Exercícios
Integral
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
O que é um problema de valor inicial?
Um foguete decola da superfície terrestre com uma aceleração constante de $20m/s^2$. Qual será sua velocidade 1 minuto depois?
Mostre que a área $A$ de um círculo de raio $r$ é $A=\pi r^{2}$.
Calcule a seguinte integral:
$ \int_4^{\infty}e^{-\frac{y}{2}}dy$.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 3x+2$ e $f(0)= 7$
$\frac{3 x^2}{2}+7 x+7$
Enuncie e demonstre o primeiro Teorema Fundamental do Cálculo.
Seja $F(x)$ tal que $F(x)=\displaystyle \int_{\pi/4}^x \cos 2t \, dt$.
Use alguma versão do Teorema Fundamental do Cálculo para encontrar $F'(x)$.
Confira se seu resultado anterior foi correto integrando e diferenciando.
Avalie a seguinte integral indefinida:
$\int (t^2+3)(t^3-2t)\ dt$
$t^6/6+t^4/4-3t^2+C$
Quais valores de $a$ e $b$ minimizam o valor de
$\int_a^b\left(x^4-2x^2\right)dx$?
Avalie a seguinte integral indefinida:
$\int x^8\ dx$
$1/9x^9+C$
Demonstre que $2\sqrt{2} \leq \int_{0}^{1}{\sqrt{x+8}dx} \leq 8$.
Derive a função $h\left( x\right) = \int_{\cos 5x}^{x^{7/3}}e^{r}\left( r^{2}+1\right) dr$.
Seja:
- $\int_0^3{s(t)dt} = 10$
- $\int_3^5{s(t)dt} = 8$
- $\int_3^5{r(t)dt} = -1$ e
- $\int_0^5{r(t)dt} = 11$
A partir destes valores, calcule as seguintes integrais:
- $\int_0^3 \big(s(t) + r(t)\big)\ dt$
- $\int_5^0 \big(s(t) - r(t)\big)\ dt$
- $\int_3^3 \big(\pi s(t) - 7r(t)\big)\ dt$
- Encontre valores para $a$ e $b$ tal que:
$\int_0^5 \big(ar(t)+bs(t)\big) \ dt=0$
- $22$
- $-7$
- $0$
- $b=-\frac{11}{18}a,\quad a\in\mathbb{R}$
O custo marginal da impressão de um pôster quando $x$ pôsteres são impressos é
$\frac{dc}{dx}=\frac{1}{2\sqrt{x}}$ reais.
Determine $c(100)-c(1)$, ou seja, a soma do custo dos pôsteres 2-100.
Avalie a seguinte integral indefinida:
$\int \sin\theta\ d\theta$
$-\cos \theta+C$
Com base no gráfico, avalie as seguintes integrais:
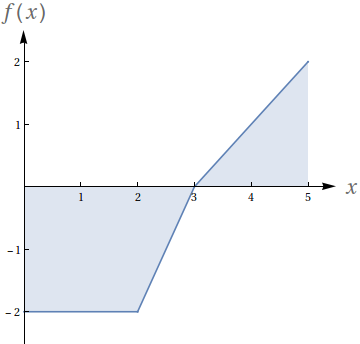
- $\int_0^2 f(x)\ dx$
- $\int_0^3 f(x)\ dx$
- $\int_0^5 f(x)\ dx$
- $\int_2^5 f(x)\ dx$
- $\int_5^3 f(x)\ dx$
- $\int_0^3 -2f(x)\ dx$
- $-4$
- $-5$
- $-3$
- 1
- $-2$
- 10
Derive a função $f\left( x\right) = \int_{x^{2}}^{e^{3x}}\cos t\sin tdt$.
Determine um número $0\leq b\leq 2$ tal que a reta $x=b$ divide a região delimitada por $y=\sqrt{4-x^{2}}$ e $y=0$ e $x=0$ em duas regiões de mesma área.
Defina o termo antiderivada com suas próprias palavras.
A antiderivada de uma função $f$ é uma função $F$ cuja derivada é a função $f$ original.
Avalie a seguinte integral indefinida:
$\int e^\pi\ dx$
$e^\pi x+C$
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f\,^{\prime \prime }\left( x\right) = 9e^{3x}+\cos x+x^{6},\;f\,^{\prime}\left( 0\right) =1\text{ e }f\left( 0\right) =2\text{ .} \end{equation*}
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 7^x$ e $f(2)= 1$
$7^x/\ln 7 + 1-49/\ln 7$
Use suas próprias palavras para definir o significado de $\int{f(x)}\ dx$.
O símbolo $\int{f(x)}\ dx$ é chamado integral indefinida de $f$ e corresponde ao conjunto de todas as antiderivadas da função $f$.
Avalie a integral $\displaystyle \int_{-1}^1 (x^5+3) \sqrt{1-x^2} \, dx$ sem fazer nenhuma conta.
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f\,^{\prime \prime }\left( x\right) = 12\sin 2x+\cos 3x+1,\;f\,^{\prime}\left( 0\right) =1\text{ e }f\left( 0\right) =0\text{ .} \end{equation*}
A antiderivada de uma função aceleração é a função _________.
Velocidade. A taxa de variação com a qual a velocidade varia de acordo com o tempo é, justamente, a aceleração.
Sendo $n$ um número positivo, mostre que
$$\displaystyle \int_{-1}^1 x^n \, dx = \left. \dfrac{x^{n+1}}{n+1} \right |_{-1}^1.$$
Se $n$ for um número negativo diferente de $-1$, esta expressão continua válida?
Durante o primeiro mês de crescimento de produtos como milho, algodão e soja, a taxa de crescimento (em gramas/dia) é proporcional ao peso presente $W$. Para determinada espécie de algodão, $dW/dt=0,21W$. Preveja o peso de uma planta no término de um mês ($t=30$), se a planta pesa 70 miligramas no início do mês.
\item Avalie a seguinte integral indefinida:
$\int dt$
$t+C$
Com base no gráfico, avalie as seguintes integrais:
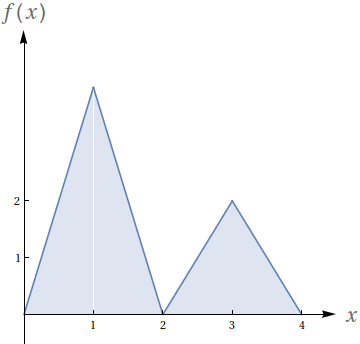
- $\int_0^2 f(x)\ dx$
- $\int_2^4 f(x)\ dx$
- $\int_2^4 2f(x)\ dx$
- $\int_0^1 4x\ dx$
- $\int_2^3 (2x-4)\ dx$
- $\int_2^3 (4x-8)\ dx$
- $4$
- $2$
- $4$
- 2
- $1$
- 2
Um objeto é solto de um helicóptero. O objeto cai cada vez mais rápido, mas sua aceleração diminui com o passar do tempo devido à resistência do ar. A aceleração foi medida nos primeiros cinco segundos, quando ele atingiu o chão, e o resultado está na tabela a seguir:
$
\begin{array}{ccccccc} \hline
t & 0 & 1 & 2 & 3 & 4 & 5 \\\hline
a & 9,81 & 5,95 & 3,61 & 2,19 & 1,33 & 0,81 \\\hline
\end{array}
$
Faça uma estimativa superior para o módulo da velocidade quando $t=5$.
Faça uma estimativa superior para o módulo da posição quando $t=5$.
Faça uma estimativa superior para a altura da queda.
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x^3$ no intervalo $[0,b]$ é $b^4/4$.
Mostre o mesmo resultado utilizando somas inferiores.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 5e^x$ e $f(0)= 10$
$5e^x+5$
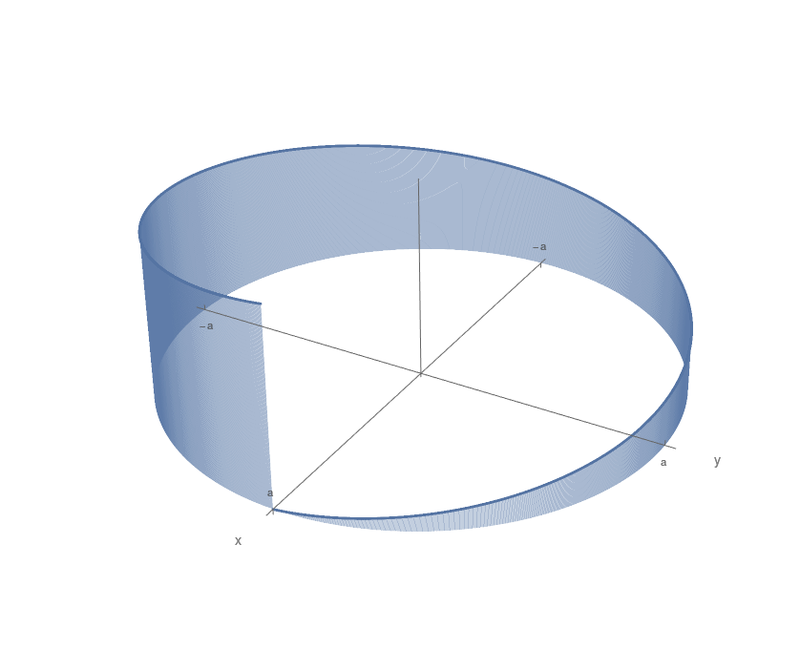
Uma superfície é criada a partir de segmentos de reta perpendiculares traçados sobre um círculo de raio $a$, perpendiculares ao plano do círculo. O comprimento de um segmento correspondente a um ponto $p$ sobre o círculo é $ks$, sendo $k$ uma constante positiva e $s$ o comprimento de arco do círculo no sentido anti-horário de $(a,0)$ até o ponto $p$.
Determine a área desta superfície, conforme a figura a seguir, em função de $k$.
Derive a função $g\left( x\right) = \int_{\tan x}^{x^{4}}\dfrac{u^{2}+1}{\sqrt{u^{2}+2u}}du$.
Avalie a seguinte integral indefinida:
$\int (2t+3)^2\ dt$
$4/3t^3+6t^2+9t+C$
Avalie a seguinte integral indefinida:
$\int 5e^\theta\ d\theta$
$5e^\theta+C$
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
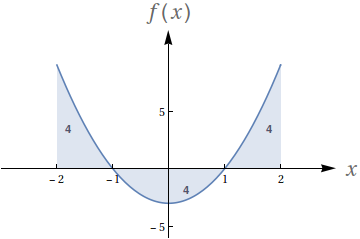
- $ \int_{-2}^{-1} f(x)\ dx$
- $ \int_1^2 f(x)\ dx$
- $ \int_{-1}^1 f(x)\ dx$
- $ \int_0^1 f(x)\ dx$
- $4$
- $4$
- $-4$
- $-2$
Se $ F(x)= { \int_1^xf(t)dt}$ e $ f(t)={ \int_{x^2}^1\frac{\sqrt{1+u^4}}{u}du}$, determine $F''(2)$.
Use o Teorema Fundamental do Cálculo e a Regra de l'Hospital para calcular o limite abaixo, justificando claramente sua resolução.
\begin{equation*}
\lim\limits_{x\rightarrow 0}\left( \dfrac{\displaystyle\int_{0}^{x}e^{t^{2}}dt}{x}\right)
\end{equation*}
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
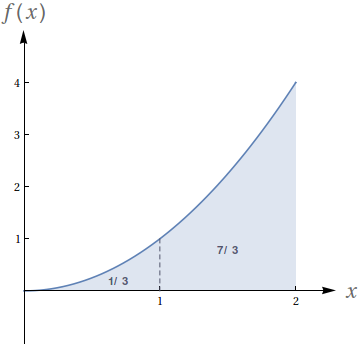
- $ \int_{0}^{2} 5x^2\ dx$
- $ \int_0^2 (x^2+3)\ dx$
- $ \int_{1}^3 (x-1)^2\ dx$
- $ \int_2^4 \big((x-2)^2+5\big)\ dx$
- $40/3$
- $26/3$
- $8/3$
- $38/3$
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função derivável, tal que $f'(x)=\alpha f(x)$ para todo $x$ e sendo $\alpha$ uma constante diferente de zero. Mostre que existe uma constante $k$ tal que, para todo $x$:
$$f(x) = k e^{\alpha x}$$
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = \sin x$ e $f(0)= 2$
$-\cos x+3$
Um objeto é atirado do nível do mar para cima com uma velocidade inicial de $100m/s$.
Supondo que a gravidade seja a única força que atua sobre este objeto superestime sua veocidade depois de $5$ segundos. Use $g=10m/s^2$.
Calcule uma estimativa inferior para a altura atingida depois de $5s$.
Avalie a seguinte integral indefinida:
$\int 3x^3\ dx$
$3/4x^4+C$
Com base no gráfico, avalie as seguintes integrais:
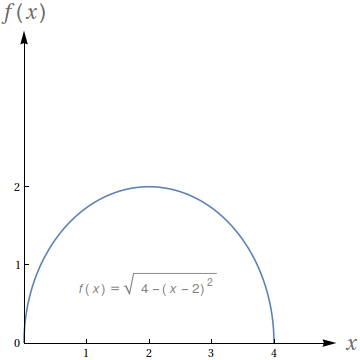
- $\int_0^2 f(x)\ dx$
- $\int_2^4 f(x)\ dx$
- $\int_0^4 f(x)\ dx$
- $\int_0^4 5f(x)\ dx$
- $\pi$
- $\pi$
- $2\pi$
- $10\pi$
Avalie a seguinte integral indefinida:
$\int (\sec x\tan x + \csc x\cot x)\ dx$
$\sec x - \csc x+C$
Este problema busca analisar o porquê de
\begin{equation*}
\int{\frac{1}{x}\ dx} = ln\left|x\right| + C
\end{equation*}
- Qual o domínio de $y = ln\ x$?
- Calcule $\frac{d}{dx}(ln\ x)$
- Qual o domínio de $y = ln(-x)$?
- Calcule $\frac{d}{dx}\left(ln(-x)\right)$
- Com base nos itens anteriores, explique o resultado apresentado no início deste problema.
Determine $f\left(x\right)$ sabendo que:
\begin{equation*} f\,^{\prime \prime }\left( x\right) = \cos 2x+6x+4,\;f\,^{\prime }\left(0\right) =2\text{ e }f\left( 0\right) =0\text{ .}\end{equation*}
Primeiramente, calcula-se a integral indefinida
$f\,^\prime(x)=\int \left(\cos 2x+6x+4\right)\,dx = 3 x^2+4 x+\frac{1}{2} \sin (2 x)+C_1$
Pelo dado do enunciado $f\, ^\prime(0)=2$. Avaliando a expressão acima para $x=0$, vê-se que $C_1=2$. Para obter $f(x)$, calcula-se novamente a integral indefinida:
$f(x)=\int \left(3 x^2+4 x+\frac{1}{2} \sin (2 x)+2\right)\,dx =x^3+2 x^2+2 x-\frac{\cos ^2(x)}{2}+C_2 $
De acordo com o enunciado, $f(0)=0$. Assim, obtém-se $C_2=\frac{1}{2}$.
Avalie a integral $\displaystyle \int_{-1}^1 x^3 \sqrt{1-x^2} \, dx$ sem fazer nenhuma conta.
Avalie a seguinte integral indefinida:
$\int (10x^2-2)\ dx$
$10/3x^3-2x+C$
O calor específico de um metal como a prata é constante a temperaturas $T$ acima de 200° K. se a temperatura do metal aumenta de $T_1$ a $T_2$, a área sob a curva $y=c/T$ de $T_1$ a $T_2$ é chamada variação de entropia $\Delta S$, que é uma medida da desordem molecular do sistema. Expresse $\Delta S$ em termos de $T_1$ e $T_2$,
Determine uma primitiva para cada uma das funções:
$f(x)=x^n$
$f(x)=sen(x)$
Use o teorema fundamental do cálculo e a regra da cadeia para calcular a derivada da função $f(x)=\int_1^{\sin x}e^{t^2} dt$. Indique claramente a justificativa de cada passagem e, em seguida, calcule $f'(\pi)$.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f''(x) = 5$ e $f'(0)= 7$, $f(0) = 3$
$5/2x^2+7x+3$
Avalie a seguinte integral indefinida:
$\int \sec^2\theta\ d\theta$
$\tan \theta+C$
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x$ no intervalo $[0,b]$ é $b^2/2$.
Mostre o mesmo resultado utilizando somas inferiores.
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f\,^{\prime \prime }\left( x\right) = \sin x-\cos x+x^{5},\;f\,^{\prime}\left( 0\right) =2\text{ e }f\left( 0\right) =0\text{ .} \end{equation*}
É mais correto se referir a uma antiderivada de $f(x)$ ou a antiderivada de $f(x)$?
O correto é uma antiderivada, já que existem infinitas antiderivadas para uma dada função.
Quais valores de $a$ e $b$ maximizam o valor de
$\int_a^b\left(x-x^2\right)dx$?
$a=0$ e $b=1$.
Encontre $f(\theta)$ que satisfaça o seguinte problema de valor inicial:
$f''(\theta) = \sin \theta$ e $f'(\pi)= 2$, $f(\pi) = 4$
$\theta-\sin (\theta)-\pi +4$
Avalie a seguinte integral indefinida:
$\int \frac{1}{\sqrt{x}}\ dx$
$2\sqrt{x}+C$
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
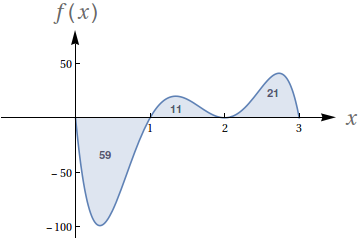
- $\int_0^1 f(x)\ dx$
- $\int_0^2 f(x)\ dx$
- $\int_0^3 f(x)\ dx$
- $\int_1^2 -3f(x)\ dx$
- $-59$
- $-48$
- $-27$
- $-33$
A atmosfera da Terra absorve aproximadamente $32\%$ da radiação proveniente do Sol. A Terra também emite radiação (a maior parte em forma de calor) e a atmosfera absorve aproximadamente $93\%$ dessa radiação. A diferença entre a radiação que entra na Terra e a que sai é chamada efeito-estufa. Modificações nesse equilíbrio podem afetar o clima da Terra. Seja $I_0$ a intensidade da radiação do Sol e $I$ a intensidade depois de percorrer uma distância $x$ na atmosfera. Se $p(h)$ é a densidade da atmosfera na altitude $h$, então a espessura ótica é $f(x)=k \displaystyle\int_0^x p(h) dh$, onde $k$ é uma constante de absorção e $I$ é dada por $I=I_0e^{-f(x)}$. Mostre que $dI/dx=-kp(x)I$.
A atmosfera da Terra absorve aproximadamente $32\%$ da radiação proveniente do Sol. A Terra também emite radiação (a maior parte em forma de calor) e a atmosfera absorve aproximadamente $93\%$ dessa radiação. A diferença entre a radiação que entra na Terra e a que sai é chamada efeito-estufa. Modoficações nesse equilíbrio podem afetar o clima da Terra. Seja $I_0$ a intensidade da radiação do Sol e $I$ a intensidade depois de percorrer uma distância $x$ na atmosfera. Se $p(h)$ é a densidade da atmosfera na altitude $h$, então a espessura ótica é $f(x)=k \displaystyle\int_0^x p(h) dh$, onde $k$ é uma constante de absorção e $I$ é dada por $I=I_0e^{-f(x)}$. Mostre que $dI/dx=-kp(x)I$.
Um objeto é lançado para cima com uma velocidade, em pés por segundo, dada por $v(t) = -32t+96$; de uma altura de $64$ pés.
- Qual a velocidade inicial do objeto?
- Em que momento o objeto tem deslocamento nulo?
- Quanto tempo leva para o objeto retornar a sua posição inicial?
- Quando o objeto alcançará uma altura de $210$ pés?
- $96ft/s$.
- $6s$.
- $6s$.
- Nunca, a altura máxima é $208ft$.
Derive a função $p\left( x\right) = \int_{2x^{-5}}^{\sin 3x}\left( v^{3}-2\right) \cos vdv$.
De acordo com s primeira lei de Kirchhoff para circuitos elétricos $V=RI+L(dI/dt)$, onde as constantes $V$, $R$ e $L$ denotam a força eletromotriz, a resistência e a indutância, respectivamente, e $I$ denota a corrente no instante $t$. Se a força eletromotriz é interrompida no instante $t=0$ e se a corrente é $I_0$ no instante da interrupção, prove que $I=I_0 e^{-Rt/L}$.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f''(x) = 24x^2+2^x-\cos x$ e $f'(0)= 5$, $f(0) = 0$
$\frac{2 x^4 \ln ^2(2)+2^x+x \ln 2) (\ln 32-1)+\ln
^2(2) \cos (x)-1-\ln ^2(2)}{\ln ^2(2)}$
Avalie a seguinte integral indefinida:
$\int \frac{5^t}{2}\ dt$
$\frac{5^t}{2\ln 5}+C$
Mostre que $\displaystyle \int_0^x \dfrac{\sin t}{t+1} \, dt > 0$
para todo $x>0$.
Demonstre que não é possível que o valor de $\int_0^1\sin(x^2)\ dx$ seja $2$. Depois, utilizando a desigualdade $\sin x \leq x$, válida para $x \geq 0$, determine um limitante superior para esta integral.
Sabemos que $\sin x \leq 1,\,\forall\,x\in\mathbb{R}$. Assim, como $\int_a^b f(x)dx \leq max\_{a \leq x \leq b} f(x) (b-a)$, podemos dizer que $\int_0^1\sin(x^2)\ dx \leq 1$.
Utilizando a desigualdade $\sin x \leq x$, podemos determinar de maneira ainda mais precisa um limitante superior para a integral.
$\int_0^1\sin(x^2)\ dx \leq \int_0^1x^2\ dx = \frac{1}{3}x^3 \vert^1_0=\frac{1}{3}$
Determine uma primitiva para cada uma das funções:
$f(x)=cosx$
$f(x)=tgx$
Considere a área entre a curva $y=x^{4}$ e o eixo $x$, primeiro no intervalo $\left[ -1,1\right] $ e depois no intervalo $\left[1,a\right] $. Determinar $a\geq 1$ tal que estas áreas sejam iguais.
Se $f(8)=12$, $f'(x)$ é contínua e ${ \int_1^8 f'(x)dx=30}$, determine o valor de $f(1)$.
Um carro está em uma rodovia a uma velocidade constante de $60mi/h$ quando vê um acidente a frente e aciona os freios. Que desaceleração constante é necessária para frear o carro em 242 pés?
Seja:
- $\int_0^2{f(x)dx} = 5$
- $\int_0^3{f(x)dx} = 7$
- $\int_0^2{g(x)dx} = -3$ e
- $\int_0^3{g(x)dx} = 5$
A partir destes valores, calcule as seguintes integrais:
- $\int_0^2 \big(f(x)+g(x)\big) \ dx$
- $\int_0^3 \big(f(x)-g(x)\big) \ dx$
- $\int_2^3 \big(3f(x)+2g(x)\big) \ dx$
- Encontre valores para $a$ e $b$ tal que:
$\int_0^3 \big(af(x)+bg(x)\big) \ dx=0$
- $2$
- $2$
- $22$
- $a=-\frac{5}{7}b,\quad b\in\mathbb{R}$
Demonstre que se $k$ é uma constante positiva, então a área entre o eixo $x$ e um arco da curva $y=\sin kx$ é $2/k$.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 4x^3-3x^2$ e $f(-1)= 9$
$x^4-x^3+7$
Use o Teorema Fundamental do Cálculo para calcular a derivada da função $g(x)={ \int_x^{x^2}\cos (t^2)dt}$.
Avalie a seguinte integral indefinida:
$\int \frac{1}{3t^2}\ dt$
$-1/(3t)+C$
Um objeto é lançado para cima com uma velocidade, em pés por segundo, dada por $v(t) = -32t+64$, de uma altura de $48$ pés.
- Qual a velocidade máxima do objeto?
- Qual o deslocamento máximo do objeto?
- Em que momento ocorre o maior deslocamento do objeto?
- Em que momento o objeto alcança a altura de $0$ pés?
Dica: encontre o momento no qual o deslocamento é $-48ft$
- $64ft/s$
- $64ft$
- $t=2$
- $t=2+\sqrt{7}\approx 4.65s$.
Determine uma primitiva para cada uma das funções:
$f(x)=1+2x+3x^2+4x^3+5x^4$
$f(x)=1+x+x^2+\ldots +x^{1000000}$
- $F(x)=1+x+x^2+x^3+x^4+x^5$
- $F(x)=x+\frac{x^2}{2}+\frac{x^3}{3}+\ldots+\frac{x^1000001}{1000001}$
Mostre que, para toda parábola dada por $y=ax^2$, com $a>0$, temos: $$\displaystyle \int_0^b a x^2 \, dx = a \dfrac{b^3}{3}.$$
Use este fato para provar que a área do setor parabólico delimitado por $y=ax^2$ e a reta $y=ab^2$ é igual a quatro terços da área do triângulo com vértices $(0,0)$, $(b,ab^2)$ e $(-b,ab^2)$. Este resultado é um caso particular do Teorema de Arquimedes sobre a área de um setor parabólico.
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
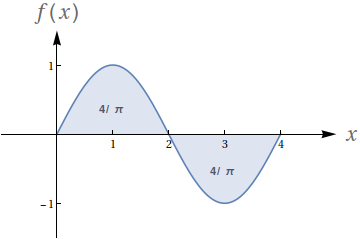
- $ \int_0^2 f(x)\ dx$
- $ \int_2^4 f(x)\ dx$
- $ \int_0^4 f(x)\ dx$
- $ \int_0^1 f(x)\ dx$
- $4/\pi$
- $-4/\pi$
- $0$
- $2/\pi$
Com base no gráfico, avalie as seguintes integrais:
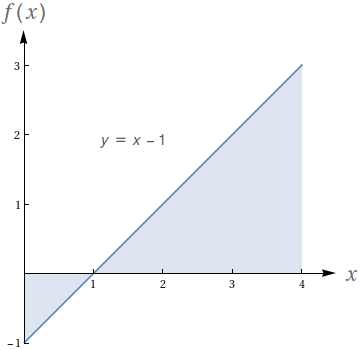
- $\int_0^1 (x-1)\ dx$
- $\int_0^2 (x-1)\ dx$
- $\int_0^3 (x-1)\ dx$
- $\int_2^3 (x-1)\ dx$
- $\int_1^4 (x-1)\ dx$
- $\int_1^4 \big((x-1)+1\big)\ dx$
- $-1/2$
- $0$
- $3/2$
- $3/2$
- $9/2$
- $15/2$
Derive a função $q\left( x\right) = \int_{e^{-2x}}^{\mathrm{tg}x}e^{\theta }\cos \theta d\theta$.
Com base no gráfico, avalie as seguintes integrais:
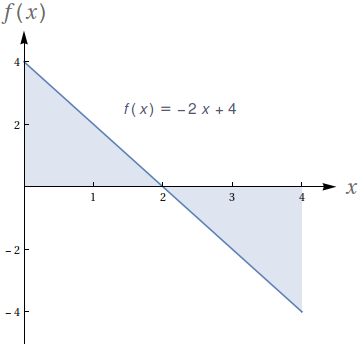
- $\int_0^1 (-2x+4)\ dx$
- $\int_0^2 (-2x+4)\ dx$
- $\int_0^3 (-2x+4)\ dx$
- $\int_1^3 (-2x+4)\ dx$
- $\int_2^4 (-2x+4)\ dx$
- $\int_0^1 (-6x+12)\ dx$
- 3
- 4
- 3
- 0
- $-4$
- 9
Calcule a seguinte integral:
$\int \dfrac{x^{3}+x}{x-1}dx.$
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x^2$ no intervalo $[0,b]$ é $b^3/3$.
Mostre o mesmo resultado utilizando somas inferiores.
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f^{\prime \prime }\left( x\right) = \dfrac{1}{x^{2}}+8e^{2x}+2,\;f^{\prime }\left( 2\right) =4e^{4}\text{ e }f\left( 1\right) =2e^{2}\text{.} \end{equation*}
Considere $y=f(x)$, para $x$ real, sendo $f$ derivável até a segunda ordem e tal que, para todo $x$, $f''(x)+f(x)=0$. Seja $g$ uma função tal que $g(x)=f'(x) \sin x - f(x) \cos x$. Mostre que $g$ é constante.

