Exercícios
Aplicações da Derivada
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Esboce o gráfico da função $f\left(x\right) =\dfrac{x^{2}-x+1}{2x-2}$, determinando o domínio, pontos de máximo e de mínimo, pontos de inflexão e assíntotas. Explicite o valor que a função assume nos pontos em questão. Justifique o seu raciocínio.
Use o método de Newton para calcular a raiz positiva de $x^2+x-1=0$ com duas casas decimais de precisão.
Suponha que em qualquer instante $t$ (em segundos) a corrente $i$ (em amperes) em um circuito de corrente alternada é $i = 2\ cos\ t+2\ sin\ t$. Qual a corrente de pico (magnitude máxim para este circuito?
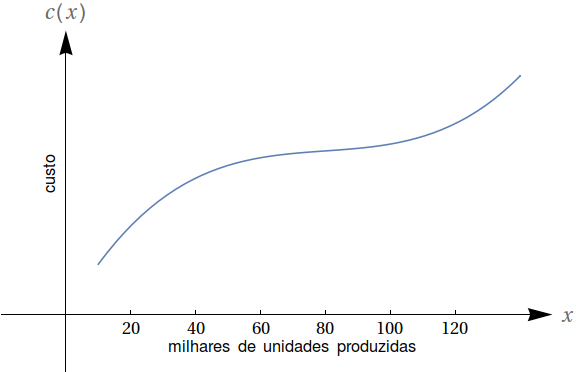
O gráfico a seguir mostra o custo hipotético $c=f(x)$ para fabricar $x$ itens. O chamado custo marginal é a mudança no custo total advinda da produção de uma unidade a mais do produto, para um certo volume de produção. Em aproximadamente qual nível de produção o custo marginal muda de decrescente para crescente?
Encontre $a$ e $b$ tais que a função $f(x)=x^3 +ax^2+b$ tenha um extremo relativo em $(2,4)$.
Estude a função $f\left( x\right) =x\ln x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
A figura abaixo mostra o gráfico do polinômio $\displaystyle y=\dfrac{1}{10}x^5(x-1)$ gerado no software Mathematica$^\textrm{TM}$ usando uma janela de $[-2;2,5]\times[-1;5]$.
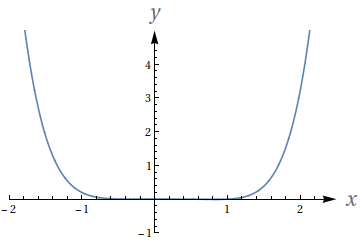
Mostre que a escolha da escala vertical faz com que o computador perca importantes aspectos do gráfico. Descreva quais são os aspectos perdidos e faça o seu próprio esboço indicando-os.
Se uma quantia $P$ é aplicada à taxa de juros de $100r \%$ ao ano, composta $m$ vezes por ano, então o montante, ao cabo de $t$ anos, é dado por $P(1+rm^{-1})^{mt}$. Considerando $m$ como um número real e fazendo m crescer indefinidamente, diz-se que a taxa é composta continuamente. Mostre que, neste caso, o montante após $t$ anos é $Pe^{rt}$.
Em cada item, esboce o gráfico de uma função contínua $f$ com as propriedades indicadas no intervalo $(-\infty,+\infty)$.
$f$ não tem extremos relativos nem absolutos.
$f$ tem um mínimo absoluto em $x=0$, mas nenhum máximo absoluto.
$f$ tem um máximo e um mínimo absolutos em $x=-5$ e $x=5$, respectivamente.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{x^{3}-x^{2}+1}{x}$.
Mostre que as funções $f(x)=(x-1)^4$ e $g(x)=x^3-3x^2+3x-2$ têm pontos estacionários em $x=1$.
O que o teste da derivada primeira diz sobre a natureza destes pontos?
Se uma função par $f(x)$ possui um valor máximo local em $x=c$, pode-se dizer algo sobre o valor de $f$ quando $x=-c$?
Ela também terá um máximo local em $x=-c$. É uma questão de simetria de seu gráfico em relação ao eixo das ordenadas.
Teorema de Rolle: Seja $f$ uma função diferenciável em $(a,b)$ e contínua em $[a,b]$; se $f(a)=f(b)=0$, então há pelo menos um ponto $c$ em $(a,b)$ tal que $f'(c)=0$. Verifique que as hipóteses do Teorema de Rolle estão satisfeitas em cada intervalo dado e ache todos os valores de $c$ naquele intervalo que satisfazem a conclusão do teorema.
$\displaystyle f(x)=\dfrac{x^2-1}{x-2},\quad [-1,1]$;
$\displaystyle f(x)=\dfrac{1}{x^2}-\dfrac{4}{3x}+\dfrac{1}{3},\quad [1,3].$
Estude a função $f\left( x\right) =x^{3}-3x^{2}-9x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
O que se pode dizer sobre os pontos de inflexão de uma curva quadrática? Justifique.
Os pontos de inflexão são os pontos nos quais a curvatura de uma curva troca de sinal, portanto, está associado com trocas de sinal da segunda derivada da função associada à curva. Curvas quadráticas terão derivadas lineares e segundas derivadas constantes. Sendo assim, como a segunda derivada de uma curva quadrática nunca trocará de sinal, uma curva quadrática nunca apresentará pontos de inflexão
Encontre os intervalos abertos nos quais $f(x)=x^3-\frac{3}{2}x^2$ é crescente e os intervalos abertos nos quais é decrescente.
Seja $f\left( x\right) =\dfrac{x^{3}}{x^{2}-1}$.
Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Considere $\frac{d}{dx}\left( \frac{x^{3}}{x^{2}-1}\right) =x^{2}\frac{x^{2}-3}{\left( x^{2}-1\right) ^{2}}$ e $\frac{d^{2}}{dx^{2}}\left(\frac{x^{3}}{x^{2}-1}\right) =2x\frac{x^{2}+3}{\left( x^{2}-1\right) ^{3}}$
(Teste da Derivada Primeira) Suponha $f$ contínua em um ponto crítico $x_0$.
Se $f'(x)>0$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e $f'(x)<0$ em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ tem um máximo relativo em $x_0$.
Se $f'(x)<0$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e $f'(x)>0$ em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ tem um mínimo relativo em $x_0$.
Se $f'(x)$ tiver o mesmo sinal $\displaystyle [f'(x)>0\ \text{ou}\ f'(x)<0]$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ não tem extremo relativo em $x_0$.
Esboce algumas curvas para mostrar que as três partes do teste da derivada primeira podem ser falsas, sem a hipótese de que $f$ é contínua em $x_0$.
Explique por que a regra de L'Hospital não se aplica ao problema $$ \lim_{x\to 0}\dfrac{x^2\sin(1/x)}{\sin x}. $$
Ache o limite acima.
Esboce o gráfico de $f(x)=x^4-5x^2+4$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
O número relativo de moléculas de gás em um recipiente que se movem a uma velocidade de $v$ $cm/s$ pode ser calculado por meio da distribuição de velocidade de Maxwell-Boltzmann, $F(v)=cv^2e^{-mv^2/(2kT)}$, sendo que $T$ é a temperatura em Kelvins, $m$ é a molécula e e $c$ e $k$ são constantes positivas. Mostre que o valor máximo de $F$ ocorre quando $v=\sqrt{2kT/m}$.
Um fazendeiro planeja cercar um pasto retangular vizinho a um rio. O pasto deve conter $180000$ metros quadrados para fornecer grama suficiente para o rebanho. Quais as dimensões do pasto para gastar a quantidade mínima de cerca se não há necessidade de cerca ao longo do rio?
Demonstre que, se $h>0$, aplicando o Método de Newton para
$f(x)=\begin{cases}
\sqrt{x},\quad \ \ x \geq 0\\
\sqrt{-x},\quad x <0
\end{cases}$,
a aproximação tende a $x_1=-h$ se $x_0=h$ e a $x_1=h$ se $x_0=-h$.
Desenhe uma figura para mostrar o que ocorre.
Estude a função $f\left( x\right) =\dfrac{x}{1+\tan x},x\in \lbrack 0,\dfrac{\pi }{2})$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Sejam $f$ e $g$ funções contínuas em $[a,b]$ e diferenciáveis em $(a,b)$. Prove: se $f(a)=g(a)$ e $f(b)=g(b)$, então há um ponto $c$ em $(a,b)$ onde $f'(c)=g'(c)$.
Prove o seguinte resultado: Se $f$ tiver um mínimo absoluto em um intervalo aberto $(a,b)$, então ele precisa ocorrer em um ponto crítico de $f$.
Suponha que, em uma aplicação do Método de Newton, o valor de $x_0$ escolhido coincidiu com uma raiz. Suponho que $f'(x_0)$ exista e não seja nula, o que acontecerá com $x_1$ e as aproximações subsequentes?
Estude a função $f\left( x\right) =xe^{-3x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Determine as abscissas dos pontos críticos das funções abaixo:
$s(t) = 2t^3 + t^2-20t +4$
$f(x) = 4x^3-5x^2-42x + 7$
$g(w) = w^4-32w$
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{x}{x^{2}+1}$.
A velocidade, no tempo $t$, de um objeto de massa $m$ em queda é $v(t)=(mg/k)(1-e^{-(k/m)t})$, onde $k$ é uma constante e $g$ denota a força da gravidade. Calcule $\lim\limits_{m \to \infty}v(t)$ e conclua que $v(t)$ é aproximadamente proporcional ao tempo $t$ se a massa é muito grande.
Ache os extremos da função $f(x)=x+3x^{3/2}$.
Esboce o gráfico da função $f\left(x\right) =e^{-x^{2}}$ explicitando domínio, intervalos de crescimento e decrescimento, concavidade, pontos de inflexdão, assíntotas, máximos e mínimos locais e globais.
Um fabricante de óleo deseja confeccionar latas cilindricas de volume igual a $1$ litro. Quais são as dimensões da lata para que o consumo de material seja o mínimo possível? Se a lata fosse esférica, o gasto de material seria maior ou menor que o gasto de material da lata cilíndrica que voce encontrou? E se a lata fosse cúbica?
Um fabricante de óleo deseja confeccionar latas cilindricas de volume igual a $1,5$ litro. Quais são as dimensões da lata para que o consumo de material seja o mínimo possível?
O efeito da luz sobre a taxa de fotossíntese pode ser descrito por $f(x)=x^a e^{(a/b)(1-x^b)}$ para $x>0$ e constantes positivas $a$ e $b$.
Mostre que $f$ tem um máximo em $x=1$.
Conclua que, se $x_0>0$ e $y_0>0$, então $g(x)=y_0f(x/x_0)$ tem máximo em $g(x_0)=y_0$.
Em estatística, a função densidade de probabilidade para a distribuição normal é definida por $f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}}e^{-z^2/2}$ com $z=\dfrac{x-\mu}{\sigma}$ para números reais $\mu$ e $\sigma>0$ ($\mu$ é a média e $\sigma^2$ é a variância da distribuição). Obtenha os extremos locais de $f$ e determine onde $f$ é crescente ou decrescente. Discuta a concavidade, ache os pontos de inflexão, determine $\lim\limits_{x \to \pm \infty}f(x)$ e esboce o gráfico de $f$.
Este exercício pretende se debruçar sobre os limites
$\lim\limits_{x \rightarrow \infty} \left(1+\frac{1}{x^2}\right)^x$ e $\lim\limits_{x \rightarrow \infty} \left(1+\frac{1}{x}\right)^x = e$.
- Use a regra de L'Hospital para mostrar que $\lim\limits_{x \rightarrow \infty} \left(1+\frac{1}{x}\right)^x = e$.
- Com o auxílio de recursos computacionais, observe as curvas de $f(x)=\left(1+\frac{1}{x^2}\right)^x$ e $g(x)=\left(1+\frac{1}{x}\right)^x$ em um único gráfico, para $x \geq 0$. Como o comportamento de $f$ se relaciona com o de $g$? Estime o valor de $\lim\limits_{x \rightarrow \infty} f(x)$.
- Confirme sua estimativa de $\lim\limits_{x \rightarrow \infty} f(x)$ através da regra de L'Hôspital.
Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =x^{3}+3x^{2}+1$.
Esboce o gŕáfico de $f\left( x\right) =\frac{e^{-x}}{x}$ .Para fazê-lo:
Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão
Dom$\left( f\right) =\left\{ x\in\mathbb{R}|x\neq0\right\} $
$f\left( x\right) \neq 0,\forall x$
A função não possui simetrias não triviais
$\lim_{x\rightarrow\infty}\frac{e^{-x}}{x}=0,\lim_{x\rightarrow-\infty}\frac{e^{-x}}{x}=\lim_{x\rightarrow-\infty}-e^{-x}=-\infty$ (este por L'Hôpital), $\lim_{x\rightarrow0^{-}}\frac{e^{-x}}{x}=-\infty$ e $\lim_{\times\rightarrow1^{+}}\frac{e^{-x}}{x}=+\infty$
- \[
f^{\prime}\left( x\right) =\frac{-e^{-x}x-e^{-x}}{x^{2}}=-e^{-x}\frac
{x+1}{x^{2}}%
\]
e temos que
\begin{align*}
f^{\prime}\left( x\right) & >0\Leftrightarrow x<-1\\
f^{\prime}\left( x\right) & <0\Leftrightarrow x>-1
\end{align*}
logo $f$ é crescente para $x<-1$ $\ $e decrescente para $x>-1$ (lembrando que $x\neq0$). O único ponto crítico de $f$ é $x=-1$, o qual é ponto de máximo, pois a derivada passa de positiva a negativa.
\begin{align*}
f"\left( x\right) & =\frac{\left( e^{-x}x-e^{-x}+e^{-x}\right)
x^{2}-\left( -e^{-x}x-e^{-x}\right) 2x}{x^{4}}\\
& =\frac{e^{-x}x^{3}+2e^{-x}x^{2}+2e^{-x}x}{x^{4}}\\
& =\frac{e^{-x}}{x^{3}}\left( x^{2}+2x+2\right)
\end{align*}
Como $e^{-x}$ e $x^{2}+2x+2$ são sempre positivos, temos que $f"\left( x\right) >0$ se $x>0$ e $f"\left( x\right) <0$ se $x<0$, ou
seja, "concavidade para baixo" se $x<0$ e "concavidade para cima" se $x>0$- Esboço do Gráfico:
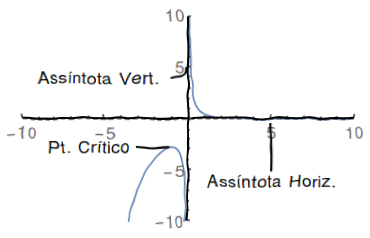
Prove que a conclusão do Teorema do Valor Médio de Cauchy pode ser escrita da seguinte forma $$ \dfrac{f(b)-f(a)}{g(b)-g(a)} = \dfrac{f'(x)}{g'(x)}, $$ sob as hipóteses adicionais de que $g(b)\neq g(a)$ e que $f'(x)$ e $g'(x)$ nunca são simultaneamente nulas sobre $(a,b)$.
Esboce o gráfico da função $f\left( x\right) =\cos x-\sin x$ . Para fazê-lo, determine:
Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão
- Dom$\left( f\right) =\mathbb{R}$
- $f\left( 0\right) =1$ e $f\left( x\right) =0$ se, e somente se, $\cos x=\sin x$ se, e somente se,
$x=\frac{\pi}{4}+k\pi$ com $k\in\mathbb{Z}$ - $f$ é periódica, com período $2\pi$
- A função não possui assíntotas verticais (pois é contínua na reta) e tampouco horizontais (pois é periódica)
- \begin{align*}
f^{\prime}\left( x\right) & =-\sin x-\cos x=0\text{ se, e somente se,}\\
\cos x & =-\sin x\text{ se, e somente se, }x=\frac{3\pi}{4}+k\pi\text{ com }k\in
\mathbb{Z}\text{.}
\end{align*}
Considerando no período $\left[ 0,2\pi\right] $ temos que
\begin{align*}
f^{\prime}\left( x\right) & >0\text{ se }x\in\left( \frac{3\pi}{4}
,\frac{7\pi}{4}\right) \text{ (intervalo de crescimento)}\\
f^{\prime}\left( x\right) & <0\text{ se }x\in\lbrack0,\frac{3\pi}{4}
)\cup(\frac{7\pi}{4},2\pi]\text{ (intervalo de crescimento)}
\end{align*} - Novamente considerando no período $\left[ 0,2\pi\right] $ temos que $\frac{3\pi}{4}$ é ponto de mínimo e $\frac{7\pi}{4}$ é ponto de máximo.
- \begin{align*}
f"\left( x\right) & =-\cos x+\sin x=0\text{ se, e somente se,}\\
\cos x & =\sin x\text{ se, e somente se, }x=\frac{\pi}{4}+k\pi\text{ com }k\in
\mathbb{Z}\text{.}
\end{align*}
Considerando no período $\left[ 0,2\pi\right] $ temos que
\begin{align*}
f"\left( x\right) & >0\text{ se }x\in\left( \frac{\pi}{4},\frac{5\pi}
{4}\right) \text{ (concavidade para cima)}\\
f"\left( x\right) & <0\text{ se }x\in\lbrack0,\frac{\pi}{4})\cup
(\frac{5\pi}{4},2\pi]\text{ (concavidade para baixo)}
\end{align*} - Esboço do Gráfico:
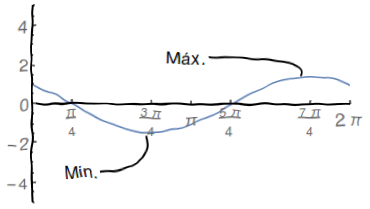
A função
$V(x)=x(10-2x)(16-2x),\quad 0<x<5$
modela o volume de uma caixa.
- Determine os valores extremos de $V$.
- Interprete quaisquer valores encontrados no item anterior em termos do volume da caixa.
Seja $f(x)=(x^3+1)/x$. Mostre que o gráfico de $y=f(x)$ tende à curva $y=x^2$ "assintotamente" no sentido de que $$ \lim_{x\to\pm\infty}\left[f(x)-x^2\right] = 0. $$ Esboce o gráfico de $y=f(x)$ mostrando o seu comportamento assintótico.
Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =x^{3}+x^{2}-5x$.
A função $f(x)=|x|$ tem valor mínimo absoluto quando $x=0$, mesmo que $f$ não seja derivável em $x=0$. Isto é consistente com o Teorema de Fermat sobre máximos e mínimos locais?
A soma dos perímetros de um triângulo equilátero e de um quadrado é $10$. Ache as dimensões do triângulo e do quadrado que produzem a área total mínima.
O modelo logístico de crescimento populacional prevê o tamanho $y(t)$ de uma população no instante $t$ por meio da fórmula $y(t)=\dfrac{k}{1+ce^{-rt}}$, onde $r$ e $k$ são constantes positivas e $c=\dfrac{k-y(0)}{y(0)}$. Os ecologistas denominam $k$ a capacidade de suporte e o interpretam como o número máximo de indivíduos que o ambiente pode sustentar. Calcule $\lim\limits_{t \to \pm \infty}y(t)$ e discuta o significado gráfico desses limites.
Estude a função $f\left( x\right) =e^{\dfrac{x-1}{x^{2}}}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Seja $ f\left( x\right) =\dfrac{x^{2}+7x+3}{x^{2}}$
Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =e^{2x}-e^{x}$.
Para calcular as coordenadas espaciais de um planeta, temos de resolver equações do tipo $x=1+0,5\sin(x)$. O traçado da função $f(x)=x-1-0,5\sin(x)$ sugere que a função possui uma raiz próxima de $x=1,5$. Utilize uma iteração do Método de Newton para melhorar essa estimativa, com $x_0=1,5$.
Faça um esboço completo do gráfico da função $y=\ln (9-x^{2}).$ Suas derivadas são: $y^{\prime }=-2x/\left( 9-x^{2}\right) $ e $y^{\prime \prime }=-\left( 18+2x^{2}\right) /\left( 9-x^{2}\right) ^{2}$. Determine explicitamente:
Domínio de definição;
Assíntotas verticais e horizontais (se houver);
Intervalos de crescimento e decrescimento;
Pontos de máximo e mínimo locais e absolutos;
Pontos de inflexão;
Concavidade.
Encontre, se existirem, o valor máximo absoluto e o valor mínimo absoluto da função $f(x)= \sqrt[3]{x^3-x^2},$ no intervalo $[0,1].$
Demonstre a Regra de L'Hospital para a indeterminação da forma $\displaystyle\dfrac{0}{0}$.
Dentre todos os retângulos inscritos numa circunferência de raio $R$, quais as dimensões daquele que tem a maior área?
Considere a função $f$ cuja derivada é $f'(x)=(x-1)^2(x+2)$.
Quais são os pontos críticos de $f$?
Em quais intervalos $f$ é crescente ou decrescente?
Em quais pontos $f$ assume valores máximos e mínimos locais?
Mostre que $|\cos x-\cos y|\leq |x-y|$ quaisquer que sejam $x$ e $y$ reais, enunciando os teoremas utilizados.
Uma caixa com base quadrada e sem tampa deve ser feita a partir de uma folha de metal, de forma que o seu volume seja de $500$ cm$^3$. Seja $S$ a área da superfície da caixa e $x$ o comprimento de um lado da base quadrada. Mostre que $\displaystyle S=x^2+2000/x$, para $x>0$, e esboce o gráfico de $S$ em função de $x$ para este caso.
Ache os pontos de máximo e de mínimo absolutos da função $f(x)=x+3x^{2/3}$.
Um retângulo tem sua base no eixo $x$ e seus dois vértices superiores na parábola $y=-x^2$. Qual é a maior área que esse retângulo pode ter? Quais são suas dimensões?
Seja $f(x)=ax^2+bx+c$, onde $a>0$. Prove que $f(x)\geq 0$ para todo $x$ se, e somente se, $b^2-ac\leq 0$. [Sugestão: ache o mínimo de $f(x)$.]
Jane está em um barco a $2 km$ da costa e deseja chegar a uma cidade litorânea, localizada $6 km$ ao longo de uma linha costeira retilínea desde o ponto (na costa) mais próximo do barco. Ela rema a $2 km/h$ e caminha a $5 km/h$. Em que ponto da costa ela deve aportar para chegar à cidade no menor tempo possível?
Esboce o gráfico de $f(x)= \frac{x^2-2x^3}{x^2-1}$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Use a derivada dada para encontrar as coordenadas $x$ de todos os pontos críticos de $f$ e classifique-os em máximo relativo, mínimo relativo ou nenhum dos dois.
$\displaystyle f'(x)=x^2(2x+1)(x-1)$;
$\displaystyle f'(x)=\dfrac{9-4x^2}{\sqrt[3]{x+1}}$.
Prove a seguinte generalização do Teorema do Valor Médio: Se $f$ é contínua e diferenciável sobre o intervalo $(a,b)$ e os limites $\displaystyle \lim_{y\to a^+}f(y)$ e $\displaystyle \lim_{y\to b^-}f(y)$ existem, então existe $x\in (a,b)$ tal que $$f'(x)=\dfrac{\displaystyle \lim_{y\to b^-}f(y)-\lim_{y\to a^+}f(y)}{b-a}.$$ (Sua prova deve começar mais ou menos assim: "Esta é uma conseqüência do Teorema do Valor Médio porque ...".)
A média geométrica de dois números reais positivos $a$ e $b$ é definida como $\sqrt{ab}$. Prove que $\sqrt{ab}=\lim\limits_{x \to \infty}\left(\dfrac{a^{1/x}+b^{1/x}}{2}\right)^x$.
Estude a função $f\left( x\right) =\sin x+\cos x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Seja $g\left( x\right) =\int_{0}^{x}f\left( t\right) dt$, onde $f\left( t\right) $ é a função cujo gráfico encontra-se abaixo.
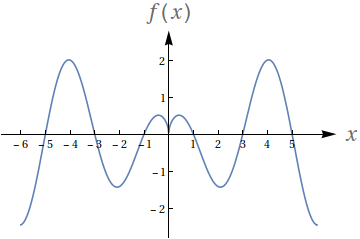
\begin{equation*} f(t) = \sqrt{|t|}\cos\left(\frac{\pi}{2}t\right) \end{equation*}
Determine os pontos de máximo e mínimo local de $g\left( x\right) $. Justifique a sua resposta
Calcule $\sqrt{5}$ com duas casas decimais de precisão, resolvendo a equação $x^2-5=0$ e use esse resultado na fórmula quadrática para obter as raízes de $x^2+x-1=0$.
Seja $ f(x)=\frac{x^3}{|x^2-1|}.$
- Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
- Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
- Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
- Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
- Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x-e^{x}$.
Uma bola esférica oca de raio $2m$ tem densidade específica $\dfrac{1}{4}$, de modo que flutua na água deslocando $\dfrac{1}{4}$ de seu próprio volume. Mostre que a profundidade $x$ à qual fica submersa é uma raiz da equação $x^3-6x^2+8=$ e use o método de Newton para calcular essa raiz com duas casas decimais de precisão. Sugestão: o volume de um segmento esférico de altura $h$ retirado de uma esfera de raio $r$ é $\pi h^2 \left(r-\dfrac{h}{3}\right)$.
Dentre todos os retângulos de perímetro fixo $L$, determine aquele de maior área. Justifique a resposta.
Encontre a área do maior retângulo que pode ser inscrito em um triângulo retângulo com catetos de comprimento $3$ e $4cm$, se dois lados do retângulo estiverem sobre o cateto.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x^n}{e^x}$.
$0$.
Sabemos que a troca de calor entre um objeto a uma temperatura $T$ e o ambiente a uma temperatura $T_{a}$ é proporcional a diferença $(T-T_{a})$. Como a variação de temperatura é proporcional a troca de calor, temos a seguinte equação diferencial $\frac{dT}{dt}=-\alpha \left( T-T_{a}\right)$ para $T\left( t\right) $ (temperatura em função do tempo. A constante $\alpha >0$ depende do calor específico e da condutividade térmica do objeto. Ache a soluçao dessa equação em função de $\alpha $ assumindo que a temperatura do ambiente $T_{a}=20^{o}C$ e a temperatura inicial $T_{0}=100^{o}C$. Qual é o limite $\lim_{t\rightarrow +\infty }T\left( t\right) $?
Prove que a equação $x^{3}-3x^{2}+6=0$ admite uma única raiz real, enquanto $x^{3}+x^{2}-5x+1=0$ admite $3$ raízes.
Para $f(x)=x^{3}-3x^{2}+6$ e $g(x)=x^{3}+x^{2}-5x+1$, queremos mostrar que $f(x)=0$ admite uma única raiz real enquanto $g(x)=0$ admite $3$ raízes. Primeiramente, analisemos as raízes de $f(x)=0$. Temos:
$f'(x)= 3x^2-6x=x(x-2)$
$f''(x)=6(x-1)$
Portanto, a segunda derivada nos diz que $f(x)$ é uma concavidade para baixo para $x<1$ e uma concavidade para cima para $x>1$, e os zeros da primeira derivada nos dizem que $f(x)$ apresenta um máximo local em $x=0$ e um mínimo local em $x=2$. Como $f(2)=2$, temos que não há raiz alguma para $x>1$, dado que a função é uma concavidade para baixo neste intervalo. A única raiz real, portanto, é algum valor $x<1$. O conhecimento do máximo local em $x=0$ nos permite inclusive dizer que é algum valor $x<0$.
Repetiremos a análise para $g(x). Temos, portanto:
$g'(x)= 2x^2+2x-5=2(x+5/3)(x-1)$
$g''(x)=6(x+1/3)$
Portanto, a segunda derivada nos diz que $g(x)$ é uma concavidade para baixo para $x<-1/3$ e uma concavidade para cima para $x>-1/3$, e os zeros da primeira derivada nos dizem que $g(x)$ apresenta um máximo local em $x=-5/3$ e um mínimo local em $x=1$. Como $g(0)=1$ e $g(1)=-2$, sabemos que há duas raízes reais de $g(x)$ no intervalo aberto $x>0$. Como $g(x)$ claramente tende para $-\infty$ para $x\rightarrow \infty$, o valor de $g(0)$ nos diz que a terceira raiz real está localizada no intervalo $x<0$. O conhecimento do máximo local em $x=-5/3$ nos permite inclusive dizer que é algum valor no intervalo aberto $x<-5/3$
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{\ln({\sin(x)})}{\ln({\sin(2x)})}$.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{\ln x}{x}$.
Mostre que se $f$ e $g$ forem funções para as quais $$ f'(x)=g(x) \quad\text{e}\quad g'(x)=f(x)$$ para todo $x$, então $f^2(x)-g^2(x)$ é uma constante.
Mostre que as funções $\displaystyle f(x)=\dfrac{1}{2}(e^x+e^{-x})$ e $\displaystyle g(x)=\dfrac{1}{2}(e^x-e^{-x})$ têm esta propriedade.
Prove que a equação $x^3-4x+2=0$ tem exatamente três raízes reais distintas.
Temos, primeiramente:
$f'(x)=3x^2-4$
$f''(x)=6x-4$
É possível ver portanto que $f(x)$ tem dois pontos críticos: $x=\pm \frac{2}{\sqrt{3}}$. Como $f''(x)>0$ para $x>0$ e $f''(x)<0$ para $x<0$, $f(x)$ tem uma concavidade para baixo em $x=-\frac{2}{\sqrt{3}}$ e uma concavidade para cima em $x=\frac{2}{\sqrt{3}}$.
Temos que $f(0)=2$. Como na concavidade em $x=\frac{2}{\sqrt{3}}$ temos $f(x)<0$, sabemos que a primeira raiz está entre $0$ e $\frac{2}{\sqrt{3}}$. É fácil observar que $\lim\limits_{x \to \infty}f(x)=\infty$, o que nos mostra uma segunda raiz. Finalmente, como $\lim\limits_{x \to -\infty}f(x)=-\infty$, temos uma terceira raiz para algum valor $x<0$, provando então que a função em questão tem três raízes distintas.
Um atleta percorreu as $26,2$ milhas da maratona de Nova York em $2,2$ horas. Demonstre que em pelo menos duas ocasiões o maratonista correu a exatas $11mi/h$, supondo que as velocidades inicial e final tenham sido zero.
Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =\dfrac{x}{x^{2}+1}$.
Esboce neste mesmo gráfico a reta $y=2x+3$. Indique a região delimitada por esta reta e pelo gráfico de $f\left(x\right) $, para $2\leq x\leq 3$. Calcule a área desta região.
Entre todos o cilindros retos que tem uma área total dada, ache o que tem volume máximo.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x \ln{x}}{x+\ln{x}}$.
$\infty$.
Seja $f\left( x\right) =x^{3}+3x.$
Estude o sinal de $f^{\prime }(x).$
Calcule $\lim\limits_{x\rightarrow +\infty }f\left(x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) .$
Utilizando as informações acima esboce o gráfico de $f\left( x\right) .$
Entre todos o cilindros retos que tem uma área total dada, ache o que tem volume máximo.
Suponha que as equações do movimento de um avião de papel, durante os $12$ segundos iniciais de vôo, são $$ x=t-2\sin t, \quad y=2-2\cos t\quad(0\leq t\leq 12). $$Quais são os pontos mais alto e mais baixo da trajetória e em que instantes eles são atingidos?
Esboce o gráfico da funçao $f\left( x\right) =\frac{x^{2}}{x-1}$, indicando domínio, limites laterais e no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.
Uma lata cilíndrica, sem tampa (mas com fundo), é feita para receber um volume de $900ml$ . Encontre as dimensoes que minimizarão o custo do metal para fazer a lata.
Estude a função $f\left( x\right) =1-e^{-x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Esboce o gráfico de $f(x)=x^3-x^2+1$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Mostre que um polinômio de terceiro grau $p\left( x\right)=ax^{3}+bx^{2}+cx+d$ ($a\neq 0$) sempre possui uma raiz real. Ilustre através de contra-exemplo que isto não é válido para polinômios de grau par, ou seja, para todo $n=2k$ par, existem polinômios de grau $n$ que não possuem raiz real.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x-\cos(x)}{x}$.
$1$.
As curvas de crescimento logístico modelam a taxa de crescimento de uma certa população em função dos fatores ambientais. Em um período prolongado de tempo, a população tende a um valor limite que representa o máximo número de indivíduos que o espaço ou alimento pode sustentar. Estas curvas são da forma $$ y(t)=\dfrac{L}{1+Ae^{-kt}}, $$ onde $y$ é a população no momento $t$ ($t\geq 0$) e $A$, $k$ e $L$ são parâmetros positivos.
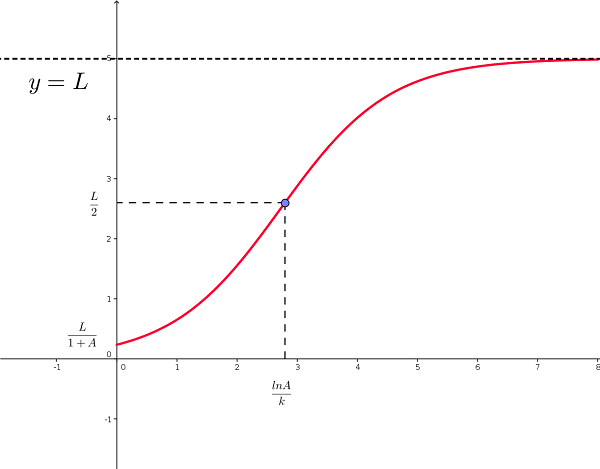
Mostre que o ponto de inflexão da curva de crescimento logístico (figura acima) ocorre no tempo $t$ solução da equação $$ \dfrac{L}{2}=\dfrac{L}{1+Ae^{-kt}}, $$ para $t$, ou seja, no instante $ t= \dfrac{\ln A}{k}$.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x+\cosh(x)}{x^2+1}$.
$\infty$.
Estude a função $f\left( x\right) =\dfrac{x^{2}}{x+1}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da função $f\left( x\right) =\left\{\begin{array}{cc} e^{-\dfrac{1}{x^{2}}} & \text{se }x\neq 0 \\ 0 & \text{se }x=0 \end{array} \right. $
Um funil de volume especificado deve ter a forma de um cone circular reto. Encontre a razão da altura pelo raio da base para que a quantidade de material empregado em sua fabricaçao seja a menor possível.
Uma página impressa deve ter $24cm^2$ de área reservada à parte escrita, uma margem de $1,5 cm$ nas partes superior e inferior e uma margem de $1cm$ nos lados. Quais as dimensões da página de menor área que preenche essas condições?
Esboce o gráfico da função $f\left( x\right) =\frac{x^{2}+3}{x-1}$, indicando domínio de definição, limites no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.
Esboce o gráfico de $f(x)=x^3-6x^2 +9x+1$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Esboce o gráfico da função $f\left( x\right) =\frac{x^{2}}{x-1}$, indicando domínio de definição, limites laterais e no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{\ln{x}}{cotg{x}}$.
Estude a função $f\left( x\right) =\sqrt{x^{2}-4}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Se uma função ímpar $f(x)$ possui um valor máximo local em $x=c$, pode-se dizer algo sobre o valor de $f$ quando $x=-c$?
Ela terá um mínimo local em $x=-c$. É uma questão de simetria de seu gráfico em relação à origem.
Um termômetro de mercúrio demorou $14s$ para subir de $-19° C$ para $100° C$ após ser retirado de um congelador e colocado em água fervendo. Considerando que, no termômetro em questão, a distância entre dois graus subsequentes é de $1mm$, demonstre que em algum instante a coluna de mercúrio subia a $8,5mm/s$.
Esboce o gráfico completo da função $\displaystyle f(x)=x\tan x,\ -\pi/2<x<\pi/2$, e localize todos os extremos relativos e pontos de inflexão. Utilize um recurso computacional gráfico a fim verificar seu resultado.
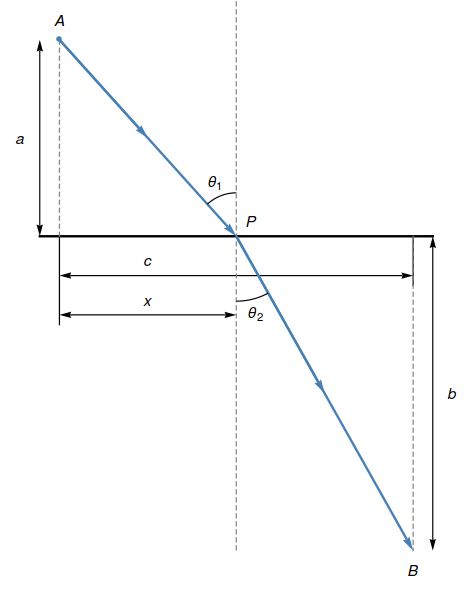
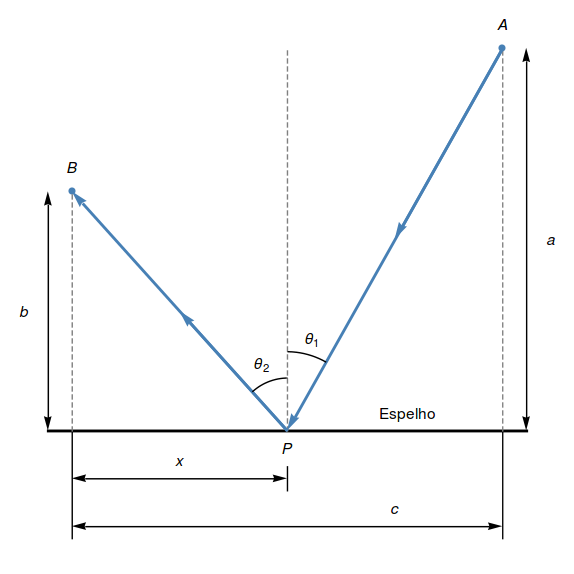
O princípio de Fermat também explica por que um raio de luz passando entre ar e água sofre um desvio de trajetória (refração). Imagine dois meios uniformes (como ar e água) e um raio de luz viajando de uma fonte $A$ em um meio para um observador $B$ em outro meio (figura abaixo). Sabe-se que a luz viaja a uma velocidade constante em um meio uniforme, porém mais vagarosamente no meio mais denso (como a água) do que no meio menos denso (como o ar). Conseqüentemente, o percurso de menor tempo entre $A$ e $B$ não é necessariamente uma reta, mas a união de dois segmentos $AP$ e $PB$, permitindo assim que a luz tome vantagem de sua maior velocidade no meio mais esparso. A Lei de Refração de Snell estabelece que a trajetória do raio de luz é tal que $$ \dfrac{\sin\theta_1}{\nu_1}= \dfrac{\sin\theta_2}{\nu_2}, $$ onde $\nu_1$ é a velocidade da luz no primeiro meio e $\nu_2$ no segundo, $\theta_1$ e $\theta_2$ são os ângulos de incidência e de refração, respectivamente (figura abaixo). Mostre que isso decorre da hipótese de que o caminho de tempo mínimo ocorre quando $\displaystyle dt/dx=0$.
Seja $f\left( x\right) =\frac{2x-1}{x-1}$
Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Domínio: Dom$\left( f\right) =\left\{ x|x\neq1\right\} =\left( -\infty,1\right) \cup\left( 1,\infty\right) $
Zeros e inteceptos: $f\left( x\right) =0\iff2x-1=0\iff x=1/2$
Simetrias: Não há.
Assíntotas:
\begin{align*}
\lim_{x\rightarrow\pm\infty}f\left( x\right) & =\lim_{x\rightarrow
\pm\infty}\frac{2x-1}{x-1}\\
& =\lim_{x\rightarrow\pm\infty}\frac{2-1/x}{1-1/x}=2
\end{align*}
\begin{align*}
\lim_{x\rightarrow1^{-}}f\left( x\right) & =\lim_{x\rightarrow1^{-}}
\frac{2x-1}{x-1}=-\infty\\
\lim_{x\rightarrow1^{+}}f\left( x\right) & =\lim_{x\rightarrow1^{-}}
\frac{2x-1}{x-1}=+\infty
\end{align*}Intervalos de crescimento e decrescimento:
\begin{align*}
f^{\prime}\left( x\right) & =\frac{2\left( x-1\right) -\left(
2x-1\right) \left( 1\right) }{\left( x-1\right) ^{2}}\\
& =\frac{-1}{\left( x-1\right) ^{2}}<0,\forall x\in Dom\left( f\right)
\end{align*}ou seja, $f$ é estritamente decrescente.
Valores máximo e mínimo locais: Não há, pois a derivada não se anula
Concavidade e pontos de Inflexão:
\[f"\left( x\right) =\frac{2}{\left( x-1\right) ^{3}}>0\iff x-1>0\iff x>1
\]
ou seja, $f$ tem concavidade para cima para $x>1$ e concavidade para baixo para $x<1$
Esboço do Gráfico:
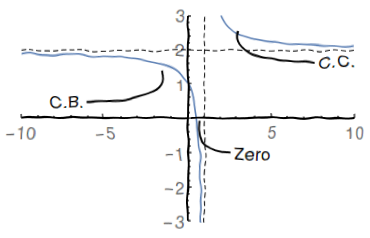
Um caminhoneiro estava em uma estrada cujo limite de velocidade era de $100km/h$. Ao passar no segundo pedágio, distante $120km$ do primeiro, o caminhoneiro recebeu uma multa, pois levou $30$ minutos para ir do primeiro ao segundo pedágio. Ele tentou contestar a multa, mas não obteve sucesso. Por que a multa foi justa?
Esboce o gráfico de $f(x)=x^2\sqrt{4-x}$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Esboce o gráfico da função $f\left(x\right) =x+\dfrac{1}{x}$.
Considere uma cápsula esférica de $1cm$ de espessura cujo volume é igual ao volume do espaço oco dentro dela. Use o método de Newton para calcular o raio externo da cápsula com duas casas decimais de precisão.
Use o Teorema do Valor Médio para mostrar que, $$\sqrt{y}-\sqrt{x}<\dfrac{y-x}{2\sqrt{x}},$$ quando $0<x<y$.
Use o resultado anterior para mostrar que se $x$ e $y$ forem positivos, então $$ \sqrt{xy} < \dfrac{1}{2}(x+y).$$ (A média aritmética é maior que a média geométrica).
Tente generalizar o resultado anterior para um conjunto amostral discreto de tamanho $n>2$.
Determine os pontos de máximo, de mínimo e de inflexão das seguintes funções (se existirem).
$y = 6x^3 + 15x^2-12x -5$
$f(x) = - 9x^2 + 14x +15$
Uma área retangular em uma fazenda será cercada por um rio e, nos outros três lados, por uma cerca elétrica feita de um fio. Com $800 m$ de fio à disposição, qual é a maior área que você pode cercar e quais são suas dimensões?
Uma página impressa deve ter $24$ $cm^{2}$ de área reservada à parte escrita, uma margem de $1,5 cm$ nas partes superior e inferior e uma margem de $1 cm$ nos lados. Discuta a existência das dimensões (e calcule quando existir) daquelas que tem área total máxima e área total mínima.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x+\dfrac{1}{x^{2}}$.
Mostre que a função $y=f(x)$ definida por $f(x)=\left\{\begin{array}{ll}\sqrt{x-r}, & \text{se} x \geq r \\ -\sqrt{r-x}, & \text{se} x<r \end{array}\right.$ tem a propriedade que para todo número real $a$, se $x_1=r+a$, então $x_2=r+a$ e, por outro lado, $x_1=r-a$, então $x_2=r+a$.
Algumas curvas são tão planas que, na prática, o Método de Newton não consegue se aproximar da raiz suficientemente para fornecer uma aproximação útil. Tente utilizar o Método de Newton em $f(x)=\left(x-1\right)^{40}$ com a estimativa inicial $x_0=2$ para observar a qualidade das aproximações. Utilizando recursos computacionais, observe o gráfico da função.
Estude a função $f\left( x\right) =\dfrac{\ln x}{x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x \sin^{-1}(x)}{x- \sin(x)}$.
$-\infty$.
Calcule o limite $\lim\limits_{x\rightarrow 7}\frac{\sqrt{x}-\sqrt{7}}{\sqrt{x+7}-\sqrt{14}}$ usando uma estratégia algébrica simples e, em seguida, usando a regra de L'Hospital. Compare os resultados.
Um fabricante produzirá caixas fechadas (com tampa) de volume igual a $27$ litros e cuja base é um retângulo com comprimento igual ao triplo da largura. Encontre as dimensões da caixa de forma que o consumo de material seja mínimo.
Determine $a$ para que a equação $x^{3}+3x^{2}-9x+a=0$ admita uma única raiz real.
Primeiramente, calculamos $f'(x)$ e $f''(x)$. Temos então
$f'(x)=3x^2+6x-9=3(x+3)(x-1)$
$f''(x)=6x+6$
Pela análise de sinal da segunda derivada, vemos que $f(x)$ é uma concavidade para baixo para $x<-1$ e uma concavidade para cima para $x>-1$, e os zeros da primeira derivada nos dizem que há um máximo local em $x=-3$ e um mínimo local em $x=1$. Assim, avaliando a função em $x=-3$ tem-se $f(-3) = 27+ a$. Qualquer valor de $a$ que torne $f(-3)<0$ garante que $f(x)$ terá apenas uma única raiz real. Finalmente, portanto, tem-se:
$a<-27$
Se uma função racional $P(x)/Q(x)$ é tal que o grau do numerador excede o grau do denominador em $1$, então o gráfico de $P(x)/Q(x)$ terá uma assíntota oblíqua, isto é, uma assíntota que não é nem horizontal nem vertical. Para ver por quê, efetuamos a divisão de $P(x)$ por $Q(x)$ obtendo $$ \dfrac{P(x)}{Q(x)}= (ax+b) + \dfrac{R(x)}{Q(x)}, $$ onde $(ax+b)$ é o quociente e $R(x)$ é o resto. Use o fato de que o grau do resto $R(x)$ é menor do que o grau do divisor $Q(x)$ para auxiliá-lo a provar que $$ \lim_{x\to \infty}\left[\dfrac{P(x)}{Q(x)}-(ax+b)\right] = 0 \quad \text{e} $$ $$ \lim_{x\to -\infty}\left[\dfrac{P(x)}{Q(x)}-(ax+b)\right] = 0. $$ Este resultado nos diz que o gráfico da equação $\displaystyle y =P(x)/Q(x)$ "tende" à reta $y=ax+b$ (assíntota oblíqua) quando $x\rightarrow +\infty$ ou $x\rightarrow -\infty$.
A trajetória de uma mosca é descrita pelas seguintes equações de movimento $$x=\dfrac{\cos t}{2+\sin t}, \quad y=3+\sin(2t)-2\sin^2t\quad (0\leq t\leq 2\pi).$$
Quais são os pontos mais alto e mais baixo do vôo?
A que distância à esquerda e à direita da origem ela voa?
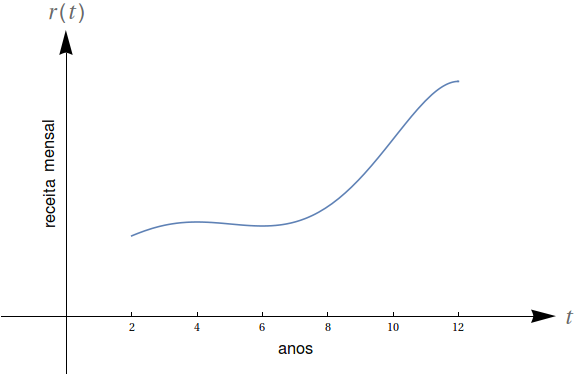
O gráfico a seguir mostra a receita mensal da empresa Fidelis Ltda. nos últimos 12 anos. Durante aproximadamente quais intervalos de tempo a receita marginal foi crescente? E decrescente?
Será construído um campo de atletismo retangular, com $x$ unidades de comprimento, tendo nas extremidades duas áreas semicirculares com raio $r$. O campo terá em volta uma pista para corrida com $400 m$ de extensão.
Expresse a área da porção retangular do campo só em função de $x$ ou só em função de $r$ (a escolha é sua).
Quais valores de $x$ e de $r$ dão à porção retangular maior área possível?
Dois corredores iniciaram uma corrida ao mesmo tempo e terminaram a corrida empatados. Prove que os dois corredores estiveram à mesma velocidade $v^*$, ainda que talvez em instantes diferentes da corrida.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x^{3}-3x^{2}+1$.
O que se pode dizer sobre os pontos de inflexão de uma curva cúbica? Justifique.
As funções da forma $$f(x)=cx^ne^{-x},\quad x>0,$$ onde $n$ é um inteiro positivo e $c=1/n!$ surgem no estudo estatístico do fluxo de tráfego.
Use um recurso gráfico computacional para gerar o gráfico de $f$ com $n=2,3,4$ e $5$ e faça uma conjectura sobre o número e a localização dos extremos relativos de $f$.
Confirme a sua conjectura usando o teste da derivada primeira.
Deixa-se cair de um balão um objeto de massa $m$. Se a força de resistência do ar é diretamente proporcional à velocidade $v(t)$ do objeto no instante $t$, então pode-se mostrar que $v(t)=(mg/k)(1-e^{-(k/m)t})$, onde $k>0$ e $g$ é uma constante gravitacional. Determine $\lim\limits_{k \to 0^+}s(t)$.
Determine os pontos de máximo, de mínimo e de inflexão das seguintes funções (se existirem).
$y = 8x^3 -51x^2 -90x +1$
$y = -x^3 – 9x^2 + 81x - 6$
Estude a função $f\left( x\right) =\sqrt[3]{x^{3}-x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Estude a função $f\left( x\right) =\dfrac{x^{3}}{x^{2}-1}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Um agricultor possui $140$ metros de cerca para construir dois currais: um deles quadrado eu outro retangular, com comprimento igual ao quádruplo da largura. Se a soma das áreas dos currais deve ser a menor possível, calcule a área do curral quadrado, apresentando todos os cálculos e/ou justificativas.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{e^x}{x^n}$.
$\infty$.
Estude a função $f\left( x\right) =e^{x}-e^{3x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Mostre que a funçao $y(x)$ com $y(0)=0$ que é definida implicitamente pela equaçao $y-x^{2}+y^{3}+xy^{2}+x^{2}y=0$ tem um extremo relativo no ponto $x=0$. Identifique esse extremo.
O Princípio de Fermat na óptica estabelece que a luz, viajando de um ponto para outro, segue aquele caminho para o qual o tempo total de percurso é mínimo. Em um meio uniforme, os caminhos de "tempo mínimo" e de "menor distância" vêm a ser iguais; assim sendo, se não obstruída, a luz viaja em linha reta. Suponha que temos uma fonte de luz (ponto $A$), um espelho plano e um observador (ponto $B$) em um meio uniforme. Se um raio de luz deixa a fonte, bate num espelho e vai até o observador, então a sua trajetória consiste de dois segmentos de reta, conforme ilustrado na figura abaixo. De acordo com o princípio de Fermat, a trajetória é tal que o tempo gasto no percurso é mínimo ou, como o meio é uniforme, a trajetória será tal que a distância total percorrida de $A$ para $B$ é a menor possível. Supondo que o mínimo ocorre quando $\displaystyle dt/dx=0$, mostre que o raio de luz irá atingir o espelho em um ponto $P$, tal que o "ângulo de incidência" $\theta_1$ é igual ao "ângulo de reflexão" $\theta_2$.
Utilize o Teorema de Valor Médio (ou o caso particular do Teorema de Rolle) para mostrar que, para qualquer valor de $c\in\mathbb{R}$, o polinômio $p\left( x\right) =x^{4}+4x+c$ tem no máximo duas raízes reais.
Estude a função $f\left( x\right) =x^{3}-3x^{2}+3x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Discuta as hipóteses necessárias para que se possa aplicar a Regra de L'Hospital.
Use a derivada dada para encontrar as coordenadas $x$ de todos os pontos críticos de $f$ e classifique-os em máximo relativo, mínimo relativo ou nenhum dos dois.
$\displaystyle f'(x)=x^3(x^2-5)$;
$\displaystyle f'(x)=xe^{-x}$.
Se um corpo de peso $P$ é arrastado ao longo de um piso horizontal por meio de uma força de grandeza $F$ e orientada segundo um ângulo $\theta$ radianos com o plano do piso, então $F=\frac{kP}{k\sin \theta +\cos \theta}$, onde $k$ é uma constante. Encontre $\cos \theta$, quando $F$ for mínimo.
Encontre os valores máximo e mínimo da função $f\left(x\right) =xe^{-x}$ no intervalo $\left[ -10,10\right]$.
$f^{\prime}\left( x\right) =e^{-x}-xe^{-x}=e^{-x}\left( 1-x\right) $.
Como $e^{-x}>0$ temos que $f\left( x\right) =0$ se e somente se $1-x=0$, ou seja, se $x=1$.
Os pontos de máximo e mínimo devem ser pontos onde $f^{\prime}\left( x\right) =0$ ou os extremos do intervalo.
Avaliamos:
$f\left( -10\right) =-10e^{10}$
$f\left( 1\right) =\frac{1}{e}$
$f\left( 10\right) =\frac{10}{e^{10}}$
Como
$-10e^{10}<\frac{10}{e^{10}}<\frac{1}{e}$
temos que o valor máximo é $f\left( 1\right) =\frac{1}{e}$ e o valor mínimo é $f\left( -10\right) =-10e^{10}$.
Você está planejando construir uma caixa retangular aberta com uma folha de papelão de $8 \times 15 pol$ recortando quadrados congruentes dos vértices da folha e dobrando suas bordas para cima. Quais são as dimensões da caixa de maior volume que você pode fazer dessa maneira? Qual é o volume?
As curvas de crescimento logístico modelam a taxa de crescimento de uma certa população em função dos fatores ambientais. Em um período prolongado de tempo, a população tende a um valor limite que representa o máximo número de indivíduos que o espaço ou alimento pode sustentar. Estas curvas são da forma $$ y(t)=\dfrac{L}{1+Ae^{-kt}}, $$ onde $y$ é a população no momento $t$ ($t\geq 0$) e $A$, $k$ e $L$ são parâmetros positivos. Suponha que uma população $y$ cresce de acordo com o modelo logístico acima.
Qual é a taxa de crescimento de $y$ em $t=0$?
Descreva como a taxa de crescimento de $y$ varia com o tempo.
Em que momento a população cresce mais rapidamente?
Estude a função $f\left( x\right) =\dfrac{3x^{2}+4x}{1+x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Você está projetando uma lata (um cilindro de revolução) de $1000 cm^3$ cuja manufatura levará o desperdício em conta. Não há desperdício ao se cortar a lateral de alumínio, mas tanto a base como o topo, ambos de raio $r$, serão recortados de quadrados que medem $2r$ de lado.
Escreva uma fórmula que forneça a quantidade total de alumínio usada para fazer uma lata.
Qual a razão $h/r$ para a lata mais econômica?
Esboce o gráfico e encontre os zeros da função $f\left( x\right) =\left| x-3\right| -\left| x+4\right| +\left| 5-x\right| $.
Uma grandeza física desconhecida é medida $n$ vezes, obtendo-se valores $x_1,x_2,\ldots,x_n$, cuja variação depende de fatores imprevisíveis, tais como temperatura, pressão atmosférica etc. Desta forma, o cientista enfrenta o problema de obter uma estimativa $\bar{x}$ de uma grandeza desconhecida $x$. Um método de se obter estimativas está baseado no princípio dos mínimos quadrados, o qual estabelece que a estimativa $\bar{x}$ deve ser escolhida de forma a minimizar a função $$ s= (x_1-\bar{x})^2+(x_2-\bar{x})^2+\ldots +(x_n-\bar{x})^2, $$que é a soma dos quadrados dos desvios entre a estimativa $\bar{x}$ e os valores medidos. Mostre que a estimativa resultante do princípio dos mínimos quadrados é dada por $$ \bar{x}= \dfrac{1}{n}(x_1+x_2+\cdots+x_n), $$ ou seja, $\bar{x}$ é a média aritmética dos valores observados.
Um peso de massa $m$ é preso a uma bola suspensa a partir de um suporte. O peso é posto em movimento movendo-se o suporte para cima e para baixo de acordo com a fórmula $h=A \cos(\omega t)$, onde $A$ e $\omega$ são constantes positivas e $t$ é o tempo. Se as forças de atrito são desprezíveis, então o deslocamento $s$ do peso em relação à sua posição inicial no instante $t$ é dada por $s=\dfrac{A \omega^2}{\omega_0^2-\omega^2}(\cos(\omega t)-\cos(\omega_0 t))$ com $\omega_0=\sqrt{k/m}$ para uma constante $k$ e com $\omega \neq \omega_0$. Calcule $\lim\limits_{\omega \to \omega_0}s$ e mostre que as oscilações resultantes aumentam em magnitude.
A altura de um corpo em movimento vertical é dada por
$s = -\frac{1}{2}gt^2+v_0t+s_0,\quad g>0$
com $s$ em metros e $t$ em segundos. Determine a altura máxima do corpo em função da velocidade inicial $v_0$, da aceleração da gravidade $g$ e da posição inicial $s_0$.
Esboce o gráfico da função $f\left( x\right) =\frac{2x^{2}}{3x^{2}-3}$ . Para fazê-lo, determine:
Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão
Dom$f=\left\{ x\in\mathbb{R}|x\neq\pm1\right\} $
$f\left( x\right) =0$ se, e somente se, $x=0$
A função é par: $f\left( -x\right) =f\left( x\right) $
Usando L'Hopital ou colocando-se $x^{2}$ em evidêncai no numerador e
denominador, obtemos que
\[
\lim_{x\rightarrow\infty}f\left( x\right) =\lim_{x\rightarrow-\infty
}f\left( x\right) =2/3
\]
\begin{align*}
\lim_{x\rightarrow-1^{+}}f\left( x\right) & =-\infty\\
\lim_{x\rightarrow-1^{-}}f\left( x\right) & =\infty\\
\lim_{x\rightarrow1^{+}}f\left( x\right) & =\infty\\
\lim_{x\rightarrow1^{-}}f\left( x\right) & =-\infty
\end{align*}\begin{align*}
f^{\prime}\left( x\right) & =\frac{4x\left( 3x^{2}-3\right)
-2x^{2}\left( 6x\right) }{\left( 3x^{2}-3\right) ^{2}}\\
& =\frac{-12x}{\left( 3x^{2}-3\right) ^{2}}
\end{align*}
logo a derivada é positiva se $x<0$ e negativa se $x>0$, ou seja $f$ é crescente para $x<0$ e decrescente para $x>0$$x=0$ é ponto de máximo da função.
A função não tem pontos de inflexão pois $\pm1\notin
Dom\left( f\right) $
\begin{align*}
f"\left( x\right) & =\frac{-12\left( 3x^{2}-3\right) ^{2}+12x2\left(
3x^{2}-3\right) 6x}{\left( 3x^{2}-3\right) ^{4}}\\
& =\frac{-12\left( 3x^{2}-3\right) +12x2\cdot6x}{\left( 3x^{2}-3\right)
^{3}}\\
& =\frac{-36x^{2}+36+12^{2}x^{2}}{\left( 3x^{2}-3\right) ^{3}}\\
& =\frac{-12x^{2}+12+48x^{2}}{\left( x^{2}-1\right) ^{3}}\\
& =12\frac{3x^{2}+1}{\left( x^{2}-1\right) ^{3}}
\end{align*}
Observando que $3x^{2}+1>0,\forall x$, temos que $f"\left( x\right) >0$ se, e somente se,
$x^{2}-1>0$ se, e somente se, $x>1$ ou $x<-1$ logo $f$ tem concavidade para cima se
$x\in(-\infty,-1)\cup\left( 1,\infty\right) $ e concavidade par baixo se
$x\in\left( -1,1\right) $.Esboço do Gráfico:
Calcule o limite $\lim\limits_{x \to 0^+}\dfrac{\ln(tg{x}+\cos{x})}{\sqrt{\ln(x^2+1)}}$.
$1$.
Estime $\pi$ através da aplicação do Método de Newton na equação $tg(x)=0$. Qual cuidado deve ser tomado, neste caso, em relação à escolha do valor inicial?

