Exercícios
Derivadas de funções trigonométricas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
A posição $s$ de uma partícula em um instante $t \geq 0$, se deslocando em um movimento retilíneo, é dada por:
$$s=10\cos(t+\pi/4).$$
- Encontre a posição inicial da partícula. Isto é, a posição em $t=0$.
- Quais são os pontos mais distantes da origem que a partícula pode alcançar? (à direita e à esquerda).
- Encontre a velocidade e a aceleração da partícula nos pontos do item anterior.
- Quando a partícula atinge a origem pela primeira vez? Encontre a velocidade, o módulo da velocidade e a aceleração neste instante.
Seja $f(x)=cossec{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
Inicialmente, determinamos a primeira derivada da função $f$:
$f'(x)=-cossec(x)cotg(x)$.
Agora, substituímos $x$ por $\dfrac{\pi}{4}$ e obtemos
$f'\left(\dfrac{\pi}{4}\right)$=-cossec\(\dfrac{\pi}{4}\)cotg\(\dfrac{\pi}{4}\)=-\dfrac{2}{\sqrt{2}}\cdot 1 = \dfrac{2}{\sqrt{2}}$.
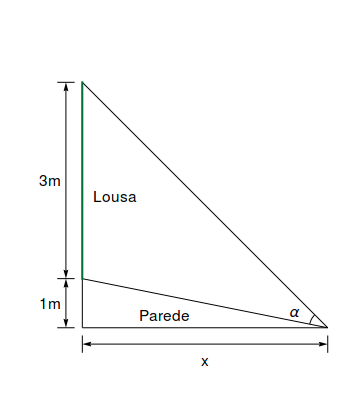
Um aluno estudioso está sentado em uma sala de aula, ao lado da parede e de frente para a lousa, como na figura abaixo. A lousa tem $3$m de largura e começa a $1$m da parede à qual o aluno está próximo. Mostre que, se a distância da parede for $x$, o ângulo de visão é
$$\alpha = \cot^{-1} \dfrac{x}{15} - \cot^{-1} \dfrac{x}{3}.$$
Determine a equação da reta tangente ao gráfico de $f(x)=tg{x}$ no ponto de abscissa $0$.
$y=x$
Calcule $f'(x)$ sendo
- $f(x)=tg{x}$
- $f(x)=sec{x}$
1. $f'(x)=sec^2(x)$.
2. $f'(x)=sec(x)tg(x)$.
Demonstre que a derivada da função cosseno é a oposta da função seno.
Seja $f(x)=\sin{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
$f'(x)=\cos(x)$ e $f'\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$.
Demonstre as seguintes regras de derivação:
- $(sec{x})'=sec{x} \cdot tg{x}$
- $(cotg{x})'=-cossec^2{x}$
- $(cossec{x})'=-cossec{x} \cdot cotg{x}$
Uma partícula tem sua posição variando com o tempo de acordo com a relação $s(t)=-2\sin(t)+3\cos(t)$ , onde $s$ é dado em metros e $t$ em segundos.
- Encontre a velocidade da partícula no instante $t$.
- Encontre a velocidade da partícula no instante $t=3$ segundos.
1. $v(t)=-3\sin(t)-2\cos(t)$.
2. $v(3)=-3\sin(3)-2\cos(3)$.
Seja $f(x)=cotg{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
$f'(x)=-cossec^2(x)$ e $f'\left(\dfrac{\pi}{4}\right)=-2$.
Se a velocidade de um objeto em metros por segundo no instante $t$ segundos é $v(t)=-\sin(t)-\cos(t)$, qual a sua posição no instante $t=4$?
$s(t)=\cos(4)-\sin(4)$
Demonstre que a derivada da função seno é a função cosseno.
Demonstre as seguintes regras de derivação:
- $(\sin{x})'=cos{x}$
- $(\cos{x})'=-\sin{x}$
- $(tg{x})'=sec^2{x}$
Demonstre que a derivada da função tangente é igual ao quadrado da função secante.