Exercícios
Derivada
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Dados $f(x) = x^2+2x$ e $x_0 = 0,1$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Determine a equação da reta tangente ao gráfico de $f(x)=\ln{x}$ no ponto de abscissa $1$. Esboce os gráficos de $f$ e da reta tangente.
Determine a derivada da função:
$f\left( x\right) =\left( sen x+\cos x\right) ^{3}.$
$3 (\cos (x)-\sin (x)) (\sin (x)+\cos (x))^2$
Uma substância radioativa decai de acordo com a fórmula $q(t)=q_0e^{-ct}$, onde $q_0$ é a quantidade inicial da substância, $c$ é uma constante positiva, e $q(t)$ é a quantidade remanescente após o tempo $t$. Mostre que a taxa na qual a substância decai é proporcional a $q(t)$.
Determine a equação da reta tangente ao gráfico de $f(x)=tg{x}$ no ponto de abscissa $0$.
$y=x$
Demonstre que a derivada da função tangente é igual ao quadrado da função secante.
Se uma droga é injetada em uma corrente sanguínea, sua concentração $C$, $t$ minutos depois, é dada por $C(t)=\frac{k}{a-b}(e^{-bt}-e^{-at})$, para constantes positivas $a$, $b$ e $k$.
- Em que instante ocorre a concentração máxima?
- Que se pode dizer sobre a concentração após um longo período de tempo?
Compute a derivada $f''(x)$ de $f(x)=\frac{x^2+1}{x}$.
$f''(x)=\dfrac{2}{x^3}$.
A taxa de crescimento $R$ de certo tipo de tumor pode ser relacionada com seu tamanho $x$, de modo aproximado, pela equação $R=r\cdot x\cdot ln(K/x)$, em que $r$ e $K$ são constantes positivas. Mostre que o tumor cresce mais rapidamente quando $x=e^{-1}K$.
Seja $f(x)=2x^2-3$. Determine a equação da reta tangente ao gráfico de $f$ nos pontos:
- $(0,f(0))$
- $(2,f(2))$
Determine a equação da reta tangente ao gráfico de $f(x)=e^x$ no ponto de abscissa $0$.
Calcule $f^{\prime }\left( x\right)$:
$\left( 1+\sqrt{x}\right) e^{x}\tan x$.
$f'(x) = \left( 1+\sqrt{x}\right) e^{x}\tan x + \dfrac{e^x \tan x}{2 \sqrt{x}} + e^x(\sqrt{x} + 1) \sec^2 x$.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =\sqrt{x},\;p=9$.
$y=\dfrac{x+9}{6}$.
Dados $f(x) = x^{-1}$ e $x_0 = 0,9$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
A linearização da função $f(x)$ em torno de um ponto $x_0$ nada mais é do que assumir que ela se comporta como uma reta que passa pelo ponto $(x_0,f(x_0))$ com inclinação $f'(x_0)$.
Neste caso temos $f(x)=x^{-1}$ e $f'(x)=-x^{-2}$. Linearizando a função em torno de $1$, temos $\frac{y-f(1)}{x-1}=f'(1)=\frac{y-1}{x-1}= -1$ portanto temos
$y=2-x$
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $x^2e^x\cos{x}$
- $e^x \sinh{x} \cos^2{x}$
Demonstre que a derivada da função seno é a função cosseno.
Seja $f(x)=\left\{\begin{array}{ll}
x^2, & \text{se } x \leq 0 \\
-x^2, & \text{se } x>0
\end{array}\right.$
- $f$ é contínua em $0$. Por quê?
- $f$ é derivável em $0$. Por quê?
1. Sim.
2. Sim.
Calcule a derivada da seguinte função:
$f\left( x\right) =\sin\left( \arccos\left( x\right) \right) .$
Um balão está subindo verticalmente acima de uma estrada a uma velocidade constante de $1$ pé por segundo. Quando ele está a $65$ pés acima do solo, uma bicicleta que se desloca a uma velocidade constante de $17$ pés por segundo passa por baixo dele. A que taxa a distância $s(t)$ entre a bicicleta e o balão aumentará três segundos depois?
Suponha que um meteorito pesado está a $s$ quilômetros do centro da Terra, e que sua velocidade de entrada na atmosfera terrestre seja inversamente proporcional a $\sqrt{s}$. Mostre que a aceleração do meteorito é inversamente proporcional a $s^2$ e interprete o resultado.
Os impulsos nervosos no corpo humano caminham ao longo de fibras nervosas que consistem em um axônio, que transporta o impulso, envolvido por uma camada de mielina. A fibra nervosa é semelhante a um cabo cilíndrico isolado, para o qual a velocidade $v$ de um impulso é dada por $v=-k(r/R)^2 \ln(r/R)$, onde $r$ é o raio do cabo e $R$ é o raio de isolamento. Ache o valor de $r/R$ que maximize $v$. Na maioria das fibras nervosas, $r/R$ vale aproximadamente $0,6$.
Uma escada de $8 m$ está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de $2 m/s$, com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a $3 m$ da parede?
Calcule a derivada da seguinte função:
$f\left( x\right) =\tan\left( x\right) \arcsin\left( x^{2}\right).$
Seja $g(x)=a^x$, em que $a>0$ e $a \neq 1$ é um real dado. Mostre que $g'(x)=a^x \ln{a}$.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =1/x^{2},\;p=1$.
$y=-2x+3$.
Sejam $f\left( x\right) $ e $g\left( x\right) $ funções
diferenciáveis e suponha que esta assuma os seguintes valores:
$\begin{array}{|c|c|}
\hline x & f\left( x\right) & g\left( x\right) & f^{\prime }\left(
x\right) & g^{\prime }\left( x\right) \\\hline
0 & 1 & 1 & 5 & 1/3 \\\hline
1 & 3 & -9 & -1/3 & -8/3 \\\hline
\end{array}$
Encontre as derivadas de:
$f\left( x\right) -3g\left( x\right) $ em $x=0;$
$f\left( g\left( x\right) \right) $ em $x=0;$
$\left( x^{11}+f\left( x\right) \right) ^{-2}$ em $x=1;$
$f\left( e^{\sin \left( x-1\right) }\right) $ em $x=1;$
- $4$
- $8/9$
- $-1/3$
- $-1/3$
A naftalina pode ser utilizada como repelente de insetos, embora possa trazer malefícios à saúde. Este composto tem a capacidade de sublimar, isto é: passa do estado sólido diretamente para o gasoso. Se uma bolinha de naftalina evapora a uma taxa proporcional à área de sua superfície, mostre que o seu raio decresce a uma taxa constante.
Calcule a derivada da seguinte função:
$f\left( x\right) =5^{x\cos\left( x^{2}\right) }.$
Seja $f(x)=cossec{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
Inicialmente, determinamos a primeira derivada da função $f$:
$f'(x)=-cossec(x)cotg(x)$.
Agora, substituímos $x$ por $\dfrac{\pi}{4}$ e obtemos
$f'\left(\dfrac{\pi}{4}\right)$=-cossec\(\dfrac{\pi}{4}\)cotg\(\dfrac{\pi}{4}\)=-\dfrac{2}{\sqrt{2}}\cdot 1 = \dfrac{2}{\sqrt{2}}$.
Suponha que $x(t)=e^{0,05t}$ e que $z(t)=e^{0,01t}$. Calcule a taxa de crescimento de $y(t)$, sabendo que $y=x^{\beta }z^{1-\beta }$, com $\beta =1/2$.
Enche-se um balão esférico a uma taxa de $4,5$ decímetros cúbicos por minuto. Calcule a taxa de variação do raio quando este medir $2$ decímetros.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{1+e^{x}}{1-e^{x}}$.
$f'(x) = \dfrac{2 e^x}{(1-e^x)^2}$.
Queremos calcular a derivada da divisão da função $1+e^x$ pela função $1-e^x$. Usando a regra da derivada do quociente, obtemos:
\[\left( \dfrac{1+e^x}{1-e^x} \right)^\prime = \dfrac{(1+e^x)^\prime \cdot (1-e^x) - (1+e^x)\cdot (1-e^x)^\prime}{(1-e^x)^2}.\]
Como
\[(1+e^x)^\prime = (1)^\prime + (e^x)^\prime = 0 + e^x = e^x\]
e, analogamente,
\[(1-e^x)^\prime = -e^x,\]
temos então que
$\dfrac{(1+e^x)^\prime \cdot (1-e^x) - (1+e^x)\cdot (1-e^x)^\prime}{(1-e^x)^2} = \dfrac{e^x (1-e^x)-(1+e^x)(-e^x)}{(1-e^x)^2} = \dfrac{e^x(1-e^x)+e^x(1+e^x)}{(1-e^x)^2}$.
Para simplificar o numerador, colocamos o fator comum $e^x$ em evidência: $e^x(1-e^x+1+e^x) = 2e^x$. Portanto, concluímos que
\[f'(x) = \dfrac{2 e^x}{(1-e^x)^2}.\]
Derive a função abaixo e avalie a derivada no ponto indicado:
$f\left( x\right) =\dfrac{\ln \left( x^{2}\right) +5x^{3}}{1+\cos^{2}x};$ avaliar em $f\,^{\prime }\left( \pi /2\right) .$.
$f'(x) = (15 x^2 + 2/x)/(\cos^2 x + 1) + (2 (5 x^3 + \log(x^2)) \sin x \cos x )/(\cos^2 x + 1)^2$.
$f'(\pi/2) = \dfrac{4}{\pi} + \dfrac{15 \pi^2}{4}$.
Escreva o polinômio $p(x)=x^4-12x^3+44x^2+2x+1$ em $x$ como um polinômio em $(x-3)$. (Só é necessário calcular o polinômio de Taylor em $3$, do mesmo grau do polinômio original. Por quê?)
Dados $f(x) = 1+x$ e $x_0 = 8,1$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
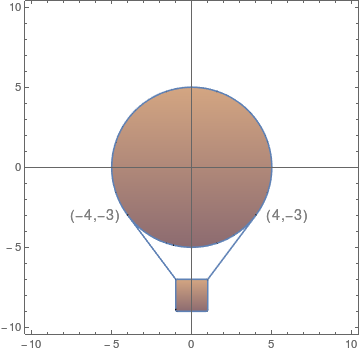
O projetista de um balão esférico (um projetista excêntrico) de ar quente com $10m$ de diâmetro quer suspender uma gôndola a $2m$ abaixo da parte inferior do balão, presa por cabos tangentes à superfície deste. Dado que os cabos, saindo da lateral do balão, tangenciam a superfície do mesmo nos pontos $(4,-3)$ e $(-4,-3)$, qual deve ser a largura da gôndola?
Encontre os dois pontos onde a curva $x^2+xy+y^2=7$ cruza o eixo x e mostre que as tangentes à curva nesses pontos são paralelas. Qual é o coeficiente angular comum dessas retas?
Derive a função abaixo e avalie a derivada no ponto indicado:
$f\left( x\right) =e^{2x^{3}}+\cos \left( \sin \left( 3x\right)\right) ;$ avaliar em $f\,^{\prime }\left( 0\right) $.
$f'(x) = 6 e^{2 x^3} x^2 - 3 \sin(\sin(3 x)) \cos(3 x)$.
$f'(0) = 0$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\arcsin\left( \cos\left( x\right) \right) .$
-\frac{\sin (x)}{\sqrt{1-\cos ^2(x)}}
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\sqrt{x^{3}+1}}{\left( x^{2}+1\right) ^{4}}.$
Calcule a derivada da função:
$y=\dfrac{x\tan 3x}{x^{2}+4}$.
$y' = -(2 x^2 \tan(3 x))/(x^2 + 4)^2 + (\tan(3 x))/(x^2 + 4) + (3 x \sec^2(3 x))/(x^2 + 4)$.
Consideremos a curva $y=-x^4 +2x^2+x$ e o ponto $P=(1,2)$ nessa curva. Verifique que a reta tangente a essa curva no ponto $P$ também é tangente à curva em outro ponto. Ache esse outro ponto.
O que podemos dizer sobre uma função $f\left( x\right) $ tal
que $f^{\prime }\left( f\left( x\right) \right) =\left( f\left( f\left(x\right) \right) \right) ^{\prime }$ para todo $x$?
Pela aplicação direta da Regra da cadeia, temos que:
$\left( f\left( f\left(x\right) \right) \right) ^{\prime }=f^{\prime }\left( f\left( x\right) \right)f^{\prime}(x)$
Para $f(x)$, portanto, temos que:
$f^{\prime }\left( f\left( x\right) \right) =f^{\prime }\left( f\left( x\right) \right)f^{\prime}(x)$
Para que a igualdade seja verdadeira, há duas possibilidades. Ou:
$f^{\prime}(x)=0,\,\forall x$
i.e., a função é uma constante (o que resultaria em $0=0$). Ou:
$f^{\prime}(x)=1,\,\forall x$
i.e., $f(x)=x+a$, sendo que $a$ é uma constante (o que resultaria em $f^{\prime }\left( f\left( x\right) \right)=f^{\prime }\left( f\left( x\right) \right)$).
Dê um exemplo de função contínua em seu domínio mas que não é diferenciável em algum(ns) ponto(s).
Qual a relação entre a continuidade e a diferenciabilidade de uma função? Demonstre.
Seja $\ell$ a reta que passa pela origem do plano cartesiano e tangencia a curva $y = x^3 + x + 16$. Qual a inclinação de $\ell$?
Dado que $\ell$ é uma reta que passa pela origem, sabemos que sua equação é do tipo $\ell(x)=ax$. Como ela tangencia a curva $y(x)$, sabemos que há um ponto $x^*$ tal que $\ell(x^*)=y(x^*)$.
Além disso, sabemos que em $x^*$ a inclinação de $\ell$ é a mesma inclinação de $y$ (por quê?), o que é equivalente a $\ell'(x^*)=y'(x^*)$.
Assim, temos:
\begin{cases}
\left.x^*\right.^3+x^*+16 = ax^* \\
3\left.x^*\right.^2+1=a
\end{cases}
Resolvendo o sistema de equações obtemos:
\begin{align*}
x^* = 2\\
a = 13
\end{align*}
Sendo, portanto, $a=13$ a resposta desejada.
Escreva o número $e$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-4}$.
Seja $g(x)=x^3+\dfrac{1}{x}$. Determine a equação da reta tangente ao gráfico de $g$ no ponto correspondente a $x=1$.
$y=2x$.
Seja $f(x)=cotg{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
$f'(x)=-cossec^2(x)$ e $f'\left(\dfrac{\pi}{4}\right)=-2$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =e^{x}\sin x\cos x$.
$f'(x) = \dfrac{1}{2} e^x ( \sin (2x) + 2 \cos (2x))$.
Calcule a derivada da seguinte função:
$f\left( x\right) =3^{2x}\ln\left( x^{2}\right) .$
$2\ 3^{2 x} \log (3) \log \left(x^2\right)+\frac{2\ 3^{2 x}}{x}$
Seja $f(x)=\sin{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
$f'(x)=\cos(x)$ e $f'\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$.
Dados $f(x) =\sin^{-1}x$ e $x_0 = \pi/12$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Calcule a derivada da seguinte função:
$f\left( x\right) =\log_{2}\left( \cos^{3}\left( x\right) \right).$
$f'(x) = -\dfrac{3 \tan x}{\log 2}$.
Dois automóveis movem-se em direção a um cruzamento em ângulo reto, um dirigindo-se para o leste à razão de $72 km/h$ e o outro para o sul à razão de $54 km/h$. Com que velocidade os carros aproximam-se um do outro no instante em que o primeiro está a $400 m$ e o segundo a $300 m$ do cruzamento?
Calcule a derivada da função:
$y=e^{x^{x}}$.
$y'=e^{x^x} x^x (\log x + 1)$.
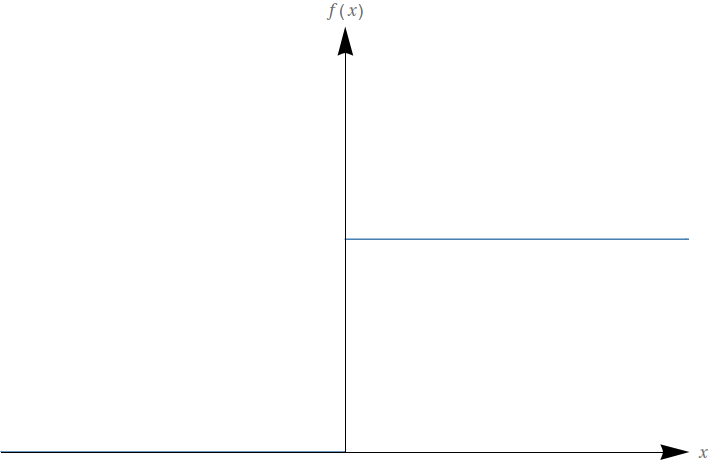
A função de Heaviside (também conhecida como função degrau), cujo gráfico pode ser visto abaixo, é muito utilizada para modelar chaves que ligam e desligam em circuitos elétricos (e também diversas aplicações). O que você tem a dizer sobre a continuidade dessa função? E sobre a diferenciabilidade?
Suponha que $x(t)=e^{0,05t}$ e que $z(t)=e^{0,01t}$. Calcule a taxa de crescimento de $y(t)$ nos seguintes casos:
- $y=x$
- $y=z$
Um invertimento de \$500,00 da juro de 7% ao ano, capitalizado continuamente, e apót $t$ anos o investimento valerá $500e^{0,07t}$.
- Aproximadamente, quando o investimento valerá \$1000,00?
- Quando o valor do investimento estará crescendo à razão de \$50,00 por ano?
Derive a função $f\left( x\right) =\left( 3^{2x+3}\right)\sqrt{\cos \left( x^{3}+x^{1/3}\right) }.$
$ 2.3^{2 x + 3} \sqrt{\cos(x^3 + x^{1/3})} \log 3 - (3^{2 x + 3} (1/(3 x^{2/3}) + 3 x^2) \sin(x^3 + x^{1/3}))/(2 \sqrt{cos(x^3 + x^{1/3})})$.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=x|x|$.
Determine a derivada da seguinte função:
$f\left( x\right) =\ln \left( 3\cos ^{5}\left( 4x\right)\right) .$
$f'(x) = -20\tan(4x)$.
Dois carros estão se encaminhando em direção a um cruzamento em ângulo reto, um seguindo a direção leste a uma velocidade de $90 km/h$ e o outro seguindo a direção sul, a $60 km/h$. Qual a taxa segundo a qual eles se aproximam um do outro no instante em que o primeiro carro está a $0,2 km$ do cruzamento e o segundo a $0,15 km$?
Dados $f(x) = \sqrt[\leftroot{-2}\uproot{2}3]{x}$ e $x_0 = 8,5$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Determine a derivada da função:
$f\left( x\right) =e^{\cos \left( x^{2}\right)}.$
Pela regra da cadeia, temos que
$f(g(x))' = f'(g(x))g'(x)$
Assim, escolhendo $f(x) = e^x$ e $g(x)=\cos(x^2)$, temos:
$(e^{\cos(x^2)}))' = e^{\cos(x^2)}(\cos(x^2))'$
Para calcular $(\cos(x^2))'$, temos que aplicar novamente a regra da cadeia. Desta vez, podemos escolher $f(x)=\cos(x)$ e $g(x)=x^2$.
Assim,
$(\cos(x^2))'= -2\sin(x^2)x$
Portanto:
$(e^{\cos(x^2)}))' = -2 e^{\cos(x^2)}x\sin(x^2)$
Um modelo de densidade urbana é uma fórmula que relaciona a densidade populacional (em número de habitantes por $km^2$) com a distância $r$ (em $km$) do centro da cidade. É considerada apropriada para certas cidades a fórmula $D=ae^{-br+cr^2}$, com $a,b$ e $c$ constantes positivas. Determine a forma do gráfico de $D$ para $r \geq 0$.
Dizemos que duas famílias de curvas são trajetórias ortogonais uma da outra se cada curva de uma família for ortogonal a cada curva da outra. Faça um esboço de gráfico da família de curvas $xy=c$ e da família $x^2-y^2=k$ no mesmo plano cartesiano, para alguns valores de $c$ e $k$ reais (se necessário, utilize algum recurso computacional). Mostre que estas famílias (de hipérboles) são ortogonais uma da outra. (Sugestão: retas tangentes são perpendiculares em um ponto de interseção se as suas inclinações são recíprocas negativas uma da outra.)
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\pi ^{x}$.
$f'(x)=ln(\pi)\pi^x$.
Calcule a derivada da função:
$y=\ln \sqrt{\dfrac{1+\sin x}{1-\sin x}}$.
$y' = \sec x$.
Demonstre que as retas tangentes às curvas $4y^3-x^2y-x+5y=0$ e $x^4-4y^3+5x+y=0$ na origem são perpendiculares.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =xe^{x}\cos x$.
$f'(x) = e^x ((x+1) \cos x - x \sin x)$.
Usando a regra da derivada do produto de duas funções, escolhendo considerar $x e^x$ como uma delas e, consequentemente, $\cos x$ como a outra, obtemos:
\[ (x e^x \cos x)^\prime = (x e^x)^\prime \cdot \cos(x)+ x e^x \cdot (\cos x)^\prime .\]
Para calcular $(x e^x)^\prime$, vamos usar novamente a regra da derivada do produto:
\[(x e^x)^\prime = (x^\prime) \cdot e^x + x\cdot (e^x)^\prime = e^x(1+x),\]
em que usamos que $(x)^\prime=1$ e $(e^x)^\prime=e^x$, além de colocar em evidência o fator comum $e^x$.
Substuindo essas expressões na igualdade inicial, temos que
\[ (x e^x \cos x)^\prime = e^x(1+x)\cos(x) - x e^x \sin x,\]
já que $(\cos x)^\prime = -\sin x$. Ou seja, obtivemos que
\[f'(x) = e^x ((x+1) \cos x - x \sin x).\]
Resolva os itens.
Considere a parábola $y=x^{2}$ e faça a seguinte construção: para cada $a\neq 0$ trace a reta normal à parábola no ponto $\left( a,a^{2}\right) $ e seja $P$ o ponto onde essa normal encontra o eixo $y$. Calcule o limite do ponto $P$ quando $a$ tende a zero.
Calcule o mesmo limite fazendo a mesma construção para a curva quártica $y=x^{4}$ em lugar da parábola.
O coeficiente angular da reta tangente, no ponto de abscissa x, ao gráfico de $y=f\left( x\right) $, é proporcional ao cubo da ordenada do ponto de tangência. Sabendo que $f\left( 0\right) =1$ e que $f\left(1\right) =1/\sqrt{2}$, determine $f$.
Mostre que o polinômio de Taylor de $f(x)=\sin(x^2)$ de grau $4n+2$ em $0$ é:$$x^2-\dfrac{x^6}{3!}+\dfrac{x^{10}}{5!}-\ldots+(-1)^n\dfrac{x^{4n+2}}{(2n+1)!}.$$ Dica: se $p$ é o polinômio de Taylor de grau $2n+1$ para $\sin$ em $0$, então $\sin x=P(x) + R(x)$, onde $\displaystyle \lim_{x \to 0} \dfrac{R(x)}{x^{2n+1}}=0$. O que isto implica em $\displaystyle \lim_{x \to 0} \dfrac{R(x^2)}{x^{4n+2}}$?
Calcule $f^{(k)}(0)$ para todo $k$.
Em geral, se $f(x)=g(x^m)$, calcule $f^{(k)}(0)$ em termos das derivadas de $g$ em $0$.
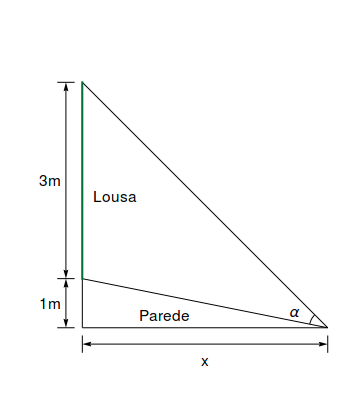
Um aluno estudioso está sentado em uma sala de aula, ao lado da parede e de frente para a lousa, como na figura abaixo. A lousa tem $3$m de largura e começa a $1$m da parede à qual o aluno está próximo. Mostre que, se a distância da parede for $x$, o ângulo de visão é
$$\alpha = \cot^{-1} \dfrac{x}{15} - \cot^{-1} \dfrac{x}{3}.$$
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =\sqrt[3]{x},\;p=1$.
$y=\dfrac{x+2}{3}$.
Seja $x$ uma função de $t$, isto é, $x=f(t)$, tal que para $t=0$, $x=1$ e para $t=1$, $x=2$. Suponha que $\dfrac{dx}{dt}>0$ para $t\geq0$; $\dfrac{d^2x}{dt^2}<0$ para $0<t<1$ e $\dfrac{d^2x}{dt^2}>0$ para $t>1$. Como você acha que deve ser o gráfico de $f$? Por quê?
A aproximação $(1+x)^k \approx 1+kx$ pode ser utilizada para cálculos rápidos.
Mostre porque esta aproximação é boa e use-a para fazer uma estimativa simples de $(1,001)^{37}$.
Compare sua estimativa com a obtida por meio de algum recurso computacional (pode ser uma calculdadora científica).
Agora utilize esta aproximação para calcular $(1,1)^{37}$ e compare com o recurso computacional. O que acontece neste caso? Justifique.
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =x^{2}+x$.
$f'(x)=2x + 1$.
O fluxo de um campo magnético através de uma bobina, em função do tempo, é dado por $F=B \cdot l^2 \sin(\omega t)$ , onde $B$ é a intensidade do campo, $l$ o comprimento da espira e $\omega$ a velocidade angular da bobina. Pela "Lei de Faraday'', temos que a tensão $v$ do circuito associado a esse campo é dada por $v=-\frac{dF}{dt}$.
- Escreva a equação do fluxo para $B = 20$, $l = 2$ e $\omega= 4$.
- Para a equação obtida no item anterior, determine a expressão de v em função de t.
Em um gerenciamento de estoques, o custo médio semanal de pedidos, pagamentos e armazenamento de mercadoria é dado por:
$$A(q)=\dfrac{km}{q}+cm+\dfrac{hq}{2},$$
onde $q$ é a quantidade de produtos pedida em períodos de baixa no estoque; $k$ é o custo (fixo) da colocação de um pedido; $c$ é o custo (também fixo) de cada item; $m$ é a quantidade de itens vendidos por mês; e $h$ é o custo mensal para manter cada item (custos de espaço, seguro, etc). Determine $dA/dq$ e $d^2A/dq^2$. Interprete os resultados.
Suco de maracujá (um bom calmante natural) é derramado a uma taxa uniforme de $20$cm$^3/$s em um copo de vidro em forma de um cone truncado (veja a figura abaixo). Se os raios superior e inferior do copo forem de $4$ e $3$cm e a altura $12$cm, com que rapidez estará subindo o nível de suco quando ele estiver na metade do copo? (Sugestão: estenda o copo para baixo para formar um cone.)

Considere a função $f(x)=\sin x.$
- Escreva o polinômio de Taylor de $f(x)$ até a terceira ordem.
- Usando o polinômio de Taylor, encontre o valor do seguinte limite: $\lim_{x\rightarrow 0}\frac{\sin x-x+2x}{3x^5}.$
Uma criança empina uma pipa a uma altura de $50$m. O vento age sobre a pipa horizontalmente a uma velocidade de $7$m$/$s em relação à criança. Com que velocidade a criança deve soltar a linha quando a pipa estiver a $100$m de distância?
Escreva a taxa de crescimento de $y$ em termos das taxas de crescimento de $k$, $l$ e $m$ para os seguintes casos. Assuma $\beta$ como uma dada constante.
- $y=k^{\beta }$
- $y=k/m$
Escreva o número $\sin 2$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-12}$.
Uma escada de $5 m$ de altura está apoiada numa parede vertical. Se a base da escada é arrastada horizontalmente da parede a $3 m/s$, a que velocidade desliza a parte superior da escada ao longo da parede quando a base encontra-se a $3 m$ da parede?
Sejam $x_0,c\in\mathbb R$ e considere a função $f(x)=e^{cx}$. Encontre $f'(x_0)$ usando a definição de derivada.
$ce^{cx_0}$.
Verifique que, para todo $x>0$, verificam-se as desigualdades:
- $e^{x}>x+1;$
- $\cos x>1-\dfrac{x^{2}}{2};$
- $\sin x<x-\dfrac{x^{3}}{3!}+\dfrac{x^{5}}{5!}.$
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=4x^4+2x$.
$f'(x)=16x^3+2$, $f''(x)=48x^2$ e $f'''(x)=96x$.
Calcule a derivada da função:
$y=\ln \left(\dfrac{\cos \sqrt{x}}{1+\sin \sqrt{x}}\right)$.
$y'=(\sin(\sqrt{x}) + 1) \sec(\sqrt{x}) \left(-\dfrac{\sin(\sqrt{x})}{2 \sqrt{x} (\sin(\sqrt{x}) + 1)} - \dfrac{\cos^2(\sqrt{x})}{2 \sqrt{x} (\sin(\sqrt{x}) + 1)^2}\right)$.
Ache uma fórmula para a soma $1+2x+3x^2 +\cdots +nx^{n-1}$.
$\dfrac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2}$, $x \neq 1$. Se $x=1$, a soma dá $\dfrac{n(n+1)}{2}$.
Calcule a derivada da função:
$y=\dfrac{2\left( 4+3\sqrt[3]{x}\right) \left( 2-\sqrt[3]{x}\right)^{3/2}}{5}$.
$y'=-\dfrac{\sqrt{2 - x^{1/3}}}{x^{1/3}}$.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=1/x$.
$f'(x)=-\dfrac{1}{x^2}$, $f''(x)=\dfrac{2}{x^3}$ e $f'''(x)=-\dfrac{6}{x^4}$.
As distribuições gamma, importantes em teoria das probabilidades, são determinadas por $f(x)=cx^ne^{-ax}$ para $x>0$, um inteiro positivo $n$, uma constante positiva $a$ e $c=\dfrac{a^{n+1}}{n!}$.
- Mostre que $f$ tem exatamente um máximo local.
- Supondo $n=4$, determine onde $f(x)$ cresce mais rapidamente.
Encontre o ponto de interseção da reta tangente ao gráfico de $y=x-\frac{1}{x}$ no ponto $(1,0)$ com o eixo $y$.
$(1,0)$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\left( x^{2}-1\right) ^{2}}{\sqrt{x^{2}+1}}.$
$f'(x) = \dfrac{x(x^2-1)(3x^2+5)}{(x^2+1)^{3/2}}$.
Determine uma reta que seja paralela a $x+y=1$ e tangente à curva $x^{2}+xy+y^{2}=3$
Seja $f(x)=\sin{x}+\cos{x}$, $0 \leq x \leq 2 \pi$.
- Estude o sinal de $f'(x)$.
- Faça um esboço do gráfico de $f$.
Encontre a equação da reta tangente ao gráfico da função $f(x)=12\sqrt[6]{x}-\frac{1}{2x^2}+\log_5(x)$ no ponto cuja coordenada horizontal é $3$.
Dados $f(x) = 2x^2+4x-3$ e $x_0 = -0,9$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $xe^x\cos{x}$
- $e^x \sin{x} \cos{x}$
Escreva a taxa de crescimento de $y$ em termos das taxas de crescimento das variáveis $k$, $l$ e $m$ para os seguintes casos. Assuma $\beta$ como uma dada constante.
- $y=(klm)^{\beta }$
- $y=(kl)^{\beta }(1/m)^{1-\beta }$
Calcule a derivada da seguinte função:
$f\left( x\right) =\tan\left( x\right) \cos^{2}\left( x\right) .$
Determine as derivadas das seguintes funções:
$f\left( x\right) =e^{\tan \left( x^{3}\right) }$.
$f\left( x\right) =\left( a\sin x+\cos bx\right)^{3};$
$f\left( x\right) =\dfrac{xe^{-3x}}{1+\cos x}.$
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =1/x^{2}$.
$f'(x) = -\dfrac{2}{x^3}$.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=\left\{\begin{array}{ll}
x^2+3x, & \text{se} x \leq 1 \\
5x-1, & \text{se} x>1
\end{array}\right.$.
Se $p$ denota o preço de venda de um artigo e $x$ é a procura correspondente (em número de artigos vendidos por di, então a relação entre $p$ e $x$ pode ser dada por $p(x)=p_0e^{-ax}$ para constantes positivas $p_0$ e $a$. Suponha $p(x)=300e^{-0,02x}$. Determine o preço de venda que maximize a receita diária.
Encontre as equações das retas que passam pelo ponto $(-1,1)$ e são tangentes à curva $x^2+4y^2-4x-8y+3=0.$
Se um raio de luz de intensidade $k$ é projetado verticalmente para baixo na água, então a sua intensidade $I(x)$ à profundidade de $x$ metros é $I(x)=ke^{-1,4x}$.
- A que taxa de intensidade o raio de luz está variando em relação à profundidade a $1$ metro?
- A que profundidade a intensidade é a metade de seu valor na superfície?
Uma partícula tem sua posição variando com o tempo de acordo com a relação $s(t)=-2\sin(t)+3\cos(t)$ , onde $s$ é dado em metros e $t$ em segundos.
- Encontre a velocidade da partícula no instante $t$.
- Encontre a velocidade da partícula no instante $t=3$ segundos.
1. $v(t)=-3\sin(t)-2\cos(t)$.
2. $v(3)=-3\sin(3)-2\cos(3)$.
Calcule a derivada da função:
$y=\sqrt{1+\sqrt{x}}$.
$y'=\dfrac{1}{4\sqrt{\sqrt{x}+1}\sqrt{x}}$.
Determine uma reta que seja tangente à elipse $x^{2}+2y^{2}=9$ e que intecepte o eixo das ordenadas no ponto de ordenada $9/4$.
Dizemos que duas famílias de curvas são trajetórias ortogonais uma da outra se cada curva de uma família for ortogonal a cada curva da outra. Faça um esboço de gráfico da família de curvas $x^2+(y-c)^2=c^2$ e da família $(x-k)^2+y^2=k^2$ no mesmo plano cartesiano, para alguns valores de $c$ e $k$ reais (se necessário, utilize algum recurso computacional). Mostre que estas famílias (de círculos) são ortogonais uma da outra. (Sugestão: retas tangentes são perpendiculares em um ponto de interseção se as suas inclinações são recíprocas negativas uma da outra.)
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\cos^{2}\left( x\right) +\sin^{2}\left(x\right) }{\sqrt{x^{3}+1}}.$
Determine o domínio de definição das funções trigonométricas inversas a seguir e expresse suas derivadas em termos de funções polinomiais:
- $g\left( x\right) =\mathrm{\arccos }\left( x\right) $;
- $g\left( x\right) =\mathrm{arcsec}\left( x\right) $;
- $g\left( x\right) =\mathrm{arccot}\left( x\right) $.
Seja $f(x)=\left\{\begin{array}{ll}
-x+3, & \text{se } x<3 \\
x-3, & \text{se } x \geq 3
\end{array}\right.$
- $f$ é contínua em $3$. Por quê?
- $f$ é derivável em $3$. Por quê?
1. Sim
2. Não
Calcule a derivada da função:
$y=\dfrac{e^{\sec \sqrt{x}}}{x}$.
$y'=\dfrac{(\tan x) e^{\sec x} \sec x)}{\sqrt{x}} - \dfrac{e^{\sec x}}{(2 x^{3/2})}$.
Prove que se $f$ for derivável em $p$, então $f$ será contínua em $p$.
Veja Guidorizzi, volume $1$, página $152$.
Se uma bola de neve derrete de tal forma que a área de sua superfície decresce a uma taxa de $1cm^{2}/\min $, encontre a taxa segundo qual o diâmetro decresce quando o diâmetro for $5 cm$.
Encontre os pontos sobre o gráfico de $p(x)=x^3-2x^2-8x+3$ nos quais a reta tangente é paralela à reta $y=4-9x.$
A corrente $I(t)$ em um circuito elétrico composto de um resistor e um indutor, no instante $t$, é dada por $I(t)=I_0e^{-Rt/L}$, onde $R$ é a resistência, $L$ a indutância e $I_0$ é a corrente no instante $t=0$. Mostre que a taxa de variação da corrente no instante $t$ é proporcional a $I(t)$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =x^{2}e^{x}$.
$f'(x)=e^x(x^2+2x)$.
Usando a regra da derivada do produto, temos que
\[f^\prime(x) = (x^2 e^x)^\prime = (x^2)' \cdot e^x + x^2 \cdot (e^x)^\prime.\]
Como $(x^2)^\prime = 2x$ e $(e^x)^\prime = e^x$, então
\[(x^2)' \cdot e^x + x^2 \cdot (e^x)^\prime = 2x e^x + x^2 e^x.\]
Colocando o fator comum $e^x$ em evidência, concluímos que
\[f^\prime (x) = e^x (x^2 + 2x).\]
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{e^{x}-e^{-x}}{2}.$
$f'\left( x\right) =\frac{e^{x}+e^{-x}}{2}.$
Mostre que se $f''(a)$ existe, então $f''(a) = \displaystyle \lim_{h \to 0} \dfrac{f(a+h) - 2f(a) + f(a-h)}{h^2}.$ (Sugestão: use o polinômio de Taylor $P_{2,a}(x)$ com $x=a+h$ e com $x=a-h$).
Conclua que $\dfrac{f(a+h) - 2f(a) + f(a-h)}{h^2}$ é uma boa aproximação para $f''(a)$, para $h$ pequeno.
Sabendo que a posição de uma partícula em função do tempo $x(t)$ é tal que $x(0)=2$, $x(1)=4$ e $x(2)=5$, utilizando a fórmula acima obtenha uma aproximação para a aceleração da partícula entre os tempos $t=0$ e $t=2$. (Escolha apropriadamente os valores de $a$ e $h$).
Em um reservatório cônico (com vértice para baixo), água é evaporada a uma taxa proporcional à área da superfície exposta ao ar. Mostre que a profundidade da água decresce a uma taxa constante que não depende das dimensões do reservatório.
O raio $r$ e a altura $h$ de um cilindro circular reto estão variando de modo a manter constante o volume $V$. Num determinado instante, $h=3cm$ e $r=1cm$ e, neste instante, a altura está variando a uma taxa de $0,2cm/s$. A que taxa está variando o volume neste instante?
Uma partícula se move na circunferência $x^2 + y^2 = a^2$ de tal modo que a componente $x$ de sua velocidade é $\dfrac{dx}{dt}=-y$. Encontre $\dfrac{dy}{dt}$ e determine se o sentido do movimento é horário ou anti-horário.
A resposta do corpo humano a uma dose de um medicamento pode ser representada pela equação:
$$R=M^2\left(\dfrac{C}{2}-\dfrac{M}{3}\right),$$
onde $C$ é uma constante positiva e $M$ a quantidade de medicamento absorvida pelo sangue. Se $R$ for uma variação da pressão sanguínea, é medida em milímetros de mercúrio; se for variação de temperatura, é medida em graus. Determine a sensibilidade do organismo ao medicamento, $dR/dM$.
Seja $f(x)=\left\{\begin{array}{ll}
x+1, & \text{se } x<2 \\
1, & \text{se } x \geq 2
\end{array}\right.$
- $f$ é contínua em $2$. Por quê?
- $f$ é derivável em $2$. Por quê?
1. Não.
2. Não
Suponha que $y=f(x)$ seja derivável em $x=a$ e que $g(x)=m(x-a)+c$ seja uma função linear, em que $m$ e $c$ sejam constantes. Se o erro entre $f$ e $g$, $E(x) = f(x)-g(x)$ for suficientemente pequeno perto de $x=a$, poderemos pensar em utilizar $g$ como aproximação linear de $f$ ao invés da linearização $L(x) = f(a)+f'(a)(x-a)$.
- Interprete as expressões $E(a)=0$ e $lim_{x\to a} \dfrac{E(x)}{x-a}=0$.
- Mostre que impondo as condições $E=0$ e $lim_{x\to a} \dfrac{E(x)}{x-a}=0$, temos $g(x)=f(a)+f'(a)(x-a)$. Interprete o resultado, relacionando com o item anterior.
Escreva o polinômio $p(x)=x^2-4x-9$ em $x$ como um polinômio em $(x-3)$. (Só é necessário calcular o polinômio de Taylor em $3$, do mesmo grau do polinômio original. Por quê?)
Calcule a derivada de ordem $n$ da função $f(x)=\sin{x}+\cos{x}$.
Demonstre que a derivada da função cosseno é a oposta da função seno.
Escreva o número $\sin 1/2$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-20}$.
Mostre que qualquer reta tangente ao gráfico da hipérbole $xy=a^2$ determina com as assíntotas um triângulo de área igual a $2a^2$.
Determine a derivada da seguinte função:
$f\left( x\right) =\left( \left( \sin x\right) \left(\cos x\right) \right) ^{3}.$
$f'(x)=3/8 \sin(2x) \sin(4x)$.
Calcule $f^{\prime }\left( x\right)$:
$\dfrac{x+\sqrt[4]{x}}{x^{2}+3}$.
$f'(x) = \dfrac{3-7x^2}{4 x^{3/4}(x^2+3)^2}$.
Calcule, pela definição, a derivada das seguntes funções:
- $f\left( x\right) =ax+b$
- $g\left( x\right) =ax^{2}+bx+c$.
1. $f'(x)=a$.
2.$f'(x)=2ax+b$.
Usa-se a técnica do carbono-14 para determinar a idade de espécimes arqueológicos ou geológicos. Este método baseia-se no fato de que o carbono-14, isótopo instável ($^{14}C$) está presente no $CO_2$ na atmosfera. As plantas assimilam carbono da atmosfera; quando morrem o $^{14}C$ acumulado começa a decair, com uma meia vida de aproximadamente 5700 anos. Medindo-se a quantidade de $^{14}C$ que resta em um espécime, é possível determinar quando o organismo morreu. Suponha que um osso fóssil acuse 20\% da quantidade de $^{14}C$ presente em um osso dos dias atuais. Dê uma aproximação da idade do osso fóssil.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{e^{x}+e^{-x}}{2}.$
$f'(x) = \frac{e^{x}-e^{-x}}{2}$.
Imagine uma estrada em que o limite de velocidade é especificado a cada ponto dela. Isto é, existe uma certa função $L$ tal que o limite de velocidade no quilômetro $x$ da estrada é $L(x)$. Dois carros, $A$ e $B$, estão viajando nesta estrada; o carro $A$ com posição $a(t)$ e o $B$ com posição $b(t)$.
Escreva uma equação para o fato de que o carro $A$ sempre anda no limite de velocidade. (A resposta não é $a'(t)=L(t)$.)
Suponha que $A$ sempre ande no limite de velocidade, e que a posição de $B$ no tempo $t$ é a posição de $A$ no tempo $t-1$. Mostre que $B$ também anda no limite da velocidade em todo o tempo.
Suponha agora que $B$ anda sempre a uma distância fixa atrás de $A$. Sobre quais condições $B$ sempre irá andar no limite de velocidade?
A base $x$ e a altura $y$ de um retângulo estão variando com o tempo. Em um dado instante, $x$ mede $3 cm$ e cresce a uma taxa de $2 cm/s$, enquanto $y$ mede $4 cm$ e decresce a uma taxa de $1 cm/s$. Determine, nesse instante, a taxa de variação da área $A$ do retângulo em relação ao tempo.
Seja
$$f(x)=\left\{\begin{array}{ll}\dfrac{\sin(x)}{x}, &\text{ se } x\neq0,\\1, &\text{ se } x=0\end{array}\right..$$
Começando com o polinômio de Taylor de ordem $2n+1$ para $\sin x$, junto com a estimativa para o termo de resto $R_{n,1}(x)=\dfrac{f^{(n+1)}(t)}{(n+1)!}(x-a){n+1}$, mostre que:
$$f(x) = \left( 1-\dfrac{x^2}{3!}+\dfrac{x^4}{5!}+\ldots+(-1)^n\dfrac{x^{2n}}{(2n+1)!} + R_{2n,0,f}(x) \right),$$
onde:
$$|R_{2n,0,f}(x)| \leq \dfrac{|x|^{2n+1}}{(2n+2)!}.$$
Determine a linearização de $f(x) = \sqrt{x+1} + \sin x$ em $x=0$. Como ela se relaciona com as linearizações individuais de $\sqrt{x+1}$ e $\sin x$ em $x=0$?
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\log _{a}x,\;a>0$ e $a\neq 1$.
$f'(x)=\dfrac{1}{xln(a)}
A que taxa o nível do líquido diminui dentro de um tanque cilíndrico vertical de raio $2$ metros se bombearmos o líquido para fora a uma taxa de $3000$ litros por minuto?
Determine a derivada da seguinte função:
$f\left( x\right) =\cos \left( x^{-2}\right)+x^{3}e^{-3x}.$
$f'(x) = -3 e^{-3 x} x^3 + 3 e^{-3 x} x^2 + (2 \sin(x^{-2}))/x^3$.
Sejam $f_1,f_2,\ldots,f_n$, $n \geq 2$, funções deriváveis em $p$. Prove, por indução finita, que $f_1+f_2+\ldots+f_n$ é derivável em $p$. Veja Guidorizzi, volume $1$, página $158$.
Um vaso em formato hemisférico de raio $7,5$cm está sendo enchido de água a uma taxa de $16$cm$^3/$s. Quando a profundidade da água está em $2,5$cm, com que velocidade o nível da água sobe?
Considere as funções trigonométricas hiperbólicas:
\begin{equation*} \sinh x=\dfrac{e^{x}-e^{-x}}{2};\;\cosh x=\dfrac{e^{x}+e^{-x}}{2}\text{.} \end{equation*}
Mostre que $\cosh ^{2}x-\sinh ^{2}x=1$.
Mostre que $\left( \sinh ^{\prime }x\right) ^{2}-\left( \cosh^{\prime }x\right) ^{2}=1$.
Encontre a equação da reta tangente à curva $y=2x^2+3$ que seja paralela à reta $8x-y+3=0$.
$y=8x+3$.
Escreva o número $\sin 1$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-17}$.
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =\dfrac{x}{x+1}$.
$f'(x) = \dfrac{1}{(x+1)^2}$.
Suponha que $x(t)=e^{0,05t}$ e que $z(t)=e^{0,01t}$. Calcule a taxa de crescimento de $y(t)$ nos seguintes casos:
- $y=xy$
- $y=x/y$
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =1/x$.
$f'(x)=-\dfrac{1}{x^2}$.
Para uma população de elefantas africanas, o peso $W(t)$ (em quilogramas) e a idade $t$ (em anos) pode ser aproximado por uma função de crescimento de Fertanlanffy $W$ tal que $W(t)=2600(1-0,51e^{-0,075t})^3$.
- Dê uma aproximação do peso e da taxa de crescimento de um elefante recém-nascido.
- Supondo que uma elefanta adulta pese $1800$ $kg$, estime sua idade e sua taxa de crescimento presente.
- Calcule e interprete $\lim\limits_{t \to \infty}W(t)$.
- Mostre que a taxa de crescimento é máxima entre as idades de $5$ e $6$ anos.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\left( x^{3}+1\right) ^{5}}{\left(x^{2}+1\right) ^{4}}.$
$\frac{x \left(x^3+1\right)^4 \left(7 x^3+15 x-8\right)}{\left(x^2+1\right)^5}$
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\ln x}{x}$.
$f'(x)=1-ln(x)$.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =x^{2}-x;\;p=1$.
$y=x-1$.
Suponha que uma gota de neblina seja uma esfera perfeita e que, por condensação, capte umidade a uma taxa proporcional à área de sua superfície. Mostre que nessas circunstâncias o raio da gota cresce a uma taxa constante.
Determine as derivadas das seguintes funções:
$f\left( x\right) =e^{\cos \left( x^{2}\right) }$.
$f\left( x\right) =\left( \sin x+\cos x\right)^{3}$.
$f\left( x\right) =x^{3}e^{-3x}.$
Calcule a derivada de ordem $1000$ da função $f(x)=e^{kx}, k \in R$.
$f^{1000}(x)=k^{1000}e^{kx}$
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =e^{x}\cos x$.
$f'(x) = e^x(\cos x - \sin x)$.
Usando a regra da derivada do produto, temos que
\[f^\prime(x) = (e^x \cos x)^\prime = (e^x)^\prime \cdot \cos(x) + e^x \cdot (\cos x)^\prime.\]
Como $(e^x)^\prime = e^x$ e $(\cos x)^\prime = -\sin x$, então
\[(e^x)^\prime \cdot \cos(x) + e^x \cdot (\cos x)^\prime = e^x \cos x + e^x (-\sin x) .\]
Colocando o fator comum $e^x$ em evidência, concluímos que
\[f^\prime (x) = e^x (\cos x- \sin x).\]Considere a seguinte função:
\begin{equation*}
f(x)= \begin{cases}
(x-b)^2 -2, \quad x\geq 0
a\sin x,\quad x<0.
\end{cases}
\end{equation*}
- Encontre os valores de $a$ e $b$ tais que $f(x)$ seja contínua e diferenciável para todo $x\in\mathbb{R}.$
- Encontre o valor de $b$ tal que a reta tangente $t$ à curva $f(x)$ no ponto $x=1$ possui inclinação 2. Escreva a equação de $t.$
- Encontre o valor de $a$ tal que a reta $s$ normal à reta tangente à $f(x)$ no ponto $x=-\pi$ possui inclinação $-\frac{1}{2}$. Escreva a equação de $s$.
Observamos que para todo $x\geq 0$ a função $(x-b)^2 -2$ é contínua e que para todo $x<0$ também a função $a\sin x$ é contínua. Logo, temos que verificar a continuidade no ponto $x=0$, isto é, deve acontecer que
$\lim_{x\rightarrow 0^-}f(x)= \lim_{x\rightarrow 0^+}f(x),$
ou seja,
$\lim_{x\rightarrow 0^-}a\sin x=\lim_{x\rightarrow 0^+} (x-b)^2 -2.$
A relação anterior implica que $0= b^2-2$, ou seja $b=\pm\sqrt{2}.$ \\
Afim de achar o valor de $a$, encontramos a derivada de $f(x)$. Observamos que, sendo $a\sin x$ e $(x-b)^2 -2$ funções diferenciáveis para todo $x\in \mathbb{R}$, a derivada de $f(x)$ é a seguinte:
$f'(x)= \begin{cases}
2(x-b), \quad x> 0
a\cos x,\quad x<0.
\end{cases}$
Como queremos que $f(x)$ seja diferenciável no ponto $x=0$ também, temos que impor
$\lim_{x\rightarrow 0^-}f'(x)= \lim_{x\rightarrow 0^+}f'(x),$
ou seja,
$\lim_{x\rightarrow 0^-}a\cos x= \lim_{x\rightarrow 0^+}2(x-b).$
A relação anterior implica que $a= -2b$, então as duplas de valores para os quais $f(x)$ é contínua e diferenciável para todo $x\in \mathbb{R}$, são $(a,b)= (2\sqrt{2}, -\sqrt{2})$ ou $(a,b)=(-2\sqrt{2}, \sqrt{2}).$
Usando a função derivada calculada no ponto anterior, temos que $f'(1)= 2(1-b),$ então, como a inclinação da reta tangente deve ser 2, obtemos $2(1-b)=2$ e logo $b= 1$. A equação de $t$ é $y= f(1)+ f'(1)(x-1)$, isto é $y= -2+1\cdot(x-1)=x-3.$
Usando a função derivada calculada no ponto anterior, temos que $f'(-\pi)= a\cos (-\pi)= -a,$ então, como a inclinação da reta normal $s$ é $-\frac{1}{2}$, deve ser $-a=2$, ou seja $a=-2$. A equação de $s$ é $y= f(-\pi)-\frac{1}{2}(x+\pi)$, isto é $y= -\frac{1}{2}x -\frac{1}{2}\pi.$
Dados $f(x) = e^{-x}$ e $x_0 = -0,1$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Calcule a derivada da função:
$y=\dfrac{1}{2}\cot ^{2}5x+\ln \sin x.$
$y'=\cot(x) - 5 \cot(5 x) \csc^2(5 x)$.
Calcule a derivada de ordem $1000$ da função $f(x)=\sin{kx}, k \in R$.
$f^{1000}(x)=k^{1000}\sin{kx}$
Sejam $f,g,h$ funções deriváveis. Verifique que $(fgh)'=f'gh+fg'h+fgh'$. Generalize.
Dica: Derive a função $Fh$, onde $F=fg$. Use a regra do produto duas vezes. Para generalizar use o princípio da indução finita.
Demonstre as seguintes regras de derivação:
- $(\sin{x})'=cos{x}$
- $(\cos{x})'=-\sin{x}$
- $(tg{x})'=sec^2{x}$
Um recipiente cheio de água com a forma de um cone invertido está sendo esvaziado à razão de $6\,cm^3/min$. A altura do cone é $24cm$ e o raio da base é $12cm$. Encontre a velocidade com que baixa o nível da água quando está a $10cm$ do fundo.
$\dfrac{dr}{dt}=-\dfrac{1}{25 \pi}$ cm/min
Uma escada de $4$m está apoiada em uma parede fazendo um ângulo $\theta$ com o chão. Considerando $h$ como a altura do chão até o ponto em que a escada encosta na parede, expresse $h$ em função de $\theta$ e, então, use $dh$ para estimar a variação em $h$ se $\theta$ varia de $60^\circ$ a $59^\circ$, de $60^\circ$ a $58^\circ$, e de $60^\circ$ a $55^\circ$. Interprete estes resultados.
Sejam $f,g,h$ funções deriváveis. Verifique que $(fgh)'=f'gh+fg'h+fgh'$. Generalize.
Seja $g(x)=log_a{x}$, em que $a>0$ e $a \neq 1$ é um real dado. Mostre que $g'(x)=\dfrac{1}{x \ln{a}}$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\sec x}{3x+2}$.
$f'(x) = \dfrac{\tan x \sec x}{3x+2}-\dfrac{3 \sec x}{(3x+2)^2}$.
Queremos calcular a derivada da divisão da função $\sec x$ pela função $3x+2$. Usando a regra da derivada do quociente, obtemos:
\[\left( \dfrac{\sec x}{3x+2} \right)^\prime = \dfrac{(\sec x)^\prime \cdot (3x+2) - (\sec x)\cdot (3x+2)^\prime}{(3x+2)^2}.\]
Como $\sec x = \dfrac{1}{\cos x}$, podemos usar a regra do quociente para calcular sua derivada:
\[(\sec x)^\prime = \left(\dfrac{1}{\cos x}\right)^\prime = \dfrac{(1)^\prime\cdot \cos(x) - 1\cdot (\cos x)^\prime}{(\cos x)^2} =\dfrac{0 - (-\sin x)}{(\cos x)^2} = \tan(x)\sec(x).\]
Por outro lado, sabemos que $(3x+2)^\prime = 3$.
Dessa forma, voltando à primeira igualdade e substituindo $(\sec x)^\prime$ e $(3x+2)^\prime$ pelas expressões encontradas, obtemos:\[\dfrac{(\sec x)^\prime \cdot (3x+2) - (\sec x)\cdot (3x+2)^\prime}{(3x+2)^2} = \dfrac{\tan(x) \sec(x) (3x+2) - (\sec x)(3)}{(3x+2)^2} .\]
Ou seja,
\[ \left( \dfrac{\sec x}{3x+2} \right)^\prime = \dfrac{\tan(x) \sec(x)}{3x+2} - \dfrac{3\sec(x)}{(3x+2)^2}. \]
A posição $s$ de uma partícula em um instante $t \geq 0$, se deslocando em um movimento retilíneo, é dada por:
$$s=10\cos(t+\pi/4).$$
- Encontre a posição inicial da partícula. Isto é, a posição em $t=0$.
- Quais são os pontos mais distantes da origem que a partícula pode alcançar? (à direita e à esquerda).
- Encontre a velocidade e a aceleração da partícula nos pontos do item anterior.
- Quando a partícula atinge a origem pela primeira vez? Encontre a velocidade, o módulo da velocidade e a aceleração neste instante.
Seja $f(x)=\sin{x}+\cos{x}$, $0 \leq x \leq 2 \pi$.
Estude o sinal de $f'(x)$.
Faça um esboço do gráfico de $f$.
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $x^2e^x\cos{x}$
- $e^x \sinh{x} \cos^2{x}$
Calcule a derivada da seguinte função:
$f\left( x\right) =\log_{2}\left( 2x\right) \log_{3}\left(3x\right) .$
$f'(x) = \dfrac{2 \ln x + \ln 6}{x \ln 2 \ln 3}$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\sqrt{x}}{x+1}$.
$f'(x) = \dfrac{1-x}{2\sqrt{x}(x+1)^2}$.
Queremos calcular a derivada da divisão da função $\sqrt{x}$ pela função $x+1$. Usando a regra da derivada do quociente, obtemos:
\[\left( \dfrac{\sqrt{x}}{x+1} \right)^\prime = \dfrac{(\sqrt{x})^\prime \cdot (x+1) - \sqrt{x}\cdot (1+x)^\prime}{(x+1)^2}.\]
Sabendo que
\[(\sqrt{x})^\prime = \left(x^{1/2}\right)^\prime = \dfrac{1}{2} x^{\left(\tfrac{1}{2}-1\right)} = \dfrac{1}{2 \sqrt{x}}\]
e que
\[(x+1)^\prime = (x)^\prime + (1)^\prime = 1 + 0 = 1,\]
podemos usar essas expressões na regra do quociente e, assim, obter que
\[\dfrac{(\sqrt{x})^\prime \cdot (x+1) - (\sqrt{x})\cdot (1+x)^\prime}{(x+1)^2} = \dfrac{\dfrac{1}{2 \sqrt{x}}(x+1)-\sqrt{x}(1)}{(x+1)^2} = \dfrac{\dfrac{x}{2 \sqrt{x}} +\dfrac{1}{2 \sqrt{x}} -\dfrac{x}{\sqrt{x}}}{(x+1)^2}.\]
Disso, podemos concluir que
\[f'(x) = \dfrac{1-x}{2\sqrt{x}(x+1)^2}.\]
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =4\sec x+\cot x$.
$f'(x) = 4 \sec x \tan x - \csc^2 x$.
Como a derivada da soma de funções é a soma de suas derivadas, temos inicialmente que
\[ (4\sec x+\cot x)^\prime = (4\sec x)^\prime + (\cot x)^\prime = 4 (\sec x)^\prime + (\cot x)^\prime .\]
Como $\sec x = \dfrac{1}{\cos x}$, podemos usar a regra do quociente para calcular sua derivada:
\[(\sec x)^\prime = \left(\dfrac{1}{\cos x}\right)^\prime = \dfrac{(1)^\prime\cdot \cos(x) - 1\cdot (\cos x)^\prime}{(\cos x)^2} =\dfrac{0 - (-\sin x)}{(\cos x)^2} = \tan(x)\sec(x).\]
De forma análoga, usaremos a regra do quociente para calcular a derivada da função $\cot x$, que é igual a $\frac{\cos x}{\sin x}$:
\[(\cot x)^\prime = \left(\dfrac{\cos x}{\sin x}\right)^\prime = \dfrac{(\cos x)^\prime\cdot \sin(x) - \cos(x)\cdot (\sin x)^\prime}{(\sin x)^2} =\dfrac{(-\sin x) \sin x - \cos(x)(\cos x)}{(\sin x)^2} = -(\csc x)^2,\]
em que usamos a identidade trigonométrica fundamental
\[(\sin x)^2 + (\cos x)^2 = 1\]
e a identidade $\csc x = \frac{1}{\sin x}$ para obter a cossecante.
Substituindo as expressões encontradas para as derivadas de $\sec x$ e de $\cot x$ na primeira igualdade, concluímos que
$f'(x) = 4 \tan(x)\sec(x) - (\csc x)^2$.
Determine a derivada de ordem $999$ da função $f(x)=\sin(x)+\cos(x)$.
Se uma massa cai uma distância $s(t)$ em $t$ segundos, e $s'$ é proporcional a $s$, então mostre que $s$ não pode ser uma função da forma $s(t)=ct^2$.
Se $s(t)=\dfrac{a}{2} t^2$, mostre que $s''(t)=a$ (a aceleração é constante) e que $[s'(t)]^2=2as(t)$ (observe que obtivemos isso trocando ligeiramente a expressão de $s(t)$).
Assumindo $a=9,8$m$/$s$^2$ (aceleração da gravidade), quantos segundos você tem para fugir de um lustre em um castelo que cai de um teto de $100$m? Se você não conseguir fugir, quão rápido o lustre vai estar quando te atingir? A que altura estava o lustre quando estava se movendo com metade desta velocidade?
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $xe^x\cos{x}$.
- $e^x \sin{x} \cos{x}$.
- $-e^x x^2 \sin (x)+e^x x^2 \cos (x)+2 e^x x \cos (x)$.
- $-e^x \sin ^2(x)+e^x \cos ^2(x)+e^x \sin (x) \cos (x)$.
Determine a derivada de ordem $n$ de:
- $f(x)=e^x$
- $f(x)=\cos{x}$
- $f(x)=\sin{x}$
- $f(x)=\ln{x}$
Calcule a derivada da função:
$y=\left( 2+\sin x\right) ^{x}$.
$y' = (\sin x + 2)^x (\log(\sin x + 2) + (x \cos x )/(\sin x + 2))$.
Suponha que em uma máquina um pistão se desloque verticalmente tal que sua posição no instante $t$ (medido em segundos) seja dado por:
$$s=A \cos(2 \pi b t ),$$
onde $A>0$ é a amplitude do movimento, e $b>0$ é a frequência (número de vezes que o pistão se desloca de cima para baixo por segundo). Qual o efeito da duplicação da frequência sobre a velocidade, a aceleração e a sobreaceleração do pistão? Relacione a sua resposta com o fato de que uma máquina quebra quando funciona rápido demais.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=4x^4+2/x$.
Calcule os valores de $a,b$ e $c$ de modo que as parábolas $y=x^2+ax+b$ e $y=-x^2 +cx$ sejam tangentes uma a outra no ponto $(1,2)$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =2^{x}$.
$f'(x)=ln(2)2^x$.
Uma escada de $10$ metros de comprimento está apoiada em uma parede vertical. Se a base da escada começa a escorregar horizontalmente a uma taxa constante de $0,6 m/s$, com que velocidade o topo da escada percorre a parede quando ele está a $6 m$ do solo?
O modelo Jenss é considerado geralmente como a fórmula mais precisa para predizer a altura de uma criança em idade pré-escolar. Se $h(x)$ denota a altura (em cm) na idade $x$ (em anos) para $\frac{1}{4} \leq x \leq 6$, então $h(x)$ pode ser aproximada por $h(x)=79,041+6,39x-e^{3,261-0,993x}$.
- Preveja a altura e a taxa de crescimento quando uma criança atinge a idade de $1$ ano.
- Quando é maior e quando é menor a taxa de crescimento?
Uma viatura de polícia, vindo do norte e se aproximando de um cruzamento em ângulo reto, está perseguindo um carro em alta velocidade, que, no cruzamento, toma a direção leste. Quando a viatura está a $0,6 km$ ao norte do cruzamento e o carro fugitivo a $0,8 km$ a leste, o radar da polícia detecta que a distância entre a viatura e o fugitivo está aumentando a $20 km/h$. Se a viatura está se deslocando a 60 km/h no instante dessa medida, qual é a velocidade do fugitivo?
Dados $f(x) = \dfrac{x}{x+1}$ e $x_0 = 1,3$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Sejam $f_1,f_2,\ldots,f_n$, $n \geq 2$, funções deriváveis em $p$. Prove, por indução finita, que $f_1+f_2+\ldots+f_n$ é derivável em $p$.
Veja Guidorizzi, volume $1$, página $158$.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =x^{2},\;p=2$.
$y=4x-4$.
Se a velocidade de um objeto em metros por segundo no instante $t$ segundos é $v(t)=-\sin(t)-\cos(t)$, qual a sua posição no instante $t=4$?
$s(t)=\cos(4)-\sin(4)$
Determine a derivada de $f\left( t\right) =t^{3}e^{-3t}$.
$-3 e^{-3t} (t-1) t^2$.
Demonstre as seguintes regras de derivação:
- $(sec{x})'=sec{x} \cdot tg{x}$
- $(cotg{x})'=-cossec^2{x}$
- $(cossec{x})'=-cossec{x} \cdot cotg{x}$
Calcule a derivada da seguinte função:
$f\left( x\right) =x^{3}\ln\left( x^{2}\right) .$
Se o raio de um círculo cresce à taxa de $30 cm/s$, a que taxa cresce a sua área em relação ao tempo, em função do raio? Dica: Use a fórmula da área do círculo.
Mostre que a linearização de $f(x)=(1+x)^k$ em $x=0$ é $L(x)=1+kx$.
Considere a curva definida pela equação $x^2y+3\ln(1-y)+x^4=1.$
- Calcule $y'.$
- Encontre a aproximação linear à curva no ponto $(1,0).$
Seja $f:\mathbb{R\rightarrow R}$ uma função.
- Defina continuidade de $f$ no ponto $p\in \mathbb{R}$.
- Defina a derivada de $f$ no ponto $p\in \mathbb{R}$. O que é a função derivada $f^{\prime }\left( x\right) ?$
- Calcule, pela definição, a derivada $g^{\prime }\left( 0\right) $ onde \begin{equation*} g\left( x\right) =\left\{ \begin{array}{cc} x^{2}\sin \left( \dfrac{1}{x^{2}}\right) & \text{se }x\neq 0 \\ 0 & \text{ se }x=0 \end{array} \right. \end{equation*}
Calcule $f'(x)$ sendo
- $f(x)=tg{x}$
- $f(x)=sec{x}$
1. $f'(x)=sec^2(x)$.
2. $f'(x)=sec(x)tg(x)$.
Dê a definição de derivada de uma função $f$ no ponto $p\in \mathbb{R}.$ O que é a função derivada $f^{\prime }(x)$?
Escreva o número $e^2$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-5}$.
Em uma esteira transportadora, areia é derrubada a uma taxa de $10$m$^3/$min no topo de um monte em formato de cone. A relação entre a altura do monte e o diâmetro da base é sempre de $3/8$.
- Qual a taxa de variação da altura?
- Qual a taxa de variação do raio, se o monte tiver $4$m de altura?

