Exercícios
Limites laterais
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x^2-1, & & \text{ se } x<-1 \\
x^3+1, & & \text{ se } -1\leq x\leq 1\\
x^2+1, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to -1^-} f(x)$
$ \lim\limits_{x\to -1^+} f(x)$
$ \lim\limits_{x\to -1} f(x)$
$f(-1)$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
- 0
- 0
- 0
- 0
- 2
- 2
- 2
- 2
Utilizando o gráfico a seguir, avalie os seguintes limites
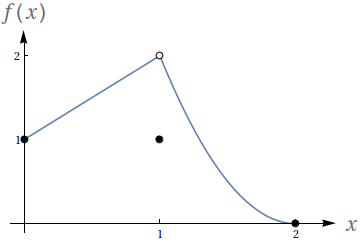
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $2$
- $2$
- $2$
- $1$
- Como $f$ não é definida para $x<0$, esse limite é indefinido.
- $1$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{3-x};$
$\lim\limits_{x\rightarrow 3^{-}}\dfrac{5}{3-x};$
$\lim\limits_{x\rightarrow 0^{+}}\dfrac{5}{x^{2}-x};$
$\lim\limits_{x\rightarrow 0^{-}}\dfrac{5}{x^{2}-x};$
$\lim\limits_{x\rightarrow 0^{+}}\dfrac{\sin x}{x^{3}-x^{2}};$
$\lim\limits_{x\rightarrow -1^{+}}\dfrac{3x^{2}-4}{1-x^{2}}$
Estime numericamente os seguintes limites para a função $f(x)= \frac{x^2+5 x-36}{x^3-5 x^2+3 x+9}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-335.64$ \\
$2.99$ & $-30350.6$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $-265.61$ \\
$3.01$ & $-29650.6$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =-\infty$.
Dê exemplo de uma função definida em $\mathbb{R}$, que não seja contínua em $2$, mas que $\lim\limits_{x \to 2^+}f(x)=\lim\limits_{x \to 2^-}f(x)$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x^2, & & \text{ se } x<2 \\
x+1, & & \text{ se } x=2\\
-x^2+2x+4, & & \text{ se } x>2
\end{array}
\right.$
$ \lim\limits_{x\to 2^-} f(x)$
$ \lim\limits_{x\to 2^+} f(x)$
$ \lim\limits_{x\to 2} f(x)$
$f(2)$
- 4
- 4
- 4
- 3
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
a(x-b)^2+c, & & \text{ se } x<b \\
a(x-b)+c, & & x \text{ se } \geq b
\end{array}
\right.,$
sendo que $a$, $b$ e $c$ são números reais.
- $ \lim\limits_{x\to b^-} f(x)$
- $ \lim\limits_{x\to b^+} f(x)$
- $ \lim\limits_{x\to b} f(x)$
- $f(b)$
- $c$
- $c$
- $c$
- $c$
Seja $f$ uma função definida num intervalo aberto $I$ e $p \in I$. Suponha que $f(x) \leq f(p)$ para todo $x \in I$. Prove que $\lim\limits_{x \to p}\dfrac{f(x)-f(p)}{x-p}=0$, desde que o limite exista.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
\frac{|x|}{x}, & & \text{ se } x\neq 0 \\
0, & & \text{ se } x=0
\end{array}
\right.$
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $ \lim\limits_{x\to 0} f(x)$
- $f(0)$
- $-1$
- $1$
- Não existe.
- $0$
Calcule os seguintes limites laterais (justifique cada passo da resolução):
$\lim\limits_{x\rightarrow1^{+}}\dfrac{\sqrt{x^{2}-1}}{x-1}.$
$\lim\limits_{x\rightarrow1^{-}}\dfrac{\sqrt{x^{2}-1}}{x-1}.$
De acordo com a teoria da relatividade, o comprimento de um objeto parece, a um observador, depender da velocidade relativa entre este e o objeto. Se o observador estabelecer o comprimento do objeto, em repouso, como $L_0$, então o comprimento, a uma velocidade $v$, parecerá:
$L=L_0\sqrt{1-\frac{v^2}{c^2}}$.
Esta equação é chamada Fórmula de Contração de Lorentz, sendo que $c$ é a velocidade da luz no vácuo, em torno de $3\times10^8m/s$. Qual o comportamento de $L$ conforme $v$ aumenta?
Determine $\lim\limits_{v\rightarrow c^- }L$. Por que o limite lateral à esquerda foi necessário, e como esta necessidade se relaciona com as Leis da Física?
Utilizando o gráfico a seguir, avalie os seguintes limites
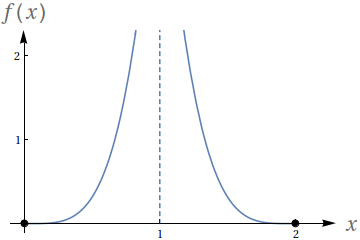
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- Não existe.
- Não existe.
- Não existe.
- Indefinido.
- $0$
- $0$
Calcule $\lim\limits_{x\rightarrow +\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-2$
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x+1, & & \text{ se } x<1 \\
1, & & \text{ se } x=1\\
x-1, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
- 2
- 0
- Não existe
- 1
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
1-\cos^2 x, & & \text{ se } x<a \\
\sin^2 x, & & \text{ se } x\geq a
\end{array},
\right.$
sendo que $a$ é um número real.
$ \lim\limits_{x\to a^-} f(x)$
$ \lim\limits_{x\to a^+} f(x)$
$ \lim\limits_{x\to a} f(x)$
$f(a)$
- $1-\cos^2 a = \sin^2 a$
- $\sin^2 a$
- $\sin^2 a$
- $\sin ^2 a$
Em matemática, a função piso, denotada por $\lfloor x\rfloor$, converte um número real ${\displaystyle x}$ no maior número inteiro menor ou igual a ${\displaystyle x}$ Essa função é importante em computação para truncamento ou arredondamento de números. Considere a função $f(x)=\lfloor 1/x\rfloor$, $x \neq 0$. Esboce o gráfico dessa função para $\dfrac{1}{4} \leq x \leq 2$ e também para $-2 \leq x \leq -\dfrac{1}{4}$. Como se comporta $f(x)$ quando $x$ tende a zero pelo lado direito? E pelo lado esquerdo? O limite $\lim\limits_{x \to 0}f(x)$ existe?
Utilizando o gráfico a seguir, avalie os seguintes limites
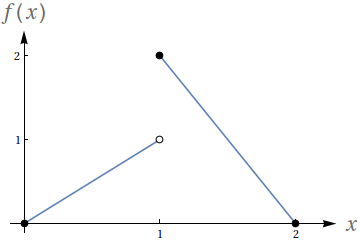
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 2^+} f(x)$
- $1$
- $2$
- Não existe.
- $2$
- $0$
- Como $f$ não é definida para $x>2$, esse limite é indefinido.
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-9 x+18}{x^2-x-6}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-0.632$ \\
$2.99$ & $-0.6032$ \\
$2.999$ & $-0.60032$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-0.6$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $-0.5686$ \\
$3.01$ & $-0.5968$ \\
$3.001$ & $-0.59968$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-0.6$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =-0.6$.
Em matemática e estatística, a função de Heaviside (ou função degrau) é uma função singular e descontínua, com valor zero quando o seu argumento é negativo e valor unitário quando o argumento é positivo. Seja $H$ a função de Heaviside. Prove, usando a definição de limite, que $\lim\limits_{x \to 0}H(x)$ não existe.
Suponha $g(x) \neq 0$, para todo $x \in Dom(g)$, $L \neq 0$ e $\lim\limits_{x \to p}g(x)=L$. Prove que $\lim\limits_{x \to p}\dfrac{1}{g(x)}=\dfrac{1}{L}$.
Veja Guidorizzi, volume $1$, página $87$.
Utilizando o gráfico a seguir, avalie os seguintes limites
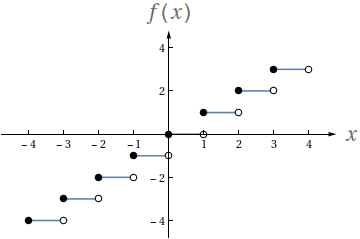
Seja $-3\leq a\leq 3$ um número inteiro
- $ \lim\limits_{x\to a^-} f(x)$
- $ \lim\limits_{x\to a^+} f(x)$
- $ \lim\limits_{x\to a} f(x)$
- $f(a)$
- $a-1$
- $a$
- Não existe.
- $a$
Utilizando o gráfico a seguir, avalie os seguintes limites
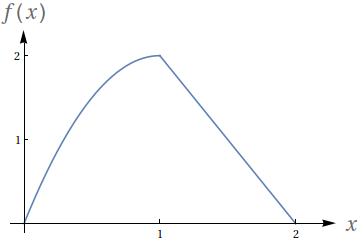
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $2$
- $2$
- $2$
- $2$
Utilizando o gráfico a seguir, avalie os seguintes limites
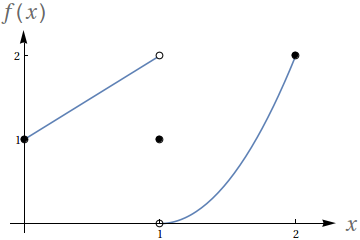
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $2$
- $0$
- Não existe.
- $1$
Utilizando o gráfico a seguir, avalie os seguintes limites
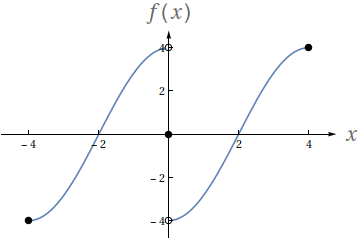
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $ \lim\limits_{x\to 0} f(x)$
- $f(0)$
- $4$
- $-4$
- Não existe.
- $0$
Mostre que
- o limite de $f(x)=\dfrac{x-2}{|\,x-2|}$, quando $x\to 2$, não existe.
- o limite de $f(x)=\left\{\begin{array}{ll} x^2+2, & x\geq -1 \\ 2x+1, & x<-1 \\ \end{array}\right.$, quando $x\to -1$, não existe.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
2x^2+5x-1, & & \text{ se } x<0 \\
\sin x, & & \text{ se } x\geq 0
\end{array}
\right.$
$ \lim\limits_{x\to 0^-} f(x)$
$ \lim\limits_{x\to 0^+} f(x)$
$ \lim\limits_{x\to 0} f(x)$
$f(0)$
- $-1$
- 0
- Não existe.
- 0
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
\cos x, & & \text{ se } x<\pi \\
\sin x, & & \text{ se } x\geq \pi
\end{array}
\right.$
$ \lim\limits_{x\to \pi^-} f(x)$
$ \lim\limits_{x\to \pi^+} f(x)$
$ \lim\limits_{x\to \pi} f(x)$
$f(\pi)$
- $-1$
- 0
- Não existe.
- 0
Dê exemplo de uma função definida em $\mathbb{R}$, que não seja contínua em $a$, mas que $\lim\limits_{x \to a^+}f(x)=\lim\limits_{x \to a^-}f(x)$.
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-1}{x^2-x-6}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-15.1224$ \\
$2.99$ & $-159.12$ \\
$2.999$ & $-1599.12$
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $16.8824$ \\
$3.01$ & $160.88$ \\
$3.001$ & $1600.88$
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x)$ não existe.
Resolva os itens:
- Mostre que $\lim\limits_{x\rightarrow 0^{+}}\left( x\ln x\right) =0$;
- Utilize o item anterior para avaliar $\lim\limits_{x\rightarrow 0^{+}}x^{x}.$
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x+1, & & \text{ se } x\leq 1 \\
x^2-5, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
2
$-4$
Não existe.
2
Utilizando o gráfico a seguir, avalie os seguintes limites
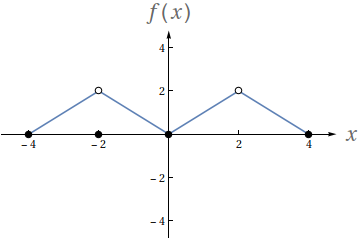
- $ \lim\limits_{x\to -2^-} f(x)$
- $ \lim\limits_{x\to -2^+} f(x)$
- $ \lim\limits_{x\to -2} f(x)$
- $f(-2)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 2^+} f(x)$
- $ \lim\limits_{x\to 2} f(x)$
- $f(2)$
- $2$
- $2$
- $2$
- $0$
- $2$
- $2$
- $2$
- Indefinido
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-11 x+30}{x^3-4 x^2-3 x+18}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $132.857$ \\
$2.99$ & $12124.4$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $108.039$ \\
$3.01$ & $11876.4$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =\infty$.

