Exercícios
Limite e continuidade
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Quais das seguintes funções f têm descontinuidade removível em $a$? Se a descontinuidade for removível em $a$, encontre a função $g$ que é igual a $f$ para $x\neq a$ e contínua em $a$.
$f(x)=\frac{x^{2}+2x-8}{x+2}$, $a=-2$.
$f(x)=\frac{x-7}{\vert x-7 \vert}$, $a=7$.
$f(x)=\frac{3- \sqrt{x}}{9-x}$, $a=9$.
Identifique as assíntotas verticais e horizontais, caso existam, da função
$f(x)=\frac{x^2+x-12}{7 x^3-14 x^2-21 x}$.
Assíntota horizontal em $y=0$; assíntotas verticais em $x=-1$ e $x=0$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0^{+}}\log _{\dfrac{1}{3}}x$.
$\infty$.
Dê exemplo de uma função definida em $\mathbb{R}$, que não seja contínua em $a$, mas que $\lim\limits_{x \to a^+}f(x)=\lim\limits_{x \to a^-}f(x)$.
Calcule, se existir, o limite $\lim\limits_{x\rightarrow 0}\sqrt x$.
$0$.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow0}\frac{\tan x}{x}$.
$1$.
Aproxime numericamente o seguinte limite
$ f(x)=\frac{x^2-9 x+18}{x^2-x-6}$
- \begin{array}{cc}
x & f(x) \\ \hline
2.9 & -0.632 \\
2.99 & -0.6032 \\
2.999 & -0.60032 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-0.6$. - \begin{array}{cc}
x & f(x) \\ \hline
3.1 & -0.5686 \\
3.01 & -0.5968 \\
3.001 & -0.59968 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-0.6$. - As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =-0.6$.
Mostre que a equação
\begin{equation*}
x^{26}+x^{2}-320=0
\end{equation*}
possui ao menos uma raiz real positiva e também uma raiz real negativa.
Use o Teorema do Valor Intermediário para provar que a equação $\tan x= 2-4x$ possui uma solução no intervalo $\bigl(-\frac{\pi}{2}, \frac{\pi}{2}\bigr).$
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = \cos x -\sin x$ no intervalo $[0.7,0.8]$.
A raiz aproximada é $x=0.78$.
Os intervalos utilizados são:
$[0.7,0.8] \quad [0.75,0.8] \quad [0.775,0.8]$
$[0.775,0.7875]\quad [0.78125,0.7875]$
(Alguns passos a mais mostrariam que $0.79$ é melhor, dado que a raiz é $\pi/4 \approx 0.78539$.)
Calcule os limites:
$\lim\limits_{x\to\pi/6} cos(sec x)$
$\lim\limits_{x\to0} \ln(1+x)$
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc} 1, & & \text{se } x=0\\ \frac{\sin x}{x}, & &\text{se } x>0 \end{array}\right.$
- $x=0$
- $x=\pi$
- Sim.
- Sim.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x+1, & & \text{ se } x<1 \\
1, & & \text{ se } x=1\\
x-1, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
- 2
- 0
- Não existe
- 1
O que significa dizer, em termos de limites, que uma função é "bem comportada"?
Calcule os seguintes limites. Pode ser útil usar a relação de inversão que há em relação às funções logarítmicas e exponenciais (isto é, $\ln(x)=y \Leftrightarrow e^y=x$) e/ou gráficos.
$\lim\limits_{x\rightarrow\infty}\log_3 x$
$\lim\limits_{x\rightarrow 0^+}\ln x$
$\lim\limits_{x\rightarrow -\infty}e^x$
Dê exemplo de uma função $f$ que seja descontínua, mas tal que $|f|$ seja contínua.
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função contínua tal que, para todo real x, tenhamos $f(f(f(x))) = x^2 + 1$. Prove que $f$ é par.
Determine os valores de $\lambda$ que tornam contínua a função $f:\mathbb{R\rightarrow R},$ da por:
\[
f\left( x\right) =\left\{
\begin{array}{c}
x^{2}+\lambda x\mbox{ se }x\leq 1 \\
\left( \lambda x\right) ^{2}-1=\lambda ^{2}x^{2}-1\mbox{ se }x>1
\end{array}
\right. \mbox{.}
\]
Se você investir $1000$ reais em uma aplicação que paga $7$% de juros compostos em $n$ vezes por ano, então em $10$ anos sua aplicação terá no total $1000(1+0,07/n)^{10n}$ reais.
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta trimestralmente ($n=4$)?
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta mensalmente ($n=12$)?
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta mensalmente ($n=365$)?
Pesquise a taxa de juros paga pela poupança, e o período em que ela é composta. Calcule a quantidade de dinheiro que você terá se investir uma certa quantia de dinheiro (pense no dinheiro você tem disponível para investir) em $1$, $2$, $5$ e $10$ anos com essa taxa e período de composição. Interprete os resultados pensando em seu futuro!
Quanto dinheiro você terá em $10$ anos se os juros forem compostos continuamente, isto é, se $n\to\infty$?
Seja $f$ uma função contínua em $[1,5]$, sendo que $f(1) = -2$ e $f(5) = -10$. Existe um valor $1<c<5$ tal que $f(c) = -9$? Por quê?
Sim, pelo Teorema do Valor Intermediário.
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
x^3-x, & & \text{se } x<1\\
x-2, & & \text{se } x\geq 1
\end{array}\right.$
- $x=0$.
- $x=1$.
- Sim.
- Não: Os limites pela direita e pela esquerda não são iguais em $x=1$.
Sabendo que $\lim\limits_{x\to2} f(x) = 3$ e $\lim\limits_{x\to2} g(x) = -1$, calcule os seguintes limites:
$\lim\limits_{x\to2}(f+g)(x)$
$\lim\limits_{x\to2}(fg)(x)$
$\lim\limits_{x\to2}(f/g)(x)$
$\lim\limits_{x\to2}f(x)^{g(x)}$
Calcule o limite $\lim\limits_{x\to e} \ln x$, em que $e$ é o número de Euler.
$1$.
A afirmação: $`` \lim\limits_{x\rightarrow p^+} f(x) = \lim\limits_{x\rightarrow p^-} f(x)\Rightarrow f \mbox{ contínua em } p. "$ é verdadeira ou falsa? Justifique.
É falsa. Só seria verdadeira se o valor dos limites laterais fosse igual a $f(p)$.
Seja $f:\mathbb{R} \to \mathbb{R}$ contínua e tal que $f(x).f(f(x))=1$, para todo $x$. Se $f(1000)=999$, calcule $f(500)$.
Dê um exemplo de uma função que seja contínua em todos os pontos da reta, exceto nos pontos da forma $k \pi$, $k \in \mathbb{Z}$.
$f(x)=1$, se $x=k \pi$, $k \in \mathbb{Z}$; $f(x)=0$, caso contrário.
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 0}\dfrac{\sin 4x}{x}$
$\lim\limits_{x\rightarrow 0}\dfrac{x}{\sin x}$
- $4$.
- $1$.
Considere uma função contínua $\phi:\mathbb{R} \to \mathbb{R}$ tal que
\[ \forall \quad {x \in \mathbb{R}},\quad \phi(x)\geq x^2.\]
Mostre que existe $a\geq 0$ tal que $\left[a,+\infty\right[$ é o contradomínio de $\phi$.
Calcule:
- $ \lim\limits_{x\to 5^-} f(x)$
- $ \lim\limits_{x\to 5^+} f(x)$
- $ \lim\limits_{x\to 5} f(x)$
- $f(5)$
- $f$ é contínua em $x=5$?
1. $20$.
2. $25$.
3. Não existe.
4. $25$
5. Não.
Dê exemplo de uma função definida em $\mathbb{R}$, que não seja contínua em $2$, mas que $\lim\limits_{x \to 2^+}f(x)=\lim\limits_{x \to 2^-}f(x)$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left(10x\right) }{\sin \left( 5x\right) }$.
$2$.
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = e^x - 2$ no intervalo $[0.65,0.7]$.
A raiz aproximada é $x=0.69$.
Os intervalos utilizados são:
$[0.65,0.7] \quad [0.675,0.7] \quad [0.6875,0.7]$
$[0.6875,0.69375]\quad [0.690625,0.69375]$
Calcule o limite a seguir, justificando as passagens.
$\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}$
0
Para todo $x\neq 0$ temos que
\begin{equation*}
\dfrac{1-\cos x}{x}=\dfrac{1-\cos x}{x}\dfrac{1+\cos x}{1+\cos x}=\dfrac{
1-\cos ^{2}x}{x}\dfrac{1}{1+\cos x}\text{.}
\end{equation*}
Como $1-\cos ^{2}x=\sin ^{2}x$ obtemos
\begin{eqnarray*}
\dfrac{1-\cos x}{x} &=&\dfrac{\sin ^{2}x}{x}\dfrac{1}{1+\cos x} \\
&=&\sin x\dfrac{\sin x}{x}\dfrac{1}{1+\cos x}.
\end{eqnarray*}
Mas
\begin{eqnarray*}
\lim\limits_{x\rightarrow 0}\sin x &=&0\;\text{(pois }\sin x\text{ é contínua)} \\
\lim\limits_{x\rightarrow 0}\dfrac{\sin x}{x} &=&1\;\text{(limite trigonométrico fundamental)} \\
\lim\limits_{x\rightarrow 0}\dfrac{1}{1+\cos x} &=&\dfrac{1}{2}\;\text{(}
\cos x\text{ cont\'{i}nua e }1+\cos \left( 0\right) \neq 0\text{).}
\end{eqnarray*}
Logo,
\begin{equation*}
\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}=\lim\limits_{x\rightarrow
0}\sin x\lim\limits_{x\rightarrow 0}\dfrac{\sin x}{x}\lim\limits_{x
\rightarrow 0}\dfrac{1}{1+\cos x}=0.
\end{equation*}
f(x)=\frac{\sqrt{1-x^2}}{1-tg x} \end{align*}
- Determine o domínio de $f$.
- Estude $f$ quanto a continuidade.
A função pode tender a valores diferentes pela esquerda e pela direita, a função pode crescer de maneira ilimitada, ou a função pode oscilar em torno de um valor.
Sejam $f$ uma função contínua num intervalo $I$, $a$ e $b$ valores em $I$. Se $f(a)$ e $f(b)$ são valores com sinais contrários, mostre que a equação $f(x)=0$ tem pelo menos uma raiz real no intervalo $\left[a,b\right]$.
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
- $\lim\limits_{x\rightarrow p}\dfrac{\tan \left( x-p\right) }{x^{2}-p^{2}}$
- $\lim\limits_{x\rightarrow p}\dfrac{\sin x-\sin p}{x-p}$
- $\lim\limits_{x\rightarrow p}\dfrac{\cos x-\cos p}{x-p}$
$f(x)=1, x \neq 0$; $f(0)=2$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\log _{3}x$.
$\infty$.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\left( 5+\dfrac{1}{x}+\dfrac{4}{x^{2}}\right)$.
$5$
É possível mostrar que, sob certas condições, a velocidade $v(t)$ de uma gota de chuva caindo no instante $t$ é:
$$v(t) = v^\star \left(1-\exp\left(-\dfrac{gt}{v} \right)\right),$$
onde $g$ é a aceleração da gravidade e $v^\star$ é a velocidade final da gota.
Calcule a velocidade para um tempo muito grande, isto é, calcule $\displaystyle \lim_{t \to \infty} v(t)$.
Considerando $v^\star = 1$m$/$s e $g=9,8$m$/$s$^2$, faça o gráfico de $v(t)$. Quanto tempo levará para a velocidade da gota atingir $99\%$ de sua velocidade final?
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
a(x-b)^2+c, & & \text{ se } x<b \\
a(x-b)+c, & & x \text{ se } \geq b
\end{array}
\right.,$
sendo que $a$, $b$ e $c$ são números reais.
- $ \lim\limits_{x\to b^-} f(x)$
- $ \lim\limits_{x\to b^+} f(x)$
- $ \lim\limits_{x\to b} f(x)$
- $f(b)$
- $c$
- $c$
- $c$
- $c$
Classifique as afirmações a seguir como verdadeiras ou falsas:
Se $ \lim\limits_{x\to 5} f(x) = \infty$, então estamos implicitamente afirmando que o limite em questão existe.
Se $ \lim\limits_{x\to \infty} f(x) = 5$, então estamos implicitamente afirmando que o limite em questão existe.
Se $ \lim\limits_{x\to 1^-} f(x) = -\infty$, então $ \lim\limits_{x\to 1^+} f(x) = \infty$.
Se $ \lim\limits_{x\to 5} f(x) = \infty$, então $f$ tem uma assíntota vertical em $x=5$.
$\infty/0$ não é uma forma indeterminada.
Falsa.
Verdadeira
Falsa
Verdadeira
Verdadeira
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(t) = \frac{1}{\sqrt{1-t^2}}$.
$(-1,1)$
Resolva os itens:
- Mostre que $\lim\limits_{x\rightarrow 0^{+}}\left( x\ln x\right) =0$;
- Utilize o item anterior para avaliar $\lim\limits_{x\rightarrow 0^{+}}x^{x}.$
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = \sin x - 1/2$ no intervalo $[0.5,0.55]$.
A raiz aproximada é $x=0.52$.
Os intervalos utilizados são:
$[0.5,0.55] \quad [0.5,0.525] \quad [0.5125,0.525]$
$[0.51875,0.525]\quad [0.521875,0.525]$.
Seja $f:\mathbb{R\rightarrow R}$ a função
definida por
\begin{equation*}
f\left( x\right) =\left\{
\begin{array}{cc}
x^{2} & \text{se }x\leq 1 \\
2x-1 & \text{se }x>1
\end{array}
\right. ,
\end{equation*}
e defina $g\left( x\right) =\lim\limits_{x\rightarrow h}\dfrac{f\left(
x+h\right) -f\left( x\right) }{h}$. Mostre que $g\left( x\right) $ é contínua.
Calcule $\displaystyle\lim_{x\rightarrow 0}\frac{\frac{2}{x} - 5\cos(\frac{1}{x^2+2x})}{-\frac{5}{x} + 2\cos(\frac{1}{x^2+2x})}$.
Existe algum número real $a$ tal que a função $f(x) = \left\{\begin{array}{ccl}\displaystyle\frac{\frac{2}{x} - 5\cos(\frac{1}{x^2+2x})}{-\frac{5}{x} + 2\cos(\frac{1}{x^2+2x})},& \mbox{se} & x\neq 0\\ a, & \mbox{se} & x=0 \end{array} \right.$ seja contínua?
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ h(k) = \sqrt{1-k}+\sqrt{k+1}$.
$[-1,1]$
De acordo com a teoria da relatividade, o comprimento de um objeto parece, a um observador, depender da velocidade relativa entre este e o objeto. Se o observador estabelecer o comprimento do objeto, em repouso, como $L_0$, então o comprimento, a uma velocidade $v$, parecerá:
$L=L_0\sqrt{1-\frac{v^2}{c^2}}$.
Esta equação é chamada Fórmula de Contração de Lorentz, sendo que $c$ é a velocidade da luz no vácuo, em torno de $3\times10^8m/s$. Qual o comportamento de $L$ conforme $v$ aumenta?
Determine $\lim\limits_{v\rightarrow c^- }L$. Por que o limite lateral à esquerda foi necessário, e como esta necessidade se relaciona com as Leis da Física?
Embora limites como $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{n}$ e $\displaystyle \lim_{n \to \infty} a^n$ possam ser avaliados utilizando conhecimentos sobre as funções logaritmo e exponencial, estes não são necessários. Neste exercício vamos calcular esses tipos de limite por meio de argumentos ``elementares''. As ferramentas básicas são desigualdades provenientes do teorema binomial, principalmente:
$$(1+h)^n \geq 1+nh, \text{ para } h > 0.$$
Mostre que $\displaystyle \lim_{n \to \infty} a^n = \infty$ se $a>1$, fazendo $a=1+h$, onde $h>0$.
Mostre que $\displaystyle \lim_{n \to \infty} a^n= 0$ se $0<a<1$.
Utilizando o gráfico a seguir, avalie os seguintes limites
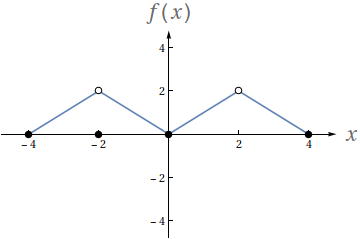
- $ \lim\limits_{x\to -2^-} f(x)$
- $ \lim\limits_{x\to -2^+} f(x)$
- $ \lim\limits_{x\to -2} f(x)$
- $f(-2)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 2^+} f(x)$
- $ \lim\limits_{x\to 2} f(x)$
- $f(2)$
- $2$
- $2$
- $2$
- $0$
- $2$
- $2$
- $2$
- Indefinido
Encontre todas as assíntotas horizontais e verticais da função $ f(x)=\frac{\sqrt{3x^2-5x+11}}{4x-7}$.
Dê exemplo de duas funções, $f$ e $g$, para ilustrar que se $g(x)\le f(x)$ para todo $x$ suficientemente próximo de $a$, então $\lim\limits_{x\rightarrow a}g(x)\le\lim\limits_{x \rightarrow a}f(x)$.
Aproxime numericamente o seguinte limite
$ f(x)=\frac{x^2-11 x+30}{x^3-4 x^2-3 x+18}$
- \begin{array}{cc}
x & f(x) \\ \hline
2.9 & 132.857 \\
2.99 & 12124.4 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =\infty$. - \begin{array}{cc}
x & f(x) \\ \hline
3.1 & 108.039 \\
3.01 & 11876.4 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$. - As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =\infty$.
$f$ é contínua em $x=0$.
$3/2$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(k) = \sqrt{1-e^k}$.
$(-\infty,0]$
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{1-2^{x}}{1-3^{x}}$.
$0$.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow1}\frac{sen(x-1)}{x^{2}+x-2}$.
$1/3$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(s) = \ln s$.
$(0,\infty)$
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
\frac{x^2+5x+4}{x^2+3x+2}, & & \text{se } x\neq -1\\
3, & &\text{se } x=-1
\end{array}\right.$
- $x=-1$
- $x=10$
- Sim.
- Sim.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x+1, & & \text{ se } x\leq 1 \\
x^2-5, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
2
$-4$
Não existe.
2
Calcule $\lim\limits_{x\rightarrow +\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-2$
Sabemos que a troca de calor entre um objeto a uma temperatura $T$ e o ambiente a uma temperatura $T_{a}$ é proporcional a diferença $(T-T_{a})$. Como a variação de temperatura é proporcional a troca de calor, temos a seguinte equação diferencial para $T\left( t\right) $ (temperatura em função do tempo $t$ ):$\frac{dT}{dt}=-\alpha \left( T-T_{a}\right) ,$ onde a constante $\alpha >0$ depende do calor específico e da condutividade térmica do objeto. Ache a solução dessa equação em função de $\alpha $ assumindo que a temperatura do ambiente $T_{a}=20^{o}C$ e a temperatura inicial $T_{0}=100^{o}C$. Qual é o limite $\lim\limits_{t\rightarrow +\infty }T\left( t\right) $?
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(N,+\infty)$, os valores da função $f(x)=1/x^2$ estejam no máximo a $0,1$ unidade de $L=0$. Encontre $N$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(N,+\infty)$, os valores da função $f(x)=x/(x+1)$ estejam no máximo a $0,01$ unidade de $L=0$. Encontre $N$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(-\infty,N)$, os valores da função $f(x)=1/x^3$ estejam no máximo a $0,001$ unidade de $L=0$. Encontre $N$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(-\infty,N)$, os valores da função $f(x)=x/(x+1)$ estejam no máximo a $0,001$ unidade de $L=0$. Encontre $N$.
Explique, usando propriedades de limites, porque $\lim\limits_{x\rightarrow 2}\frac{x^2-4}{x-2}\not = \frac{\lim\limits_{x\rightarrow 2} (x^2-4)}{\lim\limits_{x\rightarrow 2}(x-2)}$.
Note que somente podemos usar as propriedades de limite quando um limite existe e é finito. Além disso, lembre-se que limites que recaem na expressão indeterminada "$\frac{0}{0}$", podem existir ou não. Calcule os seguintes limites.
$\lim\limits_{x\rightarrow 2}\frac{x^2-4}{x-2}$
$\lim\limits_{h\rightarrow 0}\frac{(2+h)^2 - 4}{h}$
$\lim\limits_{x\rightarrow 2}\left(\frac{4}{x^2-2x}-\frac{x}{x-2}\right)$
$\lim\limits_{t\rightarrow 0}\frac{\sqrt{t^2+4}-2}{t^2}$
Identifique as assíntotas verticais e horizontais, caso existam, da função
$f(x)=\frac{2 x^2-2 x-4}{x^2+x-20}$.
Assíntota horizontal em $y=2$; assíntotas verticais em $x=-5$ e $x=4$.
Calcule o limite $\lim\limits_{x\rightarrow -\infty }\left( 2^{x}+2^{-x}\right)$.
$\infty$.
Calcule o limite:
$\lim\limits_{x\rightarrow +\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-2$.
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = x^2+2x-4$ no intervalo $[1,1.5]$.
A raiz aproximada é $x=1.23$.
Os intervalos utilizados são:
$[1,1.5] \quad [1,1.25] \quad [1.125,1.25]$
$[1.1875,1.25]\quad [1.21875,1.25]\quad [1.234375,1.25]$
$[1.234375,1.2421875]\quad [1.234375,1.2382813]$.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt[3]{3x^{3}+2x-1}}{\sqrt{x^{2}+x+4}}$.
$\sqrt[3]{3}$
Utilizando o gráfico a seguir, avalie os seguintes limites
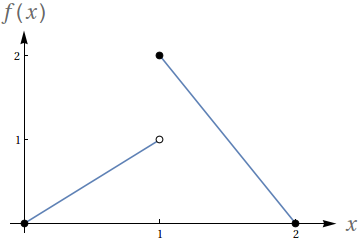
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 2^+} f(x)$
- $1$
- $2$
- Não existe.
- $2$
- $0$
- Como $f$ não é definida para $x>2$, esse limite é indefinido.
Sejam $f$ e $g$ funções contínuas. Demonstre que $h(x)=\max(f(x),g(x))$ é contínua.
Calcule o seguinte limite
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right)^{x+2}$.
Seja $f$ uma função definida em $\mathbb{R}$ e suponha que exista $M>0$ tal que $|f(x)-f(p)|\leq M|x-p|$ para todo $x$. Prove que $f$ é contínua em $p$.
Classifique as afirmações a seguir como verdadeiras ou falsas:
- Se $ \lim\limits_{x\to 5} f(x) = \infty$, então estamos implicitamente afirmando que o limite em questão existe.
- Se $ \lim\limits_{x\to 1^-} f(x) = -\infty$, então $ \lim\limits_{x\to 1^+} f(x) = \infty$.
- Se $ \lim\limits_{x\to 5} f(x) = \infty$, então $f$ tem uma assíntota vertical em $x=5$.
- $\infty/0$ não é uma forma indeterminada.
- Falsa.
- Falsa
- Verdadeira
- Verdadeira
- $\lim\limits_{x\rightarrow 1}\dfrac{\sqrt{x}-1}{\sqrt{2x+3}-\sqrt{5}}$
- $\lim\limits_{x\rightarrow 3}\dfrac{\sqrt{x}-\sqrt{3}}{x-3}$
- $\lim\limits_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}$
Seja $ f(x)=\left\{\begin{array}{ll} \sqrt{x-4} &\text{ se } x>4\\8-2x&\text{ if } x<4\end{array}\right.$.
Decida se $\lim\limits_{x\rightarrow 4}f(x)$ existe. Se o limite não existe, explique.
Aproxime numericamente o seguinte limite
$ f(x)= \frac{x^2+5 x-36}{x^3-5 x^2+3 x+9}$
- \begin{array}{cc}
x & f(x) \\ \hline
2.9 & -335.64 \\
2.99 & -30350.6 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$. - \begin{array}{cc}
x & f(x) \\ \hline
3.1 & -265.61 \\
3.01 & -29650.6 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-\infty$. - As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =-\infty$.
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-11 x+30}{x^3-4 x^2-3 x+18}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $132.857$ \\
$2.99$ & $12124.4$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $108.039$ \\
$3.01$ & $11876.4$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =\infty$.
Mostre que função $f\left( x\right) =\dfrac{1}{x^2}$ é contínua em seu domínio.
Mostre que a função $f\left( x\right) =x^{n}$ é contínua em seu domínio.
O domínio da função é $\mathbb{R}$. Logo, para $x \in \mathbb{R}$, temos:
$\lim_\limits{x \to a} x^n = a^n$
e
$f(a) = a^n$.
Isto é, $\lim_\limits{x \to a} f(x) = f(a)$, e portanto a função é contínua.
- $\lim\limits_{x\rightarrow 1}\dfrac{f\left( x\right) -f\left(1\right) }{x-1}$, onde $f\left( x\right) =\left\{ \begin{array}{cc} x^{2} & \text{se }x\leq 1 \\ 2x-1 & \text{se }x>1 \end{array} \right. $
- $\lim\limits_{x\rightarrow 2}\dfrac{f\left( x\right) -f\left(2\right) }{x-2}$, onde $f\left( x\right) =\left\{ \begin{array}{cc} x & \text{se }x\geq 2 \\ x^{2}/2 & \text{se }x<2 \end{array} \right. $
- $\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h}$, com $f\left( x\right) =x^{2}-3x$ e $f\left( x\right) =1/x$
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\dfrac{1-2^{x}}{1-3^{x}}$.
$0$.
Mostre, usando a definição, que a função $f\left( x\right) =ax+b$ é contínua em seu domínio.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x^2-1, & & \text{ se } x<-1 \\
x^3+1, & & \text{ se } -1\leq x\leq 1\\
x^2+1, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to -1^-} f(x)$
$ \lim\limits_{x\to -1^+} f(x)$
$ \lim\limits_{x\to -1} f(x)$
$f(-1)$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
- 0
- 0
- 0
- 0
- 2
- 2
- 2
- 2
Sabemos que limites que tomam a forma indeterminada ``$\infty-\infty$" exigem um pouco mais de trabalho para serem calculados. Calcule, de forma adequada, o limite $\lim\limits_{x\rightarrow\infty}\left(\sqrt{2x^2-7}-x\right)$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(x) = \sqrt{x^2-4}$.
$(-\infty,-2]\cup [2,\infty)$
Seja $f:\mathbb{R\rightarrow R}$ a função
definida por
\begin{equation*}
f\left( x\right) =\left\{
\begin{array}{cc}
x^{2}, & \text{se }x\leq 1 \\
2x-1, & \text{se }x>1
\end{array}
\right. ,
\end{equation*}
e defina $g\left( x\right) =\lim\limits_{x \rightarrow h}\dfrac{f \left(x+h \right) -f \left( x\right) }{h}$.
Mostre que $g\left( x\right) $ é contínua.
\begin{eqnarray*} g\left( x\right) &=&\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left( x+h\right) ^{2}-x^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{x^{2}+2hx+h^{2}-x^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2hx+h^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\left( 2x+h\right) =2x. \end{eqnarray*}
Já para $x>1$ temos que
\begin{eqnarray*} g\left( x\right) &=&\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ 2\left( x+h\right) -1\right] - \left[ 2x-1\right] }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2h}{h}=2. \end{eqnarray*}
Para $x=1$ temos que
\begin{eqnarray*} \lim\limits_{h\rightarrow 0^{+}}\dfrac{f\left( 1+h\right) -f\left( 1\right) }{h} &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ 2\left( 1+h\right) -1 \right] -1}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2h}{h}=2 \\ \lim\limits_{h\rightarrow 0^{-}}\dfrac{f\left( 1+h\right) -f\left( 1\right) }{h} &=&\lim\limits_{h\rightarrow 0^{-}}\dfrac{\left( 1+h\right) ^{2}-1}{h} \\ &=&\lim\limits_{h\rightarrow 0^{-}}\dfrac{2h+h^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0^{-}}\left( 2+h\right) =2. \end{eqnarray*}
Temos então que $g$ é bem definida também no ponto $x=1$ e, de modo geral, $g$ pode ser expressa por \begin{equation*} g\left( x\right) =\left\{ \begin{array}{cc} 2x & \text{se }x\leq 1 \\ 2 & \text{se }x>1 \end{array} \right. \text{.} \end{equation*}
Como as funções $h\left( x\right) =2x$ e $p\left( x\right) \equiv 2$ são contínuas, temos que $g\left( x\right) $ é contínua para todo $x\neq 1$.
Além disto, como $\lim\limits_{x\rightarrow 1^{-}}g\left( x\right) =\lim\limits_{x\rightarrow 1}2x=2=\lim\limits_{x\rightarrow 1^{+}}2=\lim\limits_{x\rightarrow 1^{+}}g\left( x\right) $, segue que $\lim\limits_{x\rightarrow 1}g\left(x\right) =2$. Mas como $g\left( 1\right) =2$, segue que a função $ g\left( x\right) $ também é contínua no ponto $x=1$.
Calcule o limite a seguir. Justifique as passagens.
$\lim\limits_{x\rightarrow +\infty }\dfrac{-x^{3}+2}{4x^{2}+89}$
Dê um exemplo de uma função tal que $\lim\limits_{x\rightarrow p}\left| f\left( x\right) \right| $ exista mas $\lim\limits_{x\rightarrow p}f\left( x\right) $ não exista.
Mostre que existe um número real que é igual a soma de seu cubo e de seu quadrado mais um. Justifique sua resposta.
Mas $f\left( -2\right) =\left( -2\right)^{3}+\left( -2\right) ^{2}-\left( -2\right) +1=-1$ e $f\left( 0\right)=1$.
Como $f\left( x\right) $ é contínua, pelo Teorema do Valor Intermediário, existe $-2<x<0$ tal que $f\left( x\right) =0$.
Resolução Alternativa:
Uma vez definida $f(x)$, pode-se ver que $\lim_{x\rightarrow+\infty}f\left( x\right)=+\infty$ e $\lim_{x\rightarrow-\infty}f\left( x\right) =-\infty $. Como $f\left( x\right)$ é contínua, pelo Teorema do Valor Intermediário, existe $x$ tal que $f\left(x\right) =0$.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{x-3}$.
Mostre, usando a definição, que a função dada por $f(x) = 3x$ é contínua para todo $x$ real.
Calcule os limites:
$\lim\limits_{x\to\pi} \frac{3x+1}{1-x}$
$\lim\limits_{x\to\pi} \frac{x^2+3x+5}{5x^2-2x-3}$
$\lim\limits_{x\to\pi} \left(\frac{x-3}{x-5}\right)^7$
Avalie o limite $\lim\limits_{x\rightarrow p}\dfrac{x^{8}-p^{8}}{x-p}$.
Calcule os limites:
$\lim\limits_{x\to6} \frac{x^2-4 x-12}{x^2-13 x+42}$
$\lim\limits_{x\to0} \frac{x^2+2 x}{x^2-2 x}$
$\lim\limits_{x\to2} \frac{x^2+6 x-16}{x^2-3 x+2}$
$-8$
$-1$
$10$
Prove que $\lim_{x\to a}f(x)=l$ se, e somente se, $\lim_{x\to a}[f(x)-l]=0$. Sugestão: Primeiro, compreenda por qual razão a afirmação anterior é óbvia; então dê uma prova formal.
Prove que $\lim_{x\to 0}f(x)=\lim_{x\to a}f(x-a)$.
Prove que $\lim_{x\to 0}f(x)=\lim_{x\to 0}f(x^3)$.
Dê um exemplo em que $\lim_{x\to 0}f(x^2)$ existe, mas $\lim_{x\to 0}f(x)$ não existe.
Enuncie e demonstre o Teorema do Confronto.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
\cos x, & & \text{ se } x<\pi \\
\sin x, & & \text{ se } x\geq \pi
\end{array}
\right.$
$ \lim\limits_{x\to \pi^-} f(x)$
$ \lim\limits_{x\to \pi^+} f(x)$
$ \lim\limits_{x\to \pi} f(x)$
$f(\pi)$
- $-1$
- 0
- Não existe.
- 0
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{e^{x^{2}}-1}{x}$.
$0$.
Suponha que você tenha as seguintes informações sobre duas funções $f$ e $g$:
$\lim\limits_{x\to 1} f(x) = 0$
$\lim\limits_{x\to 1} g(x) = 0$
$\lim\limits_{x\to 1} f(x)/g(x) = 2$
O que você pode dizer sobre o valor de $\left|\frac{f(x)}{g(x)}\right|$ quando $x \approx 1$?
Dê um exemplo de uma função definida em $\mathbb{R}$ que não seja contínua em $2$ mas que $\lim\limits_{x\rightarrow 2^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 2^{-}}f\left( x\right) .$
Determine todas as assíntotas horizontais da função $f(x) = \frac{x^2-1}{-x^2-1}$.
$y=-1$.
Seja $f:I \rightarrow \mathbb{R}$, contínua, onde I é um intervalo fechado qualquer. Prove que a imagem de $f$ é um intervalo fechado.
Calcule, por meio da definição, o limite $\lim_{x\to 2} x^3-1 = 7$.
Considere $\epsilon >0$ arbitrário. Queremos encontrar $\delta >0$ tal que quando $|x-2|<\delta$, $|f(x)-7|<\epsilon$.
Considere $|f(x)-7|<\epsilon$, lembrando que o objetivo é afirmar algo sobre $|x-2|$:
\begin{gather*}
|f(x) -7 | < \epsilon \\
|x^3-1 -7 |<\epsilon \\
| x^3-8 | < \epsilon \\
| x-2 |\cdot|x^2+2x+4| < \epsilon \\
| x-3 | < \epsilon/|x^2+2x+4| \\
\end{gather*}
Como $x$ está próximo de $2$, podemos considerar $1<x<3$. Portanto
\begin{gather*}
1^2+2\cdot1+4<x^2+2x+4<3^2+2\cdot3+4 \\
7 < x^2+2x+4 < 19 \\
\frac{1}{19} < \frac{1}{x^2+2x+4} < \frac{1}{7} \\
\frac{\epsilon}{19} < \frac{\epsilon}{x^2+2x+4} < \frac{\epsilon}{7} \\
\end{gather*}
Seja $\delta =\frac{\epsilon}{19}$. Então:
\begin{gather*}
|x-2|<\delta \\
|x-2| < \frac{\epsilon}{19}\\
|x-2| < \frac{\epsilon}{x^2+2x+4}\\
|x-2|\cdot|x^2+2x+4| < \frac{\epsilon}{x^2+2x+4}\cdot|x^2+2x+4|\\
\end{gather*}
Assumindo $x$ próximo de $2$, $x^2+2x+4$ é positivo e podemos eliminar o módulo do lado direito da equação.
\begin{gather*}
|x-2|\cdot|x^2+2x+4| < \frac{\epsilon}{x^2+2x+4}\cdot(x^2+2x+4)\\
|x^3-8| < \epsilon\\
|(x^3-1) - 7| < \epsilon,
\end{gather*}
que é o que desejávamos provar.
Calcule, pela definição, o limite $ \lim_{x\to 4} x^2+x-5 = 15$
Considere $\epsilon >0$ arbitrário. Queremos encontrar $\delta >0$ tal que quando $|x-4|<\delta$, $|f(x)-15|<\epsilon$.
Considere $|f(x)-15|<\epsilon$, lembrando que o objetivo é afirmar algo sobre $|x-4|$:
\begin{gather*}
|f(x) -15 | < \epsilon \\
|x^2+x-5 -15 |<\epsilon \\
| x^2+x-20 | < \epsilon \\
| x-4 |\cdot|x+5| < \epsilon \\
| x-4 | < \epsilon/|x+5| \\
\end{gather*}
Assumindo $x$ próximo de $4$, podemos assumir, por exemplo, que, $3<x<5$. Portanto
\begin{gather*}
3+5<x+5<5+5 \\
8 < x+5 < 10 \\
\frac{1}{10} < \frac{1}{x+5} < \frac{1}{8} \\
\frac{\epsilon}{10} < \frac{\epsilon}{x+5} < \frac{\epsilon}{8} \\
\end{gather*}
Seja $\delta =\frac{\epsilon}{10}$. Então:
\begin{gather*}
|x-4|<\delta \\
|x-4| < \frac{\epsilon}{10}\\
|x-4| < \frac{\epsilon}{x+5}\\
|x-4|\cdot|x+5| < \frac{\epsilon}{x+5}\cdot|x+5|\\
\end{gather*}
Assumindo $x$ próximo de 4, $x+5$ é positivo e podemos eliminar o módulo do lado direito da equação.
\begin{gather*}
|x-4|\cdot|x+5| < \frac{\epsilon}{x+5}\cdot(x+5)\\
|x^2+x-20| < \epsilon\\
|(x^2+x-5) -15| < \epsilon,
\end{gather*}
que é o que desejávamos provar.
Avalie o limite $\lim\limits_{x\rightarrow p}\dfrac{x^{4}-p^{4}}{x-p}$.
Considere a função $f(x) = \left\{\begin{array}{cl} x+2 & x\leq 2 \\ 3x-5 & x>2 \end{array}\right.$. Mostre que $\lim\limits_{x\to 2} f(x)$ não existe.
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow -\infty }\dfrac{5-x}{2x+3}$
$\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{x}+1}{x+3}$
- $-1/2$
- $0$
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( 5-3x+4x^{2}-x^{3}\right)$
$\lim\limits_{x\rightarrow \infty }\dfrac{5x^{3}-6x-3}{6x^{3}+2}$
- $-\infty$
- $5/6$
Justifique sua resposta.
$c=-1$ ou $c=2$.
Suponha que para todo $x$, $\left| f\left( x\right) \right| \leq x^{4}$. Calcule $\lim\limits_{x\rightarrow 0}\dfrac{f\left( x\right) }{x}.$
Encontre os seguintes limites em termos do número $\alpha = \displaystyle \lim_{n \to 0} \dfrac{\sin x}{x}$.
$\displaystyle \lim_{x \to \infty} \dfrac{\sin x}{x}$.
$\displaystyle \lim_{x \to \infty} x \sin \left(\dfrac{1}{x}\right)$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
2x^2+5x-1, & & \text{ se } x<0 \\
\sin x, & & \text{ se } x\geq 0
\end{array}
\right.$
$ \lim\limits_{x\to 0^-} f(x)$
$ \lim\limits_{x\to 0^+} f(x)$
$ \lim\limits_{x\to 0} f(x)$
$f(0)$
- $-1$
- 0
- Não existe.
- 0
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{2}+3}\right)$
$\lim\limits_{x\rightarrow -\infty }\left( x-\sqrt{x^{2}+3}\right)$
$\lim\limits_{x\rightarrow \infty } \left( \sqrt{x+1}-\sqrt{x+3}\right)$
- $0$
- $-\infty$
- $0$
Calcule, se existir, o limite $\lim\limits_{x\to 0} \frac{x+1}{x^2+3x}.$
Utilizando o gráfico a seguir, avalie os seguintes limites
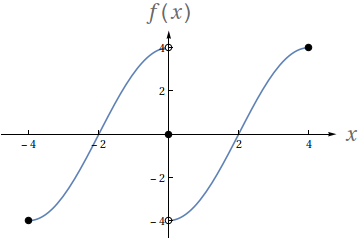
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $ \lim\limits_{x\to 0} f(x)$
- $f(0)$
- $4$
- $-4$
- Não existe.
- $0$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(x) = e^x$.
$(-\infty,\infty)$
Um $n$-ágono regular é um polígono de $n$ lados que possui todos os lados iguais e todos os ângulos de mesma medida.
- Encontre o perímetro de um $n$-ágono regular inscrito num círculo de raio $r$.
- O perímetro do $n$-ágono se aproxima de algum valor quando $n$ cresce?
- Deduza a fórmula do comprimento de uma circunferência de raio $r$.
Verifique se os seguintes limites existem. Explique.
$\lim\limits_{x\rightarrow\infty}2^{1/x}$.
$\lim\limits_{t\rightarrow\infty}\sin x$.
$\lim\limits_{x\rightarrow 2^-}\tan^{-1}\left(\frac{1}{2x-4}\right)$.
Determine se as afirmações abaixo são verdadeiras ou falsas. Justifique suas respostas ou forneça um contra exemplo.
Se $\lim\limits_{x\rightarrow a}f\left( x\right) =\infty $ e $\lim\limits_{x\rightarrow a}g\left( x\right) =0$, então $ \lim\limits_{x\rightarrow a}\dfrac{f\left( x\right) }{g\left( x\right) } =\infty $.
Sejam $p\left( x\right) $ e $q\left( x\right) $ polinômios de grau $m$ e $n$ respectivamente. Se $\lim\limits_{x\rightarrow \infty }\dfrac{p\left( x\right) }{q\left( x\right) }=0$, então $m\geq n$.
Se $\lim\limits_{x\rightarrow a}\left( f\left( x\right) g\left( x\right) \right) $ existe, então $\lim\limits_{x\rightarrow a}f\left( x\right) $ e $\lim\limits_{x\rightarrow a}g\left( x\right) $ existem e $\lim\limits_{x\rightarrow a}\left( f\left( x\right) g\left( x\right) \right) =\left( \lim\limits_{x\rightarrow a}f\left( x\right) \right) \left( \lim\limits_{x\rightarrow a}g\left( x\right) \right) .$
Se $f\left( x\right) $ e $g\left( x\right) $ são contínuas em $a$, então $\left( f+g\right) \left( x\right) $ também é contínua em $a$.
Mostre que a função $f\left( x\right) =\sqrt[n]{x}$ é contínua em seu domínio.
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-9 x+18}{x^2-x-6}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-0.632$ \\
$2.99$ & $-0.6032$ \\
$2.999$ & $-0.60032$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-0.6$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $-0.5686$ \\
$3.01$ & $-0.5968$ \\
$3.001$ & $-0.59968$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-0.6$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =-0.6$.
Mostre que a função $f\left( x\right) =\left\{ \begin{array}{cc} \dfrac{x^{3}-8}{x-2}, & \text{se }x\neq 2 \\ 12, & \text{se }x=2 \end{array}\right. $ é contínua em seu domínio.
Seja $f$ uma função contínua e decrescente em $\left[a,b\right]$. Mostre que $f$ tem uma inversa decrescente em $\left[f(b),f(a)\right]$.
Avalie o limite $\lim\limits_{x\rightarrow 0}\dfrac{\sin \left(7x\right) }{\sin \left( 23x\right) }$.
$7/23$.
Sabe-se que $f$ é contínua em $1$ e que $f(1)=2$. Mostre que existe $\delta>0$ tal que para todo $x \in D_f$ vale $1-\delta<x<1+\delta \rightarrow \dfrac{3}{2}<f(x)<\dfrac{5}{2}$.
- Se $f$ é contínua em $[0,1)$ e $[1,2)$, então $f$ é contínua em $[0,2)$.
- A soma de funções contínuas também é contínua
- Se $f$ é contínua em $[a,b]$, então $\lim_{x\to a^-}f(x) = f(a)$.
- Falso
- Verdadeiro
- Falso
Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{x}$.
$x=0$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\left( 0,27\right) ^{x}$.
$0$.
Um tanque contém 5000 litros de água pura. Água salgada contendo $30$g de sal por litro de água é bombeada para dentro do tanque a uma taxa de $25$ L$/$min. Considerando o tempo $t$ em minutos, mostre que a concentração de sal $C$ em função de $t$ (em gramas por litro) é dada por:$$C(t) = \dfrac{30 t}{200+t}.$$
O que acontece com a concentração para um tempo muito grande, isto é, para $t \to \infty$?
Calcule o seguinte limite, caso exista:
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\sin\left( 23x\right) }$
$\begin{array}{rcl} \lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\sin\left( 23x\right) } &=& \lim\limits_{x\rightarrow 0} \dfrac{ \dfrac{\sin \left( \pi x\right)}{x} }{ \dfrac{\sin\left( 23x\right)}{x} } \\ &=& \lim\limits_{x\rightarrow 0} \dfrac{ \dfrac{\pi \sin \left( \pi x\right)}{\pi x} }{ \dfrac{23\sin\left( 23x\right)}{23x} } \\ &=& \lim\limits_{x\rightarrow 0} \dfrac{\pi}{23} \dfrac{ \dfrac{ \sin \left( \pi x\right)}{\pi x} }{ \dfrac{\sin\left( 23x\right)}{23x} }. \end{array}$
Fazendo as mudanças de variáveis $y = \pi x$ e $t = 23x$, temos que
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\pi x} = \lim\limits_{y\rightarrow 0}\dfrac{\sin \left( y\right) }{y} = 1 $.
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left( 23 x\right) }{23 x} = \lim\limits_{y\rightarrow 0}\dfrac{\sin \left( t\right) }{t} = 1 $.
Onde nas últimas passagens usamos o limite fundamental do seno. Desse modo, sabendo que os limites existem, podemos substituí-los na expressão anterior:
$\begin{array}{rcl} \lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\sin\left( 23x\right) } &=& \lim\limits_{x\rightarrow 0} \dfrac{\pi}{23} \dfrac{ \dfrac{ \sin \left( \pi x\right)}{\pi x} }{ \dfrac{\sin\left( 23x\right)}{23x} } \\ &=& \dfrac{\pi}{23} \dfrac{1}{1} \\ &=& \dfrac{\pi}{23}. \end{array}$
Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{x-1}$.
$x=1$.
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-1}{x^2-x-6}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-15.1224$ \\
$2.99$ & $-159.12$ \\
$2.999$ & $-1599.12$
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $16.8824$ \\
$3.01$ & $160.88$ \\
$3.001$ & $1600.88$
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x)$ não existe.
Prove que a função $f(x)=\left\{\begin{array}{ll}
x, & \text{se x é racional}\\
-x, & \text{se x é irracional}
\end{array}\right.$ é contínua em $0$.
Utilizando o gráfico a seguir, avalie os seguintes limites
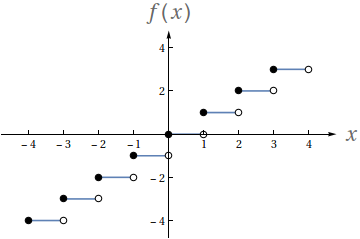
Seja $-3\leq a\leq 3$ um número inteiro
- $ \lim\limits_{x\to a^-} f(x)$
- $ \lim\limits_{x\to a^+} f(x)$
- $ \lim\limits_{x\to a} f(x)$
- $f(a)$
- $a-1$
- $a$
- Não existe.
- $a$
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
1-\cos^2 x, & & \text{ se } x<a \\
\sin^2 x, & & \text{ se } x\geq a
\end{array},
\right.$
sendo que $a$ é um número real.
$ \lim\limits_{x\to a^-} f(x)$
$ \lim\limits_{x\to a^+} f(x)$
$ \lim\limits_{x\to a} f(x)$
$f(a)$
- $1-\cos^2 a = \sin^2 a$
- $\sin^2 a$
- $\sin^2 a$
- $\sin ^2 a$
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{3x^{3}+2}\right) $.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow0}\frac{cotg (2x)}{cossec (x)}$.
$1/2$.
Calcule o limite $\lim_{x\rightarrow 0} \dfrac{3x+\tan x}{\sin x + \tan^2 x}.$
Temos que:
$\dfrac{3x+\tan x}{\sin x + \tan^2 x}= \dfrac{x}{\sin x}\cdot\dfrac{3+\dfrac{\tan x}{x}}{1+ \dfrac{\sin x}{\cos^2 x}}.$
Lembramos o limite fundamental $\lim_{x\rightarrow 0}\frac{\sin x}{x}=1$ e, além disso, observamos que
\begin{equation*}
\begin{split}
&\lim_{x\rightarrow 0}\dfrac{\sin x}{\cos^2 x}=0 \\
&\lim_{x\rightarrow 0}\dfrac{\tan x}{x}=\lim_{x\rightarrow 0}\dfrac{\sin x}{x}\cdot\dfrac{1}{\cos x}=1.
\end{split}
\end{equation*}
Então:
$\lim_{x\rightarrow 0}\dfrac{3x+\tan x}{\sin x + \tan^2 x}= \lim_{x\rightarrow 0}\dfrac{x}{\sin x}\cdot\dfrac{3+\dfrac{\tan x}{x}}{1+ \dfrac{\sin x}{\cos^2 x}} = 1\cdot\dfrac{3+1}{1+0}=4.$
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow +\infty }\dfrac{-x^{3}+2}{4x^{2}+89}$.
- Se $f$ é contínua em $c$, então $\lim_{x\to c^+}f(x) = f(c)$.
- Se $f$ é contínua em $c$, então $\lim_{x\to c}f(x)$ existe.
- Se $f$ é definida em um intervalo aberto contendo $c$, e $ \lim_{x\to c}f(x)$ existe, então $f$ é contínua em $c$.
- Verdadeiro
- Verdadeiro
- Falso
Avalie os seguintes limites de acordo com o gráfico da função:
$f(x) = x^2\sin (\pi x)$
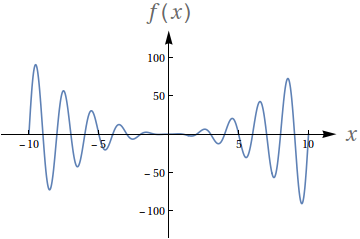
$\lim\limits_{x\to -\infty} f(x)$
$\lim\limits_{x\to \infty} f(x)$
Em matemática, a função piso, denotada por $\lfloor x\rfloor$, converte um número real ${\displaystyle x}$ no maior número inteiro menor ou igual a ${\displaystyle x}$ Essa função é importante em computação para truncamento ou arredondamento de números. Considere a função $f(x)=\lfloor 1/x\rfloor$, $x \neq 0$. Esboce o gráfico dessa função para $\dfrac{1}{4} \leq x \leq 2$ e também para $-2 \leq x \leq -\dfrac{1}{4}$. Como se comporta $f(x)$ quando $x$ tende a zero pelo lado direito? E pelo lado esquerdo? O limite $\lim\limits_{x \to 0}f(x)$ existe?
Avalie o limite $\lim\limits_{x\rightarrow p}\dfrac{x^{n}-p^{n}}{x-p}$, onde $n$ é qualquer número natural.
Calcule os seguintes limites laterais (justifique cada passo da resolução):
$\lim\limits_{x\rightarrow1^{+}}\dfrac{\sqrt{x^{2}-1}}{x-1}.$
$\lim\limits_{x\rightarrow1^{-}}\dfrac{\sqrt{x^{2}-1}}{x-1}.$
Sendo $f(x) = \left\{\begin{array}{cl} \cos x & x\leq 0 \\ x^2+3x+1 & x>0 \end{array}\right.$, calcule $\lim\limits_{x\to 0} f(x)$.
1
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow0}\frac{sen(cosx)}{sec(x)}$.
$\sin(1)$.
Mostre que existem funções $f(x)$, $g(x)$ com $\lim_{x\rightarrow p} f(x) = \lim_{x\rightarrow p} g(x) =0,$ tais que $\lim_{x\rightarrow p} (f(x)/g(x)) =\lambda$, onde $\lambda$ assume qualquer valor em $\mathbb{R} \cup \{+\infty, -\infty\}$. Escolha o ponto $p$ como achar mais conveniente.
Mostre que a função \begin{align*} f\left( x\right) =\left\{ \begin{array}{cc} \dfrac{x^{3}-4x}{x^{2}-4}, & \text{se } x\neq \pm 2 \\ 2, & \text{se } x=2 \\ -3, & \text{se } x=-2 \end{array} \right. \end{align*} é contínua em todos os pontos, com exceção do ponto $x=-2$.
Utilizando o gráfico a seguir, avalie os seguintes limites
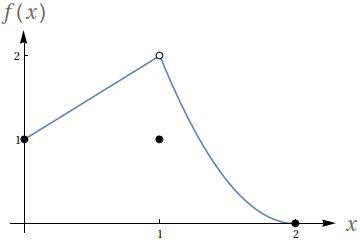
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $2$
- $2$
- $2$
- $1$
- Como $f$ não é definida para $x<0$, esse limite é indefinido.
- $1$
Calcule o seguinte limite
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{2x}\right)^{x}$.
$e^{1/2}$.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\log _{3}x$.
$\infty$.
Prove que a única função contínua $f:\mathbb{R} \to \mathbb{R}$ que satisfaz $f(f(f(x)))=x$ é a função identidade $f(x)=x$. (Sugestão: Prove que se uma função é injetiva e contínua então ela é monótona).
Em matemática e estatística, a função de Heaviside (ou função degrau) é uma função singular e descontínua, com valor zero quando o seu argumento é negativo e valor unitário quando o argumento é positivo. Seja $H$ a função de Heaviside. Prove, usando a definição de limite, que $\lim\limits_{x \to 0}H(x)$ não existe.
Admitindo-se que $\lim\limits_{x\rightarrow a}f(x)$ existe, prove que
$\lim\limits_{x\rightarrow a}f(x)=\lim\limits_{h\rightarrow0}f(a+h).$
Mostre que a equação
\begin{equation*}
x^{26}+x^{2}-320=0
\end{equation*}
possui ao menos uma raiz real positiva e também uma raiz real negativa.
Sejam $f,g:\mathbb{R} \to \mathbb{R}$ funções contínuas tais que $f(a)<g(a)$ e $f(b)>g(b)$. Mostre que existe $c \in (a,b)$ tal que $f(c)=g(c)$.
Determine os valores de $\lambda$ que tornam contínua a função
\begin{equation*} f\left( x\right) =\left\{ \begin{array} [c]{c} x^{2}+cx\text{ se }x\leq1\\ \left( cx\right) ^{2}-1=c^{2}x^{2}-1\text{ se }x>1 \end{array} \right. \text{.} \end{equation*}
Mostre que
- o limite de $f(x)=\dfrac{x-2}{|\,x-2|}$, quando $x\to 2$, não existe.
- o limite de $f(x)=\left\{\begin{array}{ll} x^2+2, & x\geq -1 \\ 2x+1, & x<-1 \\ \end{array}\right.$, quando $x\to -1$, não existe.
Considere a função $ f(x)=\left\{\begin{array}{ll} 1-2x &\text{ se} x\ne -1\\0&\text{ se } x=-1\end{array}\right.$.
Trace o gráfico de $f$.
Usando limites laterais, determine se o limite $\lim\limits_{x\rightarrow -1}f(x)$ existe ou não.
Avalie o limite $\lim\limits_{x\rightarrow p}\ln\left(\dfrac{x^{n}-p^{n}}{x-p}\right)$, onde $n$ é qualquer número natural.
Dê um exemplo para mostrar que o produto de uma função contínua por uma função descontínua, pode ser uma função contínua.
É possível que uma função $f:{\mathbb{R} \to \mathbb{R}}$
seja tal que $\lim\limits_{x\rightarrow 2^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 2^{-}}f\left(x\right)$ e ao mesmo tempo não seja contínua em $2$? Justifique e/ou dê um exemplo.
Calcule os limites:
$\lim\limits_{x\to2} \frac{x^2-10 x+16}{x^2-x-2}$
$\lim\limits_{x\to-2} \frac{x^2-5 x-14}{x^2+10 x+16}$
$\lim\limits_{x\to-1} \frac{x^2+9 x+8}{x^2-6 x-7}$
- $-2$
- $-3/2$
- $-7/8$
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{x-3}$
Seja $u=x-3$. Temos que $u$ tende a $0$ por valores positivos se $x$ tende a $3$ por valores maiores do que $3$. Logo, \begin{equation*} \lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{x-3}=\lim\limits_{u\rightarrow 0^{+}}\dfrac{5}{u}\text{.} \end{equation*} Mas dado $M>0$, temos que se $0<u<\dfrac{5}{M},$ então $M<\dfrac{5}{u}$ e temos que, por definição, $\lim\limits_{u\rightarrow 0^{+}}\dfrac{5}{u}=\infty $.
Prove que a função $f(x)=\left\{\begin{array}{ll}
x, & \text{se x é racional} \\
-x, & \text{se x é irracional}
\end{array}\right.$ é contínua em $0$.
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função contínua que satisfaz as seguintes propriedades:
- $f(n)=0$, para todo inteiro $n$;
- Se $f(a)=0$ e $f(b)=0$ então $f \left(\frac{a+b}{2} \right)$.
Mostre que $f(x)=0$, para todo real $x$.
Calcule os limites:
$\lim\limits_{x\to\pi/4} \cos x\sin x$
$\lim\limits_{x\to0} \ln x$
$\lim\limits_{x\to3} 4^{x^3-8x}$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
- $\lim\limits_{x\rightarrow 0}x\sin \left( \dfrac{1}{x}\right)$
- $\lim\limits_{x\rightarrow p}\dfrac{\sin \left(x^{2}-p^{2}\right) }{x-p}$
Utilizando o gráfico a seguir, avalie os seguintes limites
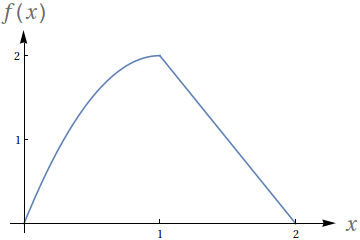
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $2$
- $2$
- $2$
- $2$
Seja $f:[a,b] \to [a,b]$ uma função contínua. Prove que $f$ possui um ponto fixo, ou seja, algum valor de $x$ tal que $f(x)=x$.
Use o Teorema do Confronto para calcular $\lim\limits_{x\rightarrow0^{+}}\sqrt{x} \,e^{\sin\left( \pi/x\right) }\text{.}$
Lembre-se de justificar porque o Teorema do Confronto pode ser útil.
Explique, usando suas palavras, o que significa escrever $\lim\limits_{x\to c} x = c$.
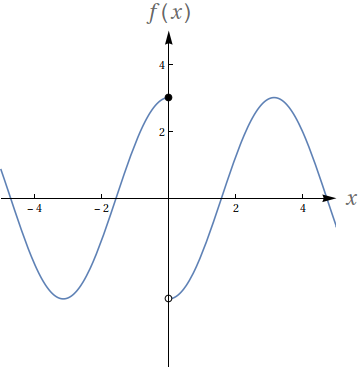
$f$ não é contínua em $x=0$.
Utilizando o gráfico, avalie os seguintes limites para a função
$ f(x) = \frac{1}{(x-3)(x-5)^2}$.
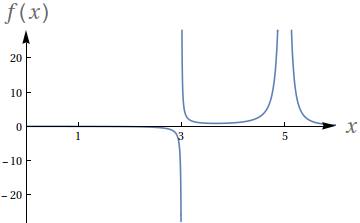
$ \lim\limits_{x\to 3^-} f(x)$
$ \lim\limits_{x\to 3^+} f(x)$
$ \lim\limits_{x\to 3} f(x)$
$ \lim\limits_{x\to 5^-} f(x)$
$ \lim\limits_{x\to 5^+} f(x)$
$ \lim\limits_{x\to 5} f(x)$
- $-\infty$
- $\infty$
- O limite não existe
- $\infty$
- $\infty$
- $\infty$
Mostre $\lim\limits_{x\to 0} \frac{x+1}{x^2+3x}$ não existe.
Prove que se $f$ e $g$ são ambas funções contínuas, então $f+g$ é contínua.
Suponha $g(x) \neq 0$, para todo $x \in Dom(g)$, $L \neq 0$ e $\lim\limits_{x \to p}g(x)=L$. Prove que $\lim\limits_{x \to p}\dfrac{1}{g(x)}=\dfrac{1}{L}$.
Veja Guidorizzi, volume $1$, página $87$.
Mostre que $f(x) = \cos x - \frac{x}{10}$ tem pelo menos dois zeros em $[0, 2\pi]$.
Classifique as afirmações a seguir como verdadeiras ou falsas:
Se $ \lim\limits_{x\to \infty} f(x) = 5$, então estamos implicitamente afirmando que o limite em questão existe.
$\infty/0$ não é uma forma indeterminada.
Verdadeira
Verdadeira
Sabe-se que $f$ é contínua em $2$ e que $f(2)=8$. Mostre que existe $\delta>0$ tal que para todo $x \in D_f$ vale $2-\delta<x<2+\delta \rightarrow f(x)>7$.
Considere $\epsilon =1$. Como $f$ é contínua em $2$, sabemos que existe $\delta >0$ tal que, para $|x-2|<\delta $ temos que $|f(x)-f(2)|<\epsilon =1$. Mas $|x-2|<\delta $ se, e somente se, $2-\delta<x<2+\delta$ e $|f(x)-f(2)|=|f(x)-8|<1$ se, e somente se, $7< f(x)<9$.
Calcule, através da definição, o limite $ \lim_{x\to 2} 5 = 5$
Seja $\epsilon >0$ dado. Queremos encontrar $\delta >0$ tal que, quando $|x-2|<\delta$, $|f(x)-5|<\epsilon$. Entretanto, como $f(x)=5$ é uma função constante, a segunda inequação é simplesmente $|5-5|<\epsilon$, o que é sempre verdade. Assim, pode-se escolher um $\delta$ qualquer; arbitrariamente, escolhe-se $\delta =\epsilon$.
Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{(x-1)^2}$.
As assíntotas verticais são os pontos $x$ tais que o limite é infinito.
Para $f(x)=\frac{x^2+1}{(x-1)^2}$ temos que:
$\lim \limits_{x \to 1} \frac{x^2+1}{(x-1)^2} = \infty$,
Logo $x=1$ é uma assíntota vertical de $f$. Como não há mais pontos no domínio de $f$ que podem levar a um limite infinito, esta é a única assíntota.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\ln \dfrac{x}{x+1}$.
$0$
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }3^{x}$.
$\infty$.
Explique, usando suas palavras, o que significa escrever $\lim\limits_{x\to c} b = b$.
Calcule, quando existirem, os seguintes limites:
$\lim\limits_{x\rightarrow 2}\dfrac{x^{2}+x-6}{ \left( x-2\right) ^{3}}$
$\lim\limits_{x\rightarrow 2}\dfrac{\sqrt{6-x}-2}{\sqrt{ 3-x}-1}$
$\lim\limits_{x\rightarrow \infty }\sqrt{3x+4}-\sqrt{3x}.$
Dê um exemplo de uma função tal que $\lim\limits_{x \rightarrow p}\left| f\left( x\right) \right| $ exista mas $ \lim\limits_{x\rightarrow p}f\left( x\right) $ não exista.
Calcule os limites:
$\lim\limits_{x\to3} x^2-3x+7$
$\lim\limits_{x\to3} x^3-3x-7$
- Como a função está definida em $x=3$, o limite pode ser calculado diretamente por substituição:
$\lim\limits_{x\rightarrow 3} x^2-3x+7 = 3^2 - 3.3 + 7 = 7$. - Como a função está definida em $x=3$, o limite pode ser calculado diretamente por substituição:
$\lim\limits_{x\rightarrow 3} x^3-3x+7 = 3^3 - 3.3 - 7 = 11$.
Calcule o limite, caso exista:
$\displaystyle \lim_{x\rightarrow \infty}\left( x-\sqrt{x^2 + 4x} \right) $
Seja $f$ uma função definida em $\mathbb{R}$ e suponha que exista $M>0$ tal que $|f(x)-f(p)|\leq M|x-p|$ para todo $x$. Prove que $f$ é contínua em $p$.
Utilizando o gráfico, avalie os seguintes limites para a função

$f(x) = \frac{1}{(x+1)^2}$
$ \lim\limits_{x\to -1^-} f(x)$
$ \lim\limits_{x\to -1^+} f(x)$
- $\infty$
- $\infty$
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\left( 2^{x}-3^{x}\right) $.
$-\infty$.
Calcule, pela definição, o limite $ \lim_{x\to 0} \sin x= 0$ (Dica: use o fato que $|\sin x| \leq |x|$, sendo uma igualdade apenas para $x=0$.)
Considere $\epsilon >0$ arbitrário. Queremos encontrar $\delta >0$ tal que quando $|x-0|<\delta$, $|f(x)-0|<\epsilon$. Em termos simples, queremos mostrar que quando $|x|<\delta$, $|\sin x| < \epsilon$.
Considere $\delta = \epsilon$. Podemos presumir que $|x|<\delta$. Usando a dica do enunciado, temos que $|\sin x | < |x| < \delta = \epsilon$. Portanto, se $|x|<\delta$, sabemos imediatamente que $|\sin x| < \epsilon$.
Responda os itens:
- Dada $f:{\mathbb{R} \to \mathbb{R}}$, defina (em termos de $\varepsilon $ e $\delta $) $\lim\limits_{x\rightarrow p}f\left( x\right) =L.$ Ilustre elaborando um gráfico para uma função genérica.
- Qual é a condição sobre esse limite para que a função seja contínua?
Considere a função \begin{align*} f\left( x\right) =\left\{ \begin{array}{cc} a-x, & \text{se } x<-1 \\ x, & \text{se } -1\leq x<1 \\ \dfrac{2}{x}+b, & \text{se } 1\leq x \end{array} \right. . \end{align*}
- Encontre os limites laterais a direita e a esquerda de $f$ nos pontos $1$ e $-1.$
- Determine os valores de $a$ e $b$ que tornam $f$ contínua em toda a reta.
- Calcule $\lim\limits_{x\rightarrow \infty }f\left(x\right) $ e $\lim\limits_{x\rightarrow -\;\infty }f\left( x\right) $.
Embora limites como $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{n}$ e $\displaystyle \lim_{n \to \infty} a^n$ possam ser avaliados utilizando conhecimentos sobre as funções logaritmo e exponencial, estes não são necessários. Neste exercício vamos calcular esses tipos de limite por meio de argumentos ``elementares''. As ferramentas básicas são desigualdades provenientes do teorema binomial, principalmente:
$$(1+h)^n \geq 1+nh, \text{ para } h > 0,$$
e, para o item 3 a seguir:
$$(1+h)^n \geq 1+nh+\dfrac{n(n-1)}{2}h^2 \geq \dfrac{n(n-1)}{2}h^2, \text{ para } h>0.$$
Mostre que $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{a}= 1$ se $a>1$, fazendo $\sqrt[\leftroot{-2}\uproot{2}n]{a}=1+h$ e estimando $h$.
Mostre que $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{a}=1 $ se $1<a<1$.
Mostre que $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{n}= 1$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(x) = \sin(e^x+x^2)$.
$(-\infty,\infty)$
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{3}-6x-3}{6x^{2}+28x+2}$.
$\infty$
Determine um intervalo de comprimento $\pi/2$ cuja equação $$2x^3+3x^2-\sqrt{|\cos(x)|}=0$$ admita uma solução real.
- $\lim\limits_{x\rightarrow -1}\sqrt[3]{\dfrac{x^{3}+1}{x+1}}$
- $\lim\limits_{x\rightarrow 1}\dfrac{\sqrt{x^{2}+3}-2}{x^{2}-1}$
- $\lim\limits_{x\rightarrow 1}\dfrac{\sqrt[3]{3x+5}-2}{x^{2}-1}$
- $\lim\limits_{h\rightarrow 0}\left( x^{2}+5xh^{2}\right) $
- $\lim\limits_{x\rightarrow 2}\dfrac{1/x-1/2}{x-2}$
Se você fosse um professor e seu(sua) aluno(a) te perguntasse ``Por que $\displaystyle \lim_{x \to 0}\dfrac{\sin x}{x}=1$?''
Como você responderia com palavras?
Que bibliografia você recomendaria?
Qual a demonstração formal?
Calcule o limite:
$\lim\limits_{x\rightarrow 1}\dfrac{\sqrt{x^{2}+3}-2}{x^{2}-1}$.
Determine os valores de $\lambda$ que tornam contínua a função $g: \left( 0,\pi\right)\mathbb{\rightarrow R},$ dada por
\[
g\left( x\right) =\left\{
\begin{array}{c}
\tan \left( x\right) \mbox{ se }x\neq \dfrac{\pi }{2} \\
\lambda \mbox{ se }x = \dfrac{\pi }{2}
\end{array}
\right.
\]
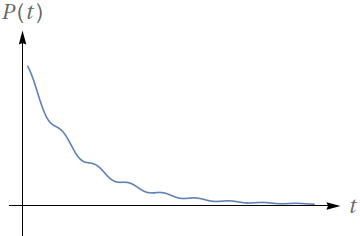
O gráfico a seguir representa o número de indivíduos de uma população ao longo do tempo.
Pode-se dizer que há uma assíntota horizontal para essa população? Justifique.
O que essa assíntota representa em termos biológicos? (Isto é, qual a interpretação da assíntota em função da população?)
Construa uma função com uma assíntota vertical em $x=5$ e uma assíntota horizontal em $y=5$.
Seja $f: \mathbb{R} \to \mathbb{R}$ uma função contínua no intervalo $\left[2,6 \right]$ com $f(2)=3$ e $f(6)=5$. Use o Teorema de Weierstrass e o Teorema do Valor Intermediário pra mostrar que a imagem de $f$ é um intervalo fechado.
Utilizando o gráfico a seguir, avalie os seguintes limites
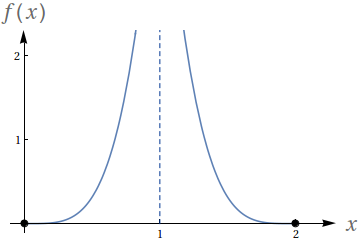
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- Não existe.
- Não existe.
- Não existe.
- Indefinido.
- $0$
- $0$
Calcule o limite $\lim_{x\rightarrow 1} \frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2}$ ou prove que não existe.
Racionalizando e aplicando diferença de quadrados temos:
\begin{equation*}
\frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2} = \frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2}\cdot \frac{\sqrt{x+1}+\sqrt{2}}{\sqrt{x+1}+\sqrt{2}}\cdot \frac{\sqrt{x^2+3}+2}{\sqrt{x^2+3}+2} =
\frac{x-1}{x^2-1}\cdot\frac{\sqrt{x^2+3}+2}{\sqrt{x+1}+\sqrt{2}}.
\end{equation*}
Logo,
$\lim_{x\rightarrow 1} \frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2}=\lim_{x\rightarrow 1}\frac{x-1}{x^2-1}\cdot\frac{\sqrt{x^2+3}+2}{\sqrt{x+1}+\sqrt{2}}=\lim_{x\rightarrow 1}\frac{1}{x+1}\cdot\frac{\sqrt{x^2+3}+2}{\sqrt{x+1}+\sqrt{2}}= \frac{1}{\sqrt{2}}.$
O que há de errado com a seguinte ``definição'' de limite?
"O limite de $f(x)$, quando $x$ tende a $a$, é $K$'' significa que para qualquer $\delta>0$, existe $\epsilon>0$ tal que $|f(x)-K|< \epsilon$, tem-se $|x-a|<\delta$."
$\epsilon$ deve ser apresentado antes, e a restrição $|x-a|<\delta$ implica em $|f(x)-K|< \epsilon$, e não o contrário.
Uma fonte de imprecisão nos cálculos feitos por computadores é a {\it subtração catastrófica}. Tal erro ocorre quando dois números aproximadamente iguais são subtraídos, e o resultado é usado como parte de outro cálculo.
Um exemplo: $(0,123456789012345-0,123456789012344)\times 10^{15}=1$.
Mas, na calculadora, obteríamos zero como resposta a esse cálculo pois ela armazena apenas 14 dígitos e os 14 primeiros dígitos são idênticos. Por vezes, pode-se evitar a subtração catastrófica fazendo um rearranjo algébrico das fórmulas. De todo modo, o melhor é estar atento à sua ocorrência, portanto, tome cuidado para resolver este exercício.
Seja $f(x)=\dfrac{x-\sin x}{x^3}$. Faça uma conjectura sobre o limite de $f$ quando $x \to 0^+$ calculando $f$ nos pontos $x=0,1$, $0,01$, $0,001$, $0,0001$.
Calcule $f$ nos pontos $x=0,00001$, $0,000001$, $0,0000001$, $0,00000001$, $0,000000001$, $0,0000000001$, e faça outra conjectura.
Que falha isso revela sobre o uso da evidência numérica para fazer conjecturas sobre limites?
Se você dispuser de um sistema de computação algébrica, um programa que pode efetuar cálculos numéricos ou simbólicos, use-o para mostrar que o valor exato desse limite é $\dfrac{1}{6}$. (Aqui, eu não posso pedir para calcular o limite à mão, de fato?)
O limite $\lim_{x\rightarrow +\infty} x^3(1+\sin x)$ existe? Explique.
Foi pedido a um torneiro mecânico que fabricasse um disco de metal circular com área de $1000cm^2$.
- Qual o raio do disco produzido?
- Se for permitido ao torneiro uma tolerância do erro de $\pm 5 cm^2$ na área do disco, quão próximo do raio ideal da parte (a) o torneiro precisa controlar o raio?
- Em termos da definição $\epsilon, \delta$ de $\lim\limits_{x \to a} f(x)=L$, o que é $x$? O que é $f(x)$? O que é $a$? O que é $L$? Qual valor de $\epsilon$ é dado? Qual o valor correspondente de $\delta$?
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\left( 1+2x\right) ^{\dfrac{1}{x}}$.
$e^2$.
O gráfico da função $f(x)=\frac{x^3+2x^2+1}{5-x^2}$ possui alguma assíntota horizontal?
Não possui.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ h(t) = \cos t$.
$(-\infty,\infty)$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
- $\lim\limits_{x\rightarrow 0}\left( 1+2x\right)^{\dfrac{1}{x}}$
- $\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}-1}{x}$
- $\lim\limits_{x\rightarrow 0}\dfrac{e^{x^{2}}-1}{x}$
Calcule o limite:
$\lim\limits_{x\rightarrow p}\dfrac{tg(x-p)}{x^{2}-p^{2}}$.
Use o teorema do valor intermediário para mostrar que $f(x)=4x^3-6x^2+3x-4$ possui um zero no intervalo $[1,2]$.
Como $f(1) = -3 < 0$ e $f(2) = 10 > 0$, temos que a função $f$ muda de sinal no intervalo $[1,2]$, e portanto, pelo teorema do valor intermediário, $f$ possui um zero nesse intervalo.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$f(x) = x^2-3x+9$.
$(-\infty,\infty)$
Mostre que $\lim\limits_{x\rightarrow p}f\left( x\right) =L$ se e somente se $\lim\limits_{x\rightarrow p}\left( f\left( x\right) -L\right) =0$.
Suponha que $f\left( x\right) \leq g\left( x\right) $ para todo $x$. Demonstre que $\lim\limits_{x\rightarrow p}f\left( x\right) \leq \lim\limits_{x\rightarrow p}g\left( x\right) $ sempre que os limites existirem.
Suponha agora que $f\left( x\right) <g\left( x\right) $ para todo $x$. Podemos afirmar que $\lim\limits_{x\rightarrow p}f\left( x\right) <\lim\limits_{x\rightarrow p}g\left( x\right) $ sempre que os limites existirem?
Seja $g$ uma função contínua em $[-3,7]$, sendo que $g(0) = 0$ e $g(2) = 25$. Existe um valor $-3<c<7$ tal que $g(c) = 15$? Por quê?
Sim, pelo Teorema do Valor Intermediário. Na realidade, é possível ser ainda mais preciso e afirmar não só que um valor $c$ existe em $(3,7)$, mas ainda que existe um valor $x$ contido em $(0,2)$.
$2$
Dê um exemplo de uma função definida em $\mathbb{R}$ que não seja contínua em $0$ mas que $\lim\limits_{x\rightarrow0^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 0^{-}}f\left( x\right) .$
Suponha que $\left| f\left( x\right) -f\left( 1\right) \right| \leq \left( x-1\right) ^{2}$. Demonstre que $f\left( x\right) $ é contínua em $1$.
Use o Teorema do Confronto para demonstrar que $\lim\limits_{x \to 0} \cos{x} = 1$.
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{3}+2}\right)$
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{2}+2}\right)$
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x+2}\right)$
- $-\infty$
- $0$
- $\infty$
Resolva os itens:
- Prove que existe $r>0$ tal que $\cos{x}-1<\dfrac{\sin{x}}{x}-1<0$ para $0<|x|<r$.
- Calcule $\lim\limits_{x \to 0}\dfrac{x-\sin{x}}{x^2}$.
Seja $f$ uma função contínua em $[-1,1]$ sendo que $f(-1) = -10$ e $f(1) = 10$. Existe um valor $-1<c<1$ tal que $f(c) = 11$? Por quê?
Não se pode dizer. O Teorema do Valor Intermediário apenas se aplica, neste caso, para valores entre $-10$ e $10$; como $11$ não pertence a este intervalo, o teorema não nos permite afirmar nada sobre a possibilidade da existência de $c$.
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{3-x};$
$\lim\limits_{x\rightarrow 3^{-}}\dfrac{5}{3-x};$
$\lim\limits_{x\rightarrow 0^{+}}\dfrac{5}{x^{2}-x};$
$\lim\limits_{x\rightarrow 0^{-}}\dfrac{5}{x^{2}-x};$
$\lim\limits_{x\rightarrow 0^{+}}\dfrac{\sin x}{x^{3}-x^{2}};$
$\lim\limits_{x\rightarrow -1^{+}}\dfrac{3x^{2}-4}{1-x^{2}}$
Determine os intervalos para os quais a função
\begin{equation*} f\left( x\right) =\left\{ \begin{array} [c]{c} x^{2}+1\text{ se }x\leq0\\ \cos x\text{ se }0<x<1\\ x^{2}+1\text{ se }1\leq x \end{array} \right. \end{equation*} é contínua. Justifique sua resposta.
As funções $x^{2}+1$ e $\cos x$ são ambas contínuas e por isto $f\left( x\right) $ é contínua para todo $x\neq0,1$. É necessário verificar a continuidade nos pontos $x=0$ e $x=1$.
Para $x=0$ temos que $\lim_{x\rightarrow0^{-}}f\left(x\right) =\lim_{x\rightarrow0^{-}}\left( x^{2}+1\right) =1$ e $\lim_{x\rightarrow0^{+}}f\left( x\right) =\lim_{x\rightarrow0^{+}}\cos x=1$, logo $f\left( x\right) $ é contínua em $x=0$, pois ambos oslimites laterais existem, são iguais e coincidem com o valor da função no ponto.
Para $x=1$ temos que $\lim_{x\rightarrow1^{-}}f\left( x\right) =\lim_{x\rightarrow0^{-}}\cos x=\cos\left( 1\right) $ e $\lim_{x\rightarrow0^{+}}f\left( x\right) =\lim_{x\rightarrow0^{+}}\left(x^{2}+1\right) =2$, e como $\cos\left( 1\right) \neq2$ temos que $f\left(x\right) $ não é contínua em $x=1$, pois apesar dos limites laterais existirem estes são distintos.
Calcule o limite a seguir:
$\lim\limits_{x \to -\infty } e^x \sin(x)$
Observe que $-1 \leq \sin(x) \leq 1$ e, portanto, como $e^x \geq 0$, $-e^x \leq e^x \sin(x) \leq e^x$.
Como $\lim\limits_{x \to -\infty} e^x = 0$ e $\lim\limits_{x \to -\infty} -e^x = 0$, então, pelo Teorema do Confronto temos $\lim\limits_{x \to -\infty} e^x \sin(x) = 0$
Considere a função $f(x) = 2^x+10$. Calcule os seguintes limites e, depois, discuta se a função $f(x)$ tem assíntotas horizontais.
$\lim\limits_{x\to -\infty} f(x)$.
$\lim\limits_{x\to \infty} f(x)$.
1. $10$.
2. $\infty$
Possui assíntota horizontal de equação $y=10$,
- $\lim\limits_{x\rightarrow p} \frac{\sin \left(x^{2}-p^{2}\right) }{x-p}$
- $\lim\limits_{y\rightarrow 3} \frac{\sin \left(y^{2}-9\right) }{y-3}$
- $\lim\limits_{x\rightarrow 4} \frac{\cos \left(x^{2}-16\right) }{x-4}$
- $\lim\limits_{x\rightarrow 0^{+}}\log _{\frac{1}{3}}x$
- $\lim\limits_{x\rightarrow 1}\ln \dfrac{x^{2}-1}{x-1}$
- $\lim\limits_{x\rightarrow p}\dfrac{x^{n}-p^{n}}{x-p}$
Seja $h$ uma função definida em $[-1,1]$, sendo que $h(-1) = -10$ e $h(1) = 10$. Existe um valor $-1<c<1$ tal que $h(c) = 0$? Por quê?
Não é possível dizer: O Teorema do Valor Intermediário só se aplica para funções contínuas, e nada foi afirmado sobre a continuidade de $h$.
Calcule o limite $\lim\limits_{x\rightarrow -3}\frac{1-x}{\sqrt{x^2+2}}$.
Como a função está definida em $x=-3$, o limite pode ser calculado diretamente por substituição:
$\lim\limits_{x\rightarrow -3}\dfrac{1-x}{\sqrt{x^2+2}} = \dfrac{1-(-3)}{\sqrt{(-3)^2+2}} = \dfrac{4}{\sqrt{11}}$.
A função $f(x) = \left\{ \begin{array}{ccc} x^2-1 & & x < 3 \\x+5 & & x\geq 3 \end{array}\right.$ é contínua em todo o seu domínio? Justifique.
Sim, é. O único ponto em que não poderia (inicialmente) ser contínua é em $x=3$. Todavia, temos $\lim\limits_{x\to 3^-} f(x)=\lim\limits_{x\to 3^+} f(x)=f(3)=8$.
Mostre que toda equação polinomial de grau ímpar, tem pelo menos uma raiz real.
Calcule o limite:
$\lim\limits_{x\rightarrow -\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-\infty$.
Defina ``$\displaystyle \lim_{x \to -\infty} f(x) = l$''.
Ache $\displaystyle \lim_{x \to -\infty} \dfrac{a_n x^n + \ldots + a_0}{b_m x^m + \ldots + b_0}$.
Mostre que $\displaystyle \lim_{x \to \infty} f(x) = \displaystyle \lim_{x \to -\infty} -f(x)$.
Mostre que $\displaystyle \lim_{x \to 0^-} \dfrac{1}{f(x)} = \displaystyle \lim_{x \to -\infty} f(x)$.
Avalie os seguintes limites de acordo com o gráfico da função:
$f(x) = \frac{1}{e^x+1}$
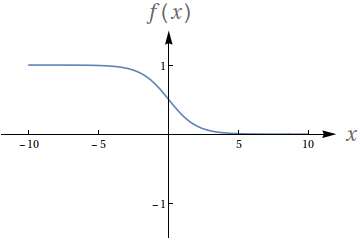
$\lim\limits_{x\to -\infty} f(x)$
$\lim\limits_{x\to \infty} f(x)$
$\lim\limits_{x\to 0^-} f(x)$
$\lim\limits_{x\to 0^+} f(x)$
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
\frac{x^2-64}{x^2-11 x+24}, & & \text{se } x\neq 8\\
5, & & \text{se } x=8
\end{array}\right.$
- $x=0$
- $x=8$
- Sim.
- Não. $\lim_{x\to 8} f(x) = 16/5 \neq f(8) = 5$.
É verdade que, ao se esticar um elástico puxando-o por suas extremidades em direções opostas, algum ponto do elástico permanecerá em sua posição inicial? Justifique sua resposta.
Avalie os seguintes limites de acordo com o gráfico da função:
$f(x) = \cos (x)$
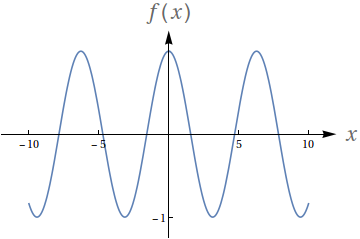
$\lim\limits_{x\to -\infty} f(x)$
$\lim\limits_{x\to \infty} f(x)$
- $\lim\limits_{x\rightarrow 4}\sqrt{x}$
- $\lim\limits_{x\rightarrow 0}\dfrac{x^{2}+3x-1}{x^{2}+2}$
- $\lim\limits_{x\rightarrow 1^{+}}\dfrac{\left| x-1\right| }{x-1}$
- $\lim\limits_{x\rightarrow 1^{-}}\dfrac{\left| x-1\right| }{x-1}$
Utilizando o gráfico a seguir, avalie os seguintes limites
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $2$
- $0$
- Não existe.
- $1$
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x^2, & & \text{ se } x<2 \\
x+1, & & \text{ se } x=2\\
-x^2+2x+4, & & \text{ se } x>2
\end{array}
\right.$
$ \lim\limits_{x\to 2^-} f(x)$
$ \lim\limits_{x\to 2^+} f(x)$
$ \lim\limits_{x\to 2} f(x)$
$f(2)$
- 4
- 4
- 4
- 3
Determine os valores para os quais a função \begin{align*} f(x) =\left\{ \begin{array} [c]{c} x^{2}+1,\text{ se }x\leq0 \\ \cos x, \text{ se } 0<x<1 \\ x^{2}+1, \text{ se }1 \leq x \end{array} \right.\end{align*} é contínua. Justifique sua resposta.
Use um recurso gráfico computacional para gerar os gráficos da função $f(x)=\dfrac{x-\sin x}{x^3}$, vide exercício ID 1703, e veja o que acontece.
Você esperaria que um problema similar ocorresse nos arredores de $x=0$ para a função $f(x)=\dfrac{1-\cos x}{x}$? Verifique se tal ocorre. Vide questão ID 958.
Mostre, usando a definição de limite, que $\displaystyle \lim_{x\to 5} 3-x = -2$
Seja $\epsilon >0$ dado. Queremos encontrar $\delta >0$ tal que, quando$|x-5|<\delta$, $|f(x)-(-2)|<\epsilon$.
Considerando $|f(x)-(-2)|<\epsilon$:
\begin{gather*}
|f(x) + 2 | < \epsilon \\
|(3-x) + 2 |<\epsilon \\
| 5-x | < \epsilon \\
-\epsilon < 5-x < \epsilon \\
-\epsilon < x-5 < \epsilon. \\
\end{gather*}
Isso implica que podemos estabelecer $\delta =\epsilon$. Portanto:
\begin{gather*}
|x-5|<\delta \\
-\delta < x-5 < \delta\\
-\epsilon < x-5 < \epsilon\\
-\epsilon < (x-3)-2 < \epsilon \\
-\epsilon < (-x+3)-(-2) < \epsilon \\
|3-x - (-2)| < \epsilon,
\end{gather*}
que é o que buscávamos provar.
Defina $\displaystyle \lim_{x \to a^+} f(x) = \infty$ e $\displaystyle \lim_{x \to a^-} f(x) = \infty$. Se estiver muito difícil, escreva em palavras.
Mostre que $\displaystyle \lim_{x \to 0^+} \dfrac{1}{x} = \infty$.
Mostre que $\displaystyle \lim_{x \to 0^+} f(x) = \infty$ se e somente se $\displaystyle \lim_{x \to \infty} f\left(\dfrac{1}{x}\right) = \infty$.
Calcule o limite $\lim\limits_{x\to p}\frac{x^{4}-p^{4}}{x-p}$
$\begin{array}{rcl} \lim\limits_{x\to p}\dfrac{x^{4}-p^{4}}{x-p} &=& \lim\limits_{x\to p} \dfrac{(x^2+p^2)(x^2-p^2)}{x-p} \\ &=& \lim\limits_{x\to p} \dfrac{(x^2+p^2)(x+p)(x-p)}{x-p} \\ &=& \lim\limits_{x\to p} (x^2+p^2)(x+p) \\ &=& (p^2 + p^2)(p+p) \\ &=& 4p^3. \end{array}$
Seja $f: \mathbb{R} \to \mathbb{R}$ uma função derivável cuja derivada é sempre positiva e tal que $f(0)=1$ e $f(4)=2$. Use o TVM para mostrar que $f(2) \neq 2$.
Uma das propriedades da potenciação é que $a^0=1$, $\forall a \neq 0$. Além disso, também sabe-se que $0^n=0,\quad \forall n>0$. A extensão destas regras para incluir, respectivamente, $a=0$ e $n=0$ levam a resultados conflitantes quanto ao valor de $0^0$(O que não implica em contradição, dado que as propriedades não foram estabelecidas para $a=0$ e $n=0$).
Sendo assim, avalie $x^x$ para $x=0,1;0,01;0,001;\ldots$. Qual o padrão observado? Com o auxílio de recursos computacionais, observe o gráfico de $y=x^x$ para valores positivos de $x$, se aproximando da origem. Para qual valor a função parece convergir para $x=0$?
Sugestão: Procure, no site, o exercício 1528. Compare os resultados obtidos.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-2x+1}{4x^{4}+2x+3}$.
$5/4$
Construa os gráficos das funções indicadas e calcule os limites:
$ f(x)=x^2$ quando $x\rightarrow\infty$
$ h(x)=3x^5$ quando $x\rightarrow -\infty$
$g(y)=\tan^{-1}(y)$ quando $y\rightarrow\infty$
$f(x)=\frac{1}{x}$ quando $x\rightarrow -\infty$
$f(x)=\frac{1}{x^7}$ quando $x\rightarrow \infty$
$f(x)=\frac{1}{x^{-2}}$ quando $x\rightarrow \infty$
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}-1}{x}$.
$2$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(t) = \sqrt{5t^2-30}$.
$(-\infty,-\sqrt{6}]\cup [\sqrt{6},\infty)$
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }3^{x}$
$\lim\limits_{x\rightarrow \infty }\left( 2^{x}-3^{x}\right)$
$\lim\limits_{x\rightarrow \infty }\left( 0,27\right) ^{x}$
1. $\infty$.
2. $-1$.
3. $0$.
Verifique que a equação $x^{179}+\frac{163}{1+x^2+\sin^2x}=119$ possui pelo menos uma solução.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 1}\ln \dfrac{x^{2}-1}{x-1}$.
$ln2$.
Identifique as assíntotas verticais e horizontais, caso existam, da função $f(x)=\frac{-3 x^2-9 x-6}{5 x^2-10 x-15}$.
Assíntota horizontal em $y=-3/5$; assíntota vertical em $x=3$.
Mostre que a função $f\left( x\right) =\dfrac{1}{x}$ é contínua em seu domínio.
Sendo $f(x) = \left\{\begin{array}{cl} x^2-x+1 & x\leq 3 \\ 2x+1 & x>3 \end{array}\right.$, calcule $\lim\limits_{x\to 3} f(x)$.
7
Calcule o seguinte limite
$\lim\limits_{x\rightarrow \infty }\left( \dfrac{x+2}{x+1}\right)^{x}$.
$e$.
Estime numericamente os seguintes limites para a função $f(x)= \frac{x^2+5 x-36}{x^3-5 x^2+3 x+9}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-335.64$ \\
$2.99$ & $-30350.6$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $-265.61$ \\
$3.01$ & $-29650.6$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =-\infty$.
Prove que se $\lim_{x\to 0}\dfrac{f(x)}{x}=l$ e $b\neq 0 $, então $\lim_{x\to 0}\dfrac{f(bx)}{x}=bl$. Dica: Escreva $\dfrac{f(bx)}{x}=b\dfrac{f(bx)}{bx}$.
O que acontece se $b=0$?
O item 1. nos permite determinar $\lim_{x\to 0}\dfrac{\sin(2x)}{x}$ em termos de $\lim_{x\to 0}\dfrac{\sin(x)}{x}$. Determine este limite de um outro modo.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
\frac{|x|}{x}, & & \text{ se } x\neq 0 \\
0, & & \text{ se } x=0
\end{array}
\right.$
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $ \lim\limits_{x\to 0} f(x)$
- $f(0)$
- $-1$
- $1$
- Não existe.
- $0$
Encontre as assíntotas horizontais e verticais ao gráfico de $f(x)=\sqrt{\frac{4x^2+1}{x^2-1}}$.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow \infty }\dfrac{-x^{4}-2x+1}{2x^{4}+2x+3}$.
Ache as assíntotas verticais e inclinadas; depois calcule os limites laterais nas assíntotas verticais da função $f\left( x\right) =\frac{x^{3}-3x-1}{x^{2}-x}.$
Calcule os limites indicados dividindo o numerador e o denominador por uma potência conveniente de $x$. Como esses limites se relacionam com as mais altas potências do numerador e do denominador?
$\lim\limits_{x\rightarrow\infty}\frac{x^4-2}{3x^4-x^3+1}$
$\lim\limits_{x\rightarrow\infty}\frac{\sqrt{2x^6-2x+1}}{x^3-x^2+2}$
$\lim\limits_{x\rightarrow -\infty}\frac{\sqrt{x^2-3}}{x+1}$
Conforme $x$ aumenta, tanto $1/x$ quanto $1/(ln\ x)$ tendem a zero. Dada a função: $f(x)=\left(\frac{1}{x}\right)^{1/(ln\ x)}$ avalie $f(x)$ para valores cada vez maiores de $x$. Qual o padrão observado? Com o auxílio de recursos computacionais, observe o gráfico de $f(x)$ para valores grandes de $x$.
Sugestão: Procure, no site, o exercício 1527. Compare os resultados obtidos.
Calcule, através da definição de limite, $\displaystyle \lim_{x\to 0} e^{2x}-1 = 0$.
Seja $\epsilon >0$ dado. Queremos $\delta >0$ tal que, quO IMECC é responsável pelos cursando $|x-0|<\delta$, $|f(x)-0|<\epsilon$.
Considerando $|f(x)-0|<\epsilon$, lembrando que o objetivo é afirmar algo sobre $|x-0|$ (i.e., $|x|$):
\begin{gather*}
|f(x) -0 | < \epsilon \\
|e^{2x}-1 |<\epsilon \\
-\epsilon< e^{2x}-1 < \epsilon \\
1-\epsilon< e^{2x} < 1+\epsilon \\
\ln (1-\epsilon) < 2x < \ln (1+\epsilon) \\
\frac{\ln (1-\epsilon)}{2} < x < \frac{\ln (1+\epsilon)}{2} \\
\end{gather*}
Seja $\delta = \min\left\{\left|\frac{\ln(1-\epsilon)}{2}\right|,\frac{\ln(1+\epsilon)}{2}\right\}=\frac{\ln(1+\epsilon)}{2}.$
Portanto:
\begin{gather*}
|x| < \delta \\
|x| <\frac{\ln(1+\epsilon)}{2}<\left|\frac{\ln(1-\epsilon)}{2}\right| \\
\frac{\ln(1-\epsilon)}{2} < x < \frac{\ln(1+\epsilon)}{2}\\
\ln(1-\epsilon)< 2x < \ln(1+\epsilon)\\
1-\epsilon < e^{2x} < 1+\epsilon\\
-\epsilon < e^{2x}-1 < \epsilon\\
|e^{2x}-1-(0)| < \epsilon,
\end{gather*}
que é o que buscávamos provar.
Dada uma função $f:{\mathbb{R} \to \mathbb{R}}$, defina sua continuidade no ponto $p\in \mathbb{R}.$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 0}\dfrac{\tan x}{x}$
$\lim\limits_{x\rightarrow 0}\dfrac{x^{3}}{\sin x}$
Seja $f$ uma função definida num intervalo aberto $I$ e $p \in I$. Suponha que $f(x) \leq f(p)$ para todo $x \in I$. Prove que $\lim\limits_{x \to p}\dfrac{f(x)-f(p)}{x-p}=0$, desde que o limite exista.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(x) = \frac{1}{1+x^2}$.
$(-\infty,\infty)$
Resolva os itens:
- Prove que existe $r>0$ tal que $\cos{x}-1<\dfrac{\sin{x}}{x}-1<0$ para $0<|x|<r$.
- Calcule $\lim\limits_{x \to 0}\dfrac{x-\sin{x}}{x^2}$.
Determine todas as funções contínuas $f:\mathbb{R} \to \mathbb{R}$ tais que $f(x+y)=f(x)f(y)$ para quaisquer x, y reais.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow -\infty }\left( 2^{x}+2^{-x}\right) $.
$-\infty$.
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right) ^{x+2}$
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{2x}\right) ^{x} $
$\lim\limits_{x\rightarrow \infty }\left( \dfrac{x+2}{x+1}\right) ^{x}$
Calcule, quando existirem, os seguintes limites (caso um limite tenda a $\pm \infty $ justifique a resposta):
$\lim\limits_{x\rightarrow 2}\dfrac{x^{2}+x-6}{\left( x-2\right) ^{3}}$
$\lim\limits_{x\rightarrow - \infty }\dfrac{5x^{5}+7x^{2}+3x+\pi }{\sqrt{7}x^{5}+4x+2}$
$\lim\limits_{x\rightarrow 0}x^{3}\cos \left( \frac{1}{x}\right)e^{x^{2}+1}$

