932

Seja $a>0$. Esboce o gráfico das funções $f(x) = \log_a x $ e $ f(x) = \log_\frac{1}{a} x$ num mesmo sistema cartesiano. Qual relação você observa entre os gráficos? Explique.

619

Determine o domínio da seguinte função:

$f\left( x\right) =\sqrt{x-\sqrt{x}}$.

$\left\{ x\geq 1\right\} $.

344

Um ponto no plano cartesiano é chamado ponto misto se uma de suas coordenadas é racional e a outra irracional. Encontre todos os polinômios com coeficientes reais tais que seus gráficos não contêm nenhum ponto misto.

924

Uma caixa retangular aberta com volume de $2 m^3$ tem a base quadrada. Expresse a área superficial da caixa como função de um dos lados da base.

Sejam $x$ a medida do lado da base da caixa e $z$ sua altura. O volume $V$ dessa caixa é dado por $V=x^2z$. Como $V=2$, temos $z=\dfrac{2}{x^2}$. A área superficial $A$ da caixa (sem tampa!) é $A=x^2+4xz$. Substituindo $z$ por $\dfrac{2}{x^2}$ obtemos $A=x^2+\dfrac{8}{x}$.

330

Uma das raízes da equação $x^2-x-a = 0$ é também raiz da equação $x^2+x-(a + 20)=0$. Qual é o valor de $a$?

928

Segundo dados de uma pesquisa, a população de certa região do país vem decrescendo em relação ao tempo t, contado em anos, aproximadamente, segundo a relação $P(t)=P(0) \cdot 2^{-0,25t}$. Sendo $P(0)$ uma constante que representa a população inicial dessa região e $P(t)$ a população $t$ anos após, determine quantos anos se passarão para que essa população fique reduzida à quarta parte da inicial.

Para que essa população fique reduzida à quarta parte da inicial devemos ter:
$P(t) = \dfrac{1}{4} P_0$.
Substituindo a expressão de $P(t)$:
$P_0 2^{-0,25 t} = 0,25 P_0$.
Com essa expressão podemos encontrar o valor de $t$.
$2^{-0,25 t} = 0,25$.
Aplicando $log_2$ dos dois lados:
$\log_2 (2^{-0,25 t}) = \log_2(0,25)$.
Utilizando propriedade de $\log$:
$-0,25 t \log_2 2 = \log_2(0,25)$.
$t = \dfrac{\log_2(0,25)}{-0,25}$.
$t = 8$ anos.

937

Determine a função inversa de:

$f(x) = x^2$
$f(x) = x^3 + 2.$

1496

Resolva os itens:

Verifique que $\sqrt{1+x^2}-|x|=\dfrac{1}{|x|+\sqrt{1+x^2}}$. Conclua que à medida que $|x|$ resce a diferença $\sqrt{1+x^2}-|x|$ se aproxima de zero.
Esboce o gráfico de $y=\sqrt{1+x^2}$.

326

Duas pequenas fábricas de calçados, $A$ e $B$, têm fabricado, respectivamente, $3000$ e $1100$ pares de sapatos por mês. Se, a partir de janeiro, a fábrica $A$ aumentar sucessivamente a produção em $70$ pares por mês e a fábrica $B$ aumentar sucessivamente a produção em $290$ pares por mês, em que mês a produção da fábrica $B$ superará a produção de $A$ pela primeira vez?

329

Qual o número de raízes distintas da equação $(x^2 – 14x + 38)^2 = 11^2$?

$3$

349

Seja $P(x)=a_0x^n+a_1x^{n-1}+\cdots+a_n$ um polinômio não nulo com coeficientes inteiros tal que $P(r)=P(s)=0$ para certos inteiros $r$ e $s$, com $0<r<s$. Prove que $a_k\leq -s$ para algum $k$.

328

Na fabricação de um lote de peças de certo produto, o custo total é igual à soma de um valor fixo de $R\$ 400,00$ com o custo de produção unitário de $R\$ 0,50$. Se o preço unitário de venda dessas peças for de $R\$ 0,85$, qual o número mínimo de peças que devem ser fabricadas e vendidas para que se comece a ter lucro?

1737

Usando as fórmulas do seno da soma e do cosseno da soma de dois ângulos, obtenha fórmulas para:

$\sin(2x), \cos(2x), \sin(3x)$ e $\cos(3x)$.

$\sin(2x) = 2 \sin x \cos x$.

$\cos(2x) = \cos^2 x - \sin^2 x$.

$\sin(3x) = \sin x (2 (\cos^2 x - \sin^2 x) + 1)$.

$\cos(3x) = \cos^3 x - 3 \sin^2 x \cos x$.

342

Encontre as raízes do polinômio $x^4-10x^3+17x^2-17x+6.$
Sugestão: Utilize o teste das raízes racionais.

1493

Dê o domínio e esboce o gráfico das seguintes funções:

$f(x)=-2+ 1/x$
$f(x)=-\dfrac{1}{x}$

1497

Sejam $a$ e $b$ reais quaisquer. Verifique que:

$\sin{a}\cos{b}=\dfrac{1}{2}(\sin(a+b)+\sin(a-b))$
$\cos{a}\cos{b}=\dfrac{1}{2}(\cos(a+b)+\cos(a-b))$

$\begin{array}{rcl} \frac{1}{2} ( \sin(a+b) + \sin(a-b) ) &=& \frac{1}{2} ( \sin a \cos b + \sin b \cos a + \sin a \cos b - \sin b \cos a ) \\ &=& \frac{1}{2} ( 2 \sin a \cos b) \\ &=& \sin a \cos b .\end{array}$

$\begin{array}{rcl} \frac{1}{2} ( \cos(a+b) + \cos(a-b) ) &=& \frac{1}{2} ( \cos a \cos b + \sin a \sin b + \cos a \cos b - \sin a \sin b ) \\ &=& \frac{1}{2} ( 2 \cos a \cos b) \\ &=& \cos a \cos b .\end{array}$

338

Seja $P(x)$ um polinômio de coeficientes inteiros com grau $d>0$. Seja $n$ o número de inteiros distintos $k$ tais que $(P(k))^2=1$. Prove que $n\leq d+2.$

919

Esboce o gráfico de $f(x) = |x-1|+3.$

1492

Dê o domínio e esboce o gráfico das seguintes funções:

$f(x)=1+1/x$
$f(x)=\dfrac{2}{x+1}$

334

Seja $P(x)$ um polinômio com coeficientes inteiros. Suponha que existam quatro inteiros distintos $a,b,c$ e $d$ tais que $P(a)=P(b)=P(c)=P(d)=5$. Prove que não existe inteiro $k$ tal que $P(k)=8$.

333

Encontre todas as funções polinomiais $f$ com coeficientes reais tais que $(x-27)f(3x)=27(x-1)f(x)$ para todo número real $x$.

1738

Usando as fórmulas pra $\sin(2x), \cos(2x), \sin(3x)$ e $\cos(3x)$, calcule $\sin\left(\dfrac{\pi}{4}\right)$, $tg\left(\dfrac{\pi}{4}\right)$, $\sin\left(\dfrac{\pi}{6}\right)$ e $\cos\left(\dfrac{\pi}{6}\right)$.

$\sin\left(\dfrac{\pi}{4}\right) = \dfrac{1}{\sqrt{2}}$.

$tg\left(\dfrac{\pi}{4}\right) = 1$.

$\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$.

$\cos\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}$.

917

Suponha que o número de carteiros necessários para distribuir, em cada dia, as correspondências entre as residências de um bairro seja dado pela função $f(x)=\frac{22x}{500+2x}$, em que $x$ é o número de residências e $f(x)$ é o número de carteiros. Se foram necessários 6 carteiros para distribuir, em um dia, estas correspondências, qual o número de residências desse bairro, que as receberam?

Substituindo $f(x) = 6$ na expressão da função:

$6 = \dfrac{22 x}{500+2x}$
$\Rightarrow 6(500+2x) = 22x$
$\Rightarrow 3000 + 12x = 22x$
$\Rightarrow 10x = 3000$
$\Rightarrow x = 300$ residências.

1494

Dê o domínio e esboce o gráfico das seguintes funções:

$f(x)=1/x^2$
$f(x)=\dfrac{1}{(x-1)^2}$

324

Um encanador $A$ cobra por serviço feito um valor fixo de $R\$ 60,00$, mais $R\$ 10,00$ por hora de trabalho. Um outro encanador $B$ cobra um valor fixo de $R\$40,00$ mais $R\$15,00$ por hora de trabalho. Considerando o menor custo para a realização de um trabalho, avalie a decisão de se contratar um ou outro encanador.

341

Encontre todos os números naturais $k$ para os quais a seguinte afirmação é verdadeira: Se $F(x)$ é um polinômio com coeficientes inteiros que satisfaz $0\leq F(c)\leq k$ para todo $c\in\{0,1,\ldots,k+1\}$ então $F(0)=F(1)=\cdots=F(k+1).$

335

Seja $f(x)=x^n+5x^{n-1}+3$, onde $n>1$ é um inteiro. Prove que $f(x)$ não pode ser expressa como um produto de polinômios não constantes com coeficientes inteiros.

1763

Prove que $\cosh'(x)=\sinh(x)$.

929

Calcule, apresentando todos os cálculos e/ou justificativas.

$log_2 (1024)+sen^2(40)+cos^2(40)$
$log_\pi [sen(30^0)+cos(60^0)]$

1498

Esboce juntas as curvas dadas no plano cartesiano e identifique cada uma com sua equação:
$y=2^x$, $y=4^x$,$y=3^{-x}$, e $y=\left( 1/2 \right)^{x}$.

931

Esboce o gráfico das funções $f(x) = \log_2 x $ e $ f(x) = \log_\frac{1}{2} x$ num mesmo sistema cartesiano. Qual relação você observa entre os gráficos? Explique.

1505

Utilizando as leis de exponenciação, simplifique a expressão a seguir:
$6^{1/3}\cdot18^{1/6}$

1507

Demonstre que $x^{ln(2)}=2^{ln(x)}$ utilizando propriedades de logaritmos e exponenciais. Utilizando recursos computacionais, observe os gráficos das duas funções, assim como a diferença entre elas. Qual seria uma explicação para o comportamento observado no gráfico de $f(x)=x^{ln(2)}-2^{ln(x)}$?

676

Mostre que a equação $x^2=x$ tem exatamente duas raízes reais.

A equação pode ser escrita na forma $x^2-x=0$, i.e, $x(x-1)=0$. As suas únicas raízes reais são $x=0$ e $x=1$. Uma outra forma de atacar este problema é perceber que os gráficos de $f(x)=x$ e $g(x)=x^2$ se intersectam exatamente duas vezes!

922

Partindo do gráfico de $h(x)=x^2$, esboce os gráficos de $f(x) =(x-1)^2$ e $ g(x) = (x +1)^2.$

660

Considere o gráfico da função $f$:

$f\left( x\right) =\left\{\begin{array}{c}-2x-2,-4\leq x\leq -2 \\x+4,-2\leq x\leq 1 \\6-x,1\leq x\leq 4\end{array}\right.$

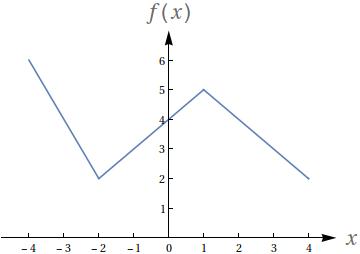
Esboce, a partir deste, os gráficos das seguintes funções:

$y=f\left( x+4\right) $
$y=f\left( x\right) +4$
$y=2f\left( x\right) $
$y=-\dfrac{1}{2}f\left( x\right) +3.$

1765

Prove que $1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots+\dfrac{x^n}{n!} \leq e^x$. Conclua que $\lim\limits_{x \to \infty} e^x/x^n=\infty$.

1500

Esboce as curvas exponenciais transladadas:
$y=2^x-1$ e $y=2^{-x}-1$.

933

Calcule:

$log_2 (8)$

$log_3 (27)$

$\log_2(8) = x$
$2^x = 8$
$2^x = 2^3$
$x = 3$.
$\log_3(27) = x$
$3^x = 27$
$3^x = 3^3$
$x = 3$.

938

Calcule $f^{-1}$ para a função $f(x)=1+3x.$

Seja $y = f(x)$. Então:
$y = 1 + 3 x$.
Isolando $x$:
$3 x = y - 1$
$x = \dfrac{y-1}{3}$.
Logo:
$f^{-1}(x) = \dfrac{x-1}{3}$.

1511

O quociente $(log_4\ x)/(log_2\ x)$ possui um valor constante. Qual valor é este?

653

Esboce o gráfico de cada uma das funções abaixo.

$y=-\sqrt{7-x^{2}}$
$y=1+\sqrt{10-x^{2}}$

654

Esboce o gráfico de cada uma das funções abaixo.

$y=2-\sqrt{16-x^{2}}$
$y=-1+\sqrt{6-(x-1)^{2}}$

1514

Dê os domínios e esboce os gráficos de $f+g$ e $\dfrac{g}{f}$ nos seguintes casos:

$f(x)=1$ e $g(x)=\dfrac{1}{(x-2)^2}$.
$f(x)=1$ e $g(x)=\sqrt{x-1}$.

930

Calcule, apresentando todos os cálculos e/ou justificativas.

$log_6 (36) +log_3 (6^4)$
$8^{\frac {2} {3}}+\sqrt{log_2 (16)}+2^{2^3}+(2^2)^{3}$

1761

Prove que $\cosh^2(x)-\sinh^2(x)=1$.

$\begin{array}{rcl} \cosh^2x - \sinh^2 x &=& \left(\dfrac{e^{-x} + e^x}{2}\right)^2 - \left(\dfrac{e^{x} - e^-x}{2}\right)^2 \\ &=& \dfrac{1}{4} (e^{-2x} + 2 e^{-x}e^x + e^{2x}) - \dfrac{1}{4} (e^{2x} - 2 e^xe^{-x} + e^{-2x}) \\ &=& \dfrac{1}{2} + \dfrac{1}{2} \\ &=& 1.\end{array}$

921

Esboce os gráficos de $f(x) =x^2-1$ e $ g(x) = x^2 +1.$

923

Esboce o gráfico de $f(x) =x^2+6x+10.$ Use completamento de quadrados.

635

Se $f(x+1)=\frac{x-1}{\pi -x},$ ache $f\left( x\right) $ e encontre o domínio de $f$.

Calculando $f((x-1)+1)$:
$f((x-1)+1)=\dfrac{(x-1)-1}{\pi-(x-1)}$
$f(x) = \dfrac{x-2}{\pi+1-x}$.
O domínio de $f$ é o conjunto de números reais menos os pontos em que o denominador é zero. Calculando esses valores:
$\pi + 1 - x = 0 \Rightarrow x = \pi + 1$.
Portanto o domínio de $f$ é: $\{x \in \mathbb{R}; x \neq \pi + 1\}$.

1506

Se Fidelis investisse $R\$1500$ em uma conta aposentadoria que rende $8\%$ de juros compostos anualmente, em quanto tempo este investimento isoladamente aumentará para $R\$5000$?

677

Mostre que a equação $\sin x +\cos x =0$ tem exatamente duas raízes reais.

327

Uma pequena indústria vende normalmente, a cada semana, $60$ caixas de certo produto, por $30$ reais a caixa. Foi feita uma experiência e observou-se que cada real de desconto nesse preço fez as vendas aumentarem em $5$ caixas. Assim, a experiência mostrou que, dentro de certos limites, a quantidade $C$ de caixas vendidas é uma função do desconto $x$, em reais. Determine uma expressão para essa função.

640

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

$y=\sqrt{x-2}$
$y=\sqrt{2-x}$

O domínio de $y$ é o conjunto de números reais em que o valor dentro da raiz é positivo. Calculando esses valores:
$x-2 > 0 \Rightarrow x > 2$.
Portanto o domínio de $y$ é: $\{x \in \mathbb{R}; x >2\}$.
O domínio de $y$ é o conjunto de números reais em que o valor dentro da raiz é positivo. Calculando esses valores:
$2-x > 0 \Rightarrow x < 2$.
Portanto o domínio de $y$ é: $\{x \in \mathbb{R}; x <2\}$.

643

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

$y=\sqrt[3]{x-2}$
$y=\displaystyle{\frac{1}{x^{2}-4}}$

1508

Uma droga é administrada por via intravenosa para combater a dor. A função
$f(t)=90-52\ ln(1+t), \quad 0 \leq t\leq4$
fornece o número de unidades da droga que permanecem no corpo após $t$ horas.

Qual foi o número inicial de unidades administradas?
Quanto estará presente após $2$ horas?
Esboce o gráfico de $f(t)$

1509

Utilizando a aproximação $ln\ 2 \approx 0,7$, pode-se derivar uma regra popular, conhecida como regra dos 70, que diz: "Para estimar quantos anos uma determinada quantia em dinheiro dobre ao ser investida a uma porcentagem $r$ composta continuamente, divida $r$ por $70$". Por exemplo, uma quantia em dinheiro investida a $7\%$ dobrará em cerca de $70/7=10$ anos. Se, em vez disso, você quiser que ela dobre em $5$ anos, deve investí-la a $70/5=14\%$. Mostre a dedução da regra dos 70.

346

Seja $P(x)$ um polinômio de grau $n$ tal que $P(k)=k/(k+1)$ para $k=0,1,\ldots n$. Encontre $P(n+1)$.

646

Seja $f\left( x\right) =\frac{1+x}{1-x}$. Mostre que $f\left( \frac{1}{1+x}\right) =\frac{2+x}{x}$, $f\left( \frac{1}{1-x}\right) =\frac{x-2}{x}$, $f\left( -x\right) =\frac{1}{f\left( x\right) }$, $f\left( 1/x\right)=-f\left( x\right) $ e que $f\left( f\left( x\right) \right) =-1/x$.

350

Enuncie o Teorema Fundamental da Álgebra (de Gauss).

"Qualquer polinômio $p(z)$ com coeficientes complexos de uma variável e de grau $n \geq 1$ tem alguma raiz complexa."

1495

Dê o domínio e esboce o gráfico das seguintes funções:

$f(x)=|x|+1/x$
$f(x)=\sqrt{|x|}$

345

Encontre as raízes do polinômio $x^4-6x^3+13x^2-12x+4.$
Sugestão: Utilize o teste das raízes racionais

639

Sejam $f(x)=\sqrt{\displaystyle{\frac{x+3}{x-3}}}$ e $g(x)=\displaystyle{\frac{\sqrt{x+3}}{\sqrt{x-3}}}$. Determine o domínio da função $f$ e o domínio da função $g$. É verdade que $f=g$?

920

Um fabricante de refrigerante quer produzir latas cilíndricas para seu produto. A lata dever ter um volume de $360 ml$. Expresse a área superficial total da lata em função do seu raio e dê o domínio da função.

Sejam $r$ o raio da base do cilindro e $h$ a sua altura. O volume $V$ do cilindro é dado por $V=\pi r^2 h$. Como $V=360$, obtemos $\pi r^2 h=360$, isto é, $h=\dfrac{360}{\pi r^2}$. A área superficial $A$ do cilindro é $A=2 \pi r^2+2 \pi r h$. Substituindo $h$ por $\dfrac{360}{\pi r^2}$ chegamos a $A=2 \pi r^2+2 \pi r \dfrac{360}{\pi r^2}$, ou seja, $A=2 \pi r^2+ \dfrac{360}{r}$. O domínio da função $A(r)$ é $\mathbb{R}^+$.

1767

Prove que $\log_{10} 2$ é irracional.

1648

Mostre que $\pi^e < e^\pi$. Sugestão: Analise a função $ln(x)/x$.

Pelas propriedades do logaritmo, podemos escrever:

$
ln(e^\pi)=\pi
$

e

$
ln(\pi^e) = e\ ln(\pi)
$

Como $\pi > e$, pode-se escrever $\pi = ae,\ a > 1$. Assim, a primeira equação pode ser escrita como:

$
ln(e^\pi)=ae
$

E a segunda equação como:

$
ln(\pi^e) = e\ ln(a\ e) = e\ ln(a)ln(e)=e\ ln(a)
$

Assim, podemos escrever a razão entre as equações como:

$
\frac{ln(\pi^e)}{ln(e^\pi)} = \frac{ln(a)}{a}
$

Analisando a equação $ln(x)/x$, vemos que para $x>1$ ela é estritamente decrescente, dado que em $x=1$ o denominador é igual a um e o numerador igual a zero e como $\frac{d(ln(x))}{dx}=\frac{1}{x}$ e $\frac{d(x)}{dx}=1$, o denominador cresce mais rapidamente para $x>1$. Assim, como $a>1$, sabemos que:

$
\frac{ln(\pi^e)}{ln(e^\pi)} = \frac{ln(a)}{a} < 1
$

Portanto:

$
ln(\pi^e) < ln(e^\pi)
$

Como $\frac{d(ln(x))}{dx}=\frac{1}{x}>0$ para $x>0$, a função logaritmo é monotônica no intervalo desejado, e portanto podemos concluir que:

$\pi^e < e^\pi$

649

Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.

$f(x)=x^{3}+x$
$f(x)=x^{4}+2x^{3}+x^{2}$

$f(-x)=(-x)^{3}+(-x) = -x^3-x = -(x^3+x) = -f(x)$, logo a função é ímpar.

$f(-x)=(-x)^{4}+2(-x)^{3}+(-x)^{2} = x^4-2x^3+x^2$, que não é igual a $f(x)$ nem $-f(x)$, logo a função não é par nem ímpar.

1768

Escreva $a^x$ em função de $e^x$. Use esse resultado para escrever $\log_a(x)$ em função de $\ln(x)$.

935

A intensidade $I$ de um terremoto, medida na escala Richter, é um número que varia de $I=0$ até $I=8,9$ para o maior terremoto conhecido. $I$ é dado pela fórmula $I=\dfrac{2}{3} log {\left(\dfrac{E}{E_0}\right)}$, em que $E$ é a energia liberada pelo terremoto em quilowatt-hora e $E_0=7 \times 10^{-3}$ kwh.

Qual a energia liberada por um terremoto de intensidade 8 na escala Richter?
Aumentando uma unidade na intensidade do terremoto, por quanto fica multiplicada a energia liberada?

636

Sejam $f\left( x\right) =\frac{x^{2}-25}{x^{2}-1}$ e $g\left(x\right) =\sqrt{x}$. Dê o domínio das seguintes funções: $f,$ $g$, $f\circ g$ e $g\circ f$.

1504

Utilizando as leis de exponenciação, simplifique a expressão a seguir:
$9^{1/3}\cdot9^{1/6}$

648

Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.

$f(x)=\tan x$
$f(x)=x^{2}+1$

656

Esboce o gráfico de cada uma das funções abaixo.

$y=|x|+x$
$y=1-x$ se $x\leq 0$ e $y=\sqrt{1-x^{2}}$ se $0\leq x\leq 1$.

1502

Esboce as curvas exponenciais transladadas:
$y=1-e^x$ e $y=1-e^{-x}$.

927

A partir de um ponto, observa-se o topo de um prédio sob um ângulo de $30^0$. Caminhando $23$m em direção ao prédio, atingimos outro ponto, de onde se vê o topo do prédio segundo um ângulo de $60^0$. Desprezando a altura do observador, calcule, em metros, a altura do prédio.

340

Sejam $a_1,a_2,\ldots,a_{100}$, $b_1,b_2,\ldots,b_{100}$ números reais distintos. Uma tabela de dimensões $100\times 100$ é preenchida com esses números tal que o número $a_i+b_j$ é inserido na célula situada exatamente abaixo da interseção da $i$-ésima linha com a $j$-ésima coluna. Dado que em cada coluna o produto de todos os números é igual a $1$, prove que em cada linha o produto de todos os números é $-1$.

641

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

$y=\sqrt{x^{2}-9}$
$y=\sqrt{-x}$

$\{x \in \mathbb{R}; x<-3 \text{ ou }x>3\}$.
$\{x \in \mathbb{R}; x<0\}$.

618

Determine o domínio da seguinte função:

$f\left( x\right) =\sqrt{x-1}+\sqrt{3-x}$.

$\left\{ 1\leq x\leq 3\right\} $.

644

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

$y=\sqrt{x+5}$
$y=\sqrt{3-2x}$

$[-5,\infty[$
$]-\infty,\frac{3}{2}]$

323

Classifique as afirmações em verdadeiras ou falsas:

Mestre Florindo, raizeiro famoso, vende suas garrafas medicinais por 5 reais, na feira de Caruaru.

Se ele vende $q$ unidades, então $R(q) = 5q$, que é a sua função receita.
Se ele tem um custo em torno de $40\%$ de sua receita, o seu custo pode ser estimado pela equação $C(q) = 2q$.
Se, além disso, o mestre gastou $R\$ 900,00$ em materiais para confecção do seu famoso produto, ele deverá vender $300$ garrafas para recuperar o seu custo total.
O lucro do mestre é dado pela função afim $L(q)=5q-900$.

Verdadeiro.
Verdadeiro.
Verdadeiro, pois o lucro total $L(q)$ é $L(q)=R(q)-C(q)-900=3q-900$ e temos que $T(q)=0$ se $q=300$.
Falso, $L(q)=3q-900$.

1260

Resolva a equação $e^{ax}=Ce^{bx}$, onde $a\neq b$.

Usando as propriedades básicas da função exponencial temos que:
\begin{align*}
e^{ax} & =Ce^{bx}\\
& \Leftrightarrow e^{-ax}e^{ax}=e^{-ax}Ce^{bx}\\
& \Leftrightarrow1=Ce^{(b-a)x}\\
& \Leftrightarrow\frac{1}{C}=e^{(b-a)x}\\
& \Leftrightarrow\ln\left( \frac{1}{C}\right) =\ln\left( e^{(b-a)x}\right)
=\left( b-a\right) x\\
& \Leftrightarrow\frac{-\ln C}{b-a}=\frac{\ln C}{a-b}=x
\end{align*}

1762

Prove que $\tanh^2(x)+\dfrac{1}{\cosh^2(x)}=1$.

1259

Resolva a equação $\ln\left( x^{2}+2x+1\right) =3$.

Como a função exponencial é estritamente monótona, temos que $\ln\left( x^{2}+2x+1\right) =3$ se, e somente se, $e^{\ln\left(x^{2}+2x+1\right) }=x^{2}+2x+1=e^{3}$. Mas $ x^{2}+2x+1=\left( x+1\right) ^{2}$. Logo $\ln\left( x^{2}+2x+1\right) =3\Leftrightarrow\left( x+1\right)^{2}=e^{3}\Leftrightarrow x+1=\pm e^{3/2}\Leftrightarrow x=\pm e^{3/2}-1$.

918

Para tranformar graus Fahrenheit em graus centígrados usa-se a fórmula $C=\dfrac{5(F-32)}{9}$, em que $F$ é o número de graus Fahrenheit e $C$ é o número de graus centígrados.

Transforme $35$ graus centígrados em graus Fahrenheit.
Qual a temperatura (em graus centígrados) em que o número de graus Fahrenheit é o dobro do número de graus centígrados?

336

Se $a$, $b$, $c$ são as raízes de $x^3-x-1=0$, calcule o valor de $\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c}.$

637

1513

Dê os domínios e esboce os gráficos de $f+g$ e $\dfrac{g}{f}$ nos seguintes casos:

$f(x)=x$ e $g(x)=x^2-1$.
$f(x)=x$ e $g(x)=\dfrac{1}{\sqrt{x}}$.

1766

Mostre, diretamente da definição, que $\log_a'(x)=\dfrac{1}{x} \cdot log_a\left(\lim\limits_{k \to 0}(1+k)^{1/k}\right)$.

638

Seja $f\left( x\right) =\left| x\right| -x$. Mostre que $f\left( x\right) =0$ para $x\geq 0$ e $f\left( x\right) =-2x$ para $x<0$. Faça o gráfico dessa função.

934

Calcule:

$log_3 (36) +log_3 (6)$
$8^{\frac {2} {3}}+\sqrt{100}+2^{2^3}+2^{(2^3)}$

1501

Esboce as curvas exponenciais transladadas:
$y=3^x+2$ e $y=3^{-x}+2$.

617

Determine o domínio da seguinte função:

$f\left( x\right) =\sqrt[4]{\dfrac{x}{x+4}}$.

$\left\{ x\geq 0\right\} \cup \left\{ x<-4\right\} $.

655

Esboce o gráfico de cada uma das funções abaixo.

$y=\sqrt{9-(2-x)^{2}}$
$y=7/2-\sqrt{13-(2+x)^{2}}$

926

Calcule o valor das seguintes expressões:

$sen(45^0)+cos(45^0)$

$\dfrac {cos(30^0)sen(60^0)} {tg(45^0)}$

$[sen^2(71,2^0)+cos^2(71,2^0)] \times cotg(45^0)$

Usando o teorema fundamental da trigonometria sabemos que o valor da expressão $sen(45^0)+cos(45^0)$ é $1$.
Este item se resolve por substituição direta: $cos(30^0)=sen(60^0)=\dfrac{\sqrt{3}}{2}$ e $tg(45^0)=1$:$\dfrac {cos(30^0)sen(60^0)} {tg(45^0)}=\left(\dfrac{\sqrt{3}}{2}\right)^2 \times 1=\dfrac{3}{4}$.
Usando o teorema fundamental da trigonometria sabemos que o valor da expressão $sen^2(71,2^0)+cos^2(71,2^0)$ é $1$. Além disso, temos que $cotg(45^0)=\dfrac{1}{tg(45^0)}=\dfrac{1}{1}=1$. Então:\\ $[sen^2(71,2^0)+cos^2(71,2^0)] \times cotg(45^0)=1 \times 1=1$.

1779

Seja $f(x)=\dfrac{1}{1+x}$. Determine:

$f(f(x))$
$f\left(\dfrac{1}{x}\right)$
$f(cx)$
$f(x+y)$
$f(x)+f(y)$

1515

Determine $f$ de modo que $g(f(x))=x$ para todo $x \in D_f$, sendo $g$ dada por:

$g(x)=\dfrac{1}{(x-2)^2}$
$g(x)=\dfrac{1}{\sqrt{x}}$

1241

Seja $x(t)$ a posição horizontal e $y(t)$ a posição vertical de um objeto no tempo $t$. Com $x(0)=y(0)=0$ e velocidade iniciais horizontal $v_x$ e vertical $v_y$, a trajetória do objeto pode ser representada pelas equações $x(t)=v_xt$ e $y(t)=-5t^2+v_y t$. Suponha que o módulo da velocidade inicial seja igual a $1$. Neste caso, o ângulo $\theta$ entre a linha horizontal (eixo $x$) e a tangente à parábola na origem $(0,0)$ satisfaz $v_x=\cos(\theta)$ e $v_y=\sin(\theta).$

Use a identidade $\sin(\theta_1+\theta_2)=\sin(\theta_1)\cos(\theta_2)+\sin(\theta_2)\cos(\theta_1)$ para provar que $\cos(\theta)\sin(\theta)=\frac{1}{2}\sin(2\theta).$
Para $v_x>0$, $v_y>0$, determine o tempo $t_f>0$ tal que $y(t_f)=0$. Escreva $t_f(\theta)$ como função de $\theta$ com domínio $]0,\frac{\pi}{2}[$.
Definimos uma função $x_f$, também com dominio $]0,\frac{\pi}{2}[$, por $x_f(\theta)=x(t_f(\theta))$. Escreva $t_f(\theta)$ como função de $\theta$ e simplifique.
Qual é a imagem de $x_f$?
Quais são os ângulos $\theta\in\,]0,\frac{\pi}{2}[$ com valores $x_f(\theta)=\frac{\sqrt{3}}{20}$, $x_f(\theta)=\frac{1}{10}$ e $x_f(\theta)=\frac{1}{5}$?

1491

Dê o domínio e esboce o gráfico das seguintes funções:

$f(x)=2/x$
$f(x)=\dfrac{2}{x-1}$

332

O consumo de combustível de um automóvel é função da sua velocidade média. Para certo automóvel, essa função é aproximadamente dada por $y = 0,03x^2-2x + 20$, sendo $y$ o consumo de combustível, em mililitros por quilômetros por hora. Nessas condições, para esse automóvel, qual velocidade média corresponde a um consumo de $120 ml/km$?

652

Esboce o gráfico de cada uma das funções abaixo.

$y=\frac{2|x+1|}{3}$
$y=\sqrt{5-x^{2}}$

647

Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.

$f(x)=\sin x$
$f(x)=\cos x$

A função $\sin x$ é ímpar pois $f(-x) = \sin (-x) = -\sin(x) = -f(x)$.

A função $\cos x$ é par pois $f(-x) = \cos (-x) = \cos(x) = f(x)$.

1516

Dê os domínios e esboce os gráficos de $f+g$ e $\dfrac{g}{f}$ no seguinte caso:

$f(x)=\left\{\begin{array}{ll}
1, & \text{se x é racional} \\
-1, & \text{se x é irracional} \end{array}\right.$

e

$g(x)=\left\{\begin{array}{ll}
-1, & \text{se x é racional} \\
1, & \text{se x é irracional} \end{array}\right.$

337

Enuncie e prove o Algoritmo de Briot-Ruffini. Dê exemplos.

657

Seja $f(x)=\frac{1+x}{1-x}$. Mostre que $f\left(\frac{1}{1+x}\right)=\frac{2+x}{x}$, $f\left(\frac{1}{1-x}\right)=\frac{x-2}{x}$, $f(-x)=\frac{1}{f(x)}$, $f(1/x)=-f(x)$, $f(f(x))=-1/x$.

343

Encontre todos os pares de inteiros $m,n\geq 3$ tais que existem infinitos inteiros positivos $a$ para os quais

$\frac{a^m+a-1}{a^n+a^2-1}$ é um inteiro.

642

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

$y=\sqrt[3]{x}$
$y=\sqrt[3]{-x}$

$\mathbb{R}$.
$\mathbb{R}$.

347

Encontre o número de polinômios de grau $5$ com coeficientes distintos pertencentes ao conjunto $\{1,2,\ldots,9\}$ que são divisíveis por $x^2-x+1$.

1503

Utilizando as leis de exponenciação, simplifique a expressão a seguir:
$16^2\cdot16^{1,75}$

645

Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.

$y=\sqrt{x^{2}-4x+3}$
$y=\sqrt{x^{2}+3x-10}$

650

Se $f(x+1)=\frac{x-1}{\pi -x}$, ache $f(x)$ e encontre o domínio de $f$.

651

Sejam $f(x)=\frac{x^{2}-25}{x^{2}-1}$ e $g(x)=\sqrt{x}$. Dê o domínio de cada uma das funções $f$, $g$, $f\circ g$ e $g\circ f$.

325

Mensalmente, pago pela prestação de minha casa $1/5$ do meu salário; metade do resto gasto em alimento e $1/3$ do que sobra coloco na poupança, restando-me ainda $R\$ 800,00$ para gastos diversos. Qual o valor colocado na poupança?

1512

Sejam $f(x)=log_x(2)$ e $g(x)=log_2(x)$:

Utilize a propriedade de quociente de logaritmos para expressar $f(x)$ e $g(x)$ em termos de logaritmos naturais.
Com o auxílio de recursos computacionais, compare os gráficos de $f(x)$ e $g(x)$.

925

A área superficial de uma caixa retangular fechada de base quadrada é igual a $20 m^2$. Determine o volume desta caixa em função do comprimento do lado de sua base.

936

Se $ f(x) = \sqrt{x} $ e $ g(x) =\sqrt{2-x},$ encontre e determine o domínio das funções:

$f \circ g (x).$
$g \circ f(x).$
$f \circ f (x).$
$g \circ g(x).$

348

Demonstre a fórmula de Báskhara usada para resolução de equações polinomiais de grau $2$.

1510

Se $(ln\ x)/x = (ln\ 2)/2$, é necessário que $x=2$? Se $(ln\ x)/x=-2ln\ 2$, é necessário que $x=\frac{1}{2}$? Justifique suas respostas.

1490

Reescreva a função $f(x)=|x-1|+|x+2|$ usando desigualdades e representação por partes. Esboce o gráfico de $f$

331

Uma das raízes da equação $x^2+mx+m^2-m-12=0$ é nula, e a outra é positiva. Qual o valor do parâmetro $m$?

339

Encontre as raízes do polinômio $x^4-7x^3+35x^2-50x+24.$

1764

Prove que $\sinh'(x)=\cosh(x)$.

1499

Esboce juntas as curvas dadas no plano cartesiano e identifique cada uma com sua equação:
$y=3^x$, $y=8^x$,$y=2^{-x}$, e $y=\left( 1/4 \right)^{x}$.

Exercícios

Funções