Exercícios
Módulo de um número real
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Dados dois números reais distintos $a$ e $b$, podemos definir uma função $f(x)$ que chamaremos "distância ao conjunto $\left\lbrace a,b \right\rbrace$" da seguinte forma: $f(x)$ é igual ao menor dos números $|x-a|$ ou $|x-b|$. Se $a=-b=1$, construa o gráfico de $f(x)$.
Dadas $a$ e $b$ constantes reais não nulas, esboce um gráfico da família de funções $f(x)=min\{|x-a|,|x-b|\}$.
Mostre que $x\neq y\Longrightarrow x^{2}+2xy<2x^{2}+2y^{2}$.
Note que $(x-y)^2+y^2>0$ sempre que $x\neq y$. Daí, $x^2-2xy+y^2+y^2>0$, que é equivalente a $2x^2+2y^2-x^2-2xy>0$, que, por sua vez, é equivalente a x^{2}+2xy<2x^{2}+2y^{2}$.
Mostre que $|x-y|<1/2,|x+2|<1/3\Longrightarrow |y+2|<5/6$.
Nos primórdios da geração comercial de eletricidade, havia uma disputa bastante acirrada entre duas formas de se distribuir energia elétrica: A disputa entre corrente alternada e corrente contínua. A corrente alternada provou-se mais eficiente para transmissão a longas distâncias, principalmente pela facilidade com que é possível elevar os níveis de tensão (e, portanto, para uma mesma potência transmitida, diminuir a corrente e consequentemente os diâmetros dos fios utilizados na transmissão, implicando em significativa economia).
Com o advento da eletrônica, na segunda metade do século XX, a corrente contínua reconquistou um papel fundamental no dia a dia da sociedade contemporânea, dado que circuitos eletrônicos são alimentados com corrente contínua. A conversão de corrente alternada é feita a partir de dispositivos chamados retificadores. Infelizmente, o funcionamento destes dispositivos foge do escopo desta disciplina.
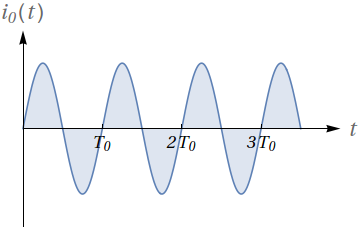
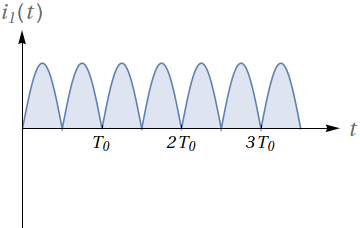
As figuras abaixo representam uma corrente $i(t)$ antes e depois de um circuito:
Responda:
- Dado que a função original seja $i_0(t)= \sin(2\pi\ 60\ t)$, qual a relação entre o seu período $T_0$ e o período da corrente retificada $i_1(t)$?
- Quais operações sobre a função $i_0(t)$ você realizaria para obter $i_1(t)$?
- Qual o valor médio, em um período, de $i_0(t)$? Qual seria sua estimativa para o valor médio de $i_1(t)$?
Resolva a equação $\left| {\frac{3x+8}{2x-3}}\right| =4$.
Temos duas possibilidades: $\frac{3x+8}{2x-3}=4$ ou $\frac{3x+8}{2x-3}=-4$. Da primeira equação obtemos $3x+8=8x-12$, i. e., $x=4$. Da segunda equação obtemos $3x+8=-8x+12$, que fornece $x=4/11$.
Sabendo que $x$ é um número negativo, simplifique a expressão $\sqrt{(x-3)^2}+\sqrt{x^2}+\sqrt{(4-3x)^2}$.
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$x\neq y\Longrightarrow |x|\neq |y|$.
$|x-y|\geq |x|-|y| \forall x,y\in \mathbb{R}$
Prove que $|x+y|=|x|+|y| \Leftrightarrow xy \geq 0$.
Resolva a equação modular $|x-2|-|x-1| =2$.
Enuncie e prove a desigualdade triangular envolvendo números reais.
Esboce o gráfico da função $f(x)=||(x-1)^2-3|-1|$.
Substitua as interrogações por expressões envolvendo $\epsilon, x_0$ e $y_0$ de modo que a afirmação abaixo seja verdadeira. Se $y_0 \neq 0$, $|y-y_0|<??$ e $|x-x_0|<??$, então $y \neq 0$ e $\left| \dfrac {x}{y}-\dfrac{x_0}{y_0}\right|<\epsilon$.
Resolva as equações:
- $|x-2|^2-5|x-2| =-6$
- $|x-2|-|x-1| =0$
Determine o conjunto solução da equação $|x|^2-5|x|+6=0$.
Mostre que a equação $|ax-b|=r$, com $r\geq 0$ e $a\neq 0$, tem como soluções os elementos do conjunto $\left\lbrace \frac{b+r}{a},\frac{b-r} {a}\right\rbrace$.
Temos duas possibilidades: $ax-b=r$ ou $ax-b=-r$. Da primeira equação obtemos $x=\dfrac{b+r}{a}$ e da segunda$x=\dfrac{b-r}{a}$.
Resolva a equação $|2x+1|=3$.
Se $2x+1\geq0$: $|2x+1| = 2x+1$, logo $2x+1=3 \Rightarrow x = 1$.
Se $2x+1<0$: $|2x+1| = -(2x+1)$, logo $-2x-1=3 \Rightarrow x = -2$.
Portanto $x=1$ ou $x=-2$.
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$x<y\Longleftrightarrow 1/y<1/x$.
$\sqrt{x^{2}}=x,\forall x\in \mathbb{R}$.
Esboce o gráfico da função $f(x)=|x^3+3x^2+3x-2|$.
Esboce o gráfico da função $f(x)=|(x-1)^2-3|$.
Obtenha a fórmula da distância entre dois pontos quaisquer no plano cartesiano. Use o teorema de Pitágoras. Veja o livro: Simmons, página $11$.
O volume de água em um tanque varia de acordo com a função $V(t)= 10 - |4-2t| -|2t - 6|$, onde $V$ é o volume medido em $m^3$ após $t$ horas, contadas a partir de $8$ h da manhã.
- Atribua um domínio para $V(t)$, considerando que um volume negativo não tem sentido na realidade.
- Faça o gráfico de $V(t)$ com $t$ no domínio estabelecido no item anterior.
- Para que valores de $t$ o tanque está enchendo?
- Para que valores de $t$ o tanque está esvaziando?
- Em qual horário o volume do tanque é constante?
Resolva as equações:
- $|x-1|^2-2|x-1| =-1$
- $|x-10|-|x+10| =0$
Qual o conjunto solução da equação $|x-2|-|x-1|+|x+3|=0$?
Para quaisquer $x,y\in \mathbb{R},$ mostre que vale $|xy|=|x||y|.$
Mostre que $|x|<x^{2}+1,\forall x\in \mathbb{R}$.
Resolva a inequação $|ax-b|<r$ na variável x, com $r>0$ e $a\neq 0$.
Se $ax-b\geq0$: $|ax-b| = ax-b$, logo $ax-b=r \Rightarrow x = \dfrac{b+r}{a}$.
Se $ax-b<0$: $|ax-b| = -(ax-b)$, logo $-ax+b=r \Rightarrow x = \dfrac{b-r}{a}$.
Portanto $x=\dfrac{b+r}{a}$ ou $x=\dfrac{b-r}{a}$.
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$|x-y|\leq |x|+|y|,\forall x,y\in \mathbb{R}$.
$x<y\Longrightarrow x^{2}<y^{2}$.
Resolva a equação modular $||x-2|-|x-1|+1| =2$.