Exercícios
Números reais
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine o conjunto de todos os números reais para os quais a expressão $\frac{\sqrt{4-x^2}}{\sqrt[3]{x-1}}$ está definida.
Classifique as afirmações em verdadeiras ou falsas.
Um número racional qualquer tem sempre um numero finito de ordens (casas) decimais.
Um número racional qualquer tem sempre um numero infinito de ordens (casas) decimais.
Um número racional qualquer não pode expressar-se em forma decimal exata.
Um número racional qualquer nunca se expressa em forma de uma decimal inexata.
F
F
F
F
Nos primórdios da geração comercial de eletricidade, havia uma disputa bastante acirrada entre duas formas de se distribuir energia elétrica: A disputa entre corrente alternada e corrente contínua. A corrente alternada provou-se mais eficiente para transmissão a longas distâncias, principalmente pela facilidade com que é possível elevar os níveis de tensão (e, portanto, para uma mesma potência transmitida, diminuir a corrente e consequentemente os diâmetros dos fios utilizados na transmissão, implicando em significativa economia).
Com o advento da eletrônica, na segunda metade do século XX, a corrente contínua reconquistou um papel fundamental no dia a dia da sociedade contemporânea, dado que circuitos eletrônicos são alimentados com corrente contínua. A conversão de corrente alternada é feita a partir de dispositivos chamados retificadores. Infelizmente, o funcionamento destes dispositivos foge do escopo desta disciplina.
As figuras abaixo representam uma corrente $i(t)$ antes e depois de um circuito:
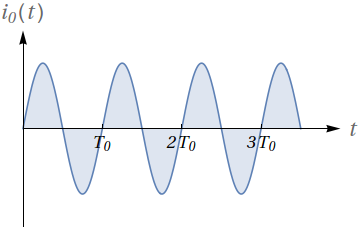
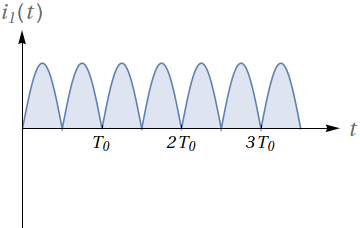
Responda:
- Dado que a função original seja $i_0(t)= \sin(2\pi\ 60\ t)$, qual a relação entre o seu período $T_0$ e o período da corrente retificada $i_1(t)$?
- Quais operações sobre a função $i_0(t)$ você realizaria para obter $i_1(t)$?
- Qual o valor médio, em um período, de $i_0(t)$? Qual seria sua estimativa para o valor médio de $i_1(t)$?
Seja o número inteiro $AB$, no qual $A$ e $B$ são os algarismos das dezenas e das unidades, respectivamente. Invertendo-se a posição dos algarismos $A$ e $B$, obtém-se um número que excede $AB$ em $27$ unidades. Se $A+B$ é um quadrado perfeito, qual o valor de $B$?
Temos que "$BA-AB$"$=10B+A-10A-B=9B-9A$. De acordo com o enunciado essa diferença é igual a $27$. Logo, $B-A=3$. Temos, portanto, $7$ possibilidades: "$BA$"$=30, 41, 52, 63, 74, 85$ ou $96$. Dentre essas possibilidades, a única em que $A+B$ é um quadrado perfeito é o caso $B=6$, $A=3$.
O produto das idades de três amigos adolescentes (entre $12$ e $19$ anos) corresponde a $4080$ anos. Qual a soma das três idades, em anos?
Decompondo o número $4080$ em fatores primos encontramos $4080=2^4 \cdot 15 \cdot 17=15 \cdot 16 \cdot 17$. Analisando essa decomposição, obtemos automaticamente que a única possibilidade que atende as exigências do enunciado é que as idades sejam $15,16$ e $17$ anos. A soma dessas idades é $15+16+17=48$ anos.
Dados dois números reais distintos $a$ e $b$, podemos definir uma função $f(x)$ que chamaremos "distância ao conjunto $\left\lbrace a,b \right\rbrace$" da seguinte forma: $f(x)$ é igual ao menor dos números $|x-a|$ ou $|x-b|$. Se $a=-b=1$, construa o gráfico de $f(x)$.
Para quaisquer $x,y\in \mathbb{R},$ mostre que vale $|xy|=|x||y|.$
Mostre que qualquer intervalo de $R$ contém algum número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Encontre os valores de $x$ para os quais cada o número $\sqrt[4]{{\frac{x^{2}-x-2}{x^{2}-4x-3}}}$ é real.
Prove que $\sqrt{6}$ é irracional.
Prove que para todo $x>0$ vale $x+\frac{1}{x}\geq 2$. Para quais números $x>0$ vale a igualdade?
Quais os valores de $x$ que satisfazem a inequação $\frac{x-3}{x-2}\leq x-1$?
Encontre os valores de $x$ para os quais cada o número $\sqrt{x^{2}+x+3}$ é real.
Este número será real se o valor dentro da raiz for maior ou igual a zero. Como $x^2 + x + 3$ têm raízes complexas e concavidade para cima, seu valor é sempre maior que zero. Portanto $\sqrt{x^2 + x + 3}$ é real para qualquer $x$ real.
O volume de água em um tanque varia de acordo com a função $V(t)= 10 - |4-2t| -|2t - 6|$, onde $V$ é o volume medido em $m^3$ após $t$ horas, contadas a partir de $8$ h da manhã.
- Atribua um domínio para $V(t)$, considerando que um volume negativo não tem sentido na realidade.
- Faça o gráfico de $V(t)$ com $t$ no domínio estabelecido no item anterior.
- Para que valores de $t$ o tanque está enchendo?
- Para que valores de $t$ o tanque está esvaziando?
- Em qual horário o volume do tanque é constante?
Sabendo-se que $\frac{x-a}{x^2+1} > \frac{x+a}{x^2}$ para todo $x$ real, determine o intevalo a que pertence o número real $a$.
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left\vert 2x^{2}-1\right\vert <1$.
Resolva as equações:
- $|x-2|^2-5|x-2| =-6$
- $|x-2|-|x-1| =0$
Sabendo que $x$ é um número negativo, simplifique a expressão $\sqrt{(x-3)^2}+\sqrt{x^2}+\sqrt{(4-3x)^2}$.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|2x-3|<5$
$|4-x|\geq 1$
Se $0<x<y$ prove que $\sqrt[3]{y-x}>\sqrt[3]{y}-\sqrt[3]{x}$.
A Lei de Ohm para circuitos elétricos, afirma que a queda de tensão em um resistor $R$ sob corrente $I$ é $V=RI$. Uma empresa recebeu pedidos de fornecimento de resistores para um circuito como o da figura a seguir. Neste circuito, $V=120V$ e, para atender as especificações de segurança e de funcionamento desejado do circuito, a corrente deve ser $I=5\pm0,1A$. Em que intervalo $R$ deve ficar para que $I$ esteja dentro da margem de segurança?
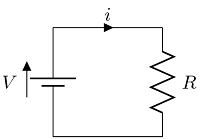
Pela Lei de Ohm, conseguimos escrever que $I=\frac{V}{R}$. Para $V=120V$ fixo, a corrente depende portanto apenas do valor da resistência, sendo inversamente proporcional a esta.
A corrente deve estar no intervalo $4,9 \leq I \ leq 5,1$. Temos que $R_{max}=\frac{120}{I_{min}}\approx 24,49$ e $R_{min}=\frac{120}{I_{max}}\approx 23,53 \Omega$.
Portanto, $23,53 \leq R \leq 24,49$.
Resolva a equação $\displaystyle \frac{x}{1-x} + \frac{x-2}{x}-1 = 0$.
Determine o conjunto solução da equação $|x|^2-5|x|+6=0$.
Para cada uma das afirmações abaixo, demonstre se verdadeiro
ou dê contra-exemplo se for falso.
- $|x-y|\leq |x|+|y|,\forall x,y\in \mathbb{R}$.
- $x<y\Longrightarrow x^{2}<y^{2}$.
- $x<y\Longleftrightarrow 1/y<1/x$.
Qual o conjunto solução da equação $|x-2|-|x-1|+|x+3|=0$?
Seja $n$ um número natural dado por $n= 2000 \cdot x$. Determine um possível valor para $x$ que torna $n$ um quadrado perfeito.
Sabemos que quando decompomos um quadrado perfeito em fatores primos, os expoentes dos números primos na decomposição são necessariamente múltiplos de $2$. Ora, decompondo $2000$ obtemos $2000=2^4 \cdot 5^3$. Se multiplicarmos $2000$ por $5$ obteremos $10000=2^4 \cdot 5^4$, que é um quadrado perfeito, a saber $100^2$. Neste caso tomamos $x=5$, mas há infinitas outras possibilidades!
Demonstre para todos números reais $a,b$ que $\max(a,b)=\frac{1}{2}(a+b)+\frac{1}{2}|b-a|,$ onde $\max(a,b)=a$ se $a\geq b$ e $\max(a,b)=b$ se $a<b$.
Mostre que $x\neq y\Longrightarrow x^{2}+2xy<2x^{2}+2y^{2}$.
Note que $(x-y)^2+y^2>0$ sempre que $x\neq y$. Daí, $x^2-2xy+y^2+y^2>0$, que é equivalente a $2x^2+2y^2-x^2-2xy>0$, que, por sua vez, é equivalente a x^{2}+2xy<2x^{2}+2y^{2}$.
Sejam $x$ e $y$ dois números reais positivos. Demonstre que $\sqrt{xy}\leq \dfrac{x+y}{2}.$
Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles.
Resolva a inequação $|ax-b|<r$ na variável x, com $r>0$ e $a\neq 0$.
Se $ax-b\geq0$: $|ax-b| = ax-b$, logo $ax-b=r \Rightarrow x = \dfrac{b+r}{a}$.
Se $ax-b<0$: $|ax-b| = -(ax-b)$, logo $-ax+b=r \Rightarrow x = \dfrac{b-r}{a}$.
Portanto $x=\dfrac{b+r}{a}$ ou $x=\dfrac{b-r}{a}$.
Mostre que a equação $|ax-b|=r$, com $r\geq 0$ e $a\neq 0$, tem como soluções os elementos do conjunto $\left\lbrace \frac{b+r}{a},\frac{b-r} {a}\right\rbrace$.
Temos duas possibilidades: $ax-b=r$ ou $ax-b=-r$. Da primeira equação obtemos $x=\dfrac{b+r}{a}$ e da segunda$x=\dfrac{b-r}{a}$.
Determine o conjunto de todos os números reais para os quais a expressão $\sqrt{x}{1-x^2}$ está definida.
Mostre que $|x|<x^{2}+1,\forall x\in \mathbb{R}$.
Qual a solução geral da dupla desigualdade $-2<x^2-3<\frac{1}{5}$?
Resolva a inequação $\frac{x^2+2x-1}{x^2-1} \geq \frac{1}{x+1}$.
Encontre a fração geratriz das dízimas seguintes:
- 2,001111...
- 2,1010101010...
- 1,23333333...
- $\begin{array}{rcl} 2,001111... &=& 2 + 0,00111... \\ &=& 2 + \dfrac{0,111...}{100} \\ &=& 2 + \dfrac{1}{100} \dfrac{1}{9} \\&=& 2 + \dfrac{1}{900} \\ &=& \dfrac{1800+1}{900} \\ &=& \dfrac{1801}{900}. \end{array} $
- $\begin{array}{rcl} 2,101010... &=& 2 + 0,101010... \\ &=& 2 + \dfrac{10}{99} \\ &=& \dfrac{198+10}{99} \\ &=& \dfrac{208}{99}. \end{array} $
- $\begin{array}{rcl} 1,2333... &=& 1,2 + 0,0333... \\ &=& \dfrac{12}{10} + \dfrac{1}{10}\dfrac{3}{9} \\ &=& \dfrac{12}{10} + \dfrac{3}{90} \\&=& \dfrac{108+3}{90} \\ &=& \dfrac{111}{90}. \end{array} $
Resolva a equação $\left| {\frac{3x+8}{2x-3}}\right| =4$.
Encontre os intervalos da reta real nos quais vale a desigualdade $\left| \frac{2x-3}{x+1}\right| \leq \frac{1}{2}.$
Resolva a equação $x^4-13x^2 + 36 = 0$.
Chamando $x^2=y$, transformamos a equação para:
$y^2 -13y + 36=0$. Resolvendo esta equação:
$\Delta = 13^2-4.1.36 = 25.$
$y = \dfrac{13 \pm \sqrt{25}}{2}.$
Assim as soluções são: $y = 9$ ou $y = 4$.
Substituindo em $y=x^2$:
$x^2 = 9 \Rightarrow x = \pm 3$.
$x^2 = 4 \Rightarrow x = \pm 2$.
Portanto as soluções são $x=-2$, $x=2$, $x=-3$ e $x=3$.
Substitua as interrogações por expressões envolvendo $\epsilon, x_0$ e $y_0$ de modo que a afirmação abaixo seja verdadeira. Se $y_0 \neq 0$, $|y-y_0|<??$ e $|x-x_0|<??$, então $y \neq 0$ e $\left| \dfrac {x}{y}-\dfrac{x_0}{y_0}\right|<\epsilon$.
Resolva a equação $|2x+1|=3$.
Temos dois casos: $2x+1=3$ ou $2x+1=-3$. Resolvendo cada uma dessas equações de primeiro grau obtemos $x=1$ e $x=-2$.
Mostre que $x^{2}-xy+y^{2}\geq 0$, $\forall x,y\in \mathbb{R}^+$ e que vale a igualdade se e somente se $x=y=0$.
Note que $x^{2}-xy+y^{2}=x^2-2xy+y^2+xy=(x-y)^2+xy \geq 0$, pois $(x-y)^2 \geq 0$ e $xy \geq 0$. O único modo de ocorrer a igualdade é quando as duas parcelas forem iguais a zero, o que ocorre se, e somente se, $x=y=0$.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$(x-1)^{2}<1-x$
$(2x-1)^{15}\leq 0$
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$2\leq {\frac{2}{3x-1}}\leq {\frac{20}{3}}$
${\frac{1}{2x+3}}\leq {\frac{x-1}{3}}\leq {\frac{1}{5}}$
Determine o conjunto solução da equação $|x|^2+|x|-6=0$.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
${\frac{3}{x}}+{\frac{x-3}{x-1}}<{\frac{2}{x-1}}$
${\frac{1}{x}}+{\frac{3}{2x}}\geq 5$
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$x<y\Longleftrightarrow 1/y<1/x$.
$\sqrt{x^{2}}=x,\forall x\in \mathbb{R}$.
Se $a$ é racional e $b$ é irracional então podemos afirmar alguma coisa sobre $a+b$ em termos de racionalidade ou irracionalidade?
Podemos afirmar que $a+b$ sempre será irracional.
Resolva a inequação $|ax-b|<r$ na variável x, com $r>0$ e $a\neq 0$.
Se $ax-b\geq0$: $|ax-b| = ax-b$, logo $ax-b<r \Rightarrow x < \dfrac{b+r}{a}$.
Se $ax-b<0$: $|ax-b| = -(ax-b)$, logo $-ax+b<r \Rightarrow x > \dfrac{b-r}{a}$.
Portanto $x<\dfrac{b+r}{a}$ ou $x>\dfrac{b-r}{a}$.
Resolva a equação $|x + 1| = 3$.
Temos dois casos: $x+1=3$ ou $x+1=-3$. Resolvendo cada uma dessas equações de primeiro grau obtemos $x=2$ e $x=-4$.
Encontre os valores de $x$ para os quais cada o número $\sqrt{7x+9}$ é real.
Este número será real se o valor dentro da raiz for maior ou igual a zero.
$\begin{array}{rcl} 7x+9 &\geq& 0 \\ 7x &\geq& -9 \\ x &\geq& -\dfrac{9}{7}. \end{array}$
Portanto o conjunto dos valores de $x$ tais que $\sqrt{7x+9}$ é real é $\{x \in \mathbb{R} ; x \geq -9/7\}$.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Suponha que exista um número inteiro $n$ tal que $0<n<1$. Então...
Prove que $\sqrt{2}+\sqrt{3}$ é irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left( 2x-3\right) \left( x^{2}+1\right) <0$.
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$|x-y|\leq |x|+|y|,\forall x,y\in \mathbb{R}$.
$x<y\Longrightarrow x^{2}<y^{2}$.
Prove que $\log2+\log3$ é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Note que $\log2+\log3=\log6$. Suponha que existam inteiros $p$ e $q$ tais que $log6=p/q$, com $p/q$ sendo fração irredutível. Use a definição de logaritmo e o teorema fundamental da aritmética para chegar a um absurdo.
Mostre que $\sqrt{xy}\leq {\frac{x+y}{2}}$$\forall x,y\geq 0$.
Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Obtenha a fórmula da distância entre dois pontos quaisquer no plano cartesiano. Use o teorema de Pitágoras. Veja o livro: Simmons, página $11$.
Use a desigualdade triangular $\left| a+b\right| \leq \left| a\right|+\left| b\right| $\emph{ }para mostrar que $\left| x-y\right| \geq \left|x\right| -\left| y\right| $ para todo $x,y\in \mathbb{R}$. Em particular, conclua que $\left| x-y^{2}\right| \geq \left| x\right| -y^{2}.$
Classifique as afirmações a seguir em verdadeiras ou falsas.
No conjunto dos números inteiros existe um elemento que é menor do que todos os outros.
O número real representado por 0,37222... é um número racional.
Toda raiz de uma equação algébrica do 2º grau é um número real.
O quadrado de qualquer número real é um número racional.
F
V
F
F
Considere o número inteiro $P = 100 \cdot 101 \cdot 102 \cdot \ldots \cdot 200$, produto de $101$ números inteiros sucessivos. Ao escrever-se $P$ como um produto de fatores primos, qual o número de vezes que o fator $7$ aparece?
Esboce o gráfico da função $f(x)=||(x-1)^2-3|-1|$.
Esboce o gráfico da função $f(x)=|(x-1)^2-3|$.
Calcule o valor de $\frac{2}{0,666 \ldots}$.
$$\begin{array}{rcl} \dfrac{2}{0.666 \ldots} &=& \dfrac{2}{\dfrac{6}{9}} \\ &=& 2 \dfrac{9}{6} \\ &=& \dfrac{9}{3} \\ &=& 3. \end{array}$$
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left\vert x-2\right\vert +\left\vert x-1\right\vert >1$.
Três números naturais e múltiplos consecutivos de 5 são tais que o triplo do menor é igual ao dobro do maior. Dentre esses números, qual o maior?
Note que todo múltiplo de $5$ pode ser escrito na forma $5n$, onde $n$ é algum número natural. Com essa ideia, podemos representar três múltiplos consecutivos de $5$ por: $5(n-1)$, $5n$ e $5(n+1)$. Como o triplo do menor é igual ao dobro do maior obtemos a equação $15(n-1)=10(n+1)$. Resolvendo essa equação encontramos $n=5$ e o maior número dentre os três é $5 \cdot 6=30$.
Mostre que $x^{2}-xy+y^{2}\geq 0$, $\forall x,y\in R$ e que vale a igualdade se e somente se $x=y=0$.
Resolva a equação modular $|x-2|-|x-1| =2$.
Encontre os valores de $x$ para os quais cada o número $\sqrt{{\frac{5x-2}{x^{2}-4}}}$ é real.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$7+|x|<{\frac{1}{x+2}}$
$\left| {\frac{2x-3}{x+1}}\right| \leq {\frac{1}{2}}$
Se duas torneiras, de igual vazão, enchem uma piscina em $5$ horas, quanto tempo três torneiras, de mesma vazão que as primeiras, encherão a piscina?
Como duas torneiras de igual vazão enchem a piscina em $5$ horas, uma única torneira encheria em $10$ horas. Ora, $3$ torneiras de igual vazão trabalhando juntas reduziriam esse tempo de $10$ horas dividindo-o por $3$. A resposta é $10/3$ horas.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
${\frac{|x-3|}{|x+7|}}>0$
$|x+4|\geq |x+1|$
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|2x+1|\leq 1$
$\left| {\frac{x}{x^{2}+1}}\right| \leq 1$
Mostre que $|x-y|<1/2,|x+2|<1/3\Longrightarrow |y+2|<5/6$.
Sejam $a, b$ racionais positivos. Prove que $\sqrt{a}+\sqrt{b}$ é racional se, e somente se, $\sqrt{a}$ e $\sqrt{b}$ forem ambos racionais. (Sugestão: multiplique por $\sqrt{a}-\sqrt{b}$).
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$x\neq y\Longrightarrow |x|\neq |y|$.
$|x-y|\geq |x|-|y| \forall x,y\in \mathbb{R}$
Prove que $\sqrt{p}$, onde $p$ é primo, é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Prove que $|x+y|=|x|+|y| \Leftrightarrow xy \geq 0$.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$(2-5x)^{20}>0$
${\frac{x-3}{x-5}}>0$
Resolva a equação modular $||x-2|-|x-1|+1| =2$.
Dadas $a$ e $b$ constantes reais não nulas, esboce um gráfico da família de funções $f(x)=min\{|x-a|,|x-b|\}$.
Prove que $\sqrt{2}$ é irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Classifique cada uma das afirmações abaixo em verdadeiras ou falsas.
Nem todo primo é ímpar.
Todo inteiro par pode ser escrito na forma $n^2+2, n \in N$.
A soma de dois inteiros ímpares é sempre um inteiro par.
Todo inteiro ímpar pode ser escrito na forma $2n-9, n \in N$.
Se $n$ é um inteiro ímpar, então $n^2$ também é ímpar.
V
F
V
V
V
Quatro números inteiros positivos e distintos, $m, n, p$ e $q$, satisfazem a equação $(7-m)(7-n)(7-p)(7-q)=4$.
Calcule a soma $m+n+p+q$.
A única maneira de escrevermos $4$ como produto de inteiros positivos, a menos de ordem dos fatores, é $4=1 \cdot 1\cdot 2 \cdot 2$. Assim, uma possibilidade é $m=n=6, p=q=5$. Há várias outras possibilidades, mas que não alterarão a soma $m+n+p+q=22$. De fato, se mudássemos os valores de $m,n,p$ e $q$, eles continuaríam sendo $1,1,2$ e $2$ em alguma ordem e a soma não mudaria, já que a adição é comutativa e associativa.
Perguntei a idade de minha professora de Matemática. Ela me contou e falou também a idade da filha, mas disse isso de modo enigmático por meio da expressão: "A soma de minha idade com a da minha filha é 44 anos. Dez anos atrás, eu tinha o triplo da idade dela."
- "Traduza" a primeira frase da expressão da professora por uma equação, representando por $x$ a idade da professora e por $y$, a idade de sua filha.
- Faça o mesmo com a segunda frase.
- Resolva o sistema obtido e dê a idade da professora e a de sua filha.
Seja $x$ a idade da professora e $y$ a idade da filha. Temos, portanto
- $x+y=44$
- $x-10=3(y-10)$, ou, reescrevendo com as incógnitas do lado esquerdo, $x-3y=-20$
- Resolver $\begin{pmatrix} 1 & 1 \\ 1 &-3 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 44 \\ -20 \end{pmatrix}$ nos dá $\begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 28 \\ 16 \end{pmatrix}$
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left\vert x-1\right\vert -\left\vert x+2\right\vert >x$.
Esboce o gráfico da função $f(x)=|x^3+3x^2+3x-2|$.
Resolva a equação $\sqrt{9x+4} + \sqrt{3x-4} = 2 \sqrt{3x}$.
Suponha que $x$ e $y$ sejam notas de provas bimestrais. Mostre que a chamada {\it média geométrica} entre $x$ e $y$, dada por $\sqrt{xy}$, poderia, se adotada como critério avaliativo, prejudicar a nota final de alguns alunos, isto é, elaé menor que ou igual à chamada {\it média aritmética} entre $x$ e $y$, que é dada por $\frac{x+y}{2}.$
Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles. Sendo assim, se o professor adotar como critério de avaliação a média geométrica em vez da aritmética, ele pode prejudicar a nota final dos alunos que tivessem a nota $x$ diferente da $y$, pois quando $x=y$ as duas médias são iguais.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|6+4x|<\left| 2-{\frac{x}{2}}\right| $
$\left| {\frac{5}{3x-2}}\right| \geq \left| {\frac{2}{x-1}}\right| $
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Pesquise sobre a diagonal de Cantor!
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Resolva a equação modular $|x-1|-2|x-2| =-3$.
Classifique as afirmações em verdadeiras ou falsas.
A soma de dois números racionais é sempre um número racional.
A soma de dois números irracionais é sempre um número irracional.
A soma de um número racional com um número irracional é sempre um número irracional.
V
F
V
Prove que $\log2$ é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Suponha que existam inteiros $p$ e $q$ tais que $log2=p/q$, com $p/q$ sendo fração irredutível. Use a definição de logaritmo e o teorema fundamental da aritmética para chegar a um absurdo.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|x+5|\geq \sqrt{2}$
$|x-1|\leq |x+1|$
Uma empresa de motores solicitou a fabricação de cilindros com área de seção transversal $A=9cm^2$ (Ou seja, com diâmetro $D=3,385cm^2$). Entretanto, o funcionário que respondeu à solicitação perguntou qual era a margem de erro permitida no diâmetro do cilindro.
Dado que para o correto funcionamento dos motores o cilindro deve ter uma área $A$ tal que $|A-9|<0,01 cm^2$, e que a área da seção transversal do cilindro é dada por $A=\pi \left(\frac{D}{2}\right)^2$, em qual intervalo deve estar o valor do diâmetro do cilindro para atender tal especificação?
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$(2-x)(x-1)$
$1-x^{2}<0$
Enuncie e prove a desigualdade triangular envolvendo números reais.
O produto de um racional diferente de zero com um irracional é racional ou irracional? Justifique.
É irracional.
Mostre que:
- $x\neq y\Longrightarrow x^{2}+2xy<2x^{2}+2y^{2}$.
- $|x|<x^{2}+1,\forall x \in \mathbb{R}$.
Sejam $a<b$ dois reais e $p \in \left]a,b \right[$. Determine $r>0$ de modo que $\left]p-r,p+r \right[ \subset \left]a,b \right[$.
Resolva a equação $\left| {\frac{3x+8}{2x-3}}\right| =4$.
Temos duas possibilidades: $\frac{3x+8}{2x-3}=4$ ou $\frac{3x+8}{2x-3}=-4$. Da primeira equação obtemos $3x+8=8x-12$, i. e., $x=4$. Da segunda equação obtemos $3x+8=-8x+12$, que fornece $x=4/11$.
Existem, para doação a escolas, $2000$ ingressos de um espetáculo e $1575$ de outro. Cada escola deve receber ingressos para somente um dos espetáculos e todas as escolas devem receber a mesma quantidade de ingressos. Distribuindo-se todos os ingressos, qual o número mínimo de escolas que poderão ser contempladas nessa doação?
Determine qual o último número $N$, escrito na sucessão dos números naturais $12345678910111213...N$, sabendo que foram escritos $3849$ algarismos.
Para cada uma das afirmações abaixo, demonstre se verdadeiro
ou dê contra-exemplo se for falso.
- $\sqrt{x^{2}}=x,\forall x \in \mathbb{R}$.
- $x\neq y\Longrightarrow |x|\neq |y|$.
- $|x-y|\geq |x|-|y| \forall x,y\in \mathbb{R}$.
Considere os números inteiros ``$abc$'' e ``$bac$'', em que $a$, $b$ e $c$ são algarismos distintos e diferentes de zero e $a>b$. A diferença $abc-bac$ é sempre um múltiplo de determinado número. Que número é esse?
Note que "$abc$"$=100a+10b+c$ e que "$bac$"$=100b+10a+c$. Assim, "$abc$"-"$bac$"$=90a-90b=90(a-b)$, que é um número sempre múltiplo de $90$ e de todos os divisores de $90$.
Mostre que:
- $|x-y|<1/2, |x+2|<1/3 \Longrightarrow |y+2|<5/6$
- $\sqrt{xy}\leq {\frac{x+y}{2}}$, $\forall x,y\geq 0$.
Se $0<x<y$ prove que $\sqrt[3]{y-x}>\sqrt[3]{y}-\sqrt[3]{x}$.
Resolva a equação $|2x+1|=3$.
Se $2x+1\geq0$: $|2x+1| = 2x+1$, logo $2x+1=3 \Rightarrow x = 1$.
Se $2x+1<0$: $|2x+1| = -(2x+1)$, logo $-2x-1=3 \Rightarrow x = -2$.
Portanto $x=1$ ou $x=-2$.
Resolva as equações:
- $|x-1|^2-2|x-1| =-1$
- $|x-10|-|x+10| =0$
O princípio da Boa Ordenação diz que todo subconjunto não-vazio de $N$ possui elemento mínimo. Demonstre que $N$, com a relação $\leq$, verifica o Princípio da Boa Ordenação.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Prove que $\sqrt{3}$ é irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\dfrac{\left( x-3\right) }{x^{2}+1}<0$.
Prove que $\log3$ é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Suponha que existam inteiros $p$ e $q$ tais que $log3=p/q$, com $p/q$ sendo fração irredutível. Use a definição de logaritmo e o teorema fundamental da aritmética para chegar a um absurdo.
Prove que a soma de um racional com um irracional é um irracional.

