Exercícios
Área de superfície de revolução
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Utilize a fórmula
\[
S=\int_{a}^{b}2\pi f\left( x\right) \sqrt{1+\left( f^{\prime}\left(
x\right) \right) ^{2}}dx
\]
para mostrar que a superfície de uma esfera de raio $R$ é $4\pi
R^{2}$.
Uma esfera de raio $R$ centrada na origem pode ser obtida pela rotação ao redor do eixo $x$ do semicírculo $x^{2}+y^{2}=R^{2}$ com $y\geq0$. Este semicírculo pode ser visto como o gráfico da função $f\left( x\right) =\sqrt{R^{2}-x^{2}}$, com $t\in\left[-R,R\right] $.
Considerando $f\left( x\right) =\sqrt{R^{2}-x^{2}}$ temos que:
\[
f^{\prime}\left( x\right) =-\frac{t}{\sqrt{R^{2}-x^{2}}}\text{.}%
\]
Usando a fórmula acima temos que:
\begin{align*}
S & =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{1+\left( f^{\prime}\left(
x\right) \right) ^{2}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{1+\frac{x^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{\frac{\left( R^{2}-x^{2}\right)
+x^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{\frac{R^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi R\frac{\sqrt{R^{2}-x^{2}}}{\sqrt{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi Rdx
\end{align*}
Temos então que:
\begin{align*} S & =\int_{-R}^{R}2\pi Rdx\\ & =\left. 2\pi Rx\right\vert _{-R}^{R}\\ & =4\pi R^{2} \end{align*}
Ache a área da superfície gerada fazendo girar a curva paramétrica $x=t^2,y=2t,0 \leq t\leq 4$, em torno do eixo $x$.
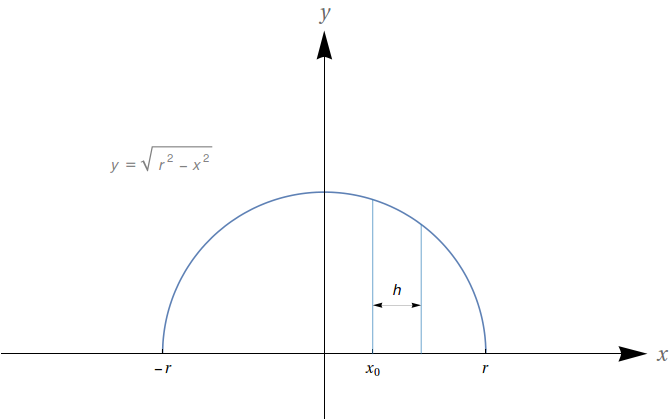
Demonstre que, ao se cortar uma cebola em fatias de igual largura, todas as fatias terão a mesma quantidade de casca.
Para isso, considere o semicírculo dado pela equação $y=\sqrt{r^2-x^2}$. A rotação deste em torno do eixo $x$ resultará numa esfera. Se escolhermos $x_0 >0$ e $h>0$ tal que $-r \leq x_0 < r$ e $x_0+h \geq r$, e o arco $AB$ localizado acima deste intervalo.
Demonstre que a área gerada pela rotação do arco $AB$ não depende de $x_0$, apenas de $h$.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=\sqrt{2}$, $3/4\leq x \leq 15/4$, eixo $x$
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=\sqrt{2x-x^2}$, $0,5\leq x \leq 1,5$, eixo $x$
Mostre que a a área lateral $S$ de um cone circular reto de altura $h$ e raio da base $r$ é $S=\pi r \sqrt{r^2+h^2}$.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=x^3/9$, $0\leq x \leq 2$, eixo $x$
Como o parabolóide é obtido pela rotação ao redor do eixo $y$ temos que o raio $r:=d/2=4$ corresponde a variação de $x$ e a altura corresponde a variação de $y$, ou seja, para $x=4$ devemos ter $y=ax^{2}=4$ donde obtemos que $a=y/x^{2}=4/4^{2}=1/4$, e consideramos a parábola $y=\frac{x^{2}}{4}$.
Como o parabolóide é obtido pela rotação ao redor do eixo $y$ devemos considerar $x$ como funçao de $y$, ou seja, $x=x\left( y\right) =2\sqrt{y}$. Temos então que:
\begin{align*}
x^{\prime}\left( y\right) & =\frac{1}{\sqrt{y}}\\
\sqrt{1+\left( x^{\prime}\left( y\right) \right) ^{2}} & =\sqrt
{1+\frac{1}{y}}=\frac{\sqrt{y+1}}{\sqrt{y}}%
\end{align*}
Temos então que a área $S$ da superfície é dada por:
\begin{align*}
S & =\int_{0}^{4}2\pi\left( 2\sqrt{y}\right) \frac{\sqrt{y+1}}{\sqrt{y}%
}dy\\
& =4\pi\int_{0}^{4}\sqrt{y+1}dy
\end{align*}
Substituindo $u=y+1,~du=dy$ obtemos:
\begin{align*}
S & =4\pi\int_{1}^{5}\sqrt{u}du\\
& =4\pi\frac{2}{3}\left. u^{3/2}\right\vert _{1}^{5}\\
& =\frac{8\pi}{3}\left( 5^{3/2}-1\right)
\end{align*}
Mostre que a área da superfície de uma esfera de raio $r$ é $4 \pi r^2$.
O laço de de $9y^2=x(3-x)^2$ é girado ao redor do eixo $y$. Calcule a área da superfície gerada por essa maneira.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$x=\frac{(e^y+e^{-y})}{2}$, $0\leq y \leq ln\ 2$, eixo $y$
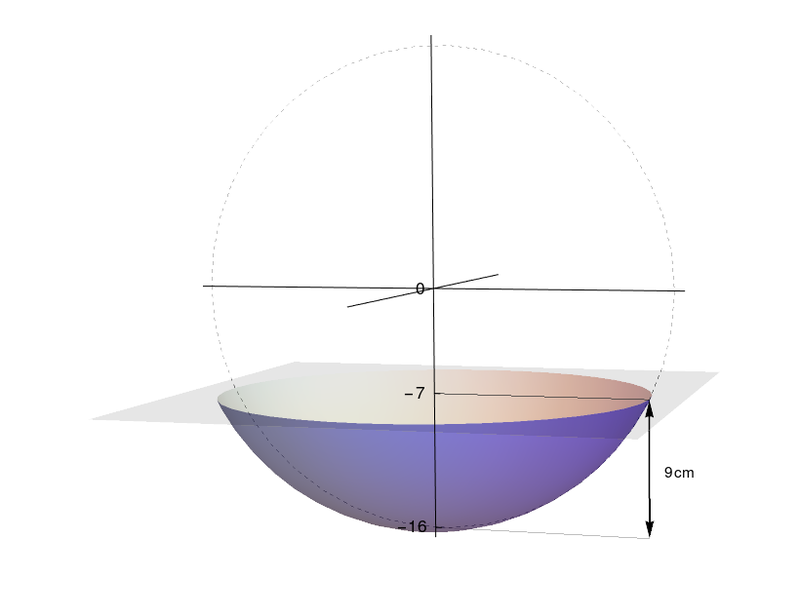
Uma empresa deseja lançar uma tigela esmaltada de branco por dentro e de vermelho por fora. A camada de esmalte terá $0,5mm$ de espessura antes de ir ao forno. O departamento de produção quer saber a quantidade de cada esmalte que precisará dispor para produzir $5000$ tigelas. Ignorando desperdício e matéria prima não utilizada, dê a sua resposta em litros. Lembre-se de que $1\ cm^3 = 1m\ell$, logo $1\ell=1000cm^3$.