Exercícios
Área entre curvas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Calcule a área do conjunto $A$ dos pontos $\left( x,y\right)$ tais que $x^{2}-1\leq y\leq x+1.$
Calcule a área no plano entre os gráficos de $f\left( x\right) =x^{3}-x$ e $g\left( x\right) =sen\left( \pi x\right) $ no intervalo $[0,1]$.
Sabemos que, no intervalo $[0,1]$, $g(x)=\sin(\pi x)>0$. Uma análise das raízes de $f(x)=x^3-x$ nos mostra que no intervalo referido, $f(x)<0$. Assim,como não há mudança de sinal de $f(x)-g(x)$, o cálculo da área entre as curvas se resumo ao cálculo da integral definida
$\int_0^1 \left(g(x)-f(x)\right)\,dx= \left.\left(-\frac{x^4}{4}+\frac{x^2}{2}-\frac{\cos (\pi x)}{\pi }\right) \right\vert_0^1=\frac{1}{4}+\frac{2}{\pi }$
Encontre a área limitada pela elipse $\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\text{.}$
Encontre a área da região no primeiro quadrante limitada pelos eixos coordenados e pela curva $y=\frac{\sqrt{9-x^2}}{3}.$
Qual das integrais a seguir, se houver alguma, serve para calcular a área da região sombreada mostrada aqui? Justifique sua resposta.
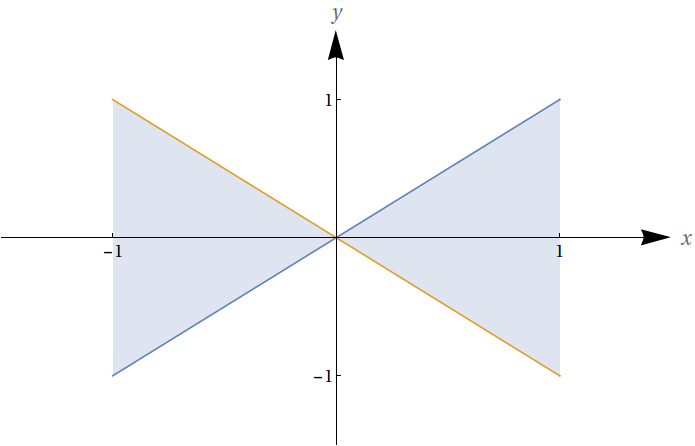 $\int_{-1}^{1} {\left(x-\left(-x\right)\right)dx} = \int_{-1}^{1} {2x\ dx}$
$\int_{-1}^{1} {\left(x-\left(-x\right)\right)dx} = \int_{-1}^{1} {2x\ dx}$- $\int_{-1}^{1} {\left(-x-x\right)dx} = \int_{-1}^{1} {-2x\ dx}$
Uma análise do resultado de ambas as integrais nos mostra, de imediato, que nenhuma delas é a adequada para o cálculo da área da figura. A segunda integral nada mais é do que a primeira integral com o sinal invertido, e portanto ambas são iguais a zero.
A questão é que no caso, se denotarmos $f_1(x)=x$ e $f_2(x)=-x$, é fácil observar que para $x>0$ $f_1(x)>f_2(x)$, e para $x<0$ $f_2(x)>f_1(x)$. Portanto, o cálculo correto da área se daria através de duas integrais, na forma
$A=\int_{-1}^{0} {\left(-x-x\right)dx}+\int_{0}^{1} {\left(x-\left(-x\right)\right)dx}$
Ou ainda, fazendo uso da simetria, poderia também se fazer:
$A=2\int_{0}^{1} {\left(x-\left(-x\right)\right)dx}=4\int_{0}^{1} {x\,dx}=2$
Seja $\mathcal{A}$ o subconjunto do plano limitado pelas retas $x=0$, $x=\frac{\pi}{2}$ e pelos gráficos de $y=\sin x$ e $y=\cos x$. Faça um esboço do conjunto $\mathcal{A}$ e calcule sua área.
Um retângulo com os lados paralelos aos eixos coordenados tem um vértice na origem e o vértice diagonalmente oposto está sobre a curva $y=kx^m$ no ponto onde $x=b$ ($b>0$, $k>0$, $m \geq 0$). Mostre que o quociente entre a área do retângulo compreendida entre a curva e o eixo $x$ depende de $m$, mas não depende de $k$ ou $b$.
A figura mostra as curvas aceleração versus tempo para dois carros movendo-se em uma pista reta, começando alinhados e acelerando a partir do repouso. O que representa a área $A$ entre as curvas no intervalo $0 \leq t \leq T$? Justifique.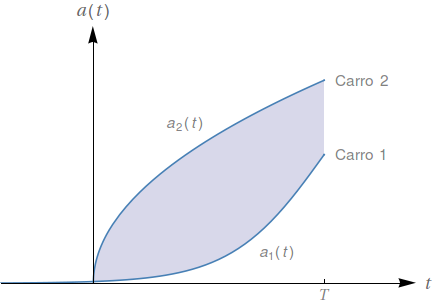
Para uma aceleração $a(t)$ qualquer, $\int_0^Ta(t)\,dt$ representa a velocidade adquirida desde o instante $t=0$, ou seja, $v(T)= v_0+\int_0^Ta(t)\,dt$. Sendo assim, a área entre as curvas representa $v_1(T)-v_2(T)$, a diferença de velocidade entre os carros no instante $t=T$.
Determine a área da região no primeiro quadrante limitada à esquerda pelo eixo $y$, abaixo pela curva $x=2\sqrt{y}$, acima à esquerda pela curva $x=\left(y-1\right)^2$ e acima à direita pela reta $x=3-y$.
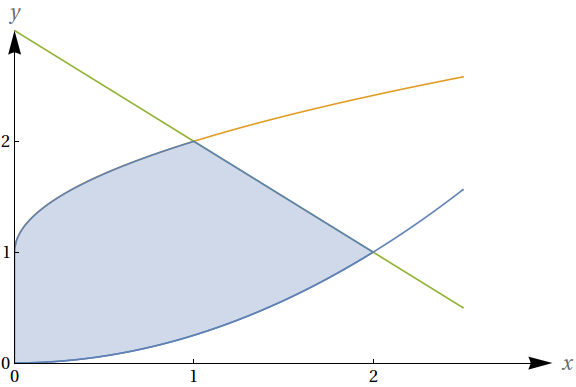
Primeiramente, devemos escrever as curvas na forma $y=f(x)$, tomando cuidado com o sinal. Após este procedimento, uma análise da figura nos permite resumir o cálculo da área $A$ como $A=A_1+A_2$, sendo que:
$A_1=\int_0^1\left (1+\sqrt{x}-\frac{1}{4}x^2\right)\,dx$
$A_2=\int_1^2\left (3-x-\frac{1}{4}x^2\right)\,dx$
Assim, temos
$A_1=\left.\left(x + \frac{2}{3} x^{3/2} - x^3/12\right)\right\vert_0^1=\frac{19}{12}$
$A_2=\left.\left(-\frac{x^3}{12}-\frac{x^2}{2}+3 x\right)\right\vert_1^2=\frac{11}{12}$
O que nos leva a $A=\frac{5}{2}=2.5$
Ache uma reta vertical $x=k$ que divida a área entre as curvas $y=x^2$ e $y=9$ em duas partes iguais.
$x=k=0$
Calcule a área no plano entre os gráficos de $f\left( x\right) =x^{3}-x$ e $g\left( x\right) =sen\left( \pi x\right) $ no intervalo $[0,1]$.
Encontre a área da região limitada pela elipse $x^2+\frac{y^2}{4}=1.$
Primeiramente, escreve-se a equação da elipse na forma $y=\pm f(x)$:
$y=\pm 2\sqrt{1-x^2}$
Observação: Nesta forma, é possível ver mais facilmente que a elipse não apresenta nenhum ponto com $\left\vert x\right\vert >1$.
Se denotarmos $f_1(x)= 2\sqrt{1-x^2}$ e $f_2(x)=- 2\sqrt{1-x^2} $, a área da região limitada pela elipse é portanto
$\int_{-1}^{1}f_1(x)-f_2(x)\,dx=2\int_{-1}^{1}f_1(x)\,dx=2 \left(\sqrt{1-x^2} x+\sin ^{-1}(x)\right)=2\pi$

