Exercícios
Comprimento de arco
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Seja $y=f(x)$ uma curva suave em $\left[a,b\right]$. Prove que se houver números não-negativos $m$ e $M$, tais que $m \leq f'(x) \leq M$ para todo $x$ em $\left[a,b\right]$, então o comprimento de arco $L$ de $y=f(x)$ satisfaz a desigualdade $(b-a)\sqrt{1+m^2} \leq L \leq (b-a) \sqrt{1+M^2}$.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=x^{3/2},\quad 0 \leq x \leq 4$
Prove que o comprimento de um arco de ciclóide é igual a $8$ vezes o tamanho do raio do seu círculo gerador. A figura abaixo mostra dois arcos e meio de ciclóide.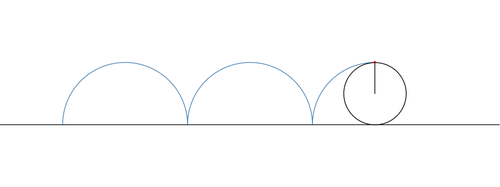
Determine o comprimento da curva a seguir no intervalo especificado.
$y=(3/4)x^{4/3}-(3/8)x^{2/3}+5,\quad 0 \leq x \leq 3$
Lembrando que o comprimento do traçado de um gráfico de uma função $f(x)$ no intervalo $[a,b]$ é dado por $\int_a^b \sqrt{1+(f'(x))^2} dx$, calcule o comprimento da circunferência de raio $r=1$.
Utilize a fórmula
\[
s\left( x\right) =\int_{a}^{x}\sqrt{1+\left( f^{\prime}\left( t\right)
\right) ^{2}}dt
\]
para mostrar que o perímetro de uma circunferência de raio $R$ é $2\pi R$.
Uma circunferência de raio $R$ centrada na origem pode ser vista como a união dos gráficos das funções $f\left(t\right) =\sqrt{R^{2}-t^{2}}$ e $g\left( t\right) =-\sqrt{R^{2}-t^{2}}$, com $t\in\left[ -R,R\right] $ Por simetria, estes dois arcos têm o mesmo comprimento, digamos $L$, e o perímetro $p$ é dado por $p=2L$.
Considerando $f\left( t\right) =\sqrt{R^{2}-t^{2}}$ temos
que:
\[
f^{\prime}\left( t\right) =-\frac{t}{\sqrt{R^{2}-t^{2}}}\text{.}%
\]
Usando a fórmula acima temos que:
\begin{align*}
L & =\int_{-R}^{R}\sqrt{1+\left( f^{\prime}\left( t\right) \right) ^{2}%
}dt\\
& =\int_{-R}^{R}\sqrt{1+\frac{t^{2}}{R^{2}-t^{2}}}dt\\
& =\int_{-R}^{R}\sqrt{\frac{\left( R^{2}-t^{2}\right) +t^{2}}{R^{2}-t^{2}}%
}dt\\
& =\int_{-R}^{R}\sqrt{\frac{R^{2}}{R^{2}-t^{2}}}dt\\
& =R\int_{-R}^{R}\frac{1}{\sqrt{R^{2}-t^{2}}}dt
\end{align*}
Fazendo a mudança de variável $t=R\sin\theta$, com $-\pi/2\leq\theta\leq\pi/2$, temos que:
\begin{align*}
\sqrt{R^{2}-t^{2}} & =\sqrt{R^{2}-R^{2}\sin^{2}\theta}\\
& =R\sqrt{1-\sin^{2}\theta}\\
& =R\cos\theta,\\
dt & =R\cos\theta d\theta
\end{align*}
Obtemos assim que:
\begin{align*}
L & =R\int_{-R}^{R}\frac{1}{\sqrt{R^{2}-t^{2}}}dt\\
& =R\int_{-\pi/2}^{\pi/2}\frac{R\cos\theta}{R\cos\theta}d\theta\\
& =R\int_{-\pi/2}^{\pi/2}d\theta\\
& \left. R\theta\right\vert _{-\pi/2}^{\pi/2}\\
& =\pi R
\end{align*}
e concluimos que:
\[
p=2L=2\pi R
\]
- Use um recurso gráfico para gerar o gráfico de uma astróide usando $a=1$.
- Ache o comprimento exato de uma astróide.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=\int_{-2}^{x}{\sqrt{3t^4-1}dt},\quad -2 \leq x \leq -1$
A ciclóide é um caminho traçado por um ponto na borda de uma roda que gira ao longo de uma reta. Use as equações paramétricas de uma ciclóide para mostrar que o comprimento $L$ de um arco de uma ciclóide é dado pela integral $L=\displaystyle\int_{0}^{2\pi} \sqrt{2(1-\cos\theta)}d \theta$
Determine o comprimento da curva a seguir no intervalo especificado.
$y=(1/3)\left(x^2+2\right)^{3/2},\quad 0 \leq x \leq 3$
Existe uma curva continuamente derivável $y=f(x)$ cujo comprimento ao longo do intervalo $0\leq x\leq a$ seja sempre $\sqrt{2}a$?
Ache o comprimento exato do arco formado pela curva $x=\dfrac{1}{8}y^4+\dfrac{1}{4}y^{-2}$ de $y=1$ até $y=4$.
Mostre que o comprimento de arco total da elipse $x=a \cos t$, $y=b \sin t$, $0 \leq t \leq 2\pi$, para $a>b>0$ é dado por $4\displaystyle\int_{0}^{\pi/2} \sqrt{1+3\sin^3 t}dt$.

