Exercícios
Aplicações da Integral
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$x=\frac{(e^y+e^{-y})}{2}$, $0\leq y \leq ln\ 2$, eixo $y$
Use camadas cilíndricas para encontrar o volume do sólido resultante quando se faz girar a área entre as curvas $y=2x-1$, $y=-2x+3$ e $x=2$ em torno do eixo $y$.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=\sqrt{2x-x^2}$, $0,5\leq x \leq 1,5$, eixo $x$
Considere um cilindro com base de diâmetro $2R$ e altura também $2R$. Considere, inscrito neste cilindro, uma esfera de raio $R$ e um cone de base circular com diâmetro $2R$ e altura $2R$. Denote por $V_{cil}$, $V_{esf}$ e $V_{cone}$, respectivamente, os volumes desses sólidos.
- Verifique as relações $V_{esf}= \frac{2}{3}V_{cil}$ e $V_{cone}=\frac{1}{3}V_{cil}.$
- Calcule $V_{cil}$, $V_{esf}$ e $V_{cone}$ usando integrais. Explicite o método que está usando.
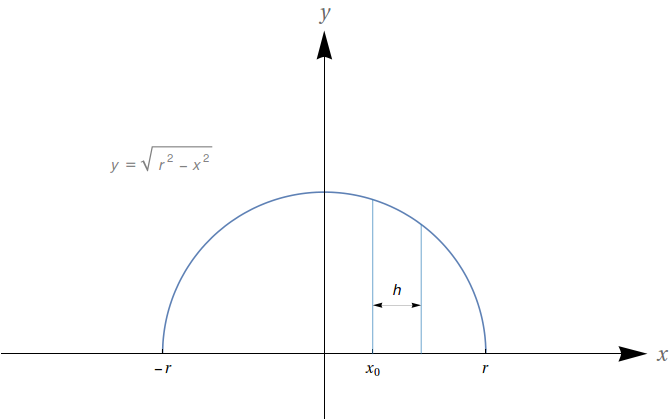
Demonstre que, ao se cortar uma cebola em fatias de igual largura, todas as fatias terão a mesma quantidade de casca.
Para isso, considere o semicírculo dado pela equação $y=\sqrt{r^2-x^2}$. A rotação deste em torno do eixo $x$ resultará numa esfera. Se escolhermos $x_0 >0$ e $h>0$ tal que $-r \leq x_0 < r$ e $x_0+h \geq r$, e o arco $AB$ localizado acima deste intervalo.
Demonstre que a área gerada pela rotação do arco $AB$ não depende de $x_0$, apenas de $h$.

Encontre o volume de uma pirâmide de base quadrada com lado $L$ e altura $h$.
Mostre que o volume de uma esfera de raio $R$ é $\dfrac{4}{3}\pi R^{3}$.
Lembrando que o comprimento do traçado de um gráfico de uma função $f(x)$ no intervalo $[a,b]$ é dado por $\int_a^b \sqrt{1+(f'(x))^2} dx$, calcule o comprimento da circunferência de raio $r=1$.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=\int_{-2}^{x}{\sqrt{3t^4-1}dt},\quad -2 \leq x \leq -1$
Usando a fórmula do volume de uma calota esférica, encontre o volume do sólido que sobra quando um buraco de raio $\dfrac{r}{2}$ é feito através do centro de uma esfera de raio $r$ e verifique a sua resposta por integração.
Considere:
- Um cilindro $CI_r$ de raio $r$ e altura $r$.
- Um cone $CO_r$ de raio $r$ e altura $r$.
- Uma pirâmide $P_r$ de base quadrada com diagonal de comprimento $2r$ e altura $r$.
Para cada um destes três sólidos, expresse o volume em forma de integral e demonstre que a relação (proporção) entre estes volumes não depende do parâmetro $r$.
Seja $y=f(x)$ uma curva suave em $\left[a,b\right]$. Prove que se houver números não-negativos $m$ e $M$, tais que $m \leq f'(x) \leq M$ para todo $x$ em $\left[a,b\right]$, então o comprimento de arco $L$ de $y=f(x)$ satisfaz a desigualdade $(b-a)\sqrt{1+m^2} \leq L \leq (b-a) \sqrt{1+M^2}$.
Mostre que se $f$ é contínua e côncava para cima em $\left[a,b\right]$, então $f_{med}>f\left(\dfrac{a-b}{2}\right)$, onde $f_{med}$ é o valor médio da função $f$ no intervalo $\left[a,b\right]$.
Calcule a área no plano entre os gráficos de $f\left( x\right) =x^{3}-x$ e $g\left( x\right) =sen\left( \pi x\right) $ no intervalo $[0,1]$.
Mostre que o comprimento de arco total da elipse $x=a \cos t$, $y=b \sin t$, $0 \leq t \leq 2\pi$, para $a>b>0$ é dado por $4\displaystyle\int_{0}^{\pi/2} \sqrt{1+3\sin^3 t}dt$.
Encontre a área da região no primeiro quadrante limitada pelos eixos coordenados e pela curva $y=\frac{\sqrt{9-x^2}}{3}.$
Ache uma reta vertical $x=k$ que divida a área entre as curvas $y=x^2$ e $y=9$ em duas partes iguais.
$x=k=0$
A região limitada pelo triângulo de vértices $(1,0),$ $(2,1)$ e $(1,1)$ gira em torno do eixo $y$ gerando um sólido $S.$ Calcule o volume de $S.$
Em $1635$, Bonaventura Cavalieri, um aluno de Galileu, estabeleceu o seguinte resultado, chamado Princípio de Cavalieiri: se dois sólidos tiverem a mesma altura, e se as áreas de suas seções transversais tomadas paralelas e a iguais distâncias de suas bases forem sempre iguais, então os sólidos têm o mesmo volume. Use esse resultado para achar o volume do cilindro oblíquo da figura.
A região no plano $xy$ limitada pela curva $y=x^2+1$ e pela reta $y=-x+3$ gira em torno do eixo $x$ gerando um sólido $S.$ Calcule o volume de $S.$
Encontre a área limitada pela elipse $\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\text{.}$
Calcule a área no plano entre os gráficos de $f\left( x\right) =x^{3}-x$ e $g\left( x\right) =sen\left( \pi x\right) $ no intervalo $[0,1]$.
Sabemos que, no intervalo $[0,1]$, $g(x)=\sin(\pi x)>0$. Uma análise das raízes de $f(x)=x^3-x$ nos mostra que no intervalo referido, $f(x)<0$. Assim,como não há mudança de sinal de $f(x)-g(x)$, o cálculo da área entre as curvas se resumo ao cálculo da integral definida
$\int_0^1 \left(g(x)-f(x)\right)\,dx= \left.\left(-\frac{x^4}{4}+\frac{x^2}{2}-\frac{\cos (\pi x)}{\pi }\right) \right\vert_0^1=\frac{1}{4}+\frac{2}{\pi }$
Mostre que a área da superfície de uma esfera de raio $r$ é $4 \pi r^2$.
Se $f_{med}[a,b]$ denota o valor médio de $f$ no intervalo $\left[a,b\right]$ e $a<c<b$, mostre que
\begin{equation*}
f_{med}[a,b]=\dfrac{c-a}{b-a}f_{med}[a,c]+\dfrac{b-c}{b-a}f_{med}[c,b]
\end{equation*}
Como o parabolóide é obtido pela rotação ao redor do eixo $y$ temos que o raio $r:=d/2=4$ corresponde a variação de $x$ e a altura corresponde a variação de $y$, ou seja, para $x=4$ devemos ter $y=ax^{2}=4$ donde obtemos que $a=y/x^{2}=4/4^{2}=1/4$, e consideramos a parábola $y=\frac{x^{2}}{4}$.
Como o parabolóide é obtido pela rotação ao redor do eixo $y$ devemos considerar $x$ como funçao de $y$, ou seja, $x=x\left( y\right) =2\sqrt{y}$. Temos então que:
\begin{align*}
x^{\prime}\left( y\right) & =\frac{1}{\sqrt{y}}\\
\sqrt{1+\left( x^{\prime}\left( y\right) \right) ^{2}} & =\sqrt
{1+\frac{1}{y}}=\frac{\sqrt{y+1}}{\sqrt{y}}%
\end{align*}
Temos então que a área $S$ da superfície é dada por:
\begin{align*}
S & =\int_{0}^{4}2\pi\left( 2\sqrt{y}\right) \frac{\sqrt{y+1}}{\sqrt{y}%
}dy\\
& =4\pi\int_{0}^{4}\sqrt{y+1}dy
\end{align*}
Substituindo $u=y+1,~du=dy$ obtemos:
\begin{align*}
S & =4\pi\int_{1}^{5}\sqrt{u}du\\
& =4\pi\frac{2}{3}\left. u^{3/2}\right\vert _{1}^{5}\\
& =\frac{8\pi}{3}\left( 5^{3/2}-1\right)
\end{align*}
Encontre o volume de um tronco de cone circular reto de altura $h$, raio da base inferior $R$ e raio da base superior $r.$
Utilize a fórmula
\[
S=\int_{a}^{b}2\pi f\left( x\right) \sqrt{1+\left( f^{\prime}\left(
x\right) \right) ^{2}}dx
\]
para mostrar que a superfície de uma esfera de raio $R$ é $4\pi
R^{2}$.
Uma esfera de raio $R$ centrada na origem pode ser obtida pela rotação ao redor do eixo $x$ do semicírculo $x^{2}+y^{2}=R^{2}$ com $y\geq0$. Este semicírculo pode ser visto como o gráfico da função $f\left( x\right) =\sqrt{R^{2}-x^{2}}$, com $t\in\left[-R,R\right] $.
Considerando $f\left( x\right) =\sqrt{R^{2}-x^{2}}$ temos que:
\[
f^{\prime}\left( x\right) =-\frac{t}{\sqrt{R^{2}-x^{2}}}\text{.}%
\]
Usando a fórmula acima temos que:
\begin{align*}
S & =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{1+\left( f^{\prime}\left(
x\right) \right) ^{2}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{1+\frac{x^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{\frac{\left( R^{2}-x^{2}\right)
+x^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{\frac{R^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi R\frac{\sqrt{R^{2}-x^{2}}}{\sqrt{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi Rdx
\end{align*}
Temos então que:
\begin{align*} S & =\int_{-R}^{R}2\pi Rdx\\ & =\left. 2\pi Rx\right\vert _{-R}^{R}\\ & =4\pi R^{2} \end{align*}
Utilize o método das cascas cilíndricas para calcular o volume de um cone circular reto de altura $h$ e base com raio $r$.
Podemos pensar no cone como a superfície de revolução obtida pela rotação de um segmento de reta. A reta em questão pode ser equacionada, por semelhança de triângulos, como
\[
\frac{y}{x}=\frac{h}{r}\text{ ou }y:=y\left( x\right) =\frac{h}{r}x\text{.}%
\]
O segmento de reta é determinado ao restringirmos $x\in\left[ 0,r\right]$. Observamos que, dado $x\in\left[ 0,r\right] $ temos que a altura $h\left( x\right) $ correspondente ao cilindro contido no cone é $h\left( x\right) =h-y\left( x\right) $. Chamando o volume de $V$, pelo método das cascas cilíndricas, obtemos que:
\begin{align*}
V & =\int_{0}^{r}\left( 2\pi x\right) \left( h-\frac{h}{r}x\right) dx\\
& =\int_{0}^{r}2\pi h\left( x-\frac{x^{2}}{r}\right) dx\\
& =2\pi h\left. \left( \frac{x^{2}}{2}-\frac{x^{3}}{3r}\right) \right\vert
_{0}^{r}\\
& =2\pi h\left( \frac{r^{2}}{2}-\frac{r^{3}}{3r}\right) \\
& =2\pi h\frac{r^{2}}{6}\\
& =\frac{\pi hr^{2}}{3}.
\end{align*}
Prove o teorema do valor médio para integrais aplicando o teorema do valor médio para derivadas(consulte Stewart, seção 4.2, para obter mais informações sobre a função $F(x)=\displaystyle\int_{a}^{x} f(t)dt$.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=(3/4)x^{4/3}-(3/8)x^{2/3}+5,\quad 0 \leq x \leq 3$
Um toro em forma de um cilindro circular reto de raio $a$ está apoiado sobre um lado. Remove-se do toro uma cunha fazendo-se um corte vertical e outro corte a um ângulo de 45°; ambos os cortes se interceptam no centro do toro (veja a figura). Ache o volume da cunha.

Mostre que a a área lateral $S$ de um cone circular reto de altura $h$ e raio da base $r$ é $S=\pi r \sqrt{r^2+h^2}$.
Ache a área da superfície gerada fazendo girar a curva paramétrica $x=t^2,y=2t,0 \leq t\leq 4$, em torno do eixo $x$.
A cápsula cônica de reentrada de um veículo espacial é desenhada de tal forma que uma secção transversal tomada $x$ pés da ponta e perpendicular ao eixo de simetria é um círculo de raio $\dfrac{1}{4}x^2$ pés. Ache o volume do cone sabendo que o seu comporimento é de $20$ pés.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=e^{-x^{2}},y=0,x=0,x=1$, ao redor do eixo $y.$
Ache o comprimento exato do arco formado pela curva $x=\dfrac{1}{8}y^4+\dfrac{1}{4}y^{-2}$ de $y=1$ até $y=4$.
Seja $\mathcal{A}$ o subconjunto do plano limitado pelas retas $x=0$, $x=\frac{\pi}{2}$ e pelos gráficos de $y=\sin x$ e $y=\cos x$. Faça um esboço do conjunto $\mathcal{A}$ e calcule sua área.
Ache o volume do sólido cuja base é a região limitada pelas curvas $y=x$ e $y=x^2$ cujas secções transversais perpendiculares ao eixo $x$ são quadrados.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=(1/3)\left(x^2+2\right)^{3/2},\quad 0 \leq x \leq 3$
Use camadas cilíndricas para encontrar o volume do sólido resultante quando se faz girar a área entre as curvas $y=\cos(x^2)$, $x-0$, $x=\dfrac{1}{2}\sqrt{\pi}$ e $y=0$ em torno do eixo $y$.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2},y^{2}=x$, ao redor do eixo $x$.
Prove que o comprimento de um arco de ciclóide é igual a $8$ vezes o tamanho do raio do seu círculo gerador. A figura abaixo mostra dois arcos e meio de ciclóide.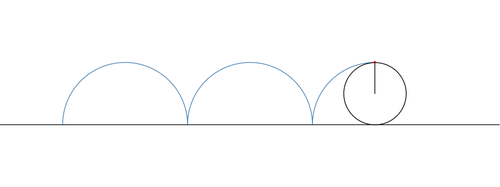
Prove que se $f$ é integrável em $\left[a,b\right]$ e $m \leq f(x) <M$ para todo $x$ em $\left[a,b\right]$, então $\displaystyle\int_{a}^{b}f(x)dx=(b-a)\mu$ para algum $\mu$ tal que $m < \mu <M$.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2},0\leq x\leq 2,y=4,x-0$ ao redor do eixo $y.$
Determine o comprimento da curva a seguir no intervalo especificado.
$y=x^{3/2},\quad 0 \leq x \leq 4$
Existe uma curva continuamente derivável $y=f(x)$ cujo comprimento ao longo do intervalo $0\leq x\leq a$ seja sempre $\sqrt{2}a$?
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2}-6x+10,y=-x^{2}+6x-6$, ao redor do eixo $y.$
A ciclóide é um caminho traçado por um ponto na borda de uma roda que gira ao longo de uma reta. Use as equações paramétricas de uma ciclóide para mostrar que o comprimento $L$ de um arco de uma ciclóide é dado pela integral $L=\displaystyle\int_{0}^{2\pi} \sqrt{2(1-\cos\theta)}d \theta$
Considere a região no plano com limite inferior dado por $y=1+x^2$ e limite superior $y=2$. Calcule os volumes quando rotacionamos essa região:
- Ao redor do eixo $x$.
- Ao redor do eixo $y$.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=x^3/9$, $0\leq x \leq 2$, eixo $x$
Calcule a área do conjunto $A$ dos pontos $\left( x,y\right)$ tais que $x^{2}-1\leq y\leq x+1.$
Uma empresa deseja lançar uma tigela esmaltada de branco por dentro e de vermelho por fora. A camada de esmalte terá $0,5mm$ de espessura antes de ir ao forno. O departamento de produção quer saber a quantidade de cada esmalte que precisará dispor para produzir $5000$ tigelas. Ignorando desperdício e matéria prima não utilizada, dê a sua resposta em litros. Lembre-se de que $1\ cm^3 = 1m\ell$, logo $1\ell=1000cm^3$.
Seja $S$ a região entre as curvas $y=x^n$ e $y=x^{n+1}$, onde $n$ é um inteiro, $n\geq 1$.
Considere o sólido $A_r$ obtido pela rotação de $S$ ao redor do eixo $x=r, r>1$ e considere o sólido $B_r$ obtido pela rotação de $S$ ao redor do eixo $y=r, r>1$. \\
Calcule o volume $V(A_r)$ de $A_r$, o volume $V(B_r)$ de $B_r$. Determine, se existir, ${\lim_{r\rightarrow\infty}\frac{V(A_r)}{V(B_r)}}$.
Um retângulo com os lados paralelos aos eixos coordenados tem um vértice na origem e o vértice diagonalmente oposto está sobre a curva $y=kx^m$ no ponto onde $x=b$ ($b>0$, $k>0$, $m \geq 0$). Mostre que o quociente entre a área do retângulo compreendida entre a curva e o eixo $x$ depende de $m$, mas não depende de $k$ ou $b$.
Encontre a área da região limitada pela elipse $x^2+\frac{y^2}{4}=1.$
Primeiramente, escreve-se a equação da elipse na forma $y=\pm f(x)$:
$y=\pm 2\sqrt{1-x^2}$
Observação: Nesta forma, é possível ver mais facilmente que a elipse não apresenta nenhum ponto com $\left\vert x\right\vert >1$.
Se denotarmos $f_1(x)= 2\sqrt{1-x^2}$ e $f_2(x)=- 2\sqrt{1-x^2} $, a área da região limitada pela elipse é portanto
$\int_{-1}^{1}f_1(x)-f_2(x)\,dx=2\int_{-1}^{1}f_1(x)\,dx=2 \left(\sqrt{1-x^2} x+\sin ^{-1}(x)\right)=2\pi$
A figura mostra as curvas aceleração versus tempo para dois carros movendo-se em uma pista reta, começando alinhados e acelerando a partir do repouso. O que representa a área $A$ entre as curvas no intervalo $0 \leq t \leq T$? Justifique.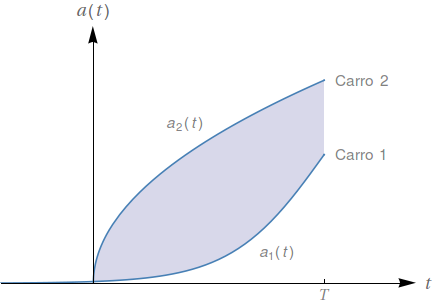
Para uma aceleração $a(t)$ qualquer, $\int_0^Ta(t)\,dt$ representa a velocidade adquirida desde o instante $t=0$, ou seja, $v(T)= v_0+\int_0^Ta(t)\,dt$. Sendo assim, a área entre as curvas representa $v_1(T)-v_2(T)$, a diferença de velocidade entre os carros no instante $t=T$.
Use camadas cilíndricas para encontrar o volume do sólido resultante quando se faz girar a área entre as curvas $y=\dfrac{1}{x^2+1}$, $x=0$, $x=1$ e $y=0$ em torno do eixo $y$.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=\sqrt{2}$, $3/4\leq x \leq 15/4$, eixo $x$
Prove que se $f$ é contínua em $\left[a,b\right]$ , então $\displaystyle\int_{a}^{b}f(x)dx=(b-a)f(\xi)$ para algum $\xi \in \left[a,b\right]$.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=e^{x},y=0,x=0,x=1$ ao redor do eixo $x.$
O laço de de $9y^2=x(3-x)^2$ é girado ao redor do eixo $y$. Calcule a área da superfície gerada por essa maneira.
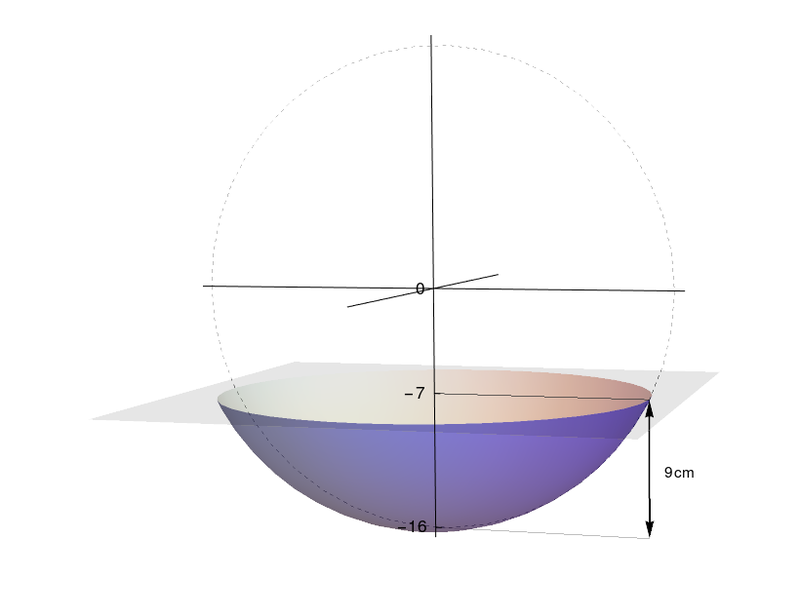
Um projetista, incumbido da tarefa de projetar uma bacia com cerca de $3L$ de capacidade, resolveu fazê-la nos moldes de uma tampa de uma casca esférica de $r=16cm$, com $9cm$ de profundidade, conforme a figura abaixo. Calcule o volume da bacia projetada e veja se a estimativa do projetista foi adequada, dado que a margem de erro do volume estabelecida pela empresa era de $15\%$.

Podemos calcular o volume da bacia através da seguinte integral:
$V=\int_{7}^{16}\pi\left(\sqrt{16^2-x^2}\right)^2\,dx=\left.\left[\pi(256x-\frac{x^3}{3})\right]\right\vert_7^{16}=1053\pi$
Lembrando que $1L=1000cm^3$ e supondo $\pi\approx3$, temos $V=3159cm^3$ (O valor real é próximo de $V=3308cm^3$). Como a margem de erro do projetista era de $15\%$, vemos que este acertou em seus cálculos.
Qual das integrais a seguir, se houver alguma, serve para calcular a área da região sombreada mostrada aqui? Justifique sua resposta.
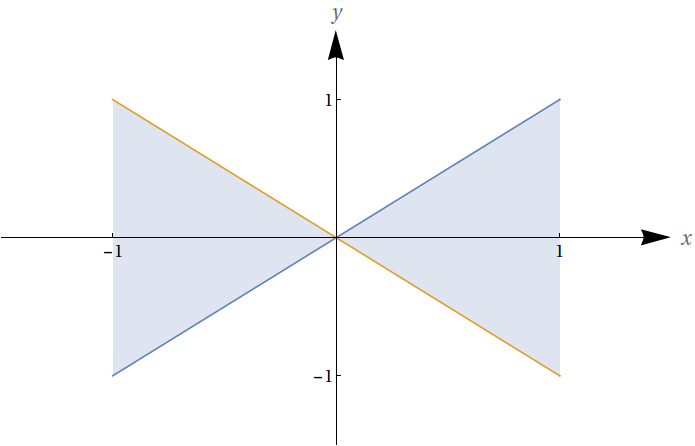 $\int_{-1}^{1} {\left(x-\left(-x\right)\right)dx} = \int_{-1}^{1} {2x\ dx}$
$\int_{-1}^{1} {\left(x-\left(-x\right)\right)dx} = \int_{-1}^{1} {2x\ dx}$- $\int_{-1}^{1} {\left(-x-x\right)dx} = \int_{-1}^{1} {-2x\ dx}$
Uma análise do resultado de ambas as integrais nos mostra, de imediato, que nenhuma delas é a adequada para o cálculo da área da figura. A segunda integral nada mais é do que a primeira integral com o sinal invertido, e portanto ambas são iguais a zero.
A questão é que no caso, se denotarmos $f_1(x)=x$ e $f_2(x)=-x$, é fácil observar que para $x>0$ $f_1(x)>f_2(x)$, e para $x<0$ $f_2(x)>f_1(x)$. Portanto, o cálculo correto da área se daria através de duas integrais, na forma
$A=\int_{-1}^{0} {\left(-x-x\right)dx}+\int_{0}^{1} {\left(x-\left(-x\right)\right)dx}$
Ou ainda, fazendo uso da simetria, poderia também se fazer:
$A=2\int_{0}^{1} {\left(x-\left(-x\right)\right)dx}=4\int_{0}^{1} {x\,dx}=2$
A região entre a curva $y^2=kx$ e a reta $x=\dfrac{1}{4}k$ é feita girar em torno da reta $x=\dfrac{1}{2}k$. Use camadas cilíndricas para encontrar o volume do sólido resultante.
$\frac{\pi k^4}{48}$
Um buraco redondo de raio $a$ é feito através do centro de uma esfera sólida de raio $r$. Use camadas cilíndricas para encontrar o volume da parte removida (suponha $r>a$).
- Use um recurso gráfico para gerar o gráfico de uma astróide usando $a=1$.
- Ache o comprimento exato de uma astróide.
Encontre o volume do sólido obtido pela rotação da região limitada por $y=x-x^{2}$ e $y=0$ ao redor da reta $x=2$.
Calcule o volume da esfera de raio $R$ de duas maneiras diferentes: a primeira através da rotação de um gráfico em torno do eixo $x$ e a segunda através da rotação de um gráfico em torno do eixo $y$.
Utilize a fórmula
\[
s\left( x\right) =\int_{a}^{x}\sqrt{1+\left( f^{\prime}\left( t\right)
\right) ^{2}}dt
\]
para mostrar que o perímetro de uma circunferência de raio $R$ é $2\pi R$.
Uma circunferência de raio $R$ centrada na origem pode ser vista como a união dos gráficos das funções $f\left(t\right) =\sqrt{R^{2}-t^{2}}$ e $g\left( t\right) =-\sqrt{R^{2}-t^{2}}$, com $t\in\left[ -R,R\right] $ Por simetria, estes dois arcos têm o mesmo comprimento, digamos $L$, e o perímetro $p$ é dado por $p=2L$.
Considerando $f\left( t\right) =\sqrt{R^{2}-t^{2}}$ temos
que:
\[
f^{\prime}\left( t\right) =-\frac{t}{\sqrt{R^{2}-t^{2}}}\text{.}%
\]
Usando a fórmula acima temos que:
\begin{align*}
L & =\int_{-R}^{R}\sqrt{1+\left( f^{\prime}\left( t\right) \right) ^{2}%
}dt\\
& =\int_{-R}^{R}\sqrt{1+\frac{t^{2}}{R^{2}-t^{2}}}dt\\
& =\int_{-R}^{R}\sqrt{\frac{\left( R^{2}-t^{2}\right) +t^{2}}{R^{2}-t^{2}}%
}dt\\
& =\int_{-R}^{R}\sqrt{\frac{R^{2}}{R^{2}-t^{2}}}dt\\
& =R\int_{-R}^{R}\frac{1}{\sqrt{R^{2}-t^{2}}}dt
\end{align*}
Fazendo a mudança de variável $t=R\sin\theta$, com $-\pi/2\leq\theta\leq\pi/2$, temos que:
\begin{align*}
\sqrt{R^{2}-t^{2}} & =\sqrt{R^{2}-R^{2}\sin^{2}\theta}\\
& =R\sqrt{1-\sin^{2}\theta}\\
& =R\cos\theta,\\
dt & =R\cos\theta d\theta
\end{align*}
Obtemos assim que:
\begin{align*}
L & =R\int_{-R}^{R}\frac{1}{\sqrt{R^{2}-t^{2}}}dt\\
& =R\int_{-\pi/2}^{\pi/2}\frac{R\cos\theta}{R\cos\theta}d\theta\\
& =R\int_{-\pi/2}^{\pi/2}d\theta\\
& \left. R\theta\right\vert _{-\pi/2}^{\pi/2}\\
& =\pi R
\end{align*}
e concluimos que:
\[
p=2L=2\pi R
\]
Determine a área da região no primeiro quadrante limitada à esquerda pelo eixo $y$, abaixo pela curva $x=2\sqrt{y}$, acima à esquerda pela curva $x=\left(y-1\right)^2$ e acima à direita pela reta $x=3-y$.
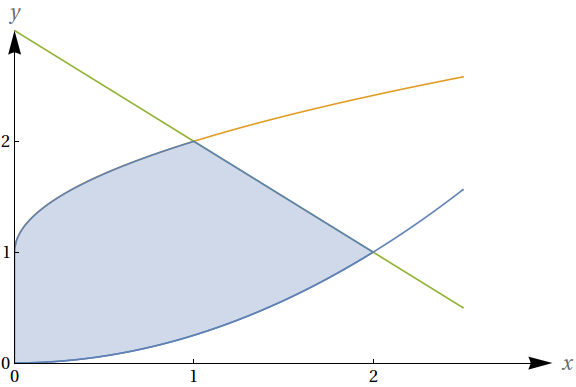
Primeiramente, devemos escrever as curvas na forma $y=f(x)$, tomando cuidado com o sinal. Após este procedimento, uma análise da figura nos permite resumir o cálculo da área $A$ como $A=A_1+A_2$, sendo que:
$A_1=\int_0^1\left (1+\sqrt{x}-\frac{1}{4}x^2\right)\,dx$
$A_2=\int_1^2\left (3-x-\frac{1}{4}x^2\right)\,dx$
Assim, temos
$A_1=\left.\left(x + \frac{2}{3} x^{3/2} - x^3/12\right)\right\vert_0^1=\frac{19}{12}$
$A_2=\left.\left(-\frac{x^3}{12}-\frac{x^2}{2}+3 x\right)\right\vert_1^2=\frac{11}{12}$
O que nos leva a $A=\frac{5}{2}=2.5$

