Exercícios
A integral definida
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
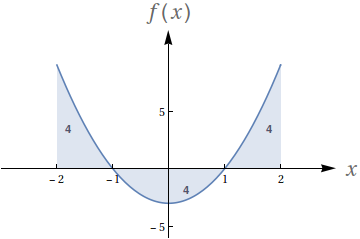
- $ \int_{-2}^{-1} f(x)\ dx$
- $ \int_1^2 f(x)\ dx$
- $ \int_{-1}^1 f(x)\ dx$
- $ \int_0^1 f(x)\ dx$
- $4$
- $4$
- $-4$
- $-2$
Avalie a integral $\displaystyle \int_{-1}^1 x^3 \sqrt{1-x^2} \, dx$ sem fazer nenhuma conta.
Demonstre que $2\sqrt{2} \leq \int_{0}^{1}{\sqrt{x+8}dx} \leq 8$.
Um objeto é lançado para cima com uma velocidade, em pés por segundo, dada por $v(t) = -32t+64$, de uma altura de $48$ pés.
- Qual a velocidade máxima do objeto?
- Qual o deslocamento máximo do objeto?
- Em que momento ocorre o maior deslocamento do objeto?
- Em que momento o objeto alcança a altura de $0$ pés?
Dica: encontre o momento no qual o deslocamento é $-48ft$
- $64ft/s$
- $64ft$
- $t=2$
- $t=2+\sqrt{7}\approx 4.65s$.
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
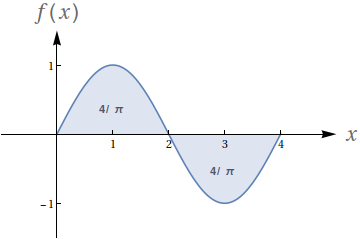
- $ \int_0^2 f(x)\ dx$
- $ \int_2^4 f(x)\ dx$
- $ \int_0^4 f(x)\ dx$
- $ \int_0^1 f(x)\ dx$
- $4/\pi$
- $-4/\pi$
- $0$
- $2/\pi$
Avalie a integral $\displaystyle \int_{-1}^1 (x^5+3) \sqrt{1-x^2} \, dx$ sem fazer nenhuma conta.
De acordo com s primeira lei de Kirchhoff para circuitos elétricos $V=RI+L(dI/dt)$, onde as constantes $V$, $R$ e $L$ denotam a força eletromotriz, a resistência e a indutância, respectivamente, e $I$ denota a corrente no instante $t$. Se a força eletromotriz é interrompida no instante $t=0$ e se a corrente é $I_0$ no instante da interrupção, prove que $I=I_0 e^{-Rt/L}$.
Quais valores de $a$ e $b$ maximizam o valor de
$\int_a^b\left(x-x^2\right)dx$?
$a=0$ e $b=1$.
O calor específico de um metal como a prata é constante a temperaturas $T$ acima de 200° K. se a temperatura do metal aumenta de $T_1$ a $T_2$, a área sob a curva $y=c/T$ de $T_1$ a $T_2$ é chamada variação de entropia $\Delta S$, que é uma medida da desordem molecular do sistema. Expresse $\Delta S$ em termos de $T_1$ e $T_2$,
Com base no gráfico, avalie as seguintes integrais:
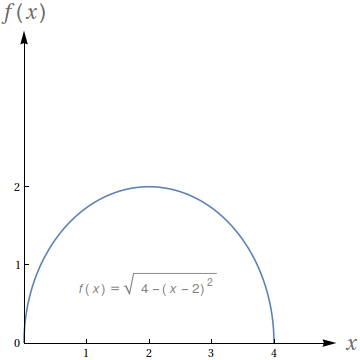
- $\int_0^2 f(x)\ dx$
- $\int_2^4 f(x)\ dx$
- $\int_0^4 f(x)\ dx$
- $\int_0^4 5f(x)\ dx$
- $\pi$
- $\pi$
- $2\pi$
- $10\pi$
Seja:
- $\int_0^2{f(x)dx} = 5$
- $\int_0^3{f(x)dx} = 7$
- $\int_0^2{g(x)dx} = -3$ e
- $\int_0^3{g(x)dx} = 5$
A partir destes valores, calcule as seguintes integrais:
- $\int_0^2 \big(f(x)+g(x)\big) \ dx$
- $\int_0^3 \big(f(x)-g(x)\big) \ dx$
- $\int_2^3 \big(3f(x)+2g(x)\big) \ dx$
- Encontre valores para $a$ e $b$ tal que:
$\int_0^3 \big(af(x)+bg(x)\big) \ dx=0$
- $2$
- $2$
- $22$
- $a=-\frac{5}{7}b,\quad b\in\mathbb{R}$
Com base no gráfico, avalie as seguintes integrais:
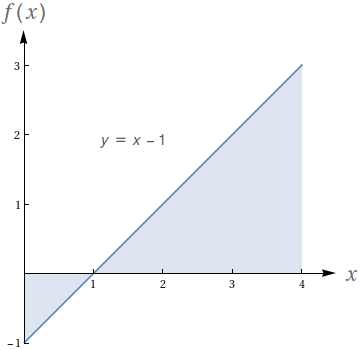
- $\int_0^1 (x-1)\ dx$
- $\int_0^2 (x-1)\ dx$
- $\int_0^3 (x-1)\ dx$
- $\int_2^3 (x-1)\ dx$
- $\int_1^4 (x-1)\ dx$
- $\int_1^4 \big((x-1)+1\big)\ dx$
- $-1/2$
- $0$
- $3/2$
- $3/2$
- $9/2$
- $15/2$
A atmosfera da Terra absorve aproximadamente $32\%$ da radiação proveniente do Sol. A Terra também emite radiação (a maior parte em forma de calor) e a atmosfera absorve aproximadamente $93\%$ dessa radiação. A diferença entre a radiação que entra na Terra e a que sai é chamada efeito-estufa. Modoficações nesse equilíbrio podem afetar o clima da Terra. Seja $I_0$ a intensidade da radiação do Sol e $I$ a intensidade depois de percorrer uma distância $x$ na atmosfera. Se $p(h)$ é a densidade da atmosfera na altitude $h$, então a espessura ótica é $f(x)=k \displaystyle\int_0^x p(h) dh$, onde $k$ é uma constante de absorção e $I$ é dada por $I=I_0e^{-f(x)}$. Mostre que $dI/dx=-kp(x)I$.
Com base no gráfico, avalie as seguintes integrais:
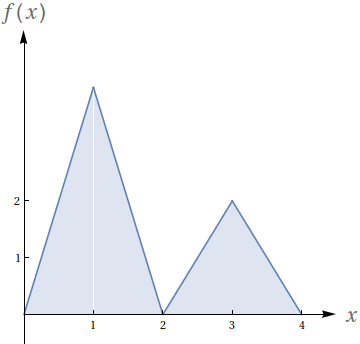
- $\int_0^2 f(x)\ dx$
- $\int_2^4 f(x)\ dx$
- $\int_2^4 2f(x)\ dx$
- $\int_0^1 4x\ dx$
- $\int_2^3 (2x-4)\ dx$
- $\int_2^3 (4x-8)\ dx$
- $4$
- $2$
- $4$
- 2
- $1$
- 2
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
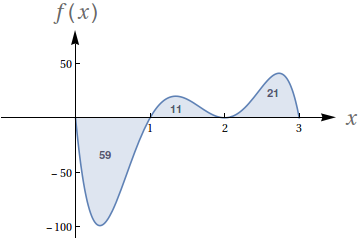
- $\int_0^1 f(x)\ dx$
- $\int_0^2 f(x)\ dx$
- $\int_0^3 f(x)\ dx$
- $\int_1^2 -3f(x)\ dx$
- $-59$
- $-48$
- $-27$
- $-33$
Durante o primeiro mês de crescimento de produtos como milho, algodão e soja, a taxa de crescimento (em gramas/dia) é proporcional ao peso presente $W$. Para determinada espécie de algodão, $dW/dt=0,21W$. Preveja o peso de uma planta no término de um mês ($t=30$), se a planta pesa 70 miligramas no início do mês.
Calcule a seguinte integral:
$\int \dfrac{x^{3}+x}{x-1}dx.$
Mostre que $\displaystyle \int_0^x \dfrac{\sin t}{t+1} \, dt > 0$
para todo $x>0$.
Um objeto é lançado para cima com uma velocidade, em pés por segundo, dada por $v(t) = -32t+96$; de uma altura de $64$ pés.
- Qual a velocidade inicial do objeto?
- Em que momento o objeto tem deslocamento nulo?
- Quanto tempo leva para o objeto retornar a sua posição inicial?
- Quando o objeto alcançará uma altura de $210$ pés?
- $96ft/s$.
- $6s$.
- $6s$.
- Nunca, a altura máxima é $208ft$.
Quais valores de $a$ e $b$ minimizam o valor de
$\int_a^b\left(x^4-2x^2\right)dx$?
Seja:
- $\int_0^3{s(t)dt} = 10$
- $\int_3^5{s(t)dt} = 8$
- $\int_3^5{r(t)dt} = -1$ e
- $\int_0^5{r(t)dt} = 11$
A partir destes valores, calcule as seguintes integrais:
- $\int_0^3 \big(s(t) + r(t)\big)\ dt$
- $\int_5^0 \big(s(t) - r(t)\big)\ dt$
- $\int_3^3 \big(\pi s(t) - 7r(t)\big)\ dt$
- Encontre valores para $a$ e $b$ tal que:
$\int_0^5 \big(ar(t)+bs(t)\big) \ dt=0$
- $22$
- $-7$
- $0$
- $b=-\frac{11}{18}a,\quad a\in\mathbb{R}$
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
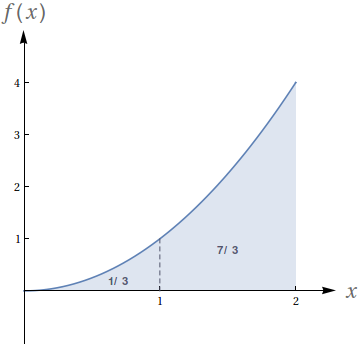
- $ \int_{0}^{2} 5x^2\ dx$
- $ \int_0^2 (x^2+3)\ dx$
- $ \int_{1}^3 (x-1)^2\ dx$
- $ \int_2^4 \big((x-2)^2+5\big)\ dx$
- $40/3$
- $26/3$
- $8/3$
- $38/3$
Calcule a seguinte integral:
$ \int_4^{\infty}e^{-\frac{y}{2}}dy$.
Com base no gráfico, avalie as seguintes integrais:
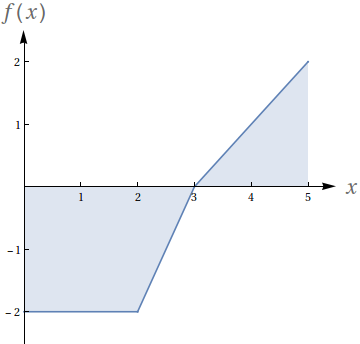
- $\int_0^2 f(x)\ dx$
- $\int_0^3 f(x)\ dx$
- $\int_0^5 f(x)\ dx$
- $\int_2^5 f(x)\ dx$
- $\int_5^3 f(x)\ dx$
- $\int_0^3 -2f(x)\ dx$
- $-4$
- $-5$
- $-3$
- 1
- $-2$
- 10
A atmosfera da Terra absorve aproximadamente $32\%$ da radiação proveniente do Sol. A Terra também emite radiação (a maior parte em forma de calor) e a atmosfera absorve aproximadamente $93\%$ dessa radiação. A diferença entre a radiação que entra na Terra e a que sai é chamada efeito-estufa. Modificações nesse equilíbrio podem afetar o clima da Terra. Seja $I_0$ a intensidade da radiação do Sol e $I$ a intensidade depois de percorrer uma distância $x$ na atmosfera. Se $p(h)$ é a densidade da atmosfera na altitude $h$, então a espessura ótica é $f(x)=k \displaystyle\int_0^x p(h) dh$, onde $k$ é uma constante de absorção e $I$ é dada por $I=I_0e^{-f(x)}$. Mostre que $dI/dx=-kp(x)I$.
Com base no gráfico, avalie as seguintes integrais:
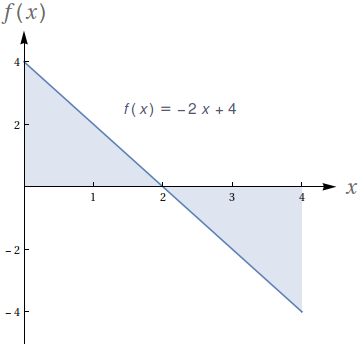
- $\int_0^1 (-2x+4)\ dx$
- $\int_0^2 (-2x+4)\ dx$
- $\int_0^3 (-2x+4)\ dx$
- $\int_1^3 (-2x+4)\ dx$
- $\int_2^4 (-2x+4)\ dx$
- $\int_0^1 (-6x+12)\ dx$
- 3
- 4
- 3
- 0
- $-4$
- 9
Demonstre que não é possível que o valor de $\int_0^1\sin(x^2)\ dx$ seja $2$. Depois, utilizando a desigualdade $\sin x \leq x$, válida para $x \geq 0$, determine um limitante superior para esta integral.
Sabemos que $\sin x \leq 1,\,\forall\,x\in\mathbb{R}$. Assim, como $\int_a^b f(x)dx \leq max\_{a \leq x \leq b} f(x) (b-a)$, podemos dizer que $\int_0^1\sin(x^2)\ dx \leq 1$.
Utilizando a desigualdade $\sin x \leq x$, podemos determinar de maneira ainda mais precisa um limitante superior para a integral.
$\int_0^1\sin(x^2)\ dx \leq \int_0^1x^2\ dx = \frac{1}{3}x^3 \vert^1_0=\frac{1}{3}$

