556

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =e^{2x}-e^{x}$.

573

Estude a função $f\left( x\right) =\sin x+\cos x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

547

Esboce o gráfico de $f(x)=x^3-x^2+1$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.

555

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x+\dfrac{1}{x^{2}}$.

577

544

Esboce o gráfico da função $f\left( x\right) =\frac{x^{2}}{x-1}$, indicando domínio de definição, limites laterais e no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.

554

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x^{3}-3x^{2}+1$.

548

Esboce o gráfico de $f(x)=x^4-5x^2+4$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.

575

Estude a função $f\left( x\right) =\dfrac{x}{1+\tan x},x\in \lbrack 0,\dfrac{\pi }{2})$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

578

Esboce o gráfico da função $f\left(x\right) =e^{-x^{2}}$ explicitando domínio, intervalos de crescimento e decrescimento, concavidade, pontos de inflexdão, assíntotas, máximos e mínimos locais e globais.

1249

Seja $f\left( x\right) =\dfrac{x^{3}}{x^{2}-1}$.

Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.

Considere $\frac{d}{dx}\left( \frac{x^{3}}{x^{2}-1}\right) =x^{2}\frac{x^{2}-3}{\left( x^{2}-1\right) ^{2}}$ e $\frac{d^{2}}{dx^{2}}\left(\frac{x^{3}}{x^{2}-1}\right) =2x\frac{x^{2}+3}{\left( x^{2}-1\right) ^{3}}$

1301

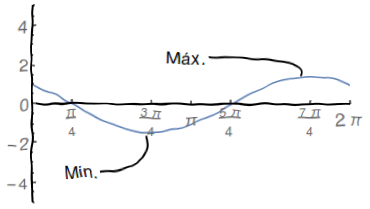
Esboce o gráfico da função $f\left( x\right) =\cos x-\sin x$ . Para fazê-lo, determine:

Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão

Dom$\left( f\right) =\mathbb{R}$
$f\left( 0\right) =1$ e $f\left( x\right) =0$ se, e somente se, $\cos x=\sin x$ se, e somente se,
$x=\frac{\pi}{4}+k\pi$ com $k\in\mathbb{Z}$
$f$ é periódica, com período $2\pi$
A função não possui assíntotas verticais (pois é contínua na reta) e tampouco horizontais (pois é periódica)
\begin{align*}
f^{\prime}\left( x\right)    & =-\sin x-\cos x=0\text{ se, e somente se,}\\
\cos x & =-\sin x\text{ se, e somente se, }x=\frac{3\pi}{4}+k\pi\text{ com }k\in
\mathbb{Z}\text{.}
\end{align*}
Considerando no período $\left[ 0,2\pi\right] $ temos que
\begin{align*}
f^{\prime}\left( x\right)    & >0\text{ se }x\in\left( \frac{3\pi}{4}
,\frac{7\pi}{4}\right) \text{ (intervalo de crescimento)}\\
f^{\prime}\left( x\right)    & <0\text{ se }x\in\lbrack0,\frac{3\pi}{4}
)\cup(\frac{7\pi}{4},2\pi]\text{ (intervalo de crescimento)}
\end{align*}
Novamente considerando no período $\left[ 0,2\pi\right] $ temos que $\frac{3\pi}{4}$ é ponto de mínimo e $\frac{7\pi}{4}$ é ponto de máximo.
\begin{align*}
f"\left( x\right)    & =-\cos x+\sin x=0\text{ se, e somente se,}\\
\cos x & =\sin x\text{ se, e somente se, }x=\frac{\pi}{4}+k\pi\text{ com }k\in
\mathbb{Z}\text{.}
\end{align*}
Considerando no período $\left[ 0,2\pi\right] $ temos que
\begin{align*}
f"\left( x\right)    & >0\text{ se }x\in\left( \frac{\pi}{4},\frac{5\pi}
{4}\right) \text{ (concavidade para cima)}\\
f"\left( x\right)    & <0\text{ se }x\in\lbrack0,\frac{\pi}{4})\cup
(\frac{5\pi}{4},2\pi]\text{ (concavidade para baixo)}
\end{align*}
Esboço do Gráfico:

560

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x-e^{x}$.

1276

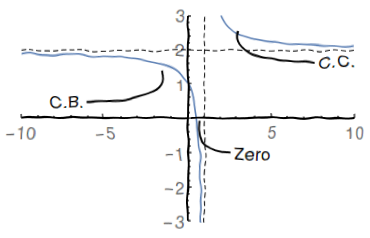
Seja $f\left( x\right) =\frac{2x-1}{x-1}$

Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.

Domínio: Dom$\left( f\right) =\left\{ x|x\neq1\right\} =\left( -\infty,1\right) \cup\left( 1,\infty\right) $
Zeros e inteceptos: $f\left( x\right) =0\iff2x-1=0\iff x=1/2$
Simetrias: Não há.
Assíntotas:
\begin{align*}
\lim_{x\rightarrow\pm\infty}f\left( x\right)   & =\lim_{x\rightarrow
\pm\infty}\frac{2x-1}{x-1}\\
& =\lim_{x\rightarrow\pm\infty}\frac{2-1/x}{1-1/x}=2
\end{align*}
\begin{align*}
\lim_{x\rightarrow1^{-}}f\left( x\right)   & =\lim_{x\rightarrow1^{-}}
\frac{2x-1}{x-1}=-\infty\\
\lim_{x\rightarrow1^{+}}f\left( x\right)   & =\lim_{x\rightarrow1^{-}}
\frac{2x-1}{x-1}=+\infty
\end{align*}
Intervalos de crescimento e decrescimento:
\begin{align*}
f^{\prime}\left( x\right) & =\frac{2\left( x-1\right) -\left(
2x-1\right) \left( 1\right) }{\left( x-1\right) ^{2}}\\
& =\frac{-1}{\left( x-1\right) ^{2}}<0,\forall x\in Dom\left( f\right)
\end{align*}
ou seja, $f$ é estritamente decrescente.
Valores máximo e mínimo locais: Não há, pois a derivada não se anula
Concavidade e pontos de Inflexão:

\[
f"\left( x\right) =\frac{2}{\left( x-1\right) ^{3}}>0\iff x-1>0\iff x>1
\]
ou seja, $f$ tem concavidade para cima para $x>1$ e concavidade para baixo para $x<1$
Esboço do Gráfico:

1566

Em estatística, a função densidade de probabilidade para a distribuição normal é definida por $f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}}e^{-z^2/2}$ com $z=\dfrac{x-\mu}{\sigma}$ para números reais $\mu$ e $\sigma>0$ ($\mu$ é a média e $\sigma^2$ é a variância da distribuição). Obtenha os extremos locais de $f$ e determine onde $f$ é crescente ou decrescente. Discuta a concavidade, ache os pontos de inflexão, determine $\lim\limits_{x \to \pm \infty}f(x)$ e esboce o gráfico de $f$.

1828

Se uma função racional $P(x)/Q(x)$ é tal que o grau do numerador excede o grau do denominador em $1$, então o gráfico de $P(x)/Q(x)$ terá uma assíntota oblíqua, isto é, uma assíntota que não é nem horizontal nem vertical. Para ver por quê, efetuamos a divisão de $P(x)$ por $Q(x)$ obtendo $$ \dfrac{P(x)}{Q(x)}= (ax+b) + \dfrac{R(x)}{Q(x)}, $$ onde $(ax+b)$ é o quociente e $R(x)$ é o resto. Use o fato de que o grau do resto $R(x)$ é menor do que o grau do divisor $Q(x)$ para auxiliá-lo a provar que $$ \lim_{x\to \infty}\left[\dfrac{P(x)}{Q(x)}-(ax+b)\right] = 0 \quad \text{e} $$ $$ \lim_{x\to -\infty}\left[\dfrac{P(x)}{Q(x)}-(ax+b)\right] = 0. $$ Este resultado nos diz que o gráfico da equação $\displaystyle y =P(x)/Q(x)$ "tende" à reta $y=ax+b$ (assíntota oblíqua) quando $x\rightarrow +\infty$ ou $x\rightarrow -\infty$.

563

Estude a função $f\left( x\right) =\sqrt{x^{2}-4}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

562

Estude a função $f\left( x\right) =x^{3}-3x^{2}+3x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

545

Esboce o gráfico de $f(x)=x^3-6x^2 +9x+1$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.

571

Estude a função $f\left( x\right) =x\ln x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

574

Estude a função $f\left( x\right) =e^{\dfrac{x-1}{x^{2}}}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

5

Esboce o gráfico da função $f\left(x\right) =x+\dfrac{1}{x}$.

559

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{x}{x^{2}+1}$.

552

Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =x^{3}+x^{2}-5x$.

1829

Seja $f(x)=(x^3+1)/x$. Mostre que o gráfico de $y=f(x)$ tende à curva $y=x^2$ "assintotamente" no sentido de que $$ \lim_{x\to\pm\infty}\left[f(x)-x^2\right] = 0. $$ Esboce o gráfico de $y=f(x)$ mostrando o seu comportamento assintótico.

553

Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =\dfrac{x}{x^{2}+1}$.

564

Estude a função $f\left( x\right) =\dfrac{x^{2}}{x+1}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

550

Faça um esboço completo do gráfico da função $y=\ln (9-x^{2}).$ Suas derivadas são: $y^{\prime }=-2x/\left( 9-x^{2}\right) $ e $y^{\prime \prime }=-\left( 18+2x^{2}\right) /\left( 9-x^{2}\right) ^{2}$. Determine explicitamente:

Domínio de definição;
Assíntotas verticais e horizontais (se houver);
Intervalos de crescimento e decrescimento;
Pontos de máximo e mínimo locais e absolutos;
Pontos de inflexão;
Concavidade.

546

Esboce o gráfico de $f(x)= \frac{x^2-2x^3}{x^2-1}$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.

1278

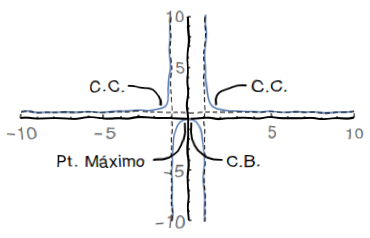
Esboce o gráfico da função $f\left( x\right) =\frac{2x^{2}}{3x^{2}-3}$ . Para fazê-lo, determine:

Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão

Dom$f=\left\{ x\in\mathbb{R}|x\neq\pm1\right\} $
$f\left( x\right) =0$ se, e somente se, $x=0$
A função é par: $f\left( -x\right) =f\left( x\right) $
Usando L'Hopital ou colocando-se $x^{2}$ em evidêncai no numerador e
denominador, obtemos que
\[
\lim_{x\rightarrow\infty}f\left( x\right) =\lim_{x\rightarrow-\infty
}f\left( x\right) =2/3
\]
\begin{align*}
\lim_{x\rightarrow-1^{+}}f\left( x\right)    & =-\infty\\
\lim_{x\rightarrow-1^{-}}f\left( x\right)    & =\infty\\
\lim_{x\rightarrow1^{+}}f\left( x\right)    & =\infty\\
\lim_{x\rightarrow1^{-}}f\left( x\right)    & =-\infty
\end{align*}
\begin{align*}
f^{\prime}\left( x\right) & =\frac{4x\left( 3x^{2}-3\right)
-2x^{2}\left( 6x\right) }{\left( 3x^{2}-3\right) ^{2}}\\
& =\frac{-12x}{\left( 3x^{2}-3\right) ^{2}}
\end{align*}
logo a derivada é positiva se $x<0$ e negativa se $x>0$, ou seja $f$ é crescente para $x<0$ e decrescente para $x>0$
$x=0$ é ponto de máximo da função.
A função não tem pontos de inflexão pois $\pm1\notin
Dom\left( f\right) $
\begin{align*}
f"\left( x\right) & =\frac{-12\left( 3x^{2}-3\right) ^{2}+12x2\left(
3x^{2}-3\right) 6x}{\left( 3x^{2}-3\right) ^{4}}\\
& =\frac{-12\left( 3x^{2}-3\right) +12x2\cdot6x}{\left( 3x^{2}-3\right)
^{3}}\\
& =\frac{-36x^{2}+36+12^{2}x^{2}}{\left( 3x^{2}-3\right) ^{3}}\\
& =\frac{-12x^{2}+12+48x^{2}}{\left( x^{2}-1\right) ^{3}}\\
& =12\frac{3x^{2}+1}{\left( x^{2}-1\right) ^{3}}
\end{align*}
Observando que $3x^{2}+1>0,\forall x$, temos que $f"\left( x\right) >0$ se, e somente se,
$x^{2}-1>0$ se, e somente se, $x>1$ ou $x<-1$ logo $f$ tem concavidade para cima se
$x\in(-\infty,-1)\cup\left( 1,\infty\right) $ e concavidade par baixo se
$x\in\left( -1,1\right) $.
Esboço do Gráfico:

580

Esboce neste mesmo gráfico a reta $y=2x+3$. Indique a região delimitada por esta reta e pelo gráfico de $f\left(x\right) $, para $2\leq x\leq 3$. Calcule a área desta região.

551

Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =x^{3}+3x^{2}+1$.

567

Estude a função $f\left( x\right) =\dfrac{3x^{2}+4x}{1+x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

1827

As curvas de crescimento logístico modelam a taxa de crescimento de uma certa população em função dos fatores ambientais. Em um período prolongado de tempo, a população tende a um valor limite que representa o máximo número de indivíduos que o espaço ou alimento pode sustentar. Estas curvas são da forma $$ y(t)=\dfrac{L}{1+Ae^{-kt}}, $$ onde $y$ é a população no momento $t$ ($t\geq 0$) e $A$, $k$ e $L$ são parâmetros positivos. Suponha que uma população $y$ cresce de acordo com o modelo logístico acima.

Qual é a taxa de crescimento de $y$ em $t=0$?
Descreva como a taxa de crescimento de $y$ varia com o tempo.
Em que momento a população cresce mais rapidamente?

1277

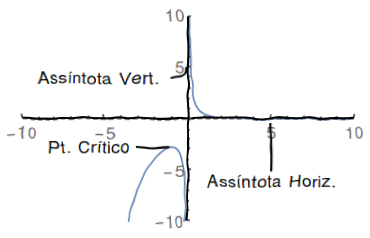
Esboce o gŕáfico de $f\left( x\right) =\frac{e^{-x}}{x}$ .Para fazê-lo:

Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão

Dom$\left( f\right) =\left\{ x\in\mathbb{R}|x\neq0\right\} $
$f\left( x\right) \neq 0,\forall x$
A função não possui simetrias não triviais
$\lim_{x\rightarrow\infty}\frac{e^{-x}}{x}=0,\lim_{x\rightarrow-\infty}\frac{e^{-x}}{x}=\lim_{x\rightarrow-\infty}-e^{-x}=-\infty$ (este por L'Hôpital), $\lim_{x\rightarrow0^{-}}\frac{e^{-x}}{x}=-\infty$ e $\lim_{\times\rightarrow1^{+}}\frac{e^{-x}}{x}=+\infty$
\[
f^{\prime}\left( x\right) =\frac{-e^{-x}x-e^{-x}}{x^{2}}=-e^{-x}\frac
{x+1}{x^{2}}%
\]
e temos que
\begin{align*}
f^{\prime}\left( x\right) & >0\Leftrightarrow x<-1\\
f^{\prime}\left( x\right) & <0\Leftrightarrow x>-1
\end{align*}
logo $f$ é crescente para $x<-1$ $\ $e decrescente para $x>-1$ (lembrando que $x\neq0$).
O único ponto crítico de $f$ é $x=-1$, o qual é ponto de máximo, pois a derivada passa de positiva a negativa.
\begin{align*}
f"\left( x\right) & =\frac{\left( e^{-x}x-e^{-x}+e^{-x}\right)
x^{2}-\left( -e^{-x}x-e^{-x}\right) 2x}{x^{4}}\\
& =\frac{e^{-x}x^{3}+2e^{-x}x^{2}+2e^{-x}x}{x^{4}}\\
& =\frac{e^{-x}}{x^{3}}\left( x^{2}+2x+2\right)
\end{align*}

Como $e^{-x}$ e $x^{2}+2x+2$ são sempre positivos, temos que $f"\left( x\right) >0$ se $x>0$ e $f"\left( x\right) <0$ se $x<0$, ou
seja, "concavidade para baixo" se $x<0$ e "concavidade para cima" se $x>0$
Esboço do Gráfico:

543

Seja $f\left( x\right) =x^{3}+3x.$

Estude o sinal de $f^{\prime }(x).$
Calcule $\lim\limits_{x\rightarrow +\infty }f\left(x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) .$
Utilizando as informações acima esboce o gráfico de $f\left( x\right) .$

1830

Esboce o gráfico completo da função $\displaystyle f(x)=x\tan x,\ -\pi/2<x<\pi/2$, e localize todos os extremos relativos e pontos de inflexão. Utilize um recurso computacional gráfico a fim verificar seu resultado.

1826

Uma caixa com base quadrada e sem tampa deve ser feita a partir de uma folha de metal, de forma que o seu volume seja de $500$ cm$^3$. Seja $S$ a área da superfície da caixa e $x$ o comprimento de um lado da base quadrada. Mostre que $\displaystyle S=x^2+2000/x$, para $x>0$, e esboce o gráfico de $S$ em função de $x$ para este caso.

557

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{x^{3}-x^{2}+1}{x}$.

558

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{\ln x}{x}$.

576

Estude a função $f\left( x\right) =\sqrt[3]{x^{3}-x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

1246

Esboce o gráfico da funçao $f\left( x\right) =\frac{x^{2}}{x-1}$, indicando domínio, limites laterais e no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.

568

Estude a função $f\left( x\right) =x^{3}-3x^{2}-9x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

570

Estude a função $f\left( x\right) =\dfrac{\ln x}{x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

569

Estude a função $f\left( x\right) =1-e^{-x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

549

Esboce o gráfico de $f(x)=x^2\sqrt{4-x}$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.

561

Determine os intervalos de decrescimento e crescimento e esboce o gráfico da função $f\left( x\right) =\left\{\begin{array}{cc} e^{-\dfrac{1}{x^{2}}} & \text{se }x\neq 0 \\ 0 & \text{se }x=0 \end{array} \right. $

1247

Seja $ f(x)=\frac{x^3}{|x^2-1|}.$

Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.

572

Estude a função $f\left( x\right) =e^{x}-e^{3x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

579

Esboce o gráfico da função $f\left(x\right) =\dfrac{x^{2}-x+1}{2x-2}$, determinando o domínio, pontos de máximo e de mínimo, pontos de inflexão e assíntotas. Explicite o valor que a função assume nos pontos em questão. Justifique o seu raciocínio.

566

Estude a função $f\left( x\right) =\dfrac{x^{3}}{x^{2}-1}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

565

Estude a função $f\left( x\right) =xe^{-3x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.

1248

Seja $ f\left( x\right) =\dfrac{x^{2}+7x+3}{x^{2}}$

Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.

Exercícios

Gráficos