Exercícios
Teste da Derivada Primeira
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Encontre os intervalos abertos nos quais $f(x)=x^3-\frac{3}{2}x^2$ é crescente e os intervalos abertos nos quais é decrescente.
Mostre que as funções $f(x)=(x-1)^4$ e $g(x)=x^3-3x^2+3x-2$ têm pontos estacionários em $x=1$.
O que o teste da derivada primeira diz sobre a natureza destes pontos?
Ache os pontos de máximo e de mínimo absolutos da função $f(x)=x+3x^{2/3}$.
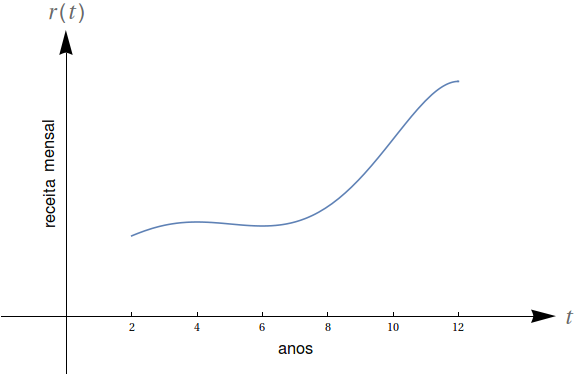
O gráfico a seguir mostra a receita mensal da empresa Fidelis Ltda. nos últimos 12 anos. Durante aproximadamente quais intervalos de tempo a receita marginal foi crescente? E decrescente?
O efeito da luz sobre a taxa de fotossíntese pode ser descrito por $f(x)=x^a e^{(a/b)(1-x^b)}$ para $x>0$ e constantes positivas $a$ e $b$.
Mostre que $f$ tem um máximo em $x=1$.
Conclua que, se $x_0>0$ e $y_0>0$, então $g(x)=y_0f(x/x_0)$ tem máximo em $g(x_0)=y_0$.
Seja $g\left( x\right) =\int_{0}^{x}f\left( t\right) dt$, onde $f\left( t\right) $ é a função cujo gráfico encontra-se abaixo.
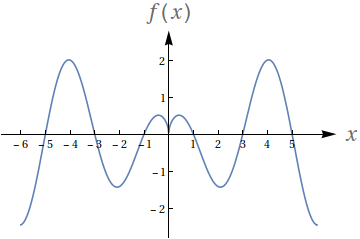
\begin{equation*} f(t) = \sqrt{|t|}\cos\left(\frac{\pi}{2}t\right) \end{equation*}
Determine os pontos de máximo e mínimo local de $g\left( x\right) $. Justifique a sua resposta
Determine as abscissas dos pontos críticos das funções abaixo:
$s(t) = 2t^3 + t^2-20t +4$
$f(x) = 4x^3-5x^2-42x + 7$
$g(w) = w^4-32w$
(Teste da Derivada Primeira) Suponha $f$ contínua em um ponto crítico $x_0$.
Se $f'(x)>0$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e $f'(x)<0$ em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ tem um máximo relativo em $x_0$.
Se $f'(x)<0$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e $f'(x)>0$ em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ tem um mínimo relativo em $x_0$.
Se $f'(x)$ tiver o mesmo sinal $\displaystyle [f'(x)>0\ \text{ou}\ f'(x)<0]$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ não tem extremo relativo em $x_0$.
Esboce algumas curvas para mostrar que as três partes do teste da derivada primeira podem ser falsas, sem a hipótese de que $f$ é contínua em $x_0$.
Encontre os valores máximo e mínimo da função $f\left(x\right) =xe^{-x}$ no intervalo $\left[ -10,10\right]$.
$f^{\prime}\left( x\right) =e^{-x}-xe^{-x}=e^{-x}\left( 1-x\right) $.
Como $e^{-x}>0$ temos que $f\left( x\right) =0$ se e somente se $1-x=0$, ou seja, se $x=1$.
Os pontos de máximo e mínimo devem ser pontos onde $f^{\prime}\left( x\right) =0$ ou os extremos do intervalo.
Avaliamos:
$f\left( -10\right) =-10e^{10}$
$f\left( 1\right) =\frac{1}{e}$
$f\left( 10\right) =\frac{10}{e^{10}}$
Como
$-10e^{10}<\frac{10}{e^{10}}<\frac{1}{e}$
temos que o valor máximo é $f\left( 1\right) =\frac{1}{e}$ e o valor mínimo é $f\left( -10\right) =-10e^{10}$.
Use a derivada dada para encontrar as coordenadas $x$ de todos os pontos críticos de $f$ e classifique-os em máximo relativo, mínimo relativo ou nenhum dos dois.
$\displaystyle f'(x)=x^3(x^2-5)$;
$\displaystyle f'(x)=xe^{-x}$.
Use a derivada dada para encontrar as coordenadas $x$ de todos os pontos críticos de $f$ e classifique-os em máximo relativo, mínimo relativo ou nenhum dos dois.
$\displaystyle f'(x)=x^2(2x+1)(x-1)$;
$\displaystyle f'(x)=\dfrac{9-4x^2}{\sqrt[3]{x+1}}$.
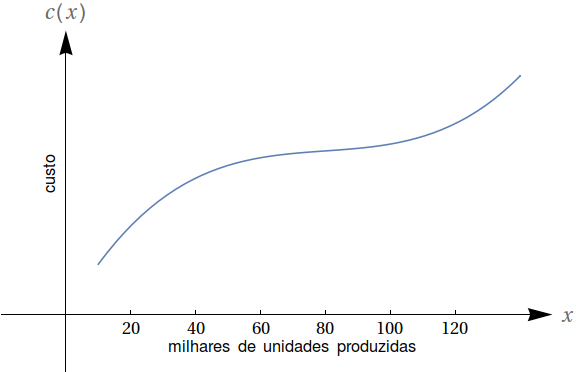
O gráfico a seguir mostra o custo hipotético $c=f(x)$ para fabricar $x$ itens. O chamado custo marginal é a mudança no custo total advinda da produção de uma unidade a mais do produto, para um certo volume de produção. Em aproximadamente qual nível de produção o custo marginal muda de decrescente para crescente?
Considere a função $f$ cuja derivada é $f'(x)=(x-1)^2(x+2)$.
Quais são os pontos críticos de $f$?
Em quais intervalos $f$ é crescente ou decrescente?
Em quais pontos $f$ assume valores máximos e mínimos locais?
As funções da forma $$f(x)=cx^ne^{-x},\quad x>0,$$ onde $n$ é um inteiro positivo e $c=1/n!$ surgem no estudo estatístico do fluxo de tráfego.
Use um recurso gráfico computacional para gerar o gráfico de $f$ com $n=2,3,4$ e $5$ e faça uma conjectura sobre o número e a localização dos extremos relativos de $f$.
Confirme a sua conjectura usando o teste da derivada primeira.
O número relativo de moléculas de gás em um recipiente que se movem a uma velocidade de $v$ $cm/s$ pode ser calculado por meio da distribuição de velocidade de Maxwell-Boltzmann, $F(v)=cv^2e^{-mv^2/(2kT)}$, sendo que $T$ é a temperatura em Kelvins, $m$ é a molécula e e $c$ e $k$ são constantes positivas. Mostre que o valor máximo de $F$ ocorre quando $v=\sqrt{2kT/m}$.
Encontre $a$ e $b$ tais que a função $f(x)=x^3 +ax^2+b$ tenha um extremo relativo em $(2,4)$.

