Exercícios
Derivabilidade e Continuidade
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Dê um exemplo de função contínua em seu domínio mas que não é diferenciável em algum(ns) ponto(s).
Qual a relação entre a continuidade e a diferenciabilidade de uma função? Demonstre.
Prove que se $f$ for derivável em $p$, então $f$ será contínua em $p$.
Veja Guidorizzi, volume $1$, página $152$.
Seja $f(x)=\left\{\begin{array}{ll}
-x+3, & \text{se } x<3 \\
x-3, & \text{se } x \geq 3
\end{array}\right.$
- $f$ é contínua em $3$. Por quê?
- $f$ é derivável em $3$. Por quê?
1. Sim
2. Não
Seja $f(x)=\left\{\begin{array}{ll}
x+1, & \text{se } x<2 \\
1, & \text{se } x \geq 2
\end{array}\right.$
- $f$ é contínua em $2$. Por quê?
- $f$ é derivável em $2$. Por quê?
1. Não.
2. Não
Seja $f(x)=\left\{\begin{array}{ll}
x^2, & \text{se } x \leq 0 \\
-x^2, & \text{se } x>0
\end{array}\right.$
- $f$ é contínua em $0$. Por quê?
- $f$ é derivável em $0$. Por quê?
1. Sim.
2. Sim.
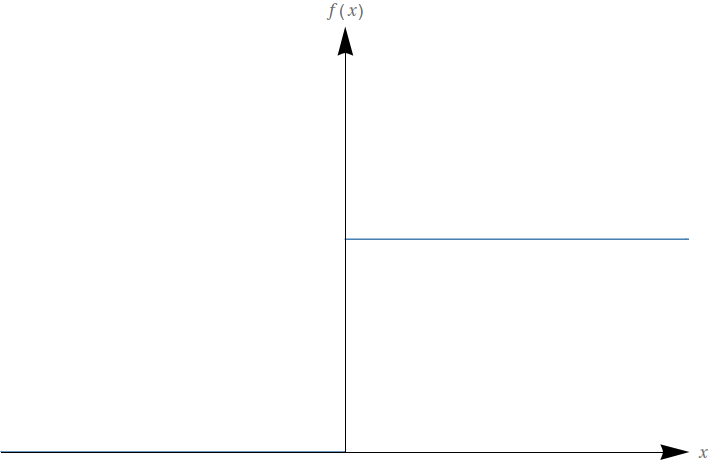
A função de Heaviside (também conhecida como função degrau), cujo gráfico pode ser visto abaixo, é muito utilizada para modelar chaves que ligam e desligam em circuitos elétricos (e também diversas aplicações). O que você tem a dizer sobre a continuidade dessa função? E sobre a diferenciabilidade?
Calcule, pela definição, a derivada das seguntes funções:
- $f\left( x\right) =ax+b$
- $g\left( x\right) =ax^{2}+bx+c$.
1. $f'(x)=a$.
2.$f'(x)=2ax+b$.
Seja $f:\mathbb{R\rightarrow R}$ uma função.
- Defina continuidade de $f$ no ponto $p\in \mathbb{R}$.
- Defina a derivada de $f$ no ponto $p\in \mathbb{R}$. O que é a função derivada $f^{\prime }\left( x\right) ?$
- Calcule, pela definição, a derivada $g^{\prime }\left( 0\right) $ onde \begin{equation*} g\left( x\right) =\left\{ \begin{array}{cc} x^{2}\sin \left( \dfrac{1}{x^{2}}\right) & \text{se }x\neq 0 \\ 0 & \text{ se }x=0 \end{array} \right. \end{equation*}

