Exercícios
Tangentes e Derivadas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =\sqrt[3]{x},\;p=1$.
$y=\dfrac{x+2}{3}$.
Encontre a equação da reta tangente à curva $y=2x^2+3$ que seja paralela à reta $8x-y+3=0$.
$y=8x+3$.
Mostre que qualquer reta tangente ao gráfico da hipérbole $xy=a^2$ determina com as assíntotas um triângulo de área igual a $2a^2$.
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =1/x^{2}$.
$f'(x) = -\dfrac{2}{x^3}$.
Considere a seguinte função:
\begin{equation*}
f(x)= \begin{cases}
(x-b)^2 -2, \quad x\geq 0
a\sin x,\quad x<0.
\end{cases}
\end{equation*}
- Encontre os valores de $a$ e $b$ tais que $f(x)$ seja contínua e diferenciável para todo $x\in\mathbb{R}.$
- Encontre o valor de $b$ tal que a reta tangente $t$ à curva $f(x)$ no ponto $x=1$ possui inclinação 2. Escreva a equação de $t.$
- Encontre o valor de $a$ tal que a reta $s$ normal à reta tangente à $f(x)$ no ponto $x=-\pi$ possui inclinação $-\frac{1}{2}$. Escreva a equação de $s$.
Observamos que para todo $x\geq 0$ a função $(x-b)^2 -2$ é contínua e que para todo $x<0$ também a função $a\sin x$ é contínua. Logo, temos que verificar a continuidade no ponto $x=0$, isto é, deve acontecer que
$\lim_{x\rightarrow 0^-}f(x)= \lim_{x\rightarrow 0^+}f(x),$
ou seja,
$\lim_{x\rightarrow 0^-}a\sin x=\lim_{x\rightarrow 0^+} (x-b)^2 -2.$
A relação anterior implica que $0= b^2-2$, ou seja $b=\pm\sqrt{2}.$ \\
Afim de achar o valor de $a$, encontramos a derivada de $f(x)$. Observamos que, sendo $a\sin x$ e $(x-b)^2 -2$ funções diferenciáveis para todo $x\in \mathbb{R}$, a derivada de $f(x)$ é a seguinte:
$f'(x)= \begin{cases}
2(x-b), \quad x> 0
a\cos x,\quad x<0.
\end{cases}$
Como queremos que $f(x)$ seja diferenciável no ponto $x=0$ também, temos que impor
$\lim_{x\rightarrow 0^-}f'(x)= \lim_{x\rightarrow 0^+}f'(x),$
ou seja,
$\lim_{x\rightarrow 0^-}a\cos x= \lim_{x\rightarrow 0^+}2(x-b).$
A relação anterior implica que $a= -2b$, então as duplas de valores para os quais $f(x)$ é contínua e diferenciável para todo $x\in \mathbb{R}$, são $(a,b)= (2\sqrt{2}, -\sqrt{2})$ ou $(a,b)=(-2\sqrt{2}, \sqrt{2}).$
Usando a função derivada calculada no ponto anterior, temos que $f'(1)= 2(1-b),$ então, como a inclinação da reta tangente deve ser 2, obtemos $2(1-b)=2$ e logo $b= 1$. A equação de $t$ é $y= f(1)+ f'(1)(x-1)$, isto é $y= -2+1\cdot(x-1)=x-3.$
Usando a função derivada calculada no ponto anterior, temos que $f'(-\pi)= a\cos (-\pi)= -a,$ então, como a inclinação da reta normal $s$ é $-\frac{1}{2}$, deve ser $-a=2$, ou seja $a=-2$. A equação de $s$ é $y= f(-\pi)-\frac{1}{2}(x+\pi)$, isto é $y= -\frac{1}{2}x -\frac{1}{2}\pi.$
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =x^{2}+x$.
$f'(x)=2x + 1$.
Seja $\ell$ a reta que passa pela origem do plano cartesiano e tangencia a curva $y = x^3 + x + 16$. Qual a inclinação de $\ell$?
Dado que $\ell$ é uma reta que passa pela origem, sabemos que sua equação é do tipo $\ell(x)=ax$. Como ela tangencia a curva $y(x)$, sabemos que há um ponto $x^*$ tal que $\ell(x^*)=y(x^*)$.
Além disso, sabemos que em $x^*$ a inclinação de $\ell$ é a mesma inclinação de $y$ (por quê?), o que é equivalente a $\ell'(x^*)=y'(x^*)$.
Assim, temos:
\begin{cases}
\left.x^*\right.^3+x^*+16 = ax^* \\
3\left.x^*\right.^2+1=a
\end{cases}
Resolvendo o sistema de equações obtemos:
\begin{align*}
x^* = 2\\
a = 13
\end{align*}
Sendo, portanto, $a=13$ a resposta desejada.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =1/x^{2},\;p=1$.
$y=-2x+3$.
Sejam $x_0,c\in\mathbb R$ e considere a função $f(x)=e^{cx}$. Encontre $f'(x_0)$ usando a definição de derivada.
$ce^{cx_0}$.
Demonstre que as retas tangentes às curvas $4y^3-x^2y-x+5y=0$ e $x^4-4y^3+5x+y=0$ na origem são perpendiculares.
Seja $f(x)=2x^2-3$. Determine a equação da reta tangente ao gráfico de $f$ nos pontos:
- $(0,f(0))$
- $(2,f(2))$
Resolva os itens.
Considere a parábola $y=x^{2}$ e faça a seguinte construção: para cada $a\neq 0$ trace a reta normal à parábola no ponto $\left( a,a^{2}\right) $ e seja $P$ o ponto onde essa normal encontra o eixo $y$. Calcule o limite do ponto $P$ quando $a$ tende a zero.
Calcule o mesmo limite fazendo a mesma construção para a curva quártica $y=x^{4}$ em lugar da parábola.
Consideremos a curva $y=-x^4 +2x^2+x$ e o ponto $P=(1,2)$ nessa curva. Verifique que a reta tangente a essa curva no ponto $P$ também é tangente à curva em outro ponto. Ache esse outro ponto.
Calcule os valores de $a,b$ e $c$ de modo que as parábolas $y=x^2+ax+b$ e $y=-x^2 +cx$ sejam tangentes uma a outra no ponto $(1,2)$.
Encontre os pontos sobre o gráfico de $p(x)=x^3-2x^2-8x+3$ nos quais a reta tangente é paralela à reta $y=4-9x.$
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =\dfrac{x}{x+1}$.
$f'(x) = \dfrac{1}{(x+1)^2}$.
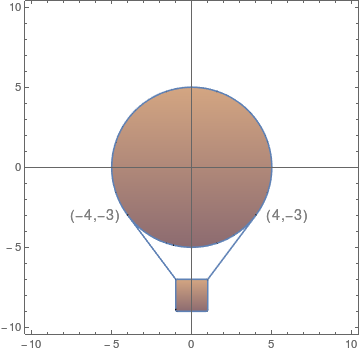
O projetista de um balão esférico (um projetista excêntrico) de ar quente com $10m$ de diâmetro quer suspender uma gôndola a $2m$ abaixo da parte inferior do balão, presa por cabos tangentes à superfície deste. Dado que os cabos, saindo da lateral do balão, tangenciam a superfície do mesmo nos pontos $(4,-3)$ e $(-4,-3)$, qual deve ser a largura da gôndola?
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =\sqrt{x},\;p=9$.
$y=\dfrac{x+9}{6}$.
Encontre a equação da reta tangente ao gráfico da função $f(x)=12\sqrt[6]{x}-\frac{1}{2x^2}+\log_5(x)$ no ponto cuja coordenada horizontal é $3$.
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =1/x$.
$f'(x)=-\dfrac{1}{x^2}$.
O coeficiente angular da reta tangente, no ponto de abscissa x, ao gráfico de $y=f\left( x\right) $, é proporcional ao cubo da ordenada do ponto de tangência. Sabendo que $f\left( 0\right) =1$ e que $f\left(1\right) =1/\sqrt{2}$, determine $f$.
Dê a definição de derivada de uma função $f$ no ponto $p\in \mathbb{R}.$ O que é a função derivada $f^{\prime }(x)$?
Encontre as equações das retas que passam pelo ponto $(-1,1)$ e são tangentes à curva $x^2+4y^2-4x-8y+3=0.$
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =x^{2}-x;\;p=1$.
$y=x-1$.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =x^{2},\;p=2$.
$y=4x-4$.
Encontre o ponto de interseção da reta tangente ao gráfico de $y=x-\frac{1}{x}$ no ponto $(1,0)$ com o eixo $y$.
$(1,0)$.

