Exercícios
MA111 - Cálculo I
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Estude a função $f\left( x\right) =x\ln x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Calcule o limite $\lim\limits_{x\rightarrow 7}\frac{\sqrt{x}-\sqrt{7}}{\sqrt{x+7}-\sqrt{14}}$ usando uma estratégia algébrica simples e, em seguida, usando a regra de L'Hospital. Compare os resultados.
Ache o comprimento exato do arco formado pela curva $x=\dfrac{1}{8}y^4+\dfrac{1}{4}y^{-2}$ de $y=1$ até $y=4$.
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função contínua tal que, para todo real x, tenhamos $f(f(f(x))) = x^2 + 1$. Prove que $f$ é par.
Seja $g\left( x\right) =\int_{0}^{x}f\left( t\right) dt$, onde $f\left( t\right) $ é a função cujo gráfico encontra-se abaixo.
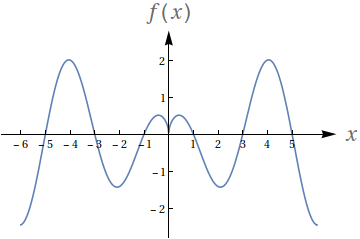
\begin{equation*} f(t) = \sqrt{|t|}\cos\left(\frac{\pi}{2}t\right) \end{equation*}
Determine os pontos de máximo e mínimo local de $g\left( x\right) $. Justifique a sua resposta
Utilizando o gráfico a seguir, avalie os seguintes limites
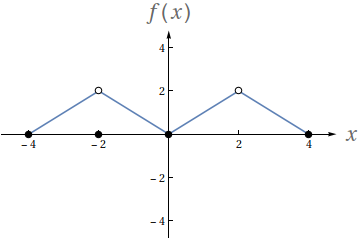
- $ \lim\limits_{x\to -2^-} f(x)$
- $ \lim\limits_{x\to -2^+} f(x)$
- $ \lim\limits_{x\to -2} f(x)$
- $f(-2)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 2^+} f(x)$
- $ \lim\limits_{x\to 2} f(x)$
- $f(2)$
- $2$
- $2$
- $2$
- $0$
- $2$
- $2$
- $2$
- Indefinido
Determine os valores para os quais a função \begin{align*} f(x) =\left\{ \begin{array} [c]{c} x^{2}+1,\text{ se }x\leq0 \\ \cos x, \text{ se } 0<x<1 \\ x^{2}+1, \text{ se }1 \leq x \end{array} \right.\end{align*} é contínua. Justifique sua resposta.
Calcule a seguinte integral:
$\int{e^{\sqrt{3x+9}}dx}$.
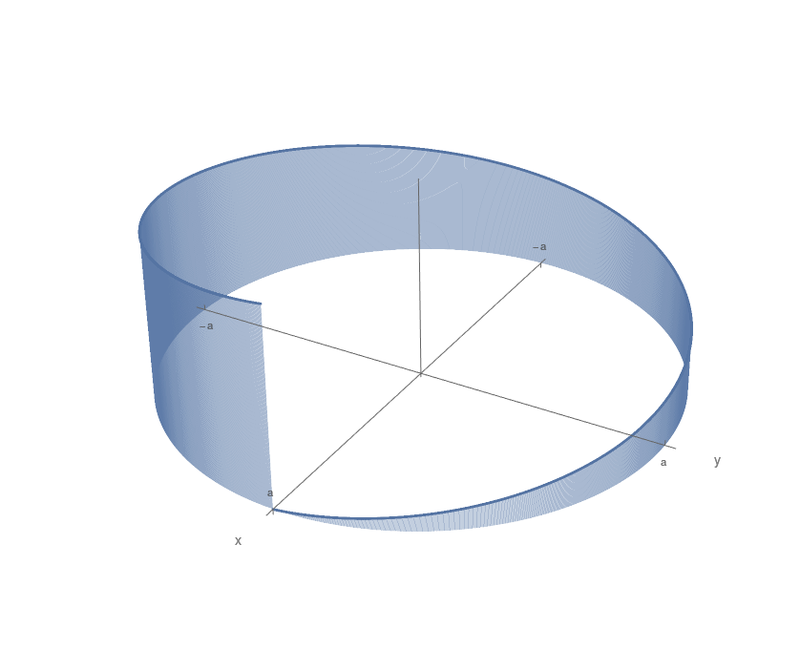
Uma superfície é criada a partir de segmentos de reta perpendiculares traçados sobre um círculo de raio $a$, perpendiculares ao plano do círculo. O comprimento de um segmento correspondente a um ponto $p$ sobre o círculo é $ks$, sendo $k$ uma constante positiva e $s$ o comprimento de arco do círculo no sentido anti-horário de $(a,0)$ até o ponto $p$.
Determine a área desta superfície, conforme a figura a seguir, em função de $k$.
Calcule a seguinte integral:
$\int{\frac{e^{2x}}{1+e^{2x}}dx}.$
A função pode tender a valores diferentes pela esquerda e pela direita, a função pode crescer de maneira ilimitada, ou a função pode oscilar em torno de um valor.
Calcule o limite:
$\lim\limits_{x\rightarrow 1}\dfrac{\sqrt{x^{2}+3}-2}{x^{2}-1}$.
Calcule o limite, caso exista:
$\displaystyle \lim_{x\rightarrow \infty}\left( x-\sqrt{x^2 + 4x} \right) $
Calcule a derivada da função:
$y=\sqrt{1+\sqrt{x}}$.
$y'=\dfrac{1}{4\sqrt{\sqrt{x}+1}\sqrt{x}}$.
O que se pode dizer sobre os pontos de inflexão de uma curva cúbica? Justifique.
Sejam $f(x)=\sqrt{\displaystyle{\frac{x+3}{x-3}}}$ e $g(x)=\displaystyle{\frac{\sqrt{x+3}}{\sqrt{x-3}}}$. Determine o domínio da função $f$ e o domínio da função $g$. É verdade que $f=g$?
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
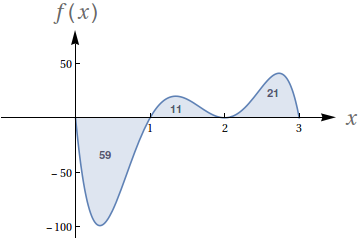
- $\int_0^1 f(x)\ dx$
- $\int_0^2 f(x)\ dx$
- $\int_0^3 f(x)\ dx$
- $\int_1^2 -3f(x)\ dx$
- $-59$
- $-48$
- $-27$
- $-33$
Este problema busca analisar o porquê de
\begin{equation*}
\int{\frac{1}{x}\ dx} = ln\left|x\right| + C
\end{equation*}
- Qual o domínio de $y = ln\ x$?
- Calcule $\frac{d}{dx}(ln\ x)$
- Qual o domínio de $y = ln(-x)$?
- Calcule $\frac{d}{dx}\left(ln(-x)\right)$
- Com base nos itens anteriores, explique o resultado apresentado no início deste problema.
Seja $f(x)=\left\{\begin{array}{ll}
-x+3, & \text{se } x<3 \\
x-3, & \text{se } x \geq 3
\end{array}\right.$
- $f$ é contínua em $3$. Por quê?
- $f$ é derivável em $3$. Por quê?
1. Sim
2. Não
Deixa-se cair de um balão um objeto de massa $m$. Se a força de resistência do ar é diretamente proporcional à velocidade $v(t)$ do objeto no instante $t$, então pode-se mostrar que $v(t)=(mg/k)(1-e^{-(k/m)t})$, onde $k>0$ e $g$ é uma constante gravitacional. Determine $\lim\limits_{k \to 0^+}s(t)$.
Calcule a derivada da função:
$y=e^{x^{x}}$.
$y'=e^{x^x} x^x (\log x + 1)$.
Calcule os seguintes limites laterais (justifique cada passo da resolução):
$\lim\limits_{x\rightarrow1^{+}}\dfrac{\sqrt{x^{2}-1}}{x-1}.$
$\lim\limits_{x\rightarrow1^{-}}\dfrac{\sqrt{x^{2}-1}}{x-1}.$
- $\lim\limits_{x\rightarrow 0^{+}}\log _{\frac{1}{3}}x$
- $\lim\limits_{x\rightarrow 1}\ln \dfrac{x^{2}-1}{x-1}$
- $\lim\limits_{x\rightarrow p}\dfrac{x^{n}-p^{n}}{x-p}$
Escreva o polinômio $p(x)=x^4-12x^3+44x^2+2x+1$ em $x$ como um polinômio em $(x-3)$. (Só é necessário calcular o polinômio de Taylor em $3$, do mesmo grau do polinômio original. Por quê?)
Mostre que a função \begin{align*} f\left( x\right) =\left\{ \begin{array}{cc} \dfrac{x^{3}-4x}{x^{2}-4}, & \text{se } x\neq \pm 2 \\ 2, & \text{se } x=2 \\ -3, & \text{se } x=-2 \end{array} \right. \end{align*} é contínua em todos os pontos, com exceção do ponto $x=-2$.
Esboce o gráfico da função $f(x)=||(x-1)^2-3|-1|$.
Dê os domínios e esboce os gráficos de $f+g$ e $\dfrac{g}{f}$ nos seguintes casos:
- $f(x)=x$ e $g(x)=x^2-1$.
- $f(x)=x$ e $g(x)=\dfrac{1}{\sqrt{x}}$.
Estude a função $f\left( x\right) =\dfrac{x^{3}}{x^{2}-1}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Um $n$-ágono regular é um polígono de $n$ lados que possui todos os lados iguais e todos os ângulos de mesma medida.
- Encontre o perímetro de um $n$-ágono regular inscrito num círculo de raio $r$.
- O perímetro do $n$-ágono se aproxima de algum valor quando $n$ cresce?
- Deduza a fórmula do comprimento de uma circunferência de raio $r$.
O produto de um racional diferente de zero com um irracional é racional ou irracional? Justifique.
É irracional.
Determine $f\left(x\right)$ sabendo que:
\begin{equation*} f\,^{\prime \prime }\left( x\right) = \cos 2x+6x+4,\;f\,^{\prime }\left(0\right) =2\text{ e }f\left( 0\right) =0\text{ .}\end{equation*}
Primeiramente, calcula-se a integral indefinida
$f\,^\prime(x)=\int \left(\cos 2x+6x+4\right)\,dx = 3 x^2+4 x+\frac{1}{2} \sin (2 x)+C_1$
Pelo dado do enunciado $f\, ^\prime(0)=2$. Avaliando a expressão acima para $x=0$, vê-se que $C_1=2$. Para obter $f(x)$, calcula-se novamente a integral indefinida:
$f(x)=\int \left(3 x^2+4 x+\frac{1}{2} \sin (2 x)+2\right)\,dx =x^3+2 x^2+2 x-\frac{\cos ^2(x)}{2}+C_2 $
De acordo com o enunciado, $f(0)=0$. Assim, obtém-se $C_2=\frac{1}{2}$.
Sendo $n$ um número positivo, mostre que
$$\displaystyle \int_{-1}^1 x^n \, dx = \left. \dfrac{x^{n+1}}{n+1} \right |_{-1}^1.$$
Se $n$ for um número negativo diferente de $-1$, esta expressão continua válida?
Mostre que existem funções $f(x)$, $g(x)$ com $\lim_{x\rightarrow p} f(x) = \lim_{x\rightarrow p} g(x) =0,$ tais que $\lim_{x\rightarrow p} (f(x)/g(x)) =\lambda$, onde $\lambda$ assume qualquer valor em $\mathbb{R} \cup \{+\infty, -\infty\}$. Escolha o ponto $p$ como achar mais conveniente.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\left( 0,27\right) ^{x}$.
$0$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(N,+\infty)$, os valores da função $f(x)=1/x^2$ estejam no máximo a $0,1$ unidade de $L=0$. Encontre $N$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(N,+\infty)$, os valores da função $f(x)=x/(x+1)$ estejam no máximo a $0,01$ unidade de $L=0$. Encontre $N$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(-\infty,N)$, os valores da função $f(x)=1/x^3$ estejam no máximo a $0,001$ unidade de $L=0$. Encontre $N$.
Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(-\infty,N)$, os valores da função $f(x)=x/(x+1)$ estejam no máximo a $0,001$ unidade de $L=0$. Encontre $N$.
Determine a equação da reta tangente ao gráfico de $f(x)=\ln{x}$ no ponto de abscissa $1$. Esboce os gráficos de $f$ e da reta tangente.
Esboce o gráfico de $f(x)=x^4-5x^2+4$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Calcule a derivada de ordem $1000$ da função $f(x)=\sin{kx}, k \in R$.
$f^{1000}(x)=k^{1000}\sin{kx}$
Seja $f$ uma função contínua e decrescente em $\left[a,b\right]$. Mostre que $f$ tem uma inversa decrescente em $\left[f(b),f(a)\right]$.
Resolva a equação modular $||x-2|-|x-1|+1| =2$.
Dados $f(x) = 1+x$ e $x_0 = 8,1$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Suponha que exista um número inteiro $n$ tal que $0<n<1$. Então...
Se um corpo de peso $P$ é arrastado ao longo de um piso horizontal por meio de uma força de grandeza $F$ e orientada segundo um ângulo $\theta$ radianos com o plano do piso, então $F=\frac{kP}{k\sin \theta +\cos \theta}$, onde $k$ é uma constante. Encontre $\cos \theta$, quando $F$ for mínimo.
Mostre que $x^{2}-xy+y^{2}\geq 0$, $\forall x,y\in R$ e que vale a igualdade se e somente se $x=y=0$.
Em cada item, esboce o gráfico de uma função contínua $f$ com as propriedades indicadas no intervalo $(-\infty,+\infty)$.
$f$ não tem extremos relativos nem absolutos.
$f$ tem um mínimo absoluto em $x=0$, mas nenhum máximo absoluto.
$f$ tem um máximo e um mínimo absolutos em $x=-5$ e $x=5$, respectivamente.
Avalie a seguinte integral indefinida:
$\int 5e^\theta\ d\theta$
$5e^\theta+C$
Determine todas as funções contínuas $f:\mathbb{R} \to \mathbb{R}$ tais que $f(x+y)=f(x)f(y)$ para quaisquer x, y reais.
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
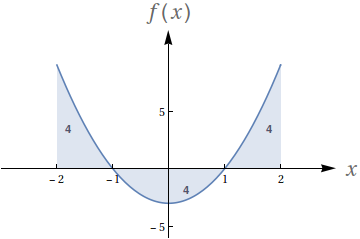
- $ \int_{-2}^{-1} f(x)\ dx$
- $ \int_1^2 f(x)\ dx$
- $ \int_{-1}^1 f(x)\ dx$
- $ \int_0^1 f(x)\ dx$
- $4$
- $4$
- $-4$
- $-2$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
- $\lim\limits_{x\rightarrow 0}\left( 1+2x\right)^{\dfrac{1}{x}}$
- $\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}-1}{x}$
- $\lim\limits_{x\rightarrow 0}\dfrac{e^{x^{2}}-1}{x}$
Uma bola esférica oca de raio $2m$ tem densidade específica $\dfrac{1}{4}$, de modo que flutua na água deslocando $\dfrac{1}{4}$ de seu próprio volume. Mostre que a profundidade $x$ à qual fica submersa é uma raiz da equação $x^3-6x^2+8=$ e use o método de Newton para calcular essa raiz com duas casas decimais de precisão. Sugestão: o volume de um segmento esférico de altura $h$ retirado de uma esfera de raio $r$ é $\pi h^2 \left(r-\dfrac{h}{3}\right)$.
Calcule a seguinte integral:
$\int_{0}^{\pi }x^{2}senx dx$.
$\pi^2-4$
Calcule:
- $ \lim\limits_{x\to 5^-} f(x)$
- $ \lim\limits_{x\to 5^+} f(x)$
- $ \lim\limits_{x\to 5} f(x)$
- $f(5)$
- $f$ é contínua em $x=5$?
1. $20$.
2. $25$.
3. Não existe.
4. $25$
5. Não.
Sejam $f_1,f_2,\ldots,f_n$, $n \geq 2$, funções deriváveis em $p$. Prove, por indução finita, que $f_1+f_2+\ldots+f_n$ é derivável em $p$. Veja Guidorizzi, volume $1$, página $158$.
Esboce o gráfico de $f(x) =x^2+6x+10.$ Use completamento de quadrados.
Determine as abscissas dos pontos críticos das funções abaixo:
$s(t) = 2t^3 + t^2-20t +4$
$f(x) = 4x^3-5x^2-42x + 7$
$g(w) = w^4-32w$
Reescreva a função $f(x)=|x-1|+|x+2|$ usando desigualdades e representação por partes. Esboce o gráfico de $f$
Determine todas as assíntotas horizontais da função $f(x) = \frac{x^2-1}{-x^2-1}$.
$y=-1$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x^2-1, & & \text{ se } x<-1 \\
x^3+1, & & \text{ se } -1\leq x\leq 1\\
x^2+1, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to -1^-} f(x)$
$ \lim\limits_{x\to -1^+} f(x)$
$ \lim\limits_{x\to -1} f(x)$
$f(-1)$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
- 0
- 0
- 0
- 0
- 2
- 2
- 2
- 2
Encontre os valores de $x$ para os quais cada o número $\sqrt{7x+9}$ é real.
Este número será real se o valor dentro da raiz for maior ou igual a zero.
$\begin{array}{rcl} 7x+9 &\geq& 0 \\ 7x &\geq& -9 \\ x &\geq& -\dfrac{9}{7}. \end{array}$
Portanto o conjunto dos valores de $x$ tais que $\sqrt{7x+9}$ é real é $\{x \in \mathbb{R} ; x \geq -9/7\}$.
Determine a derivada da função:
$f\left( x\right) =\left( sen x+\cos x\right) ^{3}.$
$3 (\cos (x)-\sin (x)) (\sin (x)+\cos (x))^2$
O terremoto de 1952 em Assam teve uma magnitude de 8,7 na escala Richter - a maior registrada até então. Se o maior terremoto em dado ano tem tem magnitude $R$, então a energia $E$ (em Joules) liberada por todos os terremotos naquele ano é estimada pela fórmula
$E=9,13 \times 10^{12} \int_{0}^{R}e^{1,25x}dx$.
Determine $E$ se $R=8$.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow +\infty }\dfrac{-x^{3}+2}{4x^{2}+89}$.
Calcule a integral a seguir:
$\int{\cos^3 x\sin\ x dx}$
$\dfrac{1}{4}cos^4(x)+C$
Esboce o gráfico da função $f\left( x\right) =\frac{x^{2}}{x-1}$, indicando domínio de definição, limites laterais e no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x \sin^{-1}(x)}{x- \sin(x)}$.
$-\infty$.
Calcule, apresentando todos os cálculos e/ou justificativas.
- $log_6 (36) +log_3 (6^4)$
- $8^{\frac {2} {3}}+\sqrt{log_2 (16)}+2^{2^3}+(2^2)^{3}$
Calcule os limites:
$\lim\limits_{x\to\pi/4} \cos x\sin x$
$\lim\limits_{x\to0} \ln x$
$\lim\limits_{x\to3} 4^{x^3-8x}$
Calcule a área no plano entre os gráficos de $f\left( x\right) =x^{3}-x$ e $g\left( x\right) =sen\left( \pi x\right) $ no intervalo $[0,1]$.
Dados $f(x) =\sin^{-1}x$ e $x_0 = \pi/12$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Calcule, quando existirem, os seguintes limites:
$\lim\limits_{x\rightarrow 2}\dfrac{x^{2}+x-6}{ \left( x-2\right) ^{3}}$
$\lim\limits_{x\rightarrow 2}\dfrac{\sqrt{6-x}-2}{\sqrt{ 3-x}-1}$
$\lim\limits_{x\rightarrow \infty }\sqrt{3x+4}-\sqrt{3x}.$
Dados $f(x) = e^{-x}$ e $x_0 = -0,1$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Encontre os valores máximo e mínimo da função $f\left(x\right) =xe^{-x}$ no intervalo $\left[ -10,10\right]$.
$f^{\prime}\left( x\right) =e^{-x}-xe^{-x}=e^{-x}\left( 1-x\right) $.
Como $e^{-x}>0$ temos que $f\left( x\right) =0$ se e somente se $1-x=0$, ou seja, se $x=1$.
Os pontos de máximo e mínimo devem ser pontos onde $f^{\prime}\left( x\right) =0$ ou os extremos do intervalo.
Avaliamos:
$f\left( -10\right) =-10e^{10}$
$f\left( 1\right) =\frac{1}{e}$
$f\left( 10\right) =\frac{10}{e^{10}}$
Como
$-10e^{10}<\frac{10}{e^{10}}<\frac{1}{e}$
temos que o valor máximo é $f\left( 1\right) =\frac{1}{e}$ e o valor mínimo é $f\left( -10\right) =-10e^{10}$.
Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =x^{3}+x^{2}-5x$.
Calcule a integral $\int \cos ^{3}xdx$.
$\frac{3}{4} x \sin (x)+\frac{1}{12} x \sin (3 x)+\frac{3 \cos (x)}{4}+\frac{1}{36} \cos(3 x)$
Consideremos a curva $y=-x^4 +2x^2+x$ e o ponto $P=(1,2)$ nessa curva. Verifique que a reta tangente a essa curva no ponto $P$ também é tangente à curva em outro ponto. Ache esse outro ponto.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\sec x}{3x+2}$.
$f'(x) = \dfrac{\tan x \sec x}{3x+2}-\dfrac{3 \sec x}{(3x+2)^2}$.
Queremos calcular a derivada da divisão da função $\sec x$ pela função $3x+2$. Usando a regra da derivada do quociente, obtemos:
\[\left( \dfrac{\sec x}{3x+2} \right)^\prime = \dfrac{(\sec x)^\prime \cdot (3x+2) - (\sec x)\cdot (3x+2)^\prime}{(3x+2)^2}.\]
Como $\sec x = \dfrac{1}{\cos x}$, podemos usar a regra do quociente para calcular sua derivada:
\[(\sec x)^\prime = \left(\dfrac{1}{\cos x}\right)^\prime = \dfrac{(1)^\prime\cdot \cos(x) - 1\cdot (\cos x)^\prime}{(\cos x)^2} =\dfrac{0 - (-\sin x)}{(\cos x)^2} = \tan(x)\sec(x).\]
Por outro lado, sabemos que $(3x+2)^\prime = 3$.
Dessa forma, voltando à primeira igualdade e substituindo $(\sec x)^\prime$ e $(3x+2)^\prime$ pelas expressões encontradas, obtemos:\[\dfrac{(\sec x)^\prime \cdot (3x+2) - (\sec x)\cdot (3x+2)^\prime}{(3x+2)^2} = \dfrac{\tan(x) \sec(x) (3x+2) - (\sec x)(3)}{(3x+2)^2} .\]
Ou seja,
\[ \left( \dfrac{\sec x}{3x+2} \right)^\prime = \dfrac{\tan(x) \sec(x)}{3x+2} - \dfrac{3\sec(x)}{(3x+2)^2}. \]
Considere a função $f$ cuja derivada é $f'(x)=(x-1)^2(x+2)$.
Quais são os pontos críticos de $f$?
Em quais intervalos $f$ é crescente ou decrescente?
Em quais pontos $f$ assume valores máximos e mínimos locais?
O coeficiente angular da reta tangente, no ponto de abscissa x, ao gráfico de $y=f\left( x\right) $, é proporcional ao cubo da ordenada do ponto de tangência. Sabendo que $f\left( 0\right) =1$ e que $f\left(1\right) =1/\sqrt{2}$, determine $f$.
Calcule os limites indicados dividindo o numerador e o denominador por uma potência conveniente de $x$. Como esses limites se relacionam com as mais altas potências do numerador e do denominador?
$\lim\limits_{x\rightarrow\infty}\frac{x^4-2}{3x^4-x^3+1}$
$\lim\limits_{x\rightarrow\infty}\frac{\sqrt{2x^6-2x+1}}{x^3-x^2+2}$
$\lim\limits_{x\rightarrow -\infty}\frac{\sqrt{x^2-3}}{x+1}$
Determine o comprimento da curva a seguir no intervalo especificado.
$y=\int_{-2}^{x}{\sqrt{3t^4-1}dt},\quad -2 \leq x \leq -1$
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = e^x - 2$ no intervalo $[0.65,0.7]$.
A raiz aproximada é $x=0.69$.
Os intervalos utilizados são:
$[0.65,0.7] \quad [0.675,0.7] \quad [0.6875,0.7]$
$[0.6875,0.69375]\quad [0.690625,0.69375]$
Para quaisquer $x,y\in \mathbb{R},$ mostre que vale $|xy|=|x||y|.$
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$x\neq y\Longrightarrow |x|\neq |y|$.
$|x-y|\geq |x|-|y| \forall x,y\in \mathbb{R}$
Calcule, se existir, o limite $\lim\limits_{x\to 0} \frac{x+1}{x^2+3x}.$
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{\ln({\sin(x)})}{\ln({\sin(2x)})}$.
Resolva a inequação $\frac{x^2+2x-1}{x^2-1} \geq \frac{1}{x+1}$.
Duas pequenas fábricas de calçados, $A$ e $B$, têm fabricado, respectivamente, $3000$ e $1100$ pares de sapatos por mês. Se, a partir de janeiro, a fábrica $A$ aumentar sucessivamente a produção em $70$ pares por mês e a fábrica $B$ aumentar sucessivamente a produção em $290$ pares por mês, em que mês a produção da fábrica $B$ superará a produção de $A$ pela primeira vez?
Calcule a área no plano entre os gráficos de $f\left( x\right) =x^{3}-x$ e $g\left( x\right) =sen\left( \pi x\right) $ no intervalo $[0,1]$.
Sabemos que, no intervalo $[0,1]$, $g(x)=\sin(\pi x)>0$. Uma análise das raízes de $f(x)=x^3-x$ nos mostra que no intervalo referido, $f(x)<0$. Assim,como não há mudança de sinal de $f(x)-g(x)$, o cálculo da área entre as curvas se resumo ao cálculo da integral definida
$\int_0^1 \left(g(x)-f(x)\right)\,dx= \left.\left(-\frac{x^4}{4}+\frac{x^2}{2}-\frac{\cos (\pi x)}{\pi }\right) \right\vert_0^1=\frac{1}{4}+\frac{2}{\pi }$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(x) = \frac{1}{1+x^2}$.
$(-\infty,\infty)$
Calcule a integral $\displaystyle\int \dfrac{1}{ax^n+bx}dx$.
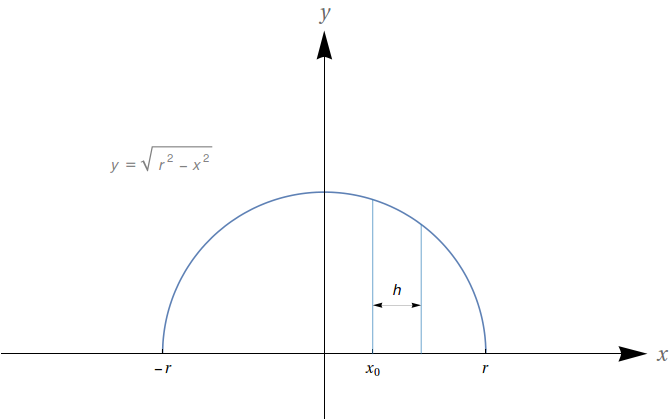
Demonstre que, ao se cortar uma cebola em fatias de igual largura, todas as fatias terão a mesma quantidade de casca.
Para isso, considere o semicírculo dado pela equação $y=\sqrt{r^2-x^2}$. A rotação deste em torno do eixo $x$ resultará numa esfera. Se escolhermos $x_0 >0$ e $h>0$ tal que $-r \leq x_0 < r$ e $x_0+h \geq r$, e o arco $AB$ localizado acima deste intervalo.
Demonstre que a área gerada pela rotação do arco $AB$ não depende de $x_0$, apenas de $h$.
Estude a função $f\left( x\right) =\sin x+\cos x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Calcule o volume da esfera de raio $R$ de duas maneiras diferentes: a primeira através da rotação de um gráfico em torno do eixo $x$ e a segunda através da rotação de um gráfico em torno do eixo $y$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
\frac{|x|}{x}, & & \text{ se } x\neq 0 \\
0, & & \text{ se } x=0
\end{array}
\right.$
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $ \lim\limits_{x\to 0} f(x)$
- $f(0)$
- $-1$
- $1$
- Não existe.
- $0$
Calcule o limite:
$\lim\limits_{x\rightarrow +\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-2$.
Resolva as equações:
- $|x-1|^2-2|x-1| =-1$
- $|x-10|-|x+10| =0$
Dados $f(x) = x^2+2x$ e $x_0 = 0,1$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Uma escada de $10$ metros de comprimento está apoiada em uma parede vertical. Se a base da escada começa a escorregar horizontalmente a uma taxa constante de $0,6 m/s$, com que velocidade o topo da escada percorre a parede quando ele está a $6 m$ do solo?
Dados $f(x) = \dfrac{x}{x+1}$ e $x_0 = 1,3$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Prove que a equação $x^3-4x+2=0$ tem exatamente três raízes reais distintas.
Temos, primeiramente:
$f'(x)=3x^2-4$
$f''(x)=6x-4$
É possível ver portanto que $f(x)$ tem dois pontos críticos: $x=\pm \frac{2}{\sqrt{3}}$. Como $f''(x)>0$ para $x>0$ e $f''(x)<0$ para $x<0$, $f(x)$ tem uma concavidade para baixo em $x=-\frac{2}{\sqrt{3}}$ e uma concavidade para cima em $x=\frac{2}{\sqrt{3}}$.
Temos que $f(0)=2$. Como na concavidade em $x=\frac{2}{\sqrt{3}}$ temos $f(x)<0$, sabemos que a primeira raiz está entre $0$ e $\frac{2}{\sqrt{3}}$. É fácil observar que $\lim\limits_{x \to \infty}f(x)=\infty$, o que nos mostra uma segunda raiz. Finalmente, como $\lim\limits_{x \to -\infty}f(x)=-\infty$, temos uma terceira raiz para algum valor $x<0$, provando então que a função em questão tem três raízes distintas.
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 0}\dfrac{\sin 4x}{x}$
$\lim\limits_{x\rightarrow 0}\dfrac{x}{\sin x}$
- $4$.
- $1$.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
${\frac{|x-3|}{|x+7|}}>0$
$|x+4|\geq |x+1|$
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x^3$ no intervalo $[0,b]$ é $b^4/4$.
Mostre o mesmo resultado utilizando somas inferiores.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|2x+1|\leq 1$
$\left| {\frac{x}{x^{2}+1}}\right| \leq 1$
Sejam $f_1,f_2,\ldots,f_n$, $n \geq 2$, funções deriváveis em $p$. Prove, por indução finita, que $f_1+f_2+\ldots+f_n$ é derivável em $p$.
Veja Guidorizzi, volume $1$, página $158$.
Sejam $f$ uma função contínua num intervalo $I$, $a$ e $b$ valores em $I$. Se $f(a)$ e $f(b)$ são valores com sinais contrários, mostre que a equação $f(x)=0$ tem pelo menos uma raiz real no intervalo $\left[a,b\right]$.
Esboce as curvas exponenciais transladadas:
$y=2^x-1$ e $y=2^{-x}-1$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\left( 2^{x}-3^{x}\right) $.
$-\infty$.
Discuta a seguinte "demonstração'':
Dada a integral $\displaystyle\int (1/x)dx$, seja $dv=dx$ e $u=1/x$, de modo que $v=x$ e $du=(-1/x^2)dx$.
Então $\displaystyle\int (1/x)dx=(1/x)x-\displaystyle\int x (-1/x^2) dx \Rightarrow \displaystyle\int (1/x)dx=1+\displaystyle\int (1/x)dx \Rightarrow 0=1.$
Prove que $\lim_{x\to a}f(x)=l$ se, e somente se, $\lim_{x\to a}[f(x)-l]=0$. Sugestão: Primeiro, compreenda por qual razão a afirmação anterior é óbvia; então dê uma prova formal.
Prove que $\lim_{x\to 0}f(x)=\lim_{x\to a}f(x-a)$.
Prove que $\lim_{x\to 0}f(x)=\lim_{x\to 0}f(x^3)$.
Dê um exemplo em que $\lim_{x\to 0}f(x^2)$ existe, mas $\lim_{x\to 0}f(x)$ não existe.
Avalie o limite $\lim\limits_{x\rightarrow p}\ln\left(\dfrac{x^{n}-p^{n}}{x-p}\right)$, onde $n$ é qualquer número natural.
Seja $P(x)$ um polinômio de grau $n$ tal que $P(k)=k/(k+1)$ para $k=0,1,\ldots n$. Encontre $P(n+1)$.
Em um reservatório cônico (com vértice para baixo), água é evaporada a uma taxa proporcional à área da superfície exposta ao ar. Mostre que a profundidade da água decresce a uma taxa constante que não depende das dimensões do reservatório.
- Use um recurso gráfico para gerar o gráfico de uma astróide usando $a=1$.
- Ache o comprimento exato de uma astróide.
Determine a derivada de ordem $999$ da função $f(x)=\sin(x)+\cos(x)$.
O fluxo de um campo magnético através de uma bobina, em função do tempo, é dado por $F=B \cdot l^2 \sin(\omega t)$ , onde $B$ é a intensidade do campo, $l$ o comprimento da espira e $\omega$ a velocidade angular da bobina. Pela "Lei de Faraday'', temos que a tensão $v$ do circuito associado a esse campo é dada por $v=-\frac{dF}{dt}$.
- Escreva a equação do fluxo para $B = 20$, $l = 2$ e $\omega= 4$.
- Para a equação obtida no item anterior, determine a expressão de v em função de t.
Determine os intervalos para os quais a função
\begin{equation*} f\left( x\right) =\left\{ \begin{array} [c]{c} x^{2}+1\text{ se }x\leq0\\ \cos x\text{ se }0<x<1\\ x^{2}+1\text{ se }1\leq x \end{array} \right. \end{equation*} é contínua. Justifique sua resposta.
As funções $x^{2}+1$ e $\cos x$ são ambas contínuas e por isto $f\left( x\right) $ é contínua para todo $x\neq0,1$. É necessário verificar a continuidade nos pontos $x=0$ e $x=1$.
Para $x=0$ temos que $\lim_{x\rightarrow0^{-}}f\left(x\right) =\lim_{x\rightarrow0^{-}}\left( x^{2}+1\right) =1$ e $\lim_{x\rightarrow0^{+}}f\left( x\right) =\lim_{x\rightarrow0^{+}}\cos x=1$, logo $f\left( x\right) $ é contínua em $x=0$, pois ambos oslimites laterais existem, são iguais e coincidem com o valor da função no ponto.
Para $x=1$ temos que $\lim_{x\rightarrow1^{-}}f\left( x\right) =\lim_{x\rightarrow0^{-}}\cos x=\cos\left( 1\right) $ e $\lim_{x\rightarrow0^{+}}f\left( x\right) =\lim_{x\rightarrow0^{+}}\left(x^{2}+1\right) =2$, e como $\cos\left( 1\right) \neq2$ temos que $f\left(x\right) $ não é contínua em $x=1$, pois apesar dos limites laterais existirem estes são distintos.
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =\dfrac{x}{x+1}$.
$f'(x) = \dfrac{1}{(x+1)^2}$.
Calcule a integral $ \int_{4}^{9}{\sqrt{x}}{\sqrt{x}-1}dx$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\left( x^{2}-1\right) ^{2}}{\sqrt{x^{2}+1}}.$
$f'(x) = \dfrac{x(x^2-1)(3x^2+5)}{(x^2+1)^{3/2}}$.
Calcule a integral a seguir utilizando decomposição de quocientes em frações parciais:
$\int{\frac{dx}{1-x^2}}$
Podemos escrever:
$\frac{1}{1-x^2}=\frac{A}{1-x}+\frac{B}{1+x}=\frac{A+Ax+B-Bx}{1-x^2}=\frac{(A+B)+(A-B)x}{2-x^2}$
Portanto, sabemos que $A+B=1$ e $A-B=0$. Temos, portanto, $A=B=\frac{1}{2}$.
Assim, reescrevemos a integral como
$\int\left(\frac{1/2}{1-x}+\frac{1/2}{1+x}\right)\,dx=\frac{1}{2}ln(1+x)+\frac{1}{2}ln(1-x)$
Mostre que:
- $|x-y|<1/2, |x+2|<1/3 \Longrightarrow |y+2|<5/6$
- $\sqrt{xy}\leq {\frac{x+y}{2}}$, $\forall x,y\geq 0$.
Determine a linearização de $f(x) = \sqrt{x+1} + \sin x$ em $x=0$. Como ela se relaciona com as linearizações individuais de $\sqrt{x+1}$ e $\sin x$ em $x=0$?
Seja $f\left( x\right) =\frac{1+x}{1-x}$. Mostre que $f\left( \frac{1}{1+x}\right) =\frac{2+x}{x}$, $f\left( \frac{1}{1-x}\right) =\frac{x-2}{x}$, $f\left( -x\right) =\frac{1}{f\left( x\right) }$, $f\left( 1/x\right)=-f\left( x\right) $ e que $f\left( f\left( x\right) \right) =-1/x$.
Mostre que a funçao $y(x)$ com $y(0)=0$ que é definida implicitamente pela equaçao $y-x^{2}+y^{3}+xy^{2}+x^{2}y=0$ tem um extremo relativo no ponto $x=0$. Identifique esse extremo.
Mostre que
- o limite de $f(x)=\dfrac{x-2}{|\,x-2|}$, quando $x\to 2$, não existe.
- o limite de $f(x)=\left\{\begin{array}{ll} x^2+2, & x\geq -1 \\ 2x+1, & x<-1 \\ \end{array}\right.$, quando $x\to -1$, não existe.
Partindo do gráfico de $h(x)=x^2$, esboce os gráficos de $f(x) =(x-1)^2$ e $ g(x) = (x +1)^2.$
Para cada uma das afirmações abaixo, demonstre se verdadeiro
ou dê contra-exemplo se for falso.
- $|x-y|\leq |x|+|y|,\forall x,y\in \mathbb{R}$.
- $x<y\Longrightarrow x^{2}<y^{2}$.
- $x<y\Longleftrightarrow 1/y<1/x$.
Calcule a seguinte integral:
$ \int_2^3 \frac{1}{x^2-1}dx$.
$\tanh ^{-1}(2)-\tanh ^{-1}(3)$
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função contínua que satisfaz as seguintes propriedades:
- $f(n)=0$, para todo inteiro $n$;
- Se $f(a)=0$ e $f(b)=0$ então $f \left(\frac{a+b}{2} \right)$.
Mostre que $f(x)=0$, para todo real $x$.
Determine qual o último número $N$, escrito na sucessão dos números naturais $12345678910111213...N$, sabendo que foram escritos $3849$ algarismos.
Encontre as raízes do polinômio $x^4-6x^3+13x^2-12x+4.$
Sugestão: Utilize o teste das raízes racionais
Mostre que a área $A$ de um círculo de raio $r$ é $A=\pi r^{2}$.
Determine o conjunto de todos os números reais para os quais a expressão $\sqrt{x}{1-x^2}$ está definida.
Encontre o número de polinômios de grau $5$ com coeficientes distintos pertencentes ao conjunto $\{1,2,\ldots,9\}$ que são divisíveis por $x^2-x+1$.
Encontre $a$ e $b$ tais que a função $f(x)=x^3 +ax^2+b$ tenha um extremo relativo em $(2,4)$.
Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.
$y=\sqrt{x-2}$
$y=\sqrt{2-x}$
- O domínio de $y$ é o conjunto de números reais em que o valor dentro da raiz é positivo. Calculando esses valores:
$x-2 > 0 \Rightarrow x > 2$.
Portanto o domínio de $y$ é: $\{x \in \mathbb{R}; x >2\}$. - O domínio de $y$ é o conjunto de números reais em que o valor dentro da raiz é positivo. Calculando esses valores:
$2-x > 0 \Rightarrow x < 2$.
Portanto o domínio de $y$ é: $\{x \in \mathbb{R}; x <2\}$.
Dê a definição de derivada de uma função $f$ no ponto $p\in \mathbb{R}.$ O que é a função derivada $f^{\prime }(x)$?
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=e^{-x^{2}},y=0,x=0,x=1$, ao redor do eixo $y.$
Avalie o limite $\lim\limits_{x\rightarrow p}\dfrac{x^{n}-p^{n}}{x-p}$, onde $n$ é qualquer número natural.
O que podemos dizer sobre uma função $f\left( x\right) $ tal
que $f^{\prime }\left( f\left( x\right) \right) =\left( f\left( f\left(x\right) \right) \right) ^{\prime }$ para todo $x$?
Pela aplicação direta da Regra da cadeia, temos que:
$\left( f\left( f\left(x\right) \right) \right) ^{\prime }=f^{\prime }\left( f\left( x\right) \right)f^{\prime}(x)$
Para $f(x)$, portanto, temos que:
$f^{\prime }\left( f\left( x\right) \right) =f^{\prime }\left( f\left( x\right) \right)f^{\prime}(x)$
Para que a igualdade seja verdadeira, há duas possibilidades. Ou:
$f^{\prime}(x)=0,\,\forall x$
i.e., a função é uma constante (o que resultaria em $0=0$). Ou:
$f^{\prime}(x)=1,\,\forall x$
i.e., $f(x)=x+a$, sendo que $a$ é uma constante (o que resultaria em $f^{\prime }\left( f\left( x\right) \right)=f^{\prime }\left( f\left( x\right) \right)$).
Seja $P(x)$ um polinômio de qualquer grau. Mostre que:
$$\displaystyle \int P(x) e^x \, dx = (P - P' + P'' -P''' + \ldots)e^x.$$
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$7+|x|<{\frac{1}{x+2}}$
$\left| {\frac{2x-3}{x+1}}\right| \leq {\frac{1}{2}}$
Seja $y=f(x)$ uma curva suave em $\left[a,b\right]$. Prove que se houver números não-negativos $m$ e $M$, tais que $m \leq f'(x) \leq M$ para todo $x$ em $\left[a,b\right]$, então o comprimento de arco $L$ de $y=f(x)$ satisfaz a desigualdade $(b-a)\sqrt{1+m^2} \leq L \leq (b-a) \sqrt{1+M^2}$.
Suponha que $x(t)=e^{0,05t}$ e que $z(t)=e^{0,01t}$. Calcule a taxa de crescimento de $y(t)$ nos seguintes casos:
- $y=xy$
- $y=x/y$
Mostre que a equação $|ax-b|=r$, com $r\geq 0$ e $a\neq 0$, tem como soluções os elementos do conjunto $\left\lbrace \frac{b+r}{a},\frac{b-r} {a}\right\rbrace$.
Temos duas possibilidades: $ax-b=r$ ou $ax-b=-r$. Da primeira equação obtemos $x=\dfrac{b+r}{a}$ e da segunda$x=\dfrac{b-r}{a}$.
A intensidade $I$ de um terremoto, medida na escala Richter, é um número que varia de $I=0$ até $I=8,9$ para o maior terremoto conhecido. $I$ é dado pela fórmula $I=\dfrac{2}{3} log {\left(\dfrac{E}{E_0}\right)}$, em que $E$ é a energia liberada pelo terremoto em quilowatt-hora e $E_0=7 \times 10^{-3}$ kwh.
- Qual a energia liberada por um terremoto de intensidade 8 na escala Richter?
- Aumentando uma unidade na intensidade do terremoto, por quanto fica multiplicada a energia liberada?
Sabe-se que $f$ é contínua em $1$ e que $f(1)=2$. Mostre que existe $\delta>0$ tal que para todo $x \in D_f$ vale $1-\delta<x<1+\delta \rightarrow \dfrac{3}{2}<f(x)<\dfrac{5}{2}$.
Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =x^{3}+3x^{2}+1$.
Mostre que toda equação polinomial de grau ímpar, tem pelo menos uma raiz real.
Avalie o limite $\lim\limits_{x\rightarrow p}\dfrac{x^{4}-p^{4}}{x-p}$.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
${\frac{3}{x}}+{\frac{x-3}{x-1}}<{\frac{2}{x-1}}$
${\frac{1}{x}}+{\frac{3}{2x}}\geq 5$
Um peso de massa $m$ é preso a uma bola suspensa a partir de um suporte. O peso é posto em movimento movendo-se o suporte para cima e para baixo de acordo com a fórmula $h=A \cos(\omega t)$, onde $A$ e $\omega$ são constantes positivas e $t$ é o tempo. Se as forças de atrito são desprezíveis, então o deslocamento $s$ do peso em relação à sua posição inicial no instante $t$ é dada por $s=\dfrac{A \omega^2}{\omega_0^2-\omega^2}(\cos(\omega t)-\cos(\omega_0 t))$ com $\omega_0=\sqrt{k/m}$ para uma constante $k$ e com $\omega \neq \omega_0$. Calcule $\lim\limits_{\omega \to \omega_0}s$ e mostre que as oscilações resultantes aumentam em magnitude.
Seja $\ell$ a reta que passa pela origem do plano cartesiano e tangencia a curva $y = x^3 + x + 16$. Qual a inclinação de $\ell$?
Dado que $\ell$ é uma reta que passa pela origem, sabemos que sua equação é do tipo $\ell(x)=ax$. Como ela tangencia a curva $y(x)$, sabemos que há um ponto $x^*$ tal que $\ell(x^*)=y(x^*)$.
Além disso, sabemos que em $x^*$ a inclinação de $\ell$ é a mesma inclinação de $y$ (por quê?), o que é equivalente a $\ell'(x^*)=y'(x^*)$.
Assim, temos:
\begin{cases}
\left.x^*\right.^3+x^*+16 = ax^* \\
3\left.x^*\right.^2+1=a
\end{cases}
Resolvendo o sistema de equações obtemos:
\begin{align*}
x^* = 2\\
a = 13
\end{align*}
Sendo, portanto, $a=13$ a resposta desejada.
Determine um número $0\leq b\leq 2$ tal que a reta $x=b$ divide a região delimitada por $y=\sqrt{4-x^{2}}$ e $y=0$ e $x=0$ em duas regiões de mesma área.
Prove que $\log_{10} 2$ é irracional.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x^n}{e^x}$.
$0$.
Mostre que $f(x) = \cos x - \frac{x}{10}$ tem pelo menos dois zeros em $[0, 2\pi]$.
Mostre que $|x-y|<1/2,|x+2|<1/3\Longrightarrow |y+2|<5/6$.
Seja $P(x)=a_0x^n+a_1x^{n-1}+\cdots+a_n$ um polinômio não nulo com coeficientes inteiros tal que $P(r)=P(s)=0$ para certos inteiros $r$ e $s$, com $0<r<s$. Prove que $a_k\leq -s$ para algum $k$.
Mostre que:
- $x\neq y\Longrightarrow x^{2}+2xy<2x^{2}+2y^{2}$.
- $|x|<x^{2}+1,\forall x \in \mathbb{R}$.
$f(x)=1, x \neq 0$; $f(0)=2$.
A que taxa o nível do líquido diminui dentro de um tanque cilíndrico vertical de raio $2$ metros se bombearmos o líquido para fora a uma taxa de $3000$ litros por minuto?
Aproxime numericamente o seguinte limite
$ f(x)=\frac{x^2-9 x+18}{x^2-x-6}$
- \begin{array}{cc}
x & f(x) \\ \hline
2.9 & -0.632 \\
2.99 & -0.6032 \\
2.999 & -0.60032 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-0.6$. - \begin{array}{cc}
x & f(x) \\ \hline
3.1 & -0.5686 \\
3.01 & -0.5968 \\
3.001 & -0.59968 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-0.6$. - As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =-0.6$.
Resolva a equação modular $|x-1|-2|x-2| =-3$.
O efeito da luz sobre a taxa de fotossíntese pode ser descrito por $f(x)=x^a e^{(a/b)(1-x^b)}$ para $x>0$ e constantes positivas $a$ e $b$.
Mostre que $f$ tem um máximo em $x=1$.
Conclua que, se $x_0>0$ e $y_0>0$, então $g(x)=y_0f(x/x_0)$ tem máximo em $g(x_0)=y_0$.
Encontre os dois pontos onde a curva $x^2+xy+y^2=7$ cruza o eixo x e mostre que as tangentes à curva nesses pontos são paralelas. Qual é o coeficiente angular comum dessas retas?
Considere $y=f(x)$, para $x$ real, sendo $f$ derivável até a segunda ordem e tal que, para todo $x$, $f''(x)+f(x)=0$. Seja $g$ uma função tal que $g(x)=f'(x) \sin x - f(x) \cos x$. Mostre que $g$ é constante.
Sejam $a_1,a_2,\ldots,a_{100}$, $b_1,b_2,\ldots,b_{100}$ números reais distintos. Uma tabela de dimensões $100\times 100$ é preenchida com esses números tal que o número $a_i+b_j$ é inserido na célula situada exatamente abaixo da interseção da $i$-ésima linha com a $j$-ésima coluna. Dado que em cada coluna o produto de todos os números é igual a $1$, prove que em cada linha o produto de todos os números é $-1$.
Existem, para doação a escolas, $2000$ ingressos de um espetáculo e $1575$ de outro. Cada escola deve receber ingressos para somente um dos espetáculos e todas as escolas devem receber a mesma quantidade de ingressos. Distribuindo-se todos os ingressos, qual o número mínimo de escolas que poderão ser contempladas nessa doação?
Na lei logística de crescimento admite-se que, no instante $t$, a taxa de crescimento $f'(t)$ de uma quantidade $f(t)$ seja dada por $f'(t)=Af(t)(B-f(t))$, com $A$ e $B$ constantes. Se $f(0)=C$, mostre que $f(t)=\dfrac{BC}{C+(B-C)e^{-ABt}}$.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=\left\{\begin{array}{ll}
x^2+3x, & \text{se} x \leq 1 \\
5x-1, & \text{se} x>1
\end{array}\right.$.
Entre todos o cilindros retos que tem uma área total dada, ache o que tem volume máximo.
Considere a área entre a curva $y=x^{4}$ e o eixo $x$, primeiro no intervalo $\left[ -1,1\right] $ e depois no intervalo $\left[1,a\right] $. Determinar $a\geq 1$ tal que estas áreas sejam iguais.
Resolva a inequação $|ax-b|<r$ na variável x, com $r>0$ e $a\neq 0$.
Se $ax-b\geq0$: $|ax-b| = ax-b$, logo $ax-b<r \Rightarrow x < \dfrac{b+r}{a}$.
Se $ax-b<0$: $|ax-b| = -(ax-b)$, logo $-ax+b<r \Rightarrow x > \dfrac{b-r}{a}$.
Portanto $x<\dfrac{b+r}{a}$ ou $x>\dfrac{b-r}{a}$.
Sejam $f(x)=\frac{x^{2}-25}{x^{2}-1}$ e $g(x)=\sqrt{x}$. Dê o domínio de cada uma das funções $f$, $g$, $f\circ g$ e $g\circ f$.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|2x-3|<5$
$|4-x|\geq 1$
Algumas curvas são tão planas que, na prática, o Método de Newton não consegue se aproximar da raiz suficientemente para fornecer uma aproximação útil. Tente utilizar o Método de Newton em $f(x)=\left(x-1\right)^{40}$ com a estimativa inicial $x_0=2$ para observar a qualidade das aproximações. Utilizando recursos computacionais, observe o gráfico da função.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=(3/4)x^{4/3}-(3/8)x^{2/3}+5,\quad 0 \leq x \leq 3$
Determine o conjunto solução da equação $|x|^2-5|x|+6=0$.
Suponha que, em uma aplicação do Método de Newton, o valor de $x_0$ escolhido coincidiu com uma raiz. Suponho que $f'(x_0)$ exista e não seja nula, o que acontecerá com $x_1$ e as aproximações subsequentes?
O que há de errado com a seguinte ``definição'' de limite?
"O limite de $f(x)$, quando $x$ tende a $a$, é $K$'' significa que para qualquer $\delta>0$, existe $\epsilon>0$ tal que $|f(x)-K|< \epsilon$, tem-se $|x-a|<\delta$."
$\epsilon$ deve ser apresentado antes, e a restrição $|x-a|<\delta$ implica em $|f(x)-K|< \epsilon$, e não o contrário.
Demonstre que a derivada da função cosseno é a oposta da função seno.
Calcule, apresentando todos os cálculos e/ou justificativas.
- $log_2 (1024)+sen^2(40)+cos^2(40)$
- $log_\pi [sen(30^0)+cos(60^0)]$
Prove que $\displaystyle\int (\ln(x))^m dx=x (\ln(x))^m -m \displaystyle\int (\ln(x))^{m-1}dx$.
Calcule os limites:
$\lim\limits_{x\to2} \frac{x^2-10 x+16}{x^2-x-2}$
$\lim\limits_{x\to-2} \frac{x^2-5 x-14}{x^2+10 x+16}$
$\lim\limits_{x\to-1} \frac{x^2+9 x+8}{x^2-6 x-7}$
- $-2$
- $-3/2$
- $-7/8$
Mostre que se $f$ e $g$ forem funções para as quais $$ f'(x)=g(x) \quad\text{e}\quad g'(x)=f(x)$$ para todo $x$, então $f^2(x)-g^2(x)$ é uma constante.
Mostre que as funções $\displaystyle f(x)=\dfrac{1}{2}(e^x+e^{-x})$ e $\displaystyle g(x)=\dfrac{1}{2}(e^x-e^{-x})$ têm esta propriedade.
Resolva a equação $\ln\left( x^{2}+2x+1\right) =3$.
Como a função exponencial é estritamente monótona, temos que $\ln\left( x^{2}+2x+1\right) =3$ se, e somente se, $e^{\ln\left(x^{2}+2x+1\right) }=x^{2}+2x+1=e^{3}$. Mas $ x^{2}+2x+1=\left( x+1\right) ^{2}$. Logo $\ln\left( x^{2}+2x+1\right) =3\Leftrightarrow\left( x+1\right)^{2}=e^{3}\Leftrightarrow x+1=\pm e^{3/2}\Leftrightarrow x=\pm e^{3/2}-1$.
Discuta as hipóteses necessárias para que se possa aplicar a Regra de L'Hospital.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f''(x) = 24x^2+2^x-\cos x$ e $f'(0)= 5$, $f(0) = 0$
$\frac{2 x^4 \ln ^2(2)+2^x+x \ln 2) (\ln 32-1)+\ln
^2(2) \cos (x)-1-\ln ^2(2)}{\ln ^2(2)}$
Utilize a fórmula
\[
S=\int_{a}^{b}2\pi f\left( x\right) \sqrt{1+\left( f^{\prime}\left(
x\right) \right) ^{2}}dx
\]
para mostrar que a superfície de uma esfera de raio $R$ é $4\pi
R^{2}$.
Uma esfera de raio $R$ centrada na origem pode ser obtida pela rotação ao redor do eixo $x$ do semicírculo $x^{2}+y^{2}=R^{2}$ com $y\geq0$. Este semicírculo pode ser visto como o gráfico da função $f\left( x\right) =\sqrt{R^{2}-x^{2}}$, com $t\in\left[-R,R\right] $.
Considerando $f\left( x\right) =\sqrt{R^{2}-x^{2}}$ temos que:
\[
f^{\prime}\left( x\right) =-\frac{t}{\sqrt{R^{2}-x^{2}}}\text{.}%
\]
Usando a fórmula acima temos que:
\begin{align*}
S & =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{1+\left( f^{\prime}\left(
x\right) \right) ^{2}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{1+\frac{x^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{\frac{\left( R^{2}-x^{2}\right)
+x^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi\sqrt{R^{2}-x^{2}}\sqrt{\frac{R^{2}}{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi R\frac{\sqrt{R^{2}-x^{2}}}{\sqrt{R^{2}-x^{2}}}dx\\
& =\int_{-R}^{R}2\pi Rdx
\end{align*}
Temos então que:
\begin{align*} S & =\int_{-R}^{R}2\pi Rdx\\ & =\left. 2\pi Rx\right\vert _{-R}^{R}\\ & =4\pi R^{2} \end{align*}
Prove que se $\lim_{x\to 0}\dfrac{f(x)}{x}=l$ e $b\neq 0 $, então $\lim_{x\to 0}\dfrac{f(bx)}{x}=bl$. Dica: Escreva $\dfrac{f(bx)}{x}=b\dfrac{f(bx)}{bx}$.
O que acontece se $b=0$?
O item 1. nos permite determinar $\lim_{x\to 0}\dfrac{\sin(2x)}{x}$ em termos de $\lim_{x\to 0}\dfrac{\sin(x)}{x}$. Determine este limite de um outro modo.
Sabemos que a troca de calor entre um objeto a uma temperatura $T$ e o ambiente a uma temperatura $T_{a}$ é proporcional a diferença $(T-T_{a})$. Como a variação de temperatura é proporcional a troca de calor, temos a seguinte equação diferencial $\frac{dT}{dt}=-\alpha \left( T-T_{a}\right)$ para $T\left( t\right) $ (temperatura em função do tempo. A constante $\alpha >0$ depende do calor específico e da condutividade térmica do objeto. Ache a soluçao dessa equação em função de $\alpha $ assumindo que a temperatura do ambiente $T_{a}=20^{o}C$ e a temperatura inicial $T_{0}=100^{o}C$. Qual é o limite $\lim_{t\rightarrow +\infty }T\left( t\right) $?
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc} 1, & & \text{se } x=0\\ \frac{\sin x}{x}, & &\text{se } x>0 \end{array}\right.$
- $x=0$
- $x=\pi$
- Sim.
- Sim.
Escreva o número $e^2$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-5}$.
Considere a região no plano com limite inferior dado por $y=1+x^2$ e limite superior $y=2$. Calcule os volumes quando rotacionamos essa região:
- Ao redor do eixo $x$.
- Ao redor do eixo $y$.
Encontre a área limitada pela elipse $\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\text{.}$
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-9 x+18}{x^2-x-6}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-0.632$ \\
$2.99$ & $-0.6032$ \\
$2.999$ & $-0.60032$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-0.6$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $-0.5686$ \\
$3.01$ & $-0.5968$ \\
$3.001$ & $-0.59968$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-0.6$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =-0.6$.
A antiderivada de uma função aceleração é a função _________.
Velocidade. A taxa de variação com a qual a velocidade varia de acordo com o tempo é, justamente, a aceleração.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\left( x^{3}+1\right) ^{5}}{\left(x^{2}+1\right) ^{4}}.$
$\frac{x \left(x^3+1\right)^4 \left(7 x^3+15 x-8\right)}{\left(x^2+1\right)^5}$
Escreva a taxa de crescimento de $y$ em termos das taxas de crescimento de $k$, $l$ e $m$ para os seguintes casos. Assuma $\beta$ como uma dada constante.
- $y=k^{\beta }$
- $y=k/m$
Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.
$y=\sqrt{x^{2}-4x+3}$
$y=\sqrt{x^{2}+3x-10}$
Para tranformar graus Fahrenheit em graus centígrados usa-se a fórmula $C=\dfrac{5(F-32)}{9}$, em que $F$ é o número de graus Fahrenheit e $C$ é o número de graus centígrados.
- Transforme $35$ graus centígrados em graus Fahrenheit.
- Qual a temperatura (em graus centígrados) em que o número de graus Fahrenheit é o dobro do número de graus centígrados?
Prove que para todo $x>0$ vale $x+\frac{1}{x}\geq 2$. Para quais números $x>0$ vale a igualdade?
Resolva os itens:
- Verifique que $\sqrt{1+x^2}-|x|=\dfrac{1}{|x|+\sqrt{1+x^2}}$. Conclua que à medida que $|x|$ resce a diferença $\sqrt{1+x^2}-|x|$ se aproxima de zero.
- Esboce o gráfico de $y=\sqrt{1+x^2}$.
Determine os valores de $\lambda$ que tornam contínua a função $g: \left( 0,\pi\right)\mathbb{\rightarrow R},$ dada por
\[
g\left( x\right) =\left\{
\begin{array}{c}
\tan \left( x\right) \mbox{ se }x\neq \dfrac{\pi }{2} \\
\lambda \mbox{ se }x = \dfrac{\pi }{2}
\end{array}
\right.
\]
Calcule a integral $\int \dfrac{x+1}{x^{2}-3x+2}dx$.
Determine um intervalo de comprimento $\pi/2$ cuja equação $$2x^3+3x^2-\sqrt{|\cos(x)|}=0$$ admita uma solução real.
Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.
$y=\sqrt[3]{x}$
$y=\sqrt[3]{-x}$
- $\mathbb{R}$.
- $\mathbb{R}$.
Aproxime numericamente o seguinte limite
$ f(x)= \frac{x^2+5 x-36}{x^3-5 x^2+3 x+9}$
- \begin{array}{cc}
x & f(x) \\ \hline
2.9 & -335.64 \\
2.99 & -30350.6 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$. - \begin{array}{cc}
x & f(x) \\ \hline
3.1 & -265.61 \\
3.01 & -29650.6 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-\infty$. - As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =-\infty$.
Justifique sua resposta.
$c=-1$ ou $c=2$.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow1}\frac{sen(x-1)}{x^{2}+x-2}$.
$1/3$.
De acordo com s primeira lei de Kirchhoff para circuitos elétricos $V=RI+L(dI/dt)$, onde as constantes $V$, $R$ e $L$ denotam a força eletromotriz, a resistência e a indutância, respectivamente, e $I$ denota a corrente no instante $t$. Se a força eletromotriz é interrompida no instante $t=0$ e se a corrente é $I_0$ no instante da interrupção, prove que $I=I_0 e^{-Rt/L}$.
Encontre os valores de $x$ para os quais cada o número $\sqrt{{\frac{5x-2}{x^{2}-4}}}$ é real.
Uma grandeza física desconhecida é medida $n$ vezes, obtendo-se valores $x_1,x_2,\ldots,x_n$, cuja variação depende de fatores imprevisíveis, tais como temperatura, pressão atmosférica etc. Desta forma, o cientista enfrenta o problema de obter uma estimativa $\bar{x}$ de uma grandeza desconhecida $x$. Um método de se obter estimativas está baseado no princípio dos mínimos quadrados, o qual estabelece que a estimativa $\bar{x}$ deve ser escolhida de forma a minimizar a função $$ s= (x_1-\bar{x})^2+(x_2-\bar{x})^2+\ldots +(x_n-\bar{x})^2, $$que é a soma dos quadrados dos desvios entre a estimativa $\bar{x}$ e os valores medidos. Mostre que a estimativa resultante do princípio dos mínimos quadrados é dada por $$ \bar{x}= \dfrac{1}{n}(x_1+x_2+\cdots+x_n), $$ ou seja, $\bar{x}$ é a média aritmética dos valores observados.
Mostre que existe um número real que é igual a soma de seu cubo e de seu quadrado mais um. Justifique sua resposta.
Mas $f\left( -2\right) =\left( -2\right)^{3}+\left( -2\right) ^{2}-\left( -2\right) +1=-1$ e $f\left( 0\right)=1$.
Como $f\left( x\right) $ é contínua, pelo Teorema do Valor Intermediário, existe $-2<x<0$ tal que $f\left( x\right) =0$.
Resolução Alternativa:
Uma vez definida $f(x)$, pode-se ver que $\lim_{x\rightarrow+\infty}f\left( x\right)=+\infty$ e $\lim_{x\rightarrow-\infty}f\left( x\right) =-\infty $. Como $f\left( x\right)$ é contínua, pelo Teorema do Valor Intermediário, existe $x$ tal que $f\left(x\right) =0$.
Uma página impressa deve ter $24$ $cm^{2}$ de área reservada à parte escrita, uma margem de $1,5 cm$ nas partes superior e inferior e uma margem de $1 cm$ nos lados. Discuta a existência das dimensões (e calcule quando existir) daquelas que tem área total máxima e área total mínima.
Uma droga é administrada por via intravenosa para combater a dor. A função
$f(t)=90-52\ ln(1+t), \quad 0 \leq t\leq4$
fornece o número de unidades da droga que permanecem no corpo após $t$ horas.
- Qual foi o número inicial de unidades administradas?
- Quanto estará presente após $2$ horas?
- Esboce o gráfico de $f(t)$
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{2}+3}\right)$
$\lim\limits_{x\rightarrow -\infty }\left( x-\sqrt{x^{2}+3}\right)$
$\lim\limits_{x\rightarrow \infty } \left( \sqrt{x+1}-\sqrt{x+3}\right)$
- $0$
- $-\infty$
- $0$
Demonstre as seguintes regras de derivação:
- $(\sin{x})'=cos{x}$
- $(\cos{x})'=-\sin{x}$
- $(tg{x})'=sec^2{x}$
Determine uma primitiva para cada uma das funções:
$f(x)=x^n$
$f(x)=sen(x)$
Faça um esboço completo do gráfico da função $y=\ln (9-x^{2}).$ Suas derivadas são: $y^{\prime }=-2x/\left( 9-x^{2}\right) $ e $y^{\prime \prime }=-\left( 18+2x^{2}\right) /\left( 9-x^{2}\right) ^{2}$. Determine explicitamente:
Domínio de definição;
Assíntotas verticais e horizontais (se houver);
Intervalos de crescimento e decrescimento;
Pontos de máximo e mínimo locais e absolutos;
Pontos de inflexão;
Concavidade.
Demonstre as seguintes regras de derivação:
- $(sec{x})'=sec{x} \cdot tg{x}$
- $(cotg{x})'=-cossec^2{x}$
- $(cossec{x})'=-cossec{x} \cdot cotg{x}$
Derive a função $g\left( x\right) = \int_{\tan x}^{x^{4}}\dfrac{u^{2}+1}{\sqrt{u^{2}+2u}}du$.
Um agricultor possui $140$ metros de cerca para construir dois currais: um deles quadrado eu outro retangular, com comprimento igual ao quádruplo da largura. Se a soma das áreas dos currais deve ser a menor possível, calcule a área do curral quadrado, apresentando todos os cálculos e/ou justificativas.
Seja $f:\mathbb{R} \to \mathbb{R}$ uma função derivável, tal que $f'(x)=\alpha f(x)$ para todo $x$ e sendo $\alpha$ uma constante diferente de zero. Mostre que existe uma constante $k$ tal que, para todo $x$:
$$f(x) = k e^{\alpha x}$$
Suponha que para todo $x$, $\left| f\left( x\right) \right| \leq x^{4}$. Calcule $\lim\limits_{x\rightarrow 0}\dfrac{f\left( x\right) }{x}.$
Prove que a função $f(x)=\left\{\begin{array}{ll}
x, & \text{se x é racional}\\
-x, & \text{se x é irracional}
\end{array}\right.$ é contínua em $0$.
Suponha que você tenha as seguintes informações sobre duas funções $f$ e $g$:
$\lim\limits_{x\to 1} f(x) = 0$
$\lim\limits_{x\to 1} g(x) = 0$
$\lim\limits_{x\to 1} f(x)/g(x) = 2$
O que você pode dizer sobre o valor de $\left|\frac{f(x)}{g(x)}\right|$ quando $x \approx 1$?
Derive a função $q\left( x\right) = \int_{e^{-2x}}^{\mathrm{tg}x}e^{\theta }\cos \theta d\theta$.
Avalie a seguinte integral indefinida:
$\int \frac{1}{3t^2}\ dt$
$-1/(3t)+C$
Qual a solução geral da dupla desigualdade $-2<x^2-3<\frac{1}{5}$?
Prove que $\displaystyle\int (sec(x))^m dx=x \dfrac{(sec(x))^{m-2}tg(x)}{m-1}+\dfrac{m-2}{m-1}\displaystyle\int (sec(x))^{m-2} dx$.
Na fabricação de um lote de peças de certo produto, o custo total é igual à soma de um valor fixo de $R\$ 400,00$ com o custo de produção unitário de $R\$ 0,50$. Se o preço unitário de venda dessas peças for de $R\$ 0,85$, qual o número mínimo de peças que devem ser fabricadas e vendidas para que se comece a ter lucro?
Calcule a integral $\displaystyle \int \dfrac{10x^2+9x+1}{2x^3+3x^2+x} \, dx$.
Utilize uma substituição trigonométrica para mostrar que $\displaystyle \int \dfrac{1}{u^2 \sqrt{a^2 - u^2}} \, du = -\dfrac{1}{a^2 u} \sqrt{a^2-u^2} + C $.
Sendo $f(x) = \left\{\begin{array}{cl} \cos x & x\leq 0 \\ x^2+3x+1 & x>0 \end{array}\right.$, calcule $\lim\limits_{x\to 0} f(x)$.
1
Dentre todos os retângulos inscritos numa circunferência de raio $R$, quais as dimensões daquele que tem a maior área?
Resolva a equação $\left| {\frac{3x+8}{2x-3}}\right| =4$.
Temos duas possibilidades: $\frac{3x+8}{2x-3}=4$ ou $\frac{3x+8}{2x-3}=-4$. Da primeira equação obtemos $3x+8=8x-12$, i. e., $x=4$. Da segunda equação obtemos $3x+8=-8x+12$, que fornece $x=4/11$.
Estude a função $f\left( x\right) =\dfrac{3x^{2}+4x}{1+x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Um atleta percorreu as $26,2$ milhas da maratona de Nova York em $2,2$ horas. Demonstre que em pelo menos duas ocasiões o maratonista correu a exatas $11mi/h$, supondo que as velocidades inicial e final tenham sido zero.
Com base no gráfico, avalie as seguintes integrais:
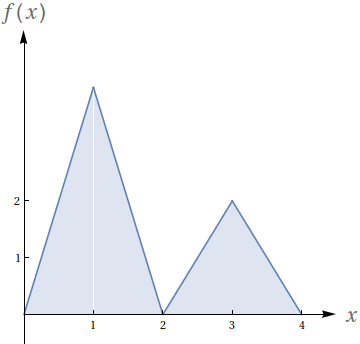
- $\int_0^2 f(x)\ dx$
- $\int_2^4 f(x)\ dx$
- $\int_2^4 2f(x)\ dx$
- $\int_0^1 4x\ dx$
- $\int_2^3 (2x-4)\ dx$
- $\int_2^3 (4x-8)\ dx$
- $4$
- $2$
- $4$
- 2
- $1$
- 2
- Se $f$ é contínua em $c$, então $\lim_{x\to c^+}f(x) = f(c)$.
- Se $f$ é contínua em $c$, então $\lim_{x\to c}f(x)$ existe.
- Se $f$ é definida em um intervalo aberto contendo $c$, e $ \lim_{x\to c}f(x)$ existe, então $f$ é contínua em $c$.
- Verdadeiro
- Verdadeiro
- Falso
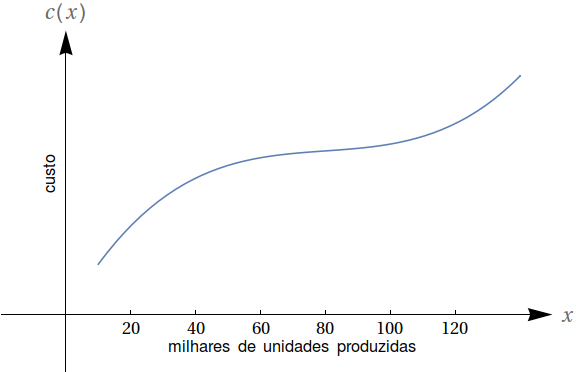
O gráfico a seguir mostra o custo hipotético $c=f(x)$ para fabricar $x$ itens. O chamado custo marginal é a mudança no custo total advinda da produção de uma unidade a mais do produto, para um certo volume de produção. Em aproximadamente qual nível de produção o custo marginal muda de decrescente para crescente?
Sendo $f(x) = \left\{\begin{array}{cl} x^2-x+1 & x\leq 3 \\ 2x+1 & x>3 \end{array}\right.$, calcule $\lim\limits_{x\to 3} f(x)$.
7
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=x^3/9$, $0\leq x \leq 2$, eixo $x$
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Calcule, através da definição de limite, $\displaystyle \lim_{x\to 0} e^{2x}-1 = 0$.
Seja $\epsilon >0$ dado. Queremos $\delta >0$ tal que, quO IMECC é responsável pelos cursando $|x-0|<\delta$, $|f(x)-0|<\epsilon$.
Considerando $|f(x)-0|<\epsilon$, lembrando que o objetivo é afirmar algo sobre $|x-0|$ (i.e., $|x|$):
\begin{gather*}
|f(x) -0 | < \epsilon \\
|e^{2x}-1 |<\epsilon \\
-\epsilon< e^{2x}-1 < \epsilon \\
1-\epsilon< e^{2x} < 1+\epsilon \\
\ln (1-\epsilon) < 2x < \ln (1+\epsilon) \\
\frac{\ln (1-\epsilon)}{2} < x < \frac{\ln (1+\epsilon)}{2} \\
\end{gather*}
Seja $\delta = \min\left\{\left|\frac{\ln(1-\epsilon)}{2}\right|,\frac{\ln(1+\epsilon)}{2}\right\}=\frac{\ln(1+\epsilon)}{2}.$
Portanto:
\begin{gather*}
|x| < \delta \\
|x| <\frac{\ln(1+\epsilon)}{2}<\left|\frac{\ln(1-\epsilon)}{2}\right| \\
\frac{\ln(1-\epsilon)}{2} < x < \frac{\ln(1+\epsilon)}{2}\\
\ln(1-\epsilon)< 2x < \ln(1+\epsilon)\\
1-\epsilon < e^{2x} < 1+\epsilon\\
-\epsilon < e^{2x}-1 < \epsilon\\
|e^{2x}-1-(0)| < \epsilon,
\end{gather*}
que é o que buscávamos provar.
Se $f$ e $g$ são funções contínuas tais que $0 \leq f(x) \leq g(x)$, para $x\geq a$, temos:
Se $\displaystyle \int_a^{+\infty} f(x) \, dx$ diverge, então $\displaystyle \int_a^{+\infty} g(x) \, dx$ diverge.
Se $\displaystyle \int_a^{+\infty} g(x) \, dx$ converge, então $\displaystyle \int_a^{+\infty} f(x) \, dx$ converge e $\displaystyle \int_a^{+\infty} f(x) \, dx \leq \int_a^{+\infty} g(x) \, dx$.
Mostre (graficamente e algebricamente) que para $x \geq 1$, temos $e^{-x^2} \leq e^{-x}$.
Calcule a integral $\displaystyle \int_1^{+\infty} e^{-x}\, dx$.
O que podemos afirmar sobre a integral $\displaystyle \int_1^{+\infty} e^{-x^2}\, dx$?
Calcule a integral $\int{\frac{\sin 10x}{4+\cos 10x}dx}.$
$\dfrac{1}{10}ln(cos(10x)+4)+C$
Esboce as curvas exponenciais transladadas:
$y=1-e^x$ e $y=1-e^{-x}$.
Escreva o número $\sin 1$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-17}$.
Para cada uma das afirmações abaixo, demonstre se verdadeiro
ou dê contra-exemplo se for falso.
- $\sqrt{x^{2}}=x,\forall x \in \mathbb{R}$.
- $x\neq y\Longrightarrow |x|\neq |y|$.
- $|x-y|\geq |x|-|y| \forall x,y\in \mathbb{R}$.
Suponha que uma população de piolhos parasitas de aves, representada por $p$, é estimada no começo do ano de $2015$ em $100 000$ em uma certa região. Um modelo matemático de crescimento da população assume que a taxa de crescimento (em milhares) após $t$ anos é dada por
$$p'(t)=(4+0,15t)^{3/2}.$$
Faça uma estimativa para o número de piolhos para o início do ano de 2025.
Prove que $\log2+\log3$ é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Note que $\log2+\log3=\log6$. Suponha que existam inteiros $p$ e $q$ tais que $log6=p/q$, com $p/q$ sendo fração irredutível. Use a definição de logaritmo e o teorema fundamental da aritmética para chegar a um absurdo.
Mostre que a função $y=f(x)$ definida por $f(x)=\left\{\begin{array}{ll}\sqrt{x-r}, & \text{se} x \geq r \\ -\sqrt{r-x}, & \text{se} x<r \end{array}\right.$ tem a propriedade que para todo número real $a$, se $x_1=r+a$, então $x_2=r+a$ e, por outro lado, $x_1=r-a$, então $x_2=r+a$.
Calcule a integral $\int_{0}^{r}\sqrt{r^{2}-x^{2}}dx$.
$\frac{1}{4}\pi r^4$
Calcule os limites:
$\lim\limits_{x\to\pi/6} cos(sec x)$
$\lim\limits_{x\to0} \ln(1+x)$
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{x-3}$
Seja $u=x-3$. Temos que $u$ tende a $0$ por valores positivos se $x$ tende a $3$ por valores maiores do que $3$. Logo, \begin{equation*} \lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{x-3}=\lim\limits_{u\rightarrow 0^{+}}\dfrac{5}{u}\text{.} \end{equation*} Mas dado $M>0$, temos que se $0<u<\dfrac{5}{M},$ então $M<\dfrac{5}{u}$ e temos que, por definição, $\lim\limits_{u\rightarrow 0^{+}}\dfrac{5}{u}=\infty $.
Enche-se um balão esférico a uma taxa de $4,5$ decímetros cúbicos por minuto. Calcule a taxa de variação do raio quando este medir $2$ decímetros.
\item Avalie a seguinte integral indefinida:
$\int dt$
$t+C$
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$|x-y|\leq |x|+|y|,\forall x,y\in \mathbb{R}$.
$x<y\Longrightarrow x^{2}<y^{2}$.
Se $a$, $b$, $c$ são as raízes de $x^3-x-1=0$, calcule o valor de $\frac{1+a}{1-a}+\frac{1+b}{1-b}+\frac{1+c}{1-c}.$
Este exercício pretende se debruçar sobre os limites
$\lim\limits_{x \rightarrow \infty} \left(1+\frac{1}{x^2}\right)^x$ e $\lim\limits_{x \rightarrow \infty} \left(1+\frac{1}{x}\right)^x = e$.
- Use a regra de L'Hospital para mostrar que $\lim\limits_{x \rightarrow \infty} \left(1+\frac{1}{x}\right)^x = e$.
- Com o auxílio de recursos computacionais, observe as curvas de $f(x)=\left(1+\frac{1}{x^2}\right)^x$ e $g(x)=\left(1+\frac{1}{x}\right)^x$ em um único gráfico, para $x \geq 0$. Como o comportamento de $f$ se relaciona com o de $g$? Estime o valor de $\lim\limits_{x \rightarrow \infty} f(x)$.
- Confirme sua estimativa de $\lim\limits_{x \rightarrow \infty} f(x)$ através da regra de L'Hôspital.
Verifique que $\displaystyle \int \text{cotg} (x) \, dx = \ln |\sin x| + k$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{e^{x}+e^{-x}}{2}.$
$f'(x) = \frac{e^{x}-e^{-x}}{2}$.
Dadas $a$ e $b$ constantes reais não nulas, esboce um gráfico da família de funções $f(x)=min\{|x-a|,|x-b|\}$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\arcsin\left( \cos\left( x\right) \right) .$
-\frac{\sin (x)}{\sqrt{1-\cos ^2(x)}}
Calcule a seguinte integral:
$\int \cos(x)\ln (\sin (x))dx $.
$sinx(ln(sinx)-1)+C$
Determine a equação da reta tangente ao gráfico de $f(x)=tg{x}$ no ponto de abscissa $0$.
$y=x$
Calcule o limite $\lim_{x\rightarrow 1} \frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2}$ ou prove que não existe.
Racionalizando e aplicando diferença de quadrados temos:
\begin{equation*}
\frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2} = \frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2}\cdot \frac{\sqrt{x+1}+\sqrt{2}}{\sqrt{x+1}+\sqrt{2}}\cdot \frac{\sqrt{x^2+3}+2}{\sqrt{x^2+3}+2} =
\frac{x-1}{x^2-1}\cdot\frac{\sqrt{x^2+3}+2}{\sqrt{x+1}+\sqrt{2}}.
\end{equation*}
Logo,
$\lim_{x\rightarrow 1} \frac{\sqrt{x+1}-\sqrt{2}}{\sqrt{x^2+3}-2}=\lim_{x\rightarrow 1}\frac{x-1}{x^2-1}\cdot\frac{\sqrt{x^2+3}+2}{\sqrt{x+1}+\sqrt{2}}=\lim_{x\rightarrow 1}\frac{1}{x+1}\cdot\frac{\sqrt{x^2+3}+2}{\sqrt{x+1}+\sqrt{2}}= \frac{1}{\sqrt{2}}.$
Mostre que $|\cos x-\cos y|\leq |x-y|$ quaisquer que sejam $x$ e $y$ reais, enunciando os teoremas utilizados.
Calcule a derivada de ordem $n$ da função $f(x)=\sin{x}+\cos{x}$.
Avalie a seguinte integral indefinida:
$\int x^8\ dx$
$1/9x^9+C$
Em uma esteira transportadora, areia é derrubada a uma taxa de $10$m$^3/$min no topo de um monte em formato de cone. A relação entre a altura do monte e o diâmetro da base é sempre de $3/8$.
- Qual a taxa de variação da altura?
- Qual a taxa de variação do raio, se o monte tiver $4$m de altura?
Seja $f: \mathbb{R} \to \mathbb{R}$ uma função contínua no intervalo $\left[2,6 \right]$ com $f(2)=3$ e $f(6)=5$. Use o Teorema de Weierstrass e o Teorema do Valor Intermediário pra mostrar que a imagem de $f$ é um intervalo fechado.
Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.
$y=\sqrt{x+5}$
$y=\sqrt{3-2x}$
- $[-5,\infty[$
- $]-\infty,\frac{3}{2}]$
Suponha que um meteorito pesado está a $s$ quilômetros do centro da Terra, e que sua velocidade de entrada na atmosfera terrestre seja inversamente proporcional a $\sqrt{s}$. Mostre que a aceleração do meteorito é inversamente proporcional a $s^2$ e interprete o resultado.
Em matemática, a função piso, denotada por $\lfloor x\rfloor$, converte um número real ${\displaystyle x}$ no maior número inteiro menor ou igual a ${\displaystyle x}$ Essa função é importante em computação para truncamento ou arredondamento de números. Considere a função $f(x)=\lfloor 1/x\rfloor$, $x \neq 0$. Esboce o gráfico dessa função para $\dfrac{1}{4} \leq x \leq 2$ e também para $-2 \leq x \leq -\dfrac{1}{4}$. Como se comporta $f(x)$ quando $x$ tende a zero pelo lado direito? E pelo lado esquerdo? O limite $\lim\limits_{x \to 0}f(x)$ existe?
A função $f(x) = \left\{ \begin{array}{ccc} x^2-1 & & x < 3 \\x+5 & & x\geq 3 \end{array}\right.$ é contínua em todo o seu domínio? Justifique.
Sim, é. O único ponto em que não poderia (inicialmente) ser contínua é em $x=3$. Todavia, temos $\lim\limits_{x\to 3^-} f(x)=\lim\limits_{x\to 3^+} f(x)=f(3)=8$.
Enuncie e demonstre o primeiro Teorema Fundamental do Cálculo.
Esboce o gráfico da função $f(x)=|x^3+3x^2+3x-2|$.
O custo marginal da impressão de um pôster quando $x$ pôsteres são impressos é
$\frac{dc}{dx}=\frac{1}{2\sqrt{x}}$ reais.
Determine $c(100)-c(1)$, ou seja, a soma do custo dos pôsteres 2-100.
Seja $h$ uma função definida em $[-1,1]$, sendo que $h(-1) = -10$ e $h(1) = 10$. Existe um valor $-1<c<1$ tal que $h(c) = 0$? Por quê?
Não é possível dizer: O Teorema do Valor Intermediário só se aplica para funções contínuas, e nada foi afirmado sobre a continuidade de $h$.
Use um recurso gráfico computacional para gerar os gráficos da função $f(x)=\dfrac{x-\sin x}{x^3}$, vide exercício ID 1703, e veja o que acontece.
Você esperaria que um problema similar ocorresse nos arredores de $x=0$ para a função $f(x)=\dfrac{1-\cos x}{x}$? Verifique se tal ocorre. Vide questão ID 958.
Seja $f(x)=2x^2-3$. Determine a equação da reta tangente ao gráfico de $f$ nos pontos:
- $(0,f(0))$
- $(2,f(2))$
Um balão está subindo verticalmente acima de uma estrada a uma velocidade constante de $1$ pé por segundo. Quando ele está a $65$ pés acima do solo, uma bicicleta que se desloca a uma velocidade constante de $17$ pés por segundo passa por baixo dele. A que taxa a distância $s(t)$ entre a bicicleta e o balão aumentará três segundos depois?
Utilizando as leis de exponenciação, simplifique a expressão a seguir:
$9^{1/3}\cdot9^{1/6}$
Enuncie e demonstre o Teorema do Confronto.
$2$
Um carro está em uma rodovia a uma velocidade constante de $60mi/h$ quando vê um acidente a frente e aciona os freios. Que desaceleração constante é necessária para frear o carro em 242 pés?
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow -\infty }\dfrac{5-x}{2x+3}$
$\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{x}+1}{x+3}$
- $-1/2$
- $0$
Determine o domínio da seguinte função:
$f\left( x\right) =\sqrt[4]{\dfrac{x}{x+4}}$.
$\left\{ x\geq 0\right\} \cup \left\{ x<-4\right\} $.
Dê exemplo de uma função $f$ que seja descontínua, mas tal que $|f|$ seja contínua.
Calcule $\displaystyle \int \sin (\ln x) \, dx$ utilizando integração por partes.
$-\dfrac{1}{2}x(cos(ln x)-sin(ln x))+C$
Esboce o gráfico de $f(x)=x^2\sqrt{4-x}$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(t) = \frac{1}{\sqrt{1-t^2}}$.
$(-1,1)$
O projetista de um balão esférico (um projetista excêntrico) de ar quente com $10m$ de diâmetro quer suspender uma gôndola a $2m$ abaixo da parte inferior do balão, presa por cabos tangentes à superfície deste. Dado que os cabos, saindo da lateral do balão, tangenciam a superfície do mesmo nos pontos $(4,-3)$ e $(-4,-3)$, qual deve ser a largura da gôndola?
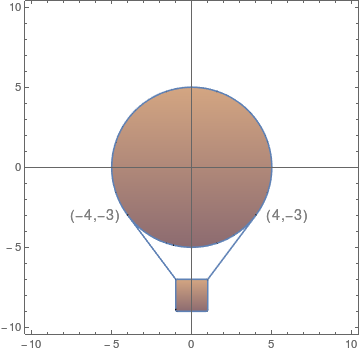
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\left( 1+2x\right) ^{\dfrac{1}{x}}$.
$e^2$.
Ache os extremos da função $f(x)=x+3x^{3/2}$.
Três números naturais e múltiplos consecutivos de 5 são tais que o triplo do menor é igual ao dobro do maior. Dentre esses números, qual o maior?
Note que todo múltiplo de $5$ pode ser escrito na forma $5n$, onde $n$ é algum número natural. Com essa ideia, podemos representar três múltiplos consecutivos de $5$ por: $5(n-1)$, $5n$ e $5(n+1)$. Como o triplo do menor é igual ao dobro do maior obtemos a equação $15(n-1)=10(n+1)$. Resolvendo essa equação encontramos $n=5$ e o maior número dentre os três é $5 \cdot 6=30$.
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left\vert x-2\right\vert +\left\vert x-1\right\vert >1$.
O raio $r$ e a altura $h$ de um cilindro circular reto estão variando de modo a manter constante o volume $V$. Num determinado instante, $h=3cm$ e $r=1cm$ e, neste instante, a altura está variando a uma taxa de $0,2cm/s$. A que taxa está variando o volume neste instante?
Escreva o número $\sin 1/2$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-20}$.
A posição $s$ de uma partícula em um instante $t \geq 0$, se deslocando em um movimento retilíneo, é dada por:
$$s=10\cos(t+\pi/4).$$
- Encontre a posição inicial da partícula. Isto é, a posição em $t=0$.
- Quais são os pontos mais distantes da origem que a partícula pode alcançar? (à direita e à esquerda).
- Encontre a velocidade e a aceleração da partícula nos pontos do item anterior.
- Quando a partícula atinge a origem pela primeira vez? Encontre a velocidade, o módulo da velocidade e a aceleração neste instante.
É possível mostrar que, sob certas condições, a velocidade $v(t)$ de uma gota de chuva caindo no instante $t$ é:
$$v(t) = v^\star \left(1-\exp\left(-\dfrac{gt}{v} \right)\right),$$
onde $g$ é a aceleração da gravidade e $v^\star$ é a velocidade final da gota.
Calcule a velocidade para um tempo muito grande, isto é, calcule $\displaystyle \lim_{t \to \infty} v(t)$.
Considerando $v^\star = 1$m$/$s e $g=9,8$m$/$s$^2$, faça o gráfico de $v(t)$. Quanto tempo levará para a velocidade da gota atingir $99\%$ de sua velocidade final?
Um projetista, incumbido da tarefa de projetar uma bacia com cerca de $3L$ de capacidade, resolveu fazê-la nos moldes de uma tampa de uma casca esférica de $r=16cm$, com $9cm$ de profundidade, conforme a figura abaixo. Calcule o volume da bacia projetada e veja se a estimativa do projetista foi adequada, dado que a margem de erro do volume estabelecida pela empresa era de $15\%$.
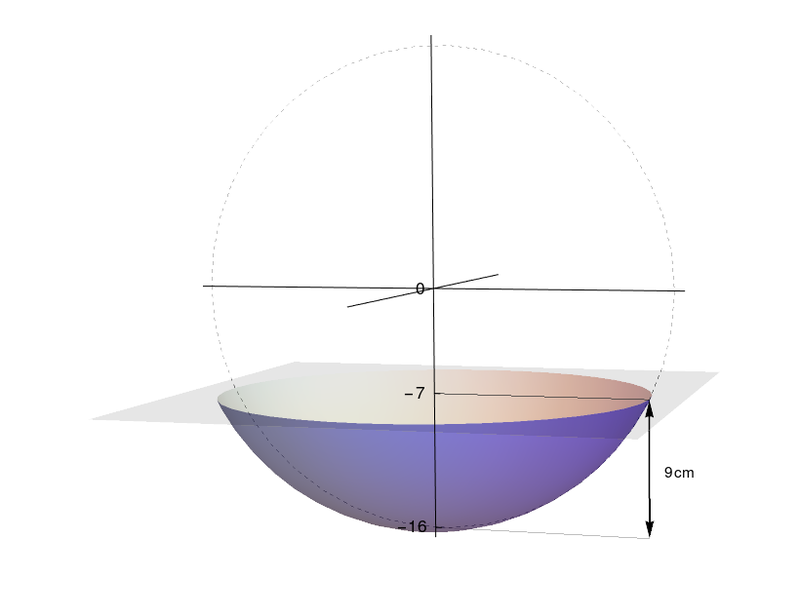
Podemos calcular o volume da bacia através da seguinte integral:
$V=\int_{7}^{16}\pi\left(\sqrt{16^2-x^2}\right)^2\,dx=\left.\left[\pi(256x-\frac{x^3}{3})\right]\right\vert_7^{16}=1053\pi$
Lembrando que $1L=1000cm^3$ e supondo $\pi\approx3$, temos $V=3159cm^3$ (O valor real é próximo de $V=3308cm^3$). Como a margem de erro do projetista era de $15\%$, vemos que este acertou em seus cálculos.
Use o método de Newton para calcular a raiz positiva de $x^2+x-1=0$ com duas casas decimais de precisão.
Identifique as assíntotas verticais e horizontais, caso existam, da função $f(x)=\frac{-3 x^2-9 x-6}{5 x^2-10 x-15}$.
Assíntota horizontal em $y=-3/5$; assíntota vertical em $x=3$.
Ache as assíntotas verticais e inclinadas; depois calcule os limites laterais nas assíntotas verticais da função $f\left( x\right) =\frac{x^{3}-3x-1}{x^{2}-x}.$
Encontre o ponto de interseção da reta tangente ao gráfico de $y=x-\frac{1}{x}$ no ponto $(1,0)$ com o eixo $y$.
$(1,0)$.
Se $p$ denota o preço de venda de um artigo e $x$ é a procura correspondente (em número de artigos vendidos por di, então a relação entre $p$ e $x$ pode ser dada por $p(x)=p_0e^{-ax}$ para constantes positivas $p_0$ e $a$. Suponha $p(x)=300e^{-0,02x}$. Determine o preço de venda que maximize a receita diária.
Verifique que $\displaystyle \int \text{cotg}^n (x) \, dx = -\dfrac{\text{cotg}^{n-1} (x) }{n-1} - \int \text{cotg}^{n-2} (x) \, dx, \, n \geq 2$.
Considere a função $f(x) = \left\{\begin{array}{cl} x+2 & x\leq 2 \\ 3x-5 & x>2 \end{array}\right.$. Mostre que $\lim\limits_{x\to 2} f(x)$ não existe.
Determine o conjunto de todos os números reais para os quais a expressão $\frac{\sqrt{4-x^2}}{\sqrt[3]{x-1}}$ está definida.
Uma partícula se move na circunferência $x^2 + y^2 = a^2$ de tal modo que a componente $x$ de sua velocidade é $\dfrac{dx}{dt}=-y$. Encontre $\dfrac{dy}{dt}$ e determine se o sentido do movimento é horário ou anti-horário.
Estime numericamente os seguintes limites para a função $f(x)= \frac{x^2+5 x-36}{x^3-5 x^2+3 x+9}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-335.64$ \\
$2.99$ & $-30350.6$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $-265.61$ \\
$3.01$ & $-29650.6$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =-\infty$.
A corrente $I(t)$ em um circuito elétrico composto de um resistor e um indutor, no instante $t$, é dada por $I(t)=I_0e^{-Rt/L}$, onde $R$ é a resistência, $L$ a indutância e $I_0$ é a corrente no instante $t=0$. Mostre que a taxa de variação da corrente no instante $t$ é proporcional a $I(t)$.
Resolva a equação $|x + 1| = 3$.
Temos dois casos: $x+1=3$ ou $x+1=-3$. Resolvendo cada uma dessas equações de primeiro grau obtemos $x=2$ e $x=-4$.
Embora limites como $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{n}$ e $\displaystyle \lim_{n \to \infty} a^n$ possam ser avaliados utilizando conhecimentos sobre as funções logaritmo e exponencial, estes não são necessários. Neste exercício vamos calcular esses tipos de limite por meio de argumentos ``elementares''. As ferramentas básicas são desigualdades provenientes do teorema binomial, principalmente:
$$(1+h)^n \geq 1+nh, \text{ para } h > 0.$$
Mostre que $\displaystyle \lim_{n \to \infty} a^n = \infty$ se $a>1$, fazendo $a=1+h$, onde $h>0$.
Mostre que $\displaystyle \lim_{n \to \infty} a^n= 0$ se $0<a<1$.
Seja $n$ um número natural dado por $n= 2000 \cdot x$. Determine um possível valor para $x$ que torna $n$ um quadrado perfeito.
Sabemos que quando decompomos um quadrado perfeito em fatores primos, os expoentes dos números primos na decomposição são necessariamente múltiplos de $2$. Ora, decompondo $2000$ obtemos $2000=2^4 \cdot 5^3$. Se multiplicarmos $2000$ por $5$ obteremos $10000=2^4 \cdot 5^4$, que é um quadrado perfeito, a saber $100^2$. Neste caso tomamos $x=5$, mas há infinitas outras possibilidades!
Calcule $\sqrt{5}$ com duas casas decimais de precisão, resolvendo a equação $x^2-5=0$ e use esse resultado na fórmula quadrática para obter as raízes de $x^2+x-1=0$.
Sejam $x$ e $y$ dois números reais positivos. Demonstre que $\sqrt{xy}\leq \dfrac{x+y}{2}.$
Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\sqrt{x}}{x+1}$.
$f'(x) = \dfrac{1-x}{2\sqrt{x}(x+1)^2}$.
Queremos calcular a derivada da divisão da função $\sqrt{x}$ pela função $x+1$. Usando a regra da derivada do quociente, obtemos:
\[\left( \dfrac{\sqrt{x}}{x+1} \right)^\prime = \dfrac{(\sqrt{x})^\prime \cdot (x+1) - \sqrt{x}\cdot (1+x)^\prime}{(x+1)^2}.\]
Sabendo que
\[(\sqrt{x})^\prime = \left(x^{1/2}\right)^\prime = \dfrac{1}{2} x^{\left(\tfrac{1}{2}-1\right)} = \dfrac{1}{2 \sqrt{x}}\]
e que
\[(x+1)^\prime = (x)^\prime + (1)^\prime = 1 + 0 = 1,\]
podemos usar essas expressões na regra do quociente e, assim, obter que
\[\dfrac{(\sqrt{x})^\prime \cdot (x+1) - (\sqrt{x})\cdot (1+x)^\prime}{(x+1)^2} = \dfrac{\dfrac{1}{2 \sqrt{x}}(x+1)-\sqrt{x}(1)}{(x+1)^2} = \dfrac{\dfrac{x}{2 \sqrt{x}} +\dfrac{1}{2 \sqrt{x}} -\dfrac{x}{\sqrt{x}}}{(x+1)^2}.\]
Disso, podemos concluir que
\[f'(x) = \dfrac{1-x}{2\sqrt{x}(x+1)^2}.\]
Considere o gráfico da função $f$:
$f\left( x\right) =\left\{\begin{array}{c}-2x-2,-4\leq x\leq -2 \\x+4,-2\leq x\leq 1 \\6-x,1\leq x\leq 4\end{array}\right.$
Esboce, a partir deste, os gráficos das seguintes funções:
$y=f\left( x+4\right) $
$y=f\left( x\right) +4$
$y=2f\left( x\right) $
$y=-\dfrac{1}{2}f\left( x\right) +3.$
Determine as derivadas das seguintes funções:
$f\left( x\right) =e^{\tan \left( x^{3}\right) }$.
$f\left( x\right) =\left( a\sin x+\cos bx\right)^{3};$
$f\left( x\right) =\dfrac{xe^{-3x}}{1+\cos x}.$
Determine a equação da reta tangente ao gráfico de $f(x)=e^x$ no ponto de abscissa $0$.
Considere os números inteiros ``$abc$'' e ``$bac$'', em que $a$, $b$ e $c$ são algarismos distintos e diferentes de zero e $a>b$. A diferença $abc-bac$ é sempre um múltiplo de determinado número. Que número é esse?
Note que "$abc$"$=100a+10b+c$ e que "$bac$"$=100b+10a+c$. Assim, "$abc$"-"$bac$"$=90a-90b=90(a-b)$, que é um número sempre múltiplo de $90$ e de todos os divisores de $90$.
O Princípio de Fermat na óptica estabelece que a luz, viajando de um ponto para outro, segue aquele caminho para o qual o tempo total de percurso é mínimo. Em um meio uniforme, os caminhos de "tempo mínimo" e de "menor distância" vêm a ser iguais; assim sendo, se não obstruída, a luz viaja em linha reta. Suponha que temos uma fonte de luz (ponto $A$), um espelho plano e um observador (ponto $B$) em um meio uniforme. Se um raio de luz deixa a fonte, bate num espelho e vai até o observador, então a sua trajetória consiste de dois segmentos de reta, conforme ilustrado na figura abaixo. De acordo com o princípio de Fermat, a trajetória é tal que o tempo gasto no percurso é mínimo ou, como o meio é uniforme, a trajetória será tal que a distância total percorrida de $A$ para $B$ é a menor possível. Supondo que o mínimo ocorre quando $\displaystyle dt/dx=0$, mostre que o raio de luz irá atingir o espelho em um ponto $P$, tal que o "ângulo de incidência" $\theta_1$ é igual ao "ângulo de reflexão" $\theta_2$.
Um fabricante produzirá caixas fechadas (com tampa) de volume igual a $27$ litros e cuja base é um retângulo com comprimento igual ao triplo da largura. Encontre as dimensões da caixa de forma que o consumo de material seja mínimo.
Durante o primeiro mês de crescimento de produtos como milho, algodão e soja, a taxa de crescimento (em gramas/dia) é proporcional ao peso presente $W$. Para determinada espécie de algodão, $dW/dt=0,21W$. Preveja o peso de uma planta no término de um mês ($t=30$), se a planta pesa 70 miligramas no início do mês.
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x \ln{x}}{x+\ln{x}}$.
$\infty$.
Determine os valores de $\lambda$ que tornam contínua a função $f:\mathbb{R\rightarrow R},$ da por:
\[
f\left( x\right) =\left\{
\begin{array}{c}
x^{2}+\lambda x\mbox{ se }x\leq 1 \\
\left( \lambda x\right) ^{2}-1=\lambda ^{2}x^{2}-1\mbox{ se }x>1
\end{array}
\right. \mbox{.}
\]
Use a desigualdade triangular $\left| a+b\right| \leq \left| a\right|+\left| b\right| $\emph{ }para mostrar que $\left| x-y\right| \geq \left|x\right| -\left| y\right| $ para todo $x,y\in \mathbb{R}$. Em particular, conclua que $\left| x-y^{2}\right| \geq \left| x\right| -y^{2}.$
Se você investir $1000$ reais em uma aplicação que paga $7$% de juros compostos em $n$ vezes por ano, então em $10$ anos sua aplicação terá no total $1000(1+0,07/n)^{10n}$ reais.
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta trimestralmente ($n=4$)?
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta mensalmente ($n=12$)?
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta mensalmente ($n=365$)?
Pesquise a taxa de juros paga pela poupança, e o período em que ela é composta. Calcule a quantidade de dinheiro que você terá se investir uma certa quantia de dinheiro (pense no dinheiro você tem disponível para investir) em $1$, $2$, $5$ e $10$ anos com essa taxa e período de composição. Interprete os resultados pensando em seu futuro!
Quanto dinheiro você terá em $10$ anos se os juros forem compostos continuamente, isto é, se $n\to\infty$?
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =4\sec x+\cot x$.
$f'(x) = 4 \sec x \tan x - \csc^2 x$.
Como a derivada da soma de funções é a soma de suas derivadas, temos inicialmente que
\[ (4\sec x+\cot x)^\prime = (4\sec x)^\prime + (\cot x)^\prime = 4 (\sec x)^\prime + (\cot x)^\prime .\]
Como $\sec x = \dfrac{1}{\cos x}$, podemos usar a regra do quociente para calcular sua derivada:
\[(\sec x)^\prime = \left(\dfrac{1}{\cos x}\right)^\prime = \dfrac{(1)^\prime\cdot \cos(x) - 1\cdot (\cos x)^\prime}{(\cos x)^2} =\dfrac{0 - (-\sin x)}{(\cos x)^2} = \tan(x)\sec(x).\]
De forma análoga, usaremos a regra do quociente para calcular a derivada da função $\cot x$, que é igual a $\frac{\cos x}{\sin x}$:
\[(\cot x)^\prime = \left(\dfrac{\cos x}{\sin x}\right)^\prime = \dfrac{(\cos x)^\prime\cdot \sin(x) - \cos(x)\cdot (\sin x)^\prime}{(\sin x)^2} =\dfrac{(-\sin x) \sin x - \cos(x)(\cos x)}{(\sin x)^2} = -(\csc x)^2,\]
em que usamos a identidade trigonométrica fundamental
\[(\sin x)^2 + (\cos x)^2 = 1\]
e a identidade $\csc x = \frac{1}{\sin x}$ para obter a cossecante.
Substituindo as expressões encontradas para as derivadas de $\sec x$ e de $\cot x$ na primeira igualdade, concluímos que
$f'(x) = 4 \tan(x)\sec(x) - (\csc x)^2$.
Demonstre a fórmula de Báskhara usada para resolução de equações polinomiais de grau $2$.
Avalie a seguinte integral indefinida:
$\int \frac{5^t}{2}\ dt$
$\frac{5^t}{2\ln 5}+C$
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{x^{3}-x^{2}+1}{x}$.
Prove que $\sqrt{2}+\sqrt{3}$ é irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Estude a função $f\left( x\right) =\dfrac{x^{2}}{x+1}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Encontre os valores de $x$ para os quais cada o número $\sqrt{x^{2}+x+3}$ é real.
Este número será real se o valor dentro da raiz for maior ou igual a zero. Como $x^2 + x + 3$ têm raízes complexas e concavidade para cima, seu valor é sempre maior que zero. Portanto $\sqrt{x^2 + x + 3}$ é real para qualquer $x$ real.
Calcule o seguinte limite
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{2x}\right)^{x}$.
$e^{1/2}$.
Verifique que a equação $x^{179}+\frac{163}{1+x^2+\sin^2x}=119$ possui pelo menos uma solução.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =e^{x}\cos x$.
$f'(x) = e^x(\cos x - \sin x)$.
Usando a regra da derivada do produto, temos que
\[f^\prime(x) = (e^x \cos x)^\prime = (e^x)^\prime \cdot \cos(x) + e^x \cdot (\cos x)^\prime.\]
Como $(e^x)^\prime = e^x$ e $(\cos x)^\prime = -\sin x$, então
\[(e^x)^\prime \cdot \cos(x) + e^x \cdot (\cos x)^\prime = e^x \cos x + e^x (-\sin x) .\]
Colocando o fator comum $e^x$ em evidência, concluímos que
\[f^\prime (x) = e^x (\cos x- \sin x).\]Uma escada de $4$m está apoiada em uma parede fazendo um ângulo $\theta$ com o chão. Considerando $h$ como a altura do chão até o ponto em que a escada encosta na parede, expresse $h$ em função de $\theta$ e, então, use $dh$ para estimar a variação em $h$ se $\theta$ varia de $60^\circ$ a $59^\circ$, de $60^\circ$ a $58^\circ$, e de $60^\circ$ a $55^\circ$. Interprete estes resultados.
Seja $f:\mathbb{R\rightarrow R}$ uma função.
- Defina continuidade de $f$ no ponto $p\in \mathbb{R}$.
- Defina a derivada de $f$ no ponto $p\in \mathbb{R}$. O que é a função derivada $f^{\prime }\left( x\right) ?$
- Calcule, pela definição, a derivada $g^{\prime }\left( 0\right) $ onde \begin{equation*} g\left( x\right) =\left\{ \begin{array}{cc} x^{2}\sin \left( \dfrac{1}{x^{2}}\right) & \text{se }x\neq 0 \\ 0 & \text{ se }x=0 \end{array} \right. \end{equation*}
Avalie a seguinte integral indefinida:
$\int (t^2+3)(t^3-2t)\ dt$
$t^6/6+t^4/4-3t^2+C$
Dê o domínio e esboce o gráfico das seguintes funções:
- $f(x)=1/x^2$
- $f(x)=\dfrac{1}{(x-1)^2}$
Quais valores de $a$ e $b$ minimizam o valor de
$\int_a^b\left(x^4-2x^2\right)dx$?
A média geométrica de dois números reais positivos $a$ e $b$ é definida como $\sqrt{ab}$. Prove que $\sqrt{ab}=\lim\limits_{x \to \infty}\left(\dfrac{a^{1/x}+b^{1/x}}{2}\right)^x$.
Calcule a integral a seguir:
$\int{\frac{\left(1+\sqrt{x}\right)^{1/3}}{\sqrt{x}}dx}$
Esboce o gráfico de $f(x)=x^3-x^2+1$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Prove que se $f$ é contínua em $\left[a,b\right]$ , então $\displaystyle\int_{a}^{b}f(x)dx=(b-a)f(\xi)$ para algum $\xi \in \left[a,b\right]$.
Qual o número de raízes distintas da equação $(x^2 – 14x + 38)^2 = 11^2$?
$3$
Explique, usando suas palavras, o que significa escrever $\lim\limits_{x\to c} x = c$.
Seja $x$ uma função de $t$, isto é, $x=f(t)$, tal que para $t=0$, $x=1$ e para $t=1$, $x=2$. Suponha que $\dfrac{dx}{dt}>0$ para $t\geq0$; $\dfrac{d^2x}{dt^2}<0$ para $0<t<1$ e $\dfrac{d^2x}{dt^2}>0$ para $t>1$. Como você acha que deve ser o gráfico de $f$? Por quê?
O gráfico da função $f(x)=\frac{x^3+2x^2+1}{5-x^2}$ possui alguma assíntota horizontal?
Não possui.
Encontre os valores de $x$ para os quais cada o número $\sqrt[4]{{\frac{x^{2}-x-2}{x^{2}-4x-3}}}$ é real.
Calcule a derivada de ordem $1000$ da função $f(x)=e^{kx}, k \in R$.
$f^{1000}(x)=k^{1000}e^{kx}$
Determine as derivadas das seguintes funções:
$f\left( x\right) =e^{\cos \left( x^{2}\right) }$.
$f\left( x\right) =\left( \sin x+\cos x\right)^{3}$.
$f\left( x\right) =x^{3}e^{-3x}.$
Dê um exemplo de uma função definida em $\mathbb{R}$ que não seja contínua em $2$ mas que $\lim\limits_{x\rightarrow 2^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 2^{-}}f\left( x\right) .$
Nos primórdios da geração comercial de eletricidade, havia uma disputa bastante acirrada entre duas formas de se distribuir energia elétrica: A disputa entre corrente alternada e corrente contínua. A corrente alternada provou-se mais eficiente para transmissão a longas distâncias, principalmente pela facilidade com que é possível elevar os níveis de tensão (e, portanto, para uma mesma potência transmitida, diminuir a corrente e consequentemente os diâmetros dos fios utilizados na transmissão, implicando em significativa economia).
Com o advento da eletrônica, na segunda metade do século XX, a corrente contínua reconquistou um papel fundamental no dia a dia da sociedade contemporânea, dado que circuitos eletrônicos são alimentados com corrente contínua. A conversão de corrente alternada é feita a partir de dispositivos chamados retificadores. Infelizmente, o funcionamento destes dispositivos foge do escopo desta disciplina.
As figuras abaixo representam uma corrente $i(t)$ antes e depois de um circuito:
Responda:
- Dado que a função original seja $i_0(t)= \sin(2\pi\ 60\ t)$, qual a relação entre o seu período $T_0$ e o período da corrente retificada $i_1(t)$?
- Quais operações sobre a função $i_0(t)$ você realizaria para obter $i_1(t)$?
- Qual o valor médio, em um período, de $i_0(t)$? Qual seria sua estimativa para o valor médio de $i_1(t)$?
Esboce o gráfico da função $f\left( x\right) =\cos x-\sin x$ . Para fazê-lo, determine:
Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão
- Dom$\left( f\right) =\mathbb{R}$
- $f\left( 0\right) =1$ e $f\left( x\right) =0$ se, e somente se, $\cos x=\sin x$ se, e somente se,
$x=\frac{\pi}{4}+k\pi$ com $k\in\mathbb{Z}$ - $f$ é periódica, com período $2\pi$
- A função não possui assíntotas verticais (pois é contínua na reta) e tampouco horizontais (pois é periódica)
- \begin{align*}
f^{\prime}\left( x\right) & =-\sin x-\cos x=0\text{ se, e somente se,}\\
\cos x & =-\sin x\text{ se, e somente se, }x=\frac{3\pi}{4}+k\pi\text{ com }k\in
\mathbb{Z}\text{.}
\end{align*}
Considerando no período $\left[ 0,2\pi\right] $ temos que
\begin{align*}
f^{\prime}\left( x\right) & >0\text{ se }x\in\left( \frac{3\pi}{4}
,\frac{7\pi}{4}\right) \text{ (intervalo de crescimento)}\\
f^{\prime}\left( x\right) & <0\text{ se }x\in\lbrack0,\frac{3\pi}{4}
)\cup(\frac{7\pi}{4},2\pi]\text{ (intervalo de crescimento)}
\end{align*} - Novamente considerando no período $\left[ 0,2\pi\right] $ temos que $\frac{3\pi}{4}$ é ponto de mínimo e $\frac{7\pi}{4}$ é ponto de máximo.
- \begin{align*}
f"\left( x\right) & =-\cos x+\sin x=0\text{ se, e somente se,}\\
\cos x & =\sin x\text{ se, e somente se, }x=\frac{\pi}{4}+k\pi\text{ com }k\in
\mathbb{Z}\text{.}
\end{align*}
Considerando no período $\left[ 0,2\pi\right] $ temos que
\begin{align*}
f"\left( x\right) & >0\text{ se }x\in\left( \frac{\pi}{4},\frac{5\pi}
{4}\right) \text{ (concavidade para cima)}\\
f"\left( x\right) & <0\text{ se }x\in\lbrack0,\frac{\pi}{4})\cup
(\frac{5\pi}{4},2\pi]\text{ (concavidade para baixo)}
\end{align*} - Esboço do Gráfico:
Usando a fórmula do volume de uma calota esférica, encontre o volume do sólido que sobra quando um buraco de raio $\dfrac{r}{2}$ é feito através do centro de uma esfera de raio $r$ e verifique a sua resposta por integração.
Se $f(x+1)=\frac{x-1}{\pi -x}$, ache $f(x)$ e encontre o domínio de $f$.
Seja $g(x)=log_a{x}$, em que $a>0$ e $a \neq 1$ é um real dado. Mostre que $g'(x)=\dfrac{1}{x \ln{a}}$.
Avalie a integral $\displaystyle \int_{-1}^1 (x^5+3) \sqrt{1-x^2} \, dx$ sem fazer nenhuma conta.
Se $ f(x) = \sqrt{x} $ e $ g(x) =\sqrt{2-x},$ encontre e determine o domínio das funções:
- $f \circ g (x).$
- $g \circ f(x).$
- $f \circ f (x).$
- $g \circ g(x).$
Jane está em um barco a $2 km$ da costa e deseja chegar a uma cidade litorânea, localizada $6 km$ ao longo de uma linha costeira retilínea desde o ponto (na costa) mais próximo do barco. Ela rema a $2 km/h$ e caminha a $5 km/h$. Em que ponto da costa ela deve aportar para chegar à cidade no menor tempo possível?
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x+1, & & \text{ se } x<1 \\
1, & & \text{ se } x=1\\
x-1, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
- 2
- 0
- Não existe
- 1
Ache uma fórmula para a soma $1+2x+3x^2 +\cdots +nx^{n-1}$.
$\dfrac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2}$, $x \neq 1$. Se $x=1$, a soma dá $\dfrac{n(n+1)}{2}$.
Calcule a integral $\int \dfrac{\sin x}{\cos ^{3}x}dx.$
Calcule a integral $\int x^{2}\ln xdx$.
$\dfrac{1}{9}x^3(3lnx-1)+C$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{e^{x}-e^{-x}}{2}.$
$f'\left( x\right) =\frac{e^{x}+e^{-x}}{2}.$
Encontre o volume de uma pirâmide de base quadrada com lado $L$ e altura $h$.
Classifique as afirmações a seguir como verdadeiras ou falsas:
Se $ \lim\limits_{x\to \infty} f(x) = 5$, então estamos implicitamente afirmando que o limite em questão existe.
$\infty/0$ não é uma forma indeterminada.
Verdadeira
Verdadeira
Conforme $x$ aumenta, tanto $1/x$ quanto $1/(ln\ x)$ tendem a zero. Dada a função: $f(x)=\left(\frac{1}{x}\right)^{1/(ln\ x)}$ avalie $f(x)$ para valores cada vez maiores de $x$. Qual o padrão observado? Com o auxílio de recursos computacionais, observe o gráfico de $f(x)$ para valores grandes de $x$.
Sugestão: Procure, no site, o exercício 1527. Compare os resultados obtidos.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$(2-5x)^{20}>0$
${\frac{x-3}{x-5}}>0$
Seja $f(x)=cossec{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
Inicialmente, determinamos a primeira derivada da função $f$:
$f'(x)=-cossec(x)cotg(x)$.
Agora, substituímos $x$ por $\dfrac{\pi}{4}$ e obtemos
$f'\left(\dfrac{\pi}{4}\right)$=-cossec\(\dfrac{\pi}{4}\)cotg\(\dfrac{\pi}{4}\)=-\dfrac{2}{\sqrt{2}}\cdot 1 = \dfrac{2}{\sqrt{2}}$.
Calcule a derivada da seguinte função:
$f\left( x\right) =3^{2x}\ln\left( x^{2}\right) .$
$2\ 3^{2 x} \log (3) \log \left(x^2\right)+\frac{2\ 3^{2 x}}{x}$
Mostre que a linearização de $f(x)=(1+x)^k$ em $x=0$ é $L(x)=1+kx$.
Classifique as afirmações em verdadeiras ou falsas.
Um número racional qualquer tem sempre um numero finito de ordens (casas) decimais.
Um número racional qualquer tem sempre um numero infinito de ordens (casas) decimais.
Um número racional qualquer não pode expressar-se em forma decimal exata.
Um número racional qualquer nunca se expressa em forma de uma decimal inexata.
F
F
F
F
Em $1635$, Bonaventura Cavalieri, um aluno de Galileu, estabeleceu o seguinte resultado, chamado Princípio de Cavalieiri: se dois sólidos tiverem a mesma altura, e se as áreas de suas seções transversais tomadas paralelas e a iguais distâncias de suas bases forem sempre iguais, então os sólidos têm o mesmo volume. Use esse resultado para achar o volume do cilindro oblíquo da figura.
Avalie a seguinte integral indefinida:
$\int e^\pi\ dx$
$e^\pi x+C$
Estude a função $f\left( x\right) =\dfrac{x}{1+\tan x},x\in \lbrack 0,\dfrac{\pi }{2})$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f''(x) = 5$ e $f'(0)= 7$, $f(0) = 3$
$5/2x^2+7x+3$
Prove que $\sqrt{6}$ é irracional.
Quais valores de $a$ e $b$ maximizam o valor de
$\int_a^b\left(x-x^2\right)dx$?
$a=0$ e $b=1$.
Calcule o seguinte limite, caso exista:
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\sin\left( 23x\right) }$
$\begin{array}{rcl} \lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\sin\left( 23x\right) } &=& \lim\limits_{x\rightarrow 0} \dfrac{ \dfrac{\sin \left( \pi x\right)}{x} }{ \dfrac{\sin\left( 23x\right)}{x} } \\ &=& \lim\limits_{x\rightarrow 0} \dfrac{ \dfrac{\pi \sin \left( \pi x\right)}{\pi x} }{ \dfrac{23\sin\left( 23x\right)}{23x} } \\ &=& \lim\limits_{x\rightarrow 0} \dfrac{\pi}{23} \dfrac{ \dfrac{ \sin \left( \pi x\right)}{\pi x} }{ \dfrac{\sin\left( 23x\right)}{23x} }. \end{array}$
Fazendo as mudanças de variáveis $y = \pi x$ e $t = 23x$, temos que
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\pi x} = \lim\limits_{y\rightarrow 0}\dfrac{\sin \left( y\right) }{y} = 1 $.
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left( 23 x\right) }{23 x} = \lim\limits_{y\rightarrow 0}\dfrac{\sin \left( t\right) }{t} = 1 $.
Onde nas últimas passagens usamos o limite fundamental do seno. Desse modo, sabendo que os limites existem, podemos substituí-los na expressão anterior:
$\begin{array}{rcl} \lim\limits_{x\rightarrow 0}\dfrac{\sin \left( \pi x\right) }{\sin\left( 23x\right) } &=& \lim\limits_{x\rightarrow 0} \dfrac{\pi}{23} \dfrac{ \dfrac{ \sin \left( \pi x\right)}{\pi x} }{ \dfrac{\sin\left( 23x\right)}{23x} } \\ &=& \dfrac{\pi}{23} \dfrac{1}{1} \\ &=& \dfrac{\pi}{23}. \end{array}$
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =\sqrt[3]{x},\;p=1$.
$y=\dfrac{x+2}{3}$.
Calcule a integral a seguir:
$\int{\cos 2x\ dx}$
$sin(x)cos(x)+C$
Com base no gráfico, avalie as seguintes integrais:
- $\int_0^2 f(x)\ dx$
- $\int_2^4 f(x)\ dx$
- $\int_0^4 f(x)\ dx$
- $\int_0^4 5f(x)\ dx$
- $\pi$
- $\pi$
- $2\pi$
- $10\pi$
Dentre todos os retângulos de perímetro fixo $L$, determine aquele de maior área. Justifique a resposta.
Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{(x-1)^2}$.
As assíntotas verticais são os pontos $x$ tais que o limite é infinito.
Para $f(x)=\frac{x^2+1}{(x-1)^2}$ temos que:
$\lim \limits_{x \to 1} \frac{x^2+1}{(x-1)^2} = \infty$,
Logo $x=1$ é uma assíntota vertical de $f$. Como não há mais pontos no domínio de $f$ que podem levar a um limite infinito, esta é a única assíntota.
Suponha que as equações do movimento de um avião de papel, durante os $12$ segundos iniciais de vôo, são $$ x=t-2\sin t, \quad y=2-2\cos t\quad(0\leq t\leq 12). $$Quais são os pontos mais alto e mais baixo da trajetória e em que instantes eles são atingidos?
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(k) = \sqrt{1-e^k}$.
$(-\infty,0]$
Dizemos que duas famílias de curvas são trajetórias ortogonais uma da outra se cada curva de uma família for ortogonal a cada curva da outra. Faça um esboço de gráfico da família de curvas $xy=c$ e da família $x^2-y^2=k$ no mesmo plano cartesiano, para alguns valores de $c$ e $k$ reais (se necessário, utilize algum recurso computacional). Mostre que estas famílias (de hipérboles) são ortogonais uma da outra. (Sugestão: retas tangentes são perpendiculares em um ponto de interseção se as suas inclinações são recíprocas negativas uma da outra.)
Utilizando o gráfico, avalie os seguintes limites para a função
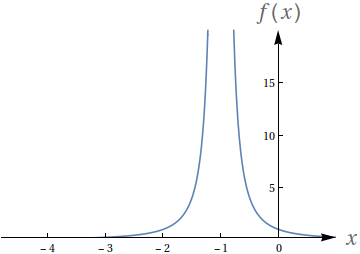
$f(x) = \frac{1}{(x+1)^2}$
$ \lim\limits_{x\to -1^-} f(x)$
$ \lim\limits_{x\to -1^+} f(x)$
- $\infty$
- $\infty$
A taxa de crescimento $R$ de certo tipo de tumor pode ser relacionada com seu tamanho $x$, de modo aproximado, pela equação $R=r\cdot x\cdot ln(K/x)$, em que $r$ e $K$ são constantes positivas. Mostre que o tumor cresce mais rapidamente quando $x=e^{-1}K$.
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 0}\dfrac{\tan x}{x}$
$\lim\limits_{x\rightarrow 0}\dfrac{x^{3}}{\sin x}$
Enuncie e prove a desigualdade triangular envolvendo números reais.
Sabendo-se que $\frac{x-a}{x^2+1} > \frac{x+a}{x^2}$ para todo $x$ real, determine o intevalo a que pertence o número real $a$.
O limite $\lim_{x\rightarrow +\infty} x^3(1+\sin x)$ existe? Explique.
Mostre que $\lim\limits_{x\rightarrow p}f\left( x\right) =L$ se e somente se $\lim\limits_{x\rightarrow p}\left( f\left( x\right) -L\right) =0$.
Suponha que $f\left( x\right) \leq g\left( x\right) $ para todo $x$. Demonstre que $\lim\limits_{x\rightarrow p}f\left( x\right) \leq \lim\limits_{x\rightarrow p}g\left( x\right) $ sempre que os limites existirem.
Suponha agora que $f\left( x\right) <g\left( x\right) $ para todo $x$. Podemos afirmar que $\lim\limits_{x\rightarrow p}f\left( x\right) <\lim\limits_{x\rightarrow p}g\left( x\right) $ sempre que os limites existirem?
Se uma função ímpar $f(x)$ possui um valor máximo local em $x=c$, pode-se dizer algo sobre o valor de $f$ quando $x=-c$?
Ela terá um mínimo local em $x=-c$. É uma questão de simetria de seu gráfico em relação à origem.
Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.
$y=\sqrt[3]{x-2}$
$y=\displaystyle{\frac{1}{x^{2}-4}}$
Prove que $\displaystyle\int (sec(x))^m dx=x \dfrac{(sec(x))^{m-2}tg(x)}{m-1}+\dfrac{m-2}{m-1}\displaystyle\int (sec(x))^{m-2} dx$, para $m$ inteiro positivo.
Prove que a função $f(x)=\left\{\begin{array}{ll}
x, & \text{se x é racional} \\
-x, & \text{se x é irracional}
\end{array}\right.$ é contínua em $0$.
Calcule a integral a seguir:
$\int{\frac{9r^2\ dr}{\sqrt{1-r^3}}}$
Calcule a seguinte integral:
$\int \cos ^{3}xdx.$
Calcule a seguinte integral:
$\int{x\sin{\frac{x}{2}}dx}$.
$4sin(x/2)-2xcos(x/2)+C$
Ache o volume do sólido cuja base é a região limitada pelas curvas $y=x$ e $y=x^2$ cujas secções transversais perpendiculares ao eixo $x$ são quadrados.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt[3]{3x^{3}+2x-1}}{\sqrt{x^{2}+x+4}}$.
$\sqrt[3]{3}$
(Teste da Derivada Primeira) Suponha $f$ contínua em um ponto crítico $x_0$.
Se $f'(x)>0$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e $f'(x)<0$ em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ tem um máximo relativo em $x_0$.
Se $f'(x)<0$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e $f'(x)>0$ em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ tem um mínimo relativo em $x_0$.
Se $f'(x)$ tiver o mesmo sinal $\displaystyle [f'(x)>0\ \text{ou}\ f'(x)<0]$ em um intervalo aberto ampliando-se à esquerda de $x_0$ e em um intervalo aberto ampliando-se à direita de $x_0$, então $f$ não tem extremo relativo em $x_0$.
Esboce algumas curvas para mostrar que as três partes do teste da derivada primeira podem ser falsas, sem a hipótese de que $f$ é contínua em $x_0$.
Prove que a conclusão do Teorema do Valor Médio de Cauchy pode ser escrita da seguinte forma $$ \dfrac{f(b)-f(a)}{g(b)-g(a)} = \dfrac{f'(x)}{g'(x)}, $$ sob as hipóteses adicionais de que $g(b)\neq g(a)$ e que $f'(x)$ e $g'(x)$ nunca são simultaneamente nulas sobre $(a,b)$.
Em matemática e estatística, a função de Heaviside (ou função degrau) é uma função singular e descontínua, com valor zero quando o seu argumento é negativo e valor unitário quando o argumento é positivo. Seja $H$ a função de Heaviside. Prove, usando a definição de limite, que $\lim\limits_{x \to 0}H(x)$ não existe.
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x$ no intervalo $[0,b]$ é $b^2/2$.
Mostre o mesmo resultado utilizando somas inferiores.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
1-\cos^2 x, & & \text{ se } x<a \\
\sin^2 x, & & \text{ se } x\geq a
\end{array},
\right.$
sendo que $a$ é um número real.
$ \lim\limits_{x\to a^-} f(x)$
$ \lim\limits_{x\to a^+} f(x)$
$ \lim\limits_{x\to a} f(x)$
$f(a)$
- $1-\cos^2 a = \sin^2 a$
- $\sin^2 a$
- $\sin^2 a$
- $\sin ^2 a$
Um aluno estudioso está sentado em uma sala de aula, ao lado da parede e de frente para a lousa, como na figura abaixo. A lousa tem $3$m de largura e começa a $1$m da parede à qual o aluno está próximo. Mostre que, se a distância da parede for $x$, o ângulo de visão é
$$\alpha = \cot^{-1} \dfrac{x}{15} - \cot^{-1} \dfrac{x}{3}.$$
Mostre que $\displaystyle \int_0^x \dfrac{\sin t}{t+1} \, dt > 0$
para todo $x>0$.
Um foguete decola da superfície terrestre com uma aceleração constante de $20m/s^2$. Qual será sua velocidade 1 minuto depois?
Mostre que a equação
\begin{equation*}
x^{26}+x^{2}-320=0
\end{equation*}
possui ao menos uma raiz real positiva e também uma raiz real negativa.
Seja $f$ uma função definida em $\mathbb{R}$ e suponha que exista $M>0$ tal que $|f(x)-f(p)|\leq M|x-p|$ para todo $x$. Prove que $f$ é contínua em $p$.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 7^x$ e $f(2)= 1$
$7^x/\ln 7 + 1-49/\ln 7$
Uma empresa de motores solicitou a fabricação de cilindros com área de seção transversal $A=9cm^2$ (Ou seja, com diâmetro $D=3,385cm^2$). Entretanto, o funcionário que respondeu à solicitação perguntou qual era a margem de erro permitida no diâmetro do cilindro.
Dado que para o correto funcionamento dos motores o cilindro deve ter uma área $A$ tal que $|A-9|<0,01 cm^2$, e que a área da seção transversal do cilindro é dada por $A=\pi \left(\frac{D}{2}\right)^2$, em qual intervalo deve estar o valor do diâmetro do cilindro para atender tal especificação?
Dê o domínio e esboce o gráfico das seguintes funções:
- $f(x)=-2+ 1/x$
- $f(x)=-\dfrac{1}{x}$
Seja $\mathcal{A}$ o subconjunto do plano limitado pelas retas $x=0$, $x=\frac{\pi}{2}$ e pelos gráficos de $y=\sin x$ e $y=\cos x$. Faça um esboço do conjunto $\mathcal{A}$ e calcule sua área.
O gráfico a seguir representa o número de indivíduos de uma população ao longo do tempo.
Pode-se dizer que há uma assíntota horizontal para essa população? Justifique.
O que essa assíntota representa em termos biológicos? (Isto é, qual a interpretação da assíntota em função da população?)
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =x^{2},\;p=2$.
$y=4x-4$.
Encontre as raízes do polinômio $x^4-10x^3+17x^2-17x+6.$
Sugestão: Utilize o teste das raízes racionais.
Sejam $f(x)=log_x(2)$ e $g(x)=log_2(x)$:
- Utilize a propriedade de quociente de logaritmos para expressar $f(x)$ e $g(x)$ em termos de logaritmos naturais.
- Com o auxílio de recursos computacionais, compare os gráficos de $f(x)$ e $g(x)$.
Um fabricante de óleo deseja confeccionar latas cilindricas de volume igual a $1,5$ litro. Quais são as dimensões da lata para que o consumo de material seja o mínimo possível?
Se $f(x+1)=\frac{x-1}{\pi -x},$ ache $f\left( x\right) $ e encontre o domínio de $f$.
Calculando $f((x-1)+1)$:
$f((x-1)+1)=\dfrac{(x-1)-1}{\pi-(x-1)}$
$f(x) = \dfrac{x-2}{\pi+1-x}$.
O domínio de $f$ é o conjunto de números reais menos os pontos em que o denominador é zero. Calculando esses valores:
$\pi + 1 - x = 0 \Rightarrow x = \pi + 1$.
Portanto o domínio de $f$ é: $\{x \in \mathbb{R}; x \neq \pi + 1\}$.
Demonstre que, se $h>0$, aplicando o Método de Newton para
$f(x)=\begin{cases}
\sqrt{x},\quad \ \ x \geq 0\\
\sqrt{-x},\quad x <0
\end{cases}$,
a aproximação tende a $x_1=-h$ se $x_0=h$ e a $x_1=h$ se $x_0=-h$.
Desenhe uma figura para mostrar o que ocorre.
Sejam $f\left( x\right) =\frac{x^{2}-25}{x^{2}-1}$ e $g\left(x\right) =\sqrt{x}$. Dê o domínio das seguintes funções: $f,$ $g$, $f\circ g$ e $g\circ f$.
Suponha que $y=f(x)$ seja derivável em $x=a$ e que $g(x)=m(x-a)+c$ seja uma função linear, em que $m$ e $c$ sejam constantes. Se o erro entre $f$ e $g$, $E(x) = f(x)-g(x)$ for suficientemente pequeno perto de $x=a$, poderemos pensar em utilizar $g$ como aproximação linear de $f$ ao invés da linearização $L(x) = f(a)+f'(a)(x-a)$.
- Interprete as expressões $E(a)=0$ e $lim_{x\to a} \dfrac{E(x)}{x-a}=0$.
- Mostre que impondo as condições $E=0$ e $lim_{x\to a} \dfrac{E(x)}{x-a}=0$, temos $g(x)=f(a)+f'(a)(x-a)$. Interprete o resultado, relacionando com o item anterior.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2}-6x+10,y=-x^{2}+6x-6$, ao redor do eixo $y.$
Se $f$ for contínua e $\int_{0}^{9}f\left( x\right) dx=9$, calcule $\int_{0}^{3}xf\left( x^{2}\right) dx.$
Prove que $\displaystyle\int \dfrac{1}{u\sqrt{a^2+u^2}}du=-\dfrac{1}{a}\ln \left|\dfrac{\sqrt{a^2+u^2}+a}{u}\right|+C$.
Calcule $\displaystyle \int \dfrac{1}{2+\sin x} \, dx$.
$\frac{2 \tan ^{-1}\left(\frac{2 \tan \left(\frac{x}{2}\right)+1}{\sqrt{3}}\right)}{\sqrt{3}}$
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=\sqrt{2x-x^2}$, $0,5\leq x \leq 1,5$, eixo $x$
Avalie a seguinte integral indefinida:
$\int \sec^2\theta\ d\theta$
$\tan \theta+C$
Utilizando o gráfico a seguir, avalie os seguintes limites
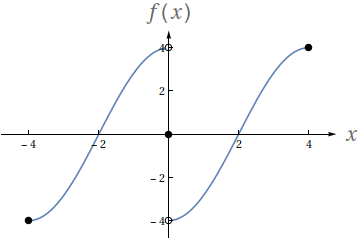
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $ \lim\limits_{x\to 0} f(x)$
- $f(0)$
- $4$
- $-4$
- Não existe.
- $0$
Use o Teorema Fundamental do Cálculo e a Regra de l'Hospital para calcular o limite abaixo, justificando claramente sua resolução.
\begin{equation*}
\lim\limits_{x\rightarrow 0}\left( \dfrac{\displaystyle\int_{0}^{x}e^{t^{2}}dt}{x}\right)
\end{equation*}
A aceleração de uma partícula que se move de um lado para o outro sobre uma reta é $a=d^2s/dt^2 = \pi^2\sin\pi t\ m/s^2$ para qualquer $t$. Se $s=0$ e $v=8m/s$ quando $t=0$, determine o valor de $s$ para $t=1\ s$.
Prove a seguinte generalização do Teorema do Valor Médio: Se $f$ é contínua e diferenciável sobre o intervalo $(a,b)$ e os limites $\displaystyle \lim_{y\to a^+}f(y)$ e $\displaystyle \lim_{y\to b^-}f(y)$ existem, então existe $x\in (a,b)$ tal que $$f'(x)=\dfrac{\displaystyle \lim_{y\to b^-}f(y)-\lim_{y\to a^+}f(y)}{b-a}.$$ (Sua prova deve começar mais ou menos assim: "Esta é uma conseqüência do Teorema do Valor Médio porque ...".)
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x+\cosh(x)}{x^2+1}$.
$\infty$.
Um recipiente cheio de água com a forma de um cone invertido está sendo esvaziado à razão de $6\,cm^3/min$. A altura do cone é $24cm$ e o raio da base é $12cm$. Encontre a velocidade com que baixa o nível da água quando está a $10cm$ do fundo.
$\dfrac{dr}{dt}=-\dfrac{1}{25 \pi}$ cm/min
Escreva o número $e$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-4}$.
Encontre todas as funções polinomiais $f$ com coeficientes reais tais que $(x-27)f(3x)=27(x-1)f(x)$ para todo número real $x$.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{3x^{3}+2}\right) $.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=1/x$.
$f'(x)=-\dfrac{1}{x^2}$, $f''(x)=\dfrac{2}{x^3}$ e $f'''(x)=-\dfrac{6}{x^4}$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{\sin \left(10x\right) }{\sin \left( 5x\right) }$.
$2$.
Considere um cilindro com base de diâmetro $2R$ e altura também $2R$. Considere, inscrito neste cilindro, uma esfera de raio $R$ e um cone de base circular com diâmetro $2R$ e altura $2R$. Denote por $V_{cil}$, $V_{esf}$ e $V_{cone}$, respectivamente, os volumes desses sólidos.
- Verifique as relações $V_{esf}= \frac{2}{3}V_{cil}$ e $V_{cone}=\frac{1}{3}V_{cil}.$
- Calcule $V_{cil}$, $V_{esf}$ e $V_{cone}$ usando integrais. Explicite o método que está usando.
Calcule a seguinte integral:
$\int_{0}^{\infty}{\frac{dx}{x^{1,001}}}$
Não converge.
Demonstre que se $k$ é uma constante positiva, então a área entre o eixo $x$ e um arco da curva $y=\sin kx$ é $2/k$.
Um vaso em formato hemisférico de raio $7,5$cm está sendo enchido de água a uma taxa de $16$cm$^3/$s. Quando a profundidade da água está em $2,5$cm, com que velocidade o nível da água sobe?
Para calcular as coordenadas espaciais de um planeta, temos de resolver equações do tipo $x=1+0,5\sin(x)$. O traçado da função $f(x)=x-1-0,5\sin(x)$ sugere que a função possui uma raiz próxima de $x=1,5$. Utilize uma iteração do Método de Newton para melhorar essa estimativa, com $x_0=1,5$.
Se $ F(x)= { \int_1^xf(t)dt}$ e $ f(t)={ \int_{x^2}^1\frac{\sqrt{1+u^4}}{u}du}$, determine $F''(2)$.
Dada uma função $f:{\mathbb{R} \to \mathbb{R}}$, defina sua continuidade no ponto $p\in \mathbb{R}.$
A função $f(x)=|x|$ tem valor mínimo absoluto quando $x=0$, mesmo que $f$ não seja derivável em $x=0$. Isto é consistente com o Teorema de Fermat sobre máximos e mínimos locais?
Dê um exemplo de uma função que seja contínua em todos os pontos da reta, exceto nos pontos da forma $k \pi$, $k \in \mathbb{Z}$.
$f(x)=1$, se $x=k \pi$, $k \in \mathbb{Z}$; $f(x)=0$, caso contrário.
Calcule a integral $\int{ \frac {1}{x^2+3x-10} dx}.$
Prove que se $f$ for derivável em $p$, então $f$ será contínua em $p$.
Veja Guidorizzi, volume $1$, página $152$.
Resolva a equação $|2x+1|=3$.
Se $2x+1\geq0$: $|2x+1| = 2x+1$, logo $2x+1=3 \Rightarrow x = 1$.
Se $2x+1<0$: $|2x+1| = -(2x+1)$, logo $-2x-1=3 \Rightarrow x = -2$.
Portanto $x=1$ ou $x=-2$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(t) = \sqrt{5t^2-30}$.
$(-\infty,-\sqrt{6}]\cup [\sqrt{6},\infty)$
A região no plano $xy$ limitada pela curva $y=x^2+1$ e pela reta $y=-x+3$ gira em torno do eixo $x$ gerando um sólido $S.$ Calcule o volume de $S.$
Prove que $\log3$ é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Suponha que existam inteiros $p$ e $q$ tais que $log3=p/q$, com $p/q$ sendo fração irredutível. Use a definição de logaritmo e o teorema fundamental da aritmética para chegar a um absurdo.
Derive a função $f\left( x\right) = \int_{x^{2}}^{e^{3x}}\cos t\sin tdt$.
Calcule, pela definição, o limite $ \lim_{x\to 0} \sin x= 0$ (Dica: use o fato que $|\sin x| \leq |x|$, sendo uma igualdade apenas para $x=0$.)
Considere $\epsilon >0$ arbitrário. Queremos encontrar $\delta >0$ tal que quando $|x-0|<\delta$, $|f(x)-0|<\epsilon$. Em termos simples, queremos mostrar que quando $|x|<\delta$, $|\sin x| < \epsilon$.
Considere $\delta = \epsilon$. Podemos presumir que $|x|<\delta$. Usando a dica do enunciado, temos que $|\sin x | < |x| < \delta = \epsilon$. Portanto, se $|x|<\delta$, sabemos imediatamente que $|\sin x| < \epsilon$.
Sabendo que $\lim\limits_{x\to2} f(x) = 3$ e $\lim\limits_{x\to2} g(x) = -1$, calcule os seguintes limites:
$\lim\limits_{x\to2}(f+g)(x)$
$\lim\limits_{x\to2}(fg)(x)$
$\lim\limits_{x\to2}(f/g)(x)$
$\lim\limits_{x\to2}f(x)^{g(x)}$
Utilize a fórmula
\[
s\left( x\right) =\int_{a}^{x}\sqrt{1+\left( f^{\prime}\left( t\right)
\right) ^{2}}dt
\]
para mostrar que o perímetro de uma circunferência de raio $R$ é $2\pi R$.
Uma circunferência de raio $R$ centrada na origem pode ser vista como a união dos gráficos das funções $f\left(t\right) =\sqrt{R^{2}-t^{2}}$ e $g\left( t\right) =-\sqrt{R^{2}-t^{2}}$, com $t\in\left[ -R,R\right] $ Por simetria, estes dois arcos têm o mesmo comprimento, digamos $L$, e o perímetro $p$ é dado por $p=2L$.
Considerando $f\left( t\right) =\sqrt{R^{2}-t^{2}}$ temos
que:
\[
f^{\prime}\left( t\right) =-\frac{t}{\sqrt{R^{2}-t^{2}}}\text{.}%
\]
Usando a fórmula acima temos que:
\begin{align*}
L & =\int_{-R}^{R}\sqrt{1+\left( f^{\prime}\left( t\right) \right) ^{2}%
}dt\\
& =\int_{-R}^{R}\sqrt{1+\frac{t^{2}}{R^{2}-t^{2}}}dt\\
& =\int_{-R}^{R}\sqrt{\frac{\left( R^{2}-t^{2}\right) +t^{2}}{R^{2}-t^{2}}%
}dt\\
& =\int_{-R}^{R}\sqrt{\frac{R^{2}}{R^{2}-t^{2}}}dt\\
& =R\int_{-R}^{R}\frac{1}{\sqrt{R^{2}-t^{2}}}dt
\end{align*}
Fazendo a mudança de variável $t=R\sin\theta$, com $-\pi/2\leq\theta\leq\pi/2$, temos que:
\begin{align*}
\sqrt{R^{2}-t^{2}} & =\sqrt{R^{2}-R^{2}\sin^{2}\theta}\\
& =R\sqrt{1-\sin^{2}\theta}\\
& =R\cos\theta,\\
dt & =R\cos\theta d\theta
\end{align*}
Obtemos assim que:
\begin{align*}
L & =R\int_{-R}^{R}\frac{1}{\sqrt{R^{2}-t^{2}}}dt\\
& =R\int_{-\pi/2}^{\pi/2}\frac{R\cos\theta}{R\cos\theta}d\theta\\
& =R\int_{-\pi/2}^{\pi/2}d\theta\\
& \left. R\theta\right\vert _{-\pi/2}^{\pi/2}\\
& =\pi R
\end{align*}
e concluimos que:
\[
p=2L=2\pi R
\]
Determine uma primitiva para cada uma das funções:
$f(x)=cosx$
$f(x)=tgx$
Um retângulo tem sua base no eixo $x$ e seus dois vértices superiores na parábola $y=-x^2$. Qual é a maior área que esse retângulo pode ter? Quais são suas dimensões?
Determine a derivada da seguinte função:
$f\left( x\right) =\cos \left( x^{-2}\right)+x^{3}e^{-3x}.$
$f'(x) = -3 e^{-3 x} x^3 + 3 e^{-3 x} x^2 + (2 \sin(x^{-2}))/x^3$.
Mostre que se $f''(a)$ existe, então $f''(a) = \displaystyle \lim_{h \to 0} \dfrac{f(a+h) - 2f(a) + f(a-h)}{h^2}.$ (Sugestão: use o polinômio de Taylor $P_{2,a}(x)$ com $x=a+h$ e com $x=a-h$).
Conclua que $\dfrac{f(a+h) - 2f(a) + f(a-h)}{h^2}$ é uma boa aproximação para $f''(a)$, para $h$ pequeno.
Sabendo que a posição de uma partícula em função do tempo $x(t)$ é tal que $x(0)=2$, $x(1)=4$ e $x(2)=5$, utilizando a fórmula acima obtenha uma aproximação para a aceleração da partícula entre os tempos $t=0$ e $t=2$. (Escolha apropriadamente os valores de $a$ e $h$).
Mostre que $x\neq y\Longrightarrow x^{2}+2xy<2x^{2}+2y^{2}$.
Note que $(x-y)^2+y^2>0$ sempre que $x\neq y$. Daí, $x^2-2xy+y^2+y^2>0$, que é equivalente a $2x^2+2y^2-x^2-2xy>0$, que, por sua vez, é equivalente a x^{2}+2xy<2x^{2}+2y^{2}$.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$2\leq {\frac{2}{3x-1}}\leq {\frac{20}{3}}$
${\frac{1}{2x+3}}\leq {\frac{x-1}{3}}\leq {\frac{1}{5}}$
Encontre os intervalos abertos nos quais $f(x)=x^3-\frac{3}{2}x^2$ é crescente e os intervalos abertos nos quais é decrescente.
Dê um exemplo para mostrar que o produto de uma função contínua por uma função descontínua, pode ser uma função contínua.
Avalie a integral $\displaystyle \int_{-1}^1 x^3 \sqrt{1-x^2} \, dx$ sem fazer nenhuma conta.
Uma cultura de bactérias cresce na taxa de $3e^{0,2t}$ por hora com $t$ em horas e $o\leq t\leq 20$.
- Quantas bactérias novas estarão na cultura depois de cinco horas?
- Quantas bactérias são introduzidas da sexta a décima quarta horas?
- Para que valor aproximado de $t$ a cultura conterá 150 bactérias novas?
Dê o domínio e esboce o gráfico das seguintes funções:
- $f(x)=|x|+1/x$
- $f(x)=\sqrt{|x|}$
Seja $P(x)$ um polinômio com coeficientes inteiros. Suponha que existam quatro inteiros distintos $a,b,c$ e $d$ tais que $P(a)=P(b)=P(c)=P(d)=5$. Prove que não existe inteiro $k$ tal que $P(k)=8$.
Resolva os itens:
- Prove que existe $r>0$ tal que $\cos{x}-1<\dfrac{\sin{x}}{x}-1<0$ para $0<|x|<r$.
- Calcule $\lim\limits_{x \to 0}\dfrac{x-\sin{x}}{x^2}$.
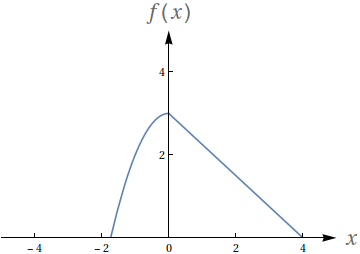
$f$ é contínua em $x=0$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\log_{2}\left( 2x\right) \log_{3}\left(3x\right) .$
$f'(x) = \dfrac{2 \ln x + \ln 6}{x \ln 2 \ln 3}$.
Se $(ln\ x)/x = (ln\ 2)/2$, é necessário que $x=2$? Se $(ln\ x)/x=-2ln\ 2$, é necessário que $x=\frac{1}{2}$? Justifique suas respostas.
Um objeto é solto de um helicóptero. O objeto cai cada vez mais rápido, mas sua aceleração diminui com o passar do tempo devido à resistência do ar. A aceleração foi medida nos primeiros cinco segundos, quando ele atingiu o chão, e o resultado está na tabela a seguir:
$
\begin{array}{ccccccc} \hline
t & 0 & 1 & 2 & 3 & 4 & 5 \\\hline
a & 9,81 & 5,95 & 3,61 & 2,19 & 1,33 & 0,81 \\\hline
\end{array}
$
Faça uma estimativa superior para o módulo da velocidade quando $t=5$.
Faça uma estimativa superior para o módulo da posição quando $t=5$.
Faça uma estimativa superior para a altura da queda.
As curvas de crescimento logístico modelam a taxa de crescimento de uma certa população em função dos fatores ambientais. Em um período prolongado de tempo, a população tende a um valor limite que representa o máximo número de indivíduos que o espaço ou alimento pode sustentar. Estas curvas são da forma $$ y(t)=\dfrac{L}{1+Ae^{-kt}}, $$ onde $y$ é a população no momento $t$ ($t\geq 0$) e $A$, $k$ e $L$ são parâmetros positivos. Suponha que uma população $y$ cresce de acordo com o modelo logístico acima.
Qual é a taxa de crescimento de $y$ em $t=0$?
Descreva como a taxa de crescimento de $y$ varia com o tempo.
Em que momento a população cresce mais rapidamente?
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x^2, & & \text{ se } x<2 \\
x+1, & & \text{ se } x=2\\
-x^2+2x+4, & & \text{ se } x>2
\end{array}
\right.$
$ \lim\limits_{x\to 2^-} f(x)$
$ \lim\limits_{x\to 2^+} f(x)$
$ \lim\limits_{x\to 2} f(x)$
$f(2)$
- 4
- 4
- 4
- 3
Um modelo de densidade urbana é uma fórmula que relaciona a densidade populacional (em número de habitantes por $km^2$) com a distância $r$ (em $km$) do centro da cidade. É considerada apropriada para certas cidades a fórmula $D=ae^{-br+cr^2}$, com $a,b$ e $c$ constantes positivas. Determine a forma do gráfico de $D$ para $r \geq 0$.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x-e^{x}$.
Calcule a seguinte integral:
$\int \dfrac{x^{3}+x}{x-1}dx.$
Seja $F(x)$ tal que $F(x)=\displaystyle \int_{\pi/4}^x \cos 2t \, dt$.
Use alguma versão do Teorema Fundamental do Cálculo para encontrar $F'(x)$.
Confira se seu resultado anterior foi correto integrando e diferenciando.
A área de um setor circular com raio $r$ e ângulo central $\theta$ é $A=\frac{1}{2} r^2 \theta$. Demonstre esta fórmula. (Dica: assuma um ângulo $0<\theta<\pi/2$ e considere o círculo centrado na origem, de forma que tenha equação $x^2+y^2=r^2$. Então $A$ é a soma da área de um triângulo e a porção restante do setor cirular. Faça um esboço do gráfico para facilitar.)
Calcule $\displaystyle\lim_{x\rightarrow 0}\frac{\frac{2}{x} - 5\cos(\frac{1}{x^2+2x})}{-\frac{5}{x} + 2\cos(\frac{1}{x^2+2x})}$.
Existe algum número real $a$ tal que a função $f(x) = \left\{\begin{array}{ccl}\displaystyle\frac{\frac{2}{x} - 5\cos(\frac{1}{x^2+2x})}{-\frac{5}{x} + 2\cos(\frac{1}{x^2+2x})},& \mbox{se} & x\neq 0\\ a, & \mbox{se} & x=0 \end{array} \right.$ seja contínua?
O princípio da Boa Ordenação diz que todo subconjunto não-vazio de $N$ possui elemento mínimo. Demonstre que $N$, com a relação $\leq$, verifica o Princípio da Boa Ordenação.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Calcule a derivada da função:
$y=\dfrac{1}{2}\cot ^{2}5x+\ln \sin x.$
$y'=\cot(x) - 5 \cot(5 x) \csc^2(5 x)$.
O que se pode dizer sobre os pontos de inflexão de uma curva quadrática? Justifique.
Os pontos de inflexão são os pontos nos quais a curvatura de uma curva troca de sinal, portanto, está associado com trocas de sinal da segunda derivada da função associada à curva. Curvas quadráticas terão derivadas lineares e segundas derivadas constantes. Sendo assim, como a segunda derivada de uma curva quadrática nunca trocará de sinal, uma curva quadrática nunca apresentará pontos de inflexão
Esboce neste mesmo gráfico a reta $y=2x+3$. Indique a região delimitada por esta reta e pelo gráfico de $f\left(x\right) $, para $2\leq x\leq 3$. Calcule a área desta região.
f(x)=\frac{\sqrt{1-x^2}}{1-tg x} \end{align*}
- Determine o domínio de $f$.
- Estude $f$ quanto a continuidade.
Um fabricante de óleo deseja confeccionar latas cilindricas de volume igual a $1$ litro. Quais são as dimensões da lata para que o consumo de material seja o mínimo possível? Se a lata fosse esférica, o gasto de material seria maior ou menor que o gasto de material da lata cilíndrica que voce encontrou? E se a lata fosse cúbica?
Considere o número inteiro $P = 100 \cdot 101 \cdot 102 \cdot \ldots \cdot 200$, produto de $101$ números inteiros sucessivos. Ao escrever-se $P$ como um produto de fatores primos, qual o número de vezes que o fator $7$ aparece?
Encontre, se existirem, o valor máximo absoluto e o valor mínimo absoluto da função $f(x)= \sqrt[3]{x^3-x^2},$ no intervalo $[0,1].$
A cápsula cônica de reentrada de um veículo espacial é desenhada de tal forma que uma secção transversal tomada $x$ pés da ponta e perpendicular ao eixo de simetria é um círculo de raio $\dfrac{1}{4}x^2$ pés. Ache o volume do cone sabendo que o seu comporimento é de $20$ pés.
Na teoria de eletromagnetismo, o potencial magnético de uma bobina circular em um ponto de seu eixo é dado por:
$$\displaystyle u = \dfrac{2\pi N I r}{k} \int_a^{\infty} \dfrac{dx}{(r^2+x^2)^{3/2}},$$
onde $N$, $I$, $r$, $k$ e $a$ são constantes com significados físicos apropriados. Calcule $u$.
Resolva a equação $e^{ax}=Ce^{bx}$, onde $a\neq b$.
Usando as propriedades básicas da função exponencial temos que:
\begin{align*}
e^{ax} & =Ce^{bx}\\
& \Leftrightarrow e^{-ax}e^{ax}=e^{-ax}Ce^{bx}\\
& \Leftrightarrow1=Ce^{(b-a)x}\\
& \Leftrightarrow\frac{1}{C}=e^{(b-a)x}\\
& \Leftrightarrow\ln\left( \frac{1}{C}\right) =\ln\left( e^{(b-a)x}\right)
=\left( b-a\right) x\\
& \Leftrightarrow\frac{-\ln C}{b-a}=\frac{\ln C}{a-b}=x
\end{align*}
Calcule a seguinte integral:
$ \int x^2\sin (\pi x)dx$.
$\dfrac{(2-\pi^2x^2)cos(\pi x+2 \pi xsin(\pi x)}{\pi^3}+C$.
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|x+5|\geq \sqrt{2}$
$|x-1|\leq |x+1|$
Utilizando o gráfico a seguir, avalie os seguintes limites
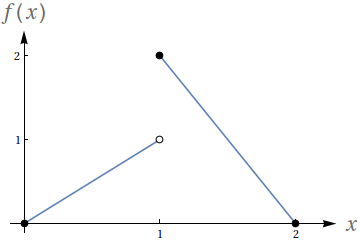
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 2^+} f(x)$
- $1$
- $2$
- Não existe.
- $2$
- $0$
- Como $f$ não é definida para $x>2$, esse limite é indefinido.
Dados $f(x) = \sqrt[\leftroot{-2}\uproot{2}3]{x}$ e $x_0 = 8,5$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
O gráfico a seguir mostra a receita mensal da empresa Fidelis Ltda. nos últimos 12 anos. Durante aproximadamente quais intervalos de tempo a receita marginal foi crescente? E decrescente?
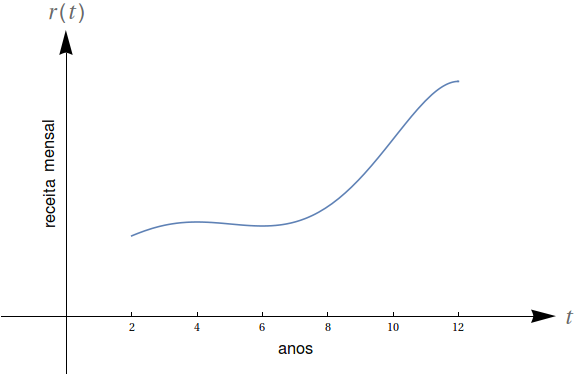
Determine $a$ para que a equação $x^{3}+3x^{2}-9x+a=0$ admita uma única raiz real.
Primeiramente, calculamos $f'(x)$ e $f''(x)$. Temos então
$f'(x)=3x^2+6x-9=3(x+3)(x-1)$
$f''(x)=6x+6$
Pela análise de sinal da segunda derivada, vemos que $f(x)$ é uma concavidade para baixo para $x<-1$ e uma concavidade para cima para $x>-1$, e os zeros da primeira derivada nos dizem que há um máximo local em $x=-3$ e um mínimo local em $x=1$. Assim, avaliando a função em $x=-3$ tem-se $f(-3) = 27+ a$. Qualquer valor de $a$ que torne $f(-3)<0$ garante que $f(x)$ terá apenas uma única raiz real. Finalmente, portanto, tem-se:
$a<-27$
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x^{3}-3x^{2}+1$.
Calcule a integral $\int e^{x}\sin xdx$.
$\dfrac{1}{2}e^x(sinx-cosx)+C$.
Use a derivada dada para encontrar as coordenadas $x$ de todos os pontos críticos de $f$ e classifique-os em máximo relativo, mínimo relativo ou nenhum dos dois.
$\displaystyle f'(x)=x^2(2x+1)(x-1)$;
$\displaystyle f'(x)=\dfrac{9-4x^2}{\sqrt[3]{x+1}}$.
Calcule os limites:
$\lim\limits_{x\to3} x^2-3x+7$
$\lim\limits_{x\to3} x^3-3x-7$
- Como a função está definida em $x=3$, o limite pode ser calculado diretamente por substituição:
$\lim\limits_{x\rightarrow 3} x^2-3x+7 = 3^2 - 3.3 + 7 = 7$. - Como a função está definida em $x=3$, o limite pode ser calculado diretamente por substituição:
$\lim\limits_{x\rightarrow 3} x^3-3x+7 = 3^3 - 3.3 - 7 = 11$.
A naftalina pode ser utilizada como repelente de insetos, embora possa trazer malefícios à saúde. Este composto tem a capacidade de sublimar, isto é: passa do estado sólido diretamente para o gasoso. Se uma bolinha de naftalina evapora a uma taxa proporcional à área de sua superfície, mostre que o seu raio decresce a uma taxa constante.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\ln \dfrac{x}{x+1}$.
$0$
Sejam $f,g,h$ funções deriváveis. Verifique que $(fgh)'=f'gh+fg'h+fgh'$. Generalize.
Dica: Derive a função $Fh$, onde $F=fg$. Use a regra do produto duas vezes. Para generalizar use o princípio da indução finita.
Uma viatura de polícia, vindo do norte e se aproximando de um cruzamento em ângulo reto, está perseguindo um carro em alta velocidade, que, no cruzamento, toma a direção leste. Quando a viatura está a $0,6 km$ ao norte do cruzamento e o carro fugitivo a $0,8 km$ a leste, o radar da polícia detecta que a distância entre a viatura e o fugitivo está aumentando a $20 km/h$. Se a viatura está se deslocando a 60 km/h no instante dessa medida, qual é a velocidade do fugitivo?
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{x-\cos(x)}{x}$.
$1$.
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f\,^{\prime \prime }\left( x\right) = \sin x-\cos x+x^{5},\;f\,^{\prime}\left( 0\right) =2\text{ e }f\left( 0\right) =0\text{ .} \end{equation*}
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{e^x}{x^n}$.
$\infty$.
Aproxime numericamente o seguinte limite
$ f(x)=\frac{x^2-11 x+30}{x^3-4 x^2-3 x+18}$
- \begin{array}{cc}
x & f(x) \\ \hline
2.9 & 132.857 \\
2.99 & 12124.4 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =\infty$. - \begin{array}{cc}
x & f(x) \\ \hline
3.1 & 108.039 \\
3.01 & 11876.4 \\
\end{array}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$. - As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =\infty$.
Avalie o limite $\lim\limits_{x\rightarrow 0}\dfrac{\sin \left(7x\right) }{\sin \left( 23x\right) }$.
$7/23$.
Um encanador $A$ cobra por serviço feito um valor fixo de $R\$ 60,00$, mais $R\$ 10,00$ por hora de trabalho. Um outro encanador $B$ cobra um valor fixo de $R\$40,00$ mais $R\$15,00$ por hora de trabalho. Considerando o menor custo para a realização de um trabalho, avalie a decisão de se contratar um ou outro encanador.
Seja $f(x)=\sin{x}+\cos{x}$, $0 \leq x \leq 2 \pi$.
- Estude o sinal de $f'(x)$.
- Faça um esboço do gráfico de $f$.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =x+\dfrac{1}{x^{2}}$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =2^{x}$.
$f'(x)=ln(2)2^x$.
Enuncie e prove o Algoritmo de Briot-Ruffini. Dê exemplos.
Esboce o gráfico da função $f\left(x\right) =\dfrac{x^{2}-x+1}{2x-2}$, determinando o domínio, pontos de máximo e de mínimo, pontos de inflexão e assíntotas. Explicite o valor que a função assume nos pontos em questão. Justifique o seu raciocínio.
Calcule, pela definição, o limite $ \lim_{x\to 4} x^2+x-5 = 15$
Considere $\epsilon >0$ arbitrário. Queremos encontrar $\delta >0$ tal que quando $|x-4|<\delta$, $|f(x)-15|<\epsilon$.
Considere $|f(x)-15|<\epsilon$, lembrando que o objetivo é afirmar algo sobre $|x-4|$:
\begin{gather*}
|f(x) -15 | < \epsilon \\
|x^2+x-5 -15 |<\epsilon \\
| x^2+x-20 | < \epsilon \\
| x-4 |\cdot|x+5| < \epsilon \\
| x-4 | < \epsilon/|x+5| \\
\end{gather*}
Assumindo $x$ próximo de $4$, podemos assumir, por exemplo, que, $3<x<5$. Portanto
\begin{gather*}
3+5<x+5<5+5 \\
8 < x+5 < 10 \\
\frac{1}{10} < \frac{1}{x+5} < \frac{1}{8} \\
\frac{\epsilon}{10} < \frac{\epsilon}{x+5} < \frac{\epsilon}{8} \\
\end{gather*}
Seja $\delta =\frac{\epsilon}{10}$. Então:
\begin{gather*}
|x-4|<\delta \\
|x-4| < \frac{\epsilon}{10}\\
|x-4| < \frac{\epsilon}{x+5}\\
|x-4|\cdot|x+5| < \frac{\epsilon}{x+5}\cdot|x+5|\\
\end{gather*}
Assumindo $x$ próximo de 4, $x+5$ é positivo e podemos eliminar o módulo do lado direito da equação.
\begin{gather*}
|x-4|\cdot|x+5| < \frac{\epsilon}{x+5}\cdot(x+5)\\
|x^2+x-20| < \epsilon\\
|(x^2+x-5) -15| < \epsilon,
\end{gather*}
que é o que desejávamos provar.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }3^{x}$.
$\infty$.
Calcule a integral $\int \frac{1}{x^2-x} dx$.
- $\lim\limits_{h\rightarrow 0}\left( x^{2}+5xh^{2}\right) $
- $\lim\limits_{x\rightarrow 2}\dfrac{1/x-1/2}{x-2}$
Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{x}$.
$x=0$.
Mostre que a equação $x^2=x$ tem exatamente duas raízes reais.
A equação pode ser escrita na forma $x^2-x=0$, i.e, $x(x-1)=0$. As suas únicas raízes reais são $x=0$ e $x=1$. Uma outra forma de atacar este problema é perceber que os gráficos de $f(x)=x$ e $g(x)=x^2$ se intersectam exatamente duas vezes!
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $xe^x\cos{x}$.
- $e^x \sin{x} \cos{x}$.
- $-e^x x^2 \sin (x)+e^x x^2 \cos (x)+2 e^x x \cos (x)$.
- $-e^x \sin ^2(x)+e^x \cos ^2(x)+e^x \sin (x) \cos (x)$.
Calcule a seguinte integral $\int \ln xdx$.
$x(lnx-1)+C$
As distribuições gamma, importantes em teoria das probabilidades, são determinadas por $f(x)=cx^ne^{-ax}$ para $x>0$, um inteiro positivo $n$, uma constante positiva $a$ e $c=\dfrac{a^{n+1}}{n!}$.
- Mostre que $f$ tem exatamente um máximo local.
- Supondo $n=4$, determine onde $f(x)$ cresce mais rapidamente.
Esboce o gráfico de cada uma das funções abaixo.
$y=-\sqrt{7-x^{2}}$
$y=1+\sqrt{10-x^{2}}$
A atmosfera da Terra absorve aproximadamente $32\%$ da radiação proveniente do Sol. A Terra também emite radiação (a maior parte em forma de calor) e a atmosfera absorve aproximadamente $93\%$ dessa radiação. A diferença entre a radiação que entra na Terra e a que sai é chamada efeito-estufa. Modificações nesse equilíbrio podem afetar o clima da Terra. Seja $I_0$ a intensidade da radiação do Sol e $I$ a intensidade depois de percorrer uma distância $x$ na atmosfera. Se $p(h)$ é a densidade da atmosfera na altitude $h$, então a espessura ótica é $f(x)=k \displaystyle\int_0^x p(h) dh$, onde $k$ é uma constante de absorção e $I$ é dada por $I=I_0e^{-f(x)}$. Mostre que $dI/dx=-kp(x)I$.
Considere a curva definida pela equação $x^2y+3\ln(1-y)+x^4=1.$
- Calcule $y'.$
- Encontre a aproximação linear à curva no ponto $(1,0).$
Sejam $f\left( x\right) $ e $g\left( x\right) $ funções
diferenciáveis e suponha que esta assuma os seguintes valores:
$\begin{array}{|c|c|}
\hline x & f\left( x\right) & g\left( x\right) & f^{\prime }\left(
x\right) & g^{\prime }\left( x\right) \\\hline
0 & 1 & 1 & 5 & 1/3 \\\hline
1 & 3 & -9 & -1/3 & -8/3 \\\hline
\end{array}$
Encontre as derivadas de:
$f\left( x\right) -3g\left( x\right) $ em $x=0;$
$f\left( g\left( x\right) \right) $ em $x=0;$
$\left( x^{11}+f\left( x\right) \right) ^{-2}$ em $x=1;$
$f\left( e^{\sin \left( x-1\right) }\right) $ em $x=1;$
- $4$
- $8/9$
- $-1/3$
- $-1/3$
Utilizando o gráfico a seguir, avalie os seguintes limites
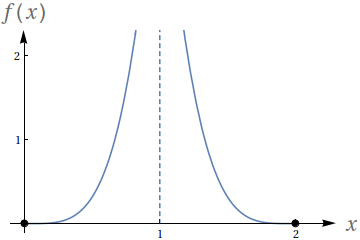
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 2^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- Não existe.
- Não existe.
- Não existe.
- Indefinido.
- $0$
- $0$
A área superficial de uma caixa retangular fechada de base quadrada é igual a $20 m^2$. Determine o volume desta caixa em função do comprimento do lado de sua base.
Calcule o limite a seguir:
$\lim\limits_{x \to -\infty } e^x \sin(x)$
Observe que $-1 \leq \sin(x) \leq 1$ e, portanto, como $e^x \geq 0$, $-e^x \leq e^x \sin(x) \leq e^x$.
Como $\lim\limits_{x \to -\infty} e^x = 0$ e $\lim\limits_{x \to -\infty} -e^x = 0$, então, pelo Teorema do Confronto temos $\lim\limits_{x \to -\infty} e^x \sin(x) = 0$
Prove que $1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots+\dfrac{x^n}{n!} \leq e^x$. Conclua que $\lim\limits_{x \to \infty} e^x/x^n=\infty$.
Mostre que $|x|<x^{2}+1,\forall x\in \mathbb{R}$.
Determine o domínio da seguinte função:
$f\left( x\right) =\sqrt{x-1}+\sqrt{3-x}$.
$\left\{ 1\leq x\leq 3\right\} $.

Utilizando o gráfico a seguir, avalie os seguintes limites
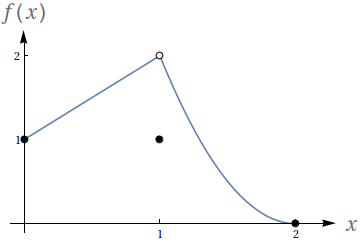
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $ \lim\limits_{x\to 0^-} f(x)$
- $ \lim\limits_{x\to 0^+} f(x)$
- $2$
- $2$
- $2$
- $1$
- Como $f$ não é definida para $x<0$, esse limite é indefinido.
- $1$
O laço de de $9y^2=x(3-x)^2$ é girado ao redor do eixo $y$. Calcule a área da superfície gerada por essa maneira.
O produto das idades de três amigos adolescentes (entre $12$ e $19$ anos) corresponde a $4080$ anos. Qual a soma das três idades, em anos?
Decompondo o número $4080$ em fatores primos encontramos $4080=2^4 \cdot 15 \cdot 17=15 \cdot 16 \cdot 17$. Analisando essa decomposição, obtemos automaticamente que a única possibilidade que atende as exigências do enunciado é que as idades sejam $15,16$ e $17$ anos. A soma dessas idades é $15+16+17=48$ anos.
Prove que $\displaystyle\int x^m \sin(x)dx=-x^m \cos(x)+m \displaystyle\int x^{m-1} \cos(x)dx$, para $m$ inteiro positivo.
Resolva a equação $x^4-13x^2 + 36 = 0$.
Chamando $x^2=y$, transformamos a equação para:
$y^2 -13y + 36=0$. Resolvendo esta equação:
$\Delta = 13^2-4.1.36 = 25.$
$y = \dfrac{13 \pm \sqrt{25}}{2}.$
Assim as soluções são: $y = 9$ ou $y = 4$.
Substituindo em $y=x^2$:
$x^2 = 9 \Rightarrow x = \pm 3$.
$x^2 = 4 \Rightarrow x = \pm 2$.
Portanto as soluções são $x=-2$, $x=2$, $x=-3$ e $x=3$.
Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.
$f(x)=x^{3}+x$
$f(x)=x^{4}+2x^{3}+x^{2}$
- $f(-x)=(-x)^{3}+(-x) = -x^3-x = -(x^3+x) = -f(x)$, logo a função é ímpar.
- $f(-x)=(-x)^{4}+2(-x)^{3}+(-x)^{2} = x^4-2x^3+x^2$, que não é igual a $f(x)$ nem $-f(x)$, logo a função não é par nem ímpar.
Calcule o limite:
$\lim\limits_{x\rightarrow p}\dfrac{tg(x-p)}{x^{2}-p^{2}}$.
Mensalmente, pago pela prestação de minha casa $1/5$ do meu salário; metade do resto gasto em alimento e $1/3$ do que sobra coloco na poupança, restando-me ainda $R\$ 800,00$ para gastos diversos. Qual o valor colocado na poupança?
Sejam $f,g,h$ funções deriváveis. Verifique que $(fgh)'=f'gh+fg'h+fgh'$. Generalize.
Seja $g(x)=a^x$, em que $a>0$ e $a \neq 1$ é um real dado. Mostre que $g'(x)=a^x \ln{a}$.
Encontre a equação da reta tangente à curva $y=2x^2+3$ que seja paralela à reta $8x-y+3=0$.
$y=8x+3$.
Classifique as afirmações em verdadeiras ou falsas.
A soma de dois números racionais é sempre um número racional.
A soma de dois números irracionais é sempre um número irracional.
A soma de um número racional com um número irracional é sempre um número irracional.
V
F
V
Determine a derivada da seguinte função:
$f\left( x\right) =\ln \left( 3\cos ^{5}\left( 4x\right)\right) .$
$f'(x) = -20\tan(4x)$.
Calcule a integral $\int_0^{1} xe^x dx$.
1
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
\frac{x^2-64}{x^2-11 x+24}, & & \text{se } x\neq 8\\
5, & & \text{se } x=8
\end{array}\right.$
- $x=0$
- $x=8$
- Sim.
- Não. $\lim_{x\to 8} f(x) = 16/5 \neq f(8) = 5$.
Mostre $\lim\limits_{x\to 0} \frac{x+1}{x^2+3x}$ não existe.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{x}{x^{2}+1}$.
Identifique as assíntotas verticais e horizontais, caso existam, da função
$f(x)=\frac{x^2+x-12}{7 x^3-14 x^2-21 x}$.
Assíntota horizontal em $y=0$; assíntotas verticais em $x=-1$ e $x=0$.
Esboce as curvas exponenciais transladadas:
$y=3^x+2$ e $y=3^{-x}+2$.
Um termômetro de mercúrio demorou $14s$ para subir de $-19° C$ para $100° C$ após ser retirado de um congelador e colocado em água fervendo. Considerando que, no termômetro em questão, a distância entre dois graus subsequentes é de $1mm$, demonstre que em algum instante a coluna de mercúrio subia a $8,5mm/s$.
Avalie a seguinte integral indefinida:
$\int (2t+3)^2\ dt$
$4/3t^3+6t^2+9t+C$
Esboce o gráfico da função $f(x)=|(x-1)^2-3|$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}-1}{x}$.
$2$.
Avalie o limite $\lim\limits_{x\rightarrow p}\dfrac{x^{8}-p^{8}}{x-p}$.
Calcule o limite $\lim\limits_{x\rightarrow -\infty }\left( 2^{x}+2^{-x}\right)$.
$\infty$.
Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{x-1}$.
$x=1$.
Qual das integrais a seguir, se houver alguma, serve para calcular a área da região sombreada mostrada aqui? Justifique sua resposta.
 $\int_{-1}^{1} {\left(x-\left(-x\right)\right)dx} = \int_{-1}^{1} {2x\ dx}$
$\int_{-1}^{1} {\left(x-\left(-x\right)\right)dx} = \int_{-1}^{1} {2x\ dx}$- $\int_{-1}^{1} {\left(-x-x\right)dx} = \int_{-1}^{1} {-2x\ dx}$
Uma análise do resultado de ambas as integrais nos mostra, de imediato, que nenhuma delas é a adequada para o cálculo da área da figura. A segunda integral nada mais é do que a primeira integral com o sinal invertido, e portanto ambas são iguais a zero.
A questão é que no caso, se denotarmos $f_1(x)=x$ e $f_2(x)=-x$, é fácil observar que para $x>0$ $f_1(x)>f_2(x)$, e para $x<0$ $f_2(x)>f_1(x)$. Portanto, o cálculo correto da área se daria através de duas integrais, na forma
$A=\int_{-1}^{0} {\left(-x-x\right)dx}+\int_{0}^{1} {\left(x-\left(-x\right)\right)dx}$
Ou ainda, fazendo uso da simetria, poderia também se fazer:
$A=2\int_{0}^{1} {\left(x-\left(-x\right)\right)dx}=4\int_{0}^{1} {x\,dx}=2$
A trombeta de Torricelli, também conhecida como trombeta de Gabriel, em referência à passagem da bíblia na qual o arcanjo Gabriel anuncia o dia do julgamento com sua trombeta, é uma figura geométrica bastante interessante. Ela é descrita a partir da rotação da função $1/x$ no domínio $x>1$ em relação ao eixo $x$. Calcule sua área e seu volume.
A área de uma superfície de revolução é dada por:
$A=\int_{a}^b 2 \pi f(x) \sqrt{1+f'(x)^2}\ dx$
Assim, temos, para a trombeta de Torricelli:
$A= \lim\limits_{a\rightarrow \infty}\left(2 \pi \int_{1}^{a}\ \frac{1}{x} \sqrt{1+\left(-\frac{1}{x^2}\right)^2}\ dx\right)$
Portanto, como $\sqrt{1+\left(-\frac{1}{x^2}\right)^2}>1$:
$A > \lim\limits_{a\rightarrow \infty}\left( 2 \pi \int_{1}^{a} \frac{1}{x} \ dx\right)= \lim\limits_{a\rightarrow \infty}\left( 2 \pi ln\ a\right)$
para $a\rightarrow \infty$, vemos que a área $A$ tende ao infinito.
Quanto ao volume, temos que:
$V= \lim\limits_{a\rightarrow \infty}\left( \pi \int_{1}^{a} \frac{1}{x^2}\ dx\right)$
Portanto, obtemos:
$V= \lim\limits_{a\rightarrow \infty}\ \pi \left(1-\frac{1}{a}\right)$
Que para $a\rightarrow \infty$ tende a $V=\pi$.
Demonstre que não é possível que o valor de $\int_0^1\sin(x^2)\ dx$ seja $2$. Depois, utilizando a desigualdade $\sin x \leq x$, válida para $x \geq 0$, determine um limitante superior para esta integral.
Sabemos que $\sin x \leq 1,\,\forall\,x\in\mathbb{R}$. Assim, como $\int_a^b f(x)dx \leq max\_{a \leq x \leq b} f(x) (b-a)$, podemos dizer que $\int_0^1\sin(x^2)\ dx \leq 1$.
Utilizando a desigualdade $\sin x \leq x$, podemos determinar de maneira ainda mais precisa um limitante superior para a integral.
$\int_0^1\sin(x^2)\ dx \leq \int_0^1x^2\ dx = \frac{1}{3}x^3 \vert^1_0=\frac{1}{3}$
Admitindo-se que $\lim\limits_{x\rightarrow a}f(x)$ existe, prove que
$\lim\limits_{x\rightarrow a}f(x)=\lim\limits_{h\rightarrow0}f(a+h).$
Esboce o gráfico de $f(x)= \frac{x^2-2x^3}{x^2-1}$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Nos exercícios abaixo determine o domínio máximo de definição de cada uma das funções dadas.
$y=\sqrt{x^{2}-9}$
$y=\sqrt{-x}$
- $\{x \in \mathbb{R}; x<-3 \text{ ou }x>3\}$.
- $\{x \in \mathbb{R}; x<0\}$.
Calcule a integral $\displaystyle \int (5x-1)^2 \, dx$ elevando ao quadrado e depois integrando as potências de $x$.
Calcule agora a integral utilizando a substituição $u=5x-1$.
As duas respostas obtidas são iguais? São equivalentes de alguma forma? Justifique.
Sejam $x_0,c\in\mathbb R$ e considere a função $f(x)=e^{cx}$. Encontre $f'(x_0)$ usando a definição de derivada.
$ce^{cx_0}$.
É possível que uma função $f:{\mathbb{R} \to \mathbb{R}}$
seja tal que $\lim\limits_{x\rightarrow 2^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 2^{-}}f\left(x\right)$ e ao mesmo tempo não seja contínua em $2$? Justifique e/ou dê um exemplo.
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=e^{x},y=0,x=0,x=1$ ao redor do eixo $x.$
Esboce o gráfico de $f(x) = |x-1|+3.$
A ciclóide é um caminho traçado por um ponto na borda de uma roda que gira ao longo de uma reta. Use as equações paramétricas de uma ciclóide para mostrar que o comprimento $L$ de um arco de uma ciclóide é dado pela integral $L=\displaystyle\int_{0}^{2\pi} \sqrt{2(1-\cos\theta)}d \theta$
Calcule a integral a seguir utilizando decomposição de quocientes em frações parciais:
$\int_{0}^{1}{\frac{x^3dx}{x^2 + 2x + 1}}$
- $\lim\limits_{x\rightarrow 1}\dfrac{f\left( x\right) -f\left(1\right) }{x-1}$, onde $f\left( x\right) =\left\{ \begin{array}{cc} x^{2} & \text{se }x\leq 1 \\ 2x-1 & \text{se }x>1 \end{array} \right. $
- $\lim\limits_{x\rightarrow 2}\dfrac{f\left( x\right) -f\left(2\right) }{x-2}$, onde $f\left( x\right) =\left\{ \begin{array}{cc} x & \text{se }x\geq 2 \\ x^{2}/2 & \text{se }x<2 \end{array} \right. $
- $\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h}$, com $f\left( x\right) =x^{2}-3x$ e $f\left( x\right) =1/x$
Encontre as equações das retas que passam pelo ponto $(-1,1)$ e são tangentes à curva $x^2+4y^2-4x-8y+3=0.$
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =\sqrt{x},\;p=9$.
$y=\dfrac{x+9}{6}$.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = \sin x$ e $f(0)= 2$
$-\cos x+3$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
- $\lim\limits_{x\rightarrow 0}x\sin \left( \dfrac{1}{x}\right)$
- $\lim\limits_{x\rightarrow p}\dfrac{\sin \left(x^{2}-p^{2}\right) }{x-p}$
Dê o domínio e esboce o gráfico das seguintes funções:
- $f(x)=1+1/x$
- $f(x)=\dfrac{2}{x+1}$
Encontre todos os números reais que satisfazem a cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$|6+4x|<\left| 2-{\frac{x}{2}}\right| $
$\left| {\frac{5}{3x-2}}\right| \geq \left| {\frac{2}{x-1}}\right| $
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f\,^{\prime \prime }\left( x\right) = 9e^{3x}+\cos x+x^{6},\;f\,^{\prime}\left( 0\right) =1\text{ e }f\left( 0\right) =2\text{ .} \end{equation*}
Use o Teorema do Confronto para demonstrar que $\lim\limits_{x \to 0} \cos{x} = 1$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow -\infty }\left( 2^{x}+2^{-x}\right) $.
$-\infty$.
Dois corredores iniciaram uma corrida ao mesmo tempo e terminaram a corrida empatados. Prove que os dois corredores estiveram à mesma velocidade $v^*$, ainda que talvez em instantes diferentes da corrida.
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$(x-1)^{2}<1-x$
$(2x-1)^{15}\leq 0$
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
- $\lim\limits_{x\rightarrow p}\dfrac{\tan \left( x-p\right) }{x^{2}-p^{2}}$
- $\lim\limits_{x\rightarrow p}\dfrac{\sin x-\sin p}{x-p}$
- $\lim\limits_{x\rightarrow p}\dfrac{\cos x-\cos p}{x-p}$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(x) = \sqrt{x^2-4}$.
$(-\infty,-2]\cup [2,\infty)$
Encontre todos os números reais que satisfazem cada uma das desigualdades abaixo. Dê o intervalo solução e ilustre a solução sobre a reta real.
$(2-x)(x-1)$
$1-x^{2}<0$
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }3^{x}$
$\lim\limits_{x\rightarrow \infty }\left( 2^{x}-3^{x}\right)$
$\lim\limits_{x\rightarrow \infty }\left( 0,27\right) ^{x}$
1. $\infty$.
2. $-1$.
3. $0$.
Esboce o gráfico de cada uma das funções abaixo.
$y=\sqrt{9-(2-x)^{2}}$
$y=7/2-\sqrt{13-(2+x)^{2}}$
Determine uma primitiva para cada uma das funções:
$f(x)=1+2x+3x^2+4x^3+5x^4$
$f(x)=1+x+x^2+\ldots +x^{1000000}$
- $F(x)=1+x+x^2+x^3+x^4+x^5$
- $F(x)=x+\frac{x^2}{2}+\frac{x^3}{3}+\ldots+\frac{x^1000001}{1000001}$
Calcule a derivada da seguinte função:
$f\left( x\right) =\sin\left( \arccos\left( x\right) \right) .$
Sabe-se que $f$ é contínua em $2$ e que $f(2)=8$. Mostre que existe $\delta>0$ tal que para todo $x \in D_f$ vale $2-\delta<x<2+\delta \rightarrow f(x)>7$.
Considere $\epsilon =1$. Como $f$ é contínua em $2$, sabemos que existe $\delta >0$ tal que, para $|x-2|<\delta $ temos que $|f(x)-f(2)|<\epsilon =1$. Mas $|x-2|<\delta $ se, e somente se, $2-\delta<x<2+\delta$ e $|f(x)-f(2)|=|f(x)-8|<1$ se, e somente se, $7< f(x)<9$.
Prove que o comprimento de um arco de ciclóide é igual a $8$ vezes o tamanho do raio do seu círculo gerador. A figura abaixo mostra dois arcos e meio de ciclóide.
Se você fosse um professor e seu(sua) aluno(a) te perguntasse ``Por que $\displaystyle \lim_{x \to 0}\dfrac{\sin x}{x}=1$?''
Como você responderia com palavras?
Que bibliografia você recomendaria?
Qual a demonstração formal?
Em um gerenciamento de estoques, o custo médio semanal de pedidos, pagamentos e armazenamento de mercadoria é dado por:
$$A(q)=\dfrac{km}{q}+cm+\dfrac{hq}{2},$$
onde $q$ é a quantidade de produtos pedida em períodos de baixa no estoque; $k$ é o custo (fixo) da colocação de um pedido; $c$ é o custo (também fixo) de cada item; $m$ é a quantidade de itens vendidos por mês; e $h$ é o custo mensal para manter cada item (custos de espaço, seguro, etc). Determine $dA/dq$ e $d^2A/dq^2$. Interprete os resultados.
Use o teorema do valor intermediário para mostrar que $f(x)=4x^3-6x^2+3x-4$ possui um zero no intervalo $[1,2]$.
Como $f(1) = -3 < 0$ e $f(2) = 10 > 0$, temos que a função $f$ muda de sinal no intervalo $[1,2]$, e portanto, pelo teorema do valor intermediário, $f$ possui um zero nesse intervalo.
O número relativo de moléculas de gás em um recipiente que se movem a uma velocidade de $v$ $cm/s$ pode ser calculado por meio da distribuição de velocidade de Maxwell-Boltzmann, $F(v)=cv^2e^{-mv^2/(2kT)}$, sendo que $T$ é a temperatura em Kelvins, $m$ é a molécula e e $c$ e $k$ são constantes positivas. Mostre que o valor máximo de $F$ ocorre quando $v=\sqrt{2kT/m}$.
Seja $f:\mathbb{R\rightarrow R}$ a função
definida por
\begin{equation*}
f\left( x\right) =\left\{
\begin{array}{cc}
x^{2} & \text{se }x\leq 1 \\
2x-1 & \text{se }x>1
\end{array}
\right. ,
\end{equation*}
e defina $g\left( x\right) =\lim\limits_{x\rightarrow h}\dfrac{f\left(
x+h\right) -f\left( x\right) }{h}$. Mostre que $g\left( x\right) $ é contínua.
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =x^{2}-x;\;p=1$.
$y=x-1$.
Calcule a seguinte integral:
$\int{e^x(x^2-2x+1)dx}$.
$e^x(x^2-4x+5)+C$
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$x=\frac{(e^y+e^{-y})}{2}$, $0\leq y \leq ln\ 2$, eixo $y$
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\log _{a}x,\;a>0$ e $a\neq 1$.
$f'(x)=\dfrac{1}{xln(a)}
Prove o teorema do valor médio para integrais aplicando o teorema do valor médio para derivadas(consulte Stewart, seção 4.2, para obter mais informações sobre a função $F(x)=\displaystyle\int_{a}^{x} f(t)dt$.
Calcule a integral a seguir utilizando substituições trigonométricas:
$\int{3\frac{dx}{\sqrt{1+9x^2}}}$
$sinh^{-1}(3x)+C$.
Prove que $\displaystyle\int x^m \sin(x)dx=-x^m \cos(x)+m \displaystyle\int x^{m-1} \cos(x)dx$.
Utilizando as leis de exponenciação, simplifique a expressão a seguir:
$6^{1/3}\cdot18^{1/6}$
Calcule a derivada da função:
$y=\dfrac{e^{\sec \sqrt{x}}}{x}$.
$y'=\dfrac{(\tan x) e^{\sec x} \sec x)}{\sqrt{x}} - \dfrac{e^{\sec x}}{(2 x^{3/2})}$.
Prove que a equação $x^{3}-3x^{2}+6=0$ admite uma única raiz real, enquanto $x^{3}+x^{2}-5x+1=0$ admite $3$ raízes.
Para $f(x)=x^{3}-3x^{2}+6$ e $g(x)=x^{3}+x^{2}-5x+1$, queremos mostrar que $f(x)=0$ admite uma única raiz real enquanto $g(x)=0$ admite $3$ raízes. Primeiramente, analisemos as raízes de $f(x)=0$. Temos:
$f'(x)= 3x^2-6x=x(x-2)$
$f''(x)=6(x-1)$
Portanto, a segunda derivada nos diz que $f(x)$ é uma concavidade para baixo para $x<1$ e uma concavidade para cima para $x>1$, e os zeros da primeira derivada nos dizem que $f(x)$ apresenta um máximo local em $x=0$ e um mínimo local em $x=2$. Como $f(2)=2$, temos que não há raiz alguma para $x>1$, dado que a função é uma concavidade para baixo neste intervalo. A única raiz real, portanto, é algum valor $x<1$. O conhecimento do máximo local em $x=0$ nos permite inclusive dizer que é algum valor $x<0$.
Repetiremos a análise para $g(x). Temos, portanto:
$g'(x)= 2x^2+2x-5=2(x+5/3)(x-1)$
$g''(x)=6(x+1/3)$
Portanto, a segunda derivada nos diz que $g(x)$ é uma concavidade para baixo para $x<-1/3$ e uma concavidade para cima para $x>-1/3$, e os zeros da primeira derivada nos dizem que $g(x)$ apresenta um máximo local em $x=-5/3$ e um mínimo local em $x=1$. Como $g(0)=1$ e $g(1)=-2$, sabemos que há duas raízes reais de $g(x)$ no intervalo aberto $x>0$. Como $g(x)$ claramente tende para $-\infty$ para $x\rightarrow \infty$, o valor de $g(0)$ nos diz que a terceira raiz real está localizada no intervalo $x<0$. O conhecimento do máximo local em $x=-5/3$ nos permite inclusive dizer que é algum valor no intervalo aberto $x<-5/3$
O modelo logístico de crescimento populacional prevê o tamanho $y(t)$ de uma população no instante $t$ por meio da fórmula $y(t)=\dfrac{k}{1+ce^{-rt}}$, onde $r$ e $k$ são constantes positivas e $c=\dfrac{k-y(0)}{y(0)}$. Os ecologistas denominam $k$ a capacidade de suporte e o interpretam como o número máximo de indivíduos que o ambiente pode sustentar. Calcule $\lim\limits_{t \to \pm \infty}y(t)$ e discuta o significado gráfico desses limites.
Um caminhoneiro estava em uma estrada cujo limite de velocidade era de $100km/h$. Ao passar no segundo pedágio, distante $120km$ do primeiro, o caminhoneiro recebeu uma multa, pois levou $30$ minutos para ir do primeiro ao segundo pedágio. Ele tentou contestar a multa, mas não obteve sucesso. Por que a multa foi justa?
Encontre a equação da reta tangente ao gráfico da função $f(x)=12\sqrt[6]{x}-\frac{1}{2x^2}+\log_5(x)$ no ponto cuja coordenada horizontal é $3$.
O modelo Jenss é considerado geralmente como a fórmula mais precisa para predizer a altura de uma criança em idade pré-escolar. Se $h(x)$ denota a altura (em cm) na idade $x$ (em anos) para $\frac{1}{4} \leq x \leq 6$, então $h(x)$ pode ser aproximada por $h(x)=79,041+6,39x-e^{3,261-0,993x}$.
- Preveja a altura e a taxa de crescimento quando uma criança atinge a idade de $1$ ano.
- Quando é maior e quando é menor a taxa de crescimento?
Entre todos o cilindros retos que tem uma área total dada, ache o que tem volume máximo.
Prove que $\cosh'(x)=\sinh(x)$.
Calcule a derivada da função:
$y=\dfrac{2\left( 4+3\sqrt[3]{x}\right) \left( 2-\sqrt[3]{x}\right)^{3/2}}{5}$.
$y'=-\dfrac{\sqrt{2 - x^{1/3}}}{x^{1/3}}$.
Determine a área da região no primeiro quadrante limitada à esquerda pelo eixo $y$, abaixo pela curva $x=2\sqrt{y}$, acima à esquerda pela curva $x=\left(y-1\right)^2$ e acima à direita pela reta $x=3-y$.
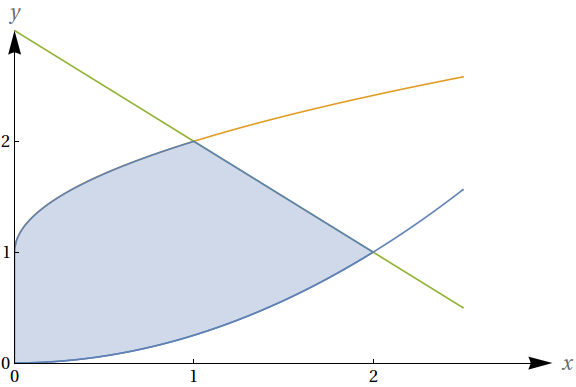
Primeiramente, devemos escrever as curvas na forma $y=f(x)$, tomando cuidado com o sinal. Após este procedimento, uma análise da figura nos permite resumir o cálculo da área $A$ como $A=A_1+A_2$, sendo que:
$A_1=\int_0^1\left (1+\sqrt{x}-\frac{1}{4}x^2\right)\,dx$
$A_2=\int_1^2\left (3-x-\frac{1}{4}x^2\right)\,dx$
Assim, temos
$A_1=\left.\left(x + \frac{2}{3} x^{3/2} - x^3/12\right)\right\vert_0^1=\frac{19}{12}$
$A_2=\left.\left(-\frac{x^3}{12}-\frac{x^2}{2}+3 x\right)\right\vert_1^2=\frac{11}{12}$
O que nos leva a $A=\frac{5}{2}=2.5$
Encontre $f(\theta)$ que satisfaça o seguinte problema de valor inicial:
$f''(\theta) = \sin \theta$ e $f'(\pi)= 2$, $f(\pi) = 4$
$\theta-\sin (\theta)-\pi +4$
Determine a função inversa de:
- $f(x) = x^2$
- $f(x) = x^3 + 2.$
Calcule a seguinte integral:
$\int_{0}^{\infty}{\frac{dx}{\sqrt{4-x}}}$
Não converge.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{3}-6x-3}{6x^{2}+28x+2}$.
$\infty$
Seja $f$ uma função definida num intervalo aberto $I$ e $p \in I$. Suponha que $f(x) \leq f(p)$ para todo $x \in I$. Prove que $\lim\limits_{x \to p}\dfrac{f(x)-f(p)}{x-p}=0$, desde que o limite exista.
Resolva a equação $\left| {\frac{3x+8}{2x-3}}\right| =4$.
Uma fonte de imprecisão nos cálculos feitos por computadores é a {\it subtração catastrófica}. Tal erro ocorre quando dois números aproximadamente iguais são subtraídos, e o resultado é usado como parte de outro cálculo.
Um exemplo: $(0,123456789012345-0,123456789012344)\times 10^{15}=1$.
Mas, na calculadora, obteríamos zero como resposta a esse cálculo pois ela armazena apenas 14 dígitos e os 14 primeiros dígitos são idênticos. Por vezes, pode-se evitar a subtração catastrófica fazendo um rearranjo algébrico das fórmulas. De todo modo, o melhor é estar atento à sua ocorrência, portanto, tome cuidado para resolver este exercício.
Seja $f(x)=\dfrac{x-\sin x}{x^3}$. Faça uma conjectura sobre o limite de $f$ quando $x \to 0^+$ calculando $f$ nos pontos $x=0,1$, $0,01$, $0,001$, $0,0001$.
Calcule $f$ nos pontos $x=0,00001$, $0,000001$, $0,0000001$, $0,00000001$, $0,000000001$, $0,0000000001$, e faça outra conjectura.
Que falha isso revela sobre o uso da evidência numérica para fazer conjecturas sobre limites?
Se você dispuser de um sistema de computação algébrica, um programa que pode efetuar cálculos numéricos ou simbólicos, use-o para mostrar que o valor exato desse limite é $\dfrac{1}{6}$. (Aqui, eu não posso pedir para calcular o limite à mão, de fato?)
Sejam $f$ e $g$ funções contínuas. Demonstre que $h(x)=\max(f(x),g(x))$ é contínua.
Calcule $f^{\prime }\left( x\right)$:
$\dfrac{x+\sqrt[4]{x}}{x^{2}+3}$.
$f'(x) = \dfrac{3-7x^2}{4 x^{3/4}(x^2+3)^2}$.
Em estatística, a função densidade de probabilidade para a distribuição normal é definida por $f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}}e^{-z^2/2}$ com $z=\dfrac{x-\mu}{\sigma}$ para números reais $\mu$ e $\sigma>0$ ($\mu$ é a média e $\sigma^2$ é a variância da distribuição). Obtenha os extremos locais de $f$ e determine onde $f$ é crescente ou decrescente. Discuta a concavidade, ache os pontos de inflexão, determine $\lim\limits_{x \to \pm \infty}f(x)$ e esboce o gráfico de $f$.
Mostre que a função $f\left( x\right) =\dfrac{1}{x}$ é contínua em seu domínio.
Classifique cada uma das afirmações abaixo em verdadeiras ou falsas.
Nem todo primo é ímpar.
Todo inteiro par pode ser escrito na forma $n^2+2, n \in N$.
A soma de dois inteiros ímpares é sempre um inteiro par.
Todo inteiro ímpar pode ser escrito na forma $2n-9, n \in N$.
Se $n$ é um inteiro ímpar, então $n^2$ também é ímpar.
V
F
V
V
V
Calcule a integral imprópria $\int_{0}^{\infty }x^{2}e^{-x}dx$
$2$.
Mostre que $\sqrt{xy}\leq {\frac{x+y}{2}}$$\forall x,y\geq 0$.
Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles.
A partir de um ponto, observa-se o topo de um prédio sob um ângulo de $30^0$. Caminhando $23$m em direção ao prédio, atingimos outro ponto, de onde se vê o topo do prédio segundo um ângulo de $60^0$. Desprezando a altura do observador, calcule, em metros, a altura do prédio.
Avalie a seguinte integral indefinida:
$\int \frac{1}{\sqrt{x}}\ dx$
$2\sqrt{x}+C$
Quais os valores de $x$ que satisfazem a inequação $\frac{x-3}{x-2}\leq x-1$?
Prove que $\displaystyle\int (\ln(x))^m dx=x (\ln(x))^m -m \displaystyle\int (\ln(x))^{m-1}dx$, para $m$ inteiro positivo.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=(1/3)\left(x^2+2\right)^{3/2},\quad 0 \leq x \leq 3$
Sociólogos utilizam a expressão "difusão social" para descrever o modo como a informação se espalha por uma população. A informação pode ser um boato, uma novidade cultural, ou notícias sobre uma inovação técnica Em uma população suficientemente grande, o número de pessoas $x$ que tem a informação é tratado como uma função derivável do tempo $t$, e a taxa de difusão é supostamente proporcional ao número de pessoas que têm a informação multiplicado pelo número de pessoas que não a tem, isto é,
$\frac{dx}{dt} = kx\left(N-x\right)$, sendo que $N$ é o número total de pessoas da população.
Suponha então que $t$ seja medido em dias, $k=1/250$ e que duas pessoas deram início a um boato no momento $t=0$ em uma população tal que $N=1000$.
Determine $x(t)$.
Quando metade da população terá ouvido o boato?
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2},y^{2}=x$, ao redor do eixo $x$.
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x^2$ no intervalo $[0,b]$ é $b^3/3$.
Mostre o mesmo resultado utilizando somas inferiores.
Seja o número inteiro $AB$, no qual $A$ e $B$ são os algarismos das dezenas e das unidades, respectivamente. Invertendo-se a posição dos algarismos $A$ e $B$, obtém-se um número que excede $AB$ em $27$ unidades. Se $A+B$ é um quadrado perfeito, qual o valor de $B$?
Temos que "$BA-AB$"$=10B+A-10A-B=9B-9A$. De acordo com o enunciado essa diferença é igual a $27$. Logo, $B-A=3$. Temos, portanto, $7$ possibilidades: "$BA$"$=30, 41, 52, 63, 74, 85$ ou $96$. Dentre essas possibilidades, a única em que $A+B$ é um quadrado perfeito é o caso $B=6$, $A=3$.
Determine o comprimento da curva a seguir no intervalo especificado.
$y=x^{3/2},\quad 0 \leq x \leq 4$
Uma força de retardamento freia o movimento de uma massa presa a uma mola alinhada com o eixo $y$, de modo que a posição da massa no instante $t$ é
$y=3 e^{-t}\cos\ t,\ \ t\geq 0$.
Calcule o valor médio de $y$ no intervalo $ 0 \leq y \leq 2\pi$
Aproximadamente $0,2383$.
Seja $f:\mathbb{R\rightarrow R}$ a função
definida por
\begin{equation*}
f\left( x\right) =\left\{
\begin{array}{cc}
x^{2}, & \text{se }x\leq 1 \\
2x-1, & \text{se }x>1
\end{array}
\right. ,
\end{equation*}
e defina $g\left( x\right) =\lim\limits_{x \rightarrow h}\dfrac{f \left(x+h \right) -f \left( x\right) }{h}$.
Mostre que $g\left( x\right) $ é contínua.
\begin{eqnarray*} g\left( x\right) &=&\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left( x+h\right) ^{2}-x^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{x^{2}+2hx+h^{2}-x^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2hx+h^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\left( 2x+h\right) =2x. \end{eqnarray*}
Já para $x>1$ temos que
\begin{eqnarray*} g\left( x\right) &=&\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ 2\left( x+h\right) -1\right] - \left[ 2x-1\right] }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2h}{h}=2. \end{eqnarray*}
Para $x=1$ temos que
\begin{eqnarray*} \lim\limits_{h\rightarrow 0^{+}}\dfrac{f\left( 1+h\right) -f\left( 1\right) }{h} &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ 2\left( 1+h\right) -1 \right] -1}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2h}{h}=2 \\ \lim\limits_{h\rightarrow 0^{-}}\dfrac{f\left( 1+h\right) -f\left( 1\right) }{h} &=&\lim\limits_{h\rightarrow 0^{-}}\dfrac{\left( 1+h\right) ^{2}-1}{h} \\ &=&\lim\limits_{h\rightarrow 0^{-}}\dfrac{2h+h^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0^{-}}\left( 2+h\right) =2. \end{eqnarray*}
Temos então que $g$ é bem definida também no ponto $x=1$ e, de modo geral, $g$ pode ser expressa por \begin{equation*} g\left( x\right) =\left\{ \begin{array}{cc} 2x & \text{se }x\leq 1 \\ 2 & \text{se }x>1 \end{array} \right. \text{.} \end{equation*}
Como as funções $h\left( x\right) =2x$ e $p\left( x\right) \equiv 2$ são contínuas, temos que $g\left( x\right) $ é contínua para todo $x\neq 1$.
Além disto, como $\lim\limits_{x\rightarrow 1^{-}}g\left( x\right) =\lim\limits_{x\rightarrow 1}2x=2=\lim\limits_{x\rightarrow 1^{+}}2=\lim\limits_{x\rightarrow 1^{+}}g\left( x\right) $, segue que $\lim\limits_{x\rightarrow 1}g\left(x\right) =2$. Mas como $g\left( 1\right) =2$, segue que a função $ g\left( x\right) $ também é contínua no ponto $x=1$.
Dê exemplo de duas funções, $f$ e $g$, para ilustrar que se $g(x)\le f(x)$ para todo $x$ suficientemente próximo de $a$, então $\lim\limits_{x\rightarrow a}g(x)\le\lim\limits_{x \rightarrow a}f(x)$.
A função de Heaviside (também conhecida como função degrau), cujo gráfico pode ser visto abaixo, é muito utilizada para modelar chaves que ligam e desligam em circuitos elétricos (e também diversas aplicações). O que você tem a dizer sobre a continuidade dessa função? E sobre a diferenciabilidade?

Utilizando o gráfico a seguir, avalie os seguintes limites
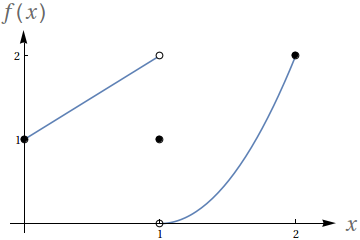
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $2$
- $0$
- Não existe.
- $1$
Se uma bola de neve derrete de tal forma que a área de sua superfície decresce a uma taxa de $1cm^{2}/\min $, encontre a taxa segundo qual o diâmetro decresce quando o diâmetro for $5 cm$.
Derive a função $f\left( x\right) =\left( 3^{2x+3}\right)\sqrt{\cos \left( x^{3}+x^{1/3}\right) }.$
$ 2.3^{2 x + 3} \sqrt{\cos(x^3 + x^{1/3})} \log 3 - (3^{2 x + 3} (1/(3 x^{2/3}) + 3 x^2) \sin(x^3 + x^{1/3}))/(2 \sqrt{cos(x^3 + x^{1/3})})$.
Determine a derivada da seguinte função:
$f\left( x\right) =\left( \left( \sin x\right) \left(\cos x\right) \right) ^{3}.$
$f'(x)=3/8 \sin(2x) \sin(4x)$.
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $x^2e^x\cos{x}$
- $e^x \sinh{x} \cos^2{x}$
Explique, usando suas palavras, o que significa escrever $\lim\limits_{x\to c} b = b$.
Calcule a integral a seguir:
$\int_{0}^{ln\ 4}{\frac{e^t dt}{\sqrt{e^{2t}+9}}}$
Aproximadamente $0,77116$
Utilizando as leis de exponenciação, simplifique a expressão a seguir:
$16^2\cdot16^{1,75}$
Calcule $\displaystyle \int x^2 \ln (x+1) \, dx$ utilizando integração por partes.
$\dfrac{1}{18}(6(x^3+1)ln(x+1)-2x^3+3x^2-6x)+C$.
- $\lim\limits_{x\rightarrow 4}\sqrt{x}$
- $\lim\limits_{x\rightarrow 0}\dfrac{x^{2}+3x-1}{x^{2}+2}$
- $\lim\limits_{x\rightarrow 1^{+}}\dfrac{\left| x-1\right| }{x-1}$
- $\lim\limits_{x\rightarrow 1^{-}}\dfrac{\left| x-1\right| }{x-1}$
A base $x$ e a altura $y$ de um retângulo estão variando com o tempo. Em um dado instante, $x$ mede $3 cm$ e cresce a uma taxa de $2 cm/s$, enquanto $y$ mede $4 cm$ e decresce a uma taxa de $1 cm/s$. Determine, nesse instante, a taxa de variação da área $A$ do retângulo em relação ao tempo.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\pi ^{x}$.
$f'(x)=ln(\pi)\pi^x$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(x) = e^x$.
$(-\infty,\infty)$
Se um raio de luz de intensidade $k$ é projetado verticalmente para baixo na água, então a sua intensidade $I(x)$ à profundidade de $x$ metros é $I(x)=ke^{-1,4x}$.
- A que taxa de intensidade o raio de luz está variando em relação à profundidade a $1$ metro?
- A que profundidade a intensidade é a metade de seu valor na superfície?
Encontre as raízes do polinômio $x^4-7x^3+35x^2-50x+24.$
Demonstre que $2\sqrt{2} \leq \int_{0}^{1}{\sqrt{x+8}dx} \leq 8$.
Um objeto é lançado para cima com uma velocidade, em pés por segundo, dada por $v(t) = -32t+96$; de uma altura de $64$ pés.
- Qual a velocidade inicial do objeto?
- Em que momento o objeto tem deslocamento nulo?
- Quanto tempo leva para o objeto retornar a sua posição inicial?
- Quando o objeto alcançará uma altura de $210$ pés?
- $96ft/s$.
- $6s$.
- $6s$.
- Nunca, a altura máxima é $208ft$.
Use camadas cilíndricas para encontrar o volume do sólido resultante quando se faz girar a área entre as curvas $y=2x-1$, $y=-2x+3$ e $x=2$ em torno do eixo $y$.
Dados $f(x) = 2x^2+4x-3$ e $x_0 = -0,9$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
Seja $f\left( x\right) =\frac{2x-1}{x-1}$
Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Domínio: Dom$\left( f\right) =\left\{ x|x\neq1\right\} =\left( -\infty,1\right) \cup\left( 1,\infty\right) $
Zeros e inteceptos: $f\left( x\right) =0\iff2x-1=0\iff x=1/2$
Simetrias: Não há.
Assíntotas:
\begin{align*}
\lim_{x\rightarrow\pm\infty}f\left( x\right) & =\lim_{x\rightarrow
\pm\infty}\frac{2x-1}{x-1}\\
& =\lim_{x\rightarrow\pm\infty}\frac{2-1/x}{1-1/x}=2
\end{align*}
\begin{align*}
\lim_{x\rightarrow1^{-}}f\left( x\right) & =\lim_{x\rightarrow1^{-}}
\frac{2x-1}{x-1}=-\infty\\
\lim_{x\rightarrow1^{+}}f\left( x\right) & =\lim_{x\rightarrow1^{-}}
\frac{2x-1}{x-1}=+\infty
\end{align*}Intervalos de crescimento e decrescimento:
\begin{align*}
f^{\prime}\left( x\right) & =\frac{2\left( x-1\right) -\left(
2x-1\right) \left( 1\right) }{\left( x-1\right) ^{2}}\\
& =\frac{-1}{\left( x-1\right) ^{2}}<0,\forall x\in Dom\left( f\right)
\end{align*}ou seja, $f$ é estritamente decrescente.
Valores máximo e mínimo locais: Não há, pois a derivada não se anula
Concavidade e pontos de Inflexão:
\[f"\left( x\right) =\frac{2}{\left( x-1\right) ^{3}}>0\iff x-1>0\iff x>1
\]
ou seja, $f$ tem concavidade para cima para $x>1$ e concavidade para baixo para $x<1$
Esboço do Gráfico:
Os impulsos nervosos no corpo humano caminham ao longo de fibras nervosas que consistem em um axônio, que transporta o impulso, envolvido por uma camada de mielina. A fibra nervosa é semelhante a um cabo cilíndrico isolado, para o qual a velocidade $v$ de um impulso é dada por $v=-k(r/R)^2 \ln(r/R)$, onde $r$ é o raio do cabo e $R$ é o raio de isolamento. Ache o valor de $r/R$ que maximize $v$. Na maioria das fibras nervosas, $r/R$ vale aproximadamente $0,6$.
Mostre que se $f$ é contínua e côncava para cima em $\left[a,b\right]$, então $f_{med}>f\left(\dfrac{a-b}{2}\right)$, onde $f_{med}$ é o valor médio da função $f$ no intervalo $\left[a,b\right]$.
Mostre que as funções $f(x)=(x-1)^4$ e $g(x)=x^3-3x^2+3x-2$ têm pontos estacionários em $x=1$.
O que o teste da derivada primeira diz sobre a natureza destes pontos?
Com base no gráfico, avalie as seguintes integrais:
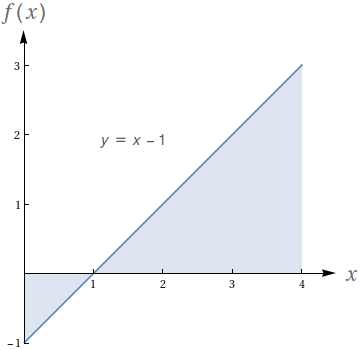
- $\int_0^1 (x-1)\ dx$
- $\int_0^2 (x-1)\ dx$
- $\int_0^3 (x-1)\ dx$
- $\int_2^3 (x-1)\ dx$
- $\int_1^4 (x-1)\ dx$
- $\int_1^4 \big((x-1)+1\big)\ dx$
- $-1/2$
- $0$
- $3/2$
- $3/2$
- $9/2$
- $15/2$
Seja $P(x)$ um polinômio de coeficientes inteiros com grau $d>0$. Seja $n$ o número de inteiros distintos $k$ tais que $(P(k))^2=1$. Prove que $n\leq d+2.$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ h(k) = \sqrt{1-k}+\sqrt{k+1}$.
$[-1,1]$
Seja $g$ uma função contínua em $[-3,7]$, sendo que $g(0) = 0$ e $g(2) = 25$. Existe um valor $-3<c<7$ tal que $g(c) = 15$? Por quê?
Sim, pelo Teorema do Valor Intermediário. Na realidade, é possível ser ainda mais preciso e afirmar não só que um valor $c$ existe em $(3,7)$, mas ainda que existe um valor $x$ contido em $(0,2)$.
Esboce juntas as curvas dadas no plano cartesiano e identifique cada uma com sua equação:
$y=2^x$, $y=4^x$,$y=3^{-x}$, e $y=\left( 1/2 \right)^{x}$.
Classifique as afirmações em verdadeiras ou falsas:
Mestre Florindo, raizeiro famoso, vende suas garrafas medicinais por 5 reais, na feira de Caruaru.
Se ele vende $q$ unidades, então $R(q) = 5q$, que é a sua função receita.
Se ele tem um custo em torno de $40\%$ de sua receita, o seu custo pode ser estimado pela equação $C(q) = 2q$.
Se, além disso, o mestre gastou $R\$ 900,00$ em materiais para confecção do seu famoso produto, ele deverá vender $300$ garrafas para recuperar o seu custo total.
O lucro do mestre é dado pela função afim $L(q)=5q-900$.
- Verdadeiro.
- Verdadeiro.
- Verdadeiro, pois o lucro total $L(q)$ é $L(q)=R(q)-C(q)-900=3q-900$ e temos que $T(q)=0$ se $q=300$.
- Falso, $L(q)=3q-900$.
Resolva os itens:
- Mostre que $\lim\limits_{x\rightarrow 0^{+}}\left( x\ln x\right) =0$;
- Utilize o item anterior para avaliar $\lim\limits_{x\rightarrow 0^{+}}x^{x}.$
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $x^2e^x\cos{x}$
- $e^x \sinh{x} \cos^2{x}$
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-1}{x^2-x-6}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $-15.1224$ \\
$2.99$ & $-159.12$ \\
$2.999$ & $-1599.12$
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $16.8824$ \\
$3.01$ & $160.88$ \\
$3.001$ & $1600.88$
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x)$ não existe.
Suponha que o número de carteiros necessários para distribuir, em cada dia, as correspondências entre as residências de um bairro seja dado pela função $f(x)=\frac{22x}{500+2x}$, em que $x$ é o número de residências e $f(x)$ é o número de carteiros. Se foram necessários 6 carteiros para distribuir, em um dia, estas correspondências, qual o número de residências desse bairro, que as receberam?
Substituindo $f(x) = 6$ na expressão da função:
$6 = \dfrac{22 x}{500+2x}$
$\Rightarrow 6(500+2x) = 22x$
$\Rightarrow 3000 + 12x = 22x$
$\Rightarrow 10x = 3000$
$\Rightarrow x = 300$ residências.
A trajetória de uma mosca é descrita pelas seguintes equações de movimento $$x=\dfrac{\cos t}{2+\sin t}, \quad y=3+\sin(2t)-2\sin^2t\quad (0\leq t\leq 2\pi).$$
Quais são os pontos mais alto e mais baixo do vôo?
A que distância à esquerda e à direita da origem ela voa?
Dê os domínios e esboce os gráficos de $f+g$ e $\dfrac{g}{f}$ no seguinte caso:
$f(x)=\left\{\begin{array}{ll}
1, & \text{se x é racional} \\
-1, & \text{se x é irracional} \end{array}\right.$
e
$g(x)=\left\{\begin{array}{ll}
-1, & \text{se x é racional} \\
1, & \text{se x é irracional} \end{array}\right.$
Encontre a fração geratriz das dízimas seguintes:
- 2,001111...
- 2,1010101010...
- 1,23333333...
- $\begin{array}{rcl} 2,001111... &=& 2 + 0,00111... \\ &=& 2 + \dfrac{0,111...}{100} \\ &=& 2 + \dfrac{1}{100} \dfrac{1}{9} \\&=& 2 + \dfrac{1}{900} \\ &=& \dfrac{1800+1}{900} \\ &=& \dfrac{1801}{900}. \end{array} $
- $\begin{array}{rcl} 2,101010... &=& 2 + 0,101010... \\ &=& 2 + \dfrac{10}{99} \\ &=& \dfrac{198+10}{99} \\ &=& \dfrac{208}{99}. \end{array} $
- $\begin{array}{rcl} 1,2333... &=& 1,2 + 0,0333... \\ &=& \dfrac{12}{10} + \dfrac{1}{10}\dfrac{3}{9} \\ &=& \dfrac{12}{10} + \dfrac{3}{90} \\&=& \dfrac{108+3}{90} \\ &=& \dfrac{111}{90}. \end{array} $
Mostre que o volume de uma esfera de raio $R$ é $\dfrac{4}{3}\pi R^{3}$.
Estime numericamente os seguintes limites para a função $f(x)=\frac{x^2-11 x+30}{x^3-4 x^2-3 x+18}$:
$\lim\limits_{x \to 3^-} f(x)$
$\lim\limits_{x \to 3^+} f(x)$
$\lim\limits_{x \to 3} f(x)$
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$2.9$ & $132.857$ \\
$2.99$ & $12124.4$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =\infty$.
\begin{tabular}{cc}
$x$ & $f(x)$ \\ \hline
$ 3.1$ & $108.039$ \\
$3.01$ & $11876.4$ \\
\end{tabular}
A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
Ao analisar as duas tabelas, parece que $\lim\limits_{x\to3}f(x) =\infty$.
Sejam $a<b$ dois reais e $p \in \left]a,b \right[$. Determine $r>0$ de modo que $\left]p-r,p+r \right[ \subset \left]a,b \right[$.
Determine o domínio da seguinte função:
$f\left( x\right) =\sqrt{x-\sqrt{x}}$.
$\left\{ x\geq 1\right\} $.
Prove que $\log2$ é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Suponha que existam inteiros $p$ e $q$ tais que $log2=p/q$, com $p/q$ sendo fração irredutível. Use a definição de logaritmo e o teorema fundamental da aritmética para chegar a um absurdo.
Mostre que um polinômio de terceiro grau $p\left( x\right)=ax^{3}+bx^{2}+cx+d$ ($a\neq 0$) sempre possui uma raiz real. Ilustre através de contra-exemplo que isto não é válido para polinômios de grau par, ou seja, para todo $n=2k$ par, existem polinômios de grau $n$ que não possuem raiz real.
Use o Teorema do Confronto para calcular $\lim\limits_{x\rightarrow0^{+}}\sqrt{x} \,e^{\sin\left( \pi/x\right) }\text{.}$
Lembre-se de justificar porque o Teorema do Confronto pode ser útil.
Calcule a seguinte integral:
$ \int_4^{\infty}e^{-\frac{y}{2}}dy$.
Calcule a derivada da função:
$y=\ln \left(\dfrac{\cos \sqrt{x}}{1+\sin \sqrt{x}}\right)$.
$y'=(\sin(\sqrt{x}) + 1) \sec(\sqrt{x}) \left(-\dfrac{\sin(\sqrt{x})}{2 \sqrt{x} (\sin(\sqrt{x}) + 1)} - \dfrac{\cos^2(\sqrt{x})}{2 \sqrt{x} (\sin(\sqrt{x}) + 1)^2}\right)$.
Uma criança empina uma pipa a uma altura de $50$m. O vento age sobre a pipa horizontalmente a uma velocidade de $7$m$/$s em relação à criança. Com que velocidade a criança deve soltar a linha quando a pipa estiver a $100$m de distância?
Calcule o seguinte limite
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right)^{x+2}$.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{1-2^{x}}{1-3^{x}}$.
$0$.
Com base no gráfico, avalie as seguintes integrais:
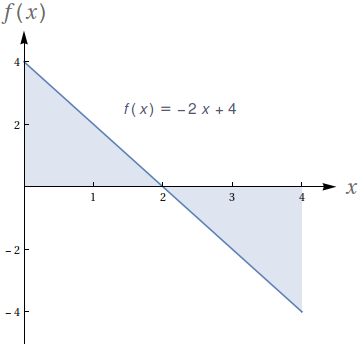
- $\int_0^1 (-2x+4)\ dx$
- $\int_0^2 (-2x+4)\ dx$
- $\int_0^3 (-2x+4)\ dx$
- $\int_1^3 (-2x+4)\ dx$
- $\int_2^4 (-2x+4)\ dx$
- $\int_0^1 (-6x+12)\ dx$
- 3
- 4
- 3
- 0
- $-4$
- 9
Dizemos que duas famílias de curvas são trajetórias ortogonais uma da outra se cada curva de uma família for ortogonal a cada curva da outra. Faça um esboço de gráfico da família de curvas $x^2+(y-c)^2=c^2$ e da família $(x-k)^2+y^2=k^2$ no mesmo plano cartesiano, para alguns valores de $c$ e $k$ reais (se necessário, utilize algum recurso computacional). Mostre que estas famílias (de círculos) são ortogonais uma da outra. (Sugestão: retas tangentes são perpendiculares em um ponto de interseção se as suas inclinações são recíprocas negativas uma da outra.)
Prove que $\sqrt{3}$ é irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Seja $ f(x)=\frac{x^3}{|x^2-1|}.$
- Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
- Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
- Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
- Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
- Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Mostre que a área da superfície de uma esfera de raio $r$ é $4 \pi r^2$.
Use o Teorema do Valor Intermediário para provar que a equação $\tan x= 2-4x$ possui uma solução no intervalo $\bigl(-\frac{\pi}{2}, \frac{\pi}{2}\bigr).$
Considere a função $f(x)=\sin x.$
- Escreva o polinômio de Taylor de $f(x)$ até a terceira ordem.
- Usando o polinômio de Taylor, encontre o valor do seguinte limite: $\lim_{x\rightarrow 0}\frac{\sin x-x+2x}{3x^5}.$
Calcule a derivada da função:
$y=\ln \sqrt{\dfrac{1+\sin x}{1-\sin x}}$.
$y' = \sec x$.
Prove que $\displaystyle\int x^me^xdx=x^me^x-m \displaystyle\int x^{m-1}e^xdx$, para $m$ inteiro positivo.
Teorema de Rolle: Seja $f$ uma função diferenciável em $(a,b)$ e contínua em $[a,b]$; se $f(a)=f(b)=0$, então há pelo menos um ponto $c$ em $(a,b)$ tal que $f'(c)=0$. Verifique que as hipóteses do Teorema de Rolle estão satisfeitas em cada intervalo dado e ache todos os valores de $c$ naquele intervalo que satisfazem a conclusão do teorema.
$\displaystyle f(x)=\dfrac{x^2-1}{x-2},\quad [-1,1]$;
$\displaystyle f(x)=\dfrac{1}{x^2}-\dfrac{4}{3x}+\dfrac{1}{3},\quad [1,3].$
Sejam $f,g:\mathbb{R} \to \mathbb{R}$ funções contínuas tais que $f(a)<g(a)$ e $f(b)>g(b)$. Mostre que existe $c \in (a,b)$ tal que $f(c)=g(c)$.
A região entre a curva $y^2=kx$ e a reta $x=\dfrac{1}{4}k$ é feita girar em torno da reta $x=\dfrac{1}{2}k$. Use camadas cilíndricas para encontrar o volume do sólido resultante.
$\frac{\pi k^4}{48}$
Considere a função \begin{align*} f\left( x\right) =\left\{ \begin{array}{cc} a-x, & \text{se } x<-1 \\ x, & \text{se } -1\leq x<1 \\ \dfrac{2}{x}+b, & \text{se } 1\leq x \end{array} \right. . \end{align*}
- Encontre os limites laterais a direita e a esquerda de $f$ nos pontos $1$ e $-1.$
- Determine os valores de $a$ e $b$ que tornam $f$ contínua em toda a reta.
- Calcule $\lim\limits_{x\rightarrow \infty }f\left(x\right) $ e $\lim\limits_{x\rightarrow -\;\infty }f\left( x\right) $.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}$.
Uma substância radioativa decai de acordo com a fórmula $q(t)=q_0e^{-ct}$, onde $q_0$ é a quantidade inicial da substância, $c$ é uma constante positiva, e $q(t)$ é a quantidade remanescente após o tempo $t$. Mostre que a taxa na qual a substância decai é proporcional a $q(t)$.
A função
$V(x)=x(10-2x)(16-2x),\quad 0<x<5$
modela o volume de uma caixa.
- Determine os valores extremos de $V$.
- Interprete quaisquer valores encontrados no item anterior em termos do volume da caixa.
Avalie os seguintes limites de acordo com o gráfico da função:
$f(x) = x^2\sin (\pi x)$
$\lim\limits_{x\to -\infty} f(x)$
$\lim\limits_{x\to \infty} f(x)$
Identifique as assíntotas verticais e horizontais, caso existam, da função
$f(x)=\frac{2 x^2-2 x-4}{x^2+x-20}$.
Assíntota horizontal em $y=2$; assíntotas verticais em $x=-5$ e $x=4$.
Calcule a derivada da seguinte função:
$f\left( x\right) =5^{x\cos\left( x^{2}\right) }.$
Dê exemplo de uma função definida em $\mathbb{R}$, que não seja contínua em $a$, mas que $\lim\limits_{x \to a^+}f(x)=\lim\limits_{x \to a^-}f(x)$.
Prove que $\tanh^2(x)+\dfrac{1}{\cosh^2(x)}=1$.
Resolva as equações:
- $|x-2|^2-5|x-2| =-6$
- $|x-2|-|x-1| =0$
Calcule a integral $\displaystyle \int \dfrac{x^5-x^4-2x^3+4x^2-15x+5}{(x^2+1)^2(x^2+4)} \, dx$.
Mostre que a equação
\begin{equation*}
x^{26}+x^{2}-320=0
\end{equation*}
possui ao menos uma raiz real positiva e também uma raiz real negativa.
As funções da forma $$f(x)=cx^ne^{-x},\quad x>0,$$ onde $n$ é um inteiro positivo e $c=1/n!$ surgem no estudo estatístico do fluxo de tráfego.
Use um recurso gráfico computacional para gerar o gráfico de $f$ com $n=2,3,4$ e $5$ e faça uma conjectura sobre o número e a localização dos extremos relativos de $f$.
Confirme a sua conjectura usando o teste da derivada primeira.
Prove que $\sqrt{p}$, onde $p$ é primo, é um número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
- Se $f$ é contínua em $[0,1)$ e $[1,2)$, então $f$ é contínua em $[0,2)$.
- A soma de funções contínuas também é contínua
- Se $f$ é contínua em $[a,b]$, então $\lim_{x\to a^-}f(x) = f(a)$.
- Falso
- Verdadeiro
- Falso
Determine uma reta que seja tangente à elipse $x^{2}+2y^{2}=9$ e que intecepte o eixo das ordenadas no ponto de ordenada $9/4$.
Uma lata cilíndrica, sem tampa (mas com fundo), é feita para receber um volume de $900ml$ . Encontre as dimensoes que minimizarão o custo do metal para fazer a lata.
Mostre que o polinômio de Taylor de $f(x)=\sin(x^2)$ de grau $4n+2$ em $0$ é:$$x^2-\dfrac{x^6}{3!}+\dfrac{x^{10}}{5!}-\ldots+(-1)^n\dfrac{x^{4n+2}}{(2n+1)!}.$$ Dica: se $p$ é o polinômio de Taylor de grau $2n+1$ para $\sin$ em $0$, então $\sin x=P(x) + R(x)$, onde $\displaystyle \lim_{x \to 0} \dfrac{R(x)}{x^{2n+1}}=0$. O que isto implica em $\displaystyle \lim_{x \to 0} \dfrac{R(x^2)}{x^{4n+2}}$?
Calcule $f^{(k)}(0)$ para todo $k$.
Em geral, se $f(x)=g(x^m)$, calcule $f^{(k)}(0)$ em termos das derivadas de $g$ em $0$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 1}\ln \dfrac{x^{2}-1}{x-1}$.
$ln2$.
Calcule o limite $\lim\limits_{x\rightarrow -3}\frac{1-x}{\sqrt{x^2+2}}$.
Como a função está definida em $x=-3$, o limite pode ser calculado diretamente por substituição:
$\lim\limits_{x\rightarrow -3}\dfrac{1-x}{\sqrt{x^2+2}} = \dfrac{1-(-3)}{\sqrt{(-3)^2+2}} = \dfrac{4}{\sqrt{11}}$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
x+1, & & \text{ se } x\leq 1 \\
x^2-5, & & \text{ se } x>1
\end{array}
\right.$
$ \lim\limits_{x\to 1^-} f(x)$
$ \lim\limits_{x\to 1^+} f(x)$
$ \lim\limits_{x\to 1} f(x)$
$f(1)$
2
$-4$
Não existe.
2
Ache a área da superfície gerada fazendo girar a curva paramétrica $x=t^2,y=2t,0 \leq t\leq 4$, em torno do eixo $x$.
Calcule $\lim\limits_{x\rightarrow +\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-2$
Se o raio de um círculo cresce à taxa de $30 cm/s$, a que taxa cresce a sua área em relação ao tempo, em função do raio? Dica: Use a fórmula da área do círculo.
Utilize o método das cascas cilíndricas para calcular o volume de um cone circular reto de altura $h$ e base com raio $r$.
Podemos pensar no cone como a superfície de revolução obtida pela rotação de um segmento de reta. A reta em questão pode ser equacionada, por semelhança de triângulos, como
\[
\frac{y}{x}=\frac{h}{r}\text{ ou }y:=y\left( x\right) =\frac{h}{r}x\text{.}%
\]
O segmento de reta é determinado ao restringirmos $x\in\left[ 0,r\right]$. Observamos que, dado $x\in\left[ 0,r\right] $ temos que a altura $h\left( x\right) $ correspondente ao cilindro contido no cone é $h\left( x\right) =h-y\left( x\right) $. Chamando o volume de $V$, pelo método das cascas cilíndricas, obtemos que:
\begin{align*}
V & =\int_{0}^{r}\left( 2\pi x\right) \left( h-\frac{h}{r}x\right) dx\\
& =\int_{0}^{r}2\pi h\left( x-\frac{x^{2}}{r}\right) dx\\
& =2\pi h\left. \left( \frac{x^{2}}{2}-\frac{x^{3}}{3r}\right) \right\vert
_{0}^{r}\\
& =2\pi h\left( \frac{r^{2}}{2}-\frac{r^{3}}{3r}\right) \\
& =2\pi h\frac{r^{2}}{6}\\
& =\frac{\pi hr^{2}}{3}.
\end{align*}
Seja $f$ uma função contínua em $[-1,1]$ sendo que $f(-1) = -10$ e $f(1) = 10$. Existe um valor $-1<c<1$ tal que $f(c) = 11$? Por quê?
Não se pode dizer. O Teorema do Valor Intermediário apenas se aplica, neste caso, para valores entre $-10$ e $10$; como $11$ não pertence a este intervalo, o teorema não nos permite afirmar nada sobre a possibilidade da existência de $c$.
Esboce o gráfico de cada uma das funções abaixo.
$y=|x|+x$
$y=1-x$ se $x\leq 0$ e $y=\sqrt{1-x^{2}}$ se $0\leq x\leq 1$.
Considere:
- Um cilindro $CI_r$ de raio $r$ e altura $r$.
- Um cone $CO_r$ de raio $r$ e altura $r$.
- Uma pirâmide $P_r$ de base quadrada com diagonal de comprimento $2r$ e altura $r$.
Para cada um destes três sólidos, expresse o volume em forma de integral e demonstre que a relação (proporção) entre estes volumes não depende do parâmetro $r$.
Utilize o Teorema de Valor Médio (ou o caso particular do Teorema de Rolle) para mostrar que, para qualquer valor de $c\in\mathbb{R}$, o polinômio $p\left( x\right) =x^{4}+4x+c$ tem no máximo duas raízes reais.
Seja $f(x)=\frac{1+x}{1-x}$. Mostre que $f\left(\frac{1}{1+x}\right)=\frac{2+x}{x}$, $f\left(\frac{1}{1-x}\right)=\frac{x-2}{x}$, $f(-x)=\frac{1}{f(x)}$, $f(1/x)=-f(x)$, $f(f(x))=-1/x$.
Determine a derivada de ordem $n$ de:
- $f(x)=e^x$
- $f(x)=\cos{x}$
- $f(x)=\sin{x}$
- $f(x)=\ln{x}$
Encontre todas as assíntotas horizontais e verticais da função $ f(x)=\frac{\sqrt{3x^2-5x+11}}{4x-7}$.
Uma área retangular em uma fazenda será cercada por um rio e, nos outros três lados, por uma cerca elétrica feita de um fio. Com $800 m$ de fio à disposição, qual é a maior área que você pode cercar e quais são suas dimensões?
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da função $f\left( x\right) =\left\{\begin{array}{cc} e^{-\dfrac{1}{x^{2}}} & \text{se }x\neq 0 \\ 0 & \text{se }x=0 \end{array} \right. $
Calcule:
- $log_2 (8)$
- $log_3 (27)$
- $\log_2(8) = x$
$2^x = 8$
$2^x = 2^3$
$x = 3$. - $\log_3(27) = x$
$3^x = 27$
$3^x = 3^3$
$x = 3$.
Calcule a derivada da seguinte função:
$f\left( x\right) =x^{3}\ln\left( x^{2}\right) .$
Se uma função racional $P(x)/Q(x)$ é tal que o grau do numerador excede o grau do denominador em $1$, então o gráfico de $P(x)/Q(x)$ terá uma assíntota oblíqua, isto é, uma assíntota que não é nem horizontal nem vertical. Para ver por quê, efetuamos a divisão de $P(x)$ por $Q(x)$ obtendo $$ \dfrac{P(x)}{Q(x)}= (ax+b) + \dfrac{R(x)}{Q(x)}, $$ onde $(ax+b)$ é o quociente e $R(x)$ é o resto. Use o fato de que o grau do resto $R(x)$ é menor do que o grau do divisor $Q(x)$ para auxiliá-lo a provar que $$ \lim_{x\to \infty}\left[\dfrac{P(x)}{Q(x)}-(ax+b)\right] = 0 \quad \text{e} $$ $$ \lim_{x\to -\infty}\left[\dfrac{P(x)}{Q(x)}-(ax+b)\right] = 0. $$ Este resultado nos diz que o gráfico da equação $\displaystyle y =P(x)/Q(x)$ "tende" à reta $y=ax+b$ (assíntota oblíqua) quando $x\rightarrow +\infty$ ou $x\rightarrow -\infty$.
Um objeto é atirado do nível do mar para cima com uma velocidade inicial de $100m/s$.
Supondo que a gravidade seja a única força que atua sobre este objeto superestime sua veocidade depois de $5$ segundos. Use $g=10m/s^2$.
Calcule uma estimativa inferior para a altura atingida depois de $5s$.
Calcule o valor de $\frac{2}{0,666 \ldots}$.
$$\begin{array}{rcl} \dfrac{2}{0.666 \ldots} &=& \dfrac{2}{\dfrac{6}{9}} \\ &=& 2 \dfrac{9}{6} \\ &=& \dfrac{9}{3} \\ &=& 3. \end{array}$$
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{3}+2}\right)$
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{2}+2}\right)$
$\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x+2}\right)$
- $-\infty$
- $0$
- $\infty$
Avalie a seguinte integral indefinida:
$\int \sin\theta\ d\theta$
$-\cos \theta+C$
Suco de maracujá (um bom calmante natural) é derramado a uma taxa uniforme de $20$cm$^3/$s em um copo de vidro em forma de um cone truncado (veja a figura abaixo). Se os raios superior e inferior do copo forem de $4$ e $3$cm e a altura $12$cm, com que rapidez estará subindo o nível de suco quando ele estiver na metade do copo? (Sugestão: estenda o copo para baixo para formar um cone.)

Calcule o seguinte limite
$\lim\limits_{x\rightarrow \infty }\left( \dfrac{x+2}{x+1}\right)^{x}$.
$e$.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\left( 5+\dfrac{1}{x}+\dfrac{4}{x^{2}}\right)$.
$5$
Seja $f\left( x\right) =\left| x\right| -x$. Mostre que $f\left( x\right) =0$ para $x\geq 0$ e $f\left( x\right) =-2x$ para $x<0$. Faça o gráfico dessa função.
Calcule o limite $\lim_{x\rightarrow 0} \dfrac{3x+\tan x}{\sin x + \tan^2 x}.$
Temos que:
$\dfrac{3x+\tan x}{\sin x + \tan^2 x}= \dfrac{x}{\sin x}\cdot\dfrac{3+\dfrac{\tan x}{x}}{1+ \dfrac{\sin x}{\cos^2 x}}.$
Lembramos o limite fundamental $\lim_{x\rightarrow 0}\frac{\sin x}{x}=1$ e, além disso, observamos que
\begin{equation*}
\begin{split}
&\lim_{x\rightarrow 0}\dfrac{\sin x}{\cos^2 x}=0 \\
&\lim_{x\rightarrow 0}\dfrac{\tan x}{x}=\lim_{x\rightarrow 0}\dfrac{\sin x}{x}\cdot\dfrac{1}{\cos x}=1.
\end{split}
\end{equation*}
Então:
$\lim_{x\rightarrow 0}\dfrac{3x+\tan x}{\sin x + \tan^2 x}= \lim_{x\rightarrow 0}\dfrac{x}{\sin x}\cdot\dfrac{3+\dfrac{\tan x}{x}}{1+ \dfrac{\sin x}{\cos^2 x}} = 1\cdot\dfrac{3+1}{1+0}=4.$
Calcule o limite $\lim\limits_{x\rightarrow \infty }\log _{3}x$.
$\infty$.
Seja
$$f(x)=\left\{\begin{array}{ll}\dfrac{\sin(x)}{x}, &\text{ se } x\neq0,\\1, &\text{ se } x=0\end{array}\right..$$
Começando com o polinômio de Taylor de ordem $2n+1$ para $\sin x$, junto com a estimativa para o termo de resto $R_{n,1}(x)=\dfrac{f^{(n+1)}(t)}{(n+1)!}(x-a){n+1}$, mostre que:
$$f(x) = \left( 1-\dfrac{x^2}{3!}+\dfrac{x^4}{5!}+\ldots+(-1)^n\dfrac{x^{2n}}{(2n+1)!} + R_{2n,0,f}(x) \right),$$
onde:
$$|R_{2n,0,f}(x)| \leq \dfrac{|x|^{2n+1}}{(2n+2)!}.$$
Considere a função $ f(x)=\left\{\begin{array}{ll} 1-2x &\text{ se} x\ne -1\\0&\text{ se } x=-1\end{array}\right.$.
Trace o gráfico de $f$.
Usando limites laterais, determine se o limite $\lim\limits_{x\rightarrow -1}f(x)$ existe ou não.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Calcule $f^{\prime }\left( x\right)$:
$\left( 1+\sqrt{x}\right) e^{x}\tan x$.
$f'(x) = \left( 1+\sqrt{x}\right) e^{x}\tan x + \dfrac{e^x \tan x}{2 \sqrt{x}} + e^x(\sqrt{x} + 1) \sec^2 x$.
Dê exemplo de uma função definida em $\mathbb{R}$, que não seja contínua em $2$, mas que $\lim\limits_{x \to 2^+}f(x)=\lim\limits_{x \to 2^-}f(x)$.
Um fabricante de refrigerante quer produzir latas cilíndricas para seu produto. A lata dever ter um volume de $360 ml$. Expresse a área superficial total da lata em função do seu raio e dê o domínio da função.
Sejam $r$ o raio da base do cilindro e $h$ a sua altura. O volume $V$ do cilindro é dado por $V=\pi r^2 h$. Como $V=360$, obtemos $\pi r^2 h=360$, isto é, $h=\dfrac{360}{\pi r^2}$. A área superficial $A$ do cilindro é $A=2 \pi r^2+2 \pi r h$. Substituindo $h$ por $\dfrac{360}{\pi r^2}$ chegamos a $A=2 \pi r^2+2 \pi r \dfrac{360}{\pi r^2}$, ou seja, $A=2 \pi r^2+ \dfrac{360}{r}$. O domínio da função $A(r)$ é $\mathbb{R}^+$.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =\dfrac{\ln x}{x}$.
Resolva a inequação $|ax-b|<r$ na variável x, com $r>0$ e $a\neq 0$.
Se $ax-b\geq0$: $|ax-b| = ax-b$, logo $ax-b=r \Rightarrow x = \dfrac{b+r}{a}$.
Se $ax-b<0$: $|ax-b| = -(ax-b)$, logo $-ax+b=r \Rightarrow x = \dfrac{b-r}{a}$.
Portanto $x=\dfrac{b+r}{a}$ ou $x=\dfrac{b-r}{a}$.
Encontre o volume do sólido obtido pela rotação da região limitada por $y=x-x^{2}$ e $y=0$ ao redor da reta $x=2$.
Esboce o gráfico da função $f\left( x\right) =\frac{2x^{2}}{3x^{2}-3}$ . Para fazê-lo, determine:
Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão
Dom$f=\left\{ x\in\mathbb{R}|x\neq\pm1\right\} $
$f\left( x\right) =0$ se, e somente se, $x=0$
A função é par: $f\left( -x\right) =f\left( x\right) $
Usando L'Hopital ou colocando-se $x^{2}$ em evidêncai no numerador e
denominador, obtemos que
\[
\lim_{x\rightarrow\infty}f\left( x\right) =\lim_{x\rightarrow-\infty
}f\left( x\right) =2/3
\]
\begin{align*}
\lim_{x\rightarrow-1^{+}}f\left( x\right) & =-\infty\\
\lim_{x\rightarrow-1^{-}}f\left( x\right) & =\infty\\
\lim_{x\rightarrow1^{+}}f\left( x\right) & =\infty\\
\lim_{x\rightarrow1^{-}}f\left( x\right) & =-\infty
\end{align*}\begin{align*}
f^{\prime}\left( x\right) & =\frac{4x\left( 3x^{2}-3\right)
-2x^{2}\left( 6x\right) }{\left( 3x^{2}-3\right) ^{2}}\\
& =\frac{-12x}{\left( 3x^{2}-3\right) ^{2}}
\end{align*}
logo a derivada é positiva se $x<0$ e negativa se $x>0$, ou seja $f$ é crescente para $x<0$ e decrescente para $x>0$$x=0$ é ponto de máximo da função.
A função não tem pontos de inflexão pois $\pm1\notin
Dom\left( f\right) $
\begin{align*}
f"\left( x\right) & =\frac{-12\left( 3x^{2}-3\right) ^{2}+12x2\left(
3x^{2}-3\right) 6x}{\left( 3x^{2}-3\right) ^{4}}\\
& =\frac{-12\left( 3x^{2}-3\right) +12x2\cdot6x}{\left( 3x^{2}-3\right)
^{3}}\\
& =\frac{-36x^{2}+36+12^{2}x^{2}}{\left( 3x^{2}-3\right) ^{3}}\\
& =\frac{-12x^{2}+12+48x^{2}}{\left( x^{2}-1\right) ^{3}}\\
& =12\frac{3x^{2}+1}{\left( x^{2}-1\right) ^{3}}
\end{align*}
Observando que $3x^{2}+1>0,\forall x$, temos que $f"\left( x\right) >0$ se, e somente se,
$x^{2}-1>0$ se, e somente se, $x>1$ ou $x<-1$ logo $f$ tem concavidade para cima se
$x\in(-\infty,-1)\cup\left( 1,\infty\right) $ e concavidade par baixo se
$x\in\left( -1,1\right) $.Esboço do Gráfico:
Calcule, por meio da definição, o limite $\lim_{x\to 2} x^3-1 = 7$.
Considere $\epsilon >0$ arbitrário. Queremos encontrar $\delta >0$ tal que quando $|x-2|<\delta$, $|f(x)-7|<\epsilon$.
Considere $|f(x)-7|<\epsilon$, lembrando que o objetivo é afirmar algo sobre $|x-2|$:
\begin{gather*}
|f(x) -7 | < \epsilon \\
|x^3-1 -7 |<\epsilon \\
| x^3-8 | < \epsilon \\
| x-2 |\cdot|x^2+2x+4| < \epsilon \\
| x-3 | < \epsilon/|x^2+2x+4| \\
\end{gather*}
Como $x$ está próximo de $2$, podemos considerar $1<x<3$. Portanto
\begin{gather*}
1^2+2\cdot1+4<x^2+2x+4<3^2+2\cdot3+4 \\
7 < x^2+2x+4 < 19 \\
\frac{1}{19} < \frac{1}{x^2+2x+4} < \frac{1}{7} \\
\frac{\epsilon}{19} < \frac{\epsilon}{x^2+2x+4} < \frac{\epsilon}{7} \\
\end{gather*}
Seja $\delta =\frac{\epsilon}{19}$. Então:
\begin{gather*}
|x-2|<\delta \\
|x-2| < \frac{\epsilon}{19}\\
|x-2| < \frac{\epsilon}{x^2+2x+4}\\
|x-2|\cdot|x^2+2x+4| < \frac{\epsilon}{x^2+2x+4}\cdot|x^2+2x+4|\\
\end{gather*}
Assumindo $x$ próximo de $2$, $x^2+2x+4$ é positivo e podemos eliminar o módulo do lado direito da equação.
\begin{gather*}
|x-2|\cdot|x^2+2x+4| < \frac{\epsilon}{x^2+2x+4}\cdot(x^2+2x+4)\\
|x^3-8| < \epsilon\\
|(x^3-1) - 7| < \epsilon,
\end{gather*}
que é o que desejávamos provar.
Derive a função $h\left( x\right) = \int_{\cos 5x}^{x^{7/3}}e^{r}\left( r^{2}+1\right) dr$.
Calcule os limites:
$\lim\limits_{x\to\pi} \frac{3x+1}{1-x}$
$\lim\limits_{x\to\pi} \frac{x^2+3x+5}{5x^2-2x-3}$
$\lim\limits_{x\to\pi} \left(\frac{x-3}{x-5}\right)^7$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ h(t) = \cos t$.
$(-\infty,\infty)$
Seja:
- $\int_0^3{s(t)dt} = 10$
- $\int_3^5{s(t)dt} = 8$
- $\int_3^5{r(t)dt} = -1$ e
- $\int_0^5{r(t)dt} = 11$
A partir destes valores, calcule as seguintes integrais:
- $\int_0^3 \big(s(t) + r(t)\big)\ dt$
- $\int_5^0 \big(s(t) - r(t)\big)\ dt$
- $\int_3^3 \big(\pi s(t) - 7r(t)\big)\ dt$
- Encontre valores para $a$ e $b$ tal que:
$\int_0^5 \big(ar(t)+bs(t)\big) \ dt=0$
- $22$
- $-7$
- $0$
- $b=-\frac{11}{18}a,\quad a\in\mathbb{R}$
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{e^{x^{2}}-1}{x}$.
$0$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(s) = \ln s$.
$(0,\infty)$
Mostre que a função $f\left( x\right) =\left\{ \begin{array}{cc} \dfrac{x^{3}-8}{x-2}, & \text{se }x\neq 2 \\ 12, & \text{se }x=2 \end{array}\right. $ é contínua em seu domínio.
Dê um exemplo de uma função definida em $\mathbb{R}$ que não seja contínua em $0$ mas que $\lim\limits_{x\rightarrow0^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 0^{-}}f\left( x\right) .$
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 5e^x$ e $f(0)= 10$
$5e^x+5$
A região limitada pelo triângulo de vértices $(1,0),$ $(2,1)$ e $(1,1)$ gira em torno do eixo $y$ gerando um sólido $S.$ Calcule o volume de $S.$
Esboce o gŕáfico de $f\left( x\right) =\frac{e^{-x}}{x}$ .Para fazê-lo:
Domínio da função
Zeros e inteceptos
Simetrias
Assíntotas horizontais e verticais
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão
Dom$\left( f\right) =\left\{ x\in\mathbb{R}|x\neq0\right\} $
$f\left( x\right) \neq 0,\forall x$
A função não possui simetrias não triviais
$\lim_{x\rightarrow\infty}\frac{e^{-x}}{x}=0,\lim_{x\rightarrow-\infty}\frac{e^{-x}}{x}=\lim_{x\rightarrow-\infty}-e^{-x}=-\infty$ (este por L'Hôpital), $\lim_{x\rightarrow0^{-}}\frac{e^{-x}}{x}=-\infty$ e $\lim_{\times\rightarrow1^{+}}\frac{e^{-x}}{x}=+\infty$
- \[
f^{\prime}\left( x\right) =\frac{-e^{-x}x-e^{-x}}{x^{2}}=-e^{-x}\frac
{x+1}{x^{2}}%
\]
e temos que
\begin{align*}
f^{\prime}\left( x\right) & >0\Leftrightarrow x<-1\\
f^{\prime}\left( x\right) & <0\Leftrightarrow x>-1
\end{align*}
logo $f$ é crescente para $x<-1$ $\ $e decrescente para $x>-1$ (lembrando que $x\neq0$). O único ponto crítico de $f$ é $x=-1$, o qual é ponto de máximo, pois a derivada passa de positiva a negativa.
\begin{align*}
f"\left( x\right) & =\frac{\left( e^{-x}x-e^{-x}+e^{-x}\right)
x^{2}-\left( -e^{-x}x-e^{-x}\right) 2x}{x^{4}}\\
& =\frac{e^{-x}x^{3}+2e^{-x}x^{2}+2e^{-x}x}{x^{4}}\\
& =\frac{e^{-x}}{x^{3}}\left( x^{2}+2x+2\right)
\end{align*}
Como $e^{-x}$ e $x^{2}+2x+2$ são sempre positivos, temos que $f"\left( x\right) >0$ se $x>0$ e $f"\left( x\right) <0$ se $x<0$, ou
seja, "concavidade para baixo" se $x<0$ e "concavidade para cima" se $x>0$- Esboço do Gráfico:
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(x) = \sin(e^x+x^2)$.
$(-\infty,\infty)$
Mostre que $\pi^e < e^\pi$. Sugestão: Analise a função $ln(x)/x$.
$
ln(e^\pi)=\pi
$
e
$
ln(\pi^e) = e\ ln(\pi)
$
Como $\pi > e$, pode-se escrever $\pi = ae,\ a > 1$. Assim, a primeira equação pode ser escrita como:
$
ln(e^\pi)=ae
$
E a segunda equação como:
$
ln(\pi^e) = e\ ln(a\ e) = e\ ln(a)ln(e)=e\ ln(a)
$
Assim, podemos escrever a razão entre as equações como:
$
\frac{ln(\pi^e)}{ln(e^\pi)} = \frac{ln(a)}{a}
$
Analisando a equação $ln(x)/x$, vemos que para $x>1$ ela é estritamente decrescente, dado que em $x=1$ o denominador é igual a um e o numerador igual a zero e como $\frac{d(ln(x))}{dx}=\frac{1}{x}$ e $\frac{d(x)}{dx}=1$, o denominador cresce mais rapidamente para $x>1$. Assim, como $a>1$, sabemos que:
$
\frac{ln(\pi^e)}{ln(e^\pi)} = \frac{ln(a)}{a} < 1
$
Portanto:
$
ln(\pi^e) < ln(e^\pi)
$
Como $\frac{d(ln(x))}{dx}=\frac{1}{x}>0$ para $x>0$, a função logaritmo é monotônica no intervalo desejado, e portanto podemos concluir que:
$\pi^e < e^\pi$
Se $a$ é racional e $b$ é irracional então podemos afirmar alguma coisa sobre $a+b$ em termos de racionalidade ou irracionalidade?
Podemos afirmar que $a+b$ sempre será irracional.
Determine $f$ de modo que $g(f(x))=x$ para todo $x \in D_f$, sendo $g$ dada por:
- $g(x)=\dfrac{1}{(x-2)^2}$
- $g(x)=\dfrac{1}{\sqrt{x}}$
A velocidade, no tempo $t$, de um objeto de massa $m$ em queda é $v(t)=(mg/k)(1-e^{-(k/m)t})$, onde $k$ é uma constante e $g$ denota a força da gravidade. Calcule $\lim\limits_{m \to \infty}v(t)$ e conclua que $v(t)$ é aproximadamente proporcional ao tempo $t$ se a massa é muito grande.
A velocidade (no instante $t$) de um ponto em movimento sobre uma reta coordenada é $\cos^2 (\pi t)$ $m/s$. Qual a distância percorrida pelo ponto em 5 segundos?
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=x|x|$.
Demonstre que $x^{ln(2)}=2^{ln(x)}$ utilizando propriedades de logaritmos e exponenciais. Utilizando recursos computacionais, observe os gráficos das duas funções, assim como a diferença entre elas. Qual seria uma explicação para o comportamento observado no gráfico de $f(x)=x^{ln(2)}-2^{ln(x)}$?
Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.
$f(x)=\tan x$
$f(x)=x^{2}+1$
Mostre que a função $f\left( x\right) =x^{n}$ é contínua em seu domínio.
O domínio da função é $\mathbb{R}$. Logo, para $x \in \mathbb{R}$, temos:
$\lim_\limits{x \to a} x^n = a^n$
e
$f(a) = a^n$.
Isto é, $\lim_\limits{x \to a} f(x) = f(a)$, e portanto a função é contínua.
Classifique as afirmações a seguir como verdadeiras ou falsas:
Se $ \lim\limits_{x\to 5} f(x) = \infty$, então estamos implicitamente afirmando que o limite em questão existe.
Se $ \lim\limits_{x\to \infty} f(x) = 5$, então estamos implicitamente afirmando que o limite em questão existe.
Se $ \lim\limits_{x\to 1^-} f(x) = -\infty$, então $ \lim\limits_{x\to 1^+} f(x) = \infty$.
Se $ \lim\limits_{x\to 5} f(x) = \infty$, então $f$ tem uma assíntota vertical em $x=5$.
$\infty/0$ não é uma forma indeterminada.
Falsa.
Verdadeira
Falsa
Verdadeira
Verdadeira
Uma escada de $8 m$ está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de $2 m/s$, com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a $3 m$ da parede?
Verifique que, para todo $x>0$, verificam-se as desigualdades:
- $e^{x}>x+1;$
- $\cos x>1-\dfrac{x^{2}}{2};$
- $\sin x<x-\dfrac{x^{3}}{3!}+\dfrac{x^{5}}{5!}.$
Seja $f(x)=\sin{x}+\cos{x}$, $0 \leq x \leq 2 \pi$.
Estude o sinal de $f'(x)$.
Faça um esboço do gráfico de $f$.
Sejam $f$ e $g$ funções contínuas tais que $0 \leq f(x) \leq g(x)$, para $x\geq a$. Utilizando conceitos de área, explique informalmente o porquê dos resultados abaixo serem verdadeiros.
Se $\displaystyle \int_a^{+\infty} f(x) \, dx$ diverge, então $\displaystyle \int_a^{+\infty} g(x) \, dx$ diverge.
Se $\displaystyle \int_a^{+\infty} g(x) \, dx$ converge, então $\displaystyle \int_a^{+\infty} f(x) \, dx$ converge e $\displaystyle \int_a^{+\infty} f(x) \, dx \leq \int_a^{+\infty} g(x) \, dx$.
Obs: estes resultados são chamados de testes de comparação para integrais impróprias.
Seja $f:\mathbb{R} \to \mathbb{R}$ contínua e tal que $f(x).f(f(x))=1$, para todo $x$. Se $f(1000)=999$, calcule $f(500)$.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =xe^{x}\cos x$.
$f'(x) = e^x ((x+1) \cos x - x \sin x)$.
Usando a regra da derivada do produto de duas funções, escolhendo considerar $x e^x$ como uma delas e, consequentemente, $\cos x$ como a outra, obtemos:
\[ (x e^x \cos x)^\prime = (x e^x)^\prime \cdot \cos(x)+ x e^x \cdot (\cos x)^\prime .\]
Para calcular $(x e^x)^\prime$, vamos usar novamente a regra da derivada do produto:
\[(x e^x)^\prime = (x^\prime) \cdot e^x + x\cdot (e^x)^\prime = e^x(1+x),\]
em que usamos que $(x)^\prime=1$ e $(e^x)^\prime=e^x$, além de colocar em evidência o fator comum $e^x$.
Substuindo essas expressões na igualdade inicial, temos que
\[ (x e^x \cos x)^\prime = e^x(1+x)\cos(x) - x e^x \sin x,\]
já que $(\cos x)^\prime = -\sin x$. Ou seja, obtivemos que
\[f'(x) = e^x ((x+1) \cos x - x \sin x).\]
Suponha que $x(t)=e^{0,05t}$ e que $z(t)=e^{0,01t}$. Calcule a taxa de crescimento de $y(t)$, sabendo que $y=x^{\beta }z^{1-\beta }$, com $\beta =1/2$.
Determine os pontos de máximo, de mínimo e de inflexão das seguintes funções (se existirem).
$y = 6x^3 + 15x^2-12x -5$
$f(x) = - 9x^2 + 14x +15$
Encontre a área da região no primeiro quadrante limitada pelos eixos coordenados e pela curva $y=\frac{\sqrt{9-x^2}}{3}.$
Calcule o limite $\lim\limits_{x \to \infty}\dfrac{\ln{x}}{cotg{x}}$.
Determine os pontos de máximo, de mínimo e de inflexão das seguintes funções (se existirem).
$y = 8x^3 -51x^2 -90x +1$
$y = -x^3 – 9x^2 + 81x - 6$
Se uma função par $f(x)$ possui um valor máximo local em $x=c$, pode-se dizer algo sobre o valor de $f$ quando $x=-c$?
Ela também terá um máximo local em $x=-c$. É uma questão de simetria de seu gráfico em relação ao eixo das ordenadas.
Obtenha a fórmula da distância entre dois pontos quaisquer no plano cartesiano. Use o teorema de Pitágoras. Veja o livro: Simmons, página $11$.
Derive a função abaixo e avalie a derivada no ponto indicado:
$f\left( x\right) =e^{2x^{3}}+\cos \left( \sin \left( 3x\right)\right) ;$ avaliar em $f\,^{\prime }\left( 0\right) $.
$f'(x) = 6 e^{2 x^3} x^2 - 3 \sin(\sin(3 x)) \cos(3 x)$.
$f'(0) = 0$.
Mostre, usando a definição, que a função dada por $f(x) = 3x$ é contínua para todo $x$ real.
Classifique as afirmações a seguir em verdadeiras ou falsas.
No conjunto dos números inteiros existe um elemento que é menor do que todos os outros.
O número real representado por 0,37222... é um número racional.
Toda raiz de uma equação algébrica do 2º grau é um número real.
O quadrado de qualquer número real é um número racional.
F
V
F
F
Suponha $g(x) \neq 0$, para todo $x \in Dom(g)$, $L \neq 0$ e $\lim\limits_{x \to p}g(x)=L$. Prove que $\lim\limits_{x \to p}\dfrac{1}{g(x)}=\dfrac{1}{L}$.
Veja Guidorizzi, volume $1$, página $87$.
Seja $ f\left( x\right) =\dfrac{x^{2}+7x+3}{x^{2}}$
Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Uma empresa deseja lançar uma tigela esmaltada de branco por dentro e de vermelho por fora. A camada de esmalte terá $0,5mm$ de espessura antes de ir ao forno. O departamento de produção quer saber a quantidade de cada esmalte que precisará dispor para produzir $5000$ tigelas. Ignorando desperdício e matéria prima não utilizada, dê a sua resposta em litros. Lembre-se de que $1\ cm^3 = 1m\ell$, logo $1\ell=1000cm^3$.

Esboce o gráfico da função $f\left(x\right) =x+\dfrac{1}{x}$.
Escreva a taxa de crescimento de $y$ em termos das taxas de crescimento das variáveis $k$, $l$ e $m$ para os seguintes casos. Assuma $\beta$ como uma dada constante.
- $y=(klm)^{\beta }$
- $y=(kl)^{\beta }(1/m)^{1-\beta }$
Considere um tanque de formato cilíndrico que é utilizado para armazenamento de produtos químicos líquidos, com diâmetro de $10$m. Sua posição é tal que suas seções transversais circulares são verticais. Se o produto químico ocupa o cilindro até $7$m de profundidade, qual porcentagem da capacidade total que está sendo utilizada?
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = x^2+2x-4$ no intervalo $[1,1.5]$.
A raiz aproximada é $x=1.23$.
Os intervalos utilizados são:
$[1,1.5] \quad [1,1.25] \quad [1.125,1.25]$
$[1.1875,1.25]\quad [1.21875,1.25]\quad [1.234375,1.25]$
$[1.234375,1.2421875]\quad [1.234375,1.2382813]$.
Encontre os intervalos da reta real nos quais vale a desigualdade $\left| \frac{2x-3}{x+1}\right| \leq \frac{1}{2}.$
O volume de água em um tanque varia de acordo com a função $V(t)= 10 - |4-2t| -|2t - 6|$, onde $V$ é o volume medido em $m^3$ após $t$ horas, contadas a partir de $8$ h da manhã.
- Atribua um domínio para $V(t)$, considerando que um volume negativo não tem sentido na realidade.
- Faça o gráfico de $V(t)$ com $t$ no domínio estabelecido no item anterior.
- Para que valores de $t$ o tanque está enchendo?
- Para que valores de $t$ o tanque está esvaziando?
- Em qual horário o volume do tanque é constante?
Avalie os seguintes limites de acordo com o gráfico da função:
$f(x) = \frac{1}{e^x+1}$
$\lim\limits_{x\to -\infty} f(x)$
$\lim\limits_{x\to \infty} f(x)$
$\lim\limits_{x\to 0^-} f(x)$
$\lim\limits_{x\to 0^+} f(x)$
Encontre o volume do sólido obtido pela rotação da região limitada pela curva dada em torno do eixo especificado. Esboce a região e o sólido.
$y=x^{2},0\leq x\leq 2,y=4,x-0$ ao redor do eixo $y.$
Resolva a equação $|2x+1|=3$.
Temos dois casos: $2x+1=3$ ou $2x+1=-3$. Resolvendo cada uma dessas equações de primeiro grau obtemos $x=1$ e $x=-2$.
Seja $f:I \rightarrow \mathbb{R}$, contínua, onde I é um intervalo fechado qualquer. Prove que a imagem de $f$ é um intervalo fechado.
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 4x^3-3x^2$ e $f(-1)= 9$
$x^4-x^3+7$
O quociente $(log_4\ x)/(log_2\ x)$ possui um valor constante. Qual valor é este?
Considere uma função contínua $\phi:\mathbb{R} \to \mathbb{R}$ tal que
\[ \forall \quad {x \in \mathbb{R}},\quad \phi(x)\geq x^2.\]
Mostre que existe $a\geq 0$ tal que $\left[a,+\infty\right[$ é o contradomínio de $\phi$.
Demonstre que as retas tangentes às curvas $4y^3-x^2y-x+5y=0$ e $x^4-4y^3+5x+y=0$ na origem são perpendiculares.
Calcule $f^{-1}$ para a função $f(x)=1+3x.$
Seja $y = f(x)$. Então:
$y = 1 + 3 x$.
Isolando $x$:
$3 x = y - 1$
$x = \dfrac{y-1}{3}$.
Logo:
$f^{-1}(x) = \dfrac{x-1}{3}$.
Encontre a área da região limitada pela elipse $x^2+\frac{y^2}{4}=1.$
Primeiramente, escreve-se a equação da elipse na forma $y=\pm f(x)$:
$y=\pm 2\sqrt{1-x^2}$
Observação: Nesta forma, é possível ver mais facilmente que a elipse não apresenta nenhum ponto com $\left\vert x\right\vert >1$.
Se denotarmos $f_1(x)= 2\sqrt{1-x^2}$ e $f_2(x)=- 2\sqrt{1-x^2} $, a área da região limitada pela elipse é portanto
$\int_{-1}^{1}f_1(x)-f_2(x)\,dx=2\int_{-1}^{1}f_1(x)\,dx=2 \left(\sqrt{1-x^2} x+\sin ^{-1}(x)\right)=2\pi$
Quatro números inteiros positivos e distintos, $m, n, p$ e $q$, satisfazem a equação $(7-m)(7-n)(7-p)(7-q)=4$.
Calcule a soma $m+n+p+q$.
A única maneira de escrevermos $4$ como produto de inteiros positivos, a menos de ordem dos fatores, é $4=1 \cdot 1\cdot 2 \cdot 2$. Assim, uma possibilidade é $m=n=6, p=q=5$. Há várias outras possibilidades, mas que não alterarão a soma $m+n+p+q=22$. De fato, se mudássemos os valores de $m,n,p$ e $q$, eles continuaríam sendo $1,1,2$ e $2$ em alguma ordem e a soma não mudaria, já que a adição é comutativa e associativa.
Estude a função $f\left( x\right) =\dfrac{\ln x}{x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Dê o domínio e esboce o gráfico das seguintes funções:
- $f(x)=2/x$
- $f(x)=\dfrac{2}{x-1}$
Esboce o gráfico de $f(x)=x^3-6x^2 +9x+1$, indicando campo de definição, intervalos de crescimento e de decrescimento, assíntotas horizontais, verticiais e inclinadas (se houver), limites no infinito, extremos relativos, estudo da concavidade, pontos de inflexão e reta tangente à curva nos pontos de inflexão.
Calcule a derivada da função:
$y=\dfrac{x\tan 3x}{x^{2}+4}$.
$y' = -(2 x^2 \tan(3 x))/(x^2 + 4)^2 + (\tan(3 x))/(x^2 + 4) + (3 x \sec^2(3 x))/(x^2 + 4)$.
Resolva os itens.
Considere a parábola $y=x^{2}$ e faça a seguinte construção: para cada $a\neq 0$ trace a reta normal à parábola no ponto $\left( a,a^{2}\right) $ e seja $P$ o ponto onde essa normal encontra o eixo $y$. Calcule o limite do ponto $P$ quando $a$ tende a zero.
Calcule o mesmo limite fazendo a mesma construção para a curva quártica $y=x^{4}$ em lugar da parábola.
Calcule, através da definição, o limite $ \lim_{x\to 2} 5 = 5$
Seja $\epsilon >0$ dado. Queremos encontrar $\delta >0$ tal que, quando $|x-2|<\delta$, $|f(x)-5|<\epsilon$. Entretanto, como $f(x)=5$ é uma função constante, a segunda inequação é simplesmente $|5-5|<\epsilon$, o que é sempre verdade. Assim, pode-se escolher um $\delta$ qualquer; arbitrariamente, escolhe-se $\delta =\epsilon$.
Mostre que a equação $\sin x +\cos x =0$ tem exatamente duas raízes reais.
Determine $f'$, $f''$ e $f'''$ sendo $f(x)=4x^4+2x$.
$f'(x)=16x^3+2$, $f''(x)=48x^2$ e $f'''(x)=96x$.
Calcule o limite:
$\lim\limits_{x\rightarrow -\infty }\left( x-\sqrt{x^{2}+4x}\right)$.
$-\infty$.
Encontre as assíntotas horizontais e verticais ao gráfico de $f(x)=\sqrt{\frac{4x^2+1}{x^2-1}}$.
Dados dois números reais distintos $a$ e $b$, podemos definir uma função $f(x)$ que chamaremos "distância ao conjunto $\left\lbrace a,b \right\rbrace$" da seguinte forma: $f(x)$ é igual ao menor dos números $|x-a|$ ou $|x-b|$. Se $a=-b=1$, construa o gráfico de $f(x)$.
Classifique as afirmações a seguir como verdadeiras ou falsas:
- Se $ \lim\limits_{x\to 5} f(x) = \infty$, então estamos implicitamente afirmando que o limite em questão existe.
- Se $ \lim\limits_{x\to 1^-} f(x) = -\infty$, então $ \lim\limits_{x\to 1^+} f(x) = \infty$.
- Se $ \lim\limits_{x\to 5} f(x) = \infty$, então $f$ tem uma assíntota vertical em $x=5$.
- $\infty/0$ não é uma forma indeterminada.
- Falsa.
- Falsa
- Verdadeira
- Verdadeira
Calcule o limite a seguir. Justifique as passagens.
$\lim\limits_{x\rightarrow +\infty }\dfrac{-x^{3}+2}{4x^{2}+89}$
Mostre que, para toda parábola dada por $y=ax^2$, com $a>0$, temos: $$\displaystyle \int_0^b a x^2 \, dx = a \dfrac{b^3}{3}.$$
Use este fato para provar que a área do setor parabólico delimitado por $y=ax^2$ e a reta $y=ab^2$ é igual a quatro terços da área do triângulo com vértices $(0,0)$, $(b,ab^2)$ e $(-b,ab^2)$. Este resultado é um caso particular do Teorema de Arquimedes sobre a área de um setor parabólico.
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
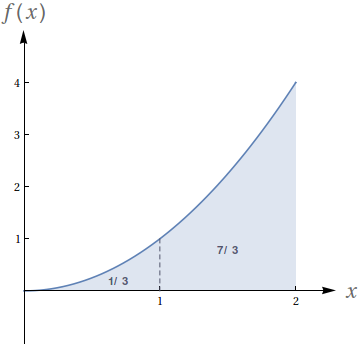
- $ \int_{0}^{2} 5x^2\ dx$
- $ \int_0^2 (x^2+3)\ dx$
- $ \int_{1}^3 (x-1)^2\ dx$
- $ \int_2^4 \big((x-2)^2+5\big)\ dx$
- $40/3$
- $26/3$
- $8/3$
- $38/3$
Seja $f\left( x\right) =\dfrac{x^{3}}{x^{2}-1}$.
Encontre o domínio de $f$, os pontos de intersecção do gráfico de $f$ com os eixos, o sinal de $f$ e analise a simetria de $f$.
Caso existam, determine as assíntotas horizontais, verticais e oblíquas de $f$.
Determine os intervalos de crescimento e decrescimento de $f$, seus pontos de máximo e mínimo locais.
Determine os intervalos onde $f$ tem concavidade para cima e para baixo e os pontos de inflexão.
Esboce o gráfico de $f$ usando as informações obtidas nos itens anteriores.
Considere $\frac{d}{dx}\left( \frac{x^{3}}{x^{2}-1}\right) =x^{2}\frac{x^{2}-3}{\left( x^{2}-1\right) ^{2}}$ e $\frac{d^{2}}{dx^{2}}\left(\frac{x^{3}}{x^{2}-1}\right) =2x\frac{x^{2}+3}{\left( x^{2}-1\right) ^{3}}$
Calcule, pela definição, a derivada das seguntes funções:
- $f\left( x\right) =ax+b$
- $g\left( x\right) =ax^{2}+bx+c$.
1. $f'(x)=a$.
2.$f'(x)=2ax+b$.
Para cada uma das afirmações abaixo, demonstre-a, se verdadeira, ou dê um contra-exemplo, se for falsa.
$x<y\Longleftrightarrow 1/y<1/x$.
$\sqrt{x^{2}}=x,\forall x\in \mathbb{R}$.
Calcule, se existir, o limite $\lim\limits_{x\rightarrow 0}\sqrt x$.
$0$.
Sabemos que a troca de calor entre um objeto a uma temperatura $T$ e o ambiente a uma temperatura $T_{a}$ é proporcional a diferença $(T-T_{a})$. Como a variação de temperatura é proporcional a troca de calor, temos a seguinte equação diferencial para $T\left( t\right) $ (temperatura em função do tempo $t$ ):$\frac{dT}{dt}=-\alpha \left( T-T_{a}\right) ,$ onde a constante $\alpha >0$ depende do calor específico e da condutividade térmica do objeto. Ache a solução dessa equação em função de $\alpha $ assumindo que a temperatura do ambiente $T_{a}=20^{o}C$ e a temperatura inicial $T_{0}=100^{o}C$. Qual é o limite $\lim\limits_{t\rightarrow +\infty }T\left( t\right) $?
Qual o conjunto solução da equação $|x-2|-|x-1|+|x+3|=0$?
Use camadas cilíndricas para encontrar o volume do sólido resultante quando se faz girar a área entre as curvas $y=\cos(x^2)$, $x-0$, $x=\dfrac{1}{2}\sqrt{\pi}$ e $y=0$ em torno do eixo $y$.
Encontre o volume de um tronco de cone circular reto de altura $h$, raio da base inferior $R$ e raio da base superior $r.$
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
2x^2+5x-1, & & \text{ se } x<0 \\
\sin x, & & \text{ se } x\geq 0
\end{array}
\right.$
$ \lim\limits_{x\to 0^-} f(x)$
$ \lim\limits_{x\to 0^+} f(x)$
$ \lim\limits_{x\to 0} f(x)$
$f(0)$
- $-1$
- 0
- Não existe.
- 0
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =e^{x}\sin x\cos x$.
$f'(x) = \dfrac{1}{2} e^x ( \sin (2x) + 2 \cos (2x))$.
Dada a função $f\left( x\right) =$ $\left| x\right| -2x$, calcule $f\left( -1\right) $, $f\left( 1/2\right) $, $f\left( -2/3\right) $. Mostre que $f\left( \left| a\right| \right) =-\left| a\right| $.
Calcule a integral $\int x^{2}e^{x^{3}}dx$.
$\dfrac{e^{x^3}}{3}+C$.
Resolva a equação $\sqrt{9x+4} + \sqrt{3x-4} = 2 \sqrt{3x}$.
Demonstre para todos números reais $a,b$ que $\max(a,b)=\frac{1}{2}(a+b)+\frac{1}{2}|b-a|,$ onde $\max(a,b)=a$ se $a\geq b$ e $\max(a,b)=b$ se $a<b$.
Esboce o gráfico e encontre os zeros da função $f\left( x\right) =\left| x-3\right| -\left| x+4\right| +\left| 5-x\right| $.
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = \cos x -\sin x$ no intervalo $[0.7,0.8]$.
A raiz aproximada é $x=0.78$.
Os intervalos utilizados são:
$[0.7,0.8] \quad [0.75,0.8] \quad [0.775,0.8]$
$[0.775,0.7875]\quad [0.78125,0.7875]$
(Alguns passos a mais mostrariam que $0.79$ é melhor, dado que a raiz é $\pi/4 \approx 0.78539$.)
Encontre $f(x)$ que satisfaça o seguinte problema de valor inicial:
$f'(x) = 3x+2$ e $f(0)= 7$
$\frac{3 x^2}{2}+7 x+7$
Construa os gráficos das funções indicadas e calcule os limites:
$ f(x)=x^2$ quando $x\rightarrow\infty$
$ h(x)=3x^5$ quando $x\rightarrow -\infty$
$g(y)=\tan^{-1}(y)$ quando $y\rightarrow\infty$
$f(x)=\frac{1}{x}$ quando $x\rightarrow -\infty$
$f(x)=\frac{1}{x^7}$ quando $x\rightarrow \infty$
$f(x)=\frac{1}{x^{-2}}$ quando $x\rightarrow \infty$
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\cos^{2}\left( x\right) +\sin^{2}\left(x\right) }{\sqrt{x^{3}+1}}.$
Suponha que em qualquer instante $t$ (em segundos) a corrente $i$ (em amperes) em um circuito de corrente alternada é $i = 2\ cos\ t+2\ sin\ t$. Qual a corrente de pico (magnitude máxim para este circuito?
Um tanque contém 5000 litros de água pura. Água salgada contendo $30$g de sal por litro de água é bombeada para dentro do tanque a uma taxa de $25$ L$/$min. Considerando o tempo $t$ em minutos, mostre que a concentração de sal $C$ em função de $t$ (em gramas por litro) é dada por:$$C(t) = \dfrac{30 t}{200+t}.$$
O que acontece com a concentração para um tempo muito grande, isto é, para $t \to \infty$?
Sabemos que limites que tomam a forma indeterminada ``$\infty-\infty$" exigem um pouco mais de trabalho para serem calculados. Calcule, de forma adequada, o limite $\lim\limits_{x\rightarrow\infty}\left(\sqrt{2x^2-7}-x\right)$.
Se uma massa cai uma distância $s(t)$ em $t$ segundos, e $s'$ é proporcional a $s$, então mostre que $s$ não pode ser uma função da forma $s(t)=ct^2$.
Se $s(t)=\dfrac{a}{2} t^2$, mostre que $s''(t)=a$ (a aceleração é constante) e que $[s'(t)]^2=2as(t)$ (observe que obtivemos isso trocando ligeiramente a expressão de $s(t)$).
Assumindo $a=9,8$m$/$s$^2$ (aceleração da gravidade), quantos segundos você tem para fugir de um lustre em um castelo que cai de um teto de $100$m? Se você não conseguir fugir, quão rápido o lustre vai estar quando te atingir? A que altura estava o lustre quando estava se movendo com metade desta velocidade?
Enuncie o Teorema Fundamental da Álgebra (de Gauss).
"Qualquer polinômio $p(z)$ com coeficientes complexos de uma variável e de grau $n \geq 1$ tem alguma raiz complexa."
Uma alternativa ao método das frações parciais é calcular integrais da forma
$$\displaystyle \int \dfrac{1}{ax^2+bx} \, dx$$
utilizando a substituição $u=a+\dfrac{b}{x}$. Mostre que com essa substituição a integral se torna:
$$\displaystyle \int \dfrac{1/x^2}{a+b/x} \, dx.$$
Substitua as interrogações por expressões envolvendo $\epsilon, x_0$ e $y_0$ de modo que a afirmação abaixo seja verdadeira. Se $y_0 \neq 0$, $|y-y_0|<??$ e $|x-x_0|<??$, então $y \neq 0$ e $\left| \dfrac {x}{y}-\dfrac{x_0}{y_0}\right|<\epsilon$.
Resolva os itens:
- Prove que existe $r>0$ tal que $\cos{x}-1<\dfrac{\sin{x}}{x}-1<0$ para $0<|x|<r$.
- Calcule $\lim\limits_{x \to 0}\dfrac{x-\sin{x}}{x^2}$.
Um toro em forma de um cilindro circular reto de raio $a$ está apoiado sobre um lado. Remove-se do toro uma cunha fazendo-se um corte vertical e outro corte a um ângulo de 45°; ambos os cortes se interceptam no centro do toro (veja a figura). Ache o volume da cunha.

Determine $f'$, $f''$ e $f'''$ sendo $f(x)=4x^4+2/x$.
Sejam $f$ e $g$ funções contínuas em $[a,b]$ e diferenciáveis em $(a,b)$. Prove: se $f(a)=g(a)$ e $f(b)=g(b)$, então há um ponto $c$ em $(a,b)$ onde $f'(c)=g'(c)$.
Esboce o gráfico da funçao $f\left( x\right) =\frac{x^{2}}{x-1}$, indicando domínio, limites laterais e no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.
Um funil de volume especificado deve ter a forma de um cone circular reto. Encontre a razão da altura pelo raio da base para que a quantidade de material empregado em sua fabricaçao seja a menor possível.
Esboce o gráfico de cada uma das funções abaixo.
$y=\frac{2|x+1|}{3}$
$y=\sqrt{5-x^{2}}$
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =x^{2}+x$.
$f'(x)=2x + 1$.
Prove que se $f$ é integrável em $\left[a,b\right]$ e $m \leq f(x) <M$ para todo $x$ em $\left[a,b\right]$, então $\displaystyle\int_{a}^{b}f(x)dx=(b-a)\mu$ para algum $\mu$ tal que $m < \mu <M$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\tan\left( x\right) \arcsin\left( x^{2}\right).$
Calcule a seguinte integral:
$ \int_0^{2\sqrt{3}}\frac{x^3}{\sqrt{16-x^2}}dx$.
A figura abaixo mostra o gráfico do polinômio $\displaystyle y=\dfrac{1}{10}x^5(x-1)$ gerado no software Mathematica$^\textrm{TM}$ usando uma janela de $[-2;2,5]\times[-1;5]$.
Mostre que a escolha da escala vertical faz com que o computador perca importantes aspectos do gráfico. Descreva quais são os aspectos perdidos e faça o seu próprio esboço indicando-os.
Utilizando a aproximação $ln\ 2 \approx 0,7$, pode-se derivar uma regra popular, conhecida como regra dos 70, que diz: "Para estimar quantos anos uma determinada quantia em dinheiro dobre ao ser investida a uma porcentagem $r$ composta continuamente, divida $r$ por $70$". Por exemplo, uma quantia em dinheiro investida a $7\%$ dobrará em cerca de $70/7=10$ anos. Se, em vez disso, você quiser que ela dobre em $5$ anos, deve investí-la a $70/5=14\%$. Mostre a dedução da regra dos 70.
Uma das propriedades da potenciação é que $a^0=1$, $\forall a \neq 0$. Além disso, também sabe-se que $0^n=0,\quad \forall n>0$. A extensão destas regras para incluir, respectivamente, $a=0$ e $n=0$ levam a resultados conflitantes quanto ao valor de $0^0$(O que não implica em contradição, dado que as propriedades não foram estabelecidas para $a=0$ e $n=0$).
Sendo assim, avalie $x^x$ para $x=0,1;0,01;0,001;\ldots$. Qual o padrão observado? Com o auxílio de recursos computacionais, observe o gráfico de $y=x^x$ para valores positivos de $x$, se aproximando da origem. Para qual valor a função parece convergir para $x=0$?
Sugestão: Procure, no site, o exercício 1528. Compare os resultados obtidos.
Esboce o gráfico das funções $f(x) = \log_2 x $ e $ f(x) = \log_\frac{1}{2} x$ num mesmo sistema cartesiano. Qual relação você observa entre os gráficos? Explique.
Foi pedido a um torneiro mecânico que fabricasse um disco de metal circular com área de $1000cm^2$.
- Qual o raio do disco produzido?
- Se for permitido ao torneiro uma tolerância do erro de $\pm 5 cm^2$ na área do disco, quão próximo do raio ideal da parte (a) o torneiro precisa controlar o raio?
- Em termos da definição $\epsilon, \delta$ de $\lim\limits_{x \to a} f(x)=L$, o que é $x$? O que é $f(x)$? O que é $a$? O que é $L$? Qual valor de $\epsilon$ é dado? Qual o valor correspondente de $\delta$?
$3/2$
Dois carros estão se encaminhando em direção a um cruzamento em ângulo reto, um seguindo a direção leste a uma velocidade de $90 km/h$ e o outro seguindo a direção sul, a $60 km/h$. Qual a taxa segundo a qual eles se aproximam um do outro no instante em que o primeiro carro está a $0,2 km$ do cruzamento e o segundo a $0,15 km$?
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f\,^{\prime \prime }\left( x\right) = 12\sin 2x+\cos 3x+1,\;f\,^{\prime}\left( 0\right) =1\text{ e }f\left( 0\right) =0\text{ .} \end{equation*}
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\log _{3}x$.
$\infty$.
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\dfrac{\left( x-3\right) }{x^{2}+1}<0$.
Determine a área da superfície gerada pela rotação da curva a seguir em torno do eixo indicado.
$y=\sqrt{2}$, $3/4\leq x \leq 15/4$, eixo $x$
Utilize uma substituição trigonométrica para mostrar que $\displaystyle \int \dfrac{u^2}{\sqrt{u^2 - a^2}} \, du = \dfrac{u}{2}\sqrt{u^2-a^2}+\dfrac{a^2}{2} \ln | u + \sqrt{u^2-a^2} | + C $.
A Lei de Ohm para circuitos elétricos, afirma que a queda de tensão em um resistor $R$ sob corrente $I$ é $V=RI$. Uma empresa recebeu pedidos de fornecimento de resistores para um circuito como o da figura a seguir. Neste circuito, $V=120V$ e, para atender as especificações de segurança e de funcionamento desejado do circuito, a corrente deve ser $I=5\pm0,1A$. Em que intervalo $R$ deve ficar para que $I$ esteja dentro da margem de segurança?
Pela Lei de Ohm, conseguimos escrever que $I=\frac{V}{R}$. Para $V=120V$ fixo, a corrente depende portanto apenas do valor da resistência, sendo inversamente proporcional a esta.
A corrente deve estar no intervalo $4,9 \leq I \ leq 5,1$. Temos que $R_{max}=\frac{120}{I_{min}}\approx 24,49$ e $R_{min}=\frac{120}{I_{max}}\approx 23,53 \Omega$.
Portanto, $23,53 \leq R \leq 24,49$.
- $\lim\limits_{x\rightarrow -1}\sqrt[3]{\dfrac{x^{3}+1}{x+1}}$
- $\lim\limits_{x\rightarrow 1}\dfrac{\sqrt{x^{2}+3}-2}{x^{2}-1}$
- $\lim\limits_{x\rightarrow 1}\dfrac{\sqrt[3]{3x+5}-2}{x^{2}-1}$
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =1/x^{2}$.
$f'(x) = -\dfrac{2}{x^3}$.
Mostre que função $f\left( x\right) =\dfrac{1}{x^2}$ é contínua em seu domínio.
Você está planejando construir uma caixa retangular aberta com uma folha de papelão de $8 \times 15 pol$ recortando quadrados congruentes dos vértices da folha e dobrando suas bordas para cima. Quais são as dimensões da caixa de maior volume que você pode fazer dessa maneira? Qual é o volume?
Seja $a>0$. Esboce o gráfico das funções $f(x) = \log_a x $ e $ f(x) = \log_\frac{1}{a} x$ num mesmo sistema cartesiano. Qual relação você observa entre os gráficos? Explique.
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right) ^{x+2}$
$\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{2x}\right) ^{x} $
$\lim\limits_{x\rightarrow \infty }\left( \dfrac{x+2}{x+1}\right) ^{x}$
Com base no gráfico, avalie as seguintes integrais:
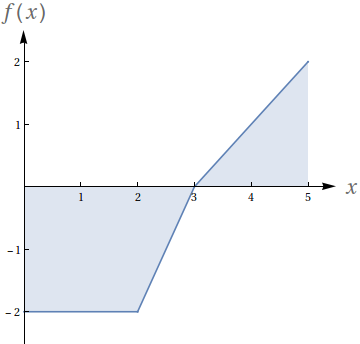
- $\int_0^2 f(x)\ dx$
- $\int_0^3 f(x)\ dx$
- $\int_0^5 f(x)\ dx$
- $\int_2^5 f(x)\ dx$
- $\int_5^3 f(x)\ dx$
- $\int_0^3 -2f(x)\ dx$
- $-4$
- $-5$
- $-3$
- 1
- $-2$
- 10
O que é um problema de valor inicial?
Prove que $\sqrt{2}$ é irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Defina $\displaystyle \lim_{x \to a^+} f(x) = \infty$ e $\displaystyle \lim_{x \to a^-} f(x) = \infty$. Se estiver muito difícil, escreva em palavras.
Mostre que $\displaystyle \lim_{x \to 0^+} \dfrac{1}{x} = \infty$.
Mostre que $\displaystyle \lim_{x \to 0^+} f(x) = \infty$ se e somente se $\displaystyle \lim_{x \to \infty} f\left(\dfrac{1}{x}\right) = \infty$.
Mostre que a a área lateral $S$ de um cone circular reto de altura $h$ e raio da base $r$ é $S=\pi r \sqrt{r^2+h^2}$.
Calcule a integral $\displaystyle \int \dfrac{dy}{\sqrt{y} e^{\sqrt{y}}}$.
Seja $f(x)=cotg{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
$f'(x)=-cossec^2(x)$ e $f'\left(\dfrac{\pi}{4}\right)=-2$.
Prove que a soma de um racional com um irracional é um irracional.
Determine uma reta que seja paralela a $x+y=1$ e tangente à curva $x^{2}+xy+y^{2}=3$
Calcule:
- $log_3 (36) +log_3 (6)$
- $8^{\frac {2} {3}}+\sqrt{100}+2^{2^3}+2^{(2^3)}$
Avalie a seguinte integral indefinida:
$\int (\sec x\tan x + \csc x\cot x)\ dx$
$\sec x - \csc x+C$
A altura de um corpo em movimento vertical é dada por
$s = -\frac{1}{2}gt^2+v_0t+s_0,\quad g>0$
com $s$ em metros e $t$ em segundos. Determine a altura máxima do corpo em função da velocidade inicial $v_0$, da aceleração da gravidade $g$ e da posição inicial $s_0$.
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
\frac{x^2+5x+4}{x^2+3x+2}, & & \text{se } x\neq -1\\
3, & &\text{se } x=-1
\end{array}\right.$
- $x=-1$
- $x=10$
- Sim.
- Sim.
Um ponto no plano cartesiano é chamado ponto misto se uma de suas coordenadas é racional e a outra irracional. Encontre todos os polinômios com coeficientes reais tais que seus gráficos não contêm nenhum ponto misto.
Calcule os seguintes limites:
$\lim\limits_{x\rightarrow \infty }\left( 5-3x+4x^{2}-x^{3}\right)$
$\lim\limits_{x\rightarrow \infty }\dfrac{5x^{3}-6x-3}{6x^{3}+2}$
- $-\infty$
- $5/6$
Estude a função $f\left( x\right) =e^{x}-e^{3x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Considere a função $f(x) = 2^x+10$. Calcule os seguintes limites e, depois, discuta se a função $f(x)$ tem assíntotas horizontais.
$\lim\limits_{x\to -\infty} f(x)$.
$\lim\limits_{x\to \infty} f(x)$.
1. $10$.
2. $\infty$
Possui assíntota horizontal de equação $y=10$,
Uma caixa com base quadrada e sem tampa deve ser feita a partir de uma folha de metal, de forma que o seu volume seja de $500$ cm$^3$. Seja $S$ a área da superfície da caixa e $x$ o comprimento de um lado da base quadrada. Mostre que $\displaystyle S=x^2+2000/x$, para $x>0$, e esboce o gráfico de $S$ em função de $x$ para este caso.
Prove que $\sinh'(x)=\cosh(x)$.
Calcule a seguinte integral:
$\int_{0}^{\infty}{\frac{dx}{x^2+1}}$
Para resolver a integral, utilizamos a substituição $x=\tan(u)$, com $dx=\frac{du}{cos^2(u)}$. A integral equivalente, com os limites de integração escolhidos no primeiro quadrante, é:
$\int_0^{\frac{\pi}{2}}\frac{du}{\cos^2(u)\left(\tan^2(u)+1\right)}=\int_0^{\frac{\pi}{2}}\frac{du}{1}=u\rvert_0^{\frac{\pi}{2}}=\frac{\pi}{2}$
Dado que os números no gráfico representam o valor das áreas demarcadas, avalie as seguintes integrais:
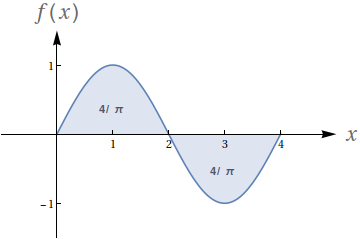
- $ \int_0^2 f(x)\ dx$
- $ \int_2^4 f(x)\ dx$
- $ \int_0^4 f(x)\ dx$
- $ \int_0^1 f(x)\ dx$
- $4/\pi$
- $-4/\pi$
- $0$
- $2/\pi$
Esboce os gráficos de $f(x) =x^2-1$ e $ g(x) = x^2 +1.$
Demonstre que $\int_{-\infty}^{\infty}{f(x)\ dx}$ pode ser diferente de $\lim\limits_{b \rightarrow \infty }\int_{-b}^{b}{f(x)\ dx}$.
Para isto, mostre que
$\int_{0}^{\infty}{\frac{2x\ dx}{x^2 +1}\ dx}$
diverge, e, portanto,
$\int_{-\infty}^{\infty}{\frac{2x\ dx}{x^2 +1}\ dx}$
também diverge. Depois, mostre que
$\lim\limits_{b \rightarrow \infty }\int_{-b}^{b}{\frac{2x\ dx}{x^2 +1}\ dx}=0$
Calcule a seguinte integral:
$\int{x^2e^{2x}dx}.$
$\dfrac{1}{4}e^{2x}(2x^2-2x+1)+C$.
O que significa dizer, em termos de limites, que uma função é "bem comportada"?
Mostre que qualquer reta tangente ao gráfico da hipérbole $xy=a^2$ determina com as assíntotas um triângulo de área igual a $2a^2$.
Uma partícula tem sua posição variando com o tempo de acordo com a relação $s(t)=-2\sin(t)+3\cos(t)$ , onde $s$ é dado em metros e $t$ em segundos.
- Encontre a velocidade da partícula no instante $t$.
- Encontre a velocidade da partícula no instante $t=3$ segundos.
1. $v(t)=-3\sin(t)-2\cos(t)$.
2. $v(3)=-3\sin(3)-2\cos(3)$.
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
\cos x, & & \text{ se } x<\pi \\
\sin x, & & \text{ se } x\geq \pi
\end{array}
\right.$
$ \lim\limits_{x\to \pi^-} f(x)$
$ \lim\limits_{x\to \pi^+} f(x)$
$ \lim\limits_{x\to \pi} f(x)$
$f(\pi)$
- $-1$
- 0
- Não existe.
- 0
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow \infty }\dfrac{-x^{4}-2x+1}{2x^{4}+2x+3}$.
Perguntei a idade de minha professora de Matemática. Ela me contou e falou também a idade da filha, mas disse isso de modo enigmático por meio da expressão: "A soma de minha idade com a da minha filha é 44 anos. Dez anos atrás, eu tinha o triplo da idade dela."
- "Traduza" a primeira frase da expressão da professora por uma equação, representando por $x$ a idade da professora e por $y$, a idade de sua filha.
- Faça o mesmo com a segunda frase.
- Resolva o sistema obtido e dê a idade da professora e a de sua filha.
Seja $x$ a idade da professora e $y$ a idade da filha. Temos, portanto
- $x+y=44$
- $x-10=3(y-10)$, ou, reescrevendo com as incógnitas do lado esquerdo, $x-3y=-20$
- Resolver $\begin{pmatrix} 1 & 1 \\ 1 &-3 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 44 \\ -20 \end{pmatrix}$ nos dá $\begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 28 \\ 16 \end{pmatrix}$
Mostre, usando a definição de limite, que $\displaystyle \lim_{x\to 5} 3-x = -2$
Seja $\epsilon >0$ dado. Queremos encontrar $\delta >0$ tal que, quando$|x-5|<\delta$, $|f(x)-(-2)|<\epsilon$.
Considerando $|f(x)-(-2)|<\epsilon$:
\begin{gather*}
|f(x) + 2 | < \epsilon \\
|(3-x) + 2 |<\epsilon \\
| 5-x | < \epsilon \\
-\epsilon < 5-x < \epsilon \\
-\epsilon < x-5 < \epsilon. \\
\end{gather*}
Isso implica que podemos estabelecer $\delta =\epsilon$. Portanto:
\begin{gather*}
|x-5|<\delta \\
-\delta < x-5 < \delta\\
-\epsilon < x-5 < \epsilon\\
-\epsilon < (x-3)-2 < \epsilon \\
-\epsilon < (-x+3)-(-2) < \epsilon \\
|3-x - (-2)| < \epsilon,
\end{gather*}
que é o que buscávamos provar.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow0}\frac{cotg (2x)}{cossec (x)}$.
$1/2$.
Dois automóveis movem-se em direção a um cruzamento em ângulo reto, um dirigindo-se para o leste à razão de $72 km/h$ e o outro para o sul à razão de $54 km/h$. Com que velocidade os carros aproximam-se um do outro no instante em que o primeiro está a $400 m$ e o segundo a $300 m$ do cruzamento?
A afirmação: $`` \lim\limits_{x\rightarrow p^+} f(x) = \lim\limits_{x\rightarrow p^-} f(x)\Rightarrow f \mbox{ contínua em } p. "$ é verdadeira ou falsa? Justifique.
É falsa. Só seria verdadeira se o valor dos limites laterais fosse igual a $f(p)$.
Prove que $\displaystyle\int x^me^xdx=x^me^x-m \displaystyle\int x^{m-1}e^xdx$.
Seja $f(x)=\left\{\begin{array}{ll}
x+1, & \text{se } x<2 \\
1, & \text{se } x \geq 2
\end{array}\right.$
- $f$ é contínua em $2$. Por quê?
- $f$ é derivável em $2$. Por quê?
1. Não.
2. Não
Use o Teorema Fundamental do Cálculo para calcular a derivada da função $g(x)={ \int_x^{x^2}\cos (t^2)dt}$.
Lembrando que o comprimento do traçado de um gráfico de uma função $f(x)$ no intervalo $[a,b]$ é dado por $\int_a^b \sqrt{1+(f'(x))^2} dx$, calcule o comprimento da circunferência de raio $r=1$.
Estude a função $f\left( x\right) =\sqrt{x^{2}-4}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Calcule a integral a seguir utilizando substituições trigonométricas:
$\int{\frac{x^3 dx}{\sqrt{x^2+4}}}$
$\dfrac{1}{3}(x^2-8)\sqrt{x^2+4}+C$.
Usando as fórmulas pra $\sin(2x), \cos(2x), \sin(3x)$ e $\cos(3x)$, calcule $\sin\left(\dfrac{\pi}{4}\right)$, $tg\left(\dfrac{\pi}{4}\right)$, $\sin\left(\dfrac{\pi}{6}\right)$ e $\cos\left(\dfrac{\pi}{6}\right)$.
$\sin\left(\dfrac{\pi}{4}\right) = \dfrac{1}{\sqrt{2}}$.
$tg\left(\dfrac{\pi}{4}\right) = 1$.
$\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$.
$\cos\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}$.
Uma escada de $5 m$ de altura está apoiada numa parede vertical. Se a base da escada é arrastada horizontalmente da parede a $3 m/s$, a que velocidade desliza a parte superior da escada ao longo da parede quando a base encontra-se a $3 m$ da parede?
Calcule a derivada da seguinte função:
$f\left( x\right) =\frac{\sqrt{x^{3}+1}}{\left( x^{2}+1\right) ^{4}}.$
Utilizando o gráfico, avalie os seguintes limites para a função
$ f(x) = \frac{1}{(x-3)(x-5)^2}$.
$ \lim\limits_{x\to 3^-} f(x)$
$ \lim\limits_{x\to 3^+} f(x)$
$ \lim\limits_{x\to 3} f(x)$
$ \lim\limits_{x\to 5^-} f(x)$
$ \lim\limits_{x\to 5^+} f(x)$
$ \lim\limits_{x\to 5} f(x)$
- $-\infty$
- $\infty$
- O limite não existe
- $\infty$
- $\infty$
- $\infty$
Existe uma curva continuamente derivável $y=f(x)$ cujo comprimento ao longo do intervalo $0\leq x\leq a$ seja sempre $\sqrt{2}a$?
A soma dos perímetros de um triângulo equilátero e de um quadrado é $10$. Ache as dimensões do triângulo e do quadrado que produzem a área total mínima.
Para uma população de elefantas africanas, o peso $W(t)$ (em quilogramas) e a idade $t$ (em anos) pode ser aproximado por uma função de crescimento de Fertanlanffy $W$ tal que $W(t)=2600(1-0,51e^{-0,075t})^3$.
- Dê uma aproximação do peso e da taxa de crescimento de um elefante recém-nascido.
- Supondo que uma elefanta adulta pese $1800$ $kg$, estime sua idade e sua taxa de crescimento presente.
- Calcule e interprete $\lim\limits_{t \to \infty}W(t)$.
- Mostre que a taxa de crescimento é máxima entre as idades de $5$ e $6$ anos.
Como o parabolóide é obtido pela rotação ao redor do eixo $y$ temos que o raio $r:=d/2=4$ corresponde a variação de $x$ e a altura corresponde a variação de $y$, ou seja, para $x=4$ devemos ter $y=ax^{2}=4$ donde obtemos que $a=y/x^{2}=4/4^{2}=1/4$, e consideramos a parábola $y=\frac{x^{2}}{4}$.
Como o parabolóide é obtido pela rotação ao redor do eixo $y$ devemos considerar $x$ como funçao de $y$, ou seja, $x=x\left( y\right) =2\sqrt{y}$. Temos então que:
\begin{align*}
x^{\prime}\left( y\right) & =\frac{1}{\sqrt{y}}\\
\sqrt{1+\left( x^{\prime}\left( y\right) \right) ^{2}} & =\sqrt
{1+\frac{1}{y}}=\frac{\sqrt{y+1}}{\sqrt{y}}%
\end{align*}
Temos então que a área $S$ da superfície é dada por:
\begin{align*}
S & =\int_{0}^{4}2\pi\left( 2\sqrt{y}\right) \frac{\sqrt{y+1}}{\sqrt{y}%
}dy\\
& =4\pi\int_{0}^{4}\sqrt{y+1}dy
\end{align*}
Substituindo $u=y+1,~du=dy$ obtemos:
\begin{align*}
S & =4\pi\int_{1}^{5}\sqrt{u}du\\
& =4\pi\frac{2}{3}\left. u^{3/2}\right\vert _{1}^{5}\\
& =\frac{8\pi}{3}\left( 5^{3/2}-1\right)
\end{align*}
Defina ``$\displaystyle \lim_{x \to -\infty} f(x) = l$''.
Ache $\displaystyle \lim_{x \to -\infty} \dfrac{a_n x^n + \ldots + a_0}{b_m x^m + \ldots + b_0}$.
Mostre que $\displaystyle \lim_{x \to \infty} f(x) = \displaystyle \lim_{x \to -\infty} -f(x)$.
Mostre que $\displaystyle \lim_{x \to 0^-} \dfrac{1}{f(x)} = \displaystyle \lim_{x \to -\infty} f(x)$.
Calcule $F'(x)$ sendo $F(x)$ igual a:
- $xe^x\cos{x}$
- $e^x \sin{x} \cos{x}$
Resolva a equação $\displaystyle \frac{x}{1-x} + \frac{x-2}{x}-1 = 0$.
Seja $f\left( x\right) =x^{3}+3x.$
Estude o sinal de $f^{\prime }(x).$
Calcule $\lim\limits_{x\rightarrow +\infty }f\left(x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) .$
Utilizando as informações acima esboce o gráfico de $f\left( x\right) .$
A atmosfera da Terra absorve aproximadamente $32\%$ da radiação proveniente do Sol. A Terra também emite radiação (a maior parte em forma de calor) e a atmosfera absorve aproximadamente $93\%$ dessa radiação. A diferença entre a radiação que entra na Terra e a que sai é chamada efeito-estufa. Modoficações nesse equilíbrio podem afetar o clima da Terra. Seja $I_0$ a intensidade da radiação do Sol e $I$ a intensidade depois de percorrer uma distância $x$ na atmosfera. Se $p(h)$ é a densidade da atmosfera na altitude $h$, então a espessura ótica é $f(x)=k \displaystyle\int_0^x p(h) dh$, onde $k$ é uma constante de absorção e $I$ é dada por $I=I_0e^{-f(x)}$. Mostre que $dI/dx=-kp(x)I$.
Mostre, usando a definição, que a função $f\left( x\right) =ax+b$ é contínua em seu domínio.
Derive a função $p\left( x\right) = \int_{2x^{-5}}^{\sin 3x}\left( v^{3}-2\right) \cos vdv$.
Considere uma força $f(x)$ que atua sobre um corpo no ponto $x$. A força varia em função do ponto $x$, segundo a função $f(x)=x^5 \sqrt{x^3+1}$. Determine o trabalho realizado se o corpo se move do ponto $x=0$ ao ponto $x=1$.
Compute a derivada $f''(x)$ de $f(x)=\frac{x^2+1}{x}$.
$f''(x)=\dfrac{2}{x^3}$.
Uma importante aplicação do Teorema do Valor Intermediário é o Método da Bissecção.
Suponha que estamos interessados em encontrar as raízes de uma função contínua $f(x)$. O Método da Bissecção é uma alternativa que pode resultar em boas aproximações para as raízes, após sucessivas aplicações do método.
Para iniciar o método, precisamos encontrar dois valores $a$ e $b$ tais que $f(a) \cdot f(b) < 0$.
Sem perda de generalidade, vamos assumir $f(a) < 0$, $f(b) > 0$ e $a<b$. O Teorema do Valor Intermediário afirma que existe um valor $c$ no intervalo $[a,b]$ tal que $f(c) = 0$. O teorema não afirma nada a respeito da localização de $c$ dentro do intervalo, apenas que ele existe.
O Método da Bissecção é, portanto, uma maneira sistemática de obter este valor $c$. Seja $d=\frac{a+b}{2}$ o meio do intervalo. Existem três possibilidades:
- $f(d) = 0 $ - Por sorte, encontramos a raiz e não é necessário prosseguir com o método.
- $f(d) < 0$ - Como $f(b)>0$, sabemos que há uma raiz no intervalo $[d,b]$. Este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
- $f(d) > 0$ - Como $f(a)<0$, sabemos que há uma raiz no intervalo $[a,d]$. Novamente, este intervalo tem metade do tamanho do intervalo original, então estamos mais próximos de obter uma boa aproximação para a raiz.
O Método da Bissecção é a aplicação sucessiva dos passos descritos até que se esteja próximo o suficiente da raiz de $f(x)$ para a aplicação desejada. Nota-se que para o caso em que $f(a)>0$ e $f(b)<0$ o método ainda funciona, mas no caso 2 o intervalo escolhido seria $[a,d]$ e no caso e $[d,b]$ (por quê?).
Utilize o Método da Bissecção para encontrar as raízes de $f(x) = \sin x - 1/2$ no intervalo $[0.5,0.55]$.
A raiz aproximada é $x=0.52$.
Os intervalos utilizados são:
$[0.5,0.55] \quad [0.5,0.525] \quad [0.5125,0.525]$
$[0.51875,0.525]\quad [0.521875,0.525]$.
A resposta do corpo humano a uma dose de um medicamento pode ser representada pela equação:
$$R=M^2\left(\dfrac{C}{2}-\dfrac{M}{3}\right),$$
onde $C$ é uma constante positiva e $M$ a quantidade de medicamento absorvida pelo sangue. Se $R$ for uma variação da pressão sanguínea, é medida em milímetros de mercúrio; se for variação de temperatura, é medida em graus. Determine a sensibilidade do organismo ao medicamento, $dR/dM$.
Encontre a área do maior retângulo que pode ser inscrito em um triângulo retângulo com catetos de comprimento $3$ e $4cm$, se dois lados do retângulo estiverem sobre o cateto.
Quais das seguintes funções f têm descontinuidade removível em $a$? Se a descontinuidade for removível em $a$, encontre a função $g$ que é igual a $f$ para $x\neq a$ e contínua em $a$.
$f(x)=\frac{x^{2}+2x-8}{x+2}$, $a=-2$.
$f(x)=\frac{x-7}{\vert x-7 \vert}$, $a=7$.
$f(x)=\frac{3- \sqrt{x}}{9-x}$, $a=9$.
Dê um exemplo de uma função tal que $\lim\limits_{x \rightarrow p}\left| f\left( x\right) \right| $ exista mas $ \lim\limits_{x\rightarrow p}f\left( x\right) $ não exista.
Seja $f$ uma função definida em $\mathbb{R}$ e suponha que exista $M>0$ tal que $|f(x)-f(p)|\leq M|x-p|$ para todo $x$. Prove que $f$ é contínua em $p$.
Se $0<x<y$ prove que $\sqrt[3]{y-x}>\sqrt[3]{y}-\sqrt[3]{x}$.
Se $0<x<y$ prove que $\sqrt[3]{y-x}>\sqrt[3]{y}-\sqrt[3]{x}$.
Defina o termo antiderivada com suas próprias palavras.
A antiderivada de uma função $f$ é uma função $F$ cuja derivada é a função $f$ original.
Derive a função abaixo e avalie a derivada no ponto indicado:
$f\left( x\right) =\dfrac{\ln \left( x^{2}\right) +5x^{3}}{1+\cos^{2}x};$ avaliar em $f\,^{\prime }\left( \pi /2\right) .$.
$f'(x) = (15 x^2 + 2/x)/(\cos^2 x + 1) + (2 (5 x^3 + \log(x^2)) \sin x \cos x )/(\cos^2 x + 1)^2$.
$f'(\pi/2) = \dfrac{4}{\pi} + \dfrac{15 \pi^2}{4}$.
Calcule a área do conjunto $A$ dos pontos $\left( x,y\right)$ tais que $x^{2}-1\leq y\leq x+1.$
Uma página impressa deve ter $24cm^2$ de área reservada à parte escrita, uma margem de $1,5 cm$ nas partes superior e inferior e uma margem de $1cm$ nos lados. Quais as dimensões da página de menor área que preenche essas condições?
O consumo de combustível de um automóvel é função da sua velocidade média. Para certo automóvel, essa função é aproximadamente dada por $y = 0,03x^2-2x + 20$, sendo $y$ o consumo de combustível, em mililitros por quilômetros por hora. Nessas condições, para esse automóvel, qual velocidade média corresponde a um consumo de $120 ml/km$?
Embora limites como $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{n}$ e $\displaystyle \lim_{n \to \infty} a^n$ possam ser avaliados utilizando conhecimentos sobre as funções logaritmo e exponencial, estes não são necessários. Neste exercício vamos calcular esses tipos de limite por meio de argumentos ``elementares''. As ferramentas básicas são desigualdades provenientes do teorema binomial, principalmente:
$$(1+h)^n \geq 1+nh, \text{ para } h > 0,$$
e, para o item 3 a seguir:
$$(1+h)^n \geq 1+nh+\dfrac{n(n-1)}{2}h^2 \geq \dfrac{n(n-1)}{2}h^2, \text{ para } h>0.$$
Mostre que $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{a}= 1$ se $a>1$, fazendo $\sqrt[\leftroot{-2}\uproot{2}n]{a}=1+h$ e estimando $h$.
Mostre que $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{a}=1 $ se $1<a<1$.
Mostre que $\displaystyle \lim_{n \to \infty} \sqrt[\leftroot{-2}\uproot{2}n]{n}= 1$.
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left\vert 2x^{2}-1\right\vert <1$.
A respiração tem um ciclo rítmico que consiste em períodos alternados de inalação e exalação. Em condições normais, um adulto tem um ciclo em média a cada $5$ segundos. Denotando por $V$ o volume de ar nos pulmões no instante $t$, a taxa de fluxo é dada por $\dfrac{dV}{dt}$.
Se a taxa máxima de fluxo é $0,6$ L$/$seg, encontre valores de $a$ e $b$ para que a fórmula $\dfrac{dV}{dt}=a \sin (bt)$ modele a respiração com os dados acima.
Utilize a expressão obtida para estimar a quantidade de ar inalada durante um ciclo completo de respiração.
Seja $ f(x)=\left\{\begin{array}{ll} \sqrt{x-4} &\text{ se } x>4\\8-2x&\text{ if } x<4\end{array}\right.$.
Decida se $\lim\limits_{x\rightarrow 4}f(x)$ existe. Se o limite não existe, explique.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =x^{2}e^{x}$.
$f'(x)=e^x(x^2+2x)$.
Usando a regra da derivada do produto, temos que
\[f^\prime(x) = (x^2 e^x)^\prime = (x^2)' \cdot e^x + x^2 \cdot (e^x)^\prime.\]
Como $(x^2)^\prime = 2x$ e $(e^x)^\prime = e^x$, então
\[(x^2)' \cdot e^x + x^2 \cdot (e^x)^\prime = 2x e^x + x^2 e^x.\]
Colocando o fator comum $e^x$ em evidência, concluímos que
\[f^\prime (x) = e^x (x^2 + 2x).\]
Encontre os seguintes limites em termos do número $\alpha = \displaystyle \lim_{n \to 0} \dfrac{\sin x}{x}$.
$\displaystyle \lim_{x \to \infty} \dfrac{\sin x}{x}$.
$\displaystyle \lim_{x \to \infty} x \sin \left(\dfrac{1}{x}\right)$.
Prove que $\cosh^2(x)-\sinh^2(x)=1$.
$\begin{array}{rcl} \cosh^2x - \sinh^2 x &=& \left(\dfrac{e^{-x} + e^x}{2}\right)^2 - \left(\dfrac{e^{x} - e^-x}{2}\right)^2 \\ &=& \dfrac{1}{4} (e^{-2x} + 2 e^{-x}e^x + e^{2x}) - \dfrac{1}{4} (e^{2x} - 2 e^xe^{-x} + e^{-2x}) \\ &=& \dfrac{1}{2} + \dfrac{1}{2} \\ &=& 1.\end{array}$
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
x^3-x, & & \text{se } x<1\\
x-2, & & \text{se } x\geq 1
\end{array}\right.$
- $x=0$.
- $x=1$.
- Sim.
- Não: Os limites pela direita e pela esquerda não são iguais em $x=1$.
Calcule a seguinte integral:
$\int_{0}^{r}\sqrt{r^{2}-x^{2}}dx.$
Calcule a integral $\displaystyle \int (1+ \sin t)^9 \cos t \, dt$, utilizando a substituição $u=1+\sin t$.
Calcule a integral $\int{\sin2\theta e^{\sin^2\theta}}d\theta.$
$e^{\sin^2\theta}+C$
Calcule a seguinte integral:
$\int e^{x}\sin xdx.$
$\dfrac{1}{2}e^x(sinx-cosx)+C$
Suponha que uma gota de neblina seja uma esfera perfeita e que, por condensação, capte umidade a uma taxa proporcional à área de sua superfície. Mostre que nessas circunstâncias o raio da gota cresce a uma taxa constante.
Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-2x+1}{4x^{4}+2x+3}$.
$5/4$
Calcule a integral $\int {\dfrac{x}{\left( x-1\right) \left( x+2\right) }}dx$.
Ache os pontos de máximo e de mínimo absolutos da função $f(x)=x+3x^{2/3}$.
Calcule a derivada da seguinte função:
$f\left( x\right) =\log_{2}\left( \cos^{3}\left( x\right) \right).$
$f'(x) = -\dfrac{3 \tan x}{\log 2}$.
Seja $g(x)=x^3+\dfrac{1}{x}$. Determine a equação da reta tangente ao gráfico de $g$ no ponto correspondente a $x=1$.
$y=2x$.
Um fazendeiro planeja cercar um pasto retangular vizinho a um rio. O pasto deve conter $180000$ metros quadrados para fornecer grama suficiente para o rebanho. Quais as dimensões do pasto para gastar a quantidade mínima de cerca se não há necessidade de cerca ao longo do rio?
Mostre que $x^{2}-xy+y^{2}\geq 0$, $\forall x,y\in \mathbb{R}^+$ e que vale a igualdade se e somente se $x=y=0$.
Note que $x^{2}-xy+y^{2}=x^2-2xy+y^2+xy=(x-y)^2+xy \geq 0$, pois $(x-y)^2 \geq 0$ e $xy \geq 0$. O único modo de ocorrer a igualdade é quando as duas parcelas forem iguais a zero, o que ocorre se, e somente se, $x=y=0$.
Estime $\pi$ através da aplicação do Método de Newton na equação $tg(x)=0$. Qual cuidado deve ser tomado, neste caso, em relação à escolha do valor inicial?
Um objeto é lançado para cima com uma velocidade, em pés por segundo, dada por $v(t) = -32t+64$, de uma altura de $48$ pés.
- Qual a velocidade máxima do objeto?
- Qual o deslocamento máximo do objeto?
- Em que momento ocorre o maior deslocamento do objeto?
- Em que momento o objeto alcança a altura de $0$ pés?
Dica: encontre o momento no qual o deslocamento é $-48ft$
- $64ft/s$
- $64ft$
- $t=2$
- $t=2+\sqrt{7}\approx 4.65s$.
Os gráficos das equações $y=e^x$, $y=0$, $x=0$ e $x=\ln 3$ formam uma região delimitada no plano. Calcule o centroide dessa região.
Mostre que qualquer intervalo de $R$ contém algum número irracional.
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
É verdade que, ao se esticar um elástico puxando-o por suas extremidades em direções opostas, algum ponto do elástico permanecerá em sua posição inicial? Justifique sua resposta.
Demonstre que a derivada da função tangente é igual ao quadrado da função secante.
Se $f_{med}[a,b]$ denota o valor médio de $f$ no intervalo $\left[a,b\right]$ e $a<c<b$, mostre que
\begin{equation*}
f_{med}[a,b]=\dfrac{c-a}{b-a}f_{med}[a,c]+\dfrac{b-c}{b-a}f_{med}[c,b]
\end{equation*}
Calcule a seguinte integral:
$ \int_{-\infty}^{e^4}\frac{\ln (x)}{x}dx$.
Calcule a derivada da função:
$y=\left( 2+\sin x\right) ^{x}$.
$y' = (\sin x + 2)^x (\log(\sin x + 2) + (x \cos x )/(\sin x + 2))$.
Se uma droga é injetada em uma corrente sanguínea, sua concentração $C$, $t$ minutos depois, é dada por $C(t)=\frac{k}{a-b}(e^{-bt}-e^{-at})$, para constantes positivas $a$, $b$ e $k$.
- Em que instante ocorre a concentração máxima?
- Que se pode dizer sobre a concentração após um longo período de tempo?
Verifique se os seguintes limites existem. Explique.
$\lim\limits_{x\rightarrow\infty}2^{1/x}$.
$\lim\limits_{t\rightarrow\infty}\sin x$.
$\lim\limits_{x\rightarrow 2^-}\tan^{-1}\left(\frac{1}{2x-4}\right)$.
Mostre que o comprimento de arco total da elipse $x=a \cos t$, $y=b \sin t$, $0 \leq t \leq 2\pi$, para $a>b>0$ é dado por $4\displaystyle\int_{0}^{\pi/2} \sqrt{1+3\sin^3 t}dt$.
Calcule o limite a seguir, justificando as passagens.
$\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}$
0
Para todo $x\neq 0$ temos que
\begin{equation*}
\dfrac{1-\cos x}{x}=\dfrac{1-\cos x}{x}\dfrac{1+\cos x}{1+\cos x}=\dfrac{
1-\cos ^{2}x}{x}\dfrac{1}{1+\cos x}\text{.}
\end{equation*}
Como $1-\cos ^{2}x=\sin ^{2}x$ obtemos
\begin{eqnarray*}
\dfrac{1-\cos x}{x} &=&\dfrac{\sin ^{2}x}{x}\dfrac{1}{1+\cos x} \\
&=&\sin x\dfrac{\sin x}{x}\dfrac{1}{1+\cos x}.
\end{eqnarray*}
Mas
\begin{eqnarray*}
\lim\limits_{x\rightarrow 0}\sin x &=&0\;\text{(pois }\sin x\text{ é contínua)} \\
\lim\limits_{x\rightarrow 0}\dfrac{\sin x}{x} &=&1\;\text{(limite trigonométrico fundamental)} \\
\lim\limits_{x\rightarrow 0}\dfrac{1}{1+\cos x} &=&\dfrac{1}{2}\;\text{(}
\cos x\text{ cont\'{i}nua e }1+\cos \left( 0\right) \neq 0\text{).}
\end{eqnarray*}
Logo,
\begin{equation*}
\lim\limits_{x\rightarrow 0}\dfrac{1-\cos x}{x}=\lim\limits_{x\rightarrow
0}\sin x\lim\limits_{x\rightarrow 0}\dfrac{\sin x}{x}\lim\limits_{x
\rightarrow 0}\dfrac{1}{1+\cos x}=0.
\end{equation*}
Utilizando o gráfico a seguir, avalie os seguintes limites
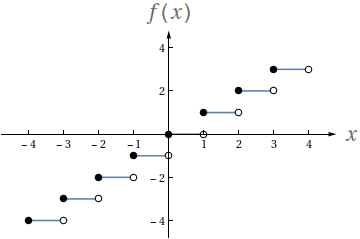
Seja $-3\leq a\leq 3$ um número inteiro
- $ \lim\limits_{x\to a^-} f(x)$
- $ \lim\limits_{x\to a^+} f(x)$
- $ \lim\limits_{x\to a} f(x)$
- $f(a)$
- $a-1$
- $a$
- Não existe.
- $a$
Uma pequena indústria vende normalmente, a cada semana, $60$ caixas de certo produto, por $30$ reais a caixa. Foi feita uma experiência e observou-se que cada real de desconto nesse preço fez as vendas aumentarem em $5$ caixas. Assim, a experiência mostrou que, dentro de certos limites, a quantidade $C$ de caixas vendidas é uma função do desconto $x$, em reais. Determine uma expressão para essa função.
Calcule o valor de $p$ para a integral a seguir convergir:
$\int_{1}^{2}{\frac{dx}{x\left(ln\ x\right)^p}}$
Sabendo que $x$ é um número negativo, simplifique a expressão $\sqrt{(x-3)^2}+\sqrt{x^2}+\sqrt{(4-3x)^2}$.
A figura mostra as curvas aceleração versus tempo para dois carros movendo-se em uma pista reta, começando alinhados e acelerando a partir do repouso. O que representa a área $A$ entre as curvas no intervalo $0 \leq t \leq T$? Justifique.
Para uma aceleração $a(t)$ qualquer, $\int_0^Ta(t)\,dt$ representa a velocidade adquirida desde o instante $t=0$, ou seja, $v(T)= v_0+\int_0^Ta(t)\,dt$. Sendo assim, a área entre as curvas representa $v_1(T)-v_2(T)$, a diferença de velocidade entre os carros no instante $t=T$.
Calcule o limite $\lim\limits_{x\to p}\frac{x^{4}-p^{4}}{x-p}$
$\begin{array}{rcl} \lim\limits_{x\to p}\dfrac{x^{4}-p^{4}}{x-p} &=& \lim\limits_{x\to p} \dfrac{(x^2+p^2)(x^2-p^2)}{x-p} \\ &=& \lim\limits_{x\to p} \dfrac{(x^2+p^2)(x+p)(x-p)}{x-p} \\ &=& \lim\limits_{x\to p} (x^2+p^2)(x+p) \\ &=& (p^2 + p^2)(p+p) \\ &=& 4p^3. \end{array}$
A velocidade de uma partícula que se move de um lado para o outro sobre uma reta é $v=ds/dt = 6\sin2t\ m/s$ para qualquer $t$. Se $s=0$ quando $t=0$, determine o valor de $s$ para $t=\pi/2\ s$.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow0}\frac{sen(cosx)}{sec(x)}$.
$\sin(1)$.
Estude a função $f\left( x\right) =1-e^{-x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Demonstre a Regra de L'Hospital para a indeterminação da forma $\displaystyle\dfrac{0}{0}$.
A aceleração (no instante $t$) de um ponto em movimento sobre uma reta coordenada é $\sin^2 (t)\cos(t)$ $m/s^2$. Em $t=0$, o ponto está na origem e sua velocidade é 10 $m/s$. Determine sua posição no instante $t$.
Se a velocidade de um objeto em metros por segundo no instante $t$ segundos é $v(t)=-\sin(t)-\cos(t)$, qual a sua posição no instante $t=4$?
$s(t)=\cos(4)-\sin(4)$
A aproximação $(1+x)^k \approx 1+kx$ pode ser utilizada para cálculos rápidos.
Mostre porque esta aproximação é boa e use-a para fazer uma estimativa simples de $(1,001)^{37}$.
Compare sua estimativa com a obtida por meio de algum recurso computacional (pode ser uma calculdadora científica).
Agora utilize esta aproximação para calcular $(1,1)^{37}$ e compare com o recurso computacional. O que acontece neste caso? Justifique.
Calcule $f'\left( x\right) $, pela definição:
$f\left( x\right) =1/x$.
$f'(x)=-\dfrac{1}{x^2}$.
Se Fidelis investisse $R\$1500$ em uma conta aposentadoria que rende $8\%$ de juros compostos anualmente, em quanto tempo este investimento isoladamente aumentará para $R\$5000$?
Calcule o valor de $p$ para a integral a seguir convergir:
$\int_{2}^{\infty}{\frac{dx}{x\left(ln\ x\right)^p}}$
Em uma reação química de dois reagentes, a velocidade da reação depende, em geral, da concentração destes. Seja $a$ a quantidade do reagente $A$ e $b$ a quantidade do reagente $B$ em $t=0$, sendo $x$ a quantidade do produto no instante $t$, a velocidade de formação de $x$ pode ser dada pela equação diferencial
$\frac{dx}{dt} = k(a-x)(b-x)$,
sendo que $k$ é uma constante para a reação. Encontre $x(t)$ se:
$a=b$
$a \neq b$
Em ambos os casos, considere $x(t=0)=0$.
Determine a derivada da função:
$f\left( x\right) =e^{\cos \left( x^{2}\right)}.$
Pela regra da cadeia, temos que
$f(g(x))' = f'(g(x))g'(x)$
Assim, escolhendo $f(x) = e^x$ e $g(x)=\cos(x^2)$, temos:
$(e^{\cos(x^2)}))' = e^{\cos(x^2)}(\cos(x^2))'$
Para calcular $(\cos(x^2))'$, temos que aplicar novamente a regra da cadeia. Desta vez, podemos escolher $f(x)=\cos(x)$ e $g(x)=x^2$.
Assim,
$(\cos(x^2))'= -2\sin(x^2)x$
Portanto:
$(e^{\cos(x^2)}))' = -2 e^{\cos(x^2)}x\sin(x^2)$
Estude a função $f\left( x\right) =x^{3}-3x^{2}-9x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Usando os limites fundamentais, encontre o limite $\lim\limits_{x\rightarrow0}\frac{\tan x}{x}$.
$1$.
As curvas de crescimento logístico modelam a taxa de crescimento de uma certa população em função dos fatores ambientais. Em um período prolongado de tempo, a população tende a um valor limite que representa o máximo número de indivíduos que o espaço ou alimento pode sustentar. Estas curvas são da forma $$ y(t)=\dfrac{L}{1+Ae^{-kt}}, $$ onde $y$ é a população no momento $t$ ($t\geq 0$) e $A$, $k$ e $L$ são parâmetros positivos.
Mostre que o ponto de inflexão da curva de crescimento logístico (figura acima) ocorre no tempo $t$ solução da equação $$ \dfrac{L}{2}=\dfrac{L}{1+Ae^{-kt}}, $$ para $t$, ou seja, no instante $ t= \dfrac{\ln A}{k}$.
Seja $f(x)=x^n+5x^{n-1}+3$, onde $n>1$ é um inteiro. Prove que $f(x)$ não pode ser expressa como um produto de polinômios não constantes com coeficientes inteiros.
Calcule a integral imprópria $\int_0^1 \frac{1}{\sqrt{1-x^2}} dx.$
$\pi/2$.
Avalie a seguinte integral indefinida:
$\int 3x^3\ dx$
$3/4x^4+C$
Considere as funções trigonométricas hiperbólicas:
\begin{equation*} \sinh x=\dfrac{e^{x}-e^{-x}}{2};\;\cosh x=\dfrac{e^{x}+e^{-x}}{2}\text{.} \end{equation*}
Mostre que $\cosh ^{2}x-\sinh ^{2}x=1$.
Mostre que $\left( \sinh ^{\prime }x\right) ^{2}-\left( \cosh^{\prime }x\right) ^{2}=1$.
Calcule e justifique os seguintes limites, quando existirem, ou justifique a inexistência:
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{3-x};$
$\lim\limits_{x\rightarrow 3^{-}}\dfrac{5}{3-x};$
$\lim\limits_{x\rightarrow 0^{+}}\dfrac{5}{x^{2}-x};$
$\lim\limits_{x\rightarrow 0^{-}}\dfrac{5}{x^{2}-x};$
$\lim\limits_{x\rightarrow 0^{+}}\dfrac{\sin x}{x^{3}-x^{2}};$
$\lim\limits_{x\rightarrow -1^{+}}\dfrac{3x^{2}-4}{1-x^{2}}$
Encontre os pontos sobre o gráfico de $p(x)=x^3-2x^2-8x+3$ nos quais a reta tangente é paralela à reta $y=4-9x.$
Determine a derivada de $f\left( t\right) =t^{3}e^{-3t}$.
$-3 e^{-3t} (t-1) t^2$.
Seja $f$ uma função contínua em $[1,5]$, sendo que $f(1) = -2$ e $f(5) = -10$. Existe um valor $1<c<5$ tal que $f(c) = -9$? Por quê?
Sim, pelo Teorema do Valor Intermediário.
Use a derivada dada para encontrar as coordenadas $x$ de todos os pontos críticos de $f$ e classifique-os em máximo relativo, mínimo relativo ou nenhum dos dois.
$\displaystyle f'(x)=x^3(x^2-5)$;
$\displaystyle f'(x)=xe^{-x}$.
Seja $f(x)=\left\{\begin{array}{ll}
x^2, & \text{se } x \leq 0 \\
-x^2, & \text{se } x>0
\end{array}\right.$
- $f$ é contínua em $0$. Por quê?
- $f$ é derivável em $0$. Por quê?
1. Sim.
2. Sim.
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{\ln x}{x}$.
$f'(x)=1-ln(x)$.
Seja $f(x)=\sin{x}$. Calcule $f'(x)$ e $f'\left(\dfrac{\pi}{4}\right)$.
$f'(x)=\cos(x)$ e $f'\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$.
Calcule $f'(x)$ sendo
- $f(x)=tg{x}$
- $f(x)=sec{x}$
1. $f'(x)=sec^2(x)$.
2. $f'(x)=sec(x)tg(x)$.
Seja $f(x)=\dfrac{1}{1+x}$. Determine:
- $f(f(x))$
- $f\left(\dfrac{1}{x}\right)$
- $f(cx)$
- $f(x+y)$
- $f(x)+f(y)$
Use suas próprias palavras para definir o significado de $\int{f(x)}\ dx$.
O símbolo $\int{f(x)}\ dx$ é chamado integral indefinida de $f$ e corresponde ao conjunto de todas as antiderivadas da função $f$.
Sejam $a, b$ racionais positivos. Prove que $\sqrt{a}+\sqrt{b}$ é racional se, e somente se, $\sqrt{a}$ e $\sqrt{b}$ forem ambos racionais. (Sugestão: multiplique por $\sqrt{a}-\sqrt{b}$).
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Escreva $a^x$ em função de $e^x$. Use esse resultado para escrever $\log_a(x)$ em função de $\ln(x)$.
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left( 2x-3\right) \left( x^{2}+1\right) <0$.
- $\lim\limits_{x\rightarrow 1}\dfrac{\sqrt{x}-1}{\sqrt{2x+3}-\sqrt{5}}$
- $\lim\limits_{x\rightarrow 3}\dfrac{\sqrt{x}-\sqrt{3}}{x-3}$
- $\lim\limits_{h\rightarrow 0}\dfrac{\sqrt{x+h}-\sqrt{x}}{h}$
Mostre, diretamente da definição, que $\log_a'(x)=\dfrac{1}{x} \cdot log_a\left(\lim\limits_{k \to 0}(1+k)^{1/k}\right)$.
Calcule o limite $\lim\limits_{x \to 0^+}\dfrac{\ln(tg{x}+\cos{x})}{\sqrt{\ln(x^2+1)}}$.
$1$.
Estude a função $f\left( x\right) =e^{\dfrac{x-1}{x^{2}}}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Seja $f: \mathbb{R} \to \mathbb{R}$ uma função derivável cuja derivada é sempre positiva e tal que $f(0)=1$ e $f(4)=2$. Use o TVM para mostrar que $f(2) \neq 2$.
Explique, usando propriedades de limites, porque $\lim\limits_{x\rightarrow 2}\frac{x^2-4}{x-2}\not = \frac{\lim\limits_{x\rightarrow 2} (x^2-4)}{\lim\limits_{x\rightarrow 2}(x-2)}$.
Note que somente podemos usar as propriedades de limite quando um limite existe e é finito. Além disso, lembre-se que limites que recaem na expressão indeterminada "$\frac{0}{0}$", podem existir ou não. Calcule os seguintes limites.
$\lim\limits_{x\rightarrow 2}\frac{x^2-4}{x-2}$
$\lim\limits_{h\rightarrow 0}\frac{(2+h)^2 - 4}{h}$
$\lim\limits_{x\rightarrow 2}\left(\frac{4}{x^2-2x}-\frac{x}{x-2}\right)$
$\lim\limits_{t\rightarrow 0}\frac{\sqrt{t^2+4}-2}{t^2}$
Um retângulo com os lados paralelos aos eixos coordenados tem um vértice na origem e o vértice diagonalmente oposto está sobre a curva $y=kx^m$ no ponto onde $x=b$ ($b>0$, $k>0$, $m \geq 0$). Mostre que o quociente entre a área do retângulo compreendida entre a curva e o eixo $x$ depende de $m$, mas não depende de $k$ ou $b$.
Ache uma reta vertical $x=k$ que divida a área entre as curvas $y=x^2$ e $y=9$ em duas partes iguais.
$x=k=0$
Suponha que $x$ e $y$ sejam notas de provas bimestrais. Mostre que a chamada {\it média geométrica} entre $x$ e $y$, dada por $\sqrt{xy}$, poderia, se adotada como critério avaliativo, prejudicar a nota final de alguns alunos, isto é, elaé menor que ou igual à chamada {\it média aritmética} entre $x$ e $y$, que é dada por $\frac{x+y}{2}.$
Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles. Sendo assim, se o professor adotar como critério de avaliação a média geométrica em vez da aritmética, ele pode prejudicar a nota final dos alunos que tivessem a nota $x$ diferente da $y$, pois quando $x=y$ as duas médias são iguais.
Suponha que $\left| f\left( x\right) -f\left( 1\right) \right| \leq \left( x-1\right) ^{2}$. Demonstre que $f\left( x\right) $ é contínua em $1$.
Dê um exemplo de uma função tal que $\lim\limits_{x\rightarrow p}\left| f\left( x\right) \right| $ exista mas $\lim\limits_{x\rightarrow p}f\left( x\right) $ não exista.
O princípio de Fermat também explica por que um raio de luz passando entre ar e água sofre um desvio de trajetória (refração). Imagine dois meios uniformes (como ar e água) e um raio de luz viajando de uma fonte $A$ em um meio para um observador $B$ em outro meio (figura abaixo). Sabe-se que a luz viaja a uma velocidade constante em um meio uniforme, porém mais vagarosamente no meio mais denso (como a água) do que no meio menos denso (como o ar). Conseqüentemente, o percurso de menor tempo entre $A$ e $B$ não é necessariamente uma reta, mas a união de dois segmentos $AP$ e $PB$, permitindo assim que a luz tome vantagem de sua maior velocidade no meio mais esparso. A Lei de Refração de Snell estabelece que a trajetória do raio de luz é tal que $$ \dfrac{\sin\theta_1}{\nu_1}= \dfrac{\sin\theta_2}{\nu_2}, $$ onde $\nu_1$ é a velocidade da luz no primeiro meio e $\nu_2$ no segundo, $\theta_1$ e $\theta_2$ são os ângulos de incidência e de refração, respectivamente (figura abaixo). Mostre que isso decorre da hipótese de que o caminho de tempo mínimo ocorre quando $\displaystyle dt/dx=0$.
Um buraco redondo de raio $a$ é feito através do centro de uma esfera sólida de raio $r$. Use camadas cilíndricas para encontrar o volume da parte removida (suponha $r>a$).
A teoria necessária para resolver esta questão pode não ser abordada em alguns cursos de Cálculo 1. Sendo, também pertinente, às disciplinas Teoria dos Números e Análise Real I.
Para aprofundar seus conhecimentos, dentro do escopo de Cálculo 1, recomendamos a leitura do Cap. 1 de Guidorizzi, vol. 1 e /ou o Prólogo de Spivak (vide Bibliografia de Cálculo 1).
Dica: Pesquise sobre a diagonal de Cantor!
Calcule $f^{\prime }\left( x\right)$:
$f\left( x\right) =\dfrac{1+e^{x}}{1-e^{x}}$.
$f'(x) = \dfrac{2 e^x}{(1-e^x)^2}$.
Queremos calcular a derivada da divisão da função $1+e^x$ pela função $1-e^x$. Usando a regra da derivada do quociente, obtemos:
\[\left( \dfrac{1+e^x}{1-e^x} \right)^\prime = \dfrac{(1+e^x)^\prime \cdot (1-e^x) - (1+e^x)\cdot (1-e^x)^\prime}{(1-e^x)^2}.\]
Como
\[(1+e^x)^\prime = (1)^\prime + (e^x)^\prime = 0 + e^x = e^x\]
e, analogamente,
\[(1-e^x)^\prime = -e^x,\]
temos então que
$\dfrac{(1+e^x)^\prime \cdot (1-e^x) - (1+e^x)\cdot (1-e^x)^\prime}{(1-e^x)^2} = \dfrac{e^x (1-e^x)-(1+e^x)(-e^x)}{(1-e^x)^2} = \dfrac{e^x(1-e^x)+e^x(1+e^x)}{(1-e^x)^2}$.
Para simplificar o numerador, colocamos o fator comum $e^x$ em evidência: $e^x(1-e^x+1+e^x) = 2e^x$. Portanto, concluímos que
\[f'(x) = \dfrac{2 e^x}{(1-e^x)^2}.\]
Use camadas cilíndricas para encontrar o volume do sólido resultante quando se faz girar a área entre as curvas $y=\dfrac{1}{x^2+1}$, $x=0$, $x=1$ e $y=0$ em torno do eixo $y$.
Suponha que em uma máquina um pistão se desloque verticalmente tal que sua posição no instante $t$ (medido em segundos) seja dado por:
$$s=A \cos(2 \pi b t ),$$
onde $A>0$ é a amplitude do movimento, e $b>0$ é a frequência (número de vezes que o pistão se desloca de cima para baixo por segundo). Qual o efeito da duplicação da frequência sobre a velocidade, a aceleração e a sobreaceleração do pistão? Relacione a sua resposta com o fato de que uma máquina quebra quando funciona rápido demais.
Seja $x(t)$ a posição horizontal e $y(t)$ a posição vertical de um objeto no tempo $t$. Com $x(0)=y(0)=0$ e velocidade iniciais horizontal $v_x$ e vertical $v_y$, a trajetória do objeto pode ser representada pelas equações $x(t)=v_xt$ e $y(t)=-5t^2+v_y t$. Suponha que o módulo da velocidade inicial seja igual a $1$. Neste caso, o ângulo $\theta$ entre a linha horizontal (eixo $x$) e a tangente à parábola na origem $(0,0)$ satisfaz $v_x=\cos(\theta)$ e $v_y=\sin(\theta).$
- Use a identidade $\sin(\theta_1+\theta_2)=\sin(\theta_1)\cos(\theta_2)+\sin(\theta_2)\cos(\theta_1)$ para provar que $\cos(\theta)\sin(\theta)=\frac{1}{2}\sin(2\theta).$
- Para $v_x>0$, $v_y>0$, determine o tempo $t_f>0$ tal que $y(t_f)=0$. Escreva $t_f(\theta)$ como função de $\theta$ com domínio $]0,\frac{\pi}{2}[$.
- Definimos uma função $x_f$, também com dominio $]0,\frac{\pi}{2}[$, por $x_f(\theta)=x(t_f(\theta))$. Escreva $t_f(\theta)$ como função de $\theta$ e simplifique.
- Qual é a imagem de $x_f$?
- Quais são os ângulos $\theta\in\,]0,\frac{\pi}{2}[$ com valores $x_f(\theta)=\frac{\sqrt{3}}{20}$, $x_f(\theta)=\frac{1}{10}$ e $x_f(\theta)=\frac{1}{5}$?
Determine $f\left(x\right)$ sabendo que: \begin{equation*} f^{\prime \prime }\left( x\right) = \dfrac{1}{x^{2}}+8e^{2x}+2,\;f^{\prime }\left( 2\right) =4e^{4}\text{ e }f\left( 1\right) =2e^{2}\text{.} \end{equation*}
Uma caixa retangular aberta com volume de $2 m^3$ tem a base quadrada. Expresse a área superficial da caixa como função de um dos lados da base.
Sejam $x$ a medida do lado da base da caixa e $z$ sua altura. O volume $V$ dessa caixa é dado por $V=x^2z$. Como $V=2$, temos $z=\dfrac{2}{x^2}$. A área superficial $A$ da caixa (sem tampa!) é $A=x^2+4xz$. Substituindo $z$ por $\dfrac{2}{x^2}$ obtemos $A=x^2+\dfrac{8}{x}$.
Estude o sinal de $f^{\prime }\left( x\right) $, calcule os limites $\lim\limits_{x\rightarrow \infty }f\left( x\right) $ e $\lim\limits_{x\rightarrow -\infty }f\left( x\right) $ e, utilizando esses dados, esboce o gráfico de $f\left( x\right) =\dfrac{x}{x^{2}+1}$.
Se uma quantia $P$ é aplicada à taxa de juros de $100r \%$ ao ano, composta $m$ vezes por ano, então o montante, ao cabo de $t$ anos, é dado por $P(1+rm^{-1})^{mt}$. Considerando $m$ como um número real e fazendo m crescer indefinidamente, diz-se que a taxa é composta continuamente. Mostre que, neste caso, o montante após $t$ anos é $Pe^{rt}$.
Imagine uma estrada em que o limite de velocidade é especificado a cada ponto dela. Isto é, existe uma certa função $L$ tal que o limite de velocidade no quilômetro $x$ da estrada é $L(x)$. Dois carros, $A$ e $B$, estão viajando nesta estrada; o carro $A$ com posição $a(t)$ e o $B$ com posição $b(t)$.
Escreva uma equação para o fato de que o carro $A$ sempre anda no limite de velocidade. (A resposta não é $a'(t)=L(t)$.)
Suponha que $A$ sempre ande no limite de velocidade, e que a posição de $B$ no tempo $t$ é a posição de $A$ no tempo $t-1$. Mostre que $B$ também anda no limite da velocidade em todo o tempo.
Suponha agora que $B$ anda sempre a uma distância fixa atrás de $A$. Sobre quais condições $B$ sempre irá andar no limite de velocidade?
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow \infty }\dfrac{1-2^{x}}{1-3^{x}}$.
$0$.
Encontre os valores de $p$ tais que a integral $\displaystyle \int_0^{+\infty} e^{px} \, dx$ converge.
Avalie os seguintes limites de acordo com o gráfico da função:
$f(x) = \cos (x)$
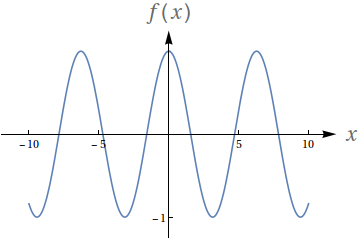
$\lim\limits_{x\to -\infty} f(x)$
$\lim\limits_{x\to \infty} f(x)$
Utilizando o gráfico a seguir, avalie os seguintes limites
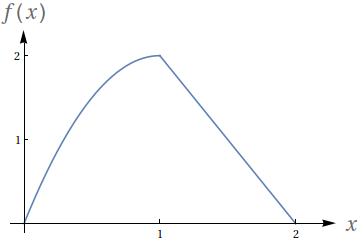
- $ \lim\limits_{x\to 1^-} f(x)$
- $ \lim\limits_{x\to 1^+} f(x)$
- $ \lim\limits_{x\to 1} f(x)$
- $f(1)$
- $2$
- $2$
- $2$
- $2$
Avalie os seguintes limites para a função definida por partes
$ f(x) = \left\{\begin{array}{ccc}
a(x-b)^2+c, & & \text{ se } x<b \\
a(x-b)+c, & & x \text{ se } \geq b
\end{array}
\right.,$
sendo que $a$, $b$ e $c$ são números reais.
- $ \lim\limits_{x\to b^-} f(x)$
- $ \lim\limits_{x\to b^+} f(x)$
- $ \lim\limits_{x\to b} f(x)$
- $f(b)$
- $c$
- $c$
- $c$
- $c$
Usa-se a técnica do carbono-14 para determinar a idade de espécimes arqueológicos ou geológicos. Este método baseia-se no fato de que o carbono-14, isótopo instável ($^{14}C$) está presente no $CO_2$ na atmosfera. As plantas assimilam carbono da atmosfera; quando morrem o $^{14}C$ acumulado começa a decair, com uma meia vida de aproximadamente 5700 anos. Medindo-se a quantidade de $^{14}C$ que resta em um espécime, é possível determinar quando o organismo morreu. Suponha que um osso fóssil acuse 20\% da quantidade de $^{14}C$ presente em um osso dos dias atuais. Dê uma aproximação da idade do osso fóssil.
Usando as fórmulas do seno da soma e do cosseno da soma de dois ângulos, obtenha fórmulas para:
$\sin(2x), \cos(2x), \sin(3x)$ e $\cos(3x)$.
$\sin(2x) = 2 \sin x \cos x$.
$\cos(2x) = \cos^2 x - \sin^2 x$.
$\sin(3x) = \sin x (2 (\cos^2 x - \sin^2 x) + 1)$.
$\cos(3x) = \cos^3 x - 3 \sin^2 x \cos x$.
Esboce o gráfico da função abaixo e resolva a inequação:
$f\left( x\right) =\left\vert x-1\right\vert -\left\vert x+2\right\vert >x$.
Determine os intervalos de decrescimento e crescimento e esboce o gráfico da seguinte função $f\left( x\right) =e^{2x}-e^{x}$.
Prove que $|x+y|=|x|+|y| \Leftrightarrow xy \geq 0$.
Um invertimento de \$500,00 da juro de 7% ao ano, capitalizado continuamente, e apót $t$ anos o investimento valerá $500e^{0,07t}$.
- Aproximadamente, quando o investimento valerá \$1000,00?
- Quando o valor do investimento estará crescendo à razão de \$50,00 por ano?
Calcule a integral a seguir utilizando substituições trigonométricas:
$\int{\frac{dx}{\sqrt{9+x^2}}}$
$sinh^{-1}(x/3)+C$.
Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0^{+}}\log _{\dfrac{1}{3}}x$.
$\infty$.
Prove que se $f$ e $g$ são ambas funções contínuas, então $f+g$ é contínua.
Calcule o limite $\lim\limits_{x\to e} \ln x$, em que $e$ é o número de Euler.
$1$.
Sejam $a$ e $b$ reais quaisquer. Verifique que:
- $\sin{a}\cos{b}=\dfrac{1}{2}(\sin(a+b)+\sin(a-b))$
- $\cos{a}\cos{b}=\dfrac{1}{2}(\cos(a+b)+\cos(a-b))$
- $\begin{array}{rcl} \frac{1}{2} ( \sin(a+b) + \sin(a-b) ) &=& \frac{1}{2} ( \sin a \cos b + \sin b \cos a + \sin a \cos b - \sin b \cos a ) \\ &=& \frac{1}{2} ( 2 \sin a \cos b) \\ &=& \sin a \cos b .\end{array}$
- $\begin{array}{rcl} \frac{1}{2} ( \cos(a+b) + \cos(a-b) ) &=& \frac{1}{2} ( \cos a \cos b + \sin a \sin b + \cos a \cos b - \sin a \sin b ) \\ &=& \frac{1}{2} ( 2 \cos a \cos b) \\ &=& \cos a \cos b .\end{array}$
Responda os itens:
- Dada $f:{\mathbb{R} \to \mathbb{R}}$, defina (em termos de $\varepsilon $ e $\delta $) $\lim\limits_{x\rightarrow p}f\left( x\right) =L.$ Ilustre elaborando um gráfico para uma função genérica.
- Qual é a condição sobre esse limite para que a função seja contínua?
Seja:
- $\int_0^2{f(x)dx} = 5$
- $\int_0^3{f(x)dx} = 7$
- $\int_0^2{g(x)dx} = -3$ e
- $\int_0^3{g(x)dx} = 5$
A partir destes valores, calcule as seguintes integrais:
- $\int_0^2 \big(f(x)+g(x)\big) \ dx$
- $\int_0^3 \big(f(x)-g(x)\big) \ dx$
- $\int_2^3 \big(3f(x)+2g(x)\big) \ dx$
- Encontre valores para $a$ e $b$ tal que:
$\int_0^3 \big(af(x)+bg(x)\big) \ dx=0$
- $2$
- $2$
- $22$
- $a=-\frac{5}{7}b,\quad b\in\mathbb{R}$
- $\lim\limits_{x\rightarrow p} \frac{\sin \left(x^{2}-p^{2}\right) }{x-p}$
- $\lim\limits_{y\rightarrow 3} \frac{\sin \left(y^{2}-9\right) }{y-3}$
- $\lim\limits_{x\rightarrow 4} \frac{\cos \left(x^{2}-16\right) }{x-4}$
Construa uma função com uma assíntota vertical em $x=5$ e uma assíntota horizontal em $y=5$.
Calcule o limite justificando as passagens.
$\lim\limits_{x\rightarrow 3^{+}}\dfrac{5}{x-3}$.
Esboce o gráfico da função $f\left( x\right) =\frac{x^{2}+3}{x-1}$, indicando domínio de definição, limites no infinito, assíntotas verticais e inclinadas, intervalos de crescimento e decrescimento e estudo da concavidade.
Resolva a equação modular $|x-2|-|x-1| =2$.
Se $f(8)=12$, $f'(x)$ é contínua e ${ \int_1^8 f'(x)dx=30}$, determine o valor de $f(1)$.
Calcule os valores de $a,b$ e $c$ de modo que as parábolas $y=x^2+ax+b$ e $y=-x^2 +cx$ sejam tangentes uma a outra no ponto $(1,2)$.
Esboce o gráfico da função $f\left(x\right) =e^{-x^{2}}$ explicitando domínio, intervalos de crescimento e decrescimento, concavidade, pontos de inflexdão, assíntotas, máximos e mínimos locais e globais.
Calcule o valor das seguintes expressões:
- $sen(45^0)+cos(45^0)$
- $\dfrac {cos(30^0)sen(60^0)} {tg(45^0)}$
- $[sen^2(71,2^0)+cos^2(71,2^0)] \times cotg(45^0)$
- Usando o teorema fundamental da trigonometria sabemos que o valor da expressão $sen(45^0)+cos(45^0)$ é $1$.
- Este item se resolve por substituição direta: $cos(30^0)=sen(60^0)=\dfrac{\sqrt{3}}{2}$ e $tg(45^0)=1$:$\dfrac {cos(30^0)sen(60^0)} {tg(45^0)}=\left(\dfrac{\sqrt{3}}{2}\right)^2 \times 1=\dfrac{3}{4}$.
- Usando o teorema fundamental da trigonometria sabemos que o valor da expressão $sen^2(71,2^0)+cos^2(71,2^0)$ é $1$. Além disso, temos que $cotg(45^0)=\dfrac{1}{tg(45^0)}=\dfrac{1}{1}=1$. Então:\\ $[sen^2(71,2^0)+cos^2(71,2^0)] \times cotg(45^0)=1 \times 1=1$.
Use o teorema fundamental do cálculo e a regra da cadeia para calcular a derivada da função $f(x)=\int_1^{\sin x}e^{t^2} dt$. Indique claramente a justificativa de cada passagem e, em seguida, calcule $f'(\pi)$.
Seja $f(x)=ax^2+bx+c$, onde $a>0$. Prove que $f(x)\geq 0$ para todo $x$ se, e somente se, $b^2-ac\leq 0$. [Sugestão: ache o mínimo de $f(x)$.]
Estude a função $f\left( x\right) =x^{3}-3x^{2}+3x$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Você está projetando uma lata (um cilindro de revolução) de $1000 cm^3$ cuja manufatura levará o desperdício em conta. Não há desperdício ao se cortar a lateral de alumínio, mas tanto a base como o topo, ambos de raio $r$, serão recortados de quadrados que medem $2r$ de lado.
Escreva uma fórmula que forneça a quantidade total de alumínio usada para fazer uma lata.
Qual a razão $h/r$ para a lata mais econômica?
Calcule a integral $\int \dfrac{x^{3}+x}{x-1}dx$.
De acordo com a teoria da relatividade, o comprimento de um objeto parece, a um observador, depender da velocidade relativa entre este e o objeto. Se o observador estabelecer o comprimento do objeto, em repouso, como $L_0$, então o comprimento, a uma velocidade $v$, parecerá:
$L=L_0\sqrt{1-\frac{v^2}{c^2}}$.
Esta equação é chamada Fórmula de Contração de Lorentz, sendo que $c$ é a velocidade da luz no vácuo, em torno de $3\times10^8m/s$. Qual o comportamento de $L$ conforme $v$ aumenta?
Determine $\lim\limits_{v\rightarrow c^- }L$. Por que o limite lateral à esquerda foi necessário, e como esta necessidade se relaciona com as Leis da Física?
Mostre que a função $f\left( x\right) =\sqrt[n]{x}$ é contínua em seu domínio.
Estude a função $f\left( x\right) =\sqrt[3]{x^{3}-x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Dê os domínios e esboce os gráficos de $f+g$ e $\dfrac{g}{f}$ nos seguintes casos:
- $f(x)=1$ e $g(x)=\dfrac{1}{(x-2)^2}$.
- $f(x)=1$ e $g(x)=\sqrt{x-1}$.
Dê um exemplo de função contínua em seu domínio mas que não é diferenciável em algum(ns) ponto(s).
Qual a relação entre a continuidade e a diferenciabilidade de uma função? Demonstre.
Uma das raízes da equação $x^2+mx+m^2-m-12=0$ é nula, e a outra é positiva. Qual o valor do parâmetro $m$?
Suponha que $x(t)=e^{0,05t}$ e que $z(t)=e^{0,01t}$. Calcule a taxa de crescimento de $y(t)$ nos seguintes casos:
- $y=x$
- $y=z$
Encontre todos os números naturais $k$ para os quais a seguinte afirmação é verdadeira: Se $F(x)$ é um polinômio com coeficientes inteiros que satisfaz $0\leq F(c)\leq k$ para todo $c\in\{0,1,\ldots,k+1\}$ então $F(0)=F(1)=\cdots=F(k+1).$
Dados $f(x) = x^{-1}$ e $x_0 = 0,9$, escolha um valor inteiro próximo a $x_0$ tal que $f(x_0)$ e $f'(x_0)$ sejam fáceis de calcular, e calcule uma linearização da função neste ponto.
A linearização da função $f(x)$ em torno de um ponto $x_0$ nada mais é do que assumir que ela se comporta como uma reta que passa pelo ponto $(x_0,f(x_0))$ com inclinação $f'(x_0)$.
Neste caso temos $f(x)=x^{-1}$ e $f'(x)=-x^{-2}$. Linearizando a função em torno de $1$, temos $\frac{y-f(1)}{x-1}=f'(1)=\frac{y-1}{x-1}= -1$ portanto temos
$y=2-x$
Demonstre que a derivada da função seno é a função cosseno.
Seja $f:[a,b] \to [a,b]$ uma função contínua. Prove que $f$ possui um ponto fixo, ou seja, algum valor de $x$ tal que $f(x)=x$.
Calcule os limites:
$\lim\limits_{x\to6} \frac{x^2-4 x-12}{x^2-13 x+42}$
$\lim\limits_{x\to0} \frac{x^2+2 x}{x^2-2 x}$
$\lim\limits_{x\to2} \frac{x^2+6 x-16}{x^2-3 x+2}$
$-8$
$-1$
$10$
Calcule a derivada da seguinte função:
$f\left( x\right) =\tan\left( x\right) \cos^{2}\left( x\right) .$
Prove o seguinte resultado: Se $f$ tiver um mínimo absoluto em um intervalo aberto $(a,b)$, então ele precisa ocorrer em um ponto crítico de $f$.
Se duas torneiras, de igual vazão, enchem uma piscina em $5$ horas, quanto tempo três torneiras, de mesma vazão que as primeiras, encherão a piscina?
Como duas torneiras de igual vazão enchem a piscina em $5$ horas, uma única torneira encheria em $10$ horas. Ora, $3$ torneiras de igual vazão trabalhando juntas reduziriam esse tempo de $10$ horas dividindo-o por $3$. A resposta é $10/3$ horas.
Determine o domínio de definição das funções trigonométricas inversas a seguir e expresse suas derivadas em termos de funções polinomiais:
- $g\left( x\right) =\mathrm{\arccos }\left( x\right) $;
- $g\left( x\right) =\mathrm{arcsec}\left( x\right) $;
- $g\left( x\right) =\mathrm{arccot}\left( x\right) $.
Explique por que a regra de L'Hospital não se aplica ao problema $$ \lim_{x\to 0}\dfrac{x^2\sin(1/x)}{\sin x}. $$
Ache o limite acima.
Prove que a única função contínua $f:\mathbb{R} \to \mathbb{R}$ que satisfaz $f(f(f(x)))=x$ é a função identidade $f(x)=x$. (Sugestão: Prove que se uma função é injetiva e contínua então ela é monótona).
Esboce juntas as curvas dadas no plano cartesiano e identifique cada uma com sua equação:
$y=3^x$, $y=8^x$,$y=2^{-x}$, e $y=\left( 1/4 \right)^{x}$.
Seja $S$ a região entre as curvas $y=x^n$ e $y=x^{n+1}$, onde $n$ é um inteiro, $n\geq 1$.
Considere o sólido $A_r$ obtido pela rotação de $S$ ao redor do eixo $x=r, r>1$ e considere o sólido $B_r$ obtido pela rotação de $S$ ao redor do eixo $y=r, r>1$. \\
Calcule o volume $V(A_r)$ de $A_r$, o volume $V(B_r)$ de $B_r$. Determine, se existir, ${\lim_{r\rightarrow\infty}\frac{V(A_r)}{V(B_r)}}$.
Calcule a integral a seguir utilizando decomposição de quocientes em frações parciais:
$\int{\frac{x^2dx}{(x-1)(x^2 + 2x + 1)}}$
Determine os valores de $\lambda$ que tornam contínua a função
\begin{equation*} f\left( x\right) =\left\{ \begin{array} [c]{c} x^{2}+cx\text{ se }x\leq1\\ \left( cx\right) ^{2}-1=c^{2}x^{2}-1\text{ se }x>1 \end{array} \right. \text{.} \end{equation*}
Determine o conjunto solução da equação $|x|^2+|x|-6=0$.
Escreva o polinômio $p(x)=x^2-4x-9$ em $x$ como um polinômio em $(x-3)$. (Só é necessário calcular o polinômio de Taylor em $3$, do mesmo grau do polinômio original. Por quê?)
Determine a equação da reta tangente em $\left( p,f\left(p\right) \right)$:
$f\left( x\right) =1/x^{2},\;p=1$.
$y=-2x+3$.
Será construído um campo de atletismo retangular, com $x$ unidades de comprimento, tendo nas extremidades duas áreas semicirculares com raio $r$. O campo terá em volta uma pista para corrida com $400 m$ de extensão.
Expresse a área da porção retangular do campo só em função de $x$ ou só em função de $r$ (a escolha é sua).
Quais valores de $x$ e de $r$ dão à porção retangular maior área possível?
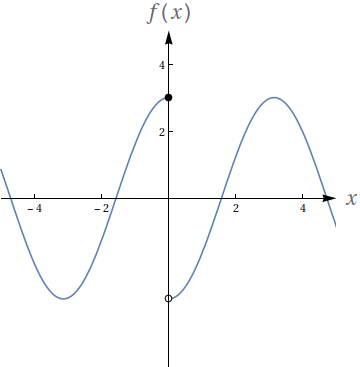
$f$ não é contínua em $x=0$.
Uma das raízes da equação $x^2-x-a = 0$ é também raiz da equação $x^2+x-(a + 20)=0$. Qual é o valor de $a$?
É mais correto se referir a uma antiderivada de $f(x)$ ou a antiderivada de $f(x)$?
O correto é uma antiderivada, já que existem infinitas antiderivadas para uma dada função.
Considere uma cápsula esférica de $1cm$ de espessura cujo volume é igual ao volume do espaço oco dentro dela. Use o método de Newton para calcular o raio externo da cápsula com duas casas decimais de precisão.
Determine se as afirmações abaixo são verdadeiras ou falsas. Justifique suas respostas ou forneça um contra exemplo.
Se $\lim\limits_{x\rightarrow a}f\left( x\right) =\infty $ e $\lim\limits_{x\rightarrow a}g\left( x\right) =0$, então $ \lim\limits_{x\rightarrow a}\dfrac{f\left( x\right) }{g\left( x\right) } =\infty $.
Sejam $p\left( x\right) $ e $q\left( x\right) $ polinômios de grau $m$ e $n$ respectivamente. Se $\lim\limits_{x\rightarrow \infty }\dfrac{p\left( x\right) }{q\left( x\right) }=0$, então $m\geq n$.
Se $\lim\limits_{x\rightarrow a}\left( f\left( x\right) g\left( x\right) \right) $ existe, então $\lim\limits_{x\rightarrow a}f\left( x\right) $ e $\lim\limits_{x\rightarrow a}g\left( x\right) $ existem e $\lim\limits_{x\rightarrow a}\left( f\left( x\right) g\left( x\right) \right) =\left( \lim\limits_{x\rightarrow a}f\left( x\right) \right) \left( \lim\limits_{x\rightarrow a}g\left( x\right) \right) .$
Se $f\left( x\right) $ e $g\left( x\right) $ são contínuas em $a$, então $\left( f+g\right) \left( x\right) $ também é contínua em $a$.
Calcule a seguinte integral:
$\int{x\cos x dx}.$
$xsinx+cosx+C$
Escreva o número $\sin 2$ como uma soma (com a notação $\Sigma$), com um erro menor que $10^{-12}$.
Seja $a$ um número real positivo e suponha que $|x|<a.$ Use o método de frações parciais para obter a fórmula $\int \frac{1}{a^2-x^2}dx=\frac{1}{2a}\ln\left(\frac{a+x}{a-x}\right) +C.$
Avalie a seguinte integral indefinida:
$\int (10x^2-2)\ dx$
$10/3x^3-2x+C$
Estude a função $f\left( x\right) =xe^{-3x}$ com relação à concavidade, pontos de inflexão, máximos e mínimos, e esboce o seu gráfico.
Esboce o gráfico de cada uma das funções abaixo.
$y=2-\sqrt{16-x^{2}}$
$y=-1+\sqrt{6-(x-1)^{2}}$
Encontre todos os pares de inteiros $m,n\geq 3$ tais que existem infinitos inteiros positivos $a$ para os quais
$\frac{a^m+a-1}{a^n+a^2-1}$ é um inteiro.
Calcule os seguintes limites. Pode ser útil usar a relação de inversão que há em relação às funções logarítmicas e exponenciais (isto é, $\ln(x)=y \Leftrightarrow e^y=x$) e/ou gráficos.
$\lim\limits_{x\rightarrow\infty}\log_3 x$
$\lim\limits_{x\rightarrow 0^+}\ln x$
$\lim\limits_{x\rightarrow -\infty}e^x$
Seja $f(x)=(x^3+1)/x$. Mostre que o gráfico de $y=f(x)$ tende à curva $y=x^2$ "assintotamente" no sentido de que $$ \lim_{x\to\pm\infty}\left[f(x)-x^2\right] = 0. $$ Esboce o gráfico de $y=f(x)$ mostrando o seu comportamento assintótico.
Considere a seguinte função:
\begin{equation*}
f(x)= \begin{cases}
(x-b)^2 -2, \quad x\geq 0
a\sin x,\quad x<0.
\end{cases}
\end{equation*}
- Encontre os valores de $a$ e $b$ tais que $f(x)$ seja contínua e diferenciável para todo $x\in\mathbb{R}.$
- Encontre o valor de $b$ tal que a reta tangente $t$ à curva $f(x)$ no ponto $x=1$ possui inclinação 2. Escreva a equação de $t.$
- Encontre o valor de $a$ tal que a reta $s$ normal à reta tangente à $f(x)$ no ponto $x=-\pi$ possui inclinação $-\frac{1}{2}$. Escreva a equação de $s$.
Observamos que para todo $x\geq 0$ a função $(x-b)^2 -2$ é contínua e que para todo $x<0$ também a função $a\sin x$ é contínua. Logo, temos que verificar a continuidade no ponto $x=0$, isto é, deve acontecer que
$\lim_{x\rightarrow 0^-}f(x)= \lim_{x\rightarrow 0^+}f(x),$
ou seja,
$\lim_{x\rightarrow 0^-}a\sin x=\lim_{x\rightarrow 0^+} (x-b)^2 -2.$
A relação anterior implica que $0= b^2-2$, ou seja $b=\pm\sqrt{2}.$ \\
Afim de achar o valor de $a$, encontramos a derivada de $f(x)$. Observamos que, sendo $a\sin x$ e $(x-b)^2 -2$ funções diferenciáveis para todo $x\in \mathbb{R}$, a derivada de $f(x)$ é a seguinte:
$f'(x)= \begin{cases}
2(x-b), \quad x> 0
a\cos x,\quad x<0.
\end{cases}$
Como queremos que $f(x)$ seja diferenciável no ponto $x=0$ também, temos que impor
$\lim_{x\rightarrow 0^-}f'(x)= \lim_{x\rightarrow 0^+}f'(x),$
ou seja,
$\lim_{x\rightarrow 0^-}a\cos x= \lim_{x\rightarrow 0^+}2(x-b).$
A relação anterior implica que $a= -2b$, então as duplas de valores para os quais $f(x)$ é contínua e diferenciável para todo $x\in \mathbb{R}$, são $(a,b)= (2\sqrt{2}, -\sqrt{2})$ ou $(a,b)=(-2\sqrt{2}, \sqrt{2}).$
Usando a função derivada calculada no ponto anterior, temos que $f'(1)= 2(1-b),$ então, como a inclinação da reta tangente deve ser 2, obtemos $2(1-b)=2$ e logo $b= 1$. A equação de $t$ é $y= f(1)+ f'(1)(x-1)$, isto é $y= -2+1\cdot(x-1)=x-3.$
Usando a função derivada calculada no ponto anterior, temos que $f'(-\pi)= a\cos (-\pi)= -a,$ então, como a inclinação da reta normal $s$ é $-\frac{1}{2}$, deve ser $-a=2$, ou seja $a=-2$. A equação de $s$ é $y= f(-\pi)-\frac{1}{2}(x+\pi)$, isto é $y= -\frac{1}{2}x -\frac{1}{2}\pi.$
Verifique que $\displaystyle \int \text{cosec}^n (x) \, dx = -\dfrac{\text{cosec}^{n-2} (x) \text{cotg} (x) }{n-1} + \dfrac{n-2}{n-1} \int \text{cosec}^{n-2} (x) \, dx, \, n \geq 2$.
Esboce o gráfico completo da função $\displaystyle f(x)=x\tan x,\ -\pi/2<x<\pi/2$, e localize todos os extremos relativos e pontos de inflexão. Utilize um recurso computacional gráfico a fim verificar seu resultado.
Prove que $\displaystyle\int \sqrt{a^2+u^2}du=\dfrac{u}{2}\sqrt{a^2+u^2}+\dfrac{a^2}{2}\ln{|u+\sqrt{a^2+u^2}|}+C$.
Segundo dados de uma pesquisa, a população de certa região do país vem decrescendo em relação ao tempo t, contado em anos, aproximadamente, segundo a relação $P(t)=P(0) \cdot 2^{-0,25t}$. Sendo $P(0)$ uma constante que representa a população inicial dessa região e $P(t)$ a população $t$ anos após, determine quantos anos se passarão para que essa população fique reduzida à quarta parte da inicial.
Para que essa população fique reduzida à quarta parte da inicial devemos ter:
$P(t) = \dfrac{1}{4} P_0$.
Substituindo a expressão de $P(t)$:
$P_0 2^{-0,25 t} = 0,25 P_0$.
Com essa expressão podemos encontrar o valor de $t$.
$2^{-0,25 t} = 0,25$.
Aplicando $log_2$ dos dois lados:
$\log_2 (2^{-0,25 t}) = \log_2(0,25)$.
Utilizando propriedade de $\log$:
$-0,25 t \log_2 2 = \log_2(0,25)$.
$t = \dfrac{\log_2(0,25)}{-0,25}$.
$t = 8$ anos.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$f(x) = x^2-3x+9$.
$(-\infty,\infty)$
O calor específico de um metal como a prata é constante a temperaturas $T$ acima de 200° K. se a temperatura do metal aumenta de $T_1$ a $T_2$, a área sob a curva $y=c/T$ de $T_1$ a $T_2$ é chamada variação de entropia $\Delta S$, que é uma medida da desordem molecular do sistema. Expresse $\Delta S$ em termos de $T_1$ e $T_2$,
Dependendo da função e limites de integração, é possível transformar uma integral imprópria em uma integral ``própria'' com mesmo valor, por meio de uma substituição apropriada.
Ilustre esse processo calculando a integral $\displaystyle \int_0^1 \sqrt{\dfrac{1+x}{1-x}} \, dx$ por meio da substituição $u=\sqrt{1-x}$.
Tente calcular diretamente a integral (utilize algum recurso computacional se a integral estiver muito difícil). Compare os resultados obtidos.
Calcule, quando existirem, os seguintes limites (caso um limite tenda a $\pm \infty $ justifique a resposta):
$\lim\limits_{x\rightarrow 2}\dfrac{x^{2}+x-6}{\left( x-2\right) ^{3}}$
$\lim\limits_{x\rightarrow - \infty }\dfrac{5x^{5}+7x^{2}+3x+\pi }{\sqrt{7}x^{5}+4x+2}$
$\lim\limits_{x\rightarrow 0}x^{3}\cos \left( \frac{1}{x}\right)e^{x^{2}+1}$
Verifique se as funções abaixo são pares, ímpares ou nenhuma das duas coisas.
$f(x)=\sin x$
$f(x)=\cos x$
- A função $\sin x$ é ímpar pois $f(-x) = \sin (-x) = -\sin(x) = -f(x)$.
- A função $\cos x$ é par pois $f(-x) = \cos (-x) = \cos(x) = f(x)$.
Use o Teorema do Valor Médio para mostrar que, $$\sqrt{y}-\sqrt{x}<\dfrac{y-x}{2\sqrt{x}},$$ quando $0<x<y$.
Use o resultado anterior para mostrar que se $x$ e $y$ forem positivos, então $$ \sqrt{xy} < \dfrac{1}{2}(x+y).$$ (A média aritmética é maior que a média geométrica).
Tente generalizar o resultado anterior para um conjunto amostral discreto de tamanho $n>2$.

