Exercícios
Funções implícitas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
A função diferenciável $z=z(x,y)$ é dada implicitamente pela equação $f\bigg(\dfrac{x}{y},\dfrac{z}{x^{\lambda}}\bigg)=0$ ($\lambda\neq 0$ um número real fixo), onde
$f(u,v)$ é suposta diferenciável e $\dfrac{\partial f}{\partial v}(u,v)\neq 0$. Verifique que
$$x\frac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=\lambda z.$$
Note que $\displaystyle \frac{\partial z}{\partial x} = \frac{\lambda z}{x} -\frac{x^{\lambda}}{y} \frac{\partial f}{\partial u} \left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\right)^{-1} $ e $\displaystyle \frac{\partial z}{\partial y} = \frac{x^{\lambda + 1}}{y^{2}} \frac{\partial f}{\partial u} \left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\right)^{-1}$.
Dado que \(\displaystyle x^3+y^2x-3=0\), determine \(\dfrac{dy}{dx}\) usando derivação implícita.
Derivando implicitamente a equação dada, temos que \(3x^2+y^2+x(2yy')-0=0\). Ou seja,
\[ \frac{dy}{dx}= -\frac{3x^2+y^2}{2xy}.\]
Suponha que a equação $F(x,y,z)=0$ defina implicitamente cada uma das três variáveis $x$,$y$ e $z$ como função das outras duas:
$z=f(x,y)$, $y=g(x,y)$ e $x=h(y,z).$ Se $F$ for diferenciável e $F_{x}$,$F_{y}$ e $F_{z}$ forem todas não nulas, mostre que
$$\frac{\partial z}{\partial x} \frac{\partial x}{\partial y}\frac{\partial y}{\partial z}=-1.$$
Note que$\displaystyle \frac{\partial z}{\partial x} = -\frac{F_{x}}{F_{z}},$$\displaystyle \frac{\partial x}{\partial y} = -\frac{F_{y}}{F_{x}}$e$\displaystyle \frac{\partial y}{\partial z} = -\frac{F_{z}}{F_{y}}.$
Suponha que a equação \(z=f(x,y)\) seja expressa na forma polar \(z=g(r,\theta)\) através da substituição \(x=r\cos\theta\) e \(y=r\sin\theta\).
Considere \(r\) e \(\theta\) como funções de \(x\) e \(y\) e use derivação implícita para mostrar que \[ \frac{\partial r}{\partial x} = \cos\theta \quad \text{e}\quad\frac{\partial\theta}{\partial x} =-\frac{\sin\theta}{r}.\]
Considere \(r\) e \(\theta\) como funções de \(x\) e \(y\) e use derivação implícita para mostrar que \[\dfrac{\partial r}{\partial y}=\sin\theta \quad \text{e}\quad \dfrac{\partial\theta}{\partial y}=\dfrac{\cos\theta}{r}.\]
Use os resultados anteriores para mostrar que \begin{align*} \dfrac{\partial z}{\partial x} & = \dfrac{\partial z}{\partial r}\cos\theta - \dfrac{1}{r}\dfrac{\partial z}{\partial\theta}\sin\theta \\ \dfrac{\partial z}{\partial y} & = \dfrac{\partial z}{\partial r}\sin\theta + \dfrac{1}{r}\dfrac{\partial z}{\partial\theta}\cos\theta\end{align*}
Use o resultado do item anterior para mostrar que \[ \left(\dfrac{\partial z}{\partial x}\right)^2 + \left(\dfrac{\partial z}{\partial y}\right)^2 = \left(\dfrac{\partial z}{\partial r}\right)^2 +\dfrac{1}{r^2}\left(\dfrac{\partial z}{\partial\theta}\right)^2. \]
Ainda usando o resultado do terceiro item, mostre que \(z=f(x,y)\) satisfaz a equação de Laplace \[ \dfrac{\partial^2z}{\partial x^2} + \dfrac{\partial^2z}{\partial y^2}= 0, \] se, e somente se, \(z=g(r,\theta)\) satisfaz a equação \[ \dfrac{\partial^2z}{\partial r^2} + \dfrac{1}{r^2}\dfrac{\partial^2z}{\partial\theta^2}+\dfrac{1}{r}\dfrac{\partial z}{\partial r} = 0. \] A última equação acima é chamada de forma polar da equação de Laplace.
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$x^{2}+y^{2}+z^{2}=3xyz$
$\displaystyle \frac{dz}{dx} = \frac{3yz - 2x}{2z - 3xy}$ e $\displaystyle \frac{dz}{dy} = \frac{3xz - 2y}{2z - 3xy} .$
A função diferenciável $z = f(x,y)$ é dada implicitamente pela equação $x^3 + y^3 + z^3 = 10$. Determine a equação do plano tangente ao gráfico de $f$ no ponto $(1,1,f(1,1))$.
$x + y + 4z = 10.$
Considere a superfície dada implicitamente por
$$x^{2}+2y^{2}+2z^{2}=-4xyz.$$
Calcule as derivadas $\dfrac{\partial z}{\partial x}$ e $\dfrac{\partial z}{\partial y}$ em um ponto genérico.
Quais os pontos nos quais as derivadas parciais calculadas no item anterior não estão definidas?
$\displaystyle \frac{\partial z}{\partial x} = -\frac{x + 2yz}{2(z + xy)} \;\;\;\text{e}\;\;\; \frac{\partial z}{\partial y} = -\frac{y + xz}{z + xy}.$
$\left\lbrace (x,y,z) \in \mathbb{R}^{3};\; z = -xy \right\rbrace$.
Encontre o valor de $\partial z/\partial x$ no ponto $(1,1,1)$ sabendo que a equação
$$xy+z^{3}x-2yz=0$$
define $z$ como uma função de duas variáveis independentes $x$ e $y$ e que a derivada parcial existe.
$\displaystyle \frac{\partial z}{\partial x} (1,1,1) = -2$.
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$xyz=\cos(x+y+z)$
$\displaystyle \frac{dz}{dx} = \frac{yz + \sin(x + y + z)}{xy + \sin(x + y + z)}$ e $\displaystyle \frac{dz}{dy} = \frac{xz + \sin(x + y + z)}{xy + \sin(x + y + z)}.$
Utilize a Equação
$$ \dfrac{dy}{dx}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}=-\dfrac{F_x}{F_y}$$
para determinar $\mathrm{d}y/\mathrm{d}x$.
$\cos(x-y)=xe^{y}$
$\displaystyle \frac{dy}{dx} = \frac{\sin(x - y) + e^{y} }{\sin(x - y) -x e^{y}} .$
Use a derivação implicíta para determinar $\partial z/\partial x$ e $\partial z/\partial y$ na expressão $x-z=\arctan(yz)$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{1 + y^{2}z^{2}}{1 + y + y^{2}z^{2}}$
$\displaystyle \frac{\partial z}{\partial y} = -\frac{z}{1 + y + y^{2}z^{2}}$.
Encontre os valores de $\partial z/ \partial x$ e $\partial z/\partial y$ no ponto indicado.
$z^{3}-xy+yz+y^{3}-2=0$, $(1,1,1).$
$\displaystyle \frac{\partial z}{\partial x}(1,1,1) = \frac{1}{4}$ e $\displaystyle \frac{\partial z}{\partial x}(1,1,1) = -\frac{3}{4}.$
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$yz=\ln(x+z)$
$\displaystyle \frac{dz}{dx} = \frac{1}{y(x+z)-1}$ e $\displaystyle \frac{dz}{dy} = \frac{z(x+z)}{y(x+z)-1}.$
De acordo com o triângulo abaixo:
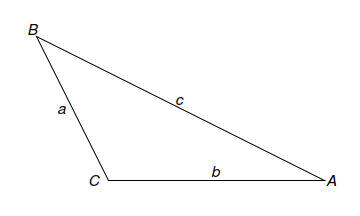
Expresse $A$ implicitamente como uma função de $a$, $b$ e $c$ e calcule $\partial A/\partial a$ e $\partial A/ \partial b.$
Expresse $a$ implicitamente como uma função de $A$, $b$ e $B$ e calcule $\partial a/ \partial A$ e $\partial a/ \partial B.$
$\displaystyle a^{2} = b^{2} + c^{2} -2bc\cos(A),\;\;\;\;\frac{\partial A}{\partial a} = \frac{a}{bc \sin (A)}\;\;\;\text{e}\;\;\;\frac{\partial A}{\partial b} = \frac{c \cos(A) - b}{bc \sin(A)}.$
$\displaystyle \frac{a}{\sin(A)} = \frac{b}{\sin(B)},\;\;\;\;\frac{\partial a}{\partial A} = \frac{a\cos(A)}{\sin(A)}\;\;\;\text{e}\;\;\;\frac{\partial a}{\partial B} = - b\csc(B) \cot(B)\sin(A).$
Utilize a Equação
$$ \dfrac{dy}{dx}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}=-\dfrac{F_x}{F_y}$$
para determinar $\mathrm{d}y/\mathrm{d}x$.
$\sqrt{xy}=1+x^{2}y$
$\displaystyle \frac{dy}{dx} = \frac{4(xy)^{3/2} - y}{x - 2x^{2}\sqrt{xy}} .$
Use a derivação implicíta para determinar $\partial z/\partial x$ e $\partial z/\partial y$ na expressão $\sin(xyz)=x+2y+3z$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{1 - yz \cos(xyz)}{xy\cos(xyz) - 3}$
$\displaystyle \frac{\partial z}{\partial y} = \frac{2 - xz \cos(xyz)}{xy\cos(xyz) - 3} $.
Encontre os valores de $\partial z/ \partial x$ e $\partial z/\partial y$ no ponto indicado.
$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-1=0$, $(2,3,6).$
$\displaystyle \frac{\partial z}{\partial x}(2,3,6) = -9$ e $\displaystyle \frac{\partial z}{\partial x}(2,3,6) = -4.$

