Exercícios
Derivadas parciais
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
O comprimento e a largura de um retângulo foram medidos como $30$ cm e $24$ cm, respectivamente, com um erro de medida de, no máximo, $0,1$ cm. Utilize as diferenciais para estimar o erro máximo cometido no cálculo da área do retângulo.
$\Delta A \approx 5.4$ cm$^{2}$.
Determine a aproximação linear da função $f(x,y) = \sqrt{20 - x^2 - 7y^2}$ em $(2,1)$ e use-a para aproximar $f(1,95; 1,08)$.
$L(x,y) = -\frac{2}{3}x - \frac{7}{3}y + \frac{20}{3}$ e $f(1,95; 1,08) \approx 2.847.$
Use a derivação implicíta para determinar $\partial z/\partial x$ e $\partial z/\partial y$ na expressão $\sin(xyz)=x+2y+3z$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{1 - yz \cos(xyz)}{xy\cos(xyz) - 3}$
$\displaystyle \frac{\partial z}{\partial y} = \frac{2 - xz \cos(xyz)}{xy\cos(xyz) - 3} $.
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização $L(x,y)$ da função naquele ponto. $f(x,y) = \dfrac{x}{x+y}, \quad (2,1)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
$L(x,y) = \frac{1}{9}x - \frac{2}{9}y + \frac{2}{3}$.
Determine as derivadas parciais de $z=\arctan \dfrac{x}{y}$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{y}{x^{2} + y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{-x}{x^{2} + y^{2}}.$
Considere a superfície dada implicitamente por
$$x^{2}+2y^{2}+2z^{2}=-4xyz.$$
Calcule as derivadas $\dfrac{\partial z}{\partial x}$ e $\dfrac{\partial z}{\partial y}$ em um ponto genérico.
Quais os pontos nos quais as derivadas parciais calculadas no item anterior não estão definidas?
$\displaystyle \frac{\partial z}{\partial x} = -\frac{x + 2yz}{2(z + xy)} \;\;\;\text{e}\;\;\; \frac{\partial z}{\partial y} = -\frac{y + xz}{z + xy}.$
$\left\lbrace (x,y,z) \in \mathbb{R}^{3};\; z = -xy \right\rbrace$.
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $y=y(x).$
Expresse $\mathrm{d} y/\mathrm{d} x$ em termos de $x$ e $y.$
$x^{2}y+\sin(y)=x$
$\displaystyle \frac{d y}{d x} = -\frac{2xy - 1}{x^{2} + \cos(y)}.$
Mostre que se \(f_x(x,y)=0\) e \(f_y(x,y)=0\) em toda uma região circular, então \(f(x,y)\) é constante nessa região.
O elipsoide $4x^{2}+2y^{2}+z^{2}=16$ intercepta o plano $y=2$ em uma elipse. Determine as equações paramétricas da reta tangente à elipse no ponto $(1,2,2).$
$x = 1 + t,$ $y = 2,$ $z = 2 - 2t$.
Seja $W(s,t)=F(u(s,t),v(s,t))$, onde $F$, $u$ e $v$ são diferenciáveis, e $u(1,0)=2$, $u_{s}(1,0)=-2$, $u_{t}(1,0)=6$, $F_{u}(2,3)=-1$, $v(1,0)=3$, $v_{s}(1,0)=5$, $v_{t}(1,0)=4$, $F_{v}(2,3)=10.$ Determine $W_{s}(1,0)$ e $W_{t}(1,0).$
$W_{s}(1,0) = 52$ e $W_{t}(1,0) = 34.$
Determine $\dfrac{ \partial f}{\partial x}$ e $\dfrac{\partial f}{\partial y}$, sendo $f(x,y)= \begin{cases}\dfrac{x+y^{4}}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= \begin{cases}\dfrac{y^{2} - x^{2} - 2xy^{4}}{(x^{2}+y^{2})^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\\text{não existe} & \quad \text{se } (x,y)=(0,0)\\\end{cases} \;\;\;\; \text{e}\\\frac{\partial f}{\partial y} &= \begin{cases}\dfrac{4x^{2}y^{3} + 2y^{5} - 2xy}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}\end{aligned}$
Suponha que, para todo $t$, $f(t^{2},2t)=t^{3}-3t$. Mostre que
$$\dfrac{\partial f}{\partial x}(1,2)=-\dfrac{\partial f}{\partial y}(1,2).$$
Tome $t = 1$ em $\displaystyle \frac{df}{dt}(t^{2},2t) = 2t \frac{\partial f}{\partial x}(t^{2},2t) + 2\frac{\partial f}{\partial y}(t^{2},2t) = 3t^{2} - 3.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=\cos^{2}(3x-y^2)$.
$\displaystyle \frac{\partial f}{\partial x} = -6\cos (3x - y^{2}) \sin(3x - y^{2}) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = 4y \cos (3x - y^{2}) \sin(3x - y^{2})$.
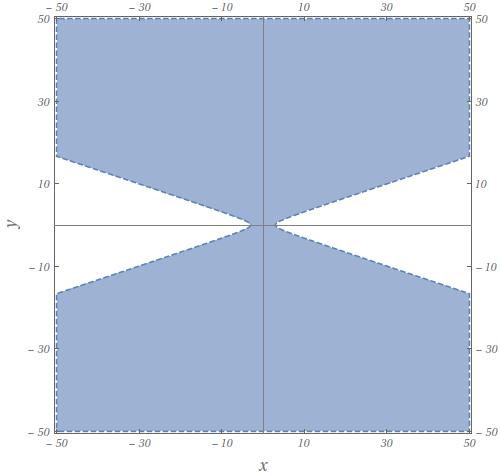
Considere a função
$$f(x,y)=\log(9-x^{2}-9y^{2}).$$
Esboce no plano $xy$ o domínio de $f.$
Calcule as derivadas parciais $f_{x}$ e $f_{y}.$
- $D_{f} = \left\lbrace (x,y) \in \mathbb{R}^{2};\; x^{2} -9y^{2} < 9 \right\rbrace$.
- $\displaystyle f_{x} = \frac{-2x}{9 - x^{2} - 9y^{2}} \;\;\;\text{e}\;\;\;f_{y} = \frac{-18y}{9 - x^{2} - 9y^{2}}$.
Determine a equação dos planos tangentes ao gráfico de $f(x,y) = - x^2 - y^2$ que passam por ambos os pontos $(1,0,7)$ e $(3,0,3)$.
$2x + 2y + z = 9$ e $2x - 2y + z = 9.$
Considere a função
$$f(x,y)=\begin{cases}\dfrac{xy}{x^{2}+y^{2}}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
A função $f$ é contínua em $(0,0)$? Justifique sua resposta.
Calcule as derivadas parciais $\dfrac{\partial f}{\partial x}(0,0)$ e $\dfrac{\partial f}{\partial y}(0,0).$
Determine $\dfrac{\partial f}{\partial x}(x,y)$ e $\dfrac{\partial f}{\partial y}(x,y)$ para $(x,y)\neq (0,0).$
$f$ é diferenciável em $(0,0)$? Justifique sua resposta.
Não, pois $\displaystyle \lim_{(x,y) \to (0,0)} f(x,y)$ não existe.
$\displaystyle \frac{\partial f}{\partial x}(0,0) = \frac{\partial f}{\partial y}(0,0) = 0$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{y^{3} - x^{2}y}{(x^{2} + y^{2})^{2}}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = \frac{x^{3} - xy^{2}}{(x^{2} + y^{2})^{2}}$.
Não, pois $f$ não é contínua em $(0,0)$ (ou: pois suas derivadas parciais não são contínuas em $(0,0)$).
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $g(x,y)=4x^{3}y^{4}+y^{3}$.
$\displaystyle \frac{\partial^{2} g}{\partial x^{2}}= 24xy^{2},\;\;\;\;\; \frac{\partial^{2} g}{\partial y^{2}}= 48x^{3} y^{2} \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} g}{\partial x\partial y}= \frac{\partial^{2} g}{\partial y\partial x}= 48x^{2}y^{3}.$
Utilize as diferenciais para estimar a quantidade de estanho em uma lata cilíndrica fechada com $8$ cm de diâmetro e $12$ cm de altura se a espessura da folha de estanho for de $0,04$ cm.
Para $V = \pi r^{2}h$ o volume da lata de raio $r$ e altura $h,$ temos $\Delta V \approx 16$ cm$^{3}.$
Seja $f(x,y)=\dfrac{1}{x^{2}+y^{2}}$. Verifique que
$x\;\dfrac{\partial ^{2}f}{\partial x^{2}}(x,y)+y\;\dfrac{\partial^{2} f}{\partial y \partial x}(x,y)=-3\dfrac{\partial f}{\partial x}(x,y)$
$\dfrac{\partial ^{2}f}{\partial x^{2}}(x,y)+\dfrac{\partial^{2} f}{\partial y^{2}}(x,y)=\dfrac{4}{(x^{2}+y^{2})^{2}}$
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= -\frac{2x}{(x^{2} + y^{2})^{2}},\;\;\;\;\; \frac{\partial^{2} f}{\partial x^{2}}= \frac{6 x^{2} - 2y^{2}}{(x^{2} + y^{2})^{3}},\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= \frac{6 y^{2} - 2x^{2}}{(x^{2} + y^{2})^{3}} \;\;\;\;\;\text{e}\\ \frac{\partial^{2} f}{\partial y\partial x} &= \frac{8xy}{(x^{2} + y^{2})^{3}}.\end{aligned}$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=x-\sqrt{y^{2}+z^{2}}$.
$\displaystyle f_{x} = 1,\;\;\;\; f_{y} = -\frac{y}{\sqrt{y^{2} + z^{2}}}\;\;\;\;\text{e}\;\;\;\; f_{z} = -\frac{z}{\sqrt{y^{2} + z^{2}}}$.
Se $z = 5x^2 + y^2$ e $(x,y)$ varia de $(1,2)$ a $(1,05; 2,1)$, compare os valores de $\Delta z$ e $dz$.
$\Delta z = 0.9225$ e $dz = 0.9$.
Se $f(u,v,w)$ é diferenciável, $u=x-y$, $v=y-z$ e $w=z-x$, mostre que
$$\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}+\frac{\partial f}{\partial z}=0.$$
Note que $\displaystyle \frac{\partial f}{\partial x} = \frac{\partial f}{\partial u} - \frac{\partial f}{\partial w}, $$\displaystyle \frac{\partial f}{\partial y} = -\frac{\partial f}{\partial u} + \frac{\partial f}{\partial v}$ e $\displaystyle \frac{\partial f}{\partial z} = -\frac{\partial f}{\partial v} + \frac{\partial f}{\partial w}.$
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = 3x^3y - xy$ em $(1,-1,f(1,-1))$.
Plano tangente: $z = -8x + 2y + 8$
Reta normal: $(x,y,z) = \left(1,-1,-2 \right) + \lambda \left(-8,2,-1 \right)$.
A fórmula de Taylor de primeira ordem para $f(\vec{a} + \vec{v})$ pode ser escrita como $ f(\vec{a}) + \nabla f(\vec{a}) \cdot \vec{v}$, já desconsiderando o termo de erro. Calcule-a para $f(x,y) = x^2/2 + y$, $\vec{a} = (0,0)$ e $\vec{v} = (1/2,1/2)$. Calcule também o erro cometido, dizendo se é um erro pequeno ou grande e por quê.
Calcule as derivadas parciais de $s = f(x,y,z,w)$ dada por $s = xw \ln{(x^2 + y^2 + z^2 + w^2)}$.
$\begin{aligned}[t]\frac{\partial s}{\partial x} &= w \left( \frac{2x^{2}}{x^{2} + y^{2} + z^{2} + w^{2}} + \ln (x^{2} + y^{2} + z^{2} + w^{2})\right),\\\frac{\partial s}{\partial y} &= \frac{2xyw}{x^{2} + y^{2} + z^{2} + w^{2}},\;\;\;\; \frac{\partial s}{\partial z} = w \frac{2xzw}{x^{2} + y^{2} + z^{2} + w^{2}}\;\;\;\;\;\text{e}\\\frac{\partial s}{\partial w} &= x \left( \frac{2w^{2}}{x^{2} + y^{2} + z^{2} + w^{2}} + \ln (x^{2} + y^{2} + z^{2} + w^{2})\right).\end{aligned}$
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}e^{\dfrac{1}{x^2 + y^2 - 1}}, & \quad \text{se } x^2 + y^2 < 1,\\0, & \quad \text{se } x^2 + y^2 \geq 1\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2}$.
Determine as derivadas parciais de primeira ordem da função $u=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdot \cdot \cdot +x_{n}^{2}}$.
$\displaystyle \frac{\partial u}{\partial x_{i}}= \frac{x_{i}}{\sqrt{x_{1}^{2}+x_{2}^{2}+\cdot \cdot \cdot +x_{n}^{2}}}$ para todo $i = 1, \cdots, n$.
Determine as derivadas parciais de $z=\dfrac{x\sin{y}}{\cos(x^{2}+y^{2})}$.
$\begin{aligned}[t]\frac{\partial z}{\partial x} &= \frac{\sin y ( \cos(x^{2} + y^{2}) + 2x^{2} \sin(x^{2} + y^{2}))}{(\cos(x^{2} + y^{2}))^{2}}\;\;\;\;\;\;\text{e}\\\frac{\partial z}{\partial y} &= \frac{x \cos y \cos(x^{2} + y^{2}) + 2xy \sin y \sin(x^{2} + y^{2})}{(\cos(x^{2} + y^{2}))^{2}}.\end{aligned}$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=e^{xy}\ln{y}$.
$\displaystyle \frac{\partial f}{\partial x} = ye^{xy}\ln y\;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = x e^{xy} \ln y + \frac{e^{xy}}{y}$.
Calcule $\mathrm{d} z/\mathrm{d} t$ por dois processos:
- substituindo as expressões para $x(t)$ e $y(t)$ em $z$ e depois derivando diretamente com relação a $t$
- aplicando a Regra da Cadeia: $\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y }\frac{dy}{dt}$.
$z=x^{2}+3y^{2}$,$x=\sin{t}$ e $y=\cos{t}.$
$\displaystyle \frac{dz}{dt} (t) = -4\sin(t)\cos(t).$
A função diferenciável $z=z(x,y)$ é dada implicitamente pela equação $f\bigg(\dfrac{x}{y},z\bigg)=0$, onde
$f(u,v)$ é suposta diferenciável e $\dfrac{\partial f}{\partial v}(u,v)\neq 0$. Verifique que
$$x\frac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=0.$$
Note que $\displaystyle \frac{\partial z}{\partial x} = - \frac{1}{y} \frac{\partial f}{\partial u} \left(\frac{x}{y},z \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},z \right)\right)^{-1}$ e $\displaystyle \frac{\partial z}{\partial y} = \frac{x}{y^{2}} \frac{\partial f}{\partial u} \left(\frac{x}{y},z \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},z \right)\right)^{-1}$.
Determine as derivadas parciais de primeira ordem da função $f(r,s)=r\ln(r^{2}+s^{2})$.
Sendo $f(r,s)=r\cdot \ln(r^{2}+s^{2})$, temos que as derivadas parciais em relação a $r$ e $s$, respectivamente, são:
$\bullet f_{r}(r,s)=1\cdot \ln(r^{2}+s^{2})+r\cdot \dfrac{1}{r^{2}+s^{2}}\cdot 2r=\ln(r^{2}+s^{2})+\dfrac{2r^{2}}{r^{2}+s^{2}}.$
$\bullet f_{s}(r,s)=0\cdot \ln(r^{2}+s^{2})+r\cdot \dfrac{1}{r^{2}+s^{2}}\cdot 2s=\dfrac{2rs}{r^{2}+s^{2}}.$
Determine as derivadas parciais de primeira ordem da função $u=te^{w/t}$.
$\displaystyle \frac{\partial u}{\partial t} = e^{w/t} \left( 1 - \frac{w}{t} \right)\;\;\;\text{e}\;\;\; \frac{\partial u}{\partial w} = e^{w/t}$.
A função $f(x,y) = \begin{cases}\dfrac{x^2y}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\\\end{cases}$ é diferenciável em $(0,0)$? Justifique.
Não.
Seja $g(x,y)=f(x^{2}+y^{2})$, onde $f:\mathbb{R}\rightarrow \mathbb{R}$ é uma função diferenciável. Mostre que
$$y\frac{\partial g}{\partial x}-x\frac{\partial g}{\partial y}=0.$$
Observe que $f$ é uma função de uma variável. Logo, utilizando a Regra da Cadeia para funções de uma variável, obtemos
$$\frac{\partial g}{\partial x}(x,y) = f'(x^2+y^2) (2x)$$
e
$$\frac{\partial g}{\partial y}(x,y) = f'(x^2+y^2) (2y).$$
Portanto
$$y\frac{\partial g}{\partial x}-x\frac{\partial g}{\partial y}=0.$$
Verifique que $\dfrac{\partial ^{2}f}{\partial x^{2}}+\dfrac{\partial ^{2}f}{\partial y^{2}}=0$, onde $f(x,y)=\ln(x^{2}+y^{2}).$
$\displaystyle \frac{\partial^{2} f}{\partial x^{2}}= \frac{2 y^{2} - 2 x^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= \frac{2 x^{2} - 2 y^{2}}{(x^{2} + y^{2})^{2}}.$
A temperatura $T$ de uma localidade do Hemisfério Norte depende da longitude $x$, da latitude $y$ e do tempo $t$, de modo que podemos escrever $T=f(x,y,t)$. Vamos medir o tempo em horas a partir do início de Janeiro.
Qual é o significado das derivadas parciais $\partial T/\partial x$, $\partial T/\partial y$ e $\partial T/\partial t$?
Honolulu (você sabe onde fica?) tem longitude de $158^{\circ}W$ e latitude de $21^{\circ}N$. Suponha que às 9 horas em $1^{\circ}$ de Janeiro esteja ventando para nordeste uma brisa quente, de forma que a oeste e a sul o ar esteja quente e a norte e leste o ar esteja mais frio. Você esperaria que $f_{x}(158,21,9)$, $f_{y}(158,21,9)$ e $f_{t}(128,21,9)$ fossem positivas ou negativas? Explique.
- $\partial T/\partial x$ é a taxa de variação da temperatura quando a longitude muda, mas a latitude e o tempo são constantes;
$\partial T/\partial y$ é a taxa de variação da temperatura quando a latitude muda, mas a longitude e o tempo são constantes;
$\partial T/\partial t$ é a taxa de variação da temperatura quando o tempo muda, mas a longitude e a latitude são constantes. - $f_{x}(158,21,9) > 0,$ $f_{y}(158,21,9) < 0$ e $f_{t}(158,21,9) > 0.$
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}\dfrac{x^3}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = 0\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$.
No item abaixo:
- expresse $\partial w/\partial u$ e $\partial w/ \partial v$ como funções de $u$ e $v$, usando a Regra da Cadeia e também expressando $w$ diretamente em termos e $u$ e $v$ antes de diferenciar;
- calcule $\partial w/\partial u$ e $\partial w/ \partial v$ no ponto dado $(u,v)$.
$w=xy+yz+xz$, $x=u+v$, $y=u-v$, $z=uv$; $(u,v)=(1/2,1).$
- $\displaystyle w(u,v) = u^{2} - v^{2} + 2u^{2}v,$$\displaystyle \frac{\partial w}{\partial u}(u,v) = 2u + 4uv$ e $\displaystyle \frac{\partial w}{\partial v}(u,v) = -2v + 2u^{2}.$
- $\displaystyle \frac{\partial w}{\partial u}(-2,0) = 3$ e $\displaystyle \frac{\partial w}{\partial v}(-2,0) = -\frac{3}{2}.$
Explique por que a função é diferenciável no ponto dado. $f(x,y) = x\sqrt{y}, \quad (1,4)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.
$t=f(u,v,w)$, onde $u=u(p,q,r,s)$, $v=v(p,q,r,s)$, $w=w(p,q,r,s)$.
$\displaystyle \frac{\partial t}{\partial p} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial p} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial p} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial p},$ $\displaystyle \frac{\partial t}{\partial q} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial q} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial q} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial q},$
$\displaystyle \frac{\partial t}{\partial r} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial r} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial r} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial r}$ e $\displaystyle \frac{\partial t}{\partial s} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial s} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial s} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial s}.$
Dado que \(\displaystyle x^3+y^2x-3=0\), determine \(\dfrac{dy}{dx}\) usando derivação implícita.
Derivando implicitamente a equação dada, temos que \(3x^2+y^2+x(2yy')-0=0\). Ou seja,
\[ \frac{dy}{dx}= -\frac{3x^2+y^2}{2xy}.\]
Suponha que \(f(x,y)\) seja uma função diferenciável no ponto \((x_0,y_0)\) e seja \(z_0=f(x_0,y_0)\). Mostre que a função \(\displaystyle g(x,y,z)=z-f(x,y)\) é diferenciável em \((x_0,y_0,z_0)\).
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = \arctan{(x - 2y)}$ em $\left(2, \dfrac{1}{2},f\left(2,\dfrac{1}{2}\right)\right)$.
Plano tangente: $4z = 2x - 4y + (\pi - 2)$
Reta normal: $(x,y,z) = \left(2,\frac{1}{2},\frac{\pi}{4} \right) + \lambda \left(\frac{1}{2},-1,-1 \right)$.
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=e^{-x}\;\sin(x+y)$.
$\displaystyle \frac{\partial f}{\partial x} = -e^{-x} \sin(x + y) + e^{-x}\cos(x + y) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = e^{-x}\cos(x + y)$.
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização $L(x,y)$ da função naquele ponto. $f(x,y) = e^{-xy} \cos{y}, \quad (\pi,0)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
$L(x,y) = 1 - \pi y$.
Calcule as derivadas parciais de $f(x,y,z) = xe^{x - y - z}$.
$\displaystyle \frac{\partial f}{\partial x} = (1 + x)e^{x - y - z},\;\;\;\; \frac{\partial f}{\partial y} = -x e^{x - y - z}\;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial f}{\partial z} = -x e^{x - y - z}.$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=e^{r}\cos{\theta}$, $r=st$, $\theta=\sqrt{s^{2}+t^{2}}$.
$\displaystyle \frac{\partial z}{\partial s} = e^{r} \left( t\cos(\theta) - \frac{s}{\sqrt{s^{2} + t^{2}}} \sin(\theta) \right) $ e $\displaystyle \frac{\partial z}{\partial t} = e^{r} \left( s\cos(\theta) - \frac{t}{\sqrt{s^{2} + t^{2}}} \sin(\theta) \right).$
Considere a função
$$f(x,y)=\begin{cases}x+y, & \quad \text{se } xy=0,\\\kappa, & \quad \text{caso contrário},\\\end{cases}$$
em que $\kappa$ é um número real. Determine as derivadas parciais de primeira ordem de $f$ em $(0,0).$
$\displaystyle \frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 1$.
Determine as derivadas parciais de $f(x,y)=e^{-x^{2}-y^{2}}$.
$\displaystyle \frac{\partial f}{\partial x} = -2xe^{-x^{2} - y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = -2ye^{-x^{2} - y^{2}}.$
Calcule $\mathrm{d} z/\mathrm{d} t$ por dois processos:
- substituindo as expressões para $x(t)$ e $y(t)$ em $z$ e depois derivando diretamente com relação a $t$
- aplicando a Regra da Cadeia: $\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y }\frac{dy}{dt}$.
$z=\ln(1+x^{2}+y^{2})$, $x=\sin{3t}$ e $y=\cos{3t}.$
$\displaystyle \frac{dz}{dt} (t) = 0.$
Explique por que a função é diferenciável no ponto dado. $f(x,y) = e^{-xy} \cos{y}, \quad (\pi,0)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
Admita que, para todo $(x,y)$,
$$4y\frac{\partial f}{\partial x}(x,y)-x\frac{\partial f}{\partial y}(x,y)=2.$$
Calcule $g^{'}(t)$, sendo $g(t)=f(2\cos{t},\sin{t})$.
$g^{'}(t) = -1.$
Se $u=f(x,y)$, onde $x=e^{s}\cos{t}$ e $y=e^{s}\sin{t}$, mostre que
$$\bigg(\dfrac{\partial u}{\partial x}\bigg)^{2}+ \bigg(\dfrac{\partial u}{\partial y}\bigg)^{2}=
e^{-2s}\bigg[ \bigg(\dfrac{\partial u}{\partial s}\bigg)^{2}+\bigg(\dfrac{\partial u}{\partial t}\bigg)^{2}\bigg].$$
Note que $\displaystyle \frac{\partial u}{\partial s} = e^{s} \cos(t) \frac{\partial u}{\partial x} + e^{s} \sin(t) \frac{\partial u}{\partial y} $e
$\displaystyle \frac{\partial u}{\partial t} = -e^{s} \sin(t) \frac{\partial u}{\partial x} + e^{s} \cos(t) \frac{\partial u}{\partial y} .$
A fórmula de Taylor de primeira ordem para $f(\vec{a} + \vec{v})$ pode ser escrita como $ f(\vec{a}) + \nabla f(\vec{a}) \cdot \vec{v}$, já desconsiderando o termo de erro. Calcule-a para $f(x,y) = x^2 + y^2$, $\vec{a} = (1,0)$ e $\vec{v} = (2,1)$. Calcule também o erro cometido, dizendo se é um erro pequeno ou grande e por quê.
Suponha que $u=f(x,y)$ e $v=g(x,y)$ verifiquem as equações de Cauchy- Riemann $u_{x}=v_{y}$ e $u_{y}=-v_{x}$. Se $x=r\cos{\theta}$ e
$y=r\sin{\theta}$, mostre que
$$\frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\partial \theta} \text{ e } \frac{\partial v}{\partial r}=-\frac{1}{r}\frac{\partial u}{\partial \theta}.$$
Note que $\displaystyle \frac{\partial u}{\partial r} = \cos(\theta) u_{x} + \sin (\theta) u_{y},$ $\displaystyle \frac{\partial v}{\partial r} = \cos(\theta) v_{x} + \sin (\theta) v_{y},$
$\displaystyle \frac{\partial u}{\partial \theta} = -r\sin(\theta) u_{x} + r \cos(\theta) u_{y}$ e $\displaystyle \frac{\partial v}{\partial \theta} = - r\sin(\theta) v_{x} + r \cos(\theta) v_{y}$.
Mostre que qualquer função da forma
$$z=f(x+at)+g(x-at)$$
é uma solução da equação de onda
$$\frac{\partial^{2} z}{\partial t^{2}}=a^{2}\frac{\partial^{2}z}{\partial x^{2}}.$$
(Sugestão: Tome $u=x+at$, $v=x-at$.)
Note que se $u = x + at$ e $v = x - at,$ então $\displaystyle \frac{\partial^{2} z}{\partial t^{2}} = a^{2}f''(u) + a^{2} g''(v)$e\\$\displaystyle \frac{\partial^{2} z}{\partial x^{2}} = f''(u) + g''(v).$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$w=xe^{y/z}$, $x=t^{2}$, $y=1-t$, $z=1+2t$.
$\displaystyle \frac{dw}{dt} = e^{\frac{y}{z}} \left(2t - \frac{x}{z} - \frac{2xy}{z^{2}} \right).$
Determine as derivadas parciais de $z=\dfrac{x^{3}+y^{2}}{x^{2}+y^{2}}$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{x^{4} + 3x^{2}y^{2} - 2xy^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{2}y(1 - x)}{(x^{2} + y^{2})^{2}}.$
Suponha que, para todo $x$,$f(3x,x^{3})=\arctan(x)$.
- Calcule $\dfrac{\partial f}{\partial x}(3,1)$ admitindo $\dfrac{\partial f}{\partial y}(3,1)=2$.
- Determine a equação do plano tangente ao gráfico de $f$ no ponto $(3,1,f(3,1))$.
- $\dfrac{\partial f}{\partial x}(3,1) = -\frac{11}{6}.$
- $\displaystyle z - \frac{\pi}{4} = -\frac{11}{6}(x - 3) + 2(y - 1).$
Determine as derivadas parciais de $z=x^{2}\ln(1+x^{2}+y^{2})$.
$\displaystyle \frac{\partial z}{\partial x} = 2x\ln(1+ x^{2} + y^{2}) + \frac{2x^{3}}{1 + x^{2} + y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{2}y}{1 + x^{2} + y^{2}}.$
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$x^{2}+y^{2}+z^{2}=3xyz$
$\displaystyle \frac{dz}{dx} = \frac{3yz - 2x}{2z - 3xy}$ e $\displaystyle \frac{dz}{dy} = \frac{3xz - 2y}{2z - 3xy} .$
Admita que, para todo $(x,y)$,
$$4y\frac{\partial f}{\partial x}(x,y)-x\frac{\partial f}{\partial y}(x,y)=0.$$
Prove que $f$ é constante sobre a elipse $\dfrac{x^{2}}{4}+y^{2}=1.$
Note que $\displaystyle \frac{dz}{dt} \left(t \right) = 0,$ para $z = f(x,y),$ $x = t$ e $\displaystyle y = \pm \sqrt{1 - \frac{t^{2}}{4}}.$
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização $L(x,y)$ da função naquele ponto. $f(x,y) = x\sqrt{y}, \quad (1,4)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
$L(x,y) = 2x + \frac{1}{4}y - 1$.
Determine a derivada parcial $f_{x}(3,4)$, onde $f(x,y)=\ln(x+\sqrt{x^{2}+y^{2}}).$
$f_{x}(3,4) = \frac{1}{5}$.
Se $R$ é a resistência equivalente de três resistores conectados em paralelo, com resistências $R_1, R_2, R_3$, então
$$\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3}.$$
Se as resistências medem, em ohms, $R_1 = 25 \Omega$, $R_2 = 40 \Omega$, $R_3 = 50 \Omega$, com margem de erro de $0,5\%$ em cada uma, estime o erro máximo no valor calculado de $R$.
$\Delta R \approx 0.059 \Omega$.
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
$z=x^{2}+xy^{3}$, $x=uv^{2}+w^{3}$, $y=u+ue^{w}$;
$\dfrac{\partial z}{\partial u}$, $\dfrac{\partial z}{\partial v}$, $\dfrac{\partial z}{\partial w}$ quando $u=2$, $v=1$, $w=0$.
$\dfrac{\partial z}{\partial u} = 85$, $\dfrac{\partial z}{\partial v} = 178$, $\dfrac{\partial z}{\partial w} = 54.$
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}\dfrac{xy}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$.
Se $z=f(x,y)$, onde $x=r^{2}+s^{2}$ e $y=2rs$, determine $\partial^{2}z/\partial r\partial s.$
$\displaystyle \frac{\partial^{2}z}{\partial r\partial s} = 4rs \frac{\partial^{2}z}{\partial x^{2}} + 4rs \frac{\partial^{2}z}{\partial y^{2}} + (4r^{2} + 4s^{2}) \frac{\partial^{2}z}{\partial x\partial y} + 2 \frac{\partial z}{\partial y}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=(xy-1)^{2}$.
$\displaystyle \frac{\partial f}{\partial x} = 2y(xy - 1)\;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = 2x (xy - 1)$.
Os lados iguais e o ângulo correspondente de um triângulo isósceles estão aumentando à razão de $3cm/h$ e $2^{\circ}/h$, respectivamente. Ache a taxa à qual a área do triângulo está aumentando no instante em que o comprimento de cada um dos
lados iguais é de $6$ metros e o ângulo correspondente é $60^{\circ}.$
$\approx 181559$ cm$^{2}/$h.
Quatro números positivos, cada um menor que $50$, são arredondados até a primeira casa decimal e depois multiplicados. Utilize os diferenciais para estimar o máximo erro possível no cálculo do produto que pode resultar do arredondamento.
Se $x,y,z,w$ são os quatro números e $p(x,y,z,w) = xyzw,$ temos $\Delta p \leq 25000.$
Suponha que $w=f(x,y)$ é diferenciável e que exista uma constante $\alpha$ tal que
$x=u\cos(\alpha)-v\sin(\alpha)$
$y=u\sin(\alpha)+v\cos(\alpha).$
Mostre que
$$\bigg(\frac{\partial w}{\partial u}\bigg)^{2}+\bigg(\frac{\partial w}{\partial v}\bigg)^{2}=\bigg(\frac{\partial w}{\partial x}\bigg)^{2}+\bigg(\frac{\partial w}{\partial y}\bigg)^{2}.$$
Note que $\displaystyle \frac{\partial w}{\partial u} = \cos(\alpha) \frac{\partial w}{\partial x} + \sin(\alpha) \frac{\partial w}{\partial y}$ e $\displaystyle \frac{\partial w}{\partial v} = -\sin(\alpha) \frac{\partial w}{\partial x} + \cos(\alpha) \frac{\partial w}{\partial y}.$
Verifique que a função $u=1/\sqrt{x^{2}+y^{2}+z^{2}}$ é uma solução da equação de Laplace tridimensional $u_{xx}+u_{yy}+u_{zz}=0.$
$\displaystyle u_{xx} = \frac{2x^{2} - y^{2} - z^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}},\;\;\; u_{yy} = \frac{2y^{2} - x^{2} - z^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}}\;\;\;\text{e}\;\;\;u_{zz} = \frac{2z^{2} - x^{2} - y^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}}$.
Determine as derivadas parciais de primeira ordem da função $u=x^{y/z}$.
$\displaystyle \frac{\partial u}{\partial x} = \frac{y}{z} x^{(y/z) - 1},\;\;\; \frac{\partial u}{\partial y} = x^{y/z} \ln x \;\;\;\text{e}\;\;\; \frac{\partial u}{\partial z} = - \frac{yx^{y/z}}{z^{2}} \ln x$.
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $f(x,y)=x^{3}y^{2}$.
$\displaystyle \frac{\partial^{2} f}{\partial x^{2}}= 2xy^{2},\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= 2x^{3}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} f}{\partial x\partial y}= \frac{\partial^{2} f}{\partial y\partial x}= 6x^{2}y.$
Seja $f(x,y)=\dfrac{x^{2}y^{2}}{x^{2}+y^{2}}.$
Calcule as derivadas parciais $\dfrac{\partial f}{\partial x}(x,y)$ e $\dfrac{\partial f}{\partial y}(x,y)$, num ponto $(x,y)\neq\;(0,0).$
Calcule o limite, se existir.
$$\lim_{(x,y)\rightarrow (0,0)}\frac{\partial f}{\partial x}(x,y)$$
$\displaystyle \frac{\partial f}{\partial x} = \frac{2xy^{4}}{(x^{2} + y^{2})^{2}} \;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = \frac{2x^{4}y}{(x^{2} + y^{2})^{2}}$.
$\displaystyle \lim_{(x,y)\rightarrow (0,0)}\frac{\partial f}{\partial x}(x,y) = 0$.
$f(t)$ e $g(x,y)$ são funções diferenciáveis tais que $g(t,f(t))=0$ para todo $t$. Suponha $f(0)=1$,
$\dfrac{\partial g}{\partial x}(0,1)=2$ e $\dfrac{\partial g}{\partial y}(0,1)=4$. Determine a equação da reta tangente a $\gamma(t)=(t,f(t))$,
no ponto $\gamma(0).$
$\displaystyle (x,y) = (0,1) + \lambda \left(1, - \frac{1}{2}\right),$ $\lambda \in \mathbb{R}.$
Determine as derivadas parciais de $z=\cos(xy)$.
$\displaystyle \frac{\partial z}{\partial x} = -y\sin(xy)\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = -x\sin(xy).$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=\displaystyle\int_{y}^{x}\cos^2t \ \mathrm{d}t$.
Sendo $f(x,y)=\displaystyle\int_{y}^{x}\cos (t^{2})\,dt$, temos que as derivadas parciais em relação a $x$ e $y$, respectivamente, são:
$\bullet \dfrac{\partial}{\partial x}f(x,y)=\dfrac{\partial}{\partial x}\bigg(\displaystyle\int_{y}^{x}\cos(t^{2})\bigg)=\cos(x^{2}).$
$\bullet \dfrac{\partial}{\partial y}f(x,y)=\dfrac{\partial}{\partial y}\bigg(\displaystyle\int_{y}^{x}\cos(t^{2})\bigg)=\dfrac{\partial}{\partial y}\bigg(-\displaystyle\int_{x}^{y}\cos(t^{2})\bigg)=-\cos(y^{2}).$
Notemos que nas soluções das derivadas parciais acima utilizamos o Teorema Fundamental do Cálculo.
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=e^{x+2y}$, $x=s/t$, $y=t/s$.
$\displaystyle \frac{\partial z}{\partial s} = e^{x + st}\left(\frac{1}{t} - \frac{2t}{s^{2}} \right) $ e $\displaystyle \frac{\partial z}{\partial t} = e^{x + st}\left(\frac{2}{s} - \frac{s}{t^{2}} \right) $.
Determine a diferencial da função $z = x^3 \ln{y^2}$.
$dz = 3x^{2} \ln (y^{2})dx + \frac{2x^{3}}{y} dy$.
Se $z=f(x,y)$, onde $f$ é diferenciável, e $x=g(t)$, $g(3)=2$, $g'(3)=5$, $f_{x}(2,7)=6$, $y=h(t)$, $h(3)=7$, $h'(3)=-4$, $f_{y}(2,7)=-8,$ determine $\mathrm{d}z/ \mathrm{d}t$ quando $t=3.$
$\displaystyle \frac{dz}{dt}(3) = 62.$
Considere a função $f(x,y) = x \ \phi\left(\frac{x}{y}\right)$, em que $\phi(u)$ é uma função derivável de uma variável. Mostre que os planos tangentes ao gráfico de $f$ passam pela origem.
Note que $x \frac{\partial f}{\partial x} (x,y) + y \frac{\partial f}{\partial y}(x,y) = f(x,y).$
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$yz=\ln(x+z)$
$\displaystyle \frac{dz}{dx} = \frac{1}{y(x+z)-1}$ e $\displaystyle \frac{dz}{dy} = \frac{z(x+z)}{y(x+z)-1}.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=e^{-xyz}$.
$\displaystyle f_{x} = -yz e^{-xyz},\;\;\;\; f_{y} = -xz e^{-xyz}\;\;\;\;\text{e}\;\;\;\; f_{z} = -xy e^{-xyz}$.
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = 4x^2 - y^2 + 2y, \quad (-1,2,4)$.
$z = -8x - 2y$.
Considere a função
$$f(x,y) = \begin{cases}\dfrac{xy}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0).\\\end{cases}$$
Mostre que $f_x(0,0)$ e $f_y(0,0)$ existem, mas $f$ não é diferenciável em $(0,0)$.
$f_{x}(0,0) = f_{y}(0,0) = 0,$ mas $\lim_{(x,y) \to (0,0)} f(x,y)$ não existe, logo $f$ é discontínua em $(0,0)$ e portanto não é diferenciável neste ponto.
A função diferenciável $z=z(x,y)$ é dada implicitamente pela equação $f\bigg(\dfrac{x}{y},\dfrac{z}{x^{\lambda}}\bigg)=0$ ($\lambda\neq 0$ um número real fixo), onde
$f(u,v)$ é suposta diferenciável e $\dfrac{\partial f}{\partial v}(u,v)\neq 0$. Verifique que
$$x\frac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=\lambda z.$$
Note que $\displaystyle \frac{\partial z}{\partial x} = \frac{\lambda z}{x} -\frac{x^{\lambda}}{y} \frac{\partial f}{\partial u} \left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\right)^{-1} $ e $\displaystyle \frac{\partial z}{\partial y} = \frac{x^{\lambda + 1}}{y^{2}} \frac{\partial f}{\partial u} \left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\right)^{-1}$.
Considere a função $F(x,y)=f\bigg(\dfrac{x}{y},\dfrac{y}{x}\bigg)$. Mostre que
$$x\dfrac{\partial F}{\partial x}+y\dfrac{\partial F}{\partial y}=0.$$
Note que$\displaystyle \frac{\partial F}{\partial x} = \frac{1}{y}\frac{\partial f}{\partial x}\left(\frac{x}{y}, \frac{y}{x} \right) - \frac{y}{x^{2}} \frac{\partial f}{\partial y}\left(\frac{x}{y}, \frac{y}{x} \right)$ e $\displaystyle \frac{\partial F}{\partial y} = -\frac{x}{y^{2}} \frac{\partial f}{\partial x}\left(\frac{x}{y}, \frac{y}{x} \right) + \frac{1}{x} \frac{\partial f}{\partial y}\left(\frac{x}{y}, \frac{y}{x} \right).$
$$x\;\dfrac{\partial z}{\partial x}+y\;\dfrac{\partial z}{\partial y}=z.$$
Primeiramente, vamos calcular $\dfrac{\partial z}{\partial x}$ e $\dfrac{\partial z}{\partial }.$ Assim,\\
$\bullet $ $\dfrac{\partial z}{\partial x}=$ $\dfrac{\partial}{\partial x}\bigg[x\cdot \sin\bigg(\dfrac{x}{y}\bigg)\bigg]=
1\cdot \sin\bigg(\dfrac{x}{y}\bigg)+x\cdot \cos \bigg(\dfrac{x}{y}\bigg)\cdot \dfrac{1}{y}$
$$=\sin\bigg(\frac{x}{y}\bigg)+\frac{x}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)$$
$\bullet $ $\dfrac{\partial z}{\partial y}=$ $\dfrac{\partial}{\partial y}\bigg[x\cdot \sin\bigg(\dfrac{x}{y}\bigg)\bigg]=
0\cdot \sin\bigg(\dfrac{x}{y}\bigg)+x\cdot \cos \bigg(\dfrac{x}{y}\bigg)\cdot \bigg(-\dfrac{x}{y^{2}}\bigg)$
$$=-\frac{x^{2}}{y^{2}}\cdot \cos\bigg(\frac{x}{y}\bigg).$$
Então,
$$x\cdot \frac{\partial z}{\partial x}+y\frac{\partial z}{\partial y}=x\cdot \bigg[\sin\bigg(\frac{x}{y}\bigg)+\frac{x}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)\bigg] +
y\cdot\bigg[ -\frac{x^{2}}{y^{2}}\cdot \cos\bigg(\frac{x}{y}\bigg)\bigg]$$
$$=x\cdot \sin\bigg(\frac{x}{y}\bigg)+\frac{x^{2}}{y}\cos\bigg(\frac{x}{y}\bigg)-\frac{x^{2}}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)$$
$$x\cdot \sin\bigg(\frac{x}{y}\bigg)=z.$$
Disseram-lhe que existe uma função $f$ cujas derivadas parciais são \[f_{x}(x,y)=x+4y \quad \mbox{e} \quad f_{y}(x,y)=3x-y,\] e cujas derivadas parciais de segunda ordem são contínuas. Você deve acreditar nisso?
Não, pois pelo Teorema de Clairaut deveria ser verdade que $f_{xy} = f_{yx},$ mas temos $f_{xy} = 4 \neq 3 = f_{yx}.$
O índice de sensação térmica $W$ é a temperatura sentida quando a temperatura real é $T$ e a velocidade do vento, $v$. Portanto, podemos escrever $W=f(T,v)$. Considerando a tabela abaixo:
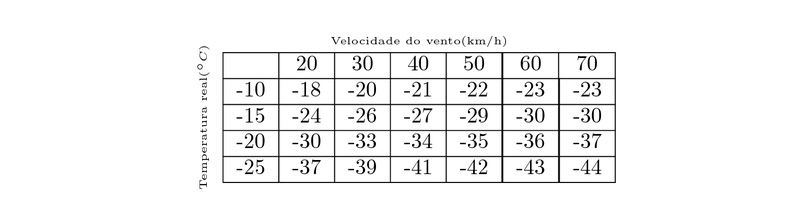
Estime os valores de $f_{T}(-15,30)$ e $f_{v}(-15,30)$. Quais são as nterpretações práticas desses valores?
Em geral, o que se pode dizer sobre o sinal de $\partial W/\partial T$ e $\partial W/\partial v$?
Qual parece ser o valor do seguinte limite
$$\lim_{v\rightarrow \infty}\frac{\partial W}{\partial v}?$$
$f_{T}(-15,30) \approx 1.3$ Isto significa que quando a temperatura real é $-15º$C e a velocidade do vento é $30$km/h, a temperatura aparente aumenta cerca de $1.3º$C para cada $1º$C que a temperatura real aumenta;\\
$f_{v}(-15,30) \approx -0.15$ Isto significa que quando a temperatura real é $-15º$C e a velocidade do vento é $30$km/h, a temperatura aparente diminui cerca de $0.15º$C para cada $1$km/h que a velocidade do vento aumenta.
$\frac{\partial W}{\partial T} > 0$ e $\frac{\partial W}{\partial v} \leq 0.$
$\lim_{v \to \infty} \frac{\partial W}{\partial v} = 0.$
O comprimento $l$, a largura $w$ e a altura $h$ de uma caixa variam com o tempo. Em certo instante, as dimensões da caixa são $l=1m$ e $w=h=2m$. $l$ e $w$ aumentam a uma taxa de $2m/s$, ao passo que $h$ diminui a uma taxa de $3m/s$. Nesse instante, determine as taxas nas quais as seguintes quantidades estão variando.
- O volume.
- A área da superfície.
- O comprimento da diagonal.
- $6$ m$^3$/s.
- $10$ m$^2$/s.
- $0$ m/s.
$z = 2x + y$ é a equação do plano tangente ao gráfico de $f(x,y)$ no ponto $(1,1,3)$. Calcule $\dfrac{\partial f}{\partial x}(1,1)$ e $\dfrac{\partial f}{\partial y}(1,1).$
$\displaystyle \frac{\partial f}{\partial x} (1,1) = 2$ e $\displaystyle \frac{\partial f}{\partial y} (1,1) = 1.$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=x^{2}y^{3}$, $x=s\cos{t}$, $y=s\sin{t}$.
$\displaystyle \frac{\partial z}{\partial s} = 2xy^{3} \cos(t) + 3x^{2}y^{2} \sin(t) $ e $\displaystyle \frac{\partial z}{\partial t} = -2sxy^{3} \sin(t) + 3 sx^{2}y^{2} \cos(t)$.
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = y \ \mbox{cos}(x-y), \quad (2,2,2)$.
$z = y$.
Use a derivação implicíta para determinar $\partial z/\partial x$ e $\partial z/\partial y$ na expressão $x-z=\arctan(yz)$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{1 + y^{2}z^{2}}{1 + y + y^{2}z^{2}}$
$\displaystyle \frac{\partial z}{\partial y} = -\frac{z}{1 + y + y^{2}z^{2}}$.
Use a definição de derivadas parciais como limites para encontrar $f_{x}(x,y)$ e $f_{y}(x,y)$, sendo $f(x,y)=x^{2}y-x^{3}y$.
$\displaystyle f_{x} = y^{2} - 3x^{2}y \;\;\;\text{e}\;\;\; f_{y} = 2xy - x^{3}$.
Determine $\partial z/\partial x$ e $\partial z/\partial y$, sendo $z=f(x)+g(y)$.
$\displaystyle \frac{\partial z}{\partial x} = f'(x)$
$\frac{\partial z}{\partial y} = g'(y)$.
Encontre os valores de $\partial z/ \partial x$ e $\partial z/\partial y$ no ponto indicado.
$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-1=0$, $(2,3,6).$
$\displaystyle \frac{\partial z}{\partial x}(2,3,6) = -9$ e $\displaystyle \frac{\partial z}{\partial x}(2,3,6) = -4.$
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = xe^{x^2 - y^2}$ em $(2,2,f(2,2))$.
Plano tangente: $z = 9x - 8y$
Reta normal: $(x,y,z) = \left(2,2,2 \right) + \lambda \left(9,-8,-1 \right)$.
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = xy$ em $\left(\dfrac{1}{2}, \dfrac{1}{2}, f\left(\dfrac{1}{2}, \dfrac{1}{2}\right)\right)$.
Plano tangente: $4z = 2x + 2y - 1$\\
Reta normal: $(x,y,z) = \left(\frac{1}{2}, \frac{1}{2}, \frac{1}{4} \right) + \lambda \left(\frac{1}{2},\frac{1}{2},-1 \right)$.
Utilize a Equação
$$ \dfrac{dy}{dx}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}=-\dfrac{F_x}{F_y}$$
para determinar $\mathrm{d}y/\mathrm{d}x$.
$\cos(x-y)=xe^{y}$
$\displaystyle \frac{dy}{dx} = \frac{\sin(x - y) + e^{y} }{\sin(x - y) -x e^{y}} .$
Determine as derivadas parciais indicadas. $w=\dfrac{x}{y+2z}$; \;\;\;\;$\dfrac{\partial^{3}w}{\partial z\partial y \partial x}$, \;\;\;\;$\dfrac{\partial^{3}w}{\partial x^{2}\partial y}$.
$\displaystyle \frac{\partial^{3}w}{\partial z\partial y \partial x} = \frac{4}{(y + 2z)^{3}}\;\;\;\text{e} \;\;\;\; \frac{\partial^{3}w}{\partial x^{2}\partial y} = 0$.
Seja $g(t)=f(3t^{2},t^{3},e^{2t})$ e suponha $\dfrac{\partial f}{\partial z}(0,0,1)=4.$
- Expresse $g^{'}(t)$ em termos das derivadas parciais de $f.$
- Calcule $g^{'}(0).$
- $\displaystyle g^{'}(t) = 6t \frac{\partial f}{\partial x}(3t^{2},t^{3},e^{2t}) + 3t^{2} \frac{\partial f}{\partial y}(3t^{2},t^{3},e^{2t}) + 2e^{2t} \frac{\partial f}{\partial z}(3t^{2},t^{3},e^{2t}).$
- $g^{'}(0) = 8.$
Determine o plano que é paralelo ao plano $z = 2x + y$ e tangente ao gráfico de $f(x,y) = x^2 + y^2$.
$z = 2x + y - \frac{5}{4}$.
$f(x,y,z)$ e $g(x,y)$ são funções diferenciáveis tais que, para todo $(x,y)$ no domínio de $g,f(x,y,g(x,y))=0$.
Suponha $g(1,1)=3$, $\dfrac{\partial f}{\partial x}(1,1,3)=2$, $\dfrac{\partial f}{\partial y}(1,1,3)=5$ e $\dfrac{\partial f}{\partial z}(1,1,3)=10.$
Determine a equação do plano tangente ao gráfico de $g$ no ponto $(1,1,3).$
$\displaystyle z - 3 = -\frac{1}{5}(x - 1) - \frac{1}{2} (y-1).$
Determine a aproximação linear da função $f(x,y,z) = \sqrt{x^2 + y^2 + z^2}$ em $(3,2,6)$ e use-a para aproximar o número $\sqrt{(3,02)^2 + (1,97)^2 + (5,99)^2}$.
Vamos determinar a aproximação linear da função $f$ em $(3,2,6)$. Primeiramente, calculamos as derivadas parcias $f_{x}$, $f_{y}$ e $f_{z}$, para todo $(x,y,z).$
$\bullet f_{x}(x,y,z)=\dfrac{1}{2}(x^{2}+y^{2}+z^{2})^{-1/2}\cdot 2x=\dfrac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}.$
$\bullet f_{y}(x,y,z)=\dfrac{1}{2}(x^{2}+y^{2}+z^{2})^{-1/2}\cdot 2y=\dfrac{y}{\sqrt{x^{2}+y^{2}+z^{2}}}.$
$\bullet f_{z}(x,y,z)=\dfrac{1}{2}(x^{2}+y^{2}+z^{2})^{-1/2}\cdot 2z=\dfrac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}.$
Agora, calculamos as derivadas parciais de $f$ no ponto $(3,2,6)$, então
$\bullet f_{x}(3,2,6)=\dfrac{3}{\sqrt{3^{2}+2^{2}+6^{2}}}=\dfrac{3}{7}.$
$\bullet f_{x}(3,2,6)=\dfrac{2}{\sqrt{3^{2}+2^{2}+6^{2}}}=\dfrac{2}{7}.$
$\bullet f_{x}(3,2,6)=\dfrac{6}{\sqrt{3^{2}+2^{2}+6^{2}}}=\dfrac{6}{7}.$
Assim, a aproximação linear da função $f$ em $(3,2,6)$ é
\begin{array}{rcl}f(x,y,z)&\approx & f(3,2,6)+f_{x}(3,2,6)(x-3)+f_{y}(3,2,6)(y-2)+f_{z}(3,2,6)(z-6)\\&=&7+\dfrac{3}{7}(x-3)+\frac{2}{7}(y-2)+\frac{6}{7}(z-6)\\&=&\dfrac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z+\bigg(7-\dfrac{9}{7}-\dfrac{4}{7}-\dfrac{36}{7}\bigg)\\&=&\dfrac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z.\end{array}
Agora, vamos aproximar o número $\sqrt{(3,02)^2 + (1,97)^2 + (5,99)^2}.$ Assim,
\begin{array}{rcl}\sqrt{(3,02)^2 + (1,97)^2 + (5,99)^2}&=&f(3,02\,,\,1,97\,,\,5,99)\\&\approx& \frac{3}{7}(3,02)+\frac{2}{7}(1,97)+\frac{6}{7}(5,99)\\&\approx& 6,9914.\end{array}
Determine as derivadas parciais de $g(x,y)=x^{y}$.
$\displaystyle \frac{\partial g}{\partial x} = yx^{y - 1}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial g}{\partial y} = x^{y} \ln x.$
Suponha que a equação $F(x,y,z)=0$ defina implicitamente cada uma das três variáveis $x$,$y$ e $z$ como função das outras duas:
$z=f(x,y)$, $y=g(x,y)$ e $x=h(y,z).$ Se $F$ for diferenciável e $F_{x}$,$F_{y}$ e $F_{z}$ forem todas não nulas, mostre que
$$\frac{\partial z}{\partial x} \frac{\partial x}{\partial y}\frac{\partial y}{\partial z}=-1.$$
Note que$\displaystyle \frac{\partial z}{\partial x} = -\frac{F_{x}}{F_{z}},$$\displaystyle \frac{\partial x}{\partial y} = -\frac{F_{y}}{F_{x}}$e$\displaystyle \frac{\partial y}{\partial z} = -\frac{F_{z}}{F_{y}}.$
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $y=y(x).$
$y^{4}+x^{2}y^{2}+x^{4}=3$
$\displaystyle \frac{d y}{d x} = - \frac{2xy^{2} + 4x^{3}}{4y^{3} + 2x^{2}y}.$
Seja $s = f(x,y,z,w)$ dada por $s = e^{\frac{x}{y} - \frac{z}{w}}$. Verifique que
$$x\dfrac{\partial s}{\partial x} + y \dfrac{\partial s}{\partial y} + z \dfrac{\partial s}{\partial z} + w \dfrac{\partial s}{\partial w} = 0.$$
$\begin{aligned}[t]\frac{\partial s}{\partial x} &= \frac{1}{y} e^{\frac{x}{y} - \frac{z}{w}},\;\;\;\;\;\frac{\partial s}{\partial y} = -\frac{x}{y^{2}} e^{\frac{x}{y} - \frac{z}{w}},\\\frac{\partial s}{\partial z} &= -\frac{1}{w} e^{\frac{x}{y} - \frac{z}{w}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial s}{\partial w} = \frac{z}{w^{2}} e^{\frac{x}{y} - \frac{z}{w}}.\end{aligned}$
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $z=e^{x^{2}-y^{2}}$.
$\begin{aligned}[t]\frac{\partial^{2} z}{\partial x^{2}} &= 2e^{x^{2} - y^{2}}(1 + 2x^{2}),\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= 2e^{x^{2} - y^{2}}(2y^{2} - 1) \;\;\;\;\;\text{e}\\\frac{\partial^{2} z}{\partial x\partial y} &= \frac{\partial^{2} z}{\partial y\partial x}= -4xye^{x^{2} - y^{2}}.\end{aligned}$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=\arcsin(x-y)$, $x=s^{2}+t^{2}$, $y=1-2st$.
$\displaystyle \frac{\partial z}{\partial s} = \displaystyle \frac{\partial z}{\partial t} = \frac{2s + 2t}{\sqrt{1 - (x - y)^{2}}}$.
Encontre os valores de $\partial z/ \partial x$ e $\partial z/\partial y$ no ponto indicado.
$z^{3}-xy+yz+y^{3}-2=0$, $(1,1,1).$
$\displaystyle \frac{\partial z}{\partial x}(1,1,1) = \frac{1}{4}$ e $\displaystyle \frac{\partial z}{\partial x}(1,1,1) = -\frac{3}{4}.$
Verifique que $x\;\dfrac{\partial ^{2}z}{\partial x \partial y}+y\;\dfrac{\partial ^{2}z}{\partial y^{2}}=0$, onde $z=(x+y)e^{x/y}.$
$\displaystyle \frac{\partial^{2} z}{\partial x \partial y}= \frac{-3xy - x^{2}}{y^{3}}e^{\frac{x}{y}} \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= \frac{3x^{2}y + x^{3}}{y^{4}}e^{\frac{x}{y}}.$
Seja $f(x,y,z) = \dfrac{x}{x^2 + y^2 + z^2}$.
Verifique que
$$x\dfrac{\partial f}{\partial x} + y\dfrac{\partial f}{\partial y} + z\dfrac{\partial f}{\partial z} = -f.$$
$\displaystyle \frac{\partial f}{\partial x} = \frac{-x^{2} + y^{2} + z^{2}}{(x^{2} + y^{2} + z^{2})^{2}},\;\;\;\; \frac{\partial f}{\partial y} = \frac{-2xy}{(x^{2} + y^{2} + z^{2})^{2}} \;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial f}{\partial z} = \frac{-2xz}{(x^{2} + y^{2} + z^{2})^{2}}.$
São mostradas as curvas de nível de uma função $f.$ Determine se as seguintes derivadas parciais são positivas ou negativas no ponto $P.$
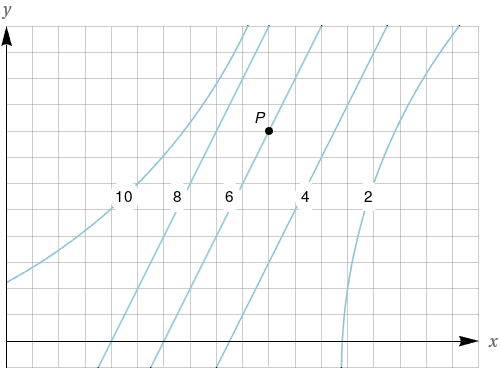
$f_{x}$
$f_{xx}$
$f_{yy}$$f_{y}$
$f_{xy}$
Negativa
Positiva
Positiva
Negativa
Positiva
De acordo com a lei dos gases ideais, a pressão, a temperatura e o volume de um gás confinado estão relacionados por \( P=kT/V\), onde \(k\) é uma constante. Use diferenciais para aproximar a variação percentual na pressão se a temperatura de um gás tiver crescido em \(3\%\) e o volume tiver crescido em \(5\%\).
Determine a diferencial da função $R = \alpha\beta^2 \cos{\lambda}$.
$dR = \beta^{2} \cos(\gamma) d\alpha + 2\gamma \beta \cos (\gamma) d\beta - \alpha \beta^{2} \sin(\gamma) d\gamma$.
A resistência total \(R\) de três resistores \(R_1\), \(R_2\) e \(R_3\) ligados em paralelo é dada por \[ \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}. \] Suponha que \(R_1\), \(R_2\) e \(R_3\) tenham sido medidos como \(100\ \Omega\), \(200\ \Omega\) e \(300\ \Omega\), respectivamente, com um erro máximo de \(10\%\) em cada um e sendo \(\Omega\)(Ohm) a unidade de medida no sistema internacional de unidades. Use diferenciais para aproximar o erro percentual máximo no valor calculado de \(R\).
Encontre o valor de $\partial z/\partial x$ no ponto $(1,1,1)$ sabendo que a equação
$$xy+z^{3}x-2yz=0$$
define $z$ como uma função de duas variáveis independentes $x$ e $y$ e que a derivada parcial existe.
$\displaystyle \frac{\partial z}{\partial x} (1,1,1) = -2$.
Determine os planos que são tangentes ao gráfico de $f(x,y) = x^2 + y^2$ e que contenham a interseção dos planos $x + y + z = 3$ e $z = 0$.
$z = 0$ e $z = 6x + 6y - 18.$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=\tan^{-1}(x/y)$, $x=e^{t}$, $y=1-e^{-t}$.
$\displaystyle \frac{dz}{dt} = \frac{xe^{-t} - ye^{t}}{x^{2} + y^{2}}.$
Determine as derivadas parciais de $f(x,y)=\sqrt[3]{x^{3}+y^{2}+3}$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{x^{2}}{\sqrt[3]{(x^{3} + y^{3} + 3)^{2}}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = \frac{2y}{3 \sqrt[3]{(x^{3} + y^{3} + 3)^{2}}} .$
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $z=z(x,y)$.
Expresse $\partial z /\partial x$ e $\partial z/\partial y$ em termos de $x$, $y$ e $z.$
$x^{3}+y^{3}+z^{3}=x+y+z$
$\displaystyle \frac{\partial z}{\partial x} = -\frac{3x^{2} - 1}{3z^{2} - 1}$ e $\displaystyle \frac{\partial z}{\partial y} = -\frac{3y^{2} - 1}{3z^{2} - 1}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=1/(x+y)$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} = -\frac{1}{(x^{2} + y^{2})^{2}}$.
Quando o tamanho das moléculas e suas forças de atração são levadas em conta, a pressão $P$, o volume $V$ e a temperatura $T$
de um mol de gás confinado estão relacionados pela {\it equação de van der Waals}
$$\bigg(P+\frac{a}{V^{2}}\bigg)(V-b)=kT,$$
em que $a$, $b$ e $k$ são constantes positivas. Se $t$ é o tempo, estabeleça uma fórmula para $\mathrm{d}T/ \mathrm{d}t$ em termos de $\mathrm{d}P/\mathrm{d} t$,
$\mathrm{d} V/\mathrm{d}t$, $P$ e $V$.
$\displaystyle \frac{dT}{dt} = \frac{1}{k} \left( \left(\frac{dP}{dt} - \frac{2a}{V^{3}} \frac{dV}{dt}\right)(V - b) + \left( P + \frac{a}{V^{2}} \right) \frac{dV}{dt} \right).$
Determine as derivadas parciais de $z=(x^{2}+y^{2})\ln(x^{2}+y^{2})$.
$\displaystyle \frac{\partial z}{\partial x} = 2x(1 + \ln(x^{2} + y^ {2}))\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = 2y(1 + \ln(x^{2} + y^ {2})).$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=x^{5}+3x^{3}y^{2}+3xy^{4}$.
$\displaystyle \frac{\partial f}{\partial x} = 5x^{4} + 9x^{2}y^{2} + 3y^{4}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = 2x^{3}y + 12xy^{3}$.
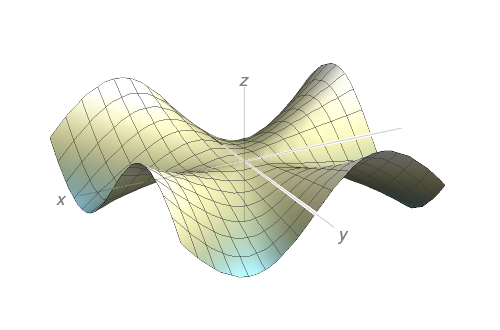
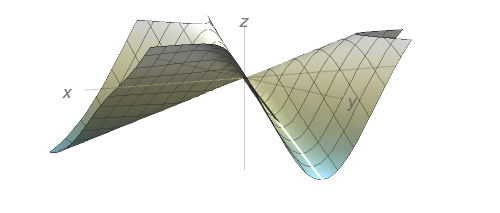
Seja
$$f(x,y)=\begin{cases}\dfrac{x^{3}y-xy^{3}}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
Use um computador para traçar o gráfico de $f$.
Determine $f_{x}(x,y)$ e $f_{y}(x,y)$ quando $(x,y)\neq (0,0).$
Determine $f_{x}(0,0)$ e $f_{y}(0,0)$ use a definição das derivadas parciais como limite.
Mostre que $f_{xy}(0,0)=-1$ e $f_{yx}(0,0)=1$
O resultado da parte (d) contradiz o Teorema de Clairaut? Use o gráfico de $f_{xy}$ e $f_{yx}$ para ilustrar sua resposta.
- Gráfico de $f$:
- $\displaystyle f_{x} = \frac{x^{4}y + 4x^{2}y^{3} - y^{5}}{(x^{2} + y^{2})^{2}}\;\;\text{e}\;\;f_{y} = \frac{x^{5} - 4x^{3}y^{2} - xy^{4} }{(x^{2} + y^{2})^{2}}$ quando $(x,y)\neq (0,0).$
- $f_{x}(0,0) = f_{y}(0,0) = 0$.
- Use $\displaystyle f_{xy}(0,0)= \lim_{h \to 0} \frac{f_{x}(0,h) - f_{x}(0,0)}{h}\;\;\text{e}\;\;f_{yx}(0,0)= \lim_{h \to 0} \frac{f_{y}(h,0) - f_{y}(0,0)}{h}$.
- Para $(x,y) \neq (0,0),$ $\displaystyle f_{xy} = {x^{6} + 9x^{4}y^{2} - 9x^{2}y^{4} - y^{6}}{(x^{2} + y^{2})^{3}}.$ Como $f_{xy}$ não é contínua na origem, não há uma contradição com o Teorema de Clairaut. Os gráficos de $f_{xy}$ e $f_{yx}$ são idênticos, exceto na origem:
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $z=z(x,y)$.
Expresse $\partial z /\partial x$ e $\partial z/\partial y$ em termos de $x$, $y$ e $z.$
$e^{x+y+z}+xyz=1$
$\displaystyle \frac{\partial z}{\partial x} = - \frac{e^{x + y + z} + yz}{e^{x + y + z} + xy}$ e $\displaystyle \frac{\partial z}{\partial y} = - \frac{e^{x + y + z} + xz}{e^{x + y + z} + xy}.$
Se $z = x^2 - xy + 3y^2$ e $(x,y)$ varia de $(3;-1)$ a $(2,96;-0,95)$, compare os valores de $\Delta z$ e $dz$.
$\Delta z = -0.7189$ e $dz = -0.73$.
Expresse $\partial z/\partial t$ em termos das derivadas parciais de $f$, sendo $z=f(x,y)$ e $x=\sin{3t}$ e $y=\cos{2t}.$
$\displaystyle \frac{dz}{dt} (t) = 3 \cos(3t) \frac{\partial f}{\partial x}(\sin(3t),\cos(2t)) - 2\sin(2t) \frac{\partial f}{\partial y}(\sin(3t),\cos(2t)).$
O raio $r$ e a altura $h$ de um cilindro circular reto aumentam à razão de $0,01cm/min$ e $0,02cm/min$, respectivamente.
- Ache a taxa de variação do volume quando $r=4cm$ e $h=7cm.$
- A que taxa a área da superfície curva está variando nesse instante?
- $0,88\pi$ cm$^{3}/$min.
- $0,3\pi$ cm$^{2}/$min.
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = x^2 + y^2$ em $(0,1,f(0,1))$.
Plano tangente: $z = 2y - 1$
Reta normal: $(x,y,z) = \left(0,1,1 \right) + \lambda \left(0,2,-1 \right)$.
No item abaixo:
- expresse $\partial w/\partial u$ e $\partial w/ \partial v$ como funções de $u$ e $v$, usando a Regra da Cadeia e também expressando $w$ diretamente em termos e $u$ e $v$ antes de diferenciar;
- calcule $\partial w/\partial u$ e $\partial w/ \partial v$ no ponto dado $(u,v)$.
$w=\ln(x^{2}+y^{2}+z^{2})$, $x=ue^{v}\sin{u}$, $y=ue^{v}\cos{u}$, $z=ue^{v}$; $(u,v)=(-2,0).$
- $\displaystyle w(u,v) = \ln(2) + 2\ln(u) + 2v,$$\displaystyle \frac{\partial w}{\partial u}(u,v) = \frac{2}{u}$ e $\displaystyle \frac{\partial w}{\partial v}(u,v) = 2.$
- $\displaystyle \frac{\partial w}{\partial u}(-2,0) = -1$ e $\displaystyle \frac{\partial w}{\partial v}(-2,0) = 2.$
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função diferenciável de uma variável real e seja $f(x,y)=(x^{2}+y^{2})\phi \bigg(\dfrac{x}{y}\bigg).$
Mostre que
$$x\;\frac{\partial f}{\partial x}+y\;\frac{\partial f}{\partial y}=2f.$$
$\displaystyle \frac{\partial f}{\partial x} = 2x \phi \left( \frac{x}{y} \right) + \frac{(x^{2} + y^{2})}{y} \phi'\left( \frac{x}{y} \right)\ \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 2y \phi \left( \frac{x}{y} \right) - \frac{x(x^{2} + y^{2})}{y^{2}} \phi'\left( \frac{x}{y} \right).$
Seja $g(t)=f(3t,2t^{2}-1).$
- Expresse $g^{'}(t)$ em termos das derivadas parciais de $f$.
- Calcule $g^{'}(0)$ admitindo $\dfrac{\partial f}{\partial x}(0,-1)=\dfrac{1}{3}.$
- $\displaystyle g'(t) = 3\frac{\partial f}{\partial x}(3t,2t^{2} - 1) + 4t \frac{\partial f}{\partial y}(3t,2t^{2} - 1).$
- $g'(0) = 1.$
A função $f(x,y) = \begin{cases}\dfrac{x^4}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\\\end{cases}$ é diferenciável em $(0,0)$? Justifique.
Sim.
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função de uma variável real, diferenciável e tal que $\phi '(1)=4.$ Seja $g(x,y)=\phi\bigg(\dfrac{x}{y}\bigg).$ Calcule
$\dfrac{\partial g}{\partial x}(1,1)$.
$\dfrac{\partial g}{\partial y}(1,1)$.
$\displaystyle \frac{\partial g}{\partial x} = \frac{1}{y} \phi'\left( \frac{x}{y} \right)$
$\displaystyle \frac{\partial g}{\partial y} = -\frac{x}{y^{2}} \phi' \left( \frac{x}{y} \right).$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=\sqrt{x^{2}+y^{2}}$, $x=e^{2t}$, $y=e^{-2t}$.
$\displaystyle \frac{dz}{dt} = \frac{2xe^{2t} - 2ye^{2t}}{\sqrt{x^{2} + y^{2}}}.$
A função $f(x,y) = \begin{cases}\dfrac{x^2 - y^2}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\\\end{cases}$ é diferenciável em $(0,0)$? Justifique.
Não.
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = \sqrt{xy}, \quad (1,1,1)$.
$x + y - 2z = 0$.
Mostre que se \(f\) é diferenciável e \(z=xf(x/y)\), então todos os pontos planos tangentes ao gráfico dessa equação passam pela origem.
Seja $w=f(x,y,z)$ uma função de três variáveis independentes. Escreva a definição formal de derivada parcial $\partial f/\partial z$ em $(x_{0},y_{0},z_{0})$. Use essa definição para encontrar $\partial f/\partial z$ em $(1,2,3)$ para $f(x,y,z)=x^{2}yz^{2}.$
$\displaystyle \frac{\partial f}{\partial z}(1,2,3) = 12$.
Determine os planos tangentes ao gráfico de $f(x,y) = 2 + x^2 + y^2$ e que contenham o eixo $x$.
$z = 2\sqrt{2} y$ e $z = -2\sqrt{2} y.$
A função $p=p(V,T)$ é dada implicitamente pela equação $pV=nRT$, onde $n$ e $R$ são constantes não-nulas (Lei dos Gases Ideais). Calcule $\dfrac{\partial p}{\partial V}$ e $\dfrac{\partial p}{\partial T}.$
$\displaystyle \frac{\partial p}{\partial V} = -\frac{nRT}{V^{2}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial p}{\partial T} = \frac{nR}{V}.$
Se $z=f(x,y)$, onde $x=r\cos{\theta}$ e $y=r\sin{\theta}$,
- Determine $\dfrac{\partial z}{\partial r}$ e $\dfrac{\partial z}{\partial \theta}.$
- Mostre que $\bigg(\dfrac{\partial z}{\partial x}\bigg)^{2}+ \bigg(\dfrac{\partial z}{\partial y}\bigg)^{2}=\bigg(\dfrac{\partial z}{\partial r}\bigg)^{2}+\dfrac{1}{r^{2}}\bigg(\dfrac{\partial z}{\partial \theta}\bigg)^{2}$.
- $\displaystyle \frac{\partial z}{\partial r} = \cos(\theta) \frac{\partial z}{\partial x} + \sin(\theta) \frac{\partial z}{\partial y} $e$\displaystyle \frac{\partial z}{\partial \theta} = -r \sin(\theta)\frac{\partial z}{\partial x} + r\cos(\theta) \frac{\partial z}{\partial y}.$
- Use $(a)$ para calcular $\bigg(\dfrac{\partial z}{\partial r}\bigg)^{2}+\dfrac{1}{r^{2}}\bigg(\dfrac{\partial z}{\partial \theta}\bigg)^{2}$.
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = 2x^2y$ em $(1,1,f(1,1))$.
Plano tangente: $z = 4x + 2y - 4$
Reta normal: $(x,y,z) = \left(1,1,2 \right) + \lambda \left(4,2,-1 \right)$.
Nos item abaixo:
- expresse $\mathrm{d} w/\mathrm{d} t$ como uma função de $t$, usando a Regra da Cadeia, expressando $w$ em termos de $t$ e diferenciando em relação a $t$;
- calcule $\mathrm{d} w/\mathrm{d} t$ no valor dado de $t$.
$w=x^{2}+y^{2}$, $x=\cos{t}+\sin{t}$, $y=\cos{t}-\sin{t}$; $t=0.$
- $\displaystyle \frac{dw}{dt}(t) = 0.$
- $\displaystyle \frac{dw}{dt}(0) = 0.$
Determine as derivadas parciais de $z=xye^{xy}$.
$\displaystyle \frac{\partial z}{\partial x} = ye^{xy} (1 + xy) \;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = xe^{xy} (1 + xy).$
Verifique que a função $f(x,y) = x^4 + y^3$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Expresse $\partial z/\partial t$ em termos das derivadas parciais de $f$, sendo $z=f(x,y)$ e $x=t^{2}$ e $y=3t.$
$\displaystyle \frac{dz}{dt} (t) = 2t \frac{\partial f}{\partial x}(t^{2},3t) + 3 \frac{\partial f}{\partial y}(t^{2},3t).$
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $z=\ln(1+x^{2}+y^{2})$.
$\begin{aligned}[t]\frac{\partial^{2} z}{\partial x^{2}} &= \frac{2 + 2y^{2} - 2x^{2}}{(1 + x^{2} + y^{2})^{2}},\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= \frac{2 + 2x^{2} - 2y^{2}}{(1 + x^{2} + y^{2})^{2}} \;\;\;\;\;\text{e}\\\frac{\partial^{2} z}{\partial x\partial y} &= \frac{\partial^{2} z}{\partial y\partial x}= \frac{-4xy}{(1 + x^{2} + y^{2})^{2}}.C\end{aligned}$
Explique por que a função é diferenciável no ponto dado. $f(x,y) = \dfrac{x}{x+y}, \quad (2,1)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
Seja $z=f(u+2v,u^{2}-v)$. Expresse $\partial z/\partial u$ e $\partial z/\partial v$ em termos das
derivadas parciais de $f$.
$\displaystyle \frac{\partial z}{\partial u}(u,v) = \frac{\partial f}{\partial x}(u + 2v,u^{2} - v) + 2u \frac{\partial f}{\partial y}(u + 2v,u^{2} - v)$ e\\ $\displaystyle \frac{\partial z}{\partial v}(u,v) = 2 \frac{\partial f}{\partial x}(u + 2v,u^{2} - v) - \frac{\partial f}{\partial y}(u + 2v,u^{2} - v).$
Utilize a Equação
$$ \dfrac{dy}{dx}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}=-\dfrac{F_x}{F_y}$$
para determinar $\mathrm{d}y/\mathrm{d}x$.
$\sqrt{xy}=1+x^{2}y$
$\displaystyle \frac{dy}{dx} = \frac{4(xy)^{3/2} - y}{x - 2x^{2}\sqrt{xy}} .$
$2x + y + 3z = 6$ é a equação do plano tangente ao gráfico de $f(x,y)$ no ponto $(1,1,1)$.
Calcule $\dfrac{\partial f}{\partial x}(1,1)$ e $\dfrac{\partial f}{\partial y}(1,1)$.
Determine a equação da reta normal no ponto $(1,1,1).$
$\displaystyle \frac{\partial f}{\partial x} (1,1) = -\frac{2}{3}$ e $\displaystyle \frac{\partial f}{\partial y} (1,1) = -\frac{1}{3}.$
$(x,y,z) = (1,1,1) + \lambda (2,1,3)$.
Determine a equação do plano que é tangente ao paraboloide $z = 2x^2 + 3y^2$ e paralelo ao plano $4x - 3y - z = 10$.
$4x - 3y - z = -\frac{11}{4}$.
Seja $z=e^{y}\phi(x-y)$, onde $\phi$ é uma função diferenciável de uma variável real. Mostre que $$\dfrac{\partial z}{\partial x}+\dfrac{\partial z}{\partial y}=z.$$
$\displaystyle \frac{\partial z}{\partial x} = e^{y}\phi'(x-y) \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = e^{y} \phi(x-y) -e^{y}\phi' (x-y).$
Verifique que a função \(\displaystyle u(x,t)=\sin(x-ct)\) é uma solução da equação da onda unidimensional \[ \dfrac{\partial^2u}{\partial t^2} = c^2\dfrac{\partial^2u}{\partial x^2}, \] onde \(c\) é uma constante que depende das características da onda.
Calculando diretamente as derivadas parciais da função dada, temos
\[\begin{array}{ll} \dfrac{\partial u}{\partial x} = \cos(x-ct), & \dfrac{\partial^2u}{\partial x^2}= -\sin(x-ct) \\ \dfrac{\partial u}{\partial t} = -c\cos(x-ct), & \dfrac{\partial^2 u}{\partial t^2}= -c^2\sin(x-ct). \end{array}\] Assim, podemos ver que \(u(x,t)\) satisfaz a equação dada.
Verifique que a função $f(x,y) = \arctan{xy}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=e^{-(x^{2}+y^{2}+z^{2})}$.
$\displaystyle f_{x} = -2xe^{-(x^{2} + y^{2} + z^{2})},\;\;\;\; f_{y} = -2ye^{-(x^{2} + y^{2} + z^{2})}\;\;\;\;\text{e}\;\;\;\; f_{z} = -2ze^{-(x^{2} + y^{2} + z^{2})}$.
A função diferenciável $z = f(x,y)$ é dada implicitamente pela equação $x^3 + y^3 + z^3 = 10$. Determine a equação do plano tangente ao gráfico de $f$ no ponto $(1,1,f(1,1))$.
$x + y + 4z = 10.$
Considere a função $f(x,y) = x \ g(x^2 - y^2)$, em que $g(u)$ é uma função derivável de uma variável. Mostre que o plano tangente ao gráfico de $f$ no ponto $(a,a,f(a,a))$ passa pela origem.
Note que $a \frac{\partial f}{\partial x} (a,a) + a \frac{\partial f}{\partial y}(a,a) = f(a,a).$
As seguintes superfícies, rotuladas $a$, $b$ e $c$ de cima para baixo, são gráficos de uma função $f$ e de suas derivadas parciais $f_{x}$ e $f_{y}$. Identifique cada superfície e dê razões para sua escolha.
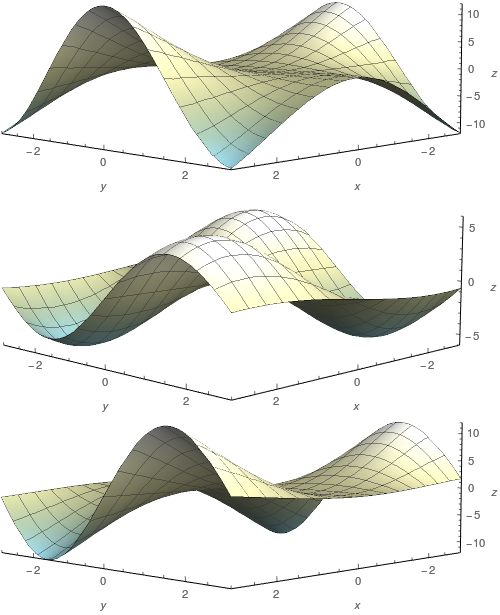
a) $f_{y},$ b) $f_{x},$ c) $f$.
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=(x^{2}+y^{2}+z^{2})^{-1/2}$.
$\begin{aligned}[t]f_{x} &= -x(x^{2} + y^{2} + z^{2})^{-3/2},\;\; f_{y} = -y(x^{2} + y^{2} + z^{2})^{-3/2}\;\;\text{e}\\f_{z} &= -z(x^{2} + y^{2} + z^{2})^{-3/2}.\end{aligned}$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=\dfrac{x-y}{x+y}$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{2y}{(x + y)^{2}}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = -\frac{2x}{(x + y)^{2}}$.
Verifique que a função $f(x,y) = x^2y$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Considere a função $z=\dfrac{xy^{2}}{x^{2}+y^{2}}.$ Verifique que $x\dfrac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=z.$
$\displaystyle \frac{\partial z}{\partial x} = \frac{y^{4} - x^{2}y^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{3}y}{(x^{2} + y^{2})^{2}}.$
Mostre que a função $f(x,y) = xy - 5y^2$ é diferenciável achando os valores $\varepsilon_1$ e $\varepsilon_2$ que satisfaçam a Definição $7$ da Seção $14.4$ do Stewart.
$\epsilon_{1} = \Delta y$ e $\epsilon_{2} = -5\Delta y$.
Encontre $\partial w/ \partial r$ quando $r=1$, $s=-1$ se $w=(x+y+z)^{2}$, $x=r-s$, $y=\cos(r+s)$, $z=\sin(r+s).$
$\displaystyle \frac{\partial w}{\partial r}(x(1,-1),y(1,-1),z(-1,1)) = 12.$
Calcule $\mathrm{d} z/\mathrm{d} t$ por dois processos:
- substituindo as expressões para $x(t)$ e $y(t)$ em $z$ e depois derivando diretamente com relação a $t$
- aplicando a Regra da Cadeia: $\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y }\frac{dy}{dt}$.
$z=\sin(xy)$, $x=3t$ e $y=t^{2}.$
$\displaystyle \frac{dz}{dt} (t) = 9t^{2}\cos(3t^{3}).$
Mostre que o plano tangente ao parabolóide $z = x^2 + y^2$ no ponto $(1,2,5)$ intercepta o plano $xy$ na reta
$$\begin{cases}2x + 4y - 5 = 0 \\z = 0\end{cases}.$$
Note que o plano tangente no ponto $(1,2,5)$ é $z = 2x + 4y - 5$.
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=x^{2}y+xy^{2}$, $x=2+t^{2}$, $y=1-t^{3}$.
$\displaystyle \frac{dz}{dt} = 4(2xy + y^{2} )^{3} - 3 (x^{2} + 2xy)t^{2}.$
Nos item abaixo:
- expresse $\mathrm{d} w/\mathrm{d} t$ como uma função de $t$, usando a Regra da Cadeia, expressando $w$ em termos de $t$ e diferenciando em relação a $t$;
- calcule $\mathrm{d} w/\mathrm{d} t$ no valor dado de $t$.
$w=x^{2}+y^{2}$, $x=\cos{t}$, $y=\sin{t}$; $t=\pi.$
- $\displaystyle \frac{dw}{dt}(t) = 0.$
- $\displaystyle \frac{dw}{dt}(\pi) = 0.$
Determine as derivadas parciais de $f(x,y)=(4xy-3y^{3})^{3}+5x^{2}y$.
$\displaystyle \frac{\partial f}{\partial x} = 12 y (4xy - 3y^{3})^{2} + 10xy\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 3(4xy - 3y^{2})^{2}(4x - 9y^{2}) + 5x^{2}.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=1+xy^{2}-2z^{2}$.
$\displaystyle f_{x} = 1+ y^{2} ,\;\;\;\; f_{y} = 2xy \;\;\;\;\text{e}\;\;\;\; f_{z} = -4z$.
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=\ln(x+2y+3z)$.
$\displaystyle f_{x} = \frac{1}{x + 2y + 3z},\;\;\;\; f_{y} = \frac{2}{x + 2y + 3z}\;\;\;\;\text{e}\;\;\;\; f_{z} = \frac{3}{x + 2y + 3z}$.
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$xyz=\cos(x+y+z)$
$\displaystyle \frac{dz}{dx} = \frac{yz + \sin(x + y + z)}{xy + \sin(x + y + z)}$ e $\displaystyle \frac{dz}{dy} = \frac{xz + \sin(x + y + z)}{xy + \sin(x + y + z)}.$
Determine as derivadas parciais de $f(x,y)=5x^{4}y^{2}+xy^{3}+4$.
$\displaystyle \frac{\partial f}{\partial x} = 20x^{3}y^{2} + y^{3}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 10x^{4}y + 3xy^{2}.$
Verifique que a função $f(x,y) = \ln{(1 + x^2 + y^2)}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
$Y=w\tan^{-1}(uv)$, $u=r+s$, $v=s+t$; $w=t+r$
$\dfrac{\partial Y}{\partial r}$, $\dfrac{\partial Y}{\partial s}$, $\dfrac{\partial Y}{\partial t}$ quando $r=1$, $s=0$, $t=1$.
$\displaystyle \frac{\partial Y}{\partial r} = 1 + \frac{\pi}{4}$ ,$\dfrac{\partial Y}{\partial s} = 2$, $\displaystyle \dfrac{\partial Y}{\partial t} = 1 + \frac{\pi}{4}.$
Verifique que a função $f(x,y) = x \cos{(x^2 + y^2)}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.
$w=f(r,s,t)$, onde $r=r(x,y)$, $s=s(x,y)$, $t=t(x,y)$.
$\displaystyle \frac{\partial w}{\partial x} = \frac{\partial w}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial w}{\partial s}\frac{\partial s}{\partial x} + \frac{\partial w}{\partial t}\frac{\partial t}{\partial x}$ e $\displaystyle \frac{\partial w}{\partial y} = \frac{\partial w}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial w}{\partial s}\frac{\partial s}{\partial y} + \frac{\partial w}{\partial t}\frac{\partial t}{\partial y}$
A lei dos gases para uma massa fixa $m$ de um gás ideal à temperatura absoluta $T$, pressão $P$ e o volume $V$ é $PV=mRT$, onde $R$ é a constante do gás. Mostre que
$$\frac{\mathrm{\partial}P}{\mathrm{\partial}V}\frac{\mathrm{\partial}V}{\mathrm{\partial}T}\frac{\mathrm{\partial}T}{\mathrm{\partial}P}=-1.$$
$\displaystyle \frac{\partial P}{\partial V} = -\frac{mRT}{V^{2}},\;\;\;\frac{\partial V}{\partial T} = \frac{mR}{P}\;\;\;\text{e}\;\;\; \frac{\partial T}{\partial P} = \frac{V}{mR}.$
Se $z=f(x,y)$ com $x=u+v$ e $y=u-v$, demonstre que
$$\frac{\partial z}{\partial u}+\frac{\partial z}{\partial v}=2 \frac{\partial f}{\partial x}.$$
Note que $\displaystyle \frac{\partial z}{\partial u} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y}$ e $\displaystyle \frac{\partial z}{\partial v} = \frac{\partial f}{\partial x} - \frac{\partial f}{\partial y}.$
Suponha que a equação \(z=f(x,y)\) seja expressa na forma polar \(z=g(r,\theta)\) através da substituição \(x=r\cos\theta\) e \(y=r\sin\theta\).
Considere \(r\) e \(\theta\) como funções de \(x\) e \(y\) e use derivação implícita para mostrar que \[ \frac{\partial r}{\partial x} = \cos\theta \quad \text{e}\quad\frac{\partial\theta}{\partial x} =-\frac{\sin\theta}{r}.\]
Considere \(r\) e \(\theta\) como funções de \(x\) e \(y\) e use derivação implícita para mostrar que \[\dfrac{\partial r}{\partial y}=\sin\theta \quad \text{e}\quad \dfrac{\partial\theta}{\partial y}=\dfrac{\cos\theta}{r}.\]
Use os resultados anteriores para mostrar que \begin{align*} \dfrac{\partial z}{\partial x} & = \dfrac{\partial z}{\partial r}\cos\theta - \dfrac{1}{r}\dfrac{\partial z}{\partial\theta}\sin\theta \\ \dfrac{\partial z}{\partial y} & = \dfrac{\partial z}{\partial r}\sin\theta + \dfrac{1}{r}\dfrac{\partial z}{\partial\theta}\cos\theta\end{align*}
Use o resultado do item anterior para mostrar que \[ \left(\dfrac{\partial z}{\partial x}\right)^2 + \left(\dfrac{\partial z}{\partial y}\right)^2 = \left(\dfrac{\partial z}{\partial r}\right)^2 +\dfrac{1}{r^2}\left(\dfrac{\partial z}{\partial\theta}\right)^2. \]
Ainda usando o resultado do terceiro item, mostre que \(z=f(x,y)\) satisfaz a equação de Laplace \[ \dfrac{\partial^2z}{\partial x^2} + \dfrac{\partial^2z}{\partial y^2}= 0, \] se, e somente se, \(z=g(r,\theta)\) satisfaz a equação \[ \dfrac{\partial^2z}{\partial r^2} + \dfrac{1}{r^2}\dfrac{\partial^2z}{\partial\theta^2}+\dfrac{1}{r}\dfrac{\partial z}{\partial r} = 0. \] A última equação acima é chamada de forma polar da equação de Laplace.
Determine o plano que passa pelos pontos $(1,1,2)$ e $(-1,1,1)$ e que seja tangente ao gráfico de $f(x,y) = xy$.
$x + 6y - 2z = 3$.
Calcule as derivadas parciais de $w = x^2 \arcsin{\dfrac{y}{z}}$.
$\displaystyle \frac{\partial w}{\partial x} = 2x \arcsin \left( \frac{t}{z}\right),\;\;\;\; \frac{\partial w}{\partial y} = \frac{x^{2}|z|}{z\sqrt{z^{2} - y^{2}}} \;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial w}{\partial z} = - \frac{x^{2}y}{|z|\sqrt{z^{2} - y^{2}}}.$
Considere a função
$$f(x,y)= \begin{cases}\dfrac{xy^{2}}{x^{2}+y^{4}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
A função é contínua em $(0,0)$? Justifique sua resposta.
Determine as derivadas parciais $\dfrac{\partial f}{\partial x}(0,0)$ e $\dfrac{\partial f}{\partial y}(0,0)$.
Não, pois $\lim_{(x,y) \to (0,0)} f(x,y)$ não existe.
$\displaystyle \frac{\partial f}{\partial x}(0,0) = \frac{\partial f}{\partial y}(0,0) = 0$.
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}\dfrac{xy^3}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = 0\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2}$.
Determine o plano que é paralelo ao plano $z = 2x + 3y$ e tangente ao gráfico de $f(x,y) = x^2 + xy$.
Considere
$$z-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})(x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})(y-y_{0})$$
o plano tangente ao gráfico de $f$. Assim,
$$z=\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot x+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot y+\bigg[ f(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot x_{0}-\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot y_{0}\bigg].$$
Como tal plano é paralelo ao plano $z=2x+3y$, obtemos que
$$\frac{\partial f}{\partial x}(x_{0},y_{0})=2\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\; \frac{\partial f}{\partial y}(x_{0},y_{0})=3.$$
Notemos que
$$\frac{\partial f}{\partial x}(x,y)=2x+y\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\; \frac{\partial f}{\partial y}(x,y)=x.$$
Assim, temos o seguinte sistema de equações
$$\left \{\begin{array}{cc}2x_{0}+y_{0}=2 \\x_{0}=3\\\end{array}\right.$$
Logo, $x_{0}=3$ e $y_{0}=-4.$ A partir desses valores temos que $f(x_{0},y_{0})=-3$, $\dfrac{\partial f}{\partial x}(x_{0},y_{0})\cdot x_{0}=6$ e
$\dfrac{\partial f}{\partial y}(x_{0},y_{0})\cdot y_{0}=-12.$ Portanto, o plano desejado tem equação
$$z=2x+3y-3-6+12,$$
ou seja,
$$z=2x+3y+3.$$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=\sin{x}\cos{y}$, $x=\pi t$, $y=\sqrt{t}$.
$\displaystyle \frac{dz}{dt} = \pi \cos(x) \cos(y) - \frac{1}{2\sqrt{t}} \sin(x) \sin(y).$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=\tan(u/v)$, $u=2s+3t$, $v=3s-2t$.
$\displaystyle \frac{\partial z}{\partial s} = \frac{2u - 3v}{v^{2}} \sec^{2}\left(\frac{u}{v} \right)$ e $\displaystyle \frac{\partial z}{\partial t} = \frac{2u + 3v}{v^{2}} \sec^{2}\left(\frac{u}{v} \right))$.
Seja $z=f(u-v,v-u)$. Verifique que
$$\frac{\partial z}{\partial u}+\frac{\partial z}{\partial v}=0.$$
Note que $\displaystyle \frac{\partial z}{\partial u}(u,v) = \frac{\partial f}{\partial x}(u-v,v-u) - \frac{\partial f}{\partial y}(u-v,v - u)$ e $\displaystyle \frac{\partial z}{\partial v}(u,v) = -\frac{\partial f}{\partial x}(u-v,v-u) + \frac{\partial f}{\partial y}(u-v,v - u).$
Se $z=\sin(x+\sin{y})$, mostre que $\dfrac{\partial z}{\partial x} \;\dfrac{\partial^{2} z}{\partial x \partial y}=\dfrac{\partial z}{\partial y}\;\dfrac{\partial^{2}z}{\partial x^{2}}$.
$\begin{aligned}[t]\frac{\partial z}{\partial x} &= \cos(x + \sin y),\;\;\; \frac{\partial z}{\partial y} = \cos(x + \sin y) \cos y,\\\frac{\partial z^{2}}{\partial x\partial y} &= -\sin (x + \sin y) \cos y\;\;\text{e}\;\; \frac{\partial^{2} z}{\partial x^{2}} = -\sin (x + \sin y).\end{aligned}$
Calcule as derivadas parciais de $w = \dfrac{xyz}{x + y + z}$.
$\displaystyle \frac{\partial w}{\partial x} = \frac{yz(y+z)}{(x+y+z)^{2}},\;\;\;\; \frac{\partial w}{\partial y} = \frac{xz(x+z)}{(x+y+z)^{2}}\;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial w}{\partial z} = \frac{xy(x+y)}{(x+y+z)^{2}}.$
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função de uma variável real, diferenciável e tal que $\phi '(1)=4.$ Seja $g(x,y)=\phi\bigg(\dfrac{x}{y}\bigg).$ Verifique que, para todo $(x,y)\in \mathbb{R}^{2}$, com $y\neq 0$, temos que
$$x\;\dfrac{\partial g}{\partial x}(x,y)+y\;\dfrac{\partial g}{\partial y}(x,y)=0.$$
Determine a diferencial da função $m = p^5q^3$.
$dm = 5p^{4}q^{3} dp + 3p^{5}q^{2} dq$.
Verifique que a função $f(x,y) = e^{x - y^2}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
$u=\sqrt{r^{2}+s^{2}}$, $r=y+x\;\cos{t}$, $s=x+y\;\sin{t}$;
$\dfrac{\partial u}{\partial x}$, $\dfrac{\partial u}{\partial y}$, $\dfrac{\partial u}{\partial t}$ quando $x=1$, $y=2$, $t=0$.
$\displaystyle \frac{\partial u}{\partial x} = \frac{4}{\sqrt{10}}$, $\displaystyle \frac{\partial u}{\partial y} = \frac{3}{\sqrt{10}}$, $\displaystyle \frac{\partial u}{\partial t}= \frac{2}{\sqrt{10}}.$
De acordo com o triângulo abaixo:
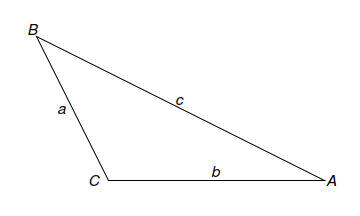
Expresse $A$ implicitamente como uma função de $a$, $b$ e $c$ e calcule $\partial A/\partial a$ e $\partial A/ \partial b.$
Expresse $a$ implicitamente como uma função de $A$, $b$ e $B$ e calcule $\partial a/ \partial A$ e $\partial a/ \partial B.$
$\displaystyle a^{2} = b^{2} + c^{2} -2bc\cos(A),\;\;\;\;\frac{\partial A}{\partial a} = \frac{a}{bc \sin (A)}\;\;\;\text{e}\;\;\;\frac{\partial A}{\partial b} = \frac{c \cos(A) - b}{bc \sin(A)}.$
$\displaystyle \frac{a}{\sin(A)} = \frac{b}{\sin(B)},\;\;\;\;\frac{\partial a}{\partial A} = \frac{a\cos(A)}{\sin(A)}\;\;\;\text{e}\;\;\;\frac{\partial a}{\partial B} = - b\csc(B) \cot(B)\sin(A).$
Mostre que se \(f\), \(f_x\) e \(f_y\) são contínuas numa região circular contendo os pontos \(A=(x_0,y_0)\) e \(B=(x_1,y_1)\), então existe um ponto \((x^\ast,y^\ast)\) no segmento que une \(A\) e \(B\) tal que \[ f(x_1,y_1)-f(x_0,y_0) = f_x(x^\ast,y^\ast)(x_1-x_0)+f_y(x^\ast,y^\ast)(y_1-y_0). \] Este resultado é a versão bidimensional do Teorema do Valor Médio. [Sugestão: expresse o segmento de reta unindo \(A\) e \(B\) na forma paramétrica e use o Teorema do Valor Médio para funções de uma variável.]
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t,$ onde
$$z=\sin{\theta}\cos{\phi}, \quad \theta=st^{2}, \quad \phi=s^{2}t.$$
Utilizando a Regra de Cadeia, obtemos
\begin{eqnarray*}
\frac{\partial z}{\partial s} & = & \frac{\partial z}{\partial \theta}\frac{\partial \theta}{\partial s}+\frac{\partial z}{\partial \phi}\frac{\partial \phi}{\partial s} \\
& = & (\cos{\theta}\cos{\phi})(t^2) + (\sin{\theta}(-\sin{\phi}))(2st) \\
& = & t^2\cos(st^2)\cos(s^2t) - 2st\sin(st^2)\sin(s^2t)
\end{eqnarray*}
e
\begin{eqnarray*}
\frac{\partial z}{\partial t} & = & \frac{\partial z}{\partial \theta}\frac{\partial \theta}{\partial t}+\frac{\partial z}{\partial \phi}\frac{\partial \phi}{\partial t} \\
& = & (\cos{\theta}\cos{\phi})(2st) + (\sin{\theta}(-\sin{\phi}))(s^2) \\
& = & 2st\cos(st^2)\cos(s^2t) - s^2\sin(st^2)\sin(s^2t).
\end{eqnarray*}
Verifique que a função $z=\ln(e^{x}+e^{y})$ é uma solução das equações diferenciais
$$\frac{\mathrm{\partial}z}{\mathrm{\partial}x} + \frac{\mathrm{\partial}z}{\mathrm{\partial}y}=1\;\;\;\;\;\;\; e\;\;\;\;\;\;\; \frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}^{2}x}+\frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}^{2}y}-\bigg(\frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}x\mathrm{\partial}y}\bigg)^{2}=0.$$
$\begin{aligned}[t]\frac{\partial z }{\partial x} &= \frac{e^{x}}{e^{x} + e^{y}},\;\;\; \frac{\partial z }{\partial y} = \frac{e^{y}}{e^{x} + e^{y}},\\\frac{\partial^{2} z }{\partial x^{2}} &= \frac{\partial^{2} z }{\partial y^{2}} = \frac{e^{x + y}}{(e^{x} + e^{y})^{2}},\;\;\; \frac{\partial^{2} z }{\partial x \partial y} = -\frac{e^{x + y}}{(e^{x} + e^{y})^{2}}.\end{aligned}$
Suponha que substituamos coordenadas polares $x=r\cos{\theta}$ e $y=r\sin{\theta}$ em uma função diferenciável $w=f(x,y).$
- Mostre que $$\frac{\partial w}{\partial r}=f_{x}\cos{\theta}+f_{y}\sin{\theta}$$ e $$\frac{1}{r}\frac{\partial w}{\partial \theta}=-f_{x}\sin{\theta}+f_{y}\cos{\theta}.$$
- Resolva as equações no item 1. para expressar $f_{x}$ e $f_{y}$ em termos de $\partial w/ \partial r$ e $\partial w/\partial \theta$.
- Mostre que $$(f_{x})^{2}+(f_{y})^{2}=\bigg(\frac{\partial w}{\partial r}\bigg)^{2}+\frac{1}{r^{2}}\bigg(\frac{\partial w}{\partial \theta}\bigg)^{2}.$$
- $\displaystyle f_{x} = \cos(\theta) \frac{\partial w}{\partial r} - \frac{\sin (\theta)}{r} \frac{\partial w}{\partial \theta}$ e $\displaystyle f_{y} = \sin(\theta) \frac{\partial w}{\partial r} + \frac{\cos (\theta)}{r} \frac{\partial w}{\partial \theta}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=(x^{2}-1)(y+2)$.
$\displaystyle \frac{\partial f}{\partial x} = 2x(y + 2) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = x^{2} - 1$.
Calcule as derivadas parciais de $f(x,y,z) = \sin{(x^2 + y^2 + z^2)}$.
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= 2x \cos (x^{2} + y^{2} + z^{2}),\;\;\;\; \frac{\partial f}{\partial y} = 2y \cos (x^{2} + y^{2} + z^{2}) \;\;\;\;\;\text{e}\\\frac{\partial f}{\partial z} &= 2z \cos (x^{2} + y^{2} + z^{2}).\end{aligned}$
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = 3(x-1)^2 + 2(y+3)^2 + 7, \quad (2,-2,12)$.
$z = 6x + 4y + 8$.
Se $z=f(x-y)$, mostre que
$$\dfrac{\partial z}{\partial x}+\dfrac{\partial z}{\partial y}=0.$$
Note que se $u = x - y,$ então $\displaystyle \frac{\partial z}{\partial x} = \frac{dz}{du}$e$\displaystyle \frac{\partial z}{\partial y} = -\frac{dz}{du}.$
Determine a derivada parcial indicada. $u=e^{r\theta}\sin{\theta}$; $\dfrac{\partial ^{3}u}{\partial r^{2}\partial \theta}$.
$\dfrac{\partial ^{3}u}{\partial r^{2}\partial \theta} = \theta e^{r\theta} (2\sin \theta + \theta \cos \theta + r\theta \sin \theta)$.

