Exercícios
Funções de várias variáveis reais
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Dada a expressão $g(x,y)=-f(x,y)$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ refletido sobre o plano $xy.$
Determine o conjunto dos pontos de continuidade da função $f(x,y) = \mbox{ln} \ \dfrac{x - y}{x^2 + y^2}$. Justifique sua resposta.
$\left\lbrace (x,y);\; x > y \right\rbrace.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy^2}{x^2 - y^2}$, caso exista.
Não existe.
Esboce o gráfico da função $f(x,y)=\sin(\sqrt{x^{2}+y^{2}})$ .Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
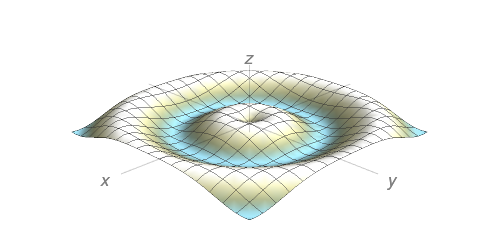
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (2,1)}\dfrac{4 - xy}{x^2 + 3y^2}$.
$\frac{2}{7}.$
Explique por que cada função é contínua ou descontínua.
A temperatura externa como função da latitude, da longitude e do tempo.
A altura acima do nível do mar como função da longitude, da latitude e do tempo.
O custo da tarifa do táxi como função da distância percorrida e do tempo gasto.
Contínua.
Descontínua.
Descontínua.
Determine o conjunto dos pontos de continuidade da função $f(x,y) = \sqrt{6 - 2x^2 - 3y^2}$. Justifique sua resposta.
$\left\lbrace (x,y);\; 2x^{2} + 3y^{2} \leq 6 \right\rbrace.$
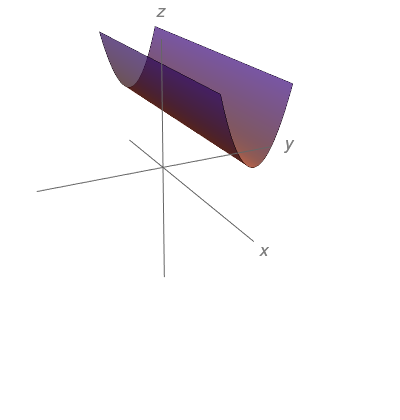
$$f(x,y)=\sqrt{x+y^{2}-3}$$
- Faça um esboço das curvas de nível de $f$ nos níveis $c=0$, $c=1$ e $c=3.$
- Quantas curvas de nível de $f$ passam pelo ponto $(3,-1)$?
As curvas de níveis de $f$ são
$$\sqrt{x+y^{2}-3}=c\,\,\,\,\mbox{ou}\,\,\,\,x+y^{2}-3=c^2\,\,\,\,\mbox{ou}\,\,\,\,x=3+c^2-y^{2},$$
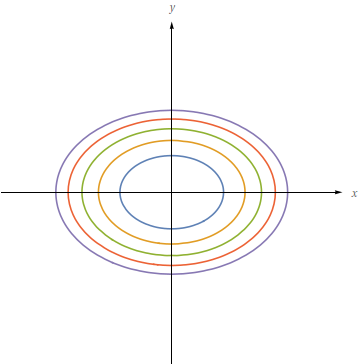
ou seja, uma família de parábolas com concavidade para a esquerda. As três curvas de níveis pedidas, obtidas considerando respectivamente $c=0$, $c=1$ e $c=3$, são
$x=3-y^{2}$, $x=4-y^{2}$ e $x=12-y^{2}.$ Elas estão apresentadas na figura abaixo.
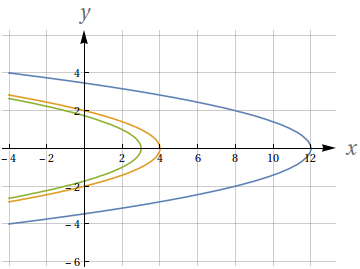
Pelo ponto $(3,-1)$ passa uma única curva de nível, isto é, $f(x,y)=1.$ Pois caso contrário o ponto $(3,-1)$ teria duas alturas diferentes, o que é impossível.
Encontre uma equação para a curva de nível da função $f(x,y)=\sqrt{x^{2}-1}$ que passa pelo ponto $(1,0)$.
$x = 1$ ou $x = -1.$
Encontre uma equação para a superfície de nível da função $f(x,y)=\ln (x^{2}+y^{2}+z^{2})$ que passa pelo ponto $(-1,2,1)$.
$x^{2} + y + z^{2} = 6.$
Defina continuidade de uma função de duas variáveis $f(x,y)$ em um ponto $(x_0, y_0)$ de seu domínio.
Dada a função
$$f(x,y) = \begin{cases} \dfrac{x^2\sqrt{y}}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\L, & \quad \text{se } (x,y) = (0,0),\end{cases}$$
é possível encontrar $L$ de maneira que $f$ seja contínua em $(0,0)$?
$f(x,y)$ é contínua em $(x_{0},y_{0}) \in D_{f}$ se
$$\lim_{(x,y) \to (x_{0},y_{0})} f(x,y) = f(x_{0},y_{0}).$$
$L = 0.$
Represente graficamente o domínio da função $z=f(x,y)$ dada por $z=\ln(2x^{2}+y^{2}-1)$.
$\left\lbrace (x,y); 2x^{2} + y^{2} > 1 \right\rbrace$
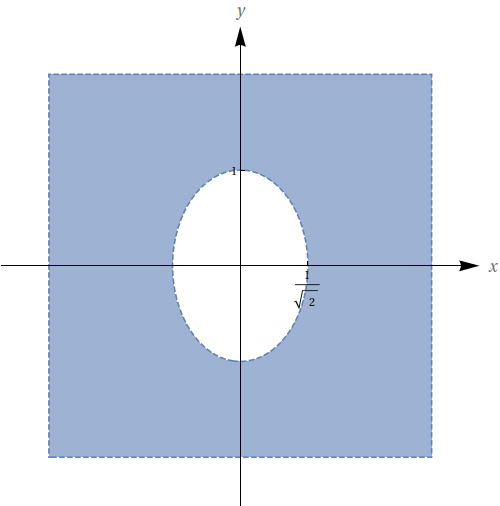
Determine \(\displaystyle \lim_{(x,y)\to (0,0)}(x^2+y^2)\ln(x^2+y^2). \)
Usando coordenadas polares, teremos que: \[\begin{array}{lll} x=r\cos\theta, & y=r\sin\theta, & r^2=x^2+y^2. \end{array} \] Além disso, como \(r=\sqrt{x^2+y^2}\geq 0\), temos que \( r\rightarrow 0^+\) se, e somente se, \( (x,y)\rightarrow (0,0) \). Assim, segue para o limite dado que \begin{align*} \lim_{(x,y)\to (0,0)}(x^2+y^2)\ln(x^2+y^2) & = \lim_{r\to 0^+} r^2\ln r^2 \\ & = \lim_{r\to 0^+}\underbrace{\dfrac{2\ln r}{1/r^2}}_{\text{do tipo}\ \infty/\infty} \\ & \stackrel{\text{L'Hospital}}{=} \lim_{r\to 0^+} \dfrac{2/r}{-2/r^3} \\ & = \lim_{r\to 0^+} (-r^2) = 0.\end{align*}
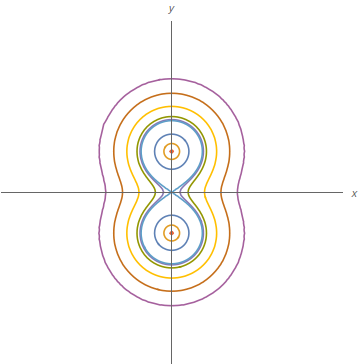
Uma placa fina de metal, localizada no plano $xy$, tem temperatura $T(x,y)$ no ponto $(x,y)$. As curvas de nível de $T$ são chamadas isotérmicas porque todos os pontos em uma isotérmica têm a mesma temperatura. Faça o esboço de algumas isotérmicas se a função temperatura for dada por
$$T(x,y)=\dfrac{100}{1+x^{2}+2y^{2}}.$$
As isotérmicas são dadas pela família de elipses: $x^{2} + 2y^{2} = \frac{100}{C} - 1,$ com $0 < C \leq 100.$
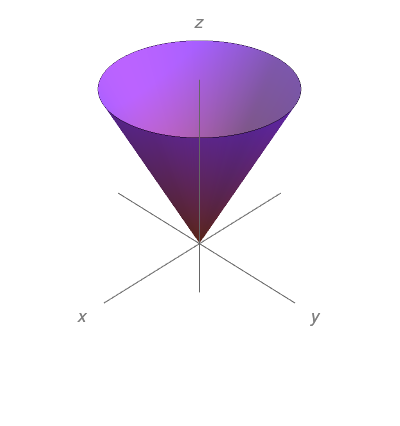
Esboce o gráfico da função $f(x,y)=\sqrt{x^{2}+y^{2}}$.
$z = \sqrt{x^{2} + y^{2}}$
Verifique que a função \(f(x,y)=\sqrt{1-x^2-y^2}\) é contínua no disco unitário fechado \(x^2+y^2\leq 1\).
O domínio de \(f\) é o disco unitário fechado \(x^2+y^2\leq 1\). Para todo ponto \((x_0,y_0)\) na fronteira do disco, temos \[ \lim_{(x,y)\to(x_0,y_0)}\sqrt{1-x^2-y^2} = \sqrt{1-x_0^2-y_0^2} = 0.\] Como o mesmo vale também para pontos interiores ao disco, temos que \(f\) é contínua no disco fechado.
Dada a função $f(x,y)=y-x$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}$.
$Im(f) = \mathbb{R}.$
As curvas de nível são as retas $y - x = C.$
Mostre que os limites não existem, considerando que \((x,y)\rightarrow (0,0) \) ao longo dos eixos coordenados.
\[ \lim_{(x,y)\to(0,0)}\dfrac{x-y}{x^2+y^2} \]
\[ \lim_{(x,y)\to(0,0)}\dfrac{\cos(xy)}{x^2+y^2} \]
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (5,-2)}(x^5 + 4x^3y - 5xy^2)$.
$2025.$
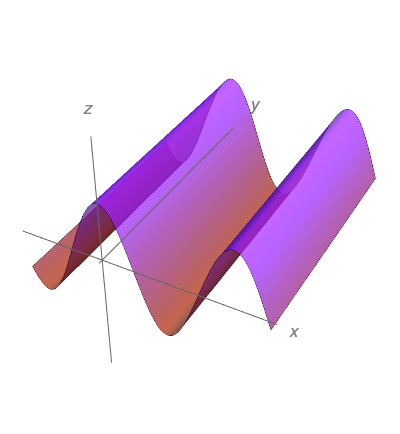
Esboce o gráfico da função $f(x,y)=\cos{x}$.
$z = \cos(x)$
Mostre (verifique) que o domínio da função $f(x,y)=\ln(x^2-y)$ consiste em todos os pontos abaixo da curva $y<x^2$.
A função $(x,y)\longmapsto\ln(x^2-y)$ só está definida para \( 0<x^2-y \), ou seja, $y<x^2$. Assim, primeiro esboçamos a parábola $y=x^2$ (como uma curva tracejada, por exemplo). A região $y<x^2$ consiste em todos os pontos abaixo dessa curva.
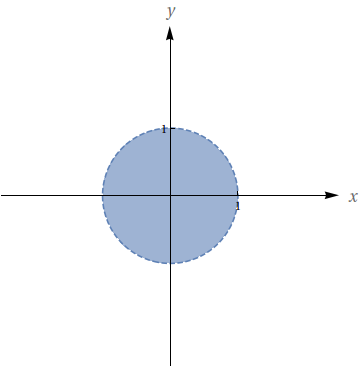
Dada $f(x,y)=\dfrac{1}{\sqrt{16-x^{2}-y^{2}}}$.
Encontre o domínio da função;
Encontre a imagem da função;
Descreva as curvas de nível da função.
O domínio de $f$ é
$$D=\{(x,y)|\, 16-x^{2}-y^{2}>0\}=\{(x,y)|\,x^{2}+y^{2}<16\}.$$
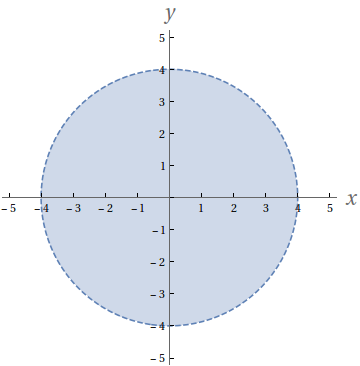
A imagem de $f$ é
$$\bigg\{z|\, z=\frac{1}{\sqrt{16-x^{2}-y^{2}}},\,(x,y)\in D\bigg\}.$$
Mas,
$$z=\frac{1}{\sqrt{16-x^{2}-y^{2}}}\geq \frac{1}{\sqrt{16}}=\frac{1}{4}.$$
Assim, a imagem de $f$ é $\bigg\{z|\, z \geq \dfrac{1}{4}\bigg\}.$
s curvas de níveis de $f$ são da forma $f(x,y)=c$, isto é,
$$\frac{1}{\sqrt{16-x^{2}-y^{2}}}=c\Leftrightarrow \sqrt{16-x^{2}-y^{2}}=\frac{1}{c}\Leftrightarrow 16-x^{2}-y^{2}=\frac{1}{c^{2}}$$
$$\Leftrightarrow x^{2}+y^{2}=16-\frac{1}{c^{2}}.$$
Assim, as curvas de níveis de $f$ são circunferências com centro na origem e raio menor do que $4.$
Dada a função $f(x,y)=\sqrt{y-x}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \left\lbrace (x,y);\; x \leq y \right\rbrace$.
$Im(f) = \left\lbrace z \in \mathbb{R};\; z \geq 0 \right\rbrace.$
As curvas de nível são as retas $y - x = C,$ com $C \geq 0.$
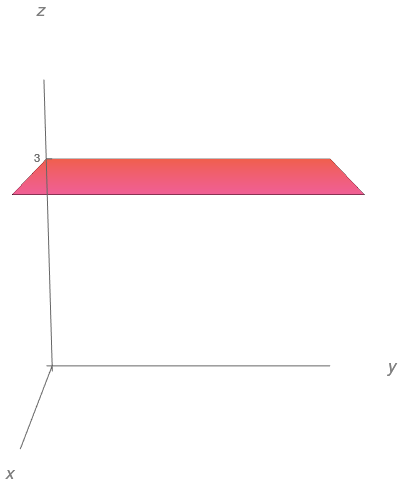
Esboce o gráfico da função $f(x,y)=3$.
$z = 3.$
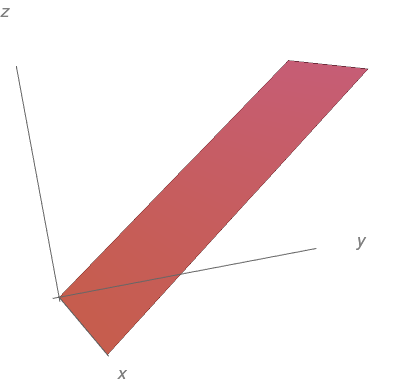
Esboce o gráfico da função $f(x,y)=y$.
$z = y.$
Encontre uma equação para a superfície de nível da função $f(x,y,z)=\sqrt{x-y}-\ln z$ que passa pelo ponto $(3,-1,1)$.
$\sqrt{x - y} - \ln(z) = 2.$
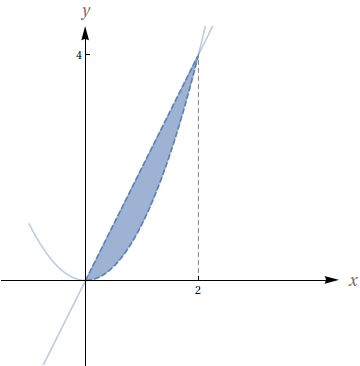
Represente graficamente o domínio da função $z=f(x,y)$ dada por $z=\sqrt{y-x^{2}}+\sqrt{2x-y}$.
$\left\lbrace (x,y); x^{2} \leq y \leq 2x \right\rbrace$
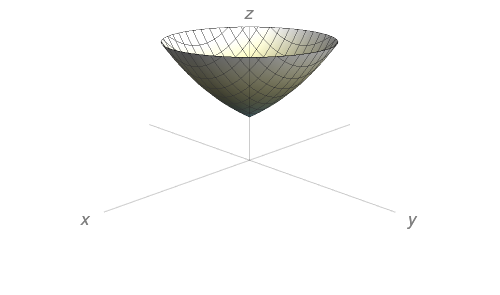
Esboce o gráfico da função $f(x,y)=e^{\sqrt{x^{2}+y^{2}}}$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{y^4}{x^4 + 3y^4}$.
Não existe.
Determine se a função
$$f(x,y) = \begin{cases}e^{\left( \dfrac{1}{x^2 + y^2 - 1} \right)}, & \quad \text{se } x^2 + y^2 < 1, \\0, & \quad \text{se } x^2 + y^2 \geq 1.\end{cases}$$
é contínua em $\displaystyle{\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)}$. Justifique sua resposta.
$0.$
Determine o maior conjunto no qual a função $f(x,y) = \begin{cases}\dfrac{xy}{x^2 + xy + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\0, & \quad \text{se } (x,y) = (0,0)\end{cases}$ é contínua.
$\left\lbrace (x,y);\; (x,y) \neq (0,0) \right\rbrace.$
Seja $f(x,y)=x^{2}e^{3xy}$.
Calcule $f(2,0).$
Determine o domínio de $f$.
Determine a imagem de $f$.
$4.$
$\mathbb{R}^{2}.$
$[0,\infty).$
- Queremos calcular $f(2,0)$ sabendo que $f(x,y)=x^{2}e^{3xy}$. Basta substituir os valores na expressão, assim temos
\[
f(2,0)=2^{2}e^{3 \cdot 2 \cdot 0}=4e^{0}=4 \cdot 1=4.
\] - Por definição, o domínio da função $f$ é o conjunto dos pontos de $\mathbb{R}^{2}$ em que a função está bem definida. Em nosso caso, o domínio é o conjunto de pontos em que a função $f(x,y)=x^{2}e^{3xy}$ está bem definida. Portanto, o domínio de $f$ é $\mathbb{R}^2$.
- A imagem da função $f$ é o conjunto dos pontos $\{ z\in \mathbb{R} | z = f(x,y) \text{ e } (x,y)\in D\}$, onde $D$ é o domínio de $f$. Observe que $x^{2} \geq 0$ e $e^{3xy}> 0$ para todo $(x,y)\in \mathbb{R}^{2}$, logo $x^{2}e^{3xy}\geq 0$ para todo $(x,y)\in \mathbb{R}^{2}$. Por exemplo, se fixarmos $x=1$ temos que a imagem da função são os pontos da forma $e^{3y}$ com $y\in \mathbb{R}$, ou seja, é todo o intervalo $(0,\infty)$. Agora, quando colocamos $x=0$ a imagem é $0$. Portanto, a imagem de $f$ é o conjunto $[0,\infty]$.
Utilize coordenadas polares $x=r\cos \theta$ e $y=r\sin \theta$, com $r \geq 0$ e $0 \leq \theta < 2 \pi$, e o teorema do confronto para calcular o limite
$$\displaystyle \lim_{(x,y) \to (0,0)}\dfrac{x^3 + y^3}{x^2 + y^2}.$$
Dica: Note que, se $(r, \theta)$ são as coordenadas polares do ponto $(x,y)$, com $r \geq 0$, então $r \to 0^+$ quando $(x,y) \to (0,0)$.
$0.$
Esboce o gráfico da função $f(x,y)=y^{2}+1$.
$z = y^{2} + 1$
Seja $f(x,y)=3x+2y.$ Calcule:
$f(1,-1)$;
$f(a,x)$;
$\dfrac{f(x+h,y)-f(x,y)}{h}$;
$\dfrac{f(x,y+k)-f(x,y)}{k}$.
$1.$
$3a + 2x.$
$3.$
$2.$
Considere a função
$$f(x,y) = \begin{cases}\dfrac{x^2 - xy}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\0, & \quad \text{se } (x,y) = (0,0).\end{cases}$$
Calcule o limite $\displaystyle \lim_{(x,y) \to (0,0)}f(x,y)$ ou mostre que esse limite não existe.
Calcule o limite $\displaystyle \lim_{(x,y) \to (1,1)}f(x,y)$ ou mostre que esse limite não existe.
$f$ é contínua em $(0,0)$? Justifique.
$f$ é contínua em $(1,1)$? Justifique.
O limite não existe.
$0.$
Não.
Sim.
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy}{y - x^3}$, caso exista.
Não existe.
Esboce o gráfico da função $f(x,y)=e^{-(x^2+y^2)}$.
Descreva em palavras como o gráfico da função \(\displaystyle g(x,y)= e^{-a(x^2+y^2)}\) está relacionado com o gráfico de \(f\), sendo \(a>0\). Mostre (verifique) que o valor de \(a\) influencia na "largura" do pico presente no gráfico da função.
Represente graficamente o domínio da função $z=f(x,y)$ dada por $f(x,y)=\dfrac{x-y}{\sqrt{1-x^{2}-y^{2}}}$.
$\left\lbrace (x,y); x^{2} + y^{2} < 1 \right\rbrace$
Considere a função
$$f(x,y) = \begin{cases}x + y, & \quad \text{se } xy = 0, \\k, & \quad \text{caso contrário},\end{cases}$$
em que $k$ é um número real. É possível escolher $k$ de modo que $f$ seja contínua em $(0,0)$? Em caso afirmativo, qual deve ser o valor de $k$?
$k = 0.$
É dada uma curva $\gamma$ que passa pelo ponto $\gamma(t_0) = (1,3)$ e cuja imagem está contida na curva de nível $x^2 + y^2 = 10$. Suponha $\gamma'(t_0) \neq \bf{0}$.
- Determine a equação da reta tangente a $\gamma$ no ponto $(1,3)$.
- Determine uma curva $\gamma(t)$ satisfazendo as condições acima.
- $(x,y) = (1,3) + \lambda (-6,2),$ $\lambda \in \mathbb{R}.$
- $\gamma(t) = (\sqrt{10} \cos(t), \sqrt{10} \sin(t)).$
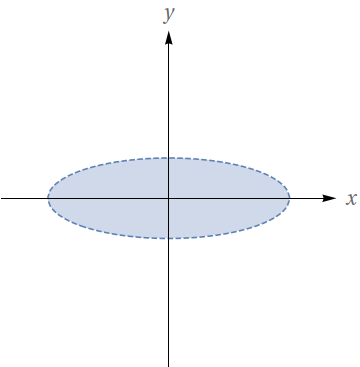
Determine e faça o esboço do domínio da função $f(x,y)=\ln(9-x^{2}-9y^{2})$.
$\left\lbrace (x,y);\; \frac{x^{2}}{9} + y^{2} < 1 \right\rbrace.$
$f(x,y) = \begin{cases}\dfrac{xy^2}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\0, & \quad \text{se } (x,y) = (0,0), \end{cases}$ é contínua em (0,0)? Justifique.
Notemos que para $(x,y)\neq (0,0)$ a função $f$ é contínua, pois $xy^{2}$ e $x^{2}+y^{2}$ são funções contínuas e $x^{2}+y^{2}\neq 0.$ Agora, estudemos a continuidade da função $f$ no ponto $(0,0).$ Temos que
$$\lim_{(x,y)\to (0,0)}f(x,y)=\lim_{(x,y)\to (0,0)}\frac{xy^{2}}{x^{2}+y^{2}}=\lim_{(x,y)\to (0,0)}x\cdot \frac{y^{2}}{x^{2}+y^{2}}.$$
Como
$$\lim_{(x,y)\to (0,0)}x=0\,\,\,\,\,\, \mbox{e}\,\,\,\,\,\, \bigg| \dfrac{y^{2}}{x^{2}+y^{2}}\bigg|\leq 1,\, \forall (x,y)\neq (0,0),$$
obtemos que
$$\lim_{(x,y)\to (0,0)}f(x,y)=0.$$
Assim,
$$\lim_{(x,y)\to (0,0)}f(x,y)=0=f(0,0).$$
Portanto, $f$ é contínua em $(0,0).$
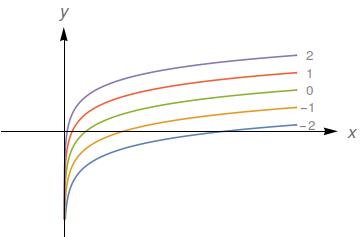
Faça o mapa de contorno da função $f(x,y)=y-\ln{x}$ mostrando várias de suas curvas de nível.
$y = \ln(x) + C.$
Mostre que os limites não existem, considerando que \((x,y)\rightarrow (0,0) \) ao longo dos eixos coordenados.
\[ \lim_{(x,y)\to(0,0)}\dfrac{3}{x^2+2y^2} \]
\[ \lim_{(x,y)\to(0,0)}\dfrac{x+y}{2x^2+y^2} \]
Dada a função $f(x,y)=x^{2}-y^{2}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}.$
$Im(f) = \mathbb{R}.$
As curvas de nível são as hipérboles $x^{2} - y^{2} = C$ com foco no eixo $x$ se $C > 0;$ com foco no eixo $y$ se $C < 0$ e as retas $y = \pm x$ se $C = 0.$
Seja $f(x,y,z)=e^{\sqrt{z-x^{2}-y^{2}}}.$
Calcule $f(2,-1,6).$
Determine o domínio de $f$.
Determine a imagem de $f$.
$e.$
$\left\lbrace (x,y,z): \;z \geq x^{2} + y^{2} \right\rbrace.$
$[1,\infty).$
Determine o maior conjunto no qual a função $G(x,y) = \ln{(x^2 + y^2 - 4)}$ é contínua.
$\left\lbrace (x,y);\;x^{2} + y^{2} > 4 \right\rbrace.$
Esboce o gráfico da função $f(x,y)=\sqrt{x^{2}+y^{2}}$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
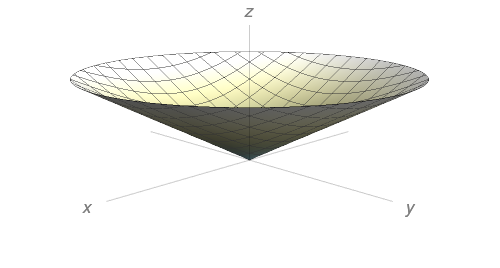
Encontre uma equação para a curva de nível da função $f(x,y)=16-x^{2}-y^{2}$ que passa pelo ponto $(2\sqrt{2},\sqrt{2})$.
$x^{2} + y^{2} = 10.$
Esboce o gráfico da função $f(x,y)=10-4x-5y$.
$z = 10 - 4x - 5y.$
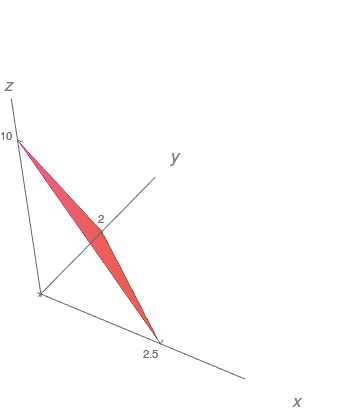
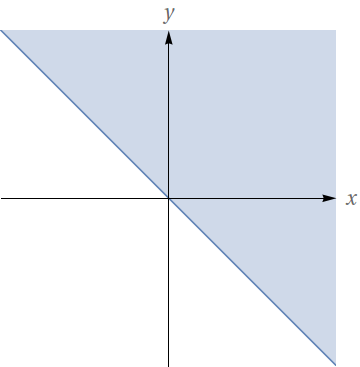
Determine e faça o esboço do domínio da função $f(x,y)=\sqrt{x+y}$.
$\left\lbrace (x,y);\; y \geq -x \right\rbrace$
Faça um esboço do diagrama de contorno da função cujo gráfico é mostrado.
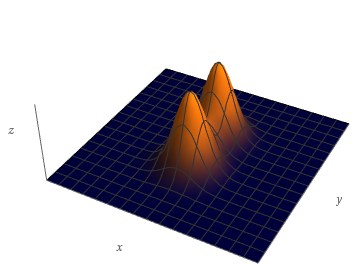
$y = 2x \pm \sqrt{C},$ $C \geq 0.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy}{\sqrt{x^2 + y^2}}$.
$0.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2}{\sqrt{x^2 + y^2}}$, caso exista.
$0.$
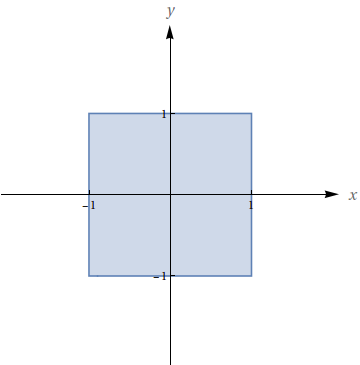
Determine e faça o esboço do domínio da função $f(x,y)=\sqrt{1-x^{2}}-\sqrt{1-y^{2}}$.
$\left\lbrace (x,y);\; -1 \leq x \leq 1,\;-1\leq y \leq 1 \right\rbrace.$
Dada a função $f(x,y)=e^{-(x^{2}+y^{2})}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}$.
$Im(f) = \left\lbrace z \in \mathbb{R};\; 0 < z \leq 1 \right\rbrace.$
As curvas de nível são as os círculos $x^{2} + y^{2} = C$ com $C > 0$ e a origem.
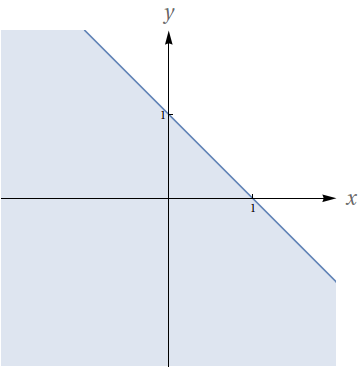
Represente graficamente o domínio da função $z=f(x,y)$ dada por $x+y-1+z^{2}=0$, $z\geq 0$.
$\left\lbrace (x,y); x + y \leq 1 \right\rbrace$
Seja $f(x,y) = \dfrac{2xy^2}{x^2 + y^4}$.
Considere a reta $\gamma(t) = (at, bt)$, com $a^2 + b^2 > 0$; mostre que, quaisquer que sejam $a$ e $b$,
$$\displaystyle \lim_{t \to 0} f(\gamma(t)) = 0.$$
Tente visualizar este resultado através das curvas de nível de $f$.
Calcule $\displaystyle \lim_{t \to 0} f(\delta(t))$, onde $\delta(t) = (t^2,t).$ (Antes de calcular o limite, tente prever o resultado olhando para as curvas de nível de $f$.)
$\displaystyle \lim_{(x,y) \to (0,0)}\dfrac{2xy^2}{x^2 + y^4}$ existe? Por quê?
Demonstração.
$1.$
Não existe.
Determine o conjunto dos pontos de continuidade da função $f(x,y) = \dfrac{x - y}{\sqrt{1 - x^2 - y^2}}$. Justifique sua resposta.
$\left\lbrace (x,y);\; x^{2} + y^{2} < 1 \right\rbrace.$
Esboce o gráfico da função $f(x,y)=g(\sqrt{x^{2}+y^{2}})$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
Dada a função $f(x,y)=xy$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}$.
$Im(f) = \mathbb{R}.$
As curvas de nível são as hipérboles $xy = C$ quando $C \neq 0$ e os eixos $x$ e $y$ quando $C = 0.$
Dada a expressão $g(x,y)=2f(x,y)$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ esticado verticalmente ao dobro.
Determine $h(x,y) = g(f(x,y))$ e o conjunto no qual $h$ é contínua, em que
$$g(t) = t^2 + \sqrt{t}, \ \ \ f(x,y) = 2x + 3y - 6.$$
$h(x,y) = (2x+3y-6)^{2} + \sqrt{2x + 3y - 6}$ é contínua em $\left\lbrace (x,y);\; y \geq -\frac{2x}{3} + 2 \right\rbrace.$
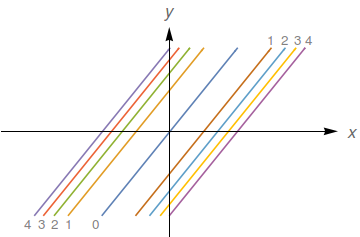
Faça o mapa de contorno da função $f(x,y)=(y-2x)^{2}$ mostrando várias de suas curvas de nível.
$y=2x\pm \sqrt{C}, C \geq0.$
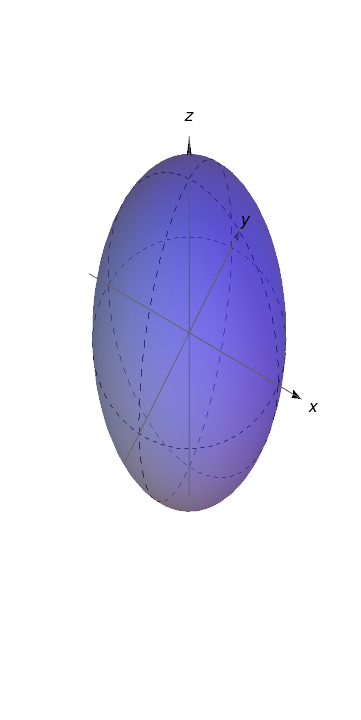
Determine e faça o esboço do domínio da função $f(x,y,z)=\ln(16-4x^{2}-4y^{2}-z^{2})$.
$\left\lbrace (x,y);\; \frac{x^{2}}{4} + \frac{y^{2}}{4} + \frac{z^{2}}{16} < 1\right\rbrace.$
Se $f(x_0,y_0) = 3$, o que podemos dizer sobre
$$\displaystyle \lim_{(x,y) \to (x_0,y_0)}f(x,y)$$
se $f$ for contínua em $(x_0,y_0)$? E se $f$ não for contínua em $(x_0,y_0)$? Justifique sua resposta.
Se $f$ for contínua em $(x_{0},y_{0}),$ então o limite é igual a $f(x_{0},y_{0}) = 3.$ Se não for contínua em $(x_{0},y_{0}),$ então o limite pode ter qualquer valor diferente de $3.$
Determine o maior conjunto no qual a função $F(x,y) = \dfrac{1}{x^2 - y}$ é contínua.
$\left\lbrace (x,y);\; y \neq x^{2} \right\rbrace.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy \ \mbox{cos} \ y}{3x^2 + y^2}$.
Não existe.
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy}{x^2 + y^2}$, caso exista.
Não existe.
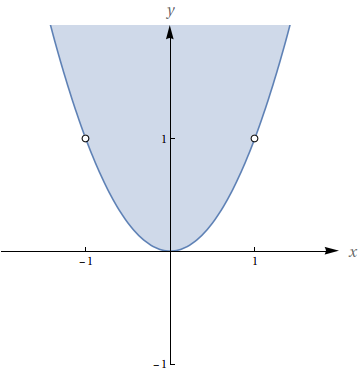
Determine e faça o esboço do domínio da função $\bigstar$ $f(x,y)=\dfrac{\sqrt{y-x^{2}}}{1-x^{2}}$.
$\left\lbrace (x,y);\; y \geq x^{2},\; x\neq \pm 1 \right\rbrace.$
Determine a equação da reta tangente à curva $\gamma$ no ponto $\gamma(t_0) = (2,5)$ sabendo-se que $\gamma'(t) \neq \bf{0}$ e que sua imagem está contida na curva de nível $xy = 10$. Qual a equação da reta normal a $\gamma$, neste ponto?
Reta tangente: $(x,y) = (2,5) + \lambda (-2,5),$ $\lambda \in \mathbb{R},$
Reta normal: $(x,y) = (2,5) + \lambda (5,2),$ $\lambda \in \mathbb{R}.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x + y}{x - y}$, caso exista.
Não existe.
Verifique que, para a função de produção de Cobb-Douglas
$$P(L,K)=1,01L^{0,75}K^{0,25}$$
discutida no Exemplo 3 da Seção 14.1 do Stewart, a produção dobrará se as quantidades de trabalho e a de capital investido forem dobradas. Determine se isto também é verdade para uma função de produção genérica
$$P(L,K)=bL^{\alpha}K^{1-\alpha}.$$
Sim.
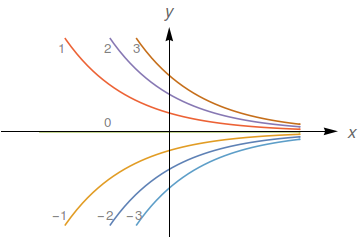
Faça o mapa de contorno da função $f(x,y)=ye^{x}$ mostrando várias de suas curvas de nível.
$y = Ce^{-x}.$
Determine e faça o esboço do domínio da função $f(x,y,z)=\sqrt{1-x^{2}-y^{2}-z^{2}}$.
$\left\lbrace (x,y);\; x^{2} + y^{2} + z^{2} \leq 1 \right\rbrace.$
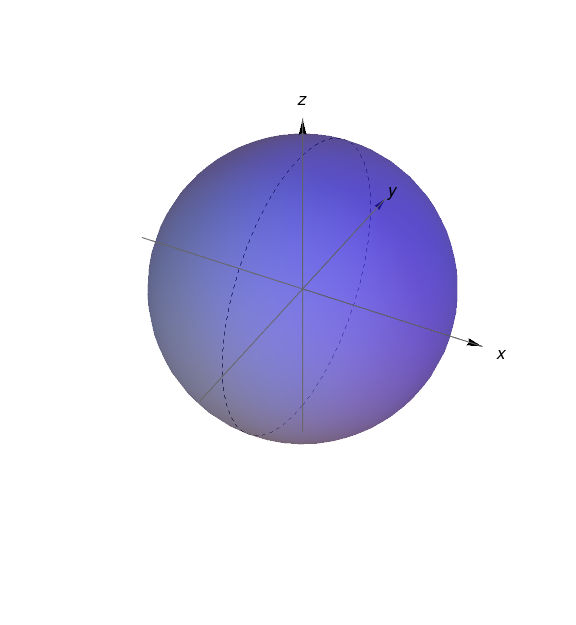
Esboce o gráfico da função $f(x,y)=\ln(\sqrt{x^{2}+y^{2}})$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
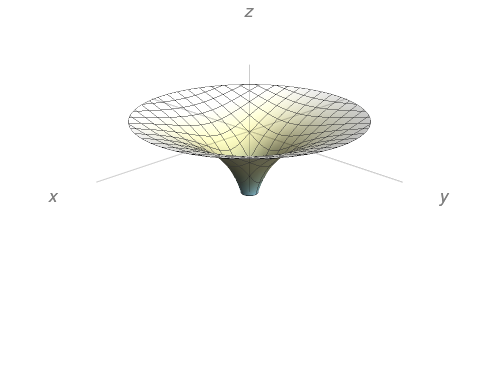
Sabendo que $\left|\sin\frac{1}{x}\right| \leq 1$, podemos dizer algo sobre
$$\displaystyle \lim_{(x,y) \to (0,0)}y\sin\dfrac{1}{x}?$$
Justifique sua resposta.
$\displaystyle \lim_{(x,y) \to (0,0)} y\sin\left(\frac{1}{x} \right) = 0.$
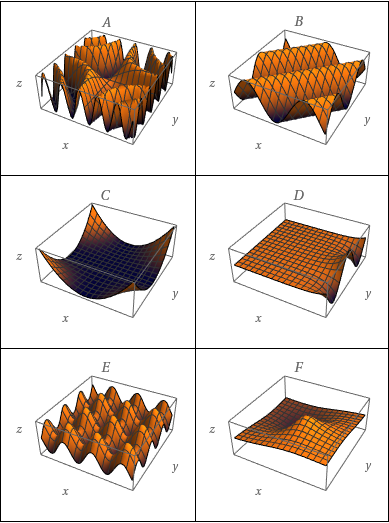
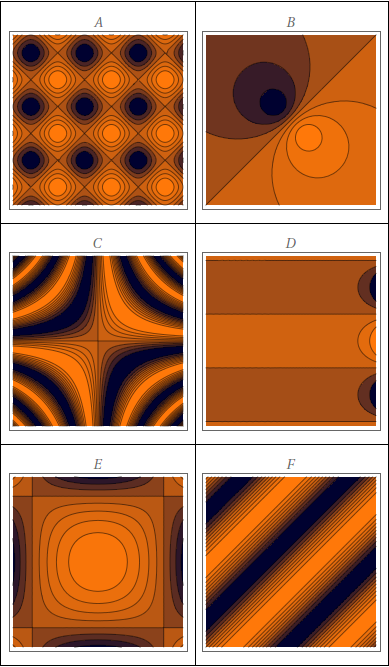
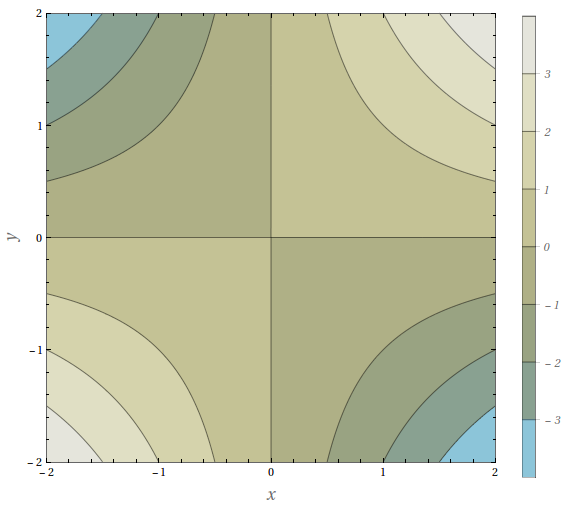
Faça uma correspondência entre a função: (i) e seu gráfico; (ii) e seus mapas de contorno. Justifique sua escolha.
$z=\sin(xy)$
$z=\sin(x-y)$
$z=(1-x^{2})(1-y^{2})$
$z=e^{x} \; \cos{y}$
$z=\sin{x}-\sin{y}$
$z=\dfrac{x-y}{1+x^{2}+y^{2}}$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy(x - y)}{x^4 + y^4}$, caso exista.
Não existe.
Dada a expressão $g(x,y)=f(x,y)+2$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ deslocado para cima por duas unidades.
O índice I de temperatura-umidade (ou simplesmente humidex) é a temperatura aparente do ar quando a temperatura real é $T$ e a umidade relativa é $h$, de modo que podemos escrever $I=f(T,h)$. A tabela seguinte com valores de $I$ foi extraída de uma tabela do Environment Canada.
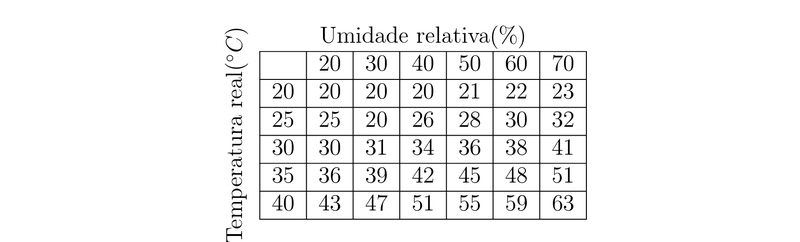
Qual é o valor de $f(35,60)$? Qual é o seu significado?
Para que valor de $h$ temos $f(30,h)=36$?
Para que valor de $T$ temos $f(T,40)=42$?
Qual o significado de $I=f(20,h)$ e $I=f(40,h)$? Compare o comportamento dessas duas funções de $h.$
48, o que significa que quando a temperatura real é $35^\circ$C e a umidade relativa é $60\%,$ o humidex é $48^\circ$C.
$50\%.$
$35^\circ$C.
$I = f(20,h)$ e $I = f(40,h)$ são funções de $h$ que fornecem os valores do humidex quando a temperatura real é $20^\circ$C e $40^\circ$C, respectivamente. Ambas as funções crescem com $h,$ porém $f(20,h)$ cresce aproximadamente a taxa constante, enquanto $f(40,h)$ cresce mais rapidamente a uma taxa crescente.
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x}{\sqrt{x^2 + y^2}}$, caso exista.
Não existe.
Dois mapas de contorno são mostrados na figura. Um é de uma função $f$ cujo gráfico é um cone. O outro é de uma função $g$ cujo gráfico é um paraboloide. Qual é qual? Por quê?
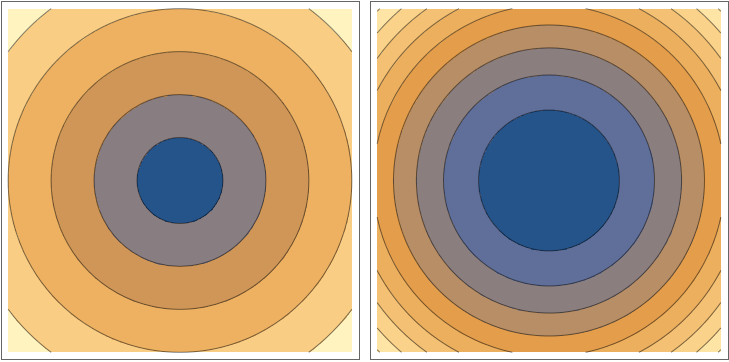
O da esquerda corresponde ao cone e o da direita ao paraboloide.
Determine o maior conjunto no qual a função $f(x,y) = \begin{cases}\dfrac{x^2y^3}{2x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\1, & \quad \text{se } (x,y) = (0,0) \end{cases}$ é contínua.
$\left\lbrace (x,y);\; (x,y) \neq (0,0) \right\rbrace.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} x \ \sin{\dfrac{1}{x^2 + y^2}}$, caso exista.
$0.$
Determine o conjunto dos pontos de continuidade da função $f(x,y) = 3x^2y^2 - 5xy + 6$. Justifique sua resposta.
$\mathbb{R}^{2}.$
Encontre uma equação para a curva de nível da função $f(x,y)=\displaystyle \int_{x}^{y}\dfrac{dt}{1+t^{2}}$ que passa pelo ponto $(-\sqrt{2},\sqrt{2})$.
$\arctan(y) - \arctan(x) = 2\arctan(\sqrt{2}).$
Suponha que $\displaystyle \lim_{(x,y) \to (3,1)}f(x,y) = 6$. O que podemos dizer do valor de $f(3,1)$? E se a função $f$ for contínua?
Nada se pode afirmar. Se $f$ for contínua em $(x_{0},y_{0}),$ $f(3,1) = 6.$
Seja $g(x,y,z)=\ln(25-x^{2}-y^{2}-z^{2}).$
Calcule $g(2,-2,4).$
Determine o domínio de $g$.
Determine a imagem de $g$.
$0.$
$\left\lbrace (x,y,z): x^{2} + y^{2} + z^{2} < 25 \right\rbrace.$
$(-\infty, \ln(25)].$
Dada a função $f(x,y)=\ln (x^{2}+y^{2})$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \left\lbrace (x,y);\; (x,y) \neq (0,0) \right\rbrace$.
$Im(f) = \mathbb{R}.$
As curvas de nível são os círculos $x^{2} + y^{2} = C$ com $C > 0.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2 + y^2}{\sqrt{x^2 + y^2 + 1} - 1}$.
$2.$
Dada a expressão $g(x,y)=2-f(x,y)$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ refletido sobre o plano $xy$ e deslocado para cima por duas unidades.
Calcule \(\displaystyle \lim_{(x,y)\to (-1,2)} \dfrac{xy}{x^2+y^2}\).
Como a função \(\displaystyle f(x,y)=\dfrac{xy}{x^2+y^2}\) é contínua no ponto \((-1,2)\) (de acumulação), basta avaliá-la neste mesmo ponto. Ou seja, \[ \lim_{(x,y)\to (-1,2)}\dfrac{xy}{x^2+y^2} = \dfrac{(-1)2}{(-1)^2+2^2} = -\dfrac{2}{5}. \]
Calcule
$$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{\mbox{sen}(x^2 + y^2)}{x^2 + y^2}.$$
Considere $t=x^{2}+y^{2}$.
Assim , se $(x,y)\rightarrow (0,0)$ temos que $t \to 0.$ Portanto,
$$\lim_{(x,y) \to (0,0)} \frac{\sin(x^{2}+y^{2})}{x^{2}+y^{2}}=\lim_{t \to 0}\frac{\sin t}{t}=1.$$
Dada a função $f(x,y)=\dfrac{y}{x^{2}}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \left\lbrace (x,y);\; (x,y) \neq (0,y) \right\rbrace$.
$Im(f) =\mathbb{R}.$
As curvas de nível são as parábolas $y = C x^{2}$ sem a origem se $C \neq 0$ e o eixo $x$ se $C \neq 0.$
Seja $f(x,y)=e^{xy}$ uma função de duas variáveis.
Determine o domínio e a imagem de $f.$
Esboce as curvas de nível de $f.$
$D_{f} = \mathbb{R}^{2}$ e $Im(f) = \left\lbrace z \in \mathbb{R};\; z > 0 \right\rbrace.$
$xy = C.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2 \ \mbox{sen}^2y}{x^2 + 2y^2}$.
$0.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2ye^y}{x^4 + 4y^2}$.
Não existe.
Não existe.
Seja $f(x,y)=\dfrac{x-y}{x+2y}$.
Determine o domínio.
Calcule $f(2u+v,v-u).$
$\left\lbrace (x,y);\; x \neq -2y \right\rbrace$
$\frac{u}{v}.$
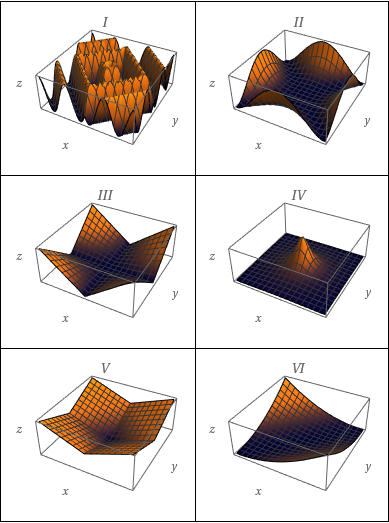
Faça uma correspondência entre a função e seu gráfico (indicado por I-VI). Dê razões para sua escolha.
$f(x,y)=|x|+|y|$.
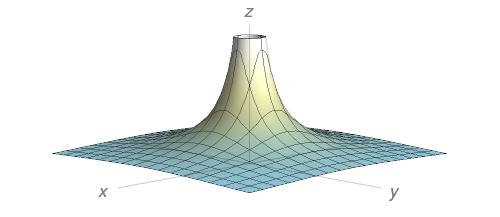
$f(x,y)=\dfrac{1}{1+x^{2}+y^{2}}$.
$f(x,y)=(x-y)^{2}$.
$f(x,y)=|xy|$.
$f(x,y)=(x^{2}-y^{2})^{2}$.
$f(x,y)=\sin(|x|+|y|)$.