Exercícios
Identificação das cônicas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+3y^2+4xy+4y-4=0$.
Identificar a cônica $x^2+3y^2-2xy+3=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Identifique a cônica descrita pela equação $x^2-6xy-7y^2+10x-30y+23=0$.
Identifique a cônica $5 x^2+12 x y= 1$ e seu parâmetros associados.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $3x^2+5y^2+4x-2y-10=0$.
Decida se a cônica $C$ determinada pela equação $\displaystyle 4x^2-4x+9y^2-18y=26$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Decida se a cônica $C$ determinada pela equação $\displaystyle 9x^2-18x+9y^2-6y=10$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Seja $A$ uma matriz $2\times 2$ real com autovalores complexos $\lambda=a\pm bi$ tais que $b\neq 0$ e $|\lambda|=1$. Mostre que toda trajetória do sistema dinâmico $\textbf{x}_{k+1}=A\textbf{x}_k$ está sobre uma elipse. [Dica: use que se $\textbf{v}$ é um autovetor associado a $\lambda=a-bi$, então a matriz $P=[ \textrm{Re}\,\textbf{v}\quad \textrm{Im}\,\textbf{v}]$ é invertível e temos que $\displaystyle A=P\left[\begin{array}{cc} a & -b \\ b & a \end{array}\right]P^{-1}$. Ponha $\displaystyle B=(PP^t)^{-1}$. Mostre que a equação quadrática $\textbf{x}^tB\textbf{x}=k$ define uma elipse para todo $k>0$, e prove que se $\textbf{x}$ está sobre esta elipse, então $A\textbf{x}$ também estará.]
Decida se a cônica $C$ determinada pela equação $\displaystyle 4y^2-4y-24x+9=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $x^2-16y^2 + 8x +128y -256 = 0$.
Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+2x+y^2+2y+2=0$.
Encontre ou mostre a impossibilidade de encontrar $\gamma\in\mathbb{R}$ tal que $\displaystyle x^2+3y^2-2xy=\gamma$ represente uma elipse.
Identifique a cônica $3 x^2-12 x y+12 y^2+ 2 \sqrt{5} x+\sqrt{5} y=0$ e seu parâmetros associados.
Na equação $x^2-y^2+2\sqrt{3}xy+6x=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Identifique a cônica descrita pela equação$7x^2+6xy-y^2-2x+10y-9=0$.
Considere a forma quadrática $2x^2+8xy+2y^2+x+y-9=0$. Escreva-a numa base conveniente e identifique qual é a cônica e seus paramêtros associados.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+5x+y-9=0$.
Seja $A$ uma matriz $2\times 2$ simétrica e $k$ um escalar. Mostre que o gráfico da equação quadrática $\textbf{x}^tA\textbf{x}=k$ é:
uma hipérbole se $k\neq 0$ e $\det A<0$;
uma elipse, círculo ou cônica imaginária se $k\neq 0$ e $\det>0$;
um par de retas ou uma cônica imaginária se $k\neq 0$ e $\det A=0$;
um par de retas ou um único ponto se $k=0$ e $\det A \neq 0$;
uma linha reta se $k=0$ e $\det A=0$.
[Dica: use o Teorema dos Eixos Principais.]
Identificar a cônica $x^2-3y^2-2xy -x-y=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Considere a forma quadrática $2x^2+8xy+2y^2+x+y-9=0$. Escrevendo-a numa base conveniente, determine:
qual o eixo que contém o(s) foco(s);
qual é a translação e a rotação associadas.
Decida se a cônica $C$ determinada pela equação $4x^2-8x-9y^2+6y-68=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Na equação $9x^2-4xy+6y^2=30$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Identificar a cônica $x^2+4y^2+4xy-2x-4y-1=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Considere a cônica definida pela equação $2xy+x-2=0.$
Determinar seu centro.
Classificar a cônica.
Esboçar seu gráfico.
Identificar a cônica $8y^2+6xy-12x-26y+11=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Seja $\mathcal{C}$ a cônica cuja equação em relação ao sistema $xy$ é dada por $29x^2 + 24xy + 36y^2 + 22x + 96y = 115$. A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue
\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad
\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]
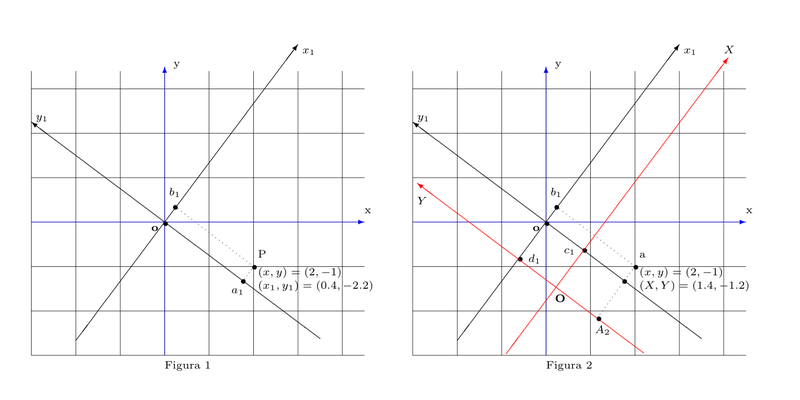
Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.
Encontre a equação de $\mathcal{C}$ nos sistemas $x_{1}y_{1}$ e $XY$.
Encontre as coordenadas dos vértices e dos focos de $\mathcal{C}$ nos três sistemas, $xy$,\,$x_{1}y_{1}$ e $XY$. Dica: Encontrar primeiro no sistema $XY$ e ir voltando.
Faça um esboço do desenho da cônica.
Identifique a cônica descrita pela equação $4x^2-12xy+9y^2-6x+9y-4=0$.
Identifique a cônica descrita pela equação $49x^2-42xy+9y^2+56x-24y+16=0$.
Decida se a cônica $C$ determinada pela equação $9y^2-9x^2+6x=1$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Decida se a cônica $C$ determinada pela equação $36x^2-24x+36y^2-36y+14=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+y^2+(1/3)xy+6x+8y-5=0$.
Identifique a cônica descrita pela equação $4x^2-4xy+y^2-2x+y+15=0$.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+(1/5)xy +y^2+2x+2y+2=0$.
Decida se a cônica $C$ determinada pela equação $y^2+x^2+3xy-10x-10y+5=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Decida se a cônica $C$ determinada pela equação $5x^2+6xy+5y^2-8 = 0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Identificar a cônica $x^2-2xy+y^2-10x-6y+25=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Sejam $F_{1}$ e $F_{2}$ dois pontos fixos do plano que distam $8$ unidades um do outro. Ou seja, $\text{dist}(F_{1},F_{2}) = 8$.
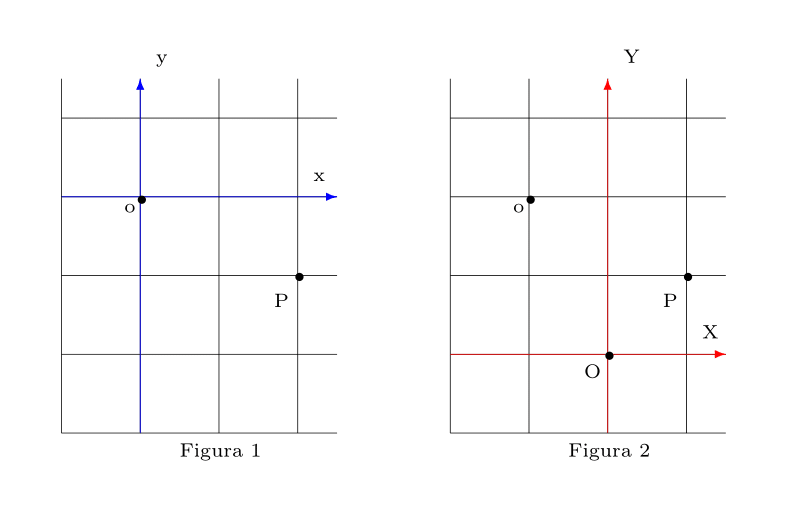
Encontre a equação do lugar geométrico dos pontos $P$ desse plano que satisfazem a condição:
\[ \text{dist}(P,F_{1}) + \text{dist}(P,F_{2}) = 10,\]
em cada um dos seguintes casos:
$F_{1} = (-c,0)$ e $F_{2} = (c,0)$, onde as coordenadas foram tomadas em relação ao sistema $xy$ da Figura 1 acima, e cada ponto $P$ tem coordenadas $(x,y)$ tomadas em relação a $\textbf{o}$.
$F_{1} = (-5,2)$ e $F_{2} = (3,2)$, onde as coordenadas foram tomadas em relação ao sistema $XY$ da Figura 2 acima, e cada ponto $P$ tem coordenadas $(X,Y)$ tomadas em relação a $\textbf{O}$.
$F_{1}$ e $F_{2}$ estão sobre o eixo $X$ do sistema $XY$ da Figura 2 acima, são simétricos em relação ao eixo $Y$, e cada ponto $P$ tem coordenadas $(x,y)$ tomadas em relação a $\textbf{o}$.
Considere a equação
$$x^{2} - 14 x y + y^{2} = 1.$$
Efetue a troca de variáveis $x = u \cos \theta + v\,\textrm{sen} \theta$ e $y = - u\, \textrm{sen} \theta + v \cos \theta$. Escolha, usando sua intuição ou fazendo as contas, $\theta$ de forma que a equação obtida em $u$ e $v$ seja a equação canônica de uma hipérbole. Explique o significado geométrico deste resultado e obtenha, nas coordenadas $x$ e $y$, as equações das retas que servem de assíntotas à tal hipérbole.
Decida se a cônica $C$ determinada pela equação $x^2+3xy+y^2=2$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Encontre ou mostre a impossibilidade de encontrar $\gamma\in\mathbb{R}$ tal que $\displaystyle x^2+\gamma y^2-4xy+ \gamma x = \gamma$ represente uma parábola.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2-2y^2+4xy-6=0$.
Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $3x^2+2xy+3y^2-6x-6y+1=0$.
Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.
Na equação $18x^2+12xy+2y^2+94\frac{\sqrt{10}}{10}x-282\frac{\sqrt{10}}{10}y+94=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2-y^2-4x+2y+2=0$.
Considere a cônica definida pela equação $x^2+xy-1=0.$
Determinar seu centro.
Classificar a cônica.
Esboçar seu gráfico.
Às vezes o gráfico de uma equação quadrática é uma reta, um par de retas ou até mesmo um único ponto. Nos referimos a tais gráficos como cônicas degeneradas. É também possível que a equação não seja satisfeita para nenhum valor real das variáveis, caso este no qual não existe um gráfico e dizemos tratar-se de uma cônica imaginária. Nos itens abaixo, identifique a cônica com a equação dada, dizendo se é degenerada ou imaginária. Quando possível, esboce também o gráfico.
$\displaystyle x^2-y^2=0$;
$\displaystyle x^2+2y^2+2=0$;
$\displaystyle 3x^2+y^2=0$.
Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $9x^2-24xy+16y^2-34x-38y+51=0$.
Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.
Identificar a cônica $4x^2+4xy+y^2-6x+3y+2=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Na equação $4x^2-20xy+25y^2-15x-6y=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Identifique a cônica descrita pela equação $16x^2+16y^2-16x+8y-59=0$.
Às vezes o gráfico de uma equação quadrática é uma reta, um par de retas ou até mesmo um único ponto. Nos referimos a tais gráficos como cônicas degeneradas. É também possível que a equação não seja satisfeita para nenhum valor real das variáveis, caso este no qual não existe um gráfico e dizemos tratar-se de uma cônica imaginária. Nos itens abaixo, identifique a cônica com a equação dada, dizendo se é degenerada ou imaginária. Quando possível, esboce também o gráfico.
$\displaystyle x^2+2xy+y^2=0$;
$\displaystyle x^2-2xy+y^2+2\sqrt{2}x-2\sqrt{2}y=0$;
$\displaystyle 2x^2+2xy+2y^2+2\sqrt{2}x-2\sqrt{2}y+6=0$.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+2y^2-4xy+y-1=0$.

