Exercícios
Mudança de coordenadas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+(1/5)xy +y^2+2x+2y+2=0$.
Identifique a cônica $5 x^2+12 x y= 1$ e seu parâmetros associados.
Reduza a equação $3x^2-3y^2-5z^2-2xy-6xz-6yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $4x^2+6y^2+4z^2-4xz+1=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Os extremos de uma corda elástica com um nó em $K(x,y)$ são presos a um ponto fixo $A(a,b)$ e um ponto $P$ sobre a borda de um pneu de raio $r$ centrado em $(0,0)$. Conforme o pneu gira, $K$ traça uma curva $C$. Encontre a equação desta curva. Assuma que a corda permanece presa e estica uniformemente (ou seja, a razão $\alpha:=|KP|/|AP|$ é constante).
Às vezes o gráfico de uma equação quadrática é uma reta, um par de retas ou até mesmo um único ponto. Nos referimos a tais gráficos como cônicas degeneradas. É também possível que a equação não seja satisfeita para nenhum valor real das variáveis, caso este no qual não existe um gráfico e dizemos tratar-se de uma cônica imaginária. Nos itens abaixo, identifique a cônica com a equação dada, dizendo se é degenerada ou imaginária. Quando possível, esboce também o gráfico.
$\displaystyle x^2-y^2=0$;
$\displaystyle x^2+2y^2+2=0$;
$\displaystyle 3x^2+y^2=0$.
Reduza a equação $3x^2+y^2-2xy+2xz-2yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $2x^2+2y^2-4z^2-5xy-2xz-2x-2y+z=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $xz = 1$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
A equação da quádrica $xz = 1$ pode ser escrita em forma matricial:
$$X^tAX-1=0,$$
onde:
$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ A=\begin{pmatrix}0 & 0 & 1/2 \\0 & 0 & 0 \\1/2 & 0 & 0\end{pmatrix}. $$
Seja:
$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}-\lambda & 0 & 1/2 \\0 & -\lambda & 0 \\1/2 & 0 & -\lambda\end{pmatrix}=-\lambda^3+\lambda/4.$$
As raízes de $P(\lambda)$ são $0$, $-1/2$ e $1/2$. Considere os sistemas lineares referentes às raízes $0$ e $1/2$: $A X = 0$ e $(A-1/2 I) X = 0$. Uma solução de norma unitária desses sistemas consiste em $U_1=(0,1,0)$ e $U_2=(1/\sqrt{2},0,1/\sqrt{2})$, respectivamente. Sejam $U_3=U_1 \times U_2 = (1/\sqrt{2},0,-1/\sqrt{2})$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $xz=1$ se transforma em:
$$\dfrac{(y')^2}{2}-\dfrac{(z')^2}{2}=1,$$
que é a equação de um cilindro hiperbólico.
Tome $x'y'$ o sistema de eixos do plano que é a translação do sistema $xy$ para a nova origem $O'=(1,1)$, i.e., $ x'=x-1$ e $y'=y-1$.
Dado o ponto $P=(1,4)$ no sistema $xy$, encontre as coordenadas de $P$ no sistema $x'y'$.
Dado o ponto $A=(2,1)$ no sistema $x'y'$, encontre as coordenadas de $A$ no sistema $xy$.
Considere a reta $\mathcal{L}$ que no sistema $xy$ tem equação $2x - 3y + 4 = 0$. Qual seria a equação de $\mathcal{L}$ no sistema $x'y'$? Mudando-se a equação, muda-se $\mathcal{L}$ de lugar? O desenho muda?
Dada a curva $\mathcal{C}$, do plano, cujos pontos têm coordenadas $(x,y)$, no sistema $xy$, satisfazendo a equação $x^2-4x+y^2-6y=12$, encontre a equação que os pontos de $\mathcal{C}$ com coordenadas $(x',y')$ no sistema $x'y'$ devem satisfazer nas variáveis $x'y'$.
Reduza a equação $7x^2 + 7y^2 + 10z^2 - 2xy - 4xz + 4yz - 12x + 12y + 60z = 24$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Seja $A$ uma matriz $2\times 2$ real com autovalores complexos $\lambda=a\pm bi$ tais que $b\neq 0$ e $|\lambda|=1$. Mostre que toda trajetória do sistema dinâmico $\textbf{x}_{k+1}=A\textbf{x}_k$ está sobre uma elipse. [Dica: use que se $\textbf{v}$ é um autovetor associado a $\lambda=a-bi$, então a matriz $P=[ \textrm{Re}\,\textbf{v}\quad \textrm{Im}\,\textbf{v}]$ é invertível e temos que $\displaystyle A=P\left[\begin{array}{cc} a & -b \\ b & a \end{array}\right]P^{-1}$. Ponha $\displaystyle B=(PP^t)^{-1}$. Mostre que a equação quadrática $\textbf{x}^tB\textbf{x}=k$ define uma elipse para todo $k>0$, e prove que se $\textbf{x}$ está sobre esta elipse, então $A\textbf{x}$ também estará.]
Reduza a equação $2x^2 + 30y^2 + 23z^2 + 72xz + 150 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $3x^2+3y^2+z^2-2xy-4x+2y+6z+5=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Considere o polinômio $p(\lambda)=\det(A-\lambda I_3)$, em que$$ A= \left[\begin{array}{ccc} a & d/2 & e/2 \\ d/2 & b & f/2 \\ e/2 & f/2 & c \end{array}\right]. $$
Sejam $\alpha$ e $\beta$ raízes reais (pois $A$ é simétrica) distintas de $p(\lambda)$. Mostre que se $X_1$ é solução de $(A-\alpha I_2)X=\vec{0}$ e $X_2$ é solução de $(A-\beta I_2)X=\vec{0}$, então $X_1$ e $X_2$ são ortogonais. (Sugestão: Mostre que $\alpha X_1\cdot X_2=\beta X_1\cdot X_2$)
Mostre que se $p(\lambda)$ tem raízes reais distintas, então sempre existe uma matriz $Q$ tal que $$ Q^tAQ = \left[\begin{array}{ccc} a' & 0 & 0 \\ 0 & b' & 0 \\ 0 & 0 & c' \end{array}\right]. $$ Conseqüentemente, a mudança de coordenadas dada por $X=QX'$ transforma a equação $$ ax^2+by^2 + cz^2 + dxy+exz+fyz+gx+hy+iz+j=0 $$ na equação $$a'x'^2+b'y'^2+c'z'^2+g'x'+h'y'+i'z + j=0, $$ onde os termos "cruzados" $xy$, $xz$ e $yz$ são eliminados.
Reduza a equação $3x^2+y^2+z^2+4yz+12x+2y-2z+9=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $4x^2-2y^2+z^2=1$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
$\dfrac{x^2}{1/4} - \dfrac{y^2}{1/2} + z^2 = 1$: hiperbolóide de uma folha.
Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um ângulo $\theta$. Explique como podemos encontrar as coordenadas $xy$ de uma reta cuja equação nas coordenadas $x'y'$ seja conhecida.
Considere a forma quadrática $2x^2+8xy+2y^2+x+y-9=0$. Escrevendo-a numa base conveniente, determine:
qual o eixo que contém o(s) foco(s);
qual é a translação e a rotação associadas.
Identificar a cônica $x^2-2xy+y^2-10x-6y+25=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+y^2+(1/3)xy+6x+8y-5=0$.
Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um
ângulo de $30^\circ$. Use a rotação \begin{align*}x & = x'\cos\theta - y'\sin\theta, \\y & = x'\sin\theta + y'\cos\theta, \end{align*}
para encontrar as coordenadas $x'y'$ da curva $y=x^2$.
Reduza a equação $-2x^2+4y^2+6z^2+2xy+6xz+6yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $4x^2+3y^2-z^2-12xy+4xz-8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Sejam $F_{1}$ e $F_{2}$ dois pontos fixos do plano que distam $8$ unidades um do outro. Ou seja, $\text{dist}(F_{1},F_{2}) = 8$.
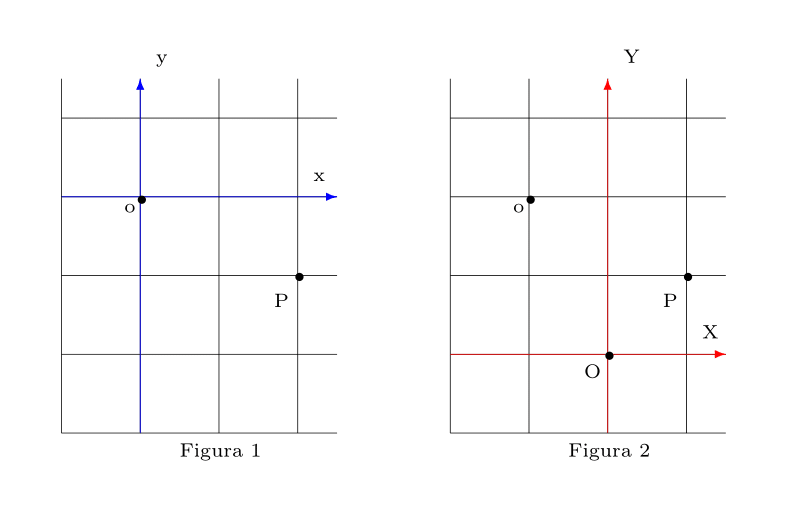
Encontre a equação do lugar geométrico dos pontos $P$ desse plano que satisfazem a condição:
\[ \text{dist}(P,F_{1}) + \text{dist}(P,F_{2}) = 10,\]
em cada um dos seguintes casos:
$F_{1} = (-c,0)$ e $F_{2} = (c,0)$, onde as coordenadas foram tomadas em relação ao sistema $xy$ da Figura 1 acima, e cada ponto $P$ tem coordenadas $(x,y)$ tomadas em relação a $\textbf{o}$.
$F_{1} = (-5,2)$ e $F_{2} = (3,2)$, onde as coordenadas foram tomadas em relação ao sistema $XY$ da Figura 2 acima, e cada ponto $P$ tem coordenadas $(X,Y)$ tomadas em relação a $\textbf{O}$.
$F_{1}$ e $F_{2}$ estão sobre o eixo $X$ do sistema $XY$ da Figura 2 acima, são simétricos em relação ao eixo $Y$, e cada ponto $P$ tem coordenadas $(x,y)$ tomadas em relação a $\textbf{o}$.
Identifique a cônica descrita pela equação $16x^2+16y^2-16x+8y-59=0$.
Encontre ou mostre a impossibilidade de encontrar $\gamma\in\mathbb{R}$ tal que $\displaystyle x^2+3y^2-2xy=\gamma$ represente uma elipse.
Reduza a equação $2xy + z = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Em cálculo de uma variável vemos que se $x_0$ é um extremo local (máximo ou mínimo) de uma função $f(x)$, então a reta tangente ao gráfico de $f$ em $x_0$ é horizontal, ou seja, $f'(x_0)=0$.
Encontre uma relação similar entre um extremo local de uma função de duas variáveis e o plano tangente ao seu gráfico.
Use esta relação para encontrar os extremos locais da função $\displaystyle f(x,y)=2x^2+2y^2-2x-6y+14$.
Verifique se sua resposta no item anterior está correta completando os quadrados em $f(x,y)$ e identificando a quádrica.
Reduza a equação $2x^2+y^2+2z^2+2xy-2yz=1 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $2x^2+3y+4z+4=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Decida se a cônica $C$ determinada pela equação $\displaystyle 9x^2-18x+9y^2-6y=10$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Reduza a equação $45x^2 + 54y^2 + 63z^2 - 36xy + 36yz - 24x - 24y + 6z + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
A equação da quádrica $45x^2 + 54y^2 + 63z^2 - 36xy + 36yz - 24x - 24y + 6z + 1 = 0$ pode ser escrita em forma matricial:
$$X^tAX+KX+1=0,$$
onde:
$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ K=\begin{pmatrix}-24 & -24 & 6\end{pmatrix}, \ A=\begin{pmatrix}45 & -18 & 0 \\-18 & 54 & 18 \\0 & 18 & 63\end{pmatrix}. $$
Seja:
$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}45-\lambda & -18 & 0 \\-18 & 54-\lambda & 18 \\0 & 18 & 63-\lambda\end{pmatrix}=-\lambda^3+162\lambda^2+-8019\lambda +118098.$$
As raízes de $P(\lambda)$ são $27$, $54$ e $81$. Considere os sistemas lineares referentes às raízes $27$ e $54$: $(A-27I) X = 0$ e $(A-54I)=0$. Uma solução de norma unitária desses sistemas são $U_1=(-2/3,-2/3,1/3)$ e $U_2=(-2/3,1/3,-2/3)$, respectivamente. Sejam $U_3=U_1 \times U_2 = (1/3,-2/3,-2/3)$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $45x^2 + 54y^2 + 63z^2 - 36xy + 36yz - 24x - 24y + 6z + 1 = 0$ se transforma em:
$$\dfrac{(x'+17/27)^2}{796/2187}+\dfrac{(y'+1/27)^2}{796/4374}+\dfrac{(z'+2/81)^2}{796/6561}=1,$$
que é a equação de um elipsóide.
Reduza a equação $x^2+z^2-xy+xz+yz-2x+2y-2z+1=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+2y^2-4xy+y-1=0$.
Identificar a cônica $x^2-3y^2-2xy -x-y=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Identificar a cônica $8y^2+6xy-12x-26y+11=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Considere a quádrica $x^2 +(m+1)y^2 +mz^2-2yz+2xy+2x+2z+4 = 0$, calcule $m$ para que a quádrica seja um parabolóide hiperbólico e obtenha sua equação reduzida.
A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue
\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]
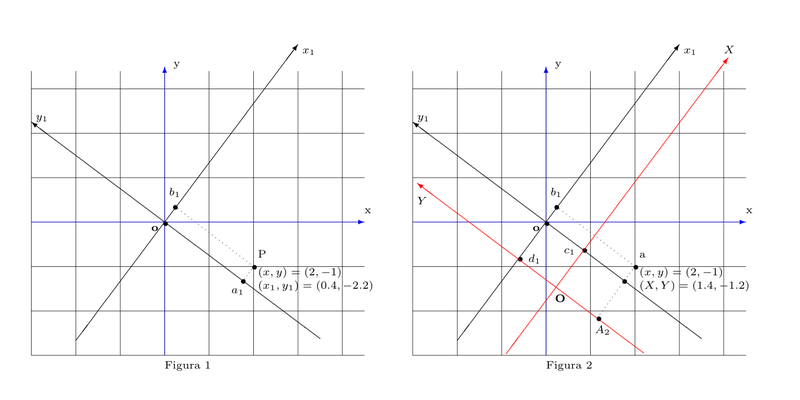
Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.
Encontre as equações das retas suporte do eixo $X$ e do eixo $Y$ em relação aos sistemas $x_{1}y_{1}$ e $xy$.
Encontre as equações das retas suporte do eixo $x_{1}$ e do eixo $y_{1}$ em relação ao sistema $xy$.
Seja $\mathcal{L}$ a reta cuja equação no sistema $xy$ é dada por $y = 2x + 1$. Encontre as equações de $\mathcal{L}$ em relação aos eixos $x_{1}y_{1}$ e $XY$.
Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $9x^2-24xy+16y^2-34x-38y+51=0$.
Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.
Reduza a equação $2xy + 2xz + 2yz - 6x - 6y - 4z = 9$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $2x^2+y^2-4xy-4yz+12x+6y+6z=1 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Em cálculo de uma variável vemos que se $x_0$ é um extremo local (máximo ou mínimo) de uma função $f(x)$, então a reta tangente ao gráfico de $f$ em $x_0$ é horizontal, ou seja, $f'(x_0)=0$.
Encontre uma relação similar entre um extremo local de uma função de duas variáveis e o plano tangente ao seu gráfico.
Use esta relação para encontrar os extremos locais da função $\displaystyle f(x,y)=-2xy$.
Verifique se sua resposta no item anterior está correta, primeiro achando uma mudança de coordenadas conveniente (rotação) e, em seguida, completando os quadrados em $f(x',y')$ de tal forma a identificar a quádrica resultante.
Reduza a equação $2x^2+2y^2-z^2+8xy-4xz-4yz=2 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $3x^2+2xy+3y^2-6x-6y+1=0$.
Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.
Reduza a equação $z^2 + 4xy + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
A equação da quádrica $z^2 + 4xy + 1 = 0$ pode ser escrita em forma matricial:
$$X^tAX+1=0,$$
onde:
$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ A=\begin{pmatrix}0 & 2 & 0 \\2 & 0 & 0 \\0 & 0 & 1\end{pmatrix}. $$
Seja:
$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}-\lambda & 2 & 0 \\2 & -\lambda & 0 \\0 & 0 & 1-\lambda\end{pmatrix}=-\lambda^3+\lambda^2+4\lambda-4.$$
As raízes de $P(\lambda)$ são $1$, $2$ e $-2$. Considere os sistemas lineares referentes às raízes $1$ e $2$, $(A-I) X = 0$ e $(A-2I) X = 0$. Uma solução de norma unitária desses sistemas consiste em $U_1=(0,0,1)$ e $U_2=(1/\sqrt{2},1/\sqrt{2},0)$, respectivamente. Sejam $U_3=U_1 \times U_2 = (-1/\sqrt{2},1/\sqrt{2},0)$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $z^2 + 4xy + 1 = 0$ se transforma em:
$$-(x')^2-\dfrac{(y')^2}{1/2}+\dfrac{(z')^2}{1/2}=1,$$
que é a equação de um hipérbolóide de duas folhas.
Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $x^2-16y^2 + 8x +128y -256 = 0$.
Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+3y^2+4xy+4y-4=0$.
Identifique a cônica descrita pela equação $4x^2-4xy+y^2-2x+y+15=0$.
Reduza a equação $x^2+y+z^2=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
$y=-(x^2+z^2)$: parabolóide elíptico.
Reduza a equação $-x^2-y^2-7z^2+16xy+8xz+8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $4x^2+4y^2+9z^2+8xy+12xz+10x+y+4z+1=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Considere a cônica definida pela equação $2xy+x-2=0.$
Determinar seu centro.
Classificar a cônica.
Esboçar seu gráfico.
Identificar a cônica $x^2+3y^2-2xy+3=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+5x+y-9=0$.
Seja $Q$ um retângulo centrado na origem, cujo lado maior mede o triplo do lado menor. Sabendo que um dos vértices de $Q$ é $V_1=(1,2)$ e que o vértice $V_2$, consecutivo a $V_1$ no sentido trigonométrico (anti-horário), é tal que $V_1V_2$ é um lado menor, determine os outros vértices de $Q$.
Tomando o ângulo $\theta=\widehat{V_10V_2}$, temos que $V_2 = R_{\theta}(V_1)$, onde $$R_\theta=\left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array} \right) $$ denota a rotação por um ângulo $\theta$ (Fig.). Sendo $P$ o ponto médio do segmento $V_1V_2$, vamos ter que $\dfrac{\theta}{2}=\widehat{POV_2}$. Sendo $V_1V_2$ um lado menor e dada a relação entre os lados (enunciado), segue que $|OP|=3|PV_2|$. Assim, o triângulo retângulo $OPV_2$ nos fornece que $$ \sin\dfrac{\theta}{2} = \dfrac{|PV_2|}{|OV_2|} \quad\text{e}\quad \cos\dfrac{\theta}{2}=\dfrac{|OP|}{|OV_2|}=\dfrac{3|PV_2|}{|OV_2|}=3\sin\dfrac{\theta}{2}, $$ o que juntamente com a relação fundamental $\sin^2\theta+\cos^2\theta=1$, resulta em $\sin^2\dfrac{\theta}{2}+9\sin^2\dfrac{\theta}{2}=1$. Ou seja, temos que $$ \sin\dfrac{\theta}{2}=\dfrac{\sqrt{10}}{10} \quad\mathrm{e}\quad\cos\dfrac{\theta}{2}=\dfrac{3\sqrt{10}}{10}.$$ Conseqüentemente, temos que $$\cos\theta= \cos(2\dfrac{\theta}{2})=\cos^2\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}= \dfrac{4}{5}\quad \text{e}$$ $$\sin\theta= \sin(2\dfrac{\theta}{2})= 2\cos\dfrac{\theta}{2}\sin\dfrac{\theta}{2}= \dfrac{3}{5} .$$ Assim, $$ V_2 = R_{\theta}(V_1)=\left(\begin{array}{cc} \dfrac{4}{5} & -\dfrac{3}{5} \\ \dfrac{3}{5} & \dfrac{4}{5} \end{array}\right)\left(\begin{array}{c} 1 \\ 2 \end{array}\right) = \left(\begin{array}{rcl} -\dfrac{2}{5} &,&\dfrac{11}{5} \end{array}\right). $$ Finalmente, como $V_3=R_{\pi}(V_1)$, $V_4=R_{\pi}(V_2)$, $cos\pi=-1$ e $\sin\pi=0$, obtemos que $$V_3=-V_1=(-1,-2) \quad \text{e}\quad V_4=-V_2=(\dfrac{2}{5},-\dfrac{11}{5}).$$
Decida se a cônica $C$ determinada pela equação $9y^2-9x^2+6x=1$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Identifique a cônica descrita pela equação $49x^2-42xy+9y^2+56x-24y+16=0$.
A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue
\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]

Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.
Encontre as coordenadas dos pontos $a_{1}$ e $b_{1}$ (Figura 1) nos sistemas $xy$ e $x_{1}y_{1}$.
Encontre as coordenadas dos pontos $c_{1}$, ,$d_{1}$, $\textbf{O}$, e $A_{2}$ (Figura 2) em relação aos eixos $xy$, $x_{1}y_{1}$ e $XY$.
Decida se a cônica $C$ determinada pela equação $\displaystyle 4x^2-4x+9y^2-18y=26$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Identifique a cônica descrita pela equação $x^2-6xy-7y^2+10x-30y+23=0$.
Reduza a equação $2z^2+5x+12y+12z+18=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+2x+y^2+2y+2=0$.
Encontre ou mostre a impossibilidade de encontrar $\gamma\in\mathbb{R}$ tal que $\displaystyle x^2+\gamma y^2-4xy+ \gamma x = \gamma$ represente uma parábola.
Seja $\mathcal{C}$ a cônica cuja equação em relação ao sistema $xy$ é dada por $29x^2 + 24xy + 36y^2 + 22x + 96y = 115$. A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue
\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad
\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]

Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.
Encontre a equação de $\mathcal{C}$ nos sistemas $x_{1}y_{1}$ e $XY$.
Encontre as coordenadas dos vértices e dos focos de $\mathcal{C}$ nos três sistemas, $xy$,\,$x_{1}y_{1}$ e $XY$. Dica: Encontrar primeiro no sistema $XY$ e ir voltando.
Faça um esboço do desenho da cônica.
Reduza a equação $3x^2+3z^2+4xy+8xz+4yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Às vezes o gráfico de uma equação quadrática é uma reta, um par de retas ou até mesmo um único ponto. Nos referimos a tais gráficos como cônicas degeneradas. É também possível que a equação não seja satisfeita para nenhum valor real das variáveis, caso este no qual não existe um gráfico e dizemos tratar-se de uma cônica imaginária. Nos itens abaixo, identifique a cônica com a equação dada, dizendo se é degenerada ou imaginária. Quando possível, esboce também o gráfico.
$\displaystyle x^2+2xy+y^2=0$;
$\displaystyle x^2-2xy+y^2+2\sqrt{2}x-2\sqrt{2}y=0$;
$\displaystyle 2x^2+2xy+2y^2+2\sqrt{2}x-2\sqrt{2}y+6=0$.
Sejam $x$, $y$ os eixos cartesianos usuais do plano. Faça a mudança de variáveis $X = x - 2$ e $Y = y + 3$, que corresponde a mudarmos a origem para o ponto $\textbf{O} = (2,-3)$.
Dado o ponto $P=(1,4)$ no sistema $xy$, encontre as coordenadas de $P$ no sistema $XY$.
Dado o ponto $A=(2,1)$ no sistema $XY$, encontre as coordenadas de $A$ no sistema $xy$.
Decida se a cônica $C$ determinada pela equação $y^2+x^2+3xy-10x-10y+5=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Reduza a equação $x^2+4y^2+9z^2-4xy+6xz-12yz+4x-8y+12z+4=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Suponha que os eixos coordenados estejam fixos, mas a posição $P(x,y)$ de um inseto é movida para uma nova posição $P'(x',y')$ através de uma rotação do ponto por um ângulo $\alpha$ em torno da origem. Naturalmente, nesta rotação o ponto $P$ estará sempre sobre um círculo fixo com centro na origem. Mostre que a nova posição do inseto será \begin{align*} x' & = x\cos\alpha - y\sin\alpha \\ y' & = x \sin\alpha + y\cos\alpha \end{align*}.
Considere o plano com o sistema cartesiano canônico $xy$ e faça uma rotação de um ângulo $\theta$, com $0\leq \theta \leq\pi/2$ obtendo o novo sistema $\overline{x}$ $\overline{y}$. Seja $(*)$ a equação:
$$(*) \ \ \ Ax^2+Bxy+Cy^2+Dx+Ey+F=0$$,
com $A$, $B$, $C$, $D$, $E$, $F$ números reais. Ao transformar $(*)$ para o sistema $\overline{x}$ $\overline{y}$ obtemos:
$$(**) \ \ \ \overline{A} \overline{x}^2+\overline{B}\overline{x} \overline{y}+ \overline{C}\overline{y}^2+ \overline{D}\overline{x}+ \overline{E}\overline{y}+\overline{F}=0$$.
Mostre que:
\begin{align*} \overline{A} & = A\cos^2\theta+B\sin\theta\cos\theta+C\sin^2\theta, \\ \overline{B} & =-2A\sin\theta\cos\theta+B(\cos^2\theta-\sin^2\theta)+2C\sin\theta\cos\theta,\\ \overline{C} & = A\sin^2\theta-B\sin\theta\cos\theta+C\cos^2\theta, \\ \overline{D} & = D\cos\theta+E\sin\theta, \\ \overline{E} & = E\cos\theta-D\sin\theta\;\;\;\;\; \text{e} \\ \overline{F} & = F. \end{align*}
Supondo $A>0$ e $F<0$, conclua, a partir de 1, que a equação $(*)$ representa uma circunferência de centro $(0,0)$ e raio $r=\sqrt{\frac{-F}{A}}$ se, e somente se, para todo $\theta$, tivermos que $A=\overline{A}$, $B=\overline{B}$, $C=\overline{C}$,
$D=\overline{D}$, $E=\overline{E}$ e $F=\overline{F}$.
Sejam
$M= \left( \begin{array}{cc}A & \frac{B}{2}\\\frac{B}{2}& C \\\end{array}\right)$, $\overline{M}= \left( \begin{array}{cc}\overline{A} & \frac{\overline{B}}{2}\\\frac{\overline{B}}{2}&\overline{C}\end{array}\right)$ e $R_{\theta}=\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$.
Mostre, a partir de 1, que $\overline{M}=R_{\theta}^{t}\cdot M\cdot R_{\theta}$ e, calculando o determinante dos dois lados da igualdade, conclua que $\Delta=B^2-4AC=\overline{B}^{2}-4\overline{A}\overline{C}$, qualquer que seja o ângulo $\theta$ (OBS: $\Delta$ é conhecido pelo nome de discriminante da equação $(*)$ e o item 3 está dizendo que ele é invariante por rotação).
Considere a equação
$$x^{2} - 14 x y + y^{2} = 1.$$
Efetue a troca de variáveis $x = u \cos \theta + v\,\textrm{sen} \theta$ e $y = - u\, \textrm{sen} \theta + v \cos \theta$. Escolha, usando sua intuição ou fazendo as contas, $\theta$ de forma que a equação obtida em $u$ e $v$ seja a equação canônica de uma hipérbole. Explique o significado geométrico deste resultado e obtenha, nas coordenadas $x$ e $y$, as equações das retas que servem de assíntotas à tal hipérbole.
Decida se a cônica $C$ determinada pela equação $4x^2-8x-9y^2+6y-68=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Reduza a equação $2x^2+y^2-4xy-4yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Identificar a cônica $x^2+4y^2+4xy-2x-4y-1=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Reduza a equação $x^2 - y^2 + z^2 + 2xz - 2y + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
A equação da quádrica $x^2 - y^2 + z^2 + 2xz - 2y + 1 = 0$ pode ser escrita em forma matricial:
$$X^tAX+KX-6=0,$$
onde:
$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ K=\begin{pmatrix}0 & -2 & 0\end{pmatrix}, \ A=\begin{pmatrix}1 & 0 & 1 \\0 & -1 & 0 \\1 & 0 & 1\end{pmatrix}. $$
Seja:
$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}1-\lambda & 0 & 1 \\0 & -1-\lambda & 0 \\1 & 0 & 1-\lambda\end{pmatrix}=-\lambda^3+\lambda^2+2\lambda.$$
As raízes de $P(\lambda)$ são $0$, $2$ e $-1$. Considere os sistemas lineares referentes às raízes $0$ e $2$: $A X = 0$ e $(A-2I)=0$. Uma solução de norma unitária desses sistemas são $U_1=(1/\sqrt{2},0,-1/\sqrt{2})$ e $U_2=(1/\sqrt{2},0,-1/\sqrt{2})$, respectivamente. Sejam $U_3=U_1 \times U_2 = (0,-1,0)$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $x^2 - y^2 + z^2 + 2xz - 2y + 1 = 0$ se transforma em:
$$\dfrac{(z'-1)^2}{2}-(y')2=1,$$
que é a equação de um cilindro hiperbólico.
Decida se a cônica $C$ determinada pela equação $\displaystyle 4y^2-4y-24x+9=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Reduza a equação $x^2+y^2+4z^2-2xy-4xz+6x+12y+18z=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2-2y^2+4xy-6=0$.
Identifique a cônica $3 x^2-12 x y+12 y^2+ 2 \sqrt{5} x+\sqrt{5} y=0$ e seu parâmetros associados.
Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um ângulo $\theta$. Explique como podemos encontrar as coordenadas $xy$ de um ponto cujas coordenadas $x'y'$ sejam conhecidas.
Na equação $4x^2-20xy+25y^2-15x-6y=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Reduza a equação $3x^2+4y^2+z^2-12x-8y-2z+16=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
$\dfrac{(x-2)^2}{1/3}+\dfrac{(y-1)^2}{1/4}+(z-1)^2=1$: elipsóide.
Considere a cônica definida pela equação $x^2+xy-1=0.$
Determinar seu centro.
Classificar a cônica.
Esboçar seu gráfico.
Reduza a equação $x^2+y^2+z^2-4xy-4xz-4yz=7 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $4x^2+y^2-8z^2+4xy-4xz+8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Reduza a equação $x^2 + y^2 + z^2 + 2xy + 2xz - 2yz + x - y + z + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um ângulo $\theta$. Mostre que, para cada valor de $\theta$, a equação $x^2+y^2=r^2$ é transformada na equação $x'^2+y'^2=r^2$. Dê uma explicação geométrica.
Na equação $x^2-y^2+2\sqrt{3}xy+6x=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Seja $A$ uma matriz $2\times 2$ simétrica e $k$ um escalar. Mostre que o gráfico da equação quadrática $\textbf{x}^tA\textbf{x}=k$ é:
uma hipérbole se $k\neq 0$ e $\det A<0$;
uma elipse, círculo ou cônica imaginária se $k\neq 0$ e $\det>0$;
um par de retas ou uma cônica imaginária se $k\neq 0$ e $\det A=0$;
um par de retas ou um único ponto se $k=0$ e $\det A \neq 0$;
uma linha reta se $k=0$ e $\det A=0$.
[Dica: use o Teorema dos Eixos Principais.]
Considere a forma quadrática $2x^2+8xy+2y^2+x+y-9=0$. Escreva-a numa base conveniente e identifique qual é a cônica e seus paramêtros associados.
Decida se a cônica $C$ determinada pela equação $x^2+3xy+y^2=2$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Reduza a equação $3x^2 + 2y^2 + 3z^2 - 2xz - 4y = 6$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
A equação da quádrica $3x^2 + 2y^2 + 3z^2 - 2xz - 4y = 6$ pode ser escrita em forma matricial:
$$X^tAX+KX-6=0,$$
onde:
$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ K=\begin{pmatrix}0 & -4 & 0\end{pmatrix}, \ A=\begin{pmatrix}3 & 0 & -1 \\0 & 2 & 0 \\-1 & 0 & 3\end{pmatrix}. $$
Seja:
$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}3-\lambda & 0 & -1 \\0 & 2-\lambda & 0 \\-1 & 0 & 3-\lambda\end{pmatrix}=-\lambda^3+8\lambda^2-20\lambda+16.$$
As raízes de $P(\lambda)$ são $2$ e $4$, sendo $2$ uma raiz dupla. Considere o sistema linear referente à raiz $2$: $(A-2I) X = 0$. Duas soluções de norma unitária desse sistema são $U_1=(1/\sqrt{2},0,1/\sqrt{2})$ e $U_2=(0,1,0)$. Sejam $U_3=U_1 \times U_2 = (-1/\sqrt{2},0,1/\sqrt{2})$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $3x^2 + 2y^2 + 3z^2 - 2xz - 4y = 6$ se transforma em:
$$\dfrac{(x')^2}{4}+\dfrac{(y'-1)^2}{4}+\dfrac{(z')^2}{2}=1,$$
que é a equação de um elipsóide.
Identificar a cônica $4x^2+4xy+y^2-6x+3y+2=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).
Reduza a equação $4x^2-8x-9y^2+6y-36z+3=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
$9z-2=(x-1)^2-\dfrac{(3y-3)^2}{4}$: parabolóide hiperbólico.
Mostre que a intersecção de um plano $\displaystyle by+cz+d=0$, em que $b^2+c^2=1$, com o cone $x^2+y^2=z^2$ é uma cônica que pode ser uma elipse, uma hipérbole ou uma parábola. (Sugestão: mude para um sistema de coordenadas $\{O,U_1,U_2,U_3\}$ tal que $U_1=\vec{i}=(1,0,0)$, $U_2=(0,b,c)$ e $U_3=(0,-c,b)$).
Considere o plano com o sistema cartesiano canônico $xy$ e faça uma rotação de um ângulo $\theta$ obtendo um novo sistema $\overline{x}$ $\overline{y}$. Seja $P$ um ponto do plano.
Se $P=(2,2)$ no sistema $xy$ e $\theta=\pi/3$, encontre as coordenadas de $P$ no sistema $\overline{x}$ $\overline{y}$.
Se $P=(2,2)$ no sistema $\overline{x}$ $\overline{y}$ e $\theta=\pi/3$, encontre as coordenadas de $P$ no sistema $xy$.
Transforme a equação $x^2+y^2=4$ para o sistema $\overline{x}$ $\overline{y}$.
Suponha que $0<\theta <\pi/2$ e que $a=\tan\theta$ ($a$=tangente de $\theta$). Transforme a equação $y=ax$ para o sistema $\overline{x}$ $\overline{y}$.
Identifique a cônica descrita pela equação $4x^2-12xy+9y^2-6x+9y-4=0$.
Reduza a equação $2x^2+4yz-4x+2y+6z+5=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $3x^2+5y^2+4x-2y-10=0$.
Reduza a equação $144x^2+100y^2+81z^2-216xz-540x-720z=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Decida se a cônica $C$ determinada pela equação $5x^2+6xy+5y^2-8 = 0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Em cálculo de uma variável vemos que se $x_0$ é um extremo local (máximo ou mínimo) de uma função $f(x)$, então a reta tangente ao gráfico de $f$ em $x_0$ é horizontal, ou seja, $f'(x_0)=0$.
Encontre uma relação similar entre um extremo local de uma função de duas variáveis e o plano tangente ao seu gráfico.
Use esta relação para encontrar os extremos locais da função $f(x,y)=x^2+y^2-2x-6y+14$.
Verifique se sua resposta no item anterior está correta completando os quadrados em $f(x,y)$ e identificando a quádrica.
Identifique a cônica descrita pela equação$7x^2+6xy-y^2-2x+10y-9=0$.
Reduza a equação $5x^2+5y^2+3z^2-2xy+2xz+2yz+2x-y=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.
Decida se a cônica $C$ determinada pela equação $36x^2-24x+36y^2-36y+14=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.
Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2-y^2-4x+2y+2=0$.
Na equação $18x^2+12xy+2y^2+94\frac{\sqrt{10}}{10}x-282\frac{\sqrt{10}}{10}y+94=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.
Na equação $9x^2-4xy+6y^2=30$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.

