Exercícios
Área e volume
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
São dados quatro vértices, $A = (-2,-1,1)$, $B = (1,1,1)$, $D = (5,1,-1)$, e $E = (1,1,-1)$, de um paralelepípedo, cuja distribuição está esquematizada no desenho abaixo.
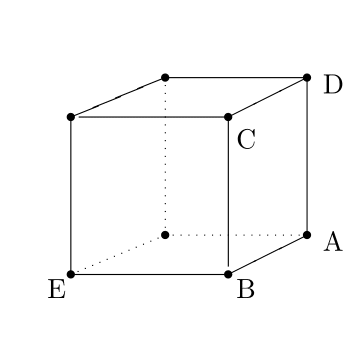
Determine as coordenadas do ponto $C$.
Encontrar o volume do paralelepípedo.
Determinar o valor da altura $h$ do paralelepípedo em relação à base $ABCD$.
Encontrar a equação do plano $\pi$ que contém a face do paralelepípedo onde está o vértice $E$ e é paralela à face $ABCD$.
Mostre que se as coordenadas dos quatro vértices de um tetraedro são
$$ (x_1,y_1,z_1),\; (x_2,y_2,z_2),\; (x_3,y_3,z_3),\; (x_4,y_4,z_4), $$
então o seu volume é dado por
$$ Vol=\frac{1}{6}\det\left(\begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \\\end{array}\right). $$
(Sugestão: Verifique primeiro que o volume do tetraedro é um sexto do volume do paralelepípedo determinados pelos seus vértices.)
A Pirâmide de Quéops, também conhecida como Grande Pirâmide de Gizé, no Egito, tem o formato muito próximo de um tetraedro regular. Pesquise as suas medidas e utilizando o produto misto, calcule aproximadamente o volume interno da pirâmide. Defina o sistema de coordenadas e os três vetores do produto misto de forma a facilitar as contas.
Mostre que
$$ u\cdot(v\times w)=\|u\|\;\|v\|\;\|w\|\;\sqrt{ \det\left(\begin{array}{ccc} 1 & \cos(u,v) & \cos(u,w) \\ \cos(u,v) & 1 & \cos(v,w) \\ \cos(u,w) & \cos(v,w) & 1 \\\end{array}\right)}, $$
onde, por exemplo, $\displaystyle \cos(u,v)=\frac{u\cdot v}{\|u \|\|v\|}$.
(Dica: Verifique primeiro que, para um tetraedro cujos vértices têm coordenadas
$$ (x_1,y_1,z_1),\; (x_2,y_2,z_2),\; (x_3,y_3,z_3),\; (x_4,y_4,z_4), $$
o seu volume é dado por
$$ Vol=\frac{1}{6}\det\left(\begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \\\end{array}\right).$$
Encontre o volume do paralelepípedo determinado pelos vetores $u$, $v$ e $w$, dados por: $u=\vec{i}+3\vec{j}+2\vec{k}$, $v=2\vec{i}+\vec{j}-\vec{k}$ e $w=\vec{i}-2\vec{j}+\vec{k}$.
$|u\cdot(v\times w)|=|-20|=20$
Sendo $\|u\|=3, \|v\|=4$ e $120^{\circ}$ o ângulo entre os vetores $u$ e $v$, calcule o volume do paralelepípedo determinado por $u\times v$, $u$ e $v$.
$108$
Sejam $A=(1,2,-1)$, $B=(5,0,1)$, $=C(2,-1,1)$ e $D=(6,1,-3)$ os vértices de um tetraedro. Calcule:
o volume deste tetraedro;
a sua altura relativa ao vértice $D$.
1. Os três vetores que determinam este tetraedro poderiam ser $
\overrightarrow{AB}$, $\overrightarrow{AC}$ e $\overrightarrow{AD}$. Como $ \overrightarrow{AB}$ $=\left( 4,-2,2\right) $, $\overrightarrow{AC}$ $ =\left( 1,-3,2\right) $ e $\overrightarrow{AD}$ $=\left( 5,-1,1\right) $ e $V_{T}=\frac{\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right] \right\vert }{6}$, então
$\left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right]
=\left\vert
\begin{array}{ccc}
4 & -2 & 2 \\
1 & -3 & 2 \\
5 & -1 & 1
\end{array}
\right\vert =36$.
Assim, concluímos que o volume do tetradro é $V_{T}=\frac{\left\vert 36\right\vert }{6}=6$.
2 . Os vetores que determinam o tetraedro são $\overrightarrow{AB},$ $
\overrightarrow{AC}$ e $\overrightarrow{AD}.$ Sabemos que o volume do
tetraedro é dado por $V_{T}=\frac{A_{b}h}{6}$, onde $A_{b}$ é a área da base e $h$ é a altura. Como a área da base é um triângulo determinado pelos vetores $\overrightarrow{AB}$ e $\overrightarrow{AC}, $ $A_{b}=\frac{\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert }{2}$.
Por outro lado, do cálculo vetorial temo que $V_{T}=\frac{\left\vert
\left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right]
\right\vert }{6}.$ Então, temos $\left\vert \left[ \overrightarrow{AB},
\overrightarrow{AC},\overrightarrow{AD}\right] \right\vert =\left\vert
\overrightarrow{AB}\times \overrightarrow{AC}\right\vert h$ $\Longrightarrow h=\frac{\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC}, \overrightarrow{AD}\right] \right\vert }{\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert }.$
Como $\overrightarrow{AB}$ $=\left( 4,-2,2\right) $, $\overrightarrow{AC}$ $
=\left( 1,-3,2\right) $e $\overrightarrow{AD}$ $=\left( 5,-1,1\right) $, temos $\left[ \overrightarrow{AB},\overrightarrow{AC}, \overrightarrow{AD} \right] =36$ e
$\overrightarrow{AB}\times \overrightarrow{AC}=\left\vert
\begin{array}{ccc}
\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\
4 & -2 & 2 \\
1 & -3 & 2
\end{array}
\right\vert =2\overrightarrow{i}-6\overrightarrow{j}-10\overrightarrow{k}.$
Logo, $\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert =2 \sqrt{35}$. Portanto, concluímos que $h=\frac{18\sqrt{35}}{35}$.
Dado que os pontos médios dos lados do triângulo $ABC$ são $M=(0,1,3)$, $N=(3,-2,2)$ e $P=(1,0,2)$, determine a área do triângulo $ABC$.
Calcule a área de um triângulo cujos vértices são: $A= (2,-1,-3)$, $B = (1,2,-4)$ e $C = (3,-1,-2)$.
$\|\vec{AB}\times\vec{AC}\|/2=\dfrac{3\sqrt{2}}{2}$
Uma piscina olímpica pode ser vista como um paralelepídeo. Pesquise as medidas padronizadas de uma piscina olímpica e e calcule, utilizando o produto misto, o volume de água utilizado para enchê-la. Defina o sistema de coordenadas e os três vetores do produto misto de forma a facilitar as contas.
A área do triângulo $ABC$ é $\sqrt{6}$. Sabendo que $A = (2,1,0), \; B = (-1,2,1)$ e que o vértice $C$ está no eixo $Y$, encontre as coordenadas de $C$.
Como $C$ está sobre o eixo $Y$, vamos escrever $C=(0,y,0)$. Pela definição de área através do produto vetorial, segue que \begin{align*} 6 = \mathrm{area}^2 & = \frac{1}{4}\|(A-B)\times (C-B)\|^2 \\ & = \frac{1}{4}\|(3,-1,-1)\times (1,y-2,-1)\|^2 \\ & = \frac{1}{4}\|(y-1,2,3y-5)\|^2 \\ & = \frac{1}{4}\left( 10y^2-32 y+30\right). \end{align*} Ou seja, ficamos com $\displaystyle 10y^2-32y+6=0$, cujas raízes são $y=3$ e $y=\frac{1}{5}$. Portanto, podemos ter $C=(0,3,0)$ ou $C=(0,\dfrac{1}{5},0)$.
Encontre o volume do paralelepípedo determinado pelos vetores $u$, $v$ e $w$, dados por: $u=\overrightarrow{AB}$, $v=\overrightarrow{AC}$ e $w=\overrightarrow{AD}$, onde $A=(1,3,4)$, $B=(3,5,3)$, $C=(2,1,6)$ e $D=(2,2,5)$.
$u\cdot(v\times w)=1$

