871

Sendo $\|u\|=3, \|v\|=4$ e $120^{\circ}$ o ângulo entre os vetores $u$ e $v$, calcule:

$\|u+v\|,$
$\|u\times(v-u)\|.$

874

Sejam $a,b,c$ três vetores não coplanares e denotemos por $[a,b,c]$ o produto misto $a\cdot(b\times c)$. Os vetores

$$a'=\frac{b\times c}{[a,b,c]},\; b'=-\frac{a\times c}{[a,b,c]},\; c'=\frac{a\times b}{[a,b,c]}$$

são chamados os vetores recíprocos aos vetores $a,b,c$.

Uma das utilidades dos vetores recíprocos consiste em encontrar as coordenadas de um vetor $v$ qualquer em termos dos vetores $a,b,c$. Isto é, queremos encontrar escalares $x,y,z$ tais que

$$ v=xa+yb+zc. $$

Mostre que, $$v = (v\cdot a')a \; + \; (v\cdot b')b \;+\; (v\cdot c')c.$$ Ou seja,
$$ x=v\cdot a', \; y=v\cdot b', \; z=v\cdot c'. $$
Mostre que se $a,b,c$ são três vetores unitários, dois a dois ortogonais e que satisfazem a regra da mão direita, então $a'=a$, $b'=b$ e $c'=c$ (ou seja, neste caso os vetores recíprocos de $a,b,c$ são eles próprios). Em particular, segue que $$v = (v\cdot a) a \; + \; (v\cdot b) b \;+\; (v\cdot c) c.$$
Verifique que se
$$ v=xa'+yb'+zc', $$
então $$v = (v\cdot a)a' \; + \; (v\cdot b)b' \;+\; (v\cdot c)c'.$$
Mostre que valem as relações
$$ a'\cdot a = b'\cdot b = c'\cdot c =1,$$
$$a'\cdot b =a'\cdot c = b'\cdot a = b'\cdot c = c'\cdot a = c'\cdot b = 0. $$
Em outras palavras, o produto escalar de vetores correspondentes é $1$, enquanto que o produto escalar de vetores não-correspondentes é $0$.
Reciprocamente, mostre que se
$$ A\cdot a = B\cdot b = C\cdot c =1,$$
$$A\cdot b = A\cdot c = B\cdot a = B\cdot c = C\cdot a = C\cdot b = 0, $$
então
$$ A=a', \; B=b', \; C=c'.$$
Conclua que os vetores recíprocos de $a',b',c'$ são exatamente $a,b,c$.

876

A área do triângulo $ABC$ é $\sqrt{6}$. Sabendo que $A = (2,1,0), \; B = (-1,2,1)$ e que o vértice $C$ está no eixo $Y$, encontre as coordenadas de $C$.

Como $C$ está sobre o eixo $Y$, vamos escrever $C=(0,y,0)$. Pela definição de área através do produto vetorial, segue que \begin{align*} 6 = \mathrm{area}^2 & = \frac{1}{4}\|(A-B)\times (C-B)\|^2 \\ & = \frac{1}{4}\|(3,-1,-1)\times (1,y-2,-1)\|^2 \\ & = \frac{1}{4}\|(y-1,2,3y-5)\|^2 \\ & = \frac{1}{4}\left( 10y^2-32 y+30\right). \end{align*} Ou seja, ficamos com $\displaystyle 10y^2-32y+6=0$, cujas raízes são $y=3$ e $y=\frac{1}{5}$. Portanto, podemos ter $C=(0,3,0)$ ou $C=(0,\dfrac{1}{5},0)$.

1418

Uma piscina olímpica pode ser vista como um paralelepídeo. Pesquise as medidas padronizadas de uma piscina olímpica e e calcule, utilizando o produto misto, o volume de água utilizado para enchê-la. Defina o sistema de coordenadas e os três vetores do produto misto de forma a facilitar as contas.

867

Determinar $u\cdot v$, sabendo que $\|u\times v\|=12$, $\|u\|=13$ e $v$ é unitário.

Usando que $\| u\times v\|=|u||v|\sin\theta$, obtemos que $\sin\theta=\dfrac{12}{13}$, onde $\theta$ é o ângulo entre os vetores $u,v\in\mathbb{R}^3$. Por conseguinte, temos que $\cos\theta=\sqrt{1-\sin^2\theta}=\sqrt{1-(\dfrac{12}{13})^2}=\dfrac{5}{13}$. Logo, $u\cdot v=|u||v|\cos\theta=13\cdot 1\dfrac{5}{13}=5$.

997

Sejam os vetores $\vec{u}=(2,1,3)$, $\vec{v}=(0,1,-1)$, $\vec{w}=(4,5,3)$. Mostre que $\vec{u}, \vec{v}$ e $\vec{w}$ são coplanares.

De fato, basta verificar que $\vec{u}\cdot(\vec{v}\times\vec{w})=0$.

1010

Encontre o volume do paralelepípedo determinado pelos vetores $u$, $v$ e $w$, dados por: $u=\overrightarrow{AB}$, $v=\overrightarrow{AC}$ e $w=\overrightarrow{AD}$, onde $A=(1,3,4)$, $B=(3,5,3)$, $C=(2,1,6)$ e $D=(2,2,5)$.

$u\cdot(v\times w)=1$

868

Verifique se os pontos $A=(1,2,4), B=(-1,0,2), C=(0,2,2) \;\mbox{e}\; D=(-2,1,3)$ estão no mesmo plano ou não.

Não estão pois $\displaystyle \vec{AB}\cdot(\vec{BC}\times\vec{AD})=-8$.

999

Dados três pontos $A = (2,1,3)$, $B = (5,-1,2)$ e $C = (1,2,-3)$, encontre um quarto ponto $D$ de forma que os pontos $A$, $B$, $C$ e $D$ sejam os vértices de um paralelogramo (Dica: Queremos $D$ de forma que $\overrightarrow{CD}$ seja paralelo a $\overrightarrow{AB}$ e tenha mesmo comprimento.).

$D=(4,4,-2)$

996

Se $u$, $v$ e $w$ são vetores no espaço então: mostre que $\langle u,v\times w\rangle = \langle v, w\times u\rangle = \langle w , v\times u\rangle$.

1000

Determine, se existir, os valores de $x$ para que o vetor $\textbf{v}=x\vec{i}+6\vec{k}$ seja paralelo ao produto vetorial de $\textbf{w}=\vec{i}+x\vec{j}+2\vec{k}$ por $\textbf{u}=2\vec{i}+\vec{j}+2\vec{k}$.

865

Determine um vetor $\vec{a}=(x,y,z)$ que satisfaça as seguintes equações:

$$\vec{a} \times \vec{j}=\vec{k}$$

$$\vec{a} {\cdot}(\vec{i}+2\vec{j})=0,$$

onde $\vec{i}$, $\vec{j}$ e $\vec{k}$ são os vetores da base canônica de $\mathbb{R}^3$.

998

Sejam $u = (2,-1,3)$, $v = (0,1,7)$ e $w = (1,4,5)$.

Mostre que existem dois números $\alpha$ e $\beta$ tais que $u\times(v\times w) = \alpha\,v + \beta\,w$.
Mostre que existem dois números $a$ e $b$ tais que $(u\times v)\times w = a\,u + b\,v$.

878

Sejam $A=(1,2,-1)$, $B=(5,0,1)$, $=C(2,-1,1)$ e $D=(6,1,-3)$ os vértices de um tetraedro. Calcule:

o volume deste tetraedro;
a sua altura relativa ao vértice $D$.

1. Os três vetores que determinam este tetraedro poderiam ser $
\overrightarrow{AB}$, $\overrightarrow{AC}$ e $\overrightarrow{AD}$. Como $ \overrightarrow{AB}$ $=\left( 4,-2,2\right) $, $\overrightarrow{AC}$ $ =\left( 1,-3,2\right) $ e $\overrightarrow{AD}$ $=\left( 5,-1,1\right) $ e $V_{T}=\frac{\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right] \right\vert }{6}$, então

$\left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right]
=\left\vert
\begin{array}{ccc}
4 & -2 & 2 \\
1 & -3 & 2 \\
5 & -1 & 1
\end{array}
\right\vert =36$.

Assim, concluímos que o volume do tetradro é $V_{T}=\frac{\left\vert 36\right\vert }{6}=6$.

2 . Os vetores que determinam o tetraedro são $\overrightarrow{AB},$ $
\overrightarrow{AC}$ e $\overrightarrow{AD}.$ Sabemos que o volume do
tetraedro é dado por $V_{T}=\frac{A_{b}h}{6}$, onde $A_{b}$ é a área da base e $h$ é a altura. Como a área da base é um triângulo determinado pelos vetores $\overrightarrow{AB}$ e $\overrightarrow{AC}, $ $A_{b}=\frac{\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert }{2}$.

Por outro lado, do cálculo vetorial temo que $V_{T}=\frac{\left\vert
\left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right]
\right\vert }{6}.$ Então, temos $\left\vert \left[ \overrightarrow{AB},
\overrightarrow{AC},\overrightarrow{AD}\right] \right\vert =\left\vert
\overrightarrow{AB}\times \overrightarrow{AC}\right\vert h$ $\Longrightarrow h=\frac{\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC}, \overrightarrow{AD}\right] \right\vert }{\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert }.$

Como $\overrightarrow{AB}$ $=\left( 4,-2,2\right) $, $\overrightarrow{AC}$ $
=\left( 1,-3,2\right) $e $\overrightarrow{AD}$ $=\left( 5,-1,1\right) $, temos $\left[ \overrightarrow{AB},\overrightarrow{AC}, \overrightarrow{AD} \right] =36$ e

$\overrightarrow{AB}\times \overrightarrow{AC}=\left\vert
\begin{array}{ccc}
\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\
4 & -2 & 2 \\
1 & -3 & 2
\end{array}
\right\vert =2\overrightarrow{i}-6\overrightarrow{j}-10\overrightarrow{k}.$

Logo, $\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert =2 \sqrt{35}$. Portanto, concluímos que $h=\frac{18\sqrt{35}}{35}$.

880

Mostre que

$$ u\cdot(v\times w)=\|u\|\;\|v\|\;\|w\|\;\sqrt{ \det\left(\begin{array}{ccc} 1 & \cos(u,v) & \cos(u,w) \\ \cos(u,v) & 1 & \cos(v,w) \\ \cos(u,w) & \cos(v,w) & 1 \\\end{array}\right)}, $$

onde, por exemplo, $\displaystyle \cos(u,v)=\frac{u\cdot v}{\|u \|\|v\|}$.

(Dica: Verifique primeiro que, para um tetraedro cujos vértices têm coordenadas

$$ (x_1,y_1,z_1),\; (x_2,y_2,z_2),\; (x_3,y_3,z_3),\; (x_4,y_4,z_4), $$

o seu volume é dado por

$$ Vol=\frac{1}{6}\det\left(\begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \\\end{array}\right).$$

1020

Calcule a área de um triângulo cujos vértices são: $A= (2,-1,-3)$, $B = (1,2,-4)$ e $C = (3,-1,-2)$.

$\|\vec{AB}\times\vec{AC}\|/2=\dfrac{3\sqrt{2}}{2}$

881

Mostre que se

$$u= u_a a + u_b b + u_c c,$$

$$v = v_a a + v_b b + v_c c,$$

$$w= w_a a + w_b b + w_c c,$$

então

$$u\cdot(v\times w)=\det\left(\begin{array}{ccc} u_a & u_b & u_c \\ v_a & v_b & v_c \\ w_a & w_b & w_c \\\end{array}\right)[a\cdot(b\times c)].$$

Se $a=i$, $b=j$ e $c=k$, como fica esta fórmula?

872

Mostre que os vetores $a, b, c$, que satisfazem a relação $$a\times b \;+\; b\times c \;+\; c\times a\; = \;0$$ são coplanares.

875

Sejam $a,b,c$ três vetores não coplanares e denotemos por $[a,b,c]$ o produto misto $a\cdot(b\times c)$. Os vetores

$$ a'=\frac{b\times c}{[a,b,c]},\; b'=-\frac{a\times c}{[a,b,c]},\; c'=\frac{a\times b}{[a,b,c]} $$ são chamados os vetores recíprocos aos vetores $a,b,c$.

Mostre que

$$ [a',b',c']=\frac{1}{[a,b,c]}. $$

1019

São dados quatro vértices, $A = (-2,-1,1)$, $B = (1,1,1)$, $D = (5,1,-1)$, e $E = (1,1,-1)$, de um paralelepípedo, cuja distribuição está esquematizada no desenho abaixo.

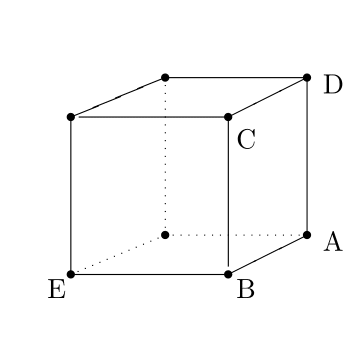
Determine as coordenadas do ponto $C$.
Encontrar o volume do paralelepípedo.
Determinar o valor da altura $h$ do paralelepípedo em relação à base $ABCD$.
Encontrar a equação do plano $\pi$ que contém a face do paralelepípedo onde está o vértice $E$ e é paralela à face $ABCD$.

866

Justificar as afirmações abaixo:

$\vec{u} \cdot (\vec{u}\times \vec{v})=0,$ para quaisquer dois vetores $\vec{u}$ e $\vec{v}.$
Se as diagonais de um paralelogramo são perpendiculares, então este paralelogramo é um losango.

869

Sabendo que $u\cdot(v\times w)=2$, calcular:

$u\cdot(w\times v)$.
$v\cdot(w\times u)$.
$(v\times w)\cdot u$.
$(u\times w)\cdot 3v$.
$u\cdot(2w\times v)$.
$(u+v)\cdot(u\times w)$.

879

Mostre que se as coordenadas dos quatro vértices de um tetraedro são

$$ (x_1,y_1,z_1),\; (x_2,y_2,z_2),\; (x_3,y_3,z_3),\; (x_4,y_4,z_4), $$

então o seu volume é dado por

$$ Vol=\frac{1}{6}\det\left(\begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \\\end{array}\right). $$

(Sugestão: Verifique primeiro que o volume do tetraedro é um sexto do volume do paralelepípedo determinados pelos seus vértices.)

1021

Sendo $\|u\|=3, \|v\|=4$ e $120^{\circ}$ o ângulo entre os vetores $u$ e $v$, calcule o volume do paralelepípedo determinado por $u\times v$, $u$ e $v$.

$108$

1404

O momento escalar ou torque sobre o ponto $P$ de uma força $\vec{F}$ aplicada a um ponto $Q$ é dado por $\|\vec{PQ} \times \vec{F}\|$. Uma força $\vec{F}$ com magnitude de $10 N$ é aplicada na direção $y$ positiva sobre o ponto $Q=(1,1,1)$ em um cubo com lados de tamanho $1m$. Determine o momento escalar de $\vec{F}$ sobre o ponto $P = (1,0,1)$. Faça um esboço do gráfico, indicando a força e o momento escalar.

1001

Responda, justificando, falso ou verdadeiro a cada uma das seguintes afirmações:

Se $u$, $v$ e $w$ são vetores no espaço, com $v$ não nulo e $v\times u=v\times w$, então $u=w$.
Se $u$, $v$ e $w$ são vetores no espaço então: $\mid u\cdot(v\times w) \mid=\mid v\cdot(u\times w) \mid=\mid w\cdot(v\times u) \mid=\mid v\cdot(w\times u) \mid$.
Se $u$, $v$ e $w$ são vetores no espaço, então $u\times (v\times w)= (u\times v)\times w$.
Se $u$, $v$ e $w$ são vetores no espaço, $u$ é não nulo e $u\times v=u\times w=\vec{0}$, então $v\times w=\vec{0}$.

873

Mostre que quaisquer vetores $a, b, c$ satisfazem a relação $$(a\times b)\cdot(c\times d)\;+\;(a\times c)\cdot(d\times b)\;+\;(a\times d)\cdot(b\times c)=0.$$

883

Usando a propriedade de que podemos trocar os sinais $\times$ e $\cdot$ em um produto misto, mais a fórmula do produto vetorial triplo: $$A\times(B\times C) = (A\cdot C)B - (A\cdot B)C,$$ mostre que $$(A\times B)\cdot (C\times D) = \det\left(\begin{array}{cc}A\cdot C & A\cdot D \\B\cdot C & B\cdot D \\\end{array}\right).$$

877

Dado que os pontos médios dos lados do triângulo $ABC$ são $M=(0,1,3)$, $N=(3,-2,2)$ e $P=(1,0,2)$, determine a área do triângulo $ABC$.

1002

Sejam $u$ e $v$ vetores no espaço. Mostre que

$(u+v)\times (u-v)=2v\times u$.
Se $u\times v$ é não nulo e $w$ é um vetor qualquer no espaço, então existem números reais $a, b$ e $c$ tais que $w=a(u\times v)+bu+cv$.
Se $u\times v$ é não nulo e $u$ é ortogonal a $v$, então $u\times (u\times v)$ é paralelo a $v$.

870

Para quais valores de $m$ os pontos $A=(m,1,2), B=(2,-2,-3), C=(5,-1,1)$ e $D=(3,-2,-2)$ são coplanares?

$m=\pm 4$

1419

A Pirâmide de Quéops, também conhecida como Grande Pirâmide de Gizé, no Egito, tem o formato muito próximo de um tetraedro regular. Pesquise as suas medidas e utilizando o produto misto, calcule aproximadamente o volume interno da pirâmide. Defina o sistema de coordenadas e os três vetores do produto misto de forma a facilitar as contas.

1402

O momento escalar ou torque sobre o ponto $P$ de uma força $\vec{F}$ aplicada a um ponto $Q$ é dado por $\|\vec{PQ} \times \vec{F}\|$. Uma força $\vec{F}$ com magnitude de $10 N$ é aplicada na direção $y$ positiva sobre o ponto $Q=(1,1,1)$ em um cubo com lados de tamanho $1m$. Determine o momento escalar de $\vec{F}$ sobre o ponto $P = (0,0,0)$. Faça um esboço do gráfico, indicando a força e o momento escalar.

1403

O momento escalar ou torque sobre o ponto $P$ de uma força $\vec{F}$ aplicada a um ponto $Q$ é dado por $\|\vec{PQ} \times \vec{F}\|$. Uma força $\vec{F}$ com magnitude de $10 N$ é aplicada na direção $y$ positiva sobre o ponto $Q=(1,1,1)$ em um cubo com lados de tamanho $1m$. Determine o momento escalar de $\vec{F}$ sobre o ponto $P = (1,0,0)$. Faça um esboço do gráfico, indicando a força e o momento escalar.

882

Mostre que se

$$u= u_a a + u_b b + u_c c,$$

$$v = v_a a + v_b b + v_c c,$$

$$w= w_a a + w_b b + w_c c,$$

então

$$(u\cdot v\times w)(a\cdot b\times c) = \det\left(\begin{array}{ccc} u\cdot a & u\cdot b & u\cdot c\\ v\cdot a & v\cdot b & v\cdot c\\ w\cdot a & w\cdot b & w\cdot c\\\end{array}\right).$$

Esta fórmula reduz o cálculo de dois determinantes (pois cada produto misto envolve o cálculo de um determinante) ao cálculo de um único.

Sugestão: Use a seguinte relação:

$$u\cdot(v\times w)=\det\left(\begin{array}{ccc} u_a & u_b & u_c \\ v_a & v_b & v_c \\ w_a & w_b & w_c \\\end{array}\right)[a\cdot(b\times c)].$$

1011

Encontre o volume do paralelepípedo determinado pelos vetores $u$, $v$ e $w$, dados por: $u=\vec{i}+3\vec{j}+2\vec{k}$, $v=2\vec{i}+\vec{j}-\vec{k}$ e $w=\vec{i}-2\vec{j}+\vec{k}$.

$|u\cdot(v\times w)|=|-20|=20$

Exercícios

Produto vetorial