Exercícios
Produto escalar
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
No triângulo $ABC$, tem-se $\vec{AP}=\frac{1}{3}\vec{AC}$ e $\vec{AQ}=\frac{1}{2}\vec{AC}.$ Expressar os vetores $\vec{BP}$ e $\vec{BQ}$ em funçãao de $\vec{BA}$ e $\vec{BC}.$
Sabendo que $\| u \| = \sqrt{2}$, $\| v \| = \sqrt{3}$ e que $u$ e $v$ formam um ângulo de ${3\pi}/4$, determinar:
$| (2u-v)\cdot(u-2v)|$.
$\|u-2v\|$.
- $| (2u-v)\cdot(u-2v)|=10+5\sqrt{3}$.
- $\|u-2v\|=2\sqrt{2+\sqrt{3}}$.
Dados os pontos $A = (2,3,0), \; B = (4,0,1)$ e $C = (0,1,2)$ no $\mathbb{R}^{3}$, determine:
O comprimento do lado $AB$.
A medida do ângulo entre os lados $BA$ e $BC$.
A área do triângulo $ABC$.
O comprimento da altura do triângulo $ABC$ relativa ao vértice $A$.
As coordenadas do ponto no lado $AC$ por onde passa a perpendicular a esse lado que contém o ponto $B$.
Desenhe o triângulo $ABC$ no espaço $\mathbb{R}^{3}$.
Mostre que as diagonais de um losango cortam-se mutuamente em seu ponto médio e que são ortogonais entre si.
Determine o conjunto de todos os vetores do espaço que são paralelos ao vetor $(1,1,1)$.
Descreva o conjunto de todos os vetores do espaço que são ortogonais ao vetor $(1,0,-1)$.
Qual o significado geométrico dos conjuntos encontrados nos itens (a) e (b)?
Encontre o ponto $Q$ do espaço tal que o vetor com origem no ponto $P=(1,0,1)$ e com extremidade em $Q$ tenha norma, direção e sentido iguais ao vetor $(1,-2,1)$.
$Q=(2,-2,2)$.
Encontre o ângulo entre os vetores $u=(2,1,0)$ e $v=(0,1,-1)$ e entre os vetores $w=(1,1,1)$ e $z=(0,-2,-2)$.
\(\arccos(\dfrac{\sqrt{10}}{10})\) e \(\arccos(-\sqrt{\dfrac{2}{3}})\), respectivamente.
Dados três pontos $A=(1,-5,8)$, $B=(5,2,4)$ e $C=(3,9,1)$, ache três pontos diferentes tais que cada um deles forma com $A,B,C$ um paralelogramo.
Sabendo que o ponto $P=(-3,m,n)$ pertence à reta que passa pelos pontos $A=(1,-2,4)$ e $B=(-1,-3,1)$, determine $m$ e $n$.
\(m=-4\) e \(n=-2\)
Sejam $u$ e $v$ dois vetores de comprimentos iguais. Mostre que para quaisquer números $a$ e $b$, os vetores $au+bv$ e $av+bu$ têm o mesmo comprimento. Interprete o resultado.
Decompor o vetor $\vec{w} = (-1,-3,-2)$ como soma de dois vetores $\vec{w} = \vec{u} + \vec{v}$, onde $\vec{u}$ é paralelo ao vetor $(0,1,3)$ e $\vec{v}$ é ortogonal a $(0,1,3)$ (Dica: $u$ pode ser escolhido como a projeção de $\vec{w}$ sobre $(0,1,3)$).
$\vec{u}=\left(0,-\frac{9}{10},-\frac{27}{10}\right)^T$ e $\vec{w}=\left(-\sqrt{\frac{10}{59}},-\frac{21}{\sqrt{590}},\frac{7}{\sqrt{590}}\right)^T$
Para o par de vetores $u=(3,1,-3)$ e $v=(2,-3,1)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.
Posto que $u \cdot v=0$, $u$ e $v$ são ortogonais. Assim, a projeção ortogonal de $v$ sobre $u$ é zero. Nesse caso, $v_1=0$ e $v_2=v$.
Decompor o vetor $w = (1,3,2)$ como soma de dois vetores $w = u + v$, onde $u$ é paralelo ao vetor $(0,1,3)$ e $v$ é ortogonal a $(0,1,3)$.
$u=(0,11/10,33/10)$ e $v=(1,9/10,-3/10)$.
Estude o ângulo entre os vetores $\vec{i}$ e $\vec{j}$ no plano. Faça o mesmo no $\mathbb{R}^{3}$ em relação a $\vec{i}$, $\vec{j}$ e $\vec{k}$.
Escrevendo os vetores $u = x\vec{i} + y\vec{j}$ e $v = a\vec{i} + b\vec{j}$, verifique que $\langle u,v\rangle = xa\langle\vec{i},\vec{i}\rangle + yb\langle\vec{j},\vec{j}\rangle$. Faça um estudo semelhante no espaço $\mathbb{R}^{3}$.
Encontre um vetor $u$ que seja ortogonal aos vetores $(2,3,-1)$ e $(2,-4,6)$ tal que $\parallel u\parallel = 3\sqrt{3}$.
$u=\pm(-3,3,3)$.
Sejam $A=(2,1,2)$, $B=(1,0,0)$ e $C=(1+\sqrt 3,\sqrt 3,-\sqrt 6)$ três pontos no espaço. Calcule os ângulos do triângulo $ABC$, e os comprimentos da mediana e da altura que saem do vértice $A$.
Mostre que o segmento que une os pontos médios de 2 lados de um triângulo é paralelo ao terceiro lado e é igual a sua metade.
$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2}\left(
\overrightarrow{AC}+\overrightarrow{CB}\right) =\frac{1}{2}\overrightarrow{AB}.$
Logo, $MN//AB$ e $\left\Vert \overrightarrow{MN}\right\Vert =\left\Vert\overrightarrow{AB}\right\Vert /2.$
Demonstre que se $\alpha$ e $\beta$ são números reais tais que $\alpha(2,3) + \beta(3,2) = \vec{0}$, então $\alpha = 0$ e $\beta = 0$.
Qual a conclusão geométrica que podemos tirar do item acima?
- $\alpha(2,3) + \beta(3,2) = \vec{0}$ resulta no sistema cujas equações são: $2\alpha+3\beta=0$ e $3\alpha+2\beta=0$.
Resolvendo o sistema, obtemos $\alpha=\dfrac{-3}{2}\beta=\dfrac{-2}{3}\beta$ que só pode ser satisfeita se $\beta=0$. E, portanto, $\alpha=0$. - Podemos concluir que esses dois vetores são linearmente independentes, isso significa que eles tem direções distintas.
Sendo $A=(3,1)$ e $B=(3,-5),$ determinar os pontos $F$ e $G$ que dividem $AB$ em três segmentos de igual comprimento.
Calcular o comprimento de $\vec{AB}.$
$F=(3,-1)$ e $G=(3,-3)$
$|\vec{AB}|=6$
Determinar os ângulos internos de um triângulo $ABC$, sendo$A=(3,-3,3)$, $B=(2,-1,2)$ e $C=(1,0,2)$.
Para o par de vetores $u=(1,2,-2)$ e $v=(3,-2,1)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.
$\textrm{proj}_{u}{v}=\dfrac{-1}{3}(1,2,-2)$.
$v_1=\dfrac{-1}{3}(1,2,-2)$.
$v_2=\dfrac{1}{3}(10,-4,1)$.
Dado um triângulo isósceles, mostre que a mediana relativa à base é a mediatriz (isto é, é perpendicular à base).
$\overrightarrow{AM}=\overrightarrow{MC}\Longrightarrow \overrightarrow{AM}=\overrightarrow{BM}-\overrightarrow{BA}=\overrightarrow{BC}-\overrightarrow{BM}\Longrightarrow \overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}.$
Também, temos que $\overrightarrow{AM}.\overrightarrow{MB}=\left\Vert \overrightarrow{BM}\right\Vert ^{2}-
\overrightarrow{BA}-\overrightarrow{MB}$.
Assim, concluímos que $\overrightarrow{AM}. \overrightarrow{MB}=\left\Vert \frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BC}\right) \right\Vert^{2}-\frac{1}{2}\overrightarrow{BA}\left( \overrightarrow{BA}+\overrightarrow{BC}\right) =\frac{1}{4}\left\Vert \overrightarrow{BA}\right\Vert ^{2}+\frac{1}{2}2\overrightarrow{BA}.\overrightarrow{BC}+\frac{1}{4}\left\Vert \overrightarrow{BC}\right\Vert ^{2}-\frac{1}{2}\left\Vert \overrightarrow{BA}\right\Vert ^{2}-\frac{1}{2}\overrightarrow{BA}.\overrightarrow{BC}=\frac{1}{2}\left\Vert \overrightarrow{BA}\right\Vert ^{2}-\frac{1}{2}\left\Vert \overrightarrow{BA}\right\Vert ^{2}=0$.
O trabalho $W$ realizado por uma força $\vec{F}$ sobre um objeto, agindo por uma distância $\vec{PQ}$, é dado por $W=\vec{F}\cdot\vec{PQ}$. Uma caixa é puxada horizontalmente por meio de uma força constante de $10N$ na direção do cabo e a um ângulo de $60^\circ$ com a horizontal. Qual é o trabalho realizado para mover a caixa ao longo de $2m$?
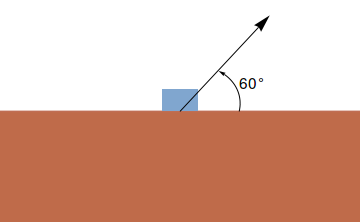
$$\vec{F} = (10\cos 60^\circ, 10 \sin 60^\circ) = (5,5\sqrt{3}).$$
Dessa forma o trabalho realizado é dado por:
$$W = \vec{F}\cdot\vec{PQ} = (5,5\sqrt{3}) \cdot(2,0) = 10 N \ m.$$
Que condições devem satisfazer os vetores $a$ e $b$ para que o vetor $a+b$ divida o ângulo formado por eles em dois ângulos iguais?
Considere um paralelogamo de lados $a$ e $b.$ O vetor soma $a+b$ representa a diagonal do paralelogramo formado pelos vetores $a$ e $b$. Caso os vetores $a$ e $b$ tenham módulos iguais, isto é, mesmo tamanho, o paralelogramo formado por esses vetores será um losango (todos os lados do paralelogramo terão a mesma medida), e a diagonal dividirá o ângulo entre os vetores $a$ e $b$ ao meio. Assim, teremos a igualdade entre dois ângulos $\alpha =\beta $ quando $\left\Vert a\right\Vert=\left\Vert b\right\Vert .$ Então, para que o vetor soma divida ao meio o ângulo entre os vetores $a$ e $b$, basta que $\left\Vert a\right\Vert =\left\Vert b\right\Vert .$
Provar, utilizando o produto escalar, que todo triângulo inscrito em uma semicircunferência é reto.
Consideremos a semicircunferência de raio $R$ com centro na origem $O$ do sistema cartesiano e situada no semiplano $y\geq 0$. Sejam $A=(R,0)$, $B=(x,y)$ e $C=(-R,0)$ três pontos sobre esta semicircunferência, sendo $B$ um ponto qualquer tal que $x^2+y^2=R^2$. Assim, teremos que
\begin{multline*}\vec{CB}\cdot\vec{AB}=(B-C)\cdot(B-A)=(x+R,y)\cdot(x-R,y)= \\ =(x+R)(x-R)+y^2 =x^2-R^2+y^2=(x^2+y^2)-R^2=R^2-R^2=0.\end{multline*} Ou seja, o triângulo inscrito $ABC$ é retângulo no vértice $B$.
Dados os vetores $a = (2,-3,6)$ e $b = (-1,2,-2)$, calcule as coordenadas do vetor $c$, bissetriz do ângulo formado pelos vetores $a$ e $b$, sabendo-se que $\|c \|= 3\sqrt{42}$.
Mostre que não existe $x$ tal que os vetores $v=(x,2,3)$ e $u=(x,-2,3)$ sejam perpendiculares.
Para que $v$ e $u$ fossem perpendiculares, seria necessário haver $x$ tal que $v\cdot u= x^2-4+9=0$, ou seja, $x$ tal que $x^2=-5$. Mas não há $x\in \mathbb{R}$ que satisfaça essa equação.
Mostre que se $X\;\mbox{e}\; Y$ são dois vetores tais que $X+Y$ é ortogonal a $X-Y$, então $\left\|X\right\|\;=\;\left\|Y\right\|$.
$X+Y$ ortogonal a $X-Y$ $\Rightarrow$ $(X+Y)\cdot(X-Y)=0$.
$(X+Y)\cdot(X-Y)=0$ $\Rightarrow$ $X\cdot X-X\cdot Y+Y\cdot X - Y\cdot Y=0\Rightarrow X\cdot X- Y\cdot Y=0 \Rightarrow X\cdot X= Y\cdot Y\Rightarrow ||X||^2=||Y||^2$ e, pela não negatividade da norma, $||X||=||Y||$.
Para o par de vetores $u=(2,0,0)$ e $v=(3,5,4)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.
$\textrm{proj}_{u}{v}=(3,0,0)$.
$v_1=(3,0,0)$ e $v_2=(0,5,4)$.
Sendo $A=(2,-5,3)$ e $B=(7,3,-1)$ vértices consecutivos de um paralelogramo $ABCD$ e $M=(4,-3,3)$ o ponto de interseção das diagonais, determine os vértices $C$ e $D$.
$C=(6,-1,3)$ e $D=(1,-9,7)$
Seja $\vec{v}\ne 0$ um vetor do $\mathbb{R}^{3}$ e sejam $\alpha$, $\beta$ e $\gamma$ os ângulos que $\vec{v}$ faz com os eixos coordenados $X$, $Y$ e $Z$, respectivamente. Mostre que:
se $\|\vec{v}\| = 1$, então $\vec{v} = (\cos(\alpha),\cos(\beta),\cos(\gamma))$ (Dica: calcular os cossenos de $\alpha$, $\beta$ e $\gamma$ fazendo o produto escalar de $\vec{v}$ com os vetores de comprimento $1$ na direção dos eixos coordenados. Como é um vetor de comprimento $1$ na direção de $X$? Isto é, sobre o eixo $X$.).
para um vetor $\vec{v}$ qualquer, vale que $\vec{v} = \|\vec{v}\|(\cos(\alpha),\cos(\beta),\cos(\gamma))$.
$\cos^{2}(\alpha) + \cos^{2}(\beta) + \cos^{2} (\gamma) = 1$.
Sejam $u=(1,-1,3)$ e $v=(3,-5,6)$ dois vetores. Encontre $\mathrm{proj}_{u+v} (2u-v)$.
$\dfrac{1}{133}(-88,132,-198)^T$
Sejam $\vec{u},\; \vec{v}$ e $\vec{w}$ três vetores. Sabendo que $\vec{u}$ é ortogonal a $\vec{v} - \vec{w}$ e $\vec{v}$ é ortogonal a $\vec{w} - \vec{u}$, verifique que $\vec{w}$ é ortogonal a $\vec{u} - \vec{v}$.
Como $\vec{u}\cdot(\vec{v}-\vec{w})=0$, temos que
$\vec{u}\cdot\vec{w}=\vec{u}\cdot\vec{v}$. Da mesma forma, como
$\vec{v}\cdot(\vec{w}-\vec{u})=0$, decorre que
$\vec{v}\cdot\vec{w}=\vec{v}\cdot\vec{u}$. Assim, usando a simetria do
produto interno euclidiano, segue que
$$
\vec{w}\cdot(\vec{u}-\vec{v})=\vec{w}\cdot\vec{u}-\vec{w}\cdot{v}=\vec{u}\cdot\vec{w}-\vec{v}\cdot\vec{w}=\vec{u}\cdot\vec{v}-\vec{v}\cdot\vec{u}=0.$$
Sejam os pontos $A=(-1,-1,2),\;B=(2,1,1) \;\mbox{e}\;C=(m,-5,3)$.
Para que valores de $m$ o triângulo $ABC$ é retângulo em $A$?
Determinar o ponto $H$, pé da altura relativa ao vértice $A$.
Sejam $u=(-1,1,1)$ e $v=(2,0,1)$ dois vetores. Encontre os vetores $w$ que são paralelos ao plano determinado por $O$, $u$ e $v$, perpendiculares a $v$ e tais que $u\cdot w=7$.
Os vetores $\vec{w}$ são da forma:
$\vec{w}=\left(-\frac{7}{3},\frac{14}{3},0\right)^T+\lambda\left(1/3,-2/3,1\right)^T$, $\lambda\in\mathbb{R}$
O vetor $w$ é ortogonal aos vetores $u=(2,3,-1)$ e $v=(1,-2,3)$ e $w\cdot(2,-1,1) = -6$. Encontre $w$.
$w=(-3,3,3)$
Dados os pontos $A=(-2,3,4)$, $B=(3,2,5)$, $C=(1,-1,2)$ e $D=(3,2,-4)$, calcular $\textrm{proj}_{CD}{AB}$.
$\textrm{proj}_{CD}{AB}=\dfrac{1}{49}(2,3,-6)$.
Considere os pontos $A = (3,-2,8)$, $B = (0,0,2)$ e $C = (2,3,2)$.
Usando vetores, mostre que o triângulo de vértices $A$, $B$ e $C$ é retângulo (Dica: O lado $BA$ é paralelo ao vetor $\stackrel{\longrightarrow}{BA}$).
Determine o ponto $H$ na aresta $AC$ para o qual os segmentos $AC$ e $HB$ são ortogonais ($=$ perpendiculares).
Determine o vetor $\stackrel{\longrightarrow}{AH}$. (Dica: $\stackrel{\longrightarrow}{AH}$ é a projeção ortogonal de $\stackrel{\longrightarrow}{AB}$ sobre $\stackrel{\longrightarrow}{AC}$.)
Calcule a área do triângulo (Dica: área do triângulo = (1/2) de base $\times$ altura).
Mostre que as três bissetrizes de um triângulo se interceptam em um único poto.
Considere o triângulo $ABC$ e bissetriz $B$ e $C$. Então eles cruzam no interior do triângulo que denotaremos por $O.$ Como $O$ está sobre a bissetriz de $B$, ele é equidistante de $AB$ e $BC.$ Mas também está na bissetriz de $C$ de forma que $O$ é equidistante de $AC$ e $BC.$ Assim, $O$ é equidistante aos três lados. Agora considere $\ AO.$ Como $AO$ divide o ângulo $\ BAC$ e passa no ponto (fora do vértice) equidistante de $AB$ e $AC$, será bissetriz de $BAC.$
Sejam $a_{1},\, a_{2},\,a_{3},\,b_{1},\, b_{2},\,b_{3}$ seis números reais quaisquer. Demonstre a desigualdade de Cauchy-Schwarz: \[ (a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3})^{2} \le (a_{1}^{2}+a_{2}^{2}+a_{3}^{2}) (b_{1}^{2}+b_{2}^{2}+b_{3}^{2}). \]
Encontre o ponto $Q$ sabendo que o mesmo é a extremidade de um vetor com origem no ponto médio do segmento que liga os pontos $P_1=(1,1,3)$ e $P_2=(-1,1,1)$ e tem norma, direção e sentido do vetor $v=(-1,0,1)$.
$(−1,1,3)$.
Sendo $A=(-2,3)\;\mbox{e}\; B=(6,-3)$ extremidades de um segmento, determinar:
Os pontos $C,\;D\;\mbox{e}\; E$ que dividem o segmento $AB$ em quatro partes de mesmo comprimento.
Os pontos $F\;\mbox{e}\; G$ que dividem o segmento $AB$ em três partes de mesmo comprimento.
Seja $O$ a origem de um sistema de coordenadas no plano. Mostre que se $ABC$ é um triângulo qualquer, suas medianas se interceptam no ponto $$M=\frac{OA+OB+OC}{3}.$$
Se de um ponto qualquer $R$ dentro de um paralelogramo $ABCD$ são traçados segmentos de reta paralelos aos lados, são formados quatro novos paralelogramos (isto é, o paralelogramo original é a união destes quatro paralelogramos menores). Mostre que as diagonais de quaisquer dois destes paralelogramos (que não sejam as diagonais que se interceptam no ponto $R$) se interceptam na reta suporte de uma das diagonais do paralelogramo original.
Sejam $A=(-1,2,3)$, $M=(-1,3,2)$ e $N=(1,1,3)$. O triângulo $ABC$ tem ângulos $A=90^\circ$ e $B=30^\circ$ e os vértices $B$ e $C$ pertencem à reta $MN$. Encontre os vértices $B$ e $C$.
Uma força $\vec{F} = (4,-6,1)$ N é aplicada a um ponto que se move uma distância de $15$ metros na direção e sentido do vetor $(1,1,1)$. Quanto trabalho foi realizado?
Dado $v_1=(1,-2,1)$, determine vetores $v_2$ e $v_3$ de modo que os três sejam mutuamente ortogonais.
$v_2=(1,1,1)$ e $v_3=(1,0,-1).$
Mostre que o vetor $\displaystyle p=b-\frac{a\cdot b}{a\cdot a}\;a$ é perpendicular ao vetor $a$.
$\displaystyle p\cdot a=b\cdot a-\frac{a\cdot b}{a\cdot a}\;a\cdot a=b\cdot a-\frac{a\cdot b}{||a||^2}||a||^2=b\cdot a-a\cdot b\,\frac{||a||^2}{||a||^2}=b\cdot a-a\cdot b=0$.
Mostre que o segmento de reta que liga um vértice de um paralelogramo ao ponto médio de um dos lados opostos trissecta a diagonal (isto é, intercepta a diagonal em um ponto que a divide em dois segmentos, um tendo um terço do comprimento da diagonal e o outro tendo dois terços do comprimento da diagonal).
Seja $ABCD$ um tetraedro e $P$ um ponto qualquer dentro dele. Ligue os vértices $A, B,C,D$ até o ponto $P$ e prolongue as linhas até que elas interceptem as faces opostas nos pontos $A',B',C',D'$, respectivamente. Mostre que vale a seguinte relação: $$\frac{PA'}{AA'}+\frac{PB'}{BB'}+\frac{PC'}{CC'}+\frac{PD'}{DD'}=1.$$
Que condições devem satisfazer os vetores $a$ e $b$ para que sejam válidas as seguintes relações?
$\|a + b \| = \|a - b \|$;
$\| a + b \| > \| a - b \|$;
$\| a + b \| < \| a - b \|$.
Para o par de vetores $u=(1,1,1)$ e $v=(3,1,-1)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.
$\textrm{proj}_{u}{u}=u$.
$v_1=u$; $v_2=(2,0,-2).$

