Exercícios
Vetores
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
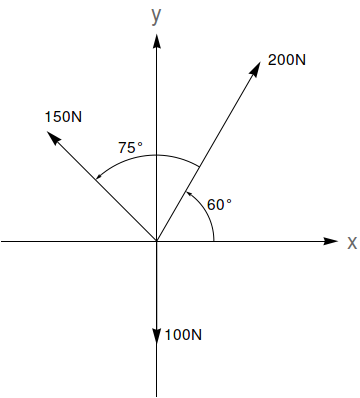
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
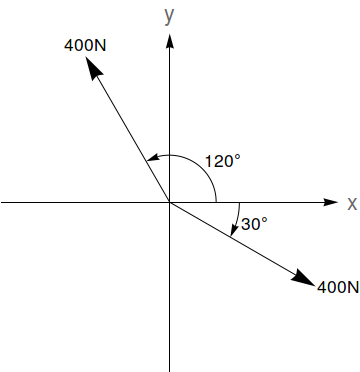
Quais são os cossenos diretores de cada eixo coordenado?
$1,0,0$; $0,1,0$; $0,0,1$.
Dados os pontos $A=(-3,2)$ e $B=(5,4)$:
Faça um esboço de $\vec{AB}$.
Calcule a distância de $A$ até $B$.
Ache o ponto médio entre $A$ e $B$.
Ache o vetor $\vec{BA}$.
Ache o ponto em $\vec{AB}$ cuja distância é 3 vezes maior de $A$ do que de $B$. Isto é, o ponto que divide $\vec{AB}$ na razão $3:1$ (existe outro ponto que está fora de $\vec{AB}$).
Ache o ponto em $\vec{AB}$ cuja coordenada $x$ é igual a $2$.
Ache o ponto em $\vec{AB}$ (extendido) cuja coordenada $y$ é igual a $5$.
Ache os pontos no eixo $x$ e no eixo $y$ que são equidistantes de $A$ e $B$.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores tais que $\cos \alpha_1=\cos \beta_1$, $\cos \gamma_1=1/3$; e a outra com ângulos diretores tais que $\cos \alpha_2=\cos \beta_2$, $\cos \gamma_2=1/4$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$\cos^{-1} (1/4) - \cos^{-1} (1/3)$.
Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(-1,0,1)$ e sua origem é o ponto médio entre os pontos $P_1=(1,1,3)$ e $P_2=(-1,1,1)$.
$(-1,1,3)$
Sejam $\vec{u}=(2,1,3)$, $\vec{v}=(0,1,-1)$ e $\vec{w}=(4,5,3)$ vetores do espaço.
Calcule $\vec{u}+\vec{v} $ e $\vec{u}-2\vec{v}+3\vec{w}$.
Determine $a$ e $b$ tais que $\vec{w}=a\vec{u}+b\vec{v}$.
- $\vec{u}+\vec{v}=(2,1,2) $ e $\vec{u}-2\vec{v}+3\vec{w}=(14,14,14)$.
- $a=2$ e $b=3$.
Sejam $\vec{OA}$ e $\vec{OB}$ dois vetores não colineares no espaço. Qual o conjunto dos pontos $P$ tais que $\vec{OP} = \lambda\vec{OA}+(1-\lambda)\vec{OB}$?
Trata-se da reta passando pelos pontos $A$ e $B$.
Quais são os cossenos diretores do vetor de $(2,-3,5)$ a $(-1,1,-7$)?
$-3/13,4/13,-12/13$.
Verifique se os seguintes pontos são colineares: $A=(0,1,-1)$, $B=(1,2,0)$ e $C=(0,2,1)$.
Os pontos não são colineares.
Mostre que o segmento que une os pontos médios de 2 lados de um triângulo é paralelo ao terceiro lado e é igual a sua metade.
Considere o triângulo $ABC,$ sendo $M$ o ponto médio do lado $AC$ e $N$ o do lado $BC.$ Assim, podemos escrever $\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\frac{1}{2} \overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2} \overrightarrow{AB}.$
Portanto, concluímos que $MN//AB$ e $\left\Vert \overrightarrow{MN}\right\Vert =\left\Vert \overrightarrow{AB}\right\Vert .$
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
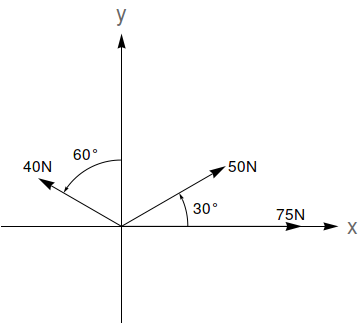
Dados os pontos $A=(1,0,1)$, $B=(-1,1,1)$ e $C=(0,1,2)$.
Determine o ponto $D$ tal que $A$, $B$, $C$ e $D$ sejam os vértices consecutivos de um paralelogramo.
Determine o ponto médio entre $A$ e $C$ e o ponto médio entre $B$ e $D$.
- \( D=(2,0,2)\)
- \(\dfrac{1}{2}(A+C)=(\dfrac{1}{2},\dfrac{1}{2},\dfrac{3}{2})=\dfrac{1}{2}(B+D)\)
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores tais que $\cos\alpha_1=1/2$, $\cos\beta_1=\sqrt{3}/2$; e a outra com ângulos diretores tais que $\cos \alpha_2=\dfrac{\sqrt{3}+1}{2\sqrt{2}}$ e $\cos\beta_2=\dfrac{\sqrt{3}-1}{2\sqrt{2}}$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$45^\circ$.
Mostre que as diagonais de um paralelogramo se cortam ao meio (Sugestão: Sejam $M$ e $N$ os pontos médios das duas diagonais. Mostre que $\overline{MN}=\vec{0}$.).
Considere o paralelogramo $ABCD$, de diagonais $AC$ e $DB.$ Seja $M$ o ponto médio de $AC.$ Vamos provar que $M$ é também ponto médio de $BD.$ Ora, $\overrightarrow{BM}=\overrightarrow{BC}+ \overrightarrow{CM}=\overrightarrow{AD}+\overrightarrow{MA}=\overrightarrow{MD}.$ Logo, $M$ é o ponto médio de $BD.$
Um ponto $(x,y,z)$ se move tal que sua distância ao ponto $(3,2,4)$ é sempre $5$. Qual figura $(x,y,z)$ traça? Faça um esboço de uma parte dessa figura (um octante). Escreva uma equação simplificada que os pontos $(x,y,z)$ devem satisfazer.
Uma esfera com centro $(3,2,4)$, raio $5$, com equação $x^2+y^2+z^2-6x-4y-8z+4=0$.
Verifique se os seguintes pontos são colineares: $A=(3,1,4)$, $B=(2,7,1)$ e $C=(0,1,5)$.
Os pontos não são colineares.
Mostre que: se um triângulo tem duas medianas iguais então ele é isósceles.
Seja o triângulo $\ ABC$, $M$ o ponto médio de $\overrightarrow{BN}$ e $N$ o de $\overrightarrow{AC}.$ Seja também $P$ a interseção de $\overrightarrow{BN}$ e $\overrightarrow{AM},$ e por hipótese, temos $\left\Vert \overrightarrow{BN}\right\Vert =\left\Vert\overrightarrow{AM}
\right\Vert .$ Observe que os triângulos $NPM$ e $APB$ são isósceles. Observe também que como $\overrightarrow{MN}$ é paralelo a $\overrightarrow{AB}$ os ângulos $N\widehat{P}A$ e $M\widehat{P}B$ são iguais. Assim, pela lei dos cossenos, temos
$\left\Vert \overrightarrow{AN}\right\Vert ^{2}=\left\Vert \overrightarrow{PN}-\overrightarrow{PA}\right\Vert ^{2}=\left\Vert \overrightarrow{PM}-\overrightarrow{PB}\right\Vert ^{2}=\left\Vert \overrightarrow{BM}\right\Vert ^{2}$
Como, $2\left\Vert \overrightarrow{AN}\right\Vert =\left\Vert \overrightarrow{AC}\right\Vert $e $2\left\Vert \overrightarrow{BM}\right\Vert =\left\Vert \overrightarrow{BC}\right\Vert ,$ então $\left\Vert \overrightarrow{AN}\right\Vert =\left\Vert \overrightarrow{BC}\right\Vert ,$ e portanto, o triângulo é isósceles.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores $\alpha_1=\beta_1=60^\circ$; e a outra com ângulos diretores tais que $\cos \alpha_2=\cos \beta_2=1/2\sqrt{2}$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$15^\circ$.
Mostre que para dois vetores $\vec{A}$ e $\vec{B}$, $\|\vec{A}\| - \|\vec{B}\| \leq \|\vec{A} \pm \vec{B}\| \leq \|\vec{A}\| + \|\vec{B}\|$. Em que condições vale a igualdade?
$\|\vec{A} - \vec{B}\|^2=\|\vec{A}\|^2+\|\vec{B}\|^2- 2\|\vec{A}\|\|\vec{B}\|\cos\theta$.
Qual é o lugar geométrico de todas as retas que passam pela origem com ângulo diretor em relação ao eixo $z$ $\gamma=30^\circ$?
Um cone sobre o eixo $z$.
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
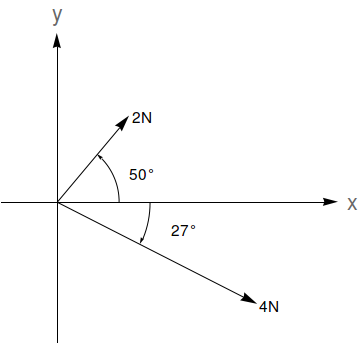
Qual é o vetor unitário na direção de $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$?
$\dfrac{x\vec{i}+y\vec{j}+z\vec{k}}{\sqrt{x^2+y^2+z^2}}$.
Seja $(4,5)$ o ponto médio de um segmento de reta tal que uma extremidade é $(-1,2)$. Ache a outra extremidade.
$(9,8)$.
Dados $A=(4,8,11)$, $B=(-3,1,4)$ e $C=(2,3,-3)$, faça uma figura esquemática, verificando que os pontos formam um triângulo, e:
Ache os tamanhos dos três lados do triângulo.
Ache os pontos médios dos três lados.
Calcule a soma dos vetores $\vec{AB}$, $\vec{BC}$ e $\vec{CA}$. Por que a soma é nula?
Ache o ponto em $AB$ cuja coordenada $y$ é $5$.
Ache os três pontos nos planos coordenados em $AB$ (extendidos).
Ache o ângulo entre $\vec{AB}$ e $\vec{BC}$ (sugestão: use a Lei dos Cossenos).
Ache os dois pontos de trisecção em $BC$ (internamente).
Ache o tamanho da altura saindo de $B$ e oposta ao lado $AC$.
Calcule a área do triângulo $ABC$.
Ache o tamanho da reta que bissecta o ângulo em $C$ (sugestão: use $\cos \theta/2 = \sqrt{(1+\cos\theta)/2}$; use trigonometria de triângulos retângulos).
Ache o raio e o centro do círculo circunscrito ao triângulo (sugestão: a hipotenusa é o diâmetro).
Ache os três pontos $D$ tais que $ABCD$ é um paralelogramo.
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
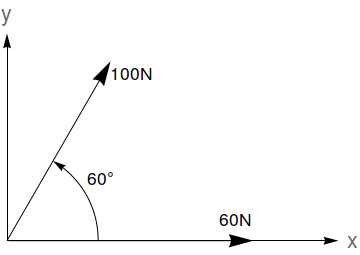
Para dois vetores $\vec{A}$ e $\vec{B}$, mostre que vale a Lei Distributiva: $m(\vec{A} + \vec{B})=m\vec{A}+m\vec{B}$ (Sugestão: mostre que $m\vec{A}+m\vec{B}$ está na mesma direção que $\vec{A}+\vec{B}$ e que $\|m\vec{A}+m\vec{B}\|$ é igual a $m$ vezes $\|\vec{A}+\vec{B}\|$). O que ocorre se $m$ for negativo?
Sejam $\vec{A}$, $\vec{B}$ e $\vec{C}$ vetores no plano, com $\|\vec{A}\|=2$, $\|\vec{B}\|=3$ e $\|\vec{C}\|=4$. O ângulo entre $\vec{A}$ e $\vec{B}$ é de $120^\circ$, entre $\vec{A}$ e $\vec{C}$ é de $135^\circ$ e entre $\vec{B}$ e $\vec{C}$ é de $105^\circ$. Faça um esboço do gráfico desses três vetores. Qual combinação linear de $\vec{A}$ e $\vec{B}$ é igual a $\vec{C}$?
$\vec{C} = -(\sqrt{2}+\sqrt{2/3})\vec{A} + -(4\sqrt{2})/(3\sqrt{3}) \vec{B}$.
Quais são os cossenos diretores da reta que passa pela origem no primeiro octante e que tem ângulos iguais com os três eixos coordenados?
$1/\sqrt{3},1/\sqrt{3},1/\sqrt{3}$.
Qual é o vetor unitário na direção de $4\vec{i}-12\vec{j}+3\vec{k}$?
$\dfrac{4\vec{i}-12\vec{j}+3\vec{k}}{13}$.
Verifique se os seguintes pontos são colineares: $A=(1,0,1)$, $B=(2,2,0)$ e $C=(0,-2,2)$.
Os pontos são colineares.
Ache os dois vetores no plano $xy$ perpendiculares a $4\vec{i}-3\vec{j}$ e de tamanho $10$.
$\pm (6\vec{i}+8\vec{j})$.
Mostre que as medianas de um triângulo interceptam-se em um único ponto. Encontre a razão em que esse ponto divide cada mediana.
Tente generalizar o item (a) para tetraedros.
$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM},$ $\overrightarrow{BH}=\frac{2}{3}\overrightarrow{BN},$ $\overrightarrow{CI}=\frac{2}{3}\overrightarrow{CP}.$
Assim, observe que
$\overrightarrow{GI}=\overrightarrow{GA}+\overrightarrow{AC}+\overrightarrow{CI}=\frac{2}{3}\overrightarrow{MC}+\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{CP}=\frac{2}{3}\overrightarrow{MP}+\frac{1}{3}\overrightarrow{AC}=\frac{1}{3}\left( \overrightarrow{BA}+\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BC}\right) =0.$
De maneira análoga, mostramos que $\overrightarrow{GH}=.$ Portanto,
concluímos que $G=H=I,$ e vale as propoções citadas acima.
b) Vamos mostrar que o centro de massa do tetraedro é a interseção das medianas. Sendo assim, seja o tetraedro $ABCD$. A mediana do tetraedro
é definida comos sendo o segmento que une um baricentro de uma das faces do tetraedro, com o seu vértice oposto.
Sejam $A^{\prime },B^{\prime },C^{\prime },D^{\prime }$, sendo respectivamente os baricentros das faces $DBC,$ $ABC,$ $ADC$ e $ADB.$
Observe que $\overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}=0,$ pois $\overrightarrow{D^{\prime }A}+
\overrightarrow{D^{\prime }B}=2\overrightarrow{D^{\prime }P},$ onde $P=\frac{A+B}{2}.$ Como $D^{\prime }$ é o baricentro do triângulo $ABC$, segue que $\overrightarrow{CD^{\prime }=}2\overrightarrow{D^{\prime }P}.$
Assim,
$\overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}=2\overrightarrow{D^{\prime }P}+\overrightarrow{D^{\prime }C}=\overrightarrow{CD^{\prime }}+\overrightarrow{D^{\prime }C}=0.$
Seja $G$ o centro de massa do tetraedro. Uma propriedade dele, é que
$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=0.$
Assim,
$3\overrightarrow{GD^{\prime }}=\overrightarrow{GA}+\overrightarrow{
AD^{\prime }}+\overrightarrow{GB}+\overrightarrow{BD^{\prime }}+
\overrightarrow{GC}+\overrightarrow{CD^{\prime }}=\overrightarrow{GA}+
\overrightarrow{GB}+\overrightarrow{GC}-\left( \overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}\right) =
\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=- \overrightarrow{GD}=\overrightarrow{DG}.$
Portanto, $3\overrightarrow{GD^{\prime }}=\overrightarrow{DG},$ ou seja, o centro de massa $G$ pertence ao segmento $\overrightarrow{DD^{\prime}}.$ De maneira análoga, mostramos que $G$ pertence aos segmentos $\overrightarrow{AA^{\prime }},$ $\overrightarrow{BB^{\prime }}, \overrightarrow{CC^{\prime }}.$ Ou seja, $G$ é o ponto de interseção das medianas.
Sejam $\vec{A}$, $\vec{B}$ e $\vec{C}$ vetores no plano, com $\|\vec{A}\|=3$, $\|\vec{B}\|=2$ e $\|\vec{C}\|=6$. O ângulo entre $\vec{A}$ e $\vec{B}$ é de $60^\circ$ e $\vec{C}$ está sobre a bissetriz deste ângulo. Faça um esboço do gráfico desses três vetores. Qual combinação linear de $\vec{A}$ e $\vec{B}$ é igual a $\vec{C}$?
$\vec{C} = 2/\sqrt{3} \vec{A} + \sqrt{3} \vec{B}$.
Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(1,-2,1)$ e sua origem é o ponto $P=(1,0,1)$.
$(2,-2,2)$.
Um vetor no espaço tem dois de seus ângulos diretores dados: $\alpha=45^\circ$ e $\beta=120^\circ$. Ache o outro ângulo diretor e faça um esboço do vetor. Quantas respostas existem? (Sugestão: use as fórmulas de cosseno diretor).
$60^\circ$, $120^\circ$. Existem duas respostas.
Um vetor no espaço tem dois de seus ângulos diretores dados: $\alpha=30^\circ$ e $\beta=60^\circ$. Ache o outro ângulo diretor e faça um esboço do vetor. Quantas respostas existem? (Sugestão: use as fórmulas de cosseno diretor).
$90^\circ$.
Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo às bases e seu comprimento é a média aritmética dos comprimentos das bases.
$\overrightarrow{MN}=\overrightarrow{NB}+\overrightarrow{BA}+\overrightarrow{AM},$ $\overrightarrow{MN}=\overrightarrow{NC}+\overrightarrow{CD}+\overrightarrow{DM}.$ Portanto, $2\overrightarrow{MN}=\overrightarrow{BA}+\overrightarrow{CD}.$
Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(1,1,1)$ e sua extremidade é o ponto $P=(1,1,1)$.
$(0,0,0)$.
Dados dois vetores $\vec{A}$ e $\vec{B}$, e $\theta$ o ângulo entre eles, ache fórmulas para $\|\vec{A} + \vec{B}\|$ e $\|\vec{A} - \vec{B}\|$ (Sugestão: use a Lei dos Cossenos).
$\|\vec{A} + \vec{B}\|^2=\|\vec{A}\|^2+\|\vec{B}\|^2 +2\|\vec{A}\|\|\vec{B}\|\cos\theta$.
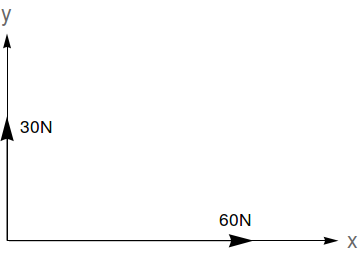
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
Demonstre que se $\alpha$ e $\beta$ são números reais tais que $\alpha(2,3) + \beta(3,2) = \vec{0}$, então $\alpha = 0$ e $\beta = 0$.
Qual a conclusão geométrica que podemos tirar do item acima?
- $\alpha(2,3) + \beta(3,2) = \vec{0}$ resulta no sistema cujas equações são: $2\alpha+3\beta=0$ e $3\alpha+2\beta=0$.
Resolvendo o sistema, obtemos $\alpha=\dfrac{-3}{2}\beta=\dfrac{-2}{3}\beta$ que só pode ser satisfeita se $\beta=0$. E, portanto, $\alpha=0$. - Podemos concluir que esses dois vetores são linearmente independentes, isso significa que eles tem direções distintas.
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).
Quais são os cossenos diretores da reta no plano $xy$ que faz $45^\circ$ com a origem?
$1/\sqrt{2},1/\sqrt{2},0$.
Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores $\alpha_1=45^\circ$, $\beta_1=45^\circ$; e a outra com ângulos diretores $\alpha_2=\beta_2=60^\circ$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).
$45^\circ$.
Considere três vetores do $\mathbb{R}^{3}$: $u = (1,0,-1)$, $v = (1,1,1)$ e $w = (x,y,z)$.
Se $w = (-1,-5,-9)$, mostre que existem escalares $a$ e $b$ tais que $w = au + bv$.
Ainda para $w = (-1,-5,-9)$, existem escalares $a', b'$ tais que $(a',b') \ne (a,b)$ e $w = a'u + b'v$?
Para todo $w$ existem escalares $a$ e $b$ tais que $w = au + bv$ como no item anterior?
Existe alguma relação entre as perguntas acima e o estudo de sistemas?
- $a=4$ e $b=-5$.
- Não.
- Não. Com apenas dois vetores não é possível gerar todos os vetores de $\mathbb{R}^3$. Por exemplo, não existem $\alpha$ e $\beta\in\mathbb{R}$ tais que $\alpha u + \beta v=(-1,5,9)$.
- Uma conclusão básica é que nem todo sistema de três equações e duas incógnitas terá solução. Mais conclusões são possíveis.
Se $(4,5)$ divide internamente um segmento de reta na razão $3:2$ e uma extremidade é $(-1,2)$, ache a outra extremidade.
$(22/3,7)$, $(23/2,19/2)$ (duas respostas internas).

