Exercícios
Teorema do Divergente
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S}{\bf a}\cdot {\bf n}\,dS=0$, onde ${\bf a}$ é um vetor constante.
Dica: Note que $\mbox{div} {\bf a} = 0.$
Use o Teorema da Divergência para encontrar todos os valores positivos \(k\) tais que \[ \mathbf{F}(\mathbf{r}) = \dfrac{\mathbf{r}}{\|\mathbf{r}\|^k} \] satisfaça a condição \(\mathrm{div\,}\mathbf{F}=0\) quando \(\mathbf{r}\neq \mathbf{0}\).
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(x^{2}+z^{2})\,{\bf i}+(y^{2}-2xy)\,{\bf j}+(4z-2yz)\,{\bf k}$ e $S$ é a superfície da região delimitada pelo cone $x=\sqrt{y^{2}+z^{2}}$ e pelo plano $x=9.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=x^{3}y\,{\bf i}-x^{2}y^{2}\,{\bf j}-x^{2}yz\,{\bf k}$ e $S$ é a superfície do sólido delimitado pelo hiperbolóide $x^{2}+y^{2}-z^{2}=1$ e pelos planos $z=-2$ e $z=2.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(\cos z+xy^{2})\,{\bf i}+xe^{-z}\,{\bf j}+(\sin y+x^{2}z)\,{\bf k}$ e $S$ é a superfície do sólido limitado pelo parabolóide $z=x^{2}+y^{2}$ e pelo plano $z=4.$
Aplique o Teorema da Divergência para achar $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS,$ sendo ${\bf F}(x,y,z)=y\,\sin x\,{\bf i}+y^{2}z\,{\bf j}+(x+3z)\,{\bf k}$ e $S$ é a superfície da região delimitada pelos planos $x=\pm 1$, $y=\pm 1$ e $z=\pm 1.$
$24.$
Seja ${\bf F}(x,y,z)=(x+y+z^{2})\,{\bf k}$ e seja $S$ a fronteira do cilindro $x^{2}+y^{2}\leq 4$ e $0\leq z \leq 3.$ Calcule $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS$ onde ${\bf n}$ é a normal exterior, isto é, ${\bf n}$ é a normal que aponta para fora do cilindro.
Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=x^{2}\,{\bf i}+xy\,{\bf j}+z\,{\bf k}$, $E$ é o sólido delimitado pelo paraboloide $z=4-x^{2}-y^{2}$ e pelo plano $xy.$
$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = 8\pi.$
Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=xy\,{\bf i}+yz\,{\bf j}+zx\,{\bf k}$, $E$ é o cilindro sólido $x^{2}+y^{2}\leq 1$, $0\leq z\leq 1.$
$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = \dfrac{\pi}{2}.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=x^{4}\,{\bf i}-x^{3}z^{2}\,{\bf j}+4xy^{2}z\,{\bf k}$ e $S$ é a superfície do sólido limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $z=x+2$ e $z=0.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S}(f\nabla g-g\nabla f)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E}(f\nabla^{2} g-g\nabla^{2} f)\,dV.$
Use o Teorema da Divergência e que $\nabla f \cdot \nabla g = \nabla g \cdot \nabla f.$
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\,x^{2}+y^{2}+z^{2}\leq 1$ e $z\geq x+y\}$ e ${\bf u}=-2xy\,{\bf i}+y^{2}\,{\bf j}+3z\,{\bf k}.$
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $S$ a fronteira de $B$ com normal exterior ${\bf n}$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, 0\leq x\leq 1,\,0\leq y\leq x$ e $0\leq z\leq 4\}$ e ${\bf u}=xy\,{\bf i}+yz\,{\bf j}+z^{2}\,{\bf k}.$
Aplique o Teorema da Divergência para achar $\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS.$, sendo ${\bf F}(x,y,z)=y^{3}e^{z}\,{\bf i}-xy\,{\bf j}+x \cdot \arctan y\,{\bf k}$ e $S$ a superfície da região delimitada pelos planos coordenados e o plano $x+y+z=1.$
Pelo Teorema do Divergente, temos
$$\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS = \displaystyle\iiint\limits_{E}\text{div }{\bf F}\,dV,$$
em que $E$ é o sólido

que pode ser escrito como
$E = \{(x,y,z) \in \mathbb{R}^3: 0 \leq x \leq 1, 0 \leq y \leq 1-x \mbox{ e } 0 \leq z \leq 1-x-y\}.$
Observe que
\begin{array}{rcl}\text{div
}{\bf F} & = & \dfrac{\partial}{\partial x}(y^3e^z) +
\dfrac{\partial}{\partial y}(-xy) + \dfrac{\partial}{\partial
z}(x\arctan{y}) \\& = & 0 - x + 0 \\& = & -x.\end{array}
Assim,
\begin{array}{rcl}\iint\limits_{S}{\bf
F}\cdot {\bf n}\,dS & = &
\displaystyle\iiint\limits_{E}{\bf F}\,dV \\& = &
\iiint\limits_{E}-x\,dV \\& = &
\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}-x\,dz dy dx \\& = &
\int_{0}^{1}\int_{0}^{1-x}-x(1-x-y)\,dy dx \\& = &
\int_{0}^{1}\left(-\frac{x}{2}+x^2-\frac{x^3}{3}\right)\,dx \\& =
& -\frac{1}{12}.\end{array}
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, x^{2}+y^{2}+z^{2}\leq 1\}$ e ${\bf u}=x\,{\bf i}+y\,{\bf j}+z^{2}\,{\bf k}.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $V(E)=\dfrac{1}{3}\displaystyle\iint\limits_{S}{\bf F}\cdot dS$, onde ${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}.$
Dica: Note que $\displaystyle\iiint\limits_{E}{\mbox{div} {\bf F}}\, dV = \iiint \limits_{E}{3}\,dV$.
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(5x^{3}+12xy^{2})\,{\bf i}+(y^{3}+e^{y}\,\sin z)\,{\bf j}+(5z^{3}+e^{y}\,\cos z)\,{\bf k}$ e $S$ é a superfície do sólido entre as esferas $x^{2}+y^{2}+z^{2}=1$ e $x^{2}+y^{2}+z^{2}=2.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S} D_{n}f\,dS=\displaystyle\iiint\limits_{E}\nabla^{2}f\,dV.$
Lembre que $D_{n} f = \nabla f \cdot {\bf b}$ e $\mbox{div} (\nabla f) = \nabla^{2} f.$
Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$, $E$ é a bola unitária $x^{2}+y^{2}+z^{2}\leq 1.$
$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = 4\pi.$
Use o Teorema do Divergente para calcular $\displaystyle\iint \limits_{S}(2x+2y+z^{2})\,dS$ onde $S$ é a esfera $x^{2}+y^{2}+z^{2}=1.$
A superfície $S$ em questão é a esfera unitária, que é a fronteira da bola unitária $B$ dada por $x^2+y^2+z^2 \leq 1$ e tem vetor normal num ponto $(x,y,z)$ igual a $(x,y,z)$ (o qual aponta para ``fora").

Observe que podemos transformar o integrando $2x+2y+z^{2}$ em $(2,2,z) \cdot (x,y,z)$ e essa escrita é interessante, já que o segundo vetor é exatamente o vetor normal a $S$. Agora estamos em condições de aplicar o Teorema do Divergente quando tomamos o campo ${\bf F}(x,y,z) = (2,2,z)$. Assim,
\begin{array}{rcl}\displaystyle\iint\limits_{S}(2x+2y+z^{2})\,dS & = & \iint\limits_{ S}(2,2,z) \cdot (x,y,z)\,dS \\& = & \int\int\int \limits_{ S}{\bf F} \cdot {\bf n}\,dS \\& = & \iiint\limits_{ B}\text{div } F\,dV \\& = & \iiint\limits_{ B}(0+0+1)\,dV \\& = & V(B) = \frac{4\pi}{3}.\end{array}
Um sólido ocupa a região $E$ com superfície $S$ e está imerso em um líquido com densidade constante $\rho$. Escolhemos um sistema de
coordenadas de modo que o plano $xy$ coincida com a superfície do líquido e valores positivos de $z$ sejam medidos para baixo, adentrando o líquido. Então, a pressão na profundidade $z$ é $p=\rho g z$, onde $g$ é a aceleração da gravidade. A força de empuxo total sobre o sólido devida $\grave{a}$ distribuição de pressão é dada pela integral de superfície
${\bf F}=-\displaystyle\iint\limits_{S} p{\bf n}\,dS$ onde ${\bf n}$ é o vetor normal unitário apontando para fora. Use o resultado do exercício anterior para mostrar que ${\bf F}=-W{\bf k}$, onde $W$ é o peso do líquido deslocado pelo sólido. (Observe que ${\bf F}$ é orientado para cima porque $z$ está orientado para baixo.) O resultado é o Princípio de Arquimedes: a força de empuxo sobre um objeto é igual ao
peso do líquido deslocado.
Note que $\displaystyle {\bf F}=-\int_{S} p {\bf n} \,dS = -\iiint_{E} \nabla p\,dV = -\iiint_{E} \nabla p\,dV = - \iiint_{E} \nabla (\rho g z)\,dV.$
Conclua usando que $W = \rho g V(E),$ onde $V(E)$ é o volume de $E.$
Seja $S$ o gráfico de $f(x,y)=x^{2}+y^{2}$, $x^{2}+y^{2}\leq 1$ e seja ${\bf n}$ a normal a $S$ com componete $z\leq 0$. Seja ${\bf F}(x,y,z)=x^{2}y\,{\bf i}-xy^{2}\,{\bf j}+{\bf k}$. Calcule $\iint \limits_{S}{\bf F}\cdot {\bf n}\, dS.$
Observe que $S$ não é uma superfície fechada (isto é, $S$ não é a fronteira de um sólido $E$). Para que possamos utilizar o Teorema do Divergente, vamos considerar a superfície $S_2$ constituída pelo parabolóide $S$ e pelo círculo $S_1$ dado por $x^2+y^2 \leq 1$ em $z=1$. Como $S_2$ é uma superfície fechada, usamos a escolha da normal ${\bf n_2}$ em $S_2$ que está apontando ``para fora". Sejam ${\bf n_1}$ a normal a $S_1$ (apontando para cima) e ${\bf n}$ a normal a $S$ (apontando para fora).
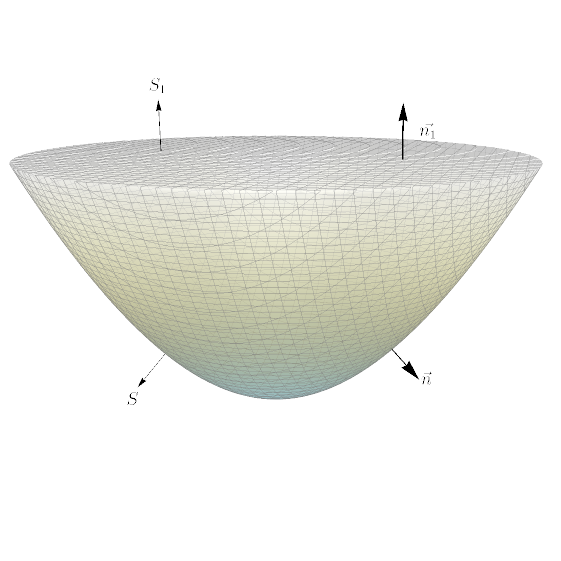
Temos
$\displaystyle\iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS = \iint\limits_{S}{\bf F}\cdot {\bf n}\,dS + \iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS,$
isto é,
$\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS = \iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS - \iint \limits_{ S_1}{\bf F}\cdot {\bf n_1}\,dS.$
Pelo Teorema do Divergente,
$$\iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS = \iiint\limits_{E}(2xy-2xy+0)\,dV = 0,$$
em que $E$ é o sólido que possui $S_2$ como fronteira.
Para determinar $\displaystyle\iint\limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS$, devemos encontrar uma parametrização para $S_1$ e determinar o vetor normal ${\bf n_1}$. Considere a seguinte parametrização de $S_1$: $r(u,v) = (u,v,1)$, com $u^2+v^2 \leq 1$. Daí, $r_u(u,v) = (1,0,0)$ e $r_v(u,v) = (0,1,0)$. Logo, $r_u \times r_v = (0,0,1)$ é um vetor normal a $S_1$. Devemos tomar ${\bf n_1} = (0,0,1)$ para que aponte para cima. Então,
$\displaystyle\iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS = \iint\limits_{D}(u^2v,-uv^2,1)\cdot(0,0,1)\,dA,$
em que $D = \{(u,v) \in \mathbb{R}^2; u^2+v^2 \leq 1\}$. Portanto,
$\displaystyle\iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS = \iint\limits_{D}1\,dA = A(D) = \pi,$
donde concluímos que
$\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS = 0 - \pi = -\pi.$
${\bf F}(x,y,z)=3x\,{\bf i}+xy\,{\bf j}+2xz\,{\bf k}$, $E$ é o cubo limitado pelos planos $x=0$, $x=1$, $y=0$, $y=1$, $z=0$ e $z=1.$
Seja ${\bf F}=(z tg^{-1}(y^{2}),z^{3}\ln(x^{2}+1),z).$ Determine o fluxo de ${\bf F}$ através da parte do parabolóide $x^{2}+y^{2}+z=2$ que está acima do plano $z=1$ e está orientada para cima. (Observe que a superfície acima não é fechada.)
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=yz\,{\bf i}+xz\,{\bf j}+xy\,{\bf k}$ e $S$ é o gráfico de $x^{2/3}+y^{2/3}+z^{2/3}=1.$
Se ${\bf F}=(xz,yz,2)$ e $E$ é a região dada por $x^{2}+y^{2}\leq 1$ e $0\leq z \leq 1,$ mostre que o Teorema do Divergente é verdadeiro neste caso. Calcule as duas integrais do enunciado do Teorema e mostre que elas têm o mesmo valor.
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3xy^{2}\,{\bf i}+xe^{z}\,{\bf j}+z^{3}\,{\bf k}$, $S$ é a superfície do sólido delimitado pelo cilindro $y^{2}+z^{2}=1$ e pelos planos $x=-1$ e $x=2.$
Seja $S$ a parte do parabolóide $z=2-x^{2}-y^{2}$ que está acima do plano $z=1.$ Calcule o fluxo do campo vetorial ${\bf F}(x,y,z)=\frac{1}{(x^{2}+y^{2}+z^{2})^{3/2}}(x,y,z)$ através de $S.$
Aplique o Teorema da Divergência para achar $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS,$ sendo ${\bf F}(x,y,z)=(x^{2}+\sin yz)\,{\bf i}+(y-xe^{-z})\,{\bf j}+z^{2}\,{\bf k}$ e $S$ a superfície da região delimitada pelo cilindro $x^{2}+y^{2}=4$ e os planos $x+z=2$ e $z=0.$
$20\pi.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S}(f\nabla g)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E}(f\nabla^{2}g+\nabla f+\nabla g)\,dV.$
Note que $\displaystyle\iint\limits_{S}(f\nabla g)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E} \mbox{div} (f\nabla g)\,dV.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=e^{x}\,\sin y\,{\bf i}+e^{x}\,\cos y\,{\bf j}+yz^{2}\,{\bf k}$ e $S$ é a superfície da caixa delimitada pelos planos $x=0$, $x=1$, $y=0$, $y=1$, $z=0$ e $z=2.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=2xz\,{\bf i}+xyz\,{\bf j}+yz\,{\bf k}$ e $S$ é a superfície da região delimitada pelos planos coordenados e os planos $x+2z=4$ e $y=2.$
Demonstre a identidade $\displaystyle\iint\limits_{S}\mbox{rot}\, {\bf F}\cdot dS=0$, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
Pelo Teorema do Divergente, temos
$\displaystyle\iint\limits_{ S}\mbox{rot} {\bf F}\cdot dS = \iiint\limits_{ E}\mbox{div} (\mbox{rot} {\bf F})\,dV,$
em que $E$ é o sólido que tem $S$ como fronteira. Observe que
\begin{align*}
&\mbox{div} (\mbox{rot} {\bf F}) =\\ & \frac{\partial}{\partial x}(R_y - Q_z) + \frac{\partial}{\partial y}(P_z - R_x) + \frac{\partial}{\partial z}(Q_x - P_y) \\ & R_{xy} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy} = 0,
\end{align*}
pois, como as derivadas de segunda ordem são contínuas, temos, pelo Teorema de Clairaut, que $P_{yz} = P_{zy}$, $Q_{zx} = Q_{xz}$ e $R_{xy} = R_{yx}$. Portanto,
$\displaystyle\iint\limits_{S}\mbox{rot}{\bf F}\cdot dS=0.$
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, x^{2}+y^{2}\leq 1,\,x^{2}+y^{2}\leq z \leq 5-x^{2}-y^{2}\}$ e ${\bf u}=3xy\,{\bf i}-\dfrac{3}{2}y^{2}\,{\bf j}+z\,{\bf k}.$
$36\pi.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3xy^{2}\,{\bf i}+xe^{z}\,{\bf j}+z^{3}\,{\bf k}$ e $S$ é a superfície do sólido delimitado pelo cilindro $y^{2}+z^{2}=1$ e pelos planos $x=-1$ e $x=2.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3x\,{\bf i}+xz\,{\bf j}+z^{2}\,{\bf k}$ e $S$ é a superfície da região delimitada pelo parabolóide $z=4-x^{2}-y^{2}$ e o plano-$xy.$
Use o Teorema do Divergente para calcular $\displaystyle\iint \limits_{S}{\bf F}\cdot dS$, onde ${\bf F}(x,y,z)=z^{2}x\,{\bf i}+(\frac{1}{3}y^{3}+tg z)\,{\bf j}+(x^{2}z+y^{2})\,{\bf k}$ e $S$ é a metade de cima da esfera $x^{2}+y^{2}+z^{2}=1.$
[Sugestão: observe que $S$ não é uma superfície fechada. Calcule primeiro as integrais sobre $S_{1}$ e $S_{2}$, onde $S_{1}$ é o círculo $x^{2}+y^{2}\leq 1$, orientado para baixo, e $S_{2}=S\cup S_{1}.$]
Note que $\dfrac{\partial}{\partial x} \left( \dfrac{x}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3x^2}{|{\bf x}|^5},$ $\dfrac{\partial}{\partial y} \left( \dfrac{y}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3y^2}{|{\bf x}|^5}$ e $\dfrac{\partial}{\partial z} \left( \dfrac{x}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3z^2}{|{\bf x}|^5}.$
Suponha que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que $f$ seja uma função escalar com derivadas parciais contínuas. Demonstre que $\displaystyle\iint\limits_{S}f{\bf n}\,dS=\iiint\limits_{E}\nabla f\,dV.$ Estas integrais de superfície e triplas de funções vetoriais são vetores definidos integrando cada função componente. [Sugestão: comece aplicando o Teorema do Divergente a ${\bf F}=f{\bf c}$, onde ${\bf c}$ é um vetor constante arbitrário.]
Note que se ${\bf n} = n_{1} {\bf i} + n_{2} {\bf j} + n_{3} {\bf k},$ então
\begin{align*} &\iint_{S} f \cdot {\bf n}\,dS \\ &= \left( \iint_{S} f n_{1}\,dS \right) {\bf i} + \left( \iint_{S} fn_{2}\,dS\right) {\bf j} + \left( \iint_{S} fn_{3}\,dS\right) {\bf k}\\ &= \left( \iiint_{E} \dfrac{\partial f}{\partial x}\,dV \right) {\bf i}+ \left( \iiint_{E} \dfrac{\partial f}{\partial y}\,dV\right) {\bf j} + \left( \iiint_{E} \dfrac{\partial f}{\partial z}\,dV \right) {\bf k}. \end{align*}
Verifique que $\mbox{div} {\bf E}=0$ para o campo elétrico ${\bf E}({\bf x})=\dfrac{\epsilon Q}{|{\bf x}|^{3}}{\bf x}.$

