2605

Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$

${\bf F}(x,y,z) = x^2z^2{\bf i} + y^2z^2{\bf j} + xyz {\bf k}$ e $S$ é a parte do parabolóide $z = x^2+y^2$ que está dentro do cilindro $x^2+y^2=4$, orientado para cima.

$0.$

2443

Calcule a integral de superfície $\displaystyle\iint\limits_{S}y^{2}dS$, onde $S$ é a parte da esfera $x^{2}+y^{2}+z^{2}=4$ que está dentro
do cilindro $x^{2}+y^{2}=1$ e acima do plano $xy.$

$\pi\left( \dfrac{32}{3} - 6\sqrt{3}\right).$

2249

Seja ${\bf F}(x,y,z)=(x+y+z^{2})\,{\bf k}$ e seja $S$ a fronteira do cilindro $x^{2}+y^{2}\leq 4$ e $0\leq z \leq 3.$ Calcule $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS$ onde ${\bf n}$ é a normal exterior, isto é, ${\bf n}$ é a normal que aponta para fora do cilindro.

2283

Determine se os pontos $P(7,10,4)$ e $Q(5,22,5)$ estão na superfície ${\bf r}(u,v)=(2u+3v,1+5u-v,2+u+v)$.

$P$ não está na superfície; $Q$ está na superfície.

3136

Em 1831, o físico Michael Faraday descobriu que uma corrente elétrica pode ser produzida variando-se o fluxo magnético através de um arco condutor. Suas experiências mostraram que a força eletromotriz $\mathbf{E}$ está relacionada com a indução magnética $\mathbf{B}$ pela equação \[ \oint_C\mathbf{E}\cdot\,d\mathbf{r} = - \iint\limits_\sigma\dfrac{\partial\mathbf{B}}{\partial t}\cdot\mathbf{n}\,dS.\] Use este resultado para fazer uma conjectura acerca da relação entre $\mathrm{rot\,}\mathbf{E}$ e $\mathbf{B}$. Explique seu raciocínio.

2297

Determine uma representação paramétrica para a superfície descrita a seguir. A superfície cortada do cilindro parabólico $z=4-y^{2}$ pelos planos $x=0$, $x=2$ e $z=0.$

$x = u,$ $y = v,$ $z = 4 - v^2,$ onde $0\leq u \leq 2$ e $-2 \leq v \leq 2.$

2258

Um sólido ocupa a região $E$ com superfície $S$ e está imerso em um líquido com densidade constante $\rho$. Escolhemos um sistema de
coordenadas de modo que o plano $xy$ coincida com a superfície do líquido e valores positivos de $z$ sejam medidos para baixo, adentrando o líquido. Então, a pressão na profundidade $z$ é $p=\rho g z$, onde $g$ é a aceleração da gravidade. A força de empuxo total sobre o sólido devida $\grave{a}$ distribuição de pressão é dada pela integral de superfície
${\bf F}=-\displaystyle\iint\limits_{S} p{\bf n}\,dS$ onde ${\bf n}$ é o vetor normal unitário apontando para fora. Use o resultado do exercício anterior para mostrar que ${\bf F}=-W{\bf k}$, onde $W$ é o peso do líquido deslocado pelo sólido. (Observe que ${\bf F}$ é orientado para cima porque $z$ está orientado para baixo.) O resultado é o Princípio de Arquimedes: a força de empuxo sobre um objeto é igual ao

peso do líquido deslocado.

Note que $\displaystyle {\bf F}=-\int_{S} p {\bf n} \,dS = -\iiint_{E} \nabla p\,dV = -\iiint_{E} \nabla p\,dV = - \iiint_{E} \nabla (\rho g z)\,dV.$

Conclua usando que $W = \rho g V(E),$ onde $V(E)$ é o volume de $E.$

2336

Determine a área da superfície dada pela parte da superfície $z=xy$ que está dentro do cilindro $x^{2}+y^{2}=1$.

$\dfrac{2\pi}{3}(2\sqrt{2} - 1)$.

2253

Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.

$V(E)=\dfrac{1}{3}\displaystyle\iint\limits_{S}{\bf F}\cdot dS$, onde ${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}.$

Dica: Note que $\displaystyle\iiint\limits_{E}{\mbox{div} {\bf F}}\, dV = \iiint \limits_{E}{3}\,dV$.

2510

Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$

${\bf F}=x{\bf i}-y{\bf j}$; $S$ é a parte no primeiro octante da esfera $x^{2}+y^{2}+z^{2}=a^{2}.$

$0.$

2257

Suponha que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que $f$ seja uma função escalar com derivadas parciais contínuas. Demonstre que $\displaystyle\iint\limits_{S}f{\bf n}\,dS=\iiint\limits_{E}\nabla f\,dV.$ Estas integrais de superfície e triplas de funções vetoriais são vetores definidos integrando cada função componente. [Sugestão: comece aplicando o Teorema do Divergente a ${\bf F}=f{\bf c}$, onde ${\bf c}$ é um vetor constante arbitrário.]

Note que se ${\bf n} = n_{1} {\bf i} + n_{2} {\bf j} + n_{3} {\bf k},$ então

\begin{align*} &\iint_{S} f \cdot {\bf n}\,dS \\ &= \left( \iint_{S} f n_{1}\,dS \right) {\bf i} + \left( \iint_{S} fn_{2}\,dS\right) {\bf j} + \left( \iint_{S} fn_{3}\,dS\right) {\bf k}\\ &= \left( \iiint_{E} \dfrac{\partial f}{\partial x}\,dV \right) {\bf i}+ \left( \iiint_{E} \dfrac{\partial f}{\partial y}\,dV\right) {\bf j} + \left( \iiint_{E} \dfrac{\partial f}{\partial z}\,dV \right) {\bf k}. \end{align*}

3138

Use o Teorema da Divergência para encontrar todos os valores positivos $k$ tais que \[ \mathbf{F}(\mathbf{r}) = \dfrac{\mathbf{r}}{\|\mathbf{r}\|^k} \] satisfaça a condição $\mathrm{div\,}\mathbf{F}=0$ quando $\mathbf{r}\neq \mathbf{0}$.

2543

Encontre o fluxo exterior do campo ${\bf F}(x,y,z)=z^{2}{\bf i}+x{\bf j}-3z{\bf k}$ através da superfície cortada do cilindro parabólico $z=4-y^{2}$ pelos planos $x=0$, $x=1$ e $z=0.$

$-32.$

2191

Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\,x^{2}+y^{2}+z^{2}\leq 1$ e $z\geq x+y\}$ e ${\bf u}=-2xy\,{\bf i}+y^{2}\,{\bf j}+3z\,{\bf k}.$

$\dfrac{3\pi}{2}.$

2612

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. Em cada caso, $C$ é orientada no sentido anti-horário quando vista de cima.

${\bf F}(x,y,z) = x^2z{\bf i} + xy^2{\bf j} + z^2{\bf k}$, $C$ é a curva de interseção do plano $x+y+z=1$ com o cilindro $x^2+y^2 = 9$.

$\dfrac{81\pi}{2}.$

2590

Use a Lei de Gauss para achar a carga contida no hemisfério sólido $x^{2}+y^{2}+z^{2} \leq a^{2}$, $z\geq 0$, se o campo elétrico for ${\bf E}(x,y,z)=x{\bf i}+y{\bf j}+2z{\bf k}$.

$\dfrac{8\pi a^3 \epsilon_{0}}{3}$.

2301

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$

Região triangular do plano $x + y + z = 1:$ $0 \leq x \leq 1, $ $0 \leq y \leq 1,$ $0 \leq z \leq 1.$

2630

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = -y^2{\bf i} + x^2{\bf j} + z^2{\bf k}$, $S$ a superfície $x^2 + \dfrac{y^2}{4} + z^2 = 2$, $z \geq 1$, sendo ${\bf n}$ a normal que aponta para cima.

$0$.

2154

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(x^{2}+z^{2})\,{\bf i}+(y^{2}-2xy)\,{\bf j}+(4z-2yz)\,{\bf k}$ e $S$ é a superfície da região delimitada pelo cone $x=\sqrt{y^{2}+z^{2}}$ e pelo plano $x=9.$

2254

Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.

$\displaystyle\iint\limits_{S} D_{n}f\,dS=\displaystyle\iiint\limits_{E}\nabla^{2}f\,dV.$

Lembre que $D_{n} f = \nabla f \cdot {\bf b}$ e $\mbox{div} (\nabla f) = \nabla^{2} f.$

2146

Aplique o Teorema da Divergência para achar $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS,$ sendo ${\bf F}(x,y,z)=(x^{2}+\sin yz)\,{\bf i}+(y-xe^{-z})\,{\bf j}+z^{2}\,{\bf k}$ e $S$ a superfície da região delimitada pelo cilindro $x^{2}+y^{2}=4$ e os planos $x+z=2$ e $z=0.$

$20\pi.$

2465

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=x{\bf i}+2y{\bf j}+3z{\bf k}$ e $S$ é o cubo com vértices $(\pm 1, \pm 1,\pm 1).$

$48.$

3149

Seja $\displaystyle \mathbf{F}(x,y,z)=f(x,y,z)\mathbf{i}+ g(x,y,z)\mathbf{j} + h(x,y,z)\mathbf{k}$ e suponha que $f$, $g$ e $h$ sejam contínuas e tenham derivadas parciais de primeira ordem contínuas numa região. Mostre que se $\mathbf{F}$ é conservativo numa região esférica aberta então $\mathrm{rot\,}\mathbf{F} = \mathbf{0}$ nessa região. [Sugestão: use que se $\mathbf{F}$ for conservativo numa região, então \[ \dfrac{\partial f}{\partial y}=\dfrac{\partial g}{\partial x},\quad \dfrac{\partial f}{\partial z}=\dfrac{\partial h}{\partial x},\quad \dfrac{\partial g}{\partial z}=\dfrac{\partial h}{\partial y} \] nessa mesma região.]

2345

Mostre que as equações paramétricas $x=a \cosh u\cos v$, $y=b\cosh u \sin v$, $z=c\sinh u$, representam um hiperboloide de uma folha.

Note que $\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} - \dfrac{z^{2}}{c^{2}} = 1$.

2615

Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial ${\bf F}$ dado e a superfície $S$.

${\bf F}(x,y,z) = y^2{\bf i} + x{\bf j} + z^2{\bf k}$, $S$ é a parte do parabolóide $z = x^2 + y^2$ que está acima do plano $z = 1$, orientado para cima.

$\displaystyle\int_{C} {\bf F} \cdot d{\bf R} = \displaystyle\iint_{S} \mbox{rot} {\bf F} \cdot d{\bf S} = \pi.$

2447

Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ sendo $g(x,y,z)=x^{2}$ e $S$ o hemisfério superior de $x^{2}+y^{2}+z^{2}=a^{2}.$

$\dfrac{2\pi a^4}{3}.$

3139

Prove a seguinte identidade \[ \iint\limits_\sigma\mathrm{rot\,}\mathbf{F}\cdot\mathbf{n}\,dS = 0, \] supondo que $\mathbf{F}$ e $\sigma$ satisfaçam as hipóteses do Teorema da Divergência.

2298

Determine uma representação paramétrica para a superfície descrita a seguir. A porção do cilindro $(x-2)^{2}+z^{2}=4$ entre os planos $y=0$ e $y=3.$

$x = 4\cos^{2}(v),$ $y = u,$ $z = 4\cos(v)\sin(v),$ onde $-\dfrac{\pi}{2}\leq v \leq \dfrac{\pi}{2}$ e $0 \leq u \leq 3.$

2346

Encontre a área da parte da esfera $x^{2}+y^{2}+z^{2}=a^{2}$ que está dentro do cilindro $x^{2}+y^{2}=ax.$

$2a^2 (\pi - 2).$

2437

Calcule a integral de superfície $\displaystyle\iint\limits_{S}x^{2}yz dS$, onde $S$ é a parte do plano $z=1+2x+3y$ que está acima do retângulo $[0,3]\times [0,2].$

$171\sqrt{14}.$

2138

Seja $S$ o gráfico de $f(x,y)=x^{2}+y^{2}$, $x^{2}+y^{2}\leq 1$ e seja ${\bf n}$ a normal a $S$ com componete $z\leq 0$. Seja ${\bf F}(x,y,z)=x^{2}y\,{\bf i}-xy^{2}\,{\bf j}+{\bf k}$. Calcule $\iint \limits_{S}{\bf F}\cdot {\bf n}\, dS.$

Observe que $S$ não é uma superfície fechada (isto é, $S$ não é a fronteira de um sólido $E$). Para que possamos utilizar o Teorema do Divergente, vamos considerar a superfície $S_2$ constituída pelo parabolóide $S$ e pelo círculo $S_1$ dado por $x^2+y^2 \leq 1$ em $z=1$. Como $S_2$ é uma superfície fechada, usamos a escolha da normal ${\bf n_2}$ em $S_2$ que está apontando ``para fora". Sejam ${\bf n_1}$ a normal a $S_1$ (apontando para cima) e ${\bf n}$ a normal a $S$ (apontando para fora).

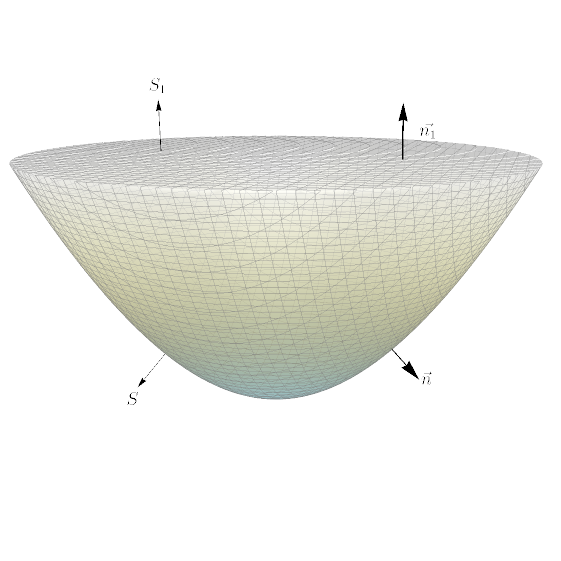
Temos
$\displaystyle\iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS = \iint\limits_{S}{\bf F}\cdot {\bf n}\,dS + \iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS,$
isto é,
$\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS = \iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS - \iint \limits_{ S_1}{\bf F}\cdot {\bf n_1}\,dS.$
Pelo Teorema do Divergente,
$$\iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS = \iiint\limits_{E}(2xy-2xy+0)\,dV = 0,$$
em que $E$ é o sólido que possui $S_2$ como fronteira.
Para determinar $\displaystyle\iint\limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS$, devemos encontrar uma parametrização para $S_1$ e determinar o vetor normal ${\bf n_1}$. Considere a seguinte parametrização de $S_1$: $r(u,v) = (u,v,1)$, com $u^2+v^2 \leq 1$. Daí, $r_u(u,v) = (1,0,0)$ e $r_v(u,v) = (0,1,0)$. Logo, $r_u \times r_v = (0,0,1)$ é um vetor normal a $S_1$. Devemos tomar ${\bf n_1} = (0,0,1)$ para que aponte para cima. Então,
$\displaystyle\iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS = \iint\limits_{D}(u^2v,-uv^2,1)\cdot(0,0,1)\,dA,$
em que $D = \{(u,v) \in \mathbb{R}^2; u^2+v^2 \leq 1\}$. Portanto,
$\displaystyle\iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS = \iint\limits_{D}1\,dA = A(D) = \pi,$
donde concluímos que
$\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS = 0 - \pi = -\pi.$

2424

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F} \cdot d{\bf r}$, com ${\bf F} (x,y,z) = yz{\bf i} + 2xz{ \bf j} + e^{xy} {\bf k} $ e $C$ é a circunferência $x^2+y^2 = 16$, $z=5$, orientada no sentido anti-horário quando vista de cima.

2512

Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$

${\bf F}=x{\bf i}+y{\bf j}+z{\bf k}$; $S$ é a parte do plano $3x+2y+z=12$ intersectada pelos planos $x=0$,$y=0$, $x=1$ e $y=2.$

$24.$

2620

Suponha que $S$ e $C$ satisfaçam as hipóteses do Teorema de Stokes e $f$ e $g$ tenham derivadas parciais de segunda ordem contínuas. Demonstre que $\displaystyle\int_C (f\nabla f)\cdot d{\bf R} = 0$

Note que $\mbox{rot} (f\nabla f) = {\bf 0}.$

2617

Seja $C$ uma curva fechada, simples e lisa que está no plano $x+y+z=1$. Mostre que a integral de linha $\displaystyle\int_C zdx - 2xdy + 3ydz$ depende apenas da área da região englobada por $C$ e não da forma de $C$ ou de sua posição no plano.

$\displaystyle\int_C zdx - 2xdy + 3ydz = \dfrac{2}{\sqrt{3}} \times $ (área da região englobada por $C$).

2305

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$

${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$,\, $v\geq 0$ e $u+v\leq 1.$

2545

Seja $S$ a superfície $z=f(x,y)$, $(x,y)\in K$, de classe $C^{1}$ num aberto contendo $K$. (Observação: trata-se da superfície dada por $x=u$, $y=v$ e $z=f(u,v)$). Seja ${\bf n}$ a normal a $S$ com componente $z>0$ e seja ${\bf F}=P{\bf i}+Q{\bf j}+R{\bf k}$ um campo vetorial contínuo na imagem de $S$. Mostre que $\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}dS=\displaystyle\iint\limits_{K}\left[ -P\dfrac{\partial f}{\partial x}(x,y)-Q\dfrac{\partial f}{\partial y}+R\right]dx dy,$ onde $P$, $Q$ e $R$ são calculadas em $(x,y,f(x,y)).$

Veja a subseção "Integrais de superfície de campos vetoriais"' da seção 16.7 do livro do Stewart.

2192

Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, x^{2}+y^{2}+z^{2}\leq 1\}$ e ${\bf u}=x\,{\bf i}+y\,{\bf j}+z^{2}\,{\bf k}.$

$\pi.$

2325

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,4-u^{2}-v^{2})$, $(u,v)\in K$, onde $K$ é o conjunto no plano $uv$ limitado pelo eixo $u$ e pela curva (em coordenadas polares) $\rho=e^{-\theta}$,$0\leq \theta \leq \pi.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\displaystyle \dfrac{1}{72} \left( \ln\left(3\dfrac{\sqrt{e^{2\pi} + 4} + e^{\pi}}{\sqrt{e^{2\pi} + 4} - e^{\pi}} \right) + 3 \ln\left(\dfrac{\sqrt{5} - 1 }{\sqrt{5} + 1 }\right) - 8e^{3\pi} \sqrt{e^{2\pi} + 4}(e^{2\pi} + 1) + 16\sqrt{5} - 6\pi \right).$

2509

Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$

${\bf F}=x{\bf i}+y{\bf j}+z{\bf k}$; $S$ é o hemisfério superior de $x^{2}+y^{2}+z^{2}=a^{2}.$

$2\pi a^3.$

2464

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=y{\bf j}-z{\bf k}$ e $S$ é formada pelo parabolóide $y=x^{2}+z^{2}$, $0 \leq y \leq 1$ e pelo círculo $x^{2}+z^{2} \leq 1$, $y=1.$

$0.$

2453

Integre $g(x,y,z)=x+y+z$ sobre a porção do plano $2x+2y+z=2$ que está no primeiro octante.

$2.$

2631

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf i} + x{\bf j} + xz{\bf k}$, $S$ a superfície $z = x+y+2$ e $x^2 + \dfrac{y^2}{4} \leq 1$, sendo ${\bf n}$ a normal que aponta para baixo.

$4\pi$.

2449

Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ onde $g(x,y,z)=x+y$ e $S$ é parte do primeiro octante do plano $2x+3y+z=6.$

$5\sqrt{14}.$

2152

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=x^{4}\,{\bf i}-x^{3}z^{2}\,{\bf j}+4xy^{2}z\,{\bf k}$ e $S$ é a superfície do sólido limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $z=x+2$ e $z=0.$

2292

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do plano $z=x+3$ que está dentro do cilindro $x^{2}+y^{2}=1.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 3 + r \cos(\theta),$ onde $0 \leq r \leq 1$ e $0\leq \theta \leq 2\pi.$

2139

Use o Teorema do Divergente para calcular $\displaystyle\iint \limits_{S}(2x+2y+z^{2})\,dS$ onde $S$ é a esfera $x^{2}+y^{2}+z^{2}=1.$

A superfície $S$ em questão é a esfera unitária, que é a fronteira da bola unitária $B$ dada por $x^2+y^2+z^2 \leq 1$ e tem vetor normal num ponto $(x,y,z)$ igual a $(x,y,z)$ (o qual aponta para ``fora").

Observe que podemos transformar o integrando $2x+2y+z^{2}$ em $(2,2,z) \cdot (x,y,z)$ e essa escrita é interessante, já que o segundo vetor é exatamente o vetor normal a $S$. Agora estamos em condições de aplicar o Teorema do Divergente quando tomamos o campo ${\bf F}(x,y,z) = (2,2,z)$. Assim,
\begin{array}{rcl}\displaystyle\iint\limits_{S}(2x+2y+z^{2})\,dS & = & \iint\limits_{ S}(2,2,z) \cdot (x,y,z)\,dS \\& = & \int\int\int \limits_{ S}{\bf F} \cdot {\bf n}\,dS \\& = & \iiint\limits_{ B}\text{div } F\,dV \\& = & \iiint\limits_{ B}(0+0+1)\,dV \\& = & V(B) = \frac{4\pi}{3}.\end{array}

2322

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{\sqrt{3}}{2}.$

2547

Um fluido tem densidade $870kg/m^{3}$ e escoa com velocidade $v=z{\bf i}+y^{2}{\bf j}+x^{2}{\bf k},$ onde $x$, $y$ e $z$ são medidos em metros e as componentes de $v$ em metros por segundo. Encontre a vazão para fora do cilindro $x^{2}+y^{2}=4$, $0\leq z\leq 1.$

$0$ kg/s.

2467

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}$ e $S$ é a parte no primeiro octante do plano $2x+3y+z=6.$

$18.$

2451

Integre $g(x,y,z)=x+y+z$ sobre a superfície do cubo cortado do primeiro octante pelos planos $x=a$, $y=a$ e $z=a.$

$9a^3.$

3143

Considere o campo vetorial $\mathbf{F}(x,y,z)=x^2\mathbf{i} + y^2\mathbf{j}+z^2\mathbf{k}$ e a superfície $\sigma$ descrita como sendo a porção do cone $z=\sqrt{x^2+y^2}$ abaixo do plano $z=1$ e tendo orientação para cima. Verifique o Teorema de Stokes calculando, separadamente, a integral de linha e a integral dupla e, em seguida, comparando os valores.

2622

Utilizando o Teorema de Stokes, transforme a integral $\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf k}$, $S$ a superfície parametrizada por ${\bf R} (u,v) = (u,v,u^2+v^2)$, $u^2+v^2 \leq 1$, sendo ${\bf n}$ a normal apontando para cima.

$0.$

2391

Calcule a integral de superfície $\displaystyle\iint\limits_{S}x^{2}z^{2}dS$, onde $S$ é a parte do cone $z^{2}=x^{2}+y^{2}$ que está entre os planos $z=1$ e $z=3.$

Temos que $S$ é a porção do cone $z^{2}=x^{2}+y^{2}$ para $1 \leq z \leq 3$, ou equivalentemente, $S$ é a parte da superfície $z=\sqrt{x^{2}+y^{2}}$ sobre a região $D=\{(x,y)| 1 \leq x^{2}+y^{2} \leq 9\}.$ Assim,
$\displaystyle\iint\limits_{S}x^{2}z^{2}dS=\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})\sqrt{\left(\dfrac{\partial z}{\partial x}\right)^{2}
+\left(\frac{\partial z}{\partial y}\right)^{2}+1}dA$
$=\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})\sqrt{\left(\frac{x}{\sqrt{x^{2}+y^{2}}}\right)^{2}+\left(\frac{y}{\sqrt{x^{2}+y^{2}}}\right)^{2}+1}dA$
$=\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})\sqrt{\frac{x^{2}+y^{2}}{x^{2}+y^{2}}+1}dA=\iint\limits_{D}\sqrt{2}x^{2}(x^{2}+y^{2})dA$
$=\sqrt{2}\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})dA.$
Por coordenadas polares, temos que $x=r\cos \theta, y=r\sin \theta, 1\leq r\leq 3 , 0\leq \theta \leq 2\pi \,\mbox{e} \, dA=r dr d\theta.$
Logo,
$\displaystyle\iint\limits_{S}x^{2}z^{2}dS=\sqrt{2}\int_{0}^{2\pi}\int_{1}^{3}(r^{2}\cos^{2}\theta)(r^{2})r dr d\theta =\sqrt{2}\int_{0}^{2\pi}\cos^{2}\theta d\theta \cdot \int_{1}^{3}r^{5}dr$

$=\sqrt{2}\cdot (\theta)\bigg|_{0}^{2\pi}\cdot \bigg(\frac{r^{6}}{6}\bigg)\bigg|_{1}^{3}=\sqrt{2}\cdot \pi \cdot \frac{1}{6}\cdot (3^{6}-1)=\frac{364\sqrt{2}}{3}\pi$

2441

Calcule a integral de superfície $\displaystyle\iint\limits_{S}z dS$, onde $S$ é a superfície $x=y+2z^{2}$, $0 \leq y\leq 1$, $0 \leq z \leq 1.$

$\dfrac{13\sqrt{2}}{12}.$

2440

Calcule a integral de superfície $\displaystyle\iint\limits_{S}\sqrt{1+x^{2}+y^{2}}dS$, onde $S$ é o helicóide com equação vetorial ${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+v{\bf k}$, $0 \leq u \leq 1$, $0 \leq v \leq \pi.$

$\dfrac{4\pi}{3}.$

2623

Utilizando o Teorema de Stokes, transforme a integral $\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf i}-x^2{\bf j}+5{\bf k}$, $S$ a superfície parametrizada por ${\bf R}(u,v) = (u,v,1-u^2)$, $u \geq 0$, $v \geq 0$, $u+v\leq 1$, sendo ${\bf n}$ a normal apontando para cima.

$-\dfrac{5}{6}.$

2303

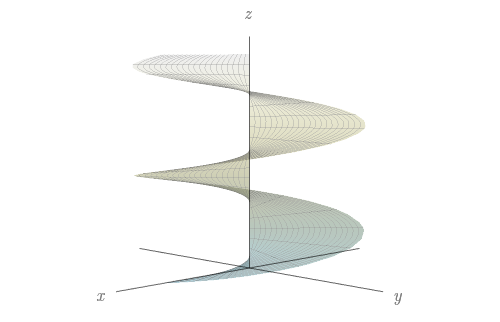
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(v\,\cos u,v\sin u,v)$, $0\leq u\leq 2\pi$,\, $0\leq v \leq h$, onde $h>0$ é um real dado.

Face lateral do cone $\sqrt{x^{2} + y^{2}} \leq z \leq h$.

2338

Determine a área da superfície $z=\frac{2}{3}(x^{3/2}+y^{3/2})$, $0\leq x \leq 1$ e $0\leq y\leq 1.$

$\dfrac{4}{15}(3^{5/2} - 2^{7/2} + 1).$

2463

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}$, $S$ é a esfera $x^{2}+y^{2}+z^{2}=9.$

$108\pi.$

2444

Calcule a integral de superfície $\displaystyle\iint\limits_{S}x dS$, onde $S$ é a superfície com equações paramétricas $x=u$, $y=v$, $z=u^{2}+v$, $0 \leq u \leq 1$, $u^{2} \leq v \leq 1.$

$\dfrac{\sqrt{2}}{10}(3\sqrt{3} - 2).$

2320

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(3\sin 2u,6\sin^{2} u, v)$,$0\leq u\leq \pi$, no ponto ${\bf r}(\pi/3,0).$

$x^{2} + (y-3)^{2} = 9.$

2343

Seja $A=\{(0,y,z)\in \mathbb{R}^{3}| z^{2}+(y-2)^{2}=1\}$; ache a área da superfície gerada pela rotação em torno do eixo $Oz$ do conjunto $A.$

$8\pi^2.$

2611

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.

${\bf F}(x,y,z) = (x^2-y){\bf i} + 4z{\bf j} + x^2{\bf k}$, $C$ é a curva de interseção do plano $z=2$ com o cone $z=\sqrt{x^2+y^2}$.

$4\pi$.

2628

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf i}$, $S$ a superfície $x^2+y^2+z^2 = 2$, $x^2+y^2\leq 1$ e $z \geq 0$, sendo ${\bf n}$ a normal apontando para cima.

$-\pi$.

2255

Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.

$\displaystyle\iint\limits_{S}(f\nabla g)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E}(f\nabla^{2}g+\nabla f+\nabla g)\,dV.$

Note que $\displaystyle\iint\limits_{S}(f\nabla g)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E} \mbox{div} (f\nabla g)\,dV.$

2144

Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$

${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$, $E$ é a bola unitária $x^{2}+y^{2}+z^{2}\leq 1.$

$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = 4\pi.$

2153

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=yz\,{\bf i}+xz\,{\bf j}+xy\,{\bf k}$ e $S$ é o gráfico de $x^{2/3}+y^{2/3}+z^{2/3}=1.$

2143

Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=xy\,{\bf i}+yz\,{\bf j}+zx\,{\bf k}$, $E$ é o cilindro sólido $x^{2}+y^{2}\leq 1$, $0\leq z\leq 1.$

$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = \dfrac{\pi}{2}.$

2621

Suponha que $S$ e $C$ satisfaçam as hipóteses do Teorema de Stokes e $f$ e $g$ tenham derivadas parciais de segunda ordem contínuas. Demonstre que $\displaystyle\int_C (f\nabla g + g\nabla f) \cdot d{\bf R} = 0$

Note que $\mbox{rot} (f\nabla g + g\nabla f) = {\bf 0}.$

2613

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.

${\bf F}(x,y,z) = (y+z,-z,y)$, $C$ é a curva obtida como interseção do cilindro $x^2+y^2=2y$ com o plano $y = z$.

$\dfrac{4\pi}{3}$.

2288

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do hiperboloide $x^{2}+y^{2}-z^{2}=1$ que está à direita do plano $xz.$

$x =u,$ $z = v,$ $y = \sqrt{1 - u^2 + v^2}.$

3147

Use o Teorema de Green para provar que\[ \int_Cf(x)\,dx + g(y)\,dy = 0\] se $f$ e $g$ forem funções diferenciáveis e $C$ for uma curva fechada simples lisa por partes.
O que isso nos diz sobre o campo vetorial \[ \mathbf{F}(x,y) = f(x)\mathbf{i}+g(y)\mathbf{j}?\]

2196

Se ${\bf F}=(xz,yz,2)$ e $E$ é a região dada por $x^{2}+y^{2}\leq 1$ e $0\leq z \leq 1,$ mostre que o Teorema do Divergente é verdadeiro neste caso. Calcule as duas integrais do enunciado do Teorema e mostre que elas têm o mesmo valor.

2252

Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.

$\displaystyle\iint\limits_{S}{\bf a}\cdot {\bf n}\,dS=0$, onde ${\bf a}$ é um vetor constante.

Dica: Note que $\mbox{div} {\bf a} = 0.$

2326

Calcule a área da superfície dada por: ${\bf r}(u,v)=\bigg(u,v,\dfrac{1}{2}u^{2}\bigg)$,$0\leq v\leq u$ e $u\leq 2.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{1}{3}\left(5\sqrt{5} - 1 \right).$

2284

Determine se os pontos $P(3,-1,5)$ e $Q(-1,3,4)$ estão na superfície ${\bf r}(u,v)=(u+v,u^{2}-v,u+v^{2})$.

$P$ está na superfície; $Q$ não está na superfície.

2439

Calcule a integral de superfície $\displaystyle\iint\limits_{S}yz dS$, onde $S$ é a superfície com equações paramétricas $x=u^{2}$, $y=u \sin v$, $z=u\cos v$, $0 \leq u \leq 1$, $0 \leq v \leq \pi/2.$

$\dfrac{5\sqrt{5}}{48} + \dfrac{1}{240}.$

2452

Integre $g(x,y,z)=xyz$ sobre a superfície do sólido retangular cortado do primeiro octante pelos planos $x=a$, $y=b$ e $z=c.$

$\dfrac{abc(ab+ac+bc)}{4}.$

2592

Considere um escoamento com velocidade ${\bf v}(x,y,z)$ e densidade $\rho(x,y,z)$, tal que ${\bf u}=\rho {\bf v}$ seja dado por ${\bf u}=x{\bf i}+y{\bf j}-2z{\bf k}$. Seja $S$ a superfície $x^{2}+y^{2}+z^{2}=4$, $z\geq \sqrt{2}$, e seja ${\bf n}$ a normal com componente $z>0$. Calcule o fluxo de ${\bf u}$ através de $S$. (Observe que, neste caso, o fluxo tem dimensões $MT^{-1}$ (massa por unidade de tempo).)

$-4\pi\sqrt{2}.$

2327

Calcule a área da superfície dada por: ${\bf r}(u,v)=(\cos u,v,\sin u)$ e $u^{2}+4v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{\pi}{2}.$

2256

Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.

$\displaystyle\iint\limits_{S}(f\nabla g-g\nabla f)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E}(f\nabla^{2} g-g\nabla^{2} f)\,dV.$

Use o Teorema da Divergência e que $\nabla f \cdot \nabla g = \nabla g \cdot \nabla f.$

3146

Sejam $\alpha$ e $\beta$ dois ângulos que satisfazem $\displaystyle 0<\beta-\alpha\leq 2\pi$ e suponha que $ r= f(\theta)$ seja uma curva polar lisa com $f(\theta)>0$ no intervalo $[\alpha,\beta]$. Use a fórmula \[ A = \dfrac{1}{2}\int_C-y\,dx+x\,dy \] para encontrar a área da região $R$ englobada pela curva $r=f(\theta)$ e os raios $\theta=\alpha$ e $\theta=\beta$.

2187

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3x\,{\bf i}+xz\,{\bf j}+z^{2}\,{\bf k}$ e $S$ é a superfície da região delimitada pelo parabolóide $z=4-x^{2}-y^{2}$ e o plano-$xy.$

2629

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = -y{\bf i} + x{\bf j} + x^2{\bf k}$, $S$ a superfície $x^2+y^2+z^2 = 4$, $\sqrt{2} \leq z \leq \sqrt{3}$ e $y \geq 0$, sendo ${\bf n}$ a normal apontando para cima.

$\pi$.

2423

A temperatura em um ponto $(x,y,z)$ em uma substância com condutividade $K=6,5$ é $u(x,y,z)=2y^{2}+2z^{2}.$ Determine a taxa de transmissão de calor nessa substância para dentro da superfície cilíndrica $y^{2}+z^{2}=6$, $0\leq x\leq 4.$

O fluxo de calor, com $u(x,y,z)=2y^{2}+2z^{2}$, é dado por

$${\bf F}(x,y,z)=-K \nabla u=-6,5(0{\bf i}+4y{\bf j}+4z{\bf k})=0{\bf i}-26y{\bf j}-26z{\bf k}.$$

Temos que $S$ é a superfície cilíndrica $y^{2}+z^{2}=6$ e $0\leq x \leq 4.$ As equações paramétricas de $S$ são:

$$x=x, y=\sqrt{6}\cos \theta \mbox{e} z=\sqrt{6}\sin \theta$$

onde $0\leq x \leq 4$ e $0\leq \theta \leq 2\pi.$

Então,

$${\bf r}(x,\theta)=x{\bf i}+\sqrt{6}\cos \theta{\bf j}+\sqrt{6}\sin \theta{\bf k}.$$

Como queremos o fluxo de calor para dentro de $S$ devemos calcular

$$\int \int\limits_{S}{\bf F}\cdot dS=\int \int\limits_{ D}{\bf F}({\bf r}(x,\theta))\cdot ({\bf r}_{x}\times {\bf r}_{\theta})dA.$$

Então,

$${\bf r}_{x}(x,\theta)={\bf i}+0{\bf j}+0{\bf k}$$

e

$${\bf r}_{\theta}(x,\theta)=0{\bf i}-\sqrt{6}\sin \theta{\bf j}-\sqrt{6}\cos \theta{\bf k}.$$

Logo,

$\begin{array}{rcl} {\bf r}_{x} \times {\bf r}_{\theta} &=& \left| \begin{array}{ccc}{\bf i} & {\bf j} & {\bf k}\\1 & 0 & 0\\0 & -\sqrt{6}\sin \theta & -\sqrt{6}\cos \theta \\ \end{array} \right| \\ &=& 0{\bf i}-\sqrt{6}\cos \theta{\bf j}-\sqrt{6}\sin \theta{\bf k}, \end{array}$

$${\bf F}({\bf r}(x,\theta))=(0{\bf i}-26\sqrt{6}\cos\theta{\bf j}-26\sqrt{6}\sin \theta{\bf k})$$

e

$${\bf F}({\bf r}(x,\theta))\cdot ({\bf r}_{x}\times {\bf r}_{\theta})=(0{\bf i}-26\sqrt{6}\cos\theta{\bf j}-26\sqrt{6}\sin \theta{\bf k}) \cdot (0{\bf i}-\sqrt{6}\cos \theta{\bf j}-\sqrt{6}\sin \theta{\bf k})=156$$

Assim, a taxa de fluxo de calor para dentro de $S$ é:

$$\int \int\limits_{S}{\bf F}\cdot dS=\int \int\limits_{ D}{\bf F}({\bf r}(x,\theta))\cdot ({\bf r}_{x}\times {\bf r}_{\theta})dA=\int \int\limits_{ D}156 dA=156\int \int\limits_{ D} 1 dA$$

$$=156\int_{0}^{2\pi}\int_{0}^{4}1dxd\theta=156\int_{0}^{2\pi}d\theta\cdot \int_{0}^{4}dx=156\cdot (\theta)\bigg|_{0}^{2\pi}\cdot (x)\bigg|_{0}^{4}=156\cdot 2\pi \cdot 4=1248 \pi.$$

2304

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=\bigg(v\cos u,v\sin u,\dfrac{1}{v^{2}}\bigg)$, $0\leq u\leq 2\pi$, $v>0.$

Gráfico de $f(x,y) = \dfrac{1}{x^2 + y^2}.$

2627

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf i}$, $S$ a superfície $z = x^2+y^2$ com $z \leq 1$, sendo ${\bf n}$ a normal com componente $z$ positiva.

$-\pi$.

2609

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.

${\bf F}(x,y,z) = (x+y^2){\bf i} + (y+z^2){\bf j} + (z+x^2){\bf k}$, $C$ é o triângulo com vértices $(1,0,0)$, $(0,1,0)$, $(0,0,1)$.

$1$.

2607

Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$

${\bf F}(x,y,z) = x{\bf i} - z{\bf j} + y{\bf k}$, $S$ é a parte do plano $x+z=1$ dentro do cilindro $x^2+y^2 = 1$, com orientação para cima.

$2\pi.$

2359

Seja $S$ a parte do cone $x^{2}=y^{2}+z^{2}$ que está dentro do cilindro $x^{2}+y^{2}=a^{2}$ e no primeiro octante. Determine a área da superfície $S.$

$\dfrac{\pi a^2}{4}$.

2347

Seja $f:K\rightarrow \mathbb{R}$ de classe $C^{1}$ no compacto $K$ com fronteira de conteúdo nulo e interior não-vazio. Mostre que a área da superfície $z=f(x,y)$ (isto é, da superfície ${\bf r}$ dada por $x=u$, $y=v$ e $z=f(u,v)$) é dada pela fórmula

$$\iint\limits_{ K}\sqrt{1+\bigg(\frac{\partial f}{\partial x}\bigg)^{2}+\bigg(\frac{\partial f}{\partial y}\bigg)^{2}}dxdy.$$

2293

Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=x^{2}+y^{2}$, \, $z\leq 4.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = r^2,$ onde $0 \leq r \leq 2$ e $0\leq \theta \leq 2\pi.$

3140

Prove a seguinte identidade \[ \iint\limits_\sigma\nabla f\cdot\mathbf{n}\,dS = \iiint\limits_G\Delta f\,dV, \] supondo que $\sigma$ e $G$ satisfaçam as hipóteses do Teorema da Diverência e que $f(x,y,z)$ cumpra os requisitos de diferenciabilidade necessários. Acima, $\displaystyle \Delta f= \dfrac{\partial^2f}{\partial x^2}+\dfrac{\partial^2f}{\partial y^2}+\dfrac{\partial^2f}{\partial z^2}$ é denominado Laplaciano de $f$.

2544

Encontre o fluxo exterior do campo ${\bf F}=2xy{\bf i}+2yz{\bf j}+2xz{\bf k}$ ao longo da superfície do cubo cortado do primeiro octante pelos planos $x=a$, $y=a$ e $z=a.$

$3\pi a^4.$

2295

Determine uma representação paramétrica para a superfície descrita a seguir. A porção no primeiro octante do cone $z=\sqrt{x^{2}+y^{2}}/2$ entre os planos $z=0$ e $z=3.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = \dfrac{r}{2},$ onde $0 \leq r \leq 6$ e $0\leq \theta \leq \dfrac{\pi}{2}.$

2194

Use o Teorema do Divergente para calcular $\displaystyle\iint \limits_{S}{\bf F}\cdot dS$, onde ${\bf F}(x,y,z)=z^{2}x\,{\bf i}+(\frac{1}{3}y^{3}+tg z)\,{\bf j}+(x^{2}z+y^{2})\,{\bf k}$ e $S$ é a metade de cima da esfera $x^{2}+y^{2}+z^{2}=1.$
[Sugestão: observe que $S$ não é uma superfície fechada. Calcule primeiro as integrais sobre $S_{1}$ e $S_{2}$, onde $S_{1}$ é o círculo $x^{2}+y^{2}\leq 1$, orientado para baixo, e $S_{2}=S\cup S_{1}.$]

Note que $\dfrac{\partial}{\partial x} \left( \dfrac{x}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3x^2}{|{\bf x}|^5},$ $\dfrac{\partial}{\partial y} \left( \dfrac{y}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3y^2}{|{\bf x}|^5}$ e $\dfrac{\partial}{\partial z} \left( \dfrac{x}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3z^2}{|{\bf x}|^5}.$

3144

Encontre o trabalho realizado pelo campo de forças \[ \mathbf{F}(x,y)= y^2\mathbf{i} + xy\mathbf{j} \] para mover uma partícula de $(0,0)$ até $(1,1)$ ao longo da parábola $y=x^2$.

2269

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=u^{2}\,{\bf i}+2u\,\sin v\,{\bf j}+u\,\cos v\,{\bf k}$; $u=1$, $v=0.$

Temos que ${\bf r}(u,v)=\underbrace{u^{2}}_{x(u,v)}\,{\bf i}+\underbrace{2u\,\sin v}_{y(u,v)}\,{\bf j}+\underbrace{u\,\cos v}_{z(u,v)}\,{\bf k}$

Primeiro, vamos calcular os vetores tangentes:

$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& 2u\,{\bf i}+2\,\sin v\,{\bf j}+\cos v\,{\bf k}\end{array}$$

e

$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& 0\,{\bf i}+2u\,\cos v\,{\bf j}-u\sin v\,{\bf k}\end{array}$$

Assim, o vetor normal ao plano tangente é:

$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i} & {\bf j} & {\bf k}\\2u & 2\sin v & \cos v\\0 & 2u\cos v & -u\sin v\\\end{array}\right|\\&=&(-2u\,\sin^{2}v-2u\cos^{2}v)\,{\bf i}+(2u^{2}\,\sin v)\,{\bf j}+(4u^{2}\,\cos v)\,{\bf k}\end{array}$$

Como $u=1$ e $v=0$ temos que o vetor normal é $-2\,{\bf i}+0\,{\bf j}+4\,{\bf k}.$

Portanto, uma equação do plano tangente no ponto ${\bf r}(1,0)=(1,0,1)$ é

$$-2\cdot(x-1)+0\cdot(y-0)+4\cdot (z-1)=0$$

$$-2x+2+4z-4=0$$

$$-2x+4z-2=0 \mbox{ou} x-2z+1=0$$

2142

Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$

${\bf F}(x,y,z)=x^{2}\,{\bf i}+xy\,{\bf j}+z\,{\bf k}$, $E$ é o sólido delimitado pelo paraboloide $z=4-x^{2}-y^{2}$ e pelo plano $xy.$

$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = 8\pi.$

3135

Seja $\sigma$ a superfície de um sólido $G$ com vetor normal unitário $\mathbf{n}$ orientado para fora de $\sigma$. Suponha que $\mathbf{F}$ seja um campo vetorial com derivadas parciais de primeira ordem contínuas em $\sigma$. Prove que \[\iint\limits_\sigma (\mathrm{rot\,}\mathbf{F})\cdot\mathbf{n}\,dS = 0.\] [Sugestão: tome $C$ uma curva fechada simples em $\sigma$ que separa a superfície em duas subsuperfícies $\sigma_1$ e $\sigma_2$ com fronteira comum $C$. Aplique o Teorema de Stokes a $\sigma_1$ e a $\sigma_2$ e some os resultados.]
O campo vetorial $\mathrm{rot\,}\mathbf{F}$ é denominado campo rotacional de $\mathbf{F}$. Em palavras, interprete a fórmula do item anterior como uma afirmação sobre o fluxo do campo rotacional.

2361

Considere a superfície parametrizada por

$${\bf r}(u,v)=(uv,u+v,u-v).$$

Determine o valor de $c$ de forma que o ponto $(c,1,0)$ pertença à superfície.
Calcule a área da parte da superfície correspondente à variação $u^{2}+v^{2}\leq 1.$

$\dfrac{1}{4}.$
$\left(\sqrt{6} - \dfrac{4}{3} \right)2\pi.$

2610

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.

${\bf F}(x,y,z) = xy{\bf i} + 2z{\bf j} + 3y{\bf k}$, $C$ é a curva de interseção do plano $x+z=5$ com o cilindro $x^2+y^2=9$.

$9\pi$.

2339

Determine a área da superfície com equações paramétricas $x=u^{2}$, $y=uv$, $z=\dfrac{1}{2}v^{2}$, $0\leq u\leq 1$, $0\leq v\leq 2.$

$4.$

2619

Suponha que $S$ e $C$ satisfaçam as hipóteses do Teorema de Stokes e $f$ e $g$ tenham derivadas parciais de segunda ordem contínuas. Demonstre que $\displaystyle\int_C (f\nabla g)\cdot d{\bf R} = \displaystyle\iint_{S} (\nabla f \times \nabla g)\cdot d{\bf S}$

Note que $\mbox{rot} (f\nabla g) = \nabla f \times \nabla g.$

2625

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf i} + x^2{\bf j} + z{\bf k}$, $S$ a superfície $x^2+y^2 = 1$, $0\leq z \leq 1$ e $y\geq 0$, sendo ${\bf n}$ a normal com componente $y\geq 0$.

$0$.

2468

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=(x^{2}+z){\bf i}+y^{2}z{\bf j}+(x^{2}+y^{2}+z){\bf k}$ e $S$ é a parte no primeiro octante do parabolóide $z=x^{2}+y^{2}$ intersectada pelo plano $z=4.$

$4\pi - \dfrac{320}{7}.$

2608

Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$

${\bf F}(x,y,z) = (e^{xy}\cos{z},(x^2+1)z,-y)$, $S$ é o hemisfério $x^2+y^2+z^2 = 1$, $x \geq 0$, orientado na direção positiva do eixo $x$.

$-2\pi$.

2290

Determine uma representação paramétrica para a superfície descrita a seguir. A parte da esfera $x^{2}+y^{2}+z^{2}=4$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}.$

$x = 2\sin(\phi)\cos(\theta),$ $y = 2\sin(\phi)\sin(\theta),$ $z = 2\cos(\phi),$ onde $0\leq \phi \leq \frac{\pi}{4}$ e $0 \leq \theta \leq 2\pi.$

2358

Calcule a área da parte da superfície esférica $x^{2}+y^{2}+z^{2}=1$ que se encontra dentro do cone $z\geq \sqrt{x^{2}+y^{2}}.$

$\pi(2 - \sqrt{2}).$

2294

Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=9-x^{2}-y^{2}$, $z\geq 0.$

$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 9 - r^2,$ onde $0 \leq r \leq 3$ e $0\leq \theta \leq 2\pi.$

2360

Encontre a área da superfície $z=1+3x+3y^{2}$ que está acima do triângulo com vértices $(0,0)$, $(0,1)$ e $(2,1).$

$\dfrac{1}{54}\left(46\sqrt{46} - 10\sqrt{10} \right).$

2589

A água do mar tem densidade $1025 kg/m^{3}$ e escoa em um campo de velocidade ${\bf v}=y{\bf i}+x{\bf j}$, onde $x$, $y$ e $z$ são medidos em metros e as componentes de ${\bf v}$ em metros por segundo. Encontre a vazão para fora do hemisfério $x^{2}+y^{2}+z^{2}=9$, $z\geq 0.$

$0$ kg/s.

2546

Determine uma fórmula para $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ semelhante à fórmula

$\displaystyle\iint\limits_{S}{\bf F}\cdot d{\bf S}=\displaystyle\iint\limits_{D}\left(-P\dfrac{\partial f}{\partial x}-Q\dfrac{\partial f}{\partial y}+R\right)dA$ para o caso onde $S$ é dada por $y=h(x,z)$ e ${\bf n}$ é o vetor normal unitário que aponta para a esquerda.

$\displaystyle \iint\limits_{S}{\bf F}\cdot d{\bf S}=\iint\limits_{D}\left(P -Q\dfrac{\partial k}{\partial y}-R\frac{\partial k}{\partial z} \right)dA.$

3145

A Lei de Coulomb afirma que a força eletrostática $\mathbf{F}(\mathbf{r})$ que uma partícula com carga $Q$ exerce sobre outra partícula com carga $q$ é dada pela fórmula \[ \mathbf{F}(\mathbf{r}) = \dfrac{q\,Q}{4\pi\epsilon_0\|\mathbf{r}\|^3}\mathbf{r}, \] onde $\mathbf{r}$ é o vetor posição da carga $q$ em relação a $Q$ e $\epsilon_0$ é uma constante positiva (chamada permissividade do meio).

Expresse o campo vetorial $\mathbf{F}(\mathbf{r})$ em forma de coordenadas $\mathbf{F}(x,y,z)$ com $Q$ na origem.
Calcule o trabalho realizado pelo campo vetorial $\mathbf{F}$ sobre uma carga $q$ que se move ao longo de um segmento de reta de $(3,0,0)$ para $(3,1,5)$.

2300

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(1,u,v)$, $0\leq u\leq 1$, $0\leq v \leq 1.$

Região quadrada do plano $x = 1:$ $0 \leq y \leq 1$ e $0 \leq z \leq 1.$

2442

Calcule a integral de superfície $\displaystyle\iint\limits_{S}y dS$, onde $S$ é a parte do parabolóide $y=x^{2}+z^{2}$ que está dentro do cilindro $x^{2}+z^{2}=4.$

$\dfrac{\pi(391\sqrt{17}+1)}{60}.$

2291

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do cilindro $y^{2}+z^{2}=16$ que está entre os planos $x=0$ e $x=5.$

$x = u,$ $y = 4\cos (\theta),$ $z = 4\sin(\theta),$ onde $0 \leq u \leq 5,$ $0 \leq \theta \leq 2\pi.$

2438

Calcule a integral de superfície $\displaystyle\iint\limits_{S}yz dS$, onde $S$ é a parte do plano $x+y+z=1$ que está no primeiro octante.

$\dfrac{\sqrt{3}}{24}.$

2445

Calcule a integral de superfície $\displaystyle\iint\limits_{S}xy dS$, onde $S$ é a superfície com equações paramétricas $x=u-v$, $y=u+v$, $z=2u+v+1$, $0 \leq u \leq 1$, $0 \leq v \leq u.$

3137

Calcule o trabalho realizado pelo campo vetorial \[ \mathbf{F}(x,y,z) = x^2\mathbf{i}+4xy^3\mathbf{j}+y^2x\mathbf{k}\] sobre uma partícula que percorre o caminho $C$ definido como o bordo da superfície $\sigma$ contida no plano $z=y$ e cuja projeção no plano $xy$ corresponde ao retângulo $R=\{(x,y)\in\mathbb{R}^2; 0\leq x\leq 1$,\ $0\leq y\leq 3\}$. O sentido de percurso é tal que a fronteira de $R$ é percorrida no sentido horário.

Note que calcular o trabalho $\displaystyle W= \oint_C\mathbf{F}\cdot\,d\mathbf{r}$ assim diretamente exigiria quatro integrações separadas, uma para cada lado do retângulo. Entretanto, usando o Teorema de Stokes podemos, em vez disso, calcular uma (única!) integral de superfície \[ W= \iint\limits_\sigma\mathrm{rot\,}\mathbf{F}\cdot\mathbf{n}\,dS \] na qual $\sigma$ é tomada com a orientação para baixo, como requerido pelo Teorema de Stokes. Como a superfície $\sigma$ está contida no plano $z=y$ e \[\mathrm{rot\,}\mathbf{F} = \left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ x^2 & 4xy^3 & xy^2 \end{array}\right| = 2xy\mathbf{i}-y^2\mathbf{j}+4y^3\mathbf{k}, \] segue então que \begin{align*} W= \iint\limits_\sigma\mathrm{rot\,}\mathbf{F}\cdot\mathbf{n}\,dS & = \iint\limits_R\mathrm{rot\,}\mathbf{F}\cdot\left( \dfrac{\partial z}{\partial x}\mathbf{i} +\dfrac{\partial z}{\partial y}\mathbf{j} - \mathbf{k}\right)\,dA \\ & = \iint\limits_R\left(2xy\mathbf{i}-y^2\mathbf{j}+4y^3\mathbf{k}\right)\cdot\left(0\mathbf{i}+\mathbf{h}-\mathbf{k}\right)\,dA \\ & = \int_0^1\int_0^3(-y^2-4y^3)\,dydx \\ & = - \int_0^1\left[\dfrac{y^3}{3}+y^4\right]_{y=0}^3\,dx \\ & = -\int_0^1 90\,dx = -90. \end{align*}

2299

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, $(u,v)\in \mathbb{R}^{2}.$.

Paraboloide de rotação $z = x^2 + y^2.$

2626

Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = x{\bf j}$, $S$ a superfície $\{(x,y,z) \in \mathbb{R}^3; 0\leq z\leq 1, x^2+y^2=1,$$x\geq 0, y\geq 0\}$, sendo ${\bf n}$ a normal com componente $x$ positiva.

$0$.

3150

Seja $\mathbf{F}(x,y)= (ye^{xy}-1)\mathbf{i} + xe^{xy}\mathbf{j}.$

Mostre que $\mathbf{F}$ é um campo vetorial conservativo.
Calcule uma função potencial de $\mathbf{F}$.
Calcule o trabalho realizado pelo campo vetorial sobre uma partícula que se move ao longo da curva representada pelas seguintes equações paramétricas \begin{align*} x & = t+ \arcsin(\sin t) \\ y & = \dfrac{2}{\pi}\arcsin(\sin t), \ \left(0\leq t\leq 8\pi\right). \end{align*}

2145

Aplique o Teorema da Divergência para achar $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS,$ sendo ${\bf F}(x,y,z)=y\,\sin x\,{\bf i}+y^{2}z\,{\bf j}+(x+3z)\,{\bf k}$ e $S$ é a superfície da região delimitada pelos planos $x=\pm 1$, $y=\pm 1$ e $z=\pm 1.$

$24.$

2251

Seja $S$ a parte do parabolóide $z=2-x^{2}-y^{2}$ que está acima do plano $z=1.$ Calcule o fluxo do campo vetorial ${\bf F}(x,y,z)=\frac{1}{(x^{2}+y^{2}+z^{2})^{3/2}}(x,y,z)$ através de $S.$

2614

Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.

${\bf F}(x,y,z) = (2xyz-2y,x^2+2x,x^2+2y)$, $C$ é a circunferência $y^2+z^2=1$, $x=2$.

$2\pi$.

2147

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=e^{x}\,\sin y\,{\bf i}+e^{x}\,\cos y\,{\bf j}+yz^{2}\,{\bf k}$ e $S$ é a superfície da caixa delimitada pelos planos $x=0$, $x=1$, $y=0$, $y=1$, $z=0$ e $z=2.$

3148

Seja $G$ um sólido com a superfície $\sigma$ orientada por vetores normais unitários para fora, suponha que $\phi$ tenha derivadas parciais de primeira e segunda ordens contínuas em algum conjunto aberto contendo $G$ e seja $D_{\mathbf{n}}\phi$ a derivada direcional de $\phi$, onde $\mathbf{n}$ é um vetor normal unitário para fora de $\sigma$. Mostre que \[ \iint\limits_\sigma D_{\mathbf{n}}\phi\,dS = \iiint\limits_G\left[\dfrac{\partial^2\phi}{\partial x^2}+ \dfrac{\partial^2\phi}{\partial y^2} + \dfrac{\partial^2\phi}{\partial z^2} \right]\,dV. \]

2409

Calcule a integral de superfície $\displaystyle\iint\limits_{S}\dfrac{z}{\sqrt{1+4x^{2}+4y^{2}}}dS$, onde $S$ é a parte do parabolóide

$z=1-x^{2}-y^{2}$ que se encontra dentro do cilindro $x^{2}+y^{2}\leq 2y.$

Parametrizando a superfície $S$, temos as equações paramétricas:

$x=u, y=v \, \mbox{e} \, z=1-u^{2}-v^{2}.$
Então,
${\bf r}(u,v)=u{\bf i}+v{\bf j}+(1-u^{2}-v^{2}){\bf k}.$
Logo,
$f({\bf r}(u,v))=\dfrac{1-u^{2}-v^{2}}{\sqrt{1-4u^{2}-4v^{2}}},$ ${\bf r}_{u}={\bf i}+0{\bf j}-2u{\bf k}$ e ${\bf r}_{v}=0{\bf i}+{\bf j}-2v{\bf k}.$
Temos que

${\bf r}_{u}\times {\bf r}_{v}=\left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k}\\ 1 & 0 & -2u\\ 0 & 1 & -2v \end{array} \right| = 2u{\bf i}+2v{\bf j}+{\bf k}$,

implicando que $|{\bf r}_{u}\times {\bf r}_{v}|=\sqrt{(2u)^{2}+(2v)^{2}+1^{2}}=\sqrt{1+4u^{2}+4v^{2}}.$ Assim,

$\displaystyle\iint\limits_{S}\dfrac{z}{\sqrt{1+4x^{2}+4y^{2}}}dS=\displaystyle\iint\limits_{D} f({\bf r}(u.v))|{\bf r}_{u}\times {\bf r}_{v}| du dv$ $=\displaystyle\iint\limits_{D} \frac{1-u^{2}-v^{2}}{\sqrt{1-4u^{2}-4v^{2}}} \sqrt{1+4u^{2}+4v^{2}} du dv=\displaystyle\iint\limits_{D}(1-u^{2}-v^{2})du dv$.
Notemos que
$D=\{(u,v)| u^{2}+v^{2}\leq 2v\}=\{(u,v)|u^{2}+(v-1)^{2}\leq 1\}.$
Em coordenadas polares teremos que
$u=r\cos \theta, v-1=r\sin \theta,$
$du dv=\left| \begin{array}{cc}
\dfrac{\partial u}{\partial r} & \dfrac{\partial u}{\partial \theta}\\
\dfrac{\partial v}{\partial r} & \dfrac{\partial v}{\partial \theta}
\end{array} \right|$, $ dr d\theta=\left| \begin{array}{cc} \cos \theta & -r\sin \theta\\ \sin \theta & r\cos \theta \end{array} \right| \, e \, du dv=r dr d\theta.$

Como $u^{2}+u^{2}=2u \Rightarrow r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=r\sin \theta \Rightarrow r=2\sin \theta,$ então $0\leq r \leq 2\sin \theta \, \mbox{e} \, 0 \leq \theta \leq \pi.$
Logo
$\displaystyle\iint\limits_{S}\dfrac{z} {\sqrt{1+4x^{2}+4y^{2}}}dS=\displaystyle\int_{0}^{\pi}\displaystyle\int_{0}^{2\sin \theta}(1-r^{2}\cos^{2} \theta-r^{2}\sin^{2}\theta)r dr d\theta$

$\displaystyle\int_{0}^{\pi}\displaystyle\int_{0}^{2\sin \theta}(1-r^{2})r dr d\theta=\displaystyle\int_{0}^{\pi}\int_{0}^{2\sin \theta}(r-r^{3})dr d\theta$ $=\displaystyle\int_{0}^{\pi}(2\sin^{2}\theta-4\sin^{4}\theta)\bigg|_{0}^{2\sin \theta}d\theta=2\int_{0}^{\pi}\sin^{2}\theta d\theta-4\int_{0}^{\pi}\sin^{4}\theta$

$=2\cdot\left(\dfrac{\theta}{2}-\frac{1}{4}\sin 2\theta\right)\bigg|_{0}^{\pi}-4\cdot \left(-\dfrac{1}{4}\sin^{3}
\theta \cos \theta+\dfrac{3}{8}\theta-\dfrac{3}{16}\sin 2\theta\right)\bigg|_{0}^{\pi}$
$=2\cdot \dfrac{\pi}{2}-4\cdot\left(\dfrac{3}{8}\pi\right)=-\dfrac{\pi}{2}.$

3042

Determine a representação paramétrica do toro obtido girando em torno do eixo $z$ o círculo do plano $xz$ com centro em $(b,0,0)$ e raio $a < b.$ [Sugestão: tome como parâmetros os ângulos $\theta$ e $\alpha$ mostrados na figura.]
Use a representação paramétrica do item anterior para achar a área do toro.

$x = b\cos(\theta) + a\cos(\alpha)\cos(\theta),$ $y = b\sin(\theta) + a\cos(\alpha)\sin(\theta),$ $z = a\sin(\alpha),$ onde $0 \leq \alpha \leq 2\pi,$ $0 \leq \theta \leq 2\pi.$
$4\pi^2 ab.$

2511

Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$

${\bf F}=2{\bf i}+5{\bf j}+3{\bf k}$; $S$ é a parte do cone $z=(x^{2}+y^{2})^{1/2}$ interior ao cilindro $x^{2}+y^{2}=1.$

$3\pi.$

2340

Determine a área da superfície dada pela parte do plano $x+2y+z=4$ que está dentro do cilindro $x^{2}+y^{2}=4$.

$4\sqrt{6}\pi.$

2140

Demonstre a identidade $\displaystyle\iint\limits_{S}\mbox{rot}\, {\bf F}\cdot dS=0$, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.

Pelo Teorema do Divergente, temos
$\displaystyle\iint\limits_{ S}\mbox{rot} {\bf F}\cdot dS = \iiint\limits_{ E}\mbox{div} (\mbox{rot} {\bf F})\,dV,$
em que $E$ é o sólido que tem $S$ como fronteira. Observe que
\begin{align*}
&\mbox{div} (\mbox{rot} {\bf F}) =\\ & \frac{\partial}{\partial x}(R_y - Q_z) + \frac{\partial}{\partial y}(P_z - R_x) + \frac{\partial}{\partial z}(Q_x - P_y) \\ & R_{xy} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy} = 0,
\end{align*}
pois, como as derivadas de segunda ordem são contínuas, temos, pelo Teorema de Clairaut, que $P_{yz} = P_{zy}$, $Q_{zx} = Q_{xz}$ e $R_{xy} = R_{yx}$. Portanto,

$\displaystyle\iint\limits_{S}\mbox{rot}{\bf F}\cdot dS=0.$

2624

Utilizando o Teorema de Stokes, transforme a integral $\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.

${\bf F}(x,y,z) = y{\bf i} + x^2{\bf j}+z{\bf k}$, $S$ a superfície parametrizada por ${\bf R}(u,v) = (u,v,2u+v+1)$, $u\geq 0$, $u+v\leq 2$, sendo ${\bf n}$ a normal apontando para baixo.

$-\dfrac{2}{3}.$

2337

Determine a área da superfície dada pela parte da superfície $y=4x+z^{2}$ que está entre os planos $x=0$, $x=1$, $z=0$ e $z=1.$

$\dfrac{\sqrt{21}}{2} + \dfrac{17}{4} \left( \ln(2 + \sqrt{21}) - \ln(\sqrt{17}) \right).$

2296

Determine uma representação paramétrica para a superfície descrita a seguir. A porção da esfera $x^{2}+y^{2}+z^{2}=3$ entre os planos $z=\sqrt{3}/2$ e $z=-\sqrt{3}/2.$

$x = \sqrt{3}\sin(\phi)\cos(\theta),$ $y = \sqrt{3}\sin(\phi)\sin(\theta),$ $z = \sqrt{3}\cos(\phi),$ onde $\dfrac{\pi}{3} \leq \phi \leq \dfrac{2\pi}{3}$ e $0 \leq \theta \leq 2\pi.$

2425

Se $S$ é uma esfera e ${\bf F}$ satisfaz as hipóteses do Teorema de Stokes, mostre que $\displaystyle\iint\limits_{S}\mbox{rot}{\bf F} \cdot d{\bf S} = 0$.

2141

Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$

${\bf F}(x,y,z)=3x\,{\bf i}+xy\,{\bf j}+2xz\,{\bf k}$, $E$ é o cubo limitado pelos planos $x=0$, $x=1$, $y=0$, $y=1$, $z=0$ e $z=1.$

$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = \dfrac{9}{2}.$

2190

Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $S$ a fronteira de $B$ com normal exterior ${\bf n}$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, 0\leq x\leq 1,\,0\leq y\leq x$ e $0\leq z\leq 4\}$ e ${\bf u}=xy\,{\bf i}+yz\,{\bf j}+z^{2}\,{\bf k}.$

$\dfrac{13\pi}{20}.$

2316

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u+v$, $y=3u^{2}$, $z=u-v$; $(2,3,0).$

$3x - y + 3z = 3.$

2302

Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,\sqrt{1-u^{2}-v^{2}},v)$, $u^{2}+v^{2}\leq 1.$

Semi superfície esférica $x^2 + y^2 + z^2 = 1,$ $y \geq 0.$

2616

Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial ${\bf F}$ dado e a superfície $S$.

${\bf F}(x,y,z) = y{\bf i} + z{\bf j} + x{\bf k}$, $S$ é o hemisfério $x^2+y^2+z^2=1$, $y \geq 0$, orientado na direção positiva do eixo $y$.

$\displaystyle\int_{C} {\bf F} \cdot d{\bf R} = \displaystyle\iint_{S} \mbox{rot} {\bf F} \cdot d{\bf S} = -\pi$.

2287

Determine uma representação paramétrica para a superfície descrita a seguir. O plano que passa pelo ponto $(1,2,-3)$ e contém os vetores ${\bf i}+{\bf j}-{\bf k}$ e ${\bf i}-{\bf j}+{\bf k}.$

$x= 1 + u + v,$ $y = 2 + u - v,$ $z = 3 - u + v.$

2149

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3xy^{2}\,{\bf i}+xe^{z}\,{\bf j}+z^{3}\,{\bf k}$ e $S$ é a superfície do sólido delimitado pelo cilindro $y^{2}+z^{2}=1$ e pelos planos $x=-1$ e $x=2.$

2323

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,2-u-v)$ e $u^{2}+v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\pi \sqrt{3}.$

2448

Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ sendo $g(x,y,z)=x^{2}+y^{2}+z^{2}$ e $S$ a parte do plano $z=y+4$ interior ao cilindro $x^{2}+y^{2}=4.$

$76\pi \sqrt{2}.$

2591

Seja ${\bf F}$ um campo inverso do quadrado, ou seja, ${\bf F}(r)=cr/|r|^{3}$ para alguma constante $c$, onde $r=x{\bf i}+y{\bf j}+z{\bf k}.$ Mostre que o fluxo de ${\bf F}$ por uma esfera $S$ com centro na origem é independente do raio de $S.$

$\displaystyle \iint\limits_{S}{\bf F}\cdot d \bf S = 4\pi c.$

2289

Determine uma representação paramétrica para a superfície descrita a seguir. A parte do paraboloide elíptico $x+y^{2}+2z^{2}=4$ que está em frente ao plano $x=0.$

$y = u,$ $z = v,$ $x = 4 - u^2 - 2v^2,$ onde $u^{2} + 2v^2 \leq 4.$

2286

Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=2\,\sin u\,{\bf i}+3\,\cos u\,{\bf j}+v\,{\bf k}$, $0\leq v\leq 2.$.

$\dfrac{x^2}{4} + \dfrac{y^{2}}{9} = 1,$ com $0\leq z \leq 2.$

3151

Enuncie o Teorema da Divergência e o Teorema de Stokes, incluindo todas as hipóteses envolvidas.

2318

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, no ponto ${\bf r}(1,1).$

$(x,y,z) = (1,1,2) + s(1,0,2) + t(0,1,2),$ $s,t \in \mathbb{R}.$

3132

Encontre a massa da lâmina descrita como sendo a porção do cilindro circular $x^2+z^2=4$ que fica diretamente acima do retângulo $\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq x\leq 1,\ 0\leq y\leq 4\}$ e tem densidade $\delta_0$ constante.

$\dfrac{4}{3}\pi\delta_0$

2348

Calcule a área da parte da superfície cilíndrica $z^{2}+x^{2}=4$ que se encontra dentro do cilindro $x^{2}+y^{2}\leq 4$ e acima do plano $xy.$

$16.$

2341

Determine a área da superfície dada pela porção do cone $z=2\sqrt{x^{2}+y^{2}}$ entre os planos $z=2$ e $z=6.$

$8\sqrt{5}\pi.$

2462

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=xze^{y}{\bf i}-xze^{y}{\bf j}+z{\bf k}$ e $S$ é a parte do plano $x+y+z=1$ no primeiro octante, com orientação para baixo.

$-\dfrac{1}{6}.$

2193

Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, x^{2}+y^{2}\leq 1,\,x^{2}+y^{2}\leq z \leq 5-x^{2}-y^{2}\}$ e ${\bf u}=3xy\,{\bf i}-\dfrac{3}{2}y^{2}\,{\bf j}+z\,{\bf k}.$

$36\pi.$

2188

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=2xz\,{\bf i}+xyz\,{\bf j}+yz\,{\bf k}$ e $S$ é a superfície da região delimitada pelos planos coordenados e os planos $x+2z=4$ e $y=2.$

2344

Determine, mas não calcule, a integral dupla da área da superfície com as equações paramétricas $x=au\cos v$, $y=bu\sin v$, $z=u^{2}$, $0\leq u\leq 2$, $0\leq v\leq 2\pi.$
Elimine os parâmetros para mostrar que a superfície é um paraboloide elíptico e escreva outra integral dupla que forneça sua área.

$\displaystyle \int^{2\pi}_{0}\int_{0}^{2} \sqrt{4b^2 u^4 \cos^{2}v + 4a^2 u^4 \sin^{2} v + a^2 b^2 u^2} dudv.$
$\displaystyle \int_{-2a}^{2a} \int^{b \sqrt{4 - \frac{x^2}{a^2}}}_{-b \sqrt{4 - \frac{x^2}{a^2}}} \sqrt{1 + \left(2\frac{x}{a^2}\right)^{2} + \left(2\frac{y}{b^2} \right)^{2}} dydx.$

2150

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=x^{3}y\,{\bf i}-x^{2}y^{2}\,{\bf j}-x^{2}yz\,{\bf k}$ e $S$ é a superfície do sólido delimitado pelo hiperbolóide $x^{2}+y^{2}-z^{2}=1$ e pelos planos $z=-2$ e $z=2.$

2618

Uma partícula se move ao longo de segmentos de reta da origem aos pontos $(1,0,0)$, $(1,2,1)$, $(0,2,1)$ e de volta para a origem sob a influência do campo de forças ${\bf F}(x,y,z) = z^2{\bf i} + 2xy{\bf j} + 4y^2{\bf k}.$ Encontre o trabalho feito.

$3$.

2189

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(5x^{3}+12xy^{2})\,{\bf i}+(y^{3}+e^{y}\,\sin z)\,{\bf j}+(5z^{3}+e^{y}\,\cos z)\,{\bf k}$ e $S$ é a superfície do sólido entre as esferas $x^{2}+y^{2}+z^{2}=1$ e $x^{2}+y^{2}+z^{2}=2.$

3041

Faça uma correspondência entre as equações e os gráficos identificados a seguir, enumerador respectivamente por $I-VI$, e justifique sua resposta. Determine quais famílias de curvas da grade têm $u$ constante e quais têm $v$ constante.

${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+v{\bf k}.$
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+\sin u{\bf k}$, $-\pi\leq u\leq \pi.$
${\bf r}(u,v)=\sin v{\bf i}+\cos u\sin 2v{\bf j}+\sin u\sin 2v{\bf k}.$
$x=(1-u)(3+\cos v)\cos 4\pi u$, $y=(1-u)(3+\cos v)\sin 4\pi u$,$z=3u+(1-u)\sin v.$
$x=\cos^{3}u\cos^{3}v$, $y=\sin^{3}u\cos^{3}v$, $z=\sin^{3}v.$
$x=(1-|u|)\cos v$, $y=(1-|u|)\sin v$, $z=u.$

IV.
I.
II.
V.
III.
VI

3134

Considere o campo vetorial \[\mathbf{F}(x,y,z)=(x-z)\mathbf{i}+(y-x)\mathbf{j}+(z-xy)\mathbf{k}. \]

Use o Teorema de Stokes para encontrar a circulação em torno do triângulo de vértices $A=(1,0,0)$, $B=(0,2,0)$ e $C=(0,0,1)$, orientado no sentido anti-horário quando visto da origem para o primeiro octante.
Encontre a densidade de circulação de $\mathbf{F}$ na origem na direção de $\mathbf{k}$, ou seja, $\displaystyle\mathrm{rot\,}\mathbf{F}(\mathbf{0})\cdot\mathbf{k}$.
Encontre o vetor unitário $\mathbf{n}$ tal que a densidade de circulação de $\mathbf{F}$ na origem seja máxima na direção de $\mathbf{n}$.

$\dfrac{3}{2}$
$-1$
$\displaystyle \mathbf{n}= -\dfrac{1}{\sqrt{2}}\mathbf{j} -\dfrac{1}{\sqrt{2}}\mathbf{k} $

2321

Determine uma representação paramétrica ${\bf r}:D\subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}$ do paraboloide elíptico $z=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}.$
Calcule a equação do plano tangente à superfície paramétrica dada no item (a) no ponto $(-a\pi,0,\pi^{2}).$

$x = u,$ $y = v,$ $z = \dfrac{u^{2}}{a^{2}}+\dfrac{v^{2}}{b^{2}},$ onde $u,v \in \mathbb{R}.$
$2\pi(x + a\pi) + a(z - \pi^{2}) = 0.$

2268

Determine a área da superfície dada pela parte de baixo da esfera $x^{2}+y^{2}+z^{2}=2$ cortada pelo cone $z=\sqrt{x^{2}+y^{2}}.$

Sejam

$$\left \{\begin{array}{cc}x=r\,\sin \phi\,\cos \theta\\y=r\,\sin \phi\,\sin \theta\\z=r\,\cos \phi\\\end{array}\right. \Rightarrow r=\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{2},\, \mbox{na\,esfera}.$$

Temos que

$$x^{2}+y^{2}+z^{2}=2 \mbox{e}\,\,\,\, z=\sqrt{x^{2}+y^{2}}\Rightarrow z^{2}+z^{2}=2\Rightarrow z^{2}=1\Rightarrow z=1\,(\mbox{pois}\, z\geq 0).$$

Logo, $\phi=\frac{\pi}{4}.$ Para a parte inferior da esfera cortado pelo cone, temos que $\phi=\pi.$

Então,

$$r(\phi,\theta)=(\sqrt{2}\,\sin \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\sin \theta)\,{\bf j}+(\sqrt{2}\,\cos \phi)\,{\bf k},$$

$$\frac{\pi}{4}\leq \phi\leq \pi\,\,\,\, \mbox{e}\,\,\,\, 0\leq \theta \leq 2\pi.$$

Isso implica que

$$r_{\phi}(\phi,\theta)=(\sqrt{2}\,\cos \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\cos \phi\,\sin \theta)\,{\bf j}-(\sqrt{2}\,\sin \phi)\,{\bf k}$$

e

$$r_{\theta}(\phi,\theta)=(-\sqrt{2}\,\sin \phi,\,\sin\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\cos \theta)\,{\bf j}+0\,{\bf k}$$

Logo,

$$\begin{array}{rcl}r_{\phi}\times r_{\theta}&=&\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\\sqrt{2}\,\cos \phi\,\cos \theta & \sqrt{2}\,\cos \phi\,\sin \theta& -\sqrt{2}\,\sin \phi\\-\sqrt{2}\,\sin \phi\,\sin \theta & \sqrt{2}\,\sin \phi\,\cos \theta & 0\end{array}\right|\\&=&(2\,\sin^{2}\phi\,\cos \theta)\,{\bf i}+(2\sin^{2}\phi\,\sin \theta)\,{\bf j}+(2\,\sin \phi \,\cos \phi)\,{\bf k}.\\\end{array}$$

Isso resulta que

$$\begin{array}{rcl}|r_{\phi}\times r_{\theta}|&=&\sqrt{4\sin^{2}\phi\,\cos^{2}\theta+4\,\sin^{4}\,\sin^{2}\theta+4\sin^{2}\phi\,\cos^{2}\phi}\\&=&\sqrt{4\,\sin^{2}\phi}=2|\sin\phi|=2\sin \phi \bigg(\mbox{pois},\, \frac{\pi}{4}\leq \phi \leq \pi\bigg).\end{array}$$

Assim,

$$A=\iint\limits_{ D}|r_{\phi}\times r_{\theta}|\,dA=\int_{\frac{\pi}{4}}^{\pi}\int_{0}^{2\pi}2\sin \phi\, d\theta d \phi=2\int_{\frac{\pi}{4}}^{\pi}\sin \phi\,d\phi \cdot \int_{0}^{2\pi}d\theta$$

$$=2\cdot (-\cos \phi)\bigg|_{\frac{\pi}{4}}^{\pi}\cdot \theta\bigg|_{0}^{2\pi}=2\cdot \bigg(1-\frac{\sqrt{2}}{2}\bigg)\cdot 2\pi=4\pi\bigg(1-\frac{\sqrt{2}}{2}\bigg)=\pi(4-2\sqrt{2})$$

2328

Determine a área da superfície dada pela parte do plano $3x+2y+z=6$ que está no primeiro octante.

$3\sqrt{14}.$

3033

Dados um hemisfério $H$ e uma parte $P$ de um paraboloide, suponha que ${\bf F}$ seja um campo vetorial sobre $\mathbb{R}^3$ cujas componentes tenham derivadas parciais contínuas. Explique por que

$$\displaystyle\iint\limits_{H}\mbox{rot}{\bf F}\cdot{\bf S} = \iint\limits_{P}\mbox{rot}{\bf F}\cdot{\bf S}.$$

Note que $H$ e $P$ satisfazem as hipóteses do Teorema de Stokes. Logo,
$$\displaystyle \iint \limits_{H} \mbox{rot } {\bf F} \cdot {\bf S} = \int \limits_{C} {\bf F} \cdot d{\bf r} = \iint \limits_{P} \mbox{rot }{\bf F}\cdot{\bf S},$$

onde $C$ é a curva de fronteira.

3141

Supondo que $\sigma$ e $G$ satisfaçam as hipóteses do Teorema da Divergência e que $f$ e $g$ sejam funções suficientemente regulares, prove as seguintes identidades (de Green):

\[\iint\limits_\sigma\left(f\nabla g\right)\cdot\mathbf{n}\,dS = \iiint\limits_G\left( f\Delta g+\nabla f\cdot\nabla g\right)\,dV, \]
\[\iint\limits_\sigma\left(f\nabla g-g\nabla f\right)\cdot\mathbf{n}\,dS = \iiint\limits_G\left( f\Delta g- g\Delta f\right)\,dV, \] onde $\displaystyle \Delta f= \dfrac{\partial^2f}{\partial x^2}+\dfrac{\partial^2f}{\partial y^2}+\dfrac{\partial^2f}{\partial z^2}$ é denominado Laplaciano de $f$.

2324

Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$ e $u^{2}+v^{2}\leq 4.$. (Sugerimos ao leitor desenhar a imagem da superfície.)

$\dfrac{\pi}{6}(17 \sqrt{17} - 1).$

2043

Aplique o Teorema da Divergência para achar $\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS.$, sendo ${\bf F}(x,y,z)=y^{3}e^{z}\,{\bf i}-xy\,{\bf j}+x \cdot \arctan y\,{\bf k}$ e $S$ a superfície da região delimitada pelos planos coordenados e o plano $x+y+z=1.$

Pelo Teorema do Divergente, temos
$$\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS = \displaystyle\iiint\limits_{E}\text{div }{\bf F}\,dV,$$
em que $E$ é o sólido

que pode ser escrito como
$E = \{(x,y,z) \in \mathbb{R}^3: 0 \leq x \leq 1, 0 \leq y \leq 1-x \mbox{ e } 0 \leq z \leq 1-x-y\}.$
Observe que
\begin{array}{rcl}\text{div }{\bf F} & = & \dfrac{\partial}{\partial x}(y^3e^z) + \dfrac{\partial}{\partial y}(-xy) + \dfrac{\partial}{\partial z}(x\arctan{y}) \\& = & 0 - x + 0 \\& = & -x.\end{array}
Assim,
\begin{array}{rcl}\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS & = & \displaystyle\iiint\limits_{E}{\bf F}\,dV \\& = & \iiint\limits_{E}-x\,dV \\& = & \int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}-x\,dz dy dx \\& = & \int_{0}^{1}\int_{0}^{1-x}-x(1-x-y)\,dy dx \\& = & \int_{0}^{1}\left(-\frac{x}{2}+x^2-\frac{x^3}{3}\right)\,dx \\& = & -\frac{1}{12}.\end{array}

2606

Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$

${\bf F}(x,y,z) = xyz{\bf i} + xy{\bf j} + x^2yz{\bf k}$ e $S$ é formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices $(\pm 1,\pm 1,\pm 1)$, com orientação para fora.

$0.$

2461

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=xy{\bf i}+yz{\bf j}+zx{\bf k}$ e $S$ é a parte do parabolóide $z=4-x^{2}-y^{2}$ que está acima do quadrado $0\leq x\leq 1$, $0\leq y\leq 1$, com orientação para cima.

$\dfrac{713}{180}.$

2541

Encontre o fluxo do campo ${\bf F}$ ao longo da porção da superfície dada no sentido especificado.

${\bf F}(x,y,z)=-{\bf i}+2{\bf j}+3{\bf k}$; $S$ é a superfície retangular $z=0$, $0\leq x\leq 2$, $0\leq y \leq 3$, sentido ${\bf k}.$

$18.$

2270

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u-v,u^{2}+v^{2},uv)$, no ponto ${\bf r}(1,1).$

Temos que ${\bf r}(u,v)=\underbrace{(u-v)}_{x(u,v)}\,{\bf i}+\underbrace{(u^{2}+v^{2})}_{y(u,v)}\,{\bf j}+\underbrace{uv}_{z(u,v)}\,{\bf k}$

Primeiro, vamos calcular os vetores tangentes:

$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& \,{\bf i}+2u\,{\bf j}+v\,{\bf k}\end{array}$$

e

$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& -\,{\bf i}+2v\,{\bf j}+u\,{\bf k}\end{array}$$

Assim, o vetor normal ao plano tangente é:

$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i}& {\bf j}&{\bf k}\\1 & 2u & v\\-1 & 2v & u\\\end{array}\right|\\&=&(-2u^{2}-2v^{2})\,{\bf i}-(u+v)\,{\bf j}+(2u+2v)\,{\bf k}\end{array}$$

Como $u=1$ e $v=1$ temos que o vetor normal é $-4\,{\bf i}-2\,{\bf j}+4\,{\bf k}.$

Portanto, uma equação do plano tangente no ponto ${\bf r}(1,1)=(0,2,1)$ é

$$-4\cdot(x-0)-2\cdot(y-2)+4\cdot (z-1)=0$$

$$-4x-2y+4+4z-4=0$$

$$-4x-2y+4z=0 \mbox{ou} 2x+y-2z=0$$

2466

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=x^{2}{\bf i}+y^{2}{\bf j}+z^{2}{\bf k}$ e $S$ é a fronteira do semicilindro sólido $0 \leq z \leq \sqrt{1-y^{2}}$, $0 \leq x \leq 2.$

$2\pi + \dfrac{8}{3}.$

2469

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=(x+y){\bf i}+z{\bf j}+xz{\bf k}$ e $S$ é a superfície do cubo de vértices $(\pm 1,\pm 1, \pm 1).$

$8.$

3133

Encontre a massa da lâmina descrita como sendo a porção do parabolóide $2z=x^2+y^2$ que fica dentro do cilindro $x^2+y^2=8$ e tem densidade $\delta_0$ constante.

2267

Determine a área da superfície dada pela parte do paraboloide hiperbólico $z=y^{2}-x^{2}$ que está entre os cilindros $x^{2}+y^{2}=1$ e $x^{2}+y^{2}=4.$

Temos que $z=f(x,y)=y^{2}-x^{2}$ com $1\leq x^{2}+y^{2}\leq 4$. Então,

$$A(S)=\iint\limits_{ D}\sqrt{1+\bigg(\frac{\partial z}{\partial x}\bigg)^{2}+\bigg(\frac{\partial z}{\partial y}\bigg)^{2}}\,dA$$

$$=\iint\limits_{ D}\sqrt{1+(2y)^{2}+(-2x)^{2}}\,dA=\iint\limits_{ D}\sqrt{1+4y^{2}+4x^{2}}\,dA.$$

Usando coordenadas polares temos que

$$x=r\,\cos \theta,\,\,\,\,\, y=r\,\sin \theta \Rightarrow 0\leq \theta\leq \frac{\pi}{2}\,\, \mbox{e}\,\, 1\leq r \leq 2.$$

Assim,

$$A(S)=\int_{0}^{2\pi}\int_{1}^{2}\sqrt{1+4r^{2}}\,r\,dr\,d\theta=\int_{0}^{2\pi}d\theta \cdot \underbrace{\int_{1}^{2}\sqrt{1+4r^{2}}r\,dr}_{\substack{u=1+4r^{2}\\ du=8r\,dr}}$$

$$=\theta\bigg|_{0}^{2\pi}\cdot \int_{5}^{17}u^{1/2}\cdot r\cdot \frac{du}{8r}=2\pi\cdot \frac{1}{8}\int_{5}^{17}u^{1/2}\,du=\frac{\pi}{4}\cdot \frac{2}{3}u^{3/2}\bigg|_{5}^{17}$$

$$=\frac{\pi}{6}\cdot(17^{3/2}-5^{3/2}).$$

2319

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(\arctan (uv),e^{u^{2}-v^{2}},u-v)$, no ponto ${\bf r}(1,-1).$

$(x,y,z) = \left(-\dfrac{\pi}{4},1,2\right) + s\left(-\dfrac{1}{2},2,1\right) + t\left(\dfrac{1}{2},2,-1\right),$ $s,t \in \mathbb{R}.$

2148

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3xy^{2}\,{\bf i}+xe^{z}\,{\bf j}+z^{3}\,{\bf k}$, $S$ é a superfície do sólido delimitado pelo cilindro $y^{2}+z^{2}=1$ e pelos planos $x=-1$ e $x=2.$

2250

Verifique que $\mbox{div} {\bf E}=0$ para o campo elétrico ${\bf E}({\bf x})=\dfrac{\epsilon Q}{|{\bf x}|^{3}}{\bf x}.$

2151

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(\cos z+xy^{2})\,{\bf i}+xe^{-z}\,{\bf j}+(\sin y+x^{2}z)\,{\bf k}$ e $S$ é a superfície do sólido limitado pelo parabolóide $z=x^{2}+y^{2}$ e pelo plano $z=4.$

2342

Determine a área da superfície dada pela porção do cilindro $x^{2}+y^{2}=1$ entre os planos $z=1$ e $z=4.$

$6\pi.$

2542

Encontre o fluxo do campo ${\bf F}$ ao longo da porção da superfície dada no sentido especificado.

${\bf F}(x,y,z)=yx^{2}{\bf i}-2{\bf j}+xz{\bf k}$; $S$ é a superfície retangular $y=0$, $-1\leq x \leq 2$, $2\leq z \leq 7$, sentido $-{\bf j}.$

$30.$

2195

Seja ${\bf F}=(z tg^{-1}(y^{2}),z^{3}\ln(x^{2}+1),z).$ Determine o fluxo de ${\bf F}$ através da parte do parabolóide $x^{2}+y^{2}+z=2$ que está acima do plano $z=1$ e está orientada para cima. (Observe que a superfície acima não é fechada.)

3142

Considere o campo vetorial $\mathbf{F}(x,y,z)=(x-y)\mathbf{i} + (y-z)\mathbf{j}+(z-x)\mathbf{k}$ e a superfície $\sigma$
descrita como sendo a porção do plano $x+y+z=1$ no primeiro octante e orientada para cima. Verifique o Teorema de Stokes
calculando, separadamente, a integral de linha e a integral dupla e, em seguida, comparando os valores.

$\dfrac{3}{2}$

2446

Calcule a integral de superfície $\displaystyle\iint\limits_{S}y dS$, onde $S$ é a superfície com equações paramétricas $x=u$, $y=v$, $z=1-u^{2}$, $0\leq u\leq 1$, $0\leq v\leq \sqrt{u}.$

2317

Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u^{2}$, $y=v^{2}$, $z=uv$; $u=1$, $v=1.$

$x + y - 2z = 0.$

2470

Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).

${\bf F}(x,y,z)=x{\bf i}-y{\bf j}+z{\bf k}$ e $S$ é a superfície do sólido delimitado pelos gráficos de $z=x^{2}+y^{2}$ e $z=4.$

$8\pi.$

2285

Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=(u+v)\,{\bf i}+(3-v)\,{\bf j}+(1+4u+5v)\,{\bf k}.$.

$4x - y - z = -4.$

2450

Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ onde $g(x,y,z)=(x^{2}+y^{2}+z^{2})^{1/2}$ e $S$ é a porção do parabolóide $2z=x^{2}+y^{2}$ interior ao cilindro $x^{2}+y^{2}=2y.$

$\dfrac{5\pi}{2}.$

Exercícios

Integrais de superfície