Exercícios
Teorema fundamental das integrais de linha
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine se ${\bf F}(x,y)=(2x-3y)\,{\bf i}+(-3x+4y-8)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = x^2 - 3xy + 2y^2 -8y + K.$
Seja ${\bf F}(x,y)=(e^{x}\,\cos y+y, x-e^{x}\,\sin y)$. Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é o arco de circunferência que une o ponto $(-\sqrt{2}/2, \sqrt{2}/2)$ ao ponto $(1,0)$. Veja a figura abaixo.
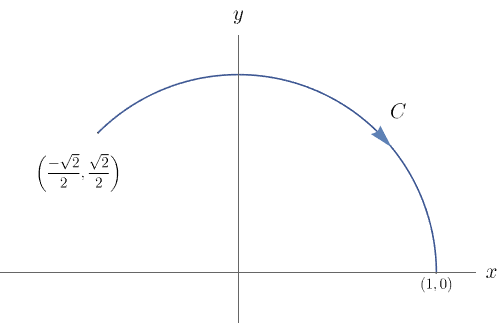
Notemos que ${\bf F}$ é um campo vetorial conservativo, pois: ${\bf F}$ é definido em todo $\mathbb{R}^{2}$; $P(x,y)=e^{x}\,\cos y+y$ e $Q(x,y)=x-e^{x}\,\sin y$ possuem derivadas parciais de primeira ordem contínuas; $\dfrac{\partial P}{\partial y}(x,y)=1-e^{x}\,\sin y=\dfrac{\partial Q}{\partial x}(x,y).$
Sendo $F$ conservativo, existe $f$ tal que $\nabla f={\bf F}.$ Vamos encontrar $f$. Temos que
$$f_{x}(x,y)=P(x,y) \mbox{ e } f_{y}(x,y)=Q(x,y).$$
Então,
$$\label{(2)}f_{x}(x,y)=e^{x}\,\cos y+y\Rightarrow f(x,y)=e^{x}\,\cos y+y+g(y).$$
Logo, temos que
$$f_{y}(x,y)=-e^{x}\,\sin y+x+g'(y).$$
Como $f_{y}(x,y)=Q(x,y)$, obtemos que
$$-e^{x}\,\sin y+x+g'(y)=x-e^{x}\,\sin y\Rightarrow g'(y)=0\Rightarrow g(y)=C.$$
Assim, tomando $C=0$ segue que
$$f(x,y)=e^{x}\,\cos y+xy.$$
Do resultado acima e pelo Teorema Fundamental da Integral de Linha, temos que
$$\int_{C}{\bf F}\cdot d{\bf r}=f(1,0)-f\bigg(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\bigg)=e-e^{-\frac{\sqrt{2}}{2}}\,\cdot\cos\bigg(\frac{\sqrt{2}}{2}\bigg)+\frac{1}{2}.$$
Calcule a integral de linha
$$\int_{C}{\bf F}\cdot d{\bf r}=\int_{C}{\bf F}\cdot r'(t)\,dt$$
onde ${\bf F}=(2xyz^{3},x^{2}z^{3},3x^{2}yz^{2})$ e $C$ é a curva dada por $r(t)=(\sin^{6}t,1-\cos t, e^{t(t-\pi/2)}$, $0\leq t\leq \pi/2.$ (Dica: verifique se ${\bf F}$ é conservativo.)
$1.$
Dados ${\bf F}(x,y,z)=yz\,{\bf i}+xz\,{\bf j}+(xy+2z)\,{\bf k}$, $C$ é o segmento de reta de $(1,0,-2)$ a $(4,6,3).$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = xyz + z^{2};$
$77.$
Determine se ${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = \dfrac{x^{2} + y^{2} + z^{2}}{2} + K.$
Suponha que ${\bf F}$ seja um campo vetorial inverso do quadrado, ou seja,
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}.$ Determine o trabalho realizado por ${\bf F}$ ao mover um objeto de um ponto $P_{1}$ por um caminho para um ponto $P_{2}$ em termos da distância $d_{1}$ e $d_{2}$ desses pontos à origem.
$c\left(\dfrac{1}{d_{1}} - \dfrac{1}{d_{2}}\right).$
Calcule $\displaystyle\int_{C}\dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy$ onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida no semiplano $y>0$, tal que $C(0)=(1,1)$ e $C(1)=(-2,3).$
$\pi.$
Mostre que, se um campo vetorial ${\bf F}=P\,{\bf i}+Q\,{\bf j}+R\,{\bf k}$ é conservativo e $P$, $Q$, $R$ têm derivadas parciais de primeira ordem contínuas, então
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}, \,\,\,\,\,\frac{\partial P}{\partial z}=\frac{\partial R}{\partial x},\,\,\,\,\,\frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}$$
Se $f$ é uma função potencial de $\mathbf{F},$ então $f_{x} = P,$ $f_{y} = Q$ e $f_{z} = R.$ Como $P, Q$ e $R$ possuem derivadas parciais de primeira ordem contínuas, então pelo Teorema de Clairaut, temos $f_{xy} = f_{yx},$ $f_{yz} = f_{zy}$ e $f_{xz} = f_{zx}.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=2y^{3/2}\,{\bf i}+3x\sqrt{y}\,{\bf j}$ ao mover um objeto de $P(1,1)$ a $Q(2,4).$
$30.$
Seja ${\bf F}=\nabla f$, onde $f(x,y)=\sin(x-2y)$. Determine curvas $C_{1}$ e $C_{2}$ que não sejam fechadas e satisfaçam a equação.
$\displaystyle\int_{C_{1}}{\bf F}\cdot d{\bf r}=0$
$\displaystyle\int_{C_{2}}{\bf F}\cdot d{\bf r}=1$
$\mathbf{r}(t) = \pi t \mathbf{i} + \pi t \mathbf{j},$ $0 \leq t \leq 1.$
$\mathbf{r}(t) = \dfrac{\pi}{2} t \mathbf{i},$ $0 \leq t \leq 1.$
Determine se ${\bf F}(x,y)=y\,{\bf i}+x\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = xy + K.$
Considere o campo
$${\bf F}(x,y,z)=(e^{z},2yz, xe^{z}+y^{2}).$$
Verifique se o campo ${\bf F}$ é conservativo.
Se ${\bf F}$ for conservativo, calcule $f(x,y,z)$ tal que $\nabla f={\bf F}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$ onde $C$ é dada por $r(t)=(\cos t, \sin t, t)$, $0\leq t\leq 2\pi.$
Sim.
$f(x,y) = x e^{z} + y^{2} z.$
$e^{2\pi} - 1.$
Determine se o conjunto $\{(x,y)|\,1<x^{2}+y^{2}<4\}$ é ou não:
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,1<x^{2}+y^{2}<4\}$ representa a região anelar entre os círculos com centro $(0,0)$ e raio $1$ e $2$. Então:
$D$ é aberto pois, em torno de cada ponto em $D$, podemos colocar um disco que se encontra inteiramente em $D$.
$D$ é conexo pois quaisquer dois pontos de $D$ podem ser conectados por um caminho em $D$.
$D$ não é simplesmente conexo pois, por exemplo, a região delimitada pela curva simples e fechada $x^{2}+y^{2}=(3/2)^2$ possui pontos que não estão em $D$, por exemplo, a origem $(0,0)$.
A figura mostra o campo vetorial ${\bf F}(x,y)=(2xy, x^{2})$ e três curvas que começam em $(1,2)$ e terminam em $(3,2).$
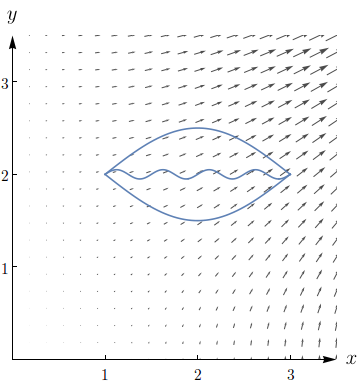
- Explique por que $\int_{c}{\bf F}\cdot d{\bf r}$ tem o mesmo valor para as três curvas.
- Qual é esse valor comum?
- ${\bf F}$ é conservativo, logo $\int_{C} \bf F \cdot d\bf r$ depende somente dos pontos inicial e final de $C.$
- $16.$
Determine se ${\bf F}(x,y)=-y\,{\bf i}+x\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
Seja ${\bf F}(x,y)=\dfrac{-y\,{\bf i}+x\,{\bf j}}{x^{2}+y^{2}}.$
Mostre que $\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}.$
Mostre que $\int_{C}{\bf F}\cdot d{\bf r}$ não é independente do caminho. [Sugestão: calcule $\int_{C_{1}}{\bf F}\cdot d{\bf r}$ e $\int_{C_{2}}{\bf F}\cdot d{\bf r}$, onde $C_{1}$ e $C_{2}$ são as metades superior e inferior do círculo $x^{2}+y^{2}=1$ de $(1,0)$ a $(-1,0)$.] Isso contraria o Teorema 6 (Seção 16.3 do Livro do James Stewart)?
$\dfrac{\partial P}{\partial y}= \dfrac{y^{2} - x^{2}}{(x^{2} + y^{2})^{2}} = \dfrac{\partial Q}{\partial x}.$
Tome $C_{1}$ a curva parametrizada por $\mathbf{r_{1}}(t) = (\cos(t), \sin(t)),$ $0 \leq t \leq \pi$ e $C_{2}$ a curva parametrizada por $\mathbf{r_{2}}(t) = (\cos(t), \sin(t)),$ de $t = 2\pi$ a $t = \pi.$ Segue que $\int_{C_{1}} \mathbf{F} \cdot d \mathbf{r} = \pi \neq -\pi = \int_{C_{2}} \mathbf{F} \cdot d \mathbf{r}.$ Como o domínio de $\mathbf{F}$ é $\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$ que não é simplesmente conexo, o resultado não contradiz o Teorema 6.
Dados ${\bf F}(x,y)=x^{2}\,{\bf i}+y^{2}\,{\bf j}$, $C$ é o arco da parábola $y=2x^{2}$ de $(-1,2)$ a $(2,8).$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y) = \dfrac{x^{3} + y^{3}}{3};$
$171.$
Determine se ${\bf F}(x,y)=(ye^{x}+\sin y)\,{\bf i}+(e^{x}+x\,\cos y)\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Primeiramente, temos que o domínio de ${\bf F}$ é todo o $\mathbb{R}^{2}$, o qual é uma região aberta e simplesmente conexa. Sendo $P(x,y)=ye^{x}+\sin y$ e $Q(x,y)=e^{x}+x\,\cos y$, temos que $P$ e $Q$ possuem derivadas de primeira ordem contínuas. Também temos que
$$\frac{\partial P}{\partial y}=e^{x}+\cos y \,\,\, \text{ e } \,\,\, \frac{\partial Q}{\partial x}=e^{x}+\cos y,$$
ou seja,
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.$$
Assim, das condições acima verificadas, temos que ${\bf F}$ é um campo conservativo. Agora, vamos determinar $f$ tal que $\nabla f={\bf F}.$ Isto é, devemos encontrar $f$ tal que
$$f_{x}(x,y)=P(x,y) \text{ e } f_{y}(x,y)=Q(x,y).$$
Como $f_{x}(x,y)=P(x,y)$ temos que
$$f_{x}(x,y)=ye^{x}+\sin y\Rightarrow f(x,y)=ye^{x}+x\,\sin y+g(y)$$
Assim obtemos que
$$f_{y}(x,y)=e^{x}+x\cos y+g'(y)$$
Mas, $f_{y}(x,y)=Q(x,y)$ logo obtemos que
$$e^{x}+x\cos y+g'(y)=e^{x}+x\,\cos y\Rightarrow g'(y)=0\Rightarrow g(y)=C.$$
Portanto,
$$f(x,y)=ye^{x}+x\sin y+C \text{ e } \nabla f={\bf F}.$$
Determine se ${\bf F}(x,y,z)=e^{y+2z}({\bf i}+x\,{\bf j}+2x\,{\bf k})$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = xe^{y + 2z} + K.$
Suponha que ${\bf F}=\nabla f$ seja um campo vetorial conservativo e
$$g(x,y,z)=\int_{(0,0,0)}^{(x,y,z)}{\bf F}\cdot d{\bf r}.$$
Mostre que $\nabla g={\bf F}.$
Como $g(x,y,z) = f(x,y,z) - f(0,0,0),$ segue que $\nabla g = \nabla f = \mathbf{F}.$
Calcule $\displaystyle\int_{C}(\sin(xy)+xy\,\cos(xy))\,dx+x^{2}\,\cos(xy)\,dy$, onde $C(t)=(t^{2}-1,t^{2}+1)$, $-1\leq t\leq 1.$
$0.$
Calcule $\displaystyle\int_{C}y\,dx+x^{2}\,dy$, onde $C$ é a curva cuja imagem é o segmento de extremidades $(1,1)$ e $(2,2)$, orientada de $(1,1)$ para $(2,2).$
$\dfrac{23}{6}.$
Calcule $\int_{C}2x\,\cos y\,dx-x^{2}\,\sin y\,dy$ ao longo dos caminhos $C$ a seguir no plano $xy.$
A parabóla $y=(x-1)^{2}$ de $(1,0)$ a $(0,1).$
O segmento de reta de $(-1,\pi)$ a $(1,0).$
O eixo $x$ de $(-1,0)$ a $(1,0).$
O astróide ${\bf r}(t)=(\cos^{3} t)\,{\bf i}+(\sin^{3}t)\,{\bf j}$, $0\leq t\leq 2\pi$, no sentido anti-horário de $(1,0)$ de volta a $(1,0).$
$-1.$
$2.$
$0.$
$0.$
Determine se o conjunto $\{(x,y)|\,x>0,\,y>0\}$ é ou não:
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x>0,\,y>0\}$ representa o primeiro quadrante, excluindo os eixos. Então:
$D$ é aberto, pois em torno de cada ponto em $D$, podemos colocar um disco que se encontra em $D.$
$D$ é conexo, pois o segmento de reta que une dois pontos quaisquer de $D$ encontra-se em $D.$
$D$ é simplesmente conexo, pois ele é conexo e não tem buracos.
Calcule a integral de linha
$$\int_{C}e^{2y}\,dx+(1+2xe^{2y})\,dy,$$
onde $C$ é a curva dada por $r(t)=(te^{t},1+\sin(\pi t/2))$, $0\leq t\leq 1.$ (Sugestão: verifique se o campo é conservativo.)
$e^{5} + 1.$
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x\neq 0\}$ consiste de todos os pontos, exceto para aqueles que encontram-se sobre o eixo y. Então:
$D$ é aberto.
Os pontos em lados opostos do eixo $y$ não podem ser conectados por um caminho que se encontra totalmente em $D$, então $D$ não é conexo.
$D$ não é simplesmente conexo, pois não é conexo.
Determine se ${\bf F}(x,y,z)=(x-y)\,{\bf i}+(x+y+z)\,{\bf j}+z^{2}\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x^{2}+y^{2}\leq 1\,$ ou\, $4\leq x^{2}+y^{2}\leq 9\}$ consiste dos pontos que estão sobre ou dentro do círculo $x^{2}+y^{2}\leq 1$ juntamente com os pontos que estão em ou entre os círculos $x^{2}+y^{2}=4$ e $x^{2}+y^{2}=9$.
$D$ não é aberto pois qualquer disco centrado em $(0,1)$ contém pontos que não estão em $D$.
$D$ não é conexo pois não existe um caminho em $D$ conectando, por exemplo, os pontos $(1,0)$ e $(2,0)$.
$D$ não é simplesmente conexo porque possui um buraco. Com efeito, a região delimitada pela curva simples e fechada $x^2+y^2=(5/2)^2$, contém pontos que não pertencem a $D$, por exemplo, o ponto $(0,3/2)$.
Calcule $\displaystyle\int_{(-1,0)}^{(1,0)}\dfrac{x}{x^{2}+y^{2}}\,dx+\dfrac{y}{x^{2}+y^{2}}\,dy$.
$\displaystyle \dfrac{\pi}{4} + \arctan\left( \dfrac{2}{3} \right).$
Considere o campo vetorial
$${\bf F}(x,y)=(1+ye^{xy})\,{\bf i}+(2y+xe^{xy})\,{\bf j}.$$
Determine se ${\bf F}$ é ou não um campo conservativo. Em caso afirmativo, encontre uma função potencial para ${\bf F}.$
Determine o trabalho realizado pelo campo vetorial ${\bf F}$ ao mover uma partícula sobre a hipérbole $x^{2} - y^{2} = 1,$ desde o ponto $(3,-\sqrt{8})$ até o ponto $(3,\sqrt{8}).$
Sim. Função potencial: $f(x,y) = x + e^{xy} + y^{2}.$
$e^{3\sqrt{8}} - e^{-3\sqrt{8}}.$
Dados ${\bf F}(x,y)=xy^{2}\,{\bf i}+x^{2}y\,{\bf j}$, $C: {\bf r}(t)=(t+\sin\frac{1}{2}\pi t, t+\cos \frac{1}{2}\pi t)$, $0\leq t\leq 1.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y) = \dfrac{x^{2}y^{2}}{2};$
$2.$
Um campo vetorial inverso do quadrado é da forma:
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$. Um exemplo de um campo inverso do quadrado é o campo gravitacional ${\bf F}=-(mMG){\bf r}/|{\bf r}|^{3}$. Determine o trabalho realizado pelo campo gravitacional quando a Terra se move do afélio (em uma distância máxima de $1,52\times 10^{8}\,km$ do Sol) ao periélio (em uma distância mínima de $1,47\times 10^{8}\,km)$. (Use os valores $m=5,97\times 10^{24}\,kg$, $M=1,99\times 10^{30}\,kg$ e $G=6,67\times 10^{-11}\,N\cdot m^{2}/kg^{2}.$)
$\approx 1,77 \times 10^{35}$ J.
Determine se ${\bf F}(x,y,z)=(e^{x}\,\cos y)\,{\bf i}-(e^{x}\,\sin y)\,{\bf j}+z\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = e^{x}\cos(y) + \dfrac{z^{2}}{2} + K.$
Dados ${\bf F}(x,y,z)=y^{2}\,\cos z\,{\bf i}+2xy\,\cos z\,{\bf j}-xy^{2}\,\sin z\,{\bf k}$, $C: {\bf r}(t)=t^{2}\,{\bf i}+\sin t\,{\bf j}+t\,{\bf k}$, $0\leq t\leq \pi.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = xy^{2} \cos(z);$
$0.$
Considere o campo vetorial
$${\bf F}(x,y)=(\ln(y^{2}+1))\,{\bf i}+\bigg(\frac{2y(x-1)}{y^{2}+1}\bigg)\,{\bf j}.$$
Determine se $F$ é ou não um campo conservativo.
Determine o trabalho realizado pelo campo vetorial ${\bf F}$ ao mover uma partícula desde o ponto $(-1,1)$ até o ponto $(2,3).$
Sim.
$\ln(10) + 2\ln(2).$
Calcule $\displaystyle\int_{(1,1)}^{(2,2)} y\,dx+x\,dy$.
$3.$
Considere o campo vetorial
$${\bf F}(x,y)=\bigg(e^{x}\ln(y)-\frac{e^{y}}{x}\bigg)\,{\bf i}+\bigg(\frac{e^{x}}{y}-e^{y}\ln(x)\bigg)\,{\bf j}.$$
O campo ${\bf F}$ é conservativo? Justifique sua resposta.
Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é qualquer caminho ligando o ponto $(1,1)$ ao ponto $(3,3).$
Sim.
$0.$
Determine se ${\bf F}(x,y)=(\ln y+2xy^{3})\,{\bf i}+(3x^{2}y^{2}+x/y)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = x^{2}y + xy^{-2} + K.$
Seja $\Omega=\{(x,y)\in \mathbb{R}^{2}|\,(x,y)\notin A\}$, onde $A$ é a semirreta $\{(x,y)\in \mathbb{R}^{2}|\,y=0\,e\,x\geq 0\}$. Calcule
$$\int_{C}\frac{-y}{x^{2}+y^{2}}\,dx+\frac{x}{x^{2}+y^{2}}\,dy,$$
onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida em $\Omega$, tal que $C(0)=(1,1)$ e $C(1)=(1,-1).$
$\dfrac{3\pi}{2}.$
Mostre que a integral de linha $\int_{C}2x\,\sin y\,dx+(x^{2}\,\cos y-3y^{2})\,dy$, onde $C$ é qualquer caminho entre $(-1,0)$ a $(5,1)$, é independente do caminho e calcule a integral.
$\mathbf{F} (x,y) = 2x \sin(y) \mathbf{i} + x^{2} \cos(y) - 3y^{2} \bf j$ é um campo conservativo com uma função potencial $f(x,y) = x^{2} \sin(y) - y^{3};$ o valor da integral é $25 \sin(1) - 1.$
Calcule $\displaystyle\int_{C}\dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy$, onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida no conjunto $\Omega=\{(x,y)\in \mathbb{R}^{2}| y>0\}\cup\{(x,y)\in \mathbb{R}^{2}|\,x<0\}$, tal que $C(0)=(1,1)$ e $C(1)=(-1,-1).$
$0.$
Seja
$${\bf F}(x,y)=\bigg(\frac{-y}{x^{2}+y^{2}},\frac{x}{x^{2}+y^{2}}+3y\bigg)$$
um campo vetorial em $\mathbb{R}^{2}$. Calcule a integral de linha do campo ${\bf F}$ ao longo das curvas
$C_{1}$ e $C_{2}$, orientadas no sentido anti-horário, onde:
$C_{1}$ é a circunferência de equação $x^{2}+y^{2}=4.$
$C_{2}$ é a fronteira do retângulo $R=\{(x,y)\in \mathbb{R}^{2}|\,-\pi \leq x \leq \pi,-3 \leq y \leq 3\}.$
$0.$
$0.$
Um campo vetorial inverso do quadrado é da forma:
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$. Um exemplo de campo inverso do quadrado é o campo elétrico ${\bf F}=\epsilon q Q{\bf r}/|{\bf r}|^{3}$. Suponha que um elétron com carga de $-1,6\times 10^{-19}\, C$ esteja localizado na origem. Uma carga positiva unitária é colocada à distância de $10^{-12}\,m$ do elétron e se move para uma posição que está à metade da distância original do elétron. Determine o trabalho realizado pelo campo elétrico. (Use o valor $\epsilon=8,985\times 10^{9}$.)
$\approx 1,4 \times 10^{4}$ J.
Determine se ${\bf F}(x,y,z)=(y\,\sin z)\,{\bf i}+(x\,\sin z)\,{\bf j}+(xy\,\cos z)\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = xy\sin(z) + K.$
A figura mostra uma curva $C$ e um mapa de contorno de uma função $f$ cujo gradiente é contínuo. Determine $\int_{C}\nabla f\cdot d{\bf r}.$
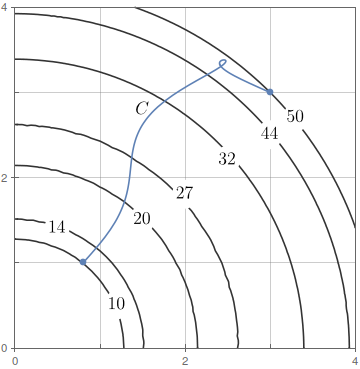
$40.$
Dados ${\bf F}(x,y,z)=e^{y}\,{\bf i}+xe^{y}\,{\bf j}+(z+1)e^{z}\,{\bf k}$, $C: {\bf r}(t)=t\,{\bf i}+t^{2}\,{\bf j}+t^{3}\,{\bf k}$, $0\leq t\leq 1.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = x e^{y} + ze^{z};$
$2e.$
Determine se ${\bf F}(x,y)=(e^{x}\,\sin y)\,{\bf i}+(e^{x}\,\cos y)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = e^{x}\sin(y) + K.$
Seja ${\bf F}:\Omega\subset \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ contínuo no aberto $\Omega$. Prove que uma condição necessária para que ${\bf F}$ seja
conservativo é que $\int_{C}{\bf F}\cdot d{\bf r}=0$ para toda curva $C$ fechada, de classe $C^{1}$ por partes, com imagem contida em $\Omega.$
Se $C$ é uma curva fechada em $\Omega$ parametrizada por $\mathbf{r}(t),$ com $a \leq t \leq b,$ $\mathbf{r}(a) = \mathbf{r}(b)$ e $\mathbf{F} = \nabla f,$ então $\int_{C}{\bf F}\cdot d{\bf r} = f(\mathbf{r}(a)) - f(\mathbf{r}(b)) = 0.$
Determine se ${\bf F}(x,y,z)=\dfrac{x}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf i}+\dfrac{y}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf j}+\dfrac{z}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = -\dfrac{1}{2(x^2 + y^{2} +z^{2})} + K.$
Determine se ${\bf F}(x,y)=e^{x}\,\cos y\,{\bf i}+e^{x}\,\sin y\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.

