Exercícios
Campos vetoriais
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Verifique que para o vetor posição \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) valem as seguintes propriedades
\(\displaystyle \mathrm{div\,}\mathbf{r} = 3\)
\(\displaystyle \nabla\dfrac{1}{\|\mathbf{r}\|} = -\dfrac{\mathbf{r}}{\|\mathbf{r}\|^3} \)
Faça uma correspondência entre as funções $f$ e os desenhos de seus campos vetoriais gradientes (rotulados de I-IV). Justifique.
- $f(x,y) = x^2+y^2$
- $f(x,y) = (x+y)^2$.
- $f(x,y) = x(x+y)$.
- $f(x,y) = \sin{\sqrt{x^2+y^2}}$.
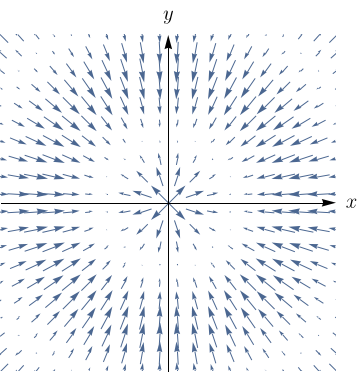
II
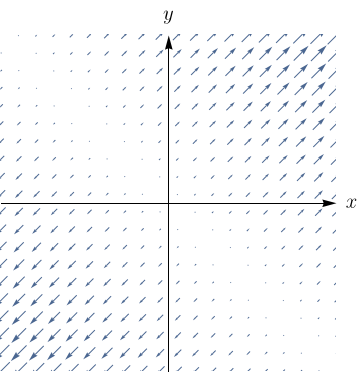
III
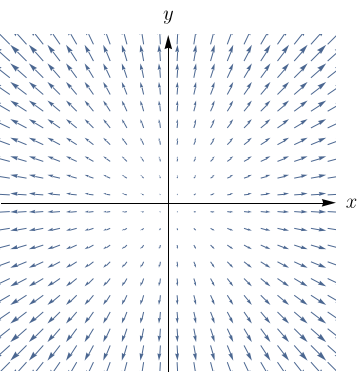
IV
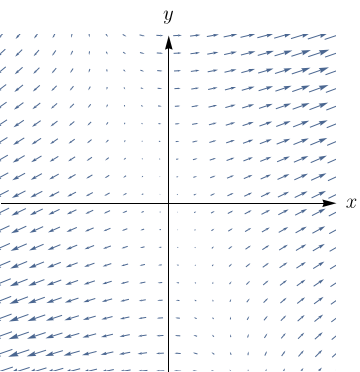
- III.
- IV.
- II.
- I.
Dado um campo vetorial \(\mathbf{F}\), uma curva \(C\) é chamada de linha de fluxo deste campo se \(\mathbf{F}\) for um vetor tangente a \(C\) em cada ponto ao longo de \(C\).
Sejam \(C\) uma linha de fluxo de \(\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}\) e \((x,y)\) um ponto em \(C\) para o qual \(y\neq 0\). Mostre que as linhas de fluxo satisfazem a equação diferencial \[ \dfrac{dy}{dx} = -\dfrac{x}{y}. \]
Resolva a equação diferencial do item anterior, por separação de variáveis, e mostre que as linhas de fluxo são círculos concêntricos centrados na origem, ou seja, da forma \(x^2+y^2=K\).
Determine o campo vetorial gradiente $\nabla f$ de $f(x,y) = \sqrt{x^2+y^2}$ e o esboce.
Sejam \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\), \(r=\|\mathbf{r}\|\), \(f\) uma função diferenciável de uma variável e \(\mathbf{F}(\mathbf{r})=f(r)\mathbf{r}\).
Mostre que \[\nabla f(r) = \dfrac{f'(r)}{r}\mathbf{r}.\]
Use o resultado anterior para mostrar que \(\displaystyle \mathbf{F}=3f(r)+rf'(r). \)
Esboce o campo vetorial $\textbf{F}=\dfrac{1}{2}(\textbf{i} + \textbf{j})$, desenhando um diagrama.
Verifique que para o vetor posição \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) valem as seguintes propriedades
\(\displaystyle \mathrm{rot\,}\mathbf{r} = \mathbf{0}\)
\(\displaystyle \nabla\|\mathbf{r}\| = \dfrac{\mathbf{r}}{\|\mathbf{r}\|} \)
Esboce o campo vetorial ${\bf F}(x,y)=(x-y)\textbf{i} + x \textbf{j}$, desenhando um diagrama.
As linhas de escoamento (ou linhas de corrente) de um campo vetorial são as trajetórias seguidas por uma partícula cujo campo de velocidade é um campo vetorial dado. Assim, os vetores do campo vetorial são tangentes a suas linhas de escoamento.
Use um esboço do campo vetorial $\textbf{F}(x,y) = x\textbf{i} - y\textbf{j}$ para desenhar algumas linhas de escoamento. Desses seus esboços é possível descobrir qual é a equação das linhas de escoamento?
Se as equações paramétricas de uma linha de escoamento são $x=x(t)$ e $y=y(t)$, explique por que essas funções satisfazem as equações diferenciais $dx/dt = x$ e $dy/dt = -y$. Resolva então as equações de forma a obter uma equação da linha de escoamento que passe pelo ponto $(1,1)$.
Uma partícula se move em um campo de velocidade $\textbf{V}(x,y) = (x^2,x+y^2)$. Se ela está na posição $(2,1)$ no instante $t=3$, estime sua posição no instante $t=3,01$.
$(2,04;1,03).$
Esboce o campo vetorial $\textbf{F}= y\textbf{i} + \dfrac{1}{2}\textbf{j}$, desenhando um diagrama.
Esboce o campo vetorial $\textbf{F}= \dfrac{y\textbf{i} - x\textbf{j}}{\sqrt{x^2+y^2}}$, desenhando um diagrama.
Determine o campo vetorial gradiente $\nabla f$ de $f(x,y) = x^2-y$ e o esboce.
Determine o campo vetorial gradiente de $f(x,y,z) = \sqrt{x^2+y^2+z^2}$.
$\nabla f(x,y,z) = \dfrac{x\textbf{i} + y\textbf{j} + z \textbf{k}}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Determine o campo vetorial gradiente de $f(x,y) = \ln(x + 2y)$.
$\nabla f(x,y) = \dfrac{\textbf{i} + 2\textbf{j}}{x + 2y}.$
- Esboce o campo vetorial $\textbf{F}(x,y) = \textbf{i} + x\textbf{j}$ e algumas linhas de escoamento. Qual é o formato que essas linhas de escoamento parecem ter?
- Se as equações paramétricas das linhas de escoamento são $x=x(t)$ e $y=y(t)$, que equações diferenciais essas funções satisfazem? Deduza que $dy/dx = x$.
- Se uma partícula está na origem no instante inicial e o campo de velocidade é dado por $\textbf{F}$, determine uma equação para a trajetória percorrida por ela.
Esboce o campo vetorial $\textbf{F}= \dfrac{y\textbf{i} + x\textbf{j}}{\sqrt{x^2+y^2}}$, desenhando um diagrama.
Encontre um campo de vetores $\textbf{G} = P(x,y)\textbf{i} + Q(x,y)\textbf{j}$ no plano $xy$ com a propriedade de que, em qualquer ponto $(a,b) \neq (0,0)$, $\textbf{G}$ é um vetor de magnitude $\sqrt{x^2+y^2}$ tangente à circunferência $x^2+y^2=a^2+b^2$ e aponta no sentido horário. (O campo é indefinido em (0,0).)
$\displaystyle \textbf{G} = \frac{y \textbf{i} - x \textbf{j}}{\sqrt{x^{2} + y^{2}}}.$

