Exercícios
Integrais de linha
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Calcule a área da região limitada pela elipse $x = a\cos{t}$, $y=b\sin{t}$, $0\leq t \leq \pi/2$, em que $a > 0$ e $b > 0$.
$\pi ab.$
Um arame fino é entortado no formato da semicircunferência $x^{2}+y^{2}=4$, $x\geq 0$. Se a densidade linear for uma constante $k$, determine a massa e o centro de massa do arame.
Massa: $k2\pi;$ centro de massa: $\displaystyle \left( \frac{4}{\pi},0 \right).$
Determine se ${\bf F}(x,y)=(ye^{x}+\sin y)\,{\bf i}+(e^{x}+x\,\cos y)\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Primeiramente, temos que o domínio de ${\bf F}$ é todo o $\mathbb{R}^{2}$, o qual é uma região aberta e simplesmente conexa. Sendo $P(x,y)=ye^{x}+\sin y$ e $Q(x,y)=e^{x}+x\,\cos y$, temos que $P$ e $Q$ possuem derivadas de primeira ordem contínuas. Também temos que
$$\frac{\partial P}{\partial y}=e^{x}+\cos y \,\,\, \text{ e } \,\,\, \frac{\partial Q}{\partial x}=e^{x}+\cos y,$$
ou seja,
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.$$
Assim, das condições acima verificadas, temos que ${\bf F}$ é um campo conservativo. Agora, vamos determinar $f$ tal que $\nabla f={\bf F}.$ Isto é, devemos encontrar $f$ tal que
$$f_{x}(x,y)=P(x,y) \text{ e } f_{y}(x,y)=Q(x,y).$$
Como $f_{x}(x,y)=P(x,y)$ temos que
$$f_{x}(x,y)=ye^{x}+\sin y\Rightarrow f(x,y)=ye^{x}+x\,\sin y+g(y)$$
Assim obtemos que
$$f_{y}(x,y)=e^{x}+x\cos y+g'(y)$$
Mas, $f_{y}(x,y)=Q(x,y)$ logo obtemos que
$$e^{x}+x\cos y+g'(y)=e^{x}+x\,\cos y\Rightarrow g'(y)=0\Rightarrow g(y)=C.$$
Portanto,
$$f(x,y)=ye^{x}+x\sin y+C \text{ e } \nabla f={\bf F}.$$
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x\neq 0\}$ consiste de todos os pontos, exceto para aqueles que encontram-se sobre o eixo y. Então:
$D$ é aberto.
Os pontos em lados opostos do eixo $y$ não podem ser conectados por um caminho que se encontra totalmente em $D$, então $D$ não é conexo.
$D$ não é simplesmente conexo, pois não é conexo.
Dados ${\bf F}(x,y)=xy^{2}\,{\bf i}+x^{2}y\,{\bf j}$, $C: {\bf r}(t)=(t+\sin\frac{1}{2}\pi t, t+\cos \frac{1}{2}\pi t)$, $0\leq t\leq 1.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y) = \dfrac{x^{2}y^{2}}{2};$
$2.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y)=e^{x-1}\,{\bf i}+xy\,{\bf j}$ e $C$ é dada por ${\bf r}(t)=t^{2}\,{\bf i}+t^{3}\,{\bf j}, 0\leq t\leq 1.$
$\displaystyle \frac{11}{8} - \frac{1}{e}.$
Determine se ${\bf F}(x,y,z)=(x-y)\,{\bf i}+(x+y+z)\,{\bf j}+z^{2}\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
Considere o campo vetorial
$${\bf F}(x,y)=(\ln(y^{2}+1))\,{\bf i}+\bigg(\frac{2y(x-1)}{y^{2}+1}\bigg)\,{\bf j}.$$
Determine se $F$ é ou não um campo conservativo.
Determine o trabalho realizado pelo campo vetorial ${\bf F}$ ao mover uma partícula desde o ponto $(-1,1)$ até o ponto $(2,3).$
Sim.
$\ln(10) + 2\ln(2).$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
$\displaystyle\int_{C}y^3 \, dx - x^3 \, dy$, $C$ é o círculo $x^2 + y^2 = 4$.
Observe que a curva $C$ com orientação positiva está nas hipóteses do Teorema de Green, assim como o campo $\mathbf{F}(x,y) = (y^3, -x^3)$. Logo,
$$\displaystyle\int_{C}y^3 \, dx - x^3 \, dy = \iint\limits_{D} \left(\frac{\partial}{\partial x}(-x^3) - \frac{\partial}{\partial y}(y^3)\right) \, dA = -3 \iint\limits_{D} (x^2 + y^2) \, dA,$$
em que $D = \{(x,y) \in \mathbb{R}^2: x^2 + y^2 \leq 4\}$. Usando coordenadas polares
$$\begin{cases}x = r \cos{\theta} \\y = r \sin{\theta}, \\\end{cases}$$
temos que a região de integração $D$ pode ser escrita como $$\{(r,\theta) \in \mathbb{R}^2: 0 \leq r \leq 2, 0 \leq \theta \leq 2 \pi\}$$ e o jacobiano dessa mudança de coordenadas é igual a $r$. Logo,
$$\iint\limits_{ D} (x^2 + y^2) dA = \displaystyle\int_{0}^{2\pi} \int_{0}^{2}r^2 \cdot r\,dr d\theta = 8\pi.$$
Portanto, $\displaystyle\int_{C}y^3 \, dx - x^3 \,dy = -24\pi$.
Verifique que para o vetor posição \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) valem as seguintes propriedades
\(\displaystyle \mathrm{rot\,}\mathbf{r} = \mathbf{0}\)
\(\displaystyle \nabla\|\mathbf{r}\| = \dfrac{\mathbf{r}}{\|\mathbf{r}\|} \)
Experiências mostram que uma corrente contínua $I$ em um fio comprido produz um campo magnético ${\bf B}$ que é tangente a qualquer círculo em um plano perpendicular ao fio cujo centro seja o eixo do fio (como na figura). A Lei de Ampère relaciona a corrente elétrica ao campo magnético criado e afirma que
$$\int_{C}{\bf B}\cdot d{\bf r}=\mu_{0}I,$$
onde $I$ é a corrente total que passa por qualquer superfície limitada por uma curva fechada $C$ e $\mu_{0}$ é uma constante, chamada permeabilidade no vácuo. Tomando $C$ como um círculo de raio $r$, mostre que o módulo $B=|{\bf B}|$ do campo magnético a uma distância $r$ do centro do fio é dado por
$$B=\frac{\mu_{0}I}{2\pi r}.$$

Note que $\textbf{B}$ é tangente a qualquer círculo que está no plano perpendicular ao fio. Logo, $\textbf{B} = |\textbf{B}| \textbf{T},$ onde $\textbf{T}$ é a tangente unitária ao círculo $\textbf{C}$ parametrizado por $x = r \cos(\theta),$ $y = r \sin(\theta).$ Daí,
$\textbf{B} = |\textbf{B}| \left(-\sin(\theta),\cos(\theta) \right)$ e
$$\int_{C} \textbf{B} \cdot d\textbf{r} = \int_{0}^{2\pi} |\textbf{B}| \left( -\sin(\theta), \cos(\theta)\right)\cdot (\left(-r \sin(\theta), r\cos(\theta) \right) d\theta = 2\pi r |\textbf{B}|.$$
Determine se ${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = \dfrac{x^{2} + y^{2} + z^{2}}{2} + K.$
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y)=(x+y^{2})\,{\bf j}$ e $C$ é a curva da figura abaixo.
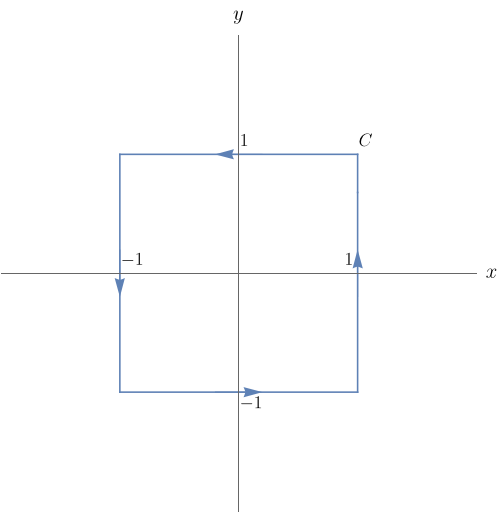
$4.$
Calcule a integral de linha, onde $C$ é a curva dada. $\displaystyle\int_{C}x^{2}y\sqrt{z}\,dz$, $C:\,x=t^{3},\, y=t,\, z=t^{2},\, 0\leq t\leq 1.$
As equações paramétricas de $C$ são
$$x=t^{3},\, y=t,\, z=t^{2},\, 0\leq t\leq 1.$$
Logo,
$$dx=3t^{2}\,dt,\, dy=dt,\, dz=2t\,dt.$$
Assim,
$$\int_{C}x^{2}y\sqrt{z}\,dz=\int_{0}^{1}((t^{3})^{2}\cdot t \cdot \sqrt{t^{2}})(2t\,dt)=2\int_{0}^{1}t^{9}\,dt$$
$$=2\cdot\frac{t^{10}}{10}\bigg|_{0}^{1}=2\cdot \frac{1}{10}=\frac{1}{5}.$$
Use o Teorema de Green para achar o trabalho realizado pela força $\mathbf{F}(x,y) = x(x+y)\mathbf{i} + xy^2\mathbf{j}$ ao mover uma partícula da origem ao longo do eixo $x$ até $(1,0)$, em seguida ao longo de um segmento de reta até $(0,1)$ e então de volta à origem ao longo do eixo $y$.
$-\dfrac{1}{12}.$
Demonstre que se $R$ é uma região no plano limitada por uma curva $C$ simples, fechada e suave por partes, então a área de $R$, denotada por $A(R)$, pode ser dada por
$$\oint_{C}x\, dy,$$
em que a curva está orientada no sentido positivo.
Temos que
$$A(R) = \iint\limits_{R} 1 \, dA.$$
A fim de utilizar o Teorema de Green, devemos encontrar funções $P$ e $Q$ que tenham derivadas de primeira ordem contínuas em um aberto que contenha a curva $C$ e o interior de $C$ e que satisfaçam a relação $\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 1$. Observe que a curva $C$ já satisfaz as hipóteses desse teorema e $C$ é a fronteira de $R$. Um exemplo de funções $P$ e $Q$ é $P(x,y) = 0$ e $Q(x,y) = x$. Portanto, pelo Teorema de Green,
$$\iint\limits_{R} 1 \, dA = \oint_{C}0 \, dx + x\, dy = \oint_{C}x\, dy.$$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}y^{3}\,ds$, $C:\,x=t^{3},\, y=t,\, 0\leq t\leq 2.$
$\displaystyle \frac{1}{54}\left(145^{3/2} - 1 \right).$
Calcule $\int_{C}{\bf E}\cdot d{\bf l}$, onde ${\bf E}(x,y)=\dfrac{1}{x^{2}+y^{2}}\dfrac{x\,{\bf i}+y\,{\bf j}}{\sqrt{x^{2}+y^{2}}}$ e $C$ é a curva dada por $x=2\,\cos t$, $y=\sin t$, com $0\leq t\leq \dfrac{\pi}{2}.$
$-\dfrac{1}{2}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=(x+y+z)\,{\bf k}$, ${\bf r}(t)=(t,t,-t^{2})$, $0\leq t\leq 1.$
$-\dfrac{11}{6}.$
Um campo vetorial inverso do quadrado é da forma:
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$. Um exemplo de campo inverso do quadrado é o campo elétrico ${\bf F}=\epsilon q Q{\bf r}/|{\bf r}|^{3}$. Suponha que um elétron com carga de $-1,6\times 10^{-19}\, C$ esteja localizado na origem. Uma carga positiva unitária é colocada à distância de $10^{-12}\,m$ do elétron e se move para uma posição que está à metade da distância original do elétron. Determine o trabalho realizado pelo campo elétrico. (Use o valor $\epsilon=8,985\times 10^{9}$.)
$\approx 1,4 \times 10^{4}$ J.
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x^{2}+y^{2}\leq 1\,$ ou\, $4\leq x^{2}+y^{2}\leq 9\}$ consiste dos pontos que estão sobre ou dentro do círculo $x^{2}+y^{2}\leq 1$ juntamente com os pontos que estão em ou entre os círculos $x^{2}+y^{2}=4$ e $x^{2}+y^{2}=9$.
$D$ não é aberto pois qualquer disco centrado em $(0,1)$ contém pontos que não estão em $D$.
$D$ não é conexo pois não existe um caminho em $D$ conectando, por exemplo, os pontos $(1,0)$ e $(2,0)$.
$D$ não é simplesmente conexo porque possui um buraco. Com efeito, a região delimitada pela curva simples e fechada $x^2+y^2=(5/2)^2$, contém pontos que não pertencem a $D$, por exemplo, o ponto $(0,3/2)$.
Determine se ${\bf F}(x,y)=-y\,{\bf i}+x\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
A figura mostra o campo vetorial ${\bf F}(x,y)=(2xy, x^{2})$ e três curvas que começam em $(1,2)$ e terminam em $(3,2).$
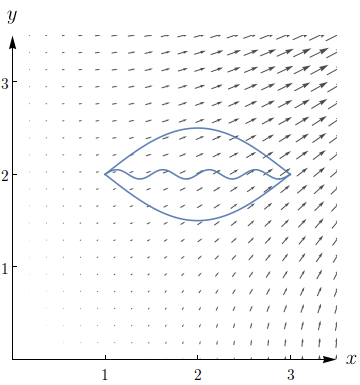
- Explique por que $\int_{c}{\bf F}\cdot d{\bf r}$ tem o mesmo valor para as três curvas.
- Qual é esse valor comum?
- ${\bf F}$ é conservativo, logo $\int_{C} \bf F \cdot d\bf r$ depende somente dos pontos inicial e final de $C.$
- $16.$
Calcule a integral de linha $\displaystyle\int_{C}(x-y)\,dx+e^{x+y}\, dy$, onde $C$ é a fronteira do triângulo de vértices $(0,0)$, $(0,1)$ e $(1,2)$, orientada no sentido anti-horário.
$\displaystyle \frac{e^{3}}{6} - \frac{e}{2} + \frac{5}{6}.$
Seja ${\bf F}(x,y)=\dfrac{-y\,{\bf i}+x\,{\bf j}}{x^{2}+y^{2}}.$
Mostre que $\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}.$
Mostre que $\int_{C}{\bf F}\cdot d{\bf r}$ não é independente do caminho. [Sugestão: calcule $\int_{C_{1}}{\bf F}\cdot d{\bf r}$ e $\int_{C_{2}}{\bf F}\cdot d{\bf r}$, onde $C_{1}$ e $C_{2}$ são as metades superior e inferior do círculo $x^{2}+y^{2}=1$ de $(1,0)$ a $(-1,0)$.] Isso contraria o Teorema 6 (Seção 16.3 do Livro do James Stewart)?
$\dfrac{\partial P}{\partial y}= \dfrac{y^{2} - x^{2}}{(x^{2} + y^{2})^{2}} = \dfrac{\partial Q}{\partial x}.$
Tome $C_{1}$ a curva parametrizada por $\mathbf{r_{1}}(t) = (\cos(t), \sin(t)),$ $0 \leq t \leq \pi$ e $C_{2}$ a curva parametrizada por $\mathbf{r_{2}}(t) = (\cos(t), \sin(t)),$ de $t = 2\pi$ a $t = \pi.$ Segue que $\int_{C_{1}} \mathbf{F} \cdot d \mathbf{r} = \pi \neq -\pi = \int_{C_{2}} \mathbf{F} \cdot d \mathbf{r}.$ Como o domínio de $\mathbf{F}$ é $\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$ que não é simplesmente conexo, o resultado não contradiz o Teorema 6.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx+y\,dy+z\,dz$, $C$ é o segmento de extremidades $(0,0,0)$ e $(1,2,1)$, percorrido no sentido de $(1,2,1)$ para $(0,0,0).$
$-3.$
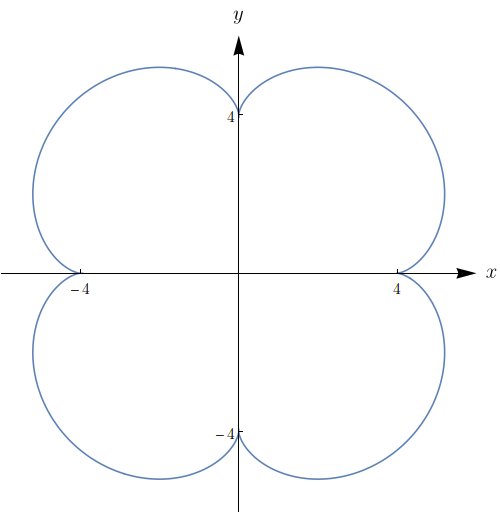
Se uma circunferência $C$ de raio $1$ rola ao longo do interior da circunferência $x^2+y^2=16$, um ponto fixo $P$ de $C$ descreve uma curva chamada epicicloide, com equações paramétricas $x = 5\cos{t}-\cos{5t}$, $y = 5\sin{t} - \sin{5t}$. Faça o gráfico da epicicloide e calcule a área da região que ela envolve.
$30\pi.$
Calcule a integral de linha
$$\int_{C}{\bf F}\cdot d{\bf r}=\int_{C}{\bf F}\cdot r'(t)\,dt$$
onde ${\bf F}=(2xyz^{3},x^{2}z^{3},3x^{2}yz^{2})$ e $C$ é a curva dada por $r(t)=(\sin^{6}t,1-\cos t, e^{t(t-\pi/2)}$, $0\leq t\leq \pi/2.$ (Dica: verifique se ${\bf F}$ é conservativo.)
$1.$
Encontre um campo de vetores $\textbf{G} = P(x,y)\textbf{i} + Q(x,y)\textbf{j}$ no plano $xy$ com a propriedade de que, em qualquer ponto $(a,b) \neq (0,0)$, $\textbf{G}$ é um vetor de magnitude $\sqrt{x^2+y^2}$ tangente à circunferência $x^2+y^2=a^2+b^2$ e aponta no sentido horário. (O campo é indefinido em (0,0).)
$\displaystyle \textbf{G} = \frac{y \textbf{i} - x \textbf{j}}{\sqrt{x^{2} + y^{2}}}.$
Suponha que ${\bf F}=\nabla f$ seja um campo vetorial conservativo e
$$g(x,y,z)=\int_{(0,0,0)}^{(x,y,z)}{\bf F}\cdot d{\bf r}.$$
Mostre que $\nabla g={\bf F}.$
Como $g(x,y,z) = f(x,y,z) - f(0,0,0),$ segue que $\nabla g = \nabla f = \mathbf{F}.$
Determine se ${\bf F}(x,y)=(\ln y+2xy^{3})\,{\bf i}+(3x^{2}y^{2}+x/y)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = x^{2}y + xy^{-2} + K.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}(y+e^{\sqrt{x}}) \, dx + (2x+\cos{y^2}) \, dy$, $C$ é a fronteira da região englobada pelas parábolas $y=x^2$ e $x=y^2$.
$\dfrac{1}{3}.$
Mostre que a integral de linha $\int_{C}2x\,\sin y\,dx+(x^{2}\,\cos y-3y^{2})\,dy$, onde $C$ é qualquer caminho entre $(-1,0)$ a $(5,1)$, é independente do caminho e calcule a integral.
$\mathbf{F} (x,y) = 2x \sin(y) \mathbf{i} + x^{2} \cos(y) - 3y^{2} \bf j$ é um campo conservativo com uma função potencial $f(x,y) = x^{2} \sin(y) - y^{3};$ o valor da integral é $25 \sin(1) - 1.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = 4x^3y^3\mathbf{i} + (3x^4y^2+5x)\mathbf{j}$, $C$ é a fronteira do quadrado de vértices $(-1,0)$, $(0,-1)$, $(1,0)$ e $(0,1)$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$10.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=xy\,{\bf i}+3y^{2}\,{\bf j}$, ${\bf r}(t)=11t^{4}\,{\bf i}+t^{3}\,{\bf j}$, $0\leq t\leq 1.$
$45.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (e^x+x^2y,e^y-xy^2)$, $C$ é a circunferência $x^2+y^2=25$, orientada no sentido horário. (Verifique a orientação da curva antes de aplicar o Teorema.)
$\dfrac{625\pi}{2}.$
Determine se o conjunto $\{(x,y)|\,1<x^{2}+y^{2}<4\}$ é ou não:
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,1<x^{2}+y^{2}<4\}$ representa a região anelar entre os círculos com centro $(0,0)$ e raio $1$ e $2$. Então:
$D$ é aberto pois, em torno de cada ponto em $D$, podemos colocar um disco que se encontra inteiramente em $D$.
$D$ é conexo pois quaisquer dois pontos de $D$ podem ser conectados por um caminho em $D$.
$D$ não é simplesmente conexo pois, por exemplo, a região delimitada pela curva simples e fechada $x^{2}+y^{2}=(3/2)^2$ possui pontos que não estão em $D$, por exemplo, a origem $(0,0)$.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xy^{4}\,ds$, $C$ é a metade direita do círculo $x^{2}+y^{2}=16.$
$\dfrac{2^{13}}{5}.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=x\,{\bf i}+(y+2)\,{\bf j}$ sobre um objeto que se move sobre um arco de cicloide ${\bf r}(t)=(t-\sin t)\,{\bf i}+(1-\cos t)\,{\bf j}$, $0\leq t\leq 2\pi.$
$2\pi^{2}.$
Calcule $\displaystyle\int_{C}y\,dx+x^{2}\,dy$, onde $C$ é a curva cuja imagem é o segmento de extremidades $(1,1)$ e $(2,2)$, orientada de $(1,1)$ para $(2,2).$
$\dfrac{23}{6}.$
Seja ${\bf F}=\nabla f$, onde $f(x,y)=\sin(x-2y)$. Determine curvas $C_{1}$ e $C_{2}$ que não sejam fechadas e satisfaçam a equação.
$\displaystyle\int_{C_{1}}{\bf F}\cdot d{\bf r}=0$
$\displaystyle\int_{C_{2}}{\bf F}\cdot d{\bf r}=1$
$\mathbf{r}(t) = \pi t \mathbf{i} + \pi t \mathbf{j},$ $0 \leq t \leq 1.$
$\mathbf{r}(t) = \dfrac{\pi}{2} t \mathbf{i},$ $0 \leq t \leq 1.$
Se um arame com densidade linear $\rho(x,y)$ está sobre uma curva plana $C$, seus momentos de inércia em relação aos eixos $x$ e $y$ são definidos por
$$I_{x}=\int_{C}y^{2}\rho(x,y)\,ds I_{y}=\int_{C}x^{2}\rho(x,y)\,ds.$$
Determine os momentos de inércia de um arame com o formato de um semicírculo $x^{2}+y^{2}=1$, $y\geq 0$, que é mais grosso perto da base do que perto do topo, se a função densidade linear em qualquer ponto for proporcional à sua distância à reta $y=1.$
$I_{x} = k\left(\dfrac{\pi}{2} - \dfrac{4}{3} \right)$ e $I_{y} = k\left(\dfrac{\pi}{2} - \dfrac{2}{3} \right).$
Sejam $A=(3,0)$, $B=(1,1)$ e $C=(0,3)$ pontos de $\mathbb{R}^{2}$ e $C$ a trajetória que vai em linha reta de $A$ até $B$ e em seguida de $B$ até $C$. Determine o trabalho ao longo de $C$ do campo de forças ${\bf F}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$, sendo
$${\bf F}(x,y)=\bigg(-\frac{y}{x^{2}+y^{2}},\frac{x}{x^{2}+y^{2}}\bigg).$$
$\displaystyle 2\arctan(2) + \arctan\left(\frac{1}{2} \right) - \arctan\left(\frac{1}{3} \right).$
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y,z)=(yz,xz,xy+2y)$ e $C$ é o segmento de reta que liga o ponto $(1,0,1)$ ao ponto $(-2,2,2).$
$-6.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xy^{3}\,ds$, $C:\,x=4\,\sin t,\, y=4\,\cos t,\, z=3t,\, 0\leq t\leq \pi/2.$
$320.$
Calcule a integral de linha $\displaystyle\int_{C}y^{2}\,dx+x\,dy -\,dz$, onde $C$ é a poligonal de vértices $A_{0}=(0,0,0)$, $A_{1}=(1,1,1)$, $A_{2}=(1,1,0)$, orientada de $A_{0}$ para $A_{2}.$
$\displaystyle \frac{5}{6}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=(e^{-y}-2x,-xe^{-y}-\sin y)$, ${\bf r}(t)=(t,\tan t)$, $0\leq t\leq \pi/4.$
$\displaystyle \cos(1) - \frac{\pi}{4}e^{-1} - \frac{\pi^{2}}{16} - 1.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}2\,dx-dy$, $C$ tem por imagem $x^{2}+y^{2}=4$, $x\geq 0$ e $y\geq 0$; sentido de percurso é de $(2,0)$ para $(0,2).$
$\displaystyle -6.$
Calcule $\displaystyle\int_{C}\dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy$, onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida no conjunto $\Omega=\{(x,y)\in \mathbb{R}^{2}| y>0\}\cup\{(x,y)\in \mathbb{R}^{2}|\,x<0\}$, tal que $C(0)=(1,1)$ e $C(1)=(-1,-1).$
$0.$
Calcule a área da região limitada pela astroide $x=\cos^3{t}$, $y = \sin^3{t}$, $0 \leq t \leq 2\pi$.
$\dfrac{3\pi}{8}.$
Considere o campo vetorial
$${\bf F}(x,y)=(1+ye^{xy})\,{\bf i}+(2y+xe^{xy})\,{\bf j}.$$
Determine se ${\bf F}$ é ou não um campo conservativo. Em caso afirmativo, encontre uma função potencial para ${\bf F}.$
Determine o trabalho realizado pelo campo vetorial ${\bf F}$ ao mover uma partícula sobre a hipérbole $x^{2} - y^{2} = 1,$ desde o ponto $(3,-\sqrt{8})$ até o ponto $(3,\sqrt{8}).$
Sim. Função potencial: $f(x,y) = x + e^{xy} + y^{2}.$
$e^{3\sqrt{8}} - e^{-3\sqrt{8}}.$
Determine se ${\bf F}(x,y,z)=(y\,\sin z)\,{\bf i}+(x\,\sin z)\,{\bf j}+(xy\,\cos z)\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = xy\sin(z) + K.$
Mostre que um campo de força constante realiza trabalho nulo sobre um partícula que dá uma única volta completa uniformemente na circunferência $x^{2}+y^{2}=1.$
Isso também é verdadeiro para um campo de força ${\bf F}({\bf x})=k{\bf x}$, onde $k$ é uma constante e $\textbf{x}=x{\bf i}+y{\bf j}$?
Dica: tome a parametrização do círculo $C$ dada por $x = cos(t)$ e $y = \sin(t),$ com $t \in [0,2\pi]$ e considere um campo constante arbitrário ${\bf F} = (a,b).$ Segue que $W = \int_{C} F\cdot d\textbf{r} = 0.$
Sim. Realize o mesmo cálculo com ${\bf F}(x,y) = (k x, ky).$
Seja $C: {\bf r}(t)=(R\,\cos t, R\,\sin t)$, $0\leq t \leq 2\pi$\,$(R>0).$ Mostre que
$$\int_{C}\frac{-y}{x^{2}+y^{2}}\,dx+\frac{x}{x^{2}+y^{2}}\,dy$$
não depende de $R.$
Note que o valor da integral é $2\pi,$ independente de $R.$
Calcule o trabalho realizado pela força $\mathbf{F}(x,y) = xy\mathbf{i}+y^2\mathbf{j}$ ao mover uma partícula da origem ao longo da reta $y=x$ até $(1,1)$ e então de volta à origem ao longo da curva $y=x^2$.
$\dfrac{1}{12}.$
Calcule a integral de linha $\displaystyle\oint_{C} xy \, dx + x^2 \, dy$, $C$ é o retângulo com vértices $(0,0)$, $(3,0)$, $(3,1)$ e $(0,1)$ por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$\dfrac{9}{2}.$
Se $\mathbf{F}(x,y) = (-y\mathbf{i} + x\mathbf{j})/(x^2+y^2)$, mostre que $\int_{C}\mathbf{F} \cdot d\mathbf{r} = 0$ para todo caminho fechado simples que não passe pela origem e nem a circunde.
Dica: como $C$ é um caminho fechado simples que não passa pela origem e não circunda a origem, então existe uma região aberta $A$ que ainda não contém a origem, mas contém $D,$ a região limitada por $C.$ Em $A,$ tanto $-y/(x^{2} + y^{2})$ quanto $x/(x^{2} + y^{2})$ possuem derivadas parciais contínuas e podemos aplicar o Teorema de Green.
Determine se ${\bf F}(x,y)=(e^{x}\,\sin y)\,{\bf i}+(e^{x}\,\cos y)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = e^{x}\sin(y) + K.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx+dy+2\,dz$, $C$ é a interseção do paraboloide $z=x^{2}+y^{2}$ com o plano $z=2x+2y-1$; caminhe no sentido anti-horário.
$0.$
Considere o campo
$${\bf F}(x,y,z)=(e^{z},2yz, xe^{z}+y^{2}).$$
Verifique se o campo ${\bf F}$ é conservativo.
Se ${\bf F}$ for conservativo, calcule $f(x,y,z)$ tal que $\nabla f={\bf F}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$ onde $C$ é dada por $r(t)=(\cos t, \sin t, t)$, $0\leq t\leq 2\pi.$
Sim.
$f(x,y) = x e^{z} + y^{2} z.$
$e^{2\pi} - 1.$
Calcule a integral de linha $\displaystyle\oint_{C} (x-y) dx + (x+y)dy$, $C$ é o círculo com centro na origem e raio 2, por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$8\pi.$
Calcule $\int_{C}2x\,\cos y\,dx-x^{2}\,\sin y\,dy$ ao longo dos caminhos $C$ a seguir no plano $xy.$
A parabóla $y=(x-1)^{2}$ de $(1,0)$ a $(0,1).$
O segmento de reta de $(-1,\pi)$ a $(1,0).$
O eixo $x$ de $(-1,0)$ a $(1,0).$
O astróide ${\bf r}(t)=(\cos^{3} t)\,{\bf i}+(\sin^{3}t)\,{\bf j}$, $0\leq t\leq 2\pi$, no sentido anti-horário de $(1,0)$ de volta a $(1,0).$
$-1.$
$2.$
$0.$
$0.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=2y^{3/2}\,{\bf i}+3x\sqrt{y}\,{\bf j}$ ao mover um objeto de $P(1,1)$ a $Q(2,4).$
$30.$
Calcule a área sob um arco da cicloide $x = t-\sin{t}$, $y = 1-\cos{t}$.
Queremos determinar a área da região $R$ mostrada na figura abaixo.
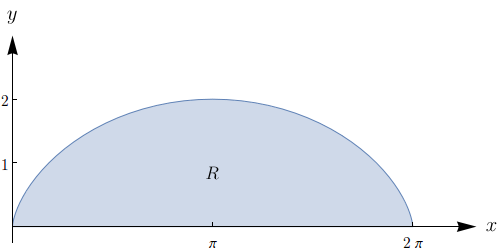
Sabemos que, se $y = f(x)$, então a integral $\int_{a}^{b}f(x)dx$ calcula a área que está abaixo do gráfico de $f$ e acima do eixo $x$, com $x$ variando entre $a$ e $b$. A princípio, poderíamos tentar encontrar uma expressão que relacionasse $x(t)$ e $y(t)$ na parametrização da cicloide, mas esse parece ser um trabalho difícil. Usaremos então o que foi provado no exercício anterior. Temos que
$$A(R) = \oint_{C}x\, dy,$$
em que $C = C_1 \cup C_2$ é a curva descrita na figura a seguir.
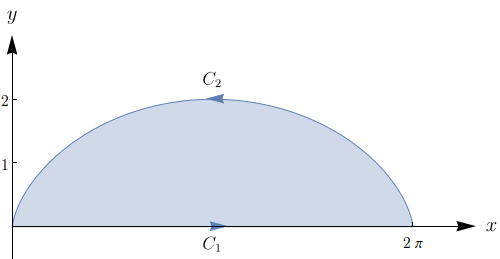
Uma parametrização de $C_1$ é $r_1(t) = (x_1(t),y_1(t)) = (t,0)$, em que $0 \leq t \leq 2\pi$. Nesse caso, $y_1'(t) = 0$. Logo,
$$\oint_{C_1}x\, dy = \int_{0}^{2\pi}(t)(0)\, dt = 0.$$
Uma parametrização de $C_2$ é $r_2(t) = (x_2(t),y_2(t)) = (t-\sin{t},1-\cos{t})$, em que $t$ varia de $2\pi$ a $0$. Nesse caso, $y_2'(t) = \sin{t}$. Logo,
$$\begin{array}{rcl}\displaystyle \oint_{C_2}x\, dy & = & \displaystyle \int_{2\pi}^{0}(t-\sin{t}) (\sin{t})\, dt \\ & = & \displaystyle \int_{0}^{2\pi}(\sin^2{t} - t\sin{t}) \, dt \\ & = & \displaystyle \int_{0}^{2\pi}\frac{1-\cos(2t)}{2}\, dt - \int_{0}^{2\pi}t\sin{t} \, dt \\ & = & \pi + 2\pi = 3\pi.\end{array}$$
Portanto, a área da região é $3\pi$.
(Observe que, para resolver a integral $\int_{0}^{2\pi}t\sin{t} \, dt$, usamos integração por partes com $u=t$ e $dv=\sin{t}\,dt$.)
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}(x^{2}y^{3}-\sqrt{x})\,dy$, $C$ é o arco da curva $y=\sqrt{x}$ de $(1,1)$ a $(4,2).$
$\dfrac{243}{8}.$
Esboce o campo vetorial $\textbf{F}=\dfrac{1}{2}(\textbf{i} + \textbf{j})$, desenhando um diagrama.
Verifique que para o vetor posição \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) valem as seguintes propriedades
\(\displaystyle \mathrm{div\,}\mathbf{r} = 3\)
\(\displaystyle \nabla\dfrac{1}{\|\mathbf{r}\|} = -\dfrac{\mathbf{r}}{\|\mathbf{r}\|^3} \)
Calcule $\int_{C}(x+y+z)\,dx+(x-2y+3z)\,dy+(2x+y-z)\,dz$, onde $C$ é a curva de $(0,0,0)$ a $(2,3,4)$ se
$C$ consiste em três segmentos de reta, o primeiro paralelo ao eixo $x$, o segundo paralelo ao eixo $y$ e o terceiro paralelo ao eixo $z$.
$C$ consite em três segmentos de reta, o primeiro paralelo ao eixo $z$, o segundo ao eixo $x$ e o terceiro paralelo ao eixo $y.$
$C$ é um segmento retilíneo.
$19.$
$35.$
$27.$
Se $C$ é o segmento de reta ligando o ponto $(x_1,y_1)$ ao ponto $(x_2,y_2)$, mostre que
$$\int_{C}x \, dy - y \, dx = x_1y_2-x_2y_1.$$
Se os vértices de um polígono, na ordem anti-horária, são
$$ (x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n), $$
mostre que a área do polígono é
$$A=\dfrac{1}{2}[(x_1y_2-x_2y_1) + (x_2y_3-x_3y_2) + \cdots + (x_{n-1}y_n - x_ny_{n-1}) + (x_ny_1-x_1y_n)].$$
Determine a área do pentágono com vértices $(0,0)$, $(2,1)$, $(1,3)$, $(0,2)$ e $(-1,1)$.
Use as equações paramétricas do segmento de reta: $x = (1-t)x_{1} + tx_{2}$ e $y = (1-t)y_{1} + ty_{2},$ $0 \leq t \leq 1.$
Aplique o Teorema de Green ao caminho $C = C_{1} \cup C_{2} \cup \cdots \cup C_{n},$ onde $C_{i}$ é o segmento ligando o ponto $(x_{i},y_{i})$ ao ponto $(x_{i + 1},y_{i + 1}),$ para cada $i = 1,\cdots, n-1.$
$\dfrac{9}{2}.$
Dados ${\bf F}(x,y,z)=y^{2}\,\cos z\,{\bf i}+2xy\,\cos z\,{\bf j}-xy^{2}\,\sin z\,{\bf k}$, $C: {\bf r}(t)=t^{2}\,{\bf i}+\sin t\,{\bf j}+t\,{\bf k}$, $0\leq t\leq \pi.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = xy^{2} \cos(z);$
$0.$
Determine o campo vetorial gradiente de $f(x,y,z) = \sqrt{x^2+y^2+z^2}$.
$\nabla f(x,y,z) = \dfrac{x\textbf{i} + y\textbf{j} + z \textbf{k}}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Mostre que, se um campo vetorial ${\bf F}=P\,{\bf i}+Q\,{\bf j}+R\,{\bf k}$ é conservativo e $P$, $Q$, $R$ têm derivadas parciais de primeira ordem contínuas, então
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}, \,\,\,\,\,\frac{\partial P}{\partial z}=\frac{\partial R}{\partial x},\,\,\,\,\,\frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}$$
Se $f$ é uma função potencial de $\mathbf{F},$ então $f_{x} = P,$ $f_{y} = Q$ e $f_{z} = R.$ Como $P, Q$ e $R$ possuem derivadas parciais de primeira ordem contínuas, então pelo Teorema de Clairaut, temos $f_{xy} = f_{yx},$ $f_{yz} = f_{zy}$ e $f_{xz} = f_{zx}.$
Considere o campo vetorial
$${\bf F}(x,y)=\bigg(e^{x}\ln(y)-\frac{e^{y}}{x}\bigg)\,{\bf i}+\bigg(\frac{e^{x}}{y}-e^{y}\ln(x)\bigg)\,{\bf j}.$$
O campo ${\bf F}$ é conservativo? Justifique sua resposta.
Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é qualquer caminho ligando o ponto $(1,1)$ ao ponto $(3,3).$
Sim.
$0.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (\sqrt{x} + y^3,x^2+\sqrt{y})$, $C$ consiste no arco da curva $y = \sin{x}$ de $(0,0)$ a $(\pi,0)$ e no segmento de reta $(\pi,0)$ a $(0,0)$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$\dfrac{4}{3} - 2\pi.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=x^{2}\,{\bf i}+(x-y)\,{\bf j}$, ${\bf r}(t)=(t,\sin t)$, $0\leq t\leq \pi.$
$\displaystyle \frac{\pi^{3}}{3} - 2.$
Determine o trabalho $W=\int_{C}{\bf F}\cdot d{\bf r}$ realizado pelo campo de força ${\bf F}(x,y)=x^{2}(x-y)\,{\bf i}+xy^{2}\,{\bf j}$ em uma partícula que se move da origem ao longo do eixo $x$ para $(1,0)$, em seguida ao longo de um segmento de arco de circunferência $x^{2}+y^{2}=1$ até $(0,1)$ e então volta à origem ao longo do eixo $y.$
$\dfrac{\pi}{8}.$
A força em um ponto $(x,y,z)$ em três dimensões é dada por ${\bf F}(x,y,z)=y\,{\bf i}+z\,{\bf j}+x\,{\bf k}$. Ache o trabalho realizado por ${\bf F}(x,y,z)$ ao longo da cúbica reversa $x=t$, $y=t^{2}$, $z=t^{3}$ de $(0,0,0)$ a $(2,4,8).$
$\dfrac{412}{15}.$
Dados ${\bf F}(x,y,z)=e^{y}\,{\bf i}+xe^{y}\,{\bf j}+(z+1)e^{z}\,{\bf k}$, $C: {\bf r}(t)=t\,{\bf i}+t^{2}\,{\bf j}+t^{3}\,{\bf k}$, $0\leq t\leq 1.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = x e^{y} + ze^{z};$
$2e.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}(2x+9z)\,ds$, $C:\,x=t,\, y=t^{2},\, z=t^{3},\, 0\leq t\leq 1.$
$\displaystyle \frac{1}{6}\left(14^{3/2} - 1\right).$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}\dfrac{-y}{4x^{2}+y^{2}}\,dx+\dfrac{x}{4x^{2}+y^{2}}\,dy$, $C$ tem por imagem a elipse $4x^{2}+y^{2}=9$ e o sentido de percurso é o anti-horário.
$\displaystyle \pi.$
As linhas de escoamento (ou linhas de corrente) de um campo vetorial são as trajetórias seguidas por uma partícula cujo campo de velocidade é um campo vetorial dado. Assim, os vetores do campo vetorial são tangentes a suas linhas de escoamento.
Use um esboço do campo vetorial $\textbf{F}(x,y) = x\textbf{i} - y\textbf{j}$ para desenhar algumas linhas de escoamento. Desses seus esboços é possível descobrir qual é a equação das linhas de escoamento?
Se as equações paramétricas de uma linha de escoamento são $x=x(t)$ e $y=y(t)$, explique por que essas funções satisfazem as equações diferenciais $dx/dt = x$ e $dy/dt = -y$. Resolva então as equações de forma a obter uma equação da linha de escoamento que passe pelo ponto $(1,1)$.
Um homem pesando $160$ lb carrega uma lata de tinta de $25$ lb por uma escada helicoidal em torno de um silo com raio de $20$ pés. Se o silo tem $90$ pés de altura e o homem dá três voltas completas em torno do silo, quanto trabalho é realizado pelo homem contra a gravidade para subir ao topo?
$16650$ ft-lb.
A força em um ponto $(x,y)$ de um plano coordenado é ${\bf F}(x,y)=(x^{2}+y^{2})\,{\bf i}+xy\,{\bf j}$. Ache o trabalho realizado por ${\bf F}(x,y)$ ao longo do gráfico de $y=x^{3}$ de $(0,0)$ a $(2,8).$
$\dfrac{1592}{21}.$
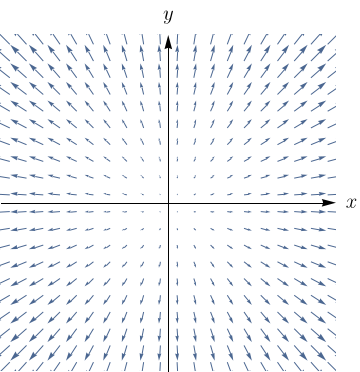
Faça uma correspondência entre as funções $f$ e os desenhos de seus campos vetoriais gradientes (rotulados de I-IV). Justifique.
- $f(x,y) = x^2+y^2$
- $f(x,y) = (x+y)^2$.
- $f(x,y) = x(x+y)$.
- $f(x,y) = \sin{\sqrt{x^2+y^2}}$.
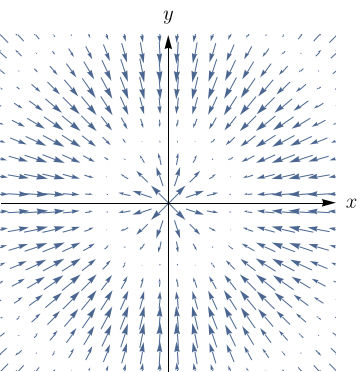
II

III
IV
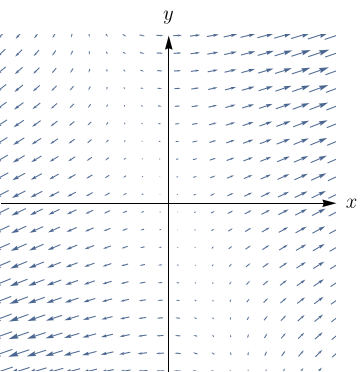
- III.
- IV.
- II.
- I.
Uma partícula desloca-se em um campo de forças dado por ${\bf F}(x,y,z)=-y\,{\bf i}+x\,{\bf j}+z\,{\bf k}.$ Calcule o trabalho realizado por ${\bf F}$ no deslocamento da partícula de ${\bf r}(a)$ até ${\bf r}(b)$, sendo dados:
${\bf r}(t)=(\cos t, \sin t,t)$, $a=0$ e $b=2\pi.$
${\bf r}(t)=(2t+1,t-1,t)$, $a=1$ e $b=2.$
${\bf r}(t)=(\cos t,0, \sin t)$, $a=0$ e $b=2\pi.$
$2\pi(1 + \pi).$
$\dfrac{9}{2}.$
$0.$
Calcule $\displaystyle\int_{C}\dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy$ onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida no semiplano $y>0$, tal que $C(0)=(1,1)$ e $C(1)=(-2,3).$
$\pi.$
Determine se ${\bf F}(x,y)=e^{x}\,\cos y\,{\bf i}+e^{x}\,\sin y\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
Calcule a integral de linha, onde $C$ é a curva dada. $\displaystyle\int_{C}x\,dx-y\,dy$, $C$ é o segmento de extremidades $(1,1)$ e $(2,3)$, percorrido no sentido de $(1,1)$ para $(2,3).$
Uma representação paramétrica para o segmento de reta $C$ é
$$\begin{array}{lr}x=1+t \\y=1+2t\\\end{array}\;\;\;\; 0\leq t \leq 1.$$
Logo,
$$\begin{array}{lr}dx=dt \\dy=2\,dt\\\end{array}$$
Assim,
$$\int_{C}x\,dx-y\,dy=\int_{0}^{1}(1+t)\cdot (dt)+(1+2t)\cdot(2\,dt)=\int_{0}^{1}(1+t+2+4t)\,dt$$
$$=\int_{0}^{1}(3+5t)\,dt=\bigg(3t+\frac{5}{2}t^{2}\bigg)\bigg|_{0}^{1}=3+\frac{5}{2}=\frac{11}{2}.$$
Determine o campo vetorial gradiente $\nabla f$ de $f(x,y) = \sqrt{x^2+y^2}$ e o esboce.
Use o Teorema de Green para determinar o trabalho realizado pelo campo de forças \(\displaystyle\mathbf{F}(x,y)=\sqrt{y}\textbf{i}+\sqrt{x}\textbf{j}\) sobre uma partícula que percorre uma vez, no sentido anti-horário, a curva fechada dada pelas equações \(y=0\), \(x=2\) e \(y=x^3/4\).
Dados ${\bf F}(x,y,z)=yz\,{\bf i}+xz\,{\bf j}+(xy+2z)\,{\bf k}$, $C$ é o segmento de reta de $(1,0,-2)$ a $(4,6,3).$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = xyz + z^{2};$
$77.$
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y)=(y,3x)$ e $C$ é a elipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$, percorrida no sentido anti-horário.
$-2\pi ab.$
Determine se ${\bf F}(x,y,z)=(e^{x}\,\cos y)\,{\bf i}-(e^{x}\,\sin y)\,{\bf j}+z\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = e^{x}\cos(y) + \dfrac{z^{2}}{2} + K.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x^{2}y\sqrt{z}\,dz$, $C:\,x=t^{3},\, y=t,\, z=t^{2},\, 0\leq t\leq 1.$
$\dfrac{1}{5}.$
Dados ${\bf F}(x,y)=x^{2}\,{\bf i}+y^{2}\,{\bf j}$, $C$ é o arco da parábola $y=2x^{2}$ de $(-1,2)$ a $(2,8).$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y) = \dfrac{x^{3} + y^{3}}{3};$
$171.$
Calcule a integral de linha $\displaystyle\oint_{C} xy \, dx + x^2y^3 \, dy$, $C$ é o triângulo com vértices $(0,0)$, $(1,0)$ e $(1,2)$ por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$\dfrac{2}{3}.$
Calcule a integral de linha $\displaystyle\int_{C}\,dx+\,dy$, onde $C$ é a poligonal de vértices $A_{0}=(0,0)$, $A_{1}=(1,2)$, $A_{2}=(-1,3)$, $A_{3}=(-2,1)$ e $A_{4}=(-1,-1)$, sendo $C$ orientada de $A_{0}$ para $A_{4}.$
$\displaystyle -2.$
Calcule $\displaystyle\int_{(-1,0)}^{(1,0)}\dfrac{x}{x^{2}+y^{2}}\,dx+\dfrac{y}{x^{2}+y^{2}}\,dy$.
$\displaystyle \dfrac{\pi}{4} + \arctan\left( \dfrac{2}{3} \right).$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xyz\,ds$, onde $C$ é a hélice ${\bf r}(t)=(\cos t,\sin t,3t)$, $0\leq t\leq 4\pi.$
$-3\sqrt{10}\pi.$
Determine o campo vetorial gradiente de $f(x,y) = \ln(x + 2y)$.
$\nabla f(x,y) = \dfrac{\textbf{i} + 2\textbf{j}}{x + 2y}.$
Calcule a área da região $R$ delimitada pela cardioide $\mathbf{r}(t) = (x(t),y(t))$, em que $x(t) = 2\cos{t}-\cos{2t}$ e $y(t) = 2\sin{t}-\sin{2t}$, $t \in [0,2\pi]$.
$6\pi.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx-y\,dy$, $C$ é o segmento de extremidades $(1,1)$ e $(2,3)$, percorrido no sentido de $(1,1)$ para $(2,3).$
$\displaystyle -\frac{5}{2}.$
Sejam \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\), \(r=\|\mathbf{r}\|\), \(f\) uma função diferenciável de uma variável e \(\mathbf{F}(\mathbf{r})=f(r)\mathbf{r}\).
Mostre que \[\nabla f(r) = \dfrac{f'(r)}{r}\mathbf{r}.\]
Use o resultado anterior para mostrar que \(\displaystyle \mathbf{F}=3f(r)+rf'(r). \)
Um campo vetorial inverso do quadrado é da forma:
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$. Um exemplo de um campo inverso do quadrado é o campo gravitacional ${\bf F}=-(mMG){\bf r}/|{\bf r}|^{3}$. Determine o trabalho realizado pelo campo gravitacional quando a Terra se move do afélio (em uma distância máxima de $1,52\times 10^{8}\,km$ do Sol) ao periélio (em uma distância mínima de $1,47\times 10^{8}\,km)$. (Use os valores $m=5,97\times 10^{24}\,kg$, $M=1,99\times 10^{30}\,kg$ e $G=6,67\times 10^{-11}\,N\cdot m^{2}/kg^{2}.$)
$\approx 1,77 \times 10^{35}$ J.
Esboce o campo vetorial $\textbf{F}= \dfrac{y\textbf{i} - x\textbf{j}}{\sqrt{x^2+y^2}}$, desenhando um diagrama.
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$, ${\bf r}(t)=(\cos t,\sin t,t)$, $0\leq t\leq 2\pi.$
$2\pi^{2}.$
Suponha que ${\bf F}$ seja um campo vetorial inverso do quadrado, ou seja,
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}.$ Determine o trabalho realizado por ${\bf F}$ ao mover um objeto de um ponto $P_{1}$ por um caminho para um ponto $P_{2}$ em termos da distância $d_{1}$ e $d_{2}$ desses pontos à origem.
$c\left(\dfrac{1}{d_{1}} - \dfrac{1}{d_{2}}\right).$
Determine se o conjunto $\{(x,y)|\,x>0,\,y>0\}$ é ou não:
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x>0,\,y>0\}$ representa o primeiro quadrante, excluindo os eixos. Então:
$D$ é aberto, pois em torno de cada ponto em $D$, podemos colocar um disco que se encontra em $D.$
$D$ é conexo, pois o segmento de reta que une dois pontos quaisquer de $D$ encontra-se em $D.$
$D$ é simplesmente conexo, pois ele é conexo e não tem buracos.
Seja $\Omega=\{(x,y)\in \mathbb{R}^{2}|\,(x,y)\notin A\}$, onde $A$ é a semirreta $\{(x,y)\in \mathbb{R}^{2}|\,y=0\,e\,x\geq 0\}$. Calcule
$$\int_{C}\frac{-y}{x^{2}+y^{2}}\,dx+\frac{x}{x^{2}+y^{2}}\,dy,$$
onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida em $\Omega$, tal que $C(0)=(1,1)$ e $C(1)=(1,-1).$
$\dfrac{3\pi}{2}.$
$$\int_{C} P\,dx+Q\,dy=\iint\limits_{B}\bigg(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\bigg)\,dxdy,$$
onde $B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(1,1)$, $C$ é a fronteira de $B$ orientada no sentido anti-horário, $P(x,y)=x^{2}-y$ e $Q(x,y)=x^{2}+y.$
$\displaystyle \int_{C} P\,dx+Q\,dy = \dfrac{7}{6} = \iint\limits_{B}\bigg(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\bigg)\,dxdy.$
Determine o campo vetorial gradiente $\nabla f$ de $f(x,y) = x^2-y$ e o esboce.
Determine o trabalho $W=\int_{C}{\bf F}\cdot d{\bf r}$ realizado pelo campo de força ${\bf F}(x,y)=x\,{\bf i}+(x^{3}+3xy^{2})\,{\bf j}$ em uma partícula que inicialmente está no ponto $(-2,0)$, se move ao longo do eixo $x$ para $(2,0)$ e ao longo da semicircunferência $y=\sqrt{4-x^{2}}$ até o ponto inicial.
Calcule a integral de linha
$$\int_{C}e^{2y}\,dx+(1+2xe^{2y})\,dy,$$
onde $C$ é a curva dada por $r(t)=(te^{t},1+\sin(\pi t/2))$, $0\leq t\leq 1.$ (Sugestão: verifique se o campo é conservativo.)
$e^{5} + 1.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=\sin{x}\,{\bf i}+\cos{y}\,{\bf j}+xz\,{\bf k}$, ${\bf r}(t)=t^{3}\,{\bf i}-t^{2}\,{\bf j}+t\,{\bf k}$, $0\leq t\leq 1.$
$\dfrac{6}{5} - \cos(1) - \sin(1).$
Seja ${\bf E}(x,y)=\dfrac{1}{x^{2}+y^{2}}\dfrac{x\,{\bf i}+y\,{\bf j}}{\sqrt{x^{2}+y^{2}}}$ e seja $C$ a curva dada por $x=t$ e $y=1-t^{4}$, $-1\leq t\leq 1.$
Que valor é razoável esperar para $\int_{C}{\bf E}\cdot d{\bf l}$? Por quê? (O ${\bf l}$ desempenha aqui o mesmo papel que ${\bf r}:{\bf l}(t)={\bf r}(t).$)
Calcule $\int_{C}{\bf E}\cdot d{\bf l}.$
$0.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}dx+xy\,dy+z\,dz$, $C$ é a interseção de $x^{2}+y^{2}+z^{2}=2$, $x\geq 0$, $y\geq 0$ e $z\geq 0$, com o plano $y=x$; o sentido de percurso é do ponto $(0,0,\sqrt{2})$ para $(1,1,0).$
$\displaystyle \frac{1}{3}.$
Determine se ${\bf F}(x,y,z)=\dfrac{x}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf i}+\dfrac{y}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf j}+\dfrac{z}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = -\dfrac{1}{2(x^2 + y^{2} +z^{2})} + K.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=x^{2}\,{\bf i}+xy\,{\bf j}$ sobre uma partícula que dá uma volta no círculo $x^{2}+y^{2}=4$ no sentido anti-horário.
$0.$
- Esboce o campo vetorial $\textbf{F}(x,y) = \textbf{i} + x\textbf{j}$ e algumas linhas de escoamento. Qual é o formato que essas linhas de escoamento parecem ter?
- Se as equações paramétricas das linhas de escoamento são $x=x(t)$ e $y=y(t)$, que equações diferenciais essas funções satisfazem? Deduza que $dy/dx = x$.
- Se uma partícula está na origem no instante inicial e o campo de velocidade é dado por $\textbf{F}$, determine uma equação para a trajetória percorrida por ela.
Calcule a integral de linha $\displaystyle\int_{C}x^{2}\,dx+y^{2}\,dy+z^{2}\,dz$, onde $C$ é o segmento de reta que liga o ponto $(1,0,1)$ ao ponto $(-2,2,2).$.
$\displaystyle \frac{2}{3}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=x^{2}\,{\bf i}+y^{2}\,{\bf j}+z^{2}\,{\bf k}$, ${\bf r}(t)=(2\cos t,3\sin t,t)$, $0\leq t\leq 2\pi.$
$\dfrac{8\pi^{3}}{3}.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C} \sin{y} \, dx + x\cos{y} \, dy$, $C$ é a elipse $x^2 + xy + y^2 = 1$.
$0.$
Calcule $\displaystyle \int_{C}{\bf E}\cdot d{\bf l}$, onde ${\bf E}(x,y)=\dfrac{1}{x^{2}+y^{2}}\dfrac{x\,{\bf i}+y\,{\bf j}}{\sqrt{x^{2}+y^{2}}}$ e $C: {\bf r}(t)=(t,1)$, $-1\leq t\leq 1.$ ( O ${\bf l}$ desempenha aqui o mesmo papel que ${\bf r}:{\bf l}(t)={\bf r}(t).$)
$0.$
A figura mostra uma curva $C$ e um mapa de contorno de uma função $f$ cujo gradiente é contínuo. Determine $\int_{C}\nabla f\cdot d{\bf r}.$

$40.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y,z)=(y+z)\,{\bf i}+(x+z)\,{\bf j}+(x+y)\,{\bf k}$ sobre uma partícula que se move ao longo do segmento de reta $(1,0,0)$ a $(3,4,2).$
$26.$
Esboce o campo vetorial ${\bf F}(x,y)=(x-y)\textbf{i} + x \textbf{j}$, desenhando um diagrama.
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y,z)=(yz,2xz,xy+2z)$ e $C$ é o segmento de reta que liga o ponto $(1,0,1)$ ao ponto $(-2,2,2).$
$-7.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=x^{2}\,{\bf j}$, ${\bf r}(t)=(t^{2},3)$, $-1\leq t\leq 1.$
$0.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}e^y \, dx + 2xe^y \, dy$, $C$ é o quadrado de lados $x=0$, $x=1$, $y=0$ e $y=1$.
$e - 1.$
Calcule o trabalho realizado pela força ${\bf F}(x,y)=xy\,{\bf i}+y^{2}\,{\bf j}$ ao mover uma partícula da origem ao longo da reta $y=x$ até $(1,1)$ e então de volta à origem ao longo da curva $y=x^{2}.$
$\dfrac{1}{12}.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xe^{yz}\,ds$, $C$ é o segmento de reta de $(0,0,0)$ a $(1,2,3).$
$\dfrac{\sqrt{14}}{12}\left(e^{6} - 1 \right).$
Use o Teorema de Green para determinar o trabalho realizado pelo campo de forças \(\displaystyle\textbf{F}(x,y)=xy\textbf{i}+(\dfrac{1}{2}x^2+xy)\textbf{j}\) sobre uma partícula que se move ao longo do caminho que começa em \((5,0)\), percorre o semicírculo superior \(x^2+y^2=25\) e retorna ao seu ponto de partida ao longo do eixo \(x\).
\(\dfrac{250}{3}\)
Calcule a integral de linha $\displaystyle\int_{C}\sqrt[3]{x}\,dx+\dfrac{dy}{1+y^{2}}$, onde $C$ é a curva na figura abaixo.

$0.$
Uma partícula se move em um campo de velocidade $\textbf{V}(x,y) = (x^2,x+y^2)$. Se ela está na posição $(2,1)$ no instante $t=3$, estime sua posição no instante $t=3,01$.
$(2,04;1,03).$
Seja ${\bf F}(x,y)=(e^{x}\,\cos y+y, x-e^{x}\,\sin y)$. Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é o arco de circunferência que une o ponto $(-\sqrt{2}/2, \sqrt{2}/2)$ ao ponto $(1,0)$. Veja a figura abaixo.
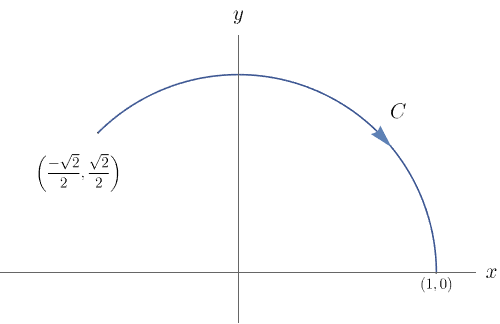
Notemos que ${\bf F}$ é um campo vetorial conservativo, pois: ${\bf F}$ é definido em todo $\mathbb{R}^{2}$; $P(x,y)=e^{x}\,\cos y+y$ e $Q(x,y)=x-e^{x}\,\sin y$ possuem derivadas parciais de primeira ordem contínuas; $\dfrac{\partial P}{\partial y}(x,y)=1-e^{x}\,\sin y=\dfrac{\partial Q}{\partial x}(x,y).$
Sendo $F$ conservativo, existe $f$ tal que $\nabla f={\bf F}.$ Vamos encontrar $f$. Temos que
$$f_{x}(x,y)=P(x,y) \mbox{ e } f_{y}(x,y)=Q(x,y).$$
Então,
$$\label{(2)}f_{x}(x,y)=e^{x}\,\cos y+y\Rightarrow f(x,y)=e^{x}\,\cos y+y+g(y).$$
Logo, temos que
$$f_{y}(x,y)=-e^{x}\,\sin y+x+g'(y).$$
Como $f_{y}(x,y)=Q(x,y)$, obtemos que
$$-e^{x}\,\sin y+x+g'(y)=x-e^{x}\,\sin y\Rightarrow g'(y)=0\Rightarrow g(y)=C.$$
Assim, tomando $C=0$ segue que
$$f(x,y)=e^{x}\,\cos y+xy.$$
Do resultado acima e pelo Teorema Fundamental da Integral de Linha, temos que
$$\int_{C}{\bf F}\cdot d{\bf r}=f(1,0)-f\bigg(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\bigg)=e-e^{-\frac{\sqrt{2}}{2}}\,\cdot\cos\bigg(\frac{\sqrt{2}}{2}\bigg)+\frac{1}{2}.$$
Calcule
$$\oint_{C} \dfrac{-y}{x^2+y^2} \, dx + \dfrac{x}{x^2 + y^2} \, dy,$$
em que $C$ é a curva

Podemos escrever $C$ como $C_1 \cup C_2$, em que $C_1$ e $C_2$ são as curvas dadas abaixo.
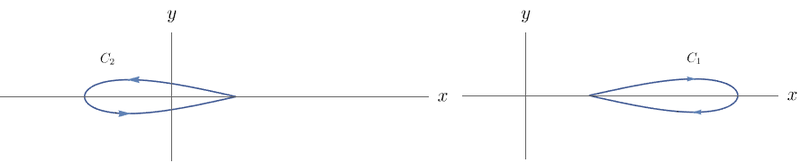
Seja $A$ um aberto simplesmente conexo que contém $C_1$ e não contém a origem. O campo $\mathbf{F}$ restrito a $A$ é conservativo, pois $A$ é aberto e simplesmente conexo, $P(x,y) = \dfrac{-y}{x^2 + y^2}$ e $Q(x,y) = \dfrac{x}{x^2 + y^2}$ possuem derivadas de primeira ordem contínuas em $A$ e $P$ e $Q$ satisfazem a relação $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$. Então,
$$\oint_{C_1}\mathbf{F} \cdot\, d\mathbf{r} = 0.$$
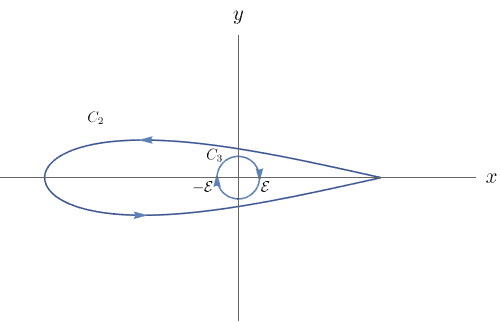
Não podemos proceder de maneira análoga em $C_2$, já que todo aberto $B$ que contém a curva $C_2$ e não contém a origem não será simplesmente conexo. Com isso, não conseguimos garantir que o campo $\mathbf{F}$ restrito a $B$ é conservativo (observe que, a princípio, não podemos afirmar que o campo é não conservativo).
A ideia para contornar esse problema é ``isolar" a origem com uma curva fechada $C_3$, a princípio arbitrária. Vamos escolher essa curva $C_3$ de maneira conveniente para que consigamos resolver o problema. Seja $\varepsilon > 0$ pequeno o suficiente para que a curva $C_3$ parametrizada por $r(t) = (\varepsilon \cos{t}, \varepsilon \sin{t})$, com $t$ variando de $2\pi$ a $0$, não intercepte a curva $C_2$ e esteja entre a curva $C_2$ e a origem.
Considere $D_1 = \{(x,y) \in \mathbb{R}^2: (x,y) \mbox{ está entre } C_2 \mbox{ e } C_3 \mbox{ e } y \geq 0\}$ e $D_2 = \{(x,y) \in \mathbb{R}^2: (x,y) \mbox{ está entre } C_2 \mbox{ e } C_3 \mbox{ e } y \leq 0\}$. As curvas que delimitam $D_1$ e $D_2$ são $C_{D_1}= C_{2}^+\cup C_{a}\cup C_{3}^+\cup C_{b}$ e $C_{D_2}=C_{2}^-\cup -C_{b}\cup C_{3}^- \cup -C_{a}$, respectivamente, e estão ilustradas a seguir.
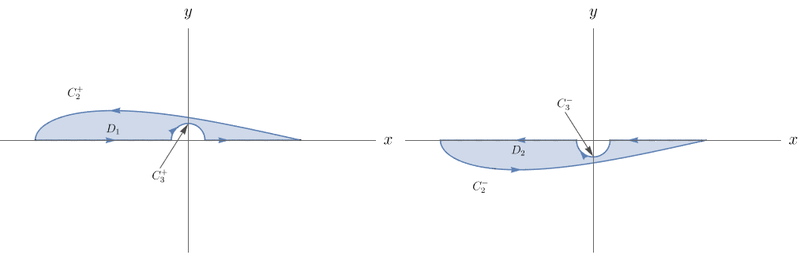
Note que
$$\oint_{C_{D_1}} \mathbf{F} \cdot d\mathbf{r} = \int_{C^+_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C_a} \mathbf{F} \cdot d\mathbf{r} + \int_{C^+_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C_b} \mathbf{F} \cdot d\mathbf{r} \qquad (\star)$$
e
$$\oint_{C_{D_2}} \mathbf{F} \cdot d\mathbf{r} = \int_{C^-_2} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_a} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_3} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_b} \mathbf{F} \cdot d\mathbf{r} \qquad (\star \star).$$
Como $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$, temos, pelo Teorema de Green,
$$\displaystyle\oint_{C_{D_1}} \mathbf{F} \cdot d\mathbf{r} = \iint\limits_{D_1} 0 \, dA = 0$$
e
$$\displaystyle\oint_{C_{D_2}} \mathbf{F} \cdot d\mathbf{r} = \iint\limits_{D_2} 0 \, dA = 0.$$
Somando as equações ($\star$) e ($\star \star$), obtemos
$$\int_{C^+_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C^+_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_3} \mathbf{F} \cdot d\mathbf{r} = 0,$$
isto é,
$$\int_{C_2} \mathbf{F} \cdot d\mathbf{r} = -\int_{C_3} \mathbf{F} \cdot d\mathbf{r} = \int_{-C_3} \mathbf{F} \cdot d\mathbf{r}.$$
Assim, basta determinar $\int_{-C_3} \mathbf{F} \cdot d\mathbf{r}$. A parametrização de $-C_3$ é $r(t) = (\varepsilon \cos{t}, \varepsilon \sin{t})$, com $t$ variando de $0$ a $2\pi$. Daí,
$$\begin{array}{rcl}\displaystyle \int_{-C_3} \mathbf{F} \cdot d\mathbf{r} & = & \displaystyle \int_{0}^{2\pi} \left(\frac{-\varepsilon \sin{t}}{\varepsilon^2},\frac{\varepsilon \cos{t}}{\varepsilon^2}\right) \cdot (-\varepsilon \sin{t}, \varepsilon \cos{t}) \, dt \\& = & \displaystyle \int_{0}^{2\pi} 1 \, dt = 2\pi.\end{array}$$
Portanto,
$$\oint_{C} \mathbf{F} \cdot d\mathbf{r} = \oint_{C_1} \mathbf{F} \cdot d\mathbf{r} + \oint_{C_2} \mathbf{F} \cdot d\mathbf{r} = 0 + 2\pi = 2\pi.$$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx+y\,dy$, $C:\,x=t^{2},\,y=\sin t$, $0\leq t\leq \pi/2.$
$\displaystyle \frac{\pi^{4}}{32} + \frac{1}{2}.$
Determine o trabalho $W = \int_{C}\mathbf{F}\cdot\, d\mathbf{r}$ realizado pelo campo de força
$$\mathbf{F}(x,y) = x\mathbf{i} + (x^3 + 3xy^2)\mathbf{j}$$
em uma partícula que inicialmente está no ponto $(-2,0)$, se move ao longo do eixo $x$ para $(2,0)$ e então se move ao longo da semicircunferência $y = \sqrt{4-x^2}$ até o ponto inicial.
$12\pi.$
Seja $D$ a região limitada por um caminho fechado e simples $C$ no plano $xy$. As coordenadas do centroide $(\bar{x},\bar{y})$ de $D$ são
$$\bar{x} = \dfrac{1}{2A}\oint_{C}x^2 \, dy \quad \quad\quad\quad \bar{y} = -\dfrac{1}{2A}\oint_{C}y^2 \, dx,$$
em que $A$ é a área de $D$. Encontre o centroide de um quarto de uma região circular de raio $a$.
$\displaystyle \left(\frac{4a}{3\pi},\frac{4a}{3\pi} \right),$ se a região for a parte do disco $x^{2} + y^{2} = a^{2}$ no primeiro quadrante.
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=(x+y)\,{\bf i}+(y-z)\,{\bf j}+z^{2}\,{\bf k}$, ${\bf r}(t)=t^{2}\,{\bf i}+t^{3}\,{\bf j}+t^{2}\,{\bf k}$, $0\leq t\leq 1.$
$\dfrac{17}{15}.$
Dado um campo vetorial \(\mathbf{F}\), uma curva \(C\) é chamada de linha de fluxo deste campo se \(\mathbf{F}\) for um vetor tangente a \(C\) em cada ponto ao longo de \(C\).
Sejam \(C\) uma linha de fluxo de \(\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}\) e \((x,y)\) um ponto em \(C\) para o qual \(y\neq 0\). Mostre que as linhas de fluxo satisfazem a equação diferencial \[ \dfrac{dy}{dx} = -\dfrac{x}{y}. \]
Resolva a equação diferencial do item anterior, por separação de variáveis, e mostre que as linhas de fluxo são círculos concêntricos centrados na origem, ou seja, da forma \(x^2+y^2=K\).
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,\sin{y}\,ds$, $C$ é o segmento de reta que liga $(0,3)$ a $(4,6).$
$\displaystyle \frac{20}{6} \left(\sin(6) - 3\cos(6) - \sin(3) \right).$
Determine se ${\bf F}(x,y,z)=e^{y+2z}({\bf i}+x\,{\bf j}+2x\,{\bf k})$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = xe^{y + 2z} + K.$
Esboce o campo vetorial $\textbf{F}= \dfrac{y\textbf{i} + x\textbf{j}}{\sqrt{x^2+y^2}}$, desenhando um diagrama.
Calcule $\displaystyle\int_{(1,1)}^{(2,2)} y\,dx+x\,dy$.
$3.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}\dfrac{-y}{x^2+y^2} \, dx + \dfrac{ x}{x^2+y^2} \, dy$, $C$ curva fechada, $C^1$ por partes, simples e fronteira de um conjunto $B$ cujo interior contém o círculo $x^2 + y^2 \leq 1$. (Sugestão: Aplique o Teorema de Green à região $K$ compreendida entre a curva $C$ e a circunferência.)
$2\pi.$
Determine se ${\bf F}(x,y)=y\,{\bf i}+x\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = xy + K.$
Um homem pesando $160$ lb carrega uma lata de tinta de $25$ lb por uma escada helicoidal em torno de um silo com raio de $20$ pés. Se o silo tem $90$ pés de altura e o homem dá três voltas completas em torno do silo. Além disso, $9$ lb de tinta vazam da lata de modo contínuo e uniforme durante a subida do homem. Quanto trabalho é realizado?
$16245$ ft-lb.
Esboce o campo vetorial $\textbf{F}= y\textbf{i} + \dfrac{1}{2}\textbf{j}$, desenhando um diagrama.
Seja ${\bf F}:\mathbb{R}^{2} \to \mathbb{R}^{2}$ um campo vetorial contínuo tal que, para todo $(x,y)$, ${\bf F}(x,y)$ é paralelo ao vetor $x\,{\bf i}+y\,{\bf j}$. Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf r}:[a,b]\to \mathbb{R}^{2}$ é uma curva de classe $C^{1}$, cuja imagem está contida na circunferência de centro na origem e raio $r>0$. Interprete geometricamente.
$0.$
Seja ${\bf F}:\Omega\subset \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ contínuo no aberto $\Omega$. Prove que uma condição necessária para que ${\bf F}$ seja
conservativo é que $\int_{C}{\bf F}\cdot d{\bf r}=0$ para toda curva $C$ fechada, de classe $C^{1}$ por partes, com imagem contida em $\Omega.$
Se $C$ é uma curva fechada em $\Omega$ parametrizada por $\mathbf{r}(t),$ com $a \leq t \leq b,$ $\mathbf{r}(a) = \mathbf{r}(b)$ e $\mathbf{F} = \nabla f,$ então $\int_{C}{\bf F}\cdot d{\bf r} = f(\mathbf{r}(a)) - f(\mathbf{r}(b)) = 0.$
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas para o caso em que $f(x,y) = 1$:
$$\iint\limits_{R} dxdy = \iint\limits_{R}\left|\dfrac{\partial(x,y)}{\partial(u,v)}\right|\, dudv.$$
Aqui, $R$ é a região do plano $xy$ que corresponde à região $S$ do plano $uv$ sob a transformação dada por $x=g(u,v)$, $y=h(u,v)$. (Sugestão: observe que o lado esquerdo é $A(R)$. Converta a integral de linha sobre $\partial R$ para uma integral de linha sobre $\partial S$ e aplique o Teorema de Green no plano $uv$.)
Dica: pelo Teorema de Green, $A(R) = \displaystyle \iint_{R} dxdy = \int_{\partial R} x dy.$ Escolhendo a orientação positiva em $\partial S$ correspondente a orientação positiva em $\partial R,$ segue que
$$\displaystyle \int_{\partial R} x dy = \int_{\partial S} g(u,v) \dfrac{\partial h}{\partial u} du + g(u,v) \frac{\partial h}{\partial v} dv.$$
Conclua utilizando o Teorema de Green no plano $uv$ e a Regra da Cadeia.
Uma partícula move-se no plano de modo que no instante $t$ sua posição é dada por ${\bf r}(t)=(t,t^{2})$. Calcule o trabalho realizado pelo campo de forças ${\bf F}(x,y)=(x+y)\,{\bf i}+(x-y)\,{\bf j}$ no deslocamento da partícula de ${\bf r}(0)$ até ${\bf r}(1).$
$1.$
Determine se ${\bf F}(x,y)=(2x-3y)\,{\bf i}+(-3x+4y-8)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = x^2 - 3xy + 2y^2 -8y + K.$
Calcule $\int_{C}\mathbf{F}\cdot\, d\mathbf{r}$, em que
$$\mathbf{F}(x,y) = (x^2+y)\mathbf{i} + (3x-y^2)\mathbf{j}$$
e $C$ é a fronteira orientada positivamente de uma região $D$ que tem área 6.
$12.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xy\,dx+(x-y)\,dy$, $C$ consiste nos segmentos de reta de $(0,0)$ a $(2,0)$ e de $(2,0)$ a $(3,2).$
$\displaystyle \frac{17}{3}.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (2x+y)\mathbf{i} + (3x-y)\mathbf{j}$, $C$ é uma curva fechada, simples, $C^1$ por partes, orientada no sentido positivo, cuja imagem é a fronteira de um compacto $B$ com área $\alpha$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$2\times$(Área de $B$).
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}(x+yz)\,dx+2x\,dy+xyz\,dz$, $C$ consiste nos segmentos de reta de $(1,0,1)$ a $(2,3,1)$ e de $(2,3,1)$ a $(2,5,2).$
$\dfrac{97}{3}.$
Seja
$${\bf F}(x,y)=\bigg(\frac{-y}{x^{2}+y^{2}},\frac{x}{x^{2}+y^{2}}+3y\bigg)$$
um campo vetorial em $\mathbb{R}^{2}$. Calcule a integral de linha do campo ${\bf F}$ ao longo das curvas
$C_{1}$ e $C_{2}$, orientadas no sentido anti-horário, onde:
$C_{1}$ é a circunferência de equação $x^{2}+y^{2}=4.$
$C_{2}$ é a fronteira do retângulo $R=\{(x,y)\in \mathbb{R}^{2}|\,-\pi \leq x \leq \pi,-3 \leq y \leq 3\}.$
$0.$
$0.$
Calcule $\displaystyle\int_{C}(\sin(xy)+xy\,\cos(xy))\,dx+x^{2}\,\cos(xy)\,dy$, onde $C(t)=(t^{2}-1,t^{2}+1)$, $-1\leq t\leq 1.$
$0.$
Calcule o trabalho realizado por uma partícula andando sobre a espiral dada por $C:\,x=t\,\cos t$, $y=t\,\sin t$, com $0\leq t\leq 2\pi$, sob a ação do campo ${\bf F}(x,y)=(x,y)$, ou seja, calcule a integral $\int_{C}x\,dx+y\,dy.$
$2\pi^{2}.$
Seja $D$ a região limitada por um caminho fechado e simples $C$ no plano $xy$. Utilize o Teorema de Green para demonstrar que as coordenadas do centroide $(\bar{x},\bar{y})$ de $D$ são
$$\bar{x} = \dfrac{1}{2A}\oint_{C}x^2 \, dy \quad \quad\quad\quad \bar{y} = -\dfrac{1}{2A}\oint_{C}y^2 \, dx,$$
em que $A$ é a área de $D$.
$\dfrac{1}{2A}\oint_{C}x^2 \, dy = \dfrac{1}{2A} \iint_{D} 2x \, dA = \bar{x}$ e $-\dfrac{1}{2A}\oint_{C}y^2 \, dx = -\dfrac{1}{2A}\iint_{D} (-2y) \, dA = \bar{y}$

