Exercícios
Em coordenadas esféricas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Identifique a superfície cuja equação é $\rho=\sin{\theta}\sin{\phi}.$
Esfera de raio $\dfrac{1}{2}$ centrada no ponto $\left(0,\dfrac{1}{2},0\right).$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}x\,dxdydz$, onde $B$ é o conjunto $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}+z^{2}\leq 1$ e $x\geq 0.$
$3\pi.$
Usando coordenadas esféricas, determine o volume do elipsoide $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}\leq 1.$
$\dfrac{4 \pi abc}{3}.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{2}(\rho\cos{\phi})\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$2\pi.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da região limitada acima pelo paraboloide $z=5-x^{2}-y^{2}$ e abaixo pelo paraboloide $z=4x^{2}+4y^{2}.$
$\dfrac{5\pi}{2}.$
Usando coordenadas esféricas, determine o centroide e o momento de inércia em relação a um diâmetro de sua base do hemisfério sólido homogêneo de raio $a.$
Centróide: $\left(0,0,\dfrac{3a}{8} \right);$ momento de inércia: $\dfrac{4 K a^5 \pi}{15},$ onde $K$ é a densidade constante.
Use coordenadas esféricas para encontrar o volume do sólido: limitado acima pela esfera \(\rho=4\) e abaixo pelo cone \(\phi=\pi/3\).
\(\dfrac{64\pi}{3}\)
Mude o ponto $(1,\sqrt{3},2\sqrt{3})$ dado em coordenadas retangulares para esféricas.
$\displaystyle \left( 4, \dfrac{\pi}{3}, \dfrac{\pi}{6} \right).$
Usando coordenadas esféricas, determine o volume da menor região cortada da esfera sólida $\rho \leq 2$ pelo plano $z=1.$
$\dfrac{5\pi}{3}.$
Seja \(G\) a região sólida dentro da esfera de raio \(2\) centrada na origem e acima do plano \(z=1\). Mostre (ou verifique) os seguintes resultados:
O volume de \(G\) é dado por \[\iiint\limits_G\,dV = \int_0^{2\pi}\int_0^{\dfrac{\pi}{3}}\int_{\sec\phi}^{2}\rho^2\sin\phi\,d\rho d\phi d\theta \]
\[\iiint\limits_G\dfrac{z}{x^2+y^2+z^2}\,dV = \int_0^{2\pi}\int_0^{\pi/3}\int_{\sec\phi}^{2}\rho\cos\phi\sin\phi\,d\rho d\phi d\theta \]
Seja $E$ o sólido limitado pelos dois planos $z=1$ e $z=2$ e lateralmente pelo cone $z=\sqrt{x^{2}+y^{2}}$. Expresse o volume de $E$ como integral tripla em coordenadas esféricas (não é necessário calcular a integral).
$\displaystyle \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{\sec(\phi)}^{2\sec(\phi)} \rho^{2}\sin(\phi)\;d\rho d\phi d\theta.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinar o volume e o centroide do sólido $E$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=1.$
Volume: $\dfrac{\pi(2 - \sqrt{2})}{3};$ centróide: $\left(0,0, \dfrac{3}{8(2 - \sqrt{2})} \right).$
Mostre que o determinante Jacobiano da mudança de coordenadas cartesianas para esféricas é $-\rho^2 \sin \varphi$.
Marque o ponto cujas coordenadas esféricas é $(1,0,0)$ e encontre as coordenadas retangulares do ponto.
$(0,0,1).$
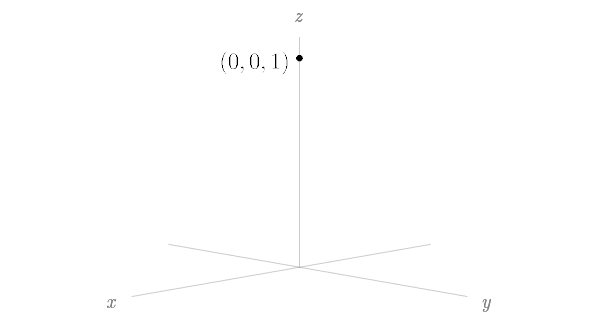
Um sólido está acima do cone $z=\sqrt{x^{2}+y^{2}}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=z.$ Escreva uma descrição do sólido em termos de desigualdades envolvendo coordenadas esféricas.
A mudança de coordenadas retangulares para coordenadas cartesianas é dada por
$$\begin{cases}x = \rho \cos{\theta} \sin{\phi} \\y = \rho \sin{\theta} \sin{\phi}\\z = \rho \cos{\phi},\end{cases}$$
em que $\rho \geq 0$, $\theta \in [0,2\pi]$ e $\phi \in [0,\pi]$. Observe que $\sin{\phi} \geq 0$ quando $\phi \in [0,\pi]$. Logo, a equação do cone em coordenadas esféricas pode ser escrita como $\rho \cos{\phi} = \sqrt{\rho^2 \sin^2{\phi}} = \rho\sin{\phi}$. A origem $(0,0,0)$ pertence ao cone e é dada por $\rho = 0$. Nos demais pontos, $\rho \neq 0$, donde $\phi = \pi/4$.
A equação da esfera em coordenadas esféricas pode ser escrita como $\rho^2=\rho\cos{\phi}$. A origem $(0,0,0)$ pertence à esfera e é dada por $\rho=0$. Nos demais pontos, $\rho \neq 0$, donde $\rho = \cos{\phi}$.
Portanto, o sólido pode ser descrito em coordenadas esféricas por
$$E = \left\{(\rho, \theta, \phi): 0 \leq \rho \leq \cos{\phi}, 0 \leq \theta \leq 2\pi \mbox{ e } 0 \leq \phi \leq \frac{\pi}{4}\right\}.$$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}x\,dxdydz$, onde $B$ é o conjunto $x\geq 0$ e $x^{2}+y^{2}+z^{2}\leq 4.$
$4\pi$.
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{3\pi/2}\int_{0}^{\pi}\int_{0}^{1}5\rho^{3}\sin^{3}{\phi}\,d\rho d\phi d\theta$.
$\dfrac{5\pi}{2}.$
Seja $D$ a região limitada abaixo pelo plano $z=0$, acima pela esfera $x^{2}+y^{2}+z^{2}=4$ e dos lados pelo cilindro $x^{2}+y^{2}=1$. Monte as integrais triplas em coordenadas esféricas que dão o volume de $D$ usando as ordens de integração a seguir.
$d\rho\,d\phi\,d\theta$;
$d\phi\,d\rho\,d\theta$.
$\displaystyle \int_{0}^{2\pi}\int_{0}^{\pi/6}\int_{0}^{2} \rho^{2}\sin(\phi)\; d\rho d\phi d\theta + \int_{0}^{2\pi}\int_{\pi/6}^{\pi/2}\int_{0}^{\csc(\phi)} \rho^{2}\sin(\phi)\; d\rho d\phi d\theta.$
$\displaystyle \int_{0}^{2\pi}\int_{1}^{2}\int_{\pi/6}^{\arcsin(1/\rho)} \rho^{2}\sin(\phi)\; d\phi d\rho d\theta + \int_{0}^{2\pi}\int_{0}^{2}\int_{0}^{\pi/6} \rho^{2}\sin(\phi)\; d\phi d\rho d\theta.$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{0}^{1}\int_{0}^{\sqrt{1-x^{2}}}\int_{\sqrt{x^{2}+y^{2}}}^{\sqrt{2-x^{2}-y^{2}}}xy\,dzdydx$.
$\dfrac{(4\sqrt{2} - 5)}{15}.$
Usando coordenadas esféricas, determine o volume da região cortada do cilindro sólido $x^{2}+y^{2}\leq 1$ pela esfera $x^{2}+y^{2}+z^{2}=4.$
$\dfrac{4\pi(8 - 3\sqrt{3})}{3}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}\sqrt{x+y}\sqrt[3]{x+2y-z}\,dxdydz$, onde $B$ é a região $1\leq x+y\leq 2$, $0\leq x+2y-z\leq 1$ e $0\leq z\leq 1.$
$\sqrt{2} - \dfrac{1}{2}.$
Usando coordenadas esféricas, determine o volume do sólido que está acima do cone $\phi=\pi/3$ e abaixo da esfera $\rho=4\cos{\phi}.$
$10\pi.$
Usando coordenadas esféricas, calcule a massa do sólido compreendido entre as esferas \(x^2+y^2+z^2=1\) e \(x^2+y^2+z^2=4\), com densidade \(\delta(x,y,z)=(x^2+y^2+z^2)^{-1/2}.\)
Usando coordenadas esféricas, determine o volume da porção da esfera sólida $\rho \leq a$ que está entre os cones $\phi=\pi/3$ e $\phi=2\pi/3.$
$\dfrac{2\pi a^{3}}{3}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}z\,dV$, onde $E$ está entre as esferas $x^{2}+y^{2}+z^{2}=1$ e $x^{2}+y^{2}+z^{2}=4$, no primeiro octante.
$\dfrac{15\pi}{16}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}xyz\,dV$, onde $E$ é o sólido limitado pelos paraboloides $z=x^{2}+y^{2}$ e $z=8-x^{2}-y^{2}.$
$0.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{(1-\cos{\phi})/2}\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$\dfrac{\pi}{3}.$
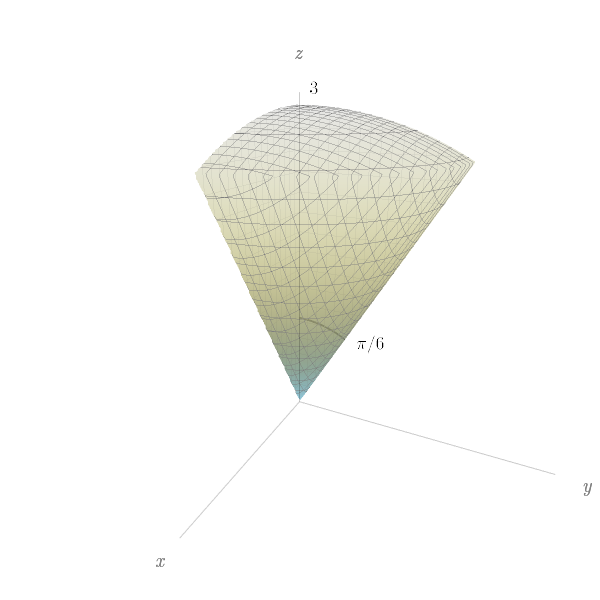
Esboce o sólido cujo volume é dado pela integral abaixo e calcule-a.
$$\int_{0}^{\pi/6}\!\!\int_{0}^{\pi/2}\!\!\int_{0}^{3}\rho^{2}\sin{\phi}\;d\rho d\theta d\phi$$
Usando coordenadas esféricas, determine o volume do sólido que está acima do plano $z=2\sqrt{3}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=16.$
$\dfrac{88\pi}{3}.$
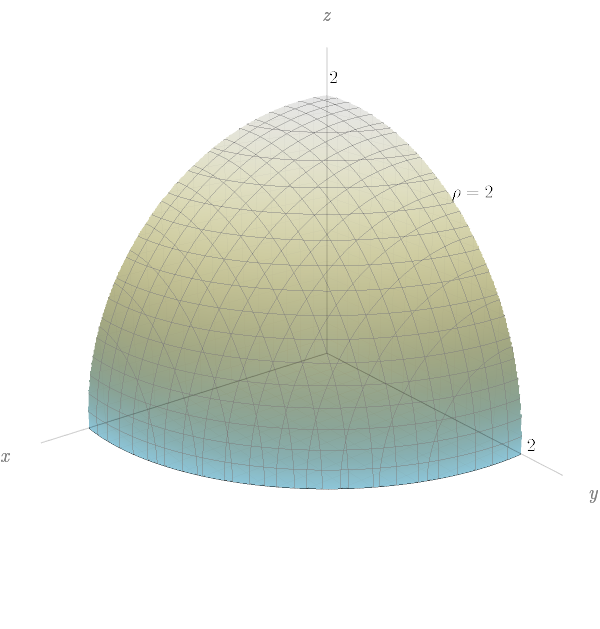
Esboce o sólido descrito por $\rho \leq 2$, $0\leq \phi \leq \pi/2$ e $0\leq \theta \leq \pi/2.$
Usando coordenadas esféricas, determine o volume do sólido que está dentro da esfera $x^{2}+y^{2}+z^{2}=4$, acima do plano $xy$ e abaixo do cone $z=\sqrt{x^{2}+y^{2}}.$
$\dfrac{8\sqrt{2}\pi}{3}.$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{-a}^{a}\int_{-\sqrt{a^{2}-y^{2}}}^{\sqrt{a^{2}-y^{2}}}\int_{-\sqrt{a^{2}-x^{2}-y^{2}}}^{\sqrt{a-x^{2}-y^{2}}}(x^{2}z+y^{2}z+z^{3})\,dzdxdy$.
$0.$
Mostre que
$$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{x^{2}+y^{2}+z^{2}}\,e^{-(x^{2}+y^{2}+z^{2})}\,dxdydz=2\pi.$$
(A integral imprópria tripla é definida como o limite da integral tripla sobre uma esfera sólida quando o raio da esfera aumenta indefinidamente.)
Note que $$\begin{split}&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{x^{2}+y^{2}+z^{2}}\,e^{-(x^{2}+y^{2}+z^{2})}\,dxdydz \\&= \lim_{R \to \infty} \int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{R} \rho e^{-\rho^2}\rho^2 \sin(\phi)\;d\rho d\phi d\theta.\end{split}$$
Usando coordenadas esféricas, determine o volume e o centroide do sólido que está acima do cone $\phi=\pi/3$ e abaixo da esfera $\rho=4\cos{\phi}.$
Volume: $10\pi;$ centróide: $(0,0,2,1).$
O centróide de uma região $E$ é dado por
$$\overline{x}=\frac{1}{vol(E)}\int_{E}x\,dV,\;\;\;\; \overline{y}=\frac{1}{vol(E)}\int_{E}y\,dV\;\; \text{e}\;\; \overline{z}=\frac{1}{vol(E)}\int_{E}z\,dV.$$
Calcule o centróide da região dada em coordenadas esféricas por $0\leq \rho \leq 1$, $0\leq\phi \leq \pi/3$ e $0\leq \theta \leq 2\pi$ (observe que, devido à simetria da região, $\overline{x}$ e $\overline{y}$ se anulam, bastando calcular a terceira coordenada).
$\overline{z} = \dfrac{9}{16}.$
Usando coordenadas esféricas, calcule a massa da esfera sólida de raio \(a\) com densidade proporcional à distância ao centro (tomando \(k\) como a constante de proporcionalidade).
\(k\pi a^4\)
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}\sqrt{x^{2}+y^{2}+z^{2}}\,dxdydz$, onde $B$ é a interseção da semi-esfera $x^{2}+y^{2}+z^{2}\leq 4$, $z\geq 0$, com o cilindro $x^{2}+y^{2}\leq 1.$
$\displaystyle \dfrac{\pi}{4}\left( 32- 14\sqrt{3} + \ln(2 + \sqrt{3})\right).$
Escreva a equação $z^{2}=x^{2}+y^{2}$ em coordenadas esféricas.
$\cos^2 \phi = \sin^2 \phi.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}xyz\,dV$, onde $E$ está entre as esferas $\rho=2$ e $\rho=4$ e acima do cone $\phi=\pi/3.$
$0.$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{0}^{2}\int_{0}^{\sqrt{4-y^{2}}}\int_{0}^{\sqrt{4-x^{2}-y^{2}}}\dfrac{1}{x^{2}+y^{2}+z^{2}}\,dzdxdy$.
$\pi.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{H}(9-x^{2}-y^{2})\,dV$, onde $H$ é o hemisfério sólido $x^{2}+y^{2}+z^{2}\leq 9$ e $z\geq 0.$
$\dfrac{486\pi}{5}.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da menor cunha esférica cortada de uma esfera de raio $a$ por dois planos que se interceptam ao longo de um diâmetro com um ângulo de $\pi/6.$
$\dfrac{\pi a^3}{9}.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{\pi}\int_{0}^{\pi}\int_{0}^{2\,\sin{\phi}}\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$\pi^2.$
Usando coordenadas esféricas, determine o volume da parte da bola $\rho\leq a$ que está entre os cones $\phi=\pi/6$ e $\phi=\pi/3.$
$\displaystyle \left( \sqrt{3} - 1 \right) \dfrac{\pi a^3}{3}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}(x^{2}+y^{2}+z^{2})^{2}\,dV$, onde $B$ é a bola com centro na origem e raio $5.$
$\dfrac{312500\pi}{7}.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da região limitada abaixo pelo plano $z=0$, lateralmente pelo cilindro $x^{2}+y^{2}=1$ e acima pelo paraboloide $z=x^{2}+y^{2}$.
$\dfrac{\pi}{2}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B} z \,dxdydz$, onde $B$ é o conjunto $1\leq x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
Usando coordenadas esféricas, o sólido pode ser descrito por
$$B = \left\{(\rho, \theta, \phi): 1 \leq \rho \leq 2, 0 \leq \theta \leq 2\pi \mbox{ e } 0 \leq \phi \leq \frac{\pi}{2}\right\}.$$
Lembre que o Jacobiano dessa transformação é $\rho^2 \sin{\phi}$. Assim, obtemos
\begin{array}{rcl}\displaystyle\iiint\limits_{B} z \,dxdydz & = & \displaystyle\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\int_{1}^{2}(\rho \cos{\phi})(\rho^2 \sin{\phi})\,d\rho d\phi d\theta \\ & = & \displaystyle\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\left.\left(\frac{\rho^4}{4} \frac{\sin{2\phi}}{2}\right|_{\rho=1}^{\rho=2}\right)\, d\phi d\theta \\ & = & \displaystyle\int_{0}^{2\pi}\left.\left(\frac{(16-1)}{8} \frac{(-\cos{2\phi)}}{2}\right|_{\phi=0}^{\rho=\frac{\pi}{2}}\right)\, d\theta \\ & = & \left.-\frac{15}{16}(-1-1) \theta \right|_{\theta=0}^{\theta=2\pi} = \frac{15\pi}{4}. \end{array}
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}z\,dxdydz$, onde $B$ é o conjunto $z\geq \sqrt{x^{2}+y^{2}}$ e $x^{2}+y^{2}+z^{2}\leq 1.$
$\dfrac{\pi}{8}.$
Use coordenadas esféricas para encontrar o volume do sólido: contido no interior do cone \(\phi=\pi/4\), entre as esferas \(\rho=1\) e \(\rho=2\).

