Exercícios
Integrais triplas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $0\leq x \leq 1$, $0\leq y \leq 1$ e \\ $x+y\leq z \leq x+y+1.$
$\displaystyle\iiint\limits_{ E}\sqrt{1-z^{2}}\;dx dy dz$, onde $E$ é o conjunto $0 \leq x \leq 1$, $0\leq z\leq 1$ e $0\leq y \leq z.$
$\dfrac{1}{2}.$
$\dfrac{1}{3}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{H}(9-x^{2}-y^{2})\,dV$, onde $H$ é o hemisfério sólido $x^{2}+y^{2}+z^{2}\leq 9$ e $z\geq 0.$
$\dfrac{486\pi}{5}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}\sqrt{x+y}\sqrt[3]{x+2y-z}\,dxdydz$, onde $B$ é a região $1\leq x+y\leq 2$, $0\leq x+2y-z\leq 1$ e $0\leq z\leq 1.$
$\sqrt{2} - \dfrac{1}{2}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}2z\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
$\displaystyle\iiint\limits_{ E}2z\;dx dy dz$, onde $E$ é o conjunto $4x^{2}+9y^{2}+z^{2}\leq 4$ e $z\geq 0.$
$8\pi.$
$0.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{2}(\rho\cos{\phi})\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$2\pi.$
Calcule a integral tripla $\displaystyle\iiint\limits_{B}xyz^{2}\,dV$, onde $B$ é a caixa retangular dada por $B=\{(x,y,z) \in \mathbb{R}^3|\;0\leq x\leq 1,\;-1\leq y\leq 2,\;0\leq z\leq 3\}$, integrando primeiro em relação a $y$, depois a $z$ e então a $x$.
$\dfrac{27}{4}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}x\,dxdydz$, onde $B$ é o conjunto $x\geq 0$ e $x^{2}+y^{2}+z^{2}\leq 4.$
$4\pi$.
Ache o centro de massa de $E$, em que:
A densidade de um ponto $P$ de um sólido cúbico $E$ de aresta $a$ é diretamente proporcional ao quadrado da distância de $P$ a um vértice fixo do cubo.
$E$ é o tetraedro delimitado pelos planos coordenados e o plano $2x+5y+z=10$ e a densidade em $P(x,y,z)$ é diretamente proporcional $\grave{a}$ distância do plano $xz$ a $P.$
$\displaystyle \left( \dfrac{7a}{12},\dfrac{7a}{12},\dfrac{7a}{12} \right).$
$\displaystyle \left( 1,\dfrac{4}{5},2 \right).$
Identifique a superfície cuja equação é $\rho=\sin{\theta}\sin{\phi}.$
Esfera de raio $\dfrac{1}{2}$ centrada no ponto $\left(0,\dfrac{1}{2},0\right).$
Determine o volume do sólido que está acima do plano $xy$, abaixo do paraboloide $z = x^2 + y^2$ e que se encontra dentro do cilindro $x^2 + y^2 = 2x$ e fora do cilindro $x^2 + y^2 = 1.$
Temos que $0\leq z\leq x^{2}+y^{2}$. Como o sólido se encontra dentro do cilindro $x^{2}+y^{2}=2x$ e fora do cilindro $x^{2}+y^{2}=1$, devemos fazer a interseção desses dois cilindros, isto é, $$\left\{\begin{array}{cc} x^{2}+y^{2}=2x\\ x^{2}+y^{2}=1\\ \end{array} \right.\Rightarrow 2x=1\Leftrightarrow x=\frac{1}{2}$$ Em coordenadas cilíndricas temos que \begin{eqnarray*} x&=&r\cos \theta\\ y&=&r\sin \theta\\ z&=&z\\ dz\,dy\,dx&=&r\,dz\,dr\,d\theta \end{eqnarray*} Da equação $x^{2}+y^{2}=1$ temos que $$r^{2}=1\Longrightarrow r=\pm 1,$$ como devemos ter $r\geq 0$, então nesse caso $r=1.$ Da equação $x^{2}+y^{2}=2x$ temos que $$r^{2}=2r\,\cos \theta \Rightarrow r=2\cos \theta.$$ Agora, sendo $x=\frac{1}{2}$ e $r=1$ temos que $$\cos \theta=\frac{1}{2}\Rightarrow \theta=\pm \frac{\pi}{3}.$$ Assim, em coordenadas cilíndricas temos que o sólido $E$ é dado por $$E=\{(\theta,\,r,\,z)|\, -\frac{\pi}{3}\leq \theta \leq \frac{\pi}{3},\, 1\leq r\leq 2 \cos \theta,\,0\leq z\leq r^{2}\}.$$ Então, $$V=\iiint\limits_{ E}1\,dV= \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int_{1}^{2\cos \theta}\int_{0}^{r^{2}}1\,r\,dz\,dr\,d\theta= \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int_{1}^{2\cos \theta}zr\bigg|_{0}^{r}\,dr\,d\theta$$ $$=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int_{1}^{2\cos \theta}r^{3}\,dr\,d\theta= \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\frac{r^{4}}{4}\bigg|_{1}^{2\cos \theta}\,d\theta =\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\bigg(4\cos^{4}\theta-\frac{1}{4}\bigg)\,d\theta$$ $$=4\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\underbrace{\cos^{4}\theta}_{\mbox{função par}}\,d\theta-\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\underbrace{\frac{1}{4}}_{\mbox{função par}}\,d\theta =8\int_{0}^{\frac{\pi}{3}}\cos^{4}\theta\,d\theta-2\int_{0}^{\frac{\pi}{3}}\frac{1}{4}\,d\theta$$ $$=8\bigg[\frac{3}{8}\theta+\frac{1}{4}\sin(2\theta)+\frac{1}{32}\sin(4\theta)\bigg]\bigg|_{0}^{\frac{\pi}{3}} -\bigg(\frac{1}{2}\theta\bigg)\bigg|_{0}^{\frac{\pi}{3}}$$ $$=8\bigg[\frac{3}{8}\cdot \frac{\pi}{3}+\frac{1}{4}\sin\bigg(\frac{2\pi}{3}\bigg)+\frac{1}{32}\sin\bigg(\frac{4\pi}{3}\bigg)\bigg]-\frac{1}{2}\cdot \frac{\pi}{3}$$ $$=\pi+\sqrt{3}-\frac{\sqrt{3}}{8}-\frac{\pi}{6}=\frac{5\pi}{6}+\frac{7\sqrt{3}}{8}.$$
Determine o volume do sólido limitado pelo cilindro $x^2 + y^2 = 4$ e pelos planos $z = 0$ e $y + z = 3$.
$12\pi.$
Determine o sólido $E$ para o qual a integral $$ \iiint\limits_{ E}(1-x^{2}-2y^{2}-3z^{2})\,dV$$ é máxima.
$E = \left\{ (x,y,z); x^2 + 2y^2 + 3z^2 \leq 1 \right\}.$
Esboce o sólido descrito pelas desigualdades $0 \leq r \leq 2$, $-\pi/2 \leq \theta \leq \pi/2$ e $0 \leq z \leq 1$.
Usando coordenadas esféricas, determine o volume da porção da esfera sólida $\rho \leq a$ que está entre os cones $\phi=\pi/3$ e $\phi=2\pi/3.$
$\dfrac{2\pi a^{3}}{3}.$
Usando coordenadas esféricas, determine o volume do sólido que está dentro da esfera $x^{2}+y^{2}+z^{2}=4$, acima do plano $xy$ e abaixo do cone $z=\sqrt{x^{2}+y^{2}}.$
$\dfrac{8\sqrt{2}\pi}{3}.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da região limitada acima pelo paraboloide $z=5-x^{2}-y^{2}$ e abaixo pelo paraboloide $z=4x^{2}+4y^{2}.$
$\dfrac{5\pi}{2}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}z\,dV$, onde $E$ é limitado pelo cilindro $y^{2}+z^{2}=9$ e pelos planos $x=0$, $y=3x$ e $z=0$ no primeiro octante.
$\displaystyle\iiint\limits_{ E}xyz\;dx dy dz$, onde $E$ é o paralelepípedo $0\leq x\leq 2$, $0\leq y\leq 1$, e $1\leq z\leq 2.$
$\dfrac{27}{8}.$
$\dfrac{3}{2}.$
Usando coordenadas esféricas, determine o volume da região cortada do cilindro sólido $x^{2}+y^{2}\leq 1$ pela esfera $x^{2}+y^{2}+z^{2}=4.$
$\dfrac{4\pi(8 - 3\sqrt{3})}{3}.$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{0}^{2}\int_{0}^{\sqrt{4-y^{2}}}\int_{0}^{\sqrt{4-x^{2}-y^{2}}}\dfrac{1}{x^{2}+y^{2}+z^{2}}\,dzdxdy$.
$\pi.$
Determine a massa e o centro de massa do cubo dado por $0\leq x\leq a$, $0\leq y\leq a$, $0\leq z\leq a$ e com função densidade:
$\rho(x,y,z)=x^{2}+y^{2}+z^{2}.$
$\rho(x,y,z)=x+y+z.$
Massa: $a^5;$ centro de massa: $\displaystyle \left(\frac{7a}{12},\frac{7a}{12},\frac{7a}{12} \right).$
Massa: $\dfrac{3a^4}{2};$ centro de massa: $\displaystyle \left(\frac{5a}{9},\frac{5a}{9},\frac{5a}{9} \right).$
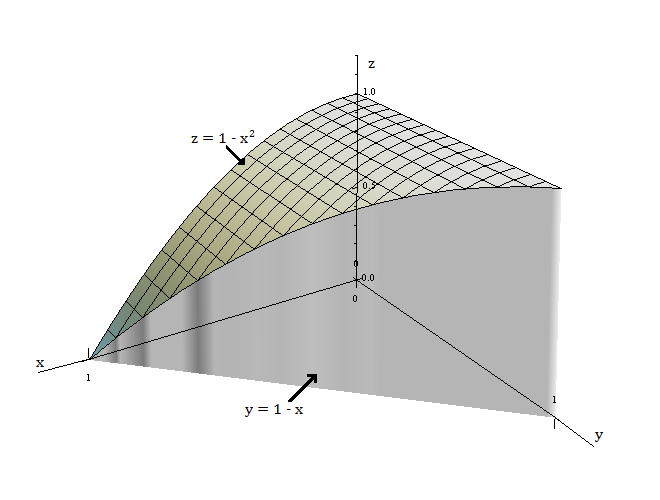
Calcule a integral tripla $\int\int\int\limits_{T}x^{2}dV$,
onde $T$ é o tetraedro sólido com vértices $(0,0,0)$, $(1,0,0)$, $(0,1,0)$ e $(0,0,1).$
Para resolvermos a integral tripla, vamos desenhar dois diagramas: um da região sólida $T$ (Figura 1) e o outro a sua projeção $D$ no plano $xy$ (Figura 2).
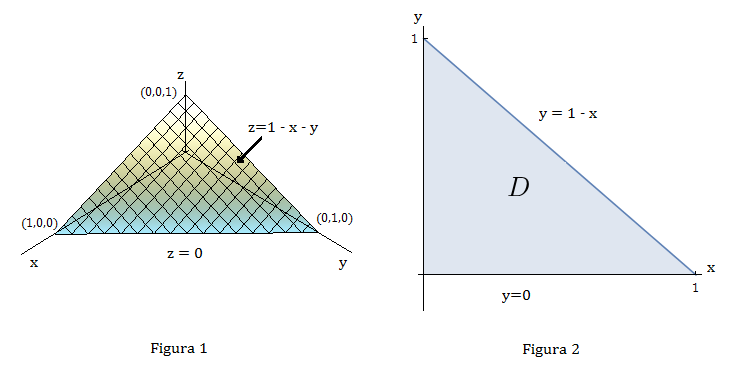
A fronteira inferior do tetraedro $T$ é o plano $z=0$ e a superior é o plano $x+y+z=1$ (ou $z=1-x-y$).
Notemos que os planos $x+y+z=1$ e $z=0$ se interceptam na reta $x+y=1$ (ou $y=1-x$) no plano $xy.$
Logo a projeção de $T$ é a região triangular da Figura 2 e temos
$$T=\{(x,y,z)|\,0\leq x \leq 1,\, 0\leq y \leq 1-x,\, 0\leq z \leq 1-x-y\}.$$
Assim,
$$\int\int\int\limits_{T}x^{2}\,dV=\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-z}x^{2}\,dz\,dy\,dx=\int_{0}^{1}\int_{0}^{1-x}x^{2}z\bigg|_{0}^{1-x-y}\,dy\,dx$$
$$=\int_{0}^{1}\int_{0}^{1-x}x^{2}(1-x-y)\,dy\,dx=\int_{0}^{1}\int_{0}^{1-x}(x^{2}-x^{3}-x^{2}y)\,dy\,dx$$
$$=\int_{0}^{1}\bigg(x^{2}y-x^{3}y-x^{2}\frac{y^{2}}{2}\bigg)\bigg|_{0}^{1-x}\,dx=\int_{0}^{1}\bigg(x^{2}(1-x)-x^{3}(1-x)-\frac{x^{2}}{2}(1-x)^{2}\bigg)dx$$
$$=\int_{0}^{1}\bigg(\frac{x^{2}}{2}-x^{3}+\frac{x^{4}}{2}\bigg)\,dx =\bigg[\frac{1}{2}\cdot\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{1}{2}\cdot\frac{x^{5}}{5}\bigg]\bigg|_{0}^{1}=\frac{1}{60}.$$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B} z \,dxdydz$, onde $B$ é o conjunto $1\leq x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
Usando coordenadas esféricas, o sólido pode ser descrito por
$$B = \left\{(\rho, \theta, \phi): 1 \leq \rho \leq 2, 0 \leq \theta \leq 2\pi \mbox{ e } 0 \leq \phi \leq \frac{\pi}{2}\right\}.$$
Lembre que o Jacobiano dessa transformação é $\rho^2 \sin{\phi}$. Assim, obtemos
\begin{array}{rcl}\displaystyle\iiint\limits_{B} z \,dxdydz & = & \displaystyle\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\int_{1}^{2}(\rho \cos{\phi})(\rho^2 \sin{\phi})\,d\rho d\phi d\theta \\ & = & \displaystyle\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\left.\left(\frac{\rho^4}{4} \frac{\sin{2\phi}}{2}\right|_{\rho=1}^{\rho=2}\right)\, d\phi d\theta \\ & = & \displaystyle\int_{0}^{2\pi}\left.\left(\frac{(16-1)}{8} \frac{(-\cos{2\phi)}}{2}\right|_{\phi=0}^{\rho=\frac{\pi}{2}}\right)\, d\theta \\ & = & \left.-\frac{15}{16}(-1-1) \theta \right|_{\theta=0}^{\theta=2\pi} = \frac{15\pi}{4}. \end{array}
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}z\,dV$, onde $E$ está entre as esferas $x^{2}+y^{2}+z^{2}=1$ e $x^{2}+y^{2}+z^{2}=4$, no primeiro octante.
$\dfrac{15\pi}{16}.$
Esboce o sólido cujo volume é dado pela integral iterada.
$\displaystyle\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2-2z}\;dy dz dx$
Usando coordenadas esféricas, calcule a massa do sólido compreendido entre as esferas \(x^2+y^2+z^2=1\) e \(x^2+y^2+z^2=4\), com densidade \(\delta(x,y,z)=(x^2+y^2+z^2)^{-1/2}.\)
Considere a integral tripla iterada $$\int_{-\sqrt{2}}^{\sqrt{2}}\int_{-\sqrt{2-x^2}}^{\sqrt{2-x^2}}\int_{x^2 + y^2}^{4-x^2-y^2} dz dy dx.$$
Transforme a integral utilizando coordenadas cilíndricas.
Calcule a integral.
Descreva o sólido cujo volume é dado por essa integral.
$\displaystyle \int_{0}^{2\pi}\int_{0}^{\sqrt{2}}\int_{ r^2}^{4-r^{2}} r dz dr d\theta.$
$4\pi.$
Região entre os parabolóides $z = x^2 + y^2$ e $z = 4 - x^2 - y^2$.
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.
$\displaystyle \int_0^4 \int_0^{2\pi}\int_r^4 r \, dz d\theta dr$
Use a integral tripla para determinar o volume do sólido dado.
O tetraedro limitado pelos planos coordenados e o plano $2x+y+z=4.$
O sólido limitado pelo paraboloide $x=y^{2}+z^{2}$ e pelo plano $x=16.$
O sólido delimitado pelo cilindro $x=y^{2}$ e pelos planos $z=0$ e $x+z=1$.
$\dfrac{16}{3}.$
$128\pi.$
$\dfrac{8}{15}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E} x^2 e^y\,dV$, onde $E$ é delimitado pelo cilindro parabólico $z=1-y^{2}$ e pelos planos $z=0$, $x=1$ e $x=-1.$
$\displaystyle\iiint\limits_{ E}x\,dV$, onde $E$ é limitado pelo paraboloide $x=4y^{2}+4z^{2}$ e pelo plano $x=4.$
$\dfrac{8}{3e}.$
$\dfrac{16\pi}{3}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}\sqrt{x^{2}+y^{2}+z^{2}}\,dxdydz$, onde $B$ é a interseção da semi-esfera $x^{2}+y^{2}+z^{2}\leq 4$, $z\geq 0$, com o cilindro $x^{2}+y^{2}\leq 1.$
$\displaystyle \dfrac{\pi}{4}\left( 32- 14\sqrt{3} + \ln(2 + \sqrt{3})\right).$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}z\,dxdydz$, onde $B$ é o conjunto $z\geq \sqrt{x^{2}+y^{2}}$ e $x^{2}+y^{2}+z^{2}\leq 1.$
$\dfrac{\pi}{8}.$
Usando coordenadas esféricas, determine o volume da parte da bola $\rho\leq a$ que está entre os cones $\phi=\pi/6$ e $\phi=\pi/3.$
$\displaystyle \left( \sqrt{3} - 1 \right) \dfrac{\pi a^3}{3}.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{3\pi/2}\int_{0}^{\pi}\int_{0}^{1}5\rho^{3}\sin^{3}{\phi}\,d\rho d\phi d\theta$.
$\dfrac{5\pi}{2}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}y\;dx dy dz$, onde $E$ é o conjunto $x^{2}+4y^{2}\leq 1$ e $0\leq z \leq 1.$
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq 4$, $x\geq 0$ e \\ $x+y\leq z \leq x+y+1.$
$0.$
$\dfrac{16}{3}.$
Seja \(G\) a região sólida dentro da esfera de raio \(2\) centrada na origem e acima do plano \(z=1\). Mostre (ou verifique) os seguintes resultados:
O volume de \(G\) é dado por \[\iiint\limits_G\,dV = \int_0^{2\pi}\int_0^{\sqrt{3}}\int_1^{\sqrt{4-r^2}}r\,dzdrd\theta \]
\[\iiint\limits_G\dfrac{z}{x^2+y^2+z^2}\,dV = \int_0^{2\pi}\int_0^{\sqrt{3}}\int_1^{\sqrt{4-r^2}}\dfrac{rz}{r^2+z^2}\,dzdrd\theta \]
Usando coordenadas esféricas, determine o volume da menor região cortada da esfera sólida $\rho \leq 2$ pelo plano $z=1.$
$\dfrac{5\pi}{3}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}e^{x^{2}}\;dx dy dz$, onde $E$ é o conjunto $0\leq x \leq 1$, $0\leq y \leq x$ e $0\leq z \leq 1.$
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}\leq y\leq x$, $0\leq z\leq x+y.$
$\dfrac{e - 1}{2}.$
$\dfrac{11}{120}.$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{0}^{1}\int_{0}^{\sqrt{1-x^{2}}}\int_{\sqrt{x^{2}+y^{2}}}^{\sqrt{2-x^{2}-y^{2}}}xy\,dzdydx$.
$\dfrac{(4\sqrt{2} - 5)}{15}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}\cos{z} \; dx dy dz$, onde $E$ é o conjunto $0\leq x \leq \dfrac{\pi}{2}$, $0\leq y \leq \dfrac{\pi}{2}$ e $x-y\leq z \leq x+y.$
$\displaystyle\iiint\limits_{ E}(y-x)\;dx dy dz$, onde $E$ é o conjunto $4\leq x+y\leq 8$, $\dfrac{1}{x}\leq y\leq \dfrac{2}{x}$, $y> x$ e $0\leq z \leq \dfrac{\sqrt[3]{xy}}{\sqrt{x+y}}.$
$2.$
$3 - 6\sqrt[3]{2} - 2\sqrt{2} + 6 \sqrt[6]{2^5}.$
Use coordenadas esféricas para encontrar o volume do sólido: limitado acima pela esfera \(\rho=4\) e abaixo pelo cone \(\phi=\pi/3\).
\(\dfrac{64\pi}{3}\)
Use a integral tripla para determinar o volume do sólido dado.
$0\leq x \leq 1$, $0\leq y \leq 1$ e $0\leq z \leq 5-x^{2}-3y^{2}.$
$0\leq x \leq 1$, $0\leq y \leq x^{2}$ e $0\leq z \leq x+y^{2}.$
$x^{2}+y^{2}\leq z \leq 4.$
$x^{2}+4y^{2}\leq z \leq 1.$
$\dfrac{11}{3}.$
$\dfrac{25}{84}.$
$8\pi.$
$\dfrac{\pi}{4}.$
Mude o ponto $(1,\sqrt{3},2\sqrt{3})$ dado em coordenadas retangulares para esféricas.
$\displaystyle \left( 4, \dfrac{\pi}{3}, \dfrac{\pi}{6} \right).$
Use a integral tripla para determinar o volume do sólido dado.
$x^{2}+y^{2}\leq 4$ e $x^{2}+y^{2}+z^{2}\leq 9.$
$x^{2}+4y^{2}+9z^{2}\leq 1.$
$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}$, $(a>0,\;b>0\;e\;c>0).$
$x^{2}+y^{2}\leq z \leq 4x+2y.$
$\left(36 - \dfrac{20\sqrt{5}}{3} \right)\pi.$
$\dfrac{2\pi}{9}.$
$\dfrac{4\pi abc}{3}.$
$\dfrac{25\pi}{4}$
Use coordenadas esféricas para encontrar o volume do sólido: contido no interior do cone \(\phi=\pi/4\), entre as esferas \(\rho=1\) e \(\rho=2\).
A figura mostra a região de integração da integral
$$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx.$$
Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.

$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx = \int_{0}^{1}\int_{0}^{y^2}\int_{0}^{1-y}f(x,y,z)\;dz dx dy $
$= \int_{0}^{1}\int_{0}^{1 - z}\int_{0}^{y^2}f(x,y,z)\;dx dy dz = \int_{0}^{1}\int_{0}^{1 - y}\int_{0}^{y^2}f(x,y,z)\;dx dz dy $
$= \int_{0}^{1}\int_{0}^{1 - \sqrt{x}}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dz dx = \int_{0}^{1}\int_{0}^{(1 - z)^2}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dx dz.$
Seja $C$ o cilindro de base circular e eixo $(Oz)$, com raio $2$ e altura $3$, com base na origem e densidade inversamente proporcional $\grave{a}$ distância ao eixo.
Determine o momento de inércia de $C$ com relação ao eixo $(Oz)$.
Se $C$ gira em torno do eixo $(Oz)$ com energia cinética $K$, qual a velocidade instantânea nos pontos de sua superfície lateral? (Fórmulas: $\bullet$ Momento de inércia: $I=\iiint\limits_{C}\rho\cdot l^{2}\,dV$, onde $\rho$ é a densidade e $l$ é a distância ao eixo; $\bullet$ Energia cinética de rotação: $K=\dfrac{1}{2}I\omega^{2}.$)
$6\pi.$
$\displaystyle \sqrt{\frac{K}{3\pi}}.$
Escreva a equação $z^{2}=x^{2}+y^{2}$ em coordenadas esféricas.
$\cos^2 \phi = \sin^2 \phi.$
Seja $E$ a região limitada pelos paraboloides $z = x^2 + y^2$ e $z = 36 - 3x^2 - 3y^2$.
Ache o volume da região $E$.
Encontre o centroide de $E$ (centro de massa no caso em que a densidade é constante).
$162\pi.$
$(0,0,15)$.
A figura mostra a região da integral
$$\int_{0}^{1}\int_{0}^{1-x^{2}}\int_{0}^{1-x}f(x,y,z)\;dy dz dx.$$
Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.
$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx = \int_{0}^{1}\int_{0}^{y^2}\int_{0}^{1-y}f(x,y,z)\;dz dx dy $
$= \int_{0}^{1}\int_{0}^{1 - z}\int_{0}^{y^2}f(x,y,z)\;dx dy dz = \int_{0}^{1}\int_{0}^{1 - y}\int_{0}^{y^2}f(x,y,z)\;dx dz dy $
$= \int_{0}^{1}\int_{0}^{1 - \sqrt{x}}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dz dx = \int_{0}^{1}\int_{0}^{(1 - z)^2}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dx dz.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinar o volume e o centroide do sólido $E$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=1.$
Volume: $\dfrac{\pi(2 - \sqrt{2})}{3};$ centróide: $\left(0,0, \dfrac{3}{8(2 - \sqrt{2})} \right).$
Para qual valor de $c$ o volume do elipsóide $x^{2}+(y/2)^{2}+(z/c)^{2}=1$ é igual a $8\pi$?
$3.$
Um cubo sólido de $2$ unidades de lado é limitado pelos planos $x=\pm 1$, $z=\pm 1$, $y=3$ e $y=5.$ Encontre o centro de massa e os momentos de inércia desse cubo.
Centro de massa: $\displaystyle \left(0,4,0 \right),$ $I_{x} = \dfrac{400}{3},$ $I_{y} = \dfrac{16}{3},$ $I_{z} = \dfrac{400}{3}.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{(1-\cos{\phi})/2}\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$\dfrac{\pi}{3}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}\sqrt{1-z^{2}}\;dx dy dz$, onde $E$ é o cubo $0\leq x\leq 1$, $0\leq y\leq 1$ e $0\leq z\leq 1.$
$\displaystyle\iiint\limits_{ E}\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq z \leq 2x.$
$\dfrac{\pi}{4}.$
$\dfrac{\pi}{2}.$
Mostre que o determinante Jacobiano da mudança de coordenadas cartesianas para esféricas é $-\rho^2 \sin \varphi$.
Vamos demonstrar a expressão geral para o volume de um cone circular de altura $h$ e raio da base $R$.
Representando o cone com vértice na origem e base no plano $z = h$, expresse $V$ por meio de uma integral dupla.
Calculando a integral, verifique que $V = \dfrac{\pi R^2 h}{3}$.
$V = 2 \displaystyle \int_{0}^{h} \int_{-\frac{R}{h}z}^{\frac{R}{h}z} \sqrt{\dfrac{R^{2}}{h^{2}} z^{2} - x^{2}} dx dz.$
Note que $\displaystyle \int_{0}^{h} \int_{-\frac{R}{h}z}^{\frac{R}{h}z} \sqrt{\dfrac{R^{2}}{h^{2}} z^{2} - x^{2}} dx dz = \dfrac{\pi R^{2}h}{6}$ é o volume da parte superior (ou inferior) do cone.
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}xyz\,dV$, onde $E$ é o sólido limitado pelos paraboloides $z=x^{2}+y^{2}$ e $z=8-x^{2}-y^{2}.$
$0.$
Seja $E$ o sólido limitado pelos dois planos $z=1$ e $z=2$ e lateralmente pelo cone $z=\sqrt{x^{2}+y^{2}}$. Expresse o volume de $E$ como integral tripla em coordenadas esféricas (não é necessário calcular a integral).
$\displaystyle \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{\sec(\phi)}^{2\sec(\phi)} \rho^{2}\sin(\phi)\;d\rho d\phi d\theta.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}(x^{2}+z^{2})\;dx dy dz$, onde $E$ é o cilindro $x^{2}+y^{2}\leq 1$ e $0\leq z \leq 1.$
$\displaystyle\iiint\limits_{ E}\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq z \leq 2x+2y-1.$
$\dfrac{7\pi}{12}.$
$\dfrac{\pi}{2}.$
Calcule as integrais mudando a ordem de integração de maneira apropriada.
$\displaystyle\int_{0}^{4}\int_{0}^{1}\int_{2y}^{2}\dfrac{4\;\cos(x^{2})}{2\sqrt{z}}\;dx dy dz$
$\displaystyle\int_{0}^{1}\int_{0}^{1}\int_{x^{2}}^{1}12xze^{zy^{2}}\;dy dx dz$
$\displaystyle\int_{0}^{1}\int_{\sqrt[3]{z}}^{1}\int_{0}^{\ln 3}\dfrac{\pi e^{2x}\;\sin(\pi y^{2})}{y^{2}}\;dx dy dz$
$2 \sin(4).$
$3e - 6.$
$4.$
O centróide de uma região $E$ é dado por
$$\overline{x}=\frac{1}{vol(E)}\int_{E}x\,dV,\;\;\;\; \overline{y}=\frac{1}{vol(E)}\int_{E}y\,dV\;\; \text{e}\;\; \overline{z}=\frac{1}{vol(E)}\int_{E}z\,dV.$$
Calcule o centróide da região dada em coordenadas esféricas por $0\leq \rho \leq 1$, $0\leq\phi \leq \pi/3$ e $0\leq \theta \leq 2\pi$ (observe que, devido à simetria da região, $\overline{x}$ e $\overline{y}$ se anulam, bastando calcular a terceira coordenada).
$\overline{z} = \dfrac{9}{16}.$
Escreva seis integrais triplas iteradas diferentes para o volume do sólido retangular no primeiro octante limitado pelos planos coordenados e pelos planos $x=1$, $y=2$ e $z=3$. Calcule uma das integrais.
$$\begin{split} 6 &= \int_{0}^{1}\int_{0}^{2}\int_{0}^{3} dz dy dx = \int_{0}^{2}\int_{0}^{1}\int_{0}^{3} dz dx dy = \int_{0}^{3}\int_{0}^{2}\int_{0}^{1} dx dy dz\\ &= \int_{0}^{2}\int_{0}^{3}\int_{0}^{1} dx dz dy = \int_{0}^{3}\int_{0}^{1}\int_{0}^{2} dy dx dz = \int_{0}^{1}\int_{0}^{3}\int_{0}^{2} dy dx dx. \end{split} $$
Marque o ponto cujas coordenadas esféricas é $(1,0,0)$ e encontre as coordenadas retangulares do ponto.
$(0,0,1).$

Suponha que o sólido tenha densidade constante $k$. Encontre os momentos de inércia para um cubo com comprimento do lado $L$ se um vértice está localizado na origem e três arestas estão nos eixos coordenados.
$\displaystyle I_{x} = I_{y} = I_{z} = \dfrac{2kL^5}{3}.$
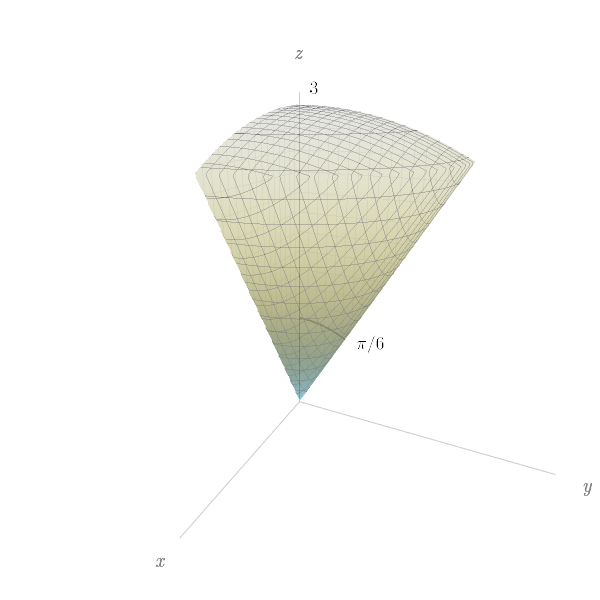
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da menor cunha esférica cortada de uma esfera de raio $a$ por dois planos que se interceptam ao longo de um diâmetro com um ângulo de $\pi/6.$
$\dfrac{\pi a^3}{9}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}x\,dxdydz$, onde $B$ é o conjunto $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}+z^{2}\leq 1$ e $x\geq 0.$
$3\pi.$
Esboce o sólido cujo volume é dado pela integral iterada.
$\displaystyle\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2-2z}\;dy dz dx$
$\displaystyle\int_{0}^{2}\int_{0}^{2-y}\int_{0}^{4-y^{2}}\;dx dz dy$
$\displaystyle\int_{0}^{1}\int_{\sqrt{1-z}}^{\sqrt{4-z}}\int_{2}^{3}\;dx dy dz$
$\displaystyle\int_{0}^{2}\int_{x^{2}}^{2x}\int_{0}^{x+y}\;dz dy dx$
(... fig)
(... fig.)
$\displaystyle \left\lbrace (x,y,z); 2 \leq x \leq 3, \sqrt{1 - z} \leq y \leq \sqrt{4 - z} , 0 \leq z \leq 1\right\rbrace.$
$\displaystyle \left\lbrace (x,y,z); 0 \leq x \leq 2, x^{2} \leq y \leq 2x , 0 \leq z \leq x + y\right\rbrace.$
Calcule, usando integração, o volume do sólido limitados pelas superfícies $z = 1$, $z = 2$ e $z = \sqrt{x^2 + y^2}.$
$\dfrac{7\pi}{6}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}2x\,dV$, onde $E=\{(x,y,z)|\;0\leq y\leq 2,\,0\leq x\leq \sqrt{4-y^{2}},\;\\ 0\leq z\leq y\}.$
$\displaystyle\iiint\limits_{ E}6xy\,dV$, onde $E$ está abaixo do plano $z=1+x+y$ e acima da região do plano $xy$ limitada pelas curvas $y=\sqrt{x}$, $y=0$ e $x=1.$
$4.$
$\dfrac{65}{28}.$
Calcule a massa do cilindro $x^{2}+y^{2}\leq 4$ e $0\leq z \leq 2$, sabendo que a densidade no ponto $(x,y,z)$ é o dobro da distância do ponto ao plano $z=0.$
$16\pi.$
Encontre o centróide e os momentos de inércia $I_{x}$, $I_{y}$ e $I_{z}$ do tetraedro cujos vértices são os pontos $(0,0,0)$, $(1,0,0)$, $(0,1,0)$ e $(0,0,1).$
Centróide: $\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4} \right),$ $I_{x} = I_{y} = I_{z} = \dfrac{1}{30}.$
Seja $D$ a região limitada abaixo pelo plano $z=0$, acima pela esfera $x^2+y^2+z^2=4$ e dos lados pelo cilindo $x^2+y^2=1$. Monte as integrais triplas em coordenadas cilíndricas que dão o volume de $D$ usando as ordens de integração a seguir.
$dzdrd\theta$
$drdzd\theta$
$d\theta dzdr$
$\displaystyle \int_{0}^{2\pi} \int_{0}^{1} \int_{0}^{\sqrt{4 - r^2}} r dz dr d\theta.$
$\displaystyle \int_{0}^{2\pi} \int_{0}^{\sqrt{3}} \int_{0}^{1} r drdzd\theta + \int_{0}^{2\pi} \int_{\sqrt{3}}^{2} \int_{0}^{\sqrt{4 - z^2}} r drdzd\theta.$
$\displaystyle \int_{0}^{1} \int_{0}^{\sqrt{4 - r^2}} \int_{0}^{2\pi} r d\theta dzdr.$
Esboce o sólido cujo volume é dado pela integral iterada.
$\displaystyle\int_{0}^{2}\int_{0}^{2-y}\int_{0}^{4-y^{2}}\;dx dz dy$
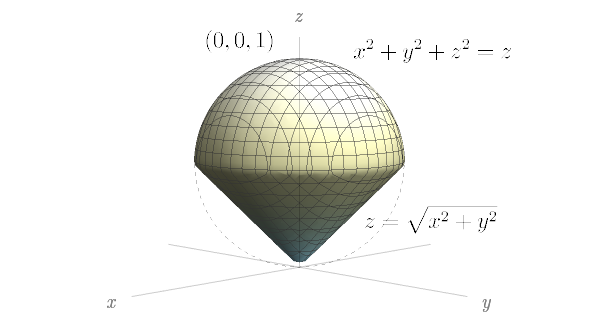
Um sólido está acima do cone $z=\sqrt{x^{2}+y^{2}}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=z.$ Escreva uma descrição do sólido em termos de desigualdades envolvendo coordenadas esféricas.
A mudança de coordenadas retangulares para coordenadas cartesianas é dada por
$$\begin{cases}x = \rho \cos{\theta} \sin{\phi} \\y = \rho \sin{\theta} \sin{\phi}\\z = \rho \cos{\phi},\end{cases}$$
em que $\rho \geq 0$, $\theta \in [0,2\pi]$ e $\phi \in [0,\pi]$. Observe que $\sin{\phi} \geq 0$ quando $\phi \in [0,\pi]$. Logo, a equação do cone em coordenadas esféricas pode ser escrita como $\rho \cos{\phi} = \sqrt{\rho^2 \sin^2{\phi}} = \rho\sin{\phi}$. A origem $(0,0,0)$ pertence ao cone e é dada por $\rho = 0$. Nos demais pontos, $\rho \neq 0$, donde $\phi = \pi/4$.
A equação da esfera em coordenadas esféricas pode ser escrita como $\rho^2=\rho\cos{\phi}$. A origem $(0,0,0)$ pertence à esfera e é dada por $\rho=0$. Nos demais pontos, $\rho \neq 0$, donde $\rho = \cos{\phi}$.
Portanto, o sólido pode ser descrito em coordenadas esféricas por
$$E = \left\{(\rho, \theta, \phi): 0 \leq \rho \leq \cos{\phi}, 0 \leq \theta \leq 2\pi \mbox{ e } 0 \leq \phi \leq \frac{\pi}{4}\right\}.$$
Calcule a integral iterada.
$\displaystyle\int_{0}^{1}\!\!\int_{0}^{z}\!\!\int_{0}^{x+z}6xz\;dy dx dz$
$\displaystyle\int_{0}^{3}\!\!\int_{0}^{1}\!\!\int_{0}^{\sqrt{1-z^{2}}}ze^{y}\;dx dz dy$
$\displaystyle\int_{0}^{\pi/2}\int_{0}^{y}\int_{0}^{x}\cos(x+y+z)\;dz dx dy$
$1.$
$\displaystyle \frac{e^3 - 1}{3}.$
$-\dfrac{1}{3}.$
Seja \(G\) a região sólida dentro da esfera de raio \(2\) centrada na origem e acima do plano \(z=1\). Mostre (ou verifique) os seguintes resultados:
O volume de \(G\) é dado por \[\iiint\limits_G\,dV = \int_0^{2\pi}\int_0^{\dfrac{\pi}{3}}\int_{\sec\phi}^{2}\rho^2\sin\phi\,d\rho d\phi d\theta \]
\[\iiint\limits_G\dfrac{z}{x^2+y^2+z^2}\,dV = \int_0^{2\pi}\int_0^{\pi/3}\int_{\sec\phi}^{2}\rho\cos\phi\sin\phi\,d\rho d\phi d\theta \]
Usando coordenadas esféricas, determine o volume do elipsoide $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}\leq 1.$
$\dfrac{4 \pi abc}{3}.$
Usando coordenadas esféricas, determine o centroide e o momento de inércia em relação a um diâmetro de sua base do hemisfério sólido homogêneo de raio $a.$
Centróide: $\left(0,0,\dfrac{3a}{8} \right);$ momento de inércia: $\dfrac{4 K a^5 \pi}{15},$ onde $K$ é a densidade constante.
Encontre a constante $a$ tal que $$\int_{0}^{1}\int_{0}^{4-a-x^{2}}\int_{a}^{4-x^{2}-y}\;dz dy dx=\frac{4}{15}.$$
$\dfrac{13}{3}$ ou $3.$
Use a integral tripla para determinar o volume do sólido dado.
$x^{2}+y^{2}\leq 1$ e $x^{2}+z^{2}\leq 1.$
$(x-a)^{2}+y^{2}\leq a^{2}$, $x^{2}+y^{2}+z^{2}\leq 4a^{2}$, $z\geq 0$ $(a>0).$
$x^{2}+y^{2}\leq a^{2}$ e $x^{2}+z^{2}\leq a^{2}$ $(a>0).$
$x^{2}+y^{2}+z^{2}\leq a^{2}$ e $z\geq \dfrac{a}{2}$ $(a>0).$
$\dfrac{16}{3}.$
$\dfrac{16a^3}{3} \left(\dfrac{\pi}{2} - \dfrac{2}{3}\right).$
$\dfrac{16a^3}{3}.$
$\dfrac{5\pi a^3}{24}.$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da região limitada abaixo pelo plano $z=0$, lateralmente pelo cilindro $x^{2}+y^{2}=1$ e acima pelo paraboloide $z=x^{2}+y^{2}$.
$\dfrac{\pi}{2}.$
Marque o ponto cujas coordenadas cilíndricas são $(2, \pi/4,1)$ e $(4, -\pi/3,5)$. Em seguida, encontre as coordenadas retangulares do ponto.
Para $(2, \pi/4,1):$ $(\sqrt{2},\sqrt{2},1)$ e para $(4, -\pi/3,5):$ $(2, -2\sqrt{3},5)$.
Seja $D$ a região limitada abaixo pelo plano $z=0$, acima pela esfera $x^{2}+y^{2}+z^{2}=4$ e dos lados pelo cilindro $x^{2}+y^{2}=1$. Monte as integrais triplas em coordenadas esféricas que dão o volume de $D$ usando as ordens de integração a seguir.
$d\rho\,d\phi\,d\theta$;
$d\phi\,d\rho\,d\theta$.
$\displaystyle \int_{0}^{2\pi}\int_{0}^{\pi/6}\int_{0}^{2} \rho^{2}\sin(\phi)\; d\rho d\phi d\theta + \int_{0}^{2\pi}\int_{\pi/6}^{\pi/2}\int_{0}^{\csc(\phi)} \rho^{2}\sin(\phi)\; d\rho d\phi d\theta.$
$\displaystyle \int_{0}^{2\pi}\int_{1}^{2}\int_{\pi/6}^{\arcsin(1/\rho)} \rho^{2}\sin(\phi)\; d\phi d\rho d\theta + \int_{0}^{2\pi}\int_{0}^{2}\int_{0}^{\pi/6} \rho^{2}\sin(\phi)\; d\phi d\rho d\theta.$
Esboce o sólido descrito por $\rho \leq 2$, $0\leq \phi \leq \pi/2$ e $0\leq \theta \leq \pi/2.$
Calcule as seguintes integrais triplas.
$\displaystyle\iiint\limits_{ E} x^2 \, dV$, em que $E$ é o sólido que está dentro do cilindro $x^2 + y^2 = 1$, acima do plano $z = 0$ e abaixo do cone $z^2 = 4x^2 + 4y^2$.
$\displaystyle\iiint\limits_{ E} xyz \, dV,$ em que $E$ é o sólido limitado pelos paraboloides $z = x^2 + y^2$, $z = 8 - x^2 - y^2$.
$\displaystyle\int_{-2}^2\int_{-\sqrt{4 - y^2}}^{\sqrt{4 - y^2}}\int_{\sqrt{x^2 + y^2}}^2 xz \, dz dx dy$
$\dfrac{2\pi}{5}$.
$0.$
$0.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}2z\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq 1$, $x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}-y^{2}\leq z \leq 1-2y^{2}.$
$\dfrac{7\pi}{2}.$
$0.$
Use a integral tripla para determinar o volume do sólido dado por $x^{2}+y^{2}\leq z\leq \sqrt{4-3x^{2}-3y^{2}}.$
Primeiramente, vamos determinar a projeção no plano $xy$ da interseção de \begin{eqnarray*} z&=&\sqrt{4-3x^{2}-3y^{2}}\\ z&=&x^{2}+y^{2}. \end{eqnarray*} Da primeira equação temos que \begin{eqnarray*} \label{1}z=\sqrt{4-3x^{2}-3y^{2}}\Leftrightarrow z^{2}=4-3x^{2}-3y^{2}\Leftrightarrow z^{2}=4-3(x^{2}+y^{2}). \end{eqnarray*} Substituindo a segunda equação na primeira, obtemos que $$z^{2}=4-z\Leftrightarrow z^{2}+3z-4=0\Leftrightarrow (z-1)(z-4)=0.$$ Logo, $z=-4$ e $z=1.$ Notemos que $z=-4$ não satisfaz as duas primeiras equações acima, então a projeção $D$ no plano $xy$ é o círculo de raio 1, isto é, $D=\{(x,y)\in \mathbb{R};\;\, x^{2}+y^{2}\leq 1\}.$ Assim, o volume, $V$, do sólido é: $$V=\iint\limits_{D}\bigg[\int_{x^{2}+y^{2}}^{\sqrt{4-3x^{2}-3y^{2}}}1\, dz\bigg]\,dA = \iint\limits_{ D}\sqrt{4-3x^{2}-3y^{2}}-(x^{2}+y^{2})\,dA.$$ Passando para coordenadas polares temos que \begin{eqnarray*} x=r\cos \theta\\ y=r\sin \theta\\ dA=r\,dr\,d\theta\\ 0\leq r\leq 1\\ 0\leq \theta \leq 2\pi.\\ \end{eqnarray*} Então, $$V=\int_{0}^{2\pi}\int_{0}^{1}(\sqrt{4-3r^{2}}-r^{2})r\,dr\,d \theta=\int_{0}^{2\pi}\int_{0}^{1}(r\sqrt{4-3r^{2}}-r^{3})\,dr\,d\theta$$ $$=\int_{0}^{2\pi}\,d\theta\cdot \bigg[\bigg(\underbrace{\int_{0}^{1}r\sqrt{4-3r^{2}}\,dr}_{\substack{ u=4-3r^{2}\\ du=-6r\,dr}}\bigg)-\bigg(\int_{0}^{1}r^{3}\,dr\bigg)\bigg]$$ $$=\theta\bigg|_{0}^{2\pi}\cdot \bigg[\bigg(\int_{4}^{1}r\cdot u^{1/2}\frac{du}{-6r}\bigg)-\bigg(\frac{r^{4}}{4}\bigg|_{0}^{1}\bigg)\bigg]$$ $$=2\pi\cdot \bigg[\bigg(-\frac{1}{6}\int_{4}^{1}u^{1/2}\,du\bigg)-\frac{1}{4}\bigg]=2\pi \cdot \bigg[\bigg(-\frac{1}{6}\cdot \frac{2}{3}u^{3/2}\bigg|_{4}^{1}\bigg)-\frac{1}{4}\bigg]$$ $$=2\pi \cdot \bigg[-\frac{1}{9}+\frac{1}{9}\cdot 8-\frac{1}{4}\bigg]=2\pi \cdot \frac{19}{36}=\frac{19\pi}{18}.$$
Mude as coordenadas de $(1,-1,4)$ de retangulares para cilíndricas.
$\displaystyle (\sqrt{2}, \dfrac{7\pi}{4}, 4).$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{-a}^{a}\int_{-\sqrt{a^{2}-y^{2}}}^{\sqrt{a^{2}-y^{2}}}\int_{-\sqrt{a^{2}-x^{2}-y^{2}}}^{\sqrt{a-x^{2}-y^{2}}}(x^{2}z+y^{2}z+z^{3})\,dzdxdy$.
$0.$
Usando coordenadas esféricas, calcule a massa da esfera sólida de raio \(a\) com densidade proporcional à distância ao centro (tomando \(k\) como a constante de proporcionalidade).
\(k\pi a^4\)
Usando coordenadas esféricas, determine o volume do sólido que está acima do plano $z=2\sqrt{3}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=16.$
$\dfrac{88\pi}{3}.$
Mostre que
$$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{x^{2}+y^{2}+z^{2}}\,e^{-(x^{2}+y^{2}+z^{2})}\,dxdydz=2\pi.$$
(A integral imprópria tripla é definida como o limite da integral tripla sobre uma esfera sólida quando o raio da esfera aumenta indefinidamente.)
Note que $$\begin{split}&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{x^{2}+y^{2}+z^{2}}\,e^{-(x^{2}+y^{2}+z^{2})}\,dxdydz \\&= \lim_{R \to \infty} \int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{R} \rho e^{-\rho^2}\rho^2 \sin(\phi)\;d\rho d\phi d\theta.\end{split}$$
Esboce o sólido cujo volume é dado pela integral abaixo e calcule-a.
$$\int_{0}^{\pi/6}\!\!\int_{0}^{\pi/2}\!\!\int_{0}^{3}\rho^{2}\sin{\phi}\;d\rho d\theta d\phi$$
Uma casca cilíndrica tem $20$ cm de comprimento, com raio interno de 6 cm e raio externo de $7$ cm. Escreva desigualdades que descrevam a casca em um sistema de coordenadas adequado. Explique como você posicionou o sistema de coordenadas em relação à casca.
$6 \leq r \leq 7,$ $0 \leq \theta \leq 2\pi,$ $0 \leq z \leq 20.$
Identifique a superfície cuja equação é dada por $z = 4 - r^2$.
$z = 4 - x^2 - y^2,$ o parabolóide circular com vértice $(0,0,4)$.
Seja \(G\) a caixa retangular definida pelas desigualdades \(a\leq x\leq b\), \(c\leq y\leq d\) e \(k\leq z\leq l\). Mostre que \[\iiint\limits_G f(x)g(y)h(z)\,dV = \left[\int_a^bf(x)\,dx\right]\left[\int_c^dg(y)\,dy\right]\left[\int_k^lh(z)\,dz\right].\]
Calcule as seguintes integrais triplas.
$\displaystyle\iiint\limits_{ E} \sqrt{x^2 + y^2} \, dV$, em que $E$ é a região que está dentro do cilindro $x^2 + y^2 = 16$ e entre os planos $z = -5$ e $z = 4$.
$\displaystyle\iiint\limits_{ E} y \, dV$, em que $E$ é o sólido que está entre os cilindros $x^2 + y^2 = 1$ e $x^2 + y^2 = 4$, acima do plano $xy$ e abaixo do plano $z = x + 2$.
$\displaystyle\iiint\limits_{ E} x \, dV$, em que $E$ está delimitidado pelos planos $z = 0$ e $z = x + y + 5$ e pelos cilindros $x^2 + y^2 = 4$ e $x^2 + y^2 = 9$.
$384\pi$.
$0$.
$\dfrac{65\pi}{4}$.
Esboce a região limitada pelos gráficos das equações e use uma integral tripla para calcular seu volume.
$z+x^{2}=4$, $y+z=4$, $y=0$ e $z=0.$
$y=2-z^{2}$, $y=z^{2}$, $x+z=4$ e $x=0.$
$y^{2}+z^{2}=1$, $x+y+z=2$ e $x=0.$
$\dfrac{128}{5}.$
$\dfrac{32}{3}.$
$2\pi.$
Usando coordenadas esféricas, determine o volume do sólido que está acima do cone $\phi=\pi/3$ e abaixo da esfera $\rho=4\cos{\phi}.$
$10\pi.$
Encontre o volume da região sólida limitada abaixo pelo plano $z = 0$, lateralmente pelo cilindro $x^2 + y^2 = 1$ e acima pelo paraboloide $z = x^2 + y^2$.
Temos que a região sólida $E$ está acima do plano $z=0$, abaixo do paraboloide $z=x^{2}+y^{2}$ e limitado lateralmente pelo cilindro $x^{2}+y^{2}=1$. Notemos que podemos dividir a região sólida em quatro porções simétricas. Assim, levando em consideração a porção da região sólida $E$ que está no primeiro octante, temos em coordenadas cilíndricas $$0\leq \theta \leq \frac{\pi}{2},\, 0\leq r \leq 1\,\, \mbox{e}\,\, 0\leq z\leq x^{2}+y^{2}=r^{2}.$$ Assim, o volume da região sólida $E$ é: $$V=\iiint\limits_{ E}1\,dV=4\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}\int_{0}^{r^{2}}1\,r\,dz\,dr\,d\theta$$ $$=4\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}zr\,\bigg|_{0}^{r^{2}}\,dr\,d\theta=4\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}r^{3}\,dr\,d\theta$$ $$=4\int_{0}^{\frac{\pi}{2}}\,d\theta\cdot \int_{0}^{1}r^{3}\,dr=4\cdot \theta\bigg|_{0}^{\frac{\pi}{2}}\cdot \frac{r^{4}}{4}\bigg|_{0}^{1}$$ $$=4\cdot \frac{\pi}{2}\cdot \frac{1}{4}=\frac{\pi}{2}.$$
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.
$\displaystyle \int_0^{\pi/2}\int_0^2\!\!\int_0^{9 - r^2} r dz dr d\theta$
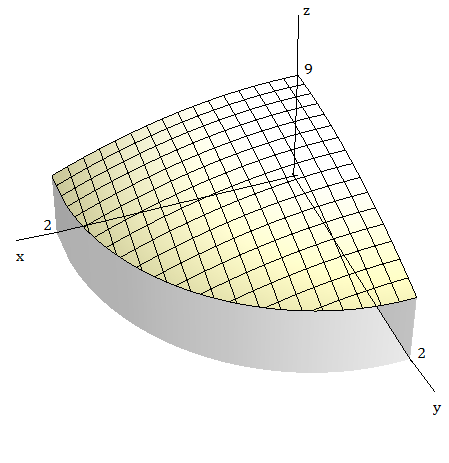
Use a integral tripla para determinar o volume do sólido dado.
$x^{2}\leq z \leq 1-y$ e $y\geq 0.$
$x^{2}+2y^{2}\leq z\leq 2a^{2}-x^{2}$ $(a>0).$
$x^{2}+y^{2}+(z-1)^{2}\leq 1$ e $z\geq x^{2}+y^{2}.$
$4x^{2}+9y^{2}+z^{2}\leq 4$ e $4x^{2}+9y^{2}\leq 1.$
$\dfrac{4}{15}.$
$\pi a^4.$
$\dfrac{71\pi}{54}.$
$\dfrac{7\pi}{12}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}xyz\,dV$, onde $E$ está entre as esferas $\rho=2$ e $\rho=4$ e acima do cone $\phi=\pi/3.$
$0.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{\pi}\int_{0}^{\pi}\int_{0}^{2\,\sin{\phi}}\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$\pi^2.$
Calcule a massa do sólido $x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0$, sendo a densidade dada por $\rho(x,y,z)=x+y.$
$\dfrac{1}{12}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}(x^{2}+y^{2}+z^{2})^{2}\,dV$, onde $B$ é a bola com centro na origem e raio $5.$
$\dfrac{312500\pi}{7}.$
Usando coordenadas esféricas, determine o volume e o centroide do sólido que está acima do cone $\phi=\pi/3$ e abaixo da esfera $\rho=4\cos{\phi}.$
Volume: $10\pi;$ centróide: $(0,0,2,1).$

