Exercícios
Aplicações
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Uma luminária tem duas lâmpadas de um tipo com tempo de vida médio de 1.000 horas. Supondo que possamos modelar a probabilidade de falha dessas lâmpadas por uma função densidade exponencial com média $\mu = 1.000$, determine a probabilidade de que ambas as lâmpadas venham a falhar dentro de um período de 1.000 horas.
Outra luminária tem somente uma lâmpada do mesmo tipo das do item anterior. Se a lâmpada queima e é trocada por outra to mesmo tipo, determine a probabilidade de que as duas venham a falhar dentro de 1.000 horas.
$(e^{-1} - 1)^2.$
$1 - 2e^{-1}.$
Utilize a integral dupla para determinar a área da região: um laço da rosácea $r=\cos(3\theta).$
$\displaystyle \frac{\pi}{12}.$
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1} \!\! \int_{0}^{1}(4-x-2y)\, dx dy.$$
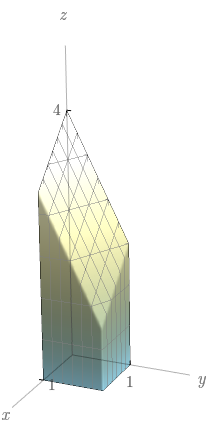
Determine o volume do sólido descrito abaixo.
Limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $y=z$, $x=0$ e $z=0$, no primeiro octante.
Cuja base é a região no plano $xy$ que é limitada pela parábola $y=4-x^{2}$ e pela reta $y=3x$, enquanto o topo do sólido é limitado pelo plano $z=x+4.$
No primeiro octante limitado pelos planos coordenados, pelo cilindro $x^{2}+y^{2}=4$ e pelo plano $z+y=3.$
$\dfrac{1}{3}.$
$\dfrac{625}{12}.$
$\dfrac{9\pi - 8}{3}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
Massa: $4;$ centro de massa: $\displaystyle \left(\frac{6}{5},\frac{12}{5} \right).$
Utilize a integral dupla para determinar a área da região: dentro da cardióide $r=1+\cos{\theta}$ e fora do círculo $r=3\cos{\theta}.$
$\displaystyle \frac{\pi}{4}.$
Calcule o centro de massa da região: $D$ o triângulo de vértices $(0,0), (0,1)$ e $(1,1)$ e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(\frac{3}{4}, \frac{2\sqrt{2} - 1}{2\sqrt{2} + 2\ln(1 + \sqrt{2})} \right).$
Utilize a integral dupla para determinar a área da região: limitada pelo eixo $x$ positivo e pela espiral $r=4\theta/3$, $0\leq \theta \leq 2\pi.$ A região se parece com uma concha de caracol.
$\dfrac{64\pi^3}{27}.$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina retangular que ocupa a região descrita pelas desigualdades \(0\leq x\leq a\) e \( 0\leq y\leq b\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ \begin{array}{lll} I_x= \dfrac{\delta ab^3}{3}, & I_y= \dfrac{\delta a^3b}{3}, & I_z= \dfrac{\delta ab(a^2+b^2)}{3}. \end{array} \]
Calcule o volume do conjunto dado.
$0\leq y\leq 1-x^{2}$ e $0\leq z\leq 1-x^{2}.$
$x^{2}+y^{2}+3\leq z\leq 4.$
$\dfrac{16}{15}.$
$\dfrac{\pi}{2}.$
Calcule o volume do conjunto dado.
$x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0.$
$x\leq y\leq 1$, $x\geq 0$, $z\geq 0$ e $z^{2}+x^{4}+x^{2}y^{2}\leq 2x^{2}.$
$\dfrac{1}{6}.$
$\dfrac{\pi(1 - \sqrt{2})}{8} + \dfrac{1}{3}.$
Uma carga elétrica é distribuída sobre o retângulo $1 \leq x \leq 3$, $0 \leq y \leq 2$, de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = 2xy + y^2$ (medida em coulombs por metro quadrado). Determine a carga total no retângulo.
$\displaystyle \frac{64}{3}$ Coulombs.
Determine o volume do sólido.
Abaixo do paraboloide $z=x^{2}+y^{2}$ e acima da região delimitada por $y=x^{2}$ e $x=y^{2}.$
Abaixo do paraboloide $z=3x^{2}+y^{2}$ e acima da região delimitada por $y=x$ e $x=y^{2}-y.$
$ $ Abaixo da superfície $z=xy$ e acima do triângulo com vértices $(1,1)$, $(4,1)$ e $(1,2).$
Limitado pelo cilindro $y^{2}+z^{2}=4$ e pelos planos $x=2y$, $x=0$ e $z=0$, no primeiro octante.
$\dfrac{6}{35}.$
$\dfrac{144}{35}.$
$\dfrac{31}{8}.$
$\dfrac{16}{3}.$
Calcule a área limitada pelas curvas $x=y^{2}-1$ e $x=2y^{2}-2.$
$\dfrac{4}{3}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $D$ delimitada pelas parábolas $y = x^2$ e $x = y^2; \quad \rho(x,y) = \sqrt{x}$.
Massa: $\dfrac{3}{14};$ centro de massa: $\displaystyle \left(\frac{14}{27},\frac{28}{55} \right).$
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento $a$, se a densidade em qualquer ponto for proporcional ao quadrado da distância do vértice oposto à hipotenusa.
$\displaystyle \left(\frac{2a}{5}, \frac{2a}{5} \right).$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq a^{2}$ e $y^{2}+z^{2}\leq a^{2}$, $a >0.$
$x^{2}+y^{2}\leq z\leq 1-x^{2}.$
$\dfrac{16a^{3}}{3}.$
$\dfrac{\pi}{2\sqrt{2}}.$
Calcule o centro de massa do quadrado $D$ dado por $0 \leq x \leq 1, \ 0 \leq y \leq 1$ e com densidade $\quad \rho(x,y) = y$.
$\displaystyle \left(\frac{1}{2}, \frac{2}{3} \right).$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq 1$ e $x+y+2\leq z \leq 4.$
$x\geq 0$, $y \geq 0$, $x+y\leq 1$ e $0\leq z\leq x^{2}+y^{2}.$
$2\pi.$
$\dfrac{1}{6}.$
Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for $\rho(x,y) = 1 + 0,1\cdot x$, é mais difícil girar a pá em torno do eixo $x$ ou do eixo $y$?
Se calcularmos os momentos de inércia sobre $x$ e $y$, poderemos determinar em qual direção será mais difíciel de girar a pá do ventilador. Notemos que a região de integração é o quadrado com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem em ambas as integrais. Então, o momento de inércia sobre o eixo $x$ é dada por: $$I_{x}=\iint\limits_{D}y^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}y^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(1+0,1x)\,dx\cdot \int_{0}^{2}y^{2}\,dy=\bigg(x+0,1\frac{x^{2}}{2}\bigg)\bigg|_{0}^{2}\cdot \bigg(\frac{y^{3}}{3}\bigg)\bigg|_{0}^{2}$$ $$=\bigg[(2+0,2)-0\bigg]\cdot \bigg[\frac{8}{3}\bigg]=\frac{17,6}{3}.$$ Da mesma forma, o momente de inércia sobre o eixo $y$ é dado por: $$I_{y}=\iint\limits{D}x^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}x^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(x^{2}+0,1x^{3})\,dx\cdot \int_{0}^{2}\,dy=\bigg(\frac{x^{3}}{3}+0,1\frac{x^{4}}{4}\bigg)\bigg|_{0}^{2}\cdot \bigg(y\bigg)\bigg|_{0}^{2}$$ $$=\bigg[\bigg(\frac{8}{3}+0,4\bigg)-0\bigg]\cdot \bigg[2-0\bigg]=\frac{18,4}{3}.$$ Como $I_{y}>I_{x}$ é mais difícil girarmos a pá do ventilador em torno do eixo $y.$
Calcule o volume do conjunto dado.
$x^{2}+4y^{2}\leq 4$ e $x+y\leq z\leq x+y+1.$
$x\geq 0$, $x\leq y\leq 1$ e $0\leq z\leq e^{y^{2}}.$
$2\pi.$
$\dfrac{e - 1}{2}.$
Encontre o volume do sólido delimitado pelo parabolóide $z=2+x^{2}+(y-2)^{2}$ e pelos planos $z=1$, $x=1$, $x=-1$, $y=0$ e $y=4.$
Observe que o sólido $E$ está abaixo da superfície $z = 2+x^2+(y-2)^2$ e acima do retângulo $[-1,1]\times [0,4]$ em $z=1$ (ver figura abaixo).

Algebricamente, $$E = \{(x,y,z) \in\mathbb{R}^3: -1 \leq x \leq 1, 0 \leq y \leq 4 \mbox{ e } 1 \leq z \leq 2 + x^2 + (y-2)^2\}.$$ Logo, o volume é dado por $$V = \iint\limits_{R}(2+x^2+(y-2)^2)\,dA - \iint\limits_{ R}\,dA,$$ em que $R = \{(x,y) \in \mathbb{R}^2; -1 \leq x \leq 1 \mbox{ e } 0 \leq y \leq 4 \}$. Assim, \begin{eqnarray*} V & = & \displaystyle\int_{-1}^{1}\int_{0}^{4}(x^2+y^2-4y+5)\,dy dx \\ & = & \displaystyle\int_{-1}^{1} \left.\left(x^2y+\frac{y^3}{3}-2y^2+5y \right|_{y=0}^{y=4} \right) \,dx \\ & = & \displaystyle\int_{-1}^{1} \left(4x^2+\frac{28}{3}\right) \,dx \\ & = & \left.\frac{4x^3}{3}+\frac{28x}{3} \right|_{x=-1}^{x=1} = \frac{64}{3}. \end{eqnarray*} Observe que, pelo Teorema de Fubini, podemos optar por calcular a integral $$\int_{0}^{4}\!\int_{-1}^{1}(x^2+y^2-4y+5)\,dy dx,$$ obtendo o mesmo resultado.
Calcule o centro de massa da região $D$ dada.
$D$ é o conjunto de todos $(x,y)$ tais que $x^3 \leq y \leq x$ e a densidade é constante e igual a 1.
$D$ é o conjunto de todos $(x,y)$ tais que $x \leq y \leq x + 1$, $0 \leq x \leq 1$, e a densidade é o produto das coordenadas do ponto.
$D$ é o conjunto de todos $(x,y)$ tais que $1 \leq x^2 + y^2 \leq 4$, $y \geq 0$, e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(0,0\right).$
$\displaystyle \left(\frac{5}{7},\frac{9}{7}\right).$
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Verifique que $$f(x,y) = \begin{cases} 4xy, & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 1,\\ 0, & \quad \text{caso contrário}, \end{cases}$$ é uma função densidade conjunta.
Se $X$ e $Y$ são variáveis aleatórias cuja função densidade conjunta é a função $f$ do item anterior, determine: (i) $P(X \geq \frac{1}{2})$, (ii) $P(X \geq \frac{1}{2}, Y \leq \frac{1}{2})$.
Determine os valores esperados de $X$ e $Y$.
Note que $$\iint_\limits{\mathbb{R}^2} f(x,y)\,dA = \int_{0}^{1} \int_{0}^{1} 4xy\, dydx = 1. $$
(i) $\dfrac{3}{4}.$ (ii) $\dfrac{3}{16}.$
$\dfrac{3}{16}.$
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste a oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade norte. Encontre o volume de água da piscina.
$1800 \pi$ m$^3.$
Encontre o volume do sólido no primeiro octante limitado pelo cilindro $z=16-x^{2}$ e pelo plano $y=5.$
$\dfrac{640}{3}.$
A fronteira de uma lâmina consiste nos semicírculos $y = \sqrt{1 - x^2}$ e $y = \sqrt{4 - x^2}$, juntamente com as partes do eixo $x$ que os une. Encontre o centro de massa da lâmina se a densidade em qualquer ponto é proporcional à sua distância da origem.
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Determine a massa e o centro de massa da lâmina que ocupa a região $\displaystyle D = \{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2, \ -1 \leq y \leq 1\}$ e tem função densidade $\rho(x,y) = xy^2.$
Massa: $\dfrac{4}{3};$ centro de massa: $\displaystyle \left(\frac{4}{3},0 \right).$
Utilize a integral dupla para determinar a área da região: cortada do primeiro quadrante pela curva $r=2(2-\sin(2\theta))^{1/2}.$
$2(\pi - 1).$
Uma lâmina ocupa parte do disco $x^2 + y^2 \leq 1$ no primeiro quadrante. Determine o centro de massa se a densidade em qualquer ponto for proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(\frac{3}{8}, \frac{3\pi}{16} \right).$
Calcule o centro de massa da região: $D = \{(x,y) \in \mathbb{R}^2: x^2 + 4y^2 \leq 1, \ y \geq 0\}$ e a densidade é proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(0, \frac{3\pi}{32} \right).$
Determine o volume do sólido limitado pelos planos coordenados e pelo plano $3x+2y+z=6.$
O sólido cujo volume deve ser calculado é $$E = \{(x,y,z) \in \mathbb{R}^3; (x,y) \in R \mbox{ e } 0 \leq z \leq 6 - 3x - 2y\},$$ em que $R$ é a projeção de $E$ no plano $xy$. Assim, o volume é dado por $$V = \displaystyle\int\!\!\!\!\int\limits_{R}(6-3x-2y)\,dA.$$ A região $R$ é tanto do tipo I como do tipo II, então é possível escrevê-la de pelo menos duas formas. Escrevendo como uma região do tipo I, obtemos: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \frac{6-3x}{2}\right\}.$$ Portanto, \begin{eqnarray*} V & = & \displaystyle\int_{0}^{2}\!\int_{0}^{\frac{6-3x}{2}}(6-3x-2y)\,dy dx \\ & = & \displaystyle\int_{0}^{2} \left.\left(6y-3xy-y^2 \right|_{y=0}^{y=\frac{6-3x}{2}} \right) \,dx \\ & = & \displaystyle\int_{0}^{2} \left(9-9x+\frac{9x^2}{4}\right) \,dx \\ & = & \left.9x-\frac{9x^2}{2}+\frac{9x^3}{12} \right|_{x=0}^{x=2} = 6. \end{eqnarray*} Observe que podemos escrever $R$ como uma região do tipo II, obtendo: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq \frac{6-2y}{3} \text{ e } 0 \leq y \leq 3\right\}.$$ Então, uma outra expressão para $V$ é $$V = \displaystyle\int_{0}^{3}\!\int_{0}^{\frac{6-2y}{3}}(6-3x-2y)\,dx dy = 6.$$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina circular que ocupa a região descrita pelas desigualdades \(0\leq x^2+y^2\leq a^2\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ I_x= I_y=\dfrac{\delta\pi a^4}{4}, \quad I_z= \dfrac{\delta\pi a^4}{2}.\]
A função densidade conjunta para um par de variáveis aleatórias $X$ e $Y$ é $$f(x,y) = \begin{cases} Cx(1 + y), & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 2,\\ 0, & \quad \text{caso contrário}.
\end{cases}$$
Determine a constante $C$.
Determine $P(X \leq 1, \ Y \leq 1)$.
Determine $P(X + Y \leq 1)$.
$\dfrac{1}{2}.$
$\dfrac{3}{8}.$
$\dfrac{5}{48}$.
Determine o valor médio de $f(x,y)=e^{y}\sqrt{x+e^{y}}$ sobre o retângulo $R=[0,4]\times [0,1].$
$\dfrac{(4 + e)^{5/2} - e^{5/2} - 5^{5/2} + 1}{15}.$
Calcule o volume do conjunto dado.
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1,0\leq z\leq x+2y\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 2, 1\leq y\leq 2, 0\leq z\leq \sqrt{xy}\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, 0\leq z\leq xye^{x^{2}-y^{2}}\}$
$ \{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, x^{2}+y^{2}\leq z\leq 2\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 1\leq x\leq 2, 0\leq y\leq 1,\;x+y\leq z\leq x+y+2\}$
$\{(x,y,z)\in \mathbb{R}^{3}|\;0\leq x\leq 1, 0\leq y\leq 1,1\leq z\leq e^{x+y}\}$
$\dfrac{3}{2}.$
$\dfrac{8\sqrt{2}(2\sqrt{2} - 1)}{9}.$
$\dfrac{(e - 1)(1 - e^{-1})}{4}.$
$\dfrac{4}{3}.$
$2.$
$e^{2}-2e.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, quando: $D$ é delimitada por $y = e^x$, $y = 0$, $x = 0$ e $x = 1; \quad \rho(x,y) = y$.
Massa: $\dfrac{1}{4}(e^{2} - 1);$ centro de massa: $\displaystyle \left(\frac{e^2 + 1}{2(e^2 - 1)},\frac{4(e^3 - 1)}{9 (e^2 - 1)} \right).$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo:$D$ a região triangular com vértices $(0,0), (2,1), (0,3)$ e $\rho(x,y) = x + y$.
Massa: $6;$ centro de massa: $\displaystyle \left(\frac{3}{4},\frac{3}{2} \right).$
Utilize o resultado $\displaystyle \int_{-\infty}^{\infty}e^{-x^{2}}\,dx=\sqrt{\pi}$ para calcular as integrais:
$\displaystyle\int_{0}^{\infty} x^{2}e^{-x^{2}}\,dx$
$\displaystyle\int_{0}^{\infty}\sqrt{x}e^{-x}\,dx$
$\displaystyle \frac{\sqrt{\pi}}{4}.$
$\displaystyle \frac{\sqrt{\pi}}{2}.$
Determine os momentos de inércia da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
$\displaystyle I_{x} = \dfrac{1}{16}(e^4 - 1),$ $I_{y} = \dfrac{1}{16}(e^4 - 1)$ e $I_{0} = \dfrac{1}{16}(e^4 + 2e^2 - 3).$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq z\leq 2x.$
$x\leq z\leq1-y^{2}$ e $x\geq 0.$
$\dfrac{\pi}{2}.$
$\dfrac{8}{15}.$
Calcule o volume do conjunto dado.
$4x+2y\geq z\geq 3x+y+1$, $x\geq 0$ e $y\geq 0.$
$0\leq z\leq \sin{y^{3}}$ e $\sqrt{x}\leq y\leq \sqrt[3]{\pi}.$
$\dfrac{1}{6}.$
$\dfrac{2}{3}.$
Utilize a integral dupla para determinar a área da região: no interior do círculo $x^{2}+(y-1)^{2}=1$ e fora do círculo $x^{2}+y^{2}=1.$
$\displaystyle \frac{\pi}{3} + \frac{\sqrt{3}}{2}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $\displaystyle D = \{(x,y) \in\mathbb{R}^2: 0 \leq y \leq \sin{(\pi x/L)}, \ 0 \leq x \leq L\}; \quad \rho(x,y) = y$.
Massa: $\dfrac{L}{4};$ centro de massa: $\displaystyle \left(\frac{L}{2},\frac{16}{9\pi} \right).$

