Exercícios
Em coordenadas polares
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{a} \int_{0}^{\sqrt{a^{2}-x^{2}}}\sqrt{a^{2}-x^{2}-y^{2}}\,dy dx$, em que $a>0.$
$\displaystyle \frac{\pi a^3}{6}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{D}e^{-x^{2}-y^{2}}\,dA$, onde $D$ é a região delimitada pelo semicírculo $x=\sqrt{4-y^{2}}$ e o eixo $y.$
$\displaystyle \frac{\pi}{2} (1 - e^{-4}).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\sqrt{x^{2}+y^{2}}\,dA$, onde $R$ é limitado pelo círculo $y=\sqrt{2x-x^{2}}$ e pela reta $y=x.$
$\displaystyle \frac{8}{9}(2 - \frac{5}{4}\sqrt{2}).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+y^{2})^{3/2}\,dA$, onde $R$ é limitado pelo círculo $x^{2}+y^{2}=4.$
$\displaystyle \frac{64\pi}{5}.$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo paraboloide $z=9-x^2-y^2$ e pelo plano $z=5.$
$8\pi.$
Uma carga elétrica é distribuída sobre um disco $x^2 + y^2 \leq 4$ de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = x + y + x^2 + y^2$ (medida em coulombs por metro quadrado). Determine a carga total do disco.
Como a carga elétrica é distribuída sobre o disco $x^2 + y^2 \leq 4$, em coordenadas polares temos que $0\leq r \leq 2$ e $0\leq \theta \leq 2\pi.$ Temos que $$Q=\iint\limits_{D}\sigma(x,y)\,dA=\iint\limits_{D}(x+y+x^{2}+y^{2})\,dA$$ $$=\int_{0}^{2\pi}\int_{0}^{2}(r\,\cos \theta+r\,\sin \theta+r^{2})r\,dr\, d \theta=\int_{0}^{2\pi}\int_{0}^{2}(r^{2}\,\cos \theta+r^{2}\,\sin \theta+r^{3})\,dr\, d \theta$$ $$=\int_{0}^{2\pi}\bigg(\frac{r^{3}}{3}\cos \theta+\frac{r^{3}}{3}\sin \theta +\frac{r^{4}}{4}\bigg)\bigg|_{0}^{2}\,d\theta= \int_{0}^{2\pi}\bigg(\frac{8}{3}\cos \theta+\frac{8}{3}\sin \theta+4\bigg)\,d\theta$$ $$=\bigg(\frac{8}{3}\sin\theta-\frac{8}{3}\cos\theta+4\theta\bigg)\bigg|_{0}^{2\pi}=\bigg(-\frac{8}{3}+8\pi\bigg)-\bigg(-\frac{8}{3}\bigg)$$ $$=-\frac{8}{3}+8\pi+\frac{8}{3}=8\pi.$$
Utilize coordenadas polares para determinar o volume do sólido dado: dentro do cilindro $x^2+y^2=4$ e do elipsoide $4x^2+4y^2+z^2=64.$
$\displaystyle \frac{8\pi}{3} (64 - 24\sqrt{3}).$
Passe para coordenadas polares e calcule.
$\displaystyle\int_{0}^{1} \int_{1-\sqrt{1-x^{2}}}^{1+\sqrt{1-x^{2}}}xy\,dy dx$
$\displaystyle\int_{-a}^{a}\!\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}\,dy dx$
Temos que a região de integração é $$R=\{(x,y)\in\mathbb{R}^2|\, 0\leq x \leq 1\,\mbox{e}\, 1-\sqrt{1-x^{2}}\leq y \leq 1+\sqrt{1-x^{2}}\}.$$

Passando para coordenadas polares temos que: $$\left\{ \begin{array}{cc} x=r\,\cos\theta \\ y=r\,\sin\theta \\ dy\,dx=r\,dr\,d\theta \\ \end{array} \right.$$ Agora, \begin{eqnarray*} x^{2}+y^{2}=2y&\Rightarrow & r^{2}\,\cos^2 \theta+r^{2}\,\sin^{2}\theta=2r\,\sin\theta\\ &\Rightarrow & r^{2}=2r \,\sin\theta\\ &\Rightarrow & r(r-2\sin\theta )=0 \\ &\Rightarrow& r=0 \mbox{ou} r=2\sin\theta.\end{eqnarray*} Logo, $\displaystyle 0\leq r \leq 2\,\sin\theta$ e $\displaystyle 0\leq\theta \leq\dfrac{\pi}{2}.$ Então, $$\int_{0}^{1}\int_{1-\sqrt{1-x^2}}^{1+\sqrt{1-x^2}}xy\,dy\,dx =\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\,\sin\theta}(r\,\cos\theta)(r\,\sin\theta)r\,dr d\theta $$
$$ =\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\,\sin\theta}r^3\,\sin\theta\, \cos\theta\,dr d\theta =\int_{0}^{\dfrac{\pi}{2}}\bigg[\frac{r^{4}} {4}\sin\theta\,\cos\theta\bigg]\bigg|_{0}^{2\,\sin\theta}\,d\theta $$ $$ =\int_0^{\frac{\pi}{2}}\frac{(2\,\sin\theta)^4}{4}\,\sin\theta\,\cos\theta\,d\theta =4\int_{0}^\frac{\pi}{2}\sin^5\theta\,\cos\theta\, d\theta.$$ Tomando, $u=\sin\theta \Rightarrow du=\cos\theta\, d\theta$ e sendo $\theta =0 \Rightarrow u=0$ e $\theta=\frac{\pi}{2}\Rightarrow u=1.$ Assim, $$\int_{0}^{1}\int_{1-\sqrt{1-x^{2}}}^{1+\sqrt{1-x^{2}}}xy\,dy dx=4\int_{0}^{1}u^{5}\,du$$ $$=4\cdot \frac{u^{6}}{6}\bigg|_{0}^{1}=\frac{2}{3}.$$Temos que a região de integração é $$R=\{(x,y)\in \mathbb{R}|\, -a\leq x \leq a,\, -\sqrt{a^{2}-x^{2}}\leq y \leq \sqrt{a^{2}-x^{2}}\}.$$
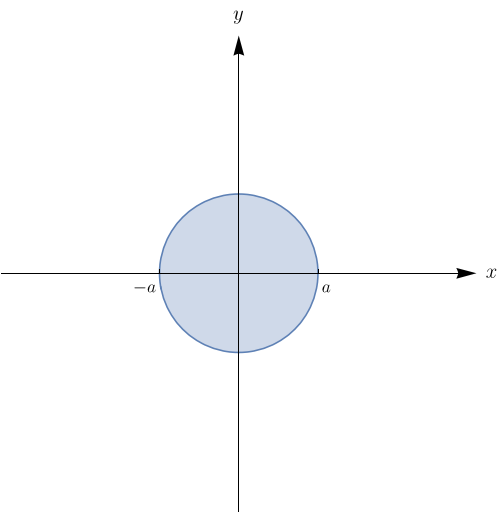
Passando para coordenadas polares temos que $$\left\{ \begin{array}{cc} x=r\,\cos\theta \\ y=r\,\sin\theta\\ dy\,dx=r\,dr\,d\theta\\ \end{array} \right. $$ Como $x^{2}+y^{2}=a^{2}\Rightarrow r^{2}\,\cos^{2}\theta+r^{2}\,\sin{2}\theta=a^{2}\Rightarrow r^{2}=a^{2}\Rightarrow r=\pm a.$ Como o raio deve ser sempre maior ou igual a zero, logo $$0\leq r\leq a \mbox{e} 0\leq \theta \leq 2\pi.$$ Então, $$\int_{-a}^{a}\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dy\,dx=\int_{0}^{2\pi}\int_{0}^{a}r\,dr\,d \theta=\int_{0}^{2\pi}d\theta \cdot \int_{0}^{a}r\,dr$$ $$=\theta\bigg |_{0}^{2\pi}\cdot \frac{r^{2}}{2}\bigg |_{0}^{a}=(2\pi)\cdot \bigg(\frac{a^{2}}{2}\bigg)=a^{2}\pi.$$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{0}^{\sqrt{1-y^{2}}}(x^{2}+y^{2})\,dx dy$
$\displaystyle \frac{\pi}{8}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\frac{x}{x^{2}+y^{2}}\,dA$, onde $R=\{(x,y)\in \mathbb{R}^{2}| x^{2}+y^{2}\leq 4, x\geq 1\}.$
$2\sqrt{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{ D}xy\,dA$, onde $D$ é o disco com centro na origem e raio 3.
$0.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\frac{x^{2}}{x^{2}+y^{2}}\,dA$, onde $R$ é a região anular limitada por $x^{2}+y^{2}=a^{2}$ e $x^{2}+y^{2}=b^{2}$, $0< a< b.$
$\displaystyle \frac{\pi}{2}(b^2 - a^2).$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo hiperboloide $-x^2-y^2+z^2=1$ e acima do plano $xy.$
$\displaystyle \frac{4\pi}{3}.$
Utilize coordenadas polares para determinar o volume do sólido dado:
dentro da esfera $x^2+y^2+z^2=16$ e fora do cilindro $x^{2}+y^{2}=4.$
$\displaystyle 32\sqrt{3}\pi.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{\ln 2} \int_{0}^{\sqrt{(\ln 2)^{2}-y^{2}}}e^{\sqrt{x^{2}+y^{2}}}\,dx dy$
$\displaystyle \frac{\pi(2\ln(2) - 1)}{2}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\,dx dy$, onde $R$ é a região, no plano $xy$, limitada pela curva (dada em coordenadas polares) $\rho=\cos(2\theta)$, $\dfrac{\pi}{8}\leq \theta \leq \dfrac{\pi}{4}.$
$\displaystyle \frac{3\pi + 2}{32}.$
Mostre que
\[ \int_0^{+\infty}\int_0^{+\infty}\dfrac{1}{(1+x^2+y^2)^2}\,dxdy= \dfrac{\pi}{4}.\]
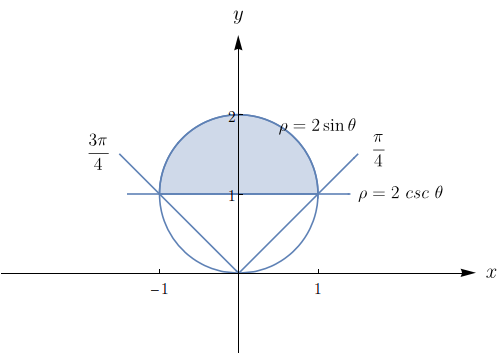
Considere a integral dada em coordenadas polares por $$\int_{0}^{\pi/4} \int_{0}^{2\cos{\theta}}r\,dr d\theta,$$ a qual representa a área de uma região $R$ do plano $xy.$
Escreva a região $R$ em coordenadas cartesianas.
Faça um esboço da região $R.$
Calcule a área da região $R.$
$R = \left\lbrace (x,y); (x - 1)^2 + y^2 \leq 1,\quad x \leq y,\quad x \geq 0,\quad y \geq 0 \right\rbrace.$
(...)
$\dfrac{\pi + 2}{4}.$
Suponha que a área de uma região no plano de coordenadas polares seja $$A=\int_{\pi/4}^{3\pi/4} \int_{\mathrm{cosec\,}{\theta}}^{2\sin{\theta}}r\,dr d\theta.$$ Esboce a região e encontre sua área.
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}x\,dx dy$, onde $R$ é a região, no plano $xy$, limitada pela curva (dada em coordenadas polares) $\rho=\cos(3\theta)$, $-\dfrac{\pi}{6}\leq \theta \leq \dfrac{\pi}{6}.$
$\displaystyle \frac{81\sqrt{3}}{320}.$
Esboce a região cuja área é dada pela integral e calcule-a: $\displaystyle\int_{0}^{\pi/2} \int_{0}^{4\cos{\theta}} r \, dr d\theta$
$2\pi;$ região de integração:
Use coordenadas polares para calcular a integral dupla
\[ \iint_R e^{-(x^2+y^2)}\,dA, \]
onde \(R\) é a região contida no círculo \(x^2+y^2=1\).
\(\displaystyle (1-e^{-1})\pi \)
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{1} \int_{0}^{\sqrt{1-x^{2}}}\,dy dx$
$\displaystyle \frac{\pi}{2}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{6} \int_{0}^{y}x\,dx dy$
$36.$
Utilize coordenadas polares para determinar o volume do sólido dado: uma esfera de raio $a.$
$\displaystyle \frac{4\pi}{3}a^3.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\arctan\left(\dfrac{y}{x}\right)\,dA$, onde $R$ é a região do primeiro quadrante limitada pelo círculo $x^{2}+y^{2}=25.$
$\displaystyle \frac{25 \pi^2}{16}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+2y)\,dx dy$, onde $R$ é o círculo $x^{2}+y^{2}\leq 4.$
$4\pi.$
Utilize coordenadas polares para determinar o volume do sólido dado: abaixo do cone $z=\sqrt{x^{2}+y^{2}}$ e acima do disco $x^{2}+y^{2}\leq 4.$
$\displaystyle \frac{16\pi}{3}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}y\,dA$, onde $R$ é a região no primeiro quadrante limitada pelo semi-círculo $x^{2}+y^{2}=2x.$
$\displaystyle \frac{2}{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\cos(x^{2}+y^{2})\,dA$, onde $R$ é a região acima do eixo do $x$ e dentro da circunferência $x^{2}+y^{2}=9.$
$\displaystyle \frac{\pi}{2} \sin(9).$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{x^{2}}^{\sqrt{2-x^{2}}}\sqrt{x^{2}+y^{2}}\,dy dx$
$\displaystyle \frac{2}{45}(1 + \sqrt{2}) + \frac{\pi}{3\sqrt{2}}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{0}^{\sqrt{x-x^{2}}}x\,dy dx$
$\displaystyle \frac{\pi}{16}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits{R}\sin(x^{2}+y^{2})\,dA$, onde $R$ é a região acima do eixo $x$ e dentro da circunferência $x^{2}+y^{2}=9.$
$\displaystyle \frac{\pi}{2}(1 - \cos(9).$
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{0} \int_{-\sqrt{1-x^{2}}}^{0}\frac{2}{1+\sqrt{x^{2}+y^{2}}}\,dy dx$
$(1 - \ln(2))\pi.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\sqrt{x^{2}+y^{2}}\,dA$, onde $R$ é limitado pelo triângulo de vértices $(0,0)$, $(3,0)$ e $(3,3).$
$\displaystyle \frac{9}{2} (\sqrt{2} + \ln(\sqrt{2} + 1)).$
Esboce a região cuja área é dada pela integral $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r\, dr d\theta$ e calcule-a:
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}e^{x^{2}+y^{2}}\,dx dy$, onde $R$ é o conjunto de todos os $(x,y)$ tais que $1\leq x^{2}+y^{2}\leq 4$, $-x\leq y\leq x$ e $x\geq 0.$
$\displaystyle \frac{\pi}{4}(e^4 - e).$
Use a integral dupla em coordenadas polares para deduzir a fórmula $$A=\int_{\alpha}^{\beta}\frac{1}{2} r^{2}\,d\theta$$ para a área da região em formato de leque entre a origem e a curva polar $r=f(\theta)$, $\alpha\leq \theta \leq \beta.$
Note que $\displaystyle A = \int_{\alpha}^{\beta}\int_{0}^{f(\theta)} r dr d\theta. $
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{1} \int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}\ln(x^{2}+y^{2}+1)\,dx dy$
$\displaystyle \pi (\ln(4) - 1).$
Calcule a integral iterada $\int_{-3}^{3} \int_{0}^{\sqrt{9-x^2}}\sin(x^{2}+y^{2})\,dy dx$, convertendo-a antes para coordenadas polares.
$\displaystyle \frac{\pi}{2}(1 - \cos(9)).$
Ao calcular por integração dupla o volume $V$ do sólido situado abaixo do gráfico de $f(x,y)=e^{x^{2}+y^{2}}$ e limitado inferiormente por uma certa região $D$ no plano $xy$, chegou-se à seguinte expressão: $$V=\int_{0}^{2} \int_{0}^{\sqrt{4-x^{2}}}e^{x^{2}+y^{2}}\,dy dx-\int_{0}^{1} \int_{0}^{\sqrt{1-x^{2}}}e^{x^{2}+y^{2}}\,dy dx.$$
Esboce a região $D.$
Expresse $V$ numa única integral dupla em coordenadas polares.
Efetue a integração para calcular $V.$
$D = \left\lbrace (x,y); 1 \leq x^{2} + y^{2} \leq 2, x \geq 0, y \geq 0 \right\rbrace.$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \int_{1}^{2} re^{r^2} dr d\theta.$
$\dfrac{\pi}{4}(e^4 - 1).$
Passe para coordenadas polares e calcule.
$\displaystyle\int_{0}^{a} \int_{0}^{x}\sqrt{x^{2}+y^{2}}\,dy dx$, em que $a>0$.
$\displaystyle\iint\limits_{ D}x\,dA$, onde $D$ é a região do primeiro quadrante compreendida entre os círculos x^2+y^2=4$ e $x^2+y^2=2x.$
Temos que a região de integração é: $$ R=\{(x,y)\in \mathbb{R}^{2}|\,0\leq x \leq a,\, 0\leq y \leq x\}.$$
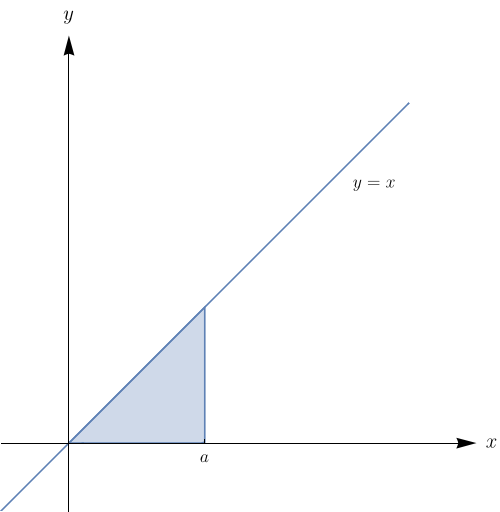
Passando para coordenadas polares temos que $$\left\{ \begin{array}{cc} x=r\,\cos \theta\\ y=r\,\sin \theta\\ dy\,dx=r\,dr\,d\theta\\ \end{array} \right. $$ Como $0\leq x \leq a$, temos que $0\leq r\leq \dfrac{a}{\cos \theta}$ e também $0\leq \theta \leq \dfrac{\pi}{4}.$ Então, $$\int_{0}^{a}\int_{0}^{x}\sqrt{x^{2}+y^{2}}\,dy\,dx= \int_{0}^{\frac{\pi}{4}}\int_{0}^{\frac{a}{\cos \theta}}\sqrt{r^{2}\,\cos^{2}\theta +r^{2}\,\sin^{2}\theta}\,r\,dr\,d\theta$$ $$=\int_{0}^{\frac{\pi} {4}}\int_{0}^\frac{a}{\cos\theta}r^{2}\,dr\,d\theta=\int_{0}^\frac{\pi}{4}\frac{r^3}{3}\bigg|_{0}^{\frac{a}{\cos \theta}}d\theta $$ $$=\frac{a^{3}}{3}\int_{0}^{\frac{\pi}{4}}\frac{1}{\cos^{3}\theta}d\theta=\frac{a^{3}}{3}\int_{0}^{\frac{\pi}{4}}\sec^{3}\theta d\theta$$ $$=\frac{a^{3}}{3}\bigg(\frac{1}{2}\sec \theta \tan \theta+\frac{1}{2}\ln|\sec \theta+\tan \theta|\bigg)\bigg|_{0}^{\frac{\pi}{4}}$$ $$=\frac{a^{3}}{6}\bigg[\bigg(\sec\frac{\pi}{4}\cdot \tan\frac{\pi}{4}+\ln\bigg|\sec\frac{\pi}{4}+\tan\frac{\pi}{4}\bigg|\bigg)- \bigg(\sec 0\cdot \tan 0+\ln|\sec 0+\tan 0|\bigg)\bigg]$$ $$=\frac{a^{3}}{6}\bigg(\sqrt{2}+\ln(\sqrt{2}+1)\bigg)$$A região de integração $R$ é descrita na figura seguinte
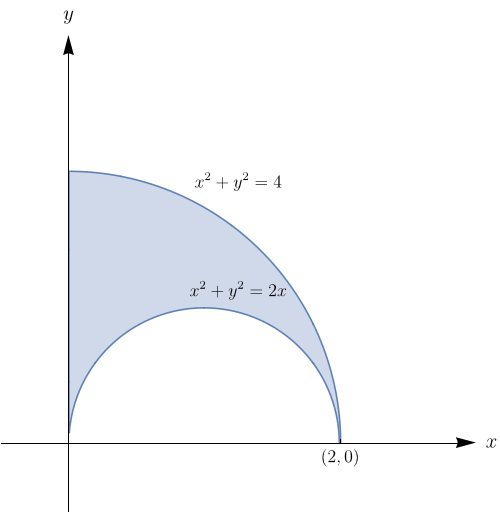
Notemos que $x^{2}+y^{2}=2x\Leftrightarrow (x-1)^{2}+y^{2}=1.$ Assim, $$\iint\limits_{ R}x\,dA=\underbrace{\iint\limits_{ \substack{x^{2}+y^{2}\leq 4\\ x\geq 0\\ y\geq 0}}x\,dA}_{(1)} -\,\,\underbrace{\iint\limits_{\substack{(x-1)^{2}+y^{2}\leq 1 \\ y\geq 0}}x\,dA}_{(2)}$$ Para a integral $(1)$ temos em coordenadas polares que $$r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=4\Rightarrow r^{2}=4\Rightarrow r=\pm 2.$$ Logo, $0\leq r\leq 2$ e $0\leq \theta \leq \dfrac{\pi}{2}.$ Para a integral $(2)$ temos em coordenadas polares que $$(r-\cos \theta-1)^{2}+r^{2}\sin^{2}\theta=1\Rightarrow r^{2}\cos^{2}\theta-2r\cos \theta+1+r^{2}\sin^{2}\theta=1$$ $$\Rightarrow r^{2}-2r\cos\theta=0\Rightarrow r(r-2\cos \theta)=0\Rightarrow r=0 \mbox{ou} r=2\cos \theta.$$ Logo, $0\leq r\leq 2\cos \theta$ e $0\leq \theta \leq \dfrac{\pi}{2}.$ Assim, $$\iint\limits_{ R}x\,dA=\int_{0}^{\frac{\pi}{2}}\int_{0}^{2}r\,\cos \theta \cdot r \,dr\,d\theta- \int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos \theta}r\cos \theta\cdot r\, dr\,d \theta$$ $$=\int_{0}^{\frac{\pi}{2}}\int_{0}^{2}r^{2}\,\cos \theta\,dr\,d\theta-\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos \theta}r^{2}\,\cos \theta\,dr\,d\theta$$ $$=\int_{0}^{\frac{\pi}{2}}\cos\,d\theta \cdot \int_{0}^{2}r^{2}\,dr-\int_{0}^{\frac{\pi}{2}}\frac{r^{3}}{3}\cos \theta \bigg|_{0}^{2\cos \theta}\,d\theta$$ $$=\bigg(\sin\theta \bigg|_{0}^{\frac{\pi}{2}}\bigg)\cdot \bigg(\frac{r^{3}}{3}\bigg|_{0}^{2}\bigg)-\frac{8}{3}\int_{0}^{\frac{\pi}{2}}\cos^{4}\theta\,d\theta$$ $$=\bigg(\sin \frac{\pi}{2}-\sin 0\bigg)\cdot \bigg(\frac{8}{3}-0\bigg)-\frac{8}{3}\bigg(\frac{1}{4}\cos^{3}\theta\,\sin \theta+\frac{3}{8}\theta+\frac{3}{16}\sin 2 \theta\bigg)\bigg|_{0}^{\frac{\pi}{2}}$$ $$=\frac{8}{3}-\frac{8}{3}\bigg[\bigg(\frac{1}{4}\cos^{3}\frac{\pi}{2}\sin \frac{\pi}{2}+\frac{3}{8}\cdot\frac{\pi}{2}+\frac{3}{16}\sin2\cdot \frac{\pi}{2}\bigg) -\bigg(\frac{1}{4}\cos^{3}0\sin 0+\frac{3}{8}\cdot 0+\frac{3}{16}\sin 0\bigg)\bigg]$$ $$=\frac{8}{3}-\frac{8}{3}\cdot \bigg(\frac{3\pi}{16}\bigg)=\frac{8}{3}-\frac{\pi}{2}=\frac{16-3\pi}{6}.$$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo cone $z^2=x^2+y^2$ e pelo cilindro $x^2+y^2=2x.$
$\dfrac{8}{9}.$
Calcule a integral dupla utilizando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+y^{2})\,dx dy$, onde $R=\{(x,y)\in \mathbb{R}^{2}| 1\leq x^{2}+y^{2}\leq 4\}.$
$\displaystyle \frac{15\pi}{2}.$
Utilize coordenadas polares para determinar o volume do sólido dado: acima do cone $z=\sqrt{x^2+y^2}$ e abaixo da esfera $x^2+y^2+z^2=1.$
$\displaystyle \frac{\pi}{3}(2 - \sqrt{2}).$
Utilize coordenadas polares para combinar a soma $$\int_{\frac{1}{\sqrt{2}}}^{1} \int_{\sqrt{1-x^{2}}}^{x}xy\,dy dx+\int_{1}^{\sqrt{2}} \int_{0}^{x}xy\,dy dx+\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx$$ em uma única integral dupla. Em seguida, calcule essa integral dupla.
Queremos combinar a soma, abaixo, de integrais em uma única: $$\underbrace{\int_\frac{1}{\sqrt{2}}^{1} \int_\sqrt{1-x^{2}}^{x}xy\,dy dx}_{1}+\underbrace{\int_{1}^{\sqrt{2}}\int_{0}^{x}xy\,dy dx}_{2}+ \underbrace{\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx}_{3}$$ Na figura abaixo, temos que a região da esquerda corresponde à região de integração da integral $(1)$, a região do meio corresponde à região de integração da integral $(2)$ e a região da esquerda corresponde à região de integração da integral $(3)$.
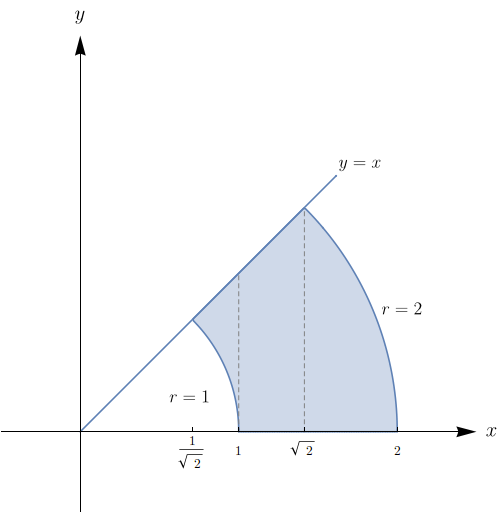
Notemos que com a junção das três regiões, podemos olhar como uma única região. Assim, em coordenadas polares teremos que $0\leq \theta \leq \frac{\pi}{4}$ e $1\leq r \leq 2.$ Então: $$\int_{\frac{1}{\sqrt{2}}}^{1} \int_{\sqrt{1-x^{2}}}^{x}xy\,dy dx+\int_{1}^{\sqrt{2}} \int_{0}^{x}xy\,dy dx+\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx$$ $$=\int_{0}^{\frac{\pi}{4}}\int_{1}^{2}(r\,\cos \theta)\cdot (r\,\sin \theta)\,r\,dr\,d\theta=\int_{0}^{\frac{\pi}{4}}\int_{1}^{2}r^{3}\cos\theta \sin \theta\,dr\,d\theta$$ $$=\underbrace{\int_{0}^{\frac{\pi}{4}}\cos \theta\, \sin \theta\,d \theta}_{\substack{ u=\sin \theta\\ du=\cos\, d\theta}}\cdot \int_{1}^{2}r^{3}\,dr =\int_{0}^{\frac{\sqrt{2}}{2}}u\,du\cdot \frac{r^{4}}{4}\bigg|_{1}^{2}$$ $$=\frac{u^{2}}{2}\bigg|_{0}^{\frac{\sqrt{2}}{2}}\cdot \bigg(\frac{16}{4}-\frac{1}{4}\bigg)=\frac{1}{4}\cdot \frac{15}{4}=\frac{15}{16}.$$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}xy\,dx dy$, onde $R$ é o círculo $x^{2}+y^{2}-2y\leq 0$, $x\geq 0.$
$\displaystyle \frac{2}{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{a} \int_{0}^{\sqrt{a^{2}-x^{2}}}\,dy dx$
$\dfrac{\pi a^2}{4}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\arctan\left(\dfrac{y}{x}\right)\,dA$, onde $R=\{(x,y) \in \mathbb{R}^2| 1\leq x^{2}+y^{2}\leq 4, 0\leq y\leq x\}.$
$\displaystyle \frac{3\pi^2}{64}.$

