Exercícios
Sobre região geral
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Considere a integral
$$\int_{0}^{2}\int_{\frac{y}{2}}^{1}ye^{x^{3}}\,dx dy.$$
Faça um esboço da região de integração.
Calcule a integral sendo explícito se vai precisar mudar a ordem de integração.
...
$\dfrac{2(e - 1)}{3}.$
Calcule $\displaystyle\iint\limits_{B} y\,dx dy$, onde $B$ é o conjunto dado.
$B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(1,1)$.
$B=\{(x,y)\in \mathbb{R}^{2}|\;-1\leq x\leq 1,\;0\leq y\leq x+2\}.$
$B$ é o conjunto de todos $(x,y)$ tais que $x^{2}+4y^{2}\leq 1.$
$B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(2,1).$
$\dfrac{1}{6}$.
$\dfrac{13}{3}$.
$0$.
$\dfrac{1}{6}$.
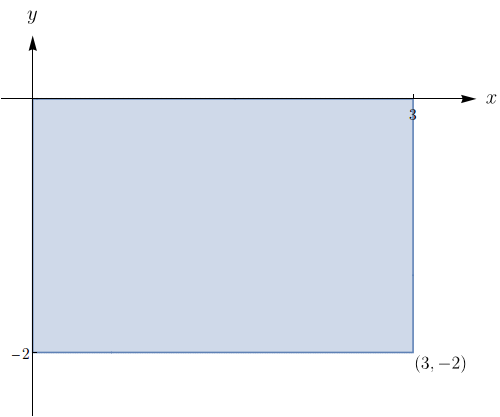
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{\pi}\!\!\int_{0}^{x}x\sin{y}\,dy dx$.
$\dfrac{\pi^{2}}{2} + 2.$
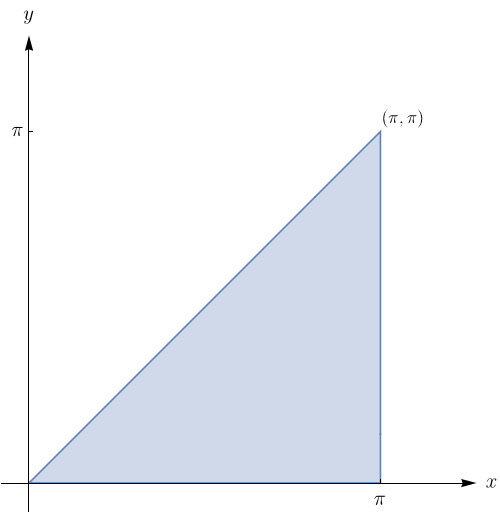
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{3}\!\!\int_{0}^{2}(4-y^{2})\,dy dx$.
$16.$
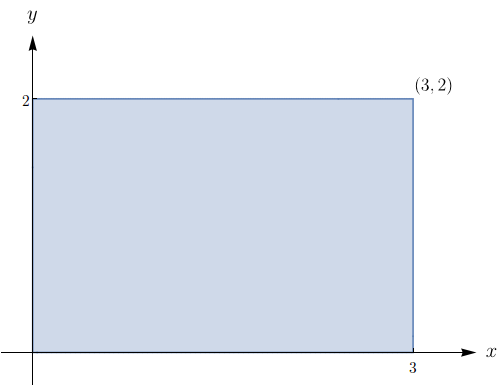
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint\limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$

$\displaystyle \int_{-1}^{1} \int_{0}^{1 - x^2} f(x,y) dy dx .$
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1}\!\!\int_{0}^{1-x}(1-x-y)\,dy dx.$$
Calcule a integral dupla.
$\displaystyle\iint\limits_{D}(2x-y)\,dA, \quad D$ limitada pelo círculo de centro na origem e raio 2.
$\displaystyle\iint\limits_{D}\dfrac{x}{y}\,dA, \quad D$ região no primeiro quadrante limitada pelas retas $y=x$, $y=2x$, $x=1$ e $x=2.$
$\displaystyle\iint\limits_{D}\dfrac{1}{xy}\,dA, \quad D$ o quadrado $1\leq x\leq 2$, \;$1\leq y\leq 2.$
$\displaystyle\iint\limits_{D}(x-\sqrt{y})\,dA, \quad D$ região triangular cortado do primeiro quadrante do plano $xy$ pela reta $x+y=1.$
$0.$
$\dfrac{3\ln(2)}{2}.$
$(\ln(2))^{2}.$
$-\dfrac{1}{10}.$
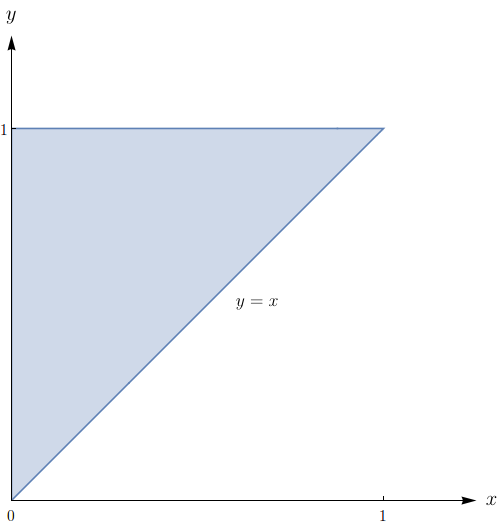
Calcule a integral trocando a ordem de integração. $\displaystyle\int_{0}^{1}\!\!\int_{x}^{1}e^{x/y}\,dy dx$.
A região de integração é do tipo I, é dada por
$$\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 1 \mbox{ e } x \leq y \leq 1\}$$
e pode ser vista geometricamente como a região esboçada na figura abaixo.
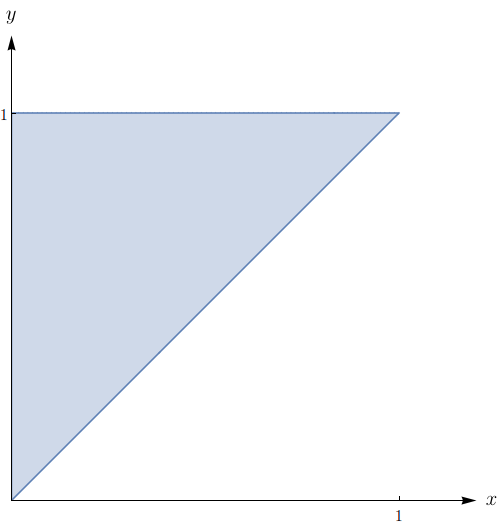
Essa região pode ser descrita como uma região do tipo II da seguinte forma:
$$\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq y \mbox{ e } 0 \leq y \leq 1\}.$$
Assim,
\begin{array}{rcl}\displaystyle\int_{0}^{1}\!\!\int_{x}^{1}e^{x/y}\,dy dx & = & \displaystyle\int_{0}^{1}\!\!\int_{0}^{y} \! e^{x/y}\,dx dy \\ & = & \displaystyle\int_{0}^{1} \! \left. ye^{x/y} \right|_{x=0}^{x=y}\,dx \\ & = & \displaystyle\int_{0}^{1} \! \left. y(e-1) \right|_{x=0}^{x=y}\,dx \\ & = & \left.(e-1) \frac{y^2}{2}\right|_{0}^{1} = \frac{e-1}{2}.\end{array}
A reta \(y=2-x\) intersecta a parábola \(y=x^2\) nos pontos \((-2,4)\) e \((1,1)\). Mostre que, se \(R\) denotar a região englobada por \(y=2-x\) e \(y=x^2\), então \[ \iint_R\left(1+2y\right)\,dA = \int_{-2}^1\int_{x^2}^{2-x}\left(1+2y\right)\,dydx = 18,9 \]
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{3}\!\!\int_{-\sqrt{9-y^{2}}}^{\sqrt{9-y^{2}}}f(x,y)\,dx dy$.
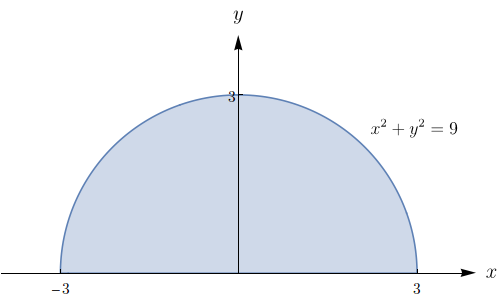
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
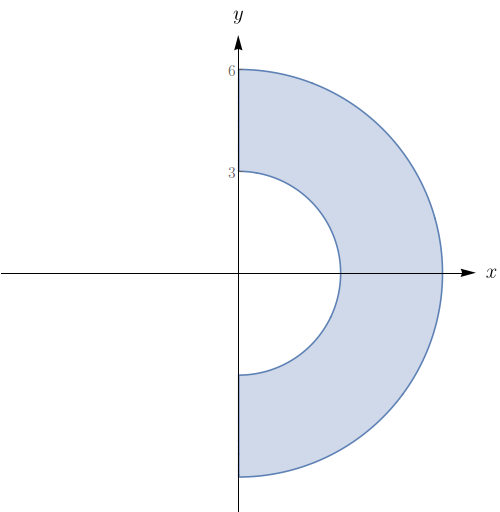
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{3}^{6} f(r\cos(\theta),r\sin(\theta)) r d r d \theta.$
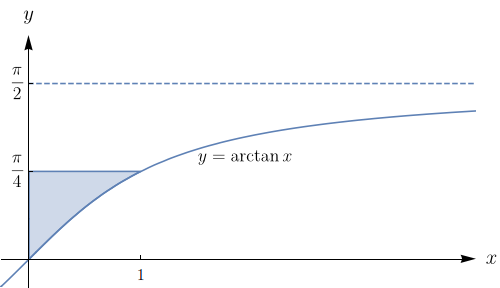
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{1}\!\!\int_{\arctan{x}}^{\pi/4}\!f(x,y)\,dy dx$.
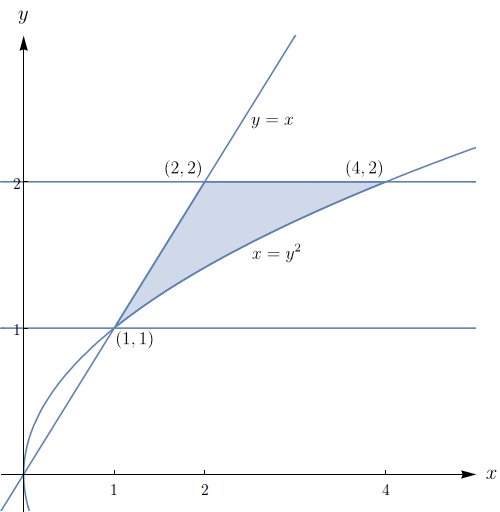
Use uma integral dupla para calcular a área da região \(R\) entre a parábola \(y=\dfrac{1}{2}x^2\) e a reta \(y = 2x\).
Denotando por \(A(R)\) a área de \(R\), teremos que \begin{align*} A(R) & = \iint_R\,dA = \int_0^4\int_{x^2/2}^{2x}\,dydx = \int_0^4\left[y\right]_{y=x^2/2}^{2x}\,dx \\ & = \int_0^4\left(2x-\dfrac{1}{2}x^2\right)\,dx = \left[x^2-\dfrac{x^3}{6}\right]_0^4= \dfrac{16}{3}. \end{align*} De outra forma, fixando primeiro a variável \(y\), teríamos \begin{align*} A(R) & = \iint_R\,dA = \int_0^8\int_{y/2}^{\sqrt{2y}}\,dxdy = \int_0^8\left[x\right]_{x=y/2}^{\sqrt{2y}}\,dy \\ & = \int_0^8\left(2y-\dfrac{1}{2}y\right)\,dy = \left[\dfrac{2\sqrt{2}}{3}y^{3/2}-\dfrac{y^2}{4}\right]_0^8= \dfrac{16}{3}. \end{align*}
Inverta a ordem de integração, integrando primeiro em $y$ e depois em $x$ para calcular a integral:
$\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}^{1}\sqrt{x^{3}+1}\,dx dy$
$\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}\sin{x^{3}}\,dx dy$
$\dfrac{2(2\sqrt{2} - 1)}{9}.$
$\dfrac{2}{3} \sin^{2}\left(\dfrac{1}{2} \right).$
Considere a integral $$\int_{0}^{1}\int_{3y}^{3}e^{x^{2}}\,dx dy.$$
Esboce a região de integração.
Calcule a integral usando a ordem de integração apropriada.
(...)
$\dfrac{e^9 - 1}{6}.$
Calcule a integral trocando a ordem de integração.
$\displaystyle\int_{0}^{4}\!\!\int_{\sqrt{x}}^{2}\dfrac{1}{y^{3}+1}\,dy dx$
$\displaystyle\int_{0}^{\pi}\!\!\int_{x}^{\pi}\dfrac{\sin{y}}{y}\,dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{x}^{2}2y^{2}\sin(xy)\,dy dx.$
$\dfrac{\ln(9)}{3}.$
$2.$
$4 - \sin(4).$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=1$ e $B$ a região compreendida entre os gráficos de $y=\sin{x}$ e $y=1-\cos{x}$, com $0\leq x\leq \dfrac{\pi}{2}.$
$f(x,y)=\sqrt{1+y^{3}}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;\sqrt{x}\leq y\leq 1 \}.$
$f(x,y)=x$ e $B$ é o conjunto de todos $(x,y)$ tais que $y\geq x^{2}$ e $x\leq y\leq x+2.$
$f(x,y)=\dfrac{y}{x+y^{2}}$ e $B$ o conjunto de todos $(x,y)$ tais que $1\leq x\leq 4$ e $0\leq y\leq \sqrt{x}.$
$2 - \dfrac{\pi}{2}.$
$\dfrac{2(2\sqrt{2} - 1)}{9}.$
$\dfrac{13}{6}.$
$\dfrac{3 \ln(2)}{2}.$
Calcule as integrais iteradas.
$\displaystyle\int_{0}^{\pi/2}\int_{0}^{\cos{\theta}}e^{\sin{\theta}}\,dr d\theta$
$\displaystyle\int_{0}^{1}\int_{0}^{v}\sqrt{1-v^{2}}\,du dv$
$e - 1.$
$\dfrac{1}{3}.$
Calcule $\int_{0}^{1}\!\int_{x}^{1}3y^{4}\cos(xy^{2})\,dy dx$. Esboce a região de integração.
$1 - \cos(1).$
Esboce a região de integração para a integral iterada $\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}^{3\sqrt{y}}f(x,y)\,dx dy$.
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=\dfrac{1}{\ln(y)}$ e $B=\bigg\{(x,y)\in \mathbb{R}^{2}|\;2\leq y\leq 3,\;0\leq x\leq \dfrac{1}{y}\bigg\}.$
$f(x,y) = xy\cos{x^{2}}$ e $B=\{(x,y) \in \mathbb{R}^{2}| \; 0 \leq x \leq 1, \; x^{2} \leq y \leq 1\}$.
$f(x,y) = \cos(2y)\sqrt{4-\sin^{2}{x}}$ e $B$ é o triângulo de vértices $(0,0)$, $\bigg(0,\dfrac{\pi}{2}\bigg)$ e $\bigg(\dfrac{\pi}{2},\dfrac{\pi}{2}\bigg).$
$f(x,y)=x+y$ e $B$ a região compreendida entre os gráficos das funções $y=x$ e $y=e^{x}$, com $0\leq x\leq 1.$
$\ln(\ln(3)) - \ln(\ln(2)).$
$\dfrac{\sin(1) - \cos(1)}{2}$.
$\dfrac{8}{3} - \sqrt{3}.$
$\dfrac{1 + e^{2}}{4}.$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=x\cos{y}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;x\geq 0,\;x^{2}\leq y\leq \pi\}.$
$f(x,y)=xy$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;x^{2}+y^{2}\leq 2,\;y\leq x\;e\;x\geq 0\}.$
$f(x,y)=x$ e $B$ o triângulo de vértices $(0,0)$, $(1,1)$ e $(2,0).$
$f(x,y)=xy\sqrt{x^{2}+y^{2}}$ e $B$ o retângulo $0\leq x\leq 1$, $0\leq y\leq 1.$
$f(x,y)=x+y$ e $B$ o paralelogramo de vértices $(0,0)$, $(1,1)$, $(3,1)$ e $(2,0).$
$-1.$
$-\dfrac{1}{4}$.
$1.$
$\dfrac{2(2\sqrt{2} - 1)}{15}.$
$4.$
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
\[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
\[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
Esboce a região de integração para a integral iterada $\displaystyle\int_{\pi}^{2\pi}\!\!\int_{\sin{y}}^{\ln(y)}f(x,y)\,dx dy$.
Esboce a região de integração e calcule a integral $\displaystyle\int_{1}^{2}\!\!\int_{y}^{y^{2}} \,dx dy$.
$\frac{5}{6}.$
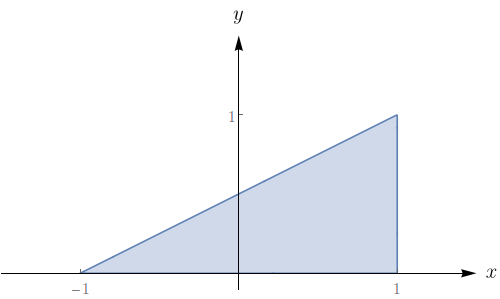
Seja \(R\) a região triangular de vértices \((0,0)\), \((3,3)\) e \((0,4)\) do plano \(xy\). Expressa como uma integral dupla, qual é área de \(R\)?
\(\displaystyle A(R)=\int_0^3\int_x^{-\frac{1}{3}x+4}\,dydx \)
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{4}\!\!\int_{0}^{\sqrt{x}} \! f(x,y)\,dy dx$.
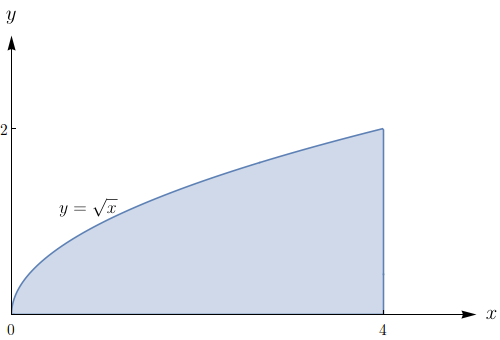
Uma região $R$ é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
$\displaystyle \int_{-1}^{1} \int_{0}^{\frac{(x + 1)}{2}} f(x,y) dy dx .$
No cálculo de uma integral dupla sobre uma região $D$, obtivemos uma soma de integrais iteradas como a que segue:
$$\int\!\!\!\!\int\limits_{\!\!\!\!\!\! D} \! f(x,y)\,dA=\int_{0}^{1}\!\!\int_{0}^{2y} \! f(x,y)\,dx dy+\int_{1}^{3}\!\!\int_{0}^{3-y} \! f(x,y)\,dx dy.$$
Esboce a região $D$ e expresse a integral dupla como uma integral iterada com ordem de integração contrária.
$\displaystyle \int_{0}^{2}\!\!\int_{\frac{x}{2}}^{3-x} \! f(x,y)\,dx dy.$
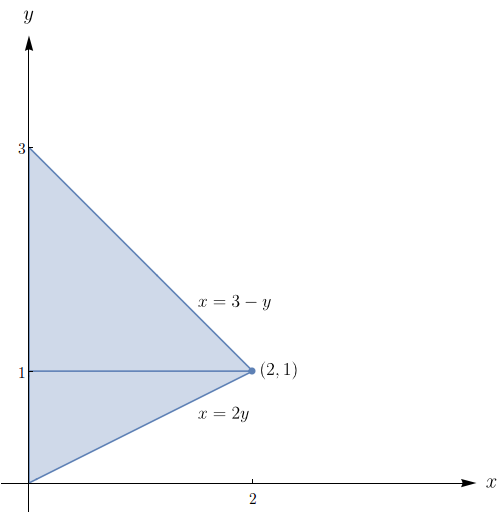
Calcule $\displaystyle\iint\limits_{B} y\,dx dy$, onde $B$ é o conjunto dado.
$B$ é a região compreendida entre os gráficos de $y=x$ e $y=x^{2}$, com $0\leq x\leq 2.$
$B$ é o paralelogramo de vértices $(-1,0)$, $(0,0)$, $(1,1)$ e $(0,1).$
$B$ é o semicírculo $x^{2}+y^{2}\leq 4$, $y\geq 0.$
$B=\{(x,y)\in \mathbb{R}^{2}|\;x\geq 0,\;x^{5}-x\leq y \leq 0\}.$
$2$.
$\dfrac{1}{2}$.
$\dfrac{16}{3}$.
$-\dfrac{16}{231}$.
Escreva a integral dupla $$\iint\limits_{R}x\cos{y}\;dA,$$ onde $R$ é limitada pelas retas $y=0$, $x=\pi/4$ e $y=x$, das duas formas possíveis (mudando a ordem de integração). Escolha uma dessas formas e calcule o valor dessa integral.
$\displaystyle \int_{0}^{\pi/4} \int_{0}^{x} x \cos(y)\;dy\;dx = \int_{0}^{\pi/4} \int_{y}^{\pi / 4} x \cos(y)\;dx\;dy = -\frac{\pi - 4}{4\sqrt{2}}.$
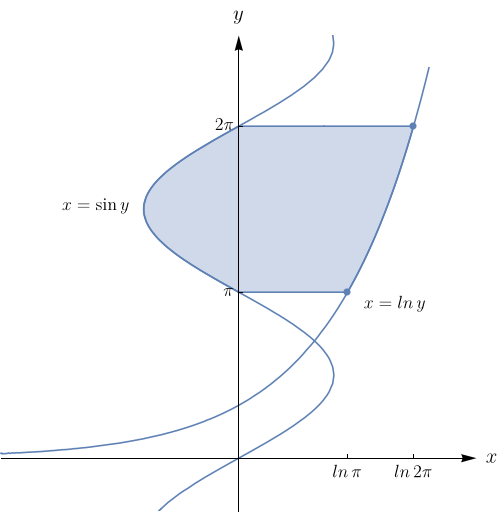
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{1}^{2}\!\!\int_{0}^{\ln(x)} \! f(x,y)\,dy dx$.
Note que a região de integração é do tipo I, é dada por
$$\{(x,y) \in \mathbb{R}^2: 1 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \ln(x)\}$$
e pode ser vista geometricamente como a região esboçada na figura abaixo.
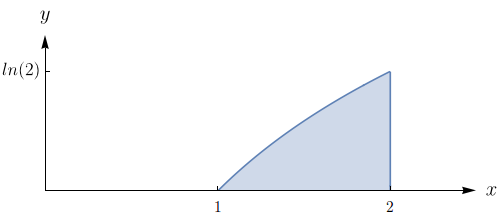
Além disso, ela pode ser descrita como uma região do tipo II da seguinte forma:
$$\{(x,y) \in \mathbb{R}^2: e^y \leq x \leq 2 \mbox{ e } 0 \leq y \leq \ln{2}\}.$$
Portanto, a integral pode ser reescrita como
$\displaystyle\int_{0}^{\ln{2}}\!\!\int_{e^y}^{2} \! f(x,y)\,dx dy$.
Esboce a região de integração e calcule a integral $\displaystyle\int_{\pi}^{2\pi}\!\!\int_{0}^{\pi}(\sin{x}+\cos{y})\,dx dy$.
$2\pi.$
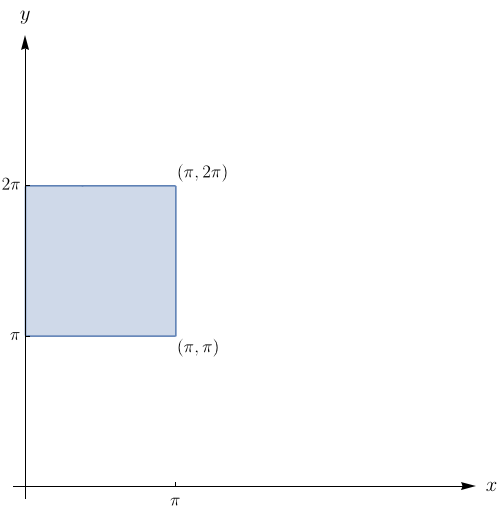
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=y^{3}e^{xy^{2}}$ e $B$ o retângulo $0\leq x\leq 1$, $1\leq y\leq 2.$
$f(x,y)=x^{5}\cos{y^{3}}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;y\geq x^{2},\;x^{2}+y^{2}\leq 2\}.$
$f(x,y)= x^{2}$ e $B$ o conjunto de todos $(x,y)$ tais que $x\leq y\leq -x^{2}+2x+2.$
$f(x,y)=x$ e $B$ a região compreendida entre os gráficos de $y=\cos{x}$ e $y=1-\cos{x}$, com $0\leq x\leq \dfrac{\pi}{2}.$
$\dfrac{e^{4} - e - 3}{2}.$
$0.$
$\dfrac{63}{20}.$
$\left(\dfrac{5}{72} -\dfrac{ \sqrt{3}}{18}\right)\pi^{2} + \left( \dfrac{4\sqrt{3}}{3} - 1 \right) \pi.$
Esboce a região de integração para a integral iterada $\displaystyle\int_{-1}^{2}\!\int_{-\sqrt{4-x^{2}}}^{4-x^{2}}f(x,y)\,dy dx$.

Calcule a integral dupla.
$\displaystyle\iint\limits_{ D}x^{3}y^{2}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq 2,\;-x\leq y\leq x\}.$
$\displaystyle\iint\limits_{D}x\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq \pi,\;0\leq y\leq \sin{x}\}.$
$\displaystyle\iint\limits_{D}x^{3}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;1\leq x\leq e,\;0\leq y\leq \ln(x)\}.$
$\displaystyle\iint\limits_{D}y^{2}e^{xy}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq y\leq 4,\;0\leq x\leq y\}.$
$\displaystyle\iint\limits_{D}y^{3}\,dA, \quad D$ região com vértices $(0,2)$, $(1,1)$ e $(3,2).$
$\dfrac{256}{21}.$
$\pi.$
$\dfrac{3e^{4} + 1}{16}.$
$\dfrac{e^{16} - 17}{2}.$
$\dfrac{147}{20}.$
Ao calcular, por integração dupla, o volume $V$ do sólido situado abaixo do parabolóide $z=x^{2}+y^{2}$ e limitado inferiormente por uma certa região $D$ no plano $xy$, chegou-se à seguinte expressão: $$V=\int_{0}^{1}\!\!\int_{0}^{y}(x^{2}+y^{2})\,dx dy+\int_{1}^{2}\int_{0}^{2-y}(x^{2}+y^{2})\,dx dy.$$
Esboce a região $D.$
Expresse $V$ numa única integral dupla iterada.
Efetue a integração para calcular $V.$
...
$\displaystyle \int_{0}^{1} \int_{x}^{2 - x} x^{2} + y^{2}\;dy\; dx$
$\dfrac{4}{3}.$
Calcule as integrais iteradas.
$\displaystyle\int_{0}^{1}\int_{0}^{x^{2}}(x+2y)\,dy dx$
$\displaystyle\int_{0}^{1}\int_{x^{2}}^{x}(1+2y)\,dy dx$
$\dfrac{9}{20}.$
$\dfrac{3}{10}.$
Considere a integral
$$\int_{0}^{1}\!\!\int_{x^{2}}^{1}x^{3}\sin{y^{3}}\,dy dx.$$
Desenhe a região de integração.
Calcule o valor da integral.
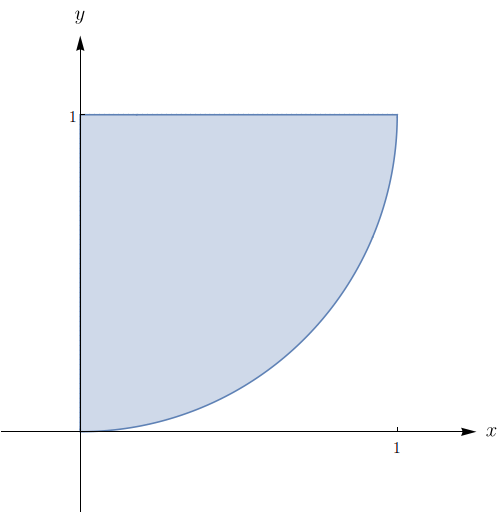
$\dfrac{1 - \cos(1)}{12}$.
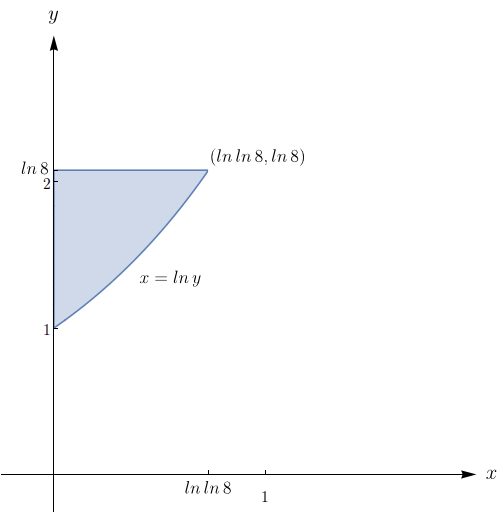
Esboce a região de integração e calcule a integral $\displaystyle\int_{1}^{\ln 8}\!\!\!\int_{0}^{\ln y}e^{x+y}\,dx dy$.
$8 \ln(8) - 16 + e.$
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{ R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
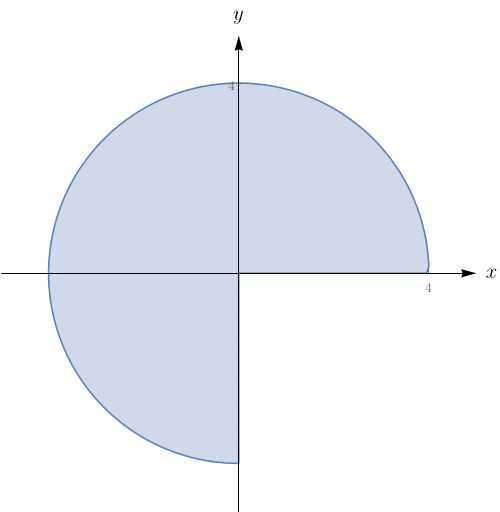
$\displaystyle \int_{0}^{\frac{3\pi}{2}} \int_{0}^{4} f(r\cos(\theta),r\sin(\theta)) r d r d \theta.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{3}\!\!\int_{-2}^{0}(x^{2}y-2xy)\,dy dx$.
$0.$