Exercícios
Iteradas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Mude a ordem de integração para mostrar que:
$$ \int_0^a \left[ \int_0^y e^{m(a-x)} f(x) \, dx \right] dy = \int_0^a (a-x) e^{m(a-x)} f(x) \, dx,$$
onde $a$ e $m$ são constantes e $a>0$.
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{\sqrt{x-x^{2}}}^{\sqrt{2x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{3a}\bigg[\int_{\frac{\sqrt{3}}{3}x}^{\sqrt{4ax-x^{2}}}f(x,y)\,dy\bigg]dx, \; a> 0.$
$\displaystyle\int_{0}^{\pi}\bigg[\int_{0}^{\sin{x}}f(x,y)\,dy\bigg]dx$
$\ \\ \begin{array}{ll} \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{y^{2}}{2}}^{\frac{1}{2} - \sqrt{\frac{1}{4} - y^{2}}}f(x,y)\,dx\bigg]dy &+ \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{1}{2}+ \sqrt{\frac{1}{4} - y^{2}}}^{1}f(x,y)\,dx\bigg]dy\\ &+ \displaystyle\int_{\frac{1}{2}}^{\sqrt{2}}\bigg[\int_{\frac{y^{2}}{2}}^{1}f(x,y)\,dx\bigg]dy \end{array} $
$\displaystyle\int_{0}^{\sqrt{3}a} \bigg[\int_{2a + \sqrt{4a^2 - y^{2}}}^{\sqrt{3} y}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{\arcsin(y)}^{\pi-\arcsin(y)}f(x,y)\,dx\bigg]dy$
Determine $\int_{0}^{5}f(x,y)\,dx$ e $\int_{0}^{1}f(x,y)\,dy$, sendo $f(x,y)=12x^{2}y^{3}.$
$\int_{0}^{5} 12x^{2}y^{3} \,dx = 500y^{3}$ e $\int_{0}^{1} 12x^{2}y^{3} \,dy = 3x^{2}.$
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
1. \[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
2. \[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{e^{y-1}}^{e^{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{2x}^{x+1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{\frac{\pi}{4}}\bigg[\int_{0}^{\tan(x)}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{e^{-1}}^{1}\bigg[\int_{0}^{1 + \ln(x)}f(x,y) \ , dy\bigg]dx + \displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{y/2}f(x,y)\,dx\bigg]dy + \int_{1}^{2}\bigg[\int_{y - 1}^{y/2}f(x,y)\,dx\bigg]dy$
$\displaystyle \int_{0}^{1}\bigg[\int_{0}^{\arctan(y)}f(x,y)\,dx \bigg]dy $
Calcule a integral iterada.
$\displaystyle\int_{1}^{3} \!\! \int_{0}^{1}(1+4xy)\, dx dy$
$\displaystyle\int_{2}^{4}\!\!\int_{-1}^{1}(x^{2}+y^{2})\,dy dx$
$10.$
$\dfrac{116}{3}.$
Suponha que a temperatura, em graus Celsius, num ponto \((x,y)\) de uma chapa metálica plana seja \( T(x,y)=10-8x^2-2y^2 \), onde \(x\) e \(y\) são medidos em metros. Calcule a temperatura média da porção retangular da chapa dada por \(0\leq x\leq 1\) e \(0\leq y\leq 2\).
\(\dfrac{14}{3}\) \({}^\circ\)C
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^5\int_1^2 4\, dxdy\)
\(\displaystyle \int_0^3\int_0^4\sqrt{25-x^2-y^2}\,dydx\)
Faça um esboço do sólido no primeiro octante compreendido pelos planos \(x=0\), \(z=0\), \(x=5\), \(z-y=0\) e \(z=-2y+6\).
Calcule o volume do sólido dividindo-o em duas partes.
Inverta a ordem de integração.
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^{2}}^{\sqrt{2-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{y-1}^{2-2y}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy + \displaystyle\int_{1}^{\sqrt{2}}\bigg[\int_{-\sqrt{2 - y^{2}}}^{\sqrt{2-y^{2}}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{0}\bigg[\int_{0}^{x + 1}f(x,y)\,dy \bigg] dx + \int_{0}^{2}\bigg[\int_{0}^{\frac{2-x}{2}}f(x,y)\,dy \bigg] dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{0}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{y}^{1}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^2}^{1}f(x,y)\,dy\bigg]dx$
Calcule a integral iterada.
$\displaystyle\int_{0}^{1}\!\!\int_{0}^{1}(u-v)^{5}\,du dv$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{\pi}r\sin^{2}{\theta}\,d\theta dr$
$0.$
$\pi.$
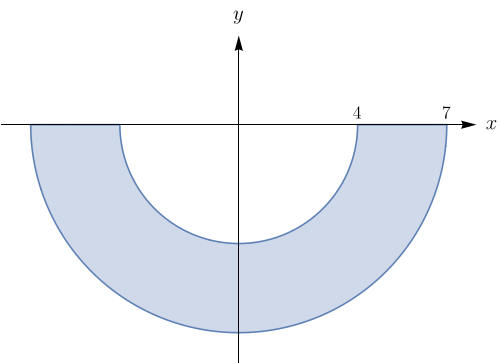
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r \, dr d\theta.$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^1\int_0^1 (2-x-y)\, dydx\)
\(\displaystyle \int_{-2}^2\int_{-2}^2(x^2+y^2)\,dxdy\)
Inverta a ordem de integração.
$\displaystyle\int_{0}^{\dfrac{\pi}{4}}\bigg[\int_{\sin{x}}^{\cos{x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{2}\bigg[\int_{\sqrt{\frac{7+5y^{2}}{3}}}^{\frac{y+7}{3}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{3}\bigg[\int_{x^{2}-2x}^{\sqrt{3x}}f(x,y)\,dy\bigg]dx$
$\displaystyle \int_{0}^{\frac{\sqrt{2}}{2}}\bigg[\int_{0}^{\arcsin{y}}f(x,y)\,dx\bigg]dy + \int_{\frac{\sqrt{2}}{2}}^{1}\bigg[\int_{0}^{\arccos{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{2}^{3}\bigg[\int_{3x - 7}^{\sqrt{\frac{3x^2 - 7}{5}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{0}\bigg[\int_{1 - \sqrt{1 + y}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy + \int_{0}^{3}\bigg[\int_{\dfrac{y^{2}}{3}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy$
Inverta a ordem de integração.
$\displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{x}f(x,y)\,dy\bigg]dx.$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{y+3}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{1}^{e^{y}}f(x,y)\,dx\bigg]dy. + \displaystyle\int_{1}^{e}\bigg[\int_{y}^{1}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{x}f(x,y)\,dy\bigg]dx + \displaystyle\int_{1}^{3}\bigg[\int_{0}^{1}f(x,y)\,dy\bigg]dx + \displaystyle\int_{3}^{4}\bigg[\int_{x-3}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}f(x,y)\,dx\bigg]dy$
Expresse a integral dupla, sobre a região $R$ indicada, como uma integral iterada e ache seu valor.
$\displaystyle\iint\limits_{R}(y+2x)\,dA; \quad R$ região retangular de vértices $(-1,-1)$, $(2,-1)$, $(2,4)$ e $(-1,4).$
$\displaystyle\iint\limits_{R}(x-y)\,dA; \quad R$ região triangular de vértices $(2,9)$, $(2,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}xy^{2}\,dA; \quad R$ região triangular de vértices $(0,0)$, $(3,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}e^{x/y}\,dA; \quad R$ região limitada pelos gráficos de $y=2x$, $y=-x$ e $y=4.$
$\displaystyle\int_{-1}^{4} \int_{-1}^{2} (y+2x)\,dx;dy = \dfrac{75}{2}.$
$\displaystyle\int_{-2}^{2} \int_{1}^{2x + 5} x - y\,dy;dx = -48.$
$\displaystyle\int_{0}^{1} \int_{-2y}^{3y} xy^{2}\,dx;dy = \dfrac{1}{2}.$
$\displaystyle\int_{0}^{4} \int_{-y}^{y/2} e^{x/y}\,dx;dy = 8(e^{1/2} - e^{-1}).$
Como não há antiderivada elementar da função \(e^{x^2}\), a integral \[ \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy \] não pode ser calculada integrando-se primeiro em relação a \(x\). Calcule essa integral expressando-a como uma integral iterada equivalente com ordem de integração invertida.
A região de integração é dada por \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq y\leq 2,\ y/2\leq x\leq 1\}\). Vamos inverter a ordem de integração sobre a região \(R\):\begin{align*} \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy & = \iint\limits_R e^{x^2}\,dA = \int_0^1\int_0^{2x} e^{x^2}\,dydx= \int_0^1\left[e^{x^2}y\right]_{y=0}^{2x}\,dx \\ & = \int_0^1 2xe^{x^2}\,dx = \left.e^{x^2}\right]_0^1 = e-1 \end{align*}
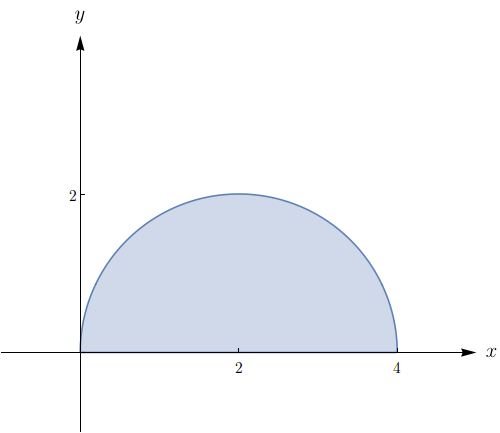
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{0}^{\pi/2}\int_{0}^{4\cos{\theta}} r \,drd\theta.$
Calcule a integral iterada.
$\displaystyle\int_{1}^{4} \int_{1}^{2}\bigg(\dfrac{x}{y}+\dfrac{y}{x}\bigg)\,dy dx$
$\displaystyle\int_{0}^{1} \int_{0}^{3}e^{x+3y}\,dx dy$
$\dfrac{21}{2} \ln(2).$
$\dfrac{(e^{3} - 1)^{2}}{3}.$
Considere a integral iterada dada por $$\int_{0}^{1} \int_{x}^{\sqrt{x}}\frac{e^{y}}{y}\,dy dx.$$
Desenhe a região de integração no plano $xy.$
Calcule a integral acima.
(...)
$e - 2.$
Calcule a integral iterada.
$\displaystyle\int_{0}^{\pi/2} \int_{0}^{\pi/2}\sin{x}\cos{y} \, dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{1}(2x+y)^{8}\,dx dy$
$1.$
$\dfrac{4^{10} - 2^{11}}{180}.$

