Exercícios
Sobre retângulo
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
A integral $\int \!\!\! \int\limits_{\!\!\!\!\!R} \! \sqrt{9 - y^2} \, dA$, em que $R = [0,4] \times [0,2]$, representa o volume de um sólido. Esboce o sólido.
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Prove que $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d.$
Note que $$ \int_{c}^{d} \left[\int_{a}^{b}f(x)g(y)\,dx\right] \;dy = \int_{c}^{d} \left[\int_{a}^{b}f(x)\,dx\right]g(y) \;dy = \left(\int_{a}^{b}f(x)\,dx\right) \int_{c}^{d} g(y) \;dy.$$
Calcule a integral dupla.
$\displaystyle\iint\limits_{R} x\sin(x+y)\,dA, \quad R=[0,\pi/6]\times [0,\pi/3].$
$\displaystyle\iint\limits_{R} xye^{x^{2}y}\,dA, \quad R=[0,1]\times [0,2].$
$\dfrac{\pi}{12}.$
$\dfrac{(e^{2} - 3)}{2}.$
Calcule a integral dupla.
$\displaystyle\iint\limits_{R} (6x^{2}y^{3}-5y^{4})\,dA, \quad R=\{(x,y) \in \mathbb{R}^2:0\leq x\leq 3,\;0\leq y\leq 1\}.$
$\displaystyle\iint\limits_{R} \dfrac{xy^{2}}{x^{2}+1}\,dA, \quad R=\{(x,y)\in \mathbb{R}^2:0\leq x\leq 1,\;-3\leq y\leq 3\}.$
$\dfrac{21}{2}.$
$9 \ln(2).$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\int\!\!\!\!\int\limits_{\!\!\!\!\!\! R} xy^{2}\,dx dy$, onde $R$ é o retângulo $1\leq x\leq 2,\;2\leq y\leq 3.$
$\displaystyle\int\!\!\!\!\int\limits_{\!\!\!\!\!\! R} x\cos(2y)\,dx dy$, onde $R$ é o retângulo $0\leq x\leq 1,\;-\dfrac{\pi}{4}\leq y\leq \dfrac{\pi}{4}.$
$\dfrac{19}{2}.$
$\dfrac{1}{2}.$
Se $f$ é uma função constante, $f(x,y) = k$, e $R = [a,b] \times [c,d],$ mostre que $\iint \limits_{R} k \, dA = k(b-a)(d-c).$
Note que se $R$ for dividida em $mn$ subretângulos, vale $$ \sum^{m}_{i = 1} \sum^{n}_{j = 1} f(x_{ij}^{*}, y_{ij}^{*}) \Delta A = k \sum^{m}_{i = 1} \sum^{n}_{j = 1} \Delta A = k (b - a) (d - c), $$ independentemente dos pontos amostrais $(x_{ij}^{*}, y_{ij}^{*})$ escolhidos.
Seja \(f(x,y)=x-2y\) e considere uma subdivisão uniforme do retângulo \(R=[0,2]\times[0,2]\) em \(16\) retângulos menores. Tome \((x_k^\ast,y_k^\ast)\) como sendo o centro do \(k\)-ésimo retângulo e aproxime a integral dupla de \(f\) sobre \(R\) pela soma de Riemann resultante.
Compare o resultado obtido no item anterior com o valor exato da integral.
Determine o volume do sólido que se encontra abaixo do plano $3x+2y+z=12$ e acima do retângulo $R=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq 1,\;-2\leq y\leq 3\}.$
$\dfrac{95}{2}.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$\sqrt{x+y}$
$\dfrac{1}{x+y}$
$\dfrac{4(9\sqrt{3} - 8\sqrt{2} + 1)}{15}.$
$\ln\left( \dfrac{27}{16}\right).$
Determine o volume do sólido que está abaixo do paraboloide elíptico $x^{2}/4+y^{2}/9+z=1$ e acima do retângulo $R=[-1,1]\times [-2,2].$
$\dfrac{166}{27}.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\iint\limits_{R} x\ln(y)\,dx dy$, onde $R$ é o retângulo $0\leq x\leq 2,\;1\leq y\leq 2.$
$\displaystyle\iint\limits_{R} xye^{x^{2}-y^{2}}\,dx dy$, onde $R$ é o retângulo $-1\leq x\leq 1,\;0\leq y\leq 3.$
$2(2\ln(2) - 1).$
$0.$
Calcule a integral dupla, identificando-a antes com o volume de um sólido.
$\displaystyle\iint\limits_{R} 3 \, dA, \quad R = \{(x,y) \in \mathbb{R}^2: -2 \leq x \leq 2, \ 1 \leq y \leq 6\}.$
$\displaystyle\iint\limits_{R} (4 - 2y) \, dA, \quad R = [0,1] \times [0,1].$
$60.$
$3.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ dada por
$y\cos(xy)$
$x\sin(\pi y)$
$\cos(1) - \dfrac{(1 + \cos(2))}{2}$
$\ln\left(\dfrac{4}{3}\right).$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\iint\limits_{R} \dfrac{\sin^{2}{x}}{1+4y^{2}}\,dx dy$, onde $R$ é o retângulo $0\leq x\leq \dfrac{\pi}{2},\;0\leq y\leq \dfrac{1}{2}.$
$\displaystyle\iint\limits_{R} \dfrac{xy\sin{x}}{1+4y^{2}}\,dx dy$, onde $R$ é o retângulo $0\leq x\leq \dfrac{\pi}{2},\;0\leq y\leq 1.$
$\dfrac{\pi^{2}}{32}.$
$\dfrac{\ln(5)}{8}.$
Estime o volume do sólido que está abaixo da superfície $z = x + 2y^2$ e acima do retângulo $R = [0,2] \times [0,4]$. Use a soma de Riemann com $m = n = 2$ e escolha os pontos amostrais como os cantos inferiores direitos.
Use a Regra do Ponto Médio para dar uma estimativa da integral do item anterior.
$\approx 44.$
$\approx 88.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{ R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$x+2y$
$x-y$
$\dfrac{5}{2}.$
$1.$
Uma piscina de 8 por 12 metros está cheia de água. A profundidade é medida em intervalos de 2 metros, começando em um canto da piscina, e os valores foram registrados na tabela. Estime o volume de água na piscina.
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & 0 & 2 & 4 & 6 & 8 & 10 & 12 \\ \hline 0 & 1 & 1,5 & 2 & 2,4 & 2,8 & 3 & 3 \\ 2 & 1 & 1,5 & 2 & 2,8 & 3 & 3,6 & 3 \\ 4 & 1 & 1,8 & 2,7 & 3 & 3,6 & 4 & 3,2 \\ 6 & 1 & 1,5 & 2 & 2,3 & 2,7 & 3 & 2,5 \\ 8 & 1 & 1 & 1 & 1 & 1,5 & 2 & 2 \\ \hline\end{array}$$
$\approx 227.$
Use um software de apoio computacional para mostrar que o volume \(V\) sob a superfície \(z=xy^3\sin(xy)\) e acima do retângulo \([0,\pi]\times[0,1]\) no plano \(xy\) é dado por \(V=3/\pi\).
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{ R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$1$
$x\cos(xy)$
$1.$
$\cos(1) - \cos(2).$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$\dfrac{1}{(x+y)^{2}}$
$\dfrac{1}{1+x^{2}+2xy+y^{2}}$
$\dfrac{3}{\pi}.$
$3\arctan(3) - 4\arctan(2) - \ln(2) + \dfrac{\ln(5)}{2} + \dfrac{\pi}{4}.$
Utilize simetria para calcular $\iint\limits_{D}(2-3x+4y)\,dA$, onde $D$ é a região limitada pelo quadrado com vértices $(\pm 5,0)$ e $(0,\pm 5).$
$100.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$ye^{xy}$
$xy^{2}$
$\dfrac{(e - 1)^{2}}{2}.$
$\dfrac{1}{2}.$
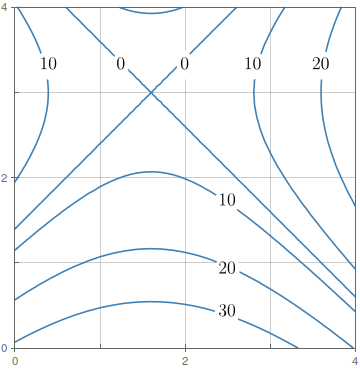
A figura mostra o mapa de contorno de $f$ no quadrado $R = [0,4] \times [0,4]$.
Use a Regra do Ponto Médio com $m = n = 2$ para estimar o valor de $\int\!\!\!\int \limits_{\!\!\!\!\!R} \! f(x,y) \, dA$.
Estime o valor médio de $f$.
