Exercícios
Integrais duplas
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Calcule $\displaystyle\iint\limits_{B} y\,dx dy$, onde $B$ é o conjunto dado.
$B$ é a região compreendida entre os gráficos de $y=x$ e $y=x^{2}$, com $0\leq x\leq 2.$
$B$ é o paralelogramo de vértices $(-1,0)$, $(0,0)$, $(1,1)$ e $(0,1).$
$B$ é o semicírculo $x^{2}+y^{2}\leq 4$, $y\geq 0.$
$B=\{(x,y)\in \mathbb{R}^{2}|\;x\geq 0,\;x^{5}-x\leq y \leq 0\}.$
$2$.
$\dfrac{1}{2}$.
$\dfrac{16}{3}$.
$-\dfrac{16}{231}$.
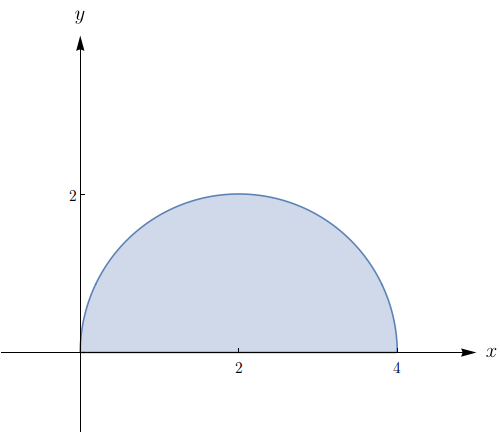
Esboce a região cuja área é dada pela integral e calcule-a: $\displaystyle\int_{0}^{\pi/2} \int_{0}^{4\cos{\theta}} r \, dr d\theta$
$2\pi;$ região de integração:
Calcule a integral dupla.
$\displaystyle\iint\limits_{R} (6x^{2}y^{3}-5y^{4})\,dA, \quad R=\{(x,y) \in \mathbb{R}^2:0\leq x\leq 3,\;0\leq y\leq 1\}.$
$\displaystyle\iint\limits_{R} \dfrac{xy^{2}}{x^{2}+1}\,dA, \quad R=\{(x,y)\in \mathbb{R}^2:0\leq x\leq 1,\;-3\leq y\leq 3\}.$
$\dfrac{21}{2}.$
$9 \ln(2).$
Calcule o centro de massa da região: $D = \{(x,y) \in \mathbb{R}^2: x^2 + 4y^2 \leq 1, \ y \geq 0\}$ e a densidade é proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(0, \frac{3\pi}{32} \right).$
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste a oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade norte. Encontre o volume de água da piscina.
$1800 \pi$ m$^3.$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq z\leq 2x.$
$x\leq z\leq1-y^{2}$ e $x\geq 0.$
$\dfrac{\pi}{2}.$
$\dfrac{8}{15}.$
Faça um esboço do sólido no primeiro octante compreendido pelos planos \(x=0\), \(z=0\), \(x=5\), \(z-y=0\) e \(z=-2y+6\).
Calcule o volume do sólido dividindo-o em duas partes.
Determine o valor médio de $f(x,y)=e^{y}\sqrt{x+e^{y}}$ sobre o retângulo $R=[0,4]\times [0,1].$
$\dfrac{(4 + e)^{5/2} - e^{5/2} - 5^{5/2} + 1}{15}.$
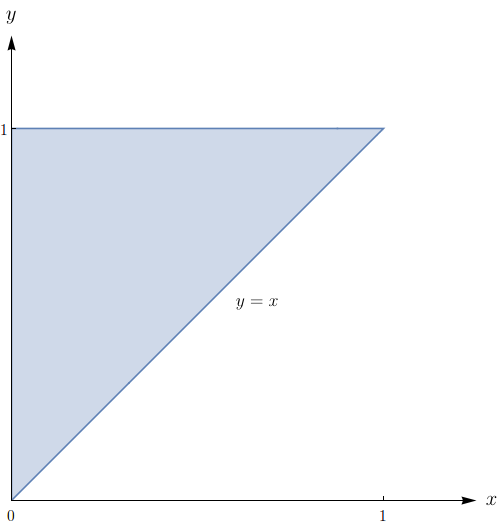
Calcule a integral trocando a ordem de integração. $\displaystyle\int_{0}^{1}\!\!\int_{x}^{1}e^{x/y}\,dy dx$.
A região de integração é do tipo I, é dada por
$$\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 1 \mbox{ e } x \leq y \leq 1\}$$
e pode ser vista geometricamente como a região esboçada na figura abaixo.
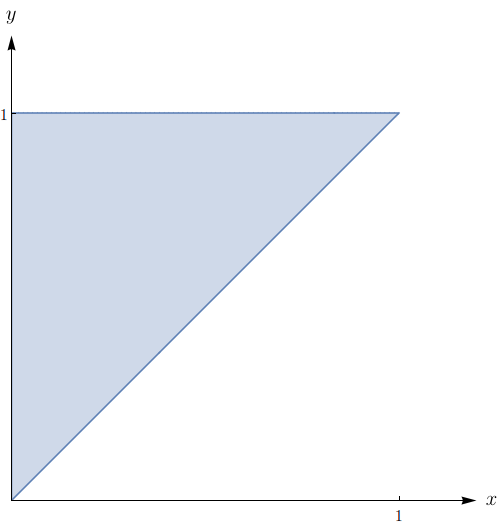
Essa região pode ser descrita como uma região do tipo II da seguinte forma:
$$\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq y \mbox{ e } 0 \leq y \leq 1\}.$$
Assim,
\begin{array}{rcl}\displaystyle\int_{0}^{1}\!\!\int_{x}^{1}e^{x/y}\,dy dx & = & \displaystyle\int_{0}^{1}\!\!\int_{0}^{y} \! e^{x/y}\,dx dy \\ & = & \displaystyle\int_{0}^{1} \! \left. ye^{x/y} \right|_{x=0}^{x=y}\,dx \\ & = & \displaystyle\int_{0}^{1} \! \left. y(e-1) \right|_{x=0}^{x=y}\,dx \\ & = & \left.(e-1) \frac{y^2}{2}\right|_{0}^{1} = \frac{e-1}{2}.\end{array}
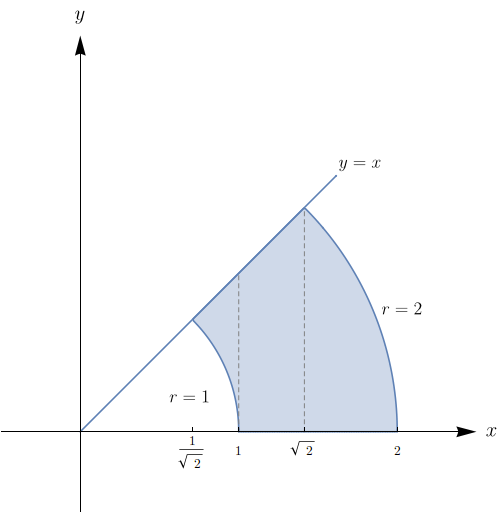
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{ D}xy\,dA$, onde $D$ é o disco com centro na origem e raio 3.
$0.$
Utilize coordenadas polares para determinar o volume do sólido dado: acima do cone $z=\sqrt{x^2+y^2}$ e abaixo da esfera $x^2+y^2+z^2=1.$
$\displaystyle \frac{\pi}{3}(2 - \sqrt{2}).$
Determine o volume do sólido que está abaixo do paraboloide elíptico $x^{2}/4+y^{2}/9+z=1$ e acima do retângulo $R=[-1,1]\times [-2,2].$
$\dfrac{166}{27}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{1} \int_{0}^{\sqrt{1-x^{2}}}\,dy dx$
$\displaystyle \frac{\pi}{2}.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\iint\limits_{R} x\ln(y)\,dx dy$, onde $R$ é o retângulo $0\leq x\leq 2,\;1\leq y\leq 2.$
$\displaystyle\iint\limits_{R} xye^{x^{2}-y^{2}}\,dx dy$, onde $R$ é o retângulo $-1\leq x\leq 1,\;0\leq y\leq 3.$
$2(2\ln(2) - 1).$
$0.$
Calcule a integral trocando a ordem de integração.
$\displaystyle\int_{0}^{4}\!\!\int_{\sqrt{x}}^{2}\dfrac{1}{y^{3}+1}\,dy dx$
$\displaystyle\int_{0}^{\pi}\!\!\int_{x}^{\pi}\dfrac{\sin{y}}{y}\,dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{x}^{2}2y^{2}\sin(xy)\,dy dx.$
$\dfrac{\ln(9)}{3}.$
$2.$
$4 - \sin(4).$
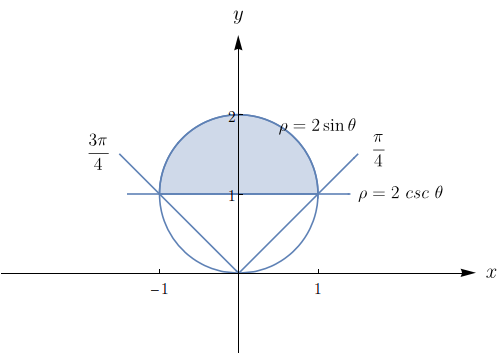
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{ R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
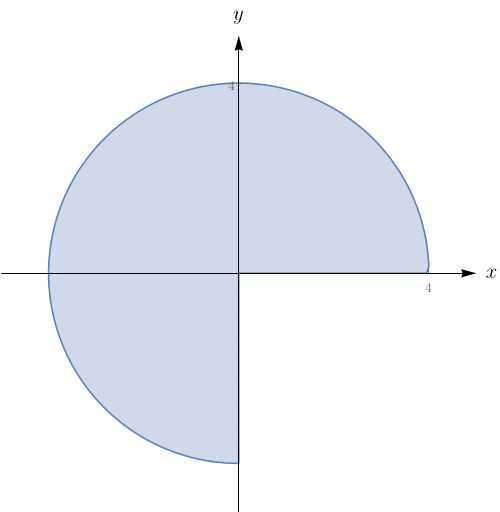
$\displaystyle \int_{0}^{\frac{3\pi}{2}} \int_{0}^{4} f(r\cos(\theta),r\sin(\theta)) r d r d \theta.$
Expresse a integral dupla, sobre a região $R$ indicada, como uma integral iterada e ache seu valor.
$\displaystyle\iint\limits_{R}(y+2x)\,dA; \quad R$ região retangular de vértices $(-1,-1)$, $(2,-1)$, $(2,4)$ e $(-1,4).$
$\displaystyle\iint\limits_{R}(x-y)\,dA; \quad R$ região triangular de vértices $(2,9)$, $(2,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}xy^{2}\,dA; \quad R$ região triangular de vértices $(0,0)$, $(3,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}e^{x/y}\,dA; \quad R$ região limitada pelos gráficos de $y=2x$, $y=-x$ e $y=4.$
$\displaystyle\int_{-1}^{4} \int_{-1}^{2} (y+2x)\,dx;dy = \dfrac{75}{2}.$
$\displaystyle\int_{-2}^{2} \int_{1}^{2x + 5} x - y\,dy;dx = -48.$
$\displaystyle\int_{0}^{1} \int_{-2y}^{3y} xy^{2}\,dx;dy = \dfrac{1}{2}.$
$\displaystyle\int_{0}^{4} \int_{-y}^{y/2} e^{x/y}\,dx;dy = 8(e^{1/2} - e^{-1}).$
Calcule a integral iterada $\int_{-3}^{3} \int_{0}^{\sqrt{9-x^2}}\sin(x^{2}+y^{2})\,dy dx$, convertendo-a antes para coordenadas polares.
$\displaystyle \frac{\pi}{2}(1 - \cos(9)).$
Considere a integral
$$\int_{0}^{1}\!\!\int_{x^{2}}^{1}x^{3}\sin{y^{3}}\,dy dx.$$
Desenhe a região de integração.
Calcule o valor da integral.
$\dfrac{1 - \cos(1)}{12}$.
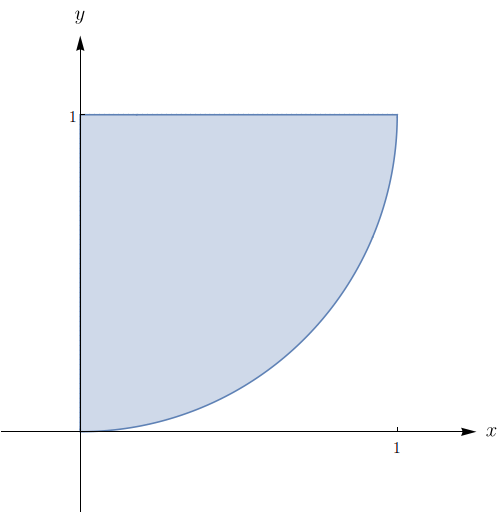
Esboce a região de integração para a integral iterada $\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}^{3\sqrt{y}}f(x,y)\,dx dy$.
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint\limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$

$\displaystyle \int_{-1}^{1} \int_{0}^{1 - x^2} f(x,y) dy dx .$
Determine $\int_{0}^{5}f(x,y)\,dx$ e $\int_{0}^{1}f(x,y)\,dy$, sendo $f(x,y)=12x^{2}y^{3}.$
$\int_{0}^{5} 12x^{2}y^{3} \,dx = 500y^{3}$ e $\int_{0}^{1} 12x^{2}y^{3} \,dy = 3x^{2}.$
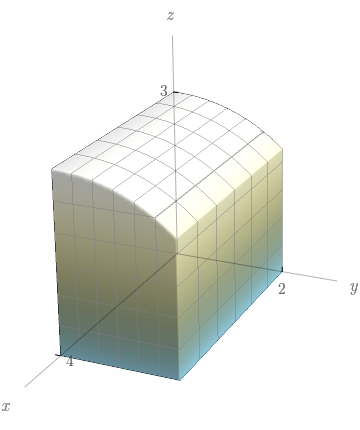
A integral $\int \!\!\! \int\limits_{\!\!\!\!\!R} \! \sqrt{9 - y^2} \, dA$, em que $R = [0,4] \times [0,2]$, representa o volume de um sólido. Esboce o sólido.
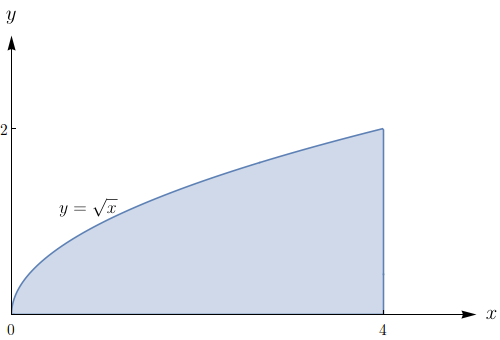
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{4}\!\!\int_{0}^{\sqrt{x}} \! f(x,y)\,dy dx$.
Calcule as integrais iteradas.
$\displaystyle\int_{0}^{1}\int_{0}^{x^{2}}(x+2y)\,dy dx$
$\displaystyle\int_{0}^{1}\int_{x^{2}}^{x}(1+2y)\,dy dx$
$\dfrac{9}{20}.$
$\dfrac{3}{10}.$
Inverta a ordem de integração.
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^{2}}^{\sqrt{2-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{y-1}^{2-2y}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy + \displaystyle\int_{1}^{\sqrt{2}}\bigg[\int_{-\sqrt{2 - y^{2}}}^{\sqrt{2-y^{2}}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{0}\bigg[\int_{0}^{x + 1}f(x,y)\,dy \bigg] dx + \int_{0}^{2}\bigg[\int_{0}^{\frac{2-x}{2}}f(x,y)\,dy \bigg] dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
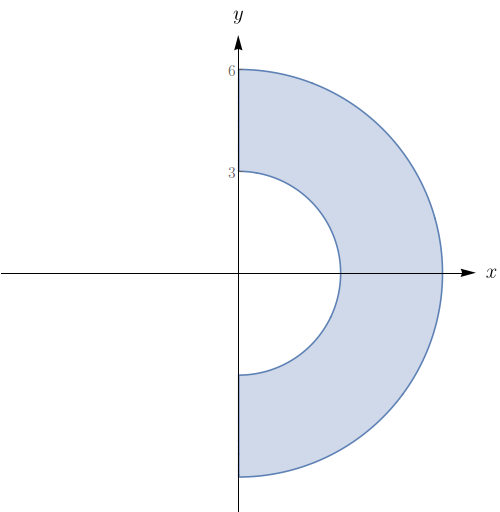
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{3}^{6} f(r\cos(\theta),r\sin(\theta)) r d r d \theta.$
Inverta a ordem de integração.
$\displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{x}f(x,y)\,dy\bigg]dx.$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{y+3}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{1}^{e^{y}}f(x,y)\,dx\bigg]dy. + \displaystyle\int_{1}^{e}\bigg[\int_{y}^{1}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{x}f(x,y)\,dy\bigg]dx + \displaystyle\int_{1}^{3}\bigg[\int_{0}^{1}f(x,y)\,dy\bigg]dx + \displaystyle\int_{3}^{4}\bigg[\int_{x-3}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}f(x,y)\,dx\bigg]dy$
Encontre o volume do sólido no primeiro octante limitado pelo cilindro $z=16-x^{2}$ e pelo plano $y=5.$
$\dfrac{640}{3}.$
Encontre a área da região descrita como sendo a parte do cone \(z=\sqrt{x^2+y^2}\) dentro do cilindro \(x^2+y^2=2x\).
A fronteira de uma lâmina consiste nos semicírculos $y = \sqrt{1 - x^2}$ e $y = \sqrt{4 - x^2}$, juntamente com as partes do eixo $x$ que os une. Encontre o centro de massa da lâmina se a densidade em qualquer ponto é proporcional à sua distância da origem.
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Calcule o volume do conjunto dado.
$0\leq y\leq 1-x^{2}$ e $0\leq z\leq 1-x^{2}.$
$x^{2}+y^{2}+3\leq z\leq 4.$
$\dfrac{16}{15}.$
$\dfrac{\pi}{2}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\frac{x}{x^{2}+y^{2}}\,dA$, onde $R=\{(x,y)\in \mathbb{R}^{2}| x^{2}+y^{2}\leq 4, x\geq 1\}.$
$2\sqrt{3}.$
Considere a integral iterada dada por $$\int_{0}^{1} \int_{x}^{\sqrt{x}}\frac{e^{y}}{y}\,dy dx.$$
Desenhe a região de integração no plano $xy.$
Calcule a integral acima.
(...)
$e - 2.$
Seja \(f(x,y)=x-2y\) e considere uma subdivisão uniforme do retângulo \(R=[0,2]\times[0,2]\) em \(16\) retângulos menores. Tome \((x_k^\ast,y_k^\ast)\) como sendo o centro do \(k\)-ésimo retângulo e aproxime a integral dupla de \(f\) sobre \(R\) pela soma de Riemann resultante.
Compare o resultado obtido no item anterior com o valor exato da integral.
Calcule a integral dupla.
$\displaystyle\iint\limits_{D}(2x-y)\,dA, \quad D$ limitada pelo círculo de centro na origem e raio 2.
$\displaystyle\iint\limits_{D}\dfrac{x}{y}\,dA, \quad D$ região no primeiro quadrante limitada pelas retas $y=x$, $y=2x$, $x=1$ e $x=2.$
$\displaystyle\iint\limits_{D}\dfrac{1}{xy}\,dA, \quad D$ o quadrado $1\leq x\leq 2$, \;$1\leq y\leq 2.$
$\displaystyle\iint\limits_{D}(x-\sqrt{y})\,dA, \quad D$ região triangular cortado do primeiro quadrante do plano $xy$ pela reta $x+y=1.$
$0.$
$\dfrac{3\ln(2)}{2}.$
$(\ln(2))^{2}.$
$-\dfrac{1}{10}.$
Calcule a integral iterada.
$\displaystyle\int_{1}^{3} \!\! \int_{0}^{1}(1+4xy)\, dx dy$
$\displaystyle\int_{2}^{4}\!\!\int_{-1}^{1}(x^{2}+y^{2})\,dy dx$
$10.$
$\dfrac{116}{3}.$
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{0}^{\pi/2}\int_{0}^{4\cos{\theta}} r \,drd\theta.$

Utilize coordenadas polares para determinar o volume do sólido dado: dentro do cilindro $x^2+y^2=4$ e do elipsoide $4x^2+4y^2+z^2=64.$
$\displaystyle \frac{8\pi}{3} (64 - 24\sqrt{3}).$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{\dfrac{\pi}{4}}\bigg[\int_{\sin{x}}^{\cos{x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{2}\bigg[\int_{\sqrt{\frac{7+5y^{2}}{3}}}^{\frac{y+7}{3}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{3}\bigg[\int_{x^{2}-2x}^{\sqrt{3x}}f(x,y)\,dy\bigg]dx$
$\displaystyle \int_{0}^{\frac{\sqrt{2}}{2}}\bigg[\int_{0}^{\arcsin{y}}f(x,y)\,dx\bigg]dy + \int_{\frac{\sqrt{2}}{2}}^{1}\bigg[\int_{0}^{\arccos{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{2}^{3}\bigg[\int_{3x - 7}^{\sqrt{\frac{3x^2 - 7}{5}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{0}\bigg[\int_{1 - \sqrt{1 + y}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy + \int_{0}^{3}\bigg[\int_{\dfrac{y^{2}}{3}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy$
Uma piscina de 8 por 12 metros está cheia de água. A profundidade é medida em intervalos de 2 metros, começando em um canto da piscina, e os valores foram registrados na tabela. Estime o volume de água na piscina.
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & 0 & 2 & 4 & 6 & 8 & 10 & 12 \\ \hline 0 & 1 & 1,5 & 2 & 2,4 & 2,8 & 3 & 3 \\ 2 & 1 & 1,5 & 2 & 2,8 & 3 & 3,6 & 3 \\ 4 & 1 & 1,8 & 2,7 & 3 & 3,6 & 4 & 3,2 \\ 6 & 1 & 1,5 & 2 & 2,3 & 2,7 & 3 & 2,5 \\ 8 & 1 & 1 & 1 & 1 & 1,5 & 2 & 2 \\ \hline\end{array}$$
$\approx 227.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\iint\limits_{R} \dfrac{\sin^{2}{x}}{1+4y^{2}}\,dx dy$, onde $R$ é o retângulo $0\leq x\leq \dfrac{\pi}{2},\;0\leq y\leq \dfrac{1}{2}.$
$\displaystyle\iint\limits_{R} \dfrac{xy\sin{x}}{1+4y^{2}}\,dx dy$, onde $R$ é o retângulo $0\leq x\leq \dfrac{\pi}{2},\;0\leq y\leq 1.$
$\dfrac{\pi^{2}}{32}.$
$\dfrac{\ln(5)}{8}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{0} \int_{-\sqrt{1-x^{2}}}^{0}\frac{2}{1+\sqrt{x^{2}+y^{2}}}\,dy dx$
$(1 - \ln(2))\pi.$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^5\int_1^2 4\, dxdy\)
\(\displaystyle \int_0^3\int_0^4\sqrt{25-x^2-y^2}\,dydx\)
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits{R}\sin(x^{2}+y^{2})\,dA$, onde $R$ é a região acima do eixo $x$ e dentro da circunferência $x^{2}+y^{2}=9.$
$\displaystyle \frac{\pi}{2}(1 - \cos(9).$
Determine os momentos de inércia da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
$\displaystyle I_{x} = \dfrac{1}{16}(e^4 - 1),$ $I_{y} = \dfrac{1}{16}(e^4 - 1)$ e $I_{0} = \dfrac{1}{16}(e^4 + 2e^2 - 3).$
Utilize coordenadas polares para determinar o volume do sólido dado: abaixo do cone $z=\sqrt{x^{2}+y^{2}}$ e acima do disco $x^{2}+y^{2}\leq 4.$
$\displaystyle \frac{16\pi}{3}.$
Considere a integral $$\int_{0}^{1}\int_{3y}^{3}e^{x^{2}}\,dx dy.$$
Esboce a região de integração.
Calcule a integral usando a ordem de integração apropriada.
(...)
$\dfrac{e^9 - 1}{6}.$
Utilize a integral dupla para determinar a área da região: um laço da rosácea $r=\cos(3\theta).$
$\displaystyle \frac{\pi}{12}.$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo hiperboloide $-x^2-y^2+z^2=1$ e acima do plano $xy.$
$\displaystyle \frac{4\pi}{3}.$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{e^{y-1}}^{e^{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{2x}^{x+1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{\frac{\pi}{4}}\bigg[\int_{0}^{\tan(x)}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{e^{-1}}^{1}\bigg[\int_{0}^{1 + \ln(x)}f(x,y) \ , dy\bigg]dx + \displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{y/2}f(x,y)\,dx\bigg]dy + \int_{1}^{2}\bigg[\int_{y - 1}^{y/2}f(x,y)\,dx\bigg]dy$
$\displaystyle \int_{0}^{1}\bigg[\int_{0}^{\arctan(y)}f(x,y)\,dx \bigg]dy $
Uma luminária tem duas lâmpadas de um tipo com tempo de vida médio de 1.000 horas. Supondo que possamos modelar a probabilidade de falha dessas lâmpadas por uma função densidade exponencial com média $\mu = 1.000$, determine a probabilidade de que ambas as lâmpadas venham a falhar dentro de um período de 1.000 horas.
Outra luminária tem somente uma lâmpada do mesmo tipo das do item anterior. Se a lâmpada queima e é trocada por outra to mesmo tipo, determine a probabilidade de que as duas venham a falhar dentro de 1.000 horas.
$(e^{-1} - 1)^2.$
$1 - 2e^{-1}.$
Encontre a área da superfície descrita como sendo a parte do plano \(2x+2y+z=8\) no primeiro octante.
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=1$ e $B$ a região compreendida entre os gráficos de $y=\sin{x}$ e $y=1-\cos{x}$, com $0\leq x\leq \dfrac{\pi}{2}.$
$f(x,y)=\sqrt{1+y^{3}}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;\sqrt{x}\leq y\leq 1 \}.$
$f(x,y)=x$ e $B$ é o conjunto de todos $(x,y)$ tais que $y\geq x^{2}$ e $x\leq y\leq x+2.$
$f(x,y)=\dfrac{y}{x+y^{2}}$ e $B$ o conjunto de todos $(x,y)$ tais que $1\leq x\leq 4$ e $0\leq y\leq \sqrt{x}.$
$2 - \dfrac{\pi}{2}.$
$\dfrac{2(2\sqrt{2} - 1)}{9}.$
$\dfrac{13}{6}.$
$\dfrac{3 \ln(2)}{2}.$
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1} \!\! \int_{0}^{1}(4-x-2y)\, dx dy.$$
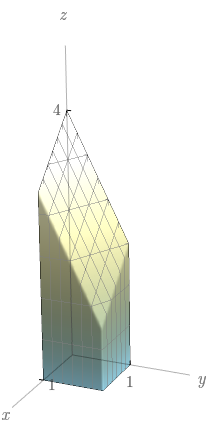
Esboce a região de integração para a integral iterada $\displaystyle\int_{-1}^{2}\!\int_{-\sqrt{4-x^{2}}}^{4-x^{2}}f(x,y)\,dy dx$.

Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq 1$ e $x+y+2\leq z \leq 4.$
$x\geq 0$, $y \geq 0$, $x+y\leq 1$ e $0\leq z\leq x^{2}+y^{2}.$
$2\pi.$
$\dfrac{1}{6}.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{1}^{\ln 8}\!\!\!\int_{0}^{\ln y}e^{x+y}\,dx dy$.
$8 \ln(8) - 16 + e.$
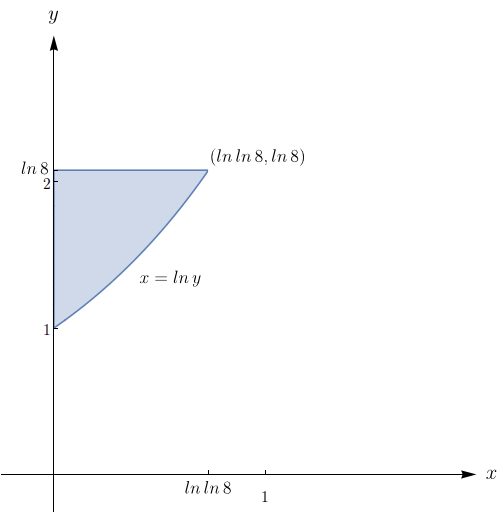
Esboce a região cuja área é dada pela integral $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r\, dr d\theta$ e calcule-a:
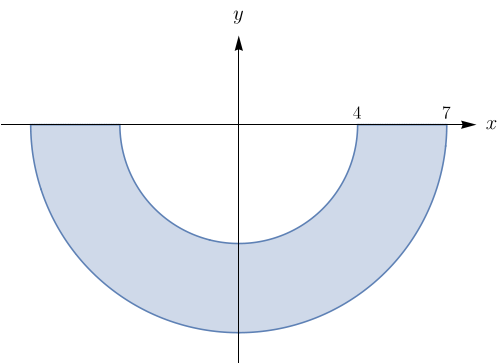
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{1}\!\!\int_{\arctan{x}}^{\pi/4}\!f(x,y)\,dy dx$.
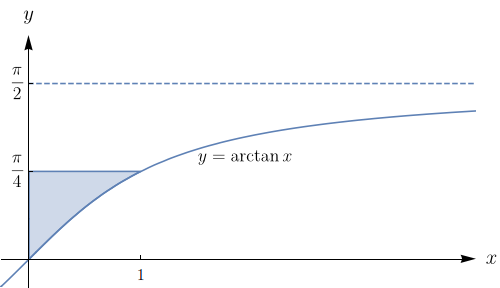
Encontre o volume do sólido delimitado pelo parabolóide $z=2+x^{2}+(y-2)^{2}$ e pelos planos $z=1$, $x=1$, $x=-1$, $y=0$ e $y=4.$
Observe que o sólido $E$ está abaixo da superfície $z = 2+x^2+(y-2)^2$ e acima do retângulo $[-1,1]\times [0,4]$ em $z=1$ (ver figura abaixo).

Algebricamente, $$E = \{(x,y,z) \in\mathbb{R}^3: -1 \leq x \leq 1, 0 \leq y \leq 4 \mbox{ e } 1 \leq z \leq 2 + x^2 + (y-2)^2\}.$$ Logo, o volume é dado por $$V = \iint\limits_{R}(2+x^2+(y-2)^2)\,dA - \iint\limits_{ R}\,dA,$$ em que $R = \{(x,y) \in \mathbb{R}^2; -1 \leq x \leq 1 \mbox{ e } 0 \leq y \leq 4 \}$. Assim, \begin{eqnarray*} V & = & \displaystyle\int_{-1}^{1}\int_{0}^{4}(x^2+y^2-4y+5)\,dy dx \\ & = & \displaystyle\int_{-1}^{1} \left.\left(x^2y+\frac{y^3}{3}-2y^2+5y \right|_{y=0}^{y=4} \right) \,dx \\ & = & \displaystyle\int_{-1}^{1} \left(4x^2+\frac{28}{3}\right) \,dx \\ & = & \left.\frac{4x^3}{3}+\frac{28x}{3} \right|_{x=-1}^{x=1} = \frac{64}{3}. \end{eqnarray*} Observe que, pelo Teorema de Fubini, podemos optar por calcular a integral $$\int_{0}^{4}\!\int_{-1}^{1}(x^2+y^2-4y+5)\,dy dx,$$ obtendo o mesmo resultado.
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{\pi}\!\!\int_{0}^{x}x\sin{y}\,dy dx$.
$\dfrac{\pi^{2}}{2} + 2.$
Calcule o volume do conjunto dado.
$x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0.$
$x\leq y\leq 1$, $x\geq 0$, $z\geq 0$ e $z^{2}+x^{4}+x^{2}y^{2}\leq 2x^{2}.$
$\dfrac{1}{6}.$
$\dfrac{\pi(1 - \sqrt{2})}{8} + \dfrac{1}{3}.$
A reta \(y=2-x\) intersecta a parábola \(y=x^2\) nos pontos \((-2,4)\) e \((1,1)\). Mostre que, se \(R\) denotar a região englobada por \(y=2-x\) e \(y=x^2\), então \[ \iint_R\left(1+2y\right)\,dA = \int_{-2}^1\int_{x^2}^{2-x}\left(1+2y\right)\,dydx = 18,9 \]
Determine o volume do sólido que se encontra abaixo do plano $3x+2y+z=12$ e acima do retângulo $R=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq 1,\;-2\leq y\leq 3\}.$
$\dfrac{95}{2}.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{1}^{2}\!\!\int_{y}^{y^{2}} \,dx dy$.
$\frac{5}{6}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+2y)\,dx dy$, onde $R$ é o círculo $x^{2}+y^{2}\leq 4.$
$4\pi.$
Uma região $R$ é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
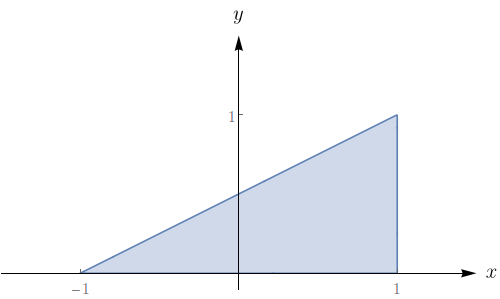
$\displaystyle \int_{-1}^{1} \int_{0}^{\frac{(x + 1)}{2}} f(x,y) dy dx .$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}xy\,dx dy$, onde $R$ é o círculo $x^{2}+y^{2}-2y\leq 0$, $x\geq 0.$
$\displaystyle \frac{2}{3}.$
Escreva a integral dupla $$\iint\limits_{R}x\cos{y}\;dA,$$ onde $R$ é limitada pelas retas $y=0$, $x=\pi/4$ e $y=x$, das duas formas possíveis (mudando a ordem de integração). Escolha uma dessas formas e calcule o valor dessa integral.
$\displaystyle \int_{0}^{\pi/4} \int_{0}^{x} x \cos(y)\;dy\;dx = \int_{0}^{\pi/4} \int_{y}^{\pi / 4} x \cos(y)\;dx\;dy = -\frac{\pi - 4}{4\sqrt{2}}.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ dada por
$y\cos(xy)$
$x\sin(\pi y)$
$\cos(1) - \dfrac{(1 + \cos(2))}{2}$
$\ln\left(\dfrac{4}{3}\right).$
Calcule o volume do conjunto dado.
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1,0\leq z\leq x+2y\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 2, 1\leq y\leq 2, 0\leq z\leq \sqrt{xy}\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, 0\leq z\leq xye^{x^{2}-y^{2}}\}$
$ \{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, x^{2}+y^{2}\leq z\leq 2\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 1\leq x\leq 2, 0\leq y\leq 1,\;x+y\leq z\leq x+y+2\}$
$\{(x,y,z)\in \mathbb{R}^{3}|\;0\leq x\leq 1, 0\leq y\leq 1,1\leq z\leq e^{x+y}\}$
$\dfrac{3}{2}.$
$\dfrac{8\sqrt{2}(2\sqrt{2} - 1)}{9}.$
$\dfrac{(e - 1)(1 - e^{-1})}{4}.$
$\dfrac{4}{3}.$
$2.$
$e^{2}-2e.$
Verifique que $$f(x,y) = \begin{cases} 4xy, & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 1,\\ 0, & \quad \text{caso contrário}, \end{cases}$$ é uma função densidade conjunta.
Se $X$ e $Y$ são variáveis aleatórias cuja função densidade conjunta é a função $f$ do item anterior, determine: (i) $P(X \geq \frac{1}{2})$, (ii) $P(X \geq \frac{1}{2}, Y \leq \frac{1}{2})$.
Determine os valores esperados de $X$ e $Y$.
Note que $$\iint_\limits{\mathbb{R}^2} f(x,y)\,dA = \int_{0}^{1} \int_{0}^{1} 4xy\, dydx = 1. $$
(i) $\dfrac{3}{4}.$ (ii) $\dfrac{3}{16}.$
$\dfrac{3}{16}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\,dx dy$, onde $R$ é a região, no plano $xy$, limitada pela curva (dada em coordenadas polares) $\rho=\cos(2\theta)$, $\dfrac{\pi}{8}\leq \theta \leq \dfrac{\pi}{4}.$
$\displaystyle \frac{3\pi + 2}{32}.$
Calcule o volume do conjunto dado.
$4x+2y\geq z\geq 3x+y+1$, $x\geq 0$ e $y\geq 0.$
$0\leq z\leq \sin{y^{3}}$ e $\sqrt{x}\leq y\leq \sqrt[3]{\pi}.$
$\dfrac{1}{6}.$
$\dfrac{2}{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{\ln 2} \int_{0}^{\sqrt{(\ln 2)^{2}-y^{2}}}e^{\sqrt{x^{2}+y^{2}}}\,dx dy$
$\displaystyle \frac{\pi(2\ln(2) - 1)}{2}.$
Calcule a integral dupla utilizando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+y^{2})\,dx dy$, onde $R=\{(x,y)\in \mathbb{R}^{2}| 1\leq x^{2}+y^{2}\leq 4\}.$
$\displaystyle \frac{15\pi}{2}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo:$D$ a região triangular com vértices $(0,0), (2,1), (0,3)$ e $\rho(x,y) = x + y$.
Massa: $6;$ centro de massa: $\displaystyle \left(\frac{3}{4},\frac{3}{2} \right).$
Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for $\rho(x,y) = 1 + 0,1\cdot x$, é mais difícil girar a pá em torno do eixo $x$ ou do eixo $y$?
Se calcularmos os momentos de inércia sobre $x$ e $y$, poderemos determinar em qual direção será mais difíciel de girar a pá do ventilador. Notemos que a região de integração é o quadrado com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem em ambas as integrais. Então, o momento de inércia sobre o eixo $x$ é dada por: $$I_{x}=\iint\limits_{D}y^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}y^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(1+0,1x)\,dx\cdot \int_{0}^{2}y^{2}\,dy=\bigg(x+0,1\frac{x^{2}}{2}\bigg)\bigg|_{0}^{2}\cdot \bigg(\frac{y^{3}}{3}\bigg)\bigg|_{0}^{2}$$ $$=\bigg[(2+0,2)-0\bigg]\cdot \bigg[\frac{8}{3}\bigg]=\frac{17,6}{3}.$$ Da mesma forma, o momente de inércia sobre o eixo $y$ é dado por: $$I_{y}=\iint\limits{D}x^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}x^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(x^{2}+0,1x^{3})\,dx\cdot \int_{0}^{2}\,dy=\bigg(\frac{x^{3}}{3}+0,1\frac{x^{4}}{4}\bigg)\bigg|_{0}^{2}\cdot \bigg(y\bigg)\bigg|_{0}^{2}$$ $$=\bigg[\bigg(\frac{8}{3}+0,4\bigg)-0\bigg]\cdot \bigg[2-0\bigg]=\frac{18,4}{3}.$$ Como $I_{y}>I_{x}$ é mais difícil girarmos a pá do ventilador em torno do eixo $y.$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=\dfrac{1}{\ln(y)}$ e $B=\bigg\{(x,y)\in \mathbb{R}^{2}|\;2\leq y\leq 3,\;0\leq x\leq \dfrac{1}{y}\bigg\}.$
$f(x,y) = xy\cos{x^{2}}$ e $B=\{(x,y) \in \mathbb{R}^{2}| \; 0 \leq x \leq 1, \; x^{2} \leq y \leq 1\}$.
$f(x,y) = \cos(2y)\sqrt{4-\sin^{2}{x}}$ e $B$ é o triângulo de vértices $(0,0)$, $\bigg(0,\dfrac{\pi}{2}\bigg)$ e $\bigg(\dfrac{\pi}{2},\dfrac{\pi}{2}\bigg).$
$f(x,y)=x+y$ e $B$ a região compreendida entre os gráficos das funções $y=x$ e $y=e^{x}$, com $0\leq x\leq 1.$
$\ln(\ln(3)) - \ln(\ln(2)).$
$\dfrac{\sin(1) - \cos(1)}{2}$.
$\dfrac{8}{3} - \sqrt{3}.$
$\dfrac{1 + e^{2}}{4}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{D}e^{-x^{2}-y^{2}}\,dA$, onde $D$ é a região delimitada pelo semicírculo $x=\sqrt{4-y^{2}}$ e o eixo $y.$
$\displaystyle \frac{\pi}{2} (1 - e^{-4}).$
Calcule a integral iterada.
$\displaystyle\int_{0}^{1}\!\!\int_{0}^{1}(u-v)^{5}\,du dv$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{\pi}r\sin^{2}{\theta}\,d\theta dr$
$0.$
$\pi.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$\dfrac{1}{(x+y)^{2}}$
$\dfrac{1}{1+x^{2}+2xy+y^{2}}$
$\dfrac{3}{\pi}.$
$3\arctan(3) - 4\arctan(2) - \ln(2) + \dfrac{\ln(5)}{2} + \dfrac{\pi}{4}.$
Utilize o resultado $\displaystyle \int_{-\infty}^{\infty}e^{-x^{2}}\,dx=\sqrt{\pi}$ para calcular as integrais:
$\displaystyle\int_{0}^{\infty} x^{2}e^{-x^{2}}\,dx$
$\displaystyle\int_{0}^{\infty}\sqrt{x}e^{-x}\,dx$
$\displaystyle \frac{\sqrt{\pi}}{4}.$
$\displaystyle \frac{\sqrt{\pi}}{2}.$
Estime o volume do sólido que está abaixo da superfície $z = x + 2y^2$ e acima do retângulo $R = [0,2] \times [0,4]$. Use a soma de Riemann com $m = n = 2$ e escolha os pontos amostrais como os cantos inferiores direitos.
Use a Regra do Ponto Médio para dar uma estimativa da integral do item anterior.
$\approx 44.$
$\approx 88.$
Determine a massa e o centro de massa da lâmina que ocupa a região $\displaystyle D = \{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2, \ -1 \leq y \leq 1\}$ e tem função densidade $\rho(x,y) = xy^2.$
Massa: $\dfrac{4}{3};$ centro de massa: $\displaystyle \left(\frac{4}{3},0 \right).$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{6} \int_{0}^{y}x\,dx dy$
$36.$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq a^{2}$ e $y^{2}+z^{2}\leq a^{2}$, $a >0.$
$x^{2}+y^{2}\leq z\leq 1-x^{2}.$
$\dfrac{16a^{3}}{3}.$
$\dfrac{\pi}{2\sqrt{2}}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $D$ delimitada pelas parábolas $y = x^2$ e $x = y^2; \quad \rho(x,y) = \sqrt{x}$.
Massa: $\dfrac{3}{14};$ centro de massa: $\displaystyle \left(\frac{14}{27},\frac{28}{55} \right).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\arctan\left(\dfrac{y}{x}\right)\,dA$, onde $R$ é a região do primeiro quadrante limitada pelo círculo $x^{2}+y^{2}=25.$
$\displaystyle \frac{25 \pi^2}{16}.$
Use um software de apoio computacional para mostrar que o volume \(V\) sob a superfície \(z=xy^3\sin(xy)\) e acima do retângulo \([0,\pi]\times[0,1]\) no plano \(xy\) é dado por \(V=3/\pi\).
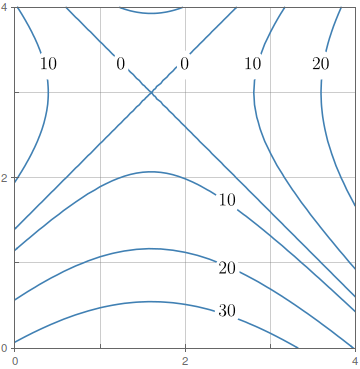
A figura mostra o mapa de contorno de $f$ no quadrado $R = [0,4] \times [0,4]$.
Use a Regra do Ponto Médio com $m = n = 2$ para estimar o valor de $\int\!\!\!\int \limits_{\!\!\!\!\!R} \! f(x,y) \, dA$.
Estime o valor médio de $f$.
Utilize a integral dupla para determinar a área da região: no interior do círculo $x^{2}+(y-1)^{2}=1$ e fora do círculo $x^{2}+y^{2}=1.$
$\displaystyle \frac{\pi}{3} + \frac{\sqrt{3}}{2}.$
Utilize coordenadas polares para determinar o volume do sólido dado:
dentro da esfera $x^2+y^2+z^2=16$ e fora do cilindro $x^{2}+y^{2}=4.$
$\displaystyle 32\sqrt{3}\pi.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Prove que $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d.$
Note que $$ \int_{c}^{d} \left[\int_{a}^{b}f(x)g(y)\,dx\right] \;dy = \int_{c}^{d} \left[\int_{a}^{b}f(x)\,dx\right]g(y) \;dy = \left(\int_{a}^{b}f(x)\,dx\right) \int_{c}^{d} g(y) \;dy.$$
Calcule a integral iterada.
$\displaystyle\int_{0}^{\pi/2} \int_{0}^{\pi/2}\sin{x}\cos{y} \, dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{1}(2x+y)^{8}\,dx dy$
$1.$
$\dfrac{4^{10} - 2^{11}}{180}.$
Use a integral dupla em coordenadas polares para deduzir a fórmula $$A=\int_{\alpha}^{\beta}\frac{1}{2} r^{2}\,d\theta$$ para a área da região em formato de leque entre a origem e a curva polar $r=f(\theta)$, $\alpha\leq \theta \leq \beta.$
Note que $\displaystyle A = \int_{\alpha}^{\beta}\int_{0}^{f(\theta)} r dr d\theta. $
Definimos a integral imprópria (sobre todo o plano $\mathbb{R}^{2}$) $$I=\displaystyle\iint\limits_{ \mathbb{R}^{2}}e^{-(x^{2}+y^{2})}\,dA=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}e^{-(x{^2}+y^{2})}\,dy dx= \lim_{a\rightarrow\infty}\displaystyle\iint\limits_{D_{a}}e^{-(x^{2}+y^{2})}\,dA,$$ onde $D_{a}$ é o disco com raio $a$ e centro na origem. Mostre que $$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}e^{-(x^{2}+y^{2})}\,dA=\pi.$$
Uma definição equivalente da integral imprópria da parte (a) é $$\iint\limits_{\mathbb{R}^{2}}e^{-(x^{2}+y^{2})}\,dA=\lim_{a\rightarrow\infty}\displaystyle\iint\limits_{S_{a}}e^{-(x^{2}+y^{2})}\,dA,$$ onde $S_{a}$ é o quadrado com vértices $(\pm a,\pm a)$. Use esse resultado para mostrar que $$\int_{-\infty}^{\infty}e^{-x^{2}}\,dx\,\int_{-\infty}^{\infty}e^{-y^{2}}\,dy=\pi.$$
Deduza que $$\int_{-\infty}^{\infty}e^{-x^{2}}\,dx=\sqrt{\pi}.$$
Fazendo a mudança de variável $t=\sqrt{2} x$, mostre que $$\int_{-\infty}^{\infty}e^{-x^{2}/2} dx=\sqrt{2\pi}.$$
(Este é um resultado fundamental em probabilidade e estatística.)
Note que $$\displaystyle\iint\limits_{D_{a}}e^{-(x^{2}+y^{2})}\,dA =\int_{0}^{2\pi}\int_{0}^{a} r e^{-r^2} dr d\theta = \pi (1 - e^{-a^2})$$ para cada $a.$
Note que $$\int\limits_{S_{a}}e^{-(x^{2}+y^{2})}\,dA = \int_{-a}^{a} \int_{-a}^{a} e^{-x^2} e^{-y^2} dxdy = \left(\int_{-a}^{a} e^{-x^2} dx\right) \left(\int_{-a}^{a} e^{-y^2} dy\right) $$ para cada $a.$
Troque $y$ por $x$ no item (b).
Note que fazendo a mudança de variável sugerida, $$\int_{-\infty}^{\infty}e^{-x^{2}/2} dx= \frac{1}{\sqrt{2}}\int_{-\infty}^{\infty}e^{-t^{2}/2} dt = \sqrt{\pi}.$$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina retangular que ocupa a região descrita pelas desigualdades \(0\leq x\leq a\) e \( 0\leq y\leq b\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ \begin{array}{lll} I_x= \dfrac{\delta ab^3}{3}, & I_y= \dfrac{\delta a^3b}{3}, & I_z= \dfrac{\delta ab(a^2+b^2)}{3}. \end{array} \]
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{3}\!\!\int_{0}^{2}(4-y^{2})\,dy dx$.
$16.$
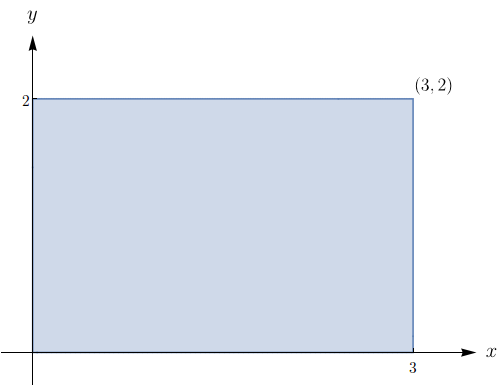
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, quando: $D$ é delimitada por $y = e^x$, $y = 0$, $x = 0$ e $x = 1; \quad \rho(x,y) = y$.
Massa: $\dfrac{1}{4}(e^{2} - 1);$ centro de massa: $\displaystyle \left(\frac{e^2 + 1}{2(e^2 - 1)},\frac{4(e^3 - 1)}{9 (e^2 - 1)} \right).$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{0}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{y}^{1}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^2}^{1}f(x,y)\,dy\bigg]dx$
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{3}\!\!\int_{-\sqrt{9-y^{2}}}^{\sqrt{9-y^{2}}}f(x,y)\,dx dy$.
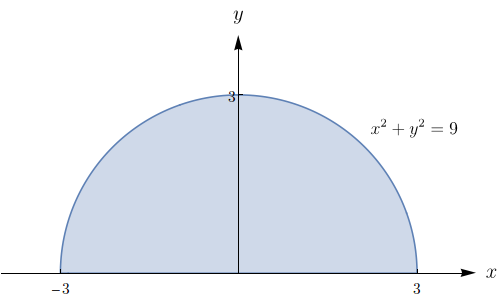
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
Massa: $4;$ centro de massa: $\displaystyle \left(\frac{6}{5},\frac{12}{5} \right).$
Seja \(R\) a região triangular de vértices \((0,0)\), \((3,3)\) e \((0,4)\) do plano \(xy\). Expressa como uma integral dupla, qual é área de \(R\)?
\(\displaystyle A(R)=\int_0^3\int_x^{-\frac{1}{3}x+4}\,dydx \)
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}y\,dA$, onde $R$ é a região no primeiro quadrante limitada pelo semi-círculo $x^{2}+y^{2}=2x.$
$\displaystyle \frac{2}{3}.$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^1\int_0^1 (2-x-y)\, dydx\)
\(\displaystyle \int_{-2}^2\int_{-2}^2(x^2+y^2)\,dxdy\)
Encontre a área da superfície descrita como sendo a parte do cilindro \(y^2+z^2=9\) que está acima do retângulo \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq x\leq 2,\ -3\leq y\leq 3\}\).
\( 6\,\pi\)
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r \, dr d\theta.$

As equações paramétricas \[\begin{array}{lll} x=u, & y=u\cos v, & z=u\sin v \end{array}\] representam o cone que resulta quando a reta \(y=x\) do plano \(xy\) é girada em torno do eixo \(x\). Determine a área de superfície da parte do cone para a qual \(0\leq u\leq 2\) e \(0\leq v\leq 2\pi\).
Sendo \(\displaystyle\{\mathbf{i},\mathbf{j},\mathbf{k}\}\) a base canônica do espaço, a superfície pode ser representada vetorialmente como \[ \mathbf{r}=u\mathbf{i}+u\cos v\mathbf{j}+u\sin v\mathbf{k} \ \ \left(0\leq u\leq 2,\ 0\leq v\leq 2\pi\right). \] Assim, teremos \begin{align*} \dfrac{\partial\mathbf{r}}{\partial u} & = \mathbf{i} + \cos v\mathbf{j} + \sin v\mathbf{k} \\ \dfrac{\partial\mathbf{r}}{\partial v} & = - u\sin v\mathbf{j} + u\cos v\mathbf{k} \\ \dfrac{\partial\mathbf{r}}{\partial u}\times\dfrac{\partial\mathbf{r}} {\partial v} & = \left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & \cos v & \sin v \\ 0 & -u\sin v & u\cos v \end{array} \right| = u\mathbf{i} -u\cos v\mathbf{j} - u\sin v\mathbf{k} \\ \|\dfrac{\partial\mathbf{r}}{\partial u}\times \dfrac{\partial\mathbf{r}}{\partial v}\| & = \sqrt{u^2+(-u\cos v)^2+(-u\sin v)^2} = |u|\sqrt{2} = u\sqrt{2}. \end{align*} Segue, portanto, que \[ S = \iint\limits_R\|\dfrac{\partial\mathbf{r}}{\partial u}\times \dfrac{\partial\mathbf{r}}{\partial v}\|\,dA = \int_0^{2\pi}\int_0^2\sqrt{2}u\,dudv = 2\sqrt{2}\int_0^{2\pi}\,dv = 4\pi\sqrt{2}. \]
Calcule o centro de massa da região $D$ dada.
$D$ é o conjunto de todos $(x,y)$ tais que $x^3 \leq y \leq x$ e a densidade é constante e igual a 1.
$D$ é o conjunto de todos $(x,y)$ tais que $x \leq y \leq x + 1$, $0 \leq x \leq 1$, e a densidade é o produto das coordenadas do ponto.
$D$ é o conjunto de todos $(x,y)$ tais que $1 \leq x^2 + y^2 \leq 4$, $y \geq 0$, e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(0,0\right).$
$\displaystyle \left(\frac{5}{7},\frac{9}{7}\right).$
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Inverta a ordem de integração, integrando primeiro em $y$ e depois em $x$ para calcular a integral:
$\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}^{1}\sqrt{x^{3}+1}\,dx dy$
$\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}\sin{x^{3}}\,dx dy$
$\dfrac{2(2\sqrt{2} - 1)}{9}.$
$\dfrac{2}{3} \sin^{2}\left(\dfrac{1}{2} \right).$
Suponha que a temperatura, em graus Celsius, num ponto \((x,y)\) de uma chapa metálica plana seja \( T(x,y)=10-8x^2-2y^2 \), onde \(x\) e \(y\) são medidos em metros. Calcule a temperatura média da porção retangular da chapa dada por \(0\leq x\leq 1\) e \(0\leq y\leq 2\).
\(\dfrac{14}{3}\) \({}^\circ\)C
Encontre a área da superfície descrita como sendo a parte do cone \(z^2=4x^2+4y^2\) que está acima da região do primeiro quadrante limitada pela reta \(y=x\) e a parábola \(y=x^2\).
\( \dfrac{\sqrt{5}}{6}\)
Utilize a integral dupla para determinar a área da região: limitada pelo eixo $x$ positivo e pela espiral $r=4\theta/3$, $0\leq \theta \leq 2\pi.$ A região se parece com uma concha de caracol.
$\dfrac{64\pi^3}{27}.$
Determine o volume do sólido descrito abaixo.
Limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $y=z$, $x=0$ e $z=0$, no primeiro octante.
Cuja base é a região no plano $xy$ que é limitada pela parábola $y=4-x^{2}$ e pela reta $y=3x$, enquanto o topo do sólido é limitado pelo plano $z=x+4.$
No primeiro octante limitado pelos planos coordenados, pelo cilindro $x^{2}+y^{2}=4$ e pelo plano $z+y=3.$
$\dfrac{1}{3}.$
$\dfrac{625}{12}.$
$\dfrac{9\pi - 8}{3}.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$\sqrt{x+y}$
$\dfrac{1}{x+y}$
$\dfrac{4(9\sqrt{3} - 8\sqrt{2} + 1)}{15}.$
$\ln\left( \dfrac{27}{16}\right).$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{ R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$1$
$x\cos(xy)$
$1.$
$\cos(1) - \cos(2).$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{a} \int_{0}^{\sqrt{a^{2}-x^{2}}}\sqrt{a^{2}-x^{2}-y^{2}}\,dy dx$, em que $a>0.$
$\displaystyle \frac{\pi a^3}{6}.$
Ao calcular, por integração dupla, o volume $V$ do sólido situado abaixo do parabolóide $z=x^{2}+y^{2}$ e limitado inferiormente por uma certa região $D$ no plano $xy$, chegou-se à seguinte expressão: $$V=\int_{0}^{1}\!\!\int_{0}^{y}(x^{2}+y^{2})\,dx dy+\int_{1}^{2}\int_{0}^{2-y}(x^{2}+y^{2})\,dx dy.$$
Esboce a região $D.$
Expresse $V$ numa única integral dupla iterada.
Efetue a integração para calcular $V.$
...
$\displaystyle \int_{0}^{1} \int_{x}^{2 - x} x^{2} + y^{2}\;dy\; dx$
$\dfrac{4}{3}.$
Considere a integral
$$\int_{0}^{2}\int_{\frac{y}{2}}^{1}ye^{x^{3}}\,dx dy.$$
Faça um esboço da região de integração.
Calcule a integral sendo explícito se vai precisar mudar a ordem de integração.
...
$\dfrac{2(e - 1)}{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{x^{2}}^{\sqrt{2-x^{2}}}\sqrt{x^{2}+y^{2}}\,dy dx$
$\displaystyle \frac{2}{45}(1 + \sqrt{2}) + \frac{\pi}{3\sqrt{2}}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\cos(x^{2}+y^{2})\,dA$, onde $R$ é a região acima do eixo do $x$ e dentro da circunferência $x^{2}+y^{2}=9.$
$\displaystyle \frac{\pi}{2} \sin(9).$
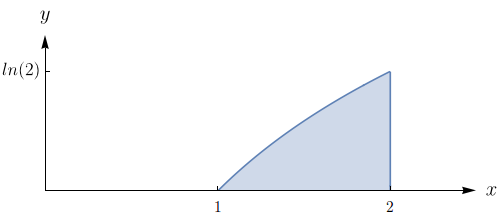
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{1}^{2}\!\!\int_{0}^{\ln(x)} \! f(x,y)\,dy dx$.
Note que a região de integração é do tipo I, é dada por
$$\{(x,y) \in \mathbb{R}^2: 1 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \ln(x)\}$$
e pode ser vista geometricamente como a região esboçada na figura abaixo.
Além disso, ela pode ser descrita como uma região do tipo II da seguinte forma:
$$\{(x,y) \in \mathbb{R}^2: e^y \leq x \leq 2 \mbox{ e } 0 \leq y \leq \ln{2}\}.$$
Portanto, a integral pode ser reescrita como
$\displaystyle\int_{0}^{\ln{2}}\!\!\int_{e^y}^{2} \! f(x,y)\,dx dy$.
Suponha que a área de uma região no plano de coordenadas polares seja $$A=\int_{\pi/4}^{3\pi/4} \int_{\mathrm{cosec\,}{\theta}}^{2\sin{\theta}}r\,dr d\theta.$$ Esboce a região e encontre sua área.
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$ye^{xy}$
$xy^{2}$
$\dfrac{(e - 1)^{2}}{2}.$
$\dfrac{1}{2}.$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo cone $z^2=x^2+y^2$ e pelo cilindro $x^2+y^2=2x.$
$\dfrac{8}{9}.$
Calcule a integral dupla, identificando-a antes com o volume de um sólido.
$\displaystyle\iint\limits_{R} 3 \, dA, \quad R = \{(x,y) \in \mathbb{R}^2: -2 \leq x \leq 2, \ 1 \leq y \leq 6\}.$
$\displaystyle\iint\limits_{R} (4 - 2y) \, dA, \quad R = [0,1] \times [0,1].$
$60.$
$3.$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=x\cos{y}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;x\geq 0,\;x^{2}\leq y\leq \pi\}.$
$f(x,y)=xy$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;x^{2}+y^{2}\leq 2,\;y\leq x\;e\;x\geq 0\}.$
$f(x,y)=x$ e $B$ o triângulo de vértices $(0,0)$, $(1,1)$ e $(2,0).$
$f(x,y)=xy\sqrt{x^{2}+y^{2}}$ e $B$ o retângulo $0\leq x\leq 1$, $0\leq y\leq 1.$
$f(x,y)=x+y$ e $B$ o paralelogramo de vértices $(0,0)$, $(1,1)$, $(3,1)$ e $(2,0).$
$-1.$
$-\dfrac{1}{4}$.
$1.$
$\dfrac{2(2\sqrt{2} - 1)}{15}.$
$4.$
Como não há antiderivada elementar da função \(e^{x^2}\), a integral \[ \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy \] não pode ser calculada integrando-se primeiro em relação a \(x\). Calcule essa integral expressando-a como uma integral iterada equivalente com ordem de integração invertida.
A região de integração é dada por \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq y\leq 2,\ y/2\leq x\leq 1\}\). Vamos inverter a ordem de integração sobre a região \(R\):\begin{align*} \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy & = \iint\limits_R e^{x^2}\,dA = \int_0^1\int_0^{2x} e^{x^2}\,dydx= \int_0^1\left[e^{x^2}y\right]_{y=0}^{2x}\,dx \\ & = \int_0^1 2xe^{x^2}\,dx = \left.e^{x^2}\right]_0^1 = e-1 \end{align*}
Utilize coordenadas polares para determinar o volume do sólido dado: uma esfera de raio $a.$
$\displaystyle \frac{4\pi}{3}a^3.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\int\!\!\!\!\int\limits_{\!\!\!\!\!\! R} xy^{2}\,dx dy$, onde $R$ é o retângulo $1\leq x\leq 2,\;2\leq y\leq 3.$
$\displaystyle\int\!\!\!\!\int\limits_{\!\!\!\!\!\! R} x\cos(2y)\,dx dy$, onde $R$ é o retângulo $0\leq x\leq 1,\;-\dfrac{\pi}{4}\leq y\leq \dfrac{\pi}{4}.$
$\dfrac{19}{2}.$
$\dfrac{1}{2}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}x\,dx dy$, onde $R$ é a região, no plano $xy$, limitada pela curva (dada em coordenadas polares) $\rho=\cos(3\theta)$, $-\dfrac{\pi}{6}\leq \theta \leq \dfrac{\pi}{6}.$
$\displaystyle \frac{81\sqrt{3}}{320}.$
Encontre a área da parte da superfície \(z=\sqrt{4-x^2}\) que fica acima do retângulo \(R\) do plano \(xy\) cujas coordenadas satisfazem \(0\leq x\leq 1\) e \(0\leq y\leq 4\).
A superfície é uma parte do cilindro \(x^2+z^2=4\) localizada no primeiro octante. Neste caso, como \(z=f(x,y)\), podemos tomar \(x=u\) e \(y=v\) como parâmetros. Assim, teremos que \(\displaystyle \mathbf{r}=u\mathbf{i}+v\mathbf{j}+f(u,v)\mathbf{k} \) e \[ \|\dfrac{\partial\mathbf{r}}{\partial u}\times \dfrac{\partial \mathbf{r}}{\partial v}\| = \sqrt{\left(\dfrac{\partial z}{\partial x}\right)^2+\left(\dfrac{\partial z}{\partial y}\right)^2+1}.\] Segue para a área que \begin{align*} S & = \iint\limits_R\sqrt{\left(\dfrac{\partial z}{\partial x}\right)^2+\left(\dfrac{\partial z}{\partial y}\right)^2+1}\,dA \\ & = \iint\limits_R\sqrt{\left(-\dfrac{x}{\sqrt{4-x^2}}\right)^2+ 0 + 1}\,dA = \int_0^4\int_0^1\dfrac{2}{\sqrt{4-x^2}}\,dxdy \\ & = 2\int_0^4\left[\arcsin\left(\dfrac{1}{2}x\right)\right]_{x=0}^1\,dy = 2\int_0^4\dfrac{\pi}{6}\,dy = \dfrac{4}{3}\pi. \end{align*}
Calcule a integral dupla.
$\displaystyle\iint\limits_{ D}x^{3}y^{2}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq 2,\;-x\leq y\leq x\}.$
$\displaystyle\iint\limits_{D}x\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq \pi,\;0\leq y\leq \sin{x}\}.$
$\displaystyle\iint\limits_{D}x^{3}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;1\leq x\leq e,\;0\leq y\leq \ln(x)\}.$
$\displaystyle\iint\limits_{D}y^{2}e^{xy}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq y\leq 4,\;0\leq x\leq y\}.$
$\displaystyle\iint\limits_{D}y^{3}\,dA, \quad D$ região com vértices $(0,2)$, $(1,1)$ e $(3,2).$
$\dfrac{256}{21}.$
$\pi.$
$\dfrac{3e^{4} + 1}{16}.$
$\dfrac{e^{16} - 17}{2}.$
$\dfrac{147}{20}.$
Utilize a integral dupla para determinar a área da região: dentro da cardióide $r=1+\cos{\theta}$ e fora do círculo $r=3\cos{\theta}.$
$\displaystyle \frac{\pi}{4}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\sqrt{x^{2}+y^{2}}\,dA$, onde $R$ é limitado pelo círculo $y=\sqrt{2x-x^{2}}$ e pela reta $y=x.$
$\displaystyle \frac{8}{9}(2 - \frac{5}{4}\sqrt{2}).$
Calcule o centro de massa do quadrado $D$ dado por $0 \leq x \leq 1, \ 0 \leq y \leq 1$ e com densidade $\quad \rho(x,y) = y$.
$\displaystyle \left(\frac{1}{2}, \frac{2}{3} \right).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+y^{2})^{3/2}\,dA$, onde $R$ é limitado pelo círculo $x^{2}+y^{2}=4.$
$\displaystyle \frac{64\pi}{5}.$
Se $f$ é uma função constante, $f(x,y) = k$, e $R = [a,b] \times [c,d],$ mostre que $\iint \limits_{R} k \, dA = k(b-a)(d-c).$
Note que se $R$ for dividida em $mn$ subretângulos, vale $$ \sum^{m}_{i = 1} \sum^{n}_{j = 1} f(x_{ij}^{*}, y_{ij}^{*}) \Delta A = k \sum^{m}_{i = 1} \sum^{n}_{j = 1} \Delta A = k (b - a) (d - c), $$ independentemente dos pontos amostrais $(x_{ij}^{*}, y_{ij}^{*})$ escolhidos.
Passe para coordenadas polares e calcule.
$\displaystyle\int_{0}^{1} \int_{1-\sqrt{1-x^{2}}}^{1+\sqrt{1-x^{2}}}xy\,dy dx$
$\displaystyle\int_{-a}^{a}\!\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}\,dy dx$
Temos que a região de integração é $$R=\{(x,y)\in\mathbb{R}^2|\, 0\leq x \leq 1\,\mbox{e}\, 1-\sqrt{1-x^{2}}\leq y \leq 1+\sqrt{1-x^{2}}\}.$$

Passando para coordenadas polares temos que: $$\left\{ \begin{array}{cc} x=r\,\cos\theta \\ y=r\,\sin\theta \\ dy\,dx=r\,dr\,d\theta \\ \end{array} \right.$$ Agora, \begin{eqnarray*} x^{2}+y^{2}=2y&\Rightarrow & r^{2}\,\cos^2 \theta+r^{2}\,\sin^{2}\theta=2r\,\sin\theta\\ &\Rightarrow & r^{2}=2r \,\sin\theta\\ &\Rightarrow & r(r-2\sin\theta )=0 \\ &\Rightarrow& r=0 \mbox{ou} r=2\sin\theta.\end{eqnarray*} Logo, $\displaystyle 0\leq r \leq 2\,\sin\theta$ e $\displaystyle 0\leq\theta \leq\dfrac{\pi}{2}.$ Então, $$\int_{0}^{1}\int_{1-\sqrt{1-x^2}}^{1+\sqrt{1-x^2}}xy\,dy\,dx =\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\,\sin\theta}(r\,\cos\theta)(r\,\sin\theta)r\,dr d\theta $$
$$ =\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\,\sin\theta}r^3\,\sin\theta\, \cos\theta\,dr d\theta =\int_{0}^{\dfrac{\pi}{2}}\bigg[\frac{r^{4}} {4}\sin\theta\,\cos\theta\bigg]\bigg|_{0}^{2\,\sin\theta}\,d\theta $$ $$ =\int_0^{\frac{\pi}{2}}\frac{(2\,\sin\theta)^4}{4}\,\sin\theta\,\cos\theta\,d\theta =4\int_{0}^\frac{\pi}{2}\sin^5\theta\,\cos\theta\, d\theta.$$ Tomando, $u=\sin\theta \Rightarrow du=\cos\theta\, d\theta$ e sendo $\theta =0 \Rightarrow u=0$ e $\theta=\frac{\pi}{2}\Rightarrow u=1.$ Assim, $$\int_{0}^{1}\int_{1-\sqrt{1-x^{2}}}^{1+\sqrt{1-x^{2}}}xy\,dy dx=4\int_{0}^{1}u^{5}\,du$$ $$=4\cdot \frac{u^{6}}{6}\bigg|_{0}^{1}=\frac{2}{3}.$$Temos que a região de integração é $$R=\{(x,y)\in \mathbb{R}|\, -a\leq x \leq a,\, -\sqrt{a^{2}-x^{2}}\leq y \leq \sqrt{a^{2}-x^{2}}\}.$$
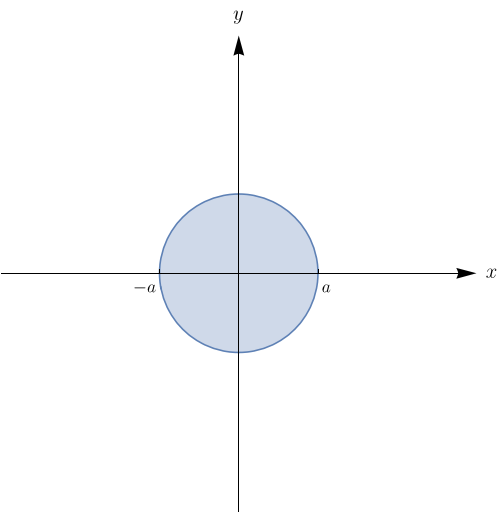
Passando para coordenadas polares temos que $$\left\{ \begin{array}{cc} x=r\,\cos\theta \\ y=r\,\sin\theta\\ dy\,dx=r\,dr\,d\theta\\ \end{array} \right. $$ Como $x^{2}+y^{2}=a^{2}\Rightarrow r^{2}\,\cos^{2}\theta+r^{2}\,\sin{2}\theta=a^{2}\Rightarrow r^{2}=a^{2}\Rightarrow r=\pm a.$ Como o raio deve ser sempre maior ou igual a zero, logo $$0\leq r\leq a \mbox{e} 0\leq \theta \leq 2\pi.$$ Então, $$\int_{-a}^{a}\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dy\,dx=\int_{0}^{2\pi}\int_{0}^{a}r\,dr\,d \theta=\int_{0}^{2\pi}d\theta \cdot \int_{0}^{a}r\,dr$$ $$=\theta\bigg |_{0}^{2\pi}\cdot \frac{r^{2}}{2}\bigg |_{0}^{a}=(2\pi)\cdot \bigg(\frac{a^{2}}{2}\bigg)=a^{2}\pi.$$
Considere a integral dada em coordenadas polares por $$\int_{0}^{\pi/4} \int_{0}^{2\cos{\theta}}r\,dr d\theta,$$ a qual representa a área de uma região $R$ do plano $xy.$
Escreva a região $R$ em coordenadas cartesianas.
Faça um esboço da região $R.$
Calcule a área da região $R.$
$R = \left\lbrace (x,y); (x - 1)^2 + y^2 \leq 1,\quad x \leq y,\quad x \geq 0,\quad y \geq 0 \right\rbrace.$
(...)
$\dfrac{\pi + 2}{4}.$
Uma carga elétrica é distribuída sobre um disco $x^2 + y^2 \leq 4$ de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = x + y + x^2 + y^2$ (medida em coulombs por metro quadrado). Determine a carga total do disco.
Como a carga elétrica é distribuída sobre o disco $x^2 + y^2 \leq 4$, em coordenadas polares temos que $0\leq r \leq 2$ e $0\leq \theta \leq 2\pi.$ Temos que $$Q=\iint\limits_{D}\sigma(x,y)\,dA=\iint\limits_{D}(x+y+x^{2}+y^{2})\,dA$$ $$=\int_{0}^{2\pi}\int_{0}^{2}(r\,\cos \theta+r\,\sin \theta+r^{2})r\,dr\, d \theta=\int_{0}^{2\pi}\int_{0}^{2}(r^{2}\,\cos \theta+r^{2}\,\sin \theta+r^{3})\,dr\, d \theta$$ $$=\int_{0}^{2\pi}\bigg(\frac{r^{3}}{3}\cos \theta+\frac{r^{3}}{3}\sin \theta +\frac{r^{4}}{4}\bigg)\bigg|_{0}^{2}\,d\theta= \int_{0}^{2\pi}\bigg(\frac{8}{3}\cos \theta+\frac{8}{3}\sin \theta+4\bigg)\,d\theta$$ $$=\bigg(\frac{8}{3}\sin\theta-\frac{8}{3}\cos\theta+4\theta\bigg)\bigg|_{0}^{2\pi}=\bigg(-\frac{8}{3}+8\pi\bigg)-\bigg(-\frac{8}{3}\bigg)$$ $$=-\frac{8}{3}+8\pi+\frac{8}{3}=8\pi.$$
Esboce a região de integração para a integral iterada $\displaystyle\int_{\pi}^{2\pi}\!\!\int_{\sin{y}}^{\ln(y)}f(x,y)\,dx dy$.
A função densidade conjunta para um par de variáveis aleatórias $X$ e $Y$ é $$f(x,y) = \begin{cases} Cx(1 + y), & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 2,\\ 0, & \quad \text{caso contrário}.
\end{cases}$$
Determine a constante $C$.
Determine $P(X \leq 1, \ Y \leq 1)$.
Determine $P(X + Y \leq 1)$.
$\dfrac{1}{2}.$
$\dfrac{3}{8}.$
$\dfrac{5}{48}$.
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{ R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$x+2y$
$x-y$
$\dfrac{5}{2}.$
$1.$
Calcule a área limitada pelas curvas $x=y^{2}-1$ e $x=2y^{2}-2.$
$\dfrac{4}{3}.$
Utilize simetria para calcular $\iint\limits_{D}(2-3x+4y)\,dA$, onde $D$ é a região limitada pelo quadrado com vértices $(\pm 5,0)$ e $(0,\pm 5).$
$100.$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{\sqrt{x-x^{2}}}^{\sqrt{2x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{3a}\bigg[\int_{\frac{\sqrt{3}}{3}x}^{\sqrt{4ax-x^{2}}}f(x,y)\,dy\bigg]dx, \; a> 0.$
$\displaystyle\int_{0}^{\pi}\bigg[\int_{0}^{\sin{x}}f(x,y)\,dy\bigg]dx$
$\ \\ \begin{array}{ll} \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{y^{2}}{2}}^{\frac{1}{2} - \sqrt{\frac{1}{4} - y^{2}}}f(x,y)\,dx\bigg]dy &+ \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{1}{2}+ \sqrt{\frac{1}{4} - y^{2}}}^{1}f(x,y)\,dx\bigg]dy\\ &+ \displaystyle\int_{\frac{1}{2}}^{\sqrt{2}}\bigg[\int_{\frac{y^{2}}{2}}^{1}f(x,y)\,dx\bigg]dy \end{array} $
$\displaystyle\int_{0}^{\sqrt{3}a} \bigg[\int_{2a + \sqrt{4a^2 - y^{2}}}^{\sqrt{3} y}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{\arcsin(y)}^{\pi-\arcsin(y)}f(x,y)\,dx\bigg]dy$
No cálculo de uma integral dupla sobre uma região $D$, obtivemos uma soma de integrais iteradas como a que segue:
$$\int\!\!\!\!\int\limits_{\!\!\!\!\!\! D} \! f(x,y)\,dA=\int_{0}^{1}\!\!\int_{0}^{2y} \! f(x,y)\,dx dy+\int_{1}^{3}\!\!\int_{0}^{3-y} \! f(x,y)\,dx dy.$$
Esboce a região $D$ e expresse a integral dupla como uma integral iterada com ordem de integração contrária.
$\displaystyle \int_{0}^{2}\!\!\int_{\frac{x}{2}}^{3-x} \! f(x,y)\,dx dy.$
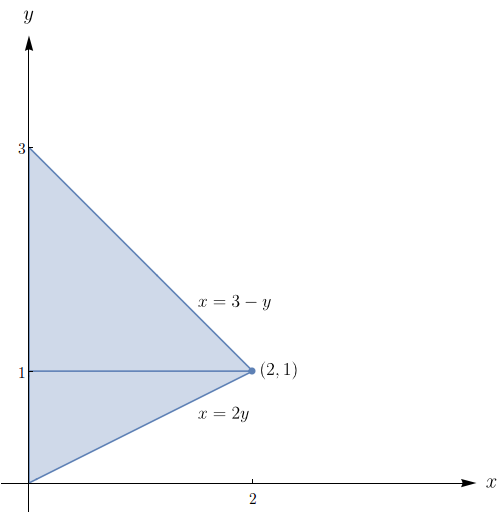
Calcule $\displaystyle\iint\limits_{B} y\,dx dy$, onde $B$ é o conjunto dado.
$B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(1,1)$.
$B=\{(x,y)\in \mathbb{R}^{2}|\;-1\leq x\leq 1,\;0\leq y\leq x+2\}.$
$B$ é o conjunto de todos $(x,y)$ tais que $x^{2}+4y^{2}\leq 1.$
$B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(2,1).$
$\dfrac{1}{6}$.
$\dfrac{13}{3}$.
$0$.
$\dfrac{1}{6}$.
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
\[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
\[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
Use uma integral dupla para calcular a área da região \(R\) entre a parábola \(y=\dfrac{1}{2}x^2\) e a reta \(y = 2x\).
Denotando por \(A(R)\) a área de \(R\), teremos que \begin{align*} A(R) & = \iint_R\,dA = \int_0^4\int_{x^2/2}^{2x}\,dydx = \int_0^4\left[y\right]_{y=x^2/2}^{2x}\,dx \\ & = \int_0^4\left(2x-\dfrac{1}{2}x^2\right)\,dx = \left[x^2-\dfrac{x^3}{6}\right]_0^4= \dfrac{16}{3}. \end{align*} De outra forma, fixando primeiro a variável \(y\), teríamos \begin{align*} A(R) & = \iint_R\,dA = \int_0^8\int_{y/2}^{\sqrt{2y}}\,dxdy = \int_0^8\left[x\right]_{x=y/2}^{\sqrt{2y}}\,dy \\ & = \int_0^8\left(2y-\dfrac{1}{2}y\right)\,dy = \left[\dfrac{2\sqrt{2}}{3}y^{3/2}-\dfrac{y^2}{4}\right]_0^8= \dfrac{16}{3}. \end{align*}
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{0}^{\sqrt{x-x^{2}}}x\,dy dx$
$\displaystyle \frac{\pi}{16}.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{\pi}^{2\pi}\!\!\int_{0}^{\pi}(\sin{x}+\cos{y})\,dx dy$.
$2\pi.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{3}\!\!\int_{-2}^{0}(x^{2}y-2xy)\,dy dx$.
$0.$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina circular que ocupa a região descrita pelas desigualdades \(0\leq x^2+y^2\leq a^2\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ I_x= I_y=\dfrac{\delta\pi a^4}{4}, \quad I_z= \dfrac{\delta\pi a^4}{2}.\]
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo paraboloide $z=9-x^2-y^2$ e pelo plano $z=5.$
$8\pi.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\frac{x^{2}}{x^{2}+y^{2}}\,dA$, onde $R$ é a região anular limitada por $x^{2}+y^{2}=a^{2}$ e $x^{2}+y^{2}=b^{2}$, $0< a< b.$
$\displaystyle \frac{\pi}{2}(b^2 - a^2).$
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
1. \[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
2. \[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
Calcule as integrais iteradas.
$\displaystyle\int_{0}^{\pi/2}\int_{0}^{\cos{\theta}}e^{\sin{\theta}}\,dr d\theta$
$\displaystyle\int_{0}^{1}\int_{0}^{v}\sqrt{1-v^{2}}\,du dv$
$e - 1.$
$\dfrac{1}{3}.$
Determine o volume do sólido limitado pelos planos coordenados e pelo plano $3x+2y+z=6.$
O sólido cujo volume deve ser calculado é $$E = \{(x,y,z) \in \mathbb{R}^3; (x,y) \in R \mbox{ e } 0 \leq z \leq 6 - 3x - 2y\},$$ em que $R$ é a projeção de $E$ no plano $xy$. Assim, o volume é dado por $$V = \displaystyle\int\!\!\!\!\int\limits_{R}(6-3x-2y)\,dA.$$ A região $R$ é tanto do tipo I como do tipo II, então é possível escrevê-la de pelo menos duas formas. Escrevendo como uma região do tipo I, obtemos: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \frac{6-3x}{2}\right\}.$$ Portanto, \begin{eqnarray*} V & = & \displaystyle\int_{0}^{2}\!\int_{0}^{\frac{6-3x}{2}}(6-3x-2y)\,dy dx \\ & = & \displaystyle\int_{0}^{2} \left.\left(6y-3xy-y^2 \right|_{y=0}^{y=\frac{6-3x}{2}} \right) \,dx \\ & = & \displaystyle\int_{0}^{2} \left(9-9x+\frac{9x^2}{4}\right) \,dx \\ & = & \left.9x-\frac{9x^2}{2}+\frac{9x^3}{12} \right|_{x=0}^{x=2} = 6. \end{eqnarray*} Observe que podemos escrever $R$ como uma região do tipo II, obtendo: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq \frac{6-2y}{3} \text{ e } 0 \leq y \leq 3\right\}.$$ Então, uma outra expressão para $V$ é $$V = \displaystyle\int_{0}^{3}\!\int_{0}^{\frac{6-2y}{3}}(6-3x-2y)\,dx dy = 6.$$
Passe para coordenadas polares e calcule.
$\displaystyle\int_{0}^{a} \int_{0}^{x}\sqrt{x^{2}+y^{2}}\,dy dx$, em que $a>0$.
$\displaystyle\iint\limits_{ D}x\,dA$, onde $D$ é a região do primeiro quadrante compreendida entre os círculos x^2+y^2=4$ e $x^2+y^2=2x.$
Temos que a região de integração é: $$ R=\{(x,y)\in \mathbb{R}^{2}|\,0\leq x \leq a,\, 0\leq y \leq x\}.$$
Passando para coordenadas polares temos que $$\left\{ \begin{array}{cc} x=r\,\cos \theta\\ y=r\,\sin \theta\\ dy\,dx=r\,dr\,d\theta\\ \end{array} \right. $$ Como $0\leq x \leq a$, temos que $0\leq r\leq \dfrac{a}{\cos \theta}$ e também $0\leq \theta \leq \dfrac{\pi}{4}.$ Então, $$\int_{0}^{a}\int_{0}^{x}\sqrt{x^{2}+y^{2}}\,dy\,dx= \int_{0}^{\frac{\pi}{4}}\int_{0}^{\frac{a}{\cos \theta}}\sqrt{r^{2}\,\cos^{2}\theta +r^{2}\,\sin^{2}\theta}\,r\,dr\,d\theta$$ $$=\int_{0}^{\frac{\pi} {4}}\int_{0}^\frac{a}{\cos\theta}r^{2}\,dr\,d\theta=\int_{0}^\frac{\pi}{4}\frac{r^3}{3}\bigg|_{0}^{\frac{a}{\cos \theta}}d\theta $$ $$=\frac{a^{3}}{3}\int_{0}^{\frac{\pi}{4}}\frac{1}{\cos^{3}\theta}d\theta=\frac{a^{3}}{3}\int_{0}^{\frac{\pi}{4}}\sec^{3}\theta d\theta$$ $$=\frac{a^{3}}{3}\bigg(\frac{1}{2}\sec \theta \tan \theta+\frac{1}{2}\ln|\sec \theta+\tan \theta|\bigg)\bigg|_{0}^{\frac{\pi}{4}}$$ $$=\frac{a^{3}}{6}\bigg[\bigg(\sec\frac{\pi}{4}\cdot \tan\frac{\pi}{4}+\ln\bigg|\sec\frac{\pi}{4}+\tan\frac{\pi}{4}\bigg|\bigg)- \bigg(\sec 0\cdot \tan 0+\ln|\sec 0+\tan 0|\bigg)\bigg]$$ $$=\frac{a^{3}}{6}\bigg(\sqrt{2}+\ln(\sqrt{2}+1)\bigg)$$A região de integração $R$ é descrita na figura seguinte
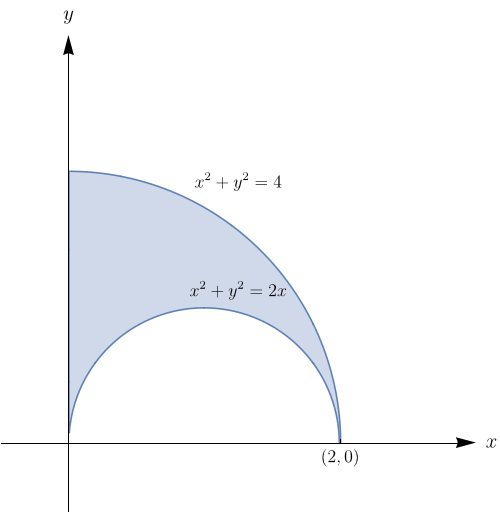
Notemos que $x^{2}+y^{2}=2x\Leftrightarrow (x-1)^{2}+y^{2}=1.$ Assim, $$\iint\limits_{ R}x\,dA=\underbrace{\iint\limits_{ \substack{x^{2}+y^{2}\leq 4\\ x\geq 0\\ y\geq 0}}x\,dA}_{(1)} -\,\,\underbrace{\iint\limits_{\substack{(x-1)^{2}+y^{2}\leq 1 \\ y\geq 0}}x\,dA}_{(2)}$$ Para a integral $(1)$ temos em coordenadas polares que $$r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=4\Rightarrow r^{2}=4\Rightarrow r=\pm 2.$$ Logo, $0\leq r\leq 2$ e $0\leq \theta \leq \dfrac{\pi}{2}.$ Para a integral $(2)$ temos em coordenadas polares que $$(r-\cos \theta-1)^{2}+r^{2}\sin^{2}\theta=1\Rightarrow r^{2}\cos^{2}\theta-2r\cos \theta+1+r^{2}\sin^{2}\theta=1$$ $$\Rightarrow r^{2}-2r\cos\theta=0\Rightarrow r(r-2\cos \theta)=0\Rightarrow r=0 \mbox{ou} r=2\cos \theta.$$ Logo, $0\leq r\leq 2\cos \theta$ e $0\leq \theta \leq \dfrac{\pi}{2}.$ Assim, $$\iint\limits_{ R}x\,dA=\int_{0}^{\frac{\pi}{2}}\int_{0}^{2}r\,\cos \theta \cdot r \,dr\,d\theta- \int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos \theta}r\cos \theta\cdot r\, dr\,d \theta$$ $$=\int_{0}^{\frac{\pi}{2}}\int_{0}^{2}r^{2}\,\cos \theta\,dr\,d\theta-\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos \theta}r^{2}\,\cos \theta\,dr\,d\theta$$ $$=\int_{0}^{\frac{\pi}{2}}\cos\,d\theta \cdot \int_{0}^{2}r^{2}\,dr-\int_{0}^{\frac{\pi}{2}}\frac{r^{3}}{3}\cos \theta \bigg|_{0}^{2\cos \theta}\,d\theta$$ $$=\bigg(\sin\theta \bigg|_{0}^{\frac{\pi}{2}}\bigg)\cdot \bigg(\frac{r^{3}}{3}\bigg|_{0}^{2}\bigg)-\frac{8}{3}\int_{0}^{\frac{\pi}{2}}\cos^{4}\theta\,d\theta$$ $$=\bigg(\sin \frac{\pi}{2}-\sin 0\bigg)\cdot \bigg(\frac{8}{3}-0\bigg)-\frac{8}{3}\bigg(\frac{1}{4}\cos^{3}\theta\,\sin \theta+\frac{3}{8}\theta+\frac{3}{16}\sin 2 \theta\bigg)\bigg|_{0}^{\frac{\pi}{2}}$$ $$=\frac{8}{3}-\frac{8}{3}\bigg[\bigg(\frac{1}{4}\cos^{3}\frac{\pi}{2}\sin \frac{\pi}{2}+\frac{3}{8}\cdot\frac{\pi}{2}+\frac{3}{16}\sin2\cdot \frac{\pi}{2}\bigg) -\bigg(\frac{1}{4}\cos^{3}0\sin 0+\frac{3}{8}\cdot 0+\frac{3}{16}\sin 0\bigg)\bigg]$$ $$=\frac{8}{3}-\frac{8}{3}\cdot \bigg(\frac{3\pi}{16}\bigg)=\frac{8}{3}-\frac{\pi}{2}=\frac{16-3\pi}{6}.$$
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{1} \int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}\ln(x^{2}+y^{2}+1)\,dx dy$
$\displaystyle \pi (\ln(4) - 1).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\sqrt{x^{2}+y^{2}}\,dA$, onde $R$ é limitado pelo triângulo de vértices $(0,0)$, $(3,0)$ e $(3,3).$
$\displaystyle \frac{9}{2} (\sqrt{2} + \ln(\sqrt{2} + 1)).$
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento $a$, se a densidade em qualquer ponto for proporcional ao quadrado da distância do vértice oposto à hipotenusa.
$\displaystyle \left(\frac{2a}{5}, \frac{2a}{5} \right).$
Use coordenadas polares para calcular a integral dupla
\[ \iint_R e^{-(x^2+y^2)}\,dA, \]
onde \(R\) é a região contida no círculo \(x^2+y^2=1\).
\(\displaystyle (1-e^{-1})\pi \)
Utilize coordenadas polares para combinar a soma $$\int_{\frac{1}{\sqrt{2}}}^{1} \int_{\sqrt{1-x^{2}}}^{x}xy\,dy dx+\int_{1}^{\sqrt{2}} \int_{0}^{x}xy\,dy dx+\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx$$ em uma única integral dupla. Em seguida, calcule essa integral dupla.
Queremos combinar a soma, abaixo, de integrais em uma única: $$\underbrace{\int_\frac{1}{\sqrt{2}}^{1} \int_\sqrt{1-x^{2}}^{x}xy\,dy dx}_{1}+\underbrace{\int_{1}^{\sqrt{2}}\int_{0}^{x}xy\,dy dx}_{2}+ \underbrace{\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx}_{3}$$ Na figura abaixo, temos que a região da esquerda corresponde à região de integração da integral $(1)$, a região do meio corresponde à região de integração da integral $(2)$ e a região da esquerda corresponde à região de integração da integral $(3)$.
Notemos que com a junção das três regiões, podemos olhar como uma única região. Assim, em coordenadas polares teremos que $0\leq \theta \leq \frac{\pi}{4}$ e $1\leq r \leq 2.$ Então: $$\int_{\frac{1}{\sqrt{2}}}^{1} \int_{\sqrt{1-x^{2}}}^{x}xy\,dy dx+\int_{1}^{\sqrt{2}} \int_{0}^{x}xy\,dy dx+\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx$$ $$=\int_{0}^{\frac{\pi}{4}}\int_{1}^{2}(r\,\cos \theta)\cdot (r\,\sin \theta)\,r\,dr\,d\theta=\int_{0}^{\frac{\pi}{4}}\int_{1}^{2}r^{3}\cos\theta \sin \theta\,dr\,d\theta$$ $$=\underbrace{\int_{0}^{\frac{\pi}{4}}\cos \theta\, \sin \theta\,d \theta}_{\substack{ u=\sin \theta\\ du=\cos\, d\theta}}\cdot \int_{1}^{2}r^{3}\,dr =\int_{0}^{\frac{\sqrt{2}}{2}}u\,du\cdot \frac{r^{4}}{4}\bigg|_{1}^{2}$$ $$=\frac{u^{2}}{2}\bigg|_{0}^{\frac{\sqrt{2}}{2}}\cdot \bigg(\frac{16}{4}-\frac{1}{4}\bigg)=\frac{1}{4}\cdot \frac{15}{4}=\frac{15}{16}.$$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=y^{3}e^{xy^{2}}$ e $B$ o retângulo $0\leq x\leq 1$, $1\leq y\leq 2.$
$f(x,y)=x^{5}\cos{y^{3}}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;y\geq x^{2},\;x^{2}+y^{2}\leq 2\}.$
$f(x,y)= x^{2}$ e $B$ o conjunto de todos $(x,y)$ tais que $x\leq y\leq -x^{2}+2x+2.$
$f(x,y)=x$ e $B$ a região compreendida entre os gráficos de $y=\cos{x}$ e $y=1-\cos{x}$, com $0\leq x\leq \dfrac{\pi}{2}.$
$\dfrac{e^{4} - e - 3}{2}.$
$0.$
$\dfrac{63}{20}.$
$\left(\dfrac{5}{72} -\dfrac{ \sqrt{3}}{18}\right)\pi^{2} + \left( \dfrac{4\sqrt{3}}{3} - 1 \right) \pi.$
Determine o volume do sólido.
Abaixo do paraboloide $z=x^{2}+y^{2}$ e acima da região delimitada por $y=x^{2}$ e $x=y^{2}.$
Abaixo do paraboloide $z=3x^{2}+y^{2}$ e acima da região delimitada por $y=x$ e $x=y^{2}-y.$
$ $ Abaixo da superfície $z=xy$ e acima do triângulo com vértices $(1,1)$, $(4,1)$ e $(1,2).$
Limitado pelo cilindro $y^{2}+z^{2}=4$ e pelos planos $x=2y$, $x=0$ e $z=0$, no primeiro octante.
$\dfrac{6}{35}.$
$\dfrac{144}{35}.$
$\dfrac{31}{8}.$
$\dfrac{16}{3}.$
Calcule a integral dupla.
$\displaystyle\iint\limits_{R} x\sin(x+y)\,dA, \quad R=[0,\pi/6]\times [0,\pi/3].$
$\displaystyle\iint\limits_{R} xye^{x^{2}y}\,dA, \quad R=[0,1]\times [0,2].$
$\dfrac{\pi}{12}.$
$\dfrac{(e^{2} - 3)}{2}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{0}^{\sqrt{1-y^{2}}}(x^{2}+y^{2})\,dx dy$
$\displaystyle \frac{\pi}{8}.$
Calcule o centro de massa da região: $D$ o triângulo de vértices $(0,0), (0,1)$ e $(1,1)$ e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(\frac{3}{4}, \frac{2\sqrt{2} - 1}{2\sqrt{2} + 2\ln(1 + \sqrt{2})} \right).$
Uma carga elétrica é distribuída sobre o retângulo $1 \leq x \leq 3$, $0 \leq y \leq 2$, de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = 2xy + y^2$ (medida em coulombs por metro quadrado). Determine a carga total no retângulo.
$\displaystyle \frac{64}{3}$ Coulombs.
Mostre que
\[ \int_0^{+\infty}\int_0^{+\infty}\dfrac{1}{(1+x^2+y^2)^2}\,dxdy= \dfrac{\pi}{4}.\]
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{a} \int_{0}^{\sqrt{a^{2}-x^{2}}}\,dy dx$
$\dfrac{\pi a^2}{4}.$
Ao calcular por integração dupla o volume $V$ do sólido situado abaixo do gráfico de $f(x,y)=e^{x^{2}+y^{2}}$ e limitado inferiormente por uma certa região $D$ no plano $xy$, chegou-se à seguinte expressão: $$V=\int_{0}^{2} \int_{0}^{\sqrt{4-x^{2}}}e^{x^{2}+y^{2}}\,dy dx-\int_{0}^{1} \int_{0}^{\sqrt{1-x^{2}}}e^{x^{2}+y^{2}}\,dy dx.$$
Esboce a região $D.$
Expresse $V$ numa única integral dupla em coordenadas polares.
Efetue a integração para calcular $V.$
$D = \left\lbrace (x,y); 1 \leq x^{2} + y^{2} \leq 2, x \geq 0, y \geq 0 \right\rbrace.$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \int_{1}^{2} re^{r^2} dr d\theta.$
$\dfrac{\pi}{4}(e^4 - 1).$
Utilize a integral dupla para determinar a área da região: cortada do primeiro quadrante pela curva $r=2(2-\sin(2\theta))^{1/2}.$
$2(\pi - 1).$
Uma lâmina ocupa parte do disco $x^2 + y^2 \leq 1$ no primeiro quadrante. Determine o centro de massa se a densidade em qualquer ponto for proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(\frac{3}{8}, \frac{3\pi}{16} \right).$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\arctan\left(\dfrac{y}{x}\right)\,dA$, onde $R=\{(x,y) \in \mathbb{R}^2| 1\leq x^{2}+y^{2}\leq 4, 0\leq y\leq x\}.$
$\displaystyle \frac{3\pi^2}{64}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}e^{x^{2}+y^{2}}\,dx dy$, onde $R$ é o conjunto de todos os $(x,y)$ tais que $1\leq x^{2}+y^{2}\leq 4$, $-x\leq y\leq x$ e $x\geq 0.$
$\displaystyle \frac{\pi}{4}(e^4 - e).$
Calcule $\int_{0}^{1}\!\int_{x}^{1}3y^{4}\cos(xy^{2})\,dy dx$. Esboce a região de integração.
$1 - \cos(1).$
Mude a ordem de integração para mostrar que:
$$ \int_0^a \left[ \int_0^y e^{m(a-x)} f(x) \, dx \right] dy = \int_0^a (a-x) e^{m(a-x)} f(x) \, dx,$$
onde $a$ e $m$ são constantes e $a>0$.
Calcule o volume do conjunto dado.
$x^{2}+4y^{2}\leq 4$ e $x+y\leq z\leq x+y+1.$
$x\geq 0$, $x\leq y\leq 1$ e $0\leq z\leq e^{y^{2}}.$
$2\pi.$
$\dfrac{e - 1}{2}.$
Calcule a integral iterada.
$\displaystyle\int_{1}^{4} \int_{1}^{2}\bigg(\dfrac{x}{y}+\dfrac{y}{x}\bigg)\,dy dx$
$\displaystyle\int_{0}^{1} \int_{0}^{3}e^{x+3y}\,dx dy$
$\dfrac{21}{2} \ln(2).$
$\dfrac{(e^{3} - 1)^{2}}{3}.$
Seja $S$ uma superfície plana paralela ao plano $xy$. Mostre que a fórmula para o cálculo de áreas de superfícies nesse caso reduz à fórmula de integrais duplas para o cálculo de área de regiões planas.
A parte da superfície \[ z= \dfrac{h}{a}\sqrt{x^2+y^2}\quad\left(a,\ h>0\right) \] entre o plano \(xy\) e o plano \(z=h\) é um cone circular reto de altura \(h\) e raio \(a\). Use uma integral dupla para mostrar que a área da superfície lateral desse cone é dada por \(\displaystyle S=\pi a\sqrt{a^2+h^2}\).
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $\displaystyle D = \{(x,y) \in\mathbb{R}^2: 0 \leq y \leq \sin{(\pi x/L)}, \ 0 \leq x \leq L\}; \quad \rho(x,y) = y$.
Massa: $\dfrac{L}{4};$ centro de massa: $\displaystyle \left(\frac{L}{2},\frac{16}{9\pi} \right).$
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1}\!\!\int_{0}^{1-x}(1-x-y)\,dy dx.$$