Exercícios
Máximos e mínimos
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=xy+2x-\ln(x^{2}y)$.
Ponto de mínimo: $\displaystyle \left(\frac{1}{2},2\right).$
Determine os pontos do cone $z^{2}=x^{2}+y^{2}$ que estão mais próximos do ponto $(4,2,0).$
$(2,1,\sqrt{5})$ e $(2,1,-\sqrt{5}).$
Mostre que $(0,0)$ é um ponto crítico de $f(x,y)=x^{2}+kxy+y^{2}$, não importando o valor da constante $k$.
Note que $f_{x} (0,0) = f_{y} (0,0) = 0.$
Encontre todos os extremos relativos de \(x^2y^2\) sujeitos à restrição \(4x^2+y^2=8\). Faça-o de duas maneiras: primeiro, usando restrições para eliminar uma variável e, em seguida, utilizando multiplicadores de Lagrange como variáveis auxiliares.
Ocorre máximo absoluto de \(4\) em \((\pm 1,\pm 2)\); mínimo absoluto de valor \(0\) em \((\pm\sqrt{2},0)\) e \((0,\pm 2\sqrt{2})\).
Seja
$$f(x,y)=k(x-y)^{2}+\frac{y^{4}}{2}-\frac{y^{2}}{2},\;\;k\neq 0.$$
Encontre os pontos críticos da função $f$.
Classifique os pontos críticos da função $f$ no caso em que $k>0$.
$(0,0), (1,1)$ e $(-1,-1).$
Pontos de mínimo: $(1,1)$ e $(-1,-1);$ ponto de sela: $(0,0).$
Determine os pontos da superfície $y^{2}=9+xz$ que estão mais próximos da origem.
$(0,3,0)$ e $(0,-3,0).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{5}+y^{5}-5x-5y$.
Ponto de mínimo: $\displaystyle \left( 1,1\right);$ ponto de máximo: $\displaystyle \left( -1,-1\right);$ pontos de sela: $\displaystyle \left(1,-1\right)$ e $\displaystyle \left(-1,1\right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{4}+y^{4}+4x+4y$.
Ponto de mínimo : $(-1,-1).$
Três alelos (versões alternativas de um gene) $A$, $B$ e $O$ determinam os quatro tipos de sangue: $A$ ($AA$ ou $AO$), $B$ ($BB$ ou $BO$), $O$ ($OO$) e $AB$. A Lei de Hardy-Weinberg afirma que a proporção de indivíduos em uma população que carregam dois alelos diferentes é $P=2pq+2pr+2rq$, onde $p$, $q$ e $r$ são as proporções de $A$, $B$ e $O$ na população. Use o fato de que $p+q+r=1$ para mostrar que $P$ é no máximo $\dfrac{2}{3}$.
É preciso maximizar de $P = 2q - 2q^{2} + 2r - 2r^{2} -2rq$ no conjunto delimitado pelas retas $q = 0,$ $r = 0$ e $q + r = 1.$ O ponto de máximo ocorre em $\displaystyle \left( \frac{1}{3}, \frac{1}{3} \right),$ no qual o valor de $P$ é justamente $\dfrac{2}{3}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}+3xy+4y^{2}-6x+2y$.
Ponto de mínimo: $\displaystyle \left( \frac{54}{7}, -\frac{22}{7} \right).$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{2}+y^{2}+x^{2}y+4$, $D=\{(x,y) \in \mathbb{R}^2: |x|\leq 1, \; |y|\leq 1\}.$
Valor máximo: $7;$ valor mínimo: $4.$
Determine o valor máximo de $f(x,y,z) = 6x + z$ sobre a curva de interseção das superfícies $x^2 + y^2 = 4$ e $z = x^2 - 2y^2$.
$16.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}-12xy+8y^{3}$.
Ponto de mínimo : $\displaystyle \left( 2,1\right);$ ponto de sela: $\displaystyle \left(0,0\right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}-12xy+8y^{3}$.
Sendo $f(x,y)=x^{3}-12xy+8y^{3}$, vamos inicialmente localizar seus pontos críticos:
$$f_{x}(x,y)=3x^{2}-12y \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; f_{y}(x,y)=-12x+24y^{2}.$$
Igualando essas derivadas parciais a zero, obtemos as equações
$$x^{2}-4y=0 \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; 2y^{2}-x=0.$$
Para resolvê-las, substituímos $x=2y^{2}$ da segunda equação na primeira. Isso resulta em
$$0=y^{4}-y=y(y^{3}-1)$$
e existem duas raízes reais $y=0$ e $y=1.$ Os dois pontos críticos de $f$ são $(0,0)$ e $(2,1).$\\
Agora vamos calcular as segundas derivadas parciais e $D(x,y)$:
$$f_{xx}(x,y)=6x\,\,\,\, f_{xy}(x,y)=-12 \;\;\;\; f_{yy}(x,y)=48y$$
$$\begin{split}D(x,y)&=f_{xx}(x,y)\cdot f_{yy}(x,y)-(f_{xy}(x,y))^{2}\\&=(6x)\cdot (48y)-(-12)^{2}=288xy-144.\end{split}$$
Como $D(0,0)=-144<0$, segue do Teste da Derivada Segunda que $(0,0)$ é um ponto de sela, ou seja, $f$ não tem nem máximo local nem mínimo local em $(0,0).$ Como $D(2,1)=432>0$ e $f_{xx}(2,1)=12>0$, vemos do Teste da Derivada Segunda que $f(2,1)=-8$ é um mínimo local.
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=xy$ em $D=\{(x,y) \in \mathbb{R}^2: x\geq 0,\;y\geq 0\;\text{e}\;2x+y\leq 5\}.$
Valor máximo: $\displaystyle \frac{25}{8};$ valor mínimo: $\displaystyle 0.$
Determine $(x,y)$, com $x^{2}+4y^{2}\leq 1$, que maximiza a soma $2x+y.$
$\displaystyle \left( \frac{4\sqrt{17}}{17}, \frac{\sqrt{17}}{34} \right).$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y) = 4x + 6y; \quad x^2 + y^2 = 13.$
Valor máximo: $26;$ valor mínimo: $-26.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x_1,x_2, \ldots, x_n) = x_1 + x_2 + \cdots + x_n; \quad x_1^2 + x_2^2 + \cdots + x_n^2 = 1.$
Valor máximo: $\sqrt{n};$ valor mínimo: $-\sqrt{n}.$
Determine três números positivos cuja soma é $100$ e cujo produto é máximo.
$\displaystyle x = y = z = \frac{100}{3}.$
Considere a função $f(x,y)=x^{2}+y^{2}+2xy-x-y+1$ no quadrado $0\leq x\leq 1$ e $0\leq y\leq 1$.
Mostre que $f$ tem um mínimo absoluto ao longo do segmento de reta $2x+2y=1$ nesse quadrado. Qual é o valor mínimo absoluto?
Encontre o valor máximo absoluto de $f$ no quadrado.
$\displaystyle \frac{3}{4}.$
$f(1,1) = 3.$
Determine as dimensões de uma caixa retangular de volume máximo tal que a soma dos comprimentos de suas 12 arestas seja uma constante $c$.
A caixa é um cubo com arestas de comprimento $\dfrac{c}{12}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}-3x^{2}+27y$.
Pontos de sela: $\displaystyle \left(3,\frac{3}{2}\right)$ e $\displaystyle \left(-3,-\frac{3}{2}\right).$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = 3x + y$ e $x^2 + 2y^2 \leq 1.$
Ponto de máximo: $\displaystyle \left( \frac{6}{\sqrt{38}}, \frac{1}{\sqrt{38}} \right)$; ponto de mínimo: $\displaystyle \left( -\frac{6}{\sqrt{38}}, -\frac{1}{\sqrt{38}} \right)$.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=\frac{1}{x^{2}}+\frac{1}{y}+xy$, $x>0$ e $y>0$.
Ponto de mínimo: $\displaystyle \left( 2^{2/5}, 2^{-1/5} \right).$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = 3x + y$ e $x^2 + 2y^2 = 1.$
Ponto de máximo: $\displaystyle \left( \frac{6}{\sqrt{38}}, \frac{1}{\sqrt{38}} \right)$; ponto de mínimo: $\displaystyle \left( -\frac{6}{\sqrt{38}}, -\frac{1}{\sqrt{38}} \right)$.
Determine a menor distância entre o ponto $(2,1,-1)$ e o plano $x+y-z=1$.
$\sqrt{3}.$
\]
Suponha que um cientista tenha razões para acreditar que duas quantidades $x$ e $y$ estejam relacionadas linearmente, ou seja, $y=mx+b$, pelo menos aproximadamente, para algum valor de $m$ e de $b$. O cientista realiza uma experiência e coleta os dados na forma de pontos $(x_{1},y_{1}), (x_{2},y_{2}), \ldots, (x_{n},y_{n})$, e então coloca-os em um gráfico. Os pontos não estão todos alinhados, de modo que o cientista quer determinar as constantes $m$ e $b$ para que a reta $y=mx+b$ ``ajuste" os pontos tanto quanto possível (veja a figura). Seja $d_{i}=y_{i}-(mx_{i}+b)$ o desvio vertical do ponto $(x_{i},y_{i})$ da reta. O {\bf método dos mínimos quadrados} determina $m$ e $b$ de modo a minimizar $\sum_{i=1}^{n}d_{i}^{2}$, a soma dos quadrados dos desvios. Mostre que, de acordo com esse método, a reta de melhor ajuste é obtida quando
$$m\sum_{i=1}^{n}x_{i}+bn=\sum_{i=1}^{n}y_{i}$$
$$m\sum_{i=1}^{n}x_{i}^{2}+b\sum_{i=1}^{n}x_{i}=\sum_{i=1}^{n}x_{i}y_{i}$$
Assim, a reta é determinada resolvendo esse sistema linear de duas equações nas incógnitas $m$ e $b.$
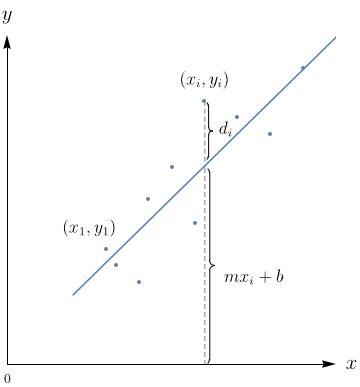
As duas equações são obtidas como pontos críticos da função $\displaystyle \sum^{n}_{i = 1} d_{i}^{2} = \sum^{n}_{i = 1} \left(y_{i} - (mx_{i} + b) \right)^{2} = f(m,b).$ Note que de fato pontos satisfazendo as equações são pontos de mínimo de $f.$
Determine os pontos da superfície $xyz = 1$ que estão mais próximos da origem.
$(1,1,1),$ $(1,-1,-1),$ $(-1,1,-1)$ e $(-1,-1,1).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=e^{x}\cos{y}$.
Não há pontos críticos.
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 + 2xy + y^2$ e $x + 2y - 1 = 0.$
Ponto de mínimo: $\displaystyle \left(-1,1 \right)$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y,z) = 2x + 6y + 10z; \quad x^2 + y^2 + z^2 = 35.$
Valor máximo: $70;$ valor mínimo: $-70.$
Determine os pontos do gráfico de $xy^{3}z^{2}=16$ mais próximos da origem.
$\displaystyle \left( \frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, \frac{2 \sqrt{2}}{\sqrt[4]{12}}\right),$ $\displaystyle \left( \frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, - \frac{2 \sqrt{2}}{\sqrt[4]{12}}\right),$ $\displaystyle \left( -\frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, \frac{2 \sqrt{2}}{\sqrt[4]{12}} \right)$ e $\displaystyle \left( -\frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, - \frac{2 \sqrt{2}}{\sqrt[4]{12}} \right).$
Determine os pontos da elipse $\mathcal{D} = \left\{ (x,y) \in \mathbb{R}^2: \frac{x^2}{8} + \frac{y^2}{2} = 1 \right\}$ que fornecem o maior e o menor valor da função $f(x,y) = xy$.
Pontos de máximo: $(2,1)$ e $(-2,-1);$ pontos de mínimo: $(-2,1)$ e $(2,-1).$
Determine os valores extremos de $f(x,y) = 2x^2 + 3y^2 - 4x - 5$ na região descrita por $x^2 + y^2 \leq 16$.
Valor máximo: $f(-2, \pm 2 \sqrt{3}) = 47$ e valor mínimo $f(1,0) = -7.$
Utilize as curvas de nível da figura para predizer a localização dos pontos críticos de $f(x,y)=3x-x^{3}-2y^{2}+y^{4}$ e se $f$ tem um ponto de sela ou um máximo ou mínimo local em cada um desses pontos. Explique seu raciocínio. Em seguida, empregue o Teste da Segunda Derivada para confirmar suas predições.
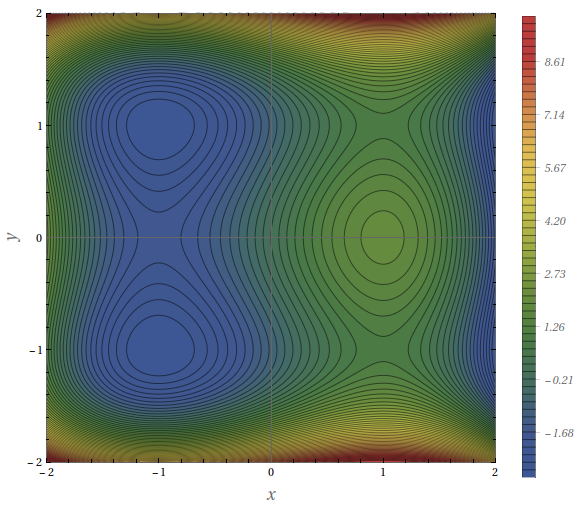
$f$ possui um ponto de máximo local em $(1,0),$ pontos de sela em $(1,1),$ $(1,-1)$ e $(-1,0)$ e pontos de mínimo local em $(-1,1)$ e $(-1,-1).$
Sejam \(\alpha\), \(\beta\) e \(\gamma\) os ângulos de um triângulo.
Use multiplicadores de Lagrange para determinar o valor máximo de \(f(\alpha,\beta,\gamma)=\cos\alpha\cos\beta\cos\gamma\) e determine os ângulos para os quais o máximo ocorre.
Expresse \(f(\alpha,\beta,\gamma)\) como uma função apenas de \(\alpha\) e \(\beta\) e use um software de apoio computacional para fazer o gráfico dessa função de duas variáveis. Confirme que o resultado obtido no item anterior é consistente com o gráfico.
\(\alpha = \beta=\gamma=\pi/3\) e valor máximo \(=1/8\).
Determine o valor máximo de $f(x,y)=x+5y$, onde $x$ e $y$ estão sujeitos às restrições: $5x+6y\leq 30$, $3x+2y\leq 12$, $x\geq 0$ e $y\geq 0.$
$25.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{2}-2xy+2y^{2}$ em $D=\{(x,y)\in \mathbb{R}^2: \;|x|+|y|\leq 1\}.$
Valor máximo: $\displaystyle 2;$ valor mínimo: $0.$
Use multiplicadores de Lagrange para demonstrar que o triângulo com área máxima, e que tem um perímetro constante $p$, é equilátero.
(Sugestão: Utilize a fórmula de Heron para a área:
$$A = \sqrt{s(s-x)(s-y)(s-z)},$$
em que $s = p/2$ e $x,y$ e $z$ são os comprimentos dos lados.)
Utilizando a fórmula de Heron temos que a área e um triânulo é
$$A=\sqrt{s(s-x)(s-y)(s-z)},$$
com $s=p/2$ e $x,\,y,\,z$ lados do triângulo.
Mas a álgebra fica mais simples se maximizarmos o quadrado da área, isto é,
$$A^{2}=f(x,y,z)=s(s-x)(s-y)(s-z).$$
A restrição é que o triângulo têm perímetro constante $p$, ou seja,
$$g(x,y,z)=x+y+z=p.$$
De acordo com o método dos multiplicadores de Lagrange, resolvemos $\nabla f=\lambda \nabla g$ e $g=p.$ Então
$$\nabla f(x,y,z)=(\,-s(s-y)(s-z),\, -s(s-x)(s-z),\,-s(s-x)(s-y)\,)$$
e
$$\lambda \nabla g(x,y,z)=\lambda (1,1,1)=(\lambda, \lambda, \lambda).$$
Logo temos as seguintes equações
\begin{array}{rcl}-s(s-y)(s-z)&=&\lambda\\-s(s-x)(s-z)&=&\lambda\\-s(s-x)(s-y)&=&\lambda\\x+y+z&=&p\end{array}
Assim, das três primeiras equações, temos que
$$-s(s-y)(s-z)=-s(s-x)(s-z)=-s(s-x)(s-y).$$
Da primeira igualdade obtemos que $s-y=s-x\Rightarrow y=x$ e da segunda igualdade obtemos que $s-z=s-y\Rightarrow z=y$, resultando que $x=y=z.$
Portanto, o triângulo com área máxima e perímetro constante $p$ é um triângulo equilátero.
Suponha que $(0,2)$ seja um ponto crítico de uma função $g$ com derivadas de segunda ordem contínuas. Em cada caso, o que se pode dizer sobre $g$?
$g_{xx}(0,2)=-1, \quad g_{xy}(0,2)=6, \quad g_{yy}(0,2)=1.$
$g_{xx}(0,2)=-1, \quad g_{xy}(0,2)=2, \quad g_{yy}(0,2)=-8.$
$g_{xx}(0,2)=4, \quad g_{xy}(0,2)=6, \quad g_{yy}(0,2)=9.$
$g$ possui um ponto de sela em $(0,2).$
$g$ possui um ponto de máximo local em $(0,2).$
Não se pode afirmar algo sobre $g$ pelo Teste da Segunda Derivada.
Para fazer essa análise sobre $g$ iremos utilizar o Teste da Segunda Derivada.
Temos que- \[ D=g_{xx}(0,2)g_{yy}(0,2)-g_{xy} ^2(0,2)=-1\cdot 1-6^2=-1-36=-37<0. \] Logo, pelo Teste da Segunda Derivada, segue que $(0,2)$ é um ponto de sela de $g$.
- Temos que \[ D=g_{xx}(0,2)g_{yy}(0,2)-g_{xy} ^2(0,2)=(-1)\cdot (-8)-2^2=8-4=4>0. \] Como $D>0$ e $g_{xx}(0,2)<0$, pelo Teste da Segunda Derivada, segue que $(0,2)$ é um ponto de máximo de $g$.
- Temos que \[ D=g_{xx}(0,2)g_{yy}(0,2)-g_{xy} ^2(0,2)=4\cdot 9-6^2=36-36=0. \] Como $D=0$ o Teste da Segunda Derivada não nos fornece nenhuma informação sobre $g$.
O plano $4x - 3y + 8z = 5$ intercepta o cone $z^2 = x^2 + y^2$ em uma elipse.
Faça os gráficos do cone, do plano e da elipse.
Use os multiplicadores de Lagrange para achar os pontos mais alto e mais baixo da elipse.
Gráficos.
Ponto mais alto: $\displaystyle \left( -\frac{4}{3}, 1,\frac{5}{3} \right)$ e ponto mais baixo: $\displaystyle \left( \frac{4}{13}, -\frac{3}{13},\frac{5}{13} \right).$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y) = x^2 + y^2; \quad xy = 1.$
Não há valor máximo; valor mínimo: $2.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}+y^{2}+x^{2}y+4$.
Pontos de mínimo: $(1,1)$ e $(-1,-1);$ ponto de sela: $(0,0).$
Considere a função
$$f(x,y)=-\frac{y^{2}}{2}+3x^{2}-2x^{3}.$$
Determine e classifique os pontos críticos de $f.$
Mostre que a curva de nível $f(x,y)=0$ com $x\geq 0$ é uma curva fechada, isto é, é a fronteira de uma região $R$ limitada do plano $xy.$ Calcule o valor máximo de $f$ nessa região $R$.
Pontos críticos: $(0,0)$ e $(1,0).$ Ponto de máximo: $(1,0);$ ponto de sela: $(0,0).$
$\max \{ f(s); s\in R \} =1$.
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 + 2y^2$ e $3x + y = 1.$
Ponto de mínimo: $\displaystyle \left( \frac{6}{19}, \frac{1}{19} \right)$.
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 + 4y^2$ e $xy = 1$, $x > 0$ e $y>0.$
Ponto de mínimo: $\displaystyle \left( \sqrt{2}, \frac{\sqrt{2}}{2} \right)$.
O plano $x + y + 2z = 2$ intercepta o paraboloide $z = x^2 + y^2$ em uma elipse. Determine os pontos dessa elipse que estão mais próximo e mais longe da origem.
Mais próximo: $\displaystyle \left( \frac{1}{2}, \frac{1}{2},\frac{1}{2} \right)$ e mais distante: $\displaystyle \left( -1,-1,2 \right).$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y,z) = yz + xy; \quad xy = 1, \quad y^2 + z^2 = 1.$
Valor máximo: $\dfrac{3}{2};$ valor mínimo: $\dfrac{1}{2}.$
Entre todos os pontos do gráfico de $z=10-x^{2}-y^{2}$ que estão acima do plano $x+2y+3z=0$, encontre o ponto mais afastado do plano.
$\displaystyle \left( \frac{1}{6}, \frac{1}{3}, \frac{355}{36} \right).$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^3 + y^3 - 3x - 3y$ e $x + 2y = 3.$
Ponto de máximo local: $\displaystyle \left(- \frac{13}{7}, \frac{17}{7} \right)$; ponto de mínimo local: $\displaystyle \left( 1,1 \right)$.
Determine o ponto da parábola $y = x^2$ mais próximo de $(14,1)$.
$(2,4).$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 - 2y^2$ e $x^2 + y^2 - 2x = 0.$
Ponto de máximo: $\displaystyle \left( 2,0 \right)$; pontos de mínimo: $\displaystyle \left( \frac{2}{3}, \frac{2\sqrt{2}}{3} \right)$ e $\displaystyle \left( \frac{2}{3}, \frac{-2\sqrt{2}}{3} \right)$.
A produção total $P$ de certo produto depende da quantidade $L$ de trabalho empregado e da quantidade $K$ de capital investido. Nas Seções 14.1 e 14.3 do livro do Stewart, foi discutido o modelo Cobb-Douglas $P = bL^\alpha K^{1-\alpha}$ seguido de certas hipóteses econômicas, em que $b$ e $\alpha$ são constantes positivas e $\alpha < 1$. Se o custo por unidade de trabalho for $m$ e o custo por unidade de capital for $n$, e uma companhia puder gastar somente uma quantidade $p$ de dinheiro como despesa total, então a maximização da produção $P$ estará sujeita à restrição $mL + nK = p$. Mostre que a produção máxima ocorre quando
$$L = \dfrac{\alpha p}{m} \quad \text{e} \quad K = \dfrac{(1 - \alpha)p}{n}.$$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y) = x^2y; \quad x^2 + 2y^2 = 6.$
Valor máximo: $4;$ valor mínimo: $-4.$
Determine o ponto da reta $x + 2y = 1$ cujo produto das coordenadas seja máximo.
$\displaystyle \left( \frac{1}{2}, \frac{1}{4} \right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=\sqrt[3]{x^{2}+2xy+4y^{2}-6x-12y}$.
Ponto de mínimo: $\displaystyle \left( 2,1\right).$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=y^{2}-x^{2}$ em $D=\{(x,y)\in \mathbb{R}^2: x^{2}+y^{2}\leq 4\}.$
Valor máximo: $\displaystyle 4;$ valor mínimo: $-4.$
Determine a menor distância entre os planos paralelos $2x+3y-z=2$ e $2x+3y-z=4.$
$\displaystyle \frac{\sqrt{14}}{7}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=e^{4y-x^{2}-y^{2}}$.
Ponto de máximo: $\displaystyle \left(0,2 \right).$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=3+xy-x-2y$, $D$ é a região triangular fechada com vértices $(1,0)$, $(5,0)$ e $(1,4).$
Valor máximo: $2;$ valor mínimo: $-2.$
Mostre que o valor máximo de $a^2b^2c^2$ sobre uma esfera de raio $r$ centrada na origem de um sistema de coordenadas cartesianas $(a,b,c)$ é $(r^2/3)^3$.
Usando o item anterior, mostre que, para números não negativos $a$, $b$ e $c$,
$$(abc)^{\frac{1}{3}} \leq \frac{a + b + c}{3},$$
isto é, a média geométrica de três números não negativos é menor que ou igual à média aritmética.
Use multiplicadores de Lagrange para maximizar $f(a,b,c) = a^{2}b^{2}c^{2}$ sujeita a restrição $a^{2} + b^{2} + c^{2} = r^{2}.$
Como $(\sqrt{a},\sqrt{b},\sqrt{c})$ está na esfera $a + b + c = r^{2},$ pelo item 1 segue que $abc = f(\sqrt{a},\sqrt{b},\sqrt{c}) \leq \left(\dfrac{r^{2}}{3}\right)^{3} = \left(\dfrac{a + b + c}{3}\right)^{3}.$
Use o método dos multiplicadores de Lagrange para determinar o ponto sobre a parábola $y = x^2$ que se encontra mais próximo do ponto $(0,1) \in \mathbb{R}^2.$
$\displaystyle \left(\frac{1}{\sqrt{2}}, \frac{1}{2} \right)$ e $\displaystyle \left(-\frac{1}{\sqrt{2}}, \frac{1}{2} \right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=9-2x+4y-x^{2}-4y^{2}$.
Ponto de máximo: $\displaystyle \left( -1, \frac{1}{2} \right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}+2xy+y^{2}-5x$.
Ponto de mínimo: $\displaystyle \left( \frac{5}{3}, -\frac{5}{3} \right);$ ponto de sela: $\displaystyle \left(-1,1\right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}-4xy+4y^{2}-x+3y+1$.
Não há pontos críticos.
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{3}-3x-y^{3}+12y$, $D$ é o quadrilátero cujos vértices são $(-2,3)$, $(2,3)$, $(2,2)$ e $(-2,-2).$
Valor máximo: $18;$ valor mínimo: $-18.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 - 2xy + y^2$ e $x^2 + y^2 = 1.$
Pontos de máximo: $\displaystyle \left( \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \right)$ e $\displaystyle \left( -\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)$; ponto de mínimo: $\displaystyle \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=-x^{2}+y^{2}+2xy+4x-2y$.
Ponto de sela: $\displaystyle \left(\frac{3}{2},-\frac{1}{2}\right).$
Determine os valores máximo e mínimo absolutos de
$$f(x,y) = x^2 + 2y^2 - x$$
no conjunto $D = \{(x,y) \in \mathbb{R}^2: x^2 + y^2 \leq 1 \}$.
Valor máximo: $\dfrac{9}{4};$ valor mínimo: $-\dfrac{1}{4}.$
Encontre os pontos da elipse $x^2 + xy + y^2 = 3$ mais próximos e mais distantes da origem.
A distância entre um ponto $(x,y)$ e a origem $(0,0)$ é
$$d=\sqrt{(x-0)^{2}+(y-0)^{2}}=\sqrt{x^{2}+y^{2}}.$$
Mas a álgebra fica mais simples se maximizarmos e minimizarmos o quadrado da distância:
$$d^{2}=f(x,y)=x^{2}+y^{2}.$$
A restrição é que os pontos pertencem a elipse, ou seja,
$$g(x,y)=x^{2}+xy+y^{2}=3$$
De acordo com os multiplicadores de Lagrange, resolvemos $\nabla f=\lambda \nabla g$ e $g=3.$ Então
$$\nabla f(x,y)=(2x,2y)$$
e
$$\lambda \nabla g(x,y)=\lambda(2x+y,x+2y)=(2x\lambda+y\lambda,2y\lambda+x \lambda).$$
Logo temos,
\begin{array}{rcl}2x=2x\lambda+y\lambda\\2y=2y\lambda+x\lambda\\x^{2}+xy+y^{2}=3\\end{array}
Se $\lambda=0$ teremos que $x=0$ e $y=0$, mas esses valores não satisfazem equação $(3)$. Logo $\lambda \neq 0$ e multiplicando
ambos os lados da equação $(1)$ por $\dfrac{y}{\lambda}$ e ambos os lados da equação $(2)$ por $\dfrac{x}{\lambda}$, obtemos que
$$\frac{2xy}{y}=2xy+y^{2}\;\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\;\; \frac{2xy}{y}=2xy+x^{2}.$$
Logo,
$$y^{2}=x^{2}\Rightarrow y=x\;\;\;\; \mbox{ou}\;\;\;\; y=-x.$$
Se $y=x$ temos que da equação $(3)$ que $x^{2}+x^{2}+x^{2}=3\Rightarrow x^{2}=1\Rightarrow x=\pm 1.$
Logo temos os pontos $(1,1)$ e $(-1, -1).$
Se $y=-x$ temos que da equação $(3)$ que $x^{2}-x^{2}+x^{2}=3\Rightarrow x^{2}=3\Rightarrow x=\pm \sqrt{3}.$
Logo temos os pontos $(\sqrt{3},-\sqrt{3})$ e $(-\sqrt{3},\sqrt{3}).$
Os valores de $f$ nesses pontos são:
$$f(1,1)=f(-1,-1)=2\;\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\;\; f(\sqrt{3},-\sqrt{3})=f(-\sqrt{3},\sqrt{3})=6.$$
Portanto, $(1,1)$ e $(-1, -1)$ são os pontos mais próximos e $(\sqrt{3},-\sqrt{3})$ e $(-\sqrt{3},\sqrt{3})$ os pontos mais afastados da origem $(0,0).$
Encontre o ponto da curva $x^2 - 2xy + y^2 - 2x - 2y + 1 = 0$ mais próximo da origem.
$\displaystyle \left( \frac{1}{4}, \frac{1}{4} \right).$
Determine os valores de máximo e mínimo de $f(x,y,z) = x^2 - yz$ em pontos da esfera $x^2 + y^2 + z^2 = 1$.
Valor máximo: $1;$ valor mínimo: $\displaystyle -\frac{1}{2}.$
Utilize as curvas de nível da figura para predizer a localização dos pontos críticos de $f(x,y)=4+x^{3}+y^{3}-3xy$ e se $f$ tem um ponto de sela ou um máximo ou mínimo local em cada um desses pontos. Explique seu raciocínio. Em seguida, empregue o Teste da Segunda Derivada para confirmar suas predições.
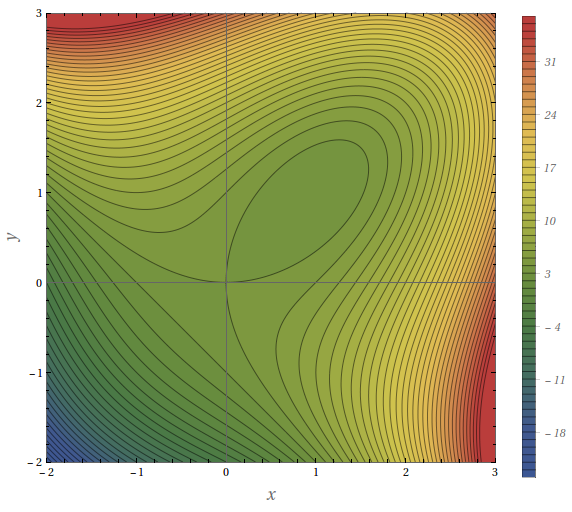
$f$ possui um ponto de sela em $(0,0)$ e um mínimo local em $(1,1).$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{2}+3xy-3x$ em $D=\{(x,y)\in \mathbb{R}^2: x\geq 0,\;y\geq 0\; \text{e} \;x+y\leq 1\}.$
Valor máximo: $\displaystyle 0;$ valor mínimo: $-2.$
Uma caixa de papelão sem tampa deve ter um volume de $32000\;cm^{3}$. Determine as dimensões que minimizem a quantidade de papelão utilizado.
$40$cm $\times$ $40$cm $\times$ $20$cm.
Embora $\nabla f = \lambda \nabla g$ seja uma condição necessária para a ocorrência de um valor extremo de $f(x,y)$ sujeito à restrição $g(x,y) = 0$, ela não garante por si só que ele exista. Como um exemplo, tente usar o método dos multiplicadores de Lagrange para encontrar um valor máximo de $f(x,y) = x + y$ sujeito à restrição $xy = 16$. O método identificará os dois pontos $(4,4)$ e $(-4,-4)$ como candidatos para a localização dos valores extremos. Ainda assim, a soma $x + y$ não tem valor máximo sobre a hipérbole. Quanto mais distante você está da origem nessa hipérbole no primeiro quadrante, maior se torna a soma $f(x,y) = x + y$.
Note que quando $x \to 0,$ tem-se $y \to \infty$ e $f(x,y) \to \infty;$ e quando $x \to -\infty,$ tem-se $y \to 0$ e $f(x,y) \to -\infty,$ logo não há valores máximo e mínimo de $f$ sujeito a esta restrição.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{4}+xy+y^{2}-6x-5y$.
Ponto de mínimo: $\displaystyle \left( 1,2\right).$
Encontre o volume máximo de uma caixa retangular que está inscrita em uma esfera de raio $r.$
$\displaystyle \frac{8}{3\sqrt{3}} r^{3}.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=(2x-x^{2})(2y-y^{2})$, $D$ é a região do plano $xy$ dada por $0\leq y\leq 2(2x-x^{2})$.
Valor máximo: $1;$ valor mínimo: $0.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=4+x^{3}+y^{3}-3xy$.
Ponto de mínimo: $(1,1);$ ponto de sela: $(0,0).$
Determine a curva de nível de $f(x,y) = x^2 + 16y^2$ que seja tangente à curva $xy = 1$, $x>0$ e $y>0$. Qual o ponto de tangência?
$x^{2} + 16 y^{2} = 8;$ o ponto de tangência é $\displaystyle \left( 2, \frac{1}{2} \right).$
Determine o volume máximo da maior caixa retangular no primeiro octante com três faces nos planos coordenados e com um vértice no plano $x+2y+3z=6.$
Vamos maximizar a função:
$$f(x,y)=x\cdot y\cdot \bigg(\dfrac{6-x-2y}{3}\bigg)=\dfrac{6xy-x^{2}y-2xy^{2}}{3},$$
então o volume máximo é $V=x \cdot y \cdot z.$
Para encontrar os pontos críticos devemos encontrar as derivadas parciais $f_{x}$ e $f_{y}.$ Assim,
$$f_{x}(x,y)=\frac{6y-2xy-2y^{2}}{3}\;\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\;\; f_{y}(x,y)=\frac{6x-x^{2}-4xy}{3}.$$
Fazendo $f_{x}=0$ e $f_{y}=0$, obtemos o seguinte sistema de equações
$$\left \{\begin{array}{cc}6y-2xy-2y^{2}=0\\6x-x^{2}-4xy=0\\\end{array}\right.$$
Da primeira equação obtemos
$$y=0 \;\;\;\;\;\;\;\; \mbox{ou}\;\;\;\;\;\;\;\; y=3-x.$$
Como, $y=0$ não satifaz as condicões, vamos analisar o caso onde $y=3-x.$ Substituindo esse valor na segunda equação obtemos
$$x=0\;\;\;\;\;\;\;\; \mbox{ou}\;\;\;\;\;\;\;\; 3x^{2}-6x=0.$$
Novamente, como $x=0$ não satisfaz as condições, vamos analisar o caso onde $3x^{2}-6=0$. Logo, obtemos
$$x=0\;\;\;\;\;\;\;\; \mbox{ou} \;\;\;\;\;\;\;\; x=2.$$
Novamente, $x=0$ não nos interessa. Assim, sendo $x=2$ obtemos que $y=1$ e $z=\dfrac{2}{3}.$ Portanto, o volume máximo da maior caixa, nas condições do exercício, será
$$V=(2)\cdot(1)\cdot \frac{2}{3}=\frac{4}{3}.$$
Determine as dimensões da caixa retangular de volume máximo, com faces paralelas aos planos coordenados, que possa ser inscrita no elipsóide $16x^{2}+4y^{2}+9z^{2}=144.$
$\displaystyle \frac{8}{\sqrt{3}} \times \frac{6}{\sqrt{3}} \times \frac{12}{\sqrt{3}}.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y,z) = x^4 + y^4 + z^4; \quad x^2 + y^2 + z^2 = 1.$
Valor máximo: $1;$ valor mínimo: $\dfrac{1}{3}.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=3x-y$ no conjunto $D$ de todas $(x,y)$ tais que $x\geq 0$, $y\geq 0$, $y-x\leq 3$, $x+y\leq 4$ e $3x+y\leq 6.$
Valor máximo: $6;$ valor mínimo: $-3.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=2x^{3}+y^{4}$, $D=\{(x,y) \in \mathbb{R}^2: x^{2}+y^{2}\leq 1\}.$
Valor máximo: $2;$ valor mínimo: $-2.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{4}+y^{4}-2x^{2}-2y^{2}$.
Pontos de mínimo: $(-1,1)$ e $(-1,-1);$ ponto de máximo: $(0,0);$ pontos de sela: $(0,1), (0,-1), (1,0)$ e $(-1,0).$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=3x-y$ em $D=\{(x,y)\in \mathbb{R}^2: x^{2}+y^{2}\leq 1\}.$
Valor máximo: $\displaystyle \frac{8\sqrt{10}}{10};$ valor mínimo: $-\sqrt{10}.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=xy^{2}$, $D=\{(x,y) \in \mathbb{R}^2: x\geq 0,\;y\geq 0,\;x^{2}+y^{2}\leq3\}.$
Valor máximo: $2;$ valor mínimo: $0.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}+2xy+y^{2}-5$.
Ponto de mínimo : $\displaystyle \left( \frac{5}{3}, -\frac{5}{3}\right);$ ponto de sela: $\displaystyle \left(-1,1\right).$
Determine o ponto do elipsóide $x^2 + 4y^2 + z^2 = 1$ que maximiza a soma $x + 2y + z$.
$\displaystyle \left( \frac{1}{\sqrt{3}}, \frac{1}{2\sqrt{3}}, \frac{1}{\sqrt{3}} \right).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=y\cos{x}$.
Sendo $f(x,y)=y\,\cos x$, vamos inicialmente localizar seus pontos críticos:
$$f_{x}(x,y)=-y\,\sin x \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; f_{y}(x,y)=\cos x.$$
Igualando essas derivadas parciais a zero, obtemos as equações
$$y\,\sin x=0 \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; \cos x=0.$$
Da segunda equação obtemos que $x=\bigg(\dfrac{\pi}{2}+n\pi\bigg)$, $n\in \mathbb{Z}.$ Da primeira equação temos que $y=0$ para todos essas $x$-valores.
Assim, os pontos críticos são $\bigg(\dfrac{\pi}{2}+n\pi,0\bigg).$ Agora,
$$f_{xx}(x,y)=-y\,\cos x,\;\;\;\;\;\; f_{xy}(x,y)=-\sin x\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\; f_{yy}(x,y)=0.$$
Então
\begin{array}{rcl}D(x,y)&=&(f_{xx}(x,y))\cdot (f_{yy}(x,y))-(f_{xy}(x,y))^{2}\\&\Rightarrow& D\bigg(\dfrac{\pi}{2}+n\pi,0\bigg)=0-\sin^{2}x=-\sin^{2}x<0.\end{array}
Portanto, cada ponto crítico é ponto de sela.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=xy-2x-y$.
Ponto de mínimo: $(2,1);$ ponto de sela: $(0,0).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=(x^{2}+y^{2})e^{y^{2}-x^{2}}$.
Ponto de mínimo: $(0,0);$ pontos de sela: $(1,0)$ e $(-1,0).$
Determine o plano tangente à superfície $\frac{x^2}{4} + \frac{y^2}{9} + \frac{z^2}{16} = 1$, com $x > 0$, $y > 0$ e $z > 0$, que forma com os planos coordenados um tetraedro de volume mínimo. (Dica: O volume do tetraedro formado pelos planos coordenados e o plano $ax + by + cz = d$ no primeiro octante é dado por $V = d^3/(6abc)$.)
$6x + 4y + 3z = 12\sqrt{3}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}+y^{3}+xy-3x-4y+5$.
Ponto de mínimo : $\displaystyle \left( 1,1\right);$ ponto de sela: $\displaystyle \left(\frac{23}{12},-\frac{5}{6}\right).$
Determine os pontos críticos da função
$$f(x,y)=-(x^{2}-1)^{2}-(x^{2}y-x-1)^{2}.$$
Calcule os valores assumidos por $f$ nos pontos críticos. É possível classificar os pontos críticos sem utilizar o críterio da derivada segunda? Se for possível, classifique-os e justifique a resposta.
$(1,2)$ e $(-1,0).$
$f(1,2) = f(-1,0) = 0.$ Note que $f(x,y) \leq 0,$ o que implica que $(1,2)$ e $(-1,0)$ são pontos de máximo.
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = xy$ e $x^2 + 4y^2 = 8.$
Pontos de máximo: $\displaystyle \left(2,1\right)$ e $(-2,-1)$; pontos de mínimo: $\displaystyle \left(-2,1\right)$ e $(2,-1)$.
Mostre que $f(x,y)=x^{2}+4y^{2}-4xy+2$ tem um número infinito de pontos críticos e que $f_{xx}f_{yy} - (f_{xy})^2 = 0$ em cada um. A seguir, mostre que $f$ tem um mínimo local (e absoluto) em cada ponto crítico.
Note que todos os pontos críticos são da forma $\displaystyle \left(x,\frac{1}{2}x \right)$ e que $f(x,y) = (x - 2y)^{2} + 2 \geq 2,$ com igualdade justamente se $\displaystyle y = \frac{1}{2}x.$
Agora, queremos ver que $f_{xx}f_{yy}-f_{xy} ^{2}=0$ em todos os pontos críticos. Para isso, calculemos as segundas derivadas de $f$ \[ f_{xx}(x,y)=2, f_{xy}(x,y)=-4 \text{ e } f_{yy}(x,y)=8. \] Daí temos que $f_{xx}f_{yy}-f_{xy} ^{2}=2\cdot 8-(-4)^{2}=16-16=0$, como queríamos.
Por fim, queremos ver que esses pontos críticos são pontos de mínimo de $f$, mas como $f_{xx}f_{yy}-f_{xy} ^{2}=0$ o Teste de Derivada Segunda é inconclusivo. Mas, note que $f$ pode ser reescrita como \[ f(x,y)=x^2+4y^2-4xy+2=(x-2y)^2+2. \]
Como $(x-2y)^2\geq 0$, segue que $f(x,y)\geq 2$ para todo $(x,y)\in \mathbb{R}^2$. Em particular, se tomamos um ponto crítico de $f$, isto é, um ponto da forma $(2y,y)$ então $f(2y,y)=2$. Provando que os pontos críticos são pontos de mínimo de $f$.
Suponha que $T(x,y)=4-x^{2}-y^{2}$ represente uma distribuição de temperatura em uma região que pode ser aproximada por um plano. Seja $D=\{(x,y)\in \mathbb{R}^2: x\geq 0,\;y\geq x\;\text{e}\;2y+x\leq 4\}$. Determine o ponto de $D$ de menor temperatura.
$(0,2).$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 - 2xy + 3y^2$ e $x^2 + 2y^2 = 1.$
Pontos de máximo: $\displaystyle \left( \frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}} \right)$ e $\displaystyle \left( -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}} \right)$; pontos de mínimo: $\displaystyle \left( \frac{2}{\sqrt{6}}, \frac{1}{\sqrt{6}} \right)$ e $\displaystyle \left( -\frac{2}{\sqrt{6}}, -\frac{1}{\sqrt{6}} \right)$.
Encontre os pontos da curva $x^2 - 6xy - 7y^2 + 80 = 0$ mais próximos da origem. Desenhe a curva.
$(1,3)$ e $(-1,-3).$ Realizando a mudança de coordenadas $x = \frac{1}{\sqrt{10}} u - \frac{3}{\sqrt{10}} v$ e $y = \frac{3}{\sqrt{10}} u + \frac{1}{\sqrt{10}} v,$ a equação da curva inicial é transformada em $\frac{u^{2}}{10} - \frac{v^{2}}{40} = 1,$.

