Exercícios
MA211 - Cálculo II
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
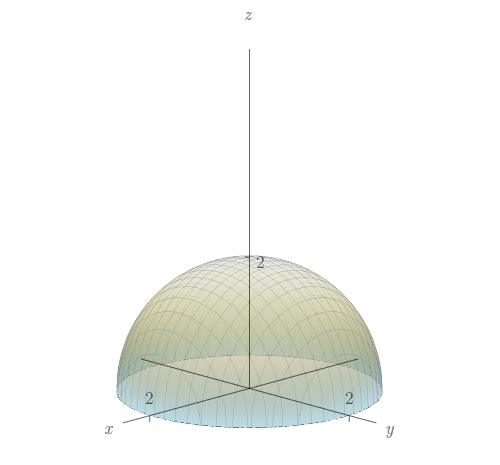
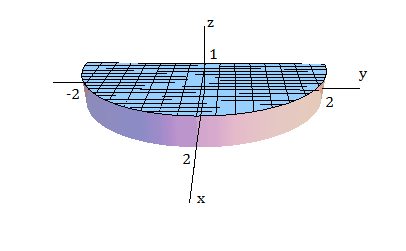
Seja \(G\) a região sólida dentro da esfera de raio \(2\) centrada na origem e acima do plano \(z=1\). Mostre (ou verifique) os seguintes resultados:
O volume de \(G\) é dado por \[\iiint\limits_G\,dV = \int_0^{2\pi}\int_0^{\sqrt{3}}\int_1^{\sqrt{4-r^2}}r\,dzdrd\theta \]
\[\iiint\limits_G\dfrac{z}{x^2+y^2+z^2}\,dV = \int_0^{2\pi}\int_0^{\sqrt{3}}\int_1^{\sqrt{4-r^2}}\dfrac{rz}{r^2+z^2}\,dzdrd\theta \]
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{1} \int_{0}^{\sqrt{1-x^{2}}}\,dy dx$
$\displaystyle \frac{\pi}{2}.$
Mostre que qualquer campo vetorial da forma
$$\mathbf{F}(x,y,z) = f(x)\mathbf{i} + g(y)\mathbf{j} + h(z)\mathbf{k},$$
em que $f,g$ e $h$ são diferenciáveis, é irrotacional.
Note que $\text{rot } \mathbf{F} = \bf{0}.$
Marque o ponto cujas coordenadas esféricas é $(1,0,0)$ e encontre as coordenadas retangulares do ponto.
$(0,0,1).$

Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=xy-2x-y$.
Ponto de mínimo: $(2,1);$ ponto de sela: $(0,0).$
Use coordenadas polares para calcular a integral dupla
\[ \iint_R e^{-(x^2+y^2)}\,dA, \]
onde \(R\) é a região contida no círculo \(x^2+y^2=1\).
\(\displaystyle (1-e^{-1})\pi \)
Determine as dimensões de uma caixa retangular de volume máximo tal que a soma dos comprimentos de suas 12 arestas seja uma constante $c$.
A caixa é um cubo com arestas de comprimento $\dfrac{c}{12}.$
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} x^2 \, dA$, em que $R$ é o conjunto de todos $(x,y)$ tais que $4x^2 + y^2 \leq 1$.
$\dfrac{\pi}{32}.$
Represente graficamente o domínio da função $z=f(x,y)$ dada por $x+y-1+z^{2}=0$, $z\geq 0$.
$\left\lbrace (x,y); x + y \leq 1 \right\rbrace$

${\bf F}(x,y,z)=3x\,{\bf i}+xy\,{\bf j}+2xz\,{\bf k}$, $E$ é o cubo limitado pelos planos $x=0$, $x=1$, $y=0$, $y=1$, $z=0$ e $z=1.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (2,1)}\dfrac{4 - xy}{x^2 + 3y^2}$.
$\frac{2}{7}.$
Ache o centro de massa de $E$, em que:
A densidade de um ponto $P$ de um sólido cúbico $E$ de aresta $a$ é diretamente proporcional ao quadrado da distância de $P$ a um vértice fixo do cubo.
$E$ é o tetraedro delimitado pelos planos coordenados e o plano $2x+5y+z=10$ e a densidade em $P(x,y,z)$ é diretamente proporcional $\grave{a}$ distância do plano $xz$ a $P.$
$\displaystyle \left( \dfrac{7a}{12},\dfrac{7a}{12},\dfrac{7a}{12} \right).$
$\displaystyle \left( 1,\dfrac{4}{5},2 \right).$
Calcule a área da região $R$ delimitada pela cardioide $\mathbf{r}(t) = (x(t),y(t))$, em que $x(t) = 2\cos{t}-\cos{2t}$ e $y(t) = 2\sin{t}-\sin{2t}$, $t \in [0,2\pi]$.
$6\pi.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$ye^{xy}$
$xy^{2}$
$\dfrac{(e - 1)^{2}}{2}.$
$\dfrac{1}{2}.$
Utilize coordenadas polares para determinar o volume do sólido dado: acima do cone $z=\sqrt{x^2+y^2}$ e abaixo da esfera $x^2+y^2+z^2=1.$
$\displaystyle \frac{\pi}{3}(2 - \sqrt{2}).$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\,dx dy$, onde $R$ é a região, no plano $xy$, limitada pela curva (dada em coordenadas polares) $\rho=\cos(2\theta)$, $\dfrac{\pi}{8}\leq \theta \leq \dfrac{\pi}{4}.$
$\displaystyle \frac{3\pi + 2}{32}.$
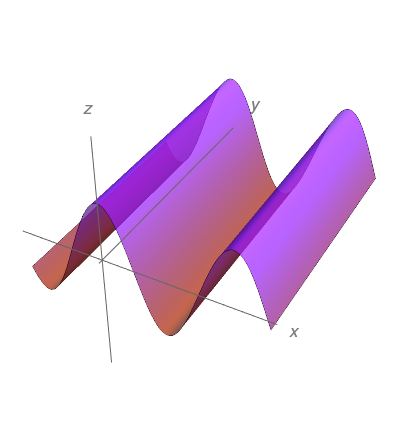
Esboce o gráfico da função $f(x,y)=\cos{x}$.
$z = \cos(x)$
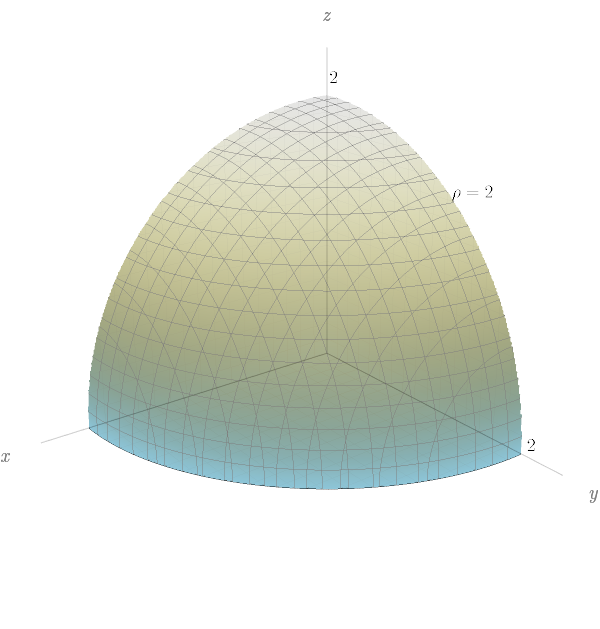
Esboce o sólido descrito por $\rho \leq 2$, $0\leq \phi \leq \pi/2$ e $0\leq \theta \leq \pi/2.$
Vamos demonstrar a expressão geral para o volume de um cone circular de altura $h$ e raio da base $R$.
Representando o cone com vértice na origem e base no plano $z = h$, expresse $V$ por meio de uma integral dupla.
Calculando a integral, verifique que $V = \dfrac{\pi R^2 h}{3}$.
$V = 2 \displaystyle \int_{0}^{h} \int_{-\frac{R}{h}z}^{\frac{R}{h}z} \sqrt{\dfrac{R^{2}}{h^{2}} z^{2} - x^{2}} dx dz.$
Note que $\displaystyle \int_{0}^{h} \int_{-\frac{R}{h}z}^{\frac{R}{h}z} \sqrt{\dfrac{R^{2}}{h^{2}} z^{2} - x^{2}} dx dz = \dfrac{\pi R^{2}h}{6}$ é o volume da parte superior (ou inferior) do cone.
Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=x^{2}+y^{2}$, \, $z\leq 4.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = r^2,$ onde $0 \leq r \leq 2$ e $0\leq \theta \leq 2\pi.$
Calcule $D_{\bf{u}}f(x_0,y_0)$, sendo dados
$f(x,y) = \arctan{\dfrac{x}{y}}$, $(x_0,y_0) = (3,3)$ e $\bf{u} = \left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$.
$\displaystyle D_{\bf{\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right)}}f(3,3) = 0.$
Calcule a área da região limitada pela elipse $x = a\cos{t}$, $y=b\sin{t}$, $0\leq t \leq \pi/2$, em que $a > 0$ e $b > 0$.
$\pi ab.$
Determine uma representação paramétrica para a superfície descrita a seguir. O paraboloide $z=9-x^{2}-y^{2}$, $z\geq 0.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 9 - r^2,$ onde $0 \leq r \leq 3$ e $0\leq \theta \leq 2\pi.$
Um homem pesando $160$ lb carrega uma lata de tinta de $25$ lb por uma escada helicoidal em torno de um silo com raio de $20$ pés. Se o silo tem $90$ pés de altura e o homem dá três voltas completas em torno do silo. Além disso, $9$ lb de tinta vazam da lata de modo contínuo e uniforme durante a subida do homem. Quanto trabalho é realizado?
$16245$ ft-lb.
Verifique que a função $z=\ln(e^{x}+e^{y})$ é uma solução das equações diferenciais
$$\frac{\mathrm{\partial}z}{\mathrm{\partial}x} + \frac{\mathrm{\partial}z}{\mathrm{\partial}y}=1\;\;\;\;\;\;\; e\;\;\;\;\;\;\; \frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}^{2}x}+\frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}^{2}y}-\bigg(\frac{\mathrm{\partial}^{2}z}{\mathrm{\partial}x\mathrm{\partial}y}\bigg)^{2}=0.$$
$\begin{aligned}[t]\frac{\partial z }{\partial x} &= \frac{e^{x}}{e^{x} + e^{y}},\;\;\; \frac{\partial z }{\partial y} = \frac{e^{y}}{e^{x} + e^{y}},\\\frac{\partial^{2} z }{\partial x^{2}} &= \frac{\partial^{2} z }{\partial y^{2}} = \frac{e^{x + y}}{(e^{x} + e^{y})^{2}},\;\;\; \frac{\partial^{2} z }{\partial x \partial y} = -\frac{e^{x + y}}{(e^{x} + e^{y})^{2}}.\end{aligned}$
Use a definição de derivadas parciais como limites para encontrar $f_{x}(x,y)$ e $f_{y}(x,y)$, sendo $f(x,y)=x^{2}y-x^{3}y$.
$\displaystyle f_{x} = y^{2} - 3x^{2}y \;\;\;\text{e}\;\;\; f_{y} = 2xy - x^{3}$.
Determine a área da superfície dada pela porção do cilindro $x^{2}+y^{2}=1$ entre os planos $z=1$ e $z=4.$
$6\pi.$
Determine se a função
$$f(x,y) = \begin{cases}e^{\left( \dfrac{1}{x^2 + y^2 - 1} \right)}, & \quad \text{se } x^2 + y^2 < 1, \\0, & \quad \text{se } x^2 + y^2 \geq 1.\end{cases}$$
é contínua em $\displaystyle{\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)}$. Justifique sua resposta.
$0.$
Determine os valores de máximo e mínimo de $f(x,y,z) = x^2 - yz$ em pontos da esfera $x^2 + y^2 + z^2 = 1$.
Valor máximo: $1;$ valor mínimo: $\displaystyle -\frac{1}{2}.$
Seja $f(x,y)=e^{xy}$ uma função de duas variáveis.
Determine o domínio e a imagem de $f.$
Esboce as curvas de nível de $f.$
$D_{f} = \mathbb{R}^{2}$ e $Im(f) = \left\lbrace z \in \mathbb{R};\; z > 0 \right\rbrace.$
$xy = C.$
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x^{2}+y^{2}\leq 1\,$ ou\, $4\leq x^{2}+y^{2}\leq 9\}$ consiste dos pontos que estão sobre ou dentro do círculo $x^{2}+y^{2}\leq 1$ juntamente com os pontos que estão em ou entre os círculos $x^{2}+y^{2}=4$ e $x^{2}+y^{2}=9$.
$D$ não é aberto pois qualquer disco centrado em $(0,1)$ contém pontos que não estão em $D$.
$D$ não é conexo pois não existe um caminho em $D$ conectando, por exemplo, os pontos $(1,0)$ e $(2,0)$.
$D$ não é simplesmente conexo porque possui um buraco. Com efeito, a região delimitada pela curva simples e fechada $x^2+y^2=(5/2)^2$, contém pontos que não pertencem a $D$, por exemplo, o ponto $(0,3/2)$.
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(\arctan (uv),e^{u^{2}-v^{2}},u-v)$, no ponto ${\bf r}(1,-1).$
$(x,y,z) = \left(-\dfrac{\pi}{4},1,2\right) + s\left(-\dfrac{1}{2},2,1\right) + t\left(\dfrac{1}{2},2,-1\right),$ $s,t \in \mathbb{R}.$
Demonstre as identidades, admitindo que as derivadas parciais apropriadas existem e são contínuas. Se $f$ for um campo escalar e $\mathbf{F}$, $\mathbf{G}$ foram campos vetoriais, então $f\mathbf{F}$, $\mathbf{F} \cdot \mathbf{G}$ e $\mathbf{F} \times \mathbf{G}$ serão definidos por
$$\begin{array}{rcl}(f\mathbf{F})(x,y,z) & = & f(x,y,z)\mathbf{F}(x,y,z) \\(\mathbf{F} \cdot \mathbf{G})(x,y,z) & = & \mathbf{F}(x,y,z) \cdot \mathbf{G}(x,y,z) \\(\mathbf{F} \times \mathbf{G})(x,y,z) & = & \mathbf{F}(x,y,z) \times \mathbf{G}(x,y,z).\end{array}$$
$\text{div }{(\mathbf{F}+\mathbf{G})} = \text{div }{\mathbf{F}}+\text{div }{\mathbf{G}}$.
$\text{div }{(f\mathbf{F})} = f\text{div }{\mathbf{F}} + \mathbf{F} \cdot \nabla{f}$.
$\text{div }{(\mathbf{F} \times \mathbf{G})} = \mathbf{G} \cdot \text{rot }{\mathbf{F}} - \mathbf{F}\cdot\text{rot }{\mathbf{G}}$.
$\text{div }{(\nabla{f} \times \nabla{g})} = 0$.
Suponhamos que ${\bf F}=P_{1}\,{\bf i}+Q_{1}\,{\bf j}+R_{1}\,{\bf k}$ e ${\bf G}=P_{2}\,{\bf i}+Q_{2}\,{\bf j}+R_{2}\,{\bf k}.$
Temos que $F+G=(P_{1}+P_{2})\,{\bf i}+(Q_{1}+Q_{2})\,{\bf j}+(R_{1}+R_{2})\,{\bf k}$. Então,
$$\begin{array}{rcl}\text{div } ({\bf F}+{\bf G})&=&\frac{\partial(P_{1}+P_{2})}{\partial x}+\frac{\partial(Q_{1}+Q_{2})}{\partial y}+\frac{\partial(R_{1}+R_{2})}{\partial z}\\&=&\frac{\partial P_{1}}{\partial x}+\frac{\partial P_{2}}{\partial x}+\frac{\partial Q_{1}}{\partial y}+\frac{\partial Q_{2}}{\partial y}+\frac{\partial R_{1}}{\partial z}+\frac{\partial R_{2}}{\partial z}\\&=&\underbrace{\frac{\partial P_{1}}{\partial x}+\frac{\partial Q_{1}}{\partial y}+\frac{\partial R_{1}}{\partial z}}+\underbrace{\frac{\partial P_{2}}{\partial x}+\frac{\partial Q_{2}}{\partial y}+\frac{\partial R_{2}}{\partial z}}\\&=& \text{div } {\bf F} + \text{div }{\bf G}.\end{array}$$
Temos que $f{\bf F}=(fP_{1})\,{\bf i}+(fQ_{1})\,{\bf j}+(fR_{1})\,{\bf k}.$ Então,
$$\begin{array}{rcl}\text{div } (f{\bf F})&=&\frac{\partial(fP_{1})}{\partial x}+\frac{\partial(fQ_{1})}{\partial y}+\frac{\partial(fR_{1})}{\partial z}\\&=&\frac{\partial f}{\partial x}\cdot P_{1}+f\cdot\frac{\partial P_{1}}{\partial x}+\frac{\partial f}{\partial y}\cdot Q_{1}+f\cdot\frac{\partial Q_{1}}{\partial y}+\frac{\partial f}{\partial z}\cdot R_{1}+f\cdot \frac{\partial R_{1}}{\partial z}\\&=&f\cdot\bigg(\underbrace{\frac{\partial P_{1}}{\partial x}+\frac{\partial Q_{1}}{\partial y}+\frac{\partial R_{1}}{\partial z}}\bigg)+\underbrace{\frac{\partial f}{\partial x}P_{1}+\frac{\partial f}{\partial y}Q_{1}+\frac{\partial f}{\partial z}R_{1}}\\&=& f\cdot \text{div } {\bf F}+ \nabla f\cdot {\bf F}\end{array}$$
Temos que ${\bf F}\times {\bf G}=(Q_{1}R_{2}-Q_{2}R_{1})\,{\bf i}+(P_{2}R_{1}-P_{1}R_{2})\,{\bf j}+(P_{1}Q_{2}-Q_{1}R_{2})\,{\bf k}.$ Então,
$$\begin{array}{rcl}\text{div } ({\bf F}\times {\bf G})&=&\frac{\partial(Q_{1}R_{2}-Q_{2}R_{1})}{\partial x}+\frac{\partial(P_{2}R_{1}-P_{1}R_{2})}{\partial y}+\frac{\partial(P_{1}Q_{2}-P_{2}Q_{1})}{\partial z}\\&=&\frac{\partial (Q_{1}R_{2})}{\partial x}-\frac{\partial (Q_{2}R_{1})}{\partial x}+\frac{\partial (P_{2}R_{1})}{\partial y}-\frac{\partial (P_{1}R_{2})}{\partial y}+\frac{\partial (P_{1}Q_{2})}{\partial z}-\frac{\partial (Q_{1}R_{2})}{\partial z}\\&=&\frac{\partial Q_{1}}{\partial x}\cdot R_{2}+Q_{1}\cdot \frac{\partial R_{2}}{\partial x}-\frac{\partial Q_{2}}{\partial x}\cdot R_{1}-Q_{2}\cdot \frac{\partial R_{1}}{\partial x}+\frac{\partial P_{2}}{\partial y}\cdot R_{1}+P_{2}\cdot \frac{\partial R_{1}}{\partial y}\\&-&\frac{\partial P_{1}}{\partial y}\cdot R_{2}-P_{1}\cdot \frac{\partial R_{2}}{\partial y}+\frac{\partial P_{1}}{\partial z}\cdot Q_{2}+P_{1}\cdot \frac{\partial Q_{2}}{\partial z}-\frac{\partial P_{2}}{\partial z}-P_{2}\cdot \frac{\partial Q_{1}}{\partial z}\\&=&P_{1}\bigg(\frac{\partial Q_{2}}{\partial z}-\frac{\partial R_{2}}{\partial y}\bigg)+Q_{1}\bigg(\frac{\partial R_{2}}{\partial x}-\frac{\partial P_{2}}{\partial z}\bigg)+R_{1}\bigg(\frac{\partial P_{2}}{\partial y}-\frac{\partial Q_{2}}{\partial x}\bigg)\\&+&P_{2}\bigg(\frac{\partial R_{1}}{\partial y}-\frac{\partial Q_{1}}{\partial z}\bigg)+Q_{2}\bigg(\frac{\partial P_{1}}{\partial z}-\frac{\partial R_{1}}{\partial x}\bigg)+R_{2}\bigg(\frac{\partial Q_{1}}{\partial x}-\frac{\partial P_{1}}{\partial y}\bigg)\\&=&\bigg[-P_{1}\bigg(\frac{\partial R_{2}}{\partial y}-\frac{\partial Q_{2}}{\partial z}\bigg)-Q_{1}\bigg(\frac{\partial P_{2}}{\partial z}-\frac{\partial R_{2}}{\partial x}\bigg)-R_{1}\bigg(\frac{\partial Q_{2}}{\partial x}-\frac{\partial P_{2}}{\partial y}\bigg)\bigg]\\&+&\bigg[P_{2}\bigg(\frac{\partial R_{1}}{\partial y}-\frac{\partial Q_{1}}{\partial z}\bigg)+Q_{2}\bigg(\frac{\partial P_{1}}{\partial z}-\frac{\partial R_{1}}{\partial x}\bigg)+R_{2}\bigg(\frac{\partial Q_{1}}{\partial x}-\frac{\partial P_{1}}{\partial y}\bigg)\bigg]\\&=&-{\bf F}\cdot \text{rot } {\bf G}+{\bf G}\cdot \text{rot } {\bf F}\\&=&{\bf G}\cdot \text{rot } {\bf F}-{\bf F}\cdot \text{rot } {\bf G}.\end{array}$$
Do item anterior temos que
$$\begin{array}{rcl}\text{div }(\nabla f\times \nabla g)&=&\nabla g \cdot \text{rot } (\nabla f)-\nabla f \cdot \text{rot } (\nabla g).\\\end{array} $$
Sabemos que, se $f$ é uma função de três variáveis que tem derivadas parciais de segunda ordem contínuas, então $\text{rot } (\nabla f)={\bf 0}.$ Deste resultado, obtemos que
$$\text{div }(\nabla f\times \nabla g) =\nabla g \cdot {\bf 0}-\nabla f \cdot {\bf 0}=0.$$
Suponha que $S$ e $C$ satisfaçam as hipóteses do Teorema de Stokes e $f$ e $g$ tenham derivadas parciais de segunda ordem contínuas. Demonstre que $\displaystyle\int_C (f\nabla f)\cdot d{\bf R} = 0$
Note que $\mbox{rot} (f\nabla f) = {\bf 0}.$
Calcule o volume do conjunto dado.
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1,0\leq z\leq x+2y\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 2, 1\leq y\leq 2, 0\leq z\leq \sqrt{xy}\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, 0\leq z\leq xye^{x^{2}-y^{2}}\}$
$ \{(x,y,z)\in \mathbb{R}^{3}| 0\leq x\leq 1, 0\leq y\leq 1, x^{2}+y^{2}\leq z\leq 2\}$
$\{(x,y,z)\in \mathbb{R}^{3}| 1\leq x\leq 2, 0\leq y\leq 1,\;x+y\leq z\leq x+y+2\}$
$\{(x,y,z)\in \mathbb{R}^{3}|\;0\leq x\leq 1, 0\leq y\leq 1,1\leq z\leq e^{x+y}\}$
$\dfrac{3}{2}.$
$\dfrac{8\sqrt{2}(2\sqrt{2} - 1)}{9}.$
$\dfrac{(e - 1)(1 - e^{-1})}{4}.$
$\dfrac{4}{3}.$
$2.$
$e^{2}-2e.$
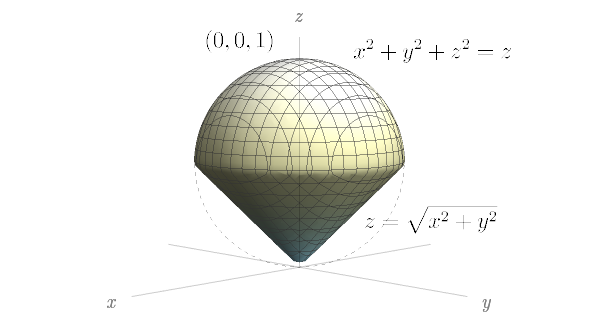
Um sólido está acima do cone $z=\sqrt{x^{2}+y^{2}}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=z.$ Escreva uma descrição do sólido em termos de desigualdades envolvendo coordenadas esféricas.
A mudança de coordenadas retangulares para coordenadas cartesianas é dada por
$$\begin{cases}x = \rho \cos{\theta} \sin{\phi} \\y = \rho \sin{\theta} \sin{\phi}\\z = \rho \cos{\phi},\end{cases}$$
em que $\rho \geq 0$, $\theta \in [0,2\pi]$ e $\phi \in [0,\pi]$. Observe que $\sin{\phi} \geq 0$ quando $\phi \in [0,\pi]$. Logo, a equação do cone em coordenadas esféricas pode ser escrita como $\rho \cos{\phi} = \sqrt{\rho^2 \sin^2{\phi}} = \rho\sin{\phi}$. A origem $(0,0,0)$ pertence ao cone e é dada por $\rho = 0$. Nos demais pontos, $\rho \neq 0$, donde $\phi = \pi/4$.
A equação da esfera em coordenadas esféricas pode ser escrita como $\rho^2=\rho\cos{\phi}$. A origem $(0,0,0)$ pertence à esfera e é dada por $\rho=0$. Nos demais pontos, $\rho \neq 0$, donde $\rho = \cos{\phi}$.
Portanto, o sólido pode ser descrito em coordenadas esféricas por
$$E = \left\{(\rho, \theta, \phi): 0 \leq \rho \leq \cos{\phi}, 0 \leq \theta \leq 2\pi \mbox{ e } 0 \leq \phi \leq \frac{\pi}{4}\right\}.$$
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = 4x^2 - y^2 + 2y, \quad (-1,2,4)$.
$z = -8x - 2y$.
Dados um hemisfério $H$ e uma parte $P$ de um paraboloide, suponha que ${\bf F}$ seja um campo vetorial sobre $\mathbb{R}^3$ cujas componentes tenham derivadas parciais contínuas. Explique por que
$$\displaystyle\iint\limits_{H}\mbox{rot}{\bf F}\cdot{\bf S} = \iint\limits_{P}\mbox{rot}{\bf F}\cdot{\bf S}.$$
Note que $H$ e $P$ satisfazem as hipóteses do Teorema de Stokes. Logo,
$$\displaystyle \iint \limits_{H} \mbox{rot } {\bf F} \cdot {\bf S} = \int \limits_{C} {\bf F} \cdot d{\bf r} = \iint \limits_{P} \mbox{rot }{\bf F}\cdot{\bf S},$$
onde $C$ é a curva de fronteira.
O plano $x + y + 2z = 2$ intercepta o paraboloide $z = x^2 + y^2$ em uma elipse. Determine os pontos dessa elipse que estão mais próximo e mais longe da origem.
Mais próximo: $\displaystyle \left( \frac{1}{2}, \frac{1}{2},\frac{1}{2} \right)$ e mais distante: $\displaystyle \left( -1,-1,2 \right).$
Expresse $\partial z/\partial t$ em termos das derivadas parciais de $f$, sendo $z=f(x,y)$ e $x=t^{2}$ e $y=3t.$
$\displaystyle \frac{dz}{dt} (t) = 2t \frac{\partial f}{\partial x}(t^{2},3t) + 3 \frac{\partial f}{\partial y}(t^{2},3t).$
Use a derivação implicíta para determinar $\partial z/\partial x$ e $\partial z/\partial y$ na expressão $\sin(xyz)=x+2y+3z$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{1 - yz \cos(xyz)}{xy\cos(xyz) - 3}$
$\displaystyle \frac{\partial z}{\partial y} = \frac{2 - xz \cos(xyz)}{xy\cos(xyz) - 3} $.
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} \dfrac{\cos{(x-y)}}{\sin{(x+y)}} \, dA$, em que $R$ é a região trapezoidal com vértices $(1,0)$, $(2,0)$, $(0,2)$ e $(0,1)$.
$1.$
Seja $f(x,y)=\dfrac{x^{2}y^{2}}{x^{2}+y^{2}}.$
Calcule as derivadas parciais $\dfrac{\partial f}{\partial x}(x,y)$ e $\dfrac{\partial f}{\partial y}(x,y)$, num ponto $(x,y)\neq\;(0,0).$
Calcule o limite, se existir.
$$\lim_{(x,y)\rightarrow (0,0)}\frac{\partial f}{\partial x}(x,y)$$
$\displaystyle \frac{\partial f}{\partial x} = \frac{2xy^{4}}{(x^{2} + y^{2})^{2}} \;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = \frac{2x^{4}y}{(x^{2} + y^{2})^{2}}$.
$\displaystyle \lim_{(x,y)\rightarrow (0,0)}\frac{\partial f}{\partial x}(x,y) = 0$.
Seja $f$ uma função de duas variáveis que tenha derivadas parciais contínuas e considere os pontos $A = (1,3)$, $B = (3,3)$, $C = (1,7)$ e $D = (6,15)$. A derivada direcional em $A$ na direção do vetor $\overrightarrow{AB}$ é 3, e a derivada direcional em $A$ na direção $\overrightarrow{AC}$ é 26. Determine a derivada direcional de $f$ em $A$ na direção do vetor $\overrightarrow{AD}$.
$\displaystyle \frac{327}{13}.$
Admita que, para todo $(x,y)$,
$$4y\frac{\partial f}{\partial x}(x,y)-x\frac{\partial f}{\partial y}(x,y)=0.$$
Prove que $f$ é constante sobre a elipse $\dfrac{x^{2}}{4}+y^{2}=1.$
Note que $\displaystyle \frac{dz}{dt} \left(t \right) = 0,$ para $z = f(x,y),$ $x = t$ e $\displaystyle y = \pm \sqrt{1 - \frac{t^{2}}{4}}.$
Mostre que a função $f(x,y) = xy - 5y^2$ é diferenciável achando os valores $\varepsilon_1$ e $\varepsilon_2$ que satisfaçam a Definição $7$ da Seção $14.4$ do Stewart.
$\epsilon_{1} = \Delta y$ e $\epsilon_{2} = -5\Delta y$.
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=2y^{3/2}\,{\bf i}+3x\sqrt{y}\,{\bf j}$ ao mover um objeto de $P(1,1)$ a $Q(2,4).$
$30.$
Uma partícula se move em um campo de velocidade $\textbf{V}(x,y) = (x^2,x+y^2)$. Se ela está na posição $(2,1)$ no instante $t=3$, estime sua posição no instante $t=3,01$.
$(2,04;1,03).$
Defina continuidade de uma função de duas variáveis $f(x,y)$ em um ponto $(x_0, y_0)$ de seu domínio.
Dada a função
$$f(x,y) = \begin{cases} \dfrac{x^2\sqrt{y}}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\L, & \quad \text{se } (x,y) = (0,0),\end{cases}$$
é possível encontrar $L$ de maneira que $f$ seja contínua em $(0,0)$?
$f(x,y)$ é contínua em $(x_{0},y_{0}) \in D_{f}$ se
$$\lim_{(x,y) \to (x_{0},y_{0})} f(x,y) = f(x_{0},y_{0}).$$
$L = 0.$
Utilize coordenadas polares para determinar o volume do sólido dado:
dentro da esfera $x^2+y^2+z^2=16$ e fora do cilindro $x^{2}+y^{2}=4.$
$\displaystyle 32\sqrt{3}\pi.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}\sqrt{x^{2}+y^{2}+z^{2}}\,dxdydz$, onde $B$ é a interseção da semi-esfera $x^{2}+y^{2}+z^{2}\leq 4$, $z\geq 0$, com o cilindro $x^{2}+y^{2}\leq 1.$
$\displaystyle \dfrac{\pi}{4}\left( 32- 14\sqrt{3} + \ln(2 + \sqrt{3})\right).$
Determine o valor máximo de $f(x,y)=x+5y$, onde $x$ e $y$ estão sujeitos às restrições: $5x+6y\leq 30$, $3x+2y\leq 12$, $x\geq 0$ e $y\geq 0.$
$25.$
Encontre o fluxo exterior do campo ${\bf F}(x,y,z)=z^{2}{\bf i}+x{\bf j}-3z{\bf k}$ através da superfície cortada do cilindro parabólico $z=4-y^{2}$ pelos planos $x=0$, $x=1$ e $z=0.$
$-32.$
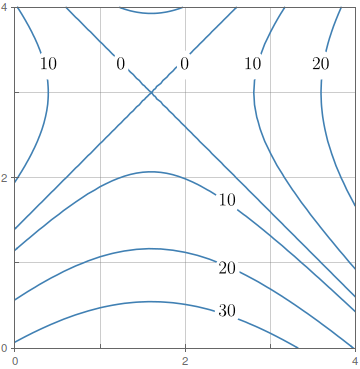
A figura mostra o mapa de contorno de $f$ no quadrado $R = [0,4] \times [0,4]$.
Use a Regra do Ponto Médio com $m = n = 2$ para estimar o valor de $\int\!\!\!\int \limits_{\!\!\!\!\!R} \! f(x,y) \, dA$.
Estime o valor médio de $f$.
Determine uma representação paramétrica para a superfície descrita a seguir. A porção no primeiro octante do cone $z=\sqrt{x^{2}+y^{2}}/2$ entre os planos $z=0$ e $z=3.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = \dfrac{r}{2},$ onde $0 \leq r \leq 6$ e $0\leq \theta \leq \dfrac{\pi}{2}.$
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F} \cdot d{\bf r}$, com ${\bf F} (x,y,z) = yz{\bf i} + 2xz{ \bf j} + e^{xy} {\bf k} $ e $C$ é a circunferência $x^2+y^2 = 16$, $z=5$, orientada no sentido anti-horário quando vista de cima.
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo paraboloide $z=9-x^2-y^2$ e pelo plano $z=5.$
$8\pi.$
Determine a derivada direcional da função no ponto dado e na direção do vetor $\bf{v}$.
$f(x,y,z) = \sqrt{xyz}, (3,2,6), \bf{v} = \left(-1,-2,2\right).$
$-1.$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=\sin{x}\cos{y}$, $x=\pi t$, $y=\sqrt{t}$.
$\displaystyle \frac{dz}{dt} = \pi \cos(x) \cos(y) - \frac{1}{2\sqrt{t}} \sin(x) \sin(y).$
Determine três números positivos cuja soma é $100$ e cujo produto é máximo.
$\displaystyle x = y = z = \frac{100}{3}.$
Ao calcular por integração dupla o volume $V$ do sólido situado abaixo do gráfico de $f(x,y)=e^{x^{2}+y^{2}}$ e limitado inferiormente por uma certa região $D$ no plano $xy$, chegou-se à seguinte expressão: $$V=\int_{0}^{2} \int_{0}^{\sqrt{4-x^{2}}}e^{x^{2}+y^{2}}\,dy dx-\int_{0}^{1} \int_{0}^{\sqrt{1-x^{2}}}e^{x^{2}+y^{2}}\,dy dx.$$
Esboce a região $D.$
Expresse $V$ numa única integral dupla em coordenadas polares.
Efetue a integração para calcular $V.$
$D = \left\lbrace (x,y); 1 \leq x^{2} + y^{2} \leq 2, x \geq 0, y \geq 0 \right\rbrace.$
$\displaystyle \int_{0}^{\frac{\pi}{2}} \int_{1}^{2} re^{r^2} dr d\theta.$
$\dfrac{\pi}{4}(e^4 - 1).$
Utilize a transformação dada para calcular a integral. $\displaystyle\iint\limits_{R} x^2 \, dA$, em que $R$ é a região limitada pela elipse $9x^2 + 4y^2 = 36$; $x = 2u$, $y = 3v$.
$6\pi.$
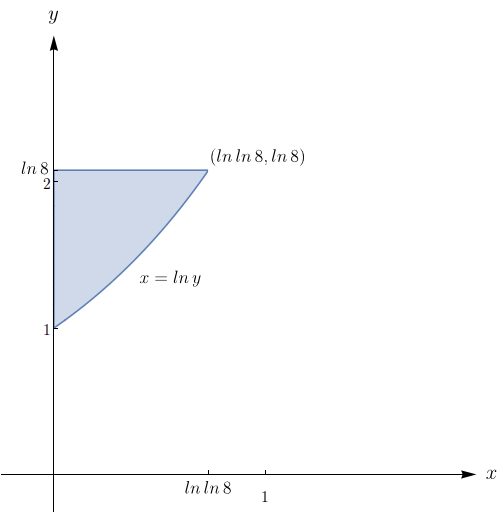
Esboce a região de integração e calcule a integral $\displaystyle\int_{1}^{\ln 8}\!\!\!\int_{0}^{\ln y}e^{x+y}\,dx dy$.
$8 \ln(8) - 16 + e.$
Passe para coordenadas polares e calcule.
$\displaystyle\int_{0}^{1} \int_{1-\sqrt{1-x^{2}}}^{1+\sqrt{1-x^{2}}}xy\,dy dx$
$\displaystyle\int_{-a}^{a}\!\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}\,dy dx$
Temos que a região de integração é $$R=\{(x,y)\in\mathbb{R}^2|\, 0\leq x \leq 1\,\mbox{e}\, 1-\sqrt{1-x^{2}}\leq y \leq 1+\sqrt{1-x^{2}}\}.$$

Passando para coordenadas polares temos que: $$\left\{ \begin{array}{cc} x=r\,\cos\theta \\ y=r\,\sin\theta \\ dy\,dx=r\,dr\,d\theta \\ \end{array} \right.$$ Agora, \begin{eqnarray*} x^{2}+y^{2}=2y&\Rightarrow & r^{2}\,\cos^2 \theta+r^{2}\,\sin^{2}\theta=2r\,\sin\theta\\ &\Rightarrow & r^{2}=2r \,\sin\theta\\ &\Rightarrow & r(r-2\sin\theta )=0 \\ &\Rightarrow& r=0 \mbox{ou} r=2\sin\theta.\end{eqnarray*} Logo, $\displaystyle 0\leq r \leq 2\,\sin\theta$ e $\displaystyle 0\leq\theta \leq\dfrac{\pi}{2}.$ Então, $$\int_{0}^{1}\int_{1-\sqrt{1-x^2}}^{1+\sqrt{1-x^2}}xy\,dy\,dx =\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\,\sin\theta}(r\,\cos\theta)(r\,\sin\theta)r\,dr d\theta $$
$$ =\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\,\sin\theta}r^3\,\sin\theta\, \cos\theta\,dr d\theta =\int_{0}^{\dfrac{\pi}{2}}\bigg[\frac{r^{4}} {4}\sin\theta\,\cos\theta\bigg]\bigg|_{0}^{2\,\sin\theta}\,d\theta $$ $$ =\int_0^{\frac{\pi}{2}}\frac{(2\,\sin\theta)^4}{4}\,\sin\theta\,\cos\theta\,d\theta =4\int_{0}^\frac{\pi}{2}\sin^5\theta\,\cos\theta\, d\theta.$$ Tomando, $u=\sin\theta \Rightarrow du=\cos\theta\, d\theta$ e sendo $\theta =0 \Rightarrow u=0$ e $\theta=\frac{\pi}{2}\Rightarrow u=1.$ Assim, $$\int_{0}^{1}\int_{1-\sqrt{1-x^{2}}}^{1+\sqrt{1-x^{2}}}xy\,dy dx=4\int_{0}^{1}u^{5}\,du$$ $$=4\cdot \frac{u^{6}}{6}\bigg|_{0}^{1}=\frac{2}{3}.$$Temos que a região de integração é $$R=\{(x,y)\in \mathbb{R}|\, -a\leq x \leq a,\, -\sqrt{a^{2}-x^{2}}\leq y \leq \sqrt{a^{2}-x^{2}}\}.$$
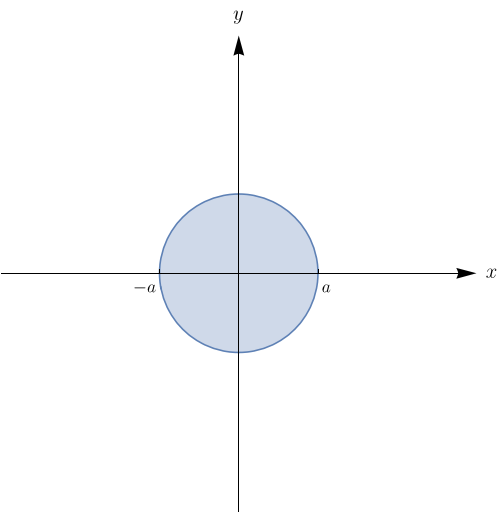
Passando para coordenadas polares temos que $$\left\{ \begin{array}{cc} x=r\,\cos\theta \\ y=r\,\sin\theta\\ dy\,dx=r\,dr\,d\theta\\ \end{array} \right. $$ Como $x^{2}+y^{2}=a^{2}\Rightarrow r^{2}\,\cos^{2}\theta+r^{2}\,\sin{2}\theta=a^{2}\Rightarrow r^{2}=a^{2}\Rightarrow r=\pm a.$ Como o raio deve ser sempre maior ou igual a zero, logo $$0\leq r\leq a \mbox{e} 0\leq \theta \leq 2\pi.$$ Então, $$\int_{-a}^{a}\int_{-\sqrt{a^{2}-x^{2}}}^{\sqrt{a^{2}-x^{2}}}dy\,dx=\int_{0}^{2\pi}\int_{0}^{a}r\,dr\,d \theta=\int_{0}^{2\pi}d\theta \cdot \int_{0}^{a}r\,dr$$ $$=\theta\bigg |_{0}^{2\pi}\cdot \frac{r^{2}}{2}\bigg |_{0}^{a}=(2\pi)\cdot \bigg(\frac{a^{2}}{2}\bigg)=a^{2}\pi.$$
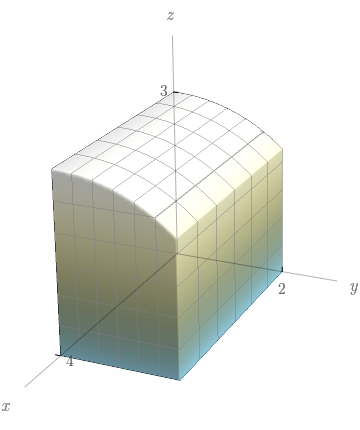
A integral $\int \!\!\! \int\limits_{\!\!\!\!\!R} \! \sqrt{9 - y^2} \, dA$, em que $R = [0,4] \times [0,2]$, representa o volume de um sólido. Esboce o sólido.
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{-a}^{a}\int_{-\sqrt{a^{2}-y^{2}}}^{\sqrt{a^{2}-y^{2}}}\int_{-\sqrt{a^{2}-x^{2}-y^{2}}}^{\sqrt{a-x^{2}-y^{2}}}(x^{2}z+y^{2}z+z^{3})\,dzdxdy$.
$0.$
Determine a imagem do conjunto $S$ sob a transformação dada. $S = \{(x,y) \in \mathbb{R}^2: 0 \leq u \leq 3, \, 0 \leq v \leq 2\}$;$x = 2u + 3v$, $y = u - v$.
O paralelogramo com vértices $(0,0),$ $(6,3),$ $(12,1),$ $(6,-2).$
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{3}\!\!\int_{-2}^{0}(x^{2}y-2xy)\,dy dx$.
$0.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=x-\sqrt{y^{2}+z^{2}}$.
$\displaystyle f_{x} = 1,\;\;\;\; f_{y} = -\frac{y}{\sqrt{y^{2} + z^{2}}}\;\;\;\;\text{e}\;\;\;\; f_{z} = -\frac{z}{\sqrt{y^{2} + z^{2}}}$.
Quatro números positivos, cada um menor que $50$, são arredondados até a primeira casa decimal e depois multiplicados. Utilize os diferenciais para estimar o máximo erro possível no cálculo do produto que pode resultar do arredondamento.
Se $x,y,z,w$ são os quatro números e $p(x,y,z,w) = xyzw,$ temos $\Delta p \leq 25000.$
Considere a integral
$$\int_{0}^{2}\int_{\frac{y}{2}}^{1}ye^{x^{3}}\,dx dy.$$
Faça um esboço da região de integração.
Calcule a integral sendo explícito se vai precisar mudar a ordem de integração.
...
$\dfrac{2(e - 1)}{3}.$
Verifique que a função $f(x,y) = e^{x - y^2}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Uma lâmina ocupa parte do disco $x^2 + y^2 \leq 1$ no primeiro quadrante. Determine o centro de massa se a densidade em qualquer ponto for proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(\frac{3}{8}, \frac{3\pi}{16} \right).$
Calcule a área da região limitada pela astroide $x=\cos^3{t}$, $y = \sin^3{t}$, $0 \leq t \leq 2\pi$.
$\dfrac{3\pi}{8}.$
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf i}$, $S$ a superfície $z = x^2+y^2$ com $z \leq 1$, sendo ${\bf n}$ a normal com componente $z$ positiva.
$-\pi$.
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, $(u,v)\in \mathbb{R}^{2}.$.
Paraboloide de rotação $z = x^2 + y^2.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{5}+y^{5}-5x-5y$.
Ponto de mínimo: $\displaystyle \left( 1,1\right);$ ponto de máximo: $\displaystyle \left( -1,-1\right);$ pontos de sela: $\displaystyle \left(1,-1\right)$ e $\displaystyle \left(-1,1\right).$
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $y=y(x).$
Expresse $\mathrm{d} y/\mathrm{d} x$ em termos de $x$ e $y.$
$x^{2}y+\sin(y)=x$
$\displaystyle \frac{d y}{d x} = -\frac{2xy - 1}{x^{2} + \cos(y)}.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}dx+xy\,dy+z\,dz$, $C$ é a interseção de $x^{2}+y^{2}+z^{2}=2$, $x\geq 0$, $y\geq 0$ e $z\geq 0$, com o plano $y=x$; o sentido de percurso é do ponto $(0,0,\sqrt{2})$ para $(1,1,0).$
$\displaystyle \frac{1}{3}.$
Use a integral tripla para determinar o volume do sólido dado.
$0\leq x \leq 1$, $0\leq y \leq 1$ e $0\leq z \leq 5-x^{2}-3y^{2}.$
$0\leq x \leq 1$, $0\leq y \leq x^{2}$ e $0\leq z \leq x+y^{2}.$
$x^{2}+y^{2}\leq z \leq 4.$
$x^{2}+4y^{2}\leq z \leq 1.$
$\dfrac{11}{3}.$
$\dfrac{25}{84}.$
$8\pi.$
$\dfrac{\pi}{4}.$
Determine as derivadas parciais de $f(x,y)=e^{-x^{2}-y^{2}}$.
$\displaystyle \frac{\partial f}{\partial x} = -2xe^{-x^{2} - y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = -2ye^{-x^{2} - y^{2}}.$
Encontre a área da superfície $z=1+3x+3y^{2}$ que está acima do triângulo com vértices $(0,0)$, $(0,1)$ e $(2,1).$
$\dfrac{1}{54}\left(46\sqrt{46} - 10\sqrt{10} \right).$
Seja $D$ a região limitada abaixo pelo plano $z=0$, acima pela esfera $x^{2}+y^{2}+z^{2}=4$ e dos lados pelo cilindro $x^{2}+y^{2}=1$. Monte as integrais triplas em coordenadas esféricas que dão o volume de $D$ usando as ordens de integração a seguir.
$d\rho\,d\phi\,d\theta$;
$d\phi\,d\rho\,d\theta$.
$\displaystyle \int_{0}^{2\pi}\int_{0}^{\pi/6}\int_{0}^{2} \rho^{2}\sin(\phi)\; d\rho d\phi d\theta + \int_{0}^{2\pi}\int_{\pi/6}^{\pi/2}\int_{0}^{\csc(\phi)} \rho^{2}\sin(\phi)\; d\rho d\phi d\theta.$
$\displaystyle \int_{0}^{2\pi}\int_{1}^{2}\int_{\pi/6}^{\arcsin(1/\rho)} \rho^{2}\sin(\phi)\; d\phi d\rho d\theta + \int_{0}^{2\pi}\int_{0}^{2}\int_{0}^{\pi/6} \rho^{2}\sin(\phi)\; d\phi d\rho d\theta.$
Mostre que os limites não existem, considerando que \((x,y)\rightarrow (0,0) \) ao longo dos eixos coordenados.
\[ \lim_{(x,y)\to(0,0)}\dfrac{x-y}{x^2+y^2} \]
\[ \lim_{(x,y)\to(0,0)}\dfrac{\cos(xy)}{x^2+y^2} \]
Calcule a integral de superfície $\displaystyle\iint\limits_{S}x dS$, onde $S$ é a superfície com equações paramétricas $x=u$, $y=v$, $z=u^{2}+v$, $0 \leq u \leq 1$, $u^{2} \leq v \leq 1.$
$\dfrac{\sqrt{2}}{10}(3\sqrt{3} - 2).$
Um homem pesando $160$ lb carrega uma lata de tinta de $25$ lb por uma escada helicoidal em torno de um silo com raio de $20$ pés. Se o silo tem $90$ pés de altura e o homem dá três voltas completas em torno do silo, quanto trabalho é realizado pelo homem contra a gravidade para subir ao topo?
$16650$ ft-lb.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}(2x+9z)\,ds$, $C:\,x=t,\, y=t^{2},\, z=t^{3},\, 0\leq t\leq 1.$
$\displaystyle \frac{1}{6}\left(14^{3/2} - 1\right).$
Dados ${\bf F}(x,y,z)=yz\,{\bf i}+xz\,{\bf j}+(xy+2z)\,{\bf k}$, $C$ é o segmento de reta de $(1,0,-2)$ a $(4,6,3).$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = xyz + z^{2};$
$77.$
Calcule a integral de linha $\displaystyle\oint_{C} xy \, dx + x^2y^3 \, dy$, $C$ é o triângulo com vértices $(0,0)$, $(1,0)$ e $(1,2)$ por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$\dfrac{2}{3}.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{2}+3xy-3x$ em $D=\{(x,y)\in \mathbb{R}^2: x\geq 0,\;y\geq 0\; \text{e} \;x+y\leq 1\}.$
Valor máximo: $\displaystyle 0;$ valor mínimo: $-2.$
Calcule a integral dupla utilizando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+y^{2})\,dx dy$, onde $R=\{(x,y)\in \mathbb{R}^{2}| 1\leq x^{2}+y^{2}\leq 4\}.$
$\displaystyle \frac{15\pi}{2}.$
Determine se ${\bf F}(x,y)=(\ln y+2xy^{3})\,{\bf i}+(3x^{2}y^{2}+x/y)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = x^{2}y + xy^{-2} + K.$
Se $z = 5x^2 + y^2$ e $(x,y)$ varia de $(1,2)$ a $(1,05; 2,1)$, compare os valores de $\Delta z$ e $dz$.
$\Delta z = 0.9225$ e $dz = 0.9$.
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (\sqrt{x} + y^3,x^2+\sqrt{y})$, $C$ consiste no arco da curva $y = \sin{x}$ de $(0,0)$ a $(\pi,0)$ e no segmento de reta $(\pi,0)$ a $(0,0)$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$\dfrac{4}{3} - 2\pi.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=e^{x}\,\sin y\,{\bf i}+e^{x}\,\cos y\,{\bf j}+yz^{2}\,{\bf k}$ e $S$ é a superfície da caixa delimitada pelos planos $x=0$, $x=1$, $y=0$, $y=1$, $z=0$ e $z=2.$
Encontre uma equação para a curva de nível da função $f(x,y)=\sqrt{x^{2}-1}$ que passa pelo ponto $(1,0)$.
$x = 1$ ou $x = -1.$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{\dfrac{\pi}{4}}\bigg[\int_{\sin{x}}^{\cos{x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{2}\bigg[\int_{\sqrt{\frac{7+5y^{2}}{3}}}^{\frac{y+7}{3}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{3}\bigg[\int_{x^{2}-2x}^{\sqrt{3x}}f(x,y)\,dy\bigg]dx$
$\displaystyle \int_{0}^{\frac{\sqrt{2}}{2}}\bigg[\int_{0}^{\arcsin{y}}f(x,y)\,dx\bigg]dy + \int_{\frac{\sqrt{2}}{2}}^{1}\bigg[\int_{0}^{\arccos{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{2}^{3}\bigg[\int_{3x - 7}^{\sqrt{\frac{3x^2 - 7}{5}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{0}\bigg[\int_{1 - \sqrt{1 + y}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy + \int_{0}^{3}\bigg[\int_{\dfrac{y^{2}}{3}}^{1 + \sqrt{1 + y}}f(x,y)\,dx\bigg]dy$
Calcule a integral de linha, onde $C$ é a curva dada. $\displaystyle\int_{C}x^{2}y\sqrt{z}\,dz$, $C:\,x=t^{3},\, y=t,\, z=t^{2},\, 0\leq t\leq 1.$
As equações paramétricas de $C$ são
$$x=t^{3},\, y=t,\, z=t^{2},\, 0\leq t\leq 1.$$
Logo,
$$dx=3t^{2}\,dt,\, dy=dt,\, dz=2t\,dt.$$
Assim,
$$\int_{C}x^{2}y\sqrt{z}\,dz=\int_{0}^{1}((t^{3})^{2}\cdot t \cdot \sqrt{t^{2}})(2t\,dt)=2\int_{0}^{1}t^{9}\,dt$$
$$=2\cdot\frac{t^{10}}{10}\bigg|_{0}^{1}=2\cdot \frac{1}{10}=\frac{1}{5}.$$
Usando coordenadas esféricas, calcule a massa da esfera sólida de raio \(a\) com densidade proporcional à distância ao centro (tomando \(k\) como a constante de proporcionalidade).
\(k\pi a^4\)
Considere a transformação do plano $xy$ no plano $uv$ dada por $u=x-2y$ e $v=3x-y$.
Inverta a transformação, isto é, obtenha as expressões da transformação do plano $uv$ no plano $xy$.
Represente geometricamente a região $R$ no plano $xy$ obtida como imagem da transformação aplicada à região delimitada por $u=0$, $u=4$, $v=1$, $v=8$.
Utilize a transformação dada para calcular a integral
$$\iint\limits_{R}\dfrac{x-2y}{3x-y} \, dA.$$
$x = \dfrac{2v - u}{5},$ $y = \dfrac{v - 3u}{5}.$
Região delimitada pelas retas $x = 2y,$ $x = 2y + 4,$ $y = 3x - 1$ e $3x - 8.$
$\dfrac{8 \ln(8)}{5}.$
Seja ${\bf F}(x,y)=\dfrac{-y\,{\bf i}+x\,{\bf j}}{x^{2}+y^{2}}.$
Mostre que $\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}.$
Mostre que $\int_{C}{\bf F}\cdot d{\bf r}$ não é independente do caminho. [Sugestão: calcule $\int_{C_{1}}{\bf F}\cdot d{\bf r}$ e $\int_{C_{2}}{\bf F}\cdot d{\bf r}$, onde $C_{1}$ e $C_{2}$ são as metades superior e inferior do círculo $x^{2}+y^{2}=1$ de $(1,0)$ a $(-1,0)$.] Isso contraria o Teorema 6 (Seção 16.3 do Livro do James Stewart)?
$\dfrac{\partial P}{\partial y}= \dfrac{y^{2} - x^{2}}{(x^{2} + y^{2})^{2}} = \dfrac{\partial Q}{\partial x}.$
Tome $C_{1}$ a curva parametrizada por $\mathbf{r_{1}}(t) = (\cos(t), \sin(t)),$ $0 \leq t \leq \pi$ e $C_{2}$ a curva parametrizada por $\mathbf{r_{2}}(t) = (\cos(t), \sin(t)),$ de $t = 2\pi$ a $t = \pi.$ Segue que $\int_{C_{1}} \mathbf{F} \cdot d \mathbf{r} = \pi \neq -\pi = \int_{C_{2}} \mathbf{F} \cdot d \mathbf{r}.$ Como o domínio de $\mathbf{F}$ é $\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$ que não é simplesmente conexo, o resultado não contradiz o Teorema 6.
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário, onde $\mathbf{F}(x,y) = x\mathbf{i} + y\mathbf{j}$, $C$ dada por $\mathbf{r}(t) = (\cos{t},\sin{t})$, $0 \leq t \leq 2\pi$ e $\mathbf{n}$ a normal exterior.
$2\pi.$
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}$ e $S$ é a parte no primeiro octante do plano $2x+3y+z=6.$
$18.$
Utilize a integral dupla para determinar a área da região: limitada pelo eixo $x$ positivo e pela espiral $r=4\theta/3$, $0\leq \theta \leq 2\pi.$ A região se parece com uma concha de caracol.
$\dfrac{64\pi^3}{27}.$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{e^{y-1}}^{e^{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{2x}^{x+1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{\frac{\pi}{4}}\bigg[\int_{0}^{\tan(x)}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{e^{-1}}^{1}\bigg[\int_{0}^{1 + \ln(x)}f(x,y) \ , dy\bigg]dx + \displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{y/2}f(x,y)\,dx\bigg]dy + \int_{1}^{2}\bigg[\int_{y - 1}^{y/2}f(x,y)\,dx\bigg]dy$
$\displaystyle \int_{0}^{1}\bigg[\int_{0}^{\arctan(y)}f(x,y)\,dx \bigg]dy $
Se ${\bf F}=(xz,yz,2)$ e $E$ é a região dada por $x^{2}+y^{2}\leq 1$ e $0\leq z \leq 1,$ mostre que o Teorema do Divergente é verdadeiro neste caso. Calcule as duas integrais do enunciado do Teorema e mostre que elas têm o mesmo valor.
Escreva a integral dupla $$\iint\limits_{R}x\cos{y}\;dA,$$ onde $R$ é limitada pelas retas $y=0$, $x=\pi/4$ e $y=x$, das duas formas possíveis (mudando a ordem de integração). Escolha uma dessas formas e calcule o valor dessa integral.
$\displaystyle \int_{0}^{\pi/4} \int_{0}^{x} x \cos(y)\;dy\;dx = \int_{0}^{\pi/4} \int_{y}^{\pi / 4} x \cos(y)\;dx\;dy = -\frac{\pi - 4}{4\sqrt{2}}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, quando: $D$ é delimitada por $y = e^x$, $y = 0$, $x = 0$ e $x = 1; \quad \rho(x,y) = y$.
Massa: $\dfrac{1}{4}(e^{2} - 1);$ centro de massa: $\displaystyle \left(\frac{e^2 + 1}{2(e^2 - 1)},\frac{4(e^3 - 1)}{9 (e^2 - 1)} \right).$
Usando coordenadas esféricas, determine o volume do elipsoide $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}\leq 1.$
$\dfrac{4 \pi abc}{3}.$
Expresse $\partial z/\partial t$ em termos das derivadas parciais de $f$, sendo $z=f(x,y)$ e $x=\sin{3t}$ e $y=\cos{2t}.$
$\displaystyle \frac{dz}{dt} (t) = 3 \cos(3t) \frac{\partial f}{\partial x}(\sin(3t),\cos(2t)) - 2\sin(2t) \frac{\partial f}{\partial y}(\sin(3t),\cos(2t)).$
Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=2\,\sin u\,{\bf i}+3\,\cos u\,{\bf j}+v\,{\bf k}$, $0\leq v\leq 2.$.
$\dfrac{x^2}{4} + \dfrac{y^{2}}{9} = 1,$ com $0\leq z \leq 2.$
Determine as derivadas parciais indicadas. $w=\dfrac{x}{y+2z}$; \;\;\;\;$\dfrac{\partial^{3}w}{\partial z\partial y \partial x}$, \;\;\;\;$\dfrac{\partial^{3}w}{\partial x^{2}\partial y}$.
$\displaystyle \frac{\partial^{3}w}{\partial z\partial y \partial x} = \frac{4}{(y + 2z)^{3}}\;\;\;\text{e} \;\;\;\; \frac{\partial^{3}w}{\partial x^{2}\partial y} = 0$.
Esboce a região de integração e calcule a integral $\displaystyle\int_{\pi}^{2\pi}\!\!\int_{0}^{\pi}(\sin{x}+\cos{y})\,dx dy$.
$2\pi.$
Se ${\bf u}(t)=(\sin{t}, \cos{t}, t)$ e ${\bf v}(t)=(t,t\cos{t},\sin{t})$, use a Fórmula $$\dfrac{d}{dt}\left[{\bf u}(t)\times{\bf v}(t)\right]={\bf u}'(t)\times{\bf v}(t)+{\bf u}(t)\times{\bf v}'(t)$$ para encontrar $$\frac{\mathrm{d}}{\mathrm{d}t}[{\bf u}(t)\times {\bf v}(t)].$$
$\left\{t^2 \sin (t)-\sin ^2(t)+\cos ^2(t)-2 t \cos (t),2 t-2 \sin (t) \cos (t),-t \sin^2(t)+t \sin (t)+t \cos ^2(t)-\cos (t)+\sin (t) \cos (t)\right\}$
Utilize as diferenciais para estimar a quantidade de estanho em uma lata cilíndrica fechada com $8$ cm de diâmetro e $12$ cm de altura se a espessura da folha de estanho for de $0,04$ cm.
Para $V = \pi r^{2}h$ o volume da lata de raio $r$ e altura $h,$ temos $\Delta V \approx 16$ cm$^{3}.$
A fronteira de uma lâmina consiste nos semicírculos $y = \sqrt{1 - x^2}$ e $y = \sqrt{4 - x^2}$, juntamente com as partes do eixo $x$ que os une. Encontre o centro de massa da lâmina se a densidade em qualquer ponto é proporcional à sua distância da origem.
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Uma carga elétrica é distribuída sobre um disco $x^2 + y^2 \leq 4$ de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = x + y + x^2 + y^2$ (medida em coulombs por metro quadrado). Determine a carga total do disco.
Como a carga elétrica é distribuída sobre o disco $x^2 + y^2 \leq 4$, em coordenadas polares temos que $0\leq r \leq 2$ e $0\leq \theta \leq 2\pi.$ Temos que $$Q=\iint\limits_{D}\sigma(x,y)\,dA=\iint\limits_{D}(x+y+x^{2}+y^{2})\,dA$$ $$=\int_{0}^{2\pi}\int_{0}^{2}(r\,\cos \theta+r\,\sin \theta+r^{2})r\,dr\, d \theta=\int_{0}^{2\pi}\int_{0}^{2}(r^{2}\,\cos \theta+r^{2}\,\sin \theta+r^{3})\,dr\, d \theta$$ $$=\int_{0}^{2\pi}\bigg(\frac{r^{3}}{3}\cos \theta+\frac{r^{3}}{3}\sin \theta +\frac{r^{4}}{4}\bigg)\bigg|_{0}^{2}\,d\theta= \int_{0}^{2\pi}\bigg(\frac{8}{3}\cos \theta+\frac{8}{3}\sin \theta+4\bigg)\,d\theta$$ $$=\bigg(\frac{8}{3}\sin\theta-\frac{8}{3}\cos\theta+4\theta\bigg)\bigg|_{0}^{2\pi}=\bigg(-\frac{8}{3}+8\pi\bigg)-\bigg(-\frac{8}{3}\bigg)$$ $$=-\frac{8}{3}+8\pi+\frac{8}{3}=8\pi.$$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{2}-2xy+2y^{2}$ em $D=\{(x,y)\in \mathbb{R}^2: \;|x|+|y|\leq 1\}.$
Valor máximo: $\displaystyle 2;$ valor mínimo: $0.$
A função densidade conjunta para um par de variáveis aleatórias $X$ e $Y$ é $$f(x,y) = \begin{cases} Cx(1 + y), & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 2,\\ 0, & \quad \text{caso contrário}.
\end{cases}$$
Determine a constante $C$.
Determine $P(X \leq 1, \ Y \leq 1)$.
Determine $P(X + Y \leq 1)$.
$\dfrac{1}{2}.$
$\dfrac{3}{8}.$
$\dfrac{5}{48}$.
Esboce o gráfico da função $f(x,y)=e^{\sqrt{x^{2}+y^{2}}}$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y,z)=(yz,2xz,xy+2z)$ e $C$ é o segmento de reta que liga o ponto $(1,0,1)$ ao ponto $(-2,2,2).$
$-7.$
Calcule a integral $\displaystyle\int_{0}^{\pi/2}(3\sin^{2}(t) \cos(t){\bf i}+3\sin(t) \cos^{2}(t){\bf j}+2\sin(t)\cos(t){\bf k})\mathrm{d}t$.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{4}+y^{4}-2x^{2}-2y^{2}$.
Pontos de mínimo: $(-1,1)$ e $(-1,-1);$ ponto de máximo: $(0,0);$ pontos de sela: $(0,1), (0,-1), (1,0)$ e $(-1,0).$
Use o Teorema de Green para achar o trabalho realizado pela força $\mathbf{F}(x,y) = x(x+y)\mathbf{i} + xy^2\mathbf{j}$ ao mover uma partícula da origem ao longo do eixo $x$ até $(1,0)$, em seguida ao longo de um segmento de reta até $(0,1)$ e então de volta à origem ao longo do eixo $y$.
$-\dfrac{1}{12}.$
Considere a função
$$f(x,y) = \begin{cases}\dfrac{xy}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0).\\\end{cases}$$
Mostre que $f_x(0,0)$ e $f_y(0,0)$ existem, mas $f$ não é diferenciável em $(0,0)$.
$f_{x}(0,0) = f_{y}(0,0) = 0,$ mas $\lim_{(x,y) \to (0,0)} f(x,y)$ não existe, logo $f$ é discontínua em $(0,0)$ e portanto não é diferenciável neste ponto.
Dado que \(\displaystyle x^3+y^2x-3=0\), determine \(\dfrac{dy}{dx}\) usando derivação implícita.
Derivando implicitamente a equação dada, temos que \(3x^2+y^2+x(2yy')-0=0\). Ou seja,
\[ \frac{dy}{dx}= -\frac{3x^2+y^2}{2xy}.\]
Mostre que $f(x,y)=x^{2}+4y^{2}-4xy+2$ tem um número infinito de pontos críticos e que $f_{xx}f_{yy} - (f_{xy})^2 = 0$ em cada um. A seguir, mostre que $f$ tem um mínimo local (e absoluto) em cada ponto crítico.
Note que todos os pontos críticos são da forma $\displaystyle \left(x,\frac{1}{2}x \right)$ e que $f(x,y) = (x - 2y)^{2} + 2 \geq 2,$ com igualdade justamente se $\displaystyle y = \frac{1}{2}x.$
Agora, queremos ver que $f_{xx}f_{yy}-f_{xy} ^{2}=0$ em todos os pontos críticos. Para isso, calculemos as segundas derivadas de $f$ \[ f_{xx}(x,y)=2, f_{xy}(x,y)=-4 \text{ e } f_{yy}(x,y)=8. \] Daí temos que $f_{xx}f_{yy}-f_{xy} ^{2}=2\cdot 8-(-4)^{2}=16-16=0$, como queríamos.
Por fim, queremos ver que esses pontos críticos são pontos de mínimo de $f$, mas como $f_{xx}f_{yy}-f_{xy} ^{2}=0$ o Teste de Derivada Segunda é inconclusivo. Mas, note que $f$ pode ser reescrita como \[ f(x,y)=x^2+4y^2-4xy+2=(x-2y)^2+2. \]
Como $(x-2y)^2\geq 0$, segue que $f(x,y)\geq 2$ para todo $(x,y)\in \mathbb{R}^2$. Em particular, se tomamos um ponto crítico de $f$, isto é, um ponto da forma $(2y,y)$ então $f(2y,y)=2$. Provando que os pontos críticos são pontos de mínimo de $f$.
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $f(x,y)=x^{3}y^{2}$.
$\displaystyle \frac{\partial^{2} f}{\partial x^{2}}= 2xy^{2},\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= 2x^{3}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} f}{\partial x\partial y}= \frac{\partial^{2} f}{\partial y\partial x}= 6x^{2}y.$
Calcule a integral iterada.
$\displaystyle\int_{1}^{3} \!\! \int_{0}^{1}(1+4xy)\, dx dy$
$\displaystyle\int_{2}^{4}\!\!\int_{-1}^{1}(x^{2}+y^{2})\,dy dx$
$10.$
$\dfrac{116}{3}.$
Nos itens abaixo:
Esboce o gráfico da curva plana com a equação vetorial dada;
Determine ${\bf r}'(t)$;
Esboce o vetor posição ${\bf r}(t)$ e o vetor tangente ${\bf r}'(t)$ para o valor dado de $t.$
${\bf r}(t)=(t-2,t^{2}+1)$ e $t=-1.$
${\bf r}(t)=\sin(t){\bf i}+2\; \cos(t){\bf j}$ e $t=\pi/4.$
${\bf r}(t)=(1+\cos{t}){\bf i}+(2+\sin{t}){\bf j}$ e $t=\pi/6.$
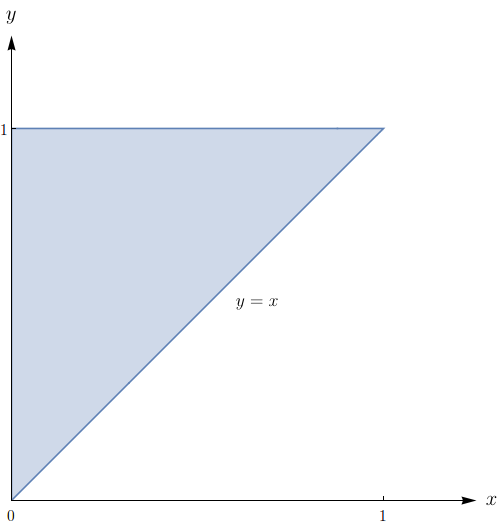
Seja $f$ uma função contínua em $[0,1]$ e seja $R$ a região triangular com vértices $(0,0), (1,0)$ e $(0,1)$. Mostre que
$$\iint\limits_{R} f(x,y) \, dA = \int_0^1 uf(u) \, du.$$
Utilize a mudança de variáveis $u = x + y$ e $v = y.$
Usando coordenadas esféricas, determine o volume do sólido que está dentro da esfera $x^{2}+y^{2}+z^{2}=4$, acima do plano $xy$ e abaixo do cone $z=\sqrt{x^{2}+y^{2}}.$
$\dfrac{8\sqrt{2}\pi}{3}.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 - 2xy + y^2$ e $x^2 + y^2 = 1.$
Pontos de máximo: $\displaystyle \left( \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}} \right)$ e $\displaystyle \left( -\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)$; ponto de mínimo: $\displaystyle \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$.
Determine a diferencial da função $m = p^5q^3$.
$dm = 5p^{4}q^{3} dp + 3p^{5}q^{2} dq$.
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas para o caso em que $f(x,y) = 1$:
$$\iint\limits_{R} dxdy = \iint\limits_{R}\left|\dfrac{\partial(x,y)}{\partial(u,v)}\right|\, dudv.$$
Aqui, $R$ é a região do plano $xy$ que corresponde à região $S$ do plano $uv$ sob a transformação dada por $x=g(u,v)$, $y=h(u,v)$. (Sugestão: observe que o lado esquerdo é $A(R)$. Converta a integral de linha sobre $\partial R$ para uma integral de linha sobre $\partial S$ e aplique o Teorema de Green no plano $uv$.)
Dica: pelo Teorema de Green, $A(R) = \displaystyle \iint_{R} dxdy = \int_{\partial R} x dy.$ Escolhendo a orientação positiva em $\partial S$ correspondente a orientação positiva em $\partial R,$ segue que
$$\displaystyle \int_{\partial R} x dy = \int_{\partial S} g(u,v) \dfrac{\partial h}{\partial u} du + g(u,v) \frac{\partial h}{\partial v} dv.$$
Conclua utilizando o Teorema de Green no plano $uv$ e a Regra da Cadeia.
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=x^{3}y\,{\bf i}-x^{2}y^{2}\,{\bf j}-x^{2}yz\,{\bf k}$ e $S$ é a superfície do sólido delimitado pelo hiperbolóide $x^{2}+y^{2}-z^{2}=1$ e pelos planos $z=-2$ e $z=2.$
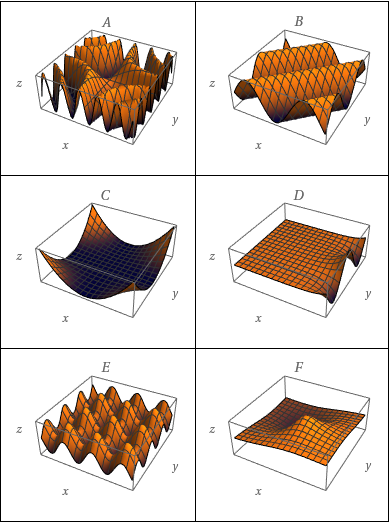
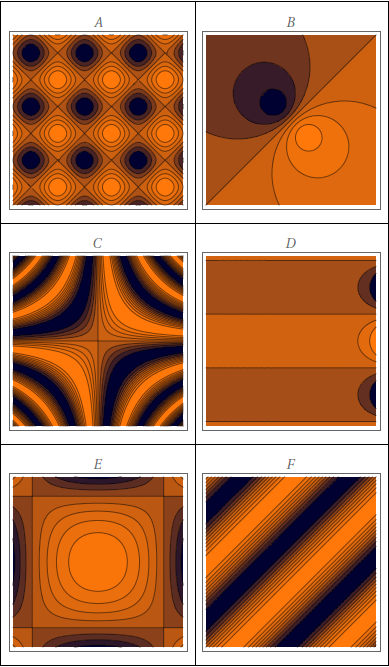
Faça uma correspondência entre a função: (i) e seu gráfico; (ii) e seus mapas de contorno. Justifique sua escolha.
$z=\sin(xy)$
$z=\sin(x-y)$
$z=(1-x^{2})(1-y^{2})$
$z=e^{x} \; \cos{y}$
$z=\sin{x}-\sin{y}$
$z=\dfrac{x-y}{1+x^{2}+y^{2}}$
$2x + y + 3z = 6$ é a equação do plano tangente ao gráfico de $f(x,y)$ no ponto $(1,1,1)$.
Calcule $\dfrac{\partial f}{\partial x}(1,1)$ e $\dfrac{\partial f}{\partial y}(1,1)$.
Determine a equação da reta normal no ponto $(1,1,1).$
$\displaystyle \frac{\partial f}{\partial x} (1,1) = -\frac{2}{3}$ e $\displaystyle \frac{\partial f}{\partial y} (1,1) = -\frac{1}{3}.$
$(x,y,z) = (1,1,1) + \lambda (2,1,3)$.
Usando coordenadas esféricas, determine o volume e o centroide do sólido que está acima do cone $\phi=\pi/3$ e abaixo da esfera $\rho=4\cos{\phi}.$
Volume: $10\pi;$ centróide: $(0,0,2,1).$
Dados ${\bf F}(x,y,z)=e^{y}\,{\bf i}+xe^{y}\,{\bf j}+(z+1)e^{z}\,{\bf k}$, $C: {\bf r}(t)=t\,{\bf i}+t^{2}\,{\bf j}+t^{3}\,{\bf k}$, $0\leq t\leq 1.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = x e^{y} + ze^{z};$
$2e.$
Seja \(f(x,y)=x-2y\) e considere uma subdivisão uniforme do retângulo \(R=[0,2]\times[0,2]\) em \(16\) retângulos menores. Tome \((x_k^\ast,y_k^\ast)\) como sendo o centro do \(k\)-ésimo retângulo e aproxime a integral dupla de \(f\) sobre \(R\) pela soma de Riemann resultante.
Compare o resultado obtido no item anterior com o valor exato da integral.
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, x^{2}+y^{2}+z^{2}\leq 1\}$ e ${\bf u}=x\,{\bf i}+y\,{\bf j}+z^{2}\,{\bf k}.$
Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.
$w=f(r,s,t)$, onde $r=r(x,y)$, $s=s(x,y)$, $t=t(x,y)$.
$\displaystyle \frac{\partial w}{\partial x} = \frac{\partial w}{\partial r}\frac{\partial r}{\partial x} + \frac{\partial w}{\partial s}\frac{\partial s}{\partial x} + \frac{\partial w}{\partial t}\frac{\partial t}{\partial x}$ e $\displaystyle \frac{\partial w}{\partial y} = \frac{\partial w}{\partial r}\frac{\partial r}{\partial y} + \frac{\partial w}{\partial s}\frac{\partial s}{\partial y} + \frac{\partial w}{\partial t}\frac{\partial t}{\partial y}$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=1$ e $B$ a região compreendida entre os gráficos de $y=\sin{x}$ e $y=1-\cos{x}$, com $0\leq x\leq \dfrac{\pi}{2}.$
$f(x,y)=\sqrt{1+y^{3}}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;\sqrt{x}\leq y\leq 1 \}.$
$f(x,y)=x$ e $B$ é o conjunto de todos $(x,y)$ tais que $y\geq x^{2}$ e $x\leq y\leq x+2.$
$f(x,y)=\dfrac{y}{x+y^{2}}$ e $B$ o conjunto de todos $(x,y)$ tais que $1\leq x\leq 4$ e $0\leq y\leq \sqrt{x}.$
$2 - \dfrac{\pi}{2}.$
$\dfrac{2(2\sqrt{2} - 1)}{9}.$
$\dfrac{13}{6}.$
$\dfrac{3 \ln(2)}{2}.$
Dada a função $f(x,y)=xy$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}$.
$Im(f) = \mathbb{R}.$
As curvas de nível são as hipérboles $xy = C$ quando $C \neq 0$ e os eixos $x$ e $y$ quando $C = 0.$
Calcule as integrais iteradas.
$\displaystyle\int_{0}^{1}\int_{0}^{x^{2}}(x+2y)\,dy dx$
$\displaystyle\int_{0}^{1}\int_{x^{2}}^{x}(1+2y)\,dy dx$
$\dfrac{9}{20}.$
$\dfrac{3}{10}.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=xy^{2}$, $D=\{(x,y) \in \mathbb{R}^2: x\geq 0,\;y\geq 0,\;x^{2}+y^{2}\leq3\}.$
Valor máximo: $2;$ valor mínimo: $0.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}(x^{2}+z^{2})\;dx dy dz$, onde $E$ é o cilindro $x^{2}+y^{2}\leq 1$ e $0\leq z \leq 1.$
$\displaystyle\iiint\limits_{ E}\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq z \leq 2x+2y-1.$
$\dfrac{7\pi}{12}.$
$\dfrac{\pi}{2}.$
O raio $r$ e a altura $h$ de um cilindro circular reto aumentam à razão de $0,01cm/min$ e $0,02cm/min$, respectivamente.
- Ache a taxa de variação do volume quando $r=4cm$ e $h=7cm.$
- A que taxa a área da superfície curva está variando nesse instante?
- $0,88\pi$ cm$^{3}/$min.
- $0,3\pi$ cm$^{2}/$min.
O elipsoide $4x^{2}+2y^{2}+z^{2}=16$ intercepta o plano $y=2$ em uma elipse. Determine as equações paramétricas da reta tangente à elipse no ponto $(1,2,2).$
$x = 1 + t,$ $y = 2,$ $z = 2 - 2t$.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}y^{3}\,ds$, $C:\,x=t^{3},\, y=t,\, 0\leq t\leq 2.$
$\displaystyle \frac{1}{54}\left(145^{3/2} - 1 \right).$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy}{\sqrt{x^2 + y^2}}$.
$0.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
$\displaystyle\int_{C}y^3 \, dx - x^3 \, dy$, $C$ é o círculo $x^2 + y^2 = 4$.
Observe que a curva $C$ com orientação positiva está nas hipóteses do Teorema de Green, assim como o campo $\mathbf{F}(x,y) = (y^3, -x^3)$. Logo,
$$\displaystyle\int_{C}y^3 \, dx - x^3 \, dy = \iint\limits_{D} \left(\frac{\partial}{\partial x}(-x^3) - \frac{\partial}{\partial y}(y^3)\right) \, dA = -3 \iint\limits_{D} (x^2 + y^2) \, dA,$$
em que $D = \{(x,y) \in \mathbb{R}^2: x^2 + y^2 \leq 4\}$. Usando coordenadas polares
$$\begin{cases}x = r \cos{\theta} \\y = r \sin{\theta}, \\\end{cases}$$
temos que a região de integração $D$ pode ser escrita como $$\{(r,\theta) \in \mathbb{R}^2: 0 \leq r \leq 2, 0 \leq \theta \leq 2 \pi\}$$ e o jacobiano dessa mudança de coordenadas é igual a $r$. Logo,
$$\iint\limits_{ D} (x^2 + y^2) dA = \displaystyle\int_{0}^{2\pi} \int_{0}^{2}r^2 \cdot r\,dr d\theta = 8\pi.$$
Portanto, $\displaystyle\int_{C}y^3 \, dx - x^3 \,dy = -24\pi$.
Determine se o campo vetorial $\mathbf{F}(x,y,z) = y\cos{xy}\mathbf{i} + x\cos{xy}\mathbf{j} - \sin{z}\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ é conservativo. $f(x,y,z) = \sin(xy) + \cos(z).$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{\ln 2} \int_{0}^{\sqrt{(\ln 2)^{2}-y^{2}}}e^{\sqrt{x^{2}+y^{2}}}\,dx dy$
$\displaystyle \frac{\pi(2\ln(2) - 1)}{2}.$
Seja $E$ a região limitada pelos paraboloides $z = x^2 + y^2$ e $z = 36 - 3x^2 - 3y^2$.
Ache o volume da região $E$.
Encontre o centroide de $E$ (centro de massa no caso em que a densidade é constante).
$162\pi.$
$(0,0,15)$.
Mostre que a integral de linha $\int_{C}2x\,\sin y\,dx+(x^{2}\,\cos y-3y^{2})\,dy$, onde $C$ é qualquer caminho entre $(-1,0)$ a $(5,1)$, é independente do caminho e calcule a integral.
$\mathbf{F} (x,y) = 2x \sin(y) \mathbf{i} + x^{2} \cos(y) - 3y^{2} \bf j$ é um campo conservativo com uma função potencial $f(x,y) = x^{2} \sin(y) - y^{3};$ o valor da integral é $25 \sin(1) - 1.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=\sqrt[3]{x^{2}+2xy+4y^{2}-6x-12y}$.
Ponto de mínimo: $\displaystyle \left( 2,1\right).$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=x^{2}\,{\bf i}+(x-y)\,{\bf j}$, ${\bf r}(t)=(t,\sin t)$, $0\leq t\leq \pi.$
$\displaystyle \frac{\pi^{3}}{3} - 2.$
Uma partícula se move no plano $xy$ de tal maneira que sua posição no instante $t$ é
$$\textbf{r}(t) = (t - \sin{t} )\textbf{i} + (1 - \cos{t})\textbf{j}.$$
Trace o gráfico de $\textbf{r}(t)$. A curva resultante é chamada de ciclóide.
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$
${\bf r}(u,v)=(u,v,1-u^{2})$, $u\geq 0$,\, $v\geq 0$ e $u+v\leq 1.$
As equações paramétricas \[\begin{array}{lll} x=u, & y=u\cos v, & z=u\sin v \end{array}\] representam o cone que resulta quando a reta \(y=x\) do plano \(xy\) é girada em torno do eixo \(x\). Determine a área de superfície da parte do cone para a qual \(0\leq u\leq 2\) e \(0\leq v\leq 2\pi\).
Sendo \(\displaystyle\{\mathbf{i},\mathbf{j},\mathbf{k}\}\) a base canônica do espaço, a superfície pode ser representada vetorialmente como \[ \mathbf{r}=u\mathbf{i}+u\cos v\mathbf{j}+u\sin v\mathbf{k} \ \ \left(0\leq u\leq 2,\ 0\leq v\leq 2\pi\right). \] Assim, teremos \begin{align*} \dfrac{\partial\mathbf{r}}{\partial u} & = \mathbf{i} + \cos v\mathbf{j} + \sin v\mathbf{k} \\ \dfrac{\partial\mathbf{r}}{\partial v} & = - u\sin v\mathbf{j} + u\cos v\mathbf{k} \\ \dfrac{\partial\mathbf{r}}{\partial u}\times\dfrac{\partial\mathbf{r}} {\partial v} & = \left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & \cos v & \sin v \\ 0 & -u\sin v & u\cos v \end{array} \right| = u\mathbf{i} -u\cos v\mathbf{j} - u\sin v\mathbf{k} \\ \|\dfrac{\partial\mathbf{r}}{\partial u}\times \dfrac{\partial\mathbf{r}}{\partial v}\| & = \sqrt{u^2+(-u\cos v)^2+(-u\sin v)^2} = |u|\sqrt{2} = u\sqrt{2}. \end{align*} Segue, portanto, que \[ S = \iint\limits_R\|\dfrac{\partial\mathbf{r}}{\partial u}\times \dfrac{\partial\mathbf{r}}{\partial v}\|\,dA = \int_0^{2\pi}\int_0^2\sqrt{2}u\,dudv = 2\sqrt{2}\int_0^{2\pi}\,dv = 4\pi\sqrt{2}. \]
Mostre que se \(f_x(x,y)=0\) e \(f_y(x,y)=0\) em toda uma região circular, então \(f(x,y)\) é constante nessa região.
Calcule $\dfrac{\mathrm{d}{\bf r}}{\mathrm{d}t}$ e $\dfrac{\mathrm{d}^{2}{\bf r}}{\mathrm{d}t^{2}}.$
- ${\bf r}(t)=(3t^{2},e^{-t},\ln(t^{2}+1))$
- ${\bf r}(t)=\sqrt[3]{t^{2}}{\bf i}+\cos(t^{2}){\bf j}+3t{\bf k}$
- ${\bf r}(t)=\sin(5t){\bf i}+\cos(4t){\bf j}-e^{-2t}{\bf k}$
Ao calcular, por integração dupla, o volume $V$ do sólido situado abaixo do parabolóide $z=x^{2}+y^{2}$ e limitado inferiormente por uma certa região $D$ no plano $xy$, chegou-se à seguinte expressão: $$V=\int_{0}^{1}\!\!\int_{0}^{y}(x^{2}+y^{2})\,dx dy+\int_{1}^{2}\int_{0}^{2-y}(x^{2}+y^{2})\,dx dy.$$
Esboce a região $D.$
Expresse $V$ numa única integral dupla iterada.
Efetue a integração para calcular $V.$
...
$\displaystyle \int_{0}^{1} \int_{x}^{2 - x} x^{2} + y^{2}\;dy\; dx$
$\dfrac{4}{3}.$
Determine a menor distância entre os planos paralelos $2x+3y-z=2$ e $2x+3y-z=4.$
$\displaystyle \frac{\sqrt{14}}{7}.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S}{\bf a}\cdot {\bf n}\,dS=0$, onde ${\bf a}$ é um vetor constante.
Dica: Note que $\mbox{div} {\bf a} = 0.$
Calcule $\int_{0}^{1}\!\int_{x}^{1}3y^{4}\cos(xy^{2})\,dy dx$. Esboce a região de integração.
$1 - \cos(1).$
Inverta a ordem de integração, integrando primeiro em $y$ e depois em $x$ para calcular a integral:
$\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}^{1}\sqrt{x^{3}+1}\,dx dy$
$\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}\sin{x^{3}}\,dx dy$
$\dfrac{2(2\sqrt{2} - 1)}{9}.$
$\dfrac{2}{3} \sin^{2}\left(\dfrac{1}{2} \right).$
Determine a equação da reta tangente à trajetória da função \newline${\bf r}(t)=\bigg(\dfrac{1}{t},
\dfrac{1}{t},t^{2}\bigg)$, no ponto ${\bf r}(2)$.
$${\bf r}(2)=\bigg(\frac{1}{2},\frac{1}{2},4\bigg)\,\,\,\,\,\, e \,\,\,\,\,\, \frac{d{\bf r}}{dt}=\bigg(-\frac{1}{t^{2}},-\frac{1}{t^{2}},2t\bigg).$$
Assim,
$$\frac{d{\bf r}}{dt}(2)=\bigg(-\frac{1}{4},-\frac{1}{4},4\bigg).$$
Portanto, a equação da reta tangente em ${\bf r}(2)$ é:
$${\bf x}={\bf r}(2)+\lambda \frac{d{\bf r}}{dt}(2),\,\, \lambda \in \mathbb{R},$$
ou seja,
$$(x,y,z)=\bigg(\frac{1}{2},\frac{1}{2},4\bigg)+\lambda \bigg(-\frac{1}{4},-\frac{1}{4},4\bigg),\,\, \lambda \in \mathbb{R}.$$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(3\sin 2u,6\sin^{2} u, v)$,$0\leq u\leq \pi$, no ponto ${\bf r}(\pi/3,0).$
$x^{2} + (y-3)^{2} = 9.$
Mostre que qualquer função da forma
$$z=f(x+at)+g(x-at)$$
é uma solução da equação de onda
$$\frac{\partial^{2} z}{\partial t^{2}}=a^{2}\frac{\partial^{2}z}{\partial x^{2}}.$$
(Sugestão: Tome $u=x+at$, $v=x-at$.)
Note que se $u = x + at$ e $v = x - at,$ então $\displaystyle \frac{\partial^{2} z}{\partial t^{2}} = a^{2}f''(u) + a^{2} g''(v)$e\\$\displaystyle \frac{\partial^{2} z}{\partial x^{2}} = f''(u) + g''(v).$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}x\,dx dy$, onde $R$ é a região, no plano $xy$, limitada pela curva (dada em coordenadas polares) $\rho=\cos(3\theta)$, $-\dfrac{\pi}{6}\leq \theta \leq \dfrac{\pi}{6}.$
$\displaystyle \frac{81\sqrt{3}}{320}.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=\ln(x+2y+3z)$.
$\displaystyle f_{x} = \frac{1}{x + 2y + 3z},\;\;\;\; f_{y} = \frac{2}{x + 2y + 3z}\;\;\;\;\text{e}\;\;\;\; f_{z} = \frac{3}{x + 2y + 3z}$.
Esboce o campo vetorial $\textbf{F}= y\textbf{i} + \dfrac{1}{2}\textbf{j}$, desenhando um diagrama.
Encontre a área da região descrita como sendo a parte do cone \(z=\sqrt{x^2+y^2}\) dentro do cilindro \(x^2+y^2=2x\).
Encontre os pontos da curva $x^2 - 6xy - 7y^2 + 80 = 0$ mais próximos da origem. Desenhe a curva.
$(1,3)$ e $(-1,-3).$ Realizando a mudança de coordenadas $x = \frac{1}{\sqrt{10}} u - \frac{3}{\sqrt{10}} v$ e $y = \frac{3}{\sqrt{10}} u + \frac{1}{\sqrt{10}} v,$ a equação da curva inicial é transformada em $\frac{u^{2}}{10} - \frac{v^{2}}{40} = 1,$.
Calcule $\int_{C}2x\,\cos y\,dx-x^{2}\,\sin y\,dy$ ao longo dos caminhos $C$ a seguir no plano $xy.$
A parabóla $y=(x-1)^{2}$ de $(1,0)$ a $(0,1).$
O segmento de reta de $(-1,\pi)$ a $(1,0).$
O eixo $x$ de $(-1,0)$ a $(1,0).$
O astróide ${\bf r}(t)=(\cos^{3} t)\,{\bf i}+(\sin^{3}t)\,{\bf j}$, $0\leq t\leq 2\pi$, no sentido anti-horário de $(1,0)$ de volta a $(1,0).$
$-1.$
$2.$
$0.$
$0.$
Determine o volume do sólido.
Abaixo do paraboloide $z=x^{2}+y^{2}$ e acima da região delimitada por $y=x^{2}$ e $x=y^{2}.$
Abaixo do paraboloide $z=3x^{2}+y^{2}$ e acima da região delimitada por $y=x$ e $x=y^{2}-y.$
$ $ Abaixo da superfície $z=xy$ e acima do triângulo com vértices $(1,1)$, $(4,1)$ e $(1,2).$
Limitado pelo cilindro $y^{2}+z^{2}=4$ e pelos planos $x=2y$, $x=0$ e $z=0$, no primeiro octante.
$\dfrac{6}{35}.$
$\dfrac{144}{35}.$
$\dfrac{31}{8}.$
$\dfrac{16}{3}.$
Determine a equação da reta tangente à curva de nível dada, no ponto dado.
$e^{2x - y} + 2x + 2y = 4$, em $\left(\dfrac{1}{2},1\right)$.
$y = -4x + 3.$
Determine se o conjunto $\{(x,y)|\,1<x^{2}+y^{2}<4\}$ é ou não:
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,1<x^{2}+y^{2}<4\}$ representa a região anelar entre os círculos com centro $(0,0)$ e raio $1$ e $2$. Então:
$D$ é aberto pois, em torno de cada ponto em $D$, podemos colocar um disco que se encontra inteiramente em $D$.
$D$ é conexo pois quaisquer dois pontos de $D$ podem ser conectados por um caminho em $D$.
$D$ não é simplesmente conexo pois, por exemplo, a região delimitada pela curva simples e fechada $x^{2}+y^{2}=(3/2)^2$ possui pontos que não estão em $D$, por exemplo, a origem $(0,0)$.
Determine uma representação paramétrica para a superfície descrita a seguir. A porção da esfera $x^{2}+y^{2}+z^{2}=3$ entre os planos $z=\sqrt{3}/2$ e $z=-\sqrt{3}/2.$
$x = \sqrt{3}\sin(\phi)\cos(\theta),$ $y = \sqrt{3}\sin(\phi)\sin(\theta),$ $z = \sqrt{3}\cos(\phi),$ onde $\dfrac{\pi}{3} \leq \phi \leq \dfrac{2\pi}{3}$ e $0 \leq \theta \leq 2\pi.$
Como não há antiderivada elementar da função \(e^{x^2}\), a integral \[ \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy \] não pode ser calculada integrando-se primeiro em relação a \(x\). Calcule essa integral expressando-a como uma integral iterada equivalente com ordem de integração invertida.
A região de integração é dada por \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq y\leq 2,\ y/2\leq x\leq 1\}\). Vamos inverter a ordem de integração sobre a região \(R\):\begin{align*} \int_0^2\int_{y/2}^1 e^{x^2}\, dxdy & = \iint\limits_R e^{x^2}\,dA = \int_0^1\int_0^{2x} e^{x^2}\,dydx= \int_0^1\left[e^{x^2}y\right]_{y=0}^{2x}\,dx \\ & = \int_0^1 2xe^{x^2}\,dx = \left.e^{x^2}\right]_0^1 = e-1 \end{align*}
Esboce o sólido descrito pelas desigualdades $0 \leq r \leq 2$, $-\pi/2 \leq \theta \leq \pi/2$ e $0 \leq z \leq 1$.
$$f(x,y)=\sqrt{x+y^{2}-3}$$
- Faça um esboço das curvas de nível de $f$ nos níveis $c=0$, $c=1$ e $c=3.$
- Quantas curvas de nível de $f$ passam pelo ponto $(3,-1)$?
As curvas de níveis de $f$ são
$$\sqrt{x+y^{2}-3}=c\,\,\,\,\mbox{ou}\,\,\,\,x+y^{2}-3=c^2\,\,\,\,\mbox{ou}\,\,\,\,x=3+c^2-y^{2},$$
ou seja, uma família de parábolas com concavidade para a esquerda. As três curvas de níveis pedidas, obtidas considerando respectivamente $c=0$, $c=1$ e $c=3$, são
$x=3-y^{2}$, $x=4-y^{2}$ e $x=12-y^{2}.$ Elas estão apresentadas na figura abaixo.
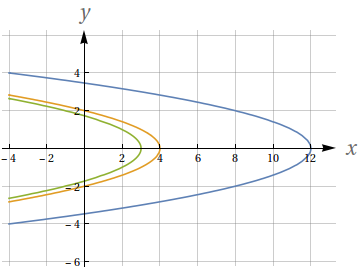
Pelo ponto $(3,-1)$ passa uma única curva de nível, isto é, $f(x,y)=1.$ Pois caso contrário o ponto $(3,-1)$ teria duas alturas diferentes, o que é impossível.
Seja $S$ a parte do parabolóide $z=2-x^{2}-y^{2}$ que está acima do plano $z=1.$ Calcule o fluxo do campo vetorial ${\bf F}(x,y,z)=\frac{1}{(x^{2}+y^{2}+z^{2})^{3/2}}(x,y,z)$ através de $S.$
Determine a área da superfície com equações paramétricas $x=u^{2}$, $y=uv$, $z=\dfrac{1}{2}v^{2}$, $0\leq u\leq 1$, $0\leq v\leq 2.$
$4.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 - 2y^2$ e $x^2 + y^2 - 2x = 0.$
Ponto de máximo: $\displaystyle \left( 2,0 \right)$; pontos de mínimo: $\displaystyle \left( \frac{2}{3}, \frac{2\sqrt{2}}{3} \right)$ e $\displaystyle \left( \frac{2}{3}, \frac{-2\sqrt{2}}{3} \right)$.
Se um arame com densidade linear $\rho(x,y)$ está sobre uma curva plana $C$, seus momentos de inércia em relação aos eixos $x$ e $y$ são definidos por
$$I_{x}=\int_{C}y^{2}\rho(x,y)\,ds I_{y}=\int_{C}x^{2}\rho(x,y)\,ds.$$
Determine os momentos de inércia de um arame com o formato de um semicírculo $x^{2}+y^{2}=1$, $y\geq 0$, que é mais grosso perto da base do que perto do topo, se a função densidade linear em qualquer ponto for proporcional à sua distância à reta $y=1.$
$I_{x} = k\left(\dfrac{\pi}{2} - \dfrac{4}{3} \right)$ e $I_{y} = k\left(\dfrac{\pi}{2} - \dfrac{2}{3} \right).$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=\displaystyle\int_{y}^{x}\cos^2t \ \mathrm{d}t$.
Sendo $f(x,y)=\displaystyle\int_{y}^{x}\cos (t^{2})\,dt$, temos que as derivadas parciais em relação a $x$ e $y$, respectivamente, são:
$\bullet \dfrac{\partial}{\partial x}f(x,y)=\dfrac{\partial}{\partial x}\bigg(\displaystyle\int_{y}^{x}\cos(t^{2})\bigg)=\cos(x^{2}).$
$\bullet \dfrac{\partial}{\partial y}f(x,y)=\dfrac{\partial}{\partial y}\bigg(\displaystyle\int_{y}^{x}\cos(t^{2})\bigg)=\dfrac{\partial}{\partial y}\bigg(-\displaystyle\int_{x}^{y}\cos(t^{2})\bigg)=-\cos(y^{2}).$
Notemos que nas soluções das derivadas parciais acima utilizamos o Teorema Fundamental do Cálculo.
Inverta a ordem de integração.
$\displaystyle\int_{1}^{e}\bigg[\int_{\ln(x)}^{x}f(x,y)\,dy\bigg]dx.$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{y+3}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{1}^{e^{y}}f(x,y)\,dx\bigg]dy. + \displaystyle\int_{1}^{e}\bigg[\int_{y}^{1}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{x}f(x,y)\,dy\bigg]dx + \displaystyle\int_{1}^{3}\bigg[\int_{0}^{1}f(x,y)\,dy\bigg]dx + \displaystyle\int_{3}^{4}\bigg[\int_{x-3}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{-1}^{1}\bigg[\int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}f(x,y)\,dx\bigg]dy$
Seja $S$ uma superfície plana paralela ao plano $xy$. Mostre que a fórmula para o cálculo de áreas de superfícies nesse caso reduz à fórmula de integrais duplas para o cálculo de área de regiões planas.
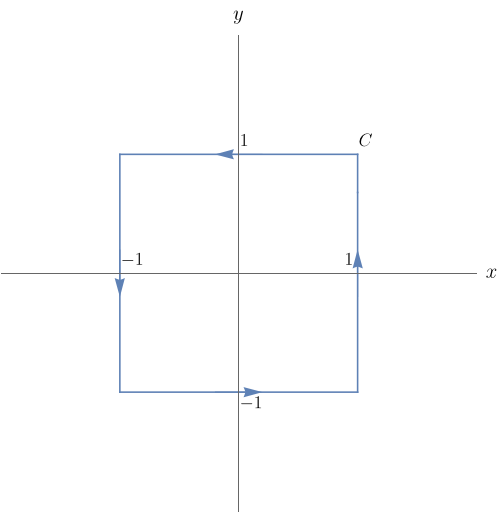
Calcule a integral de linha $\displaystyle\int_{C}\sqrt[3]{x}\,dx+\dfrac{dy}{1+y^{2}}$, onde $C$ é a curva na figura abaixo.
$0.$
Determine as derivadas parciais de $z=\arctan \dfrac{x}{y}$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{y}{x^{2} + y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{-x}{x^{2} + y^{2}}.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x + y}{x - y}$, caso exista.
Não existe.
Determine o jacobiano da transformação dada por: $x = \alpha \sin{\beta}, \quad y = \alpha \cos{\beta}$.
$-\alpha.$
Esboce o campo vetorial $\textbf{F}= \dfrac{y\textbf{i} - x\textbf{j}}{\sqrt{x^2+y^2}}$, desenhando um diagrama.
A Lei de Coulomb afirma que a força eletrostática \(\mathbf{F}(\mathbf{r})\) que uma partícula com carga \(Q\) exerce sobre outra partícula com carga \(q\) é dada pela fórmula \[ \mathbf{F}(\mathbf{r}) = \dfrac{q\,Q}{4\pi\epsilon_0\|\mathbf{r}\|^3}\mathbf{r}, \] onde \(\mathbf{r}\) é o vetor posição da carga \(q\) em relação a \(Q\) e \(\epsilon_0\) é uma constante positiva (chamada permissividade do meio).
Expresse o campo vetorial \(\mathbf{F}(\mathbf{r})\) em forma de coordenadas \(\mathbf{F}(x,y,z)\) com \(Q\) na origem.
Calcule o trabalho realizado pelo campo vetorial \(\mathbf{F}\) sobre uma carga \(q\) que se move ao longo de um segmento de reta de \((3,0,0)\) para \((3,1,5)\).
Seja $g(t)=f(3t^{2},t^{3},e^{2t})$ e suponha $\dfrac{\partial f}{\partial z}(0,0,1)=4.$
- Expresse $g^{'}(t)$ em termos das derivadas parciais de $f.$
- Calcule $g^{'}(0).$
- $\displaystyle g^{'}(t) = 6t \frac{\partial f}{\partial x}(3t^{2},t^{3},e^{2t}) + 3t^{2} \frac{\partial f}{\partial y}(3t^{2},t^{3},e^{2t}) + 2e^{2t} \frac{\partial f}{\partial z}(3t^{2},t^{3},e^{2t}).$
- $g^{'}(0) = 8.$
Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=x^{2}\,{\bf i}+xy\,{\bf j}+z\,{\bf k}$, $E$ é o sólido delimitado pelo paraboloide $z=4-x^{2}-y^{2}$ e pelo plano $xy.$
$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = 8\pi.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}+3xy+4y^{2}-6x+2y$.
Ponto de mínimo: $\displaystyle \left( \frac{54}{7}, -\frac{22}{7} \right).$
Calcule a integral dupla.
$\displaystyle\iint\limits_{ D}x^{3}y^{2}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq 2,\;-x\leq y\leq x\}.$
$\displaystyle\iint\limits_{D}x\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq \pi,\;0\leq y\leq \sin{x}\}.$
$\displaystyle\iint\limits_{D}x^{3}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;1\leq x\leq e,\;0\leq y\leq \ln(x)\}.$
$\displaystyle\iint\limits_{D}y^{2}e^{xy}\,dA, \quad D=\{(x,y) \in \mathbb{R}^2|\;0\leq y\leq 4,\;0\leq x\leq y\}.$
$\displaystyle\iint\limits_{D}y^{3}\,dA, \quad D$ região com vértices $(0,2)$, $(1,1)$ e $(3,2).$
$\dfrac{256}{21}.$
$\pi.$
$\dfrac{3e^{4} + 1}{16}.$
$\dfrac{e^{16} - 17}{2}.$
$\dfrac{147}{20}.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2 + y^2}{\sqrt{x^2 + y^2 + 1} - 1}$.
$2.$
A força em um ponto $(x,y)$ de um plano coordenado é ${\bf F}(x,y)=(x^{2}+y^{2})\,{\bf i}+xy\,{\bf j}$. Ache o trabalho realizado por ${\bf F}(x,y)$ ao longo do gráfico de $y=x^{3}$ de $(0,0)$ a $(2,8).$
$\dfrac{1592}{21}.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xy\,dx+(x-y)\,dy$, $C$ consiste nos segmentos de reta de $(0,0)$ a $(2,0)$ e de $(2,0)$ a $(3,2).$
$\displaystyle \frac{17}{3}.$
$f(x,y) = \begin{cases}\dfrac{xy^2}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\0, & \quad \text{se } (x,y) = (0,0), \end{cases}$ é contínua em (0,0)? Justifique.
Notemos que para $(x,y)\neq (0,0)$ a função $f$ é contínua, pois $xy^{2}$ e $x^{2}+y^{2}$ são funções contínuas e $x^{2}+y^{2}\neq 0.$ Agora, estudemos a continuidade da função $f$ no ponto $(0,0).$ Temos que
$$\lim_{(x,y)\to (0,0)}f(x,y)=\lim_{(x,y)\to (0,0)}\frac{xy^{2}}{x^{2}+y^{2}}=\lim_{(x,y)\to (0,0)}x\cdot \frac{y^{2}}{x^{2}+y^{2}}.$$
Como
$$\lim_{(x,y)\to (0,0)}x=0\,\,\,\,\,\, \mbox{e}\,\,\,\,\,\, \bigg| \dfrac{y^{2}}{x^{2}+y^{2}}\bigg|\leq 1,\, \forall (x,y)\neq (0,0),$$
obtemos que
$$\lim_{(x,y)\to (0,0)}f(x,y)=0.$$
Assim,
$$\lim_{(x,y)\to (0,0)}f(x,y)=0=f(0,0).$$
Portanto, $f$ é contínua em $(0,0).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}y\,dA$, onde $R$ é a região no primeiro quadrante limitada pelo semi-círculo $x^{2}+y^{2}=2x.$
$\displaystyle \frac{2}{3}.$
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$x^{2}+y^{2}+z^{2}=3xyz$
$\displaystyle \frac{dz}{dx} = \frac{3yz - 2x}{2z - 3xy}$ e $\displaystyle \frac{dz}{dy} = \frac{3xz - 2y}{2z - 3xy} .$
Determine a derivada direcional de $f$ no ponto dado e na direção indicada pelo ângulo $\theta$.
$f(x,y) = x^2y^3 - y^4, (2,1),$ $\theta = \pi/4.$
$6\sqrt{2}.$
Encontre ${\bf r}(t)$ se ${\bf r}'(t)=2t\;{\bf i}+3t^{2}\;{\bf j}+\sqrt{t}\;{\bf k}$ e ${\bf r}(1)={\bf i}+{\bf j}.$
Como ${\bf r}'(t)=2t\;{\bf i}+3t^{2}\;{\bf j}+\sqrt{t}\;{\bf k}$, temos que
$${\bf r}(t)=t^{2}\,{\bf i}+t^{3}\,{\bf j}+\frac{2}{3}t^{3/2}\,{\bf k}+C.$$
Mas, ${\bf r}(1)={\bf i}+{\bf j}$, logo
$${\bf i}+{\bf j}={\bf i}+{\bf j}+\frac{2}{3}{\bf k}+C$$
implicando que $C=\dfrac{2}{3}\,{\bf k}.$
Portanto
$${\bf r}(t)=t^{2}\,{\bf i}+t^{3}\,{\bf j}+\frac{2}{3}(t^{3/2}-1)\,{\bf k}.$$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t,$ onde
$$z=\sin{\theta}\cos{\phi}, \quad \theta=st^{2}, \quad \phi=s^{2}t.$$
Utilizando a Regra de Cadeia, obtemos
\begin{eqnarray*}
\frac{\partial z}{\partial s} & = & \frac{\partial z}{\partial \theta}\frac{\partial \theta}{\partial s}+\frac{\partial z}{\partial \phi}\frac{\partial \phi}{\partial s} \\
& = & (\cos{\theta}\cos{\phi})(t^2) + (\sin{\theta}(-\sin{\phi}))(2st) \\
& = & t^2\cos(st^2)\cos(s^2t) - 2st\sin(st^2)\sin(s^2t)
\end{eqnarray*}
e
\begin{eqnarray*}
\frac{\partial z}{\partial t} & = & \frac{\partial z}{\partial \theta}\frac{\partial \theta}{\partial t}+\frac{\partial z}{\partial \phi}\frac{\partial \phi}{\partial t} \\
& = & (\cos{\theta}\cos{\phi})(2st) + (\sin{\theta}(-\sin{\phi}))(s^2) \\
& = & 2st\cos(st^2)\cos(s^2t) - s^2\sin(st^2)\sin(s^2t).
\end{eqnarray*}
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=xy+2x-\ln(x^{2}y)$.
Ponto de mínimo: $\displaystyle \left(\frac{1}{2},2\right).$
Se $f(x_0,y_0) = 3$, o que podemos dizer sobre
$$\displaystyle \lim_{(x,y) \to (x_0,y_0)}f(x,y)$$
se $f$ for contínua em $(x_0,y_0)$? E se $f$ não for contínua em $(x_0,y_0)$? Justifique sua resposta.
Se $f$ for contínua em $(x_{0},y_{0}),$ então o limite é igual a $f(x_{0},y_{0}) = 3.$ Se não for contínua em $(x_{0},y_{0}),$ então o limite pode ter qualquer valor diferente de $3.$
Determine o trabalho $W = \int_{C}\mathbf{F}\cdot\, d\mathbf{r}$ realizado pelo campo de força
$$\mathbf{F}(x,y) = x\mathbf{i} + (x^3 + 3xy^2)\mathbf{j}$$
em uma partícula que inicialmente está no ponto $(-2,0)$, se move ao longo do eixo $x$ para $(2,0)$ e então se move ao longo da semicircunferência $y = \sqrt{4-x^2}$ até o ponto inicial.
$12\pi.$
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}$, $S$ é a esfera $x^{2}+y^{2}+z^{2}=9.$
$108\pi.$
Verifique que para o vetor posição \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) valem as seguintes propriedades
\(\displaystyle \mathrm{div\,}\mathbf{r} = 3\)
\(\displaystyle \nabla\dfrac{1}{\|\mathbf{r}\|} = -\dfrac{\mathbf{r}}{\|\mathbf{r}\|^3} \)
A função diferenciável $z = f(x,y)$ é dada implicitamente pela equação $x^3 + y^3 + z^3 = 10$. Determine a equação do plano tangente ao gráfico de $f$ no ponto $(1,1,f(1,1))$.
$x + y + 4z = 10.$
Determine a área da superfície dada pela parte de baixo da esfera $x^{2}+y^{2}+z^{2}=2$ cortada pelo cone $z=\sqrt{x^{2}+y^{2}}.$
Sejam
$$\left \{\begin{array}{cc}x=r\,\sin \phi\,\cos \theta\\y=r\,\sin \phi\,\sin \theta\\z=r\,\cos \phi\\\end{array}\right. \Rightarrow r=\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{2},\, \mbox{na\,esfera}.$$
Temos que
$$x^{2}+y^{2}+z^{2}=2 \mbox{e}\,\,\,\, z=\sqrt{x^{2}+y^{2}}\Rightarrow z^{2}+z^{2}=2\Rightarrow z^{2}=1\Rightarrow z=1\,(\mbox{pois}\, z\geq 0).$$
Logo, $\phi=\frac{\pi}{4}.$ Para a parte inferior da esfera cortado pelo cone, temos que $\phi=\pi.$
Então,
$$r(\phi,\theta)=(\sqrt{2}\,\sin \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\sin \theta)\,{\bf j}+(\sqrt{2}\,\cos \phi)\,{\bf k},$$
$$\frac{\pi}{4}\leq \phi\leq \pi\,\,\,\, \mbox{e}\,\,\,\, 0\leq \theta \leq 2\pi.$$
Isso implica que
$$r_{\phi}(\phi,\theta)=(\sqrt{2}\,\cos \phi,\,\cos\theta)\,{\bf i}+(\sqrt{2}\,\cos \phi\,\sin \theta)\,{\bf j}-(\sqrt{2}\,\sin \phi)\,{\bf k}$$
e
$$r_{\theta}(\phi,\theta)=(-\sqrt{2}\,\sin \phi,\,\sin\theta)\,{\bf i}+(\sqrt{2}\,\sin \phi\,\cos \theta)\,{\bf j}+0\,{\bf k}$$
Logo,
$$\begin{array}{rcl}r_{\phi}\times r_{\theta}&=&\left|\begin{array}{ccc}{\bf i}&{\bf j}&{\bf k}\\\sqrt{2}\,\cos \phi\,\cos \theta & \sqrt{2}\,\cos \phi\,\sin \theta& -\sqrt{2}\,\sin \phi\\-\sqrt{2}\,\sin \phi\,\sin \theta & \sqrt{2}\,\sin \phi\,\cos \theta & 0\end{array}\right|\\&=&(2\,\sin^{2}\phi\,\cos \theta)\,{\bf i}+(2\sin^{2}\phi\,\sin \theta)\,{\bf j}+(2\,\sin \phi \,\cos \phi)\,{\bf k}.\\\end{array}$$
Isso resulta que
$$\begin{array}{rcl}|r_{\phi}\times r_{\theta}|&=&\sqrt{4\sin^{2}\phi\,\cos^{2}\theta+4\,\sin^{4}\,\sin^{2}\theta+4\sin^{2}\phi\,\cos^{2}\phi}\\&=&\sqrt{4\,\sin^{2}\phi}=2|\sin\phi|=2\sin \phi \bigg(\mbox{pois},\, \frac{\pi}{4}\leq \phi \leq \pi\bigg).\end{array}$$
Assim,
$$A=\iint\limits_{ D}|r_{\phi}\times r_{\theta}|\,dA=\int_{\frac{\pi}{4}}^{\pi}\int_{0}^{2\pi}2\sin \phi\, d\theta d \phi=2\int_{\frac{\pi}{4}}^{\pi}\sin \phi\,d\phi \cdot \int_{0}^{2\pi}d\theta$$
$$=2\cdot (-\cos \phi)\bigg|_{\frac{\pi}{4}}^{\pi}\cdot \theta\bigg|_{0}^{2\pi}=2\cdot \bigg(1-\frac{\sqrt{2}}{2}\bigg)\cdot 2\pi=4\pi\bigg(1-\frac{\sqrt{2}}{2}\bigg)=\pi(4-2\sqrt{2})$$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2 \ \mbox{sen}^2y}{x^2 + 2y^2}$.
$0.$
Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro cresce.
- $\textbf{r}(t) = (t, \cos{2t}, \sin{2t})$
- $\textbf{r}(t) = (1 + t, 3t, -t)$
Determine o valor médio de $f(x,y)=e^{y}\sqrt{x+e^{y}}$ sobre o retângulo $R=[0,4]\times [0,1].$
$\dfrac{(4 + e)^{5/2} - e^{5/2} - 5^{5/2} + 1}{15}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=(e^{-y}-2x,-xe^{-y}-\sin y)$, ${\bf r}(t)=(t,\tan t)$, $0\leq t\leq \pi/4.$
$\displaystyle \cos(1) - \frac{\pi}{4}e^{-1} - \frac{\pi^{2}}{16} - 1.$
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint\limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$

$\displaystyle \int_{-1}^{1} \int_{0}^{1 - x^2} f(x,y) dy dx .$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla{r} = \dfrac{\mathbf{r}}{r}$.
$\nabla{r} = \left(\dfrac{x}{\sqrt{x^2 + y^2 + z^2}},\dfrac{y}{\sqrt{x^2 + y^2 + z^2}} ,\dfrac{z}{\sqrt{x^2 + y^2 + z^2}} \right).$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.
- ${\bf F}(x,y,z) = (2xyz-2y,x^2+2x,x^2+2y)$, $C$ é a circunferência $y^2+z^2=1$, $x=2$.
$2\pi$.
Utilize a integral dupla para determinar a área da região: dentro da cardióide $r=1+\cos{\theta}$ e fora do círculo $r=3\cos{\theta}.$
$\displaystyle \frac{\pi}{4}.$
Calcule as derivadas parciais de $w = \dfrac{xyz}{x + y + z}$.
$\displaystyle \frac{\partial w}{\partial x} = \frac{yz(y+z)}{(x+y+z)^{2}},\;\;\;\; \frac{\partial w}{\partial y} = \frac{xz(x+z)}{(x+y+z)^{2}}\;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial w}{\partial z} = \frac{xy(x+y)}{(x+y+z)^{2}}.$
Determine a área da superfície $z=\frac{2}{3}(x^{3/2}+y^{3/2})$, $0\leq x \leq 1$ e $0\leq y\leq 1.$
$\dfrac{4}{15}(3^{5/2} - 2^{7/2} + 1).$
Usando coordenadas esféricas, determine o centroide e o momento de inércia em relação a um diâmetro de sua base do hemisfério sólido homogêneo de raio $a.$
Centróide: $\left(0,0,\dfrac{3a}{8} \right);$ momento de inércia: $\dfrac{4 K a^5 \pi}{15},$ onde $K$ é a densidade constante.
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, x^{2}+y^{2}\leq 1,\,x^{2}+y^{2}\leq z \leq 5-x^{2}-y^{2}\}$ e ${\bf u}=3xy\,{\bf i}-\dfrac{3}{2}y^{2}\,{\bf j}+z\,{\bf k}.$
$36\pi.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=3x-y$ no conjunto $D$ de todas $(x,y)$ tais que $x\geq 0$, $y\geq 0$, $y-x\leq 3$, $x+y\leq 4$ e $3x+y\leq 6.$
Valor máximo: $6;$ valor mínimo: $-3.$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo hiperboloide $-x^2-y^2+z^2=1$ e acima do plano $xy.$
$\displaystyle \frac{4\pi}{3}.$
Determine a área da superfície dada pela parte do plano $3x+2y+z=6$ que está no primeiro octante.
$3\sqrt{14}.$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y) = \dfrac{y^2}{x}, (2,4).$
$4\sqrt{2}.$
Utilize a transformação dada para calcular a integral. $\displaystyle\iint\limits_{R} (x^2 - xy + y^2) \, dA$, em que $R$ é a região delimitada pela elipse $x^2 - xy + y^2 = 2$; $x = \sqrt{2}u - \sqrt{\dfrac{2}{3}}v$, $y = \sqrt{2}u + \sqrt{\dfrac{2}{3}}v$.
$\dfrac{4\pi}{\sqrt{3}}.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(\cos u,v,\sin u)$ e $u^{2}+4v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{\pi}{2}.$
Calcule o centro de massa da região: $D$ o triângulo de vértices $(0,0), (0,1)$ e $(1,1)$ e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(\frac{3}{4}, \frac{2\sqrt{2} - 1}{2\sqrt{2} + 2\ln(1 + \sqrt{2})} \right).$
Calcule as derivadas parciais de $f(x,y,z) = xe^{x - y - z}$.
$\displaystyle \frac{\partial f}{\partial x} = (1 + x)e^{x - y - z},\;\;\;\; \frac{\partial f}{\partial y} = -x e^{x - y - z}\;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial f}{\partial z} = -x e^{x - y - z}.$
Use a integral tripla para determinar o volume do sólido dado.
$x^{2}+y^{2}\leq 4$ e $x^{2}+y^{2}+z^{2}\leq 9.$
$x^{2}+4y^{2}+9z^{2}\leq 1.$
$\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}+\dfrac{z^{2}}{c^{2}}$, $(a>0,\;b>0\;e\;c>0).$
$x^{2}+y^{2}\leq z \leq 4x+2y.$
$\left(36 - \dfrac{20\sqrt{5}}{3} \right)\pi.$
$\dfrac{2\pi}{9}.$
$\dfrac{4\pi abc}{3}.$
$\dfrac{25\pi}{4}$
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função de uma variável real, diferenciável e tal que $\phi '(1)=4.$ Seja $g(x,y)=\phi\bigg(\dfrac{x}{y}\bigg).$ Calcule
$\dfrac{\partial g}{\partial x}(1,1)$.
$\dfrac{\partial g}{\partial y}(1,1)$.
$\displaystyle \frac{\partial g}{\partial x} = \frac{1}{y} \phi'\left( \frac{x}{y} \right)$
$\displaystyle \frac{\partial g}{\partial y} = -\frac{x}{y^{2}} \phi' \left( \frac{x}{y} \right).$
Encontre um campo de vetores $\textbf{G} = P(x,y)\textbf{i} + Q(x,y)\textbf{j}$ no plano $xy$ com a propriedade de que, em qualquer ponto $(a,b) \neq (0,0)$, $\textbf{G}$ é um vetor de magnitude $\sqrt{x^2+y^2}$ tangente à circunferência $x^2+y^2=a^2+b^2$ e aponta no sentido horário. (O campo é indefinido em (0,0).)
$\displaystyle \textbf{G} = \frac{y \textbf{i} - x \textbf{j}}{\sqrt{x^{2} + y^{2}}}.$
Determine se ${\bf F}(x,y)=(e^{x}\,\sin y)\,{\bf i}+(e^{x}\,\cos y)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = e^{x}\sin(y) + K.$
Utilize coordenadas polares para determinar o volume do sólido dado: dentro do cilindro $x^2+y^2=4$ e do elipsoide $4x^2+4y^2+z^2=64.$
$\displaystyle \frac{8\pi}{3} (64 - 24\sqrt{3}).$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=1+xy^{2}-2z^{2}$.
$\displaystyle f_{x} = 1+ y^{2} ,\;\;\;\; f_{y} = 2xy \;\;\;\;\text{e}\;\;\;\; f_{z} = -4z$.
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(v\,\cos u,v\sin u,v)$, $0\leq u\leq 2\pi$,\, $0\leq v \leq h$, onde $h>0$ é um real dado.
Face lateral do cone $\sqrt{x^{2} + y^{2}} \leq z \leq h$.
Determine a área da superfície dada pela parte do plano $x+2y+z=4$ que está dentro do cilindro $x^{2}+y^{2}=4$.
$4\sqrt{6}\pi.$
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=x^{2}{\bf i}+y^{2}{\bf j}+z^{2}{\bf k}$ e $S$ é a fronteira do semicilindro sólido $0 \leq z \leq \sqrt{1-y^{2}}$, $0 \leq x \leq 2.$
$2\pi + \dfrac{8}{3}.$
$z = 2x + y$ é a equação do plano tangente ao gráfico de $f(x,y)$ no ponto $(1,1,3)$. Calcule $\dfrac{\partial f}{\partial x}(1,1)$ e $\dfrac{\partial f}{\partial y}(1,1).$
$\displaystyle \frac{\partial f}{\partial x} (1,1) = 2$ e $\displaystyle \frac{\partial f}{\partial y} (1,1) = 1.$
Marque o ponto cujas coordenadas cilíndricas são $(2, \pi/4,1)$ e $(4, -\pi/3,5)$. Em seguida, encontre as coordenadas retangulares do ponto.
Para $(2, \pi/4,1):$ $(\sqrt{2},\sqrt{2},1)$ e para $(4, -\pi/3,5):$ $(2, -2\sqrt{3},5)$.
Utilize as curvas de nível da figura para predizer a localização dos pontos críticos de $f(x,y)=3x-x^{3}-2y^{2}+y^{4}$ e se $f$ tem um ponto de sela ou um máximo ou mínimo local em cada um desses pontos. Explique seu raciocínio. Em seguida, empregue o Teste da Segunda Derivada para confirmar suas predições.
$f$ possui um ponto de máximo local em $(1,0),$ pontos de sela em $(1,1),$ $(1,-1)$ e $(-1,0)$ e pontos de mínimo local em $(-1,1)$ e $(-1,-1).$
Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$
- ${\bf F}=x{\bf i}-y{\bf j}$; $S$ é a parte no primeiro octante da esfera $x^{2}+y^{2}+z^{2}=a^{2}.$
$0.$
Use a integral tripla para determinar o volume do sólido dado por $x^{2}+y^{2}\leq z\leq \sqrt{4-3x^{2}-3y^{2}}.$
Primeiramente, vamos determinar a projeção no plano $xy$ da interseção de \begin{eqnarray*} z&=&\sqrt{4-3x^{2}-3y^{2}}\\ z&=&x^{2}+y^{2}. \end{eqnarray*} Da primeira equação temos que \begin{eqnarray*} \label{1}z=\sqrt{4-3x^{2}-3y^{2}}\Leftrightarrow z^{2}=4-3x^{2}-3y^{2}\Leftrightarrow z^{2}=4-3(x^{2}+y^{2}). \end{eqnarray*} Substituindo a segunda equação na primeira, obtemos que $$z^{2}=4-z\Leftrightarrow z^{2}+3z-4=0\Leftrightarrow (z-1)(z-4)=0.$$ Logo, $z=-4$ e $z=1.$ Notemos que $z=-4$ não satisfaz as duas primeiras equações acima, então a projeção $D$ no plano $xy$ é o círculo de raio 1, isto é, $D=\{(x,y)\in \mathbb{R};\;\, x^{2}+y^{2}\leq 1\}.$ Assim, o volume, $V$, do sólido é: $$V=\iint\limits_{D}\bigg[\int_{x^{2}+y^{2}}^{\sqrt{4-3x^{2}-3y^{2}}}1\, dz\bigg]\,dA = \iint\limits_{ D}\sqrt{4-3x^{2}-3y^{2}}-(x^{2}+y^{2})\,dA.$$ Passando para coordenadas polares temos que \begin{eqnarray*} x=r\cos \theta\\ y=r\sin \theta\\ dA=r\,dr\,d\theta\\ 0\leq r\leq 1\\ 0\leq \theta \leq 2\pi.\\ \end{eqnarray*} Então, $$V=\int_{0}^{2\pi}\int_{0}^{1}(\sqrt{4-3r^{2}}-r^{2})r\,dr\,d \theta=\int_{0}^{2\pi}\int_{0}^{1}(r\sqrt{4-3r^{2}}-r^{3})\,dr\,d\theta$$ $$=\int_{0}^{2\pi}\,d\theta\cdot \bigg[\bigg(\underbrace{\int_{0}^{1}r\sqrt{4-3r^{2}}\,dr}_{\substack{ u=4-3r^{2}\\ du=-6r\,dr}}\bigg)-\bigg(\int_{0}^{1}r^{3}\,dr\bigg)\bigg]$$ $$=\theta\bigg|_{0}^{2\pi}\cdot \bigg[\bigg(\int_{4}^{1}r\cdot u^{1/2}\frac{du}{-6r}\bigg)-\bigg(\frac{r^{4}}{4}\bigg|_{0}^{1}\bigg)\bigg]$$ $$=2\pi\cdot \bigg[\bigg(-\frac{1}{6}\int_{4}^{1}u^{1/2}\,du\bigg)-\frac{1}{4}\bigg]=2\pi \cdot \bigg[\bigg(-\frac{1}{6}\cdot \frac{2}{3}u^{3/2}\bigg|_{4}^{1}\bigg)-\frac{1}{4}\bigg]$$ $$=2\pi \cdot \bigg[-\frac{1}{9}+\frac{1}{9}\cdot 8-\frac{1}{4}\bigg]=2\pi \cdot \frac{19}{36}=\frac{19\pi}{18}.$$
Determine \(\displaystyle \lim_{(x,y)\to (0,0)}(x^2+y^2)\ln(x^2+y^2). \)
Usando coordenadas polares, teremos que: \[\begin{array}{lll} x=r\cos\theta, & y=r\sin\theta, & r^2=x^2+y^2. \end{array} \] Além disso, como \(r=\sqrt{x^2+y^2}\geq 0\), temos que \( r\rightarrow 0^+\) se, e somente se, \( (x,y)\rightarrow (0,0) \). Assim, segue para o limite dado que \begin{align*} \lim_{(x,y)\to (0,0)}(x^2+y^2)\ln(x^2+y^2) & = \lim_{r\to 0^+} r^2\ln r^2 \\ & = \lim_{r\to 0^+}\underbrace{\dfrac{2\ln r}{1/r^2}}_{\text{do tipo}\ \infty/\infty} \\ & \stackrel{\text{L'Hospital}}{=} \lim_{r\to 0^+} \dfrac{2/r}{-2/r^3} \\ & = \lim_{r\to 0^+} (-r^2) = 0.\end{align*}
Verifique que $\mbox{div} {\bf E}=0$ para o campo elétrico ${\bf E}({\bf x})=\dfrac{\epsilon Q}{|{\bf x}|^{3}}{\bf x}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}(x^{2}+y^{2}+z^{2})^{2}\,dV$, onde $B$ é a bola com centro na origem e raio $5.$
$\dfrac{312500\pi}{7}.$
Determine as derivadas parciais de $z=\dfrac{x\sin{y}}{\cos(x^{2}+y^{2})}$.
$\begin{aligned}[t]\frac{\partial z}{\partial x} &= \frac{\sin y ( \cos(x^{2} + y^{2}) + 2x^{2} \sin(x^{2} + y^{2}))}{(\cos(x^{2} + y^{2}))^{2}}\;\;\;\;\;\;\text{e}\\\frac{\partial z}{\partial y} &= \frac{x \cos y \cos(x^{2} + y^{2}) + 2xy \sin y \sin(x^{2} + y^{2})}{(\cos(x^{2} + y^{2}))^{2}}.\end{aligned}$
Expresse a integral dupla, sobre a região $R$ indicada, como uma integral iterada e ache seu valor.
$\displaystyle\iint\limits_{R}(y+2x)\,dA; \quad R$ região retangular de vértices $(-1,-1)$, $(2,-1)$, $(2,4)$ e $(-1,4).$
$\displaystyle\iint\limits_{R}(x-y)\,dA; \quad R$ região triangular de vértices $(2,9)$, $(2,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}xy^{2}\,dA; \quad R$ região triangular de vértices $(0,0)$, $(3,1)$ e $(-2,1).$
$\displaystyle\iint\limits_{R}e^{x/y}\,dA; \quad R$ região limitada pelos gráficos de $y=2x$, $y=-x$ e $y=4.$
$\displaystyle\int_{-1}^{4} \int_{-1}^{2} (y+2x)\,dx;dy = \dfrac{75}{2}.$
$\displaystyle\int_{-2}^{2} \int_{1}^{2x + 5} x - y\,dy;dx = -48.$
$\displaystyle\int_{0}^{1} \int_{-2y}^{3y} xy^{2}\,dx;dy = \dfrac{1}{2}.$
$\displaystyle\int_{0}^{4} \int_{-y}^{y/2} e^{x/y}\,dx;dy = 8(e^{1/2} - e^{-1}).$
A temperatura em um ponto $(x,y,z)$ é dada por
$$T(x,y,z) = 200e^{-x^2 - 3y^2 - 9z^2},$$
em que $T$ é medido em °C e $x,y$ e $z$ em metros.
- Determine a taxa de variação da temperatura no ponto $P = (2,-1,2)$ em direção ao ponto $(3,-3,3)$.
- Qual é a direção de maior crescimento da temperatura em $P$?
- Encontre a taxa máxima de crescimento em $P$.
- $\displaystyle \frac{5200\sqrt{6}}{3e^{43}}$ ºC/m.
- $400 e^{-43} (-2,3,-18).$
- $400 e^{-43}\sqrt{337}$ ºC/m.
Seja $z=e^{y}\phi(x-y)$, onde $\phi$ é uma função diferenciável de uma variável real. Mostre que $$\dfrac{\partial z}{\partial x}+\dfrac{\partial z}{\partial y}=z.$$
$\displaystyle \frac{\partial z}{\partial x} = e^{y}\phi'(x-y) \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = e^{y} \phi(x-y) -e^{y}\phi' (x-y).$
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = x^2 + y^2$ em $(0,1,f(0,1))$.
Plano tangente: $z = 2y - 1$
Reta normal: $(x,y,z) = \left(0,1,1 \right) + \lambda \left(0,2,-1 \right)$.
Se $C$ é o segmento de reta ligando o ponto $(x_1,y_1)$ ao ponto $(x_2,y_2)$, mostre que
$$\int_{C}x \, dy - y \, dx = x_1y_2-x_2y_1.$$
Se os vértices de um polígono, na ordem anti-horária, são
$$ (x_1,y_1), (x_2,y_2), \ldots, (x_n,y_n), $$
mostre que a área do polígono é
$$A=\dfrac{1}{2}[(x_1y_2-x_2y_1) + (x_2y_3-x_3y_2) + \cdots + (x_{n-1}y_n - x_ny_{n-1}) + (x_ny_1-x_1y_n)].$$
Determine a área do pentágono com vértices $(0,0)$, $(2,1)$, $(1,3)$, $(0,2)$ e $(-1,1)$.
Use as equações paramétricas do segmento de reta: $x = (1-t)x_{1} + tx_{2}$ e $y = (1-t)y_{1} + ty_{2},$ $0 \leq t \leq 1.$
Aplique o Teorema de Green ao caminho $C = C_{1} \cup C_{2} \cup \cdots \cup C_{n},$ onde $C_{i}$ é o segmento ligando o ponto $(x_{i},y_{i})$ ao ponto $(x_{i + 1},y_{i + 1}),$ para cada $i = 1,\cdots, n-1.$
$\dfrac{9}{2}.$
Mostre que a curva com equações paramétricas $x = t^2$, $y = 1 - 3t$, $z = 1 + t^3$ passa pelos pontos $(1,4,0)$ e $(9,-8,28)$, mas não passa pelo ponto $(4,7,-6).$
Sejam \(\alpha\), \(\beta\) e \(\gamma\) os ângulos de um triângulo.
Use multiplicadores de Lagrange para determinar o valor máximo de \(f(\alpha,\beta,\gamma)=\cos\alpha\cos\beta\cos\gamma\) e determine os ângulos para os quais o máximo ocorre.
Expresse \(f(\alpha,\beta,\gamma)\) como uma função apenas de \(\alpha\) e \(\beta\) e use um software de apoio computacional para fazer o gráfico dessa função de duas variáveis. Confirme que o resultado obtido no item anterior é consistente com o gráfico.
\(\alpha = \beta=\gamma=\pi/3\) e valor máximo \(=1/8\).
Considerando um campo vetorial $\mathbf{F}$ que representa a velocidade em um fluido, a interpretação do rotacional é que partículas em um ponto $(x,y,z)$ de um fluido tendem a rodar em torno do eixo que aponta na direção de $\text{rot }\mathbf{F}(x,y,z)$. Se $\mathbf{F}$ representar a velocidade da corrente de um rio calmo, que corre somente da direção montante à jusante, podemos dizer que $\text{rot } \mathbf{F}$ é igual ou diferente de zero? Por quê? Para auxiliar na interpretação, faça um esboço do gráfico de $\mathbf{F}$ assumindo que ele não varia na direção $z$.
Igual a zero.
Determine as dimensões da caixa retangular de volume máximo, com faces paralelas aos planos coordenados, que possa ser inscrita no elipsóide $16x^{2}+4y^{2}+9z^{2}=144.$
$\displaystyle \frac{8}{\sqrt{3}} \times \frac{6}{\sqrt{3}} \times \frac{12}{\sqrt{3}}.$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=\tan(u/v)$, $u=2s+3t$, $v=3s-2t$.
$\displaystyle \frac{\partial z}{\partial s} = \frac{2u - 3v}{v^{2}} \sec^{2}\left(\frac{u}{v} \right)$ e $\displaystyle \frac{\partial z}{\partial t} = \frac{2u + 3v}{v^{2}} \sec^{2}\left(\frac{u}{v} \right))$.
Uma carga elétrica é distribuída sobre o retângulo $1 \leq x \leq 3$, $0 \leq y \leq 2$, de modo que a densidade de carga em $(x,y)$ é $\sigma(x,y) = 2xy + y^2$ (medida em coulombs por metro quadrado). Determine a carga total no retângulo.
$\displaystyle \frac{64}{3}$ Coulombs.
$f(x,y) = \sin{xy}, (1,0).$
$1.$
Esboce o gráfico da função $f(x,y)=e^{-(x^2+y^2)}$.
Descreva em palavras como o gráfico da função \(\displaystyle g(x,y)= e^{-a(x^2+y^2)}\) está relacionado com o gráfico de \(f\), sendo \(a>0\). Mostre (verifique) que o valor de \(a\) influencia na "largura" do pico presente no gráfico da função.
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = y\mathbf{j}$, $C$ a fronteira do quadrado de vértices $(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$ e $\mathbf{n}$ a normal que aponta para fora do quadrado, sendo $C$ orientada no sentido anti-horário.
$1.$
Suponha que $S$ e $C$ satisfaçam as hipóteses do Teorema de Stokes e $f$ e $g$ tenham derivadas parciais de segunda ordem contínuas. Demonstre que $\displaystyle\int_C (f\nabla g)\cdot d{\bf R} = \displaystyle\iint_{S} (\nabla f \times \nabla g)\cdot d{\bf S}$
Note que $\mbox{rot} (f\nabla g) = \nabla f \times \nabla g.$
Seja
$$f(x,y)=\begin{cases}\dfrac{x^{3}y-xy^{3}}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
Use um computador para traçar o gráfico de $f$.
Determine $f_{x}(x,y)$ e $f_{y}(x,y)$ quando $(x,y)\neq (0,0).$
Determine $f_{x}(0,0)$ e $f_{y}(0,0)$ use a definição das derivadas parciais como limite.
Mostre que $f_{xy}(0,0)=-1$ e $f_{yx}(0,0)=1$
O resultado da parte (d) contradiz o Teorema de Clairaut? Use o gráfico de $f_{xy}$ e $f_{yx}$ para ilustrar sua resposta.
- Gráfico de $f$:
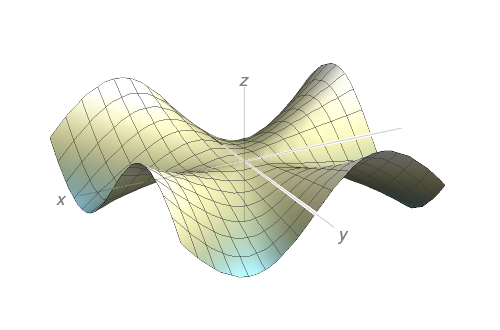
- $\displaystyle f_{x} = \frac{x^{4}y + 4x^{2}y^{3} - y^{5}}{(x^{2} + y^{2})^{2}}\;\;\text{e}\;\;f_{y} = \frac{x^{5} - 4x^{3}y^{2} - xy^{4} }{(x^{2} + y^{2})^{2}}$ quando $(x,y)\neq (0,0).$
- $f_{x}(0,0) = f_{y}(0,0) = 0$.
- Use $\displaystyle f_{xy}(0,0)= \lim_{h \to 0} \frac{f_{x}(0,h) - f_{x}(0,0)}{h}\;\;\text{e}\;\;f_{yx}(0,0)= \lim_{h \to 0} \frac{f_{y}(h,0) - f_{y}(0,0)}{h}$.
- Para $(x,y) \neq (0,0),$ $\displaystyle f_{xy} = {x^{6} + 9x^{4}y^{2} - 9x^{2}y^{4} - y^{6}}{(x^{2} + y^{2})^{3}}.$ Como $f_{xy}$ não é contínua na origem, não há uma contradição com o Teorema de Clairaut. Os gráficos de $f_{xy}$ e $f_{yx}$ são idênticos, exceto na origem:
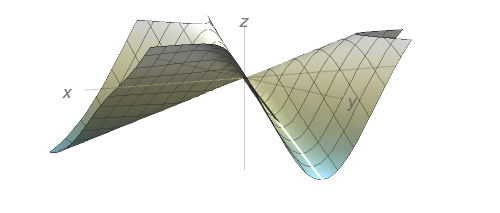
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = \dfrac{1}{\sqrt{x^2+y^2+z^2}}(x\mathbf{i} + y\mathbf{j} + z\mathbf{k})$.
$\text{rot } \mathbf{F} = \bf{0}.$ $\text{div } \mathbf{F} = \dfrac{2}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Utilizando o Teorema de Stokes, transforme a integral $\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf k}$, $S$ a superfície parametrizada por ${\bf R} (u,v) = (u,v,u^2+v^2)$, $u^2+v^2 \leq 1$, sendo ${\bf n}$ a normal apontando para cima.
$0.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $V(E)=\dfrac{1}{3}\displaystyle\iint\limits_{S}{\bf F}\cdot dS$, onde ${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}.$
Dica: Note que $\displaystyle\iiint\limits_{E}{\mbox{div} {\bf F}}\, dV = \iiint \limits_{E}{3}\,dV$.
Determine o valor máximo de $f(x,y,z) = 6x + z$ sobre a curva de interseção das superfícies $x^2 + y^2 = 4$ e $z = x^2 - 2y^2$.
$16.$
Esboce o campo vetorial $\textbf{F}= \dfrac{y\textbf{i} + x\textbf{j}}{\sqrt{x^2+y^2}}$, desenhando um diagrama.
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
$u=\sqrt{r^{2}+s^{2}}$, $r=y+x\;\cos{t}$, $s=x+y\;\sin{t}$;
$\dfrac{\partial u}{\partial x}$, $\dfrac{\partial u}{\partial y}$, $\dfrac{\partial u}{\partial t}$ quando $x=1$, $y=2$, $t=0$.
$\displaystyle \frac{\partial u}{\partial x} = \frac{4}{\sqrt{10}}$, $\displaystyle \frac{\partial u}{\partial y} = \frac{3}{\sqrt{10}}$, $\displaystyle \frac{\partial u}{\partial t}= \frac{2}{\sqrt{10}}.$
Seja $f(x,y)=\dfrac{x-y}{x+2y}$.
Determine o domínio.
Calcule $f(2u+v,v-u).$
$\left\lbrace (x,y);\; x \neq -2y \right\rbrace$
$\frac{u}{v}.$
Usando coordenadas esféricas, calcule a massa do sólido compreendido entre as esferas \(x^2+y^2+z^2=1\) e \(x^2+y^2+z^2=4\), com densidade \(\delta(x,y,z)=(x^2+y^2+z^2)^{-1/2}.\)
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
\[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
\[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
Encontre o volume máximo de uma caixa retangular que está inscrita em uma esfera de raio $r.$
$\displaystyle \frac{8}{3\sqrt{3}} r^{3}.$
Se $u=f(x,y)$, onde $x=e^{s}\cos{t}$ e $y=e^{s}\sin{t}$, mostre que
$$\bigg(\dfrac{\partial u}{\partial x}\bigg)^{2}+ \bigg(\dfrac{\partial u}{\partial y}\bigg)^{2}=
e^{-2s}\bigg[ \bigg(\dfrac{\partial u}{\partial s}\bigg)^{2}+\bigg(\dfrac{\partial u}{\partial t}\bigg)^{2}\bigg].$$
Note que $\displaystyle \frac{\partial u}{\partial s} = e^{s} \cos(t) \frac{\partial u}{\partial x} + e^{s} \sin(t) \frac{\partial u}{\partial y} $e
$\displaystyle \frac{\partial u}{\partial t} = -e^{s} \sin(t) \frac{\partial u}{\partial x} + e^{s} \cos(t) \frac{\partial u}{\partial y} .$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=e^{r}\cos{\theta}$, $r=st$, $\theta=\sqrt{s^{2}+t^{2}}$.
$\displaystyle \frac{\partial z}{\partial s} = e^{r} \left( t\cos(\theta) - \frac{s}{\sqrt{s^{2} + t^{2}}} \sin(\theta) \right) $ e $\displaystyle \frac{\partial z}{\partial t} = e^{r} \left( s\cos(\theta) - \frac{t}{\sqrt{s^{2} + t^{2}}} \sin(\theta) \right).$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=x^{5}+3x^{3}y^{2}+3xy^{4}$.
$\displaystyle \frac{\partial f}{\partial x} = 5x^{4} + 9x^{2}y^{2} + 3y^{4}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = 2x^{3}y + 12xy^{3}$.
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits{R}\sin(x^{2}+y^{2})\,dA$, onde $R$ é a região acima do eixo $x$ e dentro da circunferência $x^{2}+y^{2}=9.$
$\displaystyle \frac{\pi}{2}(1 - \cos(9).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{4}+y^{4}+4x+4y$.
Ponto de mínimo : $(-1,-1).$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=e^{-xyz}$.
$\displaystyle f_{x} = -yz e^{-xyz},\;\;\;\; f_{y} = -xz e^{-xyz}\;\;\;\;\text{e}\;\;\;\; f_{z} = -xy e^{-xyz}$.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx+y\,dy$, $C:\,x=t^{2},\,y=\sin t$, $0\leq t\leq \pi/2.$
$\displaystyle \frac{\pi^{4}}{32} + \frac{1}{2}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}\cos{z} \; dx dy dz$, onde $E$ é o conjunto $0\leq x \leq \dfrac{\pi}{2}$, $0\leq y \leq \dfrac{\pi}{2}$ e $x-y\leq z \leq x+y.$
$\displaystyle\iiint\limits_{ E}(y-x)\;dx dy dz$, onde $E$ é o conjunto $4\leq x+y\leq 8$, $\dfrac{1}{x}\leq y\leq \dfrac{2}{x}$, $y> x$ e $0\leq z \leq \dfrac{\sqrt[3]{xy}}{\sqrt{x+y}}.$
$2.$
$3 - 6\sqrt[3]{2} - 2\sqrt{2} + 6 \sqrt[6]{2^5}.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y,z) = 2x + 6y + 10z; \quad x^2 + y^2 + z^2 = 35.$
Valor máximo: $70;$ valor mínimo: $-70.$
Calcule a integral de linha $\displaystyle\int_{C}x^{2}\,dx+y^{2}\,dy+z^{2}\,dz$, onde $C$ é o segmento de reta que liga o ponto $(1,0,1)$ ao ponto $(-2,2,2).$.
$\displaystyle \frac{2}{3}.$
Suponha que o sólido tenha densidade constante $k$. Encontre os momentos de inércia para um cubo com comprimento do lado $L$ se um vértice está localizado na origem e três arestas estão nos eixos coordenados.
$\displaystyle I_{x} = I_{y} = I_{z} = \dfrac{2kL^5}{3}.$
Se ${\bf r}(t)\neq {\bf 0}$, mostre que
$$\frac{\mathrm{d}}{\mathrm{d}t}|{\bf r}(t)|=\frac{1}{|{\bf r}(t)|}{\bf r}(t)\cdot {\bf r}'(t).$$
(Sugestão: $|{\bf r}(t)|^{2}={\bf r}(t)\cdot {\bf r}(t)$).
Sabemos que $|{\bf r}(t)|^{2}={\bf r}(t)\cdot {\bf r}(t)$ ou $|{\bf r}(t)|= ({\bf r}(t)\cdot {\bf r}(t))^{1/2}.$ Então
\begin{eqnarray*}
\frac{d}{dt}|{\bf r}(t)|&=&\frac{d}{dt}[({\bf r}(t)\cdot {\bf r}(t))^{1/2}]\\
&=&\frac{1}{2}[{\bf r}(t)\cdot {\bf r}(t)]^{-1/2}[{\bf r}'(t)\cdot {\bf r}(t)+{\bf r}(t)\cdot {\bf r}'(t)]\\
&=& \frac{1}{2}[{\bf r}(t)\cdot {\bf r}(t)]^{-1/2}[2\,{\bf r}(t)\cdot {\bf r}'(t)]\\
&=&\frac{1}{2}\frac{1}{[{\bf r}(t)\cdot {\bf r}(t)]}[2\,{\bf r}(t)\cdot {\bf r}'(t)]\\
&=&\frac{1}{|{\bf r}(t)|}\,{\bf r}(t)\cdot {\bf r}'(t).
\end{eqnarray*}
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=-x^{2}+y^{2}+2xy+4x-2y$.
Ponto de sela: $\displaystyle \left(\frac{3}{2},-\frac{1}{2}\right).$
Aplique o Teorema da Divergência para achar $\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS.$, sendo ${\bf F}(x,y,z)=y^{3}e^{z}\,{\bf i}-xy\,{\bf j}+x \cdot \arctan y\,{\bf k}$ e $S$ a superfície da região delimitada pelos planos coordenados e o plano $x+y+z=1.$
Pelo Teorema do Divergente, temos
$$\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS = \displaystyle\iiint\limits_{E}\text{div }{\bf F}\,dV,$$
em que $E$ é o sólido

que pode ser escrito como
$E = \{(x,y,z) \in \mathbb{R}^3: 0 \leq x \leq 1, 0 \leq y \leq 1-x \mbox{ e } 0 \leq z \leq 1-x-y\}.$
Observe que
\begin{array}{rcl}\text{div
}{\bf F} & = & \dfrac{\partial}{\partial x}(y^3e^z) +
\dfrac{\partial}{\partial y}(-xy) + \dfrac{\partial}{\partial
z}(x\arctan{y}) \\& = & 0 - x + 0 \\& = & -x.\end{array}
Assim,
\begin{array}{rcl}\iint\limits_{S}{\bf
F}\cdot {\bf n}\,dS & = &
\displaystyle\iiint\limits_{E}{\bf F}\,dV \\& = &
\iiint\limits_{E}-x\,dV \\& = &
\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-y}-x\,dz dy dx \\& = &
\int_{0}^{1}\int_{0}^{1-x}-x(1-x-y)\,dy dx \\& = &
\int_{0}^{1}\left(-\frac{x}{2}+x^2-\frac{x^3}{3}\right)\,dx \\& =
& -\frac{1}{12}.\end{array}
Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$
${\bf F}=x{\bf i}+y{\bf j}+z{\bf k}$; $S$ é a parte do plano $3x+2y+z=12$ intersectada pelos planos $x=0$,$y=0$, $x=1$ e $y=2.$
$24.$
Esboce a região de integração para a integral iterada $\displaystyle\int_{0}^{1}\!\!\int_{\sqrt{y}}^{3\sqrt{y}}f(x,y)\,dx dy$.
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $g(x,y)=4x^{3}y^{4}+y^{3}$.
$\displaystyle \frac{\partial^{2} g}{\partial x^{2}}= 24xy^{2},\;\;\;\;\; \frac{\partial^{2} g}{\partial y^{2}}= 48x^{3} y^{2} \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} g}{\partial x\partial y}= \frac{\partial^{2} g}{\partial y\partial x}= 48x^{2}y^{3}.$
Determine o plano tangente à superfície $\frac{x^2}{4} + \frac{y^2}{9} + \frac{z^2}{16} = 1$, com $x > 0$, $y > 0$ e $z > 0$, que forma com os planos coordenados um tetraedro de volume mínimo. (Dica: O volume do tetraedro formado pelos planos coordenados e o plano $ax + by + cz = d$ no primeiro octante é dado por $V = d^3/(6abc)$.)
$6x + 4y + 3z = 12\sqrt{3}.$
Verifique que, para a função de produção de Cobb-Douglas
$$P(L,K)=1,01L^{0,75}K^{0,25}$$
discutida no Exemplo 3 da Seção 14.1 do Stewart, a produção dobrará se as quantidades de trabalho e a de capital investido forem dobradas. Determine se isto também é verdade para uma função de produção genérica
$$P(L,K)=bL^{\alpha}K^{1-\alpha}.$$
Sim.
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (2x+y)\mathbf{i} + (3x-y)\mathbf{j}$, $C$ é uma curva fechada, simples, $C^1$ por partes, orientada no sentido positivo, cuja imagem é a fronteira de um compacto $B$ com área $\alpha$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$2\times$(Área de $B$).
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf i} + x{\bf j} + xz{\bf k}$, $S$ a superfície $z = x+y+2$ e $x^2 + \dfrac{y^2}{4} \leq 1$, sendo ${\bf n}$ a normal que aponta para baixo.
$4\pi$.
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S}(f\nabla g-g\nabla f)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E}(f\nabla^{2} g-g\nabla^{2} f)\,dV.$
Use o Teorema da Divergência e que $\nabla f \cdot \nabla g = \nabla g \cdot \nabla f.$
Se $z=f(x,y)$, onde $f$ é diferenciável, e $x=g(t)$, $g(3)=2$, $g'(3)=5$, $f_{x}(2,7)=6$, $y=h(t)$, $h(3)=7$, $h'(3)=-4$, $f_{y}(2,7)=-8,$ determine $\mathrm{d}z/ \mathrm{d}t$ quando $t=3.$
$\displaystyle \frac{dz}{dt}(3) = 62.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}z\,dxdydz$, onde $B$ é o conjunto $z\geq \sqrt{x^{2}+y^{2}}$ e $x^{2}+y^{2}+z^{2}\leq 1.$
$\dfrac{\pi}{8}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}xyz\,dV$, onde $E$ está entre as esferas $\rho=2$ e $\rho=4$ e acima do cone $\phi=\pi/3.$
$0.$
Uma partícula desloca-se em um campo de forças dado por ${\bf F}(x,y,z)=-y\,{\bf i}+x\,{\bf j}+z\,{\bf k}.$ Calcule o trabalho realizado por ${\bf F}$ no deslocamento da partícula de ${\bf r}(a)$ até ${\bf r}(b)$, sendo dados:
${\bf r}(t)=(\cos t, \sin t,t)$, $a=0$ e $b=2\pi.$
${\bf r}(t)=(2t+1,t-1,t)$, $a=1$ e $b=2.$
${\bf r}(t)=(\cos t,0, \sin t)$, $a=0$ e $b=2\pi.$
$2\pi(1 + \pi).$
$\dfrac{9}{2}.$
$0.$
$f(t)$ e $g(x,y)$ são funções diferenciáveis tais que $g(t,f(t))=0$ para todo $t$. Suponha $f(0)=1$,
$\dfrac{\partial g}{\partial x}(0,1)=2$ e $\dfrac{\partial g}{\partial y}(0,1)=4$. Determine a equação da reta tangente a $\gamma(t)=(t,f(t))$,
no ponto $\gamma(0).$
$\displaystyle (x,y) = (0,1) + \lambda \left(1, - \frac{1}{2}\right),$ $\lambda \in \mathbb{R}.$
Determine a derivada direcional da função no ponto dado e na direção do vetor $\bf{v}$.
$f(x,y) = 1 + 2x\sqrt{y}, (3,4), \bf{v} = \left(4, -3\right).$
$\displaystyle \frac{23}{10}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=4+x^{3}+y^{3}-3xy$.
Ponto de mínimo: $(1,1);$ ponto de sela: $(0,0).$
A força em um ponto $(x,y,z)$ em três dimensões é dada por ${\bf F}(x,y,z)=y\,{\bf i}+z\,{\bf j}+x\,{\bf k}$. Ache o trabalho realizado por ${\bf F}(x,y,z)$ ao longo da cúbica reversa $x=t$, $y=t^{2}$, $z=t^{3}$ de $(0,0,0)$ a $(2,4,8).$
$\dfrac{412}{15}.$
Dada a função $f(x,y)=x^{2}-y^{2}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}.$
$Im(f) = \mathbb{R}.$
As curvas de nível são as hipérboles $x^{2} - y^{2} = C$ com foco no eixo $x$ se $C > 0;$ com foco no eixo $y$ se $C < 0$ e as retas $y = \pm x$ se $C = 0.$
Explique por que cada função é contínua ou descontínua.
A temperatura externa como função da latitude, da longitude e do tempo.
A altura acima do nível do mar como função da longitude, da latitude e do tempo.
O custo da tarifa do táxi como função da distância percorrida e do tempo gasto.
Contínua.
Descontínua.
Descontínua.
Calcule a área da superfície dada por: ${\bf r}(u,v)=\bigg(u,v,\dfrac{1}{2}u^{2}\bigg)$,$0\leq v\leq u$ e $u\leq 2.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{1}{3}\left(5\sqrt{5} - 1 \right).$
Determine a área da superfície dada pela parte da superfície $y=4x+z^{2}$ que está entre os planos $x=0$, $x=1$, $z=0$ e $z=1.$
$\dfrac{\sqrt{21}}{2} + \dfrac{17}{4} \left( \ln(2 + \sqrt{21}) - \ln(\sqrt{17}) \right).$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla \cdot \mathbf{r} = 3$.
$\nabla \cdot \mathbf{r} = \left(\dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \cdot \left(x,y,z \right)$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Use uma integral dupla para calcular a área da região \(R\) entre a parábola \(y=\dfrac{1}{2}x^2\) e a reta \(y = 2x\).
Denotando por \(A(R)\) a área de \(R\), teremos que \begin{align*} A(R) & = \iint_R\,dA = \int_0^4\int_{x^2/2}^{2x}\,dydx = \int_0^4\left[y\right]_{y=x^2/2}^{2x}\,dx \\ & = \int_0^4\left(2x-\dfrac{1}{2}x^2\right)\,dx = \left[x^2-\dfrac{x^3}{6}\right]_0^4= \dfrac{16}{3}. \end{align*} De outra forma, fixando primeiro a variável \(y\), teríamos \begin{align*} A(R) & = \iint_R\,dA = \int_0^8\int_{y/2}^{\sqrt{2y}}\,dxdy = \int_0^8\left[x\right]_{x=y/2}^{\sqrt{2y}}\,dy \\ & = \int_0^8\left(2y-\dfrac{1}{2}y\right)\,dy = \left[\dfrac{2\sqrt{2}}{3}y^{3/2}-\dfrac{y^2}{4}\right]_0^8= \dfrac{16}{3}. \end{align*}
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}e^{\dfrac{1}{x^2 + y^2 - 1}}, & \quad \text{se } x^2 + y^2 < 1,\\0, & \quad \text{se } x^2 + y^2 \geq 1\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2}$.
Calcule a integral de linha $\displaystyle\oint_{C} xy \, dx + x^2 \, dy$, $C$ é o retângulo com vértices $(0,0)$, $(3,0)$, $(3,1)$ e $(0,1)$ por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$\dfrac{9}{2}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=(x^{2}-1)(y+2)$.
$\displaystyle \frac{\partial f}{\partial x} = 2x(y + 2) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = x^{2} - 1$.
Faça uma correspondência entre a função e seu gráfico (indicado por I-VI). Dê razões para sua escolha.
$f(x,y)=|x|+|y|$.
$f(x,y)=\dfrac{1}{1+x^{2}+y^{2}}$.
$f(x,y)=(x-y)^{2}$.
$f(x,y)=|xy|$.
$f(x,y)=(x^{2}-y^{2})^{2}$.
$f(x,y)=\sin(|x|+|y|)$.
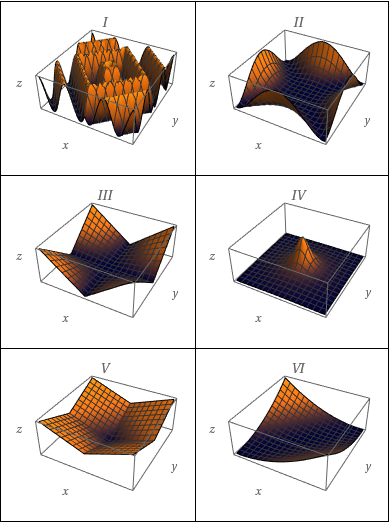
Encontre o centro de massa de uma lâmina em forma de triângulo retângulo isósceles, com os lados iguais tendo comprimento $a$, se a densidade em qualquer ponto for proporcional ao quadrado da distância do vértice oposto à hipotenusa.
$\displaystyle \left(\frac{2a}{5}, \frac{2a}{5} \right).$
Seja $f(x,y) = \dfrac{2xy^2}{x^2 + y^4}$.
Considere a reta $\gamma(t) = (at, bt)$, com $a^2 + b^2 > 0$; mostre que, quaisquer que sejam $a$ e $b$,
$$\displaystyle \lim_{t \to 0} f(\gamma(t)) = 0.$$
Tente visualizar este resultado através das curvas de nível de $f$.
Calcule $\displaystyle \lim_{t \to 0} f(\delta(t))$, onde $\delta(t) = (t^2,t).$ (Antes de calcular o limite, tente prever o resultado olhando para as curvas de nível de $f$.)
$\displaystyle \lim_{(x,y) \to (0,0)}\dfrac{2xy^2}{x^2 + y^4}$ existe? Por quê?
Demonstração.
$1.$
Não existe.
No item abaixo:
- expresse $\partial w/\partial u$ e $\partial w/ \partial v$ como funções de $u$ e $v$, usando a Regra da Cadeia e também expressando $w$ diretamente em termos e $u$ e $v$ antes de diferenciar;
- calcule $\partial w/\partial u$ e $\partial w/ \partial v$ no ponto dado $(u,v)$.
$w=xy+yz+xz$, $x=u+v$, $y=u-v$, $z=uv$; $(u,v)=(1/2,1).$
- $\displaystyle w(u,v) = u^{2} - v^{2} + 2u^{2}v,$$\displaystyle \frac{\partial w}{\partial u}(u,v) = 2u + 4uv$ e $\displaystyle \frac{\partial w}{\partial v}(u,v) = -2v + 2u^{2}.$
- $\displaystyle \frac{\partial w}{\partial u}(-2,0) = 3$ e $\displaystyle \frac{\partial w}{\partial v}(-2,0) = -\frac{3}{2}.$
Esboce a região de integração para a integral iterada $\displaystyle\int_{\pi}^{2\pi}\!\!\int_{\sin{y}}^{\ln(y)}f(x,y)\,dx dy$.
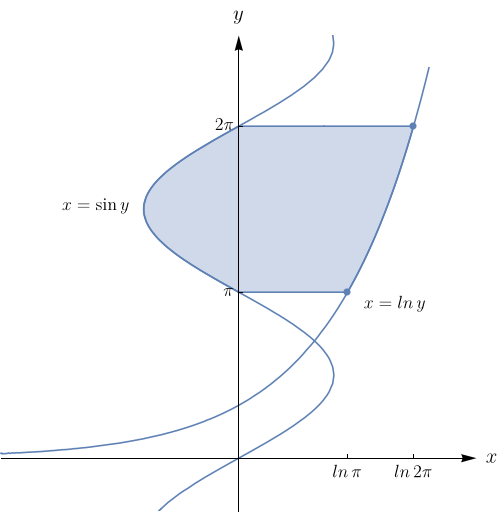
Determine a diferencial da função $R = \alpha\beta^2 \cos{\lambda}$.
$dR = \beta^{2} \cos(\gamma) d\alpha + 2\gamma \beta \cos (\gamma) d\beta - \alpha \beta^{2} \sin(\gamma) d\gamma$.
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y)=(y,3x)$ e $C$ é a elipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$, percorrida no sentido anti-horário.
$-2\pi ab.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{1}^{2}\!\!\int_{y}^{y^{2}} \,dx dy$.
$\frac{5}{6}.$
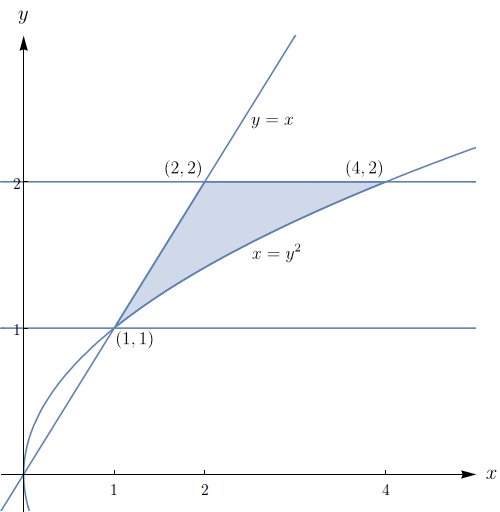
A figura mostra o campo vetorial ${\bf F}(x,y)=(2xy, x^{2})$ e três curvas que começam em $(1,2)$ e terminam em $(3,2).$
- Explique por que $\int_{c}{\bf F}\cdot d{\bf r}$ tem o mesmo valor para as três curvas.
- Qual é esse valor comum?
- ${\bf F}$ é conservativo, logo $\int_{C} \bf F \cdot d\bf r$ depende somente dos pontos inicial e final de $C.$
- $16.$
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função de uma variável real, diferenciável e tal que $\phi '(1)=4.$ Seja $g(x,y)=\phi\bigg(\dfrac{x}{y}\bigg).$ Verifique que, para todo $(x,y)\in \mathbb{R}^{2}$, com $y\neq 0$, temos que
$$x\;\dfrac{\partial g}{\partial x}(x,y)+y\;\dfrac{\partial g}{\partial y}(x,y)=0.$$
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = e^{xy}\sin{z}\mathbf{j} + y\tan^{-1}(x/z)\mathbf{k}$.
$\text{rot } \mathbf{F} = (\arctan(x/z) - e^{xy}\cos(z))\mathbf{i} - \dfrac{yz}{x^{2} + z^{2}} \mathbf{j} + ye^{xy}\sin(z) \mathbf{k}.$ $\text{div } \mathbf{F} = xe^{xy}\sin(z) - \dfrac{xy}{x^{2} + z^{2}}.$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{0}^{2}\int_{0}^{\sqrt{4-y^{2}}}\int_{0}^{\sqrt{4-x^{2}-y^{2}}}\dfrac{1}{x^{2}+y^{2}+z^{2}}\,dzdxdy$.
$\pi.$
Suponha que ${\bf F}=\nabla f$ seja um campo vetorial conservativo e
$$g(x,y,z)=\int_{(0,0,0)}^{(x,y,z)}{\bf F}\cdot d{\bf r}.$$
Mostre que $\nabla g={\bf F}.$
Como $g(x,y,z) = f(x,y,z) - f(0,0,0),$ segue que $\nabla g = \nabla f = \mathbf{F}.$
Determine os planos tangentes ao gráfico de $f(x,y) = 2 + x^2 + y^2$ e que contenham o eixo $x$.
$z = 2\sqrt{2} y$ e $z = -2\sqrt{2} y.$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $D$ delimitada pelas parábolas $y = x^2$ e $x = y^2; \quad \rho(x,y) = \sqrt{x}$.
Massa: $\dfrac{3}{14};$ centro de massa: $\displaystyle \left(\frac{14}{27},\frac{28}{55} \right).$
Utilize simetria para calcular $\iint\limits_{D}(2-3x+4y)\,dA$, onde $D$ é a região limitada pelo quadrado com vértices $(\pm 5,0)$ e $(0,\pm 5).$
$100.$
Determine o conjunto dos pontos de continuidade da função $f(x,y) = 3x^2y^2 - 5xy + 6$. Justifique sua resposta.
$\mathbb{R}^{2}.$
A primeira identidade de Green é dada por:
$$\iint\limits_{ D} f\nabla^2g \, dA = \oint_{C}f(\nabla{g}) \cdot \mathbf{n} \, ds - \iint\limits_{ D}\nabla{f} \cdot \nabla{g} \, dA,$$
em que $D$ e $C$ satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de $f$ e $g$ existem e são contínuas. (A quantidade $ \nabla{g} \cdot \mathbf{n} = D_{\mathbf{n}}g$ aparece na integral de linha. Essa é a derivada direcional na direção do vetor normal $\mathbf{n}$ e é chamada derivada normal de $g$.) Use-a para demonstrar a segunda identidade de Green:
$$\iint\limits_{ D} (f\nabla^2g - g\nabla^2f)\, dA = \oint_{C}(f\nabla{g} - g\nabla{f}) \cdot \mathbf{n} \, ds,$$
em que $D$ e $C$ satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de $f$ e $g$ existem e são contínuas.
Note que pela primeira identidade de Green,
$$\iint\limits_{ D} (f\nabla^2g - g\nabla^2f)\, dA = \oint_{C}(f\nabla{g} \cdot \mathbf{n} - g\nabla{f} \cdot \mathbf{n}) \, ds, + \iint\limits_{ D} (\nabla f \cdot \nabla g - \nabla g \cdot \nabla f)\, dA.$$
Considere a integral tripla iterada $$\int_{-\sqrt{2}}^{\sqrt{2}}\int_{-\sqrt{2-x^2}}^{\sqrt{2-x^2}}\int_{x^2 + y^2}^{4-x^2-y^2} dz dy dx.$$
Transforme a integral utilizando coordenadas cilíndricas.
Calcule a integral.
Descreva o sólido cujo volume é dado por essa integral.
$\displaystyle \int_{0}^{2\pi}\int_{0}^{\sqrt{2}}\int_{ r^2}^{4-r^{2}} r dz dr d\theta.$
$4\pi.$
Região entre os parabolóides $z = x^2 + y^2$ e $z = 4 - x^2 - y^2$.
Seja ${\bf F}(x,y,z)=(x+y+z^{2})\,{\bf k}$ e seja $S$ a fronteira do cilindro $x^{2}+y^{2}\leq 4$ e $0\leq z \leq 3.$ Calcule $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS$ onde ${\bf n}$ é a normal exterior, isto é, ${\bf n}$ é a normal que aponta para fora do cilindro.
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{6} \int_{0}^{y}x\,dx dy$
$36.$
Determine $h(x,y) = g(f(x,y))$ e o conjunto no qual $h$ é contínua, em que
$$g(t) = t^2 + \sqrt{t}, \ \ \ f(x,y) = 2x + 3y - 6.$$
$h(x,y) = (2x+3y-6)^{2} + \sqrt{2x + 3y - 6}$ é contínua em $\left\lbrace (x,y);\; y \geq -\frac{2x}{3} + 2 \right\rbrace.$
Determine se ${\bf F}(x,y)=-y\,{\bf i}+x\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{1}^{2}\!\!\int_{0}^{\ln(x)} \! f(x,y)\,dy dx$.
Note que a região de integração é do tipo I, é dada por
$$\{(x,y) \in \mathbb{R}^2: 1 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \ln(x)\}$$
e pode ser vista geometricamente como a região esboçada na figura abaixo.
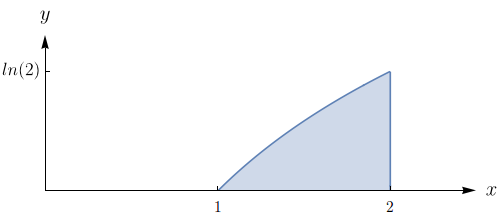
Além disso, ela pode ser descrita como uma região do tipo II da seguinte forma:
$$\{(x,y) \in \mathbb{R}^2: e^y \leq x \leq 2 \mbox{ e } 0 \leq y \leq \ln{2}\}.$$
Portanto, a integral pode ser reescrita como
$\displaystyle\int_{0}^{\ln{2}}\!\!\int_{e^y}^{2} \! f(x,y)\,dx dy$.
Calcule as seguintes integrais triplas.
$\displaystyle\iiint\limits_{ E} \sqrt{x^2 + y^2} \, dV$, em que $E$ é a região que está dentro do cilindro $x^2 + y^2 = 16$ e entre os planos $z = -5$ e $z = 4$.
$\displaystyle\iiint\limits_{ E} y \, dV$, em que $E$ é o sólido que está entre os cilindros $x^2 + y^2 = 1$ e $x^2 + y^2 = 4$, acima do plano $xy$ e abaixo do plano $z = x + 2$.
$\displaystyle\iiint\limits_{ E} x \, dV$, em que $E$ está delimitidado pelos planos $z = 0$ e $z = x + y + 5$ e pelos cilindros $x^2 + y^2 = 4$ e $x^2 + y^2 = 9$.
$384\pi$.
$0$.
$\dfrac{65\pi}{4}$.
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=x^{2}y^{3}$, $x=s\cos{t}$, $y=s\sin{t}$.
$\displaystyle \frac{\partial z}{\partial s} = 2xy^{3} \cos(t) + 3x^{2}y^{2} \sin(t) $ e $\displaystyle \frac{\partial z}{\partial t} = -2sxy^{3} \sin(t) + 3 sx^{2}y^{2} \cos(t)$.
Considere a função
$$f(x,y)=-\frac{y^{2}}{2}+3x^{2}-2x^{3}.$$
Determine e classifique os pontos críticos de $f.$
Mostre que a curva de nível $f(x,y)=0$ com $x\geq 0$ é uma curva fechada, isto é, é a fronteira de uma região $R$ limitada do plano $xy.$ Calcule o valor máximo de $f$ nessa região $R$.
Pontos críticos: $(0,0)$ e $(1,0).$ Ponto de máximo: $(1,0);$ ponto de sela: $(0,0).$
$\max \{ f(s); s\in R \} =1$.
Seja
$$f(x,y)=k(x-y)^{2}+\frac{y^{4}}{2}-\frac{y^{2}}{2},\;\;k\neq 0.$$
Encontre os pontos críticos da função $f$.
Classifique os pontos críticos da função $f$ no caso em que $k>0$.
$(0,0), (1,1)$ e $(-1,-1).$
Pontos de mínimo: $(1,1)$ e $(-1,-1);$ ponto de sela: $(0,0).$
Se $\mathbf{F}(x,y) = (-y\mathbf{i} + x\mathbf{j})/(x^2+y^2)$, mostre que $\int_{C}\mathbf{F} \cdot d\mathbf{r} = 0$ para todo caminho fechado simples que não passe pela origem e nem a circunde.
Dica: como $C$ é um caminho fechado simples que não passa pela origem e não circunda a origem, então existe uma região aberta $A$ que ainda não contém a origem, mas contém $D,$ a região limitada por $C.$ Em $A,$ tanto $-y/(x^{2} + y^{2})$ quanto $x/(x^{2} + y^{2})$ possuem derivadas parciais contínuas e podemos aplicar o Teorema de Green.
Verifique que a função $f(x,y) = x^4 + y^3$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{2\pi}\int_{0}^{\pi/4}\int_{0}^{2}(\rho\cos{\phi})\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$2\pi.$
Determine as derivadas parciais de $z=(x^{2}+y^{2})\ln(x^{2}+y^{2})$.
$\displaystyle \frac{\partial z}{\partial x} = 2x(1 + \ln(x^{2} + y^ {2}))\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = 2y(1 + \ln(x^{2} + y^ {2})).$
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=x{\bf i}+2y{\bf j}+3z{\bf k}$ e $S$ é o cubo com vértices $(\pm 1, \pm 1,\pm 1).$
$48.$
Determine se ${\bf F}(x,y)=e^{x}\,\cos y\,{\bf i}+e^{x}\,\sin y\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
Determine as derivadas parciais de $z=xye^{xy}$.
$\displaystyle \frac{\partial z}{\partial x} = ye^{xy} (1 + xy) \;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = xe^{xy} (1 + xy).$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=x^{2}\,{\bf j}$, ${\bf r}(t)=(t^{2},3)$, $-1\leq t\leq 1.$
$0.$
Encontre o fluxo do campo ${\bf F}$ ao longo da porção da superfície dada no sentido especificado.
- ${\bf F}(x,y,z)=-{\bf i}+2{\bf j}+3{\bf k}$; $S$ é a superfície retangular $z=0$, $0\leq x\leq 2$, $0\leq y \leq 3$, sentido ${\bf k}.$
$18.$
A figura mostra a região da integral
$$\int_{0}^{1}\int_{0}^{1-x^{2}}\int_{0}^{1-x}f(x,y,z)\;dy dz dx.$$
Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.
$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx = \int_{0}^{1}\int_{0}^{y^2}\int_{0}^{1-y}f(x,y,z)\;dz dx dy $
$= \int_{0}^{1}\int_{0}^{1 - z}\int_{0}^{y^2}f(x,y,z)\;dx dy dz = \int_{0}^{1}\int_{0}^{1 - y}\int_{0}^{y^2}f(x,y,z)\;dx dz dy $
$= \int_{0}^{1}\int_{0}^{1 - \sqrt{x}}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dz dx = \int_{0}^{1}\int_{0}^{(1 - z)^2}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dx dz.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}+y^{3}+xy-3x-4y+5$.
Ponto de mínimo : $\displaystyle \left( 1,1\right);$ ponto de sela: $\displaystyle \left(\frac{23}{12},-\frac{5}{6}\right).$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=\cos^{2}(3x-y^2)$.
$\displaystyle \frac{\partial f}{\partial x} = -6\cos (3x - y^{2}) \sin(3x - y^{2}) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = 4y \cos (3x - y^{2}) \sin(3x - y^{2})$.
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=e^{-x}\;\sin(x+y)$.
$\displaystyle \frac{\partial f}{\partial x} = -e^{-x} \sin(x + y) + e^{-x}\cos(x + y) \;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = e^{-x}\cos(x + y)$.
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=e^{x+2y}$, $x=s/t$, $y=t/s$.
$\displaystyle \frac{\partial z}{\partial s} = e^{x + st}\left(\frac{1}{t} - \frac{2t}{s^{2}} \right) $ e $\displaystyle \frac{\partial z}{\partial t} = e^{x + st}\left(\frac{2}{s} - \frac{s}{t^{2}} \right) $.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}(x+yz)\,dx+2x\,dy+xyz\,dz$, $C$ consiste nos segmentos de reta de $(1,0,1)$ a $(2,3,1)$ e de $(2,3,1)$ a $(2,5,2).$
$\dfrac{97}{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}xy\,dx dy$, onde $R$ é o círculo $x^{2}+y^{2}-2y\leq 0$, $x\geq 0.$
$\displaystyle \frac{2}{3}.$
Esboce o sólido cujo volume é dado pela integral iterada.
$\displaystyle\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2-2z}\;dy dz dx$
$\displaystyle\int_{0}^{2}\int_{0}^{2-y}\int_{0}^{4-y^{2}}\;dx dz dy$
$\displaystyle\int_{0}^{1}\int_{\sqrt{1-z}}^{\sqrt{4-z}}\int_{2}^{3}\;dx dy dz$
$\displaystyle\int_{0}^{2}\int_{x^{2}}^{2x}\int_{0}^{x+y}\;dz dy dx$
(... fig)
(... fig.)
$\displaystyle \left\lbrace (x,y,z); 2 \leq x \leq 3, \sqrt{1 - z} \leq y \leq \sqrt{4 - z} , 0 \leq z \leq 1\right\rbrace.$
$\displaystyle \left\lbrace (x,y,z); 0 \leq x \leq 2, x^{2} \leq y \leq 2x , 0 \leq z \leq x + y\right\rbrace.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$\dfrac{1}{(x+y)^{2}}$
$\dfrac{1}{1+x^{2}+2xy+y^{2}}$
$\dfrac{3}{\pi}.$
$3\arctan(3) - 4\arctan(2) - \ln(2) + \dfrac{\ln(5)}{2} + \dfrac{\pi}{4}.$
Esboce a região de integração para a integral iterada $\displaystyle\int_{-1}^{2}\!\int_{-\sqrt{4-x^{2}}}^{4-x^{2}}f(x,y)\,dy dx$.

Determine o volume do sólido limitado pelos planos coordenados e pelo plano $3x+2y+z=6.$
O sólido cujo volume deve ser calculado é $$E = \{(x,y,z) \in \mathbb{R}^3; (x,y) \in R \mbox{ e } 0 \leq z \leq 6 - 3x - 2y\},$$ em que $R$ é a projeção de $E$ no plano $xy$. Assim, o volume é dado por $$V = \displaystyle\int\!\!\!\!\int\limits_{R}(6-3x-2y)\,dA.$$ A região $R$ é tanto do tipo I como do tipo II, então é possível escrevê-la de pelo menos duas formas. Escrevendo como uma região do tipo I, obtemos: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2 \mbox{ e } 0 \leq y \leq \frac{6-3x}{2}\right\}.$$ Portanto, \begin{eqnarray*} V & = & \displaystyle\int_{0}^{2}\!\int_{0}^{\frac{6-3x}{2}}(6-3x-2y)\,dy dx \\ & = & \displaystyle\int_{0}^{2} \left.\left(6y-3xy-y^2 \right|_{y=0}^{y=\frac{6-3x}{2}} \right) \,dx \\ & = & \displaystyle\int_{0}^{2} \left(9-9x+\frac{9x^2}{4}\right) \,dx \\ & = & \left.9x-\frac{9x^2}{2}+\frac{9x^3}{12} \right|_{x=0}^{x=2} = 6. \end{eqnarray*} Observe que podemos escrever $R$ como uma região do tipo II, obtendo: $$R = \left\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq \frac{6-2y}{3} \text{ e } 0 \leq y \leq 3\right\}.$$ Então, uma outra expressão para $V$ é $$V = \displaystyle\int_{0}^{3}\!\int_{0}^{\frac{6-2y}{3}}(6-3x-2y)\,dx dy = 6.$$
Encontre a massa da lâmina descrita como sendo a porção do cilindro circular \(x^2+z^2=4\) que fica diretamente acima do retângulo \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq x\leq 1,\ 0\leq y\leq 4\}\) e tem densidade \(\delta_0\) constante.
\(\dfrac{4}{3}\pi\delta_0\)
Seja $f(x,y) = x \arctan{\dfrac{x}{y}}$. Calcule $D_{\bf{u}}f(1,1)$, em que $\bf{u}$ aponta na direção e sentido de máximo crescimento de $f$, no ponto $(1,1)$.
$\displaystyle D_{\bf{u}}f(1,1) = \sqrt{\left( \frac{\pi}{4} + \frac{1}{2}\right)^{2} + \frac{1}{4}}.$
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} \dfrac{\sqrt[3]{y - x}}{1 + y + x} \, dA$, em que $R$ é o triângulo de vértices $(0,0), (1,0)$ e $(0,1)$.
$0$.
Calcule $\displaystyle\int_{C}\dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy$ onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida no semiplano $y>0$, tal que $C(0)=(1,1)$ e $C(1)=(-2,3).$
$\pi.$
Seja
$${\bf F}(x,y)=\bigg(\frac{-y}{x^{2}+y^{2}},\frac{x}{x^{2}+y^{2}}+3y\bigg)$$
um campo vetorial em $\mathbb{R}^{2}$. Calcule a integral de linha do campo ${\bf F}$ ao longo das curvas
$C_{1}$ e $C_{2}$, orientadas no sentido anti-horário, onde:
$C_{1}$ é a circunferência de equação $x^{2}+y^{2}=4.$
$C_{2}$ é a fronteira do retângulo $R=\{(x,y)\in \mathbb{R}^{2}|\,-\pi \leq x \leq \pi,-3 \leq y \leq 3\}.$
$0.$
$0.$
Seja $f(x,y,z)=e^{\sqrt{z-x^{2}-y^{2}}}.$
Calcule $f(2,-1,6).$
Determine o domínio de $f$.
Determine a imagem de $f$.
$e.$
$\left\lbrace (x,y,z): \;z \geq x^{2} + y^{2} \right\rbrace.$
$[1,\infty).$
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = \sqrt{x^2 + y^2 + z^2}$
$\displaystyle \nabla f(x,y,z) = \frac{1}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Determine os planos que são tangentes ao gráfico de $f(x,y) = x^2 + y^2$ e que contenham a interseção dos planos $x + y + z = 3$ e $z = 0$.
$z = 0$ e $z = 6x + 6y - 18.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}\dfrac{-y}{4x^{2}+y^{2}}\,dx+\dfrac{x}{4x^{2}+y^{2}}\,dy$, $C$ tem por imagem a elipse $4x^{2}+y^{2}=9$ e o sentido de percurso é o anti-horário.
$\displaystyle \pi.$
O comprimento e a largura de um retângulo foram medidos como $30$ cm e $24$ cm, respectivamente, com um erro de medida de, no máximo, $0,1$ cm. Utilize as diferenciais para estimar o erro máximo cometido no cálculo da área do retângulo.
$\Delta A \approx 5.4$ cm$^{2}$.
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla \cdot (r\mathbf{r}) = 4r$.
$\nabla \cdot (r\mathbf{r}) = \left( \dfrac{x^{2}}{\sqrt{x^{2} + y^{2} + z^{2}}} + \sqrt{x^{2} + y^{2} + z^{2}} \right) + \left( \dfrac{x^{2}}{\sqrt{y^{2} + y^{2} + z^{2}}} + \sqrt{y^{2} + y^{2} + z^{2}} \right)\\ + \left( \dfrac{z^{2}}{\sqrt{x^{2} + y^{2} + z^{2}}} + \sqrt{x^{2} + y^{2} + z^{2}} \right)$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Verifique que a função $f(x,y) = x^2y$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Suponha que, para todo $t$, $f(t^{2},2t)=t^{3}-3t$. Mostre que
$$\dfrac{\partial f}{\partial x}(1,2)=-\dfrac{\partial f}{\partial y}(1,2).$$
Tome $t = 1$ em $\displaystyle \frac{df}{dt}(t^{2},2t) = 2t \frac{\partial f}{\partial x}(t^{2},2t) + 2\frac{\partial f}{\partial y}(t^{2},2t) = 3t^{2} - 3.$
Determine se ${\bf F}(x,y,z)=(y\,\sin z)\,{\bf i}+(x\,\sin z)\,{\bf j}+(xy\,\cos z)\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = xy\sin(z) + K.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}+2xy+y^{2}-5x$.
Ponto de mínimo: $\displaystyle \left( \frac{5}{3}, -\frac{5}{3} \right);$ ponto de sela: $\displaystyle \left(-1,1\right).$
Faça o mapa de contorno da função $f(x,y)=(y-2x)^{2}$ mostrando várias de suas curvas de nível.
$y=2x\pm \sqrt{C}, C \geq0.$
Calcule $\displaystyle\iint\limits_{B} y\,dx dy$, onde $B$ é o conjunto dado.
$B$ é a região compreendida entre os gráficos de $y=x$ e $y=x^{2}$, com $0\leq x\leq 2.$
$B$ é o paralelogramo de vértices $(-1,0)$, $(0,0)$, $(1,1)$ e $(0,1).$
$B$ é o semicírculo $x^{2}+y^{2}\leq 4$, $y\geq 0.$
$B=\{(x,y)\in \mathbb{R}^{2}|\;x\geq 0,\;x^{5}-x\leq y \leq 0\}.$
$2$.
$\dfrac{1}{2}$.
$\dfrac{16}{3}$.
$-\dfrac{16}{231}$.
Identifique a superfície cuja equação é dada por $z = 4 - r^2$.
$z = 4 - x^2 - y^2,$ o parabolóide circular com vértice $(0,0,4)$.
Considere o campo vetorial
$${\bf F}(x,y)=(\ln(y^{2}+1))\,{\bf i}+\bigg(\frac{2y(x-1)}{y^{2}+1}\bigg)\,{\bf j}.$$
Determine se $F$ é ou não um campo conservativo.
Determine o trabalho realizado pelo campo vetorial ${\bf F}$ ao mover uma partícula desde o ponto $(-1,1)$ até o ponto $(2,3).$
Sim.
$\ln(10) + 2\ln(2).$
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$ze^{x - y} + z^3 = 2$ em $(2,2,1)$.
Plano tangente: $x - y + 4z = 4$,
Reta normal: $(x,y,z) = (2,2,1) + \lambda (1,-1,4),$ $\lambda \in \mathbb{R}.$
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}\dfrac{x^3}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = 0\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$.
O campo vetorial $\mathbf{F}$ é mostrado no plano $xy$ e é o mesmo em todos os planos horizontais (em outras palavras, $\mathbf{F}$ é independente de $z$ e sua componente $z$ é 0).
O $\text{div }{\mathbf{F}}$ será positivo, negativo ou nulo? Justifique.
Determine se o $\text{rot }{\mathbf{F}} = 0$. Se não, em que direção rot $\mathbf{F}$ aponta?

Positivo.
$\text{rot } \bf{F} = \bf{0}.$
Considere a superfície parametrizada por
$${\bf r}(u,v)=(uv,u+v,u-v).$$
Determine o valor de $c$ de forma que o ponto $(c,1,0)$ pertença à superfície.
Calcule a área da parte da superfície correspondente à variação $u^{2}+v^{2}\leq 1.$
$\dfrac{1}{4}.$
$\left(\sqrt{6} - \dfrac{4}{3} \right)2\pi.$
Um sólido ocupa a região $E$ com superfície $S$ e está imerso em um líquido com densidade constante $\rho$. Escolhemos um sistema de
coordenadas de modo que o plano $xy$ coincida com a superfície do líquido e valores positivos de $z$ sejam medidos para baixo, adentrando o líquido. Então, a pressão na profundidade $z$ é $p=\rho g z$, onde $g$ é a aceleração da gravidade. A força de empuxo total sobre o sólido devida $\grave{a}$ distribuição de pressão é dada pela integral de superfície
${\bf F}=-\displaystyle\iint\limits_{S} p{\bf n}\,dS$ onde ${\bf n}$ é o vetor normal unitário apontando para fora. Use o resultado do exercício anterior para mostrar que ${\bf F}=-W{\bf k}$, onde $W$ é o peso do líquido deslocado pelo sólido. (Observe que ${\bf F}$ é orientado para cima porque $z$ está orientado para baixo.) O resultado é o Princípio de Arquimedes: a força de empuxo sobre um objeto é igual ao
peso do líquido deslocado.
Note que $\displaystyle {\bf F}=-\int_{S} p {\bf n} \,dS = -\iiint_{E} \nabla p\,dV = -\iiint_{E} \nabla p\,dV = - \iiint_{E} \nabla (\rho g z)\,dV.$
Conclua usando que $W = \rho g V(E),$ onde $V(E)$ é o volume de $E.$
Determine as derivadas parciais de primeira ordem da função $f(x,y)=\dfrac{x-y}{x+y}$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{2y}{(x + y)^{2}}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = -\frac{2x}{(x + y)^{2}}$.
Considere a função
$$f(x,y)=\begin{cases}\dfrac{xy}{x^{2}+y^{2}}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
A função $f$ é contínua em $(0,0)$? Justifique sua resposta.
Calcule as derivadas parciais $\dfrac{\partial f}{\partial x}(0,0)$ e $\dfrac{\partial f}{\partial y}(0,0).$
Determine $\dfrac{\partial f}{\partial x}(x,y)$ e $\dfrac{\partial f}{\partial y}(x,y)$ para $(x,y)\neq (0,0).$
$f$ é diferenciável em $(0,0)$? Justifique sua resposta.
Não, pois $\displaystyle \lim_{(x,y) \to (0,0)} f(x,y)$ não existe.
$\displaystyle \frac{\partial f}{\partial x}(0,0) = \frac{\partial f}{\partial y}(0,0) = 0$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{y^{3} - x^{2}y}{(x^{2} + y^{2})^{2}}\;\;\;\text{e}\;\;\; \frac{\partial f}{\partial y} = \frac{x^{3} - xy^{2}}{(x^{2} + y^{2})^{2}}$.
Não, pois $f$ não é contínua em $(0,0)$ (ou: pois suas derivadas parciais não são contínuas em $(0,0)$).
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$x^2 - 2y^2 + z^2 + yz = 2$ em $(2,1,-1).$
Plano tangente: $4x - 5y - z = 4$,
Reta normal: $(x,y,z) = (2,1,-1) + \lambda (4,-5,-1),$ $\lambda \in \mathbb{R}.$
Calcule o volume do conjunto dado.
$x^{2}+4y^{2}\leq 4$ e $x+y\leq z\leq x+y+1.$
$x\geq 0$, $x\leq y\leq 1$ e $0\leq z\leq e^{y^{2}}.$
$2\pi.$
$\dfrac{e - 1}{2}.$
Use a integral tripla para determinar o volume do sólido dado.
O tetraedro limitado pelos planos coordenados e o plano $2x+y+z=4.$
O sólido limitado pelo paraboloide $x=y^{2}+z^{2}$ e pelo plano $x=16.$
O sólido delimitado pelo cilindro $x=y^{2}$ e pelos planos $z=0$ e $x+z=1$.
$\dfrac{16}{3}.$
$128\pi.$
$\dfrac{8}{15}.$
Use a integral tripla para determinar o volume do sólido dado.
$x^{2}\leq z \leq 1-y$ e $y\geq 0.$
$x^{2}+2y^{2}\leq z\leq 2a^{2}-x^{2}$ $(a>0).$
$x^{2}+y^{2}+(z-1)^{2}\leq 1$ e $z\geq x^{2}+y^{2}.$
$4x^{2}+9y^{2}+z^{2}\leq 4$ e $4x^{2}+9y^{2}\leq 1.$
$\dfrac{4}{15}.$
$\pi a^4.$
$\dfrac{71\pi}{54}.$
$\dfrac{7\pi}{12}.$
Suponha que a equação $F(x,y,z)=0$ defina implicitamente cada uma das três variáveis $x$,$y$ e $z$ como função das outras duas:
$z=f(x,y)$, $y=g(x,y)$ e $x=h(y,z).$ Se $F$ for diferenciável e $F_{x}$,$F_{y}$ e $F_{z}$ forem todas não nulas, mostre que
$$\frac{\partial z}{\partial x} \frac{\partial x}{\partial y}\frac{\partial y}{\partial z}=-1.$$
Note que$\displaystyle \frac{\partial z}{\partial x} = -\frac{F_{x}}{F_{z}},$$\displaystyle \frac{\partial x}{\partial y} = -\frac{F_{y}}{F_{x}}$e$\displaystyle \frac{\partial y}{\partial z} = -\frac{F_{z}}{F_{y}}.$
Calcule o limite $\displaystyle \lim_{t \rightarrow 0}\left( \arctan(t), e^{-2t}, \dfrac{\ln{t}}{t} \right)$.
${\bf r}(t)=\left(arctg(t), e^{-2t},\frac{\ln t}{t}\right)$, temos que
$\lim\limits_{t\to 0}{\bf r}(t)=\lim\limits_{t\to 0}\left(arctg(t),e^{-2t},\frac{\ln t}{t}\right)=\left(\lim\limits_{t\to 0}arctg(t),\lim\limits_{t\to 0}e^{-2t},\lim\limits_{t\to 0}\frac{\ln t}{t}\right)$
Assim,
$\bullet \lim\limits_{t\rightarrow 0}arctg(t)=0$.
$\bullet \lim\limits_{t\to 0}e^{-2t}=1$.
$\bullet \lim\limits_{t\to 0}\dfrac{\ln t}{t}$ não existe.
Portanto, $\lim\limits_{t\to 0}\left(arctg(t),e^{-2t},\frac{\ln t}{t}\right)$ não existe.
Calcule a integral trocando a ordem de integração.
$\displaystyle\int_{0}^{4}\!\!\int_{\sqrt{x}}^{2}\dfrac{1}{y^{3}+1}\,dy dx$
$\displaystyle\int_{0}^{\pi}\!\!\int_{x}^{\pi}\dfrac{\sin{y}}{y}\,dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{x}^{2}2y^{2}\sin(xy)\,dy dx.$
$\dfrac{\ln(9)}{3}.$
$2.$
$4 - \sin(4).$
Determine a equação do plano tangente à superfície descrita parametricamente por \(x=u\cosh v\), \(y=u\sinh v\), \(z=u^2\) no ponto \((-3,0,9)\).
Esboce o sólido cujo volume é dado pela integral abaixo e calcule-a.
$$\int_{0}^{\pi/6}\!\!\int_{0}^{\pi/2}\!\!\int_{0}^{3}\rho^{2}\sin{\phi}\;d\rho d\theta d\phi$$
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{1} \int_{-\sqrt{1-y^{2}}}^{\sqrt{1-y^{2}}}\ln(x^{2}+y^{2}+1)\,dx dy$
$\displaystyle \pi (\ln(4) - 1).$
Determine a representação paramétrica do toro obtido girando em torno do eixo $z$ o círculo do plano $xz$ com centro em $(b,0,0)$ e raio $a < b.$ [Sugestão: tome como parâmetros os ângulos $\theta$ e $\alpha$ mostrados na figura.]
Use a representação paramétrica do item anterior para achar a área do toro.

$x = b\cos(\theta) + a\cos(\alpha)\cos(\theta),$ $y = b\sin(\theta) + a\cos(\alpha)\sin(\theta),$ $z = a\sin(\alpha),$ onde $0 \leq \alpha \leq 2\pi,$ $0 \leq \theta \leq 2\pi.$
$4\pi^2 ab.$
A função diferenciável $z=z(x,y)$ é dada implicitamente pela equação $f\bigg(\dfrac{x}{y},\dfrac{z}{x^{\lambda}}\bigg)=0$ ($\lambda\neq 0$ um número real fixo), onde
$f(u,v)$ é suposta diferenciável e $\dfrac{\partial f}{\partial v}(u,v)\neq 0$. Verifique que
$$x\frac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=\lambda z.$$
Note que $\displaystyle \frac{\partial z}{\partial x} = \frac{\lambda z}{x} -\frac{x^{\lambda}}{y} \frac{\partial f}{\partial u} \left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\right)^{-1} $ e $\displaystyle \frac{\partial z}{\partial y} = \frac{x^{\lambda + 1}}{y^{2}} \frac{\partial f}{\partial u} \left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},\frac{z}{x^{\lambda}} \right)\right)^{-1}$.
Utilize as curvas de nível da figura para predizer a localização dos pontos críticos de $f(x,y)=4+x^{3}+y^{3}-3xy$ e se $f$ tem um ponto de sela ou um máximo ou mínimo local em cada um desses pontos. Explique seu raciocínio. Em seguida, empregue o Teste da Segunda Derivada para confirmar suas predições.
$f$ possui um ponto de sela em $(0,0)$ e um mínimo local em $(1,1).$
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf i}$, $S$ a superfície $x^2+y^2+z^2 = 2$, $x^2+y^2\leq 1$ e $z \geq 0$, sendo ${\bf n}$ a normal apontando para cima.
$-\pi$.
Calcule o trabalho realizado pela força $\mathbf{F}(x,y) = xy\mathbf{i}+y^2\mathbf{j}$ ao mover uma partícula da origem ao longo da reta $y=x$ até $(1,1)$ e então de volta à origem ao longo da curva $y=x^2$.
$\dfrac{1}{12}.$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=x^{2}y+xy^{2}$, $x=2+t^{2}$, $y=1-t^{3}$.
$\displaystyle \frac{dz}{dt} = 4(2xy + y^{2} )^{3} - 3 (x^{2} + 2xy)t^{2}.$
Calcule a integral dupla, identificando-a antes com o volume de um sólido.
$\displaystyle\iint\limits_{R} 3 \, dA, \quad R = \{(x,y) \in \mathbb{R}^2: -2 \leq x \leq 2, \ 1 \leq y \leq 6\}.$
$\displaystyle\iint\limits_{R} (4 - 2y) \, dA, \quad R = [0,1] \times [0,1].$
$60.$
$3.$
Uma caixa de papelão sem tampa deve ter um volume de $32000\;cm^{3}$. Determine as dimensões que minimizem a quantidade de papelão utilizado.
$40$cm $\times$ $40$cm $\times$ $20$cm.
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}2z\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq 1$, $x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}-y^{2}\leq z \leq 1-2y^{2}.$
$\dfrac{7\pi}{2}.$
$0.$
Suponha que em uma certa região do espaço o potencial elétrico $V$ seja dado por $V(x,y,z) = 5x^2 - 3xy + xyz.$
- Determine a taxa de variação do potencial em $P = (3,4,5)$ na direção do vetor $\bf{v} = \bf{i} + \bf{j} - \bf{k}$.
- Em que direção $V$ varia mais rapidamente em $P$?
- Qual a taxa máxima de variação em $P$?
- Queremos determinar o valor de $D_\bf{u}f(P)$, em que $\bf{u}$ é o vetor unitário que tem mesma direção de $\bf{v}$, isto é, $\bf{u} = \frac{1}{\sqrt{3}}(1,1,-1)$. Como $V$ é diferenciável, segue que $D_\bf{u}f(P) = \nabla V(P) \cdot \mathbf{u}$. Observe que \linebreak $\nabla V(x,y,z) = (10x-3y+yz,-3x+xz,xy)$. Logo $\nabla V(P) = (38,6,12)$. Portanto, $$D_\bf{u}f(P) = \nabla V(P) \, \cdot \, \mathbf{u} = (38,6,12) \, \cdot \, \dfrac{1}{\sqrt{3}}(1,1,-1) = \dfrac{32\sqrt{3}}{3}.$$
- A direção em que $V$ varia mais rapidamente no ponto $P$ é a direção do gradiente de $V$ no ponto $P$, isto é, na direção de $\nabla V(P) = (38,6,12)$. Observe que aqui não é necessário normalizar o vetor, pois o exercício pede apenas a direção.
- A taxa de variação máxima é $|\nabla V(P)| = 2\sqrt{406}$.
Determine se ${\bf F}(x,y,z)=e^{y+2z}({\bf i}+x\,{\bf j}+2x\,{\bf k})$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = xe^{y + 2z} + K.$
Uma partícula se move ao longo de segmentos de reta da origem aos pontos $(1,0,0)$, $(1,2,1)$, $(0,2,1)$ e de volta para a origem sob a influência do campo de forças ${\bf F}(x,y,z) = z^2{\bf i} + 2xy{\bf j} + 4y^2{\bf k}.$ Encontre o trabalho feito.
$3$.
Seja $g(t)=f(3t,2t^{2}-1).$
- Expresse $g^{'}(t)$ em termos das derivadas parciais de $f$.
- Calcule $g^{'}(0)$ admitindo $\dfrac{\partial f}{\partial x}(0,-1)=\dfrac{1}{3}.$
- $\displaystyle g'(t) = 3\frac{\partial f}{\partial x}(3t,2t^{2} - 1) + 4t \frac{\partial f}{\partial y}(3t,2t^{2} - 1).$
- $g'(0) = 1.$
Calcule $\nabla f(x,y)$.
$f(x,y) = \arctan{\dfrac{x}{y}}$
$\displaystyle \nabla f(x,y) = \left(\frac{y }{x^{2} + y^{2}}, -\frac{x}{x^{2} + y^{2}} \right).$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do plano $z=x+3$ que está dentro do cilindro $x^{2}+y^{2}=1.$
$x = r \cos(\theta),$ $y = r \sin(\theta),$ $z = 3 + r \cos(\theta),$ onde $0 \leq r \leq 1$ e $0\leq \theta \leq 2\pi.$
Explique por que a função é diferenciável no ponto dado. $f(x,y) = e^{-xy} \cos{y}, \quad (\pi,0)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
Calcule $\displaystyle\int_{C}(\sin(xy)+xy\,\cos(xy))\,dx+x^{2}\,\cos(xy)\,dy$, onde $C(t)=(t^{2}-1,t^{2}+1)$, $-1\leq t\leq 1.$
$0.$
Suponha que, para todo $x$,$f(3x,x^{3})=\arctan(x)$.
- Calcule $\dfrac{\partial f}{\partial x}(3,1)$ admitindo $\dfrac{\partial f}{\partial y}(3,1)=2$.
- Determine a equação do plano tangente ao gráfico de $f$ no ponto $(3,1,f(3,1))$.
- $\dfrac{\partial f}{\partial x}(3,1) = -\frac{11}{6}.$
- $\displaystyle z - \frac{\pi}{4} = -\frac{11}{6}(x - 3) + 2(y - 1).$
Encontre o centróide e os momentos de inércia $I_{x}$, $I_{y}$ e $I_{z}$ do tetraedro cujos vértices são os pontos $(0,0,0)$, $(1,0,0)$, $(0,1,0)$ e $(0,0,1).$
Centróide: $\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4} \right),$ $I_{x} = I_{y} = I_{z} = \dfrac{1}{30}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y)=e^{x-1}\,{\bf i}+xy\,{\bf j}$ e $C$ é dada por ${\bf r}(t)=t^{2}\,{\bf i}+t^{3}\,{\bf j}, 0\leq t\leq 1.$
$\displaystyle \frac{11}{8} - \frac{1}{e}.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=x^{4}\,{\bf i}-x^{3}z^{2}\,{\bf j}+4xy^{2}z\,{\bf k}$ e $S$ é a superfície do sólido limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $z=x+2$ e $z=0.$
Determine o conjunto dos pontos de continuidade da função $f(x,y) = \sqrt{6 - 2x^2 - 3y^2}$. Justifique sua resposta.
$\left\lbrace (x,y);\; 2x^{2} + 3y^{2} \leq 6 \right\rbrace.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,4-u^{2}-v^{2})$, $(u,v)\in K$, onde $K$ é o conjunto no plano $uv$ limitado pelo eixo $u$ e pela curva (em coordenadas polares) $\rho=e^{-\theta}$,$0\leq \theta \leq \pi.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\displaystyle \dfrac{1}{72} \left( \ln\left(3\dfrac{\sqrt{e^{2\pi} + 4} + e^{\pi}}{\sqrt{e^{2\pi} + 4} - e^{\pi}} \right) + 3 \ln\left(\dfrac{\sqrt{5} - 1 }{\sqrt{5} + 1 }\right) - 8e^{3\pi} \sqrt{e^{2\pi} + 4}(e^{2\pi} + 1) + 16\sqrt{5} - 6\pi \right).$
Mostre que se \(f\), \(f_x\) e \(f_y\) são contínuas numa região circular contendo os pontos \(A=(x_0,y_0)\) e \(B=(x_1,y_1)\), então existe um ponto \((x^\ast,y^\ast)\) no segmento que une \(A\) e \(B\) tal que \[ f(x_1,y_1)-f(x_0,y_0) = f_x(x^\ast,y^\ast)(x_1-x_0)+f_y(x^\ast,y^\ast)(y_1-y_0). \] Este resultado é a versão bidimensional do Teorema do Valor Médio. [Sugestão: expresse o segmento de reta unindo \(A\) e \(B\) na forma paramétrica e use o Teorema do Valor Médio para funções de uma variável.]
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r \, dr d\theta.$
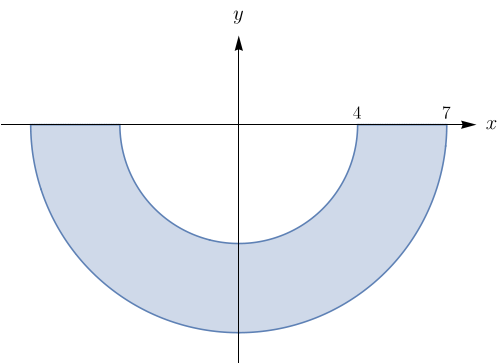
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{ R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
$\displaystyle \int_{0}^{\frac{3\pi}{2}} \int_{0}^{4} f(r\cos(\theta),r\sin(\theta)) r d r d \theta.$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=\tan^{-1}(x/y)$, $x=e^{t}$, $y=1-e^{-t}$.
$\displaystyle \frac{dz}{dt} = \frac{xe^{-t} - ye^{t}}{x^{2} + y^{2}}.$
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=1/(x+y)$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} = -\frac{1}{(x^{2} + y^{2})^{2}}$.
Determine a área da superfície dada pela parte da superfície $z=xy$ que está dentro do cilindro $x^{2}+y^{2}=1$.
$\dfrac{2\pi}{3}(2\sqrt{2} - 1)$.
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização $L(x,y)$ da função naquele ponto. $f(x,y) = x\sqrt{y}, \quad (1,4)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
$L(x,y) = 2x + \frac{1}{4}y - 1$.
Represente graficamente o domínio da função $z=f(x,y)$ dada por $f(x,y)=\dfrac{x-y}{\sqrt{1-x^{2}-y^{2}}}$.
$\left\lbrace (x,y); x^{2} + y^{2} < 1 \right\rbrace$
Determine os pontos da superfície $x^2 + 2y^2 + 3z^2 = 1$ nos quais o plano tangente é paralelo ao plano $3x - y + 3z = 1$.
$\displaystyle \left(\frac{3\sqrt{2}}{5}, - \frac{1}{5\sqrt{2}}, \frac{\sqrt{2}}{5} \right)$ e $\displaystyle \left(-\frac{3\sqrt{2}}{5}, \frac{1}{5\sqrt{2}}, -\frac{\sqrt{2}}{5} \right).$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E} x^2 e^y\,dV$, onde $E$ é delimitado pelo cilindro parabólico $z=1-y^{2}$ e pelos planos $z=0$, $x=1$ e $x=-1.$
$\displaystyle\iiint\limits_{ E}x\,dV$, onde $E$ é limitado pelo paraboloide $x=4y^{2}+4z^{2}$ e pelo plano $x=4.$
$\dfrac{8}{3e}.$
$\dfrac{16\pi}{3}.$
Determine uma reta que seja tangente à curva $x^2 + xy + y^2 = 7$ e paralela à reta $4x + 5y = 17$.
$\displaystyle y - 2 = -\frac{4}{5} (x - 1)$ ou $\displaystyle y + 2 = -\frac{4}{5} (x + 1).$
Seja ${\bf F}=(z tg^{-1}(y^{2}),z^{3}\ln(x^{2}+1),z).$ Determine o fluxo de ${\bf F}$ através da parte do parabolóide $x^{2}+y^{2}+z=2$ que está acima do plano $z=1$ e está orientada para cima. (Observe que a superfície acima não é fechada.)
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=xze^{y}{\bf i}-xze^{y}{\bf j}+z{\bf k}$ e $S$ é a parte do plano $x+y+z=1$ no primeiro octante, com orientação para baixo.
$-\dfrac{1}{6}.$
Seja ${\bf F}:\Omega\subset \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ contínuo no aberto $\Omega$. Prove que uma condição necessária para que ${\bf F}$ seja
conservativo é que $\int_{C}{\bf F}\cdot d{\bf r}=0$ para toda curva $C$ fechada, de classe $C^{1}$ por partes, com imagem contida em $\Omega.$
Se $C$ é uma curva fechada em $\Omega$ parametrizada por $\mathbf{r}(t),$ com $a \leq t \leq b,$ $\mathbf{r}(a) = \mathbf{r}(b)$ e $\mathbf{F} = \nabla f,$ então $\int_{C}{\bf F}\cdot d{\bf r} = f(\mathbf{r}(a)) - f(\mathbf{r}(b)) = 0.$
Determine e faça o esboço do domínio da função $f(x,y,z)=\sqrt{1-x^{2}-y^{2}-z^{2}}$.
$\left\lbrace (x,y);\; x^{2} + y^{2} + z^{2} \leq 1 \right\rbrace.$

$$x\;\dfrac{\partial z}{\partial x}+y\;\dfrac{\partial z}{\partial y}=z.$$
Primeiramente, vamos calcular $\dfrac{\partial z}{\partial x}$ e $\dfrac{\partial z}{\partial }.$ Assim,\\
$\bullet $ $\dfrac{\partial z}{\partial x}=$ $\dfrac{\partial}{\partial x}\bigg[x\cdot \sin\bigg(\dfrac{x}{y}\bigg)\bigg]=
1\cdot \sin\bigg(\dfrac{x}{y}\bigg)+x\cdot \cos \bigg(\dfrac{x}{y}\bigg)\cdot \dfrac{1}{y}$
$$=\sin\bigg(\frac{x}{y}\bigg)+\frac{x}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)$$
$\bullet $ $\dfrac{\partial z}{\partial y}=$ $\dfrac{\partial}{\partial y}\bigg[x\cdot \sin\bigg(\dfrac{x}{y}\bigg)\bigg]=
0\cdot \sin\bigg(\dfrac{x}{y}\bigg)+x\cdot \cos \bigg(\dfrac{x}{y}\bigg)\cdot \bigg(-\dfrac{x}{y^{2}}\bigg)$
$$=-\frac{x^{2}}{y^{2}}\cdot \cos\bigg(\frac{x}{y}\bigg).$$
Então,
$$x\cdot \frac{\partial z}{\partial x}+y\frac{\partial z}{\partial y}=x\cdot \bigg[\sin\bigg(\frac{x}{y}\bigg)+\frac{x}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)\bigg] +
y\cdot\bigg[ -\frac{x^{2}}{y^{2}}\cdot \cos\bigg(\frac{x}{y}\bigg)\bigg]$$
$$=x\cdot \sin\bigg(\frac{x}{y}\bigg)+\frac{x^{2}}{y}\cos\bigg(\frac{x}{y}\bigg)-\frac{x^{2}}{y}\cdot \cos\bigg(\frac{x}{y}\bigg)$$
$$x\cdot \sin\bigg(\frac{x}{y}\bigg)=z.$$
Encontre $\partial w/ \partial r$ quando $r=1$, $s=-1$ se $w=(x+y+z)^{2}$, $x=r-s$, $y=\cos(r+s)$, $z=\sin(r+s).$
$\displaystyle \frac{\partial w}{\partial r}(x(1,-1),y(1,-1),z(-1,1)) = 12.$
Faça um esboço do diagrama de contorno da função cujo gráfico é mostrado.
$y = 2x \pm \sqrt{C},$ $C \geq 0.$
Calcule o trabalho realizado pela força ${\bf F}(x,y)=xy\,{\bf i}+y^{2}\,{\bf j}$ ao mover uma partícula da origem ao longo da reta $y=x$ até $(1,1)$ e então de volta à origem ao longo da curva $y=x^{2}.$
$\dfrac{1}{12}.$
Uma placa fina de metal, localizada no plano $xy$, tem temperatura $T(x,y)$ no ponto $(x,y)$. As curvas de nível de $T$ são chamadas isotérmicas porque todos os pontos em uma isotérmica têm a mesma temperatura. Faça o esboço de algumas isotérmicas se a função temperatura for dada por
$$T(x,y)=\dfrac{100}{1+x^{2}+2y^{2}}.$$
As isotérmicas são dadas pela família de elipses: $x^{2} + 2y^{2} = \frac{100}{C} - 1,$ com $0 < C \leq 100.$
Mostre que $f(x,y) = \ln{(x^2+y^2)}$ satisfaz a equação de Laplace $\nabla^2f = 0$, exceto no ponto $(0,0).$
Note que se $(x,y) \neq (0,0),$ $\nabla^2f = \dfrac{\partial}{\partial x} \left[ \dfrac{2x}{x^{2} + y^{2}} \right] + \dfrac{\partial}{\partial y} \left[ \dfrac{2y}{x^{2} + y^{2}} \right].$
Determine a derivada direcional de $f(x,y,z) = xy + yz + zx$ em $P = (1,-1,3)$ na direção de $Q = (2,4,5)$.
$\displaystyle \frac{22}{\sqrt{30}}.$
Seja $g(x,y)=f(x^{2}+y^{2})$, onde $f:\mathbb{R}\rightarrow \mathbb{R}$ é uma função diferenciável. Mostre que
$$y\frac{\partial g}{\partial x}-x\frac{\partial g}{\partial y}=0.$$
Observe que $f$ é uma função de uma variável. Logo, utilizando a Regra da Cadeia para funções de uma variável, obtemos
$$\frac{\partial g}{\partial x}(x,y) = f'(x^2+y^2) (2x)$$
e
$$\frac{\partial g}{\partial y}(x,y) = f'(x^2+y^2) (2y).$$
Portanto
$$y\frac{\partial g}{\partial x}-x\frac{\partial g}{\partial y}=0.$$
Seja ${\bf F}(t)$ uma força dependendo do tempo $t$, que atua sobre uma partícula entre os instantes $t_{1}$
e $t_{2}$. Supondo ${\bf F}$ integrável em $[t_{1},t_{2}]$, o vetor
$${\bf I}=\int_{t_{1}}^{t_{2}}{\bf F}(t)\mathrm{d}t$$
denomina-se impulso de ${\bf F}$ no intervalo de tempo $[t_{1},t_{2}]$. Calcule o impulso de ${\bf F}$ no intervalo
de tempo dado.
- ${\bf F}(t)=t{\bf i}+{\bf j}+t^{2}{\bf k}$, $t_{1}=0$ e $t_{2}=2.$
- ${\bf F}(t)=\dfrac{1}{t+1}{\bf i}+t^{2}{\bf j}+{\bf k}$, $t_{1}=0$ e $t_{2}=1.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}y dS$, onde $S$ é a parte do parabolóide $y=x^{2}+z^{2}$ que está dentro do cilindro $x^{2}+z^{2}=4.$
$\dfrac{\pi(391\sqrt{17}+1)}{60}.$
Encontre o trabalho realizado pelo campo de forças \[ \mathbf{F}(x,y)= y^2\mathbf{i} + xy\mathbf{j} \] para mover uma partícula de \((0,0)\) até \((1,1)\) ao longo da parábola \(y=x^2\).
Determine os pontos da superfície $xyz = 1$ que estão mais próximos da origem.
$(1,1,1),$ $(1,-1,-1),$ $(-1,1,-1)$ e $(-1,-1,1).$
Determine $\int_{0}^{5}f(x,y)\,dx$ e $\int_{0}^{1}f(x,y)\,dy$, sendo $f(x,y)=12x^{2}y^{3}.$
$\int_{0}^{5} 12x^{2}y^{3} \,dx = 500y^{3}$ e $\int_{0}^{1} 12x^{2}y^{3} \,dy = 3x^{2}.$
Seja $W(s,t)=F(u(s,t),v(s,t))$, onde $F$, $u$ e $v$ são diferenciáveis, e $u(1,0)=2$, $u_{s}(1,0)=-2$, $u_{t}(1,0)=6$, $F_{u}(2,3)=-1$, $v(1,0)=3$, $v_{s}(1,0)=5$, $v_{t}(1,0)=4$, $F_{v}(2,3)=10.$ Determine $W_{s}(1,0)$ e $W_{t}(1,0).$
$W_{s}(1,0) = 52$ e $W_{t}(1,0) = 34.$
Calcule a integral iterada.
$\displaystyle\int_{0}^{\pi/2} \int_{0}^{\pi/2}\sin{x}\cos{y} \, dy dx$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{1}(2x+y)^{8}\,dx dy$
$1.$
$\dfrac{4^{10} - 2^{11}}{180}.$
Use o Teorema do Divergente para calcular $\displaystyle\iint \limits_{S}(2x+2y+z^{2})\,dS$ onde $S$ é a esfera $x^{2}+y^{2}+z^{2}=1.$
A superfície $S$ em questão é a esfera unitária, que é a fronteira da bola unitária $B$ dada por $x^2+y^2+z^2 \leq 1$ e tem vetor normal num ponto $(x,y,z)$ igual a $(x,y,z)$ (o qual aponta para ``fora").

Observe que podemos transformar o integrando $2x+2y+z^{2}$ em $(2,2,z) \cdot (x,y,z)$ e essa escrita é interessante, já que o segundo vetor é exatamente o vetor normal a $S$. Agora estamos em condições de aplicar o Teorema do Divergente quando tomamos o campo ${\bf F}(x,y,z) = (2,2,z)$. Assim,
\begin{array}{rcl}\displaystyle\iint\limits_{S}(2x+2y+z^{2})\,dS & = & \iint\limits_{ S}(2,2,z) \cdot (x,y,z)\,dS \\& = & \int\int\int \limits_{ S}{\bf F} \cdot {\bf n}\,dS \\& = & \iiint\limits_{ B}\text{div } F\,dV \\& = & \iiint\limits_{ B}(0+0+1)\,dV \\& = & V(B) = \frac{4\pi}{3}.\end{array}
Determine uma reta que seja tangente à elipse $2x^2 + y^2 = 3$ e paralela à reta $2x + y = 5$.
$\displaystyle y = -2x + 3$ ou$\displaystyle y = -2x - 3.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=y\cos{x}$.
Sendo $f(x,y)=y\,\cos x$, vamos inicialmente localizar seus pontos críticos:
$$f_{x}(x,y)=-y\,\sin x \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; f_{y}(x,y)=\cos x.$$
Igualando essas derivadas parciais a zero, obtemos as equações
$$y\,\sin x=0 \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; \cos x=0.$$
Da segunda equação obtemos que $x=\bigg(\dfrac{\pi}{2}+n\pi\bigg)$, $n\in \mathbb{Z}.$ Da primeira equação temos que $y=0$ para todos essas $x$-valores.
Assim, os pontos críticos são $\bigg(\dfrac{\pi}{2}+n\pi,0\bigg).$ Agora,
$$f_{xx}(x,y)=-y\,\cos x,\;\;\;\;\;\; f_{xy}(x,y)=-\sin x\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\; f_{yy}(x,y)=0.$$
Então
\begin{array}{rcl}D(x,y)&=&(f_{xx}(x,y))\cdot (f_{yy}(x,y))-(f_{xy}(x,y))^{2}\\&\Rightarrow& D\bigg(\dfrac{\pi}{2}+n\pi,0\bigg)=0-\sin^{2}x=-\sin^{2}x<0.\end{array}
Portanto, cada ponto crítico é ponto de sela.
Utilize a Equação
$$ \dfrac{dy}{dx}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}=-\dfrac{F_x}{F_y}$$
para determinar $\mathrm{d}y/\mathrm{d}x$.
$\sqrt{xy}=1+x^{2}y$
$\displaystyle \frac{dy}{dx} = \frac{4(xy)^{3/2} - y}{x - 2x^{2}\sqrt{xy}} .$
Seja $D$ a região limitada abaixo pelo plano $z=0$, acima pela esfera $x^2+y^2+z^2=4$ e dos lados pelo cilindo $x^2+y^2=1$. Monte as integrais triplas em coordenadas cilíndricas que dão o volume de $D$ usando as ordens de integração a seguir.
$dzdrd\theta$
$drdzd\theta$
$d\theta dzdr$
$\displaystyle \int_{0}^{2\pi} \int_{0}^{1} \int_{0}^{\sqrt{4 - r^2}} r dz dr d\theta.$
$\displaystyle \int_{0}^{2\pi} \int_{0}^{\sqrt{3}} \int_{0}^{1} r drdzd\theta + \int_{0}^{2\pi} \int_{\sqrt{3}}^{2} \int_{0}^{\sqrt{4 - z^2}} r drdzd\theta.$
$\displaystyle \int_{0}^{1} \int_{0}^{\sqrt{4 - r^2}} \int_{0}^{2\pi} r d\theta dzdr.$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{grad }{f}$;
$\text{rot }{(\text{grad }{f})}$;
$\text{grad }{(\text{div }{\mathbf{F}})}$.
$\text{grad }{f}$ é um campo gradiente.
$\text{rot }{(\text{grad }{f})}$ é um campo vetorial.
$\text{grad }{(\text{div }{\mathbf{F}})}$ é um campo vetorial.
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{3}-3x-y^{3}+12y$, $D$ é o quadrilátero cujos vértices são $(-2,3)$, $(2,3)$, $(2,2)$ e $(-2,-2).$
Valor máximo: $18;$ valor mínimo: $-18.$
A função $f(x,y) = \begin{cases}\dfrac{x^2 - y^2}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\\\end{cases}$ é diferenciável em $(0,0)$? Justifique.
Não.
A temperatura $T$ de uma localidade do Hemisfério Norte depende da longitude $x$, da latitude $y$ e do tempo $t$, de modo que podemos escrever $T=f(x,y,t)$. Vamos medir o tempo em horas a partir do início de Janeiro.
Qual é o significado das derivadas parciais $\partial T/\partial x$, $\partial T/\partial y$ e $\partial T/\partial t$?
Honolulu (você sabe onde fica?) tem longitude de $158^{\circ}W$ e latitude de $21^{\circ}N$. Suponha que às 9 horas em $1^{\circ}$ de Janeiro esteja ventando para nordeste uma brisa quente, de forma que a oeste e a sul o ar esteja quente e a norte e leste o ar esteja mais frio. Você esperaria que $f_{x}(158,21,9)$, $f_{y}(158,21,9)$ e $f_{t}(128,21,9)$ fossem positivas ou negativas? Explique.
- $\partial T/\partial x$ é a taxa de variação da temperatura quando a longitude muda, mas a latitude e o tempo são constantes;
$\partial T/\partial y$ é a taxa de variação da temperatura quando a latitude muda, mas a longitude e o tempo são constantes;
$\partial T/\partial t$ é a taxa de variação da temperatura quando o tempo muda, mas a longitude e a latitude são constantes. - $f_{x}(158,21,9) > 0,$ $f_{y}(158,21,9) < 0$ e $f_{t}(158,21,9) > 0.$
As equações de Maxwell relacionam o campo elétrico $\mathbf{E}$ e o campo magnético $\mathbf{H}$, quando eles variam com o tempo em uma região que não contenha carga nem corrente, como segue:
$$\text{div }{\mathbf{E}} = 0,\text{ }\text{div }{\mathbf{H}} = 0$$
$$\text{rot }{\mathbf{E}} = -\dfrac{1}{c}\dfrac{\partial\mathbf{H}}{\partial t},\text{ }\text{rot }{\mathbf{H}} = \dfrac{1}{c}\dfrac{\partial\mathbf{E}}{\partial t},$$
em que $c$ é a velocidade da luz. Use essas equações para demonstrar o seguinte:
$\nabla \times (\nabla \times \mathbf{E}) = - \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{E}}{\partial t^2}$,
$\nabla \times (\nabla \times \mathbf{H}) = - \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{H}}{\partial t^2}$,
$\nabla^2{\mathbf{E}} = \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{E}}{\partial t^2}$,
$\nabla^2{\mathbf{H}} = \dfrac{1}{c^2}\dfrac{\partial^2\mathbf{H}}{\partial t^2}$.
$\nabla \times (\nabla \times \mathbf{E}) = \nabla \times (\text{rot } \mathbf{E}) = \nabla \times \left( -\dfrac{1}{c} \dfrac{\partial \mathbf{H}}{\partial t} \right) = -\dfrac{1}{c} \dfrac{\partial}{\partial t} \text{rot } \mathbf{H} = -\dfrac{1}{c} \dfrac{\partial}{\partial t} \left(\dfrac{1}{c} \dfrac{\partial \mathbf{E}}{\partial t} \right)$
Análogo ao item 1.
Note que $\nabla^2{\mathbf{E}} = \nabla \text{div } \mathbf{E} - \text{rot } \text{rot }(\mathbf{E}).$
Análogo ao item 3.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xy^{4}\,ds$, $C$ é a metade direita do círculo $x^{2}+y^{2}=16.$
$\dfrac{2^{13}}{5}.$
Mostre que
$$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{x^{2}+y^{2}+z^{2}}\,e^{-(x^{2}+y^{2}+z^{2})}\,dxdydz=2\pi.$$
(A integral imprópria tripla é definida como o limite da integral tripla sobre uma esfera sólida quando o raio da esfera aumenta indefinidamente.)
Note que $$\begin{split}&\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\sqrt{x^{2}+y^{2}+z^{2}}\,e^{-(x^{2}+y^{2}+z^{2})}\,dxdydz \\&= \lim_{R \to \infty} \int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{R} \rho e^{-\rho^2}\rho^2 \sin(\phi)\;d\rho d\phi d\theta.\end{split}$$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = xy$ e $x^2 + 4y^2 = 8.$
Pontos de máximo: $\displaystyle \left(2,1\right)$ e $(-2,-1)$; pontos de mínimo: $\displaystyle \left(-2,1\right)$ e $(2,-1)$.
Seja $g(x,y) = f(x^2 + y^2)$, em que $f$ é uma função diferenciável. Sabendo que $f'(2) = 1$, determine a equação da reta tangente à curva de nível de $g$ que passa pelo ponto $(1,1)$.
$x + y = 2.$
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=x{\bf i}-y{\bf j}+z{\bf k}$ e $S$ é a superfície do sólido delimitado pelos gráficos de $z=x^{2}+y^{2}$ e $z=4.$
$8\pi.$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla{\ln{r}} = \dfrac{\mathbf{r}}{r^2}$.
$\nabla{\ln{r}} = \dfrac{1}{2} \nabla \ln (x^{2} + y^{2} + z^{2}).$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} e^{x+y} \, dA$, em que $R$ é dada pela inequação $|x| + |y| \leq 1$.
$e - e^{-1}.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\int\!\!\!\!\int\limits_{\!\!\!\!\!\! R} xy^{2}\,dx dy$, onde $R$ é o retângulo $1\leq x\leq 2,\;2\leq y\leq 3.$
$\displaystyle\int\!\!\!\!\int\limits_{\!\!\!\!\!\! R} x\cos(2y)\,dx dy$, onde $R$ é o retângulo $0\leq x\leq 1,\;-\dfrac{\pi}{4}\leq y\leq \dfrac{\pi}{4}.$
$\dfrac{19}{2}.$
$\dfrac{1}{2}.$
Considere a função
$$f(x,y) = \begin{cases}\dfrac{x^2 - xy}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\0, & \quad \text{se } (x,y) = (0,0).\end{cases}$$
Calcule o limite $\displaystyle \lim_{(x,y) \to (0,0)}f(x,y)$ ou mostre que esse limite não existe.
Calcule o limite $\displaystyle \lim_{(x,y) \to (1,1)}f(x,y)$ ou mostre que esse limite não existe.
$f$ é contínua em $(0,0)$? Justifique.
$f$ é contínua em $(1,1)$? Justifique.
O limite não existe.
$0.$
Não.
Sim.
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{\pi}\!\!\int_{0}^{x}x\sin{y}\,dy dx$.
$\dfrac{\pi^{2}}{2} + 2.$
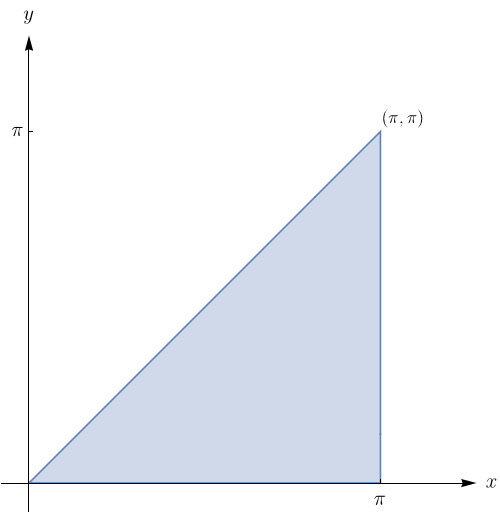
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=(x^{2}+y^{2})e^{y^{2}-x^{2}}$.
Ponto de mínimo: $(0,0);$ pontos de sela: $(1,0)$ e $(-1,0).$
Seja $z=f(u-v,v-u)$. Verifique que
$$\frac{\partial z}{\partial u}+\frac{\partial z}{\partial v}=0.$$
Note que $\displaystyle \frac{\partial z}{\partial u}(u,v) = \frac{\partial f}{\partial x}(u-v,v-u) - \frac{\partial f}{\partial y}(u-v,v - u)$ e $\displaystyle \frac{\partial z}{\partial v}(u,v) = -\frac{\partial f}{\partial x}(u-v,v-u) + \frac{\partial f}{\partial y}(u-v,v - u).$
O campo vetorial $\mathbf{F}$ é mostrado no plano $xy$ e é o mesmo em todos os planos horizontais (em outras palavras, $\mathbf{F}$ é independente de $z$ e sua componente $z$ é 0).
O $\text{div }{\mathbf{F}}$ será positivo, negativo ou nulo? Justifique.
Determine se o $\text{rot }{\mathbf{F}} = 0$. Se não, em que direção rot $\mathbf{F}$ aponta?
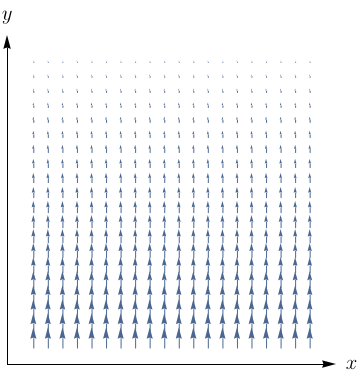
Negativo.
$\text{rot } \bf{F} = \bf{0}.$
Dada $f(x,y)=\dfrac{1}{\sqrt{16-x^{2}-y^{2}}}$.
Encontre o domínio da função;
Encontre a imagem da função;
Descreva as curvas de nível da função.
O domínio de $f$ é
$$D=\{(x,y)|\, 16-x^{2}-y^{2}>0\}=\{(x,y)|\,x^{2}+y^{2}<16\}.$$

A imagem de $f$ é
$$\bigg\{z|\, z=\frac{1}{\sqrt{16-x^{2}-y^{2}}},\,(x,y)\in D\bigg\}.$$
Mas,
$$z=\frac{1}{\sqrt{16-x^{2}-y^{2}}}\geq \frac{1}{\sqrt{16}}=\frac{1}{4}.$$
Assim, a imagem de $f$ é $\bigg\{z|\, z \geq \dfrac{1}{4}\bigg\}.$
s curvas de níveis de $f$ são da forma $f(x,y)=c$, isto é,
$$\frac{1}{\sqrt{16-x^{2}-y^{2}}}=c\Leftrightarrow \sqrt{16-x^{2}-y^{2}}=\frac{1}{c}\Leftrightarrow 16-x^{2}-y^{2}=\frac{1}{c^{2}}$$
$$\Leftrightarrow x^{2}+y^{2}=16-\frac{1}{c^{2}}.$$
Assim, as curvas de níveis de $f$ são circunferências com centro na origem e raio menor do que $4.$
Determine ${\bf r}(t)$ sabendo que
- ${\bf r}'(t)=t{\bf i}+2{\bf k}$ e ${\bf r}(0)={\bf i}+{\bf j}.$
- ${\bf r}'(t)=\sin(t){\bf i}+\cos(2t){\bf j}+\dfrac{1}{t+1}{\bf k}$, $t\geq 0$ e ${\bf r}(0)={\bf i}-{\bf j}+2{\bf k}.$
- ${\bf r}'(t)=\dfrac{1}{1+4t^{2}}{\bf i}+e^{-t}{\bf j}+{\bf k}$ e ${\bf r}(0)={\bf k}.$
Calcule a integral de linha
$$\int_{C}e^{2y}\,dx+(1+2xe^{2y})\,dy,$$
onde $C$ é a curva dada por $r(t)=(te^{t},1+\sin(\pi t/2))$, $0\leq t\leq 1.$ (Sugestão: verifique se o campo é conservativo.)
$e^{5} + 1.$
Determine $\dfrac{ \partial f}{\partial x}$ e $\dfrac{\partial f}{\partial y}$, sendo $f(x,y)= \begin{cases}\dfrac{x+y^{4}}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= \begin{cases}\dfrac{y^{2} - x^{2} - 2xy^{4}}{(x^{2}+y^{2})^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\\text{não existe} & \quad \text{se } (x,y)=(0,0)\\\end{cases} \;\;\;\; \text{e}\\\frac{\partial f}{\partial y} &= \begin{cases}\dfrac{4x^{2}y^{3} + 2y^{5} - 2xy}{x^{2}+y^{2}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}\end{aligned}$
Se $z=f(x,y)$, onde $x=r^{2}+s^{2}$ e $y=2rs$, determine $\partial^{2}z/\partial r\partial s.$
$\displaystyle \frac{\partial^{2}z}{\partial r\partial s} = 4rs \frac{\partial^{2}z}{\partial x^{2}} + 4rs \frac{\partial^{2}z}{\partial y^{2}} + (4r^{2} + 4s^{2}) \frac{\partial^{2}z}{\partial x\partial y} + 2 \frac{\partial z}{\partial y}.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=x^{2}\,{\bf i}+xy\,{\bf j}$ sobre uma partícula que dá uma volta no círculo $x^{2}+y^{2}=4$ no sentido anti-horário.
$0.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}\sqrt{x+y}\sqrt[3]{x+2y-z}\,dxdydz$, onde $B$ é a região $1\leq x+y\leq 2$, $0\leq x+2y-z\leq 1$ e $0\leq z\leq 1.$
$\sqrt{2} - \dfrac{1}{2}.$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u+v$, $y=3u^{2}$, $z=u-v$; $(2,3,0).$
$3x - y + 3z = 3.$
Calcule o trabalho realizado pelo campo vetorial \[ \mathbf{F}(x,y,z) = x^2\mathbf{i}+4xy^3\mathbf{j}+y^2x\mathbf{k}\] sobre uma partícula que percorre o caminho \(C\) definido como o bordo da superfície \(\sigma\) contida no plano \(z=y\) e cuja projeção no plano \(xy\) corresponde ao retângulo \(R=\{(x,y)\in\mathbb{R}^2; 0\leq x\leq 1\),\ \(0\leq y\leq 3\}\). O sentido de percurso é tal que a fronteira de \(R\) é percorrida no sentido horário.
Note que calcular o trabalho \(\displaystyle W= \oint_C\mathbf{F}\cdot\,d\mathbf{r}\) assim diretamente exigiria quatro integrações separadas, uma para cada lado do retângulo. Entretanto, usando o Teorema de Stokes podemos, em vez disso, calcular uma (única!) integral de superfície \[ W= \iint\limits_\sigma\mathrm{rot\,}\mathbf{F}\cdot\mathbf{n}\,dS \] na qual \(\sigma\) é tomada com a orientação para baixo, como requerido pelo Teorema de Stokes. Como a superfície \(\sigma\) está contida no plano \(z=y\) e \[\mathrm{rot\,}\mathbf{F} = \left|\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ x^2 & 4xy^3 & xy^2 \end{array}\right| = 2xy\mathbf{i}-y^2\mathbf{j}+4y^3\mathbf{k}, \] segue então que \begin{align*} W= \iint\limits_\sigma\mathrm{rot\,}\mathbf{F}\cdot\mathbf{n}\,dS & = \iint\limits_R\mathrm{rot\,}\mathbf{F}\cdot\left( \dfrac{\partial z}{\partial x}\mathbf{i} +\dfrac{\partial z}{\partial y}\mathbf{j} - \mathbf{k}\right)\,dA \\ & = \iint\limits_R\left(2xy\mathbf{i}-y^2\mathbf{j}+4y^3\mathbf{k}\right)\cdot\left(0\mathbf{i}+\mathbf{h}-\mathbf{k}\right)\,dA \\ & = \int_0^1\int_0^3(-y^2-4y^3)\,dydx \\ & = - \int_0^1\left[\dfrac{y^3}{3}+y^4\right]_{y=0}^3\,dx \\ & = -\int_0^1 90\,dx = -90. \end{align*}
Considere a função
$$f(x,y)=\log(9-x^{2}-9y^{2}).$$
Esboce no plano $xy$ o domínio de $f.$
Calcule as derivadas parciais $f_{x}$ e $f_{y}.$
- $D_{f} = \left\lbrace (x,y) \in \mathbb{R}^{2};\; x^{2} -9y^{2} < 9 \right\rbrace$.
- $\displaystyle f_{x} = \frac{-2x}{9 - x^{2} - 9y^{2}} \;\;\;\text{e}\;\;\;f_{y} = \frac{-18y}{9 - x^{2} - 9y^{2}}$.
Calcule a área da parte da superfície esférica $x^{2}+y^{2}+z^{2}=1$ que se encontra dentro do cone $z\geq \sqrt{x^{2}+y^{2}}.$
$\pi(2 - \sqrt{2}).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}+2xy+y^{2}-5$.
Ponto de mínimo : $\displaystyle \left( \frac{5}{3}, -\frac{5}{3}\right);$ ponto de sela: $\displaystyle \left(-1,1\right).$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,\sqrt{1-u^{2}-v^{2}},v)$, $u^{2}+v^{2}\leq 1.$
Semi superfície esférica $x^2 + y^2 + z^2 = 1,$ $y \geq 0.$
Calcule o centro de massa da região: $D = \{(x,y) \in \mathbb{R}^2: x^2 + 4y^2 \leq 1, \ y \geq 0\}$ e a densidade é proporcional à distância do ponto ao eixo $x$.
$\displaystyle \left(0, \frac{3\pi}{32} \right).$
Um arame fino é entortado no formato da semicircunferência $x^{2}+y^{2}=4$, $x\geq 0$. Se a densidade linear for uma constante $k$, determine a massa e o centro de massa do arame.
Massa: $k2\pi;$ centro de massa: $\displaystyle \left( \frac{4}{\pi},0 \right).$
Determine as derivadas parciais de primeira ordem da função $u=x^{y/z}$.
$\displaystyle \frac{\partial u}{\partial x} = \frac{y}{z} x^{(y/z) - 1},\;\;\; \frac{\partial u}{\partial y} = x^{y/z} \ln x \;\;\;\text{e}\;\;\; \frac{\partial u}{\partial z} = - \frac{yx^{y/z}}{z^{2}} \ln x$.
Prove a seguinte identidade \[ \iint\limits_\sigma\mathrm{rot\,}\mathbf{F}\cdot\mathbf{n}\,dS = 0, \] supondo que \(\mathbf{F}\) e \(\sigma\) satisfaçam as hipóteses do Teorema da Divergência.
Use um software de apoio computacional para mostrar que o volume \(V\) sob a superfície \(z=xy^3\sin(xy)\) e acima do retângulo \([0,\pi]\times[0,1]\) no plano \(xy\) é dado por \(V=3/\pi\).
Determine a equação da reta tangente à trajetória da função dada, no ponto dado.
- ${\bf r}(t)=(\cos (t),\sin (t),t)$ e ${\bf r}(\pi/3).$
- ${\bf r}(t)=(t^{2},t)$ e ${\bf r}(1).$
- ${\bf r}(t)=\bigg(\dfrac{1}{t},\dfrac{1}{t},t^{2}\bigg)$ e ${\bf r}(2).$
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y) = 5xy^2 - 4x^3y, P = (1,2), \bf{u} = \left( \frac{5}{13},\frac{12}{13} \right)$.
- $\nabla f(x,y) = (5y^{2} - 12x^{2}y, 10xy - 4x^{3}).$
- $\nabla f(1,2) = (-4, 16).$
- $\displaystyle \frac{172}{13}.$
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = 3x^3y - xy$ em $(1,-1,f(1,-1))$.
Plano tangente: $z = -8x + 2y + 8$
Reta normal: $(x,y,z) = \left(1,-1,-2 \right) + \lambda \left(-8,2,-1 \right)$.
Determine as derivadas parciais de $f(x,y)=(4xy-3y^{3})^{3}+5x^{2}y$.
$\displaystyle \frac{\partial f}{\partial x} = 12 y (4xy - 3y^{3})^{2} + 10xy\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 3(4xy - 3y^{2})^{2}(4x - 9y^{2}) + 5x^{2}.$
A fórmula de Taylor de primeira ordem para $f(\vec{a} + \vec{v})$ pode ser escrita como $ f(\vec{a}) + \nabla f(\vec{a}) \cdot \vec{v}$, já desconsiderando o termo de erro. Calcule-a para $f(x,y) = x^2/2 + y$, $\vec{a} = (0,0)$ e $\vec{v} = (1/2,1/2)$. Calcule também o erro cometido, dizendo se é um erro pequeno ou grande e por quê.
$$\int_{C} P\,dx+Q\,dy=\iint\limits_{B}\bigg(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\bigg)\,dxdy,$$
onde $B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(1,1)$, $C$ é a fronteira de $B$ orientada no sentido anti-horário, $P(x,y)=x^{2}-y$ e $Q(x,y)=x^{2}+y.$
$\displaystyle \int_{C} P\,dx+Q\,dy = \dfrac{7}{6} = \iint\limits_{B}\bigg(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\bigg)\,dxdy.$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla \times \mathbf{r} = \mathbf{0}$.
$\nabla \times \mathbf{r} = \left[\dfrac{\partial}{\partial y} (z) - \dfrac{\partial}{\partial z}(y) \right]\mathbf{i} + \left[\dfrac{\partial}{\partial z} (x) - \dfrac{\partial}{\partial x}(z) \right]\mathbf{j} + \left[\dfrac{\partial}{\partial x} (y) - \dfrac{\partial}{\partial y}(x) \right]\mathbf{k}.$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Mostre que o plano tangente ao parabolóide $z = x^2 + y^2$ no ponto $(1,2,5)$ intercepta o plano $xy$ na reta
$$\begin{cases}2x + 4y - 5 = 0 \\z = 0\end{cases}.$$
Note que o plano tangente no ponto $(1,2,5)$ é $z = 2x + 4y - 5$.
Sejam \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\), \(r=\|\mathbf{r}\|\), \(f\) uma função diferenciável de uma variável e \(\mathbf{F}(\mathbf{r})=f(r)\mathbf{r}\).
Mostre que \[\nabla f(r) = \dfrac{f'(r)}{r}\mathbf{r}.\]
Use o resultado anterior para mostrar que \(\displaystyle \mathbf{F}=3f(r)+rf'(r). \)
Determine a diferencial da função $z = x^3 \ln{y^2}$.
$dz = 3x^{2} \ln (y^{2})dx + \frac{2x^{3}}{y} dy$.
Determine as derivadas parciais de $f(x,y)=5x^{4}y^{2}+xy^{3}+4$.
$\displaystyle \frac{\partial f}{\partial x} = 20x^{3}y^{2} + y^{3}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 10x^{4}y + 3xy^{2}.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y) = x^2y; \quad x^2 + 2y^2 = 6.$
Valor máximo: $4;$ valor mínimo: $-4.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\cos(x^{2}+y^{2})\,dA$, onde $R$ é a região acima do eixo do $x$ e dentro da circunferência $x^{2}+y^{2}=9.$
$\displaystyle \frac{\pi}{2} \sin(9).$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B} z \,dxdydz$, onde $B$ é o conjunto $1\leq x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
Usando coordenadas esféricas, o sólido pode ser descrito por
$$B = \left\{(\rho, \theta, \phi): 1 \leq \rho \leq 2, 0 \leq \theta \leq 2\pi \mbox{ e } 0 \leq \phi \leq \frac{\pi}{2}\right\}.$$
Lembre que o Jacobiano dessa transformação é $\rho^2 \sin{\phi}$. Assim, obtemos
\begin{array}{rcl}\displaystyle\iiint\limits_{B} z \,dxdydz & = & \displaystyle\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\int_{1}^{2}(\rho \cos{\phi})(\rho^2 \sin{\phi})\,d\rho d\phi d\theta \\ & = & \displaystyle\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\left.\left(\frac{\rho^4}{4} \frac{\sin{2\phi}}{2}\right|_{\rho=1}^{\rho=2}\right)\, d\phi d\theta \\ & = & \displaystyle\int_{0}^{2\pi}\left.\left(\frac{(16-1)}{8} \frac{(-\cos{2\phi)}}{2}\right|_{\phi=0}^{\rho=\frac{\pi}{2}}\right)\, d\theta \\ & = & \left.-\frac{15}{16}(-1-1) \theta \right|_{\theta=0}^{\theta=2\pi} = \frac{15\pi}{4}. \end{array}
Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$, $E$ é a bola unitária $x^{2}+y^{2}+z^{2}\leq 1.$
$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = 4\pi.$
Seja $S$ o gráfico de $f(x,y)=x^{2}+y^{2}$, $x^{2}+y^{2}\leq 1$ e seja ${\bf n}$ a normal a $S$ com componete $z\leq 0$. Seja ${\bf F}(x,y,z)=x^{2}y\,{\bf i}-xy^{2}\,{\bf j}+{\bf k}$. Calcule $\iint \limits_{S}{\bf F}\cdot {\bf n}\, dS.$
Observe que $S$ não é uma superfície fechada (isto é, $S$ não é a fronteira de um sólido $E$). Para que possamos utilizar o Teorema do Divergente, vamos considerar a superfície $S_2$ constituída pelo parabolóide $S$ e pelo círculo $S_1$ dado por $x^2+y^2 \leq 1$ em $z=1$. Como $S_2$ é uma superfície fechada, usamos a escolha da normal ${\bf n_2}$ em $S_2$ que está apontando ``para fora". Sejam ${\bf n_1}$ a normal a $S_1$ (apontando para cima) e ${\bf n}$ a normal a $S$ (apontando para fora).
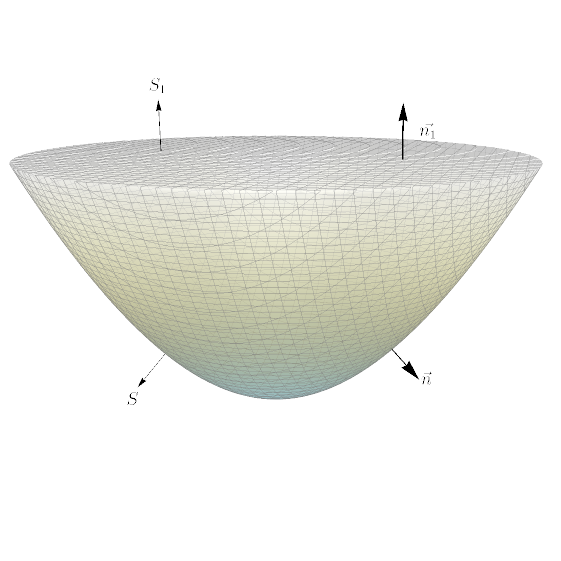
Temos
$\displaystyle\iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS = \iint\limits_{S}{\bf F}\cdot {\bf n}\,dS + \iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS,$
isto é,
$\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}\,dS = \iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS - \iint \limits_{ S_1}{\bf F}\cdot {\bf n_1}\,dS.$
Pelo Teorema do Divergente,
$$\iint\limits_{S_2}{\bf F}\cdot {\bf n_2}\,dS = \iiint\limits_{E}(2xy-2xy+0)\,dV = 0,$$
em que $E$ é o sólido que possui $S_2$ como fronteira.
Para determinar $\displaystyle\iint\limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS$, devemos encontrar uma parametrização para $S_1$ e determinar o vetor normal ${\bf n_1}$. Considere a seguinte parametrização de $S_1$: $r(u,v) = (u,v,1)$, com $u^2+v^2 \leq 1$. Daí, $r_u(u,v) = (1,0,0)$ e $r_v(u,v) = (0,1,0)$. Logo, $r_u \times r_v = (0,0,1)$ é um vetor normal a $S_1$. Devemos tomar ${\bf n_1} = (0,0,1)$ para que aponte para cima. Então,
$\displaystyle\iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS = \iint\limits_{D}(u^2v,-uv^2,1)\cdot(0,0,1)\,dA,$
em que $D = \{(u,v) \in \mathbb{R}^2; u^2+v^2 \leq 1\}$. Portanto,
$\displaystyle\iint \limits_{S_1}{\bf F}\cdot {\bf n_1}\,dS = \iint\limits_{D}1\,dA = A(D) = \pi,$
donde concluímos que
$\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS = 0 - \pi = -\pi.$
Determine os valores extremos de $f(x,y) = 2x^2 + 3y^2 - 4x - 5$ na região descrita por $x^2 + y^2 \leq 16$.
Valor máximo: $f(-2, \pm 2 \sqrt{3}) = 47$ e valor mínimo $f(1,0) = -7.$
Uma esfera astroidal tem equação \(x^{2/3}+y^{2/3}+z^{2/3}=a^{2/3}\). Encontre o volume do sólido compreendido por uma esfera astroidal usando uma integral tripla e a transformação \begin{align*} x & = \rho (\sin\phi\cos\theta)^3, \\ y & = \rho (\sin\phi\sin\theta)^3, \\ z & = \rho (\cos\phi)^3, \end{align*} para a qual \(0\leq\rho\leq a\), \(0\leq\phi\leq\pi\), \(0\leq\theta\leq 2\pi\).
\(\dfrac{4}{35}\pi a^3\)
São mostradas as curvas de nível de uma função $f.$ Determine se as seguintes derivadas parciais são positivas ou negativas no ponto $P.$
$f_{x}$
$f_{xx}$
$f_{yy}$$f_{y}$
$f_{xy}$
Negativa
Positiva
Positiva
Negativa
Positiva
Esboce o gráfico da função $f(x,y)=y$.
$z = y.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xyz\,ds$, onde $C$ é a hélice ${\bf r}(t)=(\cos t,\sin t,3t)$, $0\leq t\leq 4\pi.$
$-3\sqrt{10}\pi.$
Esboce a região cuja área é dada pela integral $\displaystyle\int_{\pi}^{2\pi} \int_{4}^{7} r\, dr d\theta$ e calcule-a:

Determine as derivadas parciais de $z=\cos(xy)$.
$\displaystyle \frac{\partial z}{\partial x} = -y\sin(xy)\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = -x\sin(xy).$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=\dfrac{1}{\ln(y)}$ e $B=\bigg\{(x,y)\in \mathbb{R}^{2}|\;2\leq y\leq 3,\;0\leq x\leq \dfrac{1}{y}\bigg\}.$
$f(x,y) = xy\cos{x^{2}}$ e $B=\{(x,y) \in \mathbb{R}^{2}| \; 0 \leq x \leq 1, \; x^{2} \leq y \leq 1\}$.
$f(x,y) = \cos(2y)\sqrt{4-\sin^{2}{x}}$ e $B$ é o triângulo de vértices $(0,0)$, $\bigg(0,\dfrac{\pi}{2}\bigg)$ e $\bigg(\dfrac{\pi}{2},\dfrac{\pi}{2}\bigg).$
$f(x,y)=x+y$ e $B$ a região compreendida entre os gráficos das funções $y=x$ e $y=e^{x}$, com $0\leq x\leq 1.$
$\ln(\ln(3)) - \ln(\ln(2)).$
$\dfrac{\sin(1) - \cos(1)}{2}$.
$\dfrac{8}{3} - \sqrt{3}.$
$\dfrac{1 + e^{2}}{4}.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{H}(9-x^{2}-y^{2})\,dV$, onde $H$ é o hemisfério sólido $x^{2}+y^{2}+z^{2}\leq 9$ e $z\geq 0.$
$\dfrac{486\pi}{5}.$
Utilize coordenadas polares $x=r\cos \theta$ e $y=r\sin \theta$, com $r \geq 0$ e $0 \leq \theta < 2 \pi$, e o teorema do confronto para calcular o limite
$$\displaystyle \lim_{(x,y) \to (0,0)}\dfrac{x^3 + y^3}{x^2 + y^2}.$$
Dica: Note que, se $(r, \theta)$ são as coordenadas polares do ponto $(x,y)$, com $r \geq 0$, então $r \to 0^+$ quando $(x,y) \to (0,0)$.
$0.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}2x\,dV$, onde $E=\{(x,y,z)|\;0\leq y\leq 2,\,0\leq x\leq \sqrt{4-y^{2}},\;\\ 0\leq z\leq y\}.$
$\displaystyle\iiint\limits_{ E}6xy\,dV$, onde $E$ está abaixo do plano $z=1+x+y$ e acima da região do plano $xy$ limitada pelas curvas $y=\sqrt{x}$, $y=0$ e $x=1.$
$4.$
$\dfrac{65}{28}.$
Encontre uma equação para a superfície de nível da função $f(x,y,z)=\sqrt{x-y}-\ln z$ que passa pelo ponto $(3,-1,1)$.
$\sqrt{x - y} - \ln(z) = 2.$
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.
- ${\bf F}(x,y,z) = (x^2-y){\bf i} + 4z{\bf j} + x^2{\bf k}$, $C$ é a curva de interseção do plano $z=2$ com o cone $z=\sqrt{x^2+y^2}$.
$4\pi$.
Dada a expressão $g(x,y)=2f(x,y)$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ esticado verticalmente ao dobro.
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$2xyz = 3$, em $\left(\dfrac{1}{2},1,3\right)$.
Plano tangente: $6x + 3y + z = 9$,
Reta normal: $(x,y,z) = \left(\frac{1}{2},1,3\right) + \lambda (6,3,1),$ $\lambda \in \mathbb{R}.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3x\,{\bf i}+xz\,{\bf j}+z^{2}\,{\bf k}$ e $S$ é a superfície da região delimitada pelo parabolóide $z=4-x^{2}-y^{2}$ e o plano-$xy.$
Determine se ${\bf F}(x,y)=(2x-3y)\,{\bf i}+(-3x+4y-8)\,{\bf j}.$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = x^2 - 3xy + 2y^2 -8y + K.$
Calcule a integral iterada $\int_{-3}^{3} \int_{0}^{\sqrt{9-x^2}}\sin(x^{2}+y^{2})\,dy dx$, convertendo-a antes para coordenadas polares.
$\displaystyle \frac{\pi}{2}(1 - \cos(9)).$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}xyz\,dV$, onde $E$ é o sólido limitado pelos paraboloides $z=x^{2}+y^{2}$ e $z=8-x^{2}-y^{2}.$
$0.$
Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial ${\bf F}$ dado e a superfície $S$.
- ${\bf F}(x,y,z) = y^2{\bf i} + x{\bf j} + z^2{\bf k}$, $S$ é a parte do parabolóide $z = x^2 + y^2$ que está acima do plano $z = 1$, orientado para cima.
$\displaystyle\int_{C} {\bf F} \cdot d{\bf R} = \displaystyle\iint_{S} \mbox{rot} {\bf F} \cdot d{\bf S} = \pi.$
Determine a equação do plano que é tangente ao paraboloide $z = 2x^2 + 3y^2$ e paralelo ao plano $4x - 3y - z = 10$.
$4x - 3y - z = -\frac{11}{4}$.
No item abaixo:
- expresse $\partial w/\partial u$ e $\partial w/ \partial v$ como funções de $u$ e $v$, usando a Regra da Cadeia e também expressando $w$ diretamente em termos e $u$ e $v$ antes de diferenciar;
- calcule $\partial w/\partial u$ e $\partial w/ \partial v$ no ponto dado $(u,v)$.
$w=\ln(x^{2}+y^{2}+z^{2})$, $x=ue^{v}\sin{u}$, $y=ue^{v}\cos{u}$, $z=ue^{v}$; $(u,v)=(-2,0).$
- $\displaystyle w(u,v) = \ln(2) + 2\ln(u) + 2v,$$\displaystyle \frac{\partial w}{\partial u}(u,v) = \frac{2}{u}$ e $\displaystyle \frac{\partial w}{\partial v}(u,v) = 2.$
- $\displaystyle \frac{\partial w}{\partial u}(-2,0) = -1$ e $\displaystyle \frac{\partial w}{\partial v}(-2,0) = 2.$
Utilize a Regra da Cadeia para determinar $\mathrm{\partial}z/\mathrm{\partial} s$ e $\mathrm{\partial}z/ \mathrm{\partial}t.$
$z=\arcsin(x-y)$, $x=s^{2}+t^{2}$, $y=1-2st$.
$\displaystyle \frac{\partial z}{\partial s} = \displaystyle \frac{\partial z}{\partial t} = \frac{2s + 2t}{\sqrt{1 - (x - y)^{2}}}$.
Calcule a integral trocando a ordem de integração. $\displaystyle\int_{0}^{1}\!\!\int_{x}^{1}e^{x/y}\,dy dx$.
A região de integração é do tipo I, é dada por
$$\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 1 \mbox{ e } x \leq y \leq 1\}$$
e pode ser vista geometricamente como a região esboçada na figura abaixo.
Essa região pode ser descrita como uma região do tipo II da seguinte forma:
$$\{(x,y) \in \mathbb{R}^2: 0 \leq x \leq y \mbox{ e } 0 \leq y \leq 1\}.$$
Assim,
\begin{array}{rcl}\displaystyle\int_{0}^{1}\!\!\int_{x}^{1}e^{x/y}\,dy dx & = & \displaystyle\int_{0}^{1}\!\!\int_{0}^{y} \! e^{x/y}\,dx dy \\ & = & \displaystyle\int_{0}^{1} \! \left. ye^{x/y} \right|_{x=0}^{x=y}\,dx \\ & = & \displaystyle\int_{0}^{1} \! \left. y(e-1) \right|_{x=0}^{x=y}\,dx \\ & = & \left.(e-1) \frac{y^2}{2}\right|_{0}^{1} = \frac{e-1}{2}.\end{array}
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = xe^{x^2 - y^2}$ em $(2,2,f(2,2))$.
Plano tangente: $z = 9x - 8y$
Reta normal: $(x,y,z) = \left(2,2,2 \right) + \lambda \left(9,-8,-1 \right)$.
Prove a seguinte identidade \[ \iint\limits_\sigma\nabla f\cdot\mathbf{n}\,dS = \iiint\limits_G\Delta f\,dV, \] supondo que \(\sigma\) e \(G\) satisfaçam as hipóteses do Teorema da Diverência e que \(f(x,y,z)\) cumpra os requisitos de diferenciabilidade necessários. Acima, \(\displaystyle \Delta f= \dfrac{\partial^2f}{\partial x^2}+\dfrac{\partial^2f}{\partial y^2}+\dfrac{\partial^2f}{\partial z^2}\) é denominado Laplaciano de \(f\).
O campo vetorial $\mathbf{F}$ é mostrado no plano $xy$ e é o mesmo em todos os planos horizontais (em outras palavras, $\mathbf{F}$ é independente de $z$ e sua componente $z$ é 0).
O $\text{div }{\mathbf{F}}$ será positivo, negativo ou nulo? Justifique.
Determine se o $\text{rot }{\mathbf{F}} = 0$. Se não, em que direção rot $\mathbf{F}$ aponta?

Nulo.
$\text{rot } \bf{F}$ aponta na direção negativa do eixo $z.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^3 + y^3 - 3x - 3y$ e $x + 2y = 3.$
Ponto de máximo local: $\displaystyle \left(- \frac{13}{7}, \frac{17}{7} \right)$; ponto de mínimo local: $\displaystyle \left( 1,1 \right)$.
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y) = x^2 + y^2; \quad xy = 1.$
Não há valor máximo; valor mínimo: $2.$
Determine a equação da reta tangente à curva de nível dada, no ponto dado.
$x^2 + xy + y^2 - 3y = 1$, em $(1,2)$.
$y - 2 = -2(x - 1).$
Suponha que a área de uma região no plano de coordenadas polares seja $$A=\int_{\pi/4}^{3\pi/4} \int_{\mathrm{cosec\,}{\theta}}^{2\sin{\theta}}r\,dr d\theta.$$ Esboce a região e encontre sua área.
Seja $\Omega=\{(x,y)\in \mathbb{R}^{2}|\,(x,y)\notin A\}$, onde $A$ é a semirreta $\{(x,y)\in \mathbb{R}^{2}|\,y=0\,e\,x\geq 0\}$. Calcule
$$\int_{C}\frac{-y}{x^{2}+y^{2}}\,dx+\frac{x}{x^{2}+y^{2}}\,dy,$$
onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida em $\Omega$, tal que $C(0)=(1,1)$ e $C(1)=(1,-1).$
$\dfrac{3\pi}{2}.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy^2}{x^2 - y^2}$, caso exista.
Não existe.
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=e^{xy}\ln{y}$.
$\displaystyle \frac{\partial f}{\partial x} = ye^{xy}\ln y\;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = x e^{xy} \ln y + \frac{e^{xy}}{y}$.
Determine a imagem do conjunto $S$ sob a transformação dada. $S$ é a região triangular com vértices $(0,0), (1,1), (0,1)$;$x = u^2$, $y = v$.
A região limitada pela reta $y = 1,$ pelo eixo $y$ e por $y = \sqrt{x}.$
Em 1831, o físico Michael Faraday descobriu que uma corrente elétrica pode ser produzida variando-se o fluxo magnético através de um arco condutor. Suas experiências mostraram que a força eletromotriz \(\mathbf{E}\) está relacionada com a indução magnética \(\mathbf{B}\) pela equação \[ \oint_C\mathbf{E}\cdot\,d\mathbf{r} = - \iint\limits_\sigma\dfrac{\partial\mathbf{B}}{\partial t}\cdot\mathbf{n}\,dS.\] Use este resultado para fazer uma conjectura acerca da relação entre \(\mathrm{rot\,}\mathbf{E}\) e \(\mathbf{B}\). Explique seu raciocínio.
Determine a derivada parcial $f_{x}(3,4)$, onde $f(x,y)=\ln(x+\sqrt{x^{2}+y^{2}}).$
$f_{x}(3,4) = \frac{1}{5}$.
A função diferenciável $z=z(x,y)$ é dada implicitamente pela equação $f\bigg(\dfrac{x}{y},z\bigg)=0$, onde
$f(u,v)$ é suposta diferenciável e $\dfrac{\partial f}{\partial v}(u,v)\neq 0$. Verifique que
$$x\frac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=0.$$
Note que $\displaystyle \frac{\partial z}{\partial x} = - \frac{1}{y} \frac{\partial f}{\partial u} \left(\frac{x}{y},z \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},z \right)\right)^{-1}$ e $\displaystyle \frac{\partial z}{\partial y} = \frac{x}{y^{2}} \frac{\partial f}{\partial u} \left(\frac{x}{y},z \right)\left(\frac{\partial f}{\partial v}\left(\frac{x}{y},z \right)\right)^{-1}$.
Suponha que $u=f(x,y)$ e $v=g(x,y)$ verifiquem as equações de Cauchy- Riemann $u_{x}=v_{y}$ e $u_{y}=-v_{x}$. Se $x=r\cos{\theta}$ e
$y=r\sin{\theta}$, mostre que
$$\frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\partial \theta} \text{ e } \frac{\partial v}{\partial r}=-\frac{1}{r}\frac{\partial u}{\partial \theta}.$$
Note que $\displaystyle \frac{\partial u}{\partial r} = \cos(\theta) u_{x} + \sin (\theta) u_{y},$ $\displaystyle \frac{\partial v}{\partial r} = \cos(\theta) v_{x} + \sin (\theta) v_{y},$
$\displaystyle \frac{\partial u}{\partial \theta} = -r\sin(\theta) u_{x} + r \cos(\theta) u_{y}$ e $\displaystyle \frac{\partial v}{\partial \theta} = - r\sin(\theta) v_{x} + r \cos(\theta) v_{y}$.
Determine o plano que passa pelos pontos $(1,1,2)$ e $(-1,1,1)$ e que seja tangente ao gráfico de $f(x,y) = xy$.
$x + 6y - 2z = 3$.
Mostre que o valor máximo de $a^2b^2c^2$ sobre uma esfera de raio $r$ centrada na origem de um sistema de coordenadas cartesianas $(a,b,c)$ é $(r^2/3)^3$.
Usando o item anterior, mostre que, para números não negativos $a$, $b$ e $c$,
$$(abc)^{\frac{1}{3}} \leq \frac{a + b + c}{3},$$
isto é, a média geométrica de três números não negativos é menor que ou igual à média aritmética.
Use multiplicadores de Lagrange para maximizar $f(a,b,c) = a^{2}b^{2}c^{2}$ sujeita a restrição $a^{2} + b^{2} + c^{2} = r^{2}.$
Como $(\sqrt{a},\sqrt{b},\sqrt{c})$ está na esfera $a + b + c = r^{2},$ pelo item 1 segue que $abc = f(\sqrt{a},\sqrt{b},\sqrt{c}) \leq \left(\dfrac{r^{2}}{3}\right)^{3} = \left(\dfrac{a + b + c}{3}\right)^{3}.$
Um fluido tem densidade $870kg/m^{3}$ e escoa com velocidade $v=z{\bf i}+y^{2}{\bf j}+x^{2}{\bf k},$ onde $x$, $y$ e $z$ são medidos em metros e as componentes de $v$ em metros por segundo. Encontre a vazão para fora do cilindro $x^{2}+y^{2}=4$, $0\leq z\leq 1.$
$0$ kg/s.
Considere a função $f(x,y) = x \ g(x^2 - y^2)$, em que $g(u)$ é uma função derivável de uma variável. Mostre que o plano tangente ao gráfico de $f$ no ponto $(a,a,f(a,a))$ passa pela origem.
Note que $a \frac{\partial f}{\partial x} (a,a) + a \frac{\partial f}{\partial y}(a,a) = f(a,a).$
Calcule a integral, transformando para coordenadas esféricas. $\displaystyle\int_{0}^{1}\int_{0}^{\sqrt{1-x^{2}}}\int_{\sqrt{x^{2}+y^{2}}}^{\sqrt{2-x^{2}-y^{2}}}xy\,dzdydx$.
$\dfrac{(4\sqrt{2} - 5)}{15}.$
Embora $\nabla f = \lambda \nabla g$ seja uma condição necessária para a ocorrência de um valor extremo de $f(x,y)$ sujeito à restrição $g(x,y) = 0$, ela não garante por si só que ele exista. Como um exemplo, tente usar o método dos multiplicadores de Lagrange para encontrar um valor máximo de $f(x,y) = x + y$ sujeito à restrição $xy = 16$. O método identificará os dois pontos $(4,4)$ e $(-4,-4)$ como candidatos para a localização dos valores extremos. Ainda assim, a soma $x + y$ não tem valor máximo sobre a hipérbole. Quanto mais distante você está da origem nessa hipérbole no primeiro quadrante, maior se torna a soma $f(x,y) = x + y$.
Note que quando $x \to 0,$ tem-se $y \to \infty$ e $f(x,y) \to \infty;$ e quando $x \to -\infty,$ tem-se $y \to 0$ e $f(x,y) \to -\infty,$ logo não há valores máximo e mínimo de $f$ sujeito a esta restrição.
Encontre os valores de $\partial z/ \partial x$ e $\partial z/\partial y$ no ponto indicado.
$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-1=0$, $(2,3,6).$
$\displaystyle \frac{\partial z}{\partial x}(2,3,6) = -9$ e $\displaystyle \frac{\partial z}{\partial x}(2,3,6) = -4.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 + 2xy + y^2$ e $x + 2y - 1 = 0.$
Ponto de mínimo: $\displaystyle \left(-1,1 \right)$
Determine e faça o esboço do domínio da função $f(x,y)=\sqrt{1-x^{2}}-\sqrt{1-y^{2}}$.
$\left\lbrace (x,y);\; -1 \leq x \leq 1,\;-1\leq y \leq 1 \right\rbrace.$
Mostre (verifique) que o domínio da função $f(x,y)=\ln(x^2-y)$ consiste em todos os pontos abaixo da curva $y<x^2$.
A função $(x,y)\longmapsto\ln(x^2-y)$ só está definida para \( 0<x^2-y \), ou seja, $y<x^2$. Assim, primeiro esboçamos a parábola $y=x^2$ (como uma curva tracejada, por exemplo). A região $y<x^2$ consiste em todos os pontos abaixo dessa curva.
Calcule $\displaystyle \int_{C}{\bf E}\cdot d{\bf l}$, onde ${\bf E}(x,y)=\dfrac{1}{x^{2}+y^{2}}\dfrac{x\,{\bf i}+y\,{\bf j}}{\sqrt{x^{2}+y^{2}}}$ e $C: {\bf r}(t)=(t,1)$, $-1\leq t\leq 1.$ ( O ${\bf l}$ desempenha aqui o mesmo papel que ${\bf r}:{\bf l}(t)={\bf r}(t).$)
$0.$
Esboce o gráfico da função $f(x,y)=10-4x-5y$.
$z = 10 - 4x - 5y.$
A figura mostra a região de integração da integral
$$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx.$$
Reescreva essa integral como uma integral iterada equivalente nas cinco outras ordens.

$\int_{0}^{1}\int_{\sqrt{x}}^{1}\int_{0}^{1-y}f(x,y,z)\;dz dy dx = \int_{0}^{1}\int_{0}^{y^2}\int_{0}^{1-y}f(x,y,z)\;dz dx dy $
$= \int_{0}^{1}\int_{0}^{1 - z}\int_{0}^{y^2}f(x,y,z)\;dx dy dz = \int_{0}^{1}\int_{0}^{1 - y}\int_{0}^{y^2}f(x,y,z)\;dx dz dy $
$= \int_{0}^{1}\int_{0}^{1 - \sqrt{x}}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dz dx = \int_{0}^{1}\int_{0}^{(1 - z)^2}\int_{\sqrt{x}}^{1-z}f(x,y,z)\;dy dx dz.$
Suponha que $S$ e $C$ satisfaçam as hipóteses do Teorema de Stokes e $f$ e $g$ tenham derivadas parciais de segunda ordem contínuas. Demonstre que $\displaystyle\int_C (f\nabla g + g\nabla f) \cdot d{\bf R} = 0$
Note que $\mbox{rot} (f\nabla g + g\nabla f) = {\bf 0}.$
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R}\dfrac{1}{\sqrt{xy}}\, dA$, em que $R$ é a região limitada pela curva $x+y = 1$ e pelos eixos coordenados.
$\pi.$
Aplique o Teorema da Divergência para achar $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS,$ sendo ${\bf F}(x,y,z)=(x^{2}+\sin yz)\,{\bf i}+(y-xe^{-z})\,{\bf j}+z^{2}\,{\bf k}$ e $S$ a superfície da região delimitada pelo cilindro $x^{2}+y^{2}=4$ e os planos $x+z=2$ e $z=0.$
$20\pi.$
Se $R$ é a resistência equivalente de três resistores conectados em paralelo, com resistências $R_1, R_2, R_3$, então
$$\dfrac{1}{R} = \dfrac{1}{R_1} + \dfrac{1}{R_2} + \dfrac{1}{R_3}.$$
Se as resistências medem, em ohms, $R_1 = 25 \Omega$, $R_2 = 40 \Omega$, $R_3 = 50 \Omega$, com margem de erro de $0,5\%$ em cada uma, estime o erro máximo no valor calculado de $R$.
$\Delta R \approx 0.059 \Omega$.
Considere o campo vetorial
$${\bf F}(x,y)=\bigg(e^{x}\ln(y)-\frac{e^{y}}{x}\bigg)\,{\bf i}+\bigg(\frac{e^{x}}{y}-e^{y}\ln(x)\bigg)\,{\bf j}.$$
O campo ${\bf F}$ é conservativo? Justifique sua resposta.
Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é qualquer caminho ligando o ponto $(1,1)$ ao ponto $(3,3).$
Sim.
$0.$
Seja \(\mathbf{F}(x,y)= (ye^{xy}-1)\mathbf{i} + xe^{xy}\mathbf{j}.\)
Mostre que \(\mathbf{F}\) é um campo vetorial conservativo.
Calcule uma função potencial de \(\mathbf{F}\).
Calcule o trabalho realizado pelo campo vetorial sobre uma partícula que se move ao longo da curva representada pelas seguintes equações paramétricas \begin{align*} x & = t+ \arcsin(\sin t) \\ y & = \dfrac{2}{\pi}\arcsin(\sin t), \ \left(0\leq t\leq 8\pi\right). \end{align*}
As curvas ${\bf r}_{1}(t)=(t,t^{2},t^{3})$ e ${\bf r}_{2}(t)=(\sin{t},\sin{2t},t)$ se interceptam na origem. Determine o ângulo
de intersecção destas com precisão de um grau.
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = xy$ em $\left(\dfrac{1}{2}, \dfrac{1}{2}, f\left(\dfrac{1}{2}, \dfrac{1}{2}\right)\right)$.
Plano tangente: $4z = 2x + 2y - 1$\\
Reta normal: $(x,y,z) = \left(\frac{1}{2}, \frac{1}{2}, \frac{1}{4} \right) + \lambda \left(\frac{1}{2},\frac{1}{2},-1 \right)$.
Faça uma correspondência entre as equações e os gráficos identificados a seguir, enumerador respectivamente por $I-VI$, e justifique sua resposta. Determine quais famílias de curvas da grade têm $u$ constante e quais têm $v$ constante.
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+v{\bf k}.$
${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+\sin u{\bf k}$, $-\pi\leq u\leq \pi.$
${\bf r}(u,v)=\sin v{\bf i}+\cos u\sin 2v{\bf j}+\sin u\sin 2v{\bf k}.$
$x=(1-u)(3+\cos v)\cos 4\pi u$, $y=(1-u)(3+\cos v)\sin 4\pi u$,$z=3u+(1-u)\sin v.$
$x=\cos^{3}u\cos^{3}v$, $y=\sin^{3}u\cos^{3}v$, $z=\sin^{3}v.$
$x=(1-|u|)\cos v$, $y=(1-|u|)\sin v$, $z=u.$
- IV.
- I.
- II.
- V.
- III.
- VI
Considere a integral dada em coordenadas polares por $$\int_{0}^{\pi/4} \int_{0}^{2\cos{\theta}}r\,dr d\theta,$$ a qual representa a área de uma região $R$ do plano $xy.$
Escreva a região $R$ em coordenadas cartesianas.
Faça um esboço da região $R.$
Calcule a área da região $R.$
$R = \left\lbrace (x,y); (x - 1)^2 + y^2 \leq 1,\quad x \leq y,\quad x \geq 0,\quad y \geq 0 \right\rbrace.$
(...)
$\dfrac{\pi + 2}{4}.$
Calcule o volume do conjunto dado.
$4x+2y\geq z\geq 3x+y+1$, $x\geq 0$ e $y\geq 0.$
$0\leq z\leq \sin{y^{3}}$ e $\sqrt{x}\leq y\leq \sqrt[3]{\pi}.$
$\dfrac{1}{6}.$
$\dfrac{2}{3}.$
Quando o tamanho das moléculas e suas forças de atração são levadas em conta, a pressão $P$, o volume $V$ e a temperatura $T$
de um mol de gás confinado estão relacionados pela {\it equação de van der Waals}
$$\bigg(P+\frac{a}{V^{2}}\bigg)(V-b)=kT,$$
em que $a$, $b$ e $k$ são constantes positivas. Se $t$ é o tempo, estabeleça uma fórmula para $\mathrm{d}T/ \mathrm{d}t$ em termos de $\mathrm{d}P/\mathrm{d} t$,
$\mathrm{d} V/\mathrm{d}t$, $P$ e $V$.
$\displaystyle \frac{dT}{dt} = \frac{1}{k} \left( \left(\frac{dP}{dt} - \frac{2a}{V^{3}} \frac{dV}{dt}\right)(V - b) + \left( P + \frac{a}{V^{2}} \right) \frac{dV}{dt} \right).$
Determine as direções em que a derivada direcional da função \linebreak $f(x,y) = x^2 + \sin{xy}$ no ponto $(1,0)$ tem valor 1.
As direções são dadas pelos vetores $(1,0)$ e $\displaystyle \left( \frac{4}{5}, -\frac{3}{5}\right).$
Determine o maior conjunto no qual a função $f(x,y) = \begin{cases}\dfrac{x^2y^3}{2x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\1, & \quad \text{se } (x,y) = (0,0) \end{cases}$ é contínua.
$\left\lbrace (x,y);\; (x,y) \neq (0,0) \right\rbrace.$
Mostre que a curva com equações paramétricas $x = t \cos{t}, \ y = t \sin{t}, \ z = t$ está no cone $z^2 = x^2 + y^2$ e use esse fato para esboçar a curva.
Encontre o volume do sólido no primeiro octante limitado pelo cilindro $z=16-x^{2}$ e pelo plano $y=5.$
$\dfrac{640}{3}.$
Determine o domínio da curva de equação vetorial
$$\textbf{r}(t) = \left( \sqrt{\dfrac{t - 2}{t + 1}}, \ln{(5 - t^2)}, e^{-t} \right).$$
Seja ${\bf F}(x,y)=(e^{x}\,\cos y+y, x-e^{x}\,\sin y)$. Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é o arco de circunferência que une o ponto $(-\sqrt{2}/2, \sqrt{2}/2)$ ao ponto $(1,0)$. Veja a figura abaixo.
Notemos que ${\bf F}$ é um campo vetorial conservativo, pois: ${\bf F}$ é definido em todo $\mathbb{R}^{2}$; $P(x,y)=e^{x}\,\cos y+y$ e $Q(x,y)=x-e^{x}\,\sin y$ possuem derivadas parciais de primeira ordem contínuas; $\dfrac{\partial P}{\partial y}(x,y)=1-e^{x}\,\sin y=\dfrac{\partial Q}{\partial x}(x,y).$
Sendo $F$ conservativo, existe $f$ tal que $\nabla f={\bf F}.$ Vamos encontrar $f$. Temos que
$$f_{x}(x,y)=P(x,y) \mbox{ e } f_{y}(x,y)=Q(x,y).$$
Então,
$$\label{(2)}f_{x}(x,y)=e^{x}\,\cos y+y\Rightarrow f(x,y)=e^{x}\,\cos y+y+g(y).$$
Logo, temos que
$$f_{y}(x,y)=-e^{x}\,\sin y+x+g'(y).$$
Como $f_{y}(x,y)=Q(x,y)$, obtemos que
$$-e^{x}\,\sin y+x+g'(y)=x-e^{x}\,\sin y\Rightarrow g'(y)=0\Rightarrow g(y)=C.$$
Assim, tomando $C=0$ segue que
$$f(x,y)=e^{x}\,\cos y+xy.$$
Do resultado acima e pelo Teorema Fundamental da Integral de Linha, temos que
$$\int_{C}{\bf F}\cdot d{\bf r}=f(1,0)-f\bigg(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\bigg)=e-e^{-\frac{\sqrt{2}}{2}}\,\cdot\cos\bigg(\frac{\sqrt{2}}{2}\bigg)+\frac{1}{2}.$$
Considere a função
$$f(x,y)= \begin{cases}\dfrac{xy^{2}}{x^{2}+y^{4}}, & \quad \text{se } (x,y)\neq (0,0),\\0, & \quad \text{se } (x,y)=(0,0).\\\end{cases}$$
A função é contínua em $(0,0)$? Justifique sua resposta.
Determine as derivadas parciais $\dfrac{\partial f}{\partial x}(0,0)$ e $\dfrac{\partial f}{\partial y}(0,0)$.
Não, pois $\lim_{(x,y) \to (0,0)} f(x,y)$ não existe.
$\displaystyle \frac{\partial f}{\partial x}(0,0) = \frac{\partial f}{\partial y}(0,0) = 0$.
Calcule $\displaystyle\int_{C}\dfrac{-y}{x^{2}+y^{2}}\,dx+\dfrac{x}{x^{2}+y^{2}}\,dy$, onde $C:[0,1]\rightarrow \mathbb{R}^{2}$ é uma curva de classe $C^{1}$ por partes, com imagem contida no conjunto $\Omega=\{(x,y)\in \mathbb{R}^{2}| y>0\}\cup\{(x,y)\in \mathbb{R}^{2}|\,x<0\}$, tal que $C(0)=(1,1)$ e $C(1)=(-1,-1).$
$0.$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=y^{3}e^{xy^{2}}$ e $B$ o retângulo $0\leq x\leq 1$, $1\leq y\leq 2.$
$f(x,y)=x^{5}\cos{y^{3}}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;y\geq x^{2},\;x^{2}+y^{2}\leq 2\}.$
$f(x,y)= x^{2}$ e $B$ o conjunto de todos $(x,y)$ tais que $x\leq y\leq -x^{2}+2x+2.$
$f(x,y)=x$ e $B$ a região compreendida entre os gráficos de $y=\cos{x}$ e $y=1-\cos{x}$, com $0\leq x\leq \dfrac{\pi}{2}.$
$\dfrac{e^{4} - e - 3}{2}.$
$0.$
$\dfrac{63}{20}.$
$\left(\dfrac{5}{72} -\dfrac{ \sqrt{3}}{18}\right)\pi^{2} + \left( \dfrac{4\sqrt{3}}{3} - 1 \right) \pi.$
Esboce o gráfico da função $f(x,y)=\sqrt{x^{2}+y^{2}}$.
$z = \sqrt{x^{2} + y^{2}}$
Suponha que $T(x,y)=4-x^{2}-y^{2}$ represente uma distribuição de temperatura em uma região que pode ser aproximada por um plano. Seja $D=\{(x,y)\in \mathbb{R}^2: x\geq 0,\;y\geq x\;\text{e}\;2y+x\leq 4\}$. Determine o ponto de $D$ de menor temperatura.
$(0,2).$
Determine se ${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = \dfrac{x^{2} + y^{2} + z^{2}}{2} + K.$
Um campo vetorial inverso do quadrado é da forma:
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$. Um exemplo de campo inverso do quadrado é o campo elétrico ${\bf F}=\epsilon q Q{\bf r}/|{\bf r}|^{3}$. Suponha que um elétron com carga de $-1,6\times 10^{-19}\, C$ esteja localizado na origem. Uma carga positiva unitária é colocada à distância de $10^{-12}\,m$ do elétron e se move para uma posição que está à metade da distância original do elétron. Determine o trabalho realizado pelo campo elétrico. (Use o valor $\epsilon=8,985\times 10^{9}$.)
$\approx 1,4 \times 10^{4}$ J.
Calcule as integrais mudando a ordem de integração de maneira apropriada.
$\displaystyle\int_{0}^{4}\int_{0}^{1}\int_{2y}^{2}\dfrac{4\;\cos(x^{2})}{2\sqrt{z}}\;dx dy dz$
$\displaystyle\int_{0}^{1}\int_{0}^{1}\int_{x^{2}}^{1}12xze^{zy^{2}}\;dy dx dz$
$\displaystyle\int_{0}^{1}\int_{\sqrt[3]{z}}^{1}\int_{0}^{\ln 3}\dfrac{\pi e^{2x}\;\sin(\pi y^{2})}{y^{2}}\;dx dy dz$
$2 \sin(4).$
$3e - 6.$
$4.$
Calcule $\nabla f(x,y)$.
$f(x,y) = e^{x^2 - y^2}$
$\displaystyle \nabla f(x,y) = e^{x^{2} - y^{2}}(2x,-2y).$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{2\pi}\int_{0}^{\pi}\int_{0}^{(1-\cos{\phi})/2}\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$\dfrac{\pi}{3}.$
Determine uma fórmula para $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ semelhante à fórmula
$\displaystyle\iint\limits_{S}{\bf F}\cdot d{\bf S}=\displaystyle\iint\limits_{D}\left(-P\dfrac{\partial f}{\partial x}-Q\dfrac{\partial f}{\partial y}+R\right)dA$ para o caso onde $S$ é dada por $y=h(x,z)$ e ${\bf n}$ é o vetor normal unitário que aponta para a esquerda.
$\displaystyle \iint\limits_{S}{\bf F}\cdot d{\bf S}=\iint\limits_{D}\left(P -Q\dfrac{\partial k}{\partial y}-R\frac{\partial k}{\partial z} \right)dA.$
Calcule o limite $\displaystyle \lim_{t \rightarrow 0}\left(\dfrac{e^t - 1}{t}, \dfrac{\sqrt{1+t}-1}{t}, \dfrac{3}{t+1}\right)$.
Consideremos ${\bf r}(t)=\bigg(\frac{e^{t}-1}{t},\frac{\sqrt{1+t}-1}{t},\frac{3}{t+1}\bigg).$
Temos que o limite de ${\bf r}$ é o vetor cujas componentes são os limites das funções componentes de ${\bf r}$, se esses limites existirem.
Então,
$\lim\limits_{t \to 0}{\bf r}(t)=\lim\limits_{t \to 0}\left(\frac{e^{t}-1}{t},\frac{\sqrt{1+t}-1}{t},\frac{3}{t+1}\right)=\left(\lim\limits_{ t\to 0}\frac{e^{t}-1}{t},\lim\limits_{t \to 0}\frac{\sqrt{1+t}-1}{t},\lim\limits_{t \to 0}\frac{3}{t+1}\right)$
Assim,
$\bullet \lim\limits_{t\rightarrow 0}\dfrac{e^{t}-1}{t}=1$.
$\bullet \lim\limits_{t\to 0}\frac{\sqrt{1+t}-1}{t}=\lim\limits_{t\to 0}\frac{(\sqrt{1+t}-1)(\sqrt{1+t}+1)}{t(\sqrt{1+t}+1)}=\lim\limits_{t\to 0}\frac{1+t-1}{t(\sqrt{1+t}+1)}=\lim\limits_{t\to 0}\frac{t}{t(\sqrt{1+t}+1)}=\lim\limits_{t\to 0}\frac{1}{\sqrt{1+t}+1}=\frac{1}{2}$.
$\bullet \lim\limits_{t\to 0}\dfrac{3}{t+1}=3$.
Portanto,
$\lim\limits_{t\to 0}\bigg(\frac{e^{t}-1}{t},\frac{\sqrt{1+t}-1}{t},\frac{3}{t+1}\bigg)=\bigg(1,\frac{1}{2},3\bigg).$
Calcule $\int_{C}{\bf E}\cdot d{\bf l}$, onde ${\bf E}(x,y)=\dfrac{1}{x^{2}+y^{2}}\dfrac{x\,{\bf i}+y\,{\bf j}}{\sqrt{x^{2}+y^{2}}}$ e $C$ é a curva dada por $x=2\,\cos t$, $y=\sin t$, com $0\leq t\leq \dfrac{\pi}{2}.$
$-\dfrac{1}{2}.$
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.
- ${\bf F}(x,y,z) = (y+z,-z,y)$, $C$ é a curva obtida como interseção do cilindro $x^2+y^2=2y$ com o plano $y = z$.
$\dfrac{4\pi}{3}$.
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = (e^x+x^2y,e^y-xy^2)$, $C$ é a circunferência $x^2+y^2=25$, orientada no sentido horário. (Verifique a orientação da curva antes de aplicar o Teorema.)
$\dfrac{625\pi}{2}.$
Considere o campo vetorial \(\mathbf{F}(x,y,z)=(x-y)\mathbf{i} + (y-z)\mathbf{j}+(z-x)\mathbf{k}\) e a superfície \(\sigma\)
descrita como sendo a porção do plano \(x+y+z=1\) no primeiro octante e orientada para cima. Verifique o Teorema de Stokes
calculando, separadamente, a integral de linha e a integral dupla e, em seguida, comparando os valores.
\(\dfrac{3}{2}\)
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{1}\!\!\int_{\arctan{x}}^{\pi/4}\!f(x,y)\,dy dx$.
Calcule $\displaystyle\int_{C}y\,dx+x^{2}\,dy$, onde $C$ é a curva cuja imagem é o segmento de extremidades $(1,1)$ e $(2,2)$, orientada de $(1,1)$ para $(2,2).$
$\dfrac{23}{6}.$
Mostre que as equações paramétricas $x=a \cosh u\cos v$, $y=b\cosh u \sin v$, $z=c\sinh u$, representam um hiperboloide de uma folha.
Note que $\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} - \dfrac{z^{2}}{c^{2}} = 1$.
A temperatura em um ponto $(x,y)$ é $T(x,y)$, medida em graus Celsius. Um inseto rasteja de modo que sua posição depois de
$t$ segundos seja dada por $x=\sqrt{1+t}$ e $y=2+\dfrac{1}{3}t$, onde $x$ e $y$ são medidas em centímetros. A função temperatura satisfaz
$T_{x}(2,3)=4$ e $T_{y}(2,3)=3$. Quão rápido a temperatura aumenta no caminho do inseto depois de três segundos?
A temperatura aumenta a uma taxa de $2º$C/s.
Suponha que a equação \(z=f(x,y)\) seja expressa na forma polar \(z=g(r,\theta)\) através da substituição \(x=r\cos\theta\) e \(y=r\sin\theta\).
Considere \(r\) e \(\theta\) como funções de \(x\) e \(y\) e use derivação implícita para mostrar que \[ \frac{\partial r}{\partial x} = \cos\theta \quad \text{e}\quad\frac{\partial\theta}{\partial x} =-\frac{\sin\theta}{r}.\]
Considere \(r\) e \(\theta\) como funções de \(x\) e \(y\) e use derivação implícita para mostrar que \[\dfrac{\partial r}{\partial y}=\sin\theta \quad \text{e}\quad \dfrac{\partial\theta}{\partial y}=\dfrac{\cos\theta}{r}.\]
Use os resultados anteriores para mostrar que \begin{align*} \dfrac{\partial z}{\partial x} & = \dfrac{\partial z}{\partial r}\cos\theta - \dfrac{1}{r}\dfrac{\partial z}{\partial\theta}\sin\theta \\ \dfrac{\partial z}{\partial y} & = \dfrac{\partial z}{\partial r}\sin\theta + \dfrac{1}{r}\dfrac{\partial z}{\partial\theta}\cos\theta\end{align*}
Use o resultado do item anterior para mostrar que \[ \left(\dfrac{\partial z}{\partial x}\right)^2 + \left(\dfrac{\partial z}{\partial y}\right)^2 = \left(\dfrac{\partial z}{\partial r}\right)^2 +\dfrac{1}{r^2}\left(\dfrac{\partial z}{\partial\theta}\right)^2. \]
Ainda usando o resultado do terceiro item, mostre que \(z=f(x,y)\) satisfaz a equação de Laplace \[ \dfrac{\partial^2z}{\partial x^2} + \dfrac{\partial^2z}{\partial y^2}= 0, \] se, e somente se, \(z=g(r,\theta)\) satisfaz a equação \[ \dfrac{\partial^2z}{\partial r^2} + \dfrac{1}{r^2}\dfrac{\partial^2z}{\partial\theta^2}+\dfrac{1}{r}\dfrac{\partial z}{\partial r} = 0. \] A última equação acima é chamada de forma polar da equação de Laplace.
Dada a função $f(x,y)=e^{-(x^{2}+y^{2})}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}$.
$Im(f) = \left\lbrace z \in \mathbb{R};\; 0 < z \leq 1 \right\rbrace.$
As curvas de nível são as os círculos $x^{2} + y^{2} = C$ com $C > 0$ e a origem.
Considere a integral $$\int_{0}^{1}\int_{3y}^{3}e^{x^{2}}\,dx dy.$$
Esboce a região de integração.
Calcule a integral usando a ordem de integração apropriada.
(...)
$\dfrac{e^9 - 1}{6}.$
Encontre a área da superfície descrita como sendo a parte do cilindro \(y^2+z^2=9\) que está acima do retângulo \(\displaystyle R=\{(x,y)\in\mathbb{R}^2;\ 0\leq x\leq 2,\ -3\leq y\leq 3\}\).
\( 6\,\pi\)
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 + 4y^2$ e $xy = 1$, $x > 0$ e $y>0.$
Ponto de mínimo: $\displaystyle \left( \sqrt{2}, \frac{\sqrt{2}}{2} \right)$.
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}-12xy+8y^{3}$.
Ponto de mínimo : $\displaystyle \left( 2,1\right);$ ponto de sela: $\displaystyle \left(0,0\right).$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}(y+e^{\sqrt{x}}) \, dx + (2x+\cos{y^2}) \, dy$, $C$ é a fronteira da região englobada pelas parábolas $y=x^2$ e $x=y^2$.
$\dfrac{1}{3}.$
Seja $s = f(x,y,z,w)$ dada por $s = e^{\frac{x}{y} - \frac{z}{w}}$. Verifique que
$$x\dfrac{\partial s}{\partial x} + y \dfrac{\partial s}{\partial y} + z \dfrac{\partial s}{\partial z} + w \dfrac{\partial s}{\partial w} = 0.$$
$\begin{aligned}[t]\frac{\partial s}{\partial x} &= \frac{1}{y} e^{\frac{x}{y} - \frac{z}{w}},\;\;\;\;\;\frac{\partial s}{\partial y} = -\frac{x}{y^{2}} e^{\frac{x}{y} - \frac{z}{w}},\\\frac{\partial s}{\partial z} &= -\frac{1}{w} e^{\frac{x}{y} - \frac{z}{w}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial s}{\partial w} = \frac{z}{w^{2}} e^{\frac{x}{y} - \frac{z}{w}}.\end{aligned}$
Calcule $\iiint\limits_{E} dV$, em que $E$ é o sólido delimitado pelo elipsoide $x^2/a^2 + y^2/b^2 + z^2/c^2 = 1$. Utilize a transformação $x = au$, $y = bv$ e $z = cw$.
A Terra não é perfeitamente esférica; como resultado da rotação, os polos foram achatados. Assim, seu formato pode ser aproximado por um elipsoide com $a = b = 6.378$ km e $c = 6.356$ km. Use o item anterior para estimar o volume da Terra.
$\dfrac{4\pi a b c}{3}.$
$\dfrac{4\pi (6378) (6378) (6356)}{3} \approx 1.083 \times 10^{12}$ km$^{3}.$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y,z) = \dfrac{x + y}{z}, (1,1,-1).$
$\sqrt{6}.$
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = x\mathbf{i} + y\mathbf{j}$, $C$ dada por $\mathbf{r}(t) = (t,t^2)$, $0 \leq t \leq 1$ e $\mathbf{n}$ a normal com componente $y < 0$.
$\dfrac{1}{3}$.
Verifique que a função \(f(x,y)=\sqrt{1-x^2-y^2}\) é contínua no disco unitário fechado \(x^2+y^2\leq 1\).
O domínio de \(f\) é o disco unitário fechado \(x^2+y^2\leq 1\). Para todo ponto \((x_0,y_0)\) na fronteira do disco, temos \[ \lim_{(x,y)\to(x_0,y_0)}\sqrt{1-x^2-y^2} = \sqrt{1-x_0^2-y_0^2} = 0.\] Como o mesmo vale também para pontos interiores ao disco, temos que \(f\) é contínua no disco fechado.
Seja \(G\) um sólido com a superfície \(\sigma\) orientada por vetores normais unitários para fora, suponha que \(\phi\) tenha derivadas parciais de primeira e segunda ordens contínuas em algum conjunto aberto contendo \(G\) e seja \(D_{\mathbf{n}}\phi\) a derivada direcional de \(\phi\), onde \(\mathbf{n}\) é um vetor normal unitário para fora de \(\sigma\). Mostre que \[ \iint\limits_\sigma D_{\mathbf{n}}\phi\,dS = \iiint\limits_G\left[\dfrac{\partial^2\phi}{\partial x^2}+ \dfrac{\partial^2\phi}{\partial y^2} + \dfrac{\partial^2\phi}{\partial z^2} \right]\,dV. \]
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo: $\displaystyle D = \{(x,y) \in\mathbb{R}^2: 0 \leq y \leq \sin{(\pi x/L)}, \ 0 \leq x \leq L\}; \quad \rho(x,y) = y$.
Massa: $\dfrac{L}{4};$ centro de massa: $\displaystyle \left(\frac{L}{2},\frac{16}{9\pi} \right).$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{E}z\,dV$, onde $E$ está entre as esferas $x^{2}+y^{2}+z^{2}=1$ e $x^{2}+y^{2}+z^{2}=4$, no primeiro octante.
$\dfrac{15\pi}{16}.$
Se $z = x^2 - xy + 3y^2$ e $(x,y)$ varia de $(3;-1)$ a $(2,96;-0,95)$, compare os valores de $\Delta z$ e $dz$.
$\Delta z = -0.7189$ e $dz = -0.73$.
Calcule a integral de superfície $\displaystyle\iint\limits_{S}x^{2}z^{2}dS$, onde $S$ é a parte do cone $z^{2}=x^{2}+y^{2}$ que está entre os planos $z=1$ e $z=3.$
Temos que $S$ é a porção do cone $z^{2}=x^{2}+y^{2}$ para $1 \leq z \leq 3$, ou equivalentemente, $S$ é a parte da superfície $z=\sqrt{x^{2}+y^{2}}$ sobre a região $D=\{(x,y)| 1 \leq x^{2}+y^{2} \leq 9\}.$ Assim,
$\displaystyle\iint\limits_{S}x^{2}z^{2}dS=\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})\sqrt{\left(\dfrac{\partial z}{\partial x}\right)^{2}
+\left(\frac{\partial z}{\partial y}\right)^{2}+1}dA$
$=\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})\sqrt{\left(\frac{x}{\sqrt{x^{2}+y^{2}}}\right)^{2}+\left(\frac{y}{\sqrt{x^{2}+y^{2}}}\right)^{2}+1}dA$
$=\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})\sqrt{\frac{x^{2}+y^{2}}{x^{2}+y^{2}}+1}dA=\iint\limits_{D}\sqrt{2}x^{2}(x^{2}+y^{2})dA$
$=\sqrt{2}\displaystyle\iint\limits_{D}x^{2}(x^{2}+y^{2})dA.$
Por coordenadas polares, temos que $x=r\cos \theta, y=r\sin \theta, 1\leq r\leq 3 , 0\leq \theta \leq 2\pi \,\mbox{e} \, dA=r dr d\theta.$
Logo,
$\displaystyle\iint\limits_{S}x^{2}z^{2}dS=\sqrt{2}\int_{0}^{2\pi}\int_{1}^{3}(r^{2}\cos^{2}\theta)(r^{2})r dr d\theta =\sqrt{2}\int_{0}^{2\pi}\cos^{2}\theta d\theta \cdot \int_{1}^{3}r^{5}dr$
$=\sqrt{2}\cdot (\theta)\bigg|_{0}^{2\pi}\cdot \bigg(\frac{r^{6}}{6}\bigg)\bigg|_{1}^{3}=\sqrt{2}\cdot \pi \cdot \frac{1}{6}\cdot (3^{6}-1)=\frac{364\sqrt{2}}{3}\pi$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinar o volume e o centroide do sólido $E$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=1.$
Volume: $\dfrac{\pi(2 - \sqrt{2})}{3};$ centróide: $\left(0,0, \dfrac{3}{8(2 - \sqrt{2})} \right).$
Suponha que $(0,2)$ seja um ponto crítico de uma função $g$ com derivadas de segunda ordem contínuas. Em cada caso, o que se pode dizer sobre $g$?
$g_{xx}(0,2)=-1, \quad g_{xy}(0,2)=6, \quad g_{yy}(0,2)=1.$
$g_{xx}(0,2)=-1, \quad g_{xy}(0,2)=2, \quad g_{yy}(0,2)=-8.$
$g_{xx}(0,2)=4, \quad g_{xy}(0,2)=6, \quad g_{yy}(0,2)=9.$
$g$ possui um ponto de sela em $(0,2).$
$g$ possui um ponto de máximo local em $(0,2).$
Não se pode afirmar algo sobre $g$ pelo Teste da Segunda Derivada.
Para fazer essa análise sobre $g$ iremos utilizar o Teste da Segunda Derivada.
Temos que- \[ D=g_{xx}(0,2)g_{yy}(0,2)-g_{xy} ^2(0,2)=-1\cdot 1-6^2=-1-36=-37<0. \] Logo, pelo Teste da Segunda Derivada, segue que $(0,2)$ é um ponto de sela de $g$.
- Temos que \[ D=g_{xx}(0,2)g_{yy}(0,2)-g_{xy} ^2(0,2)=(-1)\cdot (-8)-2^2=8-4=4>0. \] Como $D>0$ e $g_{xx}(0,2)<0$, pelo Teste da Segunda Derivada, segue que $(0,2)$ é um ponto de máximo de $g$.
- Temos que \[ D=g_{xx}(0,2)g_{yy}(0,2)-g_{xy} ^2(0,2)=4\cdot 9-6^2=36-36=0. \] Como $D=0$ o Teste da Segunda Derivada não nos fornece nenhuma informação sobre $g$.
Se uma circunferência $C$ de raio $1$ rola ao longo do interior da circunferência $x^2+y^2=16$, um ponto fixo $P$ de $C$ descreve uma curva chamada epicicloide, com equações paramétricas $x = 5\cos{t}-\cos{5t}$, $y = 5\sin{t} - \sin{5t}$. Faça o gráfico da epicicloide e calcule a área da região que ela envolve.
$30\pi.$
Mostre que a equação do plano tangente ao elipsoide $x^2/a^2 + y^2/b^2 + z^2/c^2 = 1$ no ponto $(x_0,y_0,z_0)$ pode ser escrita como
$$\dfrac{xx_0}{a^2} + \dfrac{yy_0}{b^2} + \dfrac{zz_0}{c^2} = 1.$$
Note que se $F(x,y,z) = x^2/a^2 + y^2/b^2 + z^2/c^2 - 1,$ então
$$
\nabla F(x_{0},y_{0},z_{0}) = 2 \left(\frac{x_{0}}{a^{2}},\frac{y_{0}}{b^{2}},\frac{z_{0}}{c^{2}} \right)
$$
e a equação do plano tangente em $(x_{0},y_{0},z_{0})$ é
$$
\nabla F(x_{0},y_{0},z_{0}) \cdot (x,y,z) = \nabla F(x_{0},y_{0},z_{0}) \cdot (x_{0},y_{0},z_{0}) = 2.
$$
Use a derivação implicíta para determinar $\partial z/\partial x$ e $\partial z/\partial y$ na expressão $x-z=\arctan(yz)$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{1 + y^{2}z^{2}}{1 + y + y^{2}z^{2}}$
$\displaystyle \frac{\partial z}{\partial y} = -\frac{z}{1 + y + y^{2}z^{2}}$.
Faça o mapa de contorno da função $f(x,y)=y-\ln{x}$ mostrando várias de suas curvas de nível.
$y = \ln(x) + C.$
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização $L(x,y)$ da função naquele ponto. $f(x,y) = e^{-xy} \cos{y}, \quad (\pi,0)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
$L(x,y) = 1 - \pi y$.
Usando coordenadas esféricas, determine o volume da menor região cortada da esfera sólida $\rho \leq 2$ pelo plano $z=1.$
$\dfrac{5\pi}{3}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{ D}xy\,dA$, onde $D$ é o disco com centro na origem e raio 3.
$0.$
Determine o volume do sólido que se encontra abaixo do plano $3x+2y+z=12$ e acima do retângulo $R=\{(x,y) \in \mathbb{R}^2|\;0\leq x\leq 1,\;-2\leq y\leq 3\}.$
$\dfrac{95}{2}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=(x+y)\,{\bf i}+(y-z)\,{\bf j}+z^{2}\,{\bf k}$, ${\bf r}(t)=t^{2}\,{\bf i}+t^{3}\,{\bf j}+t^{2}\,{\bf k}$, $0\leq t\leq 1.$
$\dfrac{17}{15}.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$ e $u^{2}+v^{2}\leq 4.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{\pi}{6}(17 \sqrt{17} - 1).$
Calcule a integral dupla.
$\displaystyle\iint\limits_{R} (6x^{2}y^{3}-5y^{4})\,dA, \quad R=\{(x,y) \in \mathbb{R}^2:0\leq x\leq 3,\;0\leq y\leq 1\}.$
$\displaystyle\iint\limits_{R} \dfrac{xy^{2}}{x^{2}+1}\,dA, \quad R=\{(x,y)\in \mathbb{R}^2:0\leq x\leq 1,\;-3\leq y\leq 3\}.$
$\dfrac{21}{2}.$
$9 \ln(2).$
Explique por que a função é diferenciável no ponto dado. $f(x,y) = x\sqrt{y}, \quad (1,4)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
Determine se o campo vetorial $\mathbf{F}(x,y,z) = 2xy\mathbf{i} + (x^2+2yz)\mathbf{j} + y^2\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ é conservativo. $f(x,y,z) = x^2 y + y^2 z.$
Integre $g(x,y,z)=xyz$ sobre a superfície do sólido retangular cortado do primeiro octante pelos planos $x=a$, $y=b$ e $z=c.$
$\dfrac{abc(ab+ac+bc)}{4}.$
A região limitada por $y = 1 + x^2,$ pelo eixo $x$ e pelas retas $x = 0$ e $x = 1.$
Seja $f:K\rightarrow \mathbb{R}$ de classe $C^{1}$ no compacto $K$ com fronteira de conteúdo nulo e interior não-vazio. Mostre que a área da superfície $z=f(x,y)$ (isto é, da superfície ${\bf r}$ dada por $x=u$, $y=v$ e $z=f(u,v)$) é dada pela fórmula
$$\iint\limits_{ K}\sqrt{1+\bigg(\frac{\partial f}{\partial x}\bigg)^{2}+\bigg(\frac{\partial f}{\partial y}\bigg)^{2}}dxdy.$$
Determine a área da superfície dada pela porção do cone $z=2\sqrt{x^{2}+y^{2}}$ entre os planos $z=2$ e $z=6.$
$8\sqrt{5}\pi.$
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y,z) = \sqrt{x+yz}, P = (1,3,1), \bf{u} = \left( \frac{2}{7}, \frac{3}{7}, \frac{6}{7} \right)$.
- $\displaystyle \nabla f(x,y,z) = \left(\frac{1}{2\sqrt{x + yz}}, \frac{z}{2\sqrt{x + yz}}, \frac{y}{2\sqrt{x + yz}} \right).$
- $\displaystyle \nabla f(1,3,1) = \left(\frac{1}{4}, \frac{1}{4}, \frac{3}{4}\right).$
- $\displaystyle \frac{23}{28}.$
Determine o plano que é paralelo ao plano $z = 2x + 3y$ e tangente ao gráfico de $f(x,y) = x^2 + xy$.
Considere
$$z-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})(x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})(y-y_{0})$$
o plano tangente ao gráfico de $f$. Assim,
$$z=\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot x+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot y+\bigg[ f(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot x_{0}-\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot y_{0}\bigg].$$
Como tal plano é paralelo ao plano $z=2x+3y$, obtemos que
$$\frac{\partial f}{\partial x}(x_{0},y_{0})=2\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\; \frac{\partial f}{\partial y}(x_{0},y_{0})=3.$$
Notemos que
$$\frac{\partial f}{\partial x}(x,y)=2x+y\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\; \frac{\partial f}{\partial y}(x,y)=x.$$
Assim, temos o seguinte sistema de equações
$$\left \{\begin{array}{cc}2x_{0}+y_{0}=2 \\x_{0}=3\\\end{array}\right.$$
Logo, $x_{0}=3$ e $y_{0}=-4.$ A partir desses valores temos que $f(x_{0},y_{0})=-3$, $\dfrac{\partial f}{\partial x}(x_{0},y_{0})\cdot x_{0}=6$ e
$\dfrac{\partial f}{\partial y}(x_{0},y_{0})\cdot y_{0}=-12.$ Portanto, o plano desejado tem equação
$$z=2x+3y-3-6+12,$$
ou seja,
$$z=2x+3y+3.$$
Explique por que a função é diferenciável no ponto dado. A seguir, encontre a linearização $L(x,y)$ da função naquele ponto. $f(x,y) = \dfrac{x}{x+y}, \quad (2,1)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
$L(x,y) = \frac{1}{9}x - \frac{2}{9}y + \frac{2}{3}$.
Considere o campo vetorial
$${\bf F}(x,y)=(1+ye^{xy})\,{\bf i}+(2y+xe^{xy})\,{\bf j}.$$
Determine se ${\bf F}$ é ou não um campo conservativo. Em caso afirmativo, encontre uma função potencial para ${\bf F}.$
Determine o trabalho realizado pelo campo vetorial ${\bf F}$ ao mover uma partícula sobre a hipérbole $x^{2} - y^{2} = 1,$ desde o ponto $(3,-\sqrt{8})$ até o ponto $(3,\sqrt{8}).$
Sim. Função potencial: $f(x,y) = x + e^{xy} + y^{2}.$
$e^{3\sqrt{8}} - e^{-3\sqrt{8}}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}e^{x^{2}}\;dx dy dz$, onde $E$ é o conjunto $0\leq x \leq 1$, $0\leq y \leq x$ e $0\leq z \leq 1.$
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}\leq y\leq x$, $0\leq z\leq x+y.$
$\dfrac{e - 1}{2}.$
$\dfrac{11}{120}.$
A lei dos gases para uma massa fixa $m$ de um gás ideal à temperatura absoluta $T$, pressão $P$ e o volume $V$ é $PV=mRT$, onde $R$ é a constante do gás. Mostre que
$$\frac{\mathrm{\partial}P}{\mathrm{\partial}V}\frac{\mathrm{\partial}V}{\mathrm{\partial}T}\frac{\mathrm{\partial}T}{\mathrm{\partial}P}=-1.$$
$\displaystyle \frac{\partial P}{\partial V} = -\frac{mRT}{V^{2}},\;\;\;\frac{\partial V}{\partial T} = \frac{mR}{P}\;\;\;\text{e}\;\;\; \frac{\partial T}{\partial P} = \frac{V}{mR}.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y)=x\,{\bf i}+(y+2)\,{\bf j}$ sobre um objeto que se move sobre um arco de cicloide ${\bf r}(t)=(t-\sin t)\,{\bf i}+(1-\cos t)\,{\bf j}$, $0\leq t\leq 2\pi.$
$2\pi^{2}.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{ R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$1$
$x\cos(xy)$
$1.$
$\cos(1) - \cos(2).$
Mude a ordem de integração para mostrar que:
$$ \int_0^a \left[ \int_0^y e^{m(a-x)} f(x) \, dx \right] dy = \int_0^a (a-x) e^{m(a-x)} f(x) \, dx,$$
onde $a$ e $m$ são constantes e $a>0$.
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = x^2 + y^2 + z^2$
$\displaystyle \nabla f(x,y,z) = (2x,2y,2z).$
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla\left(\dfrac{1}{r}\right) = -\dfrac{\mathbf{r}}{r^3}$.
$\nabla\left(\dfrac{1}{r}\right) =- \dfrac{\frac{1}{2\sqrt{x^2 + y^2 + z^2}} (2x)}{x^2 + y^2 + z^2} \mathbf{i} - \dfrac{-\frac{1}{2\sqrt{x^2 + y^2 + z^2}} (2y)}{x^2 + y^2 + z^2} \mathbf{j} - \dfrac{-\frac{1}{2\sqrt{x^2 + y^2 + z^2}} (2z)}{x^2 + y^2 + z^2} \mathbf{k}.$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Se $f(u,v,w)$ é diferenciável, $u=x-y$, $v=y-z$ e $w=z-x$, mostre que
$$\frac{\partial f}{\partial x}+\frac{\partial f}{\partial y}+\frac{\partial f}{\partial z}=0.$$
Note que $\displaystyle \frac{\partial f}{\partial x} = \frac{\partial f}{\partial u} - \frac{\partial f}{\partial w}, $$\displaystyle \frac{\partial f}{\partial y} = -\frac{\partial f}{\partial u} + \frac{\partial f}{\partial v}$ e $\displaystyle \frac{\partial f}{\partial z} = -\frac{\partial f}{\partial v} + \frac{\partial f}{\partial w}.$
Seja \(R\) a região triangular de vértices \((0,0)\), \((3,3)\) e \((0,4)\) do plano \(xy\). Expressa como uma integral dupla, qual é área de \(R\)?
\(\displaystyle A(R)=\int_0^3\int_x^{-\frac{1}{3}x+4}\,dydx \)
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{x^{2}}^{\sqrt{2-x^{2}}}\sqrt{x^{2}+y^{2}}\,dy dx$
$\displaystyle \frac{2}{45}(1 + \sqrt{2}) + \frac{\pi}{3\sqrt{2}}.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{3\pi/2}\int_{0}^{\pi}\int_{0}^{1}5\rho^{3}\sin^{3}{\phi}\,d\rho d\phi d\theta$.
$\dfrac{5\pi}{2}.$
Seja $f: \mathbb{R} \to \mathbb{R}$ uma função diferenciável de uma variável. Defina
$$g(x,y) = f(r), r = \sqrt{x^2 + y^2}.$$
Calcule a derivada direcional da função $g$ no ponto $(x,y) \neq (0,0)$ e na direção do vetor $(x,y)$.
$(f'(r))^{2}.$
Encontre a massa da lâmina descrita como sendo a porção do parabolóide \(2z=x^2+y^2\) que fica dentro do cilindro \(x^2+y^2=8\) e tem densidade \(\delta_0\) constante.
Suponha que $\displaystyle \lim_{(x,y) \to (3,1)}f(x,y) = 6$. O que podemos dizer do valor de $f(3,1)$? E se a função $f$ for contínua?
Nada se pode afirmar. Se $f$ for contínua em $(x_{0},y_{0}),$ $f(3,1) = 6.$
Determine se o campo vetorial $\mathbf{F}(x,y,z) = ye^{-x}\mathbf{i} + e^{-x}\mathbf{j} + 2z\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ não é conservativo.
Uma região $R$ é mostrada na figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \int_{3}^{6} f(r\cos(\theta),r\sin(\theta)) r d r d \theta.$
Seja $A=\{(0,y,z)\in \mathbb{R}^{3}| z^{2}+(y-2)^{2}=1\}$; ache a área da superfície gerada pela rotação em torno do eixo $Oz$ do conjunto $A.$
$8\pi^2.$
O índice I de temperatura-umidade (ou simplesmente humidex) é a temperatura aparente do ar quando a temperatura real é $T$ e a umidade relativa é $h$, de modo que podemos escrever $I=f(T,h)$. A tabela seguinte com valores de $I$ foi extraída de uma tabela do Environment Canada.
Qual é o valor de $f(35,60)$? Qual é o seu significado?
Para que valor de $h$ temos $f(30,h)=36$?
Para que valor de $T$ temos $f(T,40)=42$?
Qual o significado de $I=f(20,h)$ e $I=f(40,h)$? Compare o comportamento dessas duas funções de $h.$
48, o que significa que quando a temperatura real é $35^\circ$C e a umidade relativa é $60\%,$ o humidex é $48^\circ$C.
$50\%.$
$35^\circ$C.
$I = f(20,h)$ e $I = f(40,h)$ são funções de $h$ que fornecem os valores do humidex quando a temperatura real é $20^\circ$C e $40^\circ$C, respectivamente. Ambas as funções crescem com $h,$ porém $f(20,h)$ cresce aproximadamente a taxa constante, enquanto $f(40,h)$ cresce mais rapidamente a uma taxa crescente.
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}e^y \, dx + 2xe^y \, dy$, $C$ é o quadrado de lados $x=0$, $x=1$, $y=0$ e $y=1$.
$e - 1.$
Mostre que a operação de calcular o gradiente de uma função tem a propriedade fornecida. Suponha que $u$ e $v$ sejam funções de $x$ e $y$, diferenciáveis, e $a$ e $b$ sejam constantes.
$\nabla (au + bv) = a \nabla u + b \nabla v$
$\nabla\left(\dfrac{u}{v}\right) = \dfrac{v \nabla u - u \nabla v}{v^2}$
$\nabla(uv) = u \nabla v + v \nabla u$
$\nabla u^n = nu^{n-1}\nabla u$
Pelas propriedades análogas para derivadas parciais e a linearidade de vetores, os quatro itens são válidos.
Suponha que substituamos coordenadas polares $x=r\cos{\theta}$ e $y=r\sin{\theta}$ em uma função diferenciável $w=f(x,y).$
- Mostre que $$\frac{\partial w}{\partial r}=f_{x}\cos{\theta}+f_{y}\sin{\theta}$$ e $$\frac{1}{r}\frac{\partial w}{\partial \theta}=-f_{x}\sin{\theta}+f_{y}\cos{\theta}.$$
- Resolva as equações no item 1. para expressar $f_{x}$ e $f_{y}$ em termos de $\partial w/ \partial r$ e $\partial w/\partial \theta$.
- Mostre que $$(f_{x})^{2}+(f_{y})^{2}=\bigg(\frac{\partial w}{\partial r}\bigg)^{2}+\frac{1}{r^{2}}\bigg(\frac{\partial w}{\partial \theta}\bigg)^{2}.$$
- $\displaystyle f_{x} = \cos(\theta) \frac{\partial w}{\partial r} - \frac{\sin (\theta)}{r} \frac{\partial w}{\partial \theta}$ e $\displaystyle f_{y} = \sin(\theta) \frac{\partial w}{\partial r} + \frac{\cos (\theta)}{r} \frac{\partial w}{\partial \theta}.$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{R}\arctan\left(\dfrac{y}{x}\right)\,dA$, onde $R=\{(x,y) \in \mathbb{R}^2| 1\leq x^{2}+y^{2}\leq 4, 0\leq y\leq x\}.$
$\displaystyle \frac{3\pi^2}{64}.$
Determine se ${\bf F}(x,y,z)=\dfrac{x}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf i}+\dfrac{y}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf j}+\dfrac{z}{(x^{2}+y^{2}+z^{2})^{2}}\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = -\dfrac{1}{2(x^2 + y^{2} +z^{2})} + K.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=y^{2}-x^{2}$ em $D=\{(x,y)\in \mathbb{R}^2: x^{2}+y^{2}\leq 4\}.$
Valor máximo: $\displaystyle 4;$ valor mínimo: $-4.$
Seja $C: {\bf r}(t)=(R\,\cos t, R\,\sin t)$, $0\leq t \leq 2\pi$\,$(R>0).$ Mostre que
$$\int_{C}\frac{-y}{x^{2}+y^{2}}\,dx+\frac{x}{x^{2}+y^{2}}\,dy$$
não depende de $R.$
Note que o valor da integral é $2\pi,$ independente de $R.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=xy$ em $D=\{(x,y) \in \mathbb{R}^2: x\geq 0,\;y\geq 0\;\text{e}\;2x+y\leq 5\}.$
Valor máximo: $\displaystyle \frac{25}{8};$ valor mínimo: $\displaystyle 0.$
Dado um campo vetorial \(\mathbf{F}\), uma curva \(C\) é chamada de linha de fluxo deste campo se \(\mathbf{F}\) for um vetor tangente a \(C\) em cada ponto ao longo de \(C\).
Sejam \(C\) uma linha de fluxo de \(\mathbf{F}(x,y)=-y\mathbf{i}+x\mathbf{j}\) e \((x,y)\) um ponto em \(C\) para o qual \(y\neq 0\). Mostre que as linhas de fluxo satisfazem a equação diferencial \[ \dfrac{dy}{dx} = -\dfrac{x}{y}. \]
Resolva a equação diferencial do item anterior, por separação de variáveis, e mostre que as linhas de fluxo são círculos concêntricos centrados na origem, ou seja, da forma \(x^2+y^2=K\).
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}z\,dV$, onde $E$ é limitado pelo cilindro $y^{2}+z^{2}=9$ e pelos planos $x=0$, $y=3x$ e $z=0$ no primeiro octante.
$\displaystyle\iiint\limits_{ E}xyz\;dx dy dz$, onde $E$ é o paralelepípedo $0\leq x\leq 2$, $0\leq y\leq 1$, e $1\leq z\leq 2.$
$\dfrac{27}{8}.$
$\dfrac{3}{2}.$
Considere um escoamento com velocidade ${\bf v}(x,y,z)$ e densidade $\rho(x,y,z)$, tal que ${\bf u}=\rho {\bf v}$ seja dado por ${\bf u}=x{\bf i}+y{\bf j}-2z{\bf k}$. Seja $S$ a superfície $x^{2}+y^{2}+z^{2}=4$, $z\geq \sqrt{2}$, e seja ${\bf n}$ a normal com componente $z>0$. Calcule o fluxo de ${\bf u}$ através de $S$. (Observe que, neste caso, o fluxo tem dimensões $MT^{-1}$ (massa por unidade de tempo).)
$-4\pi\sqrt{2}.$
A resistência total \(R\) de três resistores \(R_1\), \(R_2\) e \(R_3\) ligados em paralelo é dada por \[ \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}. \] Suponha que \(R_1\), \(R_2\) e \(R_3\) tenham sido medidos como \(100\ \Omega\), \(200\ \Omega\) e \(300\ \Omega\), respectivamente, com um erro máximo de \(10\%\) em cada um e sendo \(\Omega\)(Ohm) a unidade de medida no sistema internacional de unidades. Use diferenciais para aproximar o erro percentual máximo no valor calculado de \(R\).
Esboce o campo vetorial $\textbf{F}=\dfrac{1}{2}(\textbf{i} + \textbf{j})$, desenhando um diagrama.
Determine as derivadas parciais de $g(x,y)=x^{y}$.
$\displaystyle \frac{\partial g}{\partial x} = yx^{y - 1}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial g}{\partial y} = x^{y} \ln x.$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(1,u,v)$, $0\leq u\leq 1$, $0\leq v \leq 1.$
Região quadrada do plano $x = 1:$ $0 \leq y \leq 1$ e $0 \leq z \leq 1.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}yz dS$, onde $S$ é a superfície com equações paramétricas $x=u^{2}$, $y=u \sin v$, $z=u\cos v$, $0 \leq u \leq 1$, $0 \leq v \leq \pi/2.$
$\dfrac{5\sqrt{5}}{48} + \dfrac{1}{240}.$
Se $z=\sin(x+\sin{y})$, mostre que $\dfrac{\partial z}{\partial x} \;\dfrac{\partial^{2} z}{\partial x \partial y}=\dfrac{\partial z}{\partial y}\;\dfrac{\partial^{2}z}{\partial x^{2}}$.
$\begin{aligned}[t]\frac{\partial z}{\partial x} &= \cos(x + \sin y),\;\;\; \frac{\partial z}{\partial y} = \cos(x + \sin y) \cos y,\\\frac{\partial z^{2}}{\partial x\partial y} &= -\sin (x + \sin y) \cos y\;\;\text{e}\;\; \frac{\partial^{2} z}{\partial x^{2}} = -\sin (x + \sin y).\end{aligned}$
Disseram-lhe que existe uma função $f$ cujas derivadas parciais são \[f_{x}(x,y)=x+4y \quad \mbox{e} \quad f_{y}(x,y)=3x-y,\] e cujas derivadas parciais de segunda ordem são contínuas. Você deve acreditar nisso?
Não, pois pelo Teorema de Clairaut deveria ser verdade que $f_{xy} = f_{yx},$ mas temos $f_{xy} = 4 \neq 3 = f_{yx}.$
Calcule o volume do conjunto dado.
$0\leq y\leq 1-x^{2}$ e $0\leq z\leq 1-x^{2}.$
$x^{2}+y^{2}+3\leq z\leq 4.$
$\dfrac{16}{15}.$
$\dfrac{\pi}{2}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}2z\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}+z^{2}\leq 4$ e $z\geq 0.$
$\displaystyle\iiint\limits_{ E}2z\;dx dy dz$, onde $E$ é o conjunto $4x^{2}+9y^{2}+z^{2}\leq 4$ e $z\geq 0.$
$8\pi.$
$0.$
A fórmula de Taylor de primeira ordem para $f(\vec{a} + \vec{v})$ pode ser escrita como $ f(\vec{a}) + \nabla f(\vec{a}) \cdot \vec{v}$, já desconsiderando o termo de erro. Calcule-a para $f(x,y) = x^2 + y^2$, $\vec{a} = (1,0)$ e $\vec{v} = (2,1)$. Calcule também o erro cometido, dizendo se é um erro pequeno ou grande e por quê.
É dada uma curva $\gamma$ que passa pelo ponto $\gamma(t_0) = (1,3)$ e cuja imagem está contida na curva de nível $x^2 + y^2 = 10$. Suponha $\gamma'(t_0) \neq \bf{0}$.
- Determine a equação da reta tangente a $\gamma$ no ponto $(1,3)$.
- Determine uma curva $\gamma(t)$ satisfazendo as condições acima.
- $(x,y) = (1,3) + \lambda (-6,2),$ $\lambda \in \mathbb{R}.$
- $\gamma(t) = (\sqrt{10} \cos(t), \sqrt{10} \sin(t)).$
Considere a função $z=\dfrac{xy^{2}}{x^{2}+y^{2}}.$ Verifique que $x\dfrac{\partial z}{\partial x}+y\dfrac{\partial z}{\partial y}=z.$
$\displaystyle \frac{\partial z}{\partial x} = \frac{y^{4} - x^{2}y^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{3}y}{(x^{2} + y^{2})^{2}}.$
Determine o campo vetorial gradiente de $f(x,y) = \ln(x + 2y)$.
$\nabla f(x,y) = \dfrac{\textbf{i} + 2\textbf{j}}{x + 2y}.$
Esboce a região limitada pelos gráficos das equações e use uma integral tripla para calcular seu volume.
$z+x^{2}=4$, $y+z=4$, $y=0$ e $z=0.$
$y=2-z^{2}$, $y=z^{2}$, $x+z=4$ e $x=0.$
$y^{2}+z^{2}=1$, $x+y+z=2$ e $x=0.$
$\dfrac{128}{5}.$
$\dfrac{32}{3}.$
$2\pi.$
Calcule $\displaystyle\int_{(1,1)}^{(2,2)} y\,dx+x\,dy$.
$3.$
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = -y{\bf i} + x{\bf j} + x^2{\bf k}$, $S$ a superfície $x^2+y^2+z^2 = 4$, $\sqrt{2} \leq z \leq \sqrt{3}$ e $y \geq 0$, sendo ${\bf n}$ a normal apontando para cima.
$\pi$.
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$\sqrt{x+y}$
$\dfrac{1}{x+y}$
$\dfrac{4(9\sqrt{3} - 8\sqrt{2} + 1)}{15}.$
$\ln\left( \dfrac{27}{16}\right).$
Considere o campo vetorial \(\mathbf{F}(x,y,z)=x^2\mathbf{i} + y^2\mathbf{j}+z^2\mathbf{k}\) e a superfície \(\sigma\) descrita como sendo a porção do cone \(z=\sqrt{x^2+y^2}\) abaixo do plano \(z=1\) e tendo orientação para cima. Verifique o Teorema de Stokes calculando, separadamente, a integral de linha e a integral dupla e, em seguida, comparando os valores.
Suponha que ${\bf F}$ seja um campo vetorial inverso do quadrado, ou seja,
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}.$ Determine o trabalho realizado por ${\bf F}$ ao mover um objeto de um ponto $P_{1}$ por um caminho para um ponto $P_{2}$ em termos da distância $d_{1}$ e $d_{2}$ desses pontos à origem.
$c\left(\dfrac{1}{d_{1}} - \dfrac{1}{d_{2}}\right).$
Seja ${\bf E}(x,y)=\dfrac{1}{x^{2}+y^{2}}\dfrac{x\,{\bf i}+y\,{\bf j}}{\sqrt{x^{2}+y^{2}}}$ e seja $C$ a curva dada por $x=t$ e $y=1-t^{4}$, $-1\leq t\leq 1.$
Que valor é razoável esperar para $\int_{C}{\bf E}\cdot d{\bf l}$? Por quê? (O ${\bf l}$ desempenha aqui o mesmo papel que ${\bf r}:{\bf l}(t)={\bf r}(t).$)
Calcule $\int_{C}{\bf E}\cdot d{\bf l}.$
$0.$
Determine uma representação paramétrica para a superfície descrita a seguir. A porção do cilindro $(x-2)^{2}+z^{2}=4$ entre os planos $y=0$ e $y=3.$
$x = 4\cos^{2}(v),$ $y = u,$ $z = 4\cos(v)\sin(v),$ onde $-\dfrac{\pi}{2}\leq v \leq \dfrac{\pi}{2}$ e $0 \leq u \leq 3.$
Calcule $\int_{C}\mathbf{F}\cdot\, d\mathbf{r}$, em que
$$\mathbf{F}(x,y) = (x^2+y)\mathbf{i} + (3x-y^2)\mathbf{j}$$
e $C$ é a fronteira orientada positivamente de uma região $D$ que tem área 6.
$12.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,\sin{y}\,ds$, $C$ é o segmento de reta que liga $(0,3)$ a $(4,6).$
$\displaystyle \frac{20}{6} \left(\sin(6) - 3\cos(6) - \sin(3) \right).$
Suponha que um cientista tenha razões para acreditar que duas quantidades $x$ e $y$ estejam relacionadas linearmente, ou seja, $y=mx+b$, pelo menos aproximadamente, para algum valor de $m$ e de $b$. O cientista realiza uma experiência e coleta os dados na forma de pontos $(x_{1},y_{1}), (x_{2},y_{2}), \ldots, (x_{n},y_{n})$, e então coloca-os em um gráfico. Os pontos não estão todos alinhados, de modo que o cientista quer determinar as constantes $m$ e $b$ para que a reta $y=mx+b$ ``ajuste" os pontos tanto quanto possível (veja a figura). Seja $d_{i}=y_{i}-(mx_{i}+b)$ o desvio vertical do ponto $(x_{i},y_{i})$ da reta. O {\bf método dos mínimos quadrados} determina $m$ e $b$ de modo a minimizar $\sum_{i=1}^{n}d_{i}^{2}$, a soma dos quadrados dos desvios. Mostre que, de acordo com esse método, a reta de melhor ajuste é obtida quando
$$m\sum_{i=1}^{n}x_{i}+bn=\sum_{i=1}^{n}y_{i}$$
$$m\sum_{i=1}^{n}x_{i}^{2}+b\sum_{i=1}^{n}x_{i}=\sum_{i=1}^{n}x_{i}y_{i}$$
Assim, a reta é determinada resolvendo esse sistema linear de duas equações nas incógnitas $m$ e $b.$
As duas equações são obtidas como pontos críticos da função $\displaystyle \sum^{n}_{i = 1} d_{i}^{2} = \sum^{n}_{i = 1} \left(y_{i} - (mx_{i} + b) \right)^{2} = f(m,b).$ Note que de fato pontos satisfazendo as equações são pontos de mínimo de $f.$
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y) = y \ln{x}, P = (1, -3), \bf{u} = \left(-\frac{4}{5}, \frac{3}{5} \right)$.
- $\nabla f(x,y) = (y/x,\ln(x)).$
- $\nabla f(1,-3) = (-3,0).$
- $\displaystyle \frac{12}{5}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}e^{x^{2}+y^{2}}\,dx dy$, onde $R$ é o conjunto de todos os $(x,y)$ tais que $1\leq x^{2}+y^{2}\leq 4$, $-x\leq y\leq x$ e $x\geq 0.$
$\displaystyle \frac{\pi}{4}(e^4 - e).$
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$, sendo:$D$ a região triangular com vértices $(0,0), (2,1), (0,3)$ e $\rho(x,y) = x + y$.
Massa: $6;$ centro de massa: $\displaystyle \left(\frac{3}{4},\frac{3}{2} \right).$
Calcule a área limitada pelas curvas $x=y^{2}-1$ e $x=2y^{2}-2.$
$\dfrac{4}{3}.$
Faça o mapa de contorno da função $f(x,y)=ye^{x}$ mostrando várias de suas curvas de nível.
$y = Ce^{-x}.$
Explique por que a função é diferenciável no ponto dado. $f(x,y) = \dfrac{x}{x+y}, \quad (2,1)$.
As derivadas $f_{x}$ e $f_{y}$ de cada $f$ existem e são contínuas no ponto dado, logo $f$ é diferenciável.
Verifique que $x\;\dfrac{\partial ^{2}z}{\partial x \partial y}+y\;\dfrac{\partial ^{2}z}{\partial y^{2}}=0$, onde $z=(x+y)e^{x/y}.$
$\displaystyle \frac{\partial^{2} z}{\partial x \partial y}= \frac{-3xy - x^{2}}{y^{3}}e^{\frac{x}{y}} \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= \frac{3x^{2}y + x^{3}}{y^{4}}e^{\frac{x}{y}}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{-1}^{0} \int_{-\sqrt{1-x^{2}}}^{0}\frac{2}{1+\sqrt{x^{2}+y^{2}}}\,dy dx$
$(1 - \ln(2))\pi.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=yz\,{\bf i}+xz\,{\bf j}+xy\,{\bf k}$ e $S$ é o gráfico de $x^{2/3}+y^{2/3}+z^{2/3}=1.$
$f(x,y,z)$ e $g(x,y)$ são funções diferenciáveis tais que, para todo $(x,y)$ no domínio de $g,f(x,y,g(x,y))=0$.
Suponha $g(1,1)=3$, $\dfrac{\partial f}{\partial x}(1,1,3)=2$, $\dfrac{\partial f}{\partial y}(1,1,3)=5$ e $\dfrac{\partial f}{\partial z}(1,1,3)=10.$
Determine a equação do plano tangente ao gráfico de $g$ no ponto $(1,1,3).$
$\displaystyle z - 3 = -\frac{1}{5}(x - 1) - \frac{1}{2} (y-1).$
Mude as coordenadas de $(1,-1,4)$ de retangulares para cilíndricas.
$\displaystyle (\sqrt{2}, \dfrac{7\pi}{4}, 4).$
Use o Teorema do Divergente para calcular $\displaystyle\iint \limits_{S}{\bf F}\cdot dS$, onde ${\bf F}(x,y,z)=z^{2}x\,{\bf i}+(\frac{1}{3}y^{3}+tg z)\,{\bf j}+(x^{2}z+y^{2})\,{\bf k}$ e $S$ é a metade de cima da esfera $x^{2}+y^{2}+z^{2}=1.$
[Sugestão: observe que $S$ não é uma superfície fechada. Calcule primeiro as integrais sobre $S_{1}$ e $S_{2}$, onde $S_{1}$ é o círculo $x^{2}+y^{2}\leq 1$, orientado para baixo, e $S_{2}=S\cup S_{1}.$]
Note que $\dfrac{\partial}{\partial x} \left( \dfrac{x}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3x^2}{|{\bf x}|^5},$ $\dfrac{\partial}{\partial y} \left( \dfrac{y}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3y^2}{|{\bf x}|^5}$ e $\dfrac{\partial}{\partial z} \left( \dfrac{x}{|{\bf x}|^3} \right) = \dfrac{|{\bf x}|^2 - 3z^2}{|{\bf x}|^5}.$
Calcule a integral iterada.
$\displaystyle\int_{1}^{4} \int_{1}^{2}\bigg(\dfrac{x}{y}+\dfrac{y}{x}\bigg)\,dy dx$
$\displaystyle\int_{0}^{1} \int_{0}^{3}e^{x+3y}\,dx dy$
$\dfrac{21}{2} \ln(2).$
$\dfrac{(e^{3} - 1)^{2}}{3}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\sqrt{x^{2}+y^{2}}\,dA$, onde $R$ é limitado pelo triângulo de vértices $(0,0)$, $(3,0)$ e $(3,3).$
$\displaystyle \frac{9}{2} (\sqrt{2} + \ln(\sqrt{2} + 1)).$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xe^{yz}\,ds$, $C$ é o segmento de reta de $(0,0,0)$ a $(1,2,3).$
$\dfrac{\sqrt{14}}{12}\left(e^{6} - 1 \right).$
Calcule a integral de linha $\displaystyle\int_{C}y^{2}\,dx+x\,dy -\,dz$, onde $C$ é a poligonal de vértices $A_{0}=(0,0,0)$, $A_{1}=(1,1,1)$, $A_{2}=(1,1,0)$, orientada de $A_{0}$ para $A_{2}.$
$\displaystyle \frac{5}{6}.$
Calcule a integral iterada.
$\displaystyle\int_{0}^{1}\!\!\int_{0}^{z}\!\!\int_{0}^{x+z}6xz\;dy dx dz$
$\displaystyle\int_{0}^{3}\!\!\int_{0}^{1}\!\!\int_{0}^{\sqrt{1-z^{2}}}ze^{y}\;dx dz dy$
$\displaystyle\int_{0}^{\pi/2}\int_{0}^{y}\int_{0}^{x}\cos(x+y+z)\;dz dx dy$
$1.$
$\displaystyle \frac{e^3 - 1}{3}.$
$-\dfrac{1}{3}.$
Calcule $\mathrm{d} z/\mathrm{d} t$ por dois processos:
- substituindo as expressões para $x(t)$ e $y(t)$ em $z$ e depois derivando diretamente com relação a $t$
- aplicando a Regra da Cadeia: $\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y }\frac{dy}{dt}$.
$z=\sin(xy)$, $x=3t$ e $y=t^{2}.$
$\displaystyle \frac{dz}{dt} (t) = 9t^{2}\cos(3t^{3}).$
Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ onde $g(x,y,z)=x+y$ e $S$ é parte do primeiro octante do plano $2x+3y+z=6.$
$5\sqrt{14}.$
Experiências mostram que uma corrente contínua $I$ em um fio comprido produz um campo magnético ${\bf B}$ que é tangente a qualquer círculo em um plano perpendicular ao fio cujo centro seja o eixo do fio (como na figura). A Lei de Ampère relaciona a corrente elétrica ao campo magnético criado e afirma que
$$\int_{C}{\bf B}\cdot d{\bf r}=\mu_{0}I,$$
onde $I$ é a corrente total que passa por qualquer superfície limitada por uma curva fechada $C$ e $\mu_{0}$ é uma constante, chamada permeabilidade no vácuo. Tomando $C$ como um círculo de raio $r$, mostre que o módulo $B=|{\bf B}|$ do campo magnético a uma distância $r$ do centro do fio é dado por
$$B=\frac{\mu_{0}I}{2\pi r}.$$

Note que $\textbf{B}$ é tangente a qualquer círculo que está no plano perpendicular ao fio. Logo, $\textbf{B} = |\textbf{B}| \textbf{T},$ onde $\textbf{T}$ é a tangente unitária ao círculo $\textbf{C}$ parametrizado por $x = r \cos(\theta),$ $y = r \sin(\theta).$ Daí,
$\textbf{B} = |\textbf{B}| \left(-\sin(\theta),\cos(\theta) \right)$ e
$$\int_{C} \textbf{B} \cdot d\textbf{r} = \int_{0}^{2\pi} |\textbf{B}| \left( -\sin(\theta), \cos(\theta)\right)\cdot (\left(-r \sin(\theta), r\cos(\theta) \right) d\theta = 2\pi r |\textbf{B}|.$$
A superfície de um lago é representada por uma região $D$ no plano $xy$, tal que a profundidade (em pés) sob o ponto correspondente a $(x,y)$ é dada por
$$f(x,y) = 300 - 2x^2 - 3y^2.$$
Se um nadador está no ponto $(4,9)$, em que direção deve nadar para que a profundidade sob ele decresça mais rapidamente?
Na direção dada pelo vetor $(16,54).$
Determine a imagem do conjunto $S$ sob a transformação dada. $S$ é o disco dado por $u^2 + v^2 \leq 1$;$x = au$, $y = bv$.
Suponha $a$ e $b$ não-nulos. Por essa mudança de coordenadas, temos que $u = x/a$ e $v = y/b$. Substituindo na equação dada, obtemos
$$\frac{x^2}{a^2}+\frac{y^2}{b^2} \leq 1,$$
isto é, o disco $S$ é transformado em uma elipse.
Mostre que, se um campo vetorial ${\bf F}=P\,{\bf i}+Q\,{\bf j}+R\,{\bf k}$ é conservativo e $P$, $Q$, $R$ têm derivadas parciais de primeira ordem contínuas, então
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}, \,\,\,\,\,\frac{\partial P}{\partial z}=\frac{\partial R}{\partial x},\,\,\,\,\,\frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}$$
Se $f$ é uma função potencial de $\mathbf{F},$ então $f_{x} = P,$ $f_{y} = Q$ e $f_{z} = R.$ Como $P, Q$ e $R$ possuem derivadas parciais de primeira ordem contínuas, então pelo Teorema de Clairaut, temos $f_{xy} = f_{yx},$ $f_{yz} = f_{zy}$ e $f_{xz} = f_{zx}.$
Considere a função
$$f(x,y) = \ln{(x^2 + y^2)}.$$
- Determine a taxa de variação máxima de $f$ em $(1,1)$ e a direção em que isso ocorre.
- Determine a derivada direcional de $f$ em $(1,1)$ na direção do vetor $\bf{v} = (3,4)$.
- Na direção do vetor $(1,1).$ O valor da taxa máxima é $\sqrt{2}.$
- $ \displaystyle \frac{7}{5}.$
Faça uma correspondência entre as funções $f$ e os desenhos de seus campos vetoriais gradientes (rotulados de I-IV). Justifique.
- $f(x,y) = x^2+y^2$
- $f(x,y) = (x+y)^2$.
- $f(x,y) = x(x+y)$.
- $f(x,y) = \sin{\sqrt{x^2+y^2}}$.
II

III
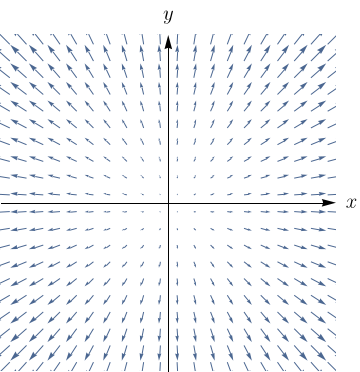
IV
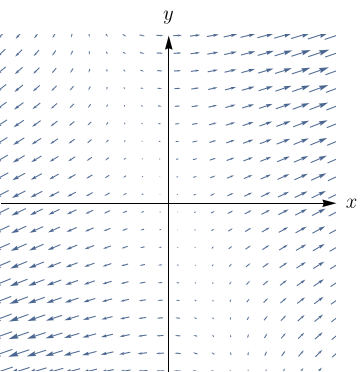
- III.
- IV.
- II.
- I.
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}\dfrac{xy}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2} \setminus \left\lbrace (0,0) \right\rbrace$.
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{3}\!\!\int_{-\sqrt{9-y^{2}}}^{\sqrt{9-y^{2}}}f(x,y)\,dx dy$.
Esboce a região cuja área é dada pela integral e calcule-a, sendo: $\displaystyle\int_{0}^{\pi/2}\int_{0}^{4\cos{\theta}} r \,drd\theta.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3xy^{2}\,{\bf i}+xe^{z}\,{\bf j}+z^{3}\,{\bf k}$ e $S$ é a superfície do sólido delimitado pelo cilindro $y^{2}+z^{2}=1$ e pelos planos $x=-1$ e $x=2.$
Encontre a área da superfície descrita como sendo a parte do cone \(z^2=4x^2+4y^2\) que está acima da região do primeiro quadrante limitada pela reta \(y=x\) e a parábola \(y=x^2\).
\( \dfrac{\sqrt{5}}{6}\)
Esboce o gráfico da função $f(x,y)=\ln(\sqrt{x^{2}+y^{2}})$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
Encontre a área da parte da esfera $x^{2}+y^{2}+z^{2}=a^{2}$ que está dentro do cilindro $x^{2}+y^{2}=ax.$
$2a^2 (\pi - 2).$
Calcule as seguintes integrais triplas.
$\displaystyle\iiint\limits_{ E} x^2 \, dV$, em que $E$ é o sólido que está dentro do cilindro $x^2 + y^2 = 1$, acima do plano $z = 0$ e abaixo do cone $z^2 = 4x^2 + 4y^2$.
$\displaystyle\iiint\limits_{ E} xyz \, dV,$ em que $E$ é o sólido limitado pelos paraboloides $z = x^2 + y^2$, $z = 8 - x^2 - y^2$.
$\displaystyle\int_{-2}^2\int_{-\sqrt{4 - y^2}}^{\sqrt{4 - y^2}}\int_{\sqrt{x^2 + y^2}}^2 xz \, dz dx dy$
$\dfrac{2\pi}{5}$.
$0.$
$0.$
Determine uma representação paramétrica para a superfície descrita a seguir. A superfície cortada do cilindro parabólico $z=4-y^{2}$ pelos planos $x=0$, $x=2$ e $z=0.$
$x = u,$ $y = v,$ $z = 4 - v^2,$ onde $0\leq u \leq 2$ e $-2 \leq v \leq 2.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=e^{x}\cos{y}$.
Não há pontos críticos.
Seja $\phi:\mathbb{R}\rightarrow \mathbb{R}$ uma função diferenciável de uma variável real e seja $f(x,y)=(x^{2}+y^{2})\phi \bigg(\dfrac{x}{y}\bigg).$
Mostre que
$$x\;\frac{\partial f}{\partial x}+y\;\frac{\partial f}{\partial y}=2f.$$
$\displaystyle \frac{\partial f}{\partial x} = 2x \phi \left( \frac{x}{y} \right) + \frac{(x^{2} + y^{2})}{y} \phi'\left( \frac{x}{y} \right)\ \;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = 2y \phi \left( \frac{x}{y} \right) - \frac{x(x^{2} + y^{2})}{y^{2}} \phi'\left( \frac{x}{y} \right).$
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = e^x\sin{y}\mathbf{i} + e^x\cos{y}\mathbf{j} + z\mathbf{k}$.
$\text{rot } \mathbf{F} = \bf{0}.$ $\text{div } \mathbf{F} = 1.$
Verifique que a função $f(x,y) = x \cos{(x^2 + y^2)}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?
$f(x,y) = \ln{||(x,y)||}$ em $(1,-1)$.
Cresce: $(1,-1)$; descresce: $(-1,1).$
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste a oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade norte. Encontre o volume de água da piscina.
$1800 \pi$ m$^3.$
Calcule.
- $\displaystyle\int_{0}^{1}(t{\bf i}+e^{t}{\bf j})\mathrm{d}t$
- $\displaystyle\int_{-1}^{1}\!\bigg(\sin(3t){\bf i}+\dfrac{1}{1+t^{2}}{\bf j}+{\bf k}\bigg)\mathrm{d}t$
- $\displaystyle\int_{1}^{2}(3{\bf i}+2{\bf j}+{\bf k})\mathrm{d}t$
Encontre uma equação para a curva de nível da função $f(x,y)=\displaystyle \int_{x}^{y}\dfrac{dt}{1+t^{2}}$ que passa pelo ponto $(-\sqrt{2},\sqrt{2})$.
$\arctan(y) - \arctan(x) = 2\arctan(\sqrt{2}).$
Seja $f(x,y)=x^{2}e^{3xy}$.
Calcule $f(2,0).$
Determine o domínio de $f$.
Determine a imagem de $f$.
$4.$
$\mathbb{R}^{2}.$
$[0,\infty).$
- Queremos calcular $f(2,0)$ sabendo que $f(x,y)=x^{2}e^{3xy}$. Basta substituir os valores na expressão, assim temos
\[
f(2,0)=2^{2}e^{3 \cdot 2 \cdot 0}=4e^{0}=4 \cdot 1=4.
\] - Por definição, o domínio da função $f$ é o conjunto dos pontos de $\mathbb{R}^{2}$ em que a função está bem definida. Em nosso caso, o domínio é o conjunto de pontos em que a função $f(x,y)=x^{2}e^{3xy}$ está bem definida. Portanto, o domínio de $f$ é $\mathbb{R}^2$.
- A imagem da função $f$ é o conjunto dos pontos $\{ z\in \mathbb{R} | z = f(x,y) \text{ e } (x,y)\in D\}$, onde $D$ é o domínio de $f$. Observe que $x^{2} \geq 0$ e $e^{3xy}> 0$ para todo $(x,y)\in \mathbb{R}^{2}$, logo $x^{2}e^{3xy}\geq 0$ para todo $(x,y)\in \mathbb{R}^{2}$. Por exemplo, se fixarmos $x=1$ temos que a imagem da função são os pontos da forma $e^{3y}$ com $y\in \mathbb{R}$, ou seja, é todo o intervalo $(0,\infty)$. Agora, quando colocamos $x=0$ a imagem é $0$. Portanto, a imagem de $f$ é o conjunto $[0,\infty]$.
Encontre o valor de $\partial z/\partial x$ no ponto $(1,1,1)$ sabendo que a equação
$$xy+z^{3}x-2yz=0$$
define $z$ como uma função de duas variáveis independentes $x$ e $y$ e que a derivada parcial existe.
$\displaystyle \frac{\partial z}{\partial x} (1,1,1) = -2$.
Determine as equações do plano tangente e da reta normal à superfície dada, no ponto dado.
$x^2 + 3y^2 + 4z^2 = 8$, em $(1,-1,1)$.
Plano tangente: $x - 3y + 4z = 8$
Reta normal: $(x,y,z) = (1,-1,1) + \lambda (2,-6,8),$ $\lambda \in \mathbb{R}.$
O centróide de uma região $E$ é dado por
$$\overline{x}=\frac{1}{vol(E)}\int_{E}x\,dV,\;\;\;\; \overline{y}=\frac{1}{vol(E)}\int_{E}y\,dV\;\; \text{e}\;\; \overline{z}=\frac{1}{vol(E)}\int_{E}z\,dV.$$
Calcule o centróide da região dada em coordenadas esféricas por $0\leq \rho \leq 1$, $0\leq\phi \leq \pi/3$ e $0\leq \theta \leq 2\pi$ (observe que, devido à simetria da região, $\overline{x}$ e $\overline{y}$ se anulam, bastando calcular a terceira coordenada).
$\overline{z} = \dfrac{9}{16}.$
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = x^2\mathbf{i}$, $C$ dada por $\mathbf{r}(t) = (2\cos{t},\sin{t})$, $0 \leq t \leq \pi$ e $\mathbf{n}$ a normal com componente $y \geq 0$.
$0$.
Determine a derivada direcional da função no ponto dado e na direção do vetor $\bf{v}$.
$f(x,y,z) = xe^y + ye^z + ze^x, (0,0,0), \bf{v} = \left(5,1,-2\right).$
$\displaystyle \frac{4}{\sqrt{30}}.$
Determine o sólido $E$ para o qual a integral $$ \iiint\limits_{ E}(1-x^{2}-2y^{2}-3z^{2})\,dV$$ é máxima.
$E = \left\{ (x,y,z); x^2 + 2y^2 + 3z^2 \leq 1 \right\}.$
Seja \(\sigma\) a superfície de um sólido \(G\) com vetor normal unitário \(\mathbf{n}\) orientado para fora de \(\sigma\). Suponha que \(\mathbf{F}\) seja um campo vetorial com derivadas parciais de primeira ordem contínuas em \(\sigma\). Prove que \[\iint\limits_\sigma (\mathrm{rot\,}\mathbf{F})\cdot\mathbf{n}\,dS = 0.\] [Sugestão: tome \(C\) uma curva fechada simples em \(\sigma\) que separa a superfície em duas subsuperfícies \(\sigma_1\) e \(\sigma_2\) com fronteira comum \(C\). Aplique o Teorema de Stokes a \(\sigma_1\) e a \(\sigma_2\) e some os resultados.]
O campo vetorial \(\mathrm{rot\,}\mathbf{F}\) é denominado campo rotacional de \(\mathbf{F}\). Em palavras, interprete a fórmula do item anterior como uma afirmação sobre o fluxo do campo rotacional.
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y)=(x+y^{2})\,{\bf j}$ e $C$ é a curva da figura abaixo.

$4.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=x^{2}+y^{2}+x^{2}y+4$, $D=\{(x,y) \in \mathbb{R}^2: |x|\leq 1, \; |y|\leq 1\}.$
Valor máximo: $7;$ valor mínimo: $4.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y,z) = yz + xy; \quad xy = 1, \quad y^2 + z^2 = 1.$
Valor máximo: $\dfrac{3}{2};$ valor mínimo: $\dfrac{1}{2}.$
Suponha que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que $f$ seja uma função escalar com derivadas parciais contínuas. Demonstre que $\displaystyle\iint\limits_{S}f{\bf n}\,dS=\iiint\limits_{E}\nabla f\,dV.$ Estas integrais de superfície e triplas de funções vetoriais são vetores definidos integrando cada função componente. [Sugestão: comece aplicando o Teorema do Divergente a ${\bf F}=f{\bf c}$, onde ${\bf c}$ é um vetor constante arbitrário.]
Note que se ${\bf n} = n_{1} {\bf i} + n_{2} {\bf j} + n_{3} {\bf k},$ então
\begin{align*} &\iint_{S} f \cdot {\bf n}\,dS \\ &= \left( \iint_{S} f n_{1}\,dS \right) {\bf i} + \left( \iint_{S} fn_{2}\,dS\right) {\bf j} + \left( \iint_{S} fn_{3}\,dS\right) {\bf k}\\ &= \left( \iiint_{E} \dfrac{\partial f}{\partial x}\,dV \right) {\bf i}+ \left( \iiint_{E} \dfrac{\partial f}{\partial y}\,dV\right) {\bf j} + \left( \iiint_{E} \dfrac{\partial f}{\partial z}\,dV \right) {\bf k}. \end{align*}
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$
Região triangular do plano $x + y + z = 1:$ $0 \leq x \leq 1, $ $0 \leq y \leq 1,$ $0 \leq z \leq 1.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}\sqrt{1-z^{2}}\;dx dy dz$, onde $E$ é o cubo $0\leq x\leq 1$, $0\leq y\leq 1$ e $0\leq z\leq 1.$
$\displaystyle\iiint\limits_{ E}\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq z \leq 2x.$
$\dfrac{\pi}{4}.$
$\dfrac{\pi}{2}.$
Determine a equação da reta tangente à curva $\gamma$ no ponto $\gamma(t_0) = (2,5)$ sabendo-se que $\gamma'(t) \neq \bf{0}$ e que sua imagem está contida na curva de nível $xy = 10$. Qual a equação da reta normal a $\gamma$, neste ponto?
Reta tangente: $(x,y) = (2,5) + \lambda (-2,5),$ $\lambda \in \mathbb{R},$
Reta normal: $(x,y) = (2,5) + \lambda (5,2),$ $\lambda \in \mathbb{R}.$
Encontre a área da superfície descrita como sendo a parte do plano \(2x+2y+z=8\) no primeiro octante.
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$z=\sqrt{x^{2}+y^{2}}$, $x=e^{2t}$, $y=e^{-2t}$.
$\displaystyle \frac{dz}{dt} = \frac{2xe^{2t} - 2ye^{2t}}{\sqrt{x^{2} + y^{2}}}.$
Calcule o centro de massa do quadrado $D$ dado por $0 \leq x \leq 1, \ 0 \leq y \leq 1$ e com densidade $\quad \rho(x,y) = y$.
$\displaystyle \left(\frac{1}{2}, \frac{2}{3} \right).$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{0}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{x}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\displaystyle\int_{y}^{1}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{y}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^2}^{1}f(x,y)\,dy\bigg]dx$
Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ sendo $g(x,y,z)=x^{2}$ e $S$ o hemisfério superior de $x^{2}+y^{2}+z^{2}=a^{2}.$
$\dfrac{2\pi a^4}{3}.$
Determine, mas não calcule, a integral dupla da área da superfície com as equações paramétricas $x=au\cos v$, $y=bu\sin v$, $z=u^{2}$, $0\leq u\leq 2$, $0\leq v\leq 2\pi.$
Elimine os parâmetros para mostrar que a superfície é um paraboloide elíptico e escreva outra integral dupla que forneça sua área.
$\displaystyle \int^{2\pi}_{0}\int_{0}^{2} \sqrt{4b^2 u^4 \cos^{2}v + 4a^2 u^4 \sin^{2} v + a^2 b^2 u^2} dudv.$
$\displaystyle \int_{-2a}^{2a} \int^{b \sqrt{4 - \frac{x^2}{a^2}}}_{-b \sqrt{4 - \frac{x^2}{a^2}}} \sqrt{1 + \left(2\frac{x}{a^2}\right)^{2} + \left(2\frac{y}{b^2} \right)^{2}} dydx.$
Utilize coordenadas polares para determinar o volume do sólido dado: uma esfera de raio $a.$
$\displaystyle \frac{4\pi}{3}a^3.$
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $z=e^{x^{2}-y^{2}}$.
$\begin{aligned}[t]\frac{\partial^{2} z}{\partial x^{2}} &= 2e^{x^{2} - y^{2}}(1 + 2x^{2}),\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= 2e^{x^{2} - y^{2}}(2y^{2} - 1) \;\;\;\;\;\text{e}\\\frac{\partial^{2} z}{\partial x\partial y} &= \frac{\partial^{2} z}{\partial y\partial x}= -4xye^{x^{2} - y^{2}}.\end{aligned}$
Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$
- ${\bf F}(x,y,z) = xyz{\bf i} + xy{\bf j} + x^2yz{\bf k}$ e $S$ é formada pelo topo e pelos quatro lados (mas não pelo fundo) do cubo com vértices $(\pm 1,\pm 1,\pm 1)$, com orientação para fora.
$0.$
Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for $\rho(x,y) = 1 + 0,1\cdot x$, é mais difícil girar a pá em torno do eixo $x$ ou do eixo $y$?
Se calcularmos os momentos de inércia sobre $x$ e $y$, poderemos determinar em qual direção será mais difíciel de girar a pá do ventilador. Notemos que a região de integração é o quadrado com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem em ambas as integrais. Então, o momento de inércia sobre o eixo $x$ é dada por: $$I_{x}=\iint\limits_{D}y^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}y^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(1+0,1x)\,dx\cdot \int_{0}^{2}y^{2}\,dy=\bigg(x+0,1\frac{x^{2}}{2}\bigg)\bigg|_{0}^{2}\cdot \bigg(\frac{y^{3}}{3}\bigg)\bigg|_{0}^{2}$$ $$=\bigg[(2+0,2)-0\bigg]\cdot \bigg[\frac{8}{3}\bigg]=\frac{17,6}{3}.$$ Da mesma forma, o momente de inércia sobre o eixo $y$ é dado por: $$I_{y}=\iint\limits{D}x^{2}\rho(x,y)\,dA=\int_{0}^{2}\int_{0}^{2}x^{2}(1+0,1x)dydx$$ $$=\int_{0}^{2}(x^{2}+0,1x^{3})\,dx\cdot \int_{0}^{2}\,dy=\bigg(\frac{x^{3}}{3}+0,1\frac{x^{4}}{4}\bigg)\bigg|_{0}^{2}\cdot \bigg(y\bigg)\bigg|_{0}^{2}$$ $$=\bigg[\bigg(\frac{8}{3}+0,4\bigg)-0\bigg]\cdot \bigg[2-0\bigg]=\frac{18,4}{3}.$$ Como $I_{y}>I_{x}$ é mais difícil girarmos a pá do ventilador em torno do eixo $y.$
Mostre que
\[ \int_0^{+\infty}\int_0^{+\infty}\dfrac{1}{(1+x^2+y^2)^2}\,dxdy= \dfrac{\pi}{4}.\]
A função $f(x,y) = \begin{cases}\dfrac{x^2y}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\\\end{cases}$ é diferenciável em $(0,0)$? Justifique.
Não.
Determine uma representação paramétrica ${\bf r}:D\subset \mathbb{R}^{2}\rightarrow \mathbb{R}^{3}$ do paraboloide elíptico $z=\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}.$
Calcule a equação do plano tangente à superfície paramétrica dada no item (a) no ponto $(-a\pi,0,\pi^{2}).$
$x = u,$ $y = v,$ $z = \dfrac{u^{2}}{a^{2}}+\dfrac{v^{2}}{b^{2}},$ onde $u,v \in \mathbb{R}.$
$2\pi(x + a\pi) + a(z - \pi^{2}) = 0.$
Demonstre a identidade $\displaystyle\iint\limits_{S}\mbox{rot}\, {\bf F}\cdot dS=0$, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
Pelo Teorema do Divergente, temos
$\displaystyle\iint\limits_{ S}\mbox{rot} {\bf F}\cdot dS = \iiint\limits_{ E}\mbox{div} (\mbox{rot} {\bf F})\,dV,$
em que $E$ é o sólido que tem $S$ como fronteira. Observe que
\begin{align*}
&\mbox{div} (\mbox{rot} {\bf F}) =\\ & \frac{\partial}{\partial x}(R_y - Q_z) + \frac{\partial}{\partial y}(P_z - R_x) + \frac{\partial}{\partial z}(Q_x - P_y) \\ & R_{xy} - Q_{xz} + P_{yz} - R_{yx} + Q_{zx} - P_{zy} = 0,
\end{align*}
pois, como as derivadas de segunda ordem são contínuas, temos, pelo Teorema de Clairaut, que $P_{yz} = P_{zy}$, $Q_{zx} = Q_{xz}$ e $R_{xy} = R_{yx}$. Portanto,
$\displaystyle\iint\limits_{S}\mbox{rot}{\bf F}\cdot dS=0.$
Determine o jacobiano da transformação dada por: $x = \dfrac{u}{u+v}, \quad y = \dfrac{v}{u-v}$.
$0.$
Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial ${\bf F}$ dado e a superfície $S$.
- ${\bf F}(x,y,z) = y{\bf i} + z{\bf j} + x{\bf k}$, $S$ é o hemisfério $x^2+y^2+z^2=1$, $y \geq 0$, orientado na direção positiva do eixo $y$.
$\displaystyle\int_{C} {\bf F} \cdot d{\bf R} = \displaystyle\iint_{S} \mbox{rot} {\bf F} \cdot d{\bf S} = -\pi$.
Seja ${\bf F}=\nabla f$, onde $f(x,y)=\sin(x-2y)$. Determine curvas $C_{1}$ e $C_{2}$ que não sejam fechadas e satisfaçam a equação.
$\displaystyle\int_{C_{1}}{\bf F}\cdot d{\bf r}=0$
$\displaystyle\int_{C_{2}}{\bf F}\cdot d{\bf r}=1$
$\mathbf{r}(t) = \pi t \mathbf{i} + \pi t \mathbf{j},$ $0 \leq t \leq 1.$
$\mathbf{r}(t) = \dfrac{\pi}{2} t \mathbf{i},$ $0 \leq t \leq 1.$
Sejam $A=(3,0)$, $B=(1,1)$ e $C=(0,3)$ pontos de $\mathbb{R}^{2}$ e $C$ a trajetória que vai em linha reta de $A$ até $B$ e em seguida de $B$ até $C$. Determine o trabalho ao longo de $C$ do campo de forças ${\bf F}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$, sendo
$${\bf F}(x,y)=\bigg(-\frac{y}{x^{2}+y^{2}},\frac{x}{x^{2}+y^{2}}\bigg).$$
$\displaystyle 2\arctan(2) + \arctan\left(\frac{1}{2} \right) - \arctan\left(\frac{1}{3} \right).$
Integre $g(x,y,z)=x+y+z$ sobre a superfície do cubo cortado do primeiro octante pelos planos $x=a$, $y=a$ e $z=a.$
$9a^3.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}-3x^{2}+27y$.
Pontos de sela: $\displaystyle \left(3,\frac{3}{2}\right)$ e $\displaystyle \left(-3,-\frac{3}{2}\right).$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\iint\limits_{R} \dfrac{\sin^{2}{x}}{1+4y^{2}}\,dx dy$, onde $R$ é o retângulo $0\leq x\leq \dfrac{\pi}{2},\;0\leq y\leq \dfrac{1}{2}.$
$\displaystyle\iint\limits_{R} \dfrac{xy\sin{x}}{1+4y^{2}}\,dx dy$, onde $R$ é o retângulo $0\leq x\leq \dfrac{\pi}{2},\;0\leq y\leq 1.$
$\dfrac{\pi^{2}}{32}.$
$\dfrac{\ln(5)}{8}.$
Calcule a integral de linha $\displaystyle\int_{C}(x-y)\,dx+e^{x+y}\, dy$, onde $C$ é a fronteira do triângulo de vértices $(0,0)$, $(0,1)$ e $(1,2)$, orientada no sentido anti-horário.
$\displaystyle \frac{e^{3}}{6} - \frac{e}{2} + \frac{5}{6}.$
Determine as equações paramétricas da reta tangente à curva formada pela intersecção do paraboloide $z = x^2 + y^2$ com o elipsoide $4x^2 + y^2 + z^2 = 9$ no ponto $(-1,1,2)$.
$(x,y,z) = (-1,1,2) + \lambda (-10, -16, -12),$ $\lambda \in \mathbb{R}.$
Um campo vetorial inverso do quadrado é da forma:
$${\bf F}({\bf r})=\frac{c{\bf r}}{|{\bf r}|^{3}}$$
para alguma constante $c$, onde ${\bf r}=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$. Um exemplo de um campo inverso do quadrado é o campo gravitacional ${\bf F}=-(mMG){\bf r}/|{\bf r}|^{3}$. Determine o trabalho realizado pelo campo gravitacional quando a Terra se move do afélio (em uma distância máxima de $1,52\times 10^{8}\,km$ do Sol) ao periélio (em uma distância mínima de $1,47\times 10^{8}\,km)$. (Use os valores $m=5,97\times 10^{24}\,kg$, $M=1,99\times 10^{30}\,kg$ e $G=6,67\times 10^{-11}\,N\cdot m^{2}/kg^{2}.$)
$\approx 1,77 \times 10^{35}$ J.
- Esboce o campo vetorial $\textbf{F}(x,y) = \textbf{i} + x\textbf{j}$ e algumas linhas de escoamento. Qual é o formato que essas linhas de escoamento parecem ter?
- Se as equações paramétricas das linhas de escoamento são $x=x(t)$ e $y=y(t)$, que equações diferenciais essas funções satisfazem? Deduza que $dy/dx = x$.
- Se uma partícula está na origem no instante inicial e o campo de velocidade é dado por $\textbf{F}$, determine uma equação para a trajetória percorrida por ela.
Esboce o sólido cujo volume é dado pela integral iterada.
$\displaystyle\int_{0}^{2}\int_{0}^{2-y}\int_{0}^{4-y^{2}}\;dx dz dy$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. $x=u^{2}$, $y=v^{2}$, $z=uv$; $u=1$, $v=1.$
$x + y - 2z = 0.$
Calcule
$$\oint_{C} \dfrac{-y}{x^2+y^2} \, dx + \dfrac{x}{x^2 + y^2} \, dy,$$
em que $C$ é a curva

Podemos escrever $C$ como $C_1 \cup C_2$, em que $C_1$ e $C_2$ são as curvas dadas abaixo.
Seja $A$ um aberto simplesmente conexo que contém $C_1$ e não contém a origem. O campo $\mathbf{F}$ restrito a $A$ é conservativo, pois $A$ é aberto e simplesmente conexo, $P(x,y) = \dfrac{-y}{x^2 + y^2}$ e $Q(x,y) = \dfrac{x}{x^2 + y^2}$ possuem derivadas de primeira ordem contínuas em $A$ e $P$ e $Q$ satisfazem a relação $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$. Então,
$$\oint_{C_1}\mathbf{F} \cdot\, d\mathbf{r} = 0.$$
Não podemos proceder de maneira análoga em $C_2$, já que todo aberto $B$ que contém a curva $C_2$ e não contém a origem não será simplesmente conexo. Com isso, não conseguimos garantir que o campo $\mathbf{F}$ restrito a $B$ é conservativo (observe que, a princípio, não podemos afirmar que o campo é não conservativo).
A ideia para contornar esse problema é ``isolar" a origem com uma curva fechada $C_3$, a princípio arbitrária. Vamos escolher essa curva $C_3$ de maneira conveniente para que consigamos resolver o problema. Seja $\varepsilon > 0$ pequeno o suficiente para que a curva $C_3$ parametrizada por $r(t) = (\varepsilon \cos{t}, \varepsilon \sin{t})$, com $t$ variando de $2\pi$ a $0$, não intercepte a curva $C_2$ e esteja entre a curva $C_2$ e a origem.
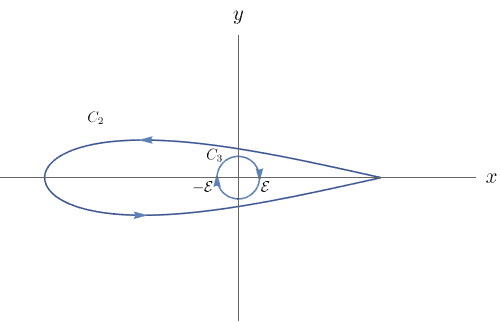
Considere $D_1 = \{(x,y) \in \mathbb{R}^2: (x,y) \mbox{ está entre } C_2 \mbox{ e } C_3 \mbox{ e } y \geq 0\}$ e $D_2 = \{(x,y) \in \mathbb{R}^2: (x,y) \mbox{ está entre } C_2 \mbox{ e } C_3 \mbox{ e } y \leq 0\}$. As curvas que delimitam $D_1$ e $D_2$ são $C_{D_1}= C_{2}^+\cup C_{a}\cup C_{3}^+\cup C_{b}$ e $C_{D_2}=C_{2}^-\cup -C_{b}\cup C_{3}^- \cup -C_{a}$, respectivamente, e estão ilustradas a seguir.
Note que
$$\oint_{C_{D_1}} \mathbf{F} \cdot d\mathbf{r} = \int_{C^+_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C_a} \mathbf{F} \cdot d\mathbf{r} + \int_{C^+_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C_b} \mathbf{F} \cdot d\mathbf{r} \qquad (\star)$$
e
$$\oint_{C_{D_2}} \mathbf{F} \cdot d\mathbf{r} = \int_{C^-_2} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_a} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_3} \mathbf{F} \cdot d\mathbf{r} + \int_{-C_b} \mathbf{F} \cdot d\mathbf{r} \qquad (\star \star).$$
Como $\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}$, temos, pelo Teorema de Green,
$$\displaystyle\oint_{C_{D_1}} \mathbf{F} \cdot d\mathbf{r} = \iint\limits_{D_1} 0 \, dA = 0$$
e
$$\displaystyle\oint_{C_{D_2}} \mathbf{F} \cdot d\mathbf{r} = \iint\limits_{D_2} 0 \, dA = 0.$$
Somando as equações ($\star$) e ($\star \star$), obtemos
$$\int_{C^+_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C^+_3} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_2} \mathbf{F} \cdot d\mathbf{r} + \int_{C^-_3} \mathbf{F} \cdot d\mathbf{r} = 0,$$
isto é,
$$\int_{C_2} \mathbf{F} \cdot d\mathbf{r} = -\int_{C_3} \mathbf{F} \cdot d\mathbf{r} = \int_{-C_3} \mathbf{F} \cdot d\mathbf{r}.$$
Assim, basta determinar $\int_{-C_3} \mathbf{F} \cdot d\mathbf{r}$. A parametrização de $-C_3$ é $r(t) = (\varepsilon \cos{t}, \varepsilon \sin{t})$, com $t$ variando de $0$ a $2\pi$. Daí,
$$\begin{array}{rcl}\displaystyle \int_{-C_3} \mathbf{F} \cdot d\mathbf{r} & = & \displaystyle \int_{0}^{2\pi} \left(\frac{-\varepsilon \sin{t}}{\varepsilon^2},\frac{\varepsilon \cos{t}}{\varepsilon^2}\right) \cdot (-\varepsilon \sin{t}, \varepsilon \cos{t}) \, dt \\& = & \displaystyle \int_{0}^{2\pi} 1 \, dt = 2\pi.\end{array}$$
Portanto,
$$\oint_{C} \mathbf{F} \cdot d\mathbf{r} = \oint_{C_1} \mathbf{F} \cdot d\mathbf{r} + \oint_{C_2} \mathbf{F} \cdot d\mathbf{r} = 0 + 2\pi = 2\pi.$$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{4}+xy+y^{2}-6x-5y$.
Ponto de mínimo: $\displaystyle \left( 1,2\right).$
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = x{\bf j}$, $S$ a superfície $\{(x,y,z) \in \mathbb{R}^3; 0\leq z\leq 1, x^2+y^2=1,$$x\geq 0, y\geq 0\}$, sendo ${\bf n}$ a normal com componente $x$ positiva.
$0$.
Calcule a integral dupla.
$\displaystyle\iint\limits_{R} x\sin(x+y)\,dA, \quad R=[0,\pi/6]\times [0,\pi/3].$
$\displaystyle\iint\limits_{R} xye^{x^{2}y}\,dA, \quad R=[0,1]\times [0,2].$
$\dfrac{\pi}{12}.$
$\dfrac{(e^{2} - 3)}{2}.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x}{\sqrt{x^2 + y^2}}$, caso exista.
Não existe.
Determine uma representação paramétrica para a superfície descrita a seguir. O plano que passa pelo ponto $(1,2,-3)$ e contém os vetores ${\bf i}+{\bf j}-{\bf k}$ e ${\bf i}-{\bf j}+{\bf k}.$
$x= 1 + u + v,$ $y = 2 + u - v,$ $z = 3 - u + v.$
Esboce a região de integração e calcule a integral $\displaystyle\int_{0}^{3}\!\!\int_{0}^{2}(4-y^{2})\,dy dx$.
$16.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\arctan\left(\dfrac{y}{x}\right)\,dA$, onde $R$ é a região do primeiro quadrante limitada pelo círculo $x^{2}+y^{2}=25.$
$\displaystyle \frac{25 \pi^2}{16}.$
Determine a massa e o centro de massa da lâmina que ocupa a região $\displaystyle D = \{(x,y) \in \mathbb{R}^2: 0 \leq x \leq 2, \ -1 \leq y \leq 1\}$ e tem função densidade $\rho(x,y) = xy^2.$
Massa: $\dfrac{4}{3};$ centro de massa: $\displaystyle \left(\frac{4}{3},0 \right).$
Determine o conjunto dos pontos de continuidade da função $f(x,y) = \dfrac{x - y}{\sqrt{1 - x^2 - y^2}}$. Justifique sua resposta.
$\left\lbrace (x,y);\; x^{2} + y^{2} < 1 \right\rbrace.$
Estime o volume do sólido que está abaixo da superfície $z = x + 2y^2$ e acima do retângulo $R = [0,2] \times [0,4]$. Use a soma de Riemann com $m = n = 2$ e escolha os pontos amostrais como os cantos inferiores direitos.
Use a Regra do Ponto Médio para dar uma estimativa da integral do item anterior.
$\approx 44.$
$\approx 88.$
Considere a integral iterada dada por $$\int_{0}^{1} \int_{x}^{\sqrt{x}}\frac{e^{y}}{y}\,dy dx.$$
Desenhe a região de integração no plano $xy.$
Calcule a integral acima.
(...)
$e - 2.$
Calcule $\nabla f(x,y)$.
$f(x,y) = x^2y$
$\displaystyle \nabla f(x,y) = (2xy,x^{2}).$
No item abaixo :
- determine o gradiente de $f$;
- calcule o gradiente no ponto $P$; e
- determine a taxa de variação de $f$ em $P$ na direção do vetor $\bf{u}$.
$f(x,y,z) = xe^{2yz}, P = (1,-3), \bf{u} = \left( \frac{2}{3}, -\frac{2}{3}, \frac{1}{3} \right)$.
- $\nabla f(x,y,z) = (e^{yz}, 2xze^{2yz}, 2xye^{2yz}).$
- $\nabla f(3,0,2) = (1,12,0).$
- $\displaystyle -\frac{22}{3}.$
Verifique que $$f(x,y) = \begin{cases} 4xy, & \quad \text{se } 0 \leq x \leq 1, \ 0 \leq y \leq 1,\\ 0, & \quad \text{caso contrário}, \end{cases}$$ é uma função densidade conjunta.
Se $X$ e $Y$ são variáveis aleatórias cuja função densidade conjunta é a função $f$ do item anterior, determine: (i) $P(X \geq \frac{1}{2})$, (ii) $P(X \geq \frac{1}{2}, Y \leq \frac{1}{2})$.
Determine os valores esperados de $X$ e $Y$.
Note que $$\iint_\limits{\mathbb{R}^2} f(x,y)\,dA = \int_{0}^{1} \int_{0}^{1} 4xy\, dydx = 1. $$
(i) $\dfrac{3}{4}.$ (ii) $\dfrac{3}{16}.$
$\dfrac{3}{16}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $0\leq x \leq 1$, $0\leq y \leq 1$ e \\ $x+y\leq z \leq x+y+1.$
$\displaystyle\iiint\limits_{ E}\sqrt{1-z^{2}}\;dx dy dz$, onde $E$ é o conjunto $0 \leq x \leq 1$, $0\leq z\leq 1$ e $0\leq y \leq z.$
$\dfrac{1}{2}.$
$\dfrac{1}{3}.$
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u-v,u^{2}+v^{2},uv)$, no ponto ${\bf r}(1,1).$
Temos que ${\bf r}(u,v)=\underbrace{(u-v)}_{x(u,v)}\,{\bf i}+\underbrace{(u^{2}+v^{2})}_{y(u,v)}\,{\bf j}+\underbrace{uv}_{z(u,v)}\,{\bf k}$
Primeiro, vamos calcular os vetores tangentes:
$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& \,{\bf i}+2u\,{\bf j}+v\,{\bf k}\end{array}$$
e
$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& -\,{\bf i}+2v\,{\bf j}+u\,{\bf k}\end{array}$$
Assim, o vetor normal ao plano tangente é:
$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i}& {\bf j}&{\bf k}\\1 & 2u & v\\-1 & 2v & u\\\end{array}\right|\\&=&(-2u^{2}-2v^{2})\,{\bf i}-(u+v)\,{\bf j}+(2u+2v)\,{\bf k}\end{array}$$
Como $u=1$ e $v=1$ temos que o vetor normal é $-4\,{\bf i}-2\,{\bf j}+4\,{\bf k}.$
Portanto, uma equação do plano tangente no ponto ${\bf r}(1,1)=(0,2,1)$ é
$$-4\cdot(x-0)-2\cdot(y-2)+4\cdot (z-1)=0$$
$$-4x-2y+4+4z-4=0$$
$$-4x-2y+4z=0 \mbox{ou} 2x+y-2z=0$$
Mostre que qualquer campo vetorial da forma
$$\mathbf{F}(x,y,z) = f(y,z)\mathbf{i} + g(x,z)\mathbf{j} + h(x,y)\mathbf{k}$$
é incompressível.
Note que $\text{div } \mathbf{F} = 0.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}x^{2}yz dS$, onde $S$ é a parte do plano $z=1+2x+3y$ que está acima do retângulo $[0,3]\times [0,2].$
$171\sqrt{14}.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}xy^{3}\,ds$, $C:\,x=4\,\sin t,\, y=4\,\cos t,\, z=3t,\, 0\leq t\leq \pi/2.$
$320.$
Seja $S$ a parte do cone $x^{2}=y^{2}+z^{2}$ que está dentro do cilindro $x^{2}+y^{2}=a^{2}$ e no primeiro octante. Determine a área da superfície $S.$
$\dfrac{\pi a^2}{4}$.
Mostre que uma função diferenciável $f$ decresce mais rapidamente em $\bf{x}$ na direção oposta à do vetor gradiente, ou seja, na direção de $-\nabla f(\bf{x})$.
Se $\bf{u}$ é um versor e $\theta$ é o ângulo entre $\nabla f$ e $\bf{u},$ então
$$
D_{\bf{u} f} = \nabla f \cdot \bf{u} = |\nabla f||\bf u| \cos(\theta) = |\nabla f|\cos(\theta).
$$
O valor mínimo de $\cos(\theta)$ é $-1$ e isto ocorre quando $\theta = \pi.$ Portanto o valor mínimo de $D_{\bf{u}} f$ é $-|\nabla f|$ e ocorre quando $\theta = \pi,$ ou seja, quando $\bf{u}$ tem a direção oposta à de $\nabla f.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=(x^{2}+y^{2}+z^{2})^{-1/2}$.
$\begin{aligned}[t]f_{x} &= -x(x^{2} + y^{2} + z^{2})^{-3/2},\;\; f_{y} = -y(x^{2} + y^{2} + z^{2})^{-3/2}\;\;\text{e}\\f_{z} &= -z(x^{2} + y^{2} + z^{2})^{-3/2}.\end{aligned}$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{a} \int_{0}^{\sqrt{a^{2}-x^{2}}}\sqrt{a^{2}-x^{2}-y^{2}}\,dy dx$, em que $a>0.$
$\displaystyle \frac{\pi a^3}{6}.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=2xz\,{\bf i}+xyz\,{\bf j}+yz\,{\bf k}$ e $S$ é a superfície da região delimitada pelos planos coordenados e os planos $x+2z=4$ e $y=2.$
Uma piscina de 8 por 12 metros está cheia de água. A profundidade é medida em intervalos de 2 metros, começando em um canto da piscina, e os valores foram registrados na tabela. Estime o volume de água na piscina.
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline & 0 & 2 & 4 & 6 & 8 & 10 & 12 \\ \hline 0 & 1 & 1,5 & 2 & 2,4 & 2,8 & 3 & 3 \\ 2 & 1 & 1,5 & 2 & 2,8 & 3 & 3,6 & 3 \\ 4 & 1 & 1,8 & 2,7 & 3 & 3,6 & 4 & 3,2 \\ 6 & 1 & 1,5 & 2 & 2,3 & 2,7 & 3 & 2,5 \\ 8 & 1 & 1 & 1 & 1 & 1,5 & 2 & 2 \\ \hline\end{array}$$
$\approx 227.$
Calcule o trabalho realizado por uma partícula andando sobre a espiral dada por $C:\,x=t\,\cos t$, $y=t\,\sin t$, com $0\leq t\leq 2\pi$, sob a ação do campo ${\bf F}(x,y)=(x,y)$, ou seja, calcule a integral $\int_{C}x\,dx+y\,dy.$
$2\pi^{2}.$
Calcule as derivadas parciais de $f(x,y,z) = \sin{(x^2 + y^2 + z^2)}$.
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= 2x \cos (x^{2} + y^{2} + z^{2}),\;\;\;\; \frac{\partial f}{\partial y} = 2y \cos (x^{2} + y^{2} + z^{2}) \;\;\;\;\;\text{e}\\\frac{\partial f}{\partial z} &= 2z \cos (x^{2} + y^{2} + z^{2}).\end{aligned}$
Calcule a integral tripla $\int\int\int\limits_{T}x^{2}dV$,
onde $T$ é o tetraedro sólido com vértices $(0,0,0)$, $(1,0,0)$, $(0,1,0)$ e $(0,0,1).$
Para resolvermos a integral tripla, vamos desenhar dois diagramas: um da região sólida $T$ (Figura 1) e o outro a sua projeção $D$ no plano $xy$ (Figura 2).
A fronteira inferior do tetraedro $T$ é o plano $z=0$ e a superior é o plano $x+y+z=1$ (ou $z=1-x-y$).
Notemos que os planos $x+y+z=1$ e $z=0$ se interceptam na reta $x+y=1$ (ou $y=1-x$) no plano $xy.$
Logo a projeção de $T$ é a região triangular da Figura 2 e temos
$$T=\{(x,y,z)|\,0\leq x \leq 1,\, 0\leq y \leq 1-x,\, 0\leq z \leq 1-x-y\}.$$
Assim,
$$\int\int\int\limits_{T}x^{2}\,dV=\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{1-x-z}x^{2}\,dz\,dy\,dx=\int_{0}^{1}\int_{0}^{1-x}x^{2}z\bigg|_{0}^{1-x-y}\,dy\,dx$$
$$=\int_{0}^{1}\int_{0}^{1-x}x^{2}(1-x-y)\,dy\,dx=\int_{0}^{1}\int_{0}^{1-x}(x^{2}-x^{3}-x^{2}y)\,dy\,dx$$
$$=\int_{0}^{1}\bigg(x^{2}y-x^{3}y-x^{2}\frac{y^{2}}{2}\bigg)\bigg|_{0}^{1-x}\,dx=\int_{0}^{1}\bigg(x^{2}(1-x)-x^{3}(1-x)-\frac{x^{2}}{2}(1-x)^{2}\bigg)dx$$
$$=\int_{0}^{1}\bigg(\frac{x^{2}}{2}-x^{3}+\frac{x^{4}}{2}\bigg)\,dx =\bigg[\frac{1}{2}\cdot\frac{x^{3}}{3}-\frac{x^{4}}{4}+\frac{1}{2}\cdot\frac{x^{5}}{5}\bigg]\bigg|_{0}^{1}=\frac{1}{60}.$$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da região limitada acima pelo paraboloide $z=5-x^{2}-y^{2}$ e abaixo pelo paraboloide $z=4x^{2}+4y^{2}.$
$\dfrac{5\pi}{2}.$
Inverta a ordem de integração.
$\displaystyle\int_{0}^{1}\bigg[\int_{\sqrt{x-x^{2}}}^{\sqrt{2x}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{3a}\bigg[\int_{\frac{\sqrt{3}}{3}x}^{\sqrt{4ax-x^{2}}}f(x,y)\,dy\bigg]dx, \; a> 0.$
$\displaystyle\int_{0}^{\pi}\bigg[\int_{0}^{\sin{x}}f(x,y)\,dy\bigg]dx$
$\ \\ \begin{array}{ll} \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{y^{2}}{2}}^{\frac{1}{2} - \sqrt{\frac{1}{4} - y^{2}}}f(x,y)\,dx\bigg]dy &+ \displaystyle\int_{0}^{\frac{1}{2}}\bigg[\int_{\frac{1}{2}+ \sqrt{\frac{1}{4} - y^{2}}}^{1}f(x,y)\,dx\bigg]dy\\ &+ \displaystyle\int_{\frac{1}{2}}^{\sqrt{2}}\bigg[\int_{\frac{y^{2}}{2}}^{1}f(x,y)\,dx\bigg]dy \end{array} $
$\displaystyle\int_{0}^{\sqrt{3}a} \bigg[\int_{2a + \sqrt{4a^2 - y^{2}}}^{\sqrt{3} y}f(x,y)\,dx\bigg]dy.$
$\displaystyle\int_{0}^{1}\bigg[\int_{\arcsin(y)}^{\pi-\arcsin(y)}f(x,y)\,dx\bigg]dy$
Dados ${\bf F}(x,y,z)=y^{2}\,\cos z\,{\bf i}+2xy\,\cos z\,{\bf j}-xy^{2}\,\sin z\,{\bf k}$, $C: {\bf r}(t)=t^{2}\,{\bf i}+\sin t\,{\bf j}+t\,{\bf k}$, $0\leq t\leq \pi.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y,z) = xy^{2} \cos(z);$
$0.$
Utilize a integral dupla para determinar a área da região: um laço da rosácea $r=\cos(3\theta).$
$\displaystyle \frac{\pi}{12}.$
Determine os pontos da superfície $y^{2}=9+xz$ que estão mais próximos da origem.
$(0,3,0)$ e $(0,-3,0).$
Utilize a Equação
$$ \dfrac{dy}{dx}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial y}}=-\dfrac{F_x}{F_y}$$
para determinar $\mathrm{d}y/\mathrm{d}x$.
$\cos(x-y)=xe^{y}$
$\displaystyle \frac{dy}{dx} = \frac{\sin(x - y) + e^{y} }{\sin(x - y) -x e^{y}} .$
Determine o jacobiano da transformação dada por: $x = uv, \quad y = \dfrac{u}{v}$.
$-\dfrac{2u}{v}.$
Determine a derivada parcial indicada. $u=e^{r\theta}\sin{\theta}$; $\dfrac{\partial ^{3}u}{\partial r^{2}\partial \theta}$.
$\dfrac{\partial ^{3}u}{\partial r^{2}\partial \theta} = \theta e^{r\theta} (2\sin \theta + \theta \cos \theta + r\theta \sin \theta)$.
Para qual valor de $c$ o volume do elipsóide $x^{2}+(y/2)^{2}+(z/c)^{2}=1$ é igual a $8\pi$?
$3.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Prove que $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d.$
Note que $$ \int_{c}^{d} \left[\int_{a}^{b}f(x)g(y)\,dx\right] \;dy = \int_{c}^{d} \left[\int_{a}^{b}f(x)\,dx\right]g(y) \;dy = \left(\int_{a}^{b}f(x)\,dx\right) \int_{c}^{d} g(y) \;dy.$$
Use a Lei de Gauss para achar a carga contida no hemisfério sólido $x^{2}+y^{2}+z^{2} \leq a^{2}$, $z\geq 0$, se o campo elétrico for ${\bf E}(x,y,z)=x{\bf i}+y{\bf j}+2z{\bf k}$.
$\dfrac{8\pi a^3 \epsilon_{0}}{3}$.
Calcule $\int_{C}(x+y+z)\,dx+(x-2y+3z)\,dy+(2x+y-z)\,dz$, onde $C$ é a curva de $(0,0,0)$ a $(2,3,4)$ se
$C$ consiste em três segmentos de reta, o primeiro paralelo ao eixo $x$, o segundo paralelo ao eixo $y$ e o terceiro paralelo ao eixo $z$.
$C$ consite em três segmentos de reta, o primeiro paralelo ao eixo $z$, o segundo ao eixo $x$ e o terceiro paralelo ao eixo $y.$
$C$ é um segmento retilíneo.
$19.$
$35.$
$27.$
Calcule a integral em coordenadas esféricas. $\displaystyle\int_{0}^{\pi}\int_{0}^{\pi}\int_{0}^{2\,\sin{\phi}}\rho^{2}\sin{\phi}\,d\rho d\phi d\theta$.
$\pi^2.$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=(2x-x^{2})(2y-y^{2})$, $D$ é a região do plano $xy$ dada por $0\leq y\leq 2(2x-x^{2})$.
Valor máximo: $1;$ valor mínimo: $0.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}\sqrt{1+x^{2}+y^{2}}dS$, onde $S$ é o helicóide com equação vetorial ${\bf r}(u,v)=u\cos v{\bf i}+u\sin v{\bf j}+v{\bf k}$, $0 \leq u \leq 1$, $0 \leq v \leq \pi.$
$\dfrac{4\pi}{3}.$
No cálculo de uma integral dupla sobre uma região $D$, obtivemos uma soma de integrais iteradas como a que segue:
$$\int\!\!\!\!\int\limits_{\!\!\!\!\!\! D} \! f(x,y)\,dA=\int_{0}^{1}\!\!\int_{0}^{2y} \! f(x,y)\,dx dy+\int_{1}^{3}\!\!\int_{0}^{3-y} \! f(x,y)\,dx dy.$$
Esboce a região $D$ e expresse a integral dupla como uma integral iterada com ordem de integração contrária.
$\displaystyle \int_{0}^{2}\!\!\int_{\frac{x}{2}}^{3-x} \! f(x,y)\,dx dy.$
Determine se ${\bf F}(x,y)=y\,{\bf i}+x\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y) = xy + K.$
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = (x^2 + y^2 + 1)^{z^2}$
$\displaystyle \nabla f(x,y,z) = (x^{2} + y^{2} + 1)^{z^{2}-1}\left(2xz^{2},2yz^{2},2z(x^{2} + y^{2} + 1)\ln(x^{2} + y^{2} + 1)\right).$
Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$
- ${\bf F}=x{\bf i}+y{\bf j}+z{\bf k}$; $S$ é o hemisfério superior de $x^{2}+y^{2}+z^{2}=a^{2}.$
$2\pi a^3.$
Determine a derivada direcional da função no ponto dado e na direção do vetor $\bf{v}$.
$g(p,q) = p^4 - p^2q^3, (2,1), \bf{v}= \left(-1,2\right).$
$\displaystyle -\frac{4\sqrt{10}}{5}.$
Determine se ${\bf F}(x,y)=(ye^{x}+\sin y)\,{\bf i}+(e^{x}+x\,\cos y)\,{\bf j}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Primeiramente, temos que o domínio de ${\bf F}$ é todo o $\mathbb{R}^{2}$, o qual é uma região aberta e simplesmente conexa. Sendo $P(x,y)=ye^{x}+\sin y$ e $Q(x,y)=e^{x}+x\,\cos y$, temos que $P$ e $Q$ possuem derivadas de primeira ordem contínuas. Também temos que
$$\frac{\partial P}{\partial y}=e^{x}+\cos y \,\,\, \text{ e } \,\,\, \frac{\partial Q}{\partial x}=e^{x}+\cos y,$$
ou seja,
$$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}.$$
Assim, das condições acima verificadas, temos que ${\bf F}$ é um campo conservativo. Agora, vamos determinar $f$ tal que $\nabla f={\bf F}.$ Isto é, devemos encontrar $f$ tal que
$$f_{x}(x,y)=P(x,y) \text{ e } f_{y}(x,y)=Q(x,y).$$
Como $f_{x}(x,y)=P(x,y)$ temos que
$$f_{x}(x,y)=ye^{x}+\sin y\Rightarrow f(x,y)=ye^{x}+x\,\sin y+g(y)$$
Assim obtemos que
$$f_{y}(x,y)=e^{x}+x\cos y+g'(y)$$
Mas, $f_{y}(x,y)=Q(x,y)$ logo obtemos que
$$e^{x}+x\cos y+g'(y)=e^{x}+x\,\cos y\Rightarrow g'(y)=0\Rightarrow g(y)=C.$$
Portanto,
$$f(x,y)=ye^{x}+x\sin y+C \text{ e } \nabla f={\bf F}.$$
Use a Regra da Cadeia para determinar $\mathrm{d}z/\mathrm{d} t$ ou $\mathrm{d}w/ \mathrm{d}t.$
$w=xe^{y/z}$, $x=t^{2}$, $y=1-t$, $z=1+2t$.
$\displaystyle \frac{dw}{dt} = e^{\frac{y}{z}} \left(2t - \frac{x}{z} - \frac{2xy}{z^{2}} \right).$
Utilize coordenadas polares para combinar a soma $$\int_{\frac{1}{\sqrt{2}}}^{1} \int_{\sqrt{1-x^{2}}}^{x}xy\,dy dx+\int_{1}^{\sqrt{2}} \int_{0}^{x}xy\,dy dx+\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx$$ em uma única integral dupla. Em seguida, calcule essa integral dupla.
Queremos combinar a soma, abaixo, de integrais em uma única: $$\underbrace{\int_\frac{1}{\sqrt{2}}^{1} \int_\sqrt{1-x^{2}}^{x}xy\,dy dx}_{1}+\underbrace{\int_{1}^{\sqrt{2}}\int_{0}^{x}xy\,dy dx}_{2}+ \underbrace{\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx}_{3}$$ Na figura abaixo, temos que a região da esquerda corresponde à região de integração da integral $(1)$, a região do meio corresponde à região de integração da integral $(2)$ e a região da esquerda corresponde à região de integração da integral $(3)$.
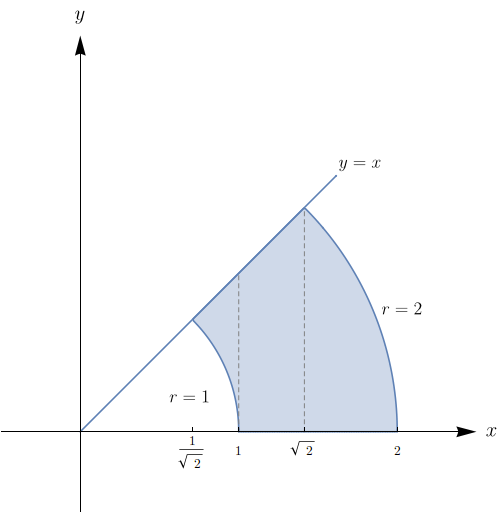
Notemos que com a junção das três regiões, podemos olhar como uma única região. Assim, em coordenadas polares teremos que $0\leq \theta \leq \frac{\pi}{4}$ e $1\leq r \leq 2.$ Então: $$\int_{\frac{1}{\sqrt{2}}}^{1} \int_{\sqrt{1-x^{2}}}^{x}xy\,dy dx+\int_{1}^{\sqrt{2}} \int_{0}^{x}xy\,dy dx+\int_{\sqrt{2}}^{2} \int_{0}^{\sqrt{4-x^{2}}}xy\,dy dx$$ $$=\int_{0}^{\frac{\pi}{4}}\int_{1}^{2}(r\,\cos \theta)\cdot (r\,\sin \theta)\,r\,dr\,d\theta=\int_{0}^{\frac{\pi}{4}}\int_{1}^{2}r^{3}\cos\theta \sin \theta\,dr\,d\theta$$ $$=\underbrace{\int_{0}^{\frac{\pi}{4}}\cos \theta\, \sin \theta\,d \theta}_{\substack{ u=\sin \theta\\ du=\cos\, d\theta}}\cdot \int_{1}^{2}r^{3}\,dr =\int_{0}^{\frac{\sqrt{2}}{2}}u\,du\cdot \frac{r^{4}}{4}\bigg|_{1}^{2}$$ $$=\frac{u^{2}}{2}\bigg|_{0}^{\frac{\sqrt{2}}{2}}\cdot \bigg(\frac{16}{4}-\frac{1}{4}\bigg)=\frac{1}{4}\cdot \frac{15}{4}=\frac{15}{16}.$$
Utilize a transformação dada para calcular a integral. $\displaystyle \iint\limits_{R}(x - 3y) \, dA$, em que $R$ é a região triangular de vértices $(0,0)$, $(2,1)$ e $(1,2)$; $x = 2u + v$, $y = u + 2v$.
$-3.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}z dS$, onde $S$ é a superfície $x=y+2z^{2}$, $0 \leq y\leq 1$, $0 \leq z \leq 1.$
$\dfrac{13\sqrt{2}}{12}.$
Sejam \(\alpha\) e \(\beta\) dois ângulos que satisfazem \(\displaystyle 0<\beta-\alpha\leq 2\pi\) e suponha que \( r= f(\theta)\) seja uma curva polar lisa com \(f(\theta)>0\) no intervalo \([\alpha,\beta]\). Use a fórmula \[ A = \dfrac{1}{2}\int_C-y\,dx+x\,dy \] para encontrar a área da região \(R\) englobada pela curva \(r=f(\theta)\) e os raios \(\theta=\alpha\) e \(\theta=\beta\).
Determine a área da superfície dada pela parte do paraboloide hiperbólico $z=y^{2}-x^{2}$ que está entre os cilindros $x^{2}+y^{2}=1$ e $x^{2}+y^{2}=4.$
Temos que $z=f(x,y)=y^{2}-x^{2}$ com $1\leq x^{2}+y^{2}\leq 4$. Então,
$$A(S)=\iint\limits_{ D}\sqrt{1+\bigg(\frac{\partial z}{\partial x}\bigg)^{2}+\bigg(\frac{\partial z}{\partial y}\bigg)^{2}}\,dA$$
$$=\iint\limits_{ D}\sqrt{1+(2y)^{2}+(-2x)^{2}}\,dA=\iint\limits_{ D}\sqrt{1+4y^{2}+4x^{2}}\,dA.$$
Usando coordenadas polares temos que
$$x=r\,\cos \theta,\,\,\,\,\, y=r\,\sin \theta \Rightarrow 0\leq \theta\leq \frac{\pi}{2}\,\, \mbox{e}\,\, 1\leq r \leq 2.$$
Assim,
$$A(S)=\int_{0}^{2\pi}\int_{1}^{2}\sqrt{1+4r^{2}}\,r\,dr\,d\theta=\int_{0}^{2\pi}d\theta \cdot \underbrace{\int_{1}^{2}\sqrt{1+4r^{2}}r\,dr}_{\substack{u=1+4r^{2}\\ du=8r\,dr}}$$
$$=\theta\bigg|_{0}^{2\pi}\cdot \int_{5}^{17}u^{1/2}\cdot r\cdot \frac{du}{8r}=2\pi\cdot \frac{1}{8}\int_{5}^{17}u^{1/2}\,du=\frac{\pi}{4}\cdot \frac{2}{3}u^{3/2}\bigg|_{5}^{17}$$
$$=\frac{\pi}{6}\cdot(17^{3/2}-5^{3/2}).$$
Use o Teorema de Green na forma $\oint_{C} \mathbf{F} \cdot \mathbf{n} \, ds = \iint\limits_{ D} \text{div }{\mathbf{F}(x,y)} \, dA$ para demonstrar a primeira identidade de Green:
$$\iint\limits_{ D} f\nabla^2g \, dA = \oint_{C}f(\nabla{g}) \cdot \mathbf{n} \, ds - \iint\limits_{ D}\nabla{f} \cdot \nabla{g} \, dA,$$
em que $D$ e $C$ satisfazem as hipóteses do Teorema de Green e as derivadas parciais apropriadas de $f$ e $g$ existem e são contínuas. (A quantidade $ \nabla{g} \cdot \mathbf{n} = D_{\mathbf{n}}g$ aparece na integral de linha. Essa é a derivada direcional na direção do vetor normal $\mathbf{n}$ e é chamada derivada normal de $g$.)
Note que $\oint_{C} f(\nabla{g}) \cdot \mathbf{n} \, ds = \iint\limits_{ D} \text{div }(f \nabla g) \, dA = \iint\limits_{ D} f\text{div }(\nabla g) + \nabla{f} \cdot \nabla{g} \, dA.$
Seja ${\bf F}:\mathbb{R}^{2} \to \mathbb{R}^{2}$ um campo vetorial contínuo tal que, para todo $(x,y)$, ${\bf F}(x,y)$ é paralelo ao vetor $x\,{\bf i}+y\,{\bf j}$. Calcule $\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf r}:[a,b]\to \mathbb{R}^{2}$ é uma curva de classe $C^{1}$, cuja imagem está contida na circunferência de centro na origem e raio $r>0$. Interprete geometricamente.
$0.$
Prove que se $\mathbf{F} \cdot \mathbf{n}$ for constante sobre $Im\,\mathbf{r}$, então o fluxo de $\mathbf{F}$ sobre $\mathbf{r}$ é o produto de $\mathbf{F} \cdot \mathbf{n}$ pelo comprimento de $\mathbf{r}$, em que $\mathbf{n}$ é normal a $\mathbf{r}$.
Direto da definição do fluxo de $\mathbf{F}$ através de $\bf{r}$ na direção $\bf{n}.$
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} \dfrac{y - 2x}{3y + 2x} \, dA$, em que $R$ é a paralelogramo de vértices $(1,2)$, $(2,4)$, $(5,2)$ e $(4,0)$.
$-4\ln(2).$
Determine se o campo vetorial $\mathbf{F}(x,y,z) = y^2z^3\mathbf{i} + 2xyz^3\mathbf{j} + 3xy^2z^2\mathbf{k}$ é conservativo ou não. Se for conservativo, determine uma função $f$ tal que $\mathbf{F} = \nabla{f}$.
$\mathbf{F}$ é conservativo. $f(x,y,z) = xy^2 z^3.$
Calcule $\nabla f(x,y)$.
$f(x,y) = \dfrac{x}{y}$
$\displaystyle \nabla f(x,y) = \left(\frac{1}{y}, -\frac{x}{y^{2}} \right).$
Determine o campo vetorial gradiente $\nabla f$ de $f(x,y) = x^2-y$ e o esboce.
Integre $g(x,y,z)=x+y+z$ sobre a porção do plano $2x+2y+z=2$ que está no primeiro octante.
$2.$
Se $g(x,y) = x^2 + y^2 - 4x$, encontre o vetor gradiente $\nabla g(1,2)$ e use-o para encontrar a reta tangente à curva de nível $g(x,y) = 1$ no ponto $(1,2)$. Esboce a curva de nível, a reta tangente e o vetor gradiente.
$\nabla g(1,2) = (1,2) = (-2,4);$ reta tangente à curva de nível $g(x,y) = 1$ em $(1,2)$: $-x + 2y = 3.$
Determine o volume do sólido limitado pelo cilindro $x^2 + y^2 = 4$ e pelos planos $z = 0$ e $y + z = 3$.
$12\pi.$
Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ sendo $g(x,y,z)=x^{2}+y^{2}+z^{2}$ e $S$ a parte do plano $z=y+4$ interior ao cilindro $x^{2}+y^{2}=4.$
$76\pi \sqrt{2}.$
Existem pontos no hiperboloide $x^2 - y^2 - z^2 = 1$ nos quais o plano tangente é paralelo ao plano $z = x + y$?
Não.
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da menor cunha esférica cortada de uma esfera de raio $a$ por dois planos que se interceptam ao longo de um diâmetro com um ângulo de $\pi/6.$
$\dfrac{\pi a^3}{9}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+y^{2})^{3/2}\,dA$, onde $R$ é limitado pelo círculo $x^{2}+y^{2}=4.$
$\displaystyle \frac{64\pi}{5}.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 + 2y^2$ e $3x + y = 1.$
Ponto de mínimo: $\displaystyle \left( \frac{6}{19}, \frac{1}{19} \right)$.
Determine as derivadas parciais de $z=x^{2}\ln(1+x^{2}+y^{2})$.
$\displaystyle \frac{\partial z}{\partial x} = 2x\ln(1+ x^{2} + y^{2}) + \frac{2x^{3}}{1 + x^{2} + y^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{2}y}{1 + x^{2} + y^{2}}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=\frac{1}{x^{2}}+\frac{1}{y}+xy$, $x>0$ e $y>0$.
Ponto de mínimo: $\displaystyle \left( 2^{2/5}, 2^{-1/5} \right).$
Encontre os valores de $\partial z/ \partial x$ e $\partial z/\partial y$ no ponto indicado.
$z^{3}-xy+yz+y^{3}-2=0$, $(1,1,1).$
$\displaystyle \frac{\partial z}{\partial x}(1,1,1) = \frac{1}{4}$ e $\displaystyle \frac{\partial z}{\partial x}(1,1,1) = -\frac{3}{4}.$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^1\int_0^1 (2-x-y)\, dydx\)
\(\displaystyle \int_{-2}^2\int_{-2}^2(x^2+y^2)\,dxdy\)
Seja $z=f(u+2v,u^{2}-v)$. Expresse $\partial z/\partial u$ e $\partial z/\partial v$ em termos das
derivadas parciais de $f$.
$\displaystyle \frac{\partial z}{\partial u}(u,v) = \frac{\partial f}{\partial x}(u + 2v,u^{2} - v) + 2u \frac{\partial f}{\partial y}(u + 2v,u^{2} - v)$ e\\ $\displaystyle \frac{\partial z}{\partial v}(u,v) = 2 \frac{\partial f}{\partial x}(u + 2v,u^{2} - v) - \frac{\partial f}{\partial y}(u + 2v,u^{2} - v).$
Encontre a constante $a$ tal que $$\int_{0}^{1}\int_{0}^{4-a-x^{2}}\int_{a}^{4-x^{2}-y}\;dz dy dx=\frac{4}{15}.$$
$\dfrac{13}{3}$ ou $3.$
Calcule a integral de linha
$$\int_{C}{\bf F}\cdot d{\bf r}=\int_{C}{\bf F}\cdot r'(t)\,dt$$
onde ${\bf F}=(2xyz^{3},x^{2}z^{3},3x^{2}yz^{2})$ e $C$ é a curva dada por $r(t)=(\sin^{6}t,1-\cos t, e^{t(t-\pi/2)}$, $0\leq t\leq \pi/2.$ (Dica: verifique se ${\bf F}$ é conservativo.)
$1.$
Calcule as integrais iteradas.
$\displaystyle\int_{0}^{\pi/2}\int_{0}^{\cos{\theta}}e^{\sin{\theta}}\,dr d\theta$
$\displaystyle\int_{0}^{1}\int_{0}^{v}\sqrt{1-v^{2}}\,du dv$
$e - 1.$
$\dfrac{1}{3}.$
Usando coordenadas esféricas, determine o volume da região cortada do cilindro sólido $x^{2}+y^{2}\leq 1$ pela esfera $x^{2}+y^{2}+z^{2}=4.$
$\dfrac{4\pi(8 - 3\sqrt{3})}{3}.$
Esboce o gráfico da função $f(x,y)=y^{2}+1$.
$z = y^{2} + 1$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}yz dS$, onde $S$ é a parte do plano $x+y+z=1$ que está no primeiro octante.
$\dfrac{\sqrt{3}}{24}.$
Determine o ponto da parábola $y = x^2$ mais próximo de $(14,1)$.
$(2,4).$
Use coordenadas esféricas para encontrar o volume do sólido: contido no interior do cone \(\phi=\pi/4\), entre as esferas \(\rho=1\) e \(\rho=2\).
Seja $f(x,y)=3x+2y.$ Calcule:
$f(1,-1)$;
$f(a,x)$;
$\dfrac{f(x+h,y)-f(x,y)}{h}$;
$\dfrac{f(x,y+k)-f(x,y)}{k}$.
$1.$
$3a + 2x.$
$3.$
$2.$
Mostre que $(0,0)$ é um ponto crítico de $f(x,y)=x^{2}+kxy+y^{2}$, não importando o valor da constante $k$.
Note que $f_{x} (0,0) = f_{y} (0,0) = 0.$
Utilize a integral dupla para determinar a área da região: no interior do círculo $x^{2}+(y-1)^{2}=1$ e fora do círculo $x^{2}+y^{2}=1.$
$\displaystyle \frac{\pi}{3} + \frac{\sqrt{3}}{2}.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S} D_{n}f\,dS=\displaystyle\iiint\limits_{E}\nabla^{2}f\,dV.$
Lembre que $D_{n} f = \nabla f \cdot {\bf b}$ e $\mbox{div} (\nabla f) = \nabla^{2} f.$
Calcule a integral dupla.
$\displaystyle\iint\limits_{D}(2x-y)\,dA, \quad D$ limitada pelo círculo de centro na origem e raio 2.
$\displaystyle\iint\limits_{D}\dfrac{x}{y}\,dA, \quad D$ região no primeiro quadrante limitada pelas retas $y=x$, $y=2x$, $x=1$ e $x=2.$
$\displaystyle\iint\limits_{D}\dfrac{1}{xy}\,dA, \quad D$ o quadrado $1\leq x\leq 2$, \;$1\leq y\leq 2.$
$\displaystyle\iint\limits_{D}(x-\sqrt{y})\,dA, \quad D$ região triangular cortado do primeiro quadrante do plano $xy$ pela reta $x+y=1.$
$0.$
$\dfrac{3\ln(2)}{2}.$
$(\ln(2))^{2}.$
$-\dfrac{1}{10}.$
Determine o volume do sólido descrito abaixo.
Limitado pelo cilindro $x^{2}+y^{2}=1$ e pelos planos $y=z$, $x=0$ e $z=0$, no primeiro octante.
Cuja base é a região no plano $xy$ que é limitada pela parábola $y=4-x^{2}$ e pela reta $y=3x$, enquanto o topo do sólido é limitado pelo plano $z=x+4.$
No primeiro octante limitado pelos planos coordenados, pelo cilindro $x^{2}+y^{2}=4$ e pelo plano $z+y=3.$
$\dfrac{1}{3}.$
$\dfrac{625}{12}.$
$\dfrac{9\pi - 8}{3}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=x^{2}\,{\bf i}+y^{2}\,{\bf j}+z^{2}\,{\bf k}$, ${\bf r}(t)=(2\cos t,3\sin t,t)$, $0\leq t\leq 2\pi.$
$\dfrac{8\pi^{3}}{3}.$
Verifique que a função $f(x,y) = \ln{(1 + x^2 + y^2)}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Esboce o gráfico da função $f(x,y)=\sin(\sqrt{x^{2}+y^{2}})$ .Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$

Mostre que se \(f\) é diferenciável e \(z=xf(x/y)\), então todos os pontos planos tangentes ao gráfico dessa equação passam pela origem.
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?
$f(x,y) = x^2 + xy + y^2$ em $(1,1)$.
Cresce: $(3,3)$; descresce: $(-3,-3).$
Determine o volume do sólido que está abaixo do paraboloide elíptico $x^{2}/4+y^{2}/9+z=1$ e acima do retângulo $R=[-1,1]\times [-2,2].$
$\dfrac{166}{27}.$
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf i} + x^2{\bf j} + z{\bf k}$, $S$ a superfície $x^2+y^2 = 1$, $0\leq z \leq 1$ e $y\geq 0$, sendo ${\bf n}$ a normal com componente $y\geq 0$.
$0$.
Mostre que se \(R\) for a região triangular de vértices \((0,0)\), \((1,0)\) e \((0,1)\), então \[\iint\limits_R f(x+y)\,dA = \int_0^1 uf(u)\,du.\]
Use o resultado anterior para calcular a integral \[ \iint\limits_R e^{x+y}\,dA. \]
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx-y\,dy$, $C$ é o segmento de extremidades $(1,1)$ e $(2,3)$, percorrido no sentido de $(1,1)$ para $(2,3).$
$\displaystyle -\frac{5}{2}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{0}^{\sqrt{x-x^{2}}}x\,dy dx$
$\displaystyle \frac{\pi}{16}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}+y^{2}+x^{2}y+4$.
Pontos de mínimo: $(1,1)$ e $(-1,-1);$ ponto de sela: $(0,0).$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{3}-12xy+8y^{3}$.
Sendo $f(x,y)=x^{3}-12xy+8y^{3}$, vamos inicialmente localizar seus pontos críticos:
$$f_{x}(x,y)=3x^{2}-12y \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; f_{y}(x,y)=-12x+24y^{2}.$$
Igualando essas derivadas parciais a zero, obtemos as equações
$$x^{2}-4y=0 \;\;\;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;\;\; 2y^{2}-x=0.$$
Para resolvê-las, substituímos $x=2y^{2}$ da segunda equação na primeira. Isso resulta em
$$0=y^{4}-y=y(y^{3}-1)$$
e existem duas raízes reais $y=0$ e $y=1.$ Os dois pontos críticos de $f$ são $(0,0)$ e $(2,1).$\\
Agora vamos calcular as segundas derivadas parciais e $D(x,y)$:
$$f_{xx}(x,y)=6x\,\,\,\, f_{xy}(x,y)=-12 \;\;\;\; f_{yy}(x,y)=48y$$
$$\begin{split}D(x,y)&=f_{xx}(x,y)\cdot f_{yy}(x,y)-(f_{xy}(x,y))^{2}\\&=(6x)\cdot (48y)-(-12)^{2}=288xy-144.\end{split}$$
Como $D(0,0)=-144<0$, segue do Teste da Derivada Segunda que $(0,0)$ é um ponto de sela, ou seja, $f$ não tem nem máximo local nem mínimo local em $(0,0).$ Como $D(2,1)=432>0$ e $f_{xx}(2,1)=12>0$, vemos do Teste da Derivada Segunda que $f(2,1)=-8$ é um mínimo local.
Existe um campo vetorial $\bf{G}$ em $\mathbb{R}^3$ tal que $\text{rot }{\bf{G}} = (x\sin{y},\cos{y},z-xy)$? Justifique.
Suponha que existe um campo vetorial $\bf G$ tal que $\text{rot } G= (x\,\sin y, \cos y,z-xy)$. Vamos calcular $\text{div } \text{rot } {\bf G}.$
Temos que
$$\text{div } \text{rot } {\bf G}=\frac{\partial (x\,\sin y) }{\partial x}+\frac{\partial (\cos{y})}{\partial y}+\frac{\partial (z-xy)}{\partial z}$$
$$=\sin y- \sin y +1=1.$$
Sabemos que se ${\bf F}=P\,{\bf i}+Q\,{\bf j}+R\,{\bf k}$ é um campo vetorial sobre $\mathbb{R}^{3}$ e $P$, $Q$ e $R$ têm derivadas parciais de segunda ordem contínuas, então $\text{div } \text{rot } {\bf F}=0.$
Como $\text{div } \text{rot } {\bf G}\neq 0$, pela contrapositiva do resultado acima, temos que ${\bf G}$ não é um campo vetorial do $\mathbb{R}^{3}.$
Determine o trabalho $W=\int_{C}{\bf F}\cdot d{\bf r}$ realizado pelo campo de força ${\bf F}(x,y)=x\,{\bf i}+(x^{3}+3xy^{2})\,{\bf j}$ em uma partícula que inicialmente está no ponto $(-2,0)$, se move ao longo do eixo $x$ para $(2,0)$ e ao longo da semicircunferência $y=\sqrt{4-x^{2}}$ até o ponto inicial.
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,1-u-v)$, $u\geq 0$, $v\geq 0$ e $u+v\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\dfrac{\sqrt{3}}{2}.$
Três alelos (versões alternativas de um gene) $A$, $B$ e $O$ determinam os quatro tipos de sangue: $A$ ($AA$ ou $AO$), $B$ ($BB$ ou $BO$), $O$ ($OO$) e $AB$. A Lei de Hardy-Weinberg afirma que a proporção de indivíduos em uma população que carregam dois alelos diferentes é $P=2pq+2pr+2rq$, onde $p$, $q$ e $r$ são as proporções de $A$, $B$ e $O$ na população. Use o fato de que $p+q+r=1$ para mostrar que $P$ é no máximo $\dfrac{2}{3}$.
É preciso maximizar de $P = 2q - 2q^{2} + 2r - 2r^{2} -2rq$ no conjunto delimitado pelas retas $q = 0,$ $r = 0$ e $q + r = 1.$ O ponto de máximo ocorre em $\displaystyle \left( \frac{1}{3}, \frac{1}{3} \right),$ no qual o valor de $P$ é justamente $\dfrac{2}{3}.$
Calcule o centro de massa da região $D$ dada.
$D$ é o conjunto de todos $(x,y)$ tais que $x^3 \leq y \leq x$ e a densidade é constante e igual a 1.
$D$ é o conjunto de todos $(x,y)$ tais que $x \leq y \leq x + 1$, $0 \leq x \leq 1$, e a densidade é o produto das coordenadas do ponto.
$D$ é o conjunto de todos $(x,y)$ tais que $1 \leq x^2 + y^2 \leq 4$, $y \geq 0$, e a densidade é proporcional à distância do ponto à origem.
$\displaystyle \left(0,0\right).$
$\displaystyle \left(\frac{5}{7},\frac{9}{7}\right).$
$\displaystyle \left(0, \frac{45}{14\pi} \right).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\sqrt{x^{2}+y^{2}}\,dA$, onde $R$ é limitado pelo círculo $y=\sqrt{2x-x^{2}}$ e pela reta $y=x.$
$\displaystyle \frac{8}{9}(2 - \frac{5}{4}\sqrt{2}).$
Utilizando o Teorema de Stokes, transforme a integral $\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf i}-x^2{\bf j}+5{\bf k}$, $S$ a superfície parametrizada por ${\bf R}(u,v) = (u,v,1-u^2)$, $u \geq 0$, $v \geq 0$, $u+v\leq 1$, sendo ${\bf n}$ a normal apontando para cima.
$-\dfrac{5}{6}.$
Determine o volume máximo da maior caixa retangular no primeiro octante com três faces nos planos coordenados e com um vértice no plano $x+2y+3z=6.$
Vamos maximizar a função:
$$f(x,y)=x\cdot y\cdot \bigg(\dfrac{6-x-2y}{3}\bigg)=\dfrac{6xy-x^{2}y-2xy^{2}}{3},$$
então o volume máximo é $V=x \cdot y \cdot z.$
Para encontrar os pontos críticos devemos encontrar as derivadas parciais $f_{x}$ e $f_{y}.$ Assim,
$$f_{x}(x,y)=\frac{6y-2xy-2y^{2}}{3}\;\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\;\; f_{y}(x,y)=\frac{6x-x^{2}-4xy}{3}.$$
Fazendo $f_{x}=0$ e $f_{y}=0$, obtemos o seguinte sistema de equações
$$\left \{\begin{array}{cc}6y-2xy-2y^{2}=0\\6x-x^{2}-4xy=0\\\end{array}\right.$$
Da primeira equação obtemos
$$y=0 \;\;\;\;\;\;\;\; \mbox{ou}\;\;\;\;\;\;\;\; y=3-x.$$
Como, $y=0$ não satifaz as condicões, vamos analisar o caso onde $y=3-x.$ Substituindo esse valor na segunda equação obtemos
$$x=0\;\;\;\;\;\;\;\; \mbox{ou}\;\;\;\;\;\;\;\; 3x^{2}-6x=0.$$
Novamente, como $x=0$ não satisfaz as condições, vamos analisar o caso onde $3x^{2}-6=0$. Logo, obtemos
$$x=0\;\;\;\;\;\;\;\; \mbox{ou} \;\;\;\;\;\;\;\; x=2.$$
Novamente, $x=0$ não nos interessa. Assim, sendo $x=2$ obtemos que $y=1$ e $z=\dfrac{2}{3}.$ Portanto, o volume máximo da maior caixa, nas condições do exercício, será
$$V=(2)\cdot(1)\cdot \frac{2}{3}=\frac{4}{3}.$$
Encontre a derivada direcional de $f(x,y) = x^2 + y^2$ na direção do versor tangente da curva
$$\bf{r}(t) = (\cos{t} + t\sin{t})\bf{i} + (\sin{t} - t\cos{t})\bf{j}, t > 0.$$
Versor tangente a $\mathbf{r}(t):$ $\mathbf{u} = \cos(t)\mathbf{i} + (\sin(t))\mathbf{j};$ $D_{\mathbf{u}} f = 2.$
Encontre $f_{x}$, $f_{y}$ e $f_{z}$ para $f(x,y,z)=e^{-(x^{2}+y^{2}+z^{2})}$.
$\displaystyle f_{x} = -2xe^{-(x^{2} + y^{2} + z^{2})},\;\;\;\; f_{y} = -2ye^{-(x^{2} + y^{2} + z^{2})}\;\;\;\;\text{e}\;\;\;\; f_{z} = -2ze^{-(x^{2} + y^{2} + z^{2})}$.
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\frac{x^{2}}{x^{2}+y^{2}}\,dA$, onde $R$ é a região anular limitada por $x^{2}+y^{2}=a^{2}$ e $x^{2}+y^{2}=b^{2}$, $0< a< b.$
$\displaystyle \frac{\pi}{2}(b^2 - a^2).$
Determine a massa e o centro de massa do cubo dado por $0\leq x\leq a$, $0\leq y\leq a$, $0\leq z\leq a$ e com função densidade:
$\rho(x,y,z)=x^{2}+y^{2}+z^{2}.$
$\rho(x,y,z)=x+y+z.$
Massa: $a^5;$ centro de massa: $\displaystyle \left(\frac{7a}{12},\frac{7a}{12},\frac{7a}{12} \right).$
Massa: $\dfrac{3a^4}{2};$ centro de massa: $\displaystyle \left(\frac{5a}{9},\frac{5a}{9},\frac{5a}{9} \right).$
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
$z=x^{2}+xy^{3}$, $x=uv^{2}+w^{3}$, $y=u+ue^{w}$;
$\dfrac{\partial z}{\partial u}$, $\dfrac{\partial z}{\partial v}$, $\dfrac{\partial z}{\partial w}$ quando $u=2$, $v=1$, $w=0$.
$\dfrac{\partial z}{\partial u} = 85$, $\dfrac{\partial z}{\partial v} = 178$, $\dfrac{\partial z}{\partial w} = 54.$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}x\,dxdydz$, onde $B$ é o conjunto $x\geq 0$ e $x^{2}+y^{2}+z^{2}\leq 4.$
$4\pi$.
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = (\ln{x},\ln{(xy)},\ln{(xyz)})$.
$\text{rot } \mathbf{F} = \dfrac{1}{y}\mathbf{i} - \dfrac{1}{x} \mathbf{j} +\dfrac{1}{x} \mathbf{k}.$ $\text{div } \mathbf{F} = \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(\cos z+xy^{2})\,{\bf i}+xe^{-z}\,{\bf j}+(\sin y+x^{2}z)\,{\bf k}$ e $S$ é a superfície do sólido limitado pelo parabolóide $z=x^{2}+y^{2}$ e pelo plano $z=4.$
Calcule $\mathrm{d} z/\mathrm{d} t$ por dois processos:
- substituindo as expressões para $x(t)$ e $y(t)$ em $z$ e depois derivando diretamente com relação a $t$
- aplicando a Regra da Cadeia: $\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y }\frac{dy}{dt}$.
$z=x^{2}+3y^{2}$,$x=\sin{t}$ e $y=\cos{t}.$
$\displaystyle \frac{dz}{dt} (t) = -4\sin(t)\cos(t).$
Seja $f(x,y)=\dfrac{1}{x^{2}+y^{2}}$. Verifique que
$x\;\dfrac{\partial ^{2}f}{\partial x^{2}}(x,y)+y\;\dfrac{\partial^{2} f}{\partial y \partial x}(x,y)=-3\dfrac{\partial f}{\partial x}(x,y)$
$\dfrac{\partial ^{2}f}{\partial x^{2}}(x,y)+\dfrac{\partial^{2} f}{\partial y^{2}}(x,y)=\dfrac{4}{(x^{2}+y^{2})^{2}}$
$\begin{aligned}[t]\frac{\partial f}{\partial x} &= -\frac{2x}{(x^{2} + y^{2})^{2}},\;\;\;\;\; \frac{\partial^{2} f}{\partial x^{2}}= \frac{6 x^{2} - 2y^{2}}{(x^{2} + y^{2})^{3}},\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= \frac{6 y^{2} - 2x^{2}}{(x^{2} + y^{2})^{3}} \;\;\;\;\;\text{e}\\ \frac{\partial^{2} f}{\partial y\partial x} &= \frac{8xy}{(x^{2} + y^{2})^{3}}.\end{aligned}$
Use o método dos multiplicadores de Lagrange para determinar o ponto sobre a parábola $y = x^2$ que se encontra mais próximo do ponto $(0,1) \in \mathbb{R}^2.$
$\displaystyle \left(\frac{1}{\sqrt{2}}, \frac{1}{2} \right)$ e $\displaystyle \left(-\frac{1}{\sqrt{2}}, \frac{1}{2} \right).$
Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$
- ${\bf F}(x,y,z) = x{\bf i} - z{\bf j} + y{\bf k}$, $S$ é a parte do plano $x+z=1$ dentro do cilindro $x^2+y^2 = 1$, com orientação para cima.
$2\pi.$
Calcule a área da superfície dada por: ${\bf r}(u,v)=(u,v,2-u-v)$ e $u^{2}+v^{2}\leq 1.$. (Sugerimos ao leitor desenhar a imagem da superfície.)
$\pi \sqrt{3}.$
Determine as equações paramétricas para a reta tangente $\grave{a}$ curva dada pelas equações paramétricas
$x=e^{-t}\; \cos{t}$, $y=e^{-t}\; \sin{t}$, $z=e^{-t}$ no ponto $(1,0,1)$.
Calcule $D_{\bf{u}}f(x_0,y_0)$, sendo dados
$f(x,y) = e^{x^2-y^2}$, $(x_0,y_0) = (1,1)$ e $\bf{u}$ o versor de $(3,4)$.
$\displaystyle D_{\bf{(3,4)}}f(1,1) = -\frac{2}{5}.$
Calcule a integral tripla.
$\displaystyle\iiint\limits_{ E}y\;dx dy dz$, onde $E$ é o conjunto $x^{2}+4y^{2}\leq 1$ e $0\leq z \leq 1.$
$\displaystyle\iiint\limits_{ E}x\;dx dy dz$, onde $E$ é o conjunto $x^{2}+y^{2}\leq 4$, $x\geq 0$ e \\ $x+y\leq z \leq x+y+1.$
$0.$
$\dfrac{16}{3}.$
Calcule a integral de linha, onde $C$ é a curva dada. $\displaystyle\int_{C}x\,dx-y\,dy$, $C$ é o segmento de extremidades $(1,1)$ e $(2,3)$, percorrido no sentido de $(1,1)$ para $(2,3).$
Uma representação paramétrica para o segmento de reta $C$ é
$$\begin{array}{lr}x=1+t \\y=1+2t\\\end{array}\;\;\;\; 0\leq t \leq 1.$$
Logo,
$$\begin{array}{lr}dx=dt \\dy=2\,dt\\\end{array}$$
Assim,
$$\int_{C}x\,dx-y\,dy=\int_{0}^{1}(1+t)\cdot (dt)+(1+2t)\cdot(2\,dt)=\int_{0}^{1}(1+t+2+4t)\,dt$$
$$=\int_{0}^{1}(3+5t)\,dt=\bigg(3t+\frac{5}{2}t^{2}\bigg)\bigg|_{0}^{1}=3+\frac{5}{2}=\frac{11}{2}.$$
Identifique e faça um esboço da imagem da superfície parametrizada dada por ${\bf r}(u,v)=\bigg(v\cos u,v\sin u,\dfrac{1}{v^{2}}\bigg)$, $0\leq u\leq 2\pi$, $v>0.$
Gráfico de $f(x,y) = \dfrac{1}{x^2 + y^2}.$
Trace a curva com equações paramétricas
\begin{eqnarray}
x & = & \sqrt{1 - 0,25 \cos^210t} \cos{t} \nonumber \\
y & = & \sqrt{1 - 0,25 \cos^210t} \sin{t} \nonumber \\
z & = & 0,5 \cos{10t}. \nonumber
\end{eqnarray}
Explique a aparência da curva, mostrando que ela está em uma esfera.
Aplique o Teorema da Divergência para achar $\displaystyle\iint \limits_{S}{\bf F}\cdot {\bf n}\,dS,$ sendo ${\bf F}(x,y,z)=y\,\sin x\,{\bf i}+y^{2}z\,{\bf j}+(x+3z)\,{\bf k}$ e $S$ é a superfície da região delimitada pelos planos $x=\pm 1$, $y=\pm 1$ e $z=\pm 1.$
$24.$
A produção total $P$ de certo produto depende da quantidade $L$ de trabalho empregado e da quantidade $K$ de capital investido. Nas Seções 14.1 e 14.3 do livro do Stewart, foi discutido o modelo Cobb-Douglas $P = bL^\alpha K^{1-\alpha}$ seguido de certas hipóteses econômicas, em que $b$ e $\alpha$ são constantes positivas e $\alpha < 1$. Se o custo por unidade de trabalho for $m$ e o custo por unidade de capital for $n$, e uma companhia puder gastar somente uma quantidade $p$ de dinheiro como despesa total, então a maximização da produção $P$ estará sujeita à restrição $mL + nK = p$. Mostre que a produção máxima ocorre quando
$$L = \dfrac{\alpha p}{m} \quad \text{e} \quad K = \dfrac{(1 - \alpha)p}{n}.$$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte da esfera $x^{2}+y^{2}+z^{2}=4$ que está acima do cone $z=\sqrt{x^{2}+y^{2}}.$
$x = 2\sin(\phi)\cos(\theta),$ $y = 2\sin(\phi)\sin(\theta),$ $z = 2\cos(\phi),$ onde $0\leq \phi \leq \frac{\pi}{4}$ e $0 \leq \theta \leq 2\pi.$
Determine $\partial z/\partial x$ e $\partial z/\partial y$, sendo $z=f(x)+g(y)$.
$\displaystyle \frac{\partial z}{\partial x} = f'(x)$
$\frac{\partial z}{\partial y} = g'(y)$.
Calcule a integral de linha $\displaystyle\oint_{C} (x-y) dx + (x+y)dy$, $C$ é o círculo com centro na origem e raio 2, por dois métodos:
diretamente; e
utilizando o Teorema de Green.
$8\pi.$
Calcule as derivadas parciais de $s = f(x,y,z,w)$ dada por $s = xw \ln{(x^2 + y^2 + z^2 + w^2)}$.
$\begin{aligned}[t]\frac{\partial s}{\partial x} &= w \left( \frac{2x^{2}}{x^{2} + y^{2} + z^{2} + w^{2}} + \ln (x^{2} + y^{2} + z^{2} + w^{2})\right),\\\frac{\partial s}{\partial y} &= \frac{2xyw}{x^{2} + y^{2} + z^{2} + w^{2}},\;\;\;\; \frac{\partial s}{\partial z} = w \frac{2xzw}{x^{2} + y^{2} + z^{2} + w^{2}}\;\;\;\;\;\text{e}\\\frac{\partial s}{\partial w} &= x \left( \frac{2w^{2}}{x^{2} + y^{2} + z^{2} + w^{2}} + \ln (x^{2} + y^{2} + z^{2} + w^{2})\right).\end{aligned}$
Determine um plano que seja tangente à superfície $x^2 + 3y^2 + 2z^2 = \dfrac{11}{6}$ e paralelo ao plano $x + y + z = 10$.
$\displaystyle x + y + z = \frac{11}{6}$ ou $\displaystyle x + y + z = -\frac{11}{6}.$
Verifique que a função \(\displaystyle u(x,t)=\sin(x-ct)\) é uma solução da equação da onda unidimensional \[ \dfrac{\partial^2u}{\partial t^2} = c^2\dfrac{\partial^2u}{\partial x^2}, \] onde \(c\) é uma constante que depende das características da onda.
Calculando diretamente as derivadas parciais da função dada, temos
\[\begin{array}{ll} \dfrac{\partial u}{\partial x} = \cos(x-ct), & \dfrac{\partial^2u}{\partial x^2}= -\sin(x-ct) \\ \dfrac{\partial u}{\partial t} = -c\cos(x-ct), & \dfrac{\partial^2 u}{\partial t^2}= -c^2\sin(x-ct). \end{array}\] Assim, podemos ver que \(u(x,t)\) satisfaz a equação dada.
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=2x^{3}+y^{4}$, $D=\{(x,y) \in \mathbb{R}^2: x^{2}+y^{2}\leq 1\}.$
Valor máximo: $2;$ valor mínimo: $-2.$
Seja $f(x,y,z) = \dfrac{x}{x^2 + y^2 + z^2}$.
Verifique que
$$x\dfrac{\partial f}{\partial x} + y\dfrac{\partial f}{\partial y} + z\dfrac{\partial f}{\partial z} = -f.$$
$\displaystyle \frac{\partial f}{\partial x} = \frac{-x^{2} + y^{2} + z^{2}}{(x^{2} + y^{2} + z^{2})^{2}},\;\;\;\; \frac{\partial f}{\partial y} = \frac{-2xy}{(x^{2} + y^{2} + z^{2})^{2}} \;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial f}{\partial z} = \frac{-2xz}{(x^{2} + y^{2} + z^{2})^{2}}.$
Determine se ${\bf F}(x,y,z)=(x-y)\,{\bf i}+(x+y+z)\,{\bf j}+z^{2}\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Não.
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.
$\displaystyle \int_0^4 \int_0^{2\pi}\int_r^4 r \, dz d\theta dr$
Determine se ${\bf F}(x,y,z)=(e^{x}\,\cos y)\,{\bf i}-(e^{x}\,\sin y)\,{\bf j}+z\,{\bf k}$ é ou não um campo vetorial conservativo. Se for, determine uma função $f$ tal que ${\bf F}=\nabla f.$
Sim. $f(x,y,z) = e^{x}\cos(y) + \dfrac{z^{2}}{2} + K.$
Calcule as derivadas parciais de $w = x^2 \arcsin{\dfrac{y}{z}}$.
$\displaystyle \frac{\partial w}{\partial x} = 2x \arcsin \left( \frac{t}{z}\right),\;\;\;\; \frac{\partial w}{\partial y} = \frac{x^{2}|z|}{z\sqrt{z^{2} - y^{2}}} \;\;\;\;\;\text{e}\;\;\;\;\;\frac{\partial w}{\partial z} = - \frac{x^{2}y}{|z|\sqrt{z^{2} - y^{2}}}.$
Seja $g(x,y,z)=\ln(25-x^{2}-y^{2}-z^{2}).$
Calcule $g(2,-2,4).$
Determine o domínio de $g$.
Determine a imagem de $g$.
$0.$
$\left\lbrace (x,y,z): x^{2} + y^{2} + z^{2} < 25 \right\rbrace.$
$(-\infty, \ln(25)].$
Existe uma direção $\bf{u}$ na qual a taxa de variação de $f(x,y) = x^2 - 3xy + 4y^2$ em $P = (1,2)$ é igual a 14? Justifique sua resposta.
Não, já que $|\nabla f(1,2)| = \sqrt{185} < 14.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = x^2 - 2xy + 3y^2$ e $x^2 + 2y^2 = 1.$
Pontos de máximo: $\displaystyle \left( \frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}} \right)$ e $\displaystyle \left( -\frac{1}{\sqrt{3}}, -\frac{1}{\sqrt{3}} \right)$; pontos de mínimo: $\displaystyle \left( \frac{2}{\sqrt{6}}, \frac{1}{\sqrt{6}} \right)$ e $\displaystyle \left( -\frac{2}{\sqrt{6}}, -\frac{1}{\sqrt{6}} \right)$.
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina retangular que ocupa a região descrita pelas desigualdades \(0\leq x\leq a\) e \( 0\leq y\leq b\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ \begin{array}{lll} I_x= \dfrac{\delta ab^3}{3}, & I_y= \dfrac{\delta a^3b}{3}, & I_z= \dfrac{\delta ab(a^2+b^2)}{3}. \end{array} \]
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2}{\sqrt{x^2 + y^2}}$, caso exista.
$0.$
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. Em cada caso, $C$ é orientada no sentido anti-horário quando vista de cima.
- ${\bf F}(x,y,z) = x^2z{\bf i} + xy^2{\bf j} + z^2{\bf k}$, $C$ é a curva de interseção do plano $x+y+z=1$ com o cilindro $x^2+y^2 = 9$.
$\dfrac{81\pi}{2}.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (5,-2)}(x^5 + 4x^3y - 5xy^2)$.
$2025.$
Determine os pontos do cone $z^{2}=x^{2}+y^{2}$ que estão mais próximos do ponto $(4,2,0).$
$(2,1,\sqrt{5})$ e $(2,1,-\sqrt{5}).$
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=(x+y){\bf i}+z{\bf j}+xz{\bf k}$ e $S$ é a superfície do cubo de vértices $(\pm 1,\pm 1, \pm 1).$
$8.$
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = 3x + y$ e $x^2 + 2y^2 = 1.$
Ponto de máximo: $\displaystyle \left( \frac{6}{\sqrt{38}}, \frac{1}{\sqrt{38}} \right)$; ponto de mínimo: $\displaystyle \left( -\frac{6}{\sqrt{38}}, -\frac{1}{\sqrt{38}} \right)$.
Determine se os pontos $P(7,10,4)$ e $Q(5,22,5)$ estão na superfície ${\bf r}(u,v)=(2u+3v,1+5u-v,2+u+v)$.
$P$ não está na superfície; $Q$ está na superfície.
Passe para coordenadas polares e calcule.
$\displaystyle\int_{0}^{a} \int_{0}^{x}\sqrt{x^{2}+y^{2}}\,dy dx$, em que $a>0$.
$\displaystyle\iint\limits_{ D}x\,dA$, onde $D$ é a região do primeiro quadrante compreendida entre os círculos x^2+y^2=4$ e $x^2+y^2=2x.$
Temos que a região de integração é: $$ R=\{(x,y)\in \mathbb{R}^{2}|\,0\leq x \leq a,\, 0\leq y \leq x\}.$$
Passando para coordenadas polares temos que $$\left\{ \begin{array}{cc} x=r\,\cos \theta\\ y=r\,\sin \theta\\ dy\,dx=r\,dr\,d\theta\\ \end{array} \right. $$ Como $0\leq x \leq a$, temos que $0\leq r\leq \dfrac{a}{\cos \theta}$ e também $0\leq \theta \leq \dfrac{\pi}{4}.$ Então, $$\int_{0}^{a}\int_{0}^{x}\sqrt{x^{2}+y^{2}}\,dy\,dx= \int_{0}^{\frac{\pi}{4}}\int_{0}^{\frac{a}{\cos \theta}}\sqrt{r^{2}\,\cos^{2}\theta +r^{2}\,\sin^{2}\theta}\,r\,dr\,d\theta$$ $$=\int_{0}^{\frac{\pi} {4}}\int_{0}^\frac{a}{\cos\theta}r^{2}\,dr\,d\theta=\int_{0}^\frac{\pi}{4}\frac{r^3}{3}\bigg|_{0}^{\frac{a}{\cos \theta}}d\theta $$ $$=\frac{a^{3}}{3}\int_{0}^{\frac{\pi}{4}}\frac{1}{\cos^{3}\theta}d\theta=\frac{a^{3}}{3}\int_{0}^{\frac{\pi}{4}}\sec^{3}\theta d\theta$$ $$=\frac{a^{3}}{3}\bigg(\frac{1}{2}\sec \theta \tan \theta+\frac{1}{2}\ln|\sec \theta+\tan \theta|\bigg)\bigg|_{0}^{\frac{\pi}{4}}$$ $$=\frac{a^{3}}{6}\bigg[\bigg(\sec\frac{\pi}{4}\cdot \tan\frac{\pi}{4}+\ln\bigg|\sec\frac{\pi}{4}+\tan\frac{\pi}{4}\bigg|\bigg)- \bigg(\sec 0\cdot \tan 0+\ln|\sec 0+\tan 0|\bigg)\bigg]$$ $$=\frac{a^{3}}{6}\bigg(\sqrt{2}+\ln(\sqrt{2}+1)\bigg)$$A região de integração $R$ é descrita na figura seguinte
Notemos que $x^{2}+y^{2}=2x\Leftrightarrow (x-1)^{2}+y^{2}=1.$ Assim, $$\iint\limits_{ R}x\,dA=\underbrace{\iint\limits_{ \substack{x^{2}+y^{2}\leq 4\\ x\geq 0\\ y\geq 0}}x\,dA}_{(1)} -\,\,\underbrace{\iint\limits_{\substack{(x-1)^{2}+y^{2}\leq 1 \\ y\geq 0}}x\,dA}_{(2)}$$ Para a integral $(1)$ temos em coordenadas polares que $$r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=4\Rightarrow r^{2}=4\Rightarrow r=\pm 2.$$ Logo, $0\leq r\leq 2$ e $0\leq \theta \leq \dfrac{\pi}{2}.$ Para a integral $(2)$ temos em coordenadas polares que $$(r-\cos \theta-1)^{2}+r^{2}\sin^{2}\theta=1\Rightarrow r^{2}\cos^{2}\theta-2r\cos \theta+1+r^{2}\sin^{2}\theta=1$$ $$\Rightarrow r^{2}-2r\cos\theta=0\Rightarrow r(r-2\cos \theta)=0\Rightarrow r=0 \mbox{ou} r=2\cos \theta.$$ Logo, $0\leq r\leq 2\cos \theta$ e $0\leq \theta \leq \dfrac{\pi}{2}.$ Assim, $$\iint\limits_{ R}x\,dA=\int_{0}^{\frac{\pi}{2}}\int_{0}^{2}r\,\cos \theta \cdot r \,dr\,d\theta- \int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos \theta}r\cos \theta\cdot r\, dr\,d \theta$$ $$=\int_{0}^{\frac{\pi}{2}}\int_{0}^{2}r^{2}\,\cos \theta\,dr\,d\theta-\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos \theta}r^{2}\,\cos \theta\,dr\,d\theta$$ $$=\int_{0}^{\frac{\pi}{2}}\cos\,d\theta \cdot \int_{0}^{2}r^{2}\,dr-\int_{0}^{\frac{\pi}{2}}\frac{r^{3}}{3}\cos \theta \bigg|_{0}^{2\cos \theta}\,d\theta$$ $$=\bigg(\sin\theta \bigg|_{0}^{\frac{\pi}{2}}\bigg)\cdot \bigg(\frac{r^{3}}{3}\bigg|_{0}^{2}\bigg)-\frac{8}{3}\int_{0}^{\frac{\pi}{2}}\cos^{4}\theta\,d\theta$$ $$=\bigg(\sin \frac{\pi}{2}-\sin 0\bigg)\cdot \bigg(\frac{8}{3}-0\bigg)-\frac{8}{3}\bigg(\frac{1}{4}\cos^{3}\theta\,\sin \theta+\frac{3}{8}\theta+\frac{3}{16}\sin 2 \theta\bigg)\bigg|_{0}^{\frac{\pi}{2}}$$ $$=\frac{8}{3}-\frac{8}{3}\bigg[\bigg(\frac{1}{4}\cos^{3}\frac{\pi}{2}\sin \frac{\pi}{2}+\frac{3}{8}\cdot\frac{\pi}{2}+\frac{3}{16}\sin2\cdot \frac{\pi}{2}\bigg) -\bigg(\frac{1}{4}\cos^{3}0\sin 0+\frac{3}{8}\cdot 0+\frac{3}{16}\sin 0\bigg)\bigg]$$ $$=\frac{8}{3}-\frac{8}{3}\cdot \bigg(\frac{3\pi}{16}\bigg)=\frac{8}{3}-\frac{\pi}{2}=\frac{16-3\pi}{6}.$$
Calcule a integral de linha $\displaystyle\int_{C}{\bf F}\cdot d{\bf r}$, onde ${\bf F}(x,y,z)=(yz,xz,xy+2y)$ e $C$ é o segmento de reta que liga o ponto $(1,0,1)$ ao ponto $(-2,2,2).$
$-6.$
Se $f$ é uma função constante, $f(x,y) = k$, e $R = [a,b] \times [c,d],$ mostre que $\iint \limits_{R} k \, dA = k(b-a)(d-c).$
Note que se $R$ for dividida em $mn$ subretângulos, vale $$ \sum^{m}_{i = 1} \sum^{n}_{j = 1} f(x_{ij}^{*}, y_{ij}^{*}) \Delta A = k \sum^{m}_{i = 1} \sum^{n}_{j = 1} \Delta A = k (b - a) (d - c), $$ independentemente dos pontos amostrais $(x_{ij}^{*}, y_{ij}^{*})$ escolhidos.
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=y{\bf j}-z{\bf k}$ e $S$ é formada pelo parabolóide $y=x^{2}+z^{2}$, $0 \leq y \leq 1$ e pelo círculo $x^{2}+z^{2} \leq 1$, $y=1.$
$0.$
Determine o trabalho realizado pelo campo de força ${\bf F}(x,y,z)=(y+z)\,{\bf i}+(x+z)\,{\bf j}+(x+y)\,{\bf k}$ sobre uma partícula que se move ao longo do segmento de reta $(1,0,0)$ a $(3,4,2).$
$26.$
Calcule
$$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{\mbox{sen}(x^2 + y^2)}{x^2 + y^2}.$$
Considere $t=x^{2}+y^{2}$.
Assim , se $(x,y)\rightarrow (0,0)$ temos que $t \to 0.$ Portanto,
$$\lim_{(x,y) \to (0,0)} \frac{\sin(x^{2}+y^{2})}{x^{2}+y^{2}}=\lim_{t \to 0}\frac{\sin t}{t}=1.$$
Se $z=f(x-y)$, mostre que
$$\dfrac{\partial z}{\partial x}+\dfrac{\partial z}{\partial y}=0.$$
Note que se $u = x - y,$ então $\displaystyle \frac{\partial z}{\partial x} = \frac{dz}{du}$e$\displaystyle \frac{\partial z}{\partial y} = -\frac{dz}{du}.$
Considere o campo
$${\bf F}(x,y,z)=(e^{z},2yz, xe^{z}+y^{2}).$$
Verifique se o campo ${\bf F}$ é conservativo.
Se ${\bf F}$ for conservativo, calcule $f(x,y,z)$ tal que $\nabla f={\bf F}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$ onde $C$ é dada por $r(t)=(\cos t, \sin t, t)$, $0\leq t\leq 2\pi.$
Sim.
$f(x,y) = x e^{z} + y^{2} z.$
$e^{2\pi} - 1.$
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = y \ \mbox{cos}(x-y), \quad (2,2,2)$.
$z = y$.
Calcule $\displaystyle\int_{(-1,0)}^{(1,0)}\dfrac{x}{x^{2}+y^{2}}\,dx+\dfrac{y}{x^{2}+y^{2}}\,dy$.
$\displaystyle \dfrac{\pi}{4} + \arctan\left( \dfrac{2}{3} \right).$
Determine o maior conjunto no qual a função $f(x,y) = \begin{cases}\dfrac{xy}{x^2 + xy + y^2}, & \quad \text{se } (x,y) \neq (0,0), \\0, & \quad \text{se } (x,y) = (0,0)\end{cases}$ é contínua.
$\left\lbrace (x,y);\; (x,y) \neq (0,0) \right\rbrace.$
Use o Teorema de Green para calcular $\int_{C}\mathbf{F} \cdot d\mathbf{r}$, onde $\mathbf{F}(x,y) = 4x^3y^3\mathbf{i} + (3x^4y^2+5x)\mathbf{j}$, $C$ é a fronteira do quadrado de vértices $(-1,0)$, $(0,-1)$, $(1,0)$ e $(0,1)$. (Verifique a orientação da curva antes de aplicar o Teorema.)
$10.$
Esboce o gráfico da função $f(x,y)=g(\sqrt{x^{2}+y^{2}})$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
Determine o campo vetorial gradiente $\nabla f$ de $f(x,y) = \sqrt{x^2+y^2}$ e o esboce.
Determine o vetor tangente unitário ${\bf T}(t)$ no ponto com valor de parâmetro $t$ dado, sendo
${\bf r}(t)=\cos(t){\bf i}+3t{\bf j}+2\sin(2t){\bf k}$ e $t=0.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{ R} f(x,y)\,dxdy$, sendo $f(x,y)$ igual a
$x+2y$
$x-y$
$\dfrac{5}{2}.$
$1.$
Mude o ponto $(1,\sqrt{3},2\sqrt{3})$ dado em coordenadas retangulares para esféricas.
$\displaystyle \left( 4, \dfrac{\pi}{3}, \dfrac{\pi}{6} \right).$
Dada a função $f(x,y)=\sqrt{y-x}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \left\lbrace (x,y);\; x \leq y \right\rbrace$.
$Im(f) = \left\lbrace z \in \mathbb{R};\; z \geq 0 \right\rbrace.$
As curvas de nível são as retas $y - x = C,$ com $C \geq 0.$
Dada a expressão $g(x,y)=f(x,y)+2$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ deslocado para cima por duas unidades.
Determine e faça o esboço do domínio da função $f(x,y)=\ln(9-x^{2}-9y^{2})$.
$\left\lbrace (x,y);\; \frac{x^{2}}{9} + y^{2} < 1 \right\rbrace.$
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = 3(x-1)^2 + 2(y+3)^2 + 7, \quad (2,-2,12)$.
$z = 6x + 4y + 8$.
Verifique que o Teorema do Divergente é verdadeiro para o campo vetorial ${\bf F}$ na região $E.$
${\bf F}(x,y,z)=xy\,{\bf i}+yz\,{\bf j}+zx\,{\bf k}$, $E$ é o cilindro sólido $x^{2}+y^{2}\leq 1$, $0\leq z\leq 1.$
$\displaystyle\iint_{S} {\bf F} \cdot d{\bf S} = \iiint_{E} \mbox{div} {\bf F} dV = \dfrac{\pi}{2}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=x^{2}-4xy+4y^{2}-x+3y+1$.
Não há pontos críticos.
Determine $(x,y)$, com $x^{2}+4y^{2}\leq 1$, que maximiza a soma $2x+y.$
$\displaystyle \left( \frac{4\sqrt{17}}{17}, \frac{\sqrt{17}}{34} \right).$
Use a integral tripla para determinar o volume do sólido dado.
$x^{2}+y^{2}\leq 1$ e $x^{2}+z^{2}\leq 1.$
$(x-a)^{2}+y^{2}\leq a^{2}$, $x^{2}+y^{2}+z^{2}\leq 4a^{2}$, $z\geq 0$ $(a>0).$
$x^{2}+y^{2}\leq a^{2}$ e $x^{2}+z^{2}\leq a^{2}$ $(a>0).$
$x^{2}+y^{2}+z^{2}\leq a^{2}$ e $z\geq \dfrac{a}{2}$ $(a>0).$
$\dfrac{16}{3}.$
$\dfrac{16a^3}{3} \left(\dfrac{\pi}{2} - \dfrac{2}{3}\right).$
$\dfrac{16a^3}{3}.$
$\dfrac{5\pi a^3}{24}.$
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$yz=\ln(x+z)$
$\displaystyle \frac{dz}{dx} = \frac{1}{y(x+z)-1}$ e $\displaystyle \frac{dz}{dy} = \frac{z(x+z)}{y(x+z)-1}.$
Se $S$ é uma esfera e ${\bf F}$ satisfaz as hipóteses do Teorema de Stokes, mostre que $\displaystyle\iint\limits_{S}\mbox{rot}{\bf F} \cdot d{\bf S} = 0$.
Determine se o conjunto $\{(x,y)|\,x>0,\,y>0\}$ é ou não:
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x>0,\,y>0\}$ representa o primeiro quadrante, excluindo os eixos. Então:
$D$ é aberto, pois em torno de cada ponto em $D$, podemos colocar um disco que se encontra em $D.$
$D$ é conexo, pois o segmento de reta que une dois pontos quaisquer de $D$ encontra-se em $D.$
$D$ é simplesmente conexo, pois ele é conexo e não tem buracos.
O plano $4x - 3y + 8z = 5$ intercepta o cone $z^2 = x^2 + y^2$ em uma elipse.
Faça os gráficos do cone, do plano e da elipse.
Use os multiplicadores de Lagrange para achar os pontos mais alto e mais baixo da elipse.
Gráficos.
Ponto mais alto: $\displaystyle \left( -\frac{4}{3}, 1,\frac{5}{3} \right)$ e ponto mais baixo: $\displaystyle \left( \frac{4}{13}, -\frac{3}{13},\frac{5}{13} \right).$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{y^4}{x^4 + 3y^4}$.
Não existe.
Defina gradiente de uma função de três variáveis. Calcule $\nabla f(x,y,z)$.
$f(x,y,z) = z \arctan{\dfrac{x}{y}}$
$\displaystyle \nabla f(x,y,z) = \left(\frac{yz}{x^{2} + y^{2}},-\frac{xz}{x^{2} + y^{2}},\arctan\left(\frac{x}{y}\right) \right).$
Determine todos os pontos nos quais a direção de maior variação da função $f(x,y) = x^2 + y^2 - 2x - 4y$ é $\bf{i} + \bf{j}$.
$\left\lbrace (x,y) \in \mathbb{R}^{2}; y =x + 1 \right\rbrace.$
Dados ${\bf F}(x,y)=x^{2}\,{\bf i}+y^{2}\,{\bf j}$, $C$ é o arco da parábola $y=2x^{2}$ de $(-1,2)$ a $(2,8).$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y) = \dfrac{x^{3} + y^{3}}{3};$
$171.$
Seja $D$ a região limitada por um caminho fechado e simples $C$ no plano $xy$. As coordenadas do centroide $(\bar{x},\bar{y})$ de $D$ são
$$\bar{x} = \dfrac{1}{2A}\oint_{C}x^2 \, dy \quad \quad\quad\quad \bar{y} = -\dfrac{1}{2A}\oint_{C}y^2 \, dx,$$
em que $A$ é a área de $D$. Encontre o centroide de um quarto de uma região circular de raio $a$.
$\displaystyle \left(\frac{4a}{3\pi},\frac{4a}{3\pi} \right),$ se a região for a parte do disco $x^{2} + y^{2} = a^{2}$ no primeiro quadrante.
Utilizando o Teorema de Stokes, transforme a integral $\displaystyle\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = -y^2{\bf i} + x^2{\bf j} + z^2{\bf k}$, $S$ a superfície $x^2 + \dfrac{y^2}{4} + z^2 = 2$, $z \geq 1$, sendo ${\bf n}$ a normal que aponta para cima.
$0$.
Encontre o fluxo do campo ${\bf F}$ ao longo da porção da superfície dada no sentido especificado.
- ${\bf F}(x,y,z)=yx^{2}{\bf i}-2{\bf j}+xz{\bf k}$; $S$ é a superfície retangular $y=0$, $-1\leq x \leq 2$, $2\leq z \leq 7$, sentido $-{\bf j}.$
$30.$
As linhas de escoamento (ou linhas de corrente) de um campo vetorial são as trajetórias seguidas por uma partícula cujo campo de velocidade é um campo vetorial dado. Assim, os vetores do campo vetorial são tangentes a suas linhas de escoamento.
Use um esboço do campo vetorial $\textbf{F}(x,y) = x\textbf{i} - y\textbf{j}$ para desenhar algumas linhas de escoamento. Desses seus esboços é possível descobrir qual é a equação das linhas de escoamento?
Se as equações paramétricas de uma linha de escoamento são $x=x(t)$ e $y=y(t)$, explique por que essas funções satisfazem as equações diferenciais $dx/dt = x$ e $dy/dt = -y$. Resolva então as equações de forma a obter uma equação da linha de escoamento que passe pelo ponto $(1,1)$.
Se $z=f(x,y)$, onde $x=r\cos{\theta}$ e $y=r\sin{\theta}$,
- Determine $\dfrac{\partial z}{\partial r}$ e $\dfrac{\partial z}{\partial \theta}.$
- Mostre que $\bigg(\dfrac{\partial z}{\partial x}\bigg)^{2}+ \bigg(\dfrac{\partial z}{\partial y}\bigg)^{2}=\bigg(\dfrac{\partial z}{\partial r}\bigg)^{2}+\dfrac{1}{r^{2}}\bigg(\dfrac{\partial z}{\partial \theta}\bigg)^{2}$.
- $\displaystyle \frac{\partial z}{\partial r} = \cos(\theta) \frac{\partial z}{\partial x} + \sin(\theta) \frac{\partial z}{\partial y} $e$\displaystyle \frac{\partial z}{\partial \theta} = -r \sin(\theta)\frac{\partial z}{\partial x} + r\cos(\theta) \frac{\partial z}{\partial y}.$
- Use $(a)$ para calcular $\bigg(\dfrac{\partial z}{\partial r}\bigg)^{2}+\dfrac{1}{r^{2}}\bigg(\dfrac{\partial z}{\partial \theta}\bigg)^{2}$.
Determine os pontos da elipse $\mathcal{D} = \left\{ (x,y) \in \mathbb{R}^2: \frac{x^2}{8} + \frac{y^2}{2} = 1 \right\}$ que fornecem o maior e o menor valor da função $f(x,y) = xy$.
Pontos de máximo: $(2,1)$ e $(-2,-1);$ pontos de mínimo: $(-2,1)$ e $(2,-1).$
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\,x^{2}+y^{2}+z^{2}\leq 1$ e $z\geq x+y\}$ e ${\bf u}=-2xy\,{\bf i}+y^{2}\,{\bf j}+3z\,{\bf k}.$
Calcule a integral iterada.
$\displaystyle\int_{0}^{1}\!\!\int_{0}^{1}(u-v)^{5}\,du dv$
$\displaystyle\int_{0}^{2}\!\!\int_{0}^{\pi}r\sin^{2}{\theta}\,d\theta dr$
$0.$
$\pi.$
Calcule a área da parte da superfície cilíndrica $z^{2}+x^{2}=4$ que se encontra dentro do cilindro $x^{2}+y^{2}\leq 4$ e acima do plano $xy.$
$16.$
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.
- ${\bf F}(x,y,z) = xy{\bf i} + 2z{\bf j} + 3y{\bf k}$, $C$ é a curva de interseção do plano $x+z=5$ com o cilindro $x^2+y^2=9$.
$9\pi$.
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $z=z(x,y)$.
Expresse $\partial z /\partial x$ e $\partial z/\partial y$ em termos de $x$, $y$ e $z.$
$x^{3}+y^{3}+z^{3}=x+y+z$
$\displaystyle \frac{\partial z}{\partial x} = -\frac{3x^{2} - 1}{3z^{2} - 1}$ e $\displaystyle \frac{\partial z}{\partial y} = -\frac{3y^{2} - 1}{3z^{2} - 1}.$
Seja \(\displaystyle \mathbf{F}(x,y,z)=f(x,y,z)\mathbf{i}+ g(x,y,z)\mathbf{j} + h(x,y,z)\mathbf{k}\) e suponha que \(f\), \(g\) e \(h\) sejam contínuas e tenham derivadas parciais de primeira ordem contínuas numa região. Mostre que se \(\mathbf{F}\) é conservativo numa região esférica aberta então \(\mathrm{rot\,}\mathbf{F} = \mathbf{0}\) nessa região. [Sugestão: use que se \(\mathbf{F}\) for conservativo numa região, então \[ \dfrac{\partial f}{\partial y}=\dfrac{\partial g}{\partial x},\quad \dfrac{\partial f}{\partial z}=\dfrac{\partial h}{\partial x},\quad \dfrac{\partial g}{\partial z}=\dfrac{\partial h}{\partial y} \] nessa mesma região.]
Determine as derivadas parciais de primeira ordem da função $f(r,s)=r\ln(r^{2}+s^{2})$.
Sendo $f(r,s)=r\cdot \ln(r^{2}+s^{2})$, temos que as derivadas parciais em relação a $r$ e $s$, respectivamente, são:
$\bullet f_{r}(r,s)=1\cdot \ln(r^{2}+s^{2})+r\cdot \dfrac{1}{r^{2}+s^{2}}\cdot 2r=\ln(r^{2}+s^{2})+\dfrac{2r^{2}}{r^{2}+s^{2}}.$
$\bullet f_{s}(r,s)=0\cdot \ln(r^{2}+s^{2})+r\cdot \dfrac{1}{r^{2}+s^{2}}\cdot 2s=\dfrac{2rs}{r^{2}+s^{2}}.$
Represente graficamente o domínio da função $z=f(x,y)$ dada por $z=\sqrt{y-x^{2}}+\sqrt{2x-y}$.
$\left\lbrace (x,y); x^{2} \leq y \leq 2x \right\rbrace$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=(x+y+z)\,{\bf k}$, ${\bf r}(t)=(t,t,-t^{2})$, $0\leq t\leq 1.$
$-\dfrac{11}{6}.$
Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$
- ${\bf F}(x,y,z) = x^2z^2{\bf i} + y^2z^2{\bf j} + xyz {\bf k}$ e $S$ é a parte do parabolóide $z = x^2+y^2$ que está dentro do cilindro $x^2+y^2=4$, orientado para cima.
$0.$
Se \(x=x(u,v,w)\), \(y=y(u,v,w)\) e \(z=z(u,v,w)\) for uma transformação injetora, então \(u=u(x,y,z)\), \(v=v(x,y,z)\) e \(w=w(x,y,z)\). Supondo a diferenciabilidade das funções, mostre que \[\dfrac{\partial(x,y,z)}{\partial(u,v,w)}\cdot\dfrac{\partial(u,v,w)}{\partial(x,y,z)} = 1.\] Use este resultado para mostrar que o volume \(V\) do paralelepípedo oblíquo limitado pelos planos \(x+y+2z=\pm 3\), \(x-2y+z=\pm 2\), \(4x+y+z=\pm 6\) é dado por \(V=16\).
Seja \(G\) a região sólida dentro da esfera de raio \(2\) centrada na origem e acima do plano \(z=1\). Mostre (ou verifique) os seguintes resultados:
O volume de \(G\) é dado por \[\iiint\limits_G\,dV = \int_0^{2\pi}\int_0^{\dfrac{\pi}{3}}\int_{\sec\phi}^{2}\rho^2\sin\phi\,d\rho d\phi d\theta \]
\[\iiint\limits_G\dfrac{z}{x^2+y^2+z^2}\,dV = \int_0^{2\pi}\int_0^{\pi/3}\int_{\sec\phi}^{2}\rho\cos\phi\sin\phi\,d\rho d\phi d\theta \]
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=(x^{2}+z){\bf i}+y^{2}z{\bf j}+(x^{2}+y^{2}+z){\bf k}$ e $S$ é a parte no primeiro octante do parabolóide $z=x^{2}+y^{2}$ intersectada pelo plano $z=4.$
$4\pi - \dfrac{320}{7}.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx+dy+2\,dz$, $C$ é a interseção do paraboloide $z=x^{2}+y^{2}$ com o plano $z=2x+2y-1$; caminhe no sentido anti-horário.
$0.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}xy dS$, onde $S$ é a superfície com equações paramétricas $x=u-v$, $y=u+v$, $z=2u+v+1$, $0 \leq u \leq 1$, $0 \leq v \leq u.$
Seja $C$ o cilindro de base circular e eixo $(Oz)$, com raio $2$ e altura $3$, com base na origem e densidade inversamente proporcional $\grave{a}$ distância ao eixo.
Determine o momento de inércia de $C$ com relação ao eixo $(Oz)$.
Se $C$ gira em torno do eixo $(Oz)$ com energia cinética $K$, qual a velocidade instantânea nos pontos de sua superfície lateral? (Fórmulas: $\bullet$ Momento de inércia: $I=\iiint\limits_{C}\rho\cdot l^{2}\,dV$, onde $\rho$ é a densidade e $l$ é a distância ao eixo; $\bullet$ Energia cinética de rotação: $K=\dfrac{1}{2}I\omega^{2}.$)
$6\pi.$
$\displaystyle \sqrt{\frac{K}{3\pi}}.$
Faça um esboço do sólido no primeiro octante compreendido pelos planos \(x=0\), \(z=0\), \(x=5\), \(z-y=0\) e \(z=-2y+6\).
Calcule o volume do sólido dividindo-o em duas partes.
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $y=y(x).$
$y^{4}+x^{2}y^{2}+x^{4}=3$
$\displaystyle \frac{d y}{d x} = - \frac{2xy^{2} + 4x^{3}}{4y^{3} + 2x^{2}y}.$
Calcule a integral de superfície $\displaystyle\iint\limits_{S}y dS$, onde $S$ é a superfície com equações paramétricas $x=u$, $y=v$, $z=1-u^{2}$, $0\leq u\leq 1$, $0\leq v\leq \sqrt{u}.$
A água do mar tem densidade $1025 kg/m^{3}$ e escoa em um campo de velocidade ${\bf v}=y{\bf i}+x{\bf j}$, onde $x$, $y$ e $z$ são medidos em metros e as componentes de ${\bf v}$ em metros por segundo. Encontre a vazão para fora do hemisfério $x^{2}+y^{2}+z^{2}=9$, $z\geq 0.$
Determine e faça o esboço do domínio da função $f(x,y)=\sqrt{x+y}$.
$\left\lbrace (x,y);\; y \geq -x \right\rbrace$
Entre todos os pontos do gráfico de $z=10-x^{2}-y^{2}$ que estão acima do plano $x+2y+3z=0$, encontre o ponto mais afastado do plano.
$\displaystyle \left( \frac{1}{6}, \frac{1}{3}, \frac{355}{36} \right).$
Use o Teorema da Divergência para encontrar todos os valores positivos \(k\) tais que \[ \mathbf{F}(\mathbf{r}) = \dfrac{\mathbf{r}}{\|\mathbf{r}\|^k} \] satisfaça a condição \(\mathrm{div\,}\mathbf{F}=0\) quando \(\mathbf{r}\neq \mathbf{0}\).
A função $p=p(V,T)$ é dada implicitamente pela equação $pV=nRT$, onde $n$ e $R$ são constantes não-nulas (Lei dos Gases Ideais). Calcule $\dfrac{\partial p}{\partial V}$ e $\dfrac{\partial p}{\partial T}.$
$\displaystyle \frac{\partial p}{\partial V} = -\frac{nRT}{V^{2}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial p}{\partial T} = \frac{nR}{V}.$
Utilize o resultado $\displaystyle \int_{-\infty}^{\infty}e^{-x^{2}}\,dx=\sqrt{\pi}$ para calcular as integrais:
$\displaystyle\int_{0}^{\infty} x^{2}e^{-x^{2}}\,dx$
$\displaystyle\int_{0}^{\infty}\sqrt{x}e^{-x}\,dx$
$\displaystyle \frac{\sqrt{\pi}}{4}.$
$\displaystyle \frac{\sqrt{\pi}}{2}.$
Encontre uma equação para a superfície de nível da função $f(x,y)=\ln (x^{2}+y^{2}+z^{2})$ que passa pelo ponto $(-1,2,1)$.
$x^{2} + y + z^{2} = 6.$
Determine a menor distância entre o ponto $(2,1,-1)$ e o plano $x+y-z=1$.
$\sqrt{3}.$
\]
Calcule, usando integração, o volume do sólido limitados pelas superfícies $z = 1$, $z = 2$ e $z = \sqrt{x^2 + y^2}.$
$\dfrac{7\pi}{6}.$
Use o Teorema de Stokes para calcular $\displaystyle\iint\limits_{ S}\mbox{rot}{\bf F}\cdot d{\bf S}.$
- ${\bf F}(x,y,z) = (e^{xy}\cos{z},(x^2+1)z,-y)$, $S$ é o hemisfério $x^2+y^2+z^2 = 1$, $x \geq 0$, orientado na direção positiva do eixo $x$.
$-2\pi$.
Usando coordenadas esféricas, determine o volume do sólido que está acima do cone $\phi=\pi/3$ e abaixo da esfera $\rho=4\cos{\phi}.$
$10\pi.$
Utilize a transformação dada para calcular a integral. $\displaystyle\iint\limits_{R} xy \, dA$, em que $R$ é a região do primeiro quadrante limitada pelas retas $y = x$ e $y = 3x$ e pelas hipérboles $xy = 1$, $xy = 3$; $x = \dfrac{u}{v}$, $y = v$.
$2 \ln 3.$
Utilize um diagrama em árvore para escrever a Regra da Cadeia para o caso dado. Suponha que todas as funções sejam diferenciáveis.
$t=f(u,v,w)$, onde $u=u(p,q,r,s)$, $v=v(p,q,r,s)$, $w=w(p,q,r,s)$.
$\displaystyle \frac{\partial t}{\partial p} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial p} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial p} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial p},$ $\displaystyle \frac{\partial t}{\partial q} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial q} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial q} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial q},$
$\displaystyle \frac{\partial t}{\partial r} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial r} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial r} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial r}$ e $\displaystyle \frac{\partial t}{\partial s} = \frac{\partial t}{\partial u}\frac{\partial u}{\partial s} + \frac{\partial t}{\partial v}\frac{\partial v}{\partial s} + \frac{\partial t}{\partial w}\frac{\partial w}{\partial s}.$
Determine a derivada da função vetorial.
- ${\bf r}(t)=(\tan (t), \sec (t), 1/t^{2})$
- ${\bf r}(t)=\sin^{-1}(t){\bf i}+\sqrt{1-t^{2}}{\bf j}+{\bf k}$
Uma região $R$ é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva $\iint \limits_{R}f(x,y)\,dA$ como uma integral iterada, onde $f$ é uma função qualquer contínua em $R.$
$\displaystyle \int_{-1}^{1} \int_{0}^{\frac{(x + 1)}{2}} f(x,y) dy dx .$
Esboce o sólido cujo volume é dado pela integral iterada.
$\displaystyle\int_{0}^{1}\int_{0}^{1-x}\int_{0}^{2-2z}\;dy dz dx$
Usando coordenadas esféricas, determine o volume da parte da bola $\rho\leq a$ que está entre os cones $\phi=\pi/6$ e $\phi=\pi/3.$
$\displaystyle \left( \sqrt{3} - 1 \right) \dfrac{\pi a^3}{3}.$
Verifique que para o vetor posição \(\mathbf{r}=x\mathbf{i}+y\mathbf{j}+z\mathbf{k}\) valem as seguintes propriedades
\(\displaystyle \mathrm{rot\,}\mathbf{r} = \mathbf{0}\)
\(\displaystyle \nabla\|\mathbf{r}\| = \dfrac{\mathbf{r}}{\|\mathbf{r}\|} \)
O índice de sensação térmica $W$ é a temperatura sentida quando a temperatura real é $T$ e a velocidade do vento, $v$. Portanto, podemos escrever $W=f(T,v)$. Considerando a tabela abaixo:
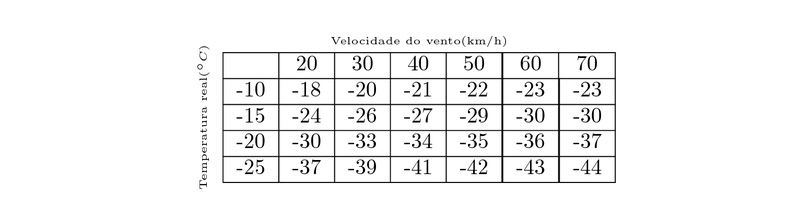
Estime os valores de $f_{T}(-15,30)$ e $f_{v}(-15,30)$. Quais são as nterpretações práticas desses valores?
Em geral, o que se pode dizer sobre o sinal de $\partial W/\partial T$ e $\partial W/\partial v$?
Qual parece ser o valor do seguinte limite
$$\lim_{v\rightarrow \infty}\frac{\partial W}{\partial v}?$$
$f_{T}(-15,30) \approx 1.3$ Isto significa que quando a temperatura real é $-15º$C e a velocidade do vento é $30$km/h, a temperatura aparente aumenta cerca de $1.3º$C para cada $1º$C que a temperatura real aumenta;\\
$f_{v}(-15,30) \approx -0.15$ Isto significa que quando a temperatura real é $-15º$C e a velocidade do vento é $30$km/h, a temperatura aparente diminui cerca de $0.15º$C para cada $1$km/h que a velocidade do vento aumenta.
$\frac{\partial W}{\partial T} > 0$ e $\frac{\partial W}{\partial v} \leq 0.$
$\lim_{v \to \infty} \frac{\partial W}{\partial v} = 0.$
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq 1$ e $x+y+2\leq z \leq 4.$
$x\geq 0$, $y \geq 0$, $x+y\leq 1$ e $0\leq z\leq x^{2}+y^{2}.$
$2\pi.$
$\dfrac{1}{6}.$
Sabendo que $\left|\sin\frac{1}{x}\right| \leq 1$, podemos dizer algo sobre
$$\displaystyle \lim_{(x,y) \to (0,0)}y\sin\dfrac{1}{x}?$$
Justifique sua resposta.
$\displaystyle \lim_{(x,y) \to (0,0)} y\sin\left(\frac{1}{x} \right) = 0.$
Determine as derivadas parciais de $f(x,y)=\sqrt[3]{x^{3}+y^{2}+3}$.
$\displaystyle \frac{\partial f}{\partial x} = \frac{x^{2}}{\sqrt[3]{(x^{3} + y^{3} + 3)^{2}}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial f}{\partial y} = \frac{2y}{3 \sqrt[3]{(x^{3} + y^{3} + 3)^{2}}} .$
Use coordenadas esféricas para encontrar o volume do sólido: limitado acima pela esfera \(\rho=4\) e abaixo pelo cone \(\phi=\pi/3\).
\(\dfrac{64\pi}{3}\)
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} x \ \sin{\dfrac{1}{x^2 + y^2}}$, caso exista.
$0.$
Admita que, para todo $(x,y)$,
$$4y\frac{\partial f}{\partial x}(x,y)-x\frac{\partial f}{\partial y}(x,y)=2.$$
Calcule $g^{'}(t)$, sendo $g(t)=f(2\cos{t},\sin{t})$.
$g^{'}(t) = -1.$
Determine a função vetorial que representa a curva obtida pela intersecção do cone $z = \sqrt{x^2 + y^2}$ com o plano $z = 1 + y$.
Encontre o ponto da curva $x^2 - 2xy + y^2 - 2x - 2y + 1 = 0$ mais próximo da origem.
$\displaystyle \left( \frac{1}{4}, \frac{1}{4} \right).$
Demonstre que se $R$ é uma região no plano limitada por uma curva $C$ simples, fechada e suave por partes, então a área de $R$, denotada por $A(R)$, pode ser dada por
$$\oint_{C}x\, dy,$$
em que a curva está orientada no sentido positivo.
Temos que
$$A(R) = \iint\limits_{R} 1 \, dA.$$
A fim de utilizar o Teorema de Green, devemos encontrar funções $P$ e $Q$ que tenham derivadas de primeira ordem contínuas em um aberto que contenha a curva $C$ e o interior de $C$ e que satisfaçam a relação $\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 1$. Observe que a curva $C$ já satisfaz as hipóteses desse teorema e $C$ é a fronteira de $R$. Um exemplo de funções $P$ e $Q$ é $P(x,y) = 0$ e $Q(x,y) = x$. Portanto, pelo Teorema de Green,
$$\iint\limits_{R} 1 \, dA = \oint_{C}0 \, dx + x\, dy = \oint_{C}x\, dy.$$
Encontre o fluxo exterior do campo ${\bf F}=2xy{\bf i}+2yz{\bf j}+2xz{\bf k}$ ao longo da superfície do cubo cortado do primeiro octante pelos planos $x=a$, $y=a$ e $z=a.$
$3\pi a^4.$
Determine uma equação do plano tangente à superfície no ponto especificado.
$z = \sqrt{xy}, \quad (1,1,1)$.
$x + y - 2z = 0$.
Calcule todas as derivadas parciais de $2^{\underline{a}}$ ordem de $z=\ln(1+x^{2}+y^{2})$.
$\begin{aligned}[t]\frac{\partial^{2} z}{\partial x^{2}} &= \frac{2 + 2y^{2} - 2x^{2}}{(1 + x^{2} + y^{2})^{2}},\;\;\;\;\; \frac{\partial^{2} z}{\partial y^{2}}= \frac{2 + 2x^{2} - 2y^{2}}{(1 + x^{2} + y^{2})^{2}} \;\;\;\;\;\text{e}\\\frac{\partial^{2} z}{\partial x\partial y} &= \frac{\partial^{2} z}{\partial y\partial x}= \frac{-4xy}{(1 + x^{2} + y^{2})^{2}}.C\end{aligned}$
Esboce a região de integração e mude a ordem de integração. $\displaystyle\int_{0}^{4}\!\!\int_{0}^{\sqrt{x}} \! f(x,y)\,dy dx$.
Seja $\mathbf{r} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k}$ e $r=|\mathbf{r}|$. Verifique a identidade $\nabla^2r^3=12r$.
$\nabla^2r^3= \dfrac{\partial}{\partial x} \left[ \dfrac{3}{2} \sqrt{x^{2} + y^{2} + z^{2}} (2x) \right] + \dfrac{\partial}{\partial y} \left[ \dfrac{3}{2} \sqrt{x^{2} + y^{2} + z^{2}} (2y) \right]\\ + \dfrac{\partial}{\partial z} \left[ \dfrac{3}{2} \sqrt{x^{2} + y^{2} + z^{2}} (2z) \right].$ (Note que: $r = \sqrt{x^{2} + y^{2} + z^{2}}.$)
Determine a aproximação linear da função $f(x,y,z) = \sqrt{x^2 + y^2 + z^2}$ em $(3,2,6)$ e use-a para aproximar o número $\sqrt{(3,02)^2 + (1,97)^2 + (5,99)^2}$.
Vamos determinar a aproximação linear da função $f$ em $(3,2,6)$. Primeiramente, calculamos as derivadas parcias $f_{x}$, $f_{y}$ e $f_{z}$, para todo $(x,y,z).$
$\bullet f_{x}(x,y,z)=\dfrac{1}{2}(x^{2}+y^{2}+z^{2})^{-1/2}\cdot 2x=\dfrac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}.$
$\bullet f_{y}(x,y,z)=\dfrac{1}{2}(x^{2}+y^{2}+z^{2})^{-1/2}\cdot 2y=\dfrac{y}{\sqrt{x^{2}+y^{2}+z^{2}}}.$
$\bullet f_{z}(x,y,z)=\dfrac{1}{2}(x^{2}+y^{2}+z^{2})^{-1/2}\cdot 2z=\dfrac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}.$
Agora, calculamos as derivadas parciais de $f$ no ponto $(3,2,6)$, então
$\bullet f_{x}(3,2,6)=\dfrac{3}{\sqrt{3^{2}+2^{2}+6^{2}}}=\dfrac{3}{7}.$
$\bullet f_{x}(3,2,6)=\dfrac{2}{\sqrt{3^{2}+2^{2}+6^{2}}}=\dfrac{2}{7}.$
$\bullet f_{x}(3,2,6)=\dfrac{6}{\sqrt{3^{2}+2^{2}+6^{2}}}=\dfrac{6}{7}.$
Assim, a aproximação linear da função $f$ em $(3,2,6)$ é
\begin{array}{rcl}f(x,y,z)&\approx & f(3,2,6)+f_{x}(3,2,6)(x-3)+f_{y}(3,2,6)(y-2)+f_{z}(3,2,6)(z-6)\\&=&7+\dfrac{3}{7}(x-3)+\frac{2}{7}(y-2)+\frac{6}{7}(z-6)\\&=&\dfrac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z+\bigg(7-\dfrac{9}{7}-\dfrac{4}{7}-\dfrac{36}{7}\bigg)\\&=&\dfrac{3}{7}x+\frac{2}{7}y+\frac{6}{7}z.\end{array}
Agora, vamos aproximar o número $\sqrt{(3,02)^2 + (1,97)^2 + (5,99)^2}.$ Assim,
\begin{array}{rcl}\sqrt{(3,02)^2 + (1,97)^2 + (5,99)^2}&=&f(3,02\,,\,1,97\,,\,5,99)\\&\approx& \frac{3}{7}(3,02)+\frac{2}{7}(1,97)+\frac{6}{7}(5,99)\\&\approx& 6,9914.\end{array}
Faça o esboço do sólido cujo volume é dado pela integral e calcule essa integral.
$\displaystyle \int_0^{\pi/2}\int_0^2\!\!\int_0^{9 - r^2} r dz dr d\theta$
Mostre que a curva com equações paramétricas $x = \sin{t}, \ y = \cos{t}, \ z = \sin^2t$ é a curva de intersecção das superfícies $z = x^2$ e $x^2 + y^2 = 1$. Use esse fato para esboçar a curva.
Calcule \(\displaystyle \lim_{(x,y)\to (-1,2)} \dfrac{xy}{x^2+y^2}\).
Como a função \(\displaystyle f(x,y)=\dfrac{xy}{x^2+y^2}\) é contínua no ponto \((-1,2)\) (de acumulação), basta avaliá-la neste mesmo ponto. Ou seja, \[ \lim_{(x,y)\to (-1,2)}\dfrac{xy}{x^2+y^2} = \dfrac{(-1)2}{(-1)^2+2^2} = -\dfrac{2}{5}. \]
Encontre $\partial f/\partial x$ e $\partial f/\partial y$ para $f(x,y)=(xy-1)^{2}$.
$\displaystyle \frac{\partial f}{\partial x} = 2y(xy - 1)\;\;\;\;\text{e}\;\;\;\; \frac{\partial f}{\partial y} = 2x (xy - 1)$.
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=u^{2}\,{\bf i}+2u\,\sin v\,{\bf j}+u\,\cos v\,{\bf k}$; $u=1$, $v=0.$
Temos que ${\bf r}(u,v)=\underbrace{u^{2}}_{x(u,v)}\,{\bf i}+\underbrace{2u\,\sin v}_{y(u,v)}\,{\bf j}+\underbrace{u\,\cos v}_{z(u,v)}\,{\bf k}$
Primeiro, vamos calcular os vetores tangentes:
$$\begin{array}{rcl}{\bf r}_{u}&=&\frac{\partial x(u,v)}{\partial u}\,{\bf i}+\frac{\partial y(u,v)}{\partial u}\,{\bf j}+\frac{\partial z(u,v)}{\partial u}\,{\bf k}\\&=& 2u\,{\bf i}+2\,\sin v\,{\bf j}+\cos v\,{\bf k}\end{array}$$
e
$$\begin{array}{rcl}{\bf r}_{v}&=&\frac{\partial x(u,v)}{\partial v}\,{\bf i}+\frac{\partial y(u,v)}{\partial v}\,{\bf j}+\frac{\partial z(u,v)}{\partial v}\,{\bf k}\\&=& 0\,{\bf i}+2u\,\cos v\,{\bf j}-u\sin v\,{\bf k}\end{array}$$
Assim, o vetor normal ao plano tangente é:
$$\begin{array}{rcl}{\bf r}_{u}\times {\bf r}_{v}&=&\left|\begin{array}{ccc}{\bf i} & {\bf j} & {\bf k}\\2u & 2\sin v & \cos v\\0 & 2u\cos v & -u\sin v\\\end{array}\right|\\&=&(-2u\,\sin^{2}v-2u\cos^{2}v)\,{\bf i}+(2u^{2}\,\sin v)\,{\bf j}+(4u^{2}\,\cos v)\,{\bf k}\end{array}$$
Como $u=1$ e $v=0$ temos que o vetor normal é $-2\,{\bf i}+0\,{\bf j}+4\,{\bf k}.$
Portanto, uma equação do plano tangente no ponto ${\bf r}(1,0)=(1,0,1)$ é
$$-2\cdot(x-1)+0\cdot(y-0)+4\cdot (z-1)=0$$
$$-2x+2+4z-4=0$$
$$-2x+4z-2=0 \mbox{ou} x-2z+1=0$$
Determine os pontos críticos da função
$$f(x,y)=-(x^{2}-1)^{2}-(x^{2}y-x-1)^{2}.$$
Calcule os valores assumidos por $f$ nos pontos críticos. É possível classificar os pontos críticos sem utilizar o críterio da derivada segunda? Se for possível, classifique-os e justifique a resposta.
$(1,2)$ e $(-1,0).$
$f(1,2) = f(-1,0) = 0.$ Note que $f(x,y) \leq 0,$ o que implica que $(1,2)$ e $(-1,0)$ são pontos de máximo.
Esboce a região cuja área é dada pela integral e calcule-a: $\displaystyle\int_{0}^{\pi/2} \int_{0}^{4\cos{\theta}} r \, dr d\theta$
$2\pi;$ região de integração:

Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(x^{2}+z^{2})\,{\bf i}+(y^{2}-2xy)\,{\bf j}+(4z-2yz)\,{\bf k}$ e $S$ é a superfície da região delimitada pelo cone $x=\sqrt{y^{2}+z^{2}}$ e pelo plano $x=9.$
Calcule a integral tripla $\displaystyle\iiint\limits_{B}xyz^{2}\,dV$, onde $B$ é a caixa retangular dada por $B=\{(x,y,z) \in \mathbb{R}^3|\;0\leq x\leq 1,\;-1\leq y\leq 2,\;0\leq z\leq 3\}$, integrando primeiro em relação a $y$, depois a $z$ e então a $x$.
$\dfrac{27}{4}.$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{rot }{f}$;
$\text{div }{\mathbf{F}}$;
$\text{grad }{\mathbf{F}}$.
$\text{rot }{f}$ não tem significado, pois $f$ é um campo escalar.
$\text{div }{\mathbf{F}}$ é um campo escalar.
$\text{grad }{\mathbf{F}}$ não tem sifnificado, pois $\bf{F}$ não é um campo escalar.
Calcule a integral de superfície $\displaystyle\iint\limits_{S}y^{2}dS$, onde $S$ é a parte da esfera $x^{2}+y^{2}+z^{2}=4$ que está dentro
do cilindro $x^{2}+y^{2}=1$ e acima do plano $xy.$
$\pi\left( \dfrac{32}{3} - 6\sqrt{3}\right).$
Dada a expressão $g(x,y)=-f(x,y)$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ refletido sobre o plano $xy.$
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R}\cos{\left(\dfrac{y - x}{y + x}\right)} \, dA$, em que $R$ é a região trapezoidal com vértices $(1,0)$, $(2,0)$, $(0,2)$ e $(0,1)$.
$\dfrac{3}{2} \sin(1).$
Dois mapas de contorno são mostrados na figura. Um é de uma função $f$ cujo gráfico é um cone. O outro é de uma função $g$ cujo gráfico é um paraboloide. Qual é qual? Por quê?
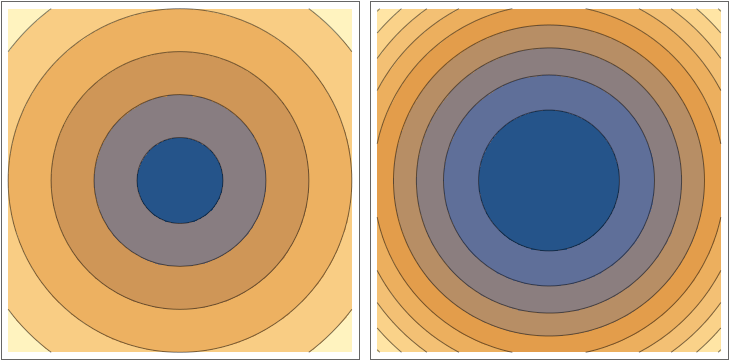
O da esquerda corresponde ao cone e o da direita ao paraboloide.
Sejam ${\bf u}(t)=t{\bf i}+{\bf j}+e^{t}{\bf k}$ e ${\bf v}(t)={\bf i}+{\bf j}+{\bf k}.$ Calcule
- $\displaystyle\int_{0}^{1}({\bf u}(t)\times{\bf v}(t))\mathrm{d}t$
- $\displaystyle\int_{0}^{1}({\bf u}(t)\cdot {\bf v}(t))\mathrm{d}t$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy}{x^2 + y^2}$, caso exista.
Não existe.
Determine a curva de nível de $f(x,y) = x^2 + 16y^2$ que seja tangente à curva $xy = 1$, $x>0$ e $y>0$. Qual o ponto de tangência?
$x^{2} + 16 y^{2} = 8;$ o ponto de tangência é $\displaystyle \left( 2, \frac{1}{2} \right).$
Determine se os pontos $P(3,-1,5)$ e $Q(-1,3,4)$ estão na superfície ${\bf r}(u,v)=(u+v,u^{2}-v,u+v^{2})$.
$P$ está na superfície; $Q$ não está na superfície.
Mostre que cada a equação a seguir define implicitamente pelo menos uma função diferenciável $z=z(x,y)$.
Expresse $\partial z /\partial x$ e $\partial z/\partial y$ em termos de $x$, $y$ e $z.$
$e^{x+y+z}+xyz=1$
$\displaystyle \frac{\partial z}{\partial x} = - \frac{e^{x + y + z} + yz}{e^{x + y + z} + xy}$ e $\displaystyle \frac{\partial z}{\partial y} = - \frac{e^{x + y + z} + xz}{e^{x + y + z} + xy}.$
Suponha que $w=f(x,y)$ é diferenciável e que exista uma constante $\alpha$ tal que
$x=u\cos(\alpha)-v\sin(\alpha)$
$y=u\sin(\alpha)+v\cos(\alpha).$
Mostre que
$$\bigg(\frac{\partial w}{\partial u}\bigg)^{2}+\bigg(\frac{\partial w}{\partial v}\bigg)^{2}=\bigg(\frac{\partial w}{\partial x}\bigg)^{2}+\bigg(\frac{\partial w}{\partial y}\bigg)^{2}.$$
Note que $\displaystyle \frac{\partial w}{\partial u} = \cos(\alpha) \frac{\partial w}{\partial x} + \sin(\alpha) \frac{\partial w}{\partial y}$ e $\displaystyle \frac{\partial w}{\partial v} = -\sin(\alpha) \frac{\partial w}{\partial x} + \cos(\alpha) \frac{\partial w}{\partial y}.$
Determine o ponto da reta $x + 2y = 1$ cujo produto das coordenadas seja máximo.
$\displaystyle \left( \frac{1}{2}, \frac{1}{4} \right).$
Encontre o volume do sólido delimitado pelo parabolóide $z=2+x^{2}+(y-2)^{2}$ e pelos planos $z=1$, $x=1$, $x=-1$, $y=0$ e $y=4.$
Observe que o sólido $E$ está abaixo da superfície $z = 2+x^2+(y-2)^2$ e acima do retângulo $[-1,1]\times [0,4]$ em $z=1$ (ver figura abaixo).

Algebricamente, $$E = \{(x,y,z) \in\mathbb{R}^3: -1 \leq x \leq 1, 0 \leq y \leq 4 \mbox{ e } 1 \leq z \leq 2 + x^2 + (y-2)^2\}.$$ Logo, o volume é dado por $$V = \iint\limits_{R}(2+x^2+(y-2)^2)\,dA - \iint\limits_{ R}\,dA,$$ em que $R = \{(x,y) \in \mathbb{R}^2; -1 \leq x \leq 1 \mbox{ e } 0 \leq y \leq 4 \}$. Assim, \begin{eqnarray*} V & = & \displaystyle\int_{-1}^{1}\int_{0}^{4}(x^2+y^2-4y+5)\,dy dx \\ & = & \displaystyle\int_{-1}^{1} \left.\left(x^2y+\frac{y^3}{3}-2y^2+5y \right|_{y=0}^{y=4} \right) \,dx \\ & = & \displaystyle\int_{-1}^{1} \left(4x^2+\frac{28}{3}\right) \,dx \\ & = & \left.\frac{4x^3}{3}+\frac{28x}{3} \right|_{x=-1}^{x=1} = \frac{64}{3}. \end{eqnarray*} Observe que, pelo Teorema de Fubini, podemos optar por calcular a integral $$\int_{0}^{4}\!\int_{-1}^{1}(x^2+y^2-4y+5)\,dy dx,$$ obtendo o mesmo resultado.
Identifique a superfície cuja equação é $\rho=\sin{\theta}\sin{\phi}.$
Esfera de raio $\dfrac{1}{2}$ centrada no ponto $\left(0,\dfrac{1}{2},0\right).$
Use o Teorema de Stokes para calcular $\displaystyle\int_C {\bf F}\cdot d{\bf R}$. $C$ é orientada no sentido anti-horário quando vista de cima.
- ${\bf F}(x,y,z) = (x+y^2){\bf i} + (y+z^2){\bf j} + (z+x^2){\bf k}$, $C$ é o triângulo com vértices $(1,0,0)$, $(0,1,0)$, $(0,0,1)$.
$1$.
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1}\!\!\int_{0}^{1-x}(1-x-y)\,dy dx.$$
Determine o maior conjunto de pontos em que a função $f(x,y) = \begin{cases}\dfrac{xy^3}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = 0\end{cases}$ é diferenciável. Justifique.
$\mathbb{R}^{2}$.
Seja $C$ uma curva fechada, simples e lisa que está no plano $x+y+z=1$. Mostre que a integral de linha $\displaystyle\int_C zdx - 2xdy + 3ydz$ depende apenas da área da região englobada por $C$ e não da forma de $C$ ou de sua posição no plano.
$\displaystyle\int_C zdx - 2xdy + 3ydz = \dfrac{2}{\sqrt{3}} \times $ (área da região englobada por $C$).
Calcule $\int_{C}\mathbf{F} \cdot \mathbf{n} \, ds$ ($\mathbf{n}$ é unitário), onde $\mathbf{F}(x,y) = x^2\mathbf{i}$, $C$ dada por $\mathbf{r}(t) = (2\cos{t},\sin{t})$, $0 \leq t \leq 2\pi$ e $\mathbf{n}$ a normal que aponta para fora da região $x^2/4+y^2\leq 1$.
$0$.
Dada a função $f(x,y)=\ln (x^{2}+y^{2})$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \left\lbrace (x,y);\; (x,y) \neq (0,0) \right\rbrace$.
$Im(f) = \mathbb{R}.$
As curvas de nível são os círculos $x^{2} + y^{2} = C$ com $C > 0.$
Calcule a massa do sólido $x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0$, sendo a densidade dada por $\rho(x,y,z)=x+y.$
$\dfrac{1}{12}.$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y,z) = \tan{(x + 2y + 3z)}, (-5,1,1).$
$\sqrt{14}.$
A temperatura em um ponto $(x,y,z)$ em uma substância com condutividade $K=6,5$ é $u(x,y,z)=2y^{2}+2z^{2}.$ Determine a taxa de transmissão de calor nessa substância para dentro da superfície cilíndrica $y^{2}+z^{2}=6$, $0\leq x\leq 4.$
O fluxo de calor, com $u(x,y,z)=2y^{2}+2z^{2}$, é dado por
$${\bf F}(x,y,z)=-K \nabla u=-6,5(0{\bf i}+4y{\bf j}+4z{\bf k})=0{\bf i}-26y{\bf j}-26z{\bf k}.$$
Temos que $S$ é a superfície cilíndrica $y^{2}+z^{2}=6$ e $0\leq x \leq 4.$ As equações paramétricas de $S$ são:
$$x=x, y=\sqrt{6}\cos \theta \mbox{e} z=\sqrt{6}\sin \theta$$
onde $0\leq x \leq 4$ e $0\leq \theta \leq 2\pi.$
Então,
$${\bf r}(x,\theta)=x{\bf i}+\sqrt{6}\cos \theta{\bf j}+\sqrt{6}\sin \theta{\bf k}.$$
Como queremos o fluxo de calor para dentro de $S$ devemos calcular
$$\int \int\limits_{S}{\bf F}\cdot dS=\int \int\limits_{ D}{\bf F}({\bf r}(x,\theta))\cdot ({\bf r}_{x}\times {\bf r}_{\theta})dA.$$
Então,
$${\bf r}_{x}(x,\theta)={\bf i}+0{\bf j}+0{\bf k}$$
e
$${\bf r}_{\theta}(x,\theta)=0{\bf i}-\sqrt{6}\sin \theta{\bf j}-\sqrt{6}\cos \theta{\bf k}.$$
Logo,
$\begin{array}{rcl} {\bf r}_{x} \times {\bf r}_{\theta} &=& \left| \begin{array}{ccc}{\bf i} & {\bf j} & {\bf k}\\1 & 0 & 0\\0 & -\sqrt{6}\sin \theta & -\sqrt{6}\cos \theta \\ \end{array} \right| \\ &=& 0{\bf i}-\sqrt{6}\cos \theta{\bf j}-\sqrt{6}\sin \theta{\bf k}, \end{array}$
$${\bf F}({\bf r}(x,\theta))=(0{\bf i}-26\sqrt{6}\cos\theta{\bf j}-26\sqrt{6}\sin \theta{\bf k})$$
e
$${\bf F}({\bf r}(x,\theta))\cdot ({\bf r}_{x}\times {\bf r}_{\theta})=(0{\bf i}-26\sqrt{6}\cos\theta{\bf j}-26\sqrt{6}\sin \theta{\bf k}) \cdot (0{\bf i}-\sqrt{6}\cos \theta{\bf j}-\sqrt{6}\sin \theta{\bf k})=156$$
Assim, a taxa de fluxo de calor para dentro de $S$ é:
$$\int \int\limits_{S}{\bf F}\cdot dS=\int \int\limits_{ D}{\bf F}({\bf r}(x,\theta))\cdot ({\bf r}_{x}\times {\bf r}_{\theta})dA=\int \int\limits_{ D}156 dA=156\int \int\limits_{ D} 1 dA$$
$$=156\int_{0}^{2\pi}\int_{0}^{4}1dxd\theta=156\int_{0}^{2\pi}d\theta\cdot \int_{0}^{4}dx=156\cdot (\theta)\bigg|_{0}^{2\pi}\cdot (x)\bigg|_{0}^{4}=156\cdot 2\pi \cdot 4=1248 \pi.$$
Passe para coordenadas polares e calcule: $\displaystyle\iint\limits_{D}e^{-x^{2}-y^{2}}\,dA$, onde $D$ é a região delimitada pelo semicírculo $x=\sqrt{4-y^{2}}$ e o eixo $y.$
$\displaystyle \frac{\pi}{2} (1 - e^{-4}).$
Verifique que a função $u=1/\sqrt{x^{2}+y^{2}+z^{2}}$ é uma solução da equação de Laplace tridimensional $u_{xx}+u_{yy}+u_{zz}=0.$
$\displaystyle u_{xx} = \frac{2x^{2} - y^{2} - z^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}},\;\;\; u_{yy} = \frac{2y^{2} - x^{2} - z^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}}\;\;\;\text{e}\;\;\;u_{zz} = \frac{2z^{2} - x^{2} - y^{2}}{(x^{2} + y^{2} + z^{2})^{5/2}}$.
Utilize as Equações
$\dfrac{\partial z}{\partial x}=-\dfrac{\dfrac{\partial F}{\partial x}}{\dfrac{\partial F}{\partial z}}$ e $\dfrac{\partial z}{\partial y}=-\dfrac{\dfrac{\partial F}{\partial y}}{\dfrac{\partial F}{\partial z}}$
para determinar $\partial z/\partial x$ e $\partial z/\partial y$.
$xyz=\cos(x+y+z)$
$\displaystyle \frac{dz}{dx} = \frac{yz + \sin(x + y + z)}{xy + \sin(x + y + z)}$ e $\displaystyle \frac{dz}{dy} = \frac{xz + \sin(x + y + z)}{xy + \sin(x + y + z)}.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{1} \int_{0}^{\sqrt{1-y^{2}}}(x^{2}+y^{2})\,dx dy$
$\displaystyle \frac{\pi}{8}.$
Calcule $D_{\bf{u}}f(x_0,y_0)$, sendo dados
$f(x,y) = xy$, $(x_0,y_0) = (1,1)$ e $\bf{u}$ o versor de $\bf{i} + \bf{j}$.
$\displaystyle D_{\bf{(1,1)}}f(1,1) = \sqrt{2}.$
Use o Teorema de Green para determinar o trabalho realizado pelo campo de forças \(\displaystyle\mathbf{F}(x,y)=\sqrt{y}\textbf{i}+\sqrt{x}\textbf{j}\) sobre uma partícula que percorre uma vez, no sentido anti-horário, a curva fechada dada pelas equações \(y=0\), \(x=2\) e \(y=x^3/4\).
Determine o maior conjunto no qual a função $G(x,y) = \ln{(x^2 + y^2 - 4)}$ é contínua.
$\left\lbrace (x,y);\;x^{2} + y^{2} > 4 \right\rbrace.$
Determine a equação dos planos tangentes ao gráfico de $f(x,y) = - x^2 - y^2$ que passam por ambos os pontos $(1,0,7)$ e $(3,0,3)$.
$2x + 2y + z = 9$ e $2x - 2y + z = 9.$
Passe para coordenadas polares e calcule: $\displaystyle\int_{0}^{a} \int_{0}^{\sqrt{a^{2}-x^{2}}}\,dy dx$
$\dfrac{\pi a^2}{4}.$
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}(x^{2}y^{3}-\sqrt{x})\,dy$, $C$ é o arco da curva $y=\sqrt{x}$ de $(1,1)$ a $(4,2).$
$\dfrac{243}{8}.$
Nos item abaixo:
- expresse $\mathrm{d} w/\mathrm{d} t$ como uma função de $t$, usando a Regra da Cadeia, expressando $w$ em termos de $t$ e diferenciando em relação a $t$;
- calcule $\mathrm{d} w/\mathrm{d} t$ no valor dado de $t$.
$w=x^{2}+y^{2}$, $x=\cos{t}$, $y=\sin{t}$; $t=\pi.$
- $\displaystyle \frac{dw}{dt}(t) = 0.$
- $\displaystyle \frac{dw}{dt}(\pi) = 0.$
Determine as derivadas parciais de $z=\dfrac{x^{3}+y^{2}}{x^{2}+y^{2}}$.
$\displaystyle \frac{\partial z}{\partial x} = \frac{x^{4} + 3x^{2}y^{2} - 2xy^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial z}{\partial y} = \frac{2x^{2}y(1 - x)}{(x^{2} + y^{2})^{2}}.$
Determine as derivadas parciais de primeira ordem da função $u=te^{w/t}$.
$\displaystyle \frac{\partial u}{\partial t} = e^{w/t} \left( 1 - \frac{w}{t} \right)\;\;\;\text{e}\;\;\; \frac{\partial u}{\partial w} = e^{w/t}$.
Esboce o campo vetorial ${\bf F}(x,y)=(x-y)\textbf{i} + x \textbf{j}$, desenhando um diagrama.
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} \sin{(4x^2 + y^2)} \, dA$, em que $R$ é o cojunto de todos $(x,y)$ tais que $4x^2 + y^2 \leq 1$ e $y \geq 0$.
$\dfrac{\pi}{4}(1 - \cos(1)).$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}\frac{x}{x^{2}+y^{2}}\,dA$, onde $R=\{(x,y)\in \mathbb{R}^{2}| x^{2}+y^{2}\leq 4, x\geq 1\}.$
$2\sqrt{3}.$
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} x \, dA$, em que $R$ é o círculo $x^2 + y^2 - x \leq 0$.
$\dfrac{\pi}{8}.$
Uma casca cilíndrica tem $20$ cm de comprimento, com raio interno de 6 cm e raio externo de $7$ cm. Escreva desigualdades que descrevam a casca em um sistema de coordenadas adequado. Explique como você posicionou o sistema de coordenadas em relação à casca.
$6 \leq r \leq 7,$ $0 \leq \theta \leq 2\pi,$ $0 \leq z \leq 20.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x_1,x_2, \ldots, x_n) = x_1 + x_2 + \cdots + x_n; \quad x_1^2 + x_2^2 + \cdots + x_n^2 = 1.$
Valor máximo: $\sqrt{n};$ valor mínimo: $-\sqrt{n}.$
Considere o campo vetorial \[\mathbf{F}(x,y,z)=(x-z)\mathbf{i}+(y-x)\mathbf{j}+(z-xy)\mathbf{k}. \]
Use o Teorema de Stokes para encontrar a circulação em torno do triângulo de vértices \(A=(1,0,0)\), \(B=(0,2,0)\) e \(C=(0,0,1)\), orientado no sentido anti-horário quando visto da origem para o primeiro octante.
Encontre a densidade de circulação de \(\mathbf{F}\) na origem na direção de \(\mathbf{k}\), ou seja, \(\displaystyle\mathrm{rot\,}\mathbf{F}(\mathbf{0})\cdot\mathbf{k}\).
Encontre o vetor unitário \(\mathbf{n}\) tal que a densidade de circulação de \(\mathbf{F}\) na origem seja máxima na direção de \(\mathbf{n}\).
\(\dfrac{3}{2}\)
\(-1\)
\(\displaystyle \mathbf{n}= -\dfrac{1}{\sqrt{2}}\mathbf{j} -\dfrac{1}{\sqrt{2}}\mathbf{k} \)
Uma partícula move-se no plano de modo que no instante $t$ sua posição é dada por ${\bf r}(t)=(t,t^{2})$. Calcule o trabalho realizado pelo campo de forças ${\bf F}(x,y)=(x+y)\,{\bf i}+(x-y)\,{\bf j}$ no deslocamento da partícula de ${\bf r}(0)$ até ${\bf r}(1).$
$1.$
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = 2x^2y$ em $(1,1,f(1,1))$.
Plano tangente: $z = 4x + 2y - 4$
Reta normal: $(x,y,z) = \left(1,1,2 \right) + \lambda \left(4,2,-1 \right)$.
Se $z=f(x,y)$ com $x=u+v$ e $y=u-v$, demonstre que
$$\frac{\partial z}{\partial u}+\frac{\partial z}{\partial v}=2 \frac{\partial f}{\partial x}.$$
Note que $\displaystyle \frac{\partial z}{\partial u} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y}$ e $\displaystyle \frac{\partial z}{\partial v} = \frac{\partial f}{\partial x} - \frac{\partial f}{\partial y}.$
Determine a taxa de variação máxima de $f$ no ponto dado e a direção em que isso ocorre.
$f(x,y,z) = \sqrt{x^2 + y^2 + z^2}, (3,6,-2).$
$1.$
Considere a integral
$$\int_{0}^{1}\!\!\int_{x^{2}}^{1}x^{3}\sin{y^{3}}\,dy dx.$$
Desenhe a região de integração.
Calcule o valor da integral.
$\dfrac{1 - \cos(1)}{12}$.
Calcule a integral de superfície $\displaystyle\iint\limits_{S}\dfrac{z}{\sqrt{1+4x^{2}+4y^{2}}}dS$, onde $S$ é a parte do parabolóide
$z=1-x^{2}-y^{2}$ que se encontra dentro do cilindro $x^{2}+y^{2}\leq 2y.$
Parametrizando a superfície $S$, temos as equações paramétricas:
$x=u, y=v \, \mbox{e} \, z=1-u^{2}-v^{2}.$
Então,
${\bf r}(u,v)=u{\bf i}+v{\bf j}+(1-u^{2}-v^{2}){\bf k}.$
Logo,
$f({\bf r}(u,v))=\dfrac{1-u^{2}-v^{2}}{\sqrt{1-4u^{2}-4v^{2}}},$ ${\bf r}_{u}={\bf i}+0{\bf j}-2u{\bf k}$ e ${\bf r}_{v}=0{\bf i}+{\bf j}-2v{\bf k}.$
Temos que
${\bf r}_{u}\times {\bf r}_{v}=\left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k}\\ 1 & 0 & -2u\\ 0 & 1 & -2v \end{array} \right| = 2u{\bf i}+2v{\bf j}+{\bf k}$,
implicando que $|{\bf r}_{u}\times {\bf r}_{v}|=\sqrt{(2u)^{2}+(2v)^{2}+1^{2}}=\sqrt{1+4u^{2}+4v^{2}}.$ Assim,
$\displaystyle\iint\limits_{S}\dfrac{z}{\sqrt{1+4x^{2}+4y^{2}}}dS=\displaystyle\iint\limits_{D} f({\bf r}(u.v))|{\bf r}_{u}\times {\bf r}_{v}| du dv$ $=\displaystyle\iint\limits_{D} \frac{1-u^{2}-v^{2}}{\sqrt{1-4u^{2}-4v^{2}}} \sqrt{1+4u^{2}+4v^{2}} du dv=\displaystyle\iint\limits_{D}(1-u^{2}-v^{2})du dv$.
Notemos que
$D=\{(u,v)| u^{2}+v^{2}\leq 2v\}=\{(u,v)|u^{2}+(v-1)^{2}\leq 1\}.$
Em coordenadas polares teremos que
$u=r\cos \theta, v-1=r\sin \theta,$
$du dv=\left| \begin{array}{cc}
\dfrac{\partial u}{\partial r} & \dfrac{\partial u}{\partial \theta}\\
\dfrac{\partial v}{\partial r} & \dfrac{\partial v}{\partial \theta}
\end{array} \right|$, $ dr d\theta=\left| \begin{array}{cc} \cos \theta & -r\sin \theta\\ \sin \theta & r\cos \theta \end{array} \right| \, e \, du dv=r dr d\theta.$
Como $u^{2}+u^{2}=2u \Rightarrow r^{2}\cos^{2}\theta+r^{2}\sin^{2}\theta=r\sin \theta \Rightarrow r=2\sin \theta,$ então $0\leq r \leq 2\sin \theta \, \mbox{e} \, 0 \leq \theta \leq \pi.$
Logo
$\displaystyle\iint\limits_{S}\dfrac{z} {\sqrt{1+4x^{2}+4y^{2}}}dS=\displaystyle\int_{0}^{\pi}\displaystyle\int_{0}^{2\sin \theta}(1-r^{2}\cos^{2} \theta-r^{2}\sin^{2}\theta)r dr d\theta$
$\displaystyle\int_{0}^{\pi}\displaystyle\int_{0}^{2\sin \theta}(1-r^{2})r dr d\theta=\displaystyle\int_{0}^{\pi}\int_{0}^{2\sin \theta}(r-r^{3})dr d\theta$ $=\displaystyle\int_{0}^{\pi}(2\sin^{2}\theta-4\sin^{4}\theta)\bigg|_{0}^{2\sin \theta}d\theta=2\int_{0}^{\pi}\sin^{2}\theta d\theta-4\int_{0}^{\pi}\sin^{4}\theta$
$=2\cdot\left(\dfrac{\theta}{2}-\frac{1}{4}\sin 2\theta\right)\bigg|_{0}^{\pi}-4\cdot \left(-\dfrac{1}{4}\sin^{3}
\theta \cos \theta+\dfrac{3}{8}\theta-\dfrac{3}{16}\sin 2\theta\right)\bigg|_{0}^{\pi}$
$=2\cdot \dfrac{\pi}{2}-4\cdot\left(\dfrac{3}{8}\pi\right)=-\dfrac{\pi}{2}.$
Demonstre a identidade abaixo, supondo que $S$ e $E$ satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda ordem contínuas.
- $\displaystyle\iint\limits_{S}(f\nabla g)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E}(f\nabla^{2}g+\nabla f+\nabla g)\,dV.$
Note que $\displaystyle\iint\limits_{S}(f\nabla g)\cdot {\bf n}\,dS=\displaystyle\iiint\limits_{E} \mbox{div} (f\nabla g)\,dV.$
Use o Teorema de Green para determinar o trabalho realizado pelo campo de forças \(\displaystyle\textbf{F}(x,y)=xy\textbf{i}+(\dfrac{1}{2}x^2+xy)\textbf{j}\) sobre uma partícula que se move ao longo do caminho que começa em \((5,0)\), percorre o semicírculo superior \(x^2+y^2=25\) e retorna ao seu ponto de partida ao longo do eixo \(x\).
\(\dfrac{250}{3}\)
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq z\leq 2x.$
$x\leq z\leq1-y^{2}$ e $x\geq 0.$
$\dfrac{\pi}{2}.$
$\dfrac{8}{15}.$
Calcule $\displaystyle\iint\limits_{B}f(x,y)\,dx dy$ sendo dados:
$f(x,y)=x\cos{y}$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;x\geq 0,\;x^{2}\leq y\leq \pi\}.$
$f(x,y)=xy$ e $B=\{(x,y)\in \mathbb{R}^{2}|\;x^{2}+y^{2}\leq 2,\;y\leq x\;e\;x\geq 0\}.$
$f(x,y)=x$ e $B$ o triângulo de vértices $(0,0)$, $(1,1)$ e $(2,0).$
$f(x,y)=xy\sqrt{x^{2}+y^{2}}$ e $B$ o retângulo $0\leq x\leq 1$, $0\leq y\leq 1.$
$f(x,y)=x+y$ e $B$ o paralelogramo de vértices $(0,0)$, $(1,1)$, $(3,1)$ e $(2,0).$
$-1.$
$-\dfrac{1}{4}$.
$1.$
$\dfrac{2(2\sqrt{2} - 1)}{15}.$
$4.$
Calcule $\displaystyle\iint\limits_{S}g(x,y,z)dS,$ onde $g(x,y,z)=(x^{2}+y^{2}+z^{2})^{1/2}$ e $S$ é a porção do parabolóide $2z=x^{2}+y^{2}$ interior ao cilindro $x^{2}+y^{2}=2y.$
$\dfrac{5\pi}{2}.$
Represente graficamente o domínio da função $z=f(x,y)$ dada por $z=\ln(2x^{2}+y^{2}-1)$.
$\left\lbrace (x,y); 2x^{2} + y^{2} > 1 \right\rbrace$
Verifique que a função $f(x,y) = \arctan{xy}$ é diferenciável.
As derivadas parciais $\frac{\partial f}{\partial x}$ e $\frac{\partial f}{\partial y}$ de cada função $f$ existem e são contínuas em todos os pontos do domínio.
Em que direção e sentido a função dada cresce mais rapidamente no ponto dado? E em que direção e sentido decresce mais rapidamente?
$f(x,y) = \sqrt{4 - x^2 - 2y^2}$ em $\left(1,\dfrac{1}{2}\right)$.
Cresce: $(-1,-1)$; descresce: $(1,1).$
Esboce o gráfico da função $f(x,y)=3$.
$z = 3.$
Seja $D$ a região limitada por um caminho fechado e simples $C$ no plano $xy$. Utilize o Teorema de Green para demonstrar que as coordenadas do centroide $(\bar{x},\bar{y})$ de $D$ são
$$\bar{x} = \dfrac{1}{2A}\oint_{C}x^2 \, dy \quad \quad\quad\quad \bar{y} = -\dfrac{1}{2A}\oint_{C}y^2 \, dx,$$
em que $A$ é a área de $D$.
$\dfrac{1}{2A}\oint_{C}x^2 \, dy = \dfrac{1}{2A} \iint_{D} 2x \, dA = \bar{x}$ e $-\dfrac{1}{2A}\oint_{C}y^2 \, dx = -\dfrac{1}{2A}\iint_{D} (-2y) \, dA = \bar{y}$
Determine a derivada direcional de $f$ no ponto dado e na direção indicada pelo ângulo $\theta$.
$f(x,y) = ye^{-x}, (0,4),$ $\theta = 2\pi/3$.
$2 + \frac{\sqrt{3}}{2}.$
Suponha que \(f(x,y)\) seja uma função diferenciável no ponto \((x_0,y_0)\) e seja \(z_0=f(x_0,y_0)\). Mostre que a função \(\displaystyle g(x,y,z)=z-f(x,y)\) é diferenciável em \((x_0,y_0,z_0)\).
Escreva seis integrais triplas iteradas diferentes para o volume do sólido retangular no primeiro octante limitado pelos planos coordenados e pelos planos $x=1$, $y=2$ e $z=3$. Calcule uma das integrais.
$$\begin{split} 6 &= \int_{0}^{1}\int_{0}^{2}\int_{0}^{3} dz dy dx = \int_{0}^{2}\int_{0}^{1}\int_{0}^{3} dz dx dy = \int_{0}^{3}\int_{0}^{2}\int_{0}^{1} dx dy dz\\ &= \int_{0}^{2}\int_{0}^{3}\int_{0}^{1} dx dz dy = \int_{0}^{3}\int_{0}^{1}\int_{0}^{2} dy dx dz = \int_{0}^{1}\int_{0}^{3}\int_{0}^{2} dy dx dx. \end{split} $$
Dados ${\bf F}(x,y)=xy^{2}\,{\bf i}+x^{2}y\,{\bf j}$, $C: {\bf r}(t)=(t+\sin\frac{1}{2}\pi t, t+\cos \frac{1}{2}\pi t)$, $0\leq t\leq 1.$
Determine uma função $f$ tal que ${\bf F}=\nabla f$.
Use o resultado anterior para calcular $\int_{C}{\bf F}\cdot d{\bf r}$ sobre a curva $C$ dada.
$f(x,y) = \dfrac{x^{2}y^{2}}{2};$
$2.$
Calcule a área sob um arco da cicloide $x = t-\sin{t}$, $y = 1-\cos{t}$.
Queremos determinar a área da região $R$ mostrada na figura abaixo.
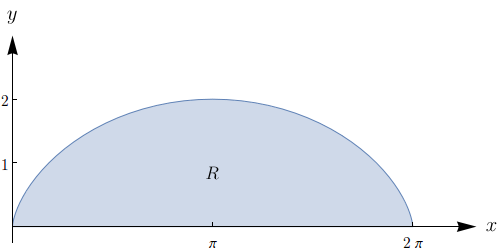
Sabemos que, se $y = f(x)$, então a integral $\int_{a}^{b}f(x)dx$ calcula a área que está abaixo do gráfico de $f$ e acima do eixo $x$, com $x$ variando entre $a$ e $b$. A princípio, poderíamos tentar encontrar uma expressão que relacionasse $x(t)$ e $y(t)$ na parametrização da cicloide, mas esse parece ser um trabalho difícil. Usaremos então o que foi provado no exercício anterior. Temos que
$$A(R) = \oint_{C}x\, dy,$$
em que $C = C_1 \cup C_2$ é a curva descrita na figura a seguir.
Uma parametrização de $C_1$ é $r_1(t) = (x_1(t),y_1(t)) = (t,0)$, em que $0 \leq t \leq 2\pi$. Nesse caso, $y_1'(t) = 0$. Logo,
$$\oint_{C_1}x\, dy = \int_{0}^{2\pi}(t)(0)\, dt = 0.$$
Uma parametrização de $C_2$ é $r_2(t) = (x_2(t),y_2(t)) = (t-\sin{t},1-\cos{t})$, em que $t$ varia de $2\pi$ a $0$. Nesse caso, $y_2'(t) = \sin{t}$. Logo,
$$\begin{array}{rcl}\displaystyle \oint_{C_2}x\, dy & = & \displaystyle \int_{2\pi}^{0}(t-\sin{t}) (\sin{t})\, dt \\ & = & \displaystyle \int_{0}^{2\pi}(\sin^2{t} - t\sin{t}) \, dt \\ & = & \displaystyle \int_{0}^{2\pi}\frac{1-\cos(2t)}{2}\, dt - \int_{0}^{2\pi}t\sin{t} \, dt \\ & = & \pi + 2\pi = 3\pi.\end{array}$$
Portanto, a área da região é $3\pi$.
(Observe que, para resolver a integral $\int_{0}^{2\pi}t\sin{t} \, dt$, usamos integração por partes com $u=t$ e $dv=\sin{t}\,dt$.)
Calcule a integral de superfície $\displaystyle\iint \limits_{ S}{\bf F}\cdot d{\bf S}$ para o campo vetorial ${\bf F}$ e superfície orientada $S$ dados abaixo. Em outras palavras, determine o fluxo de ${\bf F}$ através de $S$. Para superfícies fechadas, use a orientação positiva (para fora).
- ${\bf F}(x,y,z)=xy{\bf i}+yz{\bf j}+zx{\bf k}$ e $S$ é a parte do parabolóide $z=4-x^{2}-y^{2}$ que está acima do quadrado $0\leq x\leq 1$, $0\leq y\leq 1$, com orientação para cima.
$\dfrac{713}{180}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=\sin{x}\,{\bf i}+\cos{y}\,{\bf j}+xz\,{\bf k}$, ${\bf r}(t)=t^{3}\,{\bf i}-t^{2}\,{\bf j}+t\,{\bf k}$, $0\leq t\leq 1.$
$\dfrac{6}{5} - \cos(1) - \sin(1).$
Determine os valores máximo e mínimo absolutos de
$$f(x,y) = x^2 + 2y^2 - x$$
no conjunto $D = \{(x,y) \in \mathbb{R}^2: x^2 + y^2 \leq 1 \}$.
Valor máximo: $\dfrac{9}{4};$ valor mínimo: $-\dfrac{1}{4}.$
Seja
$$\mathbf{F}(x,y) = \dfrac{x}{(x^2+y^2)^5}\mathbf{i} + \dfrac{y}{(x^2+y^2)^5}\mathbf{j}$$
e $\mathbf{n}$ a normal unitária exterior ao círculo $x^2 + y^2 \leq 1$. Calcule $\int_{C} \mathbf{F} \cdot \mathbf{n} \, ds$, em que $C$ é dada por $\mathbf{r}(t) = (\cos{t},\sin{t})$, $0 \leq t \leq \pi$. (Sugestão: Verifique que $\mathbf{F} \cdot \mathbf{n}$ é constante.)
$\pi.$
Considere a função $F(x,y)=f\bigg(\dfrac{x}{y},\dfrac{y}{x}\bigg)$. Mostre que
$$x\dfrac{\partial F}{\partial x}+y\dfrac{\partial F}{\partial y}=0.$$
Note que$\displaystyle \frac{\partial F}{\partial x} = \frac{1}{y}\frac{\partial f}{\partial x}\left(\frac{x}{y}, \frac{y}{x} \right) - \frac{y}{x^{2}} \frac{\partial f}{\partial y}\left(\frac{x}{y}, \frac{y}{x} \right)$ e $\displaystyle \frac{\partial F}{\partial y} = -\frac{x}{y^{2}} \frac{\partial f}{\partial x}\left(\frac{x}{y}, \frac{y}{x} \right) + \frac{1}{x} \frac{\partial f}{\partial y}\left(\frac{x}{y}, \frac{y}{x} \right).$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C} \sin{y} \, dx + x\cos{y} \, dy$, $C$ é a elipse $x^2 + xy + y^2 = 1$.
$0.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y,z)=x\,{\bf i}+y\,{\bf j}+z\,{\bf k}$, ${\bf r}(t)=(\cos t,\sin t,t)$, $0\leq t\leq 2\pi.$
$2\pi^{2}.$
Determine os momentos de inércia da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
$\displaystyle I_{x} = \dfrac{1}{16}(e^4 - 1),$ $I_{y} = \dfrac{1}{16}(e^4 - 1)$ e $I_{0} = \dfrac{1}{16}(e^4 + 2e^2 - 3).$
Determine o jacobiano da transformação dada por: $x = 5u - v, \quad y = u + 3v$.
$16.$
Calcule $D_{\bf{u}}f(x_0,y_0)$, sendo dados
$f(x,y) = x^2 - 3y^2$, $(x_0,y_0) = (1,2)$ e $\bf{u}$ o versor de $2\bf{i} + \bf{j}.$
$\displaystyle D_{\bf{(2,1)}}f(1,2) = -\frac{8}{5}.$
Calcule a integral de linha $\int_{C}{\bf F}\cdot d{\bf r}$, onde $C$ é dada pela função vetorial ${\bf r}(t).$
${\bf F}(x,y)=xy\,{\bf i}+3y^{2}\,{\bf j}$, ${\bf r}(t)=11t^{4}\,{\bf i}+t^{3}\,{\bf j}$, $0\leq t\leq 1.$
$45.$
Dada a expressão $g(x,y)=2-f(x,y)$, escreva como o gráfico de $g$ é obtido a partir do gráfico de $f.$
Gráfico de $f$ refletido sobre o plano $xy$ e deslocado para cima por duas unidades.
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy \ \mbox{cos} \ y}{3x^2 + y^2}$.
Não existe.
Faça um esboço grande da curva descrita pela função vetorial ${\bf r}(t)=(t^{2},t)$, $0\leq t\leq 2$, e desenhe os vetores ${\bf r}(1)$, ${\bf r}(1,1)$ e ${\bf r}(1,1)-{\bf r}(1)$.
Desenhe o vetor ${\bf r}(1)$ começando em $(1,1)$ e compare com o vetor $$\frac{{\bf r}(1,1)-{\bf r}(1)}{0,1}.$$
Cada integral iterada abaixo representa o volume de um sólido. Faça um esboço do sólido. (Não é necessário calcular o volume.)
\(\displaystyle \int_0^5\int_1^2 4\, dxdy\)
\(\displaystyle \int_0^3\int_0^4\sqrt{25-x^2-y^2}\,dydx\)
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}2\,dx-dy$, $C$ tem por imagem $x^{2}+y^{2}=4$, $x\geq 0$ e $y\geq 0$; sentido de percurso é de $(2,0)$ para $(0,2).$
$\displaystyle -6.$
Calcule a integral de linha $\displaystyle\int_{C}\,dx+\,dy$, onde $C$ é a poligonal de vértices $A_{0}=(0,0)$, $A_{1}=(1,2)$, $A_{2}=(-1,3)$, $A_{3}=(-2,1)$ e $A_{4}=(-1,-1)$, sendo $C$ orientada de $A_{0}$ para $A_{4}.$
$\displaystyle -2.$
aberto;
conexo; e
simplesmente conexo.
Temos que o conjunto $D=\{(x,y)|\,x\neq 0\}$ consiste de todos os pontos, exceto para aqueles que encontram-se sobre o eixo y. Então:
$D$ é aberto.
Os pontos em lados opostos do eixo $y$ não podem ser conectados por um caminho que se encontra totalmente em $D$, então $D$ não é conexo.
$D$ não é simplesmente conexo, pois não é conexo.
Mostre que um campo de força constante realiza trabalho nulo sobre um partícula que dá uma única volta completa uniformemente na circunferência $x^{2}+y^{2}=1.$
Isso também é verdadeiro para um campo de força ${\bf F}({\bf x})=k{\bf x}$, onde $k$ é uma constante e $\textbf{x}=x{\bf i}+y{\bf j}$?
Dica: tome a parametrização do círculo $C$ dada por $x = cos(t)$ e $y = \sin(t),$ com $t \in [0,2\pi]$ e considere um campo constante arbitrário ${\bf F} = (a,b).$ Segue que $W = \int_{C} F\cdot d\textbf{r} = 0.$
Sim. Realize o mesmo cálculo com ${\bf F}(x,y) = (k x, ky).$
Seja \(G\) a caixa retangular definida pelas desigualdades \(a\leq x\leq b\), \(c\leq y\leq d\) e \(k\leq z\leq l\). Mostre que \[\iiint\limits_G f(x)g(y)h(z)\,dV = \left[\int_a^bf(x)\,dx\right]\left[\int_c^dg(y)\,dy\right]\left[\int_k^lh(z)\,dz\right].\]
Determine o jacobiano da transformação dada por: $x = uv, \quad y = vw, \quad z = uw$.
$2uvw.$
Determine o limite, se existir, ou mostre que o limite não existe.
$\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{x^2ye^y}{x^4 + 4y^2}$.
Não existe.
Não existe.
Inverta a ordem de integração.
$\displaystyle\int_{-1}^{1}\bigg[\int_{x^{2}}^{\sqrt{2-x^{2}}}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{y-1}^{2-2y}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{0}^{1}\bigg[\int_{x^{2}}^{1}f(x,y)\,dy\bigg]dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{-\sqrt{y}}^{\sqrt{y}}f(x,y)\,dx\bigg]dy + \displaystyle\int_{1}^{\sqrt{2}}\bigg[\int_{-\sqrt{2 - y^{2}}}^{\sqrt{2-y^{2}}}f(x,y)\,dx\bigg]dy$
$\displaystyle\int_{-1}^{0}\bigg[\int_{0}^{x + 1}f(x,y)\,dy \bigg] dx + \int_{0}^{2}\bigg[\int_{0}^{\frac{2-x}{2}}f(x,y)\,dy \bigg] dx$
$\displaystyle\int_{0}^{1}\bigg[\int_{0}^{\sqrt{y}}f(x,y)\,dx\bigg]dy$
Use o Teorema de Green para provar que\[ \int_Cf(x)\,dx + g(y)\,dy = 0\] se \(f\) e \(g\) forem funções diferenciáveis e \(C\) for uma curva fechada simples lisa por partes.
O que isso nos diz sobre o campo vetorial \[ \mathbf{F}(x,y) = f(x)\mathbf{i}+g(y)\mathbf{j}?\]
O comprimento $l$, a largura $w$ e a altura $h$ de uma caixa variam com o tempo. Em certo instante, as dimensões da caixa são $l=1m$ e $w=h=2m$. $l$ e $w$ aumentam a uma taxa de $2m/s$, ao passo que $h$ diminui a uma taxa de $3m/s$. Nesse instante, determine as taxas nas quais as seguintes quantidades estão variando.
- O volume.
- A área da superfície.
- O comprimento da diagonal.
- $6$ m$^3$/s.
- $10$ m$^2$/s.
- $0$ m/s.
Encontre a área da parte da superfície \(z=\sqrt{4-x^2}\) que fica acima do retângulo \(R\) do plano \(xy\) cujas coordenadas satisfazem \(0\leq x\leq 1\) e \(0\leq y\leq 4\).
A superfície é uma parte do cilindro \(x^2+z^2=4\) localizada no primeiro octante. Neste caso, como \(z=f(x,y)\), podemos tomar \(x=u\) e \(y=v\) como parâmetros. Assim, teremos que \(\displaystyle \mathbf{r}=u\mathbf{i}+v\mathbf{j}+f(u,v)\mathbf{k} \) e \[ \|\dfrac{\partial\mathbf{r}}{\partial u}\times \dfrac{\partial \mathbf{r}}{\partial v}\| = \sqrt{\left(\dfrac{\partial z}{\partial x}\right)^2+\left(\dfrac{\partial z}{\partial y}\right)^2+1}.\] Segue para a área que \begin{align*} S & = \iint\limits_R\sqrt{\left(\dfrac{\partial z}{\partial x}\right)^2+\left(\dfrac{\partial z}{\partial y}\right)^2+1}\,dA \\ & = \iint\limits_R\sqrt{\left(-\dfrac{x}{\sqrt{4-x^2}}\right)^2+ 0 + 1}\,dA = \int_0^4\int_0^1\dfrac{2}{\sqrt{4-x^2}}\,dxdy \\ & = 2\int_0^4\left[\arcsin\left(\dfrac{1}{2}x\right)\right]_{x=0}^1\,dy = 2\int_0^4\dfrac{\pi}{6}\,dy = \dfrac{4}{3}\pi. \end{align*}
Seja ${\bf F}$ um campo inverso do quadrado, ou seja, ${\bf F}(r)=cr/|r|^{3}$ para alguma constante $c$, onde $r=x{\bf i}+y{\bf j}+z{\bf k}.$ Mostre que o fluxo de ${\bf F}$ por uma esfera $S$ com centro na origem é independente do raio de $S.$
$\displaystyle \iint\limits_{S}{\bf F}\cdot d \bf S = 4\pi c.$
Considere o vetor unitário $\bf{u} = (\sqrt{3}/2,1/2)$ e a função
$$f(x,y) = \begin{cases}
\dfrac{xy^2}{x^2 + y^4}, & \text{se } (x,y) \neq (0,0),\\ 0, & \text{se } (x,y) = (0,0).\end{cases}$$
- Determine a derivada direcional $D_{\bf{u}}f(0,0)$.
- Explique por que o produto escalar $\nabla f(0,0) \cdot \bf{u}$ não fornece a derivada direcional de $f$ em $(0,0)$ na direção de $\bf{u}$.
- $\displaystyle \frac{\sqrt{3}}{6}.$
- Pois $f$ não é diferenciável em $(0,0),$ já que não é contínua nesse ponto.
Seja $f$ uma função de três variáveis independentes $x,y$ e $z$. Mostre que $D_{\bf{i}}f = f_x$, $D_{\bf{j}}f = f_y$ e $D_{\bf{k}}f = f_z$.
Lembre que $\bf{i} = (1,0,0),$ $\bf{j} = (0,1,0),$ $\bf{k} = (0,0,1)$ e $D_{\bf{u}}f = \nabla f \cdot \bf{u}.$
Mostre que a função vetorial
$$\textbf{r}(t) = (2\textbf{i} + 2\textbf{j} + \textbf{k}) + (\cos{t})\left( \dfrac{1}{\sqrt{2}}\textbf{i} - \dfrac{1}{\sqrt{2}}\textbf{j} \right) + (\sin{t})\left( \dfrac{1}{\sqrt{3}}\textbf{i} + \dfrac{1}{\sqrt{3}}\textbf{j} + \dfrac{1}{\sqrt{3}}\textbf{k} \right)$$
descreve o movimento de uma partícula no círculo de raio $1$ centrado no ponto $(2,2,1)$ e contido no plano $x + y - 2z = 2$.
Suponha que a temperatura, em graus Celsius, num ponto \((x,y)\) de uma chapa metálica plana seja \( T(x,y)=10-8x^2-2y^2 \), onde \(x\) e \(y\) são medidos em metros. Calcule a temperatura média da porção retangular da chapa dada por \(0\leq x\leq 1\) e \(0\leq y\leq 2\).
\(\dfrac{14}{3}\) \({}^\circ\)C
Encontre uma equação para a curva de nível da função $f(x,y)=16-x^{2}-y^{2}$ que passa pelo ponto $(2\sqrt{2},\sqrt{2})$.
$x^{2} + y^{2} = 10.$
Considere a função $f(x,y)=x^{2}+y^{2}+2xy-x-y+1$ no quadrado $0\leq x\leq 1$ e $0\leq y\leq 1$.
Mostre que $f$ tem um mínimo absoluto ao longo do segmento de reta $2x+2y=1$ nesse quadrado. Qual é o valor mínimo absoluto?
Encontre o valor máximo absoluto de $f$ no quadrado.
$\displaystyle \frac{3}{4}.$
$f(1,1) = 3.$
Escreva a equação $z^{2}=x^{2}+y^{2}$ em coordenadas esféricas.
$\cos^2 \phi = \sin^2 \phi.$
A parte da superfície \[ z= \dfrac{h}{a}\sqrt{x^2+y^2}\quad\left(a,\ h>0\right) \] entre o plano \(xy\) e o plano \(z=h\) é um cone circular reto de altura \(h\) e raio \(a\). Use uma integral dupla para mostrar que a área da superfície lateral desse cone é dada por \(\displaystyle S=\pi a\sqrt{a^2+h^2}\).
Calcule $\mathrm{d} z/\mathrm{d} t$ por dois processos:
- substituindo as expressões para $x(t)$ e $y(t)$ em $z$ e depois derivando diretamente com relação a $t$
- aplicando a Regra da Cadeia: $\frac{dz}{dt}=\frac{\partial z}{\partial x}\frac{dx}{dt}+\frac{\partial z}{\partial y }\frac{dy}{dt}$.
$z=\ln(1+x^{2}+y^{2})$, $x=\sin{3t}$ e $y=\cos{3t}.$
$\displaystyle \frac{dz}{dt} (t) = 0.$
Calcule $\displaystyle\iint\limits_{B} y\,dx dy$, onde $B$ é o conjunto dado.
$B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(1,1)$.
$B=\{(x,y)\in \mathbb{R}^{2}|\;-1\leq x\leq 1,\;0\leq y\leq x+2\}.$
$B$ é o conjunto de todos $(x,y)$ tais que $x^{2}+4y^{2}\leq 1.$
$B$ é o triângulo de vértices $(0,0)$, $(1,0)$ e $(2,1).$
$\dfrac{1}{6}$.
$\dfrac{13}{3}$.
$0$.
$\dfrac{1}{6}$.
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y,z) = x^4 + y^4 + z^4; \quad x^2 + y^2 + z^2 = 1.$
Valor máximo: $1;$ valor mínimo: $\dfrac{1}{3}.$
Mostre que os limites não existem, considerando que \((x,y)\rightarrow (0,0) \) ao longo dos eixos coordenados.
\[ \lim_{(x,y)\to(0,0)}\dfrac{3}{x^2+2y^2} \]
\[ \lim_{(x,y)\to(0,0)}\dfrac{x+y}{2x^2+y^2} \]
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x^{2}y\sqrt{z}\,dz$, $C:\,x=t^{3},\, y=t,\, z=t^{2},\, 0\leq t\leq 1.$
$\dfrac{1}{5}.$
Calcule a integral dupla usando coordenadas polares: $\displaystyle\iint\limits_{R}(x^{2}+2y)\,dx dy$, onde $R$ é o círculo $x^{2}+y^{2}\leq 4.$
$4\pi.$
Use a integral dupla em coordenadas polares para deduzir a fórmula $$A=\int_{\alpha}^{\beta}\frac{1}{2} r^{2}\,d\theta$$ para a área da região em formato de leque entre a origem e a curva polar $r=f(\theta)$, $\alpha\leq \theta \leq \beta.$
Note que $\displaystyle A = \int_{\alpha}^{\beta}\int_{0}^{f(\theta)} r dr d\theta. $
Utilize a Regra da Cadeia para determinar as derivadas parciais indicadas.
$Y=w\tan^{-1}(uv)$, $u=r+s$, $v=s+t$; $w=t+r$
$\dfrac{\partial Y}{\partial r}$, $\dfrac{\partial Y}{\partial s}$, $\dfrac{\partial Y}{\partial t}$ quando $r=1$, $s=0$, $t=1$.
$\displaystyle \frac{\partial Y}{\partial r} = 1 + \frac{\pi}{4}$ ,$\dfrac{\partial Y}{\partial s} = 2$, $\displaystyle \dfrac{\partial Y}{\partial t} = 1 + \frac{\pi}{4}.$
Dada a função $f(x,y)=y-x$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \mathbb{R}^{2}$.
$Im(f) = \mathbb{R}.$
As curvas de nível são as retas $y - x = C.$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do cilindro $y^{2}+z^{2}=16$ que está entre os planos $x=0$ e $x=5.$
$x = u,$ $y = 4\cos (\theta),$ $z = 4\sin(\theta),$ onde $0 \leq u \leq 5,$ $0 \leq \theta \leq 2\pi.$
Seja $R$ o retângulo $1\leq x\leq 2$, $0\leq y\leq 1$. Calcule $\iint\limits_{R} f(x,y)\,dxdy$, sendo $f(x,y)$ dada por
$y\cos(xy)$
$x\sin(\pi y)$
$\cos(1) - \dfrac{(1 + \cos(2))}{2}$
$\ln\left(\dfrac{4}{3}\right).$
Identifique a superfície que tem equação paramétrica ${\bf r}(u,v)=(u+v)\,{\bf i}+(3-v)\,{\bf j}+(1+4u+5v)\,{\bf k}.$.
$4x - y - z = -4.$
Determine os pontos do gráfico de $xy^{3}z^{2}=16$ mais próximos da origem.
$\displaystyle \left( \frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, \frac{2 \sqrt{2}}{\sqrt[4]{12}}\right),$ $\displaystyle \left( \frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, - \frac{2 \sqrt{2}}{\sqrt[4]{12}}\right),$ $\displaystyle \left( -\frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, \frac{2 \sqrt{2}}{\sqrt[4]{12}} \right)$ e $\displaystyle \left( -\frac{2}{\sqrt[4]{12}}, \sqrt[4]{12}, - \frac{2 \sqrt{2}}{\sqrt[4]{12}} \right).$
Calcule utilizando coordenadas esféricas. $\displaystyle\iiint\limits_{B}x\,dxdydz$, onde $B$ é o conjunto $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{9}+z^{2}\leq 1$ e $x\geq 0.$
$3\pi.$
Dada a função $f(x,y)=\dfrac{y}{x^{2}}$.
Encontre o domínio da função.
Encontre a imagem da função.
Descreva as curvas de nível da função.
$D_{f} = \left\lbrace (x,y);\; (x,y) \neq (0,y) \right\rbrace$.
$Im(f) =\mathbb{R}.$
As curvas de nível são as parábolas $y = C x^{2}$ sem a origem se $C \neq 0$ e o eixo $x$ se $C \neq 0.$
Encontre todos os extremos relativos de \(x^2y^2\) sujeitos à restrição \(4x^2+y^2=8\). Faça-o de duas maneiras: primeiro, usando restrições para eliminar uma variável e, em seguida, utilizando multiplicadores de Lagrange como variáveis auxiliares.
Ocorre máximo absoluto de \(4\) em \((\pm 1,\pm 2)\); mínimo absoluto de valor \(0\) em \((\pm\sqrt{2},0)\) e \((0,\pm 2\sqrt{2})\).
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=3x-y$ em $D=\{(x,y)\in \mathbb{R}^2: x^{2}+y^{2}\leq 1\}.$
Valor máximo: $\displaystyle \frac{8\sqrt{10}}{10};$ valor mínimo: $-\sqrt{10}.$
Utilize coordenadas polares para determinar o volume do sólido dado: delimitado pelo cone $z^2=x^2+y^2$ e pelo cilindro $x^2+y^2=2x.$
$\dfrac{8}{9}.$
Utilize a integral dupla para determinar a área da região: cortada do primeiro quadrante pela curva $r=2(2-\sin(2\theta))^{1/2}.$
$2(\pi - 1).$
Mostre que o determinante Jacobiano da mudança de coordenadas cartesianas para esféricas é $-\rho^2 \sin \varphi$.
Enuncie o Teorema da Divergência e o Teorema de Stokes, incluindo todas as hipóteses envolvidas.
Encontre os pontos da elipse $x^2 + xy + y^2 = 3$ mais próximos e mais distantes da origem.
A distância entre um ponto $(x,y)$ e a origem $(0,0)$ é
$$d=\sqrt{(x-0)^{2}+(y-0)^{2}}=\sqrt{x^{2}+y^{2}}.$$
Mas a álgebra fica mais simples se maximizarmos e minimizarmos o quadrado da distância:
$$d^{2}=f(x,y)=x^{2}+y^{2}.$$
A restrição é que os pontos pertencem a elipse, ou seja,
$$g(x,y)=x^{2}+xy+y^{2}=3$$
De acordo com os multiplicadores de Lagrange, resolvemos $\nabla f=\lambda \nabla g$ e $g=3.$ Então
$$\nabla f(x,y)=(2x,2y)$$
e
$$\lambda \nabla g(x,y)=\lambda(2x+y,x+2y)=(2x\lambda+y\lambda,2y\lambda+x \lambda).$$
Logo temos,
\begin{array}{rcl}2x=2x\lambda+y\lambda\\2y=2y\lambda+x\lambda\\x^{2}+xy+y^{2}=3\\end{array}
Se $\lambda=0$ teremos que $x=0$ e $y=0$, mas esses valores não satisfazem equação $(3)$. Logo $\lambda \neq 0$ e multiplicando
ambos os lados da equação $(1)$ por $\dfrac{y}{\lambda}$ e ambos os lados da equação $(2)$ por $\dfrac{x}{\lambda}$, obtemos que
$$\frac{2xy}{y}=2xy+y^{2}\;\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\;\; \frac{2xy}{y}=2xy+x^{2}.$$
Logo,
$$y^{2}=x^{2}\Rightarrow y=x\;\;\;\; \mbox{ou}\;\;\;\; y=-x.$$
Se $y=x$ temos que da equação $(3)$ que $x^{2}+x^{2}+x^{2}=3\Rightarrow x^{2}=1\Rightarrow x=\pm 1.$
Logo temos os pontos $(1,1)$ e $(-1, -1).$
Se $y=-x$ temos que da equação $(3)$ que $x^{2}-x^{2}+x^{2}=3\Rightarrow x^{2}=3\Rightarrow x=\pm \sqrt{3}.$
Logo temos os pontos $(\sqrt{3},-\sqrt{3})$ e $(-\sqrt{3},\sqrt{3}).$
Os valores de $f$ nesses pontos são:
$$f(1,1)=f(-1,-1)=2\;\;\;\;\;\;\;\; \mbox{e}\;\;\;\;\;\;\;\; f(\sqrt{3},-\sqrt{3})=f(-\sqrt{3},\sqrt{3})=6.$$
Portanto, $(1,1)$ e $(-1, -1)$ são os pontos mais próximos e $(\sqrt{3},-\sqrt{3})$ e $(-\sqrt{3},\sqrt{3})$ os pontos mais afastados da origem $(0,0).$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do paraboloide elíptico $x+y^{2}+2z^{2}=4$ que está em frente ao plano $x=0.$
$y = u,$ $z = v,$ $x = 4 - u^2 - 2v^2,$ onde $u^{2} + 2v^2 \leq 4.$
Calcule a massa do cilindro $x^{2}+y^{2}\leq 4$ e $0\leq z \leq 2$, sabendo que a densidade no ponto $(x,y,z)$ é o dobro da distância do ponto ao plano $z=0.$
$16\pi.$
Determine o rotacional e o divergente do campo vetorial $\mathbf{F}(x,y,z) = xyz\mathbf{i} - x^2y\mathbf{k}$.
$\text{rot } \mathbf{F} = -x^2 \mathbf{i} + 3xy \mathbf{j} -xz \mathbf{k}.$ $\text{div } \mathbf{F} = yz.$
Calcule a integral $\displaystyle\iint\limits_{R} \dfrac{e^{y - x^2}}{y - x^2} dA$, em que $R$ é o conjunto de todos $(x,y)$ tais que $1 + x^2 \leq y \leq 2 + x^2$, $y \geq x + x^2$ e $x \geq 0$, efetuando uma mudança de variáveis apropriada.
Olhando o integrando, é natural pensar que uma das novas variáveis introduzidas deva ser $y-x^2$, mas a outra, a princípio, não está pré-definida. Seja $u = y - x^2$ (escolheremos $v$ apropriadamente depois). Vamos analisar a região de integração dada.
\qquad Como $1 + x^2 \leq y \leq 2 + x^2, \text{ temos } 1 \leq y-x^2 \leq 2$, isto é, $1 \leq u \leq 2$;
\qquad Como $y \geq x + x^2$ e $x \geq 0$, temos $y-x^2 \geq x \geq 0$, isto é, $u \geq x \geq 0$.
Da análise acima, é natural pensar na outra variável como sendo $v = x$. Considere então a mudança de variáveis dada por
$$\begin{cases}x = v, \\y = u+v^2.\end{cases}$$
O Jacobiano dessa transformação é
$$\dfrac{\partial (x,y)}{\partial (u,v)} = \left| \begin{array}{cc} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{array} \right| = \left| \begin{array}{cc} 0 & 1 \\ 1 & 2v \end{array} \right| = -1.$$
Como analisamos anteriormente, a nova região de integração é
$$S = \{(u,v) \in \mathbb{R}^2: 1 \leq u \leq 2 \mbox{ e } 0 \leq v \leq u\}.$$
Assim,
\begin{array}{rcl}\displaystyle\iint\limits_{R} \dfrac{e^{y - x^2}}{y - x^2} \, dA & = & \displaystyle \iint\limits_{S} \frac{e^u}{u} \left|\frac{\partial (x,y)}{\partial (u,v)}\right|\, dv du \\& = & \displaystyle\int_{1}^{2}\int_{0}^{u} \frac{e^u}{u} (1) \, dv du \\ & = & \displaystyle\int_{1}^{2} \left.\left(\frac{v e^u}{u}\right|_{v=0}^{v=u}\right) \, du \\ & = & \displaystyle\int_{1}^{2} e^u \, du \\ & = & e^u |_{1}^{2} = e^2 - e.\end{array}
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy(x - y)}{x^4 + y^4}$, caso exista.
Não existe.
As seguintes superfícies, rotuladas $a$, $b$ e $c$ de cima para baixo, são gráficos de uma função $f$ e de suas derivadas parciais $f_{x}$ e $f_{y}$. Identifique cada superfície e dê razões para sua escolha.
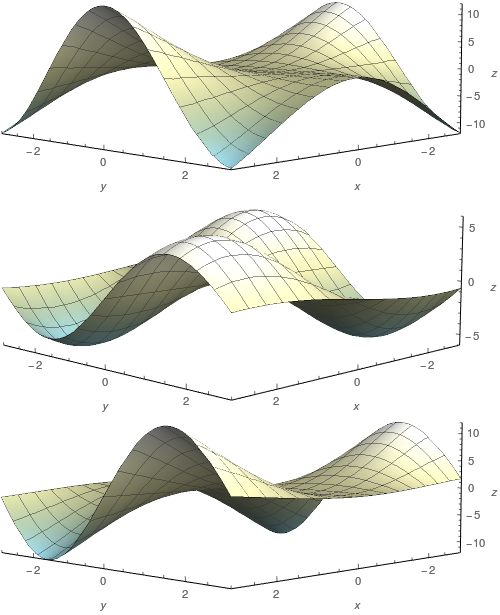
a) $f_{y},$ b) $f_{x},$ c) $f$.
Esboce o sólido cujo volume é dado pela integral iterada
$$\int_{0}^{1} \!\! \int_{0}^{1}(4-x-2y)\, dx dy.$$
Considere a função
$$f(x,y)=\begin{cases}x+y, & \quad \text{se } xy=0,\\\kappa, & \quad \text{caso contrário},\\\end{cases}$$
em que $\kappa$ é um número real. Determine as derivadas parciais de primeira ordem de $f$ em $(0,0).$
$\displaystyle \frac{\partial f}{\partial x} (0,0) = \frac{\partial f}{\partial y} (0,0) = 1$.
A figura mostra uma curva $C$ e um mapa de contorno de uma função $f$ cujo gradiente é contínuo. Determine $\int_{C}\nabla f\cdot d{\bf r}.$

$40.$
- Duas superfícies são ditas \textbf{ortogonais} em um ponto de intersecção se suas normais são perpendiculares nesse ponto. Mostre que superfícies com equação $F(x,y,z) = 0$ e $G(x,y,z) = 0$ são ortogonais em um ponto $P$, em que $\nabla F \neq 0$ e $\nabla G \neq 0$, se, e somente se, em $P$, $$F_xG_x + F_yG_y + F_zG_z = 0.$$
- Use a parte 1. para mostrar que as superfícies $z^2 = x^2 + y^2$ e $x^2 + y^2 + z^2 = r^2$ são ortogonais em todo ponto de intersecção. Você pode ver isso sem fazer os cálculos?
- Note que a direção da normal de $F$ é dada por $\nabla F,$ a de $G$ por $\nabla G$ e que duas normais em $P$ são perpendiculares se $\nabla F \cdot \nabla G = 0.$
- Tome $F = x^2 + y^2 - z^2,$ $G = x^2 + y^2 + z^2 - r^2$ e verifique $(a).$ Para "ver" isso sem calcular, note que $F = 0$ é a equação de um cone circular com vértice na origem e $G = 0$ é a equação de uma esfera centrada na origem.
Determine o maior conjunto no qual a função $F(x,y) = \dfrac{1}{x^2 - y}$ é contínua.
$\left\lbrace (x,y);\; y \neq x^{2} \right\rbrace.$
Determine o conjunto dos pontos de continuidade da função $f(x,y) = \mbox{ln} \ \dfrac{x - y}{x^2 + y^2}$. Justifique sua resposta.
$\left\lbrace (x,y);\; x > y \right\rbrace.$
Determine e faça o esboço do domínio da função $\bigstar$ $f(x,y)=\dfrac{\sqrt{y-x^{2}}}{1-x^{2}}$.
$\left\lbrace (x,y);\; y \geq x^{2},\; x\neq \pm 1 \right\rbrace.$
Um cubo sólido de $2$ unidades de lado é limitado pelos planos $x=\pm 1$, $z=\pm 1$, $y=3$ e $y=5.$ Encontre o centro de massa e os momentos de inércia desse cubo.
Centro de massa: $\displaystyle \left(0,4,0 \right),$ $I_{x} = \dfrac{400}{3},$ $I_{y} = \dfrac{16}{3},$ $I_{z} = \dfrac{400}{3}.$
Encontre o volume da região sólida limitada abaixo pelo plano $z = 0$, lateralmente pelo cilindro $x^2 + y^2 = 1$ e acima pelo paraboloide $z = x^2 + y^2$.
Temos que a região sólida $E$ está acima do plano $z=0$, abaixo do paraboloide $z=x^{2}+y^{2}$ e limitado lateralmente pelo cilindro $x^{2}+y^{2}=1$. Notemos que podemos dividir a região sólida em quatro porções simétricas. Assim, levando em consideração a porção da região sólida $E$ que está no primeiro octante, temos em coordenadas cilíndricas $$0\leq \theta \leq \frac{\pi}{2},\, 0\leq r \leq 1\,\, \mbox{e}\,\, 0\leq z\leq x^{2}+y^{2}=r^{2}.$$ Assim, o volume da região sólida $E$ é: $$V=\iiint\limits_{ E}1\,dV=4\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}\int_{0}^{r^{2}}1\,r\,dz\,dr\,d\theta$$ $$=4\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}zr\,\bigg|_{0}^{r^{2}}\,dr\,d\theta=4\int_{0}^{\frac{\pi}{2}}\int_{0}^{1}r^{3}\,dr\,d\theta$$ $$=4\int_{0}^{\frac{\pi}{2}}\,d\theta\cdot \int_{0}^{1}r^{3}\,dr=4\cdot \theta\bigg|_{0}^{\frac{\pi}{2}}\cdot \frac{r^{4}}{4}\bigg|_{0}^{1}$$ $$=4\cdot \frac{\pi}{2}\cdot \frac{1}{4}=\frac{\pi}{2}.$$
Dentre as coordenadas cilíndricas ou esféricas, utilize a que lhe parecer mais apropriada para determinaretermine o volume da região limitada abaixo pelo plano $z=0$, lateralmente pelo cilindro $x^{2}+y^{2}=1$ e acima pelo paraboloide $z=x^{2}+y^{2}$.
$\dfrac{\pi}{2}.$
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. $\displaystyle\int_{C}\dfrac{-y}{x^2+y^2} \, dx + \dfrac{ x}{x^2+y^2} \, dy$, $C$ curva fechada, $C^1$ por partes, simples e fronteira de um conjunto $B$ cujo interior contém o círculo $x^2 + y^2 \leq 1$. (Sugestão: Aplique o Teorema de Green à região $K$ compreendida entre a curva $C$ e a circunferência.)
$2\pi.$
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s).
$f(x,y) = 4x + 6y; \quad x^2 + y^2 = 13.$
Valor máximo: $26;$ valor mínimo: $-26.$
Calcule $\displaystyle\iint \limits_{S}{\bf u}\cdot {\bf n}\,dS$, sendo $S$ a fronteira de $B$ com normal exterior ${\bf n}$, sendo $B=\{(x,y,z)\in \mathbb{R}^{3}|\, 0\leq x\leq 1,\,0\leq y\leq x$ e $0\leq z\leq 4\}$ e ${\bf u}=xy\,{\bf i}+yz\,{\bf j}+z^{2}\,{\bf k}.$
Usando coordenadas esféricas, determine o volume da porção da esfera sólida $\rho \leq a$ que está entre os cones $\phi=\pi/3$ e $\phi=2\pi/3.$
$\dfrac{2\pi a^{3}}{3}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=9-2x+4y-x^{2}-4y^{2}$.
Ponto de máximo: $\displaystyle \left( -1, \frac{1}{2} \right).$
A tendência de uma lâmina de resistir a uma mudança no seu movimento de rotação em torno de um eixo é medida pelo seu momento de inércia em torno daquele eixo. Se a lâmina ocupar uma região \(R\) do plano \(xy\) e se sua densidade \(\delta(x,y)\) for uma função contínua em \(R\), então os momentos de inércia em torno dos eixos \(x\), \(y\) e \(z\) são denotados por \(I_x\), \(I_y\) e \(I_z\), respectivamente, e são definidos por \begin{align*} I_x & = \iint\limits_R y^2\delta(x,y)\,dA, \\ I_y & = \iint\limits_R x^2\delta(x,y)\,dA, \\ I_z & = \iint\limits_R (x^2+y^2)\delta(x,y)\,dA. \\ \end{align*} Considere a lâmina circular que ocupa a região descrita pelas desigualdades \(0\leq x^2+y^2\leq a^2\). Supondo que a lâmina tenha densidade \(\delta\) constante, mostre que \[ I_x= I_y=\dfrac{\delta\pi a^4}{4}, \quad I_z= \dfrac{\delta\pi a^4}{2}.\]
Considere a função $f(x,y) = x \ \phi\left(\frac{x}{y}\right)$, em que $\phi(u)$ é uma função derivável de uma variável. Mostre que os planos tangentes ao gráfico de $f$ passam pela origem.
Note que $x \frac{\partial f}{\partial x} (x,y) + y \frac{\partial f}{\partial y}(x,y) = f(x,y).$
Determine o volume do sólido que está acima do plano $xy$, abaixo do paraboloide $z = x^2 + y^2$ e que se encontra dentro do cilindro $x^2 + y^2 = 2x$ e fora do cilindro $x^2 + y^2 = 1.$
Temos que $0\leq z\leq x^{2}+y^{2}$. Como o sólido se encontra dentro do cilindro $x^{2}+y^{2}=2x$ e fora do cilindro $x^{2}+y^{2}=1$, devemos fazer a interseção desses dois cilindros, isto é, $$\left\{\begin{array}{cc} x^{2}+y^{2}=2x\\ x^{2}+y^{2}=1\\ \end{array} \right.\Rightarrow 2x=1\Leftrightarrow x=\frac{1}{2}$$ Em coordenadas cilíndricas temos que \begin{eqnarray*} x&=&r\cos \theta\\ y&=&r\sin \theta\\ z&=&z\\ dz\,dy\,dx&=&r\,dz\,dr\,d\theta \end{eqnarray*} Da equação $x^{2}+y^{2}=1$ temos que $$r^{2}=1\Longrightarrow r=\pm 1,$$ como devemos ter $r\geq 0$, então nesse caso $r=1.$ Da equação $x^{2}+y^{2}=2x$ temos que $$r^{2}=2r\,\cos \theta \Rightarrow r=2\cos \theta.$$ Agora, sendo $x=\frac{1}{2}$ e $r=1$ temos que $$\cos \theta=\frac{1}{2}\Rightarrow \theta=\pm \frac{\pi}{3}.$$ Assim, em coordenadas cilíndricas temos que o sólido $E$ é dado por $$E=\{(\theta,\,r,\,z)|\, -\frac{\pi}{3}\leq \theta \leq \frac{\pi}{3},\, 1\leq r\leq 2 \cos \theta,\,0\leq z\leq r^{2}\}.$$ Então, $$V=\iiint\limits_{ E}1\,dV= \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int_{1}^{2\cos \theta}\int_{0}^{r^{2}}1\,r\,dz\,dr\,d\theta= \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int_{1}^{2\cos \theta}zr\bigg|_{0}^{r}\,dr\,d\theta$$ $$=\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\int_{1}^{2\cos \theta}r^{3}\,dr\,d\theta= \int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\frac{r^{4}}{4}\bigg|_{1}^{2\cos \theta}\,d\theta =\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\bigg(4\cos^{4}\theta-\frac{1}{4}\bigg)\,d\theta$$ $$=4\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\underbrace{\cos^{4}\theta}_{\mbox{função par}}\,d\theta-\int_{-\frac{\pi}{3}}^{\frac{\pi}{3}}\underbrace{\frac{1}{4}}_{\mbox{função par}}\,d\theta =8\int_{0}^{\frac{\pi}{3}}\cos^{4}\theta\,d\theta-2\int_{0}^{\frac{\pi}{3}}\frac{1}{4}\,d\theta$$ $$=8\bigg[\frac{3}{8}\theta+\frac{1}{4}\sin(2\theta)+\frac{1}{32}\sin(4\theta)\bigg]\bigg|_{0}^{\frac{\pi}{3}} -\bigg(\frac{1}{2}\theta\bigg)\bigg|_{0}^{\frac{\pi}{3}}$$ $$=8\bigg[\frac{3}{8}\cdot \frac{\pi}{3}+\frac{1}{4}\sin\bigg(\frac{2\pi}{3}\bigg)+\frac{1}{32}\sin\bigg(\frac{4\pi}{3}\bigg)\bigg]-\frac{1}{2}\cdot \frac{\pi}{3}$$ $$=\pi+\sqrt{3}-\frac{\sqrt{3}}{8}-\frac{\pi}{6}=\frac{5\pi}{6}+\frac{7\sqrt{3}}{8}.$$
Esboce o gráfico da função $f(x,y)=\sqrt{x^{2}+y^{2}}$. Em geral, se $g$ é uma função de uma variável, como saber o gráfico de $f(x,y)=g(\sqrt{x^{2}+y^{2}})$ a partir do gráfico de $g$?
O gráfico de $f(x,y) = g(\sqrt{x^{2} + y^{2}})$ pode ser obtido rotacionando o gráfico de $g$ no plano $xz$ ao redor do eixo $z.$
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. $f(x,y) = \arctan{(x - 2y)}$ em $\left(2, \dfrac{1}{2},f\left(2,\dfrac{1}{2}\right)\right)$.
Plano tangente: $4z = 2x - 4y + (\pi - 2)$
Reta normal: $(x,y,z) = \left(2,\frac{1}{2},\frac{\pi}{4} \right) + \lambda \left(\frac{1}{2},-1,-1 \right)$.
Determine o plano que é paralelo ao plano $z = 2x + y$ e tangente ao gráfico de $f(x,y) = x^2 + y^2$.
$z = 2x + y - \frac{5}{4}$.
Seja $w=f(x,y,z)$ uma função de três variáveis independentes. Escreva a definição formal de derivada parcial $\partial f/\partial z$ em $(x_{0},y_{0},z_{0})$. Use essa definição para encontrar $\partial f/\partial z$ em $(1,2,3)$ para $f(x,y,z)=x^{2}yz^{2}.$
$\displaystyle \frac{\partial f}{\partial z}(1,2,3) = 12$.
Verifique que $\dfrac{\partial ^{2}f}{\partial x^{2}}+\dfrac{\partial ^{2}f}{\partial y^{2}}=0$, onde $f(x,y)=\ln(x^{2}+y^{2}).$
$\displaystyle \frac{\partial^{2} f}{\partial x^{2}}= \frac{2 y^{2} - 2 x^{2}}{(x^{2} + y^{2})^{2}}\;\;\;\;\;\text{e}\;\;\;\;\; \frac{\partial^{2} f}{\partial y^{2}}= \frac{2 x^{2} - 2 y^{2}}{(x^{2} + y^{2})^{2}}.$
De acordo com a lei dos gases ideais, a pressão, a temperatura e o volume de um gás confinado estão relacionados por \( P=kT/V\), onde \(k\) é uma constante. Use diferenciais para aproximar a variação percentual na pressão se a temperatura de um gás tiver crescido em \(3\%\) e o volume tiver crescido em \(5\%\).
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=3xy^{2}\,{\bf i}+xe^{z}\,{\bf j}+z^{3}\,{\bf k}$, $S$ é a superfície do sólido delimitado pelo cilindro $y^{2}+z^{2}=1$ e pelos planos $x=-1$ e $x=2.$
Sejam $f(x)$ e $g(x)$ duas funções contínuas, respectivamente, nos intervalos $[a,b]$ e $[c,d].$ Use o seguinte resultado $$\iint\limits_{R}f(x)g(y)\,dx dy=\bigg(\int_{a}^{b}f(x)\,dx\bigg)\bigg(\int_{c}^{d}g(y)\,dy\bigg),$$ onde $R$ é o retângulo $a\leq x\leq b$ e $c\leq y\leq d$, para calcular as integrais
$\displaystyle\iint\limits_{R} x\ln(y)\,dx dy$, onde $R$ é o retângulo $0\leq x\leq 2,\;1\leq y\leq 2.$
$\displaystyle\iint\limits_{R} xye^{x^{2}-y^{2}}\,dx dy$, onde $R$ é o retângulo $-1\leq x\leq 1,\;0\leq y\leq 3.$
$2(2\ln(2) - 1).$
$0.$
Supondo que \(\sigma\) e \(G\) satisfaçam as hipóteses do Teorema da Divergência e que \(f\) e \(g\) sejam funções suficientemente regulares, prove as seguintes identidades (de Green):
\[\iint\limits_\sigma\left(f\nabla g\right)\cdot\mathbf{n}\,dS = \iiint\limits_G\left( f\Delta g+\nabla f\cdot\nabla g\right)\,dV, \]
\[\iint\limits_\sigma\left(f\nabla g-g\nabla f\right)\cdot\mathbf{n}\,dS = \iiint\limits_G\left( f\Delta g- g\Delta f\right)\,dV, \] onde \(\displaystyle \Delta f= \dfrac{\partial^2f}{\partial x^2}+\dfrac{\partial^2f}{\partial y^2}+\dfrac{\partial^2f}{\partial z^2}\) é denominado Laplaciano de \(f\).
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} x \, dA$, em que $R$ é o conjunto, no plano $xy$, limitado pela cardioide $\rho = 1 - \cos{\theta}$.
$-\dfrac{5\pi}{4}.$
Utilize coordenadas polares para determinar o volume do sólido dado: abaixo do cone $z=\sqrt{x^{2}+y^{2}}$ e acima do disco $x^{2}+y^{2}\leq 4.$
$\displaystyle \frac{16\pi}{3}.$
Determine os valores máximos e mínimos locais e pontos de sela da função $f(x,y)=e^{4y-x^{2}-y^{2}}$.
Ponto de máximo: $\displaystyle \left(0,2 \right).$
Use multiplicadores de Lagrange para demonstrar que o triângulo com área máxima, e que tem um perímetro constante $p$, é equilátero.
(Sugestão: Utilize a fórmula de Heron para a área:
$$A = \sqrt{s(s-x)(s-y)(s-z)},$$
em que $s = p/2$ e $x,y$ e $z$ são os comprimentos dos lados.)
Utilizando a fórmula de Heron temos que a área e um triânulo é
$$A=\sqrt{s(s-x)(s-y)(s-z)},$$
com $s=p/2$ e $x,\,y,\,z$ lados do triângulo.
Mas a álgebra fica mais simples se maximizarmos o quadrado da área, isto é,
$$A^{2}=f(x,y,z)=s(s-x)(s-y)(s-z).$$
A restrição é que o triângulo têm perímetro constante $p$, ou seja,
$$g(x,y,z)=x+y+z=p.$$
De acordo com o método dos multiplicadores de Lagrange, resolvemos $\nabla f=\lambda \nabla g$ e $g=p.$ Então
$$\nabla f(x,y,z)=(\,-s(s-y)(s-z),\, -s(s-x)(s-z),\,-s(s-x)(s-y)\,)$$
e
$$\lambda \nabla g(x,y,z)=\lambda (1,1,1)=(\lambda, \lambda, \lambda).$$
Logo temos as seguintes equações
\begin{array}{rcl}-s(s-y)(s-z)&=&\lambda\\-s(s-x)(s-z)&=&\lambda\\-s(s-x)(s-y)&=&\lambda\\x+y+z&=&p\end{array}
Assim, das três primeiras equações, temos que
$$-s(s-y)(s-z)=-s(s-x)(s-z)=-s(s-x)(s-y).$$
Da primeira igualdade obtemos que $s-y=s-x\Rightarrow y=x$ e da segunda igualdade obtemos que $s-z=s-y\Rightarrow z=y$, resultando que $x=y=z.$
Portanto, o triângulo com área máxima e perímetro constante $p$ é um triângulo equilátero.
Determine a massa e o centro de massa da lâmina que ocupa a região $D$ e tem função densidade $\rho$ quando: $D$ é a região triangular delimitada pelas retas $x = 0, \ y = x$ e $2x + y = 6; \quad \rho(x,y) = x^2$.
Massa: $4;$ centro de massa: $\displaystyle \left(\frac{6}{5},\frac{12}{5} \right).$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{grad }{(\text{div }{f})}$;
$\text{div }{(\text{div }{\mathbf{F}})}$;
$\text{div }{(\text{rot }{(\text{grad }{f})})}$.
$\text{grad }{(\text{div }{f})}$ não tem significado, pois $f$ é um campo escalar.
$\text{div }{(\text{div }{\mathbf{F}})}$ não tem significado pois $\text{div } \bf{F}$ é um campo escalar.
$\text{div }{(\text{rot }{(\text{grad }{f})})}$ é um campo escalar.
Calcule a integral de linha, onde $C$ é a curva dada.
$\displaystyle\int_{C}x\,dx+y\,dy+z\,dz$, $C$ é o segmento de extremidades $(0,0,0)$ e $(1,2,1)$, percorrido no sentido de $(1,2,1)$ para $(0,0,0).$
$-3.$
Os lados iguais e o ângulo correspondente de um triângulo isósceles estão aumentando à razão de $3cm/h$ e $2^{\circ}/h$, respectivamente. Ache a taxa à qual a área do triângulo está aumentando no instante em que o comprimento de cada um dos
lados iguais é de $6$ metros e o ângulo correspondente é $60^{\circ}.$
$\approx 181559$ cm$^{2}/$h.
De acordo com o triângulo abaixo:
Expresse $A$ implicitamente como uma função de $a$, $b$ e $c$ e calcule $\partial A/\partial a$ e $\partial A/ \partial b.$
Expresse $a$ implicitamente como uma função de $A$, $b$ e $B$ e calcule $\partial a/ \partial A$ e $\partial a/ \partial B.$
$\displaystyle a^{2} = b^{2} + c^{2} -2bc\cos(A),\;\;\;\;\frac{\partial A}{\partial a} = \frac{a}{bc \sin (A)}\;\;\;\text{e}\;\;\;\frac{\partial A}{\partial b} = \frac{c \cos(A) - b}{bc \sin(A)}.$
$\displaystyle \frac{a}{\sin(A)} = \frac{b}{\sin(B)},\;\;\;\;\frac{\partial a}{\partial A} = \frac{a\cos(A)}{\sin(A)}\;\;\;\text{e}\;\;\;\frac{\partial a}{\partial B} = - b\csc(B) \cot(B)\sin(A).$
Ache $\displaystyle\iint \limits_{ S}{\bf F}\cdot {\bf n} dS$ se ${\bf n}$ é uma normal unitária superior de $S.$
${\bf F}=2{\bf i}+5{\bf j}+3{\bf k}$; $S$ é a parte do cone $z=(x^{2}+y^{2})^{1/2}$ interior ao cilindro $x^{2}+y^{2}=1.$
A reta \(y=2-x\) intersecta a parábola \(y=x^2\) nos pontos \((-2,4)\) e \((1,1)\). Mostre que, se \(R\) denotar a região englobada por \(y=2-x\) e \(y=x^2\), então \[ \iint_R\left(1+2y\right)\,dA = \int_{-2}^1\int_{x^2}^{2-x}\left(1+2y\right)\,dydx = 18,9 \]
Definimos a integral imprópria (sobre todo o plano $\mathbb{R}^{2}$) $$I=\displaystyle\iint\limits_{ \mathbb{R}^{2}}e^{-(x^{2}+y^{2})}\,dA=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}e^{-(x{^2}+y^{2})}\,dy dx= \lim_{a\rightarrow\infty}\displaystyle\iint\limits_{D_{a}}e^{-(x^{2}+y^{2})}\,dA,$$ onde $D_{a}$ é o disco com raio $a$ e centro na origem. Mostre que $$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}e^{-(x^{2}+y^{2})}\,dA=\pi.$$
Uma definição equivalente da integral imprópria da parte (a) é $$\iint\limits_{\mathbb{R}^{2}}e^{-(x^{2}+y^{2})}\,dA=\lim_{a\rightarrow\infty}\displaystyle\iint\limits_{S_{a}}e^{-(x^{2}+y^{2})}\,dA,$$ onde $S_{a}$ é o quadrado com vértices $(\pm a,\pm a)$. Use esse resultado para mostrar que $$\int_{-\infty}^{\infty}e^{-x^{2}}\,dx\,\int_{-\infty}^{\infty}e^{-y^{2}}\,dy=\pi.$$
Deduza que $$\int_{-\infty}^{\infty}e^{-x^{2}}\,dx=\sqrt{\pi}.$$
Fazendo a mudança de variável $t=\sqrt{2} x$, mostre que $$\int_{-\infty}^{\infty}e^{-x^{2}/2} dx=\sqrt{2\pi}.$$
(Este é um resultado fundamental em probabilidade e estatística.)
Note que $$\displaystyle\iint\limits_{D_{a}}e^{-(x^{2}+y^{2})}\,dA =\int_{0}^{2\pi}\int_{0}^{a} r e^{-r^2} dr d\theta = \pi (1 - e^{-a^2})$$ para cada $a.$
Note que $$\int\limits_{S_{a}}e^{-(x^{2}+y^{2})}\,dA = \int_{-a}^{a} \int_{-a}^{a} e^{-x^2} e^{-y^2} dxdy = \left(\int_{-a}^{a} e^{-x^2} dx\right) \left(\int_{-a}^{a} e^{-y^2} dy\right) $$ para cada $a.$
Troque $y$ por $x$ no item (b).
Note que fazendo a mudança de variável sugerida, $$\int_{-\infty}^{\infty}e^{-x^{2}/2} dx= \frac{1}{\sqrt{2}}\int_{-\infty}^{\infty}e^{-t^{2}/2} dt = \sqrt{\pi}.$$
Determine as derivadas parciais de primeira ordem da função $u=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdot \cdot \cdot +x_{n}^{2}}$.
$\displaystyle \frac{\partial u}{\partial x_{i}}= \frac{x_{i}}{\sqrt{x_{1}^{2}+x_{2}^{2}+\cdot \cdot \cdot +x_{n}^{2}}}$ para todo $i = 1, \cdots, n$.
Calcule o volume do conjunto dado.
$x+y+z\leq 1$, $x\geq 0$, $y\geq 0$ e $z\geq 0.$
$x\leq y\leq 1$, $x\geq 0$, $z\geq 0$ e $z^{2}+x^{4}+x^{2}y^{2}\leq 2x^{2}.$
$\dfrac{1}{6}.$
$\dfrac{\pi(1 - \sqrt{2})}{8} + \dfrac{1}{3}.$
Determine uma representação paramétrica para a superfície descrita a seguir. A parte do hiperboloide $x^{2}+y^{2}-z^{2}=1$ que está à direita do plano $xz.$
$x =u,$ $z = v,$ $y = \sqrt{1 - u^2 + v^2}.$
Determine o trabalho $W=\int_{C}{\bf F}\cdot d{\bf r}$ realizado pelo campo de força ${\bf F}(x,y)=x^{2}(x-y)\,{\bf i}+xy^{2}\,{\bf j}$ em uma partícula que se move da origem ao longo do eixo $x$ para $(1,0)$, em seguida ao longo de um segmento de arco de circunferência $x^{2}+y^{2}=1$ até $(0,1)$ e então volta à origem ao longo do eixo $y.$
$\dfrac{\pi}{8}.$
Nos item abaixo:
- expresse $\mathrm{d} w/\mathrm{d} t$ como uma função de $t$, usando a Regra da Cadeia, expressando $w$ em termos de $t$ e diferenciando em relação a $t$;
- calcule $\mathrm{d} w/\mathrm{d} t$ no valor dado de $t$.
$w=x^{2}+y^{2}$, $x=\cos{t}+\sin{t}$, $y=\cos{t}-\sin{t}$; $t=0.$
- $\displaystyle \frac{dw}{dt}(t) = 0.$
- $\displaystyle \frac{dw}{dt}(0) = 0.$
Determine o campo vetorial gradiente de $f(x,y,z) = \sqrt{x^2+y^2+z^2}$.
$\nabla f(x,y,z) = \dfrac{x\textbf{i} + y\textbf{j} + z \textbf{k}}{\sqrt{x^{2} + y^{2} + z^{2}}}.$
Seja $f$ um campo escalar e $\mathbf{F}$ um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar.
$\text{div }{(\text{grad }{f})}$;
$\text{rot }{(\text{rot }{\mathbf{F}})}$;
$(\text{grad }{f}) \times (\text{div }{\mathbf{F}})$.
$\text{div }{(\text{grad }{f})}$ é um campo escalar.
$\text{rot }{(\text{rot }{\mathbf{F}})}$ é um campo vetorial.
$(\text{grad }{f}) \times (\text{div }{\mathbf{F}})$ não tem significado pois $\text{div } \bf{F}$ é um campo escalar.
Uma luminária tem duas lâmpadas de um tipo com tempo de vida médio de 1.000 horas. Supondo que possamos modelar a probabilidade de falha dessas lâmpadas por uma função densidade exponencial com média $\mu = 1.000$, determine a probabilidade de que ambas as lâmpadas venham a falhar dentro de um período de 1.000 horas.
Outra luminária tem somente uma lâmpada do mesmo tipo das do item anterior. Se a lâmpada queima e é trocada por outra to mesmo tipo, determine a probabilidade de que as duas venham a falhar dentro de 1.000 horas.
$(e^{-1} - 1)^2.$
$1 - 2e^{-1}.$
Utilizando o Teorema de Stokes, transforme a integral $\iint_{ S}\mbox{rot}{\bf F}\cdot{\bf n}dS$ numa integral de linha e calcule.
- ${\bf F}(x,y,z) = y{\bf i} + x^2{\bf j}+z{\bf k}$, $S$ a superfície parametrizada por ${\bf R}(u,v) = (u,v,2u+v+1)$, $u\geq 0$, $u+v\leq 2$, sendo ${\bf n}$ a normal apontando para baixo.
Calcule a integral, efetuando uma mudança de variáveis apropriada. $\displaystyle\iint\limits_{R} \sin{(9x^2 + 4y^2)} \, dA$, em que $R$ é a região do primeiro quadrante limitada pela elipse $9x^2 + 4y^2 = 1$.
$\dfrac{\pi}{24}(1 - \cos(1)).$
Determine os valores máximo e mínimo absolutos de $f$ no conjunto $D.$
$f(x,y)=3+xy-x-2y$, $D$ é a região triangular fechada com vértices $(1,0)$, $(5,0)$ e $(1,4).$
Valor máximo: $2;$ valor mínimo: $-2.$
Use o Teorema do Divergente para calcular o fluxo de ${\bf F}$ através de $S,$ onde ${\bf F}(x,y,z)=(5x^{3}+12xy^{2})\,{\bf i}+(y^{3}+e^{y}\,\sin z)\,{\bf j}+(5z^{3}+e^{y}\,\cos z)\,{\bf k}$ e $S$ é a superfície do sólido entre as esferas $x^{2}+y^{2}+z^{2}=1$ e $x^{2}+y^{2}+z^{2}=2.$
Calcule $\displaystyle \lim_{(x,y) \to (0,0)} \dfrac{xy}{y - x^3}$, caso exista.
Não existe.
Usando coordenadas esféricas, determine o volume do sólido que está acima do plano $z=2\sqrt{3}$ e abaixo da esfera $x^{2}+y^{2}+z^{2}=16.$
$\dfrac{88\pi}{3}.$
A função $f(x,y) = \begin{cases}\dfrac{x^4}{x^2 + y^2}, & \quad \text{se } (x,y) \neq (0,0),\\0, & \quad \text{se } (x,y) = (0,0)\\\end{cases}$ é diferenciável em $(0,0)$? Justifique.
Sim.
Determine o ponto do elipsóide $x^2 + 4y^2 + z^2 = 1$ que maximiza a soma $x + 2y + z$.
$\displaystyle \left( \frac{1}{\sqrt{3}}, \frac{1}{2\sqrt{3}}, \frac{1}{\sqrt{3}} \right).$
Considere a função
$$f(x,y) = \begin{cases}x + y, & \quad \text{se } xy = 0, \\k, & \quad \text{caso contrário},\end{cases}$$
em que $k$ é um número real. É possível escolher $k$ de modo que $f$ seja contínua em $(0,0)$? Em caso afirmativo, qual deve ser o valor de $k$?
$k = 0.$
Considere a função
$$f(x,y) = \begin{cases}
x + y, & \quad \text{se } xy = 0,\\
1, & \quad \text{caso contrário}.
\end{cases}$$
Mostre que $f$ não possui derivada direcional em $(0,0)$ na direção de um vetor $\bf{v} = (a,b)$ com $a^2 + b^2 = 1$ e $ab \neq 0$.
Seja $\bf{v} = (a,b)$ um vetor unitário (isto é, $a^2+b^2 = 1$), em que $ab \neq 0$. A derivada direcional em $(0,0)$ na direção do vetor unitário $\bf{v}$ existe se o limite
$$\lim_{h \to 0} \frac{f(0+ah,0+bh)-f(0,0)}{h}$$
existir. Para $h \neq 0$, temos $(ah)(bh) \neq 0$. Logo $f(ah,bh) = 1$. Assim, o limite em questão se reduz a
$$\lim_{h \to 0} \frac{1}{h},$$
e esse limite não existe. Como o vetor $\bf{v}$ satisfazendo as hipóteses foi tomado arbitrariamente, concluímos que $f$ não possui derivada direcional em $(0,0)$ na direção de nenhum vetor $\bf{v} = (a,b)$ que satisfaça $a^2 + b^2 = 1$ e $ab \neq 0$.
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. ${\bf r}(u,v)=(u,v,u^{2}+v^{2})$, no ponto ${\bf r}(1,1).$
$(x,y,z) = (1,1,2) + s(1,0,2) + t(0,1,2),$ $s,t \in \mathbb{R}.$
Determine a aproximação linear da função $f(x,y) = \sqrt{20 - x^2 - 7y^2}$ em $(2,1)$ e use-a para aproximar $f(1,95; 1,08)$.
$L(x,y) = -\frac{2}{3}x - \frac{7}{3}y + \frac{20}{3}$ e $f(1,95; 1,08) \approx 2.847.$
Seja $S$ a superfície $z=f(x,y)$, $(x,y)\in K$, de classe $C^{1}$ num aberto contendo $K$. (Observação: trata-se da superfície dada por $x=u$, $y=v$ e $z=f(u,v)$). Seja ${\bf n}$ a normal a $S$ com componente $z>0$ e seja ${\bf F}=P{\bf i}+Q{\bf j}+R{\bf k}$ um campo vetorial contínuo na imagem de $S$. Mostre que $\displaystyle\iint\limits_{S}{\bf F}\cdot {\bf n}dS=\displaystyle\iint\limits_{K}\left[ -P\dfrac{\partial f}{\partial x}(x,y)-Q\dfrac{\partial f}{\partial y}+R\right]dx dy,$ onde $P$, $Q$ e $R$ são calculadas em $(x,y,f(x,y)).$
Veja a subseção "Integrais de superfície de campos vetoriais"' da seção 16.7 do livro do Stewart.
Seja
$$f(x,y) = x - y\sin{(\pi(x^2 + y^2))}.$$
- Calcule a derivada direcional de $f$ no ponto $(0,0)$ na direção de $\bf{v} = (1/2,\sqrt{3}/2)$.
- Em que direção a taxa de variação de $f$ no ponto $(0,0)$ é máxima? Qual é o valor da taxa máxima nesse ponto?
- $ \displaystyle \frac{1}{2}.$
- Na direção do vetor $(1,0).$ O valor da taxa máxima é $1.$
Mostre (verifique) que as integrais abaixo podem ser calculadas como:
1. \[ \int_1^5\int_2^{y/2}6x^2y\,dxdy = \int_1^5\left(\dfrac{1}{4}y^4-16y\right)\,dy \]
2. \[ \int_1^5\int_2^{x/2}6x^2y\,dydx = \int_1^5\left(\dfrac{3}{4}x^4-12x^2\right)\,dx \]
Estude com relação a máximos e mínimos a função dada com as restrições dadas.
$f(x,y) = 3x + y$ e $x^2 + 2y^2 \leq 1.$
Ponto de máximo: $\displaystyle \left( \frac{6}{\sqrt{38}}, \frac{1}{\sqrt{38}} \right)$; ponto de mínimo: $\displaystyle \left( -\frac{6}{\sqrt{38}}, -\frac{1}{\sqrt{38}} \right)$.
Calcule o volume do conjunto dado.
$x^{2}+y^{2}\leq a^{2}$ e $y^{2}+z^{2}\leq a^{2}$, $a >0.$
$x^{2}+y^{2}\leq z\leq 1-x^{2}.$
$\dfrac{16a^{3}}{3}.$
$\dfrac{\pi}{2\sqrt{2}}.$
Determine e faça o esboço do domínio da função $f(x,y,z)=\ln(16-4x^{2}-4y^{2}-z^{2})$.
$\left\lbrace (x,y);\; \frac{x^{2}}{4} + \frac{y^{2}}{4} + \frac{z^{2}}{16} < 1\right\rbrace.$
A temperatura $T$ em uma bola de metal é inversamente proporcional à distância do centro da bola, que tomamos como a origem. A temperatura no ponto $(1,2,2)$ é de 120°.
- Determine a taxa de variação de $T$ em $(1,2,2)$ em direção ao ponto $(2,1,3)$.
- Mostre que em qualquer ponto da bola a direção de maior crescimento na temperatura é dada por um vetor que aponta para a origem.
- $\displaystyle -\frac{40}{3\sqrt{3}}.$
- Note que $\nabla T = -360 (x^{2} + y^{2} + z^{2})^{-3/2} (x,y,z)$ sempre aponta para a origem.
Seja $E$ o sólido limitado pelos dois planos $z=1$ e $z=2$ e lateralmente pelo cone $z=\sqrt{x^{2}+y^{2}}$. Expresse o volume de $E$ como integral tripla em coordenadas esféricas (não é necessário calcular a integral).
$\displaystyle \int_{0}^{2\pi} \int_{0}^{\pi/4} \int_{\sec(\phi)}^{2\sec(\phi)} \rho^{2}\sin(\phi)\;d\rho d\phi d\theta.$
Considere a superfície dada implicitamente por
$$x^{2}+2y^{2}+2z^{2}=-4xyz.$$
Calcule as derivadas $\dfrac{\partial z}{\partial x}$ e $\dfrac{\partial z}{\partial y}$ em um ponto genérico.
Quais os pontos nos quais as derivadas parciais calculadas no item anterior não estão definidas?
$\displaystyle \frac{\partial z}{\partial x} = -\frac{x + 2yz}{2(z + xy)} \;\;\;\text{e}\;\;\; \frac{\partial z}{\partial y} = -\frac{y + xz}{z + xy}.$
$\left\lbrace (x,y,z) \in \mathbb{R}^{3};\; z = -xy \right\rbrace$.

