505

Esboce a figura correspondente às seguintes equações polares:

$r = 1$,
$r = 9$,
$\theta = \frac{\pi}{2}$,
$\theta^{2} = \frac{\pi^{2}}{16}$.

1430

Dadas duas retas que se cortam, seja $L_2$ a reta de maior ângulo de inclinação $\phi_2$ e e $L_1$ a reta de menor ângulo de

inclinação $\phi_1$. Definimos o ângulo entre $L_1$ e $L_2$ por $\theta=\phi_2-\phi_1$. Prove os resultados abaixo.

Se $L_1$ e $L_2$ não são perpendiculares, então $$ \tan\theta = \dfrac{m_2-m_1}{1+m_1m_2},$$ onde $L_1$ e $L_2$ têm inclinações $m_1$ e $m_2$.
Propriedade de Reflexão da Elipse: uma reta tangente a uma elipse em um ponto $P$ faz ângulos iguais com as retas que unem $P$ aos focos. (Sugestão: Introduza coordenadas de tal modo que a elipse seja descrita pela equação $x^2/a^2+y^2/b^2=1$ e use o item 1.)
Propridedade de Reflexão da Hipérbole: Uma reta tangente à hipérbole em um ponto $P$ faz ângulos iguais com as retas que unem $P$ aos focos. ([)Sugestão: Introduza coordenadas de tal modo que hipérbole seja descrita pela equação $x^2/a^2-y^2/b^2=1$ e use o item 1.)

287

Verificar se as retas são concorrentes e, em caso afirmativo, encontrar o ponto de interseção:

$$r_1:\;(x,y,z)=(2,4,1)+t(1,-2,3)\ \ \ {\rm e} \ \ \ \ r_2:\;(x,y,z)=(-1,2,5)+t(4,3,-2)$$

As retas não são concorrentes.

878

Sejam $A=(1,2,-1)$, $B=(5,0,1)$, $=C(2,-1,1)$ e $D=(6,1,-3)$ os vértices de um tetraedro. Calcule:

o volume deste tetraedro;
a sua altura relativa ao vértice $D$.

1. Os três vetores que determinam este tetraedro poderiam ser $
\overrightarrow{AB}$, $\overrightarrow{AC}$ e $\overrightarrow{AD}$. Como $ \overrightarrow{AB}$ $=\left( 4,-2,2\right) $, $\overrightarrow{AC}$ $ =\left( 1,-3,2\right) $ e $\overrightarrow{AD}$ $=\left( 5,-1,1\right) $ e $V_{T}=\frac{\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right] \right\vert }{6}$, então

$\left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right]
=\left\vert
\begin{array}{ccc}
4 & -2 & 2 \\
1 & -3 & 2 \\
5 & -1 & 1
\end{array}
\right\vert =36$.

Assim, concluímos que o volume do tetradro é $V_{T}=\frac{\left\vert 36\right\vert }{6}=6$.

2 . Os vetores que determinam o tetraedro são $\overrightarrow{AB},$ $
\overrightarrow{AC}$ e $\overrightarrow{AD}.$ Sabemos que o volume do
tetraedro é dado por $V_{T}=\frac{A_{b}h}{6}$, onde $A_{b}$ é a área da base e $h$ é a altura. Como a área da base é um triângulo determinado pelos vetores $\overrightarrow{AB}$ e $\overrightarrow{AC}, $ $A_{b}=\frac{\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert }{2}$.

Por outro lado, do cálculo vetorial temo que $V_{T}=\frac{\left\vert
\left[ \overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}\right]
\right\vert }{6}.$ Então, temos $\left\vert \left[ \overrightarrow{AB},
\overrightarrow{AC},\overrightarrow{AD}\right] \right\vert =\left\vert
\overrightarrow{AB}\times \overrightarrow{AC}\right\vert h$ $\Longrightarrow h=\frac{\left\vert \left[ \overrightarrow{AB},\overrightarrow{AC}, \overrightarrow{AD}\right] \right\vert }{\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert }.$

Como $\overrightarrow{AB}$ $=\left( 4,-2,2\right) $, $\overrightarrow{AC}$ $
=\left( 1,-3,2\right) $e $\overrightarrow{AD}$ $=\left( 5,-1,1\right) $, temos $\left[ \overrightarrow{AB},\overrightarrow{AC}, \overrightarrow{AD} \right] =36$ e

$\overrightarrow{AB}\times \overrightarrow{AC}=\left\vert
\begin{array}{ccc}
\overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\
4 & -2 & 2 \\
1 & -3 & 2
\end{array}
\right\vert =2\overrightarrow{i}-6\overrightarrow{j}-10\overrightarrow{k}.$

Logo, $\left\vert \overrightarrow{AB}\times \overrightarrow{AC}\right\vert =2 \sqrt{35}$. Portanto, concluímos que $h=\frac{18\sqrt{35}}{35}$.

297

Encontre condições sobre o vetor $v=(a,b,c)$ para que exista uma reta na direção de $v$ que intercepte simultaneamente as retas $r$ e $s$:

$$r:\begin{cases} x=2 + t\\
y = 5 - t
\\z = 3 + t \end{cases}\ \ \ {\rm e}\ \ \ s:\begin{cases} x= t\\
y = 1 - t
\\z = -2 + t \end{cases}$$

778

Decompor o vetor $w = (1,3,2)$ como soma de dois vetores $w = u + v$, onde $u$ é paralelo ao vetor $(0,1,3)$ e $v$ é ortogonal a $(0,1,3)$.

$u=(0,11/10,33/10)$ e $v=(1,9/10,-3/10)$.

1434

Mostre que o elipsóide obtido girando uma elipse com semi-eixo maior $a$ e semi-eixo menor $b$ em torno do eixo maior tem volume $\displaystyle V=\dfrac{4}{3}\pi ab^2$.
Mostre que o elipsóide obtido girando uma elipse com semi-eixo maior $a$ e semi-eixo menor $b$ em torno do eixo menor tem volume $\displaystyle V=\dfrac{4}{3}\pi a^2b$.

507

Seja $\ell$ a curva com equações paramétricas: $x=\dfrac{a(1+t^2)}{(1-t^2)}$ e $y=\dfrac{2bt}{(1-t^2)}$. Determine $\ell$.

390

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
0&1&0\\ 1&0&0\\ 0&0&1
\end{pmatrix}.
$

As raízes são: $x=-1$ (simples) e $x=1$ (dupla).

1375

Construa a curva cujas equações paramétricas são dadas por: $x=2\sin^2t$, $y=\sin(2t)$ e $z=2\cos t$.

308

Verifique a posição relativa do seguinte par de retas (isto é, verifique se são paralelas, concorrentes ou reversas):

\[
\left\{\begin{array}{ccr}x &=& 2-t\\y &=& 3+2t\\ z &=& 1 + t\end{array}\right., \ \ \
\left\{\begin{array}{ccr}x &=& 5-2s\\y &=& 2+4s\\ z &=& 1 + 2s\end{array}\right. .\]

São paralelas.

1056

Decida se a cônica $C$ determinada pela equação $36x^2-24x+36y^2-36y+14=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

487

Encontre uma equação em coordenadas polares para a curva cuja equação em coordenadas cartesianas é dada por $x^2-y^2=16$.

Apenas usando a definição de coordenadas polares, obtemos a seguinte equação: $\displaystyle r\sqrt{\cos(2\theta)}=4$.

1040

A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue

\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]

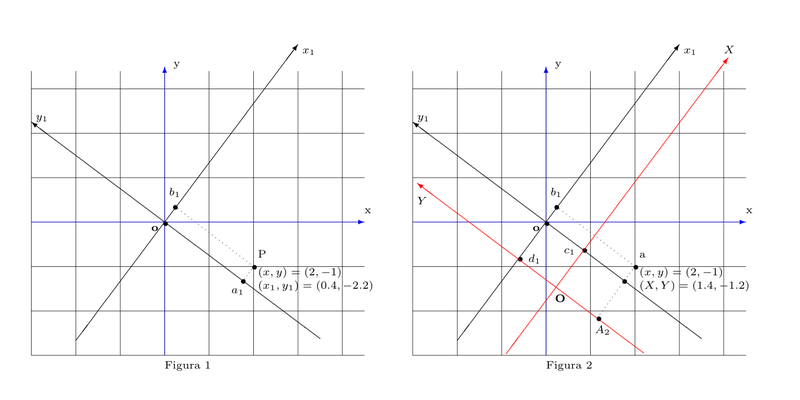
Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.

Encontre as coordenadas dos pontos $a_{1}$ e $b_{1}$ (Figura 1) nos sistemas $xy$ e $x_{1}y_{1}$.
Encontre as coordenadas dos pontos $c_{1}$, ,$d_{1}$, $\textbf{O}$, e $A_{2}$ (Figura 2) em relação aos eixos $xy$, $x_{1}y_{1}$ e $XY$.

1357

Forneça equações paramétricas para $\frac{x^2}{4}+\frac{y^2}{9}=1$, indicando os valores para o seu parâmetro $t$. Esboce suas equações paramétricas.

254

Considere o plano $\pi : ax + by + cz = 0$. Encontre as coordenadas:

da projeção ortogonal do vetor $(x,y,z)$ sobre o plano $\pi$;
da reflexão do vetor $(x,y,z)$ em relação ao plano $\pi$.

965

Mostre que a equação $x^2+y^2+2z^2+2xz-2yz=1$ representa uma superfície cilíndrica e determine a equação da curva diretriz e um vetor paralelo às retas geratrizes.

1028

Determinar a equação reduzida da hipérbole com assíntotas $3y=\pm 2x $ e vértices $(\pm 10,0).$

1567

Seja $A$ uma matriz $2\times 2$ real com autovalores complexos $\lambda=a\pm bi$ tais que $b\neq 0$ e $|\lambda|=1$. Mostre que toda trajetória do sistema dinâmico $\textbf{x}_{k+1}=A\textbf{x}_k$ está sobre uma elipse. [Dica: use que se $\textbf{v}$ é um autovetor associado a $\lambda=a-bi$, então a matriz $P=[ \textrm{Re}\,\textbf{v}\quad \textrm{Im}\,\textbf{v}]$ é invertível e temos que $\displaystyle A=P\left[\begin{array}{cc} a & -b \\ b & a \end{array}\right]P^{-1}$. Ponha $\displaystyle B=(PP^t)^{-1}$. Mostre que a equação quadrática $\textbf{x}^tB\textbf{x}=k$ define uma elipse para todo $k>0$, e prove que se $\textbf{x}$ está sobre esta elipse, então $A\textbf{x}$ também estará.]

1070

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+2y^2-4xy+y-1=0$.

302

Encontre a equação da reta $r$ que passa pelos pontos $(-2,1,-3)$ e $(-4,0,2)$.

Um vetor diretor pode ser tomado pela diferença $(-4,0,2)-(-2,1,-3)=(-2,-1,5)$. Assim, temos a seguinte forma paramétrica $$ r: (-2,1,-3)+t(-2,-1,5)\quad t\in\mathbb{R}.$$

244

Verifique que a intersecção dos planos $\pi_1:x-y=0$, $\pi_2:x+z=0$ e $\pi_3:x-y+3z+3=0$ é um ponto. Modifique o coeficiente de $y$ na equação do plano $\pi_3$ para que a intersecção $\pi_1\cap\pi_2\cap\pi_3$ seja uma reta.

1045

Decida se a cônica $C$ determinada pela equação $y^2+x^2+3xy-10x-10y+5=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

948

Obtenha a equação do lugar geométrico dos pontos que equidistam das retas $r: y=z=0$ e $l: x=y-1=0$. Que conjunto é este?

1401

Uma força $\vec{F} = (4,-6,1)$ N é aplicada a um ponto que se move uma distância de $15$ metros na direção e sentido do vetor $(1,1,1)$. Quanto trabalho foi realizado?

355

A equação $x^{2}=1$ possui apenas duas soluções reais: $x=1$ e $x=-1$. Ache todas as matrizes $2\times2$ que são soluções da equação matricial $X^{2}=I$, onde $I$ é a matriz identidade $2\times2$.

Se $X= \left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right),$ $X^2=I \rightarrow \left(\begin{array}[c]{cc}x^2+yz & wy+xy\\wz+xz & w^2+yz\end{array}\right)=\left(\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}\right).$

Cujas soluções são:

$X_1= \left(\begin{array}[c]{cc}x & y\\\frac{1-x^2}{y} & -x\end{array}\right), \forall x,y\in \mathbb{R};$ $X_2= \left(\begin{array}[c]{cc}-1 & 0\\z & 1\end{array}\right), \forall z\in \mathbb{R};$ $X_3= \left(\begin{array}[c]{cc}1 & 0\\z & -1\end{array}\right), \forall z\in \mathbb{R};$ $X_4= \left(\begin{array}[c]{cc}-1 & 0\\0 &-1\end{array}\right);$ $X_5= \left(\begin{array}[c]{cc}-1 & 0\\0 & 1\end{array}\right);$ $X_6= \left(\begin{array}[c]{cc}1 & 0\\0 & -1\end{array}\right);$ $X_7= \left(\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}\right).$

1016

Encontre os vértices (ou vértice), os focos (ou foco) e a excentricidade da cônica descrita por $4x^2+9y=144$. Esboce também o gráfico.

357

Seja \[A=\left(\begin{array}[c]{cc}2 & x^{2}\\2x-1 & 0\end{array}\right) .\]
Qual é o valor de $x$ para que tenhamos $A^{t}=A$?

$x=1$

857

Dados três pontos $A=(1,-5,8)$, $B=(5,2,4)$ e $C=(3,9,1)$, ache três pontos diferentes tais que cada um deles forma com $A,B,C$ um paralelogramo.

383

Calcule o determinante da matriz:

$
\begin{pmatrix}
\sin\alpha&\cos\alpha&1\\ \sin\beta&\cos\beta&1\\ \sin\gamma&\cos\gamma&1
\end{pmatrix}.
$

$\sin(\alpha - \beta) - \sin(\alpha - \gamma) + \sin(\beta - \gamma)$

376

Calcule o determinante da matriz:
$
\begin{pmatrix}
a&b\\ -b&a
\end{pmatrix}.
$

$a^2+b^2$

240

Determine a reta $t$, contida no plano $\pi : x-y+z=0$, e que é concorrente com as retas

$$\begin{cases} x+2y+2z=2\\ x=y \end{cases}\ \ \ {\rm e}\ \ \ \begin{cases} z=x+2\\ y=0 \end{cases}$$

Usando escalonamento, podemos ver que a primeira reta irá intersectar o plano $\pi$ no ponto $A=(2/3,2/3,0)$. Da mesma forma, a segunda reta irá intersectar $\pi$ no ponto $B=(-1,0,1)$. Assim, $t$ será a reta contida em $\pi$ e que passa por $A$ e $B$. Ou seja, tomando $B-A=(-5/3,-2/3,1)$ como vetor diretor, então podemos escrever $t$ na forma vetorial como $$ t: (2/3,2/3,0)+s(-5/3,-2/3,1),\quad s\in\mathbb{R}, $$ ou ainda, em termos de componentes, $$\begin{cases} x=\frac{2}{3}-s\frac{5}{3}, \\ y=\frac{2}{3}-s\frac{2}{3},\\ s,\quad s\in\mathbb{R}.\end{cases}$$

1437

Mostre a seguinte propriedade de Reflexão da Parábola: A reta tangente em um ponto $P$ da parábola faz ângulos iguais com a reta que passa por $P$ paralela ao eixo de simetria e com a reta que passa por $P$ e o foco. (Sugestão: Escolha os eixos coordenados de tal modo que a parábola tenha a equação $x^2=4py$.
Mostre que a reta tangente em $P(x_0,y_0)$ intersecta o eixo $y$ no ponto $Q(0,-y_0)$ e que é isósceles o triângulo cujos três vértices estão em $P$, $Q$ e o foco.

1063

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+2x+y^2+2y+2=0$.

456

Seja $M= \left( \begin{array}{cccc}a & 0 & b & 2\\a & a & 4 & 4\\0 & a & 2 & b\end{array}\right) $ a matriz ampliada (ou aumentad de um sistema linear. Para que valores de $a$ e $b$ o sistema admite:

Solução única;
Solução com uma variável livre;
Solução com duas variáveis livres;
Nenhuma solução.

1066

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+(1/5)xy +y^2+2x+2y+2=0$.

862

Mostre que as diagonais de um losango cortam-se mutuamente em seu ponto médio e que são ortogonais entre si.

1432

O que acontece com a distância entre a diretriz e o centro de uma elipse se os focos permanecerem fixados e a excentricidade tender a $0$?

951

Identifique a quádrica definida pela equação reduzida $z=4x^2+4y^2$ e esboce seu gráfico.

982

Considere três vetores do $\mathbb{R}^{3}$: $u = (1,0,-1)$, $v = (1,1,1)$ e $w = (x,y,z)$.

Se $w = (-1,-5,-9)$, mostre que existem escalares $a$ e $b$ tais que $w = au + bv$.
Ainda para $w = (-1,-5,-9)$, existem escalares $a', b'$ tais que $(a',b') \ne (a,b)$ e $w = a'u + b'v$?
Para todo $w$ existem escalares $a$ e $b$ tais que $w = au + bv$ como no item anterior?
Existe alguma relação entre as perguntas acima e o estudo de sistemas?

$a=4$ e $b=-5$.
Não.
Não. Com apenas dois vetores não é possível gerar todos os vetores de $\mathbb{R}^3$. Por exemplo, não existem $\alpha$ e $\beta\in\mathbb{R}$ tais que $\alpha u + \beta v=(-1,5,9)$.
Uma conclusão básica é que nem todo sistema de três equações e duas incógnitas terá solução. Mais conclusões são possíveis.

1397

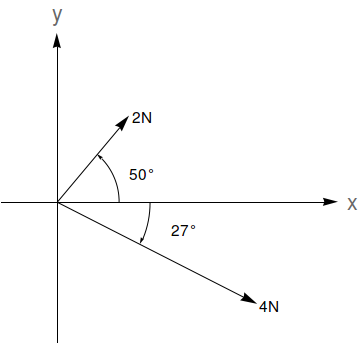
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).

860

Sendo $A=(3,1)$ e $B=(3,-5),$ determinar os pontos $F$ e $G$ que dividem $AB$ em três segmentos de igual comprimento.
Calcular o comprimento de $\vec{AB}.$

$F=(3,-1)$ e $G=(3,-3)$
$|\vec{AB}|=6$

1083

Identifique a cônica descrita pela equação $16x^2+16y^2-16x+8y-59=0$.

1042

Seja $\mathcal{C}$ a cônica cuja equação em relação ao sistema $xy$ é dada por $29x^2 + 24xy + 36y^2 + 22x + 96y = 115$. A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue
\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad
\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]

Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.

Encontre a equação de $\mathcal{C}$ nos sistemas $x_{1}y_{1}$ e $XY$.
Encontre as coordenadas dos vértices e dos focos de $\mathcal{C}$ nos três sistemas, $xy$,\,$x_{1}y_{1}$ e $XY$. Dica: Encontrar primeiro no sistema $XY$ e ir voltando.
Faça um esboço do desenho da cônica.

512

Reduza a equação $x^2+y+z^2=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

$y=-(x^2+z^2)$: parabolóide elíptico.

1472

Encontre ou mostre a impossibilidade de encontrar $\gamma\in\mathbb{R}$ tal que $\displaystyle x^2+\gamma y^2-4xy+ \gamma x = \gamma$ represente uma parábola.

415

Resolva o sistema $A\,X=B$ usando o método de Gauss-Jordan, onde: $$A=\begin{bmatrix} 1 & 0 & -1 \\ 2 & 1 & 0 \\ 0 & 1 & 1 \end{bmatrix} \text{ e } B=\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}.$$

Destaque as operações elementares usadas.

Vamos aplicar escalonamento sobre a matriz aumentada do sistema:
\begin{gather*}
\begin{pmatrix} 1 & 0 &-1&\vdots & 1 \\ 2 & 1 & 0& \vdots & 1 \\ 0 & 1 & 1 & \vdots & 1 \end{pmatrix} \begin{array}{c} L_2-2L_1\rightarrow L_2\\ \sim \end{array}
\begin{pmatrix} 1 & 0 & -1 & \vdots & 01 \\ 0 & 1 & 2 & \vdots & -1 \\ 0 & 1 & 1 & \vdots & 01 \end{pmatrix}
\begin{array}{c} L_3-L_2\rightarrow L_3 \\\sim \end{array}
\begin{pmatrix} 1 & 0 & -1 & \vdots & 1 \\ 0 & 1 & 2 & \vdots & -1 \\ 0&0&-1&\vdots&2 \end{pmatrix} \\ \begin{array}{c} \\-L_3\leftrightarrow L_3 \\ \sim \\ L_3+L_1\rightarrow L_1 \end{array} \begin{pmatrix} 1& 0& 0&\vdots & -1\\ 0& 1& 2&\vdots & -1\\ 0& 0& 1&\vdots &-2 \end{pmatrix}
\begin{array}{c} L_2-2 L_3\rightarrow L_2 \\ \sim \end{array}
\begin{pmatrix} 1& 0& 0&\vdots &-1 \\ 0 & 1& 0& \vdots& 3\\ 0& 0 & 1 &\vdots & -2 \end{pmatrix}. \end{gather*} Logo, a solução é dada por $\displaystyle (-1,3,-2)^T$.

1359

Dê equações paramétricas para a curva $y=x^3-x^2$, indicando os valores para o seu parâmetro $t$. Esboce suas parametrizações.

1086

Sejam $F_{1}$ e $F_{2}$ dois pontos fixos do plano que distam $8$ unidades um do outro. Ou seja, $\text{dist}(F_{1},F_{2}) = 8$.

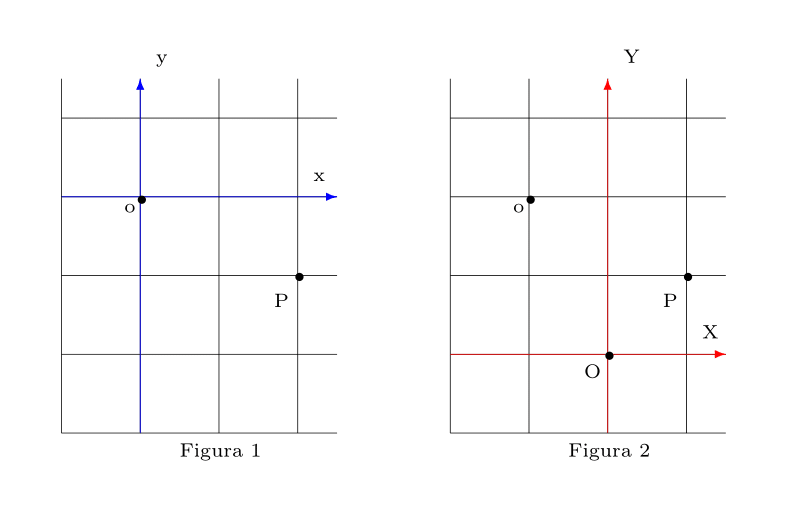
Encontre a equação do lugar geométrico dos pontos $P$ desse plano que satisfazem a condição:
\[ \text{dist}(P,F_{1}) + \text{dist}(P,F_{2}) = 10,\]
em cada um dos seguintes casos:

$F_{1} = (-c,0)$ e $F_{2} = (c,0)$, onde as coordenadas foram tomadas em relação ao sistema $xy$ da Figura 1 acima, e cada ponto $P$ tem coordenadas $(x,y)$ tomadas em relação a $\textbf{o}$.
$F_{1} = (-5,2)$ e $F_{2} = (3,2)$, onde as coordenadas foram tomadas em relação ao sistema $XY$ da Figura 2 acima, e cada ponto $P$ tem coordenadas $(X,Y)$ tomadas em relação a $\textbf{O}$.
$F_{1}$ e $F_{2}$ estão sobre o eixo $X$ do sistema $XY$ da Figura 2 acima, são simétricos em relação ao eixo $Y$, e cada ponto $P$ tem coordenadas $(x,y)$ tomadas em relação a $\textbf{o}$.

820

Para o par de vetores $u=(3,1,-3)$ e $v=(2,-3,1)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.

Posto que $u \cdot v=0$, $u$ e $v$ são ortogonais. Assim, a projeção ortogonal de $v$ sobre $u$ é zero. Nesse caso, $v_1=0$ e $v_2=v$.

718

Mostre que o plano tangente à esfera $x^2+y^2+z^2=r^2$ no ponto $(a,b,c)$ tem equação $ax+by+cz=r^2$.

362

Responda verdadeiro ou falso, justifique suas respostas.

Se $A^2 = -2\,A^4$, então $(I + A^2)^{-1} = I - 2\,A^2$.
Se $A^t = -A^2$ e $A$ é não singular, então $\det A = -1$.
Se $B = A\,A^t\,A^{-1}$, então $\det(A) = \det(B)$.
$\det(A + B) = \det A + \det B$.

Verdadeira, pois $A^2 = -2\,A^4 \Rightarrow -A^2 -2\,A^4=0$.
E $(I + A^2)^{-1} = I - 2\,A^2 \Leftrightarrow (I - 2\,A^2) (I+A^2)=I$ e $ (I+A^2) (I - 2\,A^2) =I$.
O que vale, visto que $(I - 2\,A^2) (I+A^2)=I+A^2- 2\,A^2- 2\,A^4=I-\,A^2- 2\,A^4=I-0=I$.
E $ (I+A^2) (I - 2\,A^2)=I- 2\,A^2+A^2- 2\,A^4=I-A^2- 2\,A^4=I-0=I$.
Falsa, pois $\det(A)\neq0$ e $A^t = -A^2 \Rightarrow \det(A^t)=\det(-A^2)$.
Mas $\det(A^t)=\det(A)$ e $\det(-A^2)=\det(-A)\det(A)=(-1)^n \det(A) \det(A)$, onde $n$ é a ordem da matriz $A$.
Logo $\det(A)=\det(A^t)=\det(-A^2)=(-1)^n\det(A)^2 \Rightarrow 1=(-1)^n \det(A) \Rightarrow \det(A)=(-1)^n$.
Portanto, se a matriz for de ordem par $\det(A)=1$ e se a matriz for de ordem ímpar $\det(A)=-1$.
Verdadeira.
$B = A\,A^t\,A^{-1} \Rightarrow \det(B)=\det(A)\det(A^t)\det(A^{-1})=\det(A) \det(A)\dfrac{1}{\det(A)}=\det(A)$.
Falsa, contra exemplo:
sejam $A$ e $B$ matrizes de ordem dois tais que $A=I$ e $B=2I$. Então $A+B=3I$. E $\det(A+B)=9$. Mas, como $\det(A)=1$ e $\det(B)=4$, $\det(A)+\det(B)=5\neq 9=\det(A+B)$.

1475

Seja $Q$ um retângulo centrado na origem, cujo lado maior mede o triplo do lado menor. Sabendo que um dos vértices de $Q$ é $V_1=(1,2)$ e que o vértice $V_2$, consecutivo a $V_1$ no sentido trigonométrico (anti-horário), é tal que $V_1V_2$ é um lado menor, determine os outros vértices de $Q$.

Tomando o ângulo $\theta=\widehat{V_10V_2}$, temos que $V_2 = R_{\theta}(V_1)$, onde $$R_\theta=\left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array} \right) $$ denota a rotação por um ângulo $\theta$ (Fig.). Sendo $P$ o ponto médio do segmento $V_1V_2$, vamos ter que $\dfrac{\theta}{2}=\widehat{POV_2}$. Sendo $V_1V_2$ um lado menor e dada a relação entre os lados (enunciado), segue que $|OP|=3|PV_2|$. Assim, o triângulo retângulo $OPV_2$ nos fornece que $$ \sin\dfrac{\theta}{2} = \dfrac{|PV_2|}{|OV_2|} \quad\text{e}\quad \cos\dfrac{\theta}{2}=\dfrac{|OP|}{|OV_2|}=\dfrac{3|PV_2|}{|OV_2|}=3\sin\dfrac{\theta}{2}, $$ o que juntamente com a relação fundamental $\sin^2\theta+\cos^2\theta=1$, resulta em $\sin^2\dfrac{\theta}{2}+9\sin^2\dfrac{\theta}{2}=1$. Ou seja, temos que $$ \sin\dfrac{\theta}{2}=\dfrac{\sqrt{10}}{10} \quad\mathrm{e}\quad\cos\dfrac{\theta}{2}=\dfrac{3\sqrt{10}}{10}.$$ Conseqüentemente, temos que $$\cos\theta= \cos(2\dfrac{\theta}{2})=\cos^2\dfrac{\theta}{2}-\sin\dfrac{\theta}{2}= \dfrac{4}{5}\quad \text{e}$$ $$\sin\theta= \sin(2\dfrac{\theta}{2})= 2\cos\dfrac{\theta}{2}\sin\dfrac{\theta}{2}= \dfrac{3}{5} .$$ Assim, $$ V_2 = R_{\theta}(V_1)=\left(\begin{array}{cc} \dfrac{4}{5} & -\dfrac{3}{5} \\ \dfrac{3}{5} & \dfrac{4}{5} \end{array}\right)\left(\begin{array}{c} 1 \\ 2 \end{array}\right) = \left(\begin{array}{rcl} -\dfrac{2}{5} &,&\dfrac{11}{5} \end{array}\right). $$ Finalmente, como $V_3=R_{\pi}(V_1)$, $V_4=R_{\pi}(V_2)$, $cos\pi=-1$ e $\sin\pi=0$, obtemos que $$V_3=-V_1=(-1,-2) \quad \text{e}\quad V_4=-V_2=(\dfrac{2}{5},-\dfrac{11}{5}).$$

460

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{cccccr}&x_1&-&7x_2&=&-11 \\-&x_1&+&11x_2&=&31 \\&2x_1&-&12x_2&=&-26 \\&3x_1&-&17x_2&=&-15 \\\end{array}\right. . \]

$Y = (0, 0)^T$.
Não existe solução particular $X_o$ para esse sistema. Ou seja, o sistema linear não possui solução.

428

Resolver o sistema linear: \[\left\{\begin{array}{ccccccr}2x_1&+&5x_2&+&12x_3&=& 6 \\3x_1&+&x_2&+&5x_3&=& 12 \\5x_1&+&8x_2&+&21x_3&=& 17\\\end{array}\right. .\]

Esse sistema linear não possui solução.

264

Dados o plano $x-y+z=1$ e o ponto $P=(1,0,1)$, encontre o ponto $Q$ que é simétrico a $P$ em relação ao plano dado.

298

Encontre condições sobre o vetor $v=(a,b,c)$ para que exista uma reta na direção de $v$ que intercepte simultaneamente as retas $r$ e $s$:

$$r:\begin{cases} x= 1 + t\\y = -2 - t\\z = 3 + t \end{cases}\ \ \ {\rm e}\ \ \ s:\begin{cases} x= 1 + 2t\\y = -2\\z = 3 + t \end{cases}$$

1157

Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores $\alpha_1=\beta_1=60^\circ$; e a outra com ângulos diretores tais que $\cos \alpha_2=\cos \beta_2=1/2\sqrt{2}$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).

$15^\circ$.

1208

Reduza a equação $2xy + 2xz + 2yz - 6x - 6y - 4z = 9$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1378

Construa a curva cujas equações paramétricas são dadas por: $x=\cos\theta$, $y=2\sin\theta$ e $z=3\theta$.

442

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{ccccccccccr}&&x_1&+&x_2&-&x_3&+&2x_4&=&6 \\&-&x_1&+&x_2&+&4x_3&-&3x_4&=&-2 \\&&&&x_2&+&3x_3&+&x_4&=& 5 \\&&&&x_1&+&5x_2&+&5x_3& =&14 \\\end{array}\right. . \]

Esse sistema possui infinitas soluções.

1144

Mostre que para dois vetores $\vec{A}$ e $\vec{B}$, $\|\vec{A}\| - \|\vec{B}\| \leq \|\vec{A} \pm \vec{B}\| \leq \|\vec{A}\| + \|\vec{B}\|$. Em que condições vale a igualdade?

$\|\vec{A} - \vec{B}\|^2=\|\vec{A}\|^2+\|\vec{B}\|^2- 2\|\vec{A}\|\|\vec{B}\|\cos\theta$.

449

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{ccccccccr}3x& + &3y& - &2z& - &t&=& 2\\5x& + &2y& + &z& - &2t&=& 1\\2x& - &y& + &3z& - &t&=& -1\end{array}\right. .\]

Esse sistema possui infinitas soluções.

1162

Seja $(4,5)$ o ponto médio de um segmento de reta tal que uma extremidade é $(-1,2)$. Ache a outra extremidade.

$(9,8)$.

263

Verifique que a reta $x-1=z-2 y=3$ é paralela ao plano $x+2y-z=3$ e encontre a distância perpendicular entre eles.

Escrevendo $z$ como parâmetro livre, obtemos que $v=(1,0,1)$ é um vetor diretor da reta dada e, sendo $n=(1,2,-1)$ o vetor normal ao plano, vemos que $v\cdot n=0$. Ou seja, a reta é paralela ao plano. Tomando os pontos $p=(-1,3,0)$ sobre a reta e $p_1=(3,0,0)$ sobre o plano, segue também que a distância procurada é dada por $$ \|\mathrm{proj}_{n}\overrightarrow{p_1p}\| = \sqrt{\frac{2}{3}}.$$

770

Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(1,1,1)$ e sua extremidade é o ponto $P=(1,1,1)$.

$(0,0,0)$.

1647

Em cálculo de uma variável vemos que se $x_0$ é um extremo local (máximo ou mínimo) de uma função $f(x)$, então a reta tangente ao gráfico de $f$ em $x_0$ é horizontal, ou seja, $f'(x_0)=0$.

Encontre uma relação similar entre um extremo local de uma função de duas variáveis e o plano tangente ao seu gráfico.
Use esta relação para encontrar os extremos locais da função $\displaystyle f(x,y)=-2xy$.
Verifique se sua resposta no item anterior está correta, primeiro achando uma mudança de coordenadas conveniente (rotação) e, em seguida, completando os quadrados em $f(x',y')$ de tal forma a identificar a quádrica resultante.

705

Ache as equações dos dois círculos tangentes a $2x-5y+1=0$ no ponto $(2,1)$ e com raio $r = 3$.

280

Encontrar as equações paramétricas da reta que passa por $A$ e é simultaneamente ortogornal às retas $r_1$ e $r_2$:

$$A(3,2,-1),\;\;
r_1: \begin{cases} x=3\\ y=-1. \end{cases}\ \ \ {\rm e}\ \ \
r_2: \begin{cases} y=x-3\\ z=-2x+3. \end{cases}$$

$r:(x,y,z)=(3-t',2+t',-1).$

423

Resolver o sistema linear:\[\left\{\begin{array}{rrrrrcr}1x_1+&3x_2-&7x_3+&5x_4+&2x_5&=&0 \\2x_1+&3x_2-&20x_3+&7x_4+&8x_5&=&0 \\10x_1+&22x_2-&46x_3+&34x_4+&12x_5&=&0 \\\end{array}\right. . \]

$x_3 =\dfrac{11x_1+4x_2}{5}, x_4 = \dfrac{6 x_1-x_2}{5}, x_5 = \dfrac{21 x_1 + 9 x_2}{5}, \forall x_1, x_2 \in \mathbb{R}$.

492

Encontre uma equação em coordenadas cartesianas para a curva cuja equação em coordenadas polares é dada por $r^2=2sen2\theta$.

Usando a relação entre coordenadas polares e rectangulares, obtemos a seguinte equação: $\displaystyle x^2+y^2=2\sin(2\arctan\dfrac{y}{x}), \quad x\neq 0.$

231

Considere os seguintes vetores de $\mathbb{R}^{3}$: $U=(1,0,-1)$ e $V=(0,1,0)$.

Determine a forma geral de um vetor perpendicular a $U$. Explique porque sua resposta contém duas variáveis livres.
Determine (caso existam) as equações das retas que passam pelo ponto $(1,2,3)$, são perpendiculares ao vetor $U$ e fazem ângulo de $\dfrac{\pi}{3}$ com o vetor $V$.

$(a,b,a)$.
$\left\{
\begin{array}{l}
x=1+\sqrt{3} \\
y=2+\sqrt{2}t \\
z=3+\sqrt{3}t
\end{array}
\right. $ e $\left\{
\begin{array}{l}
x=1+\sqrt{3}t \\
y=2-\sqrt{2}t \\
z=3+\sqrt{3}t
\end{array}
\right. .$

1421

Um roteador de internet sem fio é instalado de forma que o sinal chegue com mesma intensidade em qualquer ponto $(x,y)$ a uma distância de $10$m do local de instalação $(0,0)$ (desconsiderando eventuais efeitos que possam diminuir a intensidade do sinal). Um outro roteador (nas mesmas condições), é instalado na posição $(20,0)$. Um terceiro roteador deve ser colocado de forma que o sinal chegue a uma maior área possível, ao mesmo tempo que fique próximo dos outros dois roteadores. Determine os dois pontos no plano cartesiano tais que este novo roteador possa ser instalado.

1141

Sejam $\vec{A}$, $\vec{B}$ e $\vec{C}$ vetores no plano, com $\|\vec{A}\|=3$, $\|\vec{B}\|=2$ e $\|\vec{C}\|=6$. O ângulo entre $\vec{A}$ e $\vec{B}$ é de $60^\circ$ e $\vec{C}$ está sobre a bissetriz deste ângulo. Faça um esboço do gráfico desses três vetores. Qual combinação linear de $\vec{A}$ e $\vec{B}$ é igual a $\vec{C}$?

$\vec{C} = 2/\sqrt{3} \vec{A} + \sqrt{3} \vec{B}$.

1468

Mostre que, ao variar $a$, a equação polar

$$ r=a\sec\theta \quad(-\pi/2 < \theta < \pi/2 ) $$

descreve uma família de retas perpendiculares ao eixo polar.

229

Achar o ponto $N$, projeção ortogonal do ponto $P(3,-1,-4)$ no plano determinado pelos pontos $A(2,-2,3)$, $B(4,-3,-2)$ e $C(0,-4,5)$. Qual é o ponto simétrico de $P$ em relação a este plano?

$N=\left(\frac{18}{7},-\frac{17}{14},\frac{47}{14}\right),\;

P'=\left(\frac{15}{7},\frac{10}{7},-\frac{9}{14}\right)$

246

Determine o plano que passa pelos pontos $P=(1,1,-1)$ e $Q=(2,1,1)$ e que dista $1$ da reta $r=\{ (1,0,2)+t(1,0,2),t\in\mathbb{R}\}$.

984

Sejam $A=(-1,2,3)$, $M=(-1,3,2)$ e $N=(1,1,3)$. O triângulo $ABC$ tem ângulos $A=90^\circ$ e $B=30^\circ$ e os vértices $B$ e $C$ pertencem à reta $MN$. Encontre os vértices $B$ e $C$.

1469

Mostre que, quando $b$ varia, a equação polar

$$ r=b\mathrm{\,cosec\,}\theta \quad(0 < \theta < \pi ) $$

descreve uma família de retas paralelas ao eixo polar.

250

Encontre a equação geral do plano que contém os pontos $A=(1,0,0)$, $B=(1,5,-2)$ e é paralelo ao vetor $(1,-1,1)$. Determine a distância de $C=(1,-1,1)$ ao plano encontrado e a área do triângulo formado pelos vértices $A$, $B$ e $C$.

384

Calcule o determinante da matriz:

$
\begin{pmatrix}
1&1&-6&-2 \\ 4&7&4&4 \\ -2&-2&1&-2 \\ -4&-7&0&-1
\end{pmatrix}.
$

$-27$

875

Sejam $a,b,c$ três vetores não coplanares e denotemos por $[a,b,c]$ o produto misto $a\cdot(b\times c)$. Os vetores

$$ a'=\frac{b\times c}{[a,b,c]},\; b'=-\frac{a\times c}{[a,b,c]},\; c'=\frac{a\times b}{[a,b,c]} $$ são chamados os vetores recíprocos aos vetores $a,b,c$.

Mostre que

$$ [a',b',c']=\frac{1}{[a,b,c]}. $$

883

Usando a propriedade de que podemos trocar os sinais $\times$ e $\cdot$ em um produto misto, mais a fórmula do produto vetorial triplo: $$A\times(B\times C) = (A\cdot C)B - (A\cdot B)C,$$ mostre que $$(A\times B)\cdot (C\times D) = \det\left(\begin{array}{cc}A\cdot C & A\cdot D \\B\cdot C & B\cdot D \\\end{array}\right).$$

317

Encontre as equações vetoriais e paramétricas para a reta $r$ que passa pelo ponto $P_0=(1,-1,1)$, é paralela à reta $r^{\prime}: (x,y,z) = (1,0,1) + t(1,1,3/2)$ e ortogonal ao eixo $z$ .

388

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A=\begin{pmatrix}
3&4\\ 5&2
\end{pmatrix}.
$

$x=7$ ou $x=-2$

1082

Identifique a cônica descrita pela equação $49x^2-42xy+9y^2+56x-24y+16=0$.

450

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{ccccccr}2x_1&+&5x_2&+&12x_3&=& 6 \\3x_1&+&x_2&+&5x_3&=& 12 \\5x_1&+&8x_2&+&21x_3&=& 17\\\end{array}\right. .\]

Esse sistema linear não possui solução.

1206

Reduza a equação $144x^2+100y^2+81z^2-216xz-540x-720z=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1218

Reduza a equação $-x^2-y^2-7z^2+16xy+8xz+8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

354

Seja \[A=\left(\begin{array}[c]{rr}3 & -2\\-4 & 3\end{array}\right) : \]

Encontre uma matriz $B$ tal que $B^{2}=A$ (isto é, $B$ é uma "raiz quadrada'' de $A$).
Encontre todas as soluções da equação matricial $X^{2}=A$.

$B= \left(\begin{array}[c]{cc}1 & -1\\-2 & 1\end{array}\right) . $
Se $X= \left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right),$ $X^2=A \rightarrow \left(\begin{array}[c]{cc}x^2+yz & wy+xy\\wz+xz & w^2+yz\end{array}\right)=\left(\begin{array}[c]{cc}3 & -2\\-4 & 3\end{array}\right).$

Cujas 4 soluções são:

$X'= \left(\begin{array}[c]{cc}1 & -1\\-2 & 1\end{array}\right);$ $X''= \left(\begin{array}[c]{cc}-1 & 1\\2 & -1\end{array}\right);$ $X'''= \left(\begin{array}[c]{cc}\sqrt{2} & -\sqrt{2}/2\\-\sqrt{2} & \sqrt{2}\end{array}\right);$ $X''''= \left(\begin{array}[c]{cc}-\sqrt{2} & \sqrt{2}/2\\\sqrt{2} & -\sqrt{2}\end{array}\right).$

1351

Esboce o gráfico da equação paramétrica dada por $(x,y) = (3t-1,4t+2)$.

262

Encontre a distância perpendicular entre os planos (paralelos): $$ 4x-8y-z=9 \;\;\; \mbox{e}\;\;\;2x-4y-\frac{z}{2}=5.$$

O primeiro plano ($\pi_1$) tem normal, digamos, $n_1=(4,-8,-1)$ e $p_1=(0,0,-9)$ é um ponto sobre o mesmo. Note também que $p_2=(0,0,-10)$ é um ponto sobre o outro plano ($\pi_2$). Assim, segue que $$ d(\pi_1,\pi_2)=d(\pi_1,p_2)=\|\mathrm{proj\,}_{n_1}(\vec{p_1p_2})\|=\frac{1}{9}.$$

1065

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+y^2+(1/3)xy+6x+8y-5=0$.

432

Resolver o sistema linear:

\[\left\{\begin{array}{rrrrl}4x&+3y&-z&+t&=4\\x&-y&+2z&-t&=0\\5x&+2y&+z&&=4\end{array}\right. . \]

$z = 4 - 5 x - 2 y, t = 8 - 9 x - 5 y, \forall x, y \in \mathbb{R}$.

1450

Determine uma equação da superfície consistindo em todos os pontos $P(x,y,z)$ que estão duas vezes mais afastados do plano $z=-1$ que do ponto $(0,0,1)$. Identifique a superfície.

1013

A elipse $\ell$ tem focos $F_1=(1,2)$ e $F_2=(2,4)$ e vértices $A_1=(0,0)$ e $A_2=(3,6)$. Dê as equações paramétricas de $\ell$.

392

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
5&2&-3\\ 4&5&-4\\ 6&4&-4
\end{pmatrix}.
$

As raízes são: $x=1$, $x=2$ e $x=3$.

506

Mostre que os pontos em coordenadas polares $ \left(1,\frac{\pi}{3}\right)$, $ \left(\sqrt{3},\frac{\pi}{6}\right)$, e $\left(1,0\right)$ são vértices de um triângulo equilátero.

819

Sendo $A=(-2,3)\;\mbox{e}\; B=(6,-3)$ extremidades de um segmento, determinar:

Os pontos $C,\;D\;\mbox{e}\; E$ que dividem o segmento $AB$ em quatro partes de mesmo comprimento.
Os pontos $F\;\mbox{e}\; G$ que dividem o segmento $AB$ em três partes de mesmo comprimento.

782

Mostre que o segmento que une os pontos médios de 2 lados de um triângulo é paralelo ao terceiro lado e é igual a sua metade.

No triângulo $ABC,$ sejam $M$ o ponto médio de$\ AC$ e $N$ o de $BC$. Assim, podemos escrever

$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2}\left(
\overrightarrow{AC}+\overrightarrow{CB}\right) =\frac{1}{2}\overrightarrow{AB}.$

Logo, $MN//AB$ e $\left\Vert \overrightarrow{MN}\right\Vert =\left\Vert\overrightarrow{AB}\right\Vert /2.$

1

Sejam
\[A=\left(\begin{array}[c]{rrr}1 & 2 & 3\\2 & 1 & -1
\end{array}\right) \text{, }B=\left(\begin{array}[c]{rrr}-2 & 0 & 1\\3 & 0 & 1
\end{array}\right) \text{, }C=\left(\begin{array}[c]{r}-1\\2\\4\end{array}\right) \text{ e }D=\left(\begin{array}[c]{cc}2 & -1\end{array}\right) .\]
Encontre:

$A+B$;
$AC$;
$BC$;
$CD$;
$DA$;
$DB$;
$-A$;
$-D$.

\[A+B=\left(\begin{array}{ccc} -1 & 2 & 4 \\ 5 & 1 & 0 \end{array}\right);\]
\[AC=\left(\begin{array}{c} 15 \\ -4 \end{array}\right);\]
\[ BC=\left(\begin{array}{c} 6 \\ 1 \end{array}\right);\]
\[CD = \left(\begin{array}{cc} -2 & 1 \\ 4 & -2 \\ 8 & -4 \end{array}\right);\]
\[DA = \left(\begin{array}{ccc} 0 & 3 & 7 \end{array}\right);\]
\[ DB =\left(\begin{array}{ccc} -7 & 0 & 1 \end{array}\right);\]
\[ -A = \left(\begin{array}{ccc} -1 & -2 & -3 \\ -2 & -1 & 1 \end{array}\right);\]
\[ -D = \left(\begin{array}{cc} -2 & 1 \end{array}\right).\]

1230

Reduza a equação $5x^2+5y^2+3z^2-2xy+2xz+2yz+2x-y=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

380

Calcule o determinante da matriz:

$
\begin{pmatrix}
0&a&0\\ b&c&d\\ 0&e&0
\end{pmatrix}.
$

$0$

1057

Decida se a cônica $C$ determinada pela equação $4x^2-8x-9y^2+6y-68=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

370

Determine todos os valores de $\lambda$ para os quais $\det(A-\lambda I_3)=0$.

\[
A = \left( \begin{array}{ccc}
2 & -2 & 3 \\
0 & 3 & -2 \\
0 & -1 & 2
\end{array}\right). \]

\[\lambda\in\{1,2,4\}\]

265

Sejam $P=(a,b, c)$ um ponto no espa\c co e $r$ a reta $\left\{ \begin{array}{c} x+y+2z=4 \\ x-2y+z=5\end{array} \right.$. Para cada par não nulo de n\'umeros reais, $m,\,n$, considere o plano:

$$\pi_{(m,n)}: (m+n)x+(m-2n)y+(2m+n)z=4m+5n.$$
Mostre que: $P\in r$ se e somente se $P\in \pi_{(m,n)}$, para todo par não nulo $(m,n)$.

228

Calcular $k$ de modo que a reta determinada por $A(1,-1,0)$ e $B(k,1,2)$ seja paralela ao plano

$$\pi:\;\begin{cases}x=1+3h\\ y=1+2h+t\\ z=3+3t \end{cases}$$

$k=3/2$

375

Calcule o determinante da matriz:
$\begin{pmatrix}
a+b&a+c \\ d+b&d+c
\end{pmatrix}. $

$\det\left(\begin{pmatrix}a+b&a+c \\ d+b&d+c\end{pmatrix}\right)=(c-b)(a-d). $

1484

Três tipos de suplementos alimentares estão sendo desenvolvidos. Para cada grama de ração, tem-se que:

i) O suplemento 1 tem $1$ unidade de vitamina A, $3$ unidades de vitamina B e $4$ unidades de vitamina C;

ii) O suplemento 2 tem $2$, $3$, e $5$ unidades das vitaminas A, B, e C, respectivamente;

iii) O suplemento 3 tem $3$ unidades das vitaminas A e C, e não contém vitamina B.

Se são necessárias $11$ unidades de vitamina A, $9$ de vitamina B, e $20$ de vitamina C,

Encontre todas as possíveis quantidades dos suplementos 1, 2, e 3, que fornecem a quantidade de vitaminas desejada.
Qual o sistema homogêneo associado?
O sistema homogêneo associado aceita solução não nula?
Qual a relação entre a resposta dos itens anteriores?
Se o suplemento 1 custa $6$ reais por grama e os outros dois custam $1$, existe uma solução custando exatamente $10$ reais?

1376

Construa a curva cujas equações paramétricas são dadas por: $x=e^t$, $y=e^{-t}$ e $z=t$.

1075

Identificar a cônica $x^2-2xy+y^2-10x-6y+25=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).

1156

Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores $\alpha_1=45^\circ$, $\beta_1=45^\circ$; e a outra com ângulos diretores $\alpha_2=\beta_2=60^\circ$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).

$45^\circ$.

1479

Um silo com formato cônico de raio $r=1$ m e altura $h=2$ m é preenchido com trigo em $70\%$ de sua capacidade.

Quanto mais de trigo podemos colocar a fim de preenchê-lo completamente?

994

Seja $\vec{v}\ne 0$ um vetor do $\mathbb{R}^{3}$ e sejam $\alpha$, $\beta$ e $\gamma$ os ângulos que $\vec{v}$ faz com os eixos coordenados $X$, $Y$ e $Z$, respectivamente. Mostre que:

se $\|\vec{v}\| = 1$, então $\vec{v} = (\cos(\alpha),\cos(\beta),\cos(\gamma))$ (Dica: calcular os cossenos de $\alpha$, $\beta$ e $\gamma$ fazendo o produto escalar de $\vec{v}$ com os vetores de comprimento $1$ na direção dos eixos coordenados. Como é um vetor de comprimento $1$ na direção de $X$? Isto é, sobre o eixo $X$.).
para um vetor $\vec{v}$ qualquer, vale que $\vec{v} = \|\vec{v}\|(\cos(\alpha),\cos(\beta),\cos(\gamma))$.
$\cos^{2}(\alpha) + \cos^{2}(\beta) + \cos^{2} (\gamma) = 1$.

421

Resolver o sistema linear:

\[\left\{\begin{array}{cccccr}&x_1&-&7x_2&=&-11 \\-&x_1&+&11x_2&=&31 \\&2x_1&-&12x_2&=&-26 \\&3x_1&-&17x_2&=&-15 \\\end{array}\right. . \]

O sistema não possui solução.

420

Resolver o sistema linear:

\[\left\{\begin{array}{ccccccccccr}&&x_1&+&x_2&-&x_3&+&2x_4&=&6 \\&-&x_1&+&x_2&+&4x_3&-&3x_4&=&-2 \\&&&&x_2&+&3x_3&+&x_4&=& 5 \\&&&&x_1&+&5x_2&+&5x_3& =&14 \\\end{array}\right. . \]

$x_2 = \dfrac{13-2 x_1}{5}, x_3 = \dfrac{1+x_1}{5}, x_4 = \dfrac{9-x_1}{5}, \forall x_1\in\mathbb{R}.$

454

Examine o sitema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[ \left\{\begin{array}{rrrrl}x&+5y&+4z&-13z&=3\\3x&-y&+2z&+5t &=2\\2x&+2y&+3z&-4t&=1\end{array}\right. .\]

Esse sistema linear não possui solução.

1145

Para dois vetores $\vec{A}$ e $\vec{B}$, mostre que vale a Lei Distributiva: $m(\vec{A} + \vec{B})=m\vec{A}+m\vec{B}$ (Sugestão: mostre que $m\vec{A}+m\vec{B}$ está na mesma direção que $\vec{A}+\vec{B}$ e que $\|m\vec{A}+m\vec{B}\|$ é igual a $m$ vezes $\|\vec{A}+\vec{B}\|$). O que ocorre se $m$ for negativo?

1348

Considere a curva no espaço descrita pela espiral $S(t) = \left( \frac{\cos(t)}{\sqrt{1 + t^2}}, \frac{\sin(t)}{\sqrt{1 + t^2}}, \frac{t}{\sqrt{1 + t^2}} \right)$. Qual a relação entre esta curva e a hélice cilíndrica $H(t) = (\cos(t), \sin(t), t)$? Esboce a imagem de $S$. Compare o movimento de uma partícula $p$ ao longo de $S$ com o movimento de uma outra partícula ao longo de $H$.

1007

Dado um plano qualquer com um sistema de coordenadas $xy$, encontre os vértices (ou vértice), os focos (ou foco) e a excentricidade da cônica descrita por $4x^2+9y=144$. Esboce o gráfico.

996

Se $u$, $v$ e $w$ são vetores no espaço então: mostre que $\langle u,v\times w\rangle = \langle v, w\times u\rangle = \langle w , v\times u\rangle$.

1373

Construa a curva cujas equações paramétricas são dadas por: $x=t$, $y=2t^2$ e $z=3t^3$.

453

Examine o sitema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{rrrrl}4x&+3y&-z&+t&=4\\x&-y&+2z&-t&=0\\5x&+2y&+z&&=4\end{array}\right. . \]

Esse sistema linear possui infinitas soluções.

444

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{rrrcr}2x_1+&3x_2-&5x_3&=& 2 \\2x_1+&3x_2-&x_3&=& 8 \\6x_1+ &9x_2-&7x_3&=& 18 \\\end{array}\right. . \]

Esse sistema possui infinitas soluções.

1361

Dê equações paramétricas para a curva $y^2-8x-8y+8=0$, indicando os valores para o seu parâmetro $t$. Esboce suas parametrizações.

701

Ache a equação do círculo com centro $(-2,5)$ e raio $r = 3$.

$(x+2)^2+(y-5)^2=9$, ou seja, $x^2+y^2+4x-10y+20=0$.

309

Verifique a posição relativa do seguinte par de retas (isto é, verifique se são paralelas, concorrentes ou reversas):

\[
\left\{\begin{array}{ccr}x &=& 1-2t\\y &=& -1-t\\ z &=& 3 + 3t\end{array}\right., \ \ \
\left\{\begin{array}{ccr}x &=& 3+4s\\y &=& -4+2s\\ z &=& 1 + s\end{array}\right. .
\]

São reversas.

1407

Mostre que os dois lados não paralelos de um trapézio e a reta que liga os pontos médios dos lados paralelos são concorrentes.

993

Sejam $\vec{u},\; \vec{v}$ e $\vec{w}$ três vetores. Sabendo que $\vec{u}$ é ortogonal a $\vec{v} - \vec{w}$ e $\vec{v}$ é ortogonal a $\vec{w} - \vec{u}$, verifique que $\vec{w}$ é ortogonal a $\vec{u} - \vec{v}$.

Como $\vec{u}\cdot(\vec{v}-\vec{w})=0$, temos que $\vec{u}\cdot\vec{w}=\vec{u}\cdot\vec{v}$. Da mesma forma, como $\vec{v}\cdot(\vec{w}-\vec{u})=0$, decorre que $\vec{v}\cdot\vec{w}=\vec{v}\cdot\vec{u}$. Assim, usando a simetria do produto interno euclidiano, segue que
$$ \vec{w}\cdot(\vec{u}-\vec{v})=\vec{w}\cdot\vec{u}-\vec{w}\cdot{v}=\vec{u}\cdot\vec{w}-\vec{v}\cdot\vec{w}=\vec{u}\cdot\vec{v}-\vec{v}\cdot\vec{u}=0.$$

707

Identifique o círculo $x^2+y^2-2x-4y+5=0$, dando o seu centro e raio.

Ao completarmos quadrados, ficamos com $(x-1)^2+(y-2)^2=0$. Trata-se de um único ponto (círculo degenerado), a saber, o ponto $(1,2)$.

499

Encontre uma equação em coordenadas cartesianas para a superfície cuja equação em coordenadas cilíndricas é dada por $r=3\cos\theta$.

1439

Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um
ângulo de $30^\circ$. Use a rotação \begin{align*}x & = x'\cos\theta - y'\sin\theta, \\y & = x'\sin\theta + y'\cos\theta, \end{align*}
para encontrar as coordenadas $x'y'$ da curva $y=x^2$.

320

Para o par de retas $r$ e $r^{\prime}$ abaixo encontre o ponto de interseção, $r\cap r^{\prime}$, se existir. E nos casos em que a interseção é vazia decida se elas são paralelas ou reversas.

$r:$ $(x,y,z) = (-1,-4,2) + t(2,-5,3)$ e

$r^{\prime}:$ $\frac{x-3}{2}=\frac{y+14}{5}=\frac{z-8}{-3} .$

Usando escalonamento, podemos verificar que a intersecção ocorre em $t=2$ e, logo, corresponde ao ponto $r\cap r'=(3,-14,8)$.

1394

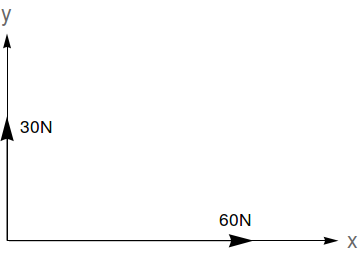
A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).

1002

Sejam $u$ e $v$ vetores no espaço. Mostre que

$(u+v)\times (u-v)=2v\times u$.
Se $u\times v$ é não nulo e $w$ é um vetor qualquer no espaço, então existem números reais $a, b$ e $c$ tais que $w=a(u\times v)+bu+cv$.
Se $u\times v$ é não nulo e $u$ é ortogonal a $v$, então $u\times (u\times v)$ é paralelo a $v$.

1000

Determine, se existir, os valores de $x$ para que o vetor $\textbf{v}=x\vec{i}+6\vec{k}$ seja paralelo ao produto vetorial de $\textbf{w}=\vec{i}+x\vec{j}+2\vec{k}$ por $\textbf{u}=2\vec{i}+\vec{j}+2\vec{k}$.

710

Verifique se a equação $x^2-6x+y^2-4y+z^2+14z+58=0$ descreve uma esfera. Em caso afirmativo, identifique o centro e o raio.

Completamos quadrados para reescrevê-la como $\displaystyle (x-3)^2+(y-2)^2+(z+7)^2=4$. Ou seja, neste caso, a equação descreve uma esfera de raio $2$ e centro em $(3,2,-7)$.

817

Sejam os pontos $A=(-1,-1,2),\;B=(2,1,1) \;\mbox{e}\;C=(m,-5,3)$.

Para que valores de $m$ o triângulo $ABC$ é retângulo em $A$?
Determinar o ponto $H$, pé da altura relativa ao vértice $A$.

316

Encontre as equações vetoriais e paramétricas para a reta $r$ que tem vetor diretor $v=(1,1,-1)$ e passa pelo ponto $P_o=(0,1,7)$.

Equação vetorial: $$ \vec{r}=P_0+tv =(0,1,7)+t(1,1,-1),\quad t\in\mathbb{R}. $$ Ou, ainda, $$ \begin{cases} x=t,\\y=1+t,\\z=7-t,\quad t\in\mathbb{R}.\end{cases} $$

368

Determine todas as matrizes $D$, $2\times 2$ e diagonais, que satisfazem: $DB=BD$ para toda matriz, $2\times 2$, $B$.
Determine todas as matrizes $A$, $2\times 2$, que satisfazem: $AB=BA$ para toda matriz $B$, $2\times 2$.
Tente generalizar a) e b) para matrizes $n\times n$.

485

Sejam $\mathcal{C}$ a circunferência de equação $x^2+y^2=r^2$. Se $r=1$ e $l$ é a reta de equação $3x+4y=5$ então mostre que $l$ é tangente a $\mathcal{C}$. Encontre o ponto de tangência.

Basta dividir ambos os lados da equação equação da reta dada e confrontar com a afirmação vista no exercício anterior. Ou seja, a reta $l$ tem equação $\dfrac{3}{5}x+\dfrac{4}{5}y=1$. Assim, pelo visto no exercício anterior, vemos que $l$ é a reta tangente a $\mathcal{C}$ pelo ponto $(3/5,4/5)$.

498

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por $x^2+y^2=9$.

999

Dados três pontos $A = (2,1,3)$, $B = (5,-1,2)$ e $C = (1,2,-3)$, encontre um quarto ponto $D$ de forma que os pontos $A$, $B$, $C$ e $D$ sejam os vértices de um paralelogramo (Dica: Queremos $D$ de forma que $\overrightarrow{CD}$ seja paralelo a $\overrightarrow{AB}$ e tenha mesmo comprimento.).

$D=(4,4,-2)$

232

Encontre a equação da reta $r$ que passa pelos pontos $A=(3,5,3)$ e $B=(1,1,1)$.
Considere $s$ a reta $(x,y,z)=(1,2,3)+t(1,2,1).$ Verifique se as retas $r$ e $s$ são paralelas, reversas ou concorrentes.
Ache, se possível, uma equação geral do plano que contém as retas $r$ e $s$.
Calcule a distância entre as retas $r$ e $s$.

$\left\{
\begin{array}{l}
x=1+2t \\
y=1+4t \\
z=1+2t
\end{array}
\right. $.
Paralelas.
$3x-2y+z=2.$
$\sqrt{\frac{7}{3}}.$

854

Dados os vetores $a = (2,-3,6)$ e $b = (-1,2,-2)$, calcule as coordenadas do vetor $c$, bissetriz do ângulo formado pelos vetores $a$ e $b$, sabendo-se que $\|c \|= 3\sqrt{42}$.

227

Estabeleça as equações gerais dos planos bissetores dos ângulos formados pelos planos $xOy$ e $yOz$.

$x-y=0$

401

Resolver o sistema linear:\[\left\{\begin{array}{rrrrrcr}1x_1+&3x_2-&7x_3+&5x_4+&2x_5&=&0 \\2x_1+&3x_2-&20x_3+&7x_4+&8x_5&=&0 \\10x_1+&22x_2-&46x_3+&34x_4+&12x_5&=&0 \\\end{array}\right. . \]

$x_3 =\dfrac{11x_1+4x_2}{5}, x_4 = \dfrac{6 x_1-x_2}{5}, x_5 = \dfrac{21 x_1 + 9 x_2}{5}, \forall x_1, x_2 \in \mathbb{R}$.

293

Determine, caso exista, uma reta que passa por $P$ e intercepta $r$ e $s$ nos pontos $A$ e $B$ de modo que os segmentos $AP$ e $BP$ sejam congruentes, nos seguintes casos:

$P=(1,1,9)$, $r=\{ (0,-4,1)+t(2,1,0),t\in\mathbb{R}\}$ e $s=\{(0,-3,-3+t(1,0,2),t\in\mathbb{R}\}$
$P=(1,2,3)$, $r=\{ t(1,0,1),t\in\mathbb{R}\}$ e $s=\{(1,1,1)+t(2,1,1),t\in\mathbb{R}\}$

Interprete geometricamente.

702

Ache a equação do círculo com centro $(5,2)$ e passando pelo ponto $(2,3)$.

A equação do círculo é dada por $(x-5)^2+(y-2)^2=d^2$, onde $d$ é o seu raio. Como é dado um ponto sobre o mesmo, obtemos então que $d=\sqrt{(2-5)^2+(3-2)^2}=\sqrt{10}$.

967

Determine a equação da superfície de revolução gerada pela rotação da curva dada por $9x^2+4y^2=36$ e $z=0$ em torno do eixo $y$.

1163

Se $(4,5)$ divide internamente um segmento de reta na razão $3:2$ e uma extremidade é $(-1,2)$, ache a outra extremidade.

$(22/3,7)$, $(23/2,19/2)$ (duas respostas internas).

1037

Considere o plano com o sistema cartesiano canônico $xy$ e faça uma rotação de um ângulo $\theta$, com $0\leq \theta \leq\pi/2$ obtendo o novo sistema $\overline{x}$ $\overline{y}$. Seja $(*)$ a equação:

$$(*) \ \ \ Ax^2+Bxy+Cy^2+Dx+Ey+F=0$$,

com $A$, $B$, $C$, $D$, $E$, $F$ números reais. Ao transformar $(*)$ para o sistema $\overline{x}$ $\overline{y}$ obtemos:

$$(**) \ \ \ \overline{A} \overline{x}^2+\overline{B}\overline{x} \overline{y}+ \overline{C}\overline{y}^2+ \overline{D}\overline{x}+ \overline{E}\overline{y}+\overline{F}=0$$.

Mostre que:
\begin{align*} \overline{A} & = A\cos^2\theta+B\sin\theta\cos\theta+C\sin^2\theta, \\ \overline{B} & =-2A\sin\theta\cos\theta+B(\cos^2\theta-\sin^2\theta)+2C\sin\theta\cos\theta,\\ \overline{C} & = A\sin^2\theta-B\sin\theta\cos\theta+C\cos^2\theta, \\ \overline{D} & = D\cos\theta+E\sin\theta, \\ \overline{E} & = E\cos\theta-D\sin\theta\;\;\;\;\; \text{e} \\ \overline{F} & = F. \end{align*}
Supondo $A>0$ e $F<0$, conclua, a partir de 1, que a equação $(*)$ representa uma circunferência de centro $(0,0)$ e raio $r=\sqrt{\frac{-F}{A}}$ se, e somente se, para todo $\theta$, tivermos que $A=\overline{A}$, $B=\overline{B}$, $C=\overline{C}$,
$D=\overline{D}$, $E=\overline{E}$ e $F=\overline{F}$.
Sejam
$M= \left( \begin{array}{cc}A & \frac{B}{2}\\\frac{B}{2}& C \\\end{array}\right)$, $\overline{M}= \left( \begin{array}{cc}\overline{A} & \frac{\overline{B}}{2}\\\frac{\overline{B}}{2}&\overline{C}\end{array}\right)$ e $R_{\theta}=\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$.

Mostre, a partir de 1, que $\overline{M}=R_{\theta}^{t}\cdot M\cdot R_{\theta}$ e, calculando o determinante dos dois lados da igualdade, conclua que $\Delta=B^2-4AC=\overline{B}^{2}-4\overline{A}\overline{C}$, qualquer que seja o ângulo $\theta$ (OBS: $\Delta$ é conhecido pelo nome de discriminante da equação $(*)$ e o item 3 está dizendo que ele é invariante por rotação).

373

Sabendo-se que para toda matriz $A\in \mathbb{R}^{n\times n}$ com $\det(A)\neq 0$ existe uma matriz $\overline{A}$, também $n\times n$, tal que $\overline{A}A=I_n$, mostre que:

se $B$ e $C$ são matrizes $n\times n$ tais que $BC=I_n$, então $CB=I_n$.
se $\det(B)\neq 0$ ($B$ matriz $n\times n$), então existe uma única $B^{-1}$ tal que $BB^{-1}=B^{-1}B=I_n$.

976

Qual(is) das quádricas abaixo representa(m) uma superfície de rotação?

$ 3x^2+y^2-2z^2=1$,
$\frac{x^2}{6}+\frac{y^2}{5}+\frac{z^2}{3}=1$,
$x^2+ y^2-z^2=0$.

1147

Qual é o vetor unitário na direção de $\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}$?

$\dfrac{x\vec{i}+y\vec{j}+z\vec{k}}{\sqrt{x^2+y^2+z^2}}$.

978

Diga qual é a cônica obtida pela intersecção do cone

$$x^{2} + y^{2} - z^{2} = 0$$

com o plano

$$x - y + z\;\sqrt{2/3} = 5 \sqrt{2/3} .$$

Explique seu raciocínio.

273

A reta $r$ passa pelo ponto $A(4,-3,-2)$ e é paralela à reta

$$\begin{cases} x=1+3t\\ y=2-4t\\ z=3-t. \end{cases}$$

Se $P(m,n,-5)\in r$, determinar $m$ e $n$.

$m=13,\;n=-15.$

Seja $r$ a reta que passa pelo ponto $A(4,-3,-2).$ Encontramos, primeiramente o vetor fornece a direção da reta $s$, que por sinal também fornece a direção da reta $r$, pois as retas $r$ e $s$ são paralelas. O vetor direção da reta pode ser encontrado observando os elementos que acompanham o parâmetro $t$ na equação da reta $s.$ Temos o vetor direção da reta $s$ dada por $v=3\overrightarrow{i}-4\overrightarrow{j}-\overrightarrow{k}.$

Nesse sentido, podemos escrever a equação de $r$, pois temos um ponto $A(4,-3,-2)$ e sua direção:
$$\begin{cases} x=4+3\overline{t}\\ y=-3-4\overline{t}\\ z=-2-\overline{t} \end{cases}$$,

onde $\overline{t}$ é o parâmetro. Usamos $\overline{t}$ pois os parâmetros da reta $r$ são diferentes dos parâmetros da reta $s$. Assim, temos um valor de $z$ no ponto $P$, então podemos encontrar o valor de $\overline{t}$ correspondente, isto é, $-5=-2-\overline{t} \Longrightarrow \overline{t}=3.$ Substituindo, $ \overline{t}=3$ na equação obtida para a reta $r$, obtemos as coordenadas de $P$, isto é $m=4+3\overline{t} \Longrightarrow m=13$ e $n=-2-\overline{t}\Longrightarrow n=-15.$ Portanto, concluímos que os valores de $m=13$ e $n=-15$ e o ponto é dado por $P\left( 13,-15,5\right)$.

510

Reduza a equação $4x^2-2y^2+z^2=1$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

$\dfrac{x^2}{1/4} - \dfrac{y^2}{1/2} + z^2 = 1$: hiperbolóide de uma folha.

1627

Suponha que os eixos coordenados estejam fixos, mas a posição $P(x,y)$ de um inseto é movida para uma nova posição $P'(x',y')$ através de uma rotação do ponto por um ângulo $\alpha$ em torno da origem. Naturalmente, nesta rotação o ponto $P$ estará sempre sobre um círculo fixo com centro na origem. Mostre que a nova posição do inseto será \begin{align*} x' & = x\cos\alpha - y\sin\alpha \\ y' & = x \sin\alpha + y\cos\alpha \end{align*}.

1354

Esboce o gráfico da equação paramétrica dada por $(x,y)=(cos(t),tan(t))$.

719

Ache a equação da esfera que passa pelos pontos $(0,0,1)$, $(1,0,0)$, $(0,1,0)$ e cujo centro está no plano $x+y-z=0$.

275

Determinar as equações paramétricas e representar graficamente a reta que passa por $A(3,-2,4)$ e é paralela ao eixo dos $x$.

$r:(x,y,z)=(3+t,-2,4);$

Seja $r$ a reta que passa pelo ponto $A(3,-2,4).$ Como a reta $r$ deve ser pararela aos eixos $x$, considere o vetor canônico $\left( 1,0,0\right)$, que por sinal será o vetor direção do eixo dos $x$ e consequentemente o vetor direção da reta $r$, pois é paralela ao eixo dos x e dado por $\ v=\overrightarrow{i}$. Nesse sentido, como temos um vetor direção e o ponto $A(3,-2,4)$, concluímos que as equações paramétricas são dadas por $$\begin{cases} x=3+t\\ y=-2\\ z=4. \end{cases}$$

452

Seja o sistema linear $AX = B$, onde

\[A=\begin{pmatrix}1&\phantom{-}2&-3\\3&-1&\phantom{-}5\\1&\phantom{-}1&a^{2}-16\end{pmatrix}\quad\text{e}\quad B = \begin{pmatrix}4\\2\\a+14\end{pmatrix}.\]

Determine o valor (ou valores) de $a$ para que o sistema tenha solução única.
Exitem valores de $a$ para os quais o sistema tem infinitas soluções?
Exitem valores de $a$ para os quais o sistema não tem solução?

247

Encontre a equação da reta simétrica à reta $r$ em relação ao plano $\pi$:

$$r:\begin{cases} x= 1 + 2t\\
y = -2 + 7t
\\z = -2 + 5t \end{cases}\ \ \ {\rm e}\ \ \ \pi:x-y+z=1.$$

413

Determine os coeficientes $a$, $b$, $c$ e $d$ da função polinomial $p(x)=ax^3+bx^2+cx+d$, cujo gráfico passa pelos pontos $P_1=(0,10)$, $P_2=(1,7)$, $P_3=(3,-11)$ e $P_4=(4,-14)$.
Determine coeficientes $a, b$ e $c$ da equação do círculo, $x^2+y^2+ax+by+c=0$, que passa pelos pontos $P_1=(-2,7)$, $P_2=(-4,5)$ e $P_3=(4,-3)$.

$a = 1/6$, $b = -1$, $c = -13/6$, $d=10$.
$a= -2$, $b = -4$, $c = -29$.

243

Considere as retas $r=\{ (1,1,0)+t(0,1,1), t\in\mathbb{R}\}$ e $s:\frac{x-1}{2}=y=z$. Sejam $A$ o ponto de intersecção de $s$ e $\pi : x-y+z=2$; $B$ e $C$ as intersecções de $r$ com os planos coordenados $xz$ e $xy$ respectivamente. Calcule a área do triângulo $ABC$.

$\frac{\sqrt{3}}{2}$

1038

Sejam $x$, $y$ os eixos cartesianos usuais do plano. Faça a mudança de variáveis $X = x - 2$ e $Y = y + 3$, que corresponde a mudarmos a origem para o ponto $\textbf{O} = (2,-3)$.

Dado o ponto $P=(1,4)$ no sistema $xy$, encontre as coordenadas de $P$ no sistema $XY$.
Dado o ponto $A=(2,1)$ no sistema $XY$, encontre as coordenadas de $A$ no sistema $xy$.

1470

Mostre que, em um sistema de coordenadas polares, a distância $d$ entre os pontos $(r_1,\theta_1)$ e $(r_2,\theta_2)$ é dada por
$$ d=\sqrt{r_1^2+r_2^2-2r_1r_2\cos(\theta_1-\theta_2)}. $$
Mostre que, se $0\leq \theta_1 < \theta_2 \leq \pi$ e se $r_1$ e $r_2$ forem positivos, então a área $A$ do triângulo com vértices $(0,0)$, $(r_1,\theta_1)$ e $(r_2,\theta_2)$ é dada por
$$ A= \dfrac{1}{2}r_1r_2\sin(\theta_2-\theta_1). $$
Encontre a distância entre os focos cujas coordenadas polares são $(3,\pi/6)$ e $(2,\pi/3)$.
Encontre a área do triângulo cujos vértices em coordenadas polares são $(0,0)$, $(1,5\pi/6)$ e $(2,\pi/3)$.

1205

Reduza a equação $2x^2 + 30y^2 + 23z^2 + 72xz + 150 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1027

Determine a área do quadrado de lados paralelos aos eixos coordenados e inscrito na elipse com vértices $A_1=(10,0)$, $A_2=(-10,0)$, $B_1=(0,6)$, $B_2=(0, -6)$.

1460

Considere o hiperbolóide de uma folha $H$ dado pela equação $x^2+y^2=1+z^2$. Mostre que por cada um dos seus pontos passam duas retas inteiramente contidas na superfície $H$. Generalize para qualquer hiperbolóide de uma folha. (Sugestão: $x^2+y^2=1+z^2\Leftrightarrow(x+z)(x-z)=(1+y)(1-y)$.)

853

Provar, utilizando o produto escalar, que todo triângulo inscrito em uma semicircunferência é reto.

Consideremos a semicircunferência de raio $R$ com centro na origem $O$ do sistema cartesiano e situada no semiplano $y\geq 0$. Sejam $A=(R,0)$, $B=(x,y)$ e $C=(-R,0)$ três pontos sobre esta semicircunferência, sendo $B$ um ponto qualquer tal que $x^2+y^2=R^2$. Assim, teremos que
\begin{multline*}\vec{CB}\cdot\vec{AB}=(B-C)\cdot(B-A)=(x+R,y)\cdot(x-R,y)= \\ =(x+R)(x-R)+y^2 =x^2-R^2+y^2=(x^2+y^2)-R^2=R^2-R^2=0.\end{multline*} Ou seja, o triângulo inscrito $ABC$ é retângulo no vértice $B$.

286

Verificar se as retas são concorrentes e, em caso afirmativo, encontrar o ponto de interseção:

$$r_1:\;\begin{cases}x=2-t\\ y=3-5t\\ z=6-6t. \end{cases}\ \ \ {\rm e } \ \ \ \begin{cases}x=-3+6h\\ y=1+7h\\ z=-1+13h\end{cases}$$

$P=(3,8,12)$.

995

Dados os pontos $A = (2,3,0), \; B = (4,0,1)$ e $C = (0,1,2)$ no $\mathbb{R}^{3}$, determine:

O comprimento do lado $AB$.
A medida do ângulo entre os lados $BA$ e $BC$.
A área do triângulo $ABC$.
O comprimento da altura do triângulo $ABC$ relativa ao vértice $A$.
As coordenadas do ponto no lado $AC$ por onde passa a perpendicular a esse lado que contém o ponto $B$.
Desenhe o triângulo $ABC$ no espaço $\mathbb{R}^{3}$.

861

No triângulo $ABC$, tem-se $\vec{AP}=\frac{1}{3}\vec{AC}$ e $\vec{AQ}=\frac{1}{2}\vec{AC}.$ Expressar os vetores $\vec{BP}$ e $\vec{BQ}$ em funçãao de $\vec{BA}$ e $\vec{BC}.$

1441

Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um ângulo $\theta$. Explique como podemos encontrar as coordenadas $xy$ de um ponto cujas coordenadas $x'y'$ sejam conhecidas.

713

Uma corda da circunferência $x^2+y^2=25$ se encontra sobre a reta cuja equação é $x-7y+25=$. Qual o comprimento dessa corda?

966

Mostre que a equação $17x^2+2y^2+z^2-8xy-6xz-2=0$ representa uma superfície cilíndrica e determine a equação da curva diretriz e um vetor paralelo às retas geratrizes.

282

Encontrar as equações paramétricas da reta que passa por $A$ e é simultaneamente ortogornal às retas $r_1$ e $r_2$: $A$ é a interseção de $r_1$ e $r_2$; $$r_1:\;x-2=\frac{y+1}{2}=\frac{z}{3}\ \ \ {\rm e}\ \ \ r_2:\;\begin{cases} x=1-y\\ z=2+2y. \end{cases}$$

$r:(x,y,z)=(-2+t',3-5t',2+2t').$

1486

Em cálculo de uma variável vemos que se $x_0$ é um extremo local (máximo ou mínimo) de uma função $f(x)$, então a reta tangente ao gráfico de $f$ em $x_0$ é horizontal, ou seja, $f'(x_0)=0$.

Encontre uma relação similar entre um extremo local de uma função de duas variáveis e o plano tangente ao seu gráfico.
Use esta relação para encontrar os extremos locais da função $f(x,y)=x^2+y^2-2x-6y+14$.
Verifique se sua resposta no item anterior está correta completando os quadrados em $f(x,y)$ e identificando a quádrica.

1033

Um próton é lançado ao longo da reta $y = \frac{1}{2} x$ em direção ao núcleo de um átomo localizado na origem. Se o próton é defletido em direção à linha $y = -\frac{1}{2} x$, ao longo de um trecho de hipérbole, dê a equação para a trajetória do próton.

1012

Seja $\ell$ a curva com equações paramétricas $x=a(1+t^2)/(1-t^2)$, $y=2bt/(1-t^2)$. Determine $\ell$.

407

Resolver o sistema linear: \[\left\{\begin{array}{ccccccccccr}x_1&-&2x_2&+&3x_3&+&2x_4&+&x_5&=&10 \\2x_1&-&4x_2&+&8x_3&+&3x_4&+&10x_5&=& 7 \\3x_1&-&6x_2&+&10x_3&+&6x_4&+&5x_5&=&27\\\end{array}\right..\]

$x_3 = \dfrac{-19+2 x1- 4 x2}{3}, x_4 = \dfrac{ 41 - 4 x_1 + 8 x_2}{3}, x_5 = \dfrac{5- x_1+2 x_2}{3}, \forall x_1, x_2\in \mathbb{R}$.

1214

Reduza a equação $45x^2 + 54y^2 + 63z^2 - 36xy + 36yz - 24x - 24y + 6z + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

A equação da quádrica $45x^2 + 54y^2 + 63z^2 - 36xy + 36yz - 24x - 24y + 6z + 1 = 0$ pode ser escrita em forma matricial:

$$X^tAX+KX+1=0,$$

onde:

$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ K=\begin{pmatrix}-24 & -24 & 6\end{pmatrix}, \ A=\begin{pmatrix}45 & -18 & 0 \\-18 & 54 & 18 \\0 & 18 & 63\end{pmatrix}. $$

Seja:

$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}45-\lambda & -18 & 0 \\-18 & 54-\lambda & 18 \\0 & 18 & 63-\lambda\end{pmatrix}=-\lambda^3+162\lambda^2+-8019\lambda +118098.$$

As raízes de $P(\lambda)$ são $27$, $54$ e $81$. Considere os sistemas lineares referentes às raízes $27$ e $54$: $(A-27I) X = 0$ e $(A-54I)=0$. Uma solução de norma unitária desses sistemas são $U_1=(-2/3,-2/3,1/3)$ e $U_2=(-2/3,1/3,-2/3)$, respectivamente. Sejam $U_3=U_1 \times U_2 = (1/3,-2/3,-2/3)$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $45x^2 + 54y^2 + 63z^2 - 36xy + 36yz - 24x - 24y + 6z + 1 = 0$ se transforma em:

$$\dfrac{(x'+17/27)^2}{796/2187}+\dfrac{(y'+1/27)^2}{796/4374}+\dfrac{(z'+2/81)^2}{796/6561}=1,$$

que é a equação de um elipsóide.

427

Resolver o sistema linear: \[\left\{\begin{array}{ccccccccr}3x& + &3y& - &2z& - &t&=& 2\\5x& + &2y& + &z& - &2t&=& 1\\2x& - &y& + &3z& - &t&=& -1\end{array}\right. .\]

$z = \dfrac{-3+x+4y}{5}, t =\dfrac{-4+13 x+7 y}{5}, \forall x, y \in \mathbb{R}.$

277

Determinar as equações paramétricas e representar graficamente a reta que passa por $A(-2,3,4)$ e é ortogonal ao mesmo tempo aos eixos dos $x$ e dos $y$.

$r:(x,y,z)=(-2,3,4+t);$

1215

Considere a quádrica $x^2 +(m+1)y^2 +mz^2-2yz+2xy+2x+2z+4 = 0$, calcule $m$ para que a quádrica seja um parabolóide hiperbólico e obtenha sua equação reduzida.

1221

Reduza a equação $3x^2+y^2-2xy+2xz-2yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

968

Determine a equação da superfície de revolução gerada pela rotação da curva dada por $yz=1$ e $x=0$ em torno do eixo $z$.

398

Resolver o sistema linear:

\[\left\{\begin{array}{ccccccccccr}&&x_1&+&x_2&-&x_3&+&2x_4&=&6 \\&-&x_1&+&x_2&+&4x_3&-&3x_4&=&-2 \\&&&&x_2&+&3x_3&+&x_4&=& 5 \\&&&&x_1&+&5x_2&+&5x_3& =&14 \\\end{array}\right. . \]

$x_2 = \dfrac{13-2 x_1}{5}, x_3 = \dfrac{1+x_1}{5}, x_4 = \dfrac{9-x_1}{5}, \forall x_1\in\mathbb{R}.$

712

Ache as retas tangentes ao círculo $x^2+y^2=4x$ que passam pelo ponto $(3,2)$.

291

Se $V$ é o vetor que satisfaz as condições:

$V$ é ortogonal aos vetores $(1,0,2)$ e $(-2,1,0);$
$\left\| V\right\| =\sqrt{21};$
o ângulo entre $V$ e o vetor $(0,1,2)$ é menor que $90^{\circ }.$

Encontre o ponto final do representante de $V$ que tem ponto inicial em $(9,0,-2)$.

$(11,4,-3)$.

855

Que condições devem satisfazer os vetores $a$ e $b$ para que sejam válidas as seguintes relações?

$\|a + b \| = \|a - b \|$;
$\| a + b \| > \| a - b \|$;
$\| a + b \| < \| a - b \|$.

478

Sabemos que se $B$ é uma base de $R^3$ formada pelos vetores $U,V$ e $W$, então as leis de mudança de base entre a base usual e a base $B$ são $$ P_B = [U,V,W]^{-1}P\ \ {\rm e}\ \ P = [U,V,W]P_B$$ Determine a mudança de base entre a base $B$ e uma base $B^{\prime}$ distinta da usual.

435

Considere a matriz $ A = \left[ \begin{array}{ccc} 1 & 2 & 3\\ 1 & 1 & 2 \\ 0 & 1 & 2\end{array}\right]$.

Calcule o $det(A^n)$, para todo número natural $n$.
Usando escalonamento encontre a matriz inversa $A^{-1}$.

Como $\det(A)=-1$ e $\det(A^n)=\det(A)^n$, $\det(A)^n=(-1)^n$.
$ A^{-1} = \left[ \begin{array}{ccc} 0 & 1 & -1\\ 2 & -2 & -1 \\ -1 & 1 & 1\end{array}\right]$.

237

Considere as retas $r$ e $s$ dadas pelas equações:

\[
r:\ x\ =\ \frac{y}{2}\ =\ z, \ s:\left\{
\begin{array}{ccl}
x & = & -4+t \\
y & = & 2+2t \\
z & = & t , \ \ \ \ \ \ \ \ \mathrm{onde}\ \ t\in \mathbb{R}
\end{array}
\right. \ \
\]

Determine a equação da reta paralela a $r$ e a $s$, contida no mesmo plano de $r$ e $s$ e que seja equidistante de $r$ e de $s$.

$\left\{
\begin{array}{l}
x=-2+t \\
y=1+2t \\
z=t
\end{array}
\right. $

1239

Reduza a equação $2x^2+4yz-4x+2y+6z+5=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1236

Reduza a equação $2x^2+2y^2-4z^2-5xy-2xz-2x-2y+z=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

414

Um construtor tem contratos para construir 3 estilos de casa: moderno, mediterrâneo e colonial. A quantidade de material empregada em cada tipo de casa é dada pela tabela:

\[
\begin{array}{lccccc}
& \text{Ferro} & \text{Madeira} & \text{Vidro} &
\text{Tinta} & \text{Tijolo}\\
\text{Moderno} & 5 & 20 & 16 & 7 & 17\\
\text{Mediterrâneo} & 7 & 18 & 12 & 9 & 21\\
\text{Colonial} & 6 & 25 & 8 & 5 & 13
\end{array}
\]

Se ele pretende construir 5, 7 e 12 casas dos tipos moderno, mediterrâneo e colonial, respectivamente, quantas unidades de cada material serão empregadas?
Suponha que os preços por unidade de ferro, madeira, vidro, tinta e tijolo sejam, respectivamente, 15, 8, 5, 1 e 10. Qual é o preço unitário de cada tipo de casa?
Qual é o custo total do material empregado?

As quantidades de ferro, madeira, vidro, tinta e tijolo serão 146, 526, 260,158 e 388, respectivamente.
O preço unitário dos tipos moderno, mediterrâneo e colonial serão 492, 528 e 465, respectivamente.
O custo total do material empregado para construir 5 casas do estilo moderno, 7 casas do estilo mediterrâneo e 12 casas do estilo colonial é 11736.

1438

Seja $a$ o semi-eixo maior da órbita de um planeta em torno do Sol, e seja $T$ o seu período. Pelas Leis de Kepler, a órbita é elíptica com o Sol em um dos focos, e $T=a^{3/2}$. Mostre que se $T$ for medido em dias e $a$ em quilômetros, então $\displaystyle T=(365\times 10^{-9})\left(\dfrac{a}{150}\right)^{3/2}$.
Use o resultado do item anterior para encontrar o período do planeta Mercúrio, em dias, dado que o seu semi-eixo maior é $a=57,95\times 10^6$ km.
Escolha um sistema de coordenadas polares com o Sol no pólo e encontre uma equação para a órbita de Mercúrio naquele sistema de coordenadas, dado que a excentricidade da órbita é $e=0,206$.
Use um recurso gráfico computacional para gerar a órbita de Mercúrio a partir da equação obtida no item 3.

1068

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+3y^2+4xy+4y-4=0$.

288

Verificar se as retas são concorrentes e, em caso afirmativo, encontrar o ponto de interseção:

$$r_1:\;\begin{cases}x=2+t\\ y=4-t\\ z=-t. \end{cases}\ \ \ {\rm e } \ \ \ \begin{cases} y=6-x\\ z=2-x\end{cases}$$

As retas são coincidentes.

1011

Encontre o volume do paralelepípedo determinado pelos vetores $u$, $v$ e $w$, dados por: $u=\vec{i}+3\vec{j}+2\vec{k}$, $v=2\vec{i}+\vec{j}-\vec{k}$ e $w=\vec{i}-2\vec{j}+\vec{k}$.

$|u\cdot(v\times w)|=|-20|=20$

1220

Reduza a equação $3x^2-3y^2-5z^2-2xy-6xz-6yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

225

Dado o ponto $P(5,2,3)$ e o plano $\pi:\;2x+y+z=0$, determinar:

equações paramétricas da reta que passa por $P$ e é perpendicular a $\pi$;
a projeção ortogonal de $P$ sobre o plano $\pi$;
o ponto $P'$ simétrico de $P$ em relação a $\pi$;
a distância de $P$ a o plano $\pi$.

$r:(x,y,z)=(5+2t,2+t,3+t)$.
$P_{\bot}=(0,-\frac{1}{2},\frac{1}{2})$.
$P'=(-5,-3,-2)$.
$5\dfrac{\sqrt{6}}{2}$.

249

Encontre a equação da reta simétrica à reta $r$ em relação ao plano $\pi$:

$$r:\begin{cases} x= 1 + t\\
y = -2 - t
\\z = -1 + t \end{cases}\ \ \ {\rm e}\ \ \ \pi:x-y+z=2.$$

1374

Construa a curva cujas equações paramétricas são dadas por: $x=\sin\theta$, $y=\mathrm{cosec\,}\theta$ e $z=\cos\theta$.

1445

Encontre a inclinação da reta tangente à curva paramétrica $(x(t),y(t))=(3\cos t,4\sin t)$, em $t=\pi/4$ e $7\pi/4$, sem eliminar o parâmetro.
Verifique suas respostas do item anterior eliminando o parâmetro e diferenciando uma função apropriada de $x$.

500

Encontre uma equação em coordenadas cartesianas para a superfície cuja equação em coordenadas cilíndricas é dada por $z^2\sin\theta=r^3$.

1476

Mostre que a intersecção de um plano $\displaystyle by+cz+d=0$, em que $b^2+c^2=1$, com o cone $x^2+y^2=z^2$ é uma cônica que pode ser uma elipse, uma hipérbole ou uma parábola. (Sugestão: mude para um sistema de coordenadas $\{O,U_1,U_2,U_3\}$ tal que $U_1=\vec{i}=(1,0,0)$, $U_2=(0,b,c)$ e $U_3=(0,-c,b)$).

455

Examine o sitema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left \{\begin{array}{rrrrl}x&-y&+2z&-t&=0\\3x&+y&+3z&+t&=0\\x&-y&-z&-5t&=0\end{array}\right..\]

Esse sistema linear possui infinitas soluções.

869

Sabendo que $u\cdot(v\times w)=2$, calcular:

$u\cdot(w\times v)$.
$v\cdot(w\times u)$.
$(v\times w)\cdot u$.
$(u\times w)\cdot 3v$.
$u\cdot(2w\times v)$.
$(u+v)\cdot(u\times w)$.

1055

Decida se a cônica $C$ determinada pela equação $\displaystyle 4y^2-4y-24x+9=0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

305

Encontre a equação da reta $r$ que passa por $A=(2,1,-1)$ e é perpendicular à reta $s: (2,0,0) + t(3,1,-1)$.

Inicialmente, vamos determinar o ponto $P_0$ sobre $s$ tal que $(P_0-A)\cdot(3,1,-1)=0$. Para isso, temos que $(P_0-A)=(2+3t,t,-t)-(2,1,-1)=(3t,t-1,1-t)$. Segue que $$(P_0-A)\cdot(3,1,-1)=0\Longleftrightarrow 9t+(t-1)-(1-t)=0 \Longleftrightarrow 11t=2\Longleftrightarrow t=11/2.$$ Logo, $$ P_0-A=(\frac{6}{11},-\frac{9}{11},\frac{9}{11})=\frac{3}{11}(2,-3,3), $$ e podemos tomar o vetor $(2,-3,3)$ como diretor. Assim, a reta procurada pode ser descrita parametricamente por $$ r: (2,1,-1) + t(2,-3,3),\quad t\in\mathbb{R}.$$

1444

As funções trigonométricas seno hiperbólico e cosseno hiperbólico são definidas, respectivamente, por

$$\cosh t=\dfrac{e^t+e^{-t}}{2}\quad\text{e}\quad \sinh t\dfrac{e^t-e^{-t}}{2}, \quad t\in\mathbb{R},$$

e vale a relação $\cosh^2 t-\sinh^2 t=1$.

Mostre que as equações paramétricas da hipérbole de equação $\displaystyle \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ são $$ x=\pm a\cosh t, \quad y=b\sinh t.$$
Mostre que não existem funções contínuas $f_1$ e $f_2$ tais que a hipérbole possa ser escrita como $x=f_1(t)$ e $y=f_2(t)$.

1061

Considere a equação

$$x^{2} - 14 x y + y^{2} = 1.$$

Efetue a troca de variáveis $x = u \cos \theta + v\,\textrm{sen} \theta$ e $y = - u\, \textrm{sen} \theta + v \cos \theta$. Escolha, usando sua intuição ou fazendo as contas, $\theta$ de forma que a equação obtida em $u$ e $v$ seja a equação canônica de uma hipérbole. Explique o significado geométrico deste resultado e obtenha, nas coordenadas $x$ e $y$, as equações das retas que servem de assíntotas à tal hipérbole.

451

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{ccccccccccr}x_1&-&2x_2&+&3x_3&+&2x_4&+&x_5&=&10 \\2x_1&-&4x_2&+&8x_3&+&3x_4&+&10x_5&=& 7 \\3x_1&-&6x_2&+&10x_3&+&6x_4&+&5x_5&=&27\\\end{array}\right..\]

Esse sistema linear possui infinitas soluções.

1389

Uma liga de metal $L_1$ contém $20\%$ de ouro e $80\%$ de prata e uma liga $L_2$ tem $65\%$ de ouro e $35\%$ de prata. Quanto gramas de cada liga são necessários para se formar $100$ gramas de uma liga com quantidade igual de ouro e prata?

Serão necessárias aproximadamente 33.3333 gramas da liga $L_1$ e 66.6667 gramas da liga $L_2$.

422

Resolver o sistema linear:

\[\left\{\begin{array}{rrrcr}2x_1+&3x_2-&5x_3&=& 2 \\2x_1+&3x_2-&x_3&=& 8 \\6x_1+ &9x_2-&7x_3&=& 18 \\\end{array}\right. . \]

$x_2 =\dfrac{19-4x_1}{6}, x3 =\dfrac{3}{2}, \forall x_1 \in \mathbb{R}$.

290

Dados o ponto $A(3,4,-2)$ e a reta

$$r:\;\begin{cases}x=1+t\\ y=2-t\\ z=4+2t\end{cases},$$

determinar as equações paramétricas da reta que passa por $A$ e é perpendicular a $r$,
calcular a distância de $A$ a $r$,
determinar o ponto simétrico de $A$ em relação a $r$.

$\begin{cases}
x=3-4t\\
y=4\\
z=-2+2t
\end{cases}$;
$2\sqrt{5}$;
$A'=(-5,4,2)$

767

Verifique se os seguintes pontos são colineares: $A=(3,1,4)$, $B=(2,7,1)$ e $C=(0,1,5)$.

Os pontos não são colineares.

394

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
0&0&1\\ 0&1&0\\ 1&0&0
\end{pmatrix}.
$

$x_1=-1$, $x_2=1$, $x_3=1$.

431

Verifique se as matrizes abaixo estão na forma escalonada. Usando operações de linha equivalência escalone as (encontre a forma escalonada das) que não estiverem na forma escalonada.

$ \begin{pmatrix}1&0&0\\0&1&0\\0&0&1\\1&0&0\end{pmatrix}.,$
$ \begin{pmatrix}1&1&0\\0&0&1\\0&0&0\end{pmatrix}. $

399

Resolver o sistema linear:

\[\left\{\begin{array}{cccccr}&x_1&-&7x_2&=&-11 \\-&x_1&+&11x_2&=&31 \\&2x_1&-&12x_2&=&-26 \\&3x_1&-&17x_2&=&-15 \\\end{array}\right. . \]

O sistema não possui solução.

1409

Dois piolhos andam em trajetórias retilíneas no espaço. No instante $t$, as posições $(x,y,z)$ dos piolhos 1 e 2 são dadas pelas retas $r_1$ e $r_2$:

$$r_1: \ x=4-t, \ y=1+2t, \ z=2+t;$$

$$r_2: x=t, \ y=1+t, \ z=1+2t.$$

Suponha que a distância esteja em centímetros e o tempo em minutos.

Determine a distância entre os piolhos no instante $t=0$.
Use um recurso gráfico para fazer o gráfico da distância entre os piolhos como uma função do tempo de $t=0$ a $t=5$.
O que o gráfico nos diz sobre a distância entre os piolhos?
Quão perto ficam os piolhos?

1035

Encontre a equação da parábola que tem foco no ponto $F = (1,1)$ e tem reta diretriz com equação $y = -x - 2$.

830

Seja $O$ a origem de um sistema de coordenadas no plano. Mostre que se $ABC$ é um triângulo qualquer, suas medianas se interceptam no ponto $$M=\frac{OA+OB+OC}{3}.$$

457

Sabendo que o sistema

$ \left\{\begin{array}{rrrl}x&+y&+z&=1\\mx&+2y&+3z&=0\\m^2x&+4y&+9z&=1\end{array}\right.$

admite uma única solução, podemos concluir que $m$ pode assumir todos os valores no intervalo real:

$[0,1]$
$[1,2]$
$[3,4)$
$[0,4]$.

1415

Responda falso ou verdadeiro para cada uma das afirmações abaixo (justifique suas respostas).

Se $A$ e $B$ são duas matrizes $n\times n$ e $AB=BA$, então $(AB)^{p}=A^{p}B^{p}$ para todo número natural $p$.
Se $A$ e $B$ são matrizes $n\times n$ tais que $AB={\bf 0}$, então $BA={\bf 0}$.
Se $A$ é uma matriz $n\times n$ e $A^4 - 3A^2 + 7A -I_n={\bf 0}$ então $A$ é invertível (isto é, $AB=BA=I_n$ para alguma matriz $B$, $n\times n$).

765

Mostre que as diagonais de um paralelogramo se cortam ao meio (Sugestão: Sejam $M$ e $N$ os pontos médios das duas diagonais. Mostre que $\overline{MN}=\vec{0}$.).

Considere o paralelogramo $ABCD$, de diagonais $AC$ e $DB.$ Seja $M$ o ponto médio de $AC.$ Vamos provar que $M$ é também ponto médio de $BD.$ Ora, $\overrightarrow{BM}=\overrightarrow{BC}+ \overrightarrow{CM}=\overrightarrow{AD}+\overrightarrow{MA}=\overrightarrow{MD}.$ Logo, $M$ é o ponto médio de $BD.$

369

Responda falso ou verdadeiro para cada uma das afirmações abaixo (justifique suas respostas).

Se $A$ é matriz $n\times n$ e $A^2={\bf 0}$, então $A={\bf 0}$, onde ${\bf 0}$ é a matriz nula.
A única matriz $n\times n $ simétrica e anti-simétrica ao mesmo tempo é a matriz nula.
Se $A$ é uma matriz $n\times n$ e $A^{2}=I_n$, então $A=I_n$ ou $A=-I_n$ ($I_n$ é a matriz identidade $n\times n$).

Falsa. Contra-exemplo: $A= \left( \begin{array}{cc}
0 & 0 \\
1 & 0
\end{array}\right)$ é não-nula e $A^2={\bf 0}$.
Falsa. Qualquer matriz diagonal é simétrica e anti-seimétrica ao mesmo tempo.
Falsa. Contra-exemplo: $A= \left( \begin{array}{cc}
-1 & 0 \\
z & 1
\end{array}\right)$ é diferente de $I_2$ e de $-I_2$ mas $A^2=I_2$.

1371

Construa a curva cujas equações paramétricas são dadas por: $x=t$, $y=t$ e $z=1-t^2$.

1142

Sejam $\vec{A}$, $\vec{B}$ e $\vec{C}$ vetores no plano, com $\|\vec{A}\|=2$, $\|\vec{B}\|=3$ e $\|\vec{C}\|=4$. O ângulo entre $\vec{A}$ e $\vec{B}$ é de $120^\circ$, entre $\vec{A}$ e $\vec{C}$ é de $135^\circ$ e entre $\vec{B}$ e $\vec{C}$ é de $105^\circ$. Faça um esboço do gráfico desses três vetores. Qual combinação linear de $\vec{A}$ e $\vec{B}$ é igual a $\vec{C}$?

$\vec{C} = -(\sqrt{2}+\sqrt{2/3})\vec{A} + -(4\sqrt{2})/(3\sqrt{3}) \vec{B}$.

859

Sabendo que o ponto $P=(-3,m,n)$ pertence à reta que passa pelos pontos $A=(1,-2,4)$ e $B=(-1,-3,1)$, determine $m$ e $n$.

$m=-4$ e $n=-2$

1001

Responda, justificando, falso ou verdadeiro a cada uma das seguintes afirmações:

Se $u$, $v$ e $w$ são vetores no espaço, com $v$ não nulo e $v\times u=v\times w$, então $u=w$.
Se $u$, $v$ e $w$ são vetores no espaço então: $\mid u\cdot(v\times w) \mid=\mid v\cdot(u\times w) \mid=\mid w\cdot(v\times u) \mid=\mid v\cdot(w\times u) \mid$.
Se $u$, $v$ e $w$ são vetores no espaço, então $u\times (v\times w)= (u\times v)\times w$.
Se $u$, $v$ e $w$ são vetores no espaço, $u$ é não nulo e $u\times v=u\times w=\vec{0}$, então $v\times w=\vec{0}$.

1151

Qual é o lugar geométrico de todas as retas que passam pela origem com ângulo diretor em relação ao eixo $z$ $\gamma=30^\circ$?

Um cone sobre o eixo $z$.

1478

Um homem deseja construir uma ampulheta dispondo de $v$ m$^3$ de uma certa areia. Considerando que a ampulheta possa ser "modelada" como uma porção simétrica de uma superfície cônica, encontre a equação do cone, com abertura no eixo $z$, que contém essa ampulheta.

490

Encontre uma equação em coordenadas polares para a curva cuja equação em coordenadas cartesianas é dada por $x^3+y^3-6xy=0$.

Pela definição de coordenadas polares, obtemos a seguinte equação: $$r=\frac{6\cos(\theta)\sin(\theta)}{\cos^3(\theta)+\sin^3(\theta)} \quad \theta\in[0,2\pi].$$

1352

Esboce o gráfico da equação paramétrica dada por $(x,y)=(t^2-1,t^2+1)$.

446

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{cccccr}2x_1+&1x_2+&4x_3+&x_4&=&-5 \\2x_1+&8x_2-&10x_3+&8x_4&=&2 \\&&-9x_3+&2x_4&=&2\\4x_1+&1x_2+&6x_3+&5x_4&=&-3\\4x_1+&5x_2-&8x_3+&8x_4&=&-3\\\end{array}\right . .\]

Esse sistema possui uma única solução.

711

Ache a equação da reta tangente a $x^2+y^2=25$ no ponto $(-3,4)$.

1646

Em cálculo de uma variável vemos que se $x_0$ é um extremo local (máximo ou mínimo) de uma função $f(x)$, então a reta tangente ao gráfico de $f$ em $x_0$ é horizontal, ou seja, $f'(x_0)=0$.

Encontre uma relação similar entre um extremo local de uma função de duas variáveis e o plano tangente ao seu gráfico.
Use esta relação para encontrar os extremos locais da função $\displaystyle f(x,y)=2x^2+2y^2-2x-6y+14$.
Verifique se sua resposta no item anterior está correta completando os quadrados em $f(x,y)$ e identificando a quádrica.

1212

Reduza a equação $xz = 1$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

A equação da quádrica $xz = 1$ pode ser escrita em forma matricial:

$$X^tAX-1=0,$$

onde:

$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ A=\begin{pmatrix}0 & 0 & 1/2 \\0 & 0 & 0 \\1/2 & 0 & 0\end{pmatrix}. $$

Seja:

$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}-\lambda & 0 & 1/2 \\0 & -\lambda & 0 \\1/2 & 0 & -\lambda\end{pmatrix}=-\lambda^3+\lambda/4.$$

As raízes de $P(\lambda)$ são $0$, $-1/2$ e $1/2$. Considere os sistemas lineares referentes às raízes $0$ e $1/2$: $A X = 0$ e $(A-1/2 I) X = 0$. Uma solução de norma unitária desses sistemas consiste em $U_1=(0,1,0)$ e $U_2=(1/\sqrt{2},0,1/\sqrt{2})$, respectivamente. Sejam $U_3=U_1 \times U_2 = (1/\sqrt{2},0,-1/\sqrt{2})$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $xz=1$ se transforma em:

$$\dfrac{(y')^2}{2}-\dfrac{(z')^2}{2}=1,$$

que é a equação de um cilindro hiperbólico.

445

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{rrrrrcr}1x_1+&3x_2-&7x_3+&5x_4+&2x_5&=&0 \\2x_1+&3x_2-&20x_3+&7x_4+&8x_5&=&0 \\10x_1+&22x_2-&46x_3+&34x_4+&12x_5&=&0 \\\end{array}\right. . \]

Esse sistema possui infinitas soluções.

775

Sejam $u$ e $v$ dois vetores de comprimentos iguais. Mostre que para quaisquer números $a$ e $b$, os vetores $au+bv$ e $av+bu$ têm o mesmo comprimento. Interprete o resultado.

956

Identifique a quádrica definida pela equação reduzida $x^2+ y^2-z^2=0$ e esboce seu gráfico.

468

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{ccccccr}2x_1&+&5x_2&+&12x_3&=& 6 \\3x_1&+&x_2&+&5x_3&=& 12 \\5x_1&+&8x_2&+&21x_3&=& 17\\\end{array}\right. .\]

717

Ache a equação do círculo que passa pelos pontos $(a,0)$, $(b,0)$ e $(0,c)$. Ache também seu centro, raio, e faça um esboço de seu gráfico.

395

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
-2&2&-2\\2&1&-4\\ -2&-4&1
\end{pmatrix}.
$

$x_1=-3$, $x_2=-3$, $x_3=6$.

366

Sejam $A$ e $B$ duas matrizes quadradas $n\times n$.

Mostre que $(A+B)^2=A^2+AB+BA+B^2$.
Suponha que:
$A= \left( \begin{array}{cc}
1 & 0 \\
1 & 1
\end{array}\right) \;\; \mbox{e}\;\;
B= \left( \begin{array}{cc}
0 & 1 \\
1 & 1
\end{array}\right) $.
Verifique que $AB\neq BA$. Conclua que neste caso, $(A+B)^2\neq A^2+2AB+B^2$.
Mostre que: Se $A$ e $B$ são duas matrizes quadradas $n\times n$, então $(A+B)^2=A^2+2AB+B^2$, se e somente se, $AB=BA$.

1031

Qual a distância de um ponto $(x,y)$ ao ponto $(c,0)$?
Qual a distância de um ponto $(x,y)$ ao ponto $(-c,0)$?
Use sua resposta anterior para obter a equação de uma elipse com focos $(c,0)$ e $(-c,0)$.
Simplifique sua equação o máximo possível. Isso exigirá certa manipulação algébrica mas, ao final, podemos obter uma forma simplificada para elipses deste tipo.
Quais são as intersecções desta elipse com os eixos $x$ e $y$?
Como muda a sua equação se os focos forem $(0,c)$ e $(0,-c)$?

1481

Uma liga de metal $L_1$ contém $20\%$ de ouro e $80\%$ de prata, uma liga $L_2$ tem $65\%$ de ouro e $35\%$ de prata, e uma liga $L_3$ tem mesma quantidade de ouro e prata.

Escreva um sistema linear cuja solução dê a quantidade de gramas de cada liga necessários para se formar $100$ gramas de uma liga com $60$ gramas de ouro e $40$ gramas de prata.
Este problema tem solução única? Justifique utilizando conceitos sobre sistemas lineares.
Determine a(s) solução(ões) do sistema linear.

Se $x$, $y$ e $z$ designam as quantidades, em gramas, das ligas $L_1$, $L_2$ e $L_3$, respectivamente, o sistema pode ser escrito como a seguir
$$ \left\{ \begin{array}{rcrcc}0,2 x &+&0,65 y &+ &0,5 z & = &60\\0,8 x &+&0,35 y &+ &0,5 z & = &40\end{array} \right. $$
Existem infinitas soluções para este problema. Por que?
As soluções são dadas por $y=\dfrac{200}{3}+2x$, $z=\dfrac{100}{3}-3x$.
Como $x$, $y$ e $z$ representam pesos, a solução só fará sentido para $x,y,z \in \mathbb{R}^+$. Logo, é preciso que $x\leq\dfrac{100}{9}$ gramas.

981

Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(1,-2,1)$ e sua origem é o ponto $P=(1,0,1)$.

$(2,-2,2)$.

270

Sejam $a$, $b$, $c$, $d$ números reais tais que $ax+by+cz+d>0$ para quaisquer $x$, $y$, $z\in\mathbb{R}$. Mostre que $a=b=c=0$ e $d>0$.

1211

Reduza a equação $3x^2 + 2y^2 + 3z^2 - 2xz - 4y = 6$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

A equação da quádrica $3x^2 + 2y^2 + 3z^2 - 2xz - 4y = 6$ pode ser escrita em forma matricial:

$$X^tAX+KX-6=0,$$

onde:

$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ K=\begin{pmatrix}0 & -4 & 0\end{pmatrix}, \ A=\begin{pmatrix}3 & 0 & -1 \\0 & 2 & 0 \\-1 & 0 & 3\end{pmatrix}. $$

Seja:

$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}3-\lambda & 0 & -1 \\0 & 2-\lambda & 0 \\-1 & 0 & 3-\lambda\end{pmatrix}=-\lambda^3+8\lambda^2-20\lambda+16.$$

As raízes de $P(\lambda)$ são $2$ e $4$, sendo $2$ uma raiz dupla. Considere o sistema linear referente à raiz $2$: $(A-2I) X = 0$. Duas soluções de norma unitária desse sistema são $U_1=(1/\sqrt{2},0,1/\sqrt{2})$ e $U_2=(0,1,0)$. Sejam $U_3=U_1 \times U_2 = (-1/\sqrt{2},0,1/\sqrt{2})$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $3x^2 + 2y^2 + 3z^2 - 2xz - 4y = 6$ se transforma em:

$$\dfrac{(x')^2}{4}+\dfrac{(y'-1)^2}{4}+\dfrac{(z')^2}{2}=1,$$

que é a equação de um elipsóide.

299

Encontre condições sobre o vetor $v=(a,b,c)$ para que exista uma reta na direção de $v$ que intercepte simultaneamente as retas $r$ e $s$:

$$r:\begin{cases} x= 2 + t\\y = 5 - t\\z = 3 + t \end{cases}\ \ \ {\rm e}\ \ \ s:\begin{cases} x= t\\y = 1 - t\\z = -2 \end{cases}$$

417

Use o processo de inversão (Gauss-Jordan) para obter a inversa da matriz $A$ e verifique que a matriz obtida é de fato a inversa de $A$, onde: $$ A = \begin{bmatrix} 6 & 4 & 3 & 0 \\ 1 & 1 & 0 & 0 \\ -3 & -2 & -1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$$

461

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{rrrcr}2x_1+&3x_2-&5x_3&=& 2 \\2x_1+&3x_2-&x_3&=& 8 \\6x_1+ &9x_2-&7x_3&=& 18 \\\end{array}\right. . \]

$Y = x_1 \left(1, \dfrac{-2}{3}, 0\right)^T$, $\forall x_1\in\mathbb{R}$.

$X_o = \left(0, \dfrac{19}{6},\dfrac{ 3}{2}\right)^T$.

$X_o + Y = \left(x_1, \dfrac{19}{6}-\dfrac{2 x_1}{3},\dfrac{ 3}{2}\right)^T$, $\forall x_1\in\mathbb{R}$.

508

A elipse $\ell$ tem focos $F_1=(1,2)$, $F_2=(2,4)$ e vértices $A_1=(0,0)$, $A_2=(3,6)$. Dê as equações paramétricas de $\ell$.

1404

O momento escalar ou torque sobre o ponto $P$ de uma força $\vec{F}$ aplicada a um ponto $Q$ é dado por $\|\vec{PQ} \times \vec{F}\|$. Uma força $\vec{F}$ com magnitude de $10 N$ é aplicada na direção $y$ positiva sobre o ponto $Q=(1,1,1)$ em um cubo com lados de tamanho $1m$. Determine o momento escalar de $\vec{F}$ sobre o ponto $P = (1,0,1)$. Faça um esboço do gráfico, indicando a força e o momento escalar.

781

Encontre o ponto $Q$ do espaço tal que o vetor com origem no ponto $P=(1,0,1)$ e com extremidade em $Q$ tenha norma, direção e sentido iguais ao vetor $(1,-2,1)$.

$Q=(2,-2,2)$.

285

Verificar se as retas são concorrentes e, em caso afirmativo, encontrar o ponto de interseção:

$$r_1:\;\begin{cases} y=2x-3\\ z=-x-10. \end{cases}\ \ \ {\rm e } \ \ \ r_2:\; \begin{cases}y=3x+7\\ z=x+1\end{cases}$$

As retas não são concorrentes.

1231

Reduza a equação $x^2+z^2-xy+xz+yz-2x+2y-2z+1=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

292

Considere as retas $r$ e $s$ de respectivas equações

\[
r:\ \frac{x-2}{2}\ =\ y\ =\ z+1, \ s:\ x\ =\ y+1\ =\ z-
2
\]

Verifique se as retas $r$ e $s$ são paralelas, concorrentes ou reversas.
Determine a equação da reta $t$ perpendicular e concorrente com as retas $r$ e $s$.
Calcule o ângulo e a distância entre as retas $r$ e $s$.

Reversas.
$\left\{
\begin{array}{l}
x=-4 \\
y=-5-t \\
z=-2+t
\end{array}
\right. .$
Ângulo $\left( r,s\right) =\arccos \frac{4}{\sqrt{18}} $; dist$(r,s)=\sqrt{8}.$

1043

Decida se a cônica $C$ determinada pela equação $5x^2+6xy+5y^2-8 = 0$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

1362

Forneça equações paramétricas para o ramo positivo da curva $9x^2-4y^2+90x+32y+125=0$, indicando valores para o parâmetro $t$. Esboce suas parametrizações.

1234

Reduza a equação $2z^2+5x+12y+12z+18=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1424

Mostre que quaisquer que sejam $u$, $v$ e $w$ em $\mathbb{R}^2$, eles são linearmente dependentes.

990

Estude o ângulo entre os vetores $\vec{i}$ e $\vec{j}$ no plano. Faça o mesmo no $\mathbb{R}^{3}$ em relação a $\vec{i}$, $\vec{j}$ e $\vec{k}$.
Escrevendo os vetores $u = x\vec{i} + y\vec{j}$ e $v = a\vec{i} + b\vec{j}$, verifique que $\langle u,v\rangle = xa\langle\vec{i},\vec{i}\rangle + yb\langle\vec{j},\vec{j}\rangle$. Faça um estudo semelhante no espaço $\mathbb{R}^{3}$.

1485

Suponha que:

$$ \left\{ \begin{array}{rcrcc}a x &+& b y & = & 0\\c x &+& d y & = & 0 \end{array} \right. ,$$

sejam duas equações de retas, onde $a$, $b$, $c$ e $d$ são números reais.

O que significa, geometricamente, o fato de que os termos independentes são nulos?
Como estudar a existência/tipo de interseções entre essas duas retas usando sistemas lineares?

Significa que ambas as retas passam pela origem do plano cartesiano. Afinal, ponto $(x,y)=(0,0)$ satisfaz ambas as equações do sistema.
Posto que as duas retas passam pelas origem, esse tipo de sistema possui sempre ao menos uma solução, ponto de interseção das retas, a origem. Restando a possibilidade de, se o determinante da matriz dos coeficientes for nulo, que as retas sejam coincidentes.

1350

Suponha que uma partícula $p$ tenha trajetória descrita pela curva $C(t) = (\cos(t), \sin(t), 0).$ Ou seja, $p$ se move ao longo de um círculo no plano $xy$. Seja $\epsilon >0$ um número real (pequeno). Podemos perturbar o movimento de $p$, no instante $t$, empurrando-a um pouco em alguma outra direção. Dada a curva $D(t) = \left(\cos\left(\frac{3}{2}t\right)\cos\left(t\right), \cos\left(\frac{3}{2}t\right)\sin\left(t\right), \sin\left(\frac{3}{2}t\right)\right)$, considere a nova trajetória "perturbada" $E(t) = C(t) + \epsilon D(t)$. Esboce $E(t)$ com $\epsilon = 1/4$ e com $t$ em radianos. Como muda a imagem (traço) da curva se trocarmos o fator $\frac{3}{2}$ por outro número, digamos, $\frac{5}{3}$ ou $\frac{8}{5}$? E se o coeficiente for irracional?

295

Ache os pontos de $r:x-1=2y=z$ que equidistam de $s=\{ (2,t,0),t\in\mathbb{R}\}$ e do eixo $x$.

418

Use o método de inversão por escalonamento para obter, se possível, a inversa das seguintes matrizes:

$A= \begin{bmatrix} 1 & 1 & 1 \\ 2 & 1 & 4 \\ 2 & 3 & 5 \end{bmatrix} $;
$B=\begin{bmatrix} 1 & 2 & 3 \\ 1 & 1 & 2 \\ 0 & 1 & 1 \end{bmatrix} $.

359

Considere as matrizes

\[A=\left(\begin{array}[c]{rrr}2 & -3 & -5\\-1 & 4 & 5\\1 & -3 & -4\end{array}\right) \text{, }B=\left(
\begin{array} [c]{rrr}-1 & 3 & 5\\1 & -3 & -5\\-1 & 3 & 5\end{array}\right) \text{ e }C=\left(
\begin{array}[c]{rrr} 2 & -2 & -4\\-1 & 3 & 4\\
1 & -2 & -3 \end{array}\right) .\]

Mostre que $AB=BA=0$, $AC=A$ e $CA=C$.
Use os resultados do item anterior para mostrar que $ACB=CBA$, $A^{2}-B^{2}=(A+B)(A-B)$ e $(A\pm B)^{2}=A^{2}+B^{2}$.

1051

Na equação $x^2-y^2+2\sqrt{3}xy+6x=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.

973

Dadas a equação da curva diretriz $x^2+z^2=1$, $y=0$ e um vetor $V=(4,1,0)$ paralelo às retas geratrizes, determine a equação da superfície cilíndrica.

1017

Encontre os vértices (ou vértice), os focos (ou foco) e a excentricidade da cônica descrita por $49x^2-9y^2=441$. Esboce também o gráfico.

480

Considere a reta $r=\{(x,y):2x-3y=1\}\subset\mathbb{R}^2$. Seja $B$ a base formada pelos vetores $(3,2)$ e $(1,0)$ e $x^{\prime}$ e $y^{\prime}$ coordenadas definidas em $\mathbb{R}^2$ pela origem usual e pela base $B$. Ache a equação de $r$ nas coordenadas $x^{\prime}$ e $y^{\prime}$.

385

Calcule o determinante da matriz:

$
\begin{pmatrix}
1&2&3&4\\ 5&6&7&8\\ 9&10&0&0\\ 11&12&0&0
\end{pmatrix}.
$

$8$

1143

Dados dois vetores $\vec{A}$ e $\vec{B}$, e $\theta$ o ângulo entre eles, ache fórmulas para $\|\vec{A} + \vec{B}\|$ e $\|\vec{A} - \vec{B}\|$ (Sugestão: use a Lei dos Cossenos).

$\|\vec{A} + \vec{B}\|^2=\|\vec{A}\|^2+\|\vec{B}\|^2 +2\|\vec{A}\|\|\vec{B}\|\cos\theta$.

1153

Quais são os cossenos diretores da reta no plano $xy$ que faz $45^\circ$ com a origem?

$1/\sqrt{2},1/\sqrt{2},0$.

437

Encontre a inversa da matriz abaixo (se existir):

\[\begin{pmatrix}a & b \\ -b & a\end{pmatrix}.\]

A inversa existirá desde que $a\neq 0$ ou $b\neq 0$, nesse caso será dada por \[\begin{pmatrix}\dfrac{a}{a^2+b^2} & \dfrac{-b}{a^2+b^2} \\ \dfrac{b}{a^2+b^2} & \dfrac{a}{a^2+b^2}\end{pmatrix}.\]

313

Encontre a equação de uma reta mediatriz do segmento de extremos $A = (1,1,1)$ e $B = (3,3,3)$.

O ponto médio do segmento é dado por $M=\dfrac{1}{2}(A+B)=(2,2,2)$. Já para um vetor diretor, podemos escolher qualquer vetor que seja ortogonal a $B-A=2(1,1,1)$. Por exemplo, tomando o vetor $(1,-1,0)$ como diretor, teremos a seguinte forma paramétrica para uma mediatriz: $$ (2,2,2)+t(1,-1,0),\quad t\in\mathbb{R}.$$

322

Sejam a reta $r: \ x-1=y=z$ e os pontos $A(1,1,1)$ e $B(0,0,1)$. Encontre o ponto de $r$ que é equidistante de $A$ e $B$.

1419

A Pirâmide de Quéops, também conhecida como Grande Pirâmide de Gizé, no Egito, tem o formato muito próximo de um tetraedro regular. Pesquise as suas medidas e utilizando o produto misto, calcule aproximadamente o volume interno da pirâmide. Defina o sistema de coordenadas e os três vetores do produto misto de forma a facilitar as contas.

312

Verifique a posição relativa do seguinte par de retas (isto é, verifique se são paralelas, concorrentes ou reversas):

\[(2,1,-1) + t(3,2,-1), \ \ \ \left\{\begin{array}{ccr}x &=& -1+2s\\y &=& 3s\\ z &=& 4 + 5s\end{array}\right. \]

São reversas.

866

Justificar as afirmações abaixo:

$\vec{u} \cdot (\vec{u}\times \vec{v})=0,$ para quaisquer dois vetores $\vec{u}$ e $\vec{v}.$
Se as diagonais de um paralelogramo são perpendiculares, então este paralelogramo é um losango.

1154

Quais são os cossenos diretores da reta que passa pela origem no primeiro octante e que tem ângulos iguais com os três eixos coordenados?

$1/\sqrt{3},1/\sqrt{3},1/\sqrt{3}$.

1433

Mostre que os ramos direito e esquerdo da hipérbole $\displaystyle \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ podem ser representados parametricamente por

$$ x= a\sec t, \quad y=b\tan t, \quad(-\pi/2 < t < \pi/2) $$

$$ x= -a\sec t, \quad y=b\tan t, \quad(-\pi/2 < t < \pi/2). $$

Use um recurso gráfico para gerar ambos os ramos da hipérbole $x^2-y^2=1$ em um mesmo gráfico.

1428

Uma viga metálica fina, com extremidades nas coordenadas $A=(2,5,3)$ e $B=(1,1,0)$, deve ser dividida em três partes iguais. Determine os pontos $C$ e $D$ que realizam esta divisão.

245

Dados os planos $\pi_1:x-y=0$, $\pi_2:x+y-z+1=0$ e $\pi_3:x+y+2z-2=0$, determine o plano que contém $\pi_1\cap\pi_2$ e é perpendicular a $\pi_3$.

289

Determinar o ângulo entre a reta que passa por $A(3,-1,4)$ e $B(1,3,2)$ e a sua projeção ortogonal no plano $xy$.

$\theta=\arccos \left(\frac{5}{\sqrt{30}}\right)$

1480

Uma indústria produz três produtos $p_1,p_2,p_3$, com duas matérias prima distintas, $m_1$ e $m_2$. Para a fabricação de cada unidade de $p_1$ são utilizados $1$ unidade de $m_1$ e $2$ unidades de $m_2$; para cada unidade de $p_2$, $1$ unidade de $m_1$ e $1$ unidade de $m_2$; e para cada unidade de $p_3$, $1$ unidade de $m_1$ e $4$ unidades de $m_2$.

Escreva um sistema linear que relacione as quantidades de $x$ unidades de $p_1$, $y$ unidades de $p_2$ e $z$ unidades de $p_3$ que podem ser produzidas com $200$ unidades de $m_1$ e $300$ unidades de $m_2$.
Utilizando conhecimentos sobre sistemas lineares, responda se há apenas uma configuração possível de produção dos produtos $p_1$, $p_2$ e $p_3$. Determine esta(s) configuração(ões) e interprete.

$$ \left\{ \begin{array}{rcrcc}x &+& y &+ & z & = &200\\2x &+& y &+ &4 z & = &300\end{array} \right. $$
Há infinitas configurações possíveis respeitando $y=\dfrac{500-2x}{3}$ e $z=\dfrac{100-x}{3}$ desde que $x,y,z \in\mathbb{I}^+$, logo $x\leq 100$.

1050

Na equação $4x^2-20xy+25y^2-15x-6y=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.

301

Encontre a equação da reta $r$ que passa por (1,-2,3), e tem vetor diretor $(-1,2,-3)$.

Parametricamente: $$ r: (1,-2,3) + t(-1,2,-3)\quad t\in\mathbb{R}.$$

714

As equações dos lados de um triângulo são $9x+2y+13=0$, $3x+8y-47=0$ e $x-y-1=0$. Encontrar a equação da circunferência circunscrita a esse triângulo.

1008

Dado um plano qualquer com um sistema de coordenadas $xy$, encontre os vértices (ou vértice), os focos (ou foco) e a excentricidade da cônica descrita por $49x^2-9y^2=441$. Esboce o gráfico.

448

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz, em função do parâmetro $\lambda$.

\[\left\{\begin{array}{ccccl}x_1-&2x_2-&x_3+&x_4&=-2 \\2x_1+&7x_2+&3x_3+&x_4&=\ \, 6 \\11x_1+&11x_2+&4x_3+&8x_4&=\ \, 8\\10x_1+&2x_2+&&8x_4&=\ \, \lambda \\\end{array}\right. .\]

1451

Dada a superfície $4x^2+y^2+z^2=9$, identifique a cônica obtida ao fixar:

$x=0$;
$y=0$;
$z=1$.

812

Seja $ABCD$ um tetraedro e $P$ um ponto qualquer dentro dele. Ligue os vértices $A, B,C,D$ até o ponto $P$ e prolongue as linhas até que elas interceptem as faces opostas nos pontos $A',B',C',D'$, respectivamente. Mostre que vale a seguinte relação: $$\frac{PA'}{AA'}+\frac{PB'}{BB'}+\frac{PC'}{CC'}+\frac{PD'}{DD'}=1.$$

1461

Mostre que por cada ponto do parabolóide hiperbólico $z=x^2-y^2$ passam duas retas inteiramente contidas nele.

1041

A mudança de coordenadas entre os sistemas $xy$ e $x_{1}y_{1}$ é feita através de uma matriz ortogonal $U$, como segue

\[ \begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{\,4}{5}} \\{\frac{\,-4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\quad \text{ e }\quad\begin{pmatrix}x\\ y\end{pmatrix} = \begin{pmatrix}{\frac{\,3}{5}} & {\frac{-4}{5}} \\ {\frac{\,4}{5}} & {\frac{\,3}{5}} \end{pmatrix}\begin{pmatrix}x_{1}\\ y_{1}\end{pmatrix},\quad \text{ lembrar que } U^{-1} = U^{t}.\]

Já a mudança entre os sistemas $x_{1}y_{1}$ e $XY$ é dada por $X = x_{1}+1$, $Y = y_{1}+1$.

Encontre as equações das retas suporte do eixo $X$ e do eixo $Y$ em relação aos sistemas $x_{1}y_{1}$ e $xy$.
Encontre as equações das retas suporte do eixo $x_{1}$ e do eixo $y_{1}$ em relação ao sistema $xy$.
Seja $\mathcal{L}$ a reta cuja equação no sistema $xy$ é dada por $y = 2x + 1$. Encontre as equações de $\mathcal{L}$ em relação aos eixos $x_{1}y_{1}$ e $XY$.

772

Sejam $\vec{u}=(2,1,3)$, $\vec{v}=(0,1,-1)$ e $\vec{w}=(4,5,3)$ vetores do espaço.

Calcule $\vec{u}+\vec{v} $ e $\vec{u}-2\vec{v}+3\vec{w}$.
Determine $a$ e $b$ tais que $\vec{w}=a\vec{u}+b\vec{v}$.

$\vec{u}+\vec{v}=(2,1,2) $ e $\vec{u}-2\vec{v}+3\vec{w}=(14,14,14)$.
$a=2$ e $b=3$.

867

Determinar $u\cdot v$, sabendo que $\|u\times v\|=12$, $\|u\|=13$ e $v$ é unitário.

Usando que $\| u\times v\|=|u||v|\sin\theta$, obtemos que $\sin\theta=\dfrac{12}{13}$, onde $\theta$ é o ângulo entre os vetores $u,v\in\mathbb{R}^3$. Por conseguinte, temos que $\cos\theta=\sqrt{1-\sin^2\theta}=\sqrt{1-(\dfrac{12}{13})^2}=\dfrac{5}{13}$. Logo, $u\cdot v=|u||v|\cos\theta=13\cdot 1\dfrac{5}{13}=5$.

1148

Ache os dois vetores no plano $xy$ perpendiculares a $4\vec{i}-3\vec{j}$ e de tamanho $10$.

$\pm (6\vec{i}+8\vec{j})$.

1399

A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).

479

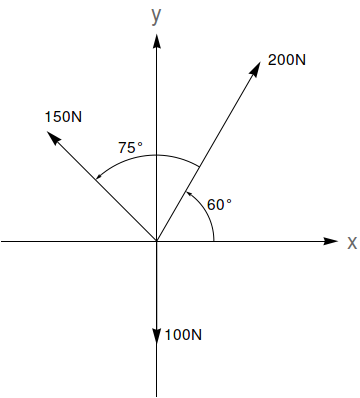
Considere o círculo $C$ de raio $1$ e centrado na origem do sistema usual de coordenadas do $\mathbb{R}^2$. Lembre-se que a equação de $C$ é $x^2+y^2=1$. Considere o sistema $\{ Q,i,j\}$, onde $Q=(-3,2)$. Ache a equação de $C$ no novo sistema de coordenadas.

864

Encontre o ângulo entre os vetores $u=(2,1,0)$ e $v=(0,1,-1)$ e entre os vetores $w=(1,1,1)$ e $z=(0,-2,-2)$.

$\arccos(\dfrac{\sqrt{10}}{10})$ e $\arccos(-\sqrt{\dfrac{2}{3}})$, respectivamente.

1222

Reduza a equação $-2x^2+4y^2+6z^2+2xy+6xz+6yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

266

Dados os dois pontos $A=(x_1,y_1,z_1)$ e $B=(x_2,y_2,z_2)$, mostre que o lugar geométrico dos pontos do espaço que equidistam de $A$ e $B$ é um plano que passa pelo ponto médio do segmento $AB$ e é perpendicular à reta que contém $A$ e $B$.

715

Qual a equação da circunferência que passa pelos pontos $(1,2)$, $(3,4)$ e que tem centro sobre o eixo $y$?

1025

Determinar a equação reduzida da seguinte cônica e fazer um esboço gráfico da mesma: hipérbole com focos no eixo $x$, assíntotas $y=\pm 2 x $ e o ponto $P=(5,6).$

1006

Identifique a seguinte cônica, determinando sua excentricidade, sua equação cartesiana, a equação cartesiana da diretriz e as coordenadas cartesianas do(s) foco(s) e do(s) vértice(s): $r=\frac{4}{2-3cos\theta}$.

1353

Esboce o gráfico da equação paramétrica dada por $(x,y)=( t^2-2t,t)$.

238

Considere a reta $r$ e o plano $\pi $ de respectivas equações

\[
\frac{x-2}{2}\ =\ y-2\ =\ \frac{z-3}{3}\, \ \mathrm{e}, \ x+y+z\ =\ 1.
\]

Encontre uma equação paramétrica para a reta que é a projeção ortogonal de $r$ sobre $\pi$.

$\left\{
\begin{array}{l}
x=0 \\
y=1-t \\
z=t
\end{array}
\right. $

1598

Às vezes o gráfico de uma equação quadrática é uma reta, um par de retas ou até mesmo um único ponto. Nos referimos a tais gráficos como cônicas degeneradas. É também possível que a equação não seja satisfeita para nenhum valor real das variáveis, caso este no qual não existe um gráfico e dizemos tratar-se de uma cônica imaginária. Nos itens abaixo, identifique a cônica com a equação dada, dizendo se é degenerada ou imaginária. Quando possível, esboce também o gráfico.

$\displaystyle x^2-y^2=0$;
$\displaystyle x^2+2y^2+2=0$;
$\displaystyle 3x^2+y^2=0$.

985

Sejam $u=(-1,1,1)$ e $v=(2,0,1)$ dois vetores. Encontre os vetores $w$ que são paralelos ao plano determinado por $O$, $u$ e $v$, perpendiculares a $v$ e tais que $u\cdot w=7$.

Os vetores $\vec{w}$ são da forma:

$\vec{w}=\left(-\frac{7}{3},\frac{14}{3},0\right)^T+\lambda\left(1/3,-2/3,1\right)^T$, $\lambda\in\mathbb{R}$

1223

Reduza a equação $4x^2+y^2-8z^2+4xy-4xz+8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

484

Sejam $\mathcal{C}$ a circunferência de equação $x^2+y^2=r^2$ e $P=(x_1,y_1)$ um ponto em $\mathcal{C}$. Mostre que a equação da reta tangente à circunferência por $P$ é $x_1x+y_1y=r^2$. (Lembre que a reta tangente em $P$ sempre é perpendicular ao vetor $\vec{OP}$, com $O$ sendo o centro de $\mathcal{C}$.)

Um ponto $x=(x,y)$ qualquer sobre a reta tangente a $\mathcal{C}$ pelo ponto $P$ deverá satisfazer $(x-P)\cdot\overrightarrow{OP}=0$. Ou seja, $\vec{x}$ deverá cumprir $(x-x_1)x_1+(y-y_1)y_1=0$ pela condição de perpendicularidade. Como $P\in\mathcal{C}$, então $x_1^2+y_1^2=r^2$ e a condição anterior fica $\displaystyle xx_1+yy_1=r^2$.

389

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
\cos a& \sin a\\ -\sin a&\cos a
\end{pmatrix}.
$

$\displaystyle \cos a\pm \sqrt{\cos^2a-1}$

1386

Uma indústria produz três produtos $p_1,p_2,p_3$, com duas matérias prima distintas, $m_1$ e $m_2$. Para a fabricação de cada unidade de $p_1$ são utilizados $1$ unidade de $m_1$ e $2$ unidades de $m_2$; para cada unidade de $p_2$, $1$ unidade de $m_1$ e $1$ unidade de $m_2$; e para cada unidade de $p_3$, $1$ unidade de $m_1$ e $4$ unidades de $m_2$. Utilizando matrizes, determine quantas unidades de $m_1$ e $m_2$ são necessárias na produção de $x$ unidades de $p_1$, $y$ unidades de $p_2$ e $z$ unidades de $p_3$.

Seja $A$ a matriz $2 \times 3$ tal que sua primeira linha contenha informações sobre $m_1$ e a segunda linha informações sobre $m_2$, e a primeira, segunda e terceira colunas informações sobre $p_1$, $p_2$ e $p_3$, respectivamente:

$$A=\begin{pmatrix}1 & 1 & 1 \\ 2& 1& 4 \end{pmatrix} \text{ e } X=\begin{pmatrix}x\\y\\z\end{pmatrix},$$

então a multiplicação $AX$ nos dá o vetor tal que a sua primeira linha seja a quantidade de $m_1$ necessária e sua segunda linha a quantidade de $m_2$:

$$AX=\begin{pmatrix} x+y+z \\ 2x+y+4z \end{pmatrix}.$$

405

Resolver o sistema linear: \[\left\{\begin{array}{ccccccccr}3x& + &3y& - &2z& - &t&=& 2\\5x& + &2y& + &z& - &2t&=& 1\\2x& - &y& + &3z& - &t&=& -1\end{array}\right. .\]

$z = \dfrac{-3+x+4y}{5}, t =\dfrac{-4+13 x+7 y}{5}, \forall x, y \in \mathbb{R}.$

1360

Dê equações paramétricas para a curva $y=x^2-x^4$, indicando os valores para o seu parâmetro $t$. Esboce suas parametrizações.

441

Encontre a inversa da matriz abaixo (se existir):

\[\begin{pmatrix}1 & 3 & -7 \\ 0 & 1 & -2 \\0 & 0 & 1\end{pmatrix}.\]

\[\begin{pmatrix}1 & -3 & -1 \\ 0 & 1 & -2 \\0 & 0 & 1\end{pmatrix}.\]

408

Sejam

$A= \left( \begin{array}{ccc}1 & -2 & -1\\1 & 0 & -1\\4 & -1 & 0\end{array}\right)$ e $X= \left( \begin{array}{c}x\\y\\z\\\end{array}\right)$.

Verifique que: $xA_1+yA_2+zA_3=AX$, sendo $A_j$ a $j$-ésima coluna de $A$ para $j=1$, 2, 3.
Usando 1. verifique que: a segunda coluna de $C=A^2$ é $C_2=-2A_1 - A_3$.
Tente generalizar o que foi feito em e para a seguinte situação: Sejam $A$ uma matriz $m\times n$, $B$ uma matriz $n\times k$ e $C=AB$. Se $C_j$ é a $j$-ésima coluna de $C$, encontre $C_j$ em termos das $n$ colunas de $A$ e da $j$-ésima coluna de $B$.

425

Resolver o sistema linear em função do parâmetro $\lambda$:

\[\left\{\begin{array}{cccl}2x_1+&3x_2+&x_3&=1 \\x_1+&6x_2+&x_3&=3 \\2x_1-&3x_2+&2x_3&=\lambda\\x_1+&3x_2+&2x_3&=1 \\\end{array}\right.. \]

$x_1 =\dfrac{-1}{4}, x_2 =\dfrac{7}{12}, x_3 =\dfrac{-1}{4}, \lambda = \dfrac{-11}{4}.$

997

Sejam os vetores $\vec{u}=(2,1,3)$, $\vec{v}=(0,1,-1)$, $\vec{w}=(4,5,3)$. Mostre que $\vec{u}, \vec{v}$ e $\vec{w}$ são coplanares.

De fato, basta verificar que $\vec{u}\cdot(\vec{v}\times\vec{w})=0$.

443

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz.

\[\left\{\begin{array}{cccccr}&x_1&-&7x_2&=&-11 \\-&x_1&+&11x_2&=&31 \\&2x_1&-&12x_2&=&-26 \\&3x_1&-&17x_2&=&-15 \\\end{array}\right. . \]

O sistema não possui solução.

1367

Construa a curva cujas equações paramétricas são dadas por: $x=-2t-3$, $y=t+5$ e $z=4t-7$.

440

Encontre a inversa da matriz abaixo (se existir):

\[\begin{pmatrix}2 & 2 & -1 \\ 2 & -1 & 2 \\-1 & 2 & 2\end{pmatrix}.\]

\[\begin{pmatrix}2/9 & 2/9 & -1/9 \\ 2/9 & -1/9 & 2/9 \\-1/9 & 2/9 & 2/9\end{pmatrix}.\]

239

Considere a reta
\[
r:\left\{
\begin{array}{ccl}
x & = & 1 \\
y & = & -z
\end{array}
\right.
\]
e o ponto $A\ =\ (1,1,1)$. Determine a equação do plano $\pi $ que é paralelo à reta $r$, passa por $A$ e é tal que a sua reta normal pelo ponto $A$ seja perpendicular e concorrente com a reta $r$.

$y+z=2$

1364

Dê uma representação paramétrica para as seguintes superfícies:

parabolóide elíptico $x=5y^2+2z^2-10$;
parte do parabolóide elíptico $x=5y^2+2z^2-10$ que está em frente ao plano $yz$.

a). Como a superfície está na forma $x=f(y,z)$, podemos tomar $y$ e $z$ como parâmetros, obtendo assim o seguinte conjunto de equações paramétricas $$x=5u^2+2v^2-10, \quad y = u \ \textrm{e}\ z=v.$$ Ou seja, temos a representação paramétrica $$ \sigma(u,v)= (5u^2+2v^2-10,u,v), \quad u,v\in\mathbb{R}. $$ b). Trata-se de uma restrição da representação paramétrica anterior. Entretanto, como queremos apenas a parte da superfície em frente ao plano $yz$, consideramos $x\geq 0$. Ou seja, devemos considerar $5u^2+2v^2-10 \geq 0$ ou $5u^2+2v^2 \geq 10$.

496

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por $x^2-y^2=3z^2$.

Usando a definição de coordenadas cilíndricas, a equação dada fica: $\displaystyle r^2\cos(2\theta)=3z^2$.

352

Considere a multiplicação de matrizes $3\times3$ abaixo, em que os pontos de interrogação representam coeficientes desconhecidos:

\[\left(\begin{array}[c]{rrr}9 & -8 & 4\\? & -7 & 2\\? & -4 & ?\end{array}\right) \left(\begin{array}[c]{rrr}-5 & -9 & ?\\? & 5 & ?\\4 & -8 & -7\end{array}\right) =\left(\begin{array}
[c]{ccc}c_{11} & c_{12} & c_{13}\\c_{21} & c_{22} & c_{23}\\c_{31} & c_{32} & c_{33}\end{array}\right) .\]

Só é possível determinar um coeficiente da matriz produto. Qual é ele e qual é o seu valor?

Lembre-se que a multiplicação de matrizes é feita entre linhas 'vezes' colunas. Note que, na primeira matriz apenas a primeira linha está completada (não tem ?), enquanto na outra matriz apenas a segunda coluna não contém um símbolo ?. Assim, na matriz produto, apenas a entrada $c_{12}$ estará bem-definida e seu valor será:

\[\left(\begin{array}{ccc} 9 & -8 & 4 \end{array}\right) \left(\begin{array}{c} -9 \\ 5 \\ -8 \end{array}\right) = -9^2- 8\cdot 5 -4\cdot 8 = -153.\]

470

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{rrrrl}4x&+3y&-z&+t&=4\\x&-y&+2z&-t&=0\\5x&+2y&+z&&=4\end{array}\right. . \]

402

Resolver o sistema linear:

\[\left\{\begin{array}{cccccr}2x_1+&1x_2+&4x_3+&x_4&=&-5 \\2x_1+&8x_2-&10x_3+&8x_4&=&2 \\&&-9x_3+&2x_4&=&2\\4x_1+&1x_2+&6x_3+&5x_4&=&-3\\4x_1+&5x_2-&8x_3+&8x_4&=&-3\\\end{array}\right . .\]

$x_1 = -\dfrac{27}{7}, x_2=\dfrac{-5}{7}, x_3 =\dfrac{2}{7} , x_4 =\dfrac{16}{7}.$

975

Qual(is) das quádricas abaixo representa(m) uma superfície obtida pela rotação de uma parábola em torno do eixo z?

$ 6x^2+3y^2-z^2=-2$,
$z=4x^2+4y^2$,
$\frac{x^2}{10}+\frac{y^2}{9}+\frac{z^2}{5}=1$,
$-x^2+ y^2+z^2=0$.

465

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$, em função do parâmetro $\lambda$:

\[\left\{\begin{array}{cccl}2x_1+&3x_2+&x_3&=1 \\x_1+&6x_2+&x_3&=3 \\2x_1-&3x_2+&2x_3&=\lambda\\x_1+&3x_2+&2x_3&=1 \\\end{array}\right.. \]

1448

Se uma esfera $\displaystyle \dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}+\dfrac{z^2}{a^2}=1$ de raio $a$ for comprimida na direção $z$, então a superfície resultante, chamada de esferóide oblato, tem uma equação da forma $\displaystyle \dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}+\dfrac{z^2}{c^2}=1$, onde $c<a$. A rotação da Terra causa um achatamento nos pólos, portanto sua forma é freqüentemente modelada como um esferóide oblato em vez de uma esfera. Um dos modelos usados pelos satélites de posicionamento global é o Sistema Geodésico Mundial de 1984 (WGS-84), que trata a Terra como uma esfera oblata, cujo raio equatorial é $6378,1370$ km e cujo raio polar (a distância do centro da Terra aos pólos) é $6356,5231$ km. Use o modelo WGS-84 para encontrar uma equação para a superfície da Terra em relação ao sistema de coordenadas com origem no centro de massa da Terra, eixo $z$ apontando para o pólo norte e plano $xy$ contendo o equador.

1235

Reduza a equação $x^2+y^2+4z^2-2xy-4xz+6x+12y+18z=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1079

Identifique a cônica $5 x^2+12 x y= 1$ e seu parâmetros associados.

1081

Identifique a cônica descrita pela equação $4x^2-4xy+y^2-2x+y+15=0$.

703

Ache a equação do círculo tangente ao eixo $y$ na origem e com raio $r = a$.

$(x-a)^2+y^2=a^2$

1642

Quais dos seguintes objetos não podem ser associados a elipsóides, pelo aspecto da sua superfície externa?

Um ovo.
Um bola de rugby.
Uma câmara de ar.
Uma bola de futebol.
Um charuto.

O aspecto de uma bola de rugby lembra bastante o de um elipsóide, o que não ocorre com as demais opções.

281

Encontrar as equações paramétricas da reta que passa por $A$ e é simultaneamente ortogornal às retas $r_1$ e $r_2$:

$$A(0,0,0),\;\;r_1:\;\frac{x}{2}=y=\frac{z-3}{2}\ \ \ {\rm e}\ \ \ r_2:\;\begin{cases} x=3t\\ y=-t+1\\ z=2. \end{cases}$$

$r:(x,y,z)=(2t,6t,-5t).$

1010

Encontre o volume do paralelepípedo determinado pelos vetores $u$, $v$ e $w$, dados por: $u=\overrightarrow{AB}$, $v=\overrightarrow{AC}$ e $w=\overrightarrow{AD}$, onde $A=(1,3,4)$, $B=(3,5,3)$, $C=(2,1,6)$ e $D=(2,2,5)$.

$u\cdot(v\times w)=1$

1225

Reduza a equação $2x^2+2y^2-z^2+8xy-4xz-4yz=2 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

353

Ache $x,y,z$ e $w$ tais que
\[\left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right) \left(\begin{array}[c]{cc}2 & 3\\3 & 4\end{array}\right) =\left(\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}\right) .\]
Mostre que não existem $x,y,z$ e $w$ tais que
\[\left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right) \left(\begin{array}[c]{cc}1 & 0\\0 & 0\end{array}\right) =\left(\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}\right) . \]
Existem $x,y,z$ e $w$ tais que
\[\left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right) \left(\begin{array}[c]{cc}1 & 1\\1 & 1\end{array}\right) =\left(
\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}
\right) ?\]

$x=-4$; $ y=3$; $z=3$; $w=-2$.
\[\left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right) \left(\begin{array}[c]{cc}1 & 0\\0 & 0\end{array}\right) =\left(\begin{array}[c]{cc}x & 0\\z & 0\end{array}\right) =\left(\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}\right) . \]
Mas $0=1$ é absurdo.
\[\left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right) \left(\begin{array}[c]{cc}1 & 1\\1 & 1\end{array}\right) =\left(
\begin{array}[c]{cc}x+y & x+y\\w+z & w+z\end{array}
\right)=\left(
\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}
\right) .\]
Portanto, o sistema é sobredeterminado e impassível de solução.

954

Identifique a quádrica definida pela equação reduzida $3x^2+y^2-2z^2=1$ e esboce seu gráfico.

416

Sejam $U=\begin{bmatrix} c & 4 & 1 \\ 0 & d+1 & 3 \\ 0 & 0 & c^2-4 \end{bmatrix}$, $M=\begin{bmatrix} -1 & 1 & -1 \\ -4 & 9 & -3 \\ 2 & 3 & 3 \end{bmatrix}$ e $N=\begin{bmatrix} 1 & -5 & 4 \\ -2 & 2 & 0 \\ -3 & -1 & -1 \end{bmatrix}$.

Determine, se possível, $c$ e $d$ tais que $A=M\,U$ seja invertível;
Determine, se possível, $c$ e $d$ tais que $B=N\,U$ seja invertível.

Posto que $\det(M)=0$ e $\det(A)=\det(M)\det(U)$, não há valores de $c$ e $d$ tais que $A$ seja invertível.
$\det(N)=40$, logo, se $\det(U)\neq0$, $B=NU$ será invertível, de novo porque $\det(B)=\det(N)\det(U)$. Os valores de $c$ e $d$ para os quais $\det(U)\neq$ são $c,\, d\in\mathbb{R}$ tais que $c\neq 0,$ $c\neq\pm 2$ e $d\neq -1$.

1443

Considere o sistema linear:

$$ \left\{ \begin{array}{rcrcc}a x &+& b y & = & c\\(\alpha a) x &+& (\alpha b) y & = & d\end{array} \right. ,$$

onde $a$, $b$, $c$, $d$, $\alpha$ são números reais.

Mostre que, se $d=\alpha c$, o sistema tem infinitas soluções em função de um parâmetro $\lambda$ real, dadas por: $x=\dfrac{c-b\lambda}{a}$ e $y=\lambda$.
Mostre que, se $d \neq \alpha c$, o sistema não admite solução.

863

Mostre que não existe $x$ tal que os vetores $v=(x,2,3)$ e $u=(x,-2,3)$ sejam perpendiculares.

Para que $v$ e $u$ fossem perpendiculares, seria necessário haver $x$ tal que $v\cdot u= x^2-4+9=0$, ou seja, $x$ tal que $x^2=-5$. Mas não há $x\in \mathbb{R}$ que satisfaça essa equação.

1398

A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).

709

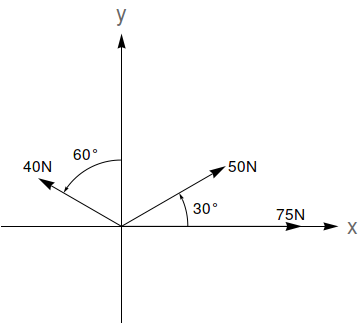
Verifique se a equação $x^2+y^2+z^2-2x-4y+10=0$ descreve uma esfera. Em caso afirmativo, identifique o centro e o raio.

Completando quadrados, vemos que não descreve uma esfera.

469

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{ccccccccccr}x_1&-&2x_2&+&3x_3&+&2x_4&+&x_5&=&10 \\2x_1&-&4x_2&+&8x_3&+&3x_4&+&10x_5&=& 7 \\3x_1&-&6x_2&+&10x_3&+&6x_4&+&5x_5&=&27\\\end{array}\right..\]

832

Mostre que o segmento de reta que liga um vértice de um paralelogramo ao ponto médio de um dos lados opostos trissecta a diagonal (isto é, intercepta a diagonal em um ponto que a divide em dois segmentos, um tendo um terço do comprimento da diagonal e o outro tendo dois terços do comprimento da diagonal).

476

Sejam $(x,y,z)$ coordenadas em relação ao sistema usual de $\mathbb{R}^3$, $S_0=\{O,i,j,k\}$. Considere o paralelepípedo $P$ com vértices $(0,0,0)$, $(3,0,0)$, $(0,2,0)$, $(0,0,1)$ (quais são os outros quatro?). Determine os vetores que representam as quatro diagonais de $P$. Escolha três deles e mostre que formam uma base de $R^3$. Chame esta base de $\beta =\{V_1,V_2,V_3\}$.

1210

Reduza a equação $z^2 + 4xy + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

A equação da quádrica $z^2 + 4xy + 1 = 0$ pode ser escrita em forma matricial:

$$X^tAX+1=0,$$

onde:

$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ A=\begin{pmatrix}0 & 2 & 0 \\2 & 0 & 0 \\0 & 0 & 1\end{pmatrix}. $$

Seja:

$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}-\lambda & 2 & 0 \\2 & -\lambda & 0 \\0 & 0 & 1-\lambda\end{pmatrix}=-\lambda^3+\lambda^2+4\lambda-4.$$

As raízes de $P(\lambda)$ são $1$, $2$ e $-2$. Considere os sistemas lineares referentes às raízes $1$ e $2$, $(A-I) X = 0$ e $(A-2I) X = 0$. Uma solução de norma unitária desses sistemas consiste em $U_1=(0,0,1)$ e $U_2=(1/\sqrt{2},1/\sqrt{2},0)$, respectivamente. Sejam $U_3=U_1 \times U_2 = (-1/\sqrt{2},1/\sqrt{2},0)$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $z^2 + 4xy + 1 = 0$ se transforma em:

$$-(x')^2-\dfrac{(y')^2}{1/2}+\dfrac{(z')^2}{1/2}=1,$$

que é a equação de um hipérbolóide de duas folhas.

823

Para o par de vetores $u=(1,2,-2)$ e $v=(3,-2,1)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.

$\textrm{proj}_{u}{v}=\dfrac{-1}{3}(1,2,-2)$.
$v_1=\dfrac{-1}{3}(1,2,-2)$.
$v_2=\dfrac{1}{3}(10,-4,1)$.

1146

Qual é o vetor unitário na direção de $4\vec{i}-12\vec{j}+3\vec{k}$?

$\dfrac{4\vec{i}-12\vec{j}+3\vec{k}}{13}$.

259

Encontre a equação do plano $\pi$ que é perpendicular ao plano $x+3y-z=7$ e contém os pontos $A=(2,0,5)$ e $B=(0,2,-1)$.

Consideremos os vetores $v_1=(1,3,-1)$ (normal ao plano perpendicular) e $v_2=B-A=(-2,2,-6)$. Note que estes vetores estão contidos no plano procurado e não são paralelos, com $v_1\times v_2=(-16,8,8)$. Logo, o plano procurado pode ser descrito por $$\pi: -16x+8y+8z=(-16,8,8)\cdot A=8\Longleftrightarrow -2x+y+z=1. $$

511

Reduza a equação $3x^2+4y^2+z^2-12x-8y-2z+16=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

$\dfrac{(x-2)^2}{1/3}+\dfrac{(y-1)^2}{1/4}+(z-1)^2=1$: elipsóide.

1039

Tome $x'y'$ o sistema de eixos do plano que é a translação do sistema $xy$ para a nova origem $O'=(1,1)$, i.e., $ x'=x-1$ e $y'=y-1$.

Dado o ponto $P=(1,4)$ no sistema $xy$, encontre as coordenadas de $P$ no sistema $x'y'$.
Dado o ponto $A=(2,1)$ no sistema $x'y'$, encontre as coordenadas de $A$ no sistema $xy$.
Considere a reta $\mathcal{L}$ que no sistema $xy$ tem equação $2x - 3y + 4 = 0$. Qual seria a equação de $\mathcal{L}$ no sistema $x'y'$? Mudando-se a equação, muda-se $\mathcal{L}$ de lugar? O desenho muda?
Dada a curva $\mathcal{C}$, do plano, cujos pontos têm coordenadas $(x,y)$, no sistema $xy$, satisfazendo a equação $x^2-4x+y^2-6y=12$, encontre a equação que os pontos de $\mathcal{C}$ com coordenadas $(x',y')$ no sistema $x'y'$ devem satisfazer nas variáveis $x'y'$.

1363

Determine a superfície dada pela representação paramétrica $\sigma(u,v) = (u, u\cos v, u\sin v)$.

Vamos, primeiro, escrever as equações paramétricas $x=u$, $y = u\cos v$ e $z=u\sin v$. Somando os quadrado de $y$ e $z$, temos $$ y^2 + z^2 = u^2\cos^2v+u^2\sin^2v= u^2(\cos^2v+\sin^2v)=u^2=x^2.$$ Assim, somos capazes de eliminar os parâmetros e então a equação em $x$, $y$ e $z$ fica dada por $x^2= y^2+z^2$. O prévio conhecimento da forma reduzida das superfícies quádricas nos permite dizer que se trata de um cone abrindo-se ao longo do eixo $x$.

771

Determine a extremidade ou a origem do segmento orientado quando o mesmo: representa o vetor $v=(-1,0,1)$ e sua origem é o ponto médio entre os pontos $P_1=(1,1,3)$ e $P_2=(-1,1,1)$.

$(-1,1,3)$

1227

Reduza a equação $4x^2+6y^2+4z^2-4xz+1=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

464

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{cccccr}2x_1+&1x_2+&4x_3+&x_4&=&-5 \\2x_1+&8x_2-&10x_3+&8x_4&=&2 \\&&-9x_3+&2x_4&=&2\\4x_1+&1x_2+&6x_3+&5x_4&=&-3\\4x_1+&5x_2-&8x_3+&8x_4&=&-3\\\end{array}\right . .\]

486

Sejam $\mathcal{C}$ a circunferência de equação $x^2+y^2=r^2$ e $P=(x_1,y_1)$ um ponto no exterior da circunferência. Sejam também $P_2=(x_2,y_2)$, $P_3=(x_3,y_3)$ os pontos de $\mathcal{C}$ tais que as retas $l_2$ que passa por $P$ e $P_2$, e $l_3$ que passa por $P$ e $P_3$ são tangentes à circunferência. Então mostre que a reta (secante) que passa por $P_2$ e $P_3$ tem equação $x_1x+y_1y=r^2$. (Sugestão: encontre as equações das retas $l_2$ e $l_3$ e use o fato de que $P$ está em ambas.)

1216

Reduza a equação $x^2 + y^2 + z^2 + 2xy + 2xz - 2yz + x - y + z + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1159

Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores tais que $\cos\alpha_1=1/2$, $\cos\beta_1=\sqrt{3}/2$; e a outra com ângulos diretores tais que $\cos \alpha_2=\dfrac{\sqrt{3}+1}{2\sqrt{2}}$ e $\cos\beta_2=\dfrac{\sqrt{3}-1}{2\sqrt{2}}$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).

$45^\circ$.

374

Calcule o determinante da matriz: $\begin{pmatrix}
\sin\alpha&\cos\alpha \\ \sin\beta&\cos\beta
\end{pmatrix}.$

$\displaystyle \sin(\alpha-\beta)$

1440

Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um ângulo $\theta$. Mostre que, para cada valor de $\theta$, a equação $x^2+y^2=r^2$ é transformada na equação $x'^2+y'^2=r^2$. Dê uma explicação geométrica.

424

Resolver o sistema linear:

\[\left\{\begin{array}{cccccr}2x_1+&1x_2+&4x_3+&x_4&=&-5 \\2x_1+&8x_2-&10x_3+&8x_4&=&2 \\&&-9x_3+&2x_4&=&2\\4x_1+&1x_2+&6x_3+&5x_4&=&-3\\4x_1+&5x_2-&8x_3+&8x_4&=&-3\\\end{array}\right . .\]

$x_1 = -\dfrac{27}{7}, x_2=\dfrac{-5}{7}, x_3 =\dfrac{2}{7} , x_4 =\dfrac{16}{7}.$

991

Considere os pontos $A = (3,-2,8)$, $B = (0,0,2)$ e $C = (2,3,2)$.

Usando vetores, mostre que o triângulo de vértices $A$, $B$ e $C$ é retângulo (Dica: O lado $BA$ é paralelo ao vetor $\stackrel{\longrightarrow}{BA}$).
Determine o ponto $H$ na aresta $AC$ para o qual os segmentos $AC$ e $HB$ são ortogonais ($=$ perpendiculares).
Determine o vetor $\stackrel{\longrightarrow}{AH}$. (Dica: $\stackrel{\longrightarrow}{AH}$ é a projeção ortogonal de $\stackrel{\longrightarrow}{AB}$ sobre $\stackrel{\longrightarrow}{AC}$.)
Calcule a área do triângulo (Dica: área do triângulo = (1/2) de base $\times$ altura).

1442

Suponha que o sistema de coordenadas $x'y'$ tenha sido obtido pela rotação de um sistema de coordenadas $xy$ por um ângulo $\theta$. Explique como podemos encontrar as coordenadas $xy$ de uma reta cuja equação nas coordenadas $x'y'$ seja conhecida.

271

Os seguintes pares de retas $r_1$ e $r_2$ são paralelas ou concorrentes. Encontre uma equação geral do plano que as contém.

$$r_1:\;\begin{cases}y=2x-3\\z=-x+2\end{cases}\ \ \ {\rm e}\ \
\ r_2: \begin{cases}\text{ $\frac{x-1}{3}=\frac{z-1}{-1}$}\\
y=-1.\end{cases}$$

As retas são concorrentes em $P(1,-1,1)$; $\pi: x+y+3z-3=0$.

977

Mostre que a projeção no plano $yz$ da curva correspondente à intersecção das superfícies $x = 1 - y^{2}$ e $x = y^{2} + z^{2}$ é uma elipse. Explique bem seu raciocínio.

1408

Mostre que as duas diagonais do trapézio e a reta que passa pelos pontos médios dos lados paralelos são concorrentes.

1446

Encontre a inclinação da reta tangente à curva paramétrica $x=t/2$, $y=t^2+1$ em $t=-1$ e $t=1$ sem eliminar o parâmetro.
Verifique suas respostas do item anterior eliminando o parâmetro e diferenciando uma função apropriada de $x$.

992

Decompor o vetor $\vec{w} = (-1,-3,-2)$ como soma de dois vetores $\vec{w} = \vec{u} + \vec{v}$, onde $\vec{u}$ é paralelo ao vetor $(0,1,3)$ e $\vec{v}$ é ortogonal a $(0,1,3)$ (Dica: $u$ pode ser escolhido como a projeção de $\vec{w}$ sobre $(0,1,3)$).

$\vec{u}=\left(0,-\frac{9}{10},-\frac{27}{10}\right)^T$ e $\vec{w}=\left(-\sqrt{\frac{10}{59}},-\frac{21}{\sqrt{590}},\frac{7}{\sqrt{590}}\right)^T$

776

Dado um triângulo isósceles, mostre que a mediana relativa à base é a mediatriz (isto é, é perpendicular à base).

Seja o triângulo isósceles $ABC$ onde $M$ é a mediana do segmento $\ AC.$ Então, temos

$\overrightarrow{AM}=\overrightarrow{MC}\Longrightarrow \overrightarrow{AM}=\overrightarrow{BM}-\overrightarrow{BA}=\overrightarrow{BC}-\overrightarrow{BM}\Longrightarrow \overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}.$

Também, temos que $\overrightarrow{AM}.\overrightarrow{MB}=\left\Vert \overrightarrow{BM}\right\Vert ^{2}-
\overrightarrow{BA}-\overrightarrow{MB}$.

Assim, concluímos que $\overrightarrow{AM}. \overrightarrow{MB}=\left\Vert \frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BC}\right) \right\Vert^{2}-\frac{1}{2}\overrightarrow{BA}\left( \overrightarrow{BA}+\overrightarrow{BC}\right) =\frac{1}{4}\left\Vert \overrightarrow{BA}\right\Vert ^{2}+\frac{1}{2}2\overrightarrow{BA}.\overrightarrow{BC}+\frac{1}{4}\left\Vert \overrightarrow{BC}\right\Vert ^{2}-\frac{1}{2}\left\Vert \overrightarrow{BA}\right\Vert ^{2}-\frac{1}{2}\overrightarrow{BA}.\overrightarrow{BC}=\frac{1}{2}\left\Vert \overrightarrow{BA}\right\Vert ^{2}-\frac{1}{2}\left\Vert \overrightarrow{BA}\right\Vert ^{2}=0$.

311

Verifique a posição relativa do seguinte par de retas (isto é, verifique se são paralelas, concorrentes ou reversas):

\[r:(2,4,1) + t(1,-2,3), \ \ \ s:(-1,3,2) + s(4,-1,2) .\]

São concorrentes.

987

Sejam $u=(1,-1,3)$ e $v=(3,-5,6)$ dois vetores. Encontre $\mathrm{proj}_{u+v} (2u-v)$.

$\dfrac{1}{133}(-88,132,-198)^T$

1459

Classifique a superfície $\displaystyle z^2-\dfrac{x^2}{36}-\dfrac{y^2}{25}=1$ como elipsóide, hiperbolóide de uma folha, hiperbolóide de duas folhas, cone elíptico, parabolóide elíptico ou parabolóide hiperbólico.

1366

Construa a curva cujas equações paramétricas são dadas por: $x=t+2$, $y=2t-4$ e $z=1-t$.

363

Sejam $A\in M_{2\times 3}$, $B\in M_{3\times 1}$ e $C\in M_{3\times 3}$. Quais dos produtos existem?

$A\,B$;
$B\,A$;
$A\,B^t$;
$A\,C$;
$A\,C^t$;
$A\,B\,C$;
$A\,C\,B$.

Apenas os produtos 1, 3, 4, 5 e 7estão definidos.

768

Verifique se os seguintes pontos são colineares: $A=(0,1,-1)$, $B=(1,2,0)$ e $C=(0,2,1)$.

Os pontos não são colineares.

1238

Reduza a equação $4x^2+4y^2+9z^2+8xy+12xz+10x+y+4z+1=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

438

Encontre a inversa da matriz abaixo (se existir):

\[\begin{pmatrix}\cos x & \sin x \\ - \sin x & \cos x\end{pmatrix}.\]

\[\begin{pmatrix}\cos x & -\sin x \\ \sin x & \cos x\end{pmatrix}.\]

1085

Identifique a cônica descrita pela equação$7x^2+6xy-y^2-2x+10y-9=0$.

1396

A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).

1411

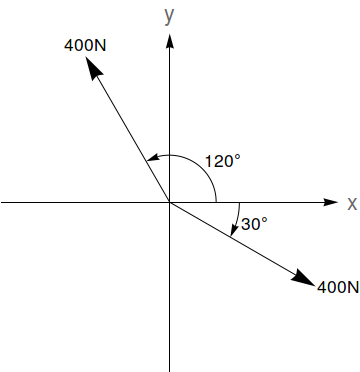
Em um sistema de coordenadas ortogonal, um detonador de bomba está localizado no ponto $P=(2,1,2)$. Para ativá-lo, é preciso acender a extremidade $A=(2,1,1)$ de uma haste de combustível paralela ao vetor $\vec{u}=(1,0,2)$, cuja extremidade $B$ toca o ponto inicial de um caminho de pólvora que segue em linha reta até o detonador. O fogo se propaga com velocidade unitária na haste e no caminho de pólvora e este está contido no plano $\pi : x+2y-z-2=0$. Mostre que a explosão ocorre entre $3$ e $4$ segundos após o início do processo.

824

Mostre que as três bissetrizes de um triângulo se interceptam em um único poto.

Considere o triângulo $ABC$ e bissetriz $B$ e $C$. Então eles cruzam no interior do triângulo que denotaremos por $O.$ Como $O$ está sobre a bissetriz de $B$, ele é equidistante de $AB$ e $BC.$ Mas também está na bissetriz de $C$ de forma que $O$ é equidistante de $AC$ e $BC.$ Assim, $O$ é equidistante aos três lados. Agora considere $\ AO.$ Como $AO$ divide o ângulo $\ BAC$ e passa no ponto (fora do vértice) equidistante de $AB$ e $AC$, será bissetriz de $BAC.$

876

A área do triângulo $ABC$ é $\sqrt{6}$. Sabendo que $A = (2,1,0), \; B = (-1,2,1)$ e que o vértice $C$ está no eixo $Y$, encontre as coordenadas de $C$.

Como $C$ está sobre o eixo $Y$, vamos escrever $C=(0,y,0)$. Pela definição de área através do produto vetorial, segue que \begin{align*} 6 = \mathrm{area}^2 & = \frac{1}{4}\|(A-B)\times (C-B)\|^2 \\ & = \frac{1}{4}\|(3,-1,-1)\times (1,y-2,-1)\|^2 \\ & = \frac{1}{4}\|(y-1,2,3y-5)\|^2 \\ & = \frac{1}{4}\left( 10y^2-32 y+30\right). \end{align*} Ou seja, ficamos com $\displaystyle 10y^2-32y+6=0$, cujas raízes são $y=3$ e $y=\frac{1}{5}$. Portanto, podemos ter $C=(0,3,0)$ ou $C=(0,\dfrac{1}{5},0)$.

1149

Um vetor no espaço tem dois de seus ângulos diretores dados: $\alpha=30^\circ$ e $\beta=60^\circ$. Ache o outro ângulo diretor e faça um esboço do vetor. Quantas respostas existem? (Sugestão: use as fórmulas de cosseno diretor).

$90^\circ$.

979

Mostre que o segmento que une os pontos médios de 2 lados de um triângulo é paralelo ao terceiro lado e é igual a sua metade.

Considere o triângulo $ABC,$ sendo $M$ o ponto médio do lado $AC$ e $N$ o do lado $BC.$ Assim, podemos escrever $\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\frac{1}{2} \overrightarrow{AC}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2} \overrightarrow{AB}.$

Portanto, concluímos que $MN//AB$ e $\left\Vert \overrightarrow{MN}\right\Vert =\left\Vert \overrightarrow{AB}\right\Vert .$

493

Encontre uma equação em coordenadas cartesianas para a curva cuja equação em coordenadas polares é dada por $r=\frac{6}{2-3sen\theta}$.

1087

Considere a forma quadrática $2x^2+8xy+2y^2+x+y-9=0$. Escrevendo-a numa base conveniente, determine:

qual o eixo que contém o(s) foco(s);
qual é a translação e a rotação associadas.

361

Verdadeiro ou Falso? Justifique.

Se $A=\left(\begin{array}[c]{rr}-2 & 1\\3 & 2\end{array}\right) $, então $A^{2}=\left(\begin{array}[c]{rr} 4 & 1\\9 & 4\end{array}\right) $.
$(A+B)^{t}=B^{t}+A^{t}.$
Se $AB=0$, então $A=0$ ou $B=0$.
Se $AB=0$, então $BA=0$.
Se podemos efetuar o produto $AA$, então $A$ é uma matriz quadrada.
$(-A)(-B)=-(AB).$
Sejam $A$ e $B$ duas matrizes. Se $A=0$, então $BA$ sempre existe.

Falso, pois efetuando a multiplicação temos que
\[A^2=7I_2.\]
Verdadeiro. Não confundir com a transposta do produto.
Falso! Como contra-exemplos, podemos tomar:
\[A=\left(\begin{array}{cc} 1 & 1 \\ 0 & 0 \end{array}\right) \quad\text{e}\quad B=\left(\begin{array}{cc} 1 & 0 \\ -1 & 0 \end{array}\right).\] Note que $AB=\mathbf{0}$, não sendo nenhuma delas nula.
Falso também. Ainda pegando os dois exemplos anteriores, note que
\[BA=\left(\begin{array}{cc} 1&0\\-1&0\end{array}\right)\left(\begin{array}{cc} 1&1\\0&0\end{array}\right) = \left(\begin{array}{cc} 1 & 1\\ -1 & -1 \end{array}\right).\]
Verdadeiro. Supondo que $A$ fosse $m\times n$, como o produto $A\cdot A$ existe, isso implica que devemos ter $m=n$.
Falso, pois
\[(-A)(-B)=[(-1)A][(-1B)]=(-1)[A(-B)]=(-1)[A(-1)B]=(-1)(-1)[AB]=AB.\]
Falso. Note que, para que exista $BA$, o número de colunas de $B$ dever ser igual ao número de linhas de $A$ que, por sua vez, não tem nada a ver com ser nula. Por exemplo, considerando $A$ como sendo uma matriz $2\times 3$ nula e $B$ uma matriz $2\times 3$ qualquer, temos que o produto $BA$ não fica definido.

1638

Às vezes o gráfico de uma equação quadrática é uma reta, um par de retas ou até mesmo um único ponto. Nos referimos a tais gráficos como cônicas degeneradas. É também possível que a equação não seja satisfeita para nenhum valor real das variáveis, caso este no qual não existe um gráfico e dizemos tratar-se de uma cônica imaginária. Nos itens abaixo, identifique a cônica com a equação dada, dizendo se é degenerada ou imaginária. Quando possível, esboce também o gráfico.

$\displaystyle x^2+2xy+y^2=0$;
$\displaystyle x^2-2xy+y^2+2\sqrt{2}x-2\sqrt{2}y=0$;
$\displaystyle 2x^2+2xy+2y^2+2\sqrt{2}x-2\sqrt{2}y+6=0$.

503

Para cada um dos pontos abaixo faça a mudança de coordenadas de polares para cartesianas:

$ (3,\frac{\pi}{4})$,
$ (6,\frac{2\pi}{3})$,
$ (-2,\frac{\pi}{6})$,
$ (4,-36^{o})$,
$ (-3,150^{o})$,
$ (1,\frac{187\pi}{6})$,
$ (-2,-\frac{16\pi}{3})$.

1046

Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $x^2-16y^2 + 8x +128y -256 = 0$.

Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.

1036

Considere o plano com o sistema cartesiano canônico $xy$ e faça uma rotação de um ângulo $\theta$ obtendo um novo sistema $\overline{x}$ $\overline{y}$. Seja $P$ um ponto do plano.

Se $P=(2,2)$ no sistema $xy$ e $\theta=\pi/3$, encontre as coordenadas de $P$ no sistema $\overline{x}$ $\overline{y}$.
Se $P=(2,2)$ no sistema $\overline{x}$ $\overline{y}$ e $\theta=\pi/3$, encontre as coordenadas de $P$ no sistema $xy$.
Transforme a equação $x^2+y^2=4$ para o sistema $\overline{x}$ $\overline{y}$.
Suponha que $0<\theta <\pi/2$ e que $a=\tan\theta$ ($a$=tangente de $\theta$). Transforme a equação $y=ax$ para o sistema $\overline{x}$ $\overline{y}$.

1474

Considere o sistema linear:

$$ \left\{ \begin{array}{rcrcrcc}a x &+& b y &+& cz & = & c\\(\alpha a) x &+& (\alpha b)y &+& (\alpha c) z & = & d \\(\beta a) x &+& (\beta b)y &+& (\beta c) z & = & e\end{array} \right. ,$$

onde $a$, $b$, $c$, $d$, $e$, $\alpha$ e $\beta$ são números reais.

Mostre que, se $d=\alpha c$ e $e=\beta c$, o sistema tem infinitas soluções em função de um único parâmetro real.
Mostre que, se $d=\alpha c$ e $e\neq\beta c$, ou, se $d\neq\alpha c$ e $e=\beta c$, o sistema tem infinitas soluções em função de dois parâmetros reais.
Mostre que, se $d\neq\alpha c$ e $e\neq\beta c$, o sistema tem solução única.

257

Encontre a equação do plano $\pi$ que passa pelos pontos $A=(0,0,2)$, $B=(2,4,1)$ e $C=(-2,3,3)$

$\pi:7x+14z=28$

1023

Determinar a equação reduzida da seguinte cônica: hipérbole com assíntotas $y=\pm x$ e um ponto da hipérbole $P=(2,7)$.

816

Mostre que se $X\;\mbox{e}\; Y$ são dois vetores tais que $X+Y$ é ortogonal a $X-Y$, então $\left\|X\right\|\;=\;\left\|Y\right\|$.

$X+Y$ ortogonal a $X-Y$ $\Rightarrow$ $(X+Y)\cdot(X-Y)=0$.
$(X+Y)\cdot(X-Y)=0$ $\Rightarrow$ $X\cdot X-X\cdot Y+Y\cdot X - Y\cdot Y=0\Rightarrow X\cdot X- Y\cdot Y=0 \Rightarrow X\cdot X= Y\cdot Y\Rightarrow ||X||^2=||Y||^2$ e, pela não negatividade da norma, $||X||=||Y||$.

952

Identifique a quádrica definida pela equação reduzida $\dfrac{x^2}{10}+\dfrac{y^2}{9}+\dfrac{z^2}{5}=1$ e esboce seu gráfico.

1406

No tetraedro $ABCD$, seja $X$ um ponto tal que $\vec{AX}$ = $m\vec{XD}$. Determine os valores de $m$ para os quais os vetores $\vec{AX}+\vec{AC}$, $\vec{BX}+\vec{BC}$ e $(1-m)\vec{BC}+\vec{AB}$ sejam linearmente independentes.

1347

Suponha que uma partícula se mova no espaço e tenha posição $H(t) = (\cos(t), \sin(t), t)$ no instante $t$ (hélice cilíndrica). Esboce a trajetória da partícula. Qual a sua direção no instante $t$?

1232

Reduza a equação $x^2+4y^2+9z^2-4xy+6xz-12yz+4x-8y+12z+4=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1431

Como é afetado o formato de uma hipérbole quando sua excentricidade tende a $1$? E quando tende a $+\infty$? Esboce algumas figuras para ilustrar suas conclusões.

815

Mostre que o vetor $\displaystyle p=b-\frac{a\cdot b}{a\cdot a}\;a$ é perpendicular ao vetor $a$.

$\displaystyle p\cdot a=b\cdot a-\frac{a\cdot b}{a\cdot a}\;a\cdot a=b\cdot a-\frac{a\cdot b}{||a||^2}||a||^2=b\cdot a-a\cdot b\,\frac{||a||^2}{||a||^2}=b\cdot a-a\cdot b=0$.

429

Resolver o sistema linear: \[\left\{\begin{array}{ccccccccccr}x_1&-&2x_2&+&3x_3&+&2x_4&+&x_5&=&10 \\2x_1&-&4x_2&+&8x_3&+&3x_4&+&10x_5&=& 7 \\3x_1&-&6x_2&+&10x_3&+&6x_4&+&5x_5&=&27\\\end{array}\right..\]

$x_3 = \dfrac{-19+2 x1- 4 x2}{3}, x_4 = \dfrac{ 41 - 4 x_1 + 8 x_2}{3}, x_5 = \dfrac{5- x_1+2 x_2}{3}, \forall x_1, x_2\in \mathbb{R}$.

226

Dada a reta $r:\;(x,y,z)=(3+t,1-2t,-1+2t)$, determinar as equações reduzidas das retas projeções de $r$ sobre os planos $xOy$ e $xOz$.

$r_{xOy}=(3+t',1-2t',0),\;r_{xOz}=(3+t,0,-1+2t)$

1226

Reduza a equação $2x^2+y^2+2z^2+2xy-2yz=1 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1034

Um homem parado num ponto $Q=(x,y)$ ouve o estampido de um rifle localizado no ponto $P_1=(1000,0)$ e o som do projétil atingindo o alvo no ponto $P_2=(-1000,0)$ ao mesmo tempo. Se o projétil viaja a $2000$ pés/s e o som a $1100$ pés/s, ache uma equação relacionando $x$ e $y$.

1358

Forneça equações paramétricas para $\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$, indicando os valores para o seu parâmetro $t$. Esboce suas equações paramétricas.

1395

A resultante de $n$ forças $\vec{F_1}, \vec{F_2}, \ldots, \vec{F_n}$ (que podem ser representadas por vetores) é dada pela soma $\vec{F_1}+\vec{F_2}+\ldots,\vec{F_n}$. A magnitude de uma força $\vec{F}$ é dada pela norma $\|\vec{F}\|$. Dadas as forças na figura abaixo, determine a magnitude da força resultante e o ângulo que ela faz com o eixo $x$ positivo (sugestão: use a Lei dos Cossenos e a Lei dos Senos).

881

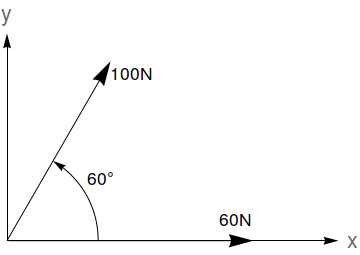
Mostre que se

$$u= u_a a + u_b b + u_c c,$$

$$v = v_a a + v_b b + v_c c,$$

$$w= w_a a + w_b b + w_c c,$$

então

$$u\cdot(v\times w)=\det\left(\begin{array}{ccc} u_a & u_b & u_c \\ v_a & v_b & v_c \\ w_a & w_b & w_c \\\end{array}\right)[a\cdot(b\times c)].$$

Se $a=i$, $b=j$ e $c=k$, como fica esta fórmula?

1240

Reduza a equação $3x^2+3y^2+z^2-2xy-4x+2y+6z+5=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1150

Um vetor no espaço tem dois de seus ângulos diretores dados: $\alpha=45^\circ$ e $\beta=120^\circ$. Ache o outro ângulo diretor e faça um esboço do vetor. Quantas respostas existem? (Sugestão: use as fórmulas de cosseno diretor).

$60^\circ$, $120^\circ$. Existem duas respostas.

1370

Construa a curva cujas equações paramétricas são dadas por: $x=4\sin^2\theta$, $y=2\cos\theta$ e $z=2\sin\theta$.

307

Encontre a equação da reta $r$ que passa por $(1,-2,3)$, é concorrente com a reta $\left\{\begin{array}{ccr}x &=& 2 + 3t\\ y &=& 1 + 2t\\z &=& -1\end{array}\right.$ e tem vetor diretor ortogonal ao vetor $(1,-3,1)$.

761

Mostre que: se um triângulo tem duas medianas iguais então ele é isósceles.

Seja o triângulo $\ ABC$, $M$ o ponto médio de $\overrightarrow{BN}$ e $N$ o de $\overrightarrow{AC}.$ Seja também $P$ a interseção de $\overrightarrow{BN}$ e $\overrightarrow{AM},$ e por hipótese, temos $\left\Vert \overrightarrow{BN}\right\Vert =\left\Vert\overrightarrow{AM}
\right\Vert .$ Observe que os triângulos $NPM$ e $APB$ são isósceles. Observe também que como $\overrightarrow{MN}$ é paralelo a $\overrightarrow{AB}$ os ângulos $N\widehat{P}A$ e $M\widehat{P}B$ são iguais. Assim, pela lei dos cossenos, temos

$\left\Vert \overrightarrow{AN}\right\Vert ^{2}=\left\Vert \overrightarrow{PN}-\overrightarrow{PA}\right\Vert ^{2}=\left\Vert \overrightarrow{PM}-\overrightarrow{PB}\right\Vert ^{2}=\left\Vert \overrightarrow{BM}\right\Vert ^{2}$

Como, $2\left\Vert \overrightarrow{AN}\right\Vert =\left\Vert \overrightarrow{AC}\right\Vert $e $2\left\Vert \overrightarrow{BM}\right\Vert =\left\Vert \overrightarrow{BC}\right\Vert ,$ então $\left\Vert \overrightarrow{AN}\right\Vert =\left\Vert \overrightarrow{BC}\right\Vert ,$ e portanto, o triângulo é isósceles.

391

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
5&6&-3\\ -1&0&1\\ 1&2&1
\end{pmatrix}.
$

$x=2$ é uma raíz tripla.

1477

Considere o polinômio $p(\lambda)=\det(A-\lambda I_3)$, em que$$ A= \left[\begin{array}{ccc} a & d/2 & e/2 \\ d/2 & b & f/2 \\ e/2 & f/2 & c \end{array}\right]. $$

Sejam $\alpha$ e $\beta$ raízes reais (pois $A$ é simétrica) distintas de $p(\lambda)$. Mostre que se $X_1$ é solução de $(A-\alpha I_2)X=\vec{0}$ e $X_2$ é solução de $(A-\beta I_2)X=\vec{0}$, então $X_1$ e $X_2$ são ortogonais. (Sugestão: Mostre que $\alpha X_1\cdot X_2=\beta X_1\cdot X_2$)
Mostre que se $p(\lambda)$ tem raízes reais distintas, então sempre existe uma matriz $Q$ tal que $$ Q^tAQ = \left[\begin{array}{ccc} a' & 0 & 0 \\ 0 & b' & 0 \\ 0 & 0 & c' \end{array}\right]. $$ Conseqüentemente, a mudança de coordenadas dada por $X=QX'$ transforma a equação $$ ax^2+by^2 + cz^2 + dxy+exz+fyz+gx+hy+iz+j=0 $$ na equação $$a'x'^2+b'y'^2+c'z'^2+g'x'+h'y'+i'z + j=0, $$ onde os termos "cruzados" $xy$, $xz$ e $yz$ são eliminados.

319

Para o par de retas $r$ e $r^{\prime}$ abaixo encontre o ponto de interseção, $r\cap r^{\prime}$, se existir. E nos casos em que a interseção é vazia decida se elas são paralelas ou reversas.

$r:$ $(x,y,z) = (2,-3,-2) + t(4,-1,3) \;\;\;$ e $r^{\prime}:$ $\left\{ \begin{array}{c} 3x+2y+z=-2 \\ x-y+2z=1\end{array} \right. .$

Usando escalonamento, podemos obter que a intersecção ocorre para $t=0$. Assim, o ponto de intersecção consiste em $(2,-3,-2)$.

458

Sejam $A$ uma matriz $n\times m$, ${\bf 0}$ a matriz nula $m\times 1$ e $B$ uma matriz $m\times 1$.

Sabendo que $Y_{1}$ e $Y_{2}$ são duas matrizes $m\times 1$ que são soluções do sistema $AX = {\bf 0}$ e que $a$ e $b$ são dois números reais, mostre que $Y_{3} = aY_{1} + bY_{2}$ também é solução do sistema $AX = {\bf 0}$.
Sabendo que $X_{1}$ e $X_{2}$ são duas matrizes $m\times 1$, que são soluções do sistema $AX = B$, mostre que $X_{3} = X_{1} - X_{2}$ é uma solução do sistema $AX = {\bf 0}$.
Sabendo que $U$ e $V$ são duas matrizes $m\times 1$ onde $U$ é uma solução do sistema $AX = {\bf 0}$ e $V$ é uma solução do sistema $AX = B$ mostre que $Z = U + V$ também é solução do sistema $AX = B$.

1058

Decida se a cônica $C$ determinada pela equação $9y^2-9x^2+6x=1$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

980

Demonstre que se $\alpha$ e $\beta$ são números reais tais que $\alpha(2,3) + \beta(3,2) = \vec{0}$, então $\alpha = 0$ e $\beta = 0$.
Qual a conclusão geométrica que podemos tirar do item acima?

$\alpha(2,3) + \beta(3,2) = \vec{0}$ resulta no sistema cujas equações são: $2\alpha+3\beta=0$ e $3\alpha+2\beta=0$.
Resolvendo o sistema, obtemos $\alpha=\dfrac{-3}{2}\beta=\dfrac{-2}{3}\beta$ que só pode ser satisfeita se $\beta=0$. E, portanto, $\alpha=0$.
Podemos concluir que esses dois vetores são linearmente independentes, isso significa que eles tem direções distintas.

1053

Decida se a cônica $C$ determinada pela equação $\displaystyle 9x^2-18x+9y^2-6y=10$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

491

Encontre uma equação em coordenadas cartesianas para a curva cuja equação em coordenadas polares é dada por $r=\frac{5}{2-2cos\theta}$.

Usando a definição de coordenadas cartesianas, obtemos: $\displaystyle 2+\frac{5}{x-\sqrt{x^2+y^2}}=0. $

1466

Use um recurso computacional para investigar como a família de curvas polares $r=1+a\cos(n\theta)$ é afetada pela mudança nos valores de $a$ e $n$, sendo $a$ um número real positivo e $n$ um inteiro positivo.

409

Resolver o sistema linear:

\[\left\{\begin{array}{rrrrl}4x&+3y&-z&+t&=4\\x&-y&+2z&-t&=0\\5x&+2y&+z&&=4\end{array}\right. . \]

$z = 4 - 5 x - 2 y, t = 8 - 9 x - 5 y, \forall x, y \in \mathbb{R}$.

433

Resolver o sistema linear:

\[ \left\{\begin{array}{rrrrl}x&+5y&+4z&-13z&=3\\3x&-y&+2z&+5t &=2\\2x&+2y&+3z&-4t&=1\end{array}\right. .\]

Esse sistema linear não possui solução.

371

Determine todos os valores de $\lambda$ para os quais $\det(A-\lambda I_3)=0$, onde

\[
A = \left( \begin{array}{ccc}
2 & 2 & 3 \\
1 & 2 & 1 \\
2 & -2 & 1
\end{array}\right) .\]

$\lambda=-1$, $2$ ou $4$.

296

Um quadrado $ABCD$ tem a diagonal $BD$ contida na reta $\displaystyle \begin{cases} x=1\\ y=z\end{cases}$. Sabendo que $A=(0,0,0)$, determine os vértices $B$, $C$ e $D$.

1391

Seja $f: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ uma função definida por $f(x,y) = (2x+y,x-y)$. Ache o(s) valor(es) de $\lambda$ para que a equação $f(x,y) = \lambda(x,y)$ possua solução $(x,y) \neq 0$.

$\lambda=\dfrac{1 + \sqrt{13}}{2}$ ou $\lambda=\dfrac{1 - \sqrt{13}}{2}$.

439

Encontre a inversa da matriz abaixo (se existir):

\[\begin{pmatrix}1 & 0 & 0 \\ 0 & 5 & 0 \\0 & 0 & 6\end{pmatrix}.\]

\[\begin{pmatrix}1 & 0 & 0 \\ 0 & 1/5 & 0 \\0 & 0 & 1/6\end{pmatrix}.\]

1436

Mostre que o elipsóide obtido girando uma elipse com semi-eixo maior $a$ e semi-eixo menor $b$ em torno do eixo menor tem área de superfície

$$ S= 2\pi ab\left(\dfrac{a}{b}+\dfrac{b}{c}\ln\dfrac{a+c}{b}\right), $$

onde $c=\sqrt{a^2-b^2}$.

251

Determine a equação do plano $\pi_1$ que passa por $A = (10/3, 1,-1), B = (1, 9/2,-1) \text{ e } C = (1,-1, 5/6)$.
Determine a equação do plano $\pi_2$ que passa por $D = (-1, 4,-1), E = (3/2,-1, 10)$ e é paralelo ao eixo $z$.
Escreva as equações paramétricas para a reta $r$, interseção dos planos $\pi_1$ e $\pi_2$.
Qual o ângulo entre os planos $\pi_1$ e $\pi_2$?
Qual o ponto $P$ de $\pi_1$ que está mais próximo da origem? (Sugestão: este ponto é tal que $ \overrightarrow{OP}$ é ortogonal ao plano $\pi_1$.)

272

Os seguintes pares de retas $r_1$ e $r_2$ são paralelas ou concorrentes. Encontre uma equação geral do plano que as contém.

$$r_1:\;\begin{cases}x=1+2t\\
y=-2+3t\\ z=3-t\end{cases}\ \ \ {\rm e}\ \ \ r_2: \begin{cases}x=1+2t\\
y=-2-t\\ z=3+2t.\end{cases}$$

As retas são concorrentes em $P(1,-2,3)$; $\pi: 5x-6y-8z+7=0$.

473

Considere o subconjunto de vetores $\mathcal{B} =\{(1,1,0),(0,1,1),(1,0,1)\}$.

Mostre que $\mathcal{B}$ é uma base para $\mathbb{R}^{3}$.
Encontre a matriz de mudança de coordenadas $A$ da base canônica $\{i,j,k\}$ de $\mathbb{R}^{3}$ para a base $\mathcal{B}$. Qual é matriz de mudança de coordenadas $A^{\prime}$ da base $\mathcal{B}$ para a base canônica?
Quais são as coordenadas dos vetores canônicos $i,j$ e $k$ em relação à base $\mathcal{B}$?
Se o ponto $P$ tem coordenadas $(1,-2,5)$ no sistema $\{O,i,j,k\}$, quais são as coordenadas de $P$ no sistema $\{O,\mathcal{B}\}$?

Pois $\det\left[\begin{array}[c]{ccc}1 & 0 & 1\\1 & 1 & 0\\0 & 1 & 1\end{array}\right] =2\neq0$.
$A^{\prime}=\left[\begin{array}[c]{ccc}1 & 0 & 1\\1 & 1 & 0\\0 & 1 & 1\end{array}\right] ;A=(A^{\prime})^{-1}=\left[\begin{array}[c]{rrr}\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\\-\overset{}{\frac{1}{2}} & \frac{1}{2} & \frac{1}{2}\\\overset{}{\frac{1}{2}} & -\frac{1}{2} & \frac{1}{2}\end{array}\right] $.
São as colunas de $A$, respectivamente: $\left(\frac{1}{2},-\frac{1}{2},\frac{1}{2}\right) ,\left( \frac{1}{2},\frac{1}{2},-\frac{1}{2}\right) $ e $\left( -\frac{1}{2},\frac{1}{2},\frac{1}{2}\right) $.
$(-3,1,4).$

766

Dados os pontos $A=(1,0,1)$, $B=(-1,1,1)$ e $C=(0,1,2)$.

Determine o ponto $D$ tal que $A$, $B$, $C$ e $D$ sejam os vértices consecutivos de um paralelogramo.
Determine o ponto médio entre $A$ e $C$ e o ponto médio entre $B$ e $D$.

$ D=(2,0,2)$
$\dfrac{1}{2}(A+C)=(\dfrac{1}{2},\dfrac{1}{2},\dfrac{3}{2})=\dfrac{1}{2}(B+D)$

258

Encontre a equação do plano $\pi$, sabendo que $C=(-5,1,2)\in \pi$ e $\pi$ é perpendicular à reta que passa pelos pontos $A=(2,2,-4)$ e $B=(7,-1,3)$.

Podemos tomar $B-A=(5,-3,7)$ como vetor normal ao plano e, sendo $(B-A)\cdot C=-25-3+14=-14$, segue que $$\pi:5x-3y+7z=-14.$$

233

Seja $\pi $ o plano que contém as retas

\[
r_{1}:\left\{
\begin{array}{ccc}
x & \;=\; & 2t \\
y & \;=\; & t \\
z & \;=\; & 2-t
\end{array}
\right. \mathrm{onde}\ \;\;t\in \Bbb{R}\;\;\;\;\ \ \ \ \ \ \mathrm{e}\ \ \ \
\ \ \;\;r_{2}:\left\{
\begin{array}{ccc}
z & \;= & \;2 \\
x & \;= & y
\end{array}
\right.
\]

Determine a equação de $\pi $.
Escreva o vetor $\vec{V}=2\vec{\imath}+1\vec{\jmath}+2\vec{k}$ como a soma de 2 vetores $\vec{U_{1}}$ e $\vec{U_{2}}$, sendo $\vec{U_{1}}$ paralelo a $\pi $ e $\vec{U_{2}}$ ortogonal a $\pi $.

$x-y+z=2.$
$\overrightarrow{U}_{1}=(1,2,1)$ e $\overrightarrow{U}_{2}=(1,-1,1).$

1379

Um construtor tem contratos para construir 3 estilos de casa: moderno, mediterrâneo e colonial. A quantidade de material empregada em cada tipo de casa é dada pela tabela:

\[
\begin{array}{lccccc}
& \text{Ferro} & \text{Madeira} & \text{Vidro} &
\text{Tinta} & \text{Tijolo}\\
\text{Moderno} & 5 & 20 & 16 & 7 & 17\\
\text{Mediterrâneo} & 7 & 18 & 12 & 9 & 21\\
\text{Colonial} & 6 & 25 & 8 & 5 & 13
\end{array}
\]

Se ele pretende construir 5, 7 e 12 casas dos tipos moderno, mediterrâneo e colonial, respectivamente, quantas unidades de cada material serão empregadas?
Suponha que os preços por unidade de ferro, madeira, vidro, tinta e tijolo sejam, respectivamente, 15, 8, 5, 1 e 10. Qual é o preço unitário de cada tipo de casa?
Qual e o custo total do material empregado?

As quantidades de ferro, madeira, vidro, tinta e tijolo serão 146, 526, 260,158 e 388, respectivamente.
O preço unitário dos tipos moderno, mediterrâneo e colonial serão 492, 528 e 465, respectivamente.
O custo total do material empregado para construir 5 casas do estilo moderno, 7 casas do estilo mediterrâneo e 12 casas do estilo colonial é 11736.

1213

Reduza a equação $x^2 - y^2 + z^2 + 2xz - 2y + 1 = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

A equação da quádrica $x^2 - y^2 + z^2 + 2xz - 2y + 1 = 0$ pode ser escrita em forma matricial:

$$X^tAX+KX-6=0,$$

onde:

$$X=\begin{pmatrix}x \\ y \\ z\end{pmatrix}, \ K=\begin{pmatrix}0 & -2 & 0\end{pmatrix}, \ A=\begin{pmatrix}1 & 0 & 1 \\0 & -1 & 0 \\1 & 0 & 1\end{pmatrix}. $$

Seja:

$$P(\lambda)=\det(A-\lambda I)=\det\begin{pmatrix}1-\lambda & 0 & 1 \\0 & -1-\lambda & 0 \\1 & 0 & 1-\lambda\end{pmatrix}=-\lambda^3+\lambda^2+2\lambda.$$

As raízes de $P(\lambda)$ são $0$, $2$ e $-1$. Considere os sistemas lineares referentes às raízes $0$ e $2$: $A X = 0$ e $(A-2I)=0$. Uma solução de norma unitária desses sistemas são $U_1=(1/\sqrt{2},0,-1/\sqrt{2})$ e $U_2=(1/\sqrt{2},0,-1/\sqrt{2})$, respectivamente. Sejam $U_3=U_1 \times U_2 = (0,-1,0)$, $Q=(U_1,U_2,U_3)$ e $X'=\begin{pmatrix}x' \\ y' \\ z'\end{pmatrix}.$ Dessa forma, com a mudança de coordenadas dada por $X=QX'$, a equação $x^2 - y^2 + z^2 + 2xz - 2y + 1 = 0$ se transforma em:

$$\dfrac{(z'-1)^2}{2}-(y')2=1,$$

que é a equação de um cilindro hiperbólico.

1077

Considere a forma quadrática $2x^2+8xy+2y^2+x+y-9=0$. Escreva-a numa base conveniente e identifique qual é a cônica e seus paramêtros associados.

1368

Construa a curva cujas equações paramétricas são dadas por: $x=2t$, $y=4t^2$ e $z=t$.

494

Encontre uma equação em coordenadas cartesianas para a curva cuja equação em coordenadas polares é dada por $r^2=cos\theta$.

764

Demonstre que o segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo às bases e seu comprimento é a média aritmética dos comprimentos das bases.

Seja o trapézio $ABCD$, onde $\overrightarrow{AB}$ é a base menor, e $\overrightarrow{DC}$ é a base maior. Seja $M$ o ponto médio de $\overrightarrow{AD}$ e $N$ o de $\overrightarrow{BC}.$ Assim, temos

$\overrightarrow{MN}=\overrightarrow{NB}+\overrightarrow{BA}+\overrightarrow{AM},$ $\overrightarrow{MN}=\overrightarrow{NC}+\overrightarrow{CD}+\overrightarrow{DM}.$ Portanto, $2\overrightarrow{MN}=\overrightarrow{BA}+\overrightarrow{CD}.$

513

Reduza a equação $4x^2-8x-9y^2+6y-36z+3=0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

$9z-2=(x-1)^2-\dfrac{(3y-3)^2}{4}$: parabolóide hiperbólico.

763

Sejam $\vec{OA}$ e $\vec{OB}$ dois vetores não colineares no espaço. Qual o conjunto dos pontos $P$ tais que $\vec{OP} = \lambda\vec{OA}+(1-\lambda)\vec{OB}$?

Trata-se da reta passando pelos pontos $A$ e $B$.

1644

Mostre que o conjunto dos pontos do espaço que satisfazem uma equação da forma $f(x,y)=0$ ou $f(x,z)=0$ ou $f(y,z)=0$ representa uma superfície cilíndrica que tem retas geratrizes paralelas ao eixo cuja variável não aparece na equação. Equação esta que é também a equação da curva diretriz no plano coordenado correspondente às variáveis que aparecem na equação.

364

Calcule os produtos:

$\begin{pmatrix}\phantom{-}3 & 1\\ -1 &2\end{pmatrix} \cdot \begin{pmatrix}\phantom{-}0 & 5\\ -1 &6\end{pmatrix}$;
$\begin{pmatrix}\phantom{-}3\\ -1\\ \phantom{-}2\end{pmatrix}\cdot
\begin{pmatrix}2 & -6 & 7\end{pmatrix}$;
$\left(\begin{array}{ccc}1 & -4 & 5\end{array}\right)\cdot
\left(\begin{array}{c}\phantom{-}3\\ \phantom{-}4\\
-1\end{array}\right)$;
$A\cdot A^t$, onde $A=\begin{pmatrix}1&2&3\\ 3&2&1\end{pmatrix}$;
$\begin{pmatrix}2& -4 & 6\\ 5 &\phantom{-}2 & 7 \\ 1& \phantom{-}0&4 \end{pmatrix} \cdot \begin{pmatrix}5& 0 & \phantom{-}0\\ 0 &2 & \phantom{-}0 \\ 0& 0&-1\end{pmatrix}$;
$\begin{pmatrix}2&-1&3 \\ 0&\phantom{-}1&2\end{pmatrix}\cdot \begin{pmatrix}-2&\phantom{-}1\\ \phantom{-}0&\phantom{-}2\\ \phantom{-}1&-1\end{pmatrix}\cdot\begin{pmatrix}2 & -1\\ 3 & \phantom{-}0\end{pmatrix}$;
$\begin{pmatrix} \cos \alpha &- \sin \alpha \\ \sin \alpha & \phantom{-}\cos \alpha \end{pmatrix} \cdot \begin{pmatrix}
\cos \alpha & -\sin \alpha \\ \sin \alpha& \phantom{-}\cos \alpha \\
\end{pmatrix}$.

\[\left(\begin{array}{cc} -1 & 21 \\ -2 & 7 \end{array}\right);\]
\[\left(\begin{array}{ccc} 6 & -18 & 21 \\ -2 &6 & -7 \\ 4 & -12 & 14 \end{array}\right);\]
$\displaystyle -18;$
\[\left(\begin{array}{cc} 14 & 10 \\ 10 & 14\end{array}\right);\]
\[\left(\begin{array}{ccc} 10 & -8 & -6\\ 25 & 4 & -7\\ 5& 0 -4 \end{array}\right);\]
\[\begin{pmatrix} -11 & 1\\ 4 &-2 \end{pmatrix};\]
\[\begin{pmatrix} \cos(2\alpha) & -\sin(2\alpha) \\ \sin(2\alpha) & \cos(2\alpha) \end{pmatrix}.\]

721

Encontre a equação dos planos que contém a reta $r$ e são tangentes à esfera $S$, dados por:

$r:\dfrac{x+6}{2}=y+3=z+1$ e $S:x^2+y^2+z^2-4x+2y-4z+4=0$.

1604

Os extremos de uma corda elástica com um nó em $K(x,y)$ são presos a um ponto fixo $A(a,b)$ e um ponto $P$ sobre a borda de um pneu de raio $r$ centrado em $(0,0)$. Conforme o pneu gira, $K$ traça uma curva $C$. Encontre a equação desta curva. Assuma que a corda permanece presa e estica uniformemente (ou seja, a razão $\alpha:=|KP|/|AP|$ é constante).

706

Identifique o círculo $x^2+y^2-4x+6y=12$, dando o seu centro e raio.

Centro igual $(2,-3)$ e com raio $5$.

365

Sejam
$A= \left( \begin{array}{ccc}1 & -2 & -1\\1 & 0 & -1\\4 & -1 & 0\end{array}\right)$ e $X= \left( \begin{array}{c}x\\y\\z\\\end{array}\right)$.

Verifique que: $xA_1+yA_2+zA_3=AX$, sendo $A_j$ a $j$-ésima coluna de $A$, para $j=1$, 2, 3.
Verifique que a segunda coluna de $C=A^2$ é $C_2=-2A_1 - A_3$.
Tente generalizar o que foi feito em a) e b) para a seguinte situação: Sejam $A$ uma matriz $m\times n$, $B$ uma matriz $n\times k$ e $C=AB$. Se $C_j$ é a $j$-ésima coluna de $C$, encontre $C_j$ em termos das $n$ colunas de $A$ e da $j$-ésima coluna de $B$.

260

Encontre a equação do plano $\pi$ que é perpendicular a cada um dos planos $x-y-2z=0$ e $2x+y-4z-5=0$ e contém o ponto $A=(4,0,-2)$.

$$\pi: 2x+z=6$$

983

Sejam $A=(2,1,2)$, $B=(1,0,0)$ e $C=(1+\sqrt 3,\sqrt 3,-\sqrt 6)$ três pontos no espaço. Calcule os ângulos do triângulo $ABC$, e os comprimentos da mediana e da altura que saem do vértice $A$.

1355

Dê equações paramétricas para o círculo centrado na origem de raio 1, indicando os domínios onde o parâmetro $t$ assume valores. Esboce suas parametrizações.

1004

Identifique a seguinte cônica, determinando sua excentricidade, sua equação cartesiana, a equação cartesiana da diretriz e as coordenadas cartesianas do(s) foco(s) e do(s) vértice(s): $r=\frac{6}{3+sen\theta}$.

822

Para o par de vetores $u=(1,1,1)$ e $v=(3,1,-1)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.

$\textrm{proj}_{u}{u}=u$.

$v_1=u$; $v_2=(2,0,-2).$

387

Calcule o determinante da matriz:

$
\begin{pmatrix}
1&-2&3&2\\ 0&2&-1&1\\ 0&0&-1&1\\ 2&0&0&3
\end{pmatrix}.
$

$14$

382

Calcule o determinante da matriz:

$
\begin{pmatrix}
a&b&c\\ b&c&a\\ c&a&b
\end{pmatrix}.
$

$-a^3 - b^3 + 3 a b c - c^3$.

1423

Suponha que $u_1,\ldots, u_n$ gerem $\mathbb{R}^n$. Mostre que dados vetores quaisquer em $\mathbb{R}^n$, $u_{n+1}, \ldots, u_m$, então $u_1, \ldots, u_n, u_{n+1}, \ldots, u_m$ geram $\mathbb{R}^n$.

1422

Encontre $\lambda \in \mathbb{R}$ para que $v_1=(2 \lambda,1)$, $v_2=(\lambda + 1, \lambda + 1)$:

Sejam paralelos;
Não sejam paralelos;
$v_1$ e $v_2$ formem uma base para $\mathbb{R}^2$.

$\lambda=-1$ ou $\lambda=1/2$.
$\lambda\neq -1$ ou $\lambda\neq 1/2$.
$\lambda\neq -1$ ou $\lambda\neq 1/2$.

1377

Construa a curva cujas equações paramétricas são dadas por: $x=2\cos\theta$, $y=2\sin\theta$ e $z=2\theta$.

482

Dados: a esfera $\mathcal{S}$ de centro $C=(h,k,p)$ e raio $r$ e $P=(x_1,y_1,z_1)$ um ponto da esfera, mostre que: $\pi\cap \mathcal{S}=\{P\}$, onde $\pi$ é o plano que é normal ao vetor $\vec{CP}$ e passa por $P$. Tal plano é chamado de plano tangente à esfera por $P$.

242

Existe alguma reta paralela a $r=\{ (0,1,1)+t(1,-1,-1), t\in\mathbb{R}\}$, contida no plano $\pi : x-2y+3z-1=0$? Por quê?

Sim, pois o vetor diretor de $r$ está contido no plano $\pi$, haja visto que $(1,-1,-1)\cdot(1,-2,3)=0$. De outra forma, podemos deduzir (como?) que $v_1=(2,1,0)$ e $v_2=(-3,0,1)$ formam um par gerador para $\pi$ e que o vetor diretor da reta $r$ pode ser escrito como combinação deste par. Ou seja, se escalonarmos a matriz cujas linhas são estes três vetores, então obteremos uma linha nula na forma escalonada reduzida.

447

Examine o sistema linear a seguir, verificando se tem solução ou não, ou quantas são as possíveis soluções, utilizando resultados sobre posto de matriz, em função do parâmetro $\lambda$.

\[\left\{\begin{array}{cccl}2x_1+&3x_2+&x_3&=1 \\x_1+&6x_2+&x_3&=3 \\2x_1-&3x_2+&2x_3&=\lambda\\x_1+&3x_2+&2x_3&=1 \\\end{array}\right.. \]

358

Dadas as matrizes
\[A=\left(\begin{array}[c]{rrr}1 & -3 & 2\\2 & 1 & -3\\4 & -3 & -1\end{array}\right) \text{, }B=\left(\begin{array}[c]{rrrr}1 & 4 & 1 & 0\\2 & 1 & 1 & 1\\1 & -2 & 1 & 2\end{array}\right) \text{ e }C=\left(\begin{array}[c]{rrrr}2 & 1 & -1 & -2\\3 & -2 & -1 & -1\\2 & -5 & -1 & 0\end{array}\right) ,\]
mostre que $AB=AC$.

$AB=\left(\begin{array}[c]{rrrr}-3 & -3 & 0 & 1\\1 & 15 & 0 & -5\\-3 & 15 & 0 & -5\end{array}\right) $ e $AC=\left(\begin{array}[c]{rrrr}-3 & -3 & 0 & 1\\1 & 15 & 0 & -5\\-3 & 15 & 0 & -5\end{array}\right) $.

1005

Identifique a seguinte cônica, determinando sua excentricidade, sua equação cartesiana, a equação cartesiana da diretriz e as coordenadas cartesianas do(s) foco(s) e do(s) vértice(s): $r=\frac{3}{2+4cos\theta}$.

306

Encontre a equação da reta $r$ que passa por $(-3,2,-1)$ e é paralela à reta $s : \left\{\begin{array}{ccr}x &=& -3z-1\\ y &=& 4z + 3\end{array}\right.$.

Note que, como dada acima, $z$ aparece como parâmetro livre, tendo $s$, portanto, vetor diretor $(-3,4,1)$. Assim, sendo $r$ paralela a esta, então pode ser descrita, parametricamente, por $$ r: (-3,2,-1)+t(-3,4,1), \quad t\in\mathbb{R}. $$

1020

Calcule a área de um triângulo cujos vértices são: $A= (2,-1,-3)$, $B = (1,2,-4)$ e $C = (3,-1,-2)$.

$\|\vec{AB}\times\vec{AC}\|/2=\dfrac{3\sqrt{2}}{2}$

1009

Dado um plano qualquer com um sistema de coordenadas $xy$, encontre os vértices (ou vértice), os focos (ou foco) e a excentricidade da cônica descrita por $3x^2-14y=0$. Esboce o gráfico.

483

Dada a esfera $S: x^2 + y^2 + z^2 - 4x - 2y -11 = 0$.

Encontre o seu centro e seu raio.
Encontre a equação do plano tangente à esfera e que passa pelo ponto $P=(2,1,4)\in S$.

Completando quadrados, temos que $(x-2)^2+(y-1)^2+z^2=16$. Ou seja, a esfera tem centro $C=(2,1,0)$ e raio 4.
O plano tangente terá normal $n=P-C=(0,0,4)$ e passa por $P$ (enunciado). Logo, ele é dado por $\displaystyle z=4$.

1390

No processo de escalonamento de um sistema linear, se uma linha se anular, mostre que ela era uma combinação linear das outras.

1022

Determinar a equação reduzida da seguinte cônica: elipse com vértices $A_1=(5,0), \, A_2=(-5,0), \, B_1=(0,2), \, B_2=(0, -2)$.

969

Mostre que a equação $x^2+y^2-z^3=0$ representa uma superfície de revolução e determine o seu eixo de revolução e a equação da curva geratriz.

1026

Determinar a equação reduzida da seguinte cônica e fazer um esboço gráfico da mesma: parábola com vértice na origem e foco $F=(3,0).$

489

Encontre uma equação em coordenadas polares para a curva cuja equação em coordenadas cartesianas é dada por $(x^2+y^2)^2=4(x^2-y^2)$.

Apenas usando a definição de coordenadas polares, obtemos a seguinte equação: $\displaystyle r=2\sqrt{\cos(2\theta)}$, com $\theta\in[0,2\pi]$.

300

As equações a seguir representam as trajetórias retilíneas de duas partículas com velocidade uniforme. Determine se as trajetórias se interceptam. Em caso afirmativo, determine se há colisão entre as partículas.

$\alpha(t) =(1+t,-2t,3-t)$ e $\beta(t) = (-2+t,6-2t,6-t)$.
$\gamma(t) = (1+t,-2t,3-t)$ e $\delta(t) = (-1+t,4-2t,-3-t)$.
$\varepsilon(t) = (1+t,-2t,3-t)$ e $\eta(t) =(6+t,-10-t,-2-t)$.
$\theta(t) = (1+t,-2t,3-t)$ e $\lambda(t) = (6+2t,-10-2t,-2-2t)$.
$\mu(t) =(1+t,-2t,3-t)$ e $\nu(t) = (5+t,-10-t,-2-t)$.

1449

Determine uma equação da superfície consistindo em todos os pontos $P(x,y,z)$ que estão eqüidistantes do ponto $(0,0,1)$ e do plano $z=-1$. Identifique a superfície.

1048

Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $3x^2+2xy+3y^2-6x-6y+1=0$.

Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.

1219

Reduza a equação $2x^2+y^2-4xy-4yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1387

Uma liga de metal $L_1$ contém $20\%$ de ouro e $80\%$ de prata e uma liga $L_2$ tem $65\%$ de ouro e $35\%$ de prata. Quanto gramas de cada liga são necessários para se formar $100$ gramas de uma liga com quantidade igual de ouro e prata?

Serão necessárias aproximadamente 33.3333 gramas da liga $L_1$ e 66.6667 gramas da liga $L_2$.

1435

Mostre que o elipsóide obtido girando uma elipse com semi-eixo maior $a$ e semi-eixo menor $b$ em torno do eixo maior tem área de superfície

$$ S= 2\pi ab\left(\dfrac{b}{a}+\dfrac{a}{c}\arcsin\dfrac{c}{a}\right), $$

onde $c=\sqrt{a^2-b^2}$.

283

Verificar se as retas são concorrentes e, em caso afirmativo, encontrar o ponto de interseção:

$$r_1:\;\begin{cases} y=2x-3\\ z=-x+5 \end{cases}\ \ \ {\rm e } \ \ \ r_2:\;\begin{cases}y=3x+7\\ z=x+1\end{cases}$$

As retas não são concorrentes.

393

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e
$
A = \begin{pmatrix}
4&-2&2\\ -5&7&-5\\ -6&6&-4
\end{pmatrix}.
$

As raízes são: $x=3$ e $x=2$, esta última com multiplicidade dupla.

426

Resolver o sistema linear em função do parâmetro $\lambda$:

\[\left\{\begin{array}{ccccl}x_1-&2x_2-&x_3+&x_4&=-2 \\2x_1+&7x_2+&3x_3+&x_4&=\ \, 6 \\11x_1+&11x_2+&4x_3+&8x_4&=\ \, 8\\10x_1+&2x_2+&&8x_4&=\ \, \lambda \\\end{array}\right. .\]

$x_3 = 2 - \dfrac{x_1- 9 x_2}{4} , x_4 = -\dfrac{5x_1-x_2}{4}, \lambda = 0, \forall x_1,x_2\in\mathbb{R}$.

1161

Dados $A=(4,8,11)$, $B=(-3,1,4)$ e $C=(2,3,-3)$, faça uma figura esquemática, verificando que os pontos formam um triângulo, e:

Ache os tamanhos dos três lados do triângulo.
Ache os pontos médios dos três lados.
Calcule a soma dos vetores $\vec{AB}$, $\vec{BC}$ e $\vec{CA}$. Por que a soma é nula?
Ache o ponto em $AB$ cuja coordenada $y$ é $5$.
Ache os três pontos nos planos coordenados em $AB$ (extendidos).
Ache o ângulo entre $\vec{AB}$ e $\vec{BC}$ (sugestão: use a Lei dos Cossenos).
Ache os dois pontos de trisecção em $BC$ (internamente).
Ache o tamanho da altura saindo de $B$ e oposta ao lado $AC$.
Calcule a área do triângulo $ABC$.
Ache o tamanho da reta que bissecta o ângulo em $C$ (sugestão: use $\cos \theta/2 = \sqrt{(1+\cos\theta)/2}$; use trigonometria de triângulos retângulos).
Ache o raio e o centro do círculo circunscrito ao triângulo (sugestão: a hipotenusa é o diâmetro).
Ache os três pontos $D$ tais que $ABCD$ é um paralelogramo.

777

Encontre um vetor $u$ que seja ortogonal aos vetores $(2,3,-1)$ e $(2,-4,6)$ tal que $\parallel u\parallel = 3\sqrt{3}$.

$u=\pm(-3,3,3)$.

463

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{rrrrrcr}1x_1+&3x_2-&7x_3+&5x_4+&2x_5&=&0 \\2x_1+&3x_2-&20x_3+&7x_4+&8x_5&=&0 \\10x_1+&22x_2-&46x_3+&34x_4+&12x_5&=&0 \\\end{array}\right. . \]

$Y = x_ 1\left ( 1,0, \dfrac {11} {5}, \dfrac {6} {5},\dfrac {21} {5} \right)^T+x_2\left ( 0,1, \dfrac {4} {5}, \dfrac {-1} {5},\dfrac {9} {5} \right)^T$, $\forall x_1, x_2\in\mathbb {R}$.

870

Para quais valores de $m$ os pontos $A=(m,1,2), B=(2,-2,-3), C=(5,-1,1)$ e $D=(3,-2,-2)$ são coplanares?

$m=\pm 4$

1400

O trabalho $W$ realizado por uma força $\vec{F}$ sobre um objeto, agindo por uma distância $\vec{PQ}$, é dado por $W=\vec{F}\cdot\vec{PQ}$. Uma caixa é puxada horizontalmente por meio de uma força constante de $10N$ na direção do cabo e a um ângulo de $60^\circ$ com a horizontal. Qual é o trabalho realizado para mover a caixa ao longo de $2m$?

Considerando um sistema de coordenadas tal que a caixa esteja inicialmente na origem e tenha posição final $(2,0)$, isto é, se move no eixo $x$, temos que a distância percorrida por ela é $\vec{PQ} = (2,0)$. Decompondo a força nas componentes vertical e horizonal:
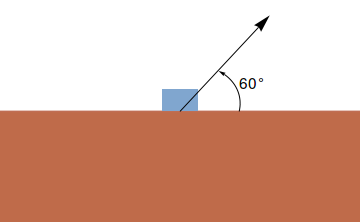
$$\vec{F} = (10\cos 60^\circ, 10 \sin 60^\circ) = (5,5\sqrt{3}).$$

Dessa forma o trabalho realizado é dado por:

$$W = \vec{F}\cdot\vec{PQ} = (5,5\sqrt{3}) \cdot(2,0) = 10 N \ m.$$

488

Encontre uma equação em coordenadas polares para a curva cuja equação em coordenadas cartesianas é dada por $2xy=25$.

Apenas utilizando a definição de coordenadas polares, obtemos a seguinte equação: $\displaystyle r=\dfrac{5}{\sqrt{\sin(2\theta)}}$, com $\displaystyle \theta\in(0,\pi)\cup (\pi,2\pi)$.

974

Dadas a equação da curva diretriz $4x^2+z^2+4z=0$, $y=0$ e um vetor $V=(4,1,0)$ paralelo às retas geratrizes, determine a equação da superfície cilíndrica.

410

Resolver o sistema linear:

\[ \left\{\begin{array}{rrrrl}x&+5y&+4z&-13z&=3\\3x&-y&+2z&+5t &=2\\2x&+2y&+3z&-4t&=1\end{array}\right. .\]

Esse sistema linear não possui solução.

879

Mostre que se as coordenadas dos quatro vértices de um tetraedro são

$$ (x_1,y_1,z_1),\; (x_2,y_2,z_2),\; (x_3,y_3,z_3),\; (x_4,y_4,z_4), $$

então o seu volume é dado por

$$ Vol=\frac{1}{6}\det\left(\begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \\\end{array}\right). $$

(Sugestão: Verifique primeiro que o volume do tetraedro é um sexto do volume do paralelepípedo determinados pelos seus vértices.)

1229

Reduza a equação $x^2+y^2+z^2-4xy-4xz-4yz=7 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

880

Mostre que

$$ u\cdot(v\times w)=\|u\|\;\|v\|\;\|w\|\;\sqrt{ \det\left(\begin{array}{ccc} 1 & \cos(u,v) & \cos(u,w) \\ \cos(u,v) & 1 & \cos(v,w) \\ \cos(u,w) & \cos(v,w) & 1 \\\end{array}\right)}, $$

onde, por exemplo, $\displaystyle \cos(u,v)=\frac{u\cdot v}{\|u \|\|v\|}$.

(Dica: Verifique primeiro que, para um tetraedro cujos vértices têm coordenadas

$$ (x_1,y_1,z_1),\; (x_2,y_2,z_2),\; (x_3,y_3,z_3),\; (x_4,y_4,z_4), $$

o seu volume é dado por

$$ Vol=\frac{1}{6}\det\left(\begin{array}{cccc} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \\\end{array}\right).$$

877

Dado que os pontos médios dos lados do triângulo $ABC$ são $M=(0,1,3)$, $N=(3,-2,2)$ e $P=(1,0,2)$, determine a área do triângulo $ABC$.

1209

Reduza a equação $7x^2 + 7y^2 + 10z^2 - 2xy - 4xz + 4yz - 12x + 12y + 60z = 24$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1164

Um ponto $(x,y,z)$ se move tal que sua distância ao ponto $(3,2,4)$ é sempre $5$. Qual figura $(x,y,z)$ traça? Faça um esboço de uma parte dessa figura (um octante). Escreva uma equação simplificada que os pontos $(x,y,z)$ devem satisfazer.

Uma esfera com centro $(3,2,4)$, raio $5$, com equação $x^2+y^2+z^2-6x-4y-8z+4=0$.

1059

Considere a cônica definida pela equação $2xy+x-2=0.$

Determinar seu centro.
Classificar a cônica.
Esboçar seu gráfico.

255

Considere os pontos $A=(1,1,0)$, $B=(3,2,-1)$, $C=(0,1,-2)$ e $D=(1,3,-1)$.

Encontre as retas: $r_1$ contendo o segmento $AB$ e $r_2$ contendo o segmento $CD$. Determine a posição relativa desta retas.
Use o produto misto para encontrar a equação do plano $\pi$ contendo o segmento $AB$ e que seja paralelo a $r_2$.
Calcule as distâncias $d(\pi, r_2)$ e $d(r_1, r_2)$.

1483

Mostre que um sistema linear homogêneo de $m$ equações e $n$ incógnitas sempre tem soluções não triviais se $m < n$.

241

Obtenha o plano que contém a reta $r = \{ (1,1,0)+t(2,1,2), t\in\mathbb{R}\}$ e é paralelo à reta $s:\frac{x+1}{2}=y=z+3$.

Um vetor diretor para a reta $s$ é dado por $v_s=(2,1,0)$. Já para $r$, $v_r=(2,1,2)$ é o vetor diretor. Fazendo $v_r\times v_s=(-1,2,3)$ obtemos, dessa forma, um vetor normal ao plano procurado. Como esse plano deve conter o ponto $(1,1,0)$, então o mesmo pode ser descrito como: $$(x-1,y-1,z)\cdot(-1,2,3)=0\Longleftrightarrow -x+2y+3z=-1.$$

1471

Encontre ou mostre a impossibilidade de encontrar $\gamma\in\mathbb{R}$ tal que $\displaystyle x^2+3y^2-2xy=\gamma$ represente uma elipse.

253

Determine a equação do plano $\pi_1$ que passa por $A = (10, 1,-1)$, $B = (1, 9,-1) \text{ e } C = (1,-1, 5)$.
Determine a equação do plano $\pi_2$ que passa por $D = (-1, 4,-1)$, $E = (3,-1, 10)$ e é paralelo ao eixo $z$.
Escreva as equações paramétricas para a reta $r$, interseção dos planos $\pi_1$ e $\pi_2$.
Qual o ângulo entre os planos $\pi_1$ e $\pi_2$?
Qual o ponto $P$ de $\pi_1$ que está mais próximo da origem? (Sugestão: este ponto é tal que $\overrightarrow{OP}$ é ortogonal ao plano $\pi_1$.)

856

Que condições devem satisfazer os vetores $a$ e $b$ para que o vetor $a+b$ divida o ângulo formado por eles em dois ângulos iguais?

Considere um paralelogamo de lados $a$ e $b.$ O vetor soma $a+b$ representa a diagonal do paralelogramo formado pelos vetores $a$ e $b$. Caso os vetores $a$ e $b$ tenham módulos iguais, isto é, mesmo tamanho, o paralelogramo formado por esses vetores será um losango (todos os lados do paralelogramo terão a mesma medida), e a diagonal dividirá o ângulo entre os vetores $a$ e $b$ ao meio. Assim, teremos a igualdade entre dois ângulos $\alpha =\beta $ quando $\left\Vert a\right\Vert=\left\Vert b\right\Vert .$ Então, para que o vetor soma divida ao meio o ângulo entre os vetores $a$ e $b$, basta que $\left\Vert a\right\Vert =\left\Vert b\right\Vert .$

274

Seja o triângulo de vértices $A(-1,4,-2),\; B(3,-3,6)$ e $C(2,-1,4)$. Escrever as equações paramétricas da reta que passa pelo ponto médio do lado $AB$ e pelo vértice oposto $C$.

$r:\begin{cases}x=2+2t\\ y=-1-3t\\ z=4+4t.\end{cases}$

234

Considere o ponto $A=(3,4,-2)$ e a reta $ r:\left\{
\begin{array}{ccc}
x & \;=\; & 1+t \\
y & \;=\; & 2-t \\
z & \;=\; & 4+2t
\end{array}
\right. $, onde $t\in \mathbb{R}.$

Escreva a equação do plano $\pi $ perpendicular a $r$ que passa por $A$.
Determine a reta que passa por $A$ e é perpendicular a $r$.

$x-y+2z=-5.$
$\left\{
\begin{array}{l}
x=3-4t \\
y=4 \\
z=-2+2t
\end{array}
\right. .$

481

Considere a reta $r=\{(x,y):2x-3y=1\}\subset\mathbb{R}^2$. Seja $B$ a base formada pelos vetores $(3,2)$ e $(1,0)$ e $x^{\prime}$ e $y^{\prime}$ coordenadas definidas em $\mathbb{R}^2$ pela origem usual e pela base $B$. Ache a equação de $r$ nas coordenadas $x^{\prime}$ e $y^{\prime}$.

1069

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2-2y^2+4xy-6=0$.

1052

Na equação $18x^2+12xy+2y^2+94\frac{\sqrt{10}}{10}x-282\frac{\sqrt{10}}{10}y+94=0$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.

256

Encontre a equação do plano $\pi$ que passa pelo ponto $P=(3,1,2)$ e tem vetor normal $N=(1,2,-3)$.

$x+2y-3z=-1$

276

Determinar as equações paramétricas e representar graficamente a reta que passa por $A(2,2,4)$ e é perpendicular ao plano $xOz$.

$r:(x,y,z)=(2,2+t,4);$

1071

Identificar a cônica $x^2-3y^2-2xy -x-y=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).

972

Dadas a equação da curva diretriz $x^2-y^2=1$, $z=0$ e um vetor $V=(0,2,-1)$ paralelo às retas geratrizes, determine a equação da superfície cilíndrica.

947

Obtenha a equação do lugar geométrico dos pontos que equidistam do plano $\pi: x=2$ e do ponto $P=(-2,0,0)$. Que conjunto é este?

467

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{ccccccccr}3x& + &3y& - &2z& - &t&=& 2\\5x& + &2y& + &z& - &2t&=& 1\\2x& - &y& + &3z& - &t&=& -1\end{array}\right. .\]

248

Encontre a equação da reta simétrica à reta $r$ em relação ao plano $\pi$:

$$r:\begin{cases} x - 2y = 4\\
3y + z = -8\end{cases}\ \ \ {\rm e}\ \ \ \pi:x-y+z=0.$$

386

Calcule o determinante da matriz:

$
\begin{pmatrix}
a&b&c&d\\ -b&a&d&-c\\ -c&-d&a&b\\ -d&c&-b&a
\end{pmatrix}.
$

$(a^2 + b^2 + c^2 + d^2)^2$

779

Demonstre que se $\alpha$ e $\beta$ são números reais tais que $\alpha(2,3) + \beta(3,2) = \vec{0}$, então $\alpha = 0$ e $\beta = 0$.
Qual a conclusão geométrica que podemos tirar do item acima?

$\alpha(2,3) + \beta(3,2) = \vec{0}$ resulta no sistema cujas equações são: $2\alpha+3\beta=0$ e $3\alpha+2\beta=0$.
Resolvendo o sistema, obtemos $\alpha=\dfrac{-3}{2}\beta=\dfrac{-2}{3}\beta$ que só pode ser satisfeita se $\beta=0$. E, portanto, $\alpha=0$.
Podemos concluir que esses dois vetores são linearmente independentes, isso significa que eles tem direções distintas.

1062

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $3x^2+5y^2+4x-2y-10=0$.

949

Determine a equação do lugar geométrico dos pontos $P=(x,y,z)$ tais que a soma das distâncias de $P$ aos dois pontos $(2,0,0)$ e $(-2,0,0)$ é igual a $6$. Que lugar geométrico é este?

882

Mostre que se

$$u= u_a a + u_b b + u_c c,$$

$$v = v_a a + v_b b + v_c c,$$

$$w= w_a a + w_b b + w_c c,$$

então

$$(u\cdot v\times w)(a\cdot b\times c) = \det\left(\begin{array}{ccc} u\cdot a & u\cdot b & u\cdot c\\ v\cdot a & v\cdot b & v\cdot c\\ w\cdot a & w\cdot b & w\cdot c\\\end{array}\right).$$

Esta fórmula reduz o cálculo de dois determinantes (pois cada produto misto envolve o cálculo de um determinante) ao cálculo de um único.

Sugestão: Use a seguinte relação:

$$u\cdot(v\times w)=\det\left(\begin{array}{ccc} u_a & u_b & u_c \\ v_a & v_b & v_c \\ w_a & w_b & w_c \\\end{array}\right)[a\cdot(b\times c)].$$

269

Considere os pontos $A = (4,3,-2)$, $B = (5,5,-1)$, $C = (6,4,-3)$ e $D = (7,6,0)$. Pede-se:

A equação do plano $\pi$ que passa por $A$, $B$ e $C$. Mostre também que $D$ não está em $\pi$.
As equações paramétricas da reta $r$ que passa por $D$ e é perpendicular ao plano $\pi$ (do item 1).
O ponto de interseção entre a reta $r$ (do item 2) e o plano $\pi$ (do item 1).
A distância do ponto $D$ ao plano $\pi$ (do item 1).
A área do triângulo de vértices $A$, $B$ e $C$ (área do triângulo $=1/2$ área do paralelogramo).
O volume do tetraedro de vértices $A$, $B$, $C$ e $D$. (Volume do tetraedro $= 1/6$ volume do paralelepípedo).
A altura do tetraedro $ABCD$.

Dica: Os itens 5 e 6 requerem produto vetorial. A solução baseada na geometria plana não é o propósito da geometria analítica.

1429

Considere a matriz diagonal $ A = diag\{a, b\},$ onde $a,b\in\mathbb{R}$, e seja $\Delta$ um triângulo com vértices $0$, $u$ e $v$, onde $u$ e $v$ são pontos na circunferência $S^1$ de equação $x^2+y^2=1$. Seja $A\Delta$ o triângulo
de vértices $0$, $A\cdot u$ e $A\cdot u$.

Mostre que os vértices $A\cdot u$ e $A\cdot v$ estão na elipse $E$ de equação $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$.
Mostre que se $S(\Delta$) for a área de $\Delta$ e $S(A\Delta$) for a área de $A\Delta$, então $S(A\Delta)=abS(\Delta)=S(\Delta)\,\det A$.
Mostre que a relação do item anterior é preservada para qualquer polígono inscrito na circunferência.
Inspirando-se no processo clássico para o cálculo da área do círculo, pense na área da região limitada pela elipse $E$ como sendo
o limite das áreas dos polígonos inscritos em $E$, quando o lado maior tende a zero. Conclua que esta área é dada por $\pi ab$.

970

Mostre que a equação $y^6-x^2-z^2=0$ representa uma superfície de revolução e determine o seu eixo de revolução e a equação da curva geratriz.

377

Calcule o determinante da matriz:

$
\begin{pmatrix}
1+x_1y_1&1+x_1y_2 \\ 1+x_2y_1&1+x_2y_2
\end{pmatrix}.
$

$(x_1-x_2)(y_1-y_2)$.

1403

O momento escalar ou torque sobre o ponto $P$ de uma força $\vec{F}$ aplicada a um ponto $Q$ é dado por $\|\vec{PQ} \times \vec{F}\|$. Uma força $\vec{F}$ com magnitude de $10 N$ é aplicada na direção $y$ positiva sobre o ponto $Q=(1,1,1)$ em um cubo com lados de tamanho $1m$. Determine o momento escalar de $\vec{F}$ sobre o ponto $P = (1,0,0)$. Faça um esboço do gráfico, indicando a força e o momento escalar.

1467

Mostre que se o gráfico polar de $r=f(\theta)$ for girado no sentido anti-horário em torno da origem por um ângulo $\alpha$, então $r=f(\theta-\alpha)$ é uma equação para a curva girada. (Sugestão: se $(r_0,\theta_0)$ for um ponto qualquer do gráfico original, então $(r_0,\theta_0+\alpha)$ é um ponto no gráfico girado.)

303

Encontre a equação da reta $r$ que passa pelo ponto (-1,2,3) e é paralela a reta que passa por $(1,0,-1)$ e tem $(-2,1,-3)$ como vetor diretor.

Como é paralela à reta mencionada, então terá o vetor diretor em comum com aquela. Assim, a reta procurada é dada parametricamente como $$ r: (-1,2,3) + t(-2,1,-3)\quad t\in\mathbb{R}.$$

294

Calcule o cosseno do ângulo entre a diagonal de um cubo e suas arestas.

Consideraremos o cubo com arestas paralelas aos eixos coordenados. Sejam a origem $\left( 0,0,0\right) $ e os pontos $\left( k,0,0\right) ,\left(
0,k,0\right) $ e $\left( 0,0,k\right) $ quatro vértices do cubo. Considere agora o vetor diagonal, isto é, o vetor $\overline{d}$ obtido considerando a origem e o vértice oposto $\left( k,k,k\right) $. Então, o ângulo $\theta $ entre o vetor diagonal e a aresta $u_{x}=\left(k,0,0\right) $ é obtido como segue:

$\overline{d}.u_{x}=\left( k,k,k\right) .\left( k,0,0\right) =\left\vert
\overline{d}\right\vert .\left\vert \overline{u_{x}}\right\vert \cos \theta ,
$ $k^{2}=\sqrt{3k^{2}}k\cos \theta .$

Logo, $\cos \theta =\frac{1}{\sqrt{3}},$ e $\theta =arc\cos \left( \frac{1}{
\sqrt{3}}\right) ,$ onde escolhemos a determinação do $\arccos $ em $
\left( 0,\pi \right) $. Os ângulos com as arestas são iguais. Observe que o ângulo obtido é sempre independente da escolha de $k.$

1080

Identifique a cônica descrita pela equação $4x^2-12xy+9y^2-6x+9y-4=0$.

404

Resolver o sistema linear em função do parâmetro $\lambda$:

\[\left\{\begin{array}{ccccl}x_1-&2x_2-&x_3+&x_4&=-2 \\2x_1+&7x_2+&3x_3+&x_4&=\ \, 6 \\11x_1+&11x_2+&4x_3+&8x_4&=\ \, 8\\10x_1+&2x_2+&&8x_4&=\ \, \lambda \\\end{array}\right. .\]

$x_3 = 2 - \dfrac{x_1- 9 x_2}{4} , x_4 = -\dfrac{5x_1-x_2}{4}, \lambda = 0, \forall x_1,x_2\in\mathbb{R}$.

1365

Determine a curva definida pela intersecção das superfícies cilíndricas $x^2+z^2=1$ e $y^2=4x$.

708

Ache a equação do círculo que passa pelos pontos $(4,0)$, $(0,3)$ e a origem.

1388

Seja $f: \mathbb{R}^2 \rightarrow \mathbb{R}^2$ uma função definida por $f(x,y) =(2x+y,x-y)$. Ache o(s) valor(es) de $\lambda$ para que a equação $f(x,y) = \lambda(x,y)$ possua solução $(x,y) \neq 0$.

$\lambda=\dfrac{1 + \sqrt{13}}{2}$ ou $\lambda=\dfrac{1 - \sqrt{13}}{2}$.

310

Verifique a posição relativa do seguinte par de retas (isto é, verifique se são paralelas, concorrentes ou reversas):

\[
\left\{\begin{array}{ccr}x &=& 1+2t\\y &=& -3-t\\ z &=& t\end{array}\right., \ \
\left\{\begin{array}{ccr}x &=& 1/2+3/2s\\y &=& -1+s\\ z &=& 1/3s \end{array} \right. .
\]

São reversas.

1356

Dê equações paramétricas para o círculo centrado em $(h,k)$ e de raio 1, indicando o domínio onde o parâmetro $t$ assume valores. Esboce suas parametrizações.

381

Calcule o determinante da matriz:

$
\begin{pmatrix}
1&1&1\\ a&b&c\\ a^2&b^2&c^2
\end{pmatrix}.
$

$-(a - b)(a - c)(b - c)$

814

Dados os pontos $A=(-2,3,4)$, $B=(3,2,5)$, $C=(1,-1,2)$ e $D=(3,2,-4)$, calcular $\textrm{proj}_{CD}{AB}$.

$\textrm{proj}_{CD}{AB}=\dfrac{1}{49}(2,3,-6)$.

1076

Identificar a cônica $4x^2+4xy+y^2-6x+3y+2=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).

1021

Sendo $\|u\|=3, \|v\|=4$ e $120^{\circ}$ o ângulo entre os vetores $u$ e $v$, calcule o volume do paralelepípedo determinado por $u\times v$, $u$ e $v$.

$108$

871

Sendo $\|u\|=3, \|v\|=4$ e $120^{\circ}$ o ângulo entre os vetores $u$ e $v$, calcule:

$\|u+v\|,$
$\|u\times(v-u)\|.$

372

Determine todos os valores de $\lambda$ para os quais $\det(A-\lambda I_3)=0$, onde

\[A = \left( \begin{array}{ccc}
1 & 0 & 0 \\
-1 & 3 & 0 \\
3 & 2 & -2 \end{array}\right). \]

As raízes são: $\lambda=-2$, $\lambda=1$ e $\lambda=3$.

356

Os únicos números reais cujos quadrados são eles próprios são $0$ e $1$. Ache todas as matrizes quadradas $A$, $2\times2$, tais que $A^{2}=A.$

Se $A= \left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right),$ $A^2=A \rightarrow \left(\begin{array}[c]{cc}x^2+yz & wy+xy\\wz+xz & w^2+yz\end{array}\right)=\left(\begin{array}[c]{cc}x & y\\z & w\end{array}\right).$

Cujas soluções são:

$X_1= \left(\begin{array}[c]{cc}x & y\\\frac{x-x^2}{y} & 1-x\end{array}\right), \forall x,y\in \mathbb{R};$ $X_2= \left(\begin{array}[c]{cc}0 & 0\\z & 1\end{array}\right), \forall z\in \mathbb{R};$ $X_3= \left(\begin{array}[c]{cc}1 & 0\\z & 0\end{array}\right), \forall z\in \mathbb{R};$ $X_4= \left(\begin{array}[c]{cc}0 & 0\\0 &0\end{array}\right);$ $X_5= \left(\begin{array}[c]{cc}0 & 0\\0 & 1\end{array}\right);$ $X_6= \left(\begin{array}[c]{cc}1 & 0\\0 & 0\end{array}\right);$ $X_7= \left(\begin{array}[c]{cc}1 & 0\\0 & 1\end{array}\right).$

989

Determine o conjunto de todos os vetores do espaço que são paralelos ao vetor $(1,1,1)$.
Descreva o conjunto de todos os vetores do espaço que são ortogonais ao vetor $(1,0,-1)$.
Qual o significado geométrico dos conjuntos encontrados nos itens (a) e (b)?

813

Dado $v_1=(1,-2,1)$, determine vetores $v_2$ e $v_3$ de modo que os três sejam mutuamente ortogonais.

$v_2=(1,1,1)$ e $v_3=(1,0,-1).$

1420

Um roteador de internet sem fio é instalado de forma que o sinal chegue com mesma intensidade em qualquer ponto $(x,y)$ a uma distância $r$ do local de instalação $(a,b)$ (desconsiderando eventuais efeitos que possam diminuir a intensidade do sinal). Determine a equação do lugar geométrico no plano cartesiano tal que a internet possa ser utilizada sem problemas.

430

Verifique se as matrizes abaixo estão na forma escalonada. Usando operações de linha equivalência escalone as (encontre a forma escalonada das) que não estiverem na forma escalonada.

$ \begin{pmatrix}1&-2&-1&0\\1&\phantom{-}0&-1&1\\0&\phantom{-}1&\phantom{-}0&2\end{pmatrix}, $
$ \begin{pmatrix}1&0&0&5&0\\0&1&0&2&0\\0&0&1&1&0\\0&0&0&0&1\end{pmatrix}. $

971

Dadas a equação da curva diretriz $y^2=4x$, $z=0$ e um vetor $V=(1,-1,1)$ paralelo às retas geratrizes, determine a equação da superfície cilíndrica.

400

Resolver o sistema linear:

\[\left\{\begin{array}{rrrcr}2x_1+&3x_2-&5x_3&=& 2 \\2x_1+&3x_2-&x_3&=& 8 \\6x_1+ &9x_2-&7x_3&=& 18 \\\end{array}\right. . \]

$x_2 =\dfrac{19-4x_1}{6}, x3 =\dfrac{3}{2}, \forall x_1 \in \mathbb{R}$.

495

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por $x^2+y^2+4z^2=16$.

Usando a definição, a equação dada fica: $\displaystyle r^2+4z^2=16$.

261

Encontre a distância entre o plano $\pi: 2x+2y-z=6$ e o ponto $P=(2,2,-4)$.

Vamos utilizar o conceito de distância dado na referência R. J. Santos-Matrizes, Vetores e Geometria Analítica. Neste caso, precisamos tomar um ponto (arbitrário) sobre o plano. Vamos tomar $P_1=(3,0,0)$ em $\pi$. Assim, sendo $N=(2,2,-1)$ a normal ao plano, $$ d(P,\pi)=\|\mathrm{proj}_N\vec{P_1P}\|=2.$$

1372

Construa a curva cujas equações paramétricas são dadas por: $x=\sin^2\theta$, $y=\sin\theta\cos\theta$ e $z=\cos\theta$.

434

Resolver o sistema linear:

\[\left \{\begin{array}{rrrrl}x&-y&+2z&-t&=0\\3x&+y&+3z&+t&=0\\x&-y&-z&-5t&=0\end{array}\right..\]

$y = \dfrac{-6 x}{5}, z = \dfrac{-4 x}{5}, t = \dfrac{3 x}{5}, \forall x \in \mathbb{R}$.

411

Resolver o sistema linear:

\[\left \{\begin{array}{rrrrl}x&-y&+2z&-t&=0\\3x&+y&+3z&+t&=0\\x&-y&-z&-5t&=0\end{array}\right..\]

$y = \dfrac{-6 x}{5}, z = \dfrac{-4 x}{5}, t = \dfrac{3 x}{5}, \forall x \in \mathbb{R}$.

1054

Decida se a cônica $C$ determinada pela equação $\displaystyle 4x^2-4x+9y^2-18y=26$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

1452

Dada a superfície $4x^2+z^2-y^2=9$, identifique a cônica obtida ao fixar:

$x=0$;
$y=0$;
$z=1$.

267

Considere as retas $r$ e $r^{\prime}$ dadas por:

$r$: $x=0$, $y=2+t$ e $z=1+t$ $r^{\prime}$: $ x-2=z+1$ e $y=3$.

Mostre que $r$ e $r^{\prime}$ são reversas.
Encontre dois planos paralelos $\pi$ e $\alpha$ tais que $r\subset \pi$ e $r^{\prime}\subset \alpha$. Pergunta: Podem existir outros planos com as propriedades de $\pi$ e $\alpha$?
Encontre a distância entre os planos $\pi$ e $\alpha$ do item anterior.
Encontre $P$ em $r$ e $Q$ em $r^{\prime}$ tais que a reta que passa por $P$ e $Q$ seja perpendicular a $r$ e $r^{\prime}$.

314

Dada a reta $r = \left\{\begin{array}{rcl}x &=& 1+m\lambda\\y &=& 2+n\lambda\\ z &=& 1+(n-1)\lambda\end{array}\right.$, determine, se possível, $m$ e $n$ em cada um dos seguintes casos:

$r$ é paralela ao eixo $Y$;
$r$ é paralela ao plano $XY$;
$r$ passa pela origem.

Devemos ter $m=0$ e $n=1$.
Para este caso: $n=1$ e $m$ pode ser qualquer.
$m=1$ e $n=2$.

1233

Reduza a equação $2x^2+3y+4z+4=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1044

Decida se a cônica $C$ determinada pela equação $x^2+3xy+y^2=2$ é degenerada ou não. Se não for degenerada, encontre os vértices (ou vértice), os focos (ou foco) e esboce o gráfico.

436

Encontre a inversa da matriz abaixo (se existir):

\[\begin{pmatrix}1 & 2 \\ 3 & 5\end{pmatrix}.\]

\[\begin{pmatrix}-5 & 2 \\ 3 & -1\end{pmatrix}.\]

1072

Identificar a cônica $x^2+4y^2+4xy-2x-4y-1=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).

1024

Determinar a equação reduzida da seguinte cônica e fazer um esboço gráfico da mesma: elipse com vértices $A_1=(10,0), \, A_2=(-10,0), \, B_1=(0,6), \, B_2=(0, -6).$

1064

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2-y^2-4x+2y+2=0$.

403

Resolver o sistema linear em função do parâmetro $\lambda$:

\[\left\{\begin{array}{cccl}2x_1+&3x_2+&x_3&=1 \\x_1+&6x_2+&x_3&=3 \\2x_1-&3x_2+&2x_3&=\lambda\\x_1+&3x_2+&2x_3&=1 \\\end{array}\right.. \]

$x_1 =\dfrac{-1}{4}, x_2 =\dfrac{7}{12}, x_3 =\dfrac{-1}{4}, \lambda = \dfrac{-11}{4}.$

466

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$, em função do parâmetro $\lambda$:

\[\left\{\begin{array}{ccccl}x_1-&2x_2-&x_3+&x_4&=-2 \\2x_1+&7x_2+&3x_3+&x_4&=\ \, 6 \\11x_1+&11x_2+&4x_3+&8x_4&=\ \, 8\\10x_1+&2x_2+&&8x_4&=\ \, \lambda \\\end{array}\right. .\]

235

Considere a reta $r$ e o plano $\pi$ de respectivas equações

\[
\frac{x}{2}\ =\ \frac{1-y}{4}\ =\ z-3, \]
\[ x+y+2z\ =\ 1.\]
Determine a equação paramétrica da reta $s$ que é igual a projeção ortogonal da reta $r$ sobre o plano $\pi$.

$\left\{
\begin{array}{l}
x=-1+2t \\
y=-4t \\
z=1+t
\end{array}
\right. .$

1014

A hipérbole $\ell$ tem focos $F_1$ e $F_2$ e vértices $A_1$ e $A_2$. Encontrar equações paramétricas de $\ell$ se

$F_1=(2,0)$, $F_2=(8,0)$, $A_1=(3,0)$, $A_2=(7,0)$;
$F_1=(0,0)$, $F_2=(4,8)$, $A_1=(1,2)$, $A_2=(3,6)$.

268

Considere os planos $\alpha : x - y + z - 3=0$ e $\beta: 2m^{2}x - (m+1)y + 2z=0$.

Determine $m$ para que os planos $\alpha$ e $\beta$ possam ser paralelos, concorrentes, e concorrentes ortogonais (Um $m$ para cada caso, se for possível).
Para $m=-1$ encontre a equação da reta interseção entre $\alpha$ e $\beta$.

953

Identifique a quádrica definida pela equação reduzida $-x^2+ y^2+z^2=0$ e esboce seu gráfico.

720

Ache a esfera que tem centro na reta $r: \left\{ \begin{array}{c} x=2z-3 \\ y = z-1 \end{array} \right.$ e passa pelos pontos $(6,-1,3)$ e $(0,7,5)$.

378

Calcule o determinante da matriz:
$
\begin{pmatrix}
1&a\\ 1&b\
\end{pmatrix}.
$

$b-a$

1402

O momento escalar ou torque sobre o ponto $P$ de uma força $\vec{F}$ aplicada a um ponto $Q$ é dado por $\|\vec{PQ} \times \vec{F}\|$. Uma força $\vec{F}$ com magnitude de $10 N$ é aplicada na direção $y$ positiva sobre o ponto $Q=(1,1,1)$ em um cubo com lados de tamanho $1m$. Determine o momento escalar de $\vec{F}$ sobre o ponto $P = (0,0,0)$. Faça um esboço do gráfico, indicando a força e o momento escalar.

367

Seja $M= \left( \begin{array}{cc}0 & 1 \\-1 & 0\end{array}\right)$.

Mostre que: Se $A$ é uma matriz $2\times 2$ qualquer, então $AM=MA$, se e somente se, $A= \left( \begin{array}{cc}
a & b \\
-b & a
\end{array}\right)$.
Mostre que se $A$ e $B$ são matrizes $2\times 2$ que comutam com $M$, então $A$ e $B$ comutam entre si, isto é, $AB=BA$.

Seja $A= \left( \begin{array}{cc}a & b \\c & d\end{array}\right)$, tal que $AM=MA$.
Deseja-se que $AM=\left( \begin{array}{cc}-b & a \\-d & c\end{array}\right)=MA= \left( \begin{array}{cc}c & b \\-a & -b\end{array}\right)$.
Logo, é necessário que $c=-b$ e $d=a$, de onde $A= \left( \begin{array}{cc}a & b \\-b & a\end{array}\right)$.
Se $A$ e $B$ são matrizes $2\times 2$ que comutam com $M$, de acordo com o item anterior, $A= \left( \begin{array}{cc}a & b \\-b & a\end{array}\right)$ e $B= \left( \begin{array}{cc}c & d \\-d & c\end{array}\right)$.
Calculando $AB$ e $BA$, obtém-se $AB= \left( \begin{array}{cc}ac-bd & ad+bc \\-bc-ad & -bd+ac\end{array}\right)=BA$ .

471

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[ \left\{\begin{array}{rrrrl}x&+5y&+4z&-13z&=3\\3x&-y&+2z&+5t &=2\\2x&+2y&+3z&-4t&=1\end{array}\right. .\]

1416

Mostre que o sistema linear:

$$ \left\{ \begin{array}{ccccccccc}a_{11} x_1 &+& a_{12} x_2 &+& \ldots &+& a_{1n} x_n &=& b_1 \\a_{21} x_1 &+& a_{22} x_2 &+& \ldots &+& a_{2n} x_n &=& b_2 \\\vdots && \vdots && && \vdots && \vdots \\a_{n1} x_1 &+& a_{n2} x_2 &+& \ldots &+&a_{nn} x_n &= &b_n \\ \end{array} \right.$$
pode ser escrito em forma matricial $Ax=b$, onde:

$$A=\begin{pmatrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots && \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{pmatrix}, x = \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix}, b = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n\end{pmatrix}.$$

1228

Reduza a equação $2x^2+y^2-4xy-4yz+12x+6y+6z=1 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

419

Considere a matriz $$A = \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 3 & -2 & a \\ 2 & 2a-2 & -a-2& 3a-1 \\ 3 & a + 2 & -3 & 2a + 1 \end{bmatrix}.$$ Determine o conjunto solução do sistema $A\,X = B$, em que $B = \begin{bmatrix} 4 & 3 & 1 & 6\end{bmatrix}^t$, para todos os valores de $a$.

Para $a=5$, o sistema não possui solução.

Para $a=1$, o sistema possui infinitas soluções com $x=2-w$, $y=z=1$ e $w\in\mathbb{R}$.

Para $a\neq 5$ e $a\neq 1$, $x = \dfrac{4a-11}{a-5}$, $y = \dfrac{4}{5-a}$, $z = \dfrac{4}{5-a}$, $w = \dfrac{1}{5-a}$.

872

Mostre que os vetores $a, b, c$, que satisfazem a relação $$a\times b \;+\; b\times c \;+\; c\times a\; = \;0$$ são coplanares.

1160

Dados os pontos $A=(-3,2)$ e $B=(5,4)$:

Faça um esboço de $\vec{AB}$.
Calcule a distância de $A$ até $B$.
Ache o ponto médio entre $A$ e $B$.
Ache o vetor $\vec{BA}$.
Ache o ponto em $\vec{AB}$ cuja distância é 3 vezes maior de $A$ do que de $B$. Isto é, o ponto que divide $\vec{AB}$ na razão $3:1$ (existe outro ponto que está fora de $\vec{AB}$).
Ache o ponto em $\vec{AB}$ cuja coordenada $x$ é igual a $2$.
Ache o ponto em $\vec{AB}$ (extendido) cuja coordenada $y$ é igual a $5$.
Ache os pontos no eixo $x$ e no eixo $y$ que são equidistantes de $A$ e $B$.

1237

Reduza a equação $3x^2+y^2+z^2+4yz+12x+2y-2z+9=0 $ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1032

A fim de esboçarmos uma hipérbole, precisamos indicar: centro, focos, vértices e assíntotas. Os pontos sobre a curva mais próximos do centro (sobre o eixo maior) são os vértices. Os vértices distam $a$ do centro e as assíntotas são da forma $y=\pm(\frac{a}{b}) x$ (se os focos estiverem sobre o eixo $y$) ou $y=\pm(\frac{b}{a}) x$ (se estiverem sobre o eixo $x$), onde $a^2+b^2=c^2$. A excentricidade de uma hipérbole é definida como $\frac{c}{a}$.

Esboce o gráfico de $25x^2-16y^2=400$.
Dê a equação da hipérbole com vértices $(0,\pm3)$ e excentricidade $e=5/3$.
Esboce o gráfico da curva $9x^2-y^2=-36$.

1207

Reduza a equação $2xy + z = 0$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1458

Classifique a superfície $\displaystyle \dfrac{x^2}{36}+\dfrac{y^2}{25}-z^2=0$ como elipsóide, hiperbolóide de uma folha, hiperbolóide de duas folhas, cone elíptico, parabolóide elíptico ou parabolóide hiperbólico.

1067

Identifique a curva $\ell$ consistindo de todos os pontos $P=(x,y)$ cujas coordenadas satisfazem a equação $x^2+5x+y-9=0$.

950

Identifique a quádrica definida pela equação reduzida $6x^2+3y^2-z^2=-2$ e esboce seu gráfico.

1155

Quais são os cossenos diretores do vetor de $(2,-3,5)$ a $(-1,1,-7$)?

$-3/13,4/13,-12/13$.

1453

Dada a superfície $4x^2+y^2-z=0$, identifique a cônica obtida ao fixar:

$x=0$;
$y=0$;
$z=1$.

475

Os vetores $(1,1,0,-1),(1,2,1,3),(1,1,-9,2),(16,-13,1,3)$ formam uma base para $\mathbb{R}^{4}$?

Sim, porque são 4 vetores linearmente independentes, e dim $\mathbb{R}^{4}=4$.

858

Sendo $A=(2,-5,3)$ e $B=(7,3,-1)$ vértices consecutivos de um paralelogramo $ABCD$ e $M=(4,-3,3)$ o ponto de interseção das diagonais, determine os vértices $C$ e $D$.

$C=(6,-1,3)$ e $D=(1,-9,7)$

1482

Mostre que um sistema de equações lineares homogêneo de $n$ equações e $n$ incógnitas admite solução(ões) não trivial(is) se e somente se o determinante da matriz dos coeficientes for nulo.

1152

Quais são os cossenos diretores de cada eixo coordenado?

$1,0,0$; $0,1,0$; $0,0,1$.

1392

Mostre que todo sistema linear homogêneo (isto é, cujos termos independentes são todos iguais a zero) de três equações com quatro incógnitas possui uma infinidade de soluções.

1047

Seja $C$ o lugar geométrico dos pontos $P = (x,y)$ de um plano cujas coordenadas $x$ e $y$ satisfazem a equação $9x^2-24xy+16y^2-34x-38y+51=0$.

Qual a natureza da cônica $C$?
Escrever a forma canônica da equação de $C$.
Caso $C$ seja uma elipse ou uma hipérbole, encontre os focos e a excentricidade. Caso seja uma hipérbole, encontre também as equações das retas assíntotas no sistema $xy$ original.

1568

Seja $A$ uma matriz $2\times 2$ simétrica e $k$ um escalar. Mostre que o gráfico da equação quadrática $\textbf{x}^tA\textbf{x}=k$ é:

uma hipérbole se $k\neq 0$ e $\det A<0$;
uma elipse, círculo ou cônica imaginária se $k\neq 0$ e $\det>0$;
um par de retas ou uma cônica imaginária se $k\neq 0$ e $\det A=0$;
um par de retas ou um único ponto se $k=0$ e $\det A \neq 0$;
uma linha reta se $k=0$ e $\det A=0$.

[Dica: use o Teorema dos Eixos Principais.]

865

Determine um vetor $\vec{a}=(x,y,z)$ que satisfaça as seguintes equações:

$$\vec{a} \times \vec{j}=\vec{k}$$

$$\vec{a} {\cdot}(\vec{i}+2\vec{j})=0,$$

onde $\vec{i}$, $\vec{j}$ e $\vec{k}$ são os vetores da base canônica de $\mathbb{R}^3$.

1073

Identificar a cônica $x^2+3y^2-2xy+3=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).

831

Se de um ponto qualquer $R$ dentro de um paralelogramo $ABCD$ são traçados segmentos de reta paralelos aos lados, são formados quatro novos paralelogramos (isto é, o paralelogramo original é a união destes quatro paralelogramos menores). Mostre que as diagonais de quaisquer dois destes paralelogramos (que não sejam as diagonais que se interceptam no ponto $R$) se interceptam na reta suporte de uma das diagonais do paralelogramo original.

1078

Identifique a cônica $3 x^2-12 x y+12 y^2+ 2 \sqrt{5} x+\sqrt{5} y=0$ e seu parâmetros associados.

988

Sejam $a_{1},\, a_{2},\,a_{3},\,b_{1},\, b_{2},\,b_{3}$ seis números reais quaisquer. Demonstre a desigualdade de Cauchy-Schwarz: \[ (a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3})^{2} \le (a_{1}^{2}+a_{2}^{2}+a_{3}^{2}) (b_{1}^{2}+b_{2}^{2}+b_{3}^{2}). \]

762

Mostre que as medianas de um triângulo interceptam-se em um único ponto. Encontre a razão em que esse ponto divide cada mediana.
Tente generalizar o item (a) para tetraedros.

a) Sejam o triângulo $ABC$, $M$ o ponto médio de $\overrightarrow{BC}$, $N$ o de $\overrightarrow{CA}$ e $P$ o de $\overrightarrow{AB}.$ Sejam também os pontos $G,$ $H$ e $I$ tais que

$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM},$ $\overrightarrow{BH}=\frac{2}{3}\overrightarrow{BN},$ $\overrightarrow{CI}=\frac{2}{3}\overrightarrow{CP}.$

Assim, observe que
$\overrightarrow{GI}=\overrightarrow{GA}+\overrightarrow{AC}+\overrightarrow{CI}=\frac{2}{3}\overrightarrow{MC}+\frac{1}{3}\overrightarrow{AC}+\frac{2}{3}\overrightarrow{CP}=\frac{2}{3}\overrightarrow{MP}+\frac{1}{3}\overrightarrow{AC}=\frac{1}{3}\left( \overrightarrow{BA}+\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BC}\right) =0.$

De maneira análoga, mostramos que $\overrightarrow{GH}=.$ Portanto,

concluímos que $G=H=I,$ e vale as propoções citadas acima.

b) Vamos mostrar que o centro de massa do tetraedro é a interseção das medianas. Sendo assim, seja o tetraedro $ABCD$. A mediana do tetraedro
é definida comos sendo o segmento que une um baricentro de uma das faces do tetraedro, com o seu vértice oposto.

Sejam $A^{\prime },B^{\prime },C^{\prime },D^{\prime }$, sendo respectivamente os baricentros das faces $DBC,$ $ABC,$ $ADC$ e $ADB.$
Observe que $\overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}=0,$ pois $\overrightarrow{D^{\prime }A}+
\overrightarrow{D^{\prime }B}=2\overrightarrow{D^{\prime }P},$ onde $P=\frac{A+B}{2}.$ Como $D^{\prime }$ é o baricentro do triângulo $ABC$, segue que $\overrightarrow{CD^{\prime }=}2\overrightarrow{D^{\prime }P}.$
Assim,

$\overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}=2\overrightarrow{D^{\prime }P}+\overrightarrow{D^{\prime }C}=\overrightarrow{CD^{\prime }}+\overrightarrow{D^{\prime }C}=0.$

Seja $G$ o centro de massa do tetraedro. Uma propriedade dele, é que

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=0.$

Assim,

$3\overrightarrow{GD^{\prime }}=\overrightarrow{GA}+\overrightarrow{
AD^{\prime }}+\overrightarrow{GB}+\overrightarrow{BD^{\prime }}+
\overrightarrow{GC}+\overrightarrow{CD^{\prime }}=\overrightarrow{GA}+
\overrightarrow{GB}+\overrightarrow{GC}-\left( \overrightarrow{D^{\prime }A}+\overrightarrow{D^{\prime }B}+\overrightarrow{D^{\prime }C}\right) =
\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=- \overrightarrow{GD}=\overrightarrow{DG}.$

Portanto, $3\overrightarrow{GD^{\prime }}=\overrightarrow{DG},$ ou seja, o centro de massa $G$ pertence ao segmento $\overrightarrow{DD^{\prime}}.$ De maneira análoga, mostramos que $G$ pertence aos segmentos $\overrightarrow{AA^{\prime }},$ $\overrightarrow{BB^{\prime }}, \overrightarrow{CC^{\prime }}.$ Ou seja, $G$ é o ponto de interseção das medianas.

833

Sabendo que $\| u \| = \sqrt{2}$, $\| v \| = \sqrt{3}$ e que $u$ e $v$ formam um ângulo de ${3\pi}/4$, determinar:

$| (2u-v)\cdot(u-2v)|$.
$\|u-2v\|$.

$| (2u-v)\cdot(u-2v)|=10+5\sqrt{3}$.
$\|u-2v\|=2\sqrt{2+\sqrt{3}}$.

1019

São dados quatro vértices, $A = (-2,-1,1)$, $B = (1,1,1)$, $D = (5,1,-1)$, e $E = (1,1,-1)$, de um paralelepípedo, cuja distribuição está esquematizada no desenho abaixo.

Determine as coordenadas do ponto $C$.
Encontrar o volume do paralelepípedo.
Determinar o valor da altura $h$ do paralelepípedo em relação à base $ABCD$.
Encontrar a equação do plano $\pi$ que contém a face do paralelepípedo onde está o vértice $E$ e é paralela à face $ABCD$.

1060

Considere a cônica definida pela equação $x^2+xy-1=0.$

Determinar seu centro.
Classificar a cônica.
Esboçar seu gráfico.

284

Verificar se as retas são concorrentes e, em caso afirmativo, encontrar o ponto de interseção:

$$r_1:\; \begin{cases}\frac{x-2}{3}=\frac{y+1}{-3}=\frac{z-2}{4} \end{cases}\ \ \ {\rm e } \ \ \ r_2:\; \begin{cases}x=-1+t\\ y=4-t\\ z=-8+3t\end{cases}$$

As retas não são concorrentes.

704

Ache a equação do círculo com centro $C=(3,-2)$ tangente a $2x-y=0$.

Visto que seu centro é dado, nos basta então encontrar seu raio. Para isso, vamos determinar o ponto de tangencia, digamos, $P=(x_1,y_1)$. Você pode notar, inicialmente, que a reta dada passa pela origem e tem diretor $\vec{v}=(1,2)$. Assim, devemos ter que $\displaystyle (P-C)\cdot\vec{v}=0$, ou seja, $(x_1-3,y_1+2)\cdot (1,2)=0\Longrightarrow x_1+2y_1=-1$. Por outro lado, como $P$ é um ponto da reta
dada, deve cumprir sua equação. Enfim, $P$ pode ser obtido pelo sisteminha $$\begin{cases} x_1+2y_1=-1,
\\ 2x_1-y_1=0, \end{cases}\Leftrightarrow \left(\begin{array}{cccc} 1&2 & \vdots & -1 \\ 2 & -1 & \vdots & 0 \end{array}\right)
\begin{array}{c} {}\\ \sim \\ {}\end{array} \left(\begin{array}{cccc} 1 & 2 & \vdots & -1 \\ 0& -5 & \vdots & 2\end{array}\right). $$ Donde obtemos a solução $$ x_1=\frac{1}{5} \quad\text{e}\quad y_1=-\frac{2}{5}. $$ Segue que o raio é dado então por $r=\|P-c\|=2\sqrt{\dfrac{13}{5}}$. Portanto, a equação procurada do círculo é dada por $$ (x-3)^2+(y+2)^2=\frac{52}{5}.$$

873

Mostre que quaisquer vetores $a, b, c$ satisfazem a relação $$(a\times b)\cdot(c\times d)\;+\;(a\times c)\cdot(d\times b)\;+\;(a\times d)\cdot(b\times c)=0.$$

1015

Encontre a equação da parábola que tem foco no ponto $F = (1,1)$ e tem reta diretriz com equação $y = -x - 2$.

1454

Classifique a superfície $\displaystyle \dfrac{x^2}{36}+\dfrac{y^2}{25}-z=0$ como elipsóide, hiperbolóide de uma folha, hiperbolóide de duas folhas, cone elíptico, parabolóide elíptico ou parabolóide hiperbólico.

1049

Na equação $9x^2-4xy+6y^2=30$, elimine, por meio de uma rotação, o termo $xy$. Identifique o conjunto solução e nos casos em que for uma cônica encontre as coordenadas, no sistema inicial, do(s) foco(s) e esboce o gráfico.

1003

Identifique a seguinte cônica, determinando sua excentricidade, sua equação cartesiana, a equação cartesiana da diretriz e as coordenadas cartesianas do(s) foco(s) e do(s) vértice(s): $r=\frac{5}{2-2cos\theta}$.

1447

Se uma esfera $\displaystyle \dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}+\dfrac{z^2}{a^2}=1$ de raio $a$ for comprimida na direção $z$, então a superfície resultante, chamada de esferóide oblato, tem uma equação da forma $\displaystyle \dfrac{x^2}{a^2}+\dfrac{y^2}{a^2}+\dfrac{z^2}{c^2}=1$, onde $c<a$. Mostre que o esferóide oblato tem um traço circular de raio $a$ no plano $xy$ e um traço elíptico no plano $xz$, com eixo maior de comprimento $2a$ ao longo do eixo $x$ e eixo menor de comprimento $2c$ ao longo do eixo $z$.

868

Verifique se os pontos $A=(1,2,4), B=(-1,0,2), C=(0,2,2) \;\mbox{e}\; D=(-2,1,3)$ estão no mesmo plano ou não.

Não estão pois $\displaystyle \vec{AB}\cdot(\vec{BC}\times\vec{AD})=-8$.

998

Sejam $u = (2,-1,3)$, $v = (0,1,7)$ e $w = (1,4,5)$.

Mostre que existem dois números $\alpha$ e $\beta$ tais que $u\times(v\times w) = \alpha\,v + \beta\,w$.
Mostre que existem dois números $a$ e $b$ tais que $(u\times v)\times w = a\,u + b\,v$.

1369

Construa a curva cujas equações paramétricas são dadas por: $x=\cos\theta$, $y=\cos^2\theta$ e $z=\sin\theta$.

497

Encontre uma equação em coordenadas cilíndricas para a superfície cuja equação em coordenadas cartesianas é dada por $x^2+y^2+z^2=9z$.

1427

Uma viga metálica fina, com extremidades nas coordenadas $A=(-1,4,7)$ e $B=(3,-2,-1)$, deve ser dividida em duas partes iguais. Determine o ponto $C$ que realiza esta divisão.

406

Resolver o sistema linear: \[\left\{\begin{array}{ccccccr}2x_1&+&5x_2&+&12x_3&=& 6 \\3x_1&+&x_2&+&5x_3&=& 12 \\5x_1&+&8x_2&+&21x_3&=& 17\\\end{array}\right. .\]

Esse sistema linear não possui solução.

1410

Seja $T$ a temperatura em um ponto $(x,y,z)$ sobre a reta dada por $$x=t, y=1+t, z=3-2t.$$ A temperatura varia com o espaço de tal forma que $T=25 x^2 y z$. Utilize um recurso computacional para encontrar uma aproximação para a temperatura máxima na parte da reta que se estende do plano $xz$ ao plano $xy$.

1417

Mostre que o sistema linear:
$$ \left\{ \begin{array}{ccccc}a_{11} x &+& a_{12} y & = & b_1\\a_{21} x &+& a_{22} y & = & b_2 \end{array} \right.$$

pode ser escrito em forma matricial $AX=b$, onde:

$$A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}, X = \begin{pmatrix} x \\ y \end{pmatrix}, b = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}.$$

304

Encontre a equação da reta $r$ que passa por $(1,2,-1)$ e é paralela ao eixo $X$.

Ser paralela ao eixo $x$ nos diz que podemos tomar $(1,0,0)$ como um diretor. Assim, a reta pode ser descrita parametricamente como $$ r: (1,2,-1)+t(1,0,0)\quad t\in\mathbb{R}.$$

1643

O lugar geométrico dos pontos do espaço que satisfaz a equação $\displaystyle x^{2/3}+y^{2/3}+z^{2/3}=a^{2/3}$ é denominado esfera astroidal. Mostre que essa superfície pode ser representada parametricamente como \begin{align*} x& = a(\sin u\cos v)^3 \\ y& = a(\sin u\sin v)^3 \\ z & = a (\cos u)^3, \quad (0\leq u\leq \pi, \ 0\leq v\leq 2\pi). \end{align*} Tente esboçar o seu gráfico.

315

Encontre as equações vetoriais e paramétricas para a reta $r$ que passa pelos pontos $A=(1,0,1)$ e $B=(2,3,1)$.

Um vetor diretor pode ser tomado como sendo um mútiplo de $B-A=(1,3,0)$. Assim, a reta procurada terá a seguinte representação vetorial $$\vec{r}= (1,0,1) + t(1,3,0),\quad t\in\mathbb{R}$$ ou, parametricamente $$ \begin{cases} x=1+t, \\ y=3t,\\ z=1, \quad t\in\mathbb{R}.\end{cases}$$

1455

Classifique a superfície $\displaystyle \dfrac{x^2}{36}+\dfrac{y^2}{25}+z^2=1$ como elipsóide, hiperbolóide de uma folha, hiperbolóide de duas folhas, cone elíptico, parabolóide elíptico ou parabolóide hiperbólico.

252

Determine a equação do plano $\pi_1$ que passa por $A = (3, 1,-1), B = (1, 2,-1) \text{ e } C = (1,-1, 0)$.
Determine a equação do plano $\pi_2$ que passa por $D = (-1, 4,-1), E = (2,-1,0)$ e é paralelo ao eixo $y$.
Escreva as equações paramétricas para a reta $r$, interseção dos planos $\pi_1$ e $\pi_2$.
Qual o ângulo entre os planos $\pi_1$ e $\pi_2$?
Qual o ponto $P$ de $\pi_1$ que está mais próximo da origem? (Sugestão: este ponto é tal que $\overrightarrow{OP}$ é ortogonal ao plano $\pi_1$.)

379

Calcule o determinante da matriz:

$
\begin{pmatrix}
1&1&-1\\ -1&0&1\\ -1&-1&0
\end{pmatrix}.
$

$-1$

716

Ache a equação do círculo que passa pelos pontos $(3,4)$, $(-1,2)$ e $(-2,4)$. Ache também seu centro, raio, e faça um esboço de seu gráfico.

412

Dada uma matriz $A = CD$, onde $C^{-1} = \left[\begin{array}{cc} 3 & 2 \\ 1 &3\end{array}\right]$ e $ D^{-1} =\left[\begin{array}{cr} 2 & 5 \\ 3 & -2\end{array}\right]$, resolva o sistema $AX = B$, sabendo que $B=\left[\begin{array}{c} -1 \\0 \end{array}\right]$.

Se $AX=B$ com $A=CD$, tem-se $CDX=B$.

Multiplicando a última expressão por $C^{-1}$ à esquerda: $C^{-1}CDX=C^{-1}B \Rightarrow I_2DX=C^{-1}B$ ou $DX=C^{-1}B$.

E então, multiplicando a expressão resultante por $D^{-1}$ à esquerda: $D^{-1}DX=D^{-1}C^{-1}B$ e $I_2X=D^{-1}C^{-1}B$ ou, equivalentemente, $X=D^{-1}C^{-1}B$.

Como $C^{-1}$ e $D^{-1}$ são dadas, basta realizar as multiplicações, obtendo-se $B=\left[\begin{array}{c} -11 \\7 \end{array}\right]$.

1380

Um construtor tem contratos para construir 3 estilos de casa: moderno, mediterrâneo e colonial. A quantidade de material empregada em cada tipo de casa é dada pela tabela:

\[
\begin{array}{lccccc}
& \text{Ferro} & \text{Madeira} & \text{Vidro} &
\text{Tinta} & \text{Tijolo}\\
\text{Moderno} & 5 & 20 & 16 & 7 & 17\\
\text{Mediterrâneo} & 7 & 18 & 12 & 9 & 21\\
\text{Colonial} & 6 & 25 & 8 & 5 & 13
\end{array}
\]

Se ele pretende construir 5, 7 e 12 casas dos tipos moderno, mediterrâneo e colonial, respectivamente, quantas unidades de cada material serão empregadas?
Suponha que os preços por unidade de ferro, madeira, vidro, tinta e tijolo sejam, respectivamente, 15, 8, 5, 1 e 10. Qual é o preço unitário de cada tipo de casa?
Qual é o custo total do material empregado?

As quantidades de ferro, madeira, vidro, tinta e tijolo serão 146, 526, 260,158 e 388, respectivamente.
O preço unitário dos tipos moderno, mediterrâneo e colonial serão 492, 528 e 465, respectivamente.
O custo total do material empregado para construir 5 casas do estilo moderno, 7 casas do estilo mediterrâneo e 12 casas do estilo colonial é 11736.

1457

Classifique a superfície $\displaystyle \dfrac{x^2}{36}+\dfrac{y^2}{25}-z^2=1$ como elipsóide, hiperbolóide de uma folha, hiperbolóide de duas folhas, cone elíptico, parabolóide elíptico ou parabolóide hiperbólico.

1217

Reduza a equação $4x^2+3y^2-z^2-12xy+4xz-8yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

1084

Identifique a cônica descrita pela equação $x^2-6xy-7y^2+10x-30y+23=0$.

278

Determinar as equações paramétricas e representar graficamente a reta que passa por $A(4,-3,-2)$ e tem a direção de $3i\;-\;2j$.

$r:(x,y,z)=(4+3t,-3-2t,-2)$.

780

Encontre o ponto $Q$ sabendo que o mesmo é a extremidade de um vetor com origem no ponto médio do segmento que liga os pontos $P_1=(1,1,3)$ e $P_2=(-1,1,1)$ e tem norma, direção e sentido do vetor $v=(-1,0,1)$.

$(−1,1,3)$.

1456

Classifique a superfície $\displaystyle \dfrac{x^2}{36}-\dfrac{y^2}{25}+z=0$ como elipsóide, hiperbolóide de uma folha, hiperbolóide de duas folhas, cone elíptico, parabolóide elíptico ou parabolóide hiperbólico.

504

Para cada um dos pontos abaixo faça a mudança de coordenadas de cartesianas para polares:

$(7,7)$,
$(1,-\sqrt{3})$,
$(-3,-3\sqrt{3})$,
$(0,7)$,
$(0,-2)$.

509

A hipérbole $\ell$ tem focos $F_1$, $F_2$ e vértices $A_1$, $A_2$. Encontrar equações paramétricas de $\ell$ se

$F_1=(2,0)$, $F_2=(8,0)$, $A_1=(3,0)$, $A_2=(7,0)$;
$F_1=(0,0)$, $F_2=(4,8)$, $A_1=(1,2)$, $A_2=(3,6)$.

1158

Ache o ângulo entre duas retas no espaço que passam pela origem, no primeiro octante, sendo uma delas com ângulos diretores tais que $\cos \alpha_1=\cos \beta_1$, $\cos \gamma_1=1/3$; e a outra com ângulos diretores tais que $\cos \alpha_2=\cos \beta_2$, $\cos \gamma_2=1/4$ (Sugestão: cada par de retas forma um plano que contém um dos eixos coordenados -- por quê?).

$\cos^{-1} (1/4) - \cos^{-1} (1/3)$.

1426

Um trecho de uma estrada passa sob três viadutos. Aproximadamente, a estrada pode ser considerada como pertencente ao plano $\pi: 5x+4y+20z-20=0$, e os viadutos têm seus pontos mais baixos nas retas: $r_1: X=(5,6,3)+t(4,0,-1)$, $r_2: X=(3,3,4)+t(0,5,-1)$ e $r_3=(2,6,4)+t(4,5,-2)$. As medidas são consideradas em metros. Determine aproximadamente a altura máxima dos veículos que podem trafegar na estrada.

396

Resolva a equação $f(x)=0$, onde $f(x)=\det(A-xI)$ e

$
A = \begin{pmatrix}
2&-2&0\\ -2&3&-2\\
0&-2&4
\end{pmatrix}.
$

$x=0$, $x=3$ e $x=6$

1645

Mostre que a equação de uma superfície cônica com vértice num ponto $P_0=(x_0,y_0,z_0)$ e curva diretriz situada no plano $z=c$ com equação $f(x,y)=0$ é $$f(x_0+\dfrac{c-z_0}{z-z_0}(x-x_0), y_0+\dfrac{c-z_0)}{z-z_0}(y-y_0))=0. $$

769

Verifique se os seguintes pontos são colineares: $A=(1,0,1)$, $B=(2,2,0)$ e $C=(0,-2,2)$.

Os pontos são colineares.

236

Considere a reta $r$ de equação \[
\frac{x-1}{2}\ =\ y-2\ =\ \frac{z-2}{3}
\] e considere o plano $\pi $ de equação $2x+y+z=-2$. Determine a equação do plano $\alpha $ que contém a reta $r$ e é perpendicular ao plano $\pi $.

$-x+2y=3.$

360

Sejam $A,B$ e $C$ matrizes reais tais que $AB=AC$. Se existir uma matriz $Y$ tal que $YA=I$, onde $I$ é a matriz identidade, então podemos concluir que $B=C$?

Sim, pois se $Y$ é uma inversa à esquerda de $A$, então podemos multiplicar ambos os lados, à esquerda, da equação $AB=BC$ e então teremos que
\[ B=IB=(YA)B=Y(AB)=Y(AC)=(YA)C=IC=C.\]

477

Nesta questão, todos os sistemas de coordenadas têm mesma origem $O$. Sejam $(x,y,z)$ coordenadas em relação à base usual $\{i,j,k\}$; $(u,v,w)$ coordenadas em relação à base $\beta =\{j,i,i-j+k\}$ e $(r,s,t)$ coordenadas em relação à base $\gamma =\{k,i-j,i+j\}$. Dado um ponto $P\in\mathbb{R}^3$, escrito na base $\beta$ como $P_{\beta} = (3,2,1)$, ache $P_{\gamma}$, isto é, $P$ na base $\gamma$.

1074

Identificar a cônica $8y^2+6xy-12x-26y+11=0$ e calcular os focos, diretrizes, e assíntotas (quando couber).

874

Sejam $a,b,c$ três vetores não coplanares e denotemos por $[a,b,c]$ o produto misto $a\cdot(b\times c)$. Os vetores

$$a'=\frac{b\times c}{[a,b,c]},\; b'=-\frac{a\times c}{[a,b,c]},\; c'=\frac{a\times b}{[a,b,c]}$$

são chamados os vetores recíprocos aos vetores $a,b,c$.

Uma das utilidades dos vetores recíprocos consiste em encontrar as coordenadas de um vetor $v$ qualquer em termos dos vetores $a,b,c$. Isto é, queremos encontrar escalares $x,y,z$ tais que

$$ v=xa+yb+zc. $$

Mostre que, $$v = (v\cdot a')a \; + \; (v\cdot b')b \;+\; (v\cdot c')c.$$ Ou seja,
$$ x=v\cdot a', \; y=v\cdot b', \; z=v\cdot c'. $$
Mostre que se $a,b,c$ são três vetores unitários, dois a dois ortogonais e que satisfazem a regra da mão direita, então $a'=a$, $b'=b$ e $c'=c$ (ou seja, neste caso os vetores recíprocos de $a,b,c$ são eles próprios). Em particular, segue que $$v = (v\cdot a) a \; + \; (v\cdot b) b \;+\; (v\cdot c) c.$$
Verifique que se
$$ v=xa'+yb'+zc', $$
então $$v = (v\cdot a)a' \; + \; (v\cdot b)b' \;+\; (v\cdot c)c'.$$
Mostre que valem as relações
$$ a'\cdot a = b'\cdot b = c'\cdot c =1,$$
$$a'\cdot b =a'\cdot c = b'\cdot a = b'\cdot c = c'\cdot a = c'\cdot b = 0. $$
Em outras palavras, o produto escalar de vetores correspondentes é $1$, enquanto que o produto escalar de vetores não-correspondentes é $0$.
Reciprocamente, mostre que se
$$ A\cdot a = B\cdot b = C\cdot c =1,$$
$$A\cdot b = A\cdot c = B\cdot a = B\cdot c = C\cdot a = C\cdot b = 0, $$
então
$$ A=a', \; B=b', \; C=c'.$$
Conclua que os vetores recíprocos de $a',b',c'$ são exatamente $a,b,c$.

474

Considere o subconjunto de vetores $\mathcal{B} =\{(1,1,-2),(1,-1,0),(1,1,1)\}$.

Mostre que $\mathcal{B}$ é uma base para $\mathbb{R}^{3}$.
Encontre a matriz de mudança de coordenadas $A$ da base canônica $\{i,j,k\}$ de $\mathbb{R}^{3}$ para a base $\mathcal{B}$. Qual é matriz de mudança de coordenadas $A^{\prime}$ da base $\mathcal{B}$ para a base canônica?
Quais são as coordenadas dos vetores canônicos $i,j$ e $k$ em relação à base $\mathcal{B}$?
Se o ponto $P$ tem coordenadas $(1,-2,5)$ no sistema $\{O,i,j,k\}$, quais são as coordenadas de $P$ no sistema $\{O,\mathcal{B}\}$?

Como eles são ortogonais dois a dois e dim $\!\mathbb{R}^{3}=3$, eles são L.I.
$A^{\prime}=\left[\begin{array}[c]{rrr}1 & 1 & 1\\1 & -1 & 1\\-2 & 0 & 1\end{array}\right] ;A=(A^{\prime})^{-1}=\left[\begin{array}[c]{rrr}
\frac{1}{6} & \frac{1}{6} & -\frac{1}{3}\\\overset{}{\frac{1}{2}} & -\frac{1}{2} & 0\\\overset{}{\frac{1}{3}} & \frac{1}{3} & \frac{1}{3}\end{array}\right] $.
São as colunas de $A$, respectivamente: $\left(
\frac{1}{6},\frac{1}{2},\frac{1}{3}\right) ,\left( \frac{1}{6},-\frac{1}%
{2},\frac{1}{3}\right) $ e $\left( -\frac{1}{3},0,\frac{1}{3}\right) $.
$\left( -\frac{11}{6},\frac{3}{2},\frac{4}{3}\right) $.

1641

Um navio ao mar está no ponto $A$ que está localizado a $60^\circ$ de longitude oeste e $40^\circ$ de latitude norte. O navio viaja ao ponto $B$ que está a $40^\circ$ de longitude oeste e $20^\circ$ de latitude norte. Supondo que a Terra seja uma esfera com raio de $6370$ Km, determine a menor distância que o navio pode pode viajar indo de $A$ para $B$, dado que a menor distância entre os dois pontos sobre uma esfera está ao longo do arco do círculo máximo que une os pontos. [Sugestão: usando o sistema de coordenadas esféricas, considere o ângulo entre os vetores do centro da Terra aos pontos $A$ e $B$. Se o termo "círculo máximo" lhe for estranho, consulte um dicionário.]

351

Qual é o valor de $c_{23}$ na multiplicação das matrizes abaixo?

\[\left(\begin{array}[c]{rr}1 & -2\\5 & -2\\-4 & 4\\-1 & 2\end{array}\right) \left(\begin{array}
[c]{rrrr}-5 & 1 & 5 & -4\\-2 & 5 & 2 & 2\end{array}
\right) =\left(\begin{array}[c]{cccc}c_{11} & c_{12} & c_{13} & c_{14}\\c_{21} & c_{22} & c_{23} & c_{24}\\c_{31} & c_{32} & c_{33} & c_{34}\\c_{41} & c_{42} & c_{43} & c_{44}\end{array}\right) .\]

Note que, como o enunciado apenas pede o valor da entrada $c_{23}$, basta multiplicar a linha $2$ da primeira matriz pela coluna $3$ da outra:

\[c_{23}=\left(\begin{array}{cc} 5 & -2 \end{array}\right)\left(\begin{array}{c} 5 \\ 2 \end{array}\right) = 5\cdot5 -2\cdot2 =21.\]

501

Encontre uma equação em coordenadas cartesianas para a superfície cuja equação em coordenadas esféricas é dada por $r=2\tan\theta$.

Usando a definição de coordenadas esféricas, a equação dada fica: $\displaystyle (x^2+y^2)(z^2-4)+z^4=0$.

1349

A cúbica retorcida $T(t) = (t, t^2, t^3)$ (e suas primas) aparece em geometria algébrica. Mostre que se $a$, $b$, $c$ e $d$ são números reais distintos, então os pontos $T(a)$, $T(b)$, $T(c)$ e $T(d)$ não pertencem a um único plano em $\mathbb{R}^3$. (Dica: primeiro resolva o problema correspondente para a parábola em $\mathbb{R}^2$.)

1418

Uma piscina olímpica pode ser vista como um paralelepídeo. Pesquise as medidas padronizadas de uma piscina olímpica e e calcule, utilizando o produto misto, o volume de água utilizado para enchê-la. Defina o sistema de coordenadas e os três vetores do produto misto de forma a facilitar as contas.

1224

Reduza a equação $3x^2+3z^2+4xy+8xz+4yz$ de forma a identificar a quádrica que ela representa e esboce o seu gráfico.

821

Para o par de vetores $u=(2,0,0)$ e $v=(3,5,4)$, encontrar a projeção ortogonal de $v$ sobre $u$ e decompor $v$ como soma de $v_{1}$ com $v_{2}$, sendo $v_{1} \parallel u$ e $v_{2}\perp u$.

$\textrm{proj}_{u}{v}=(3,0,0)$.

$v_1=(3,0,0)$ e $v_2=(0,5,4)$.

502

Encontre uma equação em coordenadas cartesianas para a superfície cuja equação em coordenadas esféricas é dada por $r=9\sec\phi$.

Usando a definição, a equação dada fica: $\displaystyle x^2+y^2+z^2=\frac{81}{x^2}(x^2+y^2).$

1640

As coordenadas esféricas estão relacionadas com as coordenadas em longitude e latitude usadas na navegação. Para ver como, vamos definir um sistema de coordenadas retangulares satisfazendo a regra da mão direita, com sua origem no centro da Terra, o seu eixo $z$ positivo passando pelo Pólo Norte e o seu eixo $x$ positivo passando pelo meridiano principal. Supondo a Terra uma esfera de raio $\rho=4000$ milhas, então cada ponto sobre a Terra tem coordenadas esféricas da forma $(4000,\theta,\phi)$, onde $\phi$ e $\theta$ determinam a latitude e a longitude do ponto. É comum especificar longitudes em graus leste ou oeste do meridiano principal e latitudes em graus norte ou sul do Equador. A cidade de New Orleans, nos EUA, está localizada a $90^\circ$ de longitude oeste e $30^\circ$ de latitude norte. Determine as coordenadas esféricas e retangulares associadas a esta localização (suponha que a distância esteja em milhas).

Uma longitude de $90^\circ$ oeste corresponde a $\theta=360^\circ-90^\circ=270^\circ$ ou $\theta=3\pi/2$ radianos; enquanto $30^\circ$ de latitude norte corresponde a $\phi=90^\circ-30^\circ=60^\circ$ ou $\phi=\pi/3$ radianos. Assim, as coordenadas esféricas $(\rho, \theta,\phi)$ de New Orleans são $(4000,3\pi/2,\pi/3)$. Para determinarmos as coordenadas rectangulares, aplicamos as fórmulas de conversão de esféricas para retangulares. Assim, obteremos \begin{align*} x &=4000\sin\dfrac{\pi}{3}\cos\dfrac{3\pi}{2}=4000\dfrac{\sqrt{3}}{2}(0)= 0\ \text{milhas} \\ y & = 4000\sin\dfrac{\pi}{3}\sin\dfrac{3\pi}{2}=4000\dfrac{\sqrt{3}}{2}(-1)=-2000\sqrt{3}\ \text{milhas} \\ z& = 4000\cos\dfrac{\pi}{3}=4000(\dfrac{1}{2})=2000\ \text{milhas}.\end{align*}

955

Identifique a quádrica definida pela equação reduzida $\dfrac{x^2}{6}+\dfrac{y^2}{5}+\dfrac{z^2}{3}=1$ e esboce seu gráfico.

321

Para o par de retas $r$ e $r^{\prime}$ abaixo encontre o ponto de interseção, $r\cap r^{\prime}$, se existir. E nos casos em que a interseção é vazia decida se elas são paralelas ou reversas.

$r:$ $\left\{ \begin{array}{c} 3x-y-z=0 \\ 8x-2y-3z=-1\end{array} \right.$ e $r^{\prime}: \left\{ \begin{array}{c}x-3y+z=-3 \\ 3x-y-z=-5\end{array} \right. .$

Neste caso, a intersecção é vazia e as retas são paralelas. De fato, note que os vetores $(3,-1,-1)\times(8, -2, -3)=(1,1,2)$ e $(1, -3, 1)\times(3,-1,-1)=(4,4,8)$ são múltiplos entre si (linearmente dependentes).

279

Determinar as equações paramétricas e representar graficamente a reta que passa por $A(4,-3,-2)$ e $B(3,3,4)$.

$r:(x,y,z)=(3-t,3+6t,4+6t).$

986

O vetor $w$ é ortogonal aos vetores $u=(2,3,-1)$ e $v=(1,-2,3)$ e $w\cdot(2,-1,1) = -6$. Encontre $w$.

$w=(-3,3,3)$

318

Encontre as equações vetoriais e paramétricas para a reta $r$ que é perpendicular ao plano $2x-y+2z=4$ e passa pelo ponto de interseção das retas $r_1$ e $r_2$ dadas por: $$
r_1: \left\{\begin{array}{ccr}
x&=&t \\ y&=&2+t \\ z&=&1+t
\end{array}\right.,\,\,\, t\in \mathbb{R} \;\;\;\;\;\; \mbox{e} \;\;\;\;\;\;
r_2:\left\{\begin{array}{ccr}
x&=&-1+2s \\ y&=&1+s \\ z&=&0
\end{array}
\right.,\;\;s\in \mathbb{R}.$$

Usando escalonamento, obtemos que o ponto de intersecção ocorre para os valores $s=0$ e $t=-1$ dos respectivos parâmetros. Ou seja, as retas $r_1$ e $r_2$ se intersectam no ponto $(-1,1,0)$. Como $r$ é perpendicular ao plano, então podemos tomar a normal $(2,-1,2)$ como um vetor diretor. Portanto, a reta procurada pode ser descrita vetorialmente como $$\vec{r}=(-1,1,0)+t(2,-1,2),\quad t\in\mathbb{R},$$ ou ainda, parametricamente, como sendo $$\begin{cases} x=-1+2t,\\y=1-t,\\z=2t,\quad t\in\mathbb{R}. \end{cases}$$

459

Seja $X_{o}$ uma solução particular de um sistema $AX = B$, e $Y$ a solução geral do sistema homogêneo associado, $AX = {\bf 0}$. Temos então que $X_{o} + Y$ é a solução geral do sistema $AX = B$.

Encontre as soluções gerais do sistema homogêneo associado ao sistema linear a seguir. Encontre também a solução geral do sistema da forma $X_{o} + Y$.

\[\left\{\begin{array}{ccccccccccr}&&x_1&+&x_2&-&x_3&+&2x_4&=&6 \\&-&x_1&+&x_2&+&4x_3&-&3x_4&=&-2 \\&&&&x_2&+&3x_3&+&x_4&=& 5 \\&&&&x_1&+&5x_2&+&5x_3& =&14 \\\end{array}\right. . \]

$Y=(0,0,0,0)^T$.
$X_o=(4,1,1,1)^T$.
$X_o+Y=(4,1,1,1)^T$.

834

Determinar os ângulos internos de um triângulo $ABC$, sendo$A=(3,-3,3)$, $B=(2,-1,2)$ e $C=(1,0,2)$.

1018

Encontre os vértices (ou vértice), os focos (ou foco) e a excentricidade da cônica descrita por $3x^2-14y=0$. Esboce também o gráfico.

Exercícios

MA141 - Geometria Analítica