Equações e Inequações

913

Determine o conjunto de todos os números reais para os quais a expressão $\frac{\sqrt{4-x^2}}{\sqrt[3]{x-1}}$ está definida.

914

Qual a solução geral da dupla desigualdade $-2<x^2-3<\frac{1}{5}$?

904

Resolva a equação $|x + 1| = 3$.

Temos dois casos: $x+1=3$ ou $x+1=-3$. Resolvendo cada uma dessas equações de primeiro grau obtemos $x=2$ e $x=-4$.

915

Determine o conjunto de todos os números reais para os quais a expressão $\sqrt{x}{1-x^2}$ está definida.

909

Resolva a inequação $|ax-b|<r$ na variável x, com $r>0$ e $a\neq 0$.

Se $ax-b\geq0$: $|ax-b| = ax-b$, logo $ax-b<r \Rightarrow x < \dfrac{b+r}{a}$.
Se $ax-b<0$: $|ax-b| = -(ax-b)$, logo $-ax+b<r \Rightarrow x > \dfrac{b-r}{a}$.
Portanto $x<\dfrac{b+r}{a}$ ou $x>\dfrac{b-r}{a}$.

906

Perguntei a idade de minha professora de Matemática. Ela me contou e falou também a idade da filha, mas disse isso de modo enigmático por meio da expressão: "A soma de minha idade com a da minha filha é 44 anos. Dez anos atrás, eu tinha o triplo da idade dela."

"Traduza" a primeira frase da expressão da professora por uma equação, representando por $x$ a idade da professora e por $y$, a idade de sua filha.
Faça o mesmo com a segunda frase.
Resolva o sistema obtido e dê a idade da professora e a de sua filha.

Seja $x$ a idade da professora e $y$ a idade da filha. Temos, portanto

$x+y=44$
$x-10=3(y-10)$, ou, reescrevendo com as incógnitas do lado esquerdo, $x-3y=-20$
Resolver $\begin{pmatrix} 1 & 1 \\ 1 &-3 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 44 \\ -20 \end{pmatrix}$ nos dá $\begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 28 \\ 16 \end{pmatrix}$

608

Use a desigualdade triangular $\left| a+b\right| \leq \left| a\right|+\left| b\right| $\emph{ }para mostrar que $\left| x-y\right| \geq \left|x\right| -\left| y\right| $ para todo $x,y\in \mathbb{R}$. Em particular, conclua que $\left| x-y^{2}\right| \geq \left| x\right| -y^{2}.$

911

Sabendo-se que $\frac{x-a}{x^2+1} > \frac{x+a}{x^2}$ para todo $x$ real, determine o intevalo a que pertence o número real $a$.

610

Mostre que $\sqrt{xy}\leq {\frac{x+y}{2}}$$\forall x,y\geq 0$.

Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles.

1464

A Lei de Ohm para circuitos elétricos, afirma que a queda de tensão em um resistor $R$ sob corrente $I$ é $V=RI$. Uma empresa recebeu pedidos de fornecimento de resistores para um circuito como o da figura a seguir. Neste circuito, $V=120V$ e, para atender as especificações de segurança e de funcionamento desejado do circuito, a corrente deve ser $I=5\pm0,1A$. Em que intervalo $R$ deve ficar para que $I$ esteja dentro da margem de segurança?

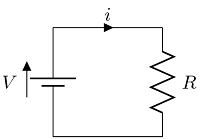
fig_intervalo_1.reduzida.png

Pela Lei de Ohm, conseguimos escrever que $I=\frac{V}{R}$. Para $V=120V$ fixo, a corrente depende portanto apenas do valor da resistência, sendo inversamente proporcional a esta.

A corrente deve estar no intervalo $4,9 \leq I \ leq 5,1$. Temos que $R_{max}=\frac{120}{I_{min}}\approx 24,49$ e $R_{min}=\frac{120}{I_{max}}\approx 23,53 \Omega$.

Portanto, $23,53 \leq R \leq 24,49$.

912

Resolva a inequação $\frac{x^2+2x-1}{x^2-1} \geq \frac{1}{x+1}$.

611

Suponha que $x$ e $y$ sejam notas de provas bimestrais. Mostre que a chamada {\it média geométrica} entre $x$ e $y$, dada por $\sqrt{xy}$, poderia, se adotada como critério avaliativo, prejudicar a nota final de alguns alunos, isto é, elaé menor que ou igual à chamada {\it média aritmética} entre $x$ e $y$, que é dada por $\frac{x+y}{2}.$

Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles. Sendo assim, se o professor adotar como critério de avaliação a média geométrica em vez da aritmética, ele pode prejudicar a nota final dos alunos que tivessem a nota $x$ diferente da $y$, pois quando $x=y$ as duas médias são iguais.

901

Resolva a equação $x^4-13x^2 + 36 = 0$.

Chamando $x^2=y$, transformamos a equação para:
$y^2 -13y + 36=0$. Resolvendo esta equação:
$\Delta = 13^2-4.1.36 = 25.$
$y = \dfrac{13 \pm \sqrt{25}}{2}.$
Assim as soluções são: $y = 9$ ou $y = 4$.
Substituindo em $y=x^2$:
$x^2 = 9 \Rightarrow x = \pm 3$.
$x^2 = 4 \Rightarrow x = \pm 2$.
Portanto as soluções são $x=-2$, $x=2$, $x=-3$ e $x=3$.

902

Resolva a equação $\displaystyle \frac{x}{1-x} + \frac{x-2}{x}-1 = 0$.

916

Determine o conjunto solução da equação $|x|^2+|x|-6=0$.

1465

Uma empresa de motores solicitou a fabricação de cilindros com área de seção transversal $A=9cm^2$ (Ou seja, com diâmetro $D=3,385cm^2$). Entretanto, o funcionário que respondeu à solicitação perguntou qual era a margem de erro permitida no diâmetro do cilindro.
Dado que para o correto funcionamento dos motores o cilindro deve ter uma área $A$ tal que $|A-9|<0,01 cm^2$, e que a área da seção transversal do cilindro é dada por $A=\pi \left(\frac{D}{2}\right)^2$, em qual intervalo deve estar o valor do diâmetro do cilindro para atender tal especificação?

615

Esboce o gráfico da função abaixo e resolva a inequação:

$f\left( x\right) =\left\vert x-1\right\vert -\left\vert x+2\right\vert >x$.

905

Resolva a equação modular $|x-1|-2|x-2| =-3$.

614

Esboce o gráfico da função abaixo e resolva a inequação:

$f\left( x\right) =\left\vert x-2\right\vert +\left\vert x-1\right\vert >1$.

1199

Resolva a equação $\left| {\frac{3x+8}{2x-3}}\right| =4$.

616

Esboce o gráfico da função abaixo e resolva a inequação:

$f\left( x\right) =\left\vert 2x^{2}-1\right\vert <1$.

903

Resolva a equação $\sqrt{9x+4} + \sqrt{3x-4} = 2 \sqrt{3x}$.

613

Esboce o gráfico da função abaixo e resolva a inequação:

$f\left( x\right) =\dfrac{\left( x-3\right) }{x^{2}+1}<0$.

910

Quais os valores de $x$ que satisfazem a inequação $\frac{x-3}{x-2}\leq x-1$?

908

Resolva a equação $|2x+1|=3$.

Temos dois casos: $2x+1=3$ ou $2x+1=-3$. Resolvendo cada uma dessas equações de primeiro grau obtemos $x=1$ e $x=-2$.

609

Sejam $x$ e $y$ dois números reais positivos. Demonstre que $\sqrt{xy}\leq \dfrac{x+y}{2}.$

Elevando ambos os membros da expressão $\sqrt{xy}\leq \dfrac{x+y}{2}$ ao quadrado obtemos $xy\leq \dfrac{x^2+2xy+y^2}{4}$. Simplificando chegamos a $x^2-2xy+y^2=(x-y)^2 \geq0$. Como a última expressão obtida é verdadeira e todas as expressões são equivalentes entre si, segue o resultado. Esse resultado diz que a média geométrica entre dois dois números reais positivos é sempre menor que, ou igual, à média aritmética entre eles.

612

Esboce o gráfico da função abaixo e resolva a inequação:

$f\left( x\right) =\left( 2x-3\right) \left( x^{2}+1\right) <0$.