LISTA DE DISCIPLINAS

| MA111 - Cálculo I | Limite e continuidade | Limites infinitos e Assíntotas verticais

Limites infinitos e Assíntotas verticais

Selecione os exercícios por

Dificuldade

Categoria

Outros

Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.

1030   

Utilizando o gráfico, avalie os seguintes limites para a  função

$ f(x) = \frac{1}{(x-3)(x-5)^2}$.

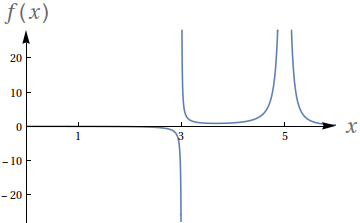
fig_assintotas_verticais_2.png

  1. $ \lim\limits_{x\to 3^-} f(x)$

  2. $ \lim\limits_{x\to 3^+} f(x)$

  3. $ \lim\limits_{x\to 3} f(x)$

  4. $ \lim\limits_{x\to 5^-} f(x)$

  5. $ \lim\limits_{x\to 5^+} f(x)$

  6. $ \lim\limits_{x\to 5} f(x)$

  1. $-\infty$
  2. $\infty$
  3. O limite não existe
  4. $\infty$
  5. $\infty$
  6. $\infty$

1342   

Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{x-1}$.



$x=1$.

1029   

Utilizando o gráfico, avalie os seguintes limites para a  função

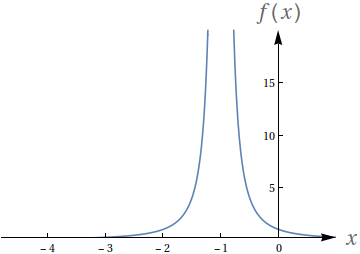
fig_assintotas_verticais_1.png
$f(x) = \frac{1}{(x+1)^2}$

  1. $ \lim\limits_{x\to -1^-} f(x)$

  2. $ \lim\limits_{x\to -1^+} f(x)$

  1. $\infty$
  2.  $\infty$

1341   

Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{(x-1)^2}$.


As assíntotas verticais são os pontos $x$ tais que o limite é infinito.

Para $f(x)=\frac{x^2+1}{(x-1)^2}$ temos que:

$\lim \limits_{x \to 1} \frac{x^2+1}{(x-1)^2} = \infty$,

Logo $x=1$ é uma assíntota vertical de $f$. Como não há mais pontos no domínio de $f$ que podem levar a um limite infinito, esta é a única assíntota.

1714   

  1. Defina $\displaystyle \lim_{x \to a^+} f(x) = \infty$ e $\displaystyle \lim_{x \to a^-} f(x) = \infty$. Se estiver muito difícil, escreva em palavras.

  2. Mostre que $\displaystyle \lim_{x \to 0^+} \dfrac{1}{x} = \infty$.

  3. Mostre que $\displaystyle \lim_{x \to 0^+} f(x) = \infty$ se e somente se $\displaystyle \lim_{x \to \infty} f\left(\dfrac{1}{x}\right) = \infty$.

751   

Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 1}\ln \dfrac{x^{2}-1}{x-1}$.

$ln2$.

749   

Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{e^{x^{2}}-1}{x}$.

$0$.

750   

Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0^{+}}\log _{\dfrac{1}{3}}x$.

$\infty$.

1130   

Aproxime numericamente o seguinte limite
  $ f(x)= \frac{x^2+5 x-36}{x^3-5 x^2+3 x+9}$


  1.  \begin{array}{cc}
      x & f(x) \\ \hline
      2.9 & -335.64 \\
       2.99 & -30350.6 \\
        \end{array}
       A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-\infty$.  
  2.   \begin{array}{cc}
      x & f(x) \\ \hline
       3.1 & -265.61 \\
       3.01 & -29650.6 \\
        \end{array}
        A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =-\infty$.
  3. As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =-\infty$.

1129   

Aproxime numericamente o seguinte limite
  $ f(x)=\frac{x^2-9 x+18}{x^2-x-6}$

  1.  \begin{array}{cc}
      x & f(x) \\ \hline
      2.9 & -0.632 \\
      2.99 & -0.6032 \\
      2.999 & -0.60032 \\
      \end{array}
    A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =-0.6$.
  2.  \begin{array}{cc}
      x & f(x) \\ \hline
       3.1 & -0.5686 \\
      3.01 & -0.5968 \\
      3.001 & -0.59968 \\
        \end{array}
    A tabela parece indicar que   $\lim\limits_{x\to3^+}f(x) =-0.6$.
  3. As tabelas parecem indicar que   $\lim\limits_{x\to3}f(x) =-0.6$.

748   

Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\dfrac{e^{2x}-1}{x}$.

$2$.

746   

Ache as assíntotas verticais e inclinadas; depois calcule os limites laterais nas assíntotas verticais da função $f\left( x\right) =\frac{x^{3}-3x-1}{x^{2}-x}.$

747   

Calcule o seguinte limite:
$\lim\limits_{x\rightarrow 0}\left( 1+2x\right) ^{\dfrac{1}{x}}$.

$e^2$.

1131   

Aproxime numericamente o seguinte limite

  $ f(x)=\frac{x^2-11 x+30}{x^3-4 x^2-3 x+18}$


  1.   \begin{array}{cc}
      x & f(x) \\ \hline
      2.9 & 132.857 \\
       2.99 & 12124.4 \\
        \end{array}
       A tabela parece indicar que $\lim\limits_{x\to3^-}f(x) =\infty$.
  2.     \begin{array}{cc}
      x & f(x) \\ \hline
       3.1 & 108.039 \\
       3.01 & 11876.4 \\
        \end{array}
        A tabela parece indicar que $\lim\limits_{x\to3^+}f(x) =\infty$.
  3.   As tabelas parecem indicar que $\lim\limits_{x\to3}f(x) =\infty$.

1343   

Obtenha as assíntotas verticais de $f(x)=\frac{x^2+1}{x}$.



$x=0$.

1132   

Classifique as afirmações a seguir como verdadeiras ou falsas:

  1.      Se $ \lim\limits_{x\to 5} f(x) = \infty$, então estamos implicitamente afirmando que o limite em questão existe.
  2.      Se $ \lim\limits_{x\to 1^-} f(x) = -\infty$, então $ \lim\limits_{x\to 1^+} f(x) = \infty$.
  3.      Se $ \lim\limits_{x\to 5} f(x) = \infty$, então $f$ tem uma assíntota vertical em $x=5$.
  4.      $\infty/0$ não é uma forma indeterminada.


    

  1.  Falsa.
  2.  Falsa
  3.  Verdadeira
  4.  Verdadeira