LISTA DE DISCIPLINAS

| MA111 - Cálculo I | Limite e continuidade | Limites no infinito e Assíntotas horizontais

Limites no infinito e Assíntotas horizontais

Selecione os exercícios por

Dificuldade

Categoria

Outros

Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.

48   

Classifique as afirmações a seguir como verdadeiras ou falsas:

  1. Se $ \lim\limits_{x\to \infty} f(x) = 5$, então estamos implicitamente afirmando que o limite em questão existe.

  2. $\infty/0$ não é uma forma indeterminada.

  1. Verdadeira

  2. Verdadeira

724   

Calcule o limite:


$\lim\limits_{x\rightarrow -\infty }\left( x-\sqrt{x^{2}+4x}\right)$.

$-\infty$.

32   

Calcule os seguintes limites:

  1. $\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{2}+3}\right)$

  2. $\lim\limits_{x\rightarrow -\infty }\left( x-\sqrt{x^{2}+3}\right)$

  3. $\lim\limits_{x\rightarrow \infty } \left( \sqrt{x+1}-\sqrt{x+3}\right)$

  1. $0$
  2. $-\infty$
  3. $0$

729   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow -\infty }\left( 2^{x}+2^{-x}\right) $.

$-\infty$.

730   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow \infty }\log _{3}x$.

$\infty$.

1712   

  1. Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(N,+\infty)$, os valores da função $f(x)=1/x^2$ estejam no máximo a $0,1$ unidade de $L=0$. Encontre $N$.

  2. Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(N,+\infty)$, os valores da função $f(x)=x/(x+1)$ estejam no máximo a $0,01$ unidade de $L=0$. Encontre $N$.

  3. Seja $N$ um número positivo tal que, para cada $x$ no intervalo $(-\infty,N)$, os valores da função $f(x)=1/x^3$ estejam no máximo a $0,001$ unidade de $L=0$. Encontre $N$.

  4. Seja $N$ um número positivo tal que, para cada $x$ no intervalo  $(-\infty,N)$, os valores da função $f(x)=x/(x+1)$ estejam no máximo a $0,001$ unidade de $L=0$. Encontre $N$.

42   

Determine todas as assíntotas horizontais da função $f(x) = \frac{x^2-1}{-x^2-1}$.

$y=-1$.

725   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow \infty }3^{x}$.

$\infty$.

731   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow \infty }\ln \dfrac{x}{x+1}$.

$0$

40   

Calcule o limite $\lim\limits_{x\rightarrow \infty }\log _{3}x$.

$\infty$.

34   

Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{3}-6x-3}{6x^{2}+28x+2}$.

  $\infty$

55   

Sabemos que limites que tomam a forma indeterminada ``$\infty-\infty$" exigem um pouco mais de trabalho para serem calculados. Calcule, de forma adequada, o limite $\lim\limits_{x\rightarrow\infty}\left(\sqrt{2x^2-7}-x\right)$.

30   

Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{4}-2x+1}{4x^{4}+2x+3}$.

$5/4$

6   

Calcule o limite $\lim\limits_{x\rightarrow \infty }\left( 5+\dfrac{1}{x}+\dfrac{4}{x^{2}}\right)$.

$5$

1711   

É possível mostrar que, sob certas condições, a velocidade $v(t)$ de uma gota de chuva caindo no instante $t$ é:

$$v(t) = v^\star \left(1-\exp\left(-\dfrac{gt}{v} \right)\right),$$

onde $g$ é a aceleração da gravidade e $v^\star$ é a velocidade final da gota.

  1. Calcule a velocidade para um tempo muito grande, isto é, calcule $\displaystyle \lim_{t \to \infty} v(t)$.

  2. Considerando $v^\star = 1$m$/$s e $g=9,8$m$/$s$^2$, faça o gráfico de $v(t)$. Quanto tempo levará para a velocidade da gota atingir $99\%$ de sua velocidade final?

52   

Construa os gráficos das funções indicadas e calcule os limites:

  1. $ f(x)=x^2$ quando $x\rightarrow\infty$

  2. $ h(x)=3x^5$  quando $x\rightarrow -\infty$

  3. $g(y)=\tan^{-1}(y)$ quando $y\rightarrow\infty$

  4. $f(x)=\frac{1}{x}$  quando $x\rightarrow -\infty$

  5. $f(x)=\frac{1}{x^7}$  quando $x\rightarrow \infty$

  6. $f(x)=\frac{1}{x^{-2}}$  quando $x\rightarrow \infty$

1709   

Encontre os seguintes limites em termos do número $\alpha = \displaystyle \lim_{n \to 0} \dfrac{\sin x}{x}$.

  1. $\displaystyle \lim_{x \to \infty} \dfrac{\sin x}{x}$.

  2. $\displaystyle \lim_{x \to \infty} x \sin \left(\dfrac{1}{x}\right)$.

39   

Calcule o limite $\lim\limits_{x\rightarrow -\infty }\left( 2^{x}+2^{-x}\right)$.

$\infty$.

49   

Avalie os seguintes limites de acordo com o gráfico da função:

$f(x) = \frac{1}{e^x+1}$

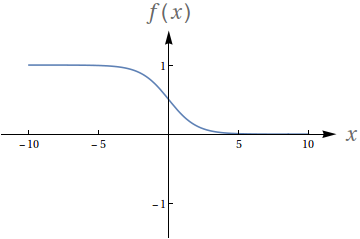
fig_assintotas_horizontais_21.png

  1. $\lim\limits_{x\to -\infty} f(x)$

  2. $\lim\limits_{x\to \infty} f(x)$

  3. $\lim\limits_{x\to 0^-} f(x)$

  4. $\lim\limits_{x\to 0^+} f(x)$

728   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow \infty }\dfrac{1-2^{x}}{1-3^{x}}$.

$0$.

44   

Calcule o limite $\lim\limits_{x\to e} \ln x$, em que $e$ é o número de Euler.

$1$.

54   

Calcule os seguintes limites. Pode ser útil usar a relação de inversão que há em relação às funções logarítmicas e exponenciais (isto é, $\ln(x)=y \Leftrightarrow e^y=x$) e/ou gráficos.

  1. $\lim\limits_{x\rightarrow\infty}\log_3 x$

  2. $\lim\limits_{x\rightarrow 0^+}\ln x$

  3. $\lim\limits_{x\rightarrow -\infty}e^x$

37   

Calcule os seguintes limites:

  1. $\lim\limits_{x\rightarrow \infty }3^{x}$

  2. $\lim\limits_{x\rightarrow \infty }\left( 2^{x}-3^{x}\right)$

  3. $\lim\limits_{x\rightarrow \infty }\left( 0,27\right) ^{x}$

1. $\infty$.

2. $-1$.

3. $0$.

33   

Calcule os seguintes limites:

  1. $\lim\limits_{x\rightarrow \infty }\left( 5-3x+4x^{2}-x^{3}\right)$

  2. $\lim\limits_{x\rightarrow \infty }\dfrac{5x^{3}-6x-3}{6x^{3}+2}$

  1. $-\infty$
  2. $5/6$

1710   

  1. Um tanque contém 5000 litros de água pura. Água salgada contendo $30$g de sal por litro de água é bombeada para dentro do tanque a uma taxa de $25$ L$/$min. Considerando o tempo $t$ em minutos, mostre que a concentração de sal $C$ em função de $t$ (em gramas por litro) é dada por:$$C(t) = \dfrac{30 t}{200+t}.$$

  2. O que acontece com a concentração para um tempo muito grande, isto é, para $t \to \infty$?

47   

O gráfico da função $f(x)=\frac{x^3+2x^2+1}{5-x^2}$ possui alguma assíntota horizontal?

Não possui.

38   

Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{1-2^{x}}{1-3^{x}}$.

$0$.

46   

Sabendo que $\lim\limits_{x\to2} f(x) = 3$ e $\lim\limits_{x\to2} g(x) = -1$, calcule os seguintes limites:

  1. $\lim\limits_{x\to2}(f+g)(x)$

  2. $\lim\limits_{x\to2}(fg)(x)$

  3. $\lim\limits_{x\to2}(f/g)(x)$

  4. $\lim\limits_{x\to2}f(x)^{g(x)}$

1713   

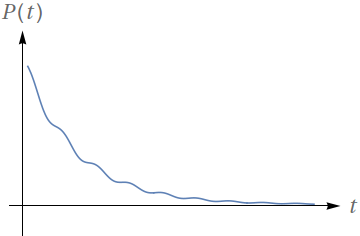
O gráfico a seguir representa o número de indivíduos de uma população ao longo do tempo.

  1. Pode-se dizer que há uma assíntota horizontal para essa população? Justifique.

  2. O que essa assíntota representa em termos biológicos? (Isto é, qual a interpretação da assíntota em função da população?)

fig_assintotas_populacao.png

31   

Calcule o limite $\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt[3]{3x^{3}+2x-1}}{\sqrt{x^{2}+x+4}}$.

  $\sqrt[3]{3}$

726   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow \infty }\left( 2^{x}-3^{x}\right) $.

$-\infty$.

727   

Calcule o seguinte limite:

$\lim\limits_{x\rightarrow \infty }\left( 0,27\right) ^{x}$.

$0$.

51   

Avalie os seguintes limites de acordo com o gráfico da função:

$f(x) = \cos (x)$

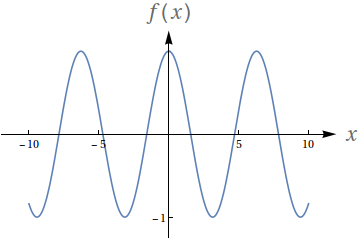
fig_assintotas_horizontais_23.png

  1. $\lim\limits_{x\to -\infty} f(x)$

  2. $\lim\limits_{x\to \infty} f(x)$

53   

Calcule os limites indicados dividindo o numerador e o denominador por uma potência conveniente de $x$. Como esses limites se relacionam com as mais altas potências do numerador e do denominador?

  1. $\lim\limits_{x\rightarrow\infty}\frac{x^4-2}{3x^4-x^3+1}$

  2. $\lim\limits_{x\rightarrow\infty}\frac{\sqrt{2x^6-2x+1}}{x^3-x^2+2}$

  3. $\lim\limits_{x\rightarrow -\infty}\frac{\sqrt{x^2-3}}{x+1}$

35   

Calcule os seguintes limites:

  1. $\lim\limits_{x\rightarrow -\infty }\dfrac{5-x}{2x+3}$

  2. $\lim\limits_{x\rightarrow \infty }\dfrac{\sqrt{x}+1}{x+3}$

  1.   $-1/2$
  2.   $0$

45   

A função $f(x) = \left\{ \begin{array}{ccc} x^2-1 & & x < 3 \\x+5 & & x\geq 3 \end{array}\right.$ é contínua em todo o seu domínio? Justifique.

Sim, é. O único ponto em que não poderia  (inicialmente) ser contínua é em $x=3$. Todavia, temos $\lim\limits_{x\to 3^-} f(x)=\lim\limits_{x\to 3^+} f(x)=f(3)=8$.

43   

Considere a função $f(x) = 2^x+10$. Calcule os seguintes limites e, depois, discuta se a função $f(x)$ tem assíntotas horizontais.

  1. $\lim\limits_{x\to -\infty} f(x)$.

  2. $\lim\limits_{x\to \infty} f(x)$.

1. $10$.

2. $\infty$

Possui assíntota horizontal de equação $y=10$,

1708   

Defina ``$\displaystyle \lim_{x \to -\infty} f(x) = l$''.

  1. Ache $\displaystyle \lim_{x \to -\infty} \dfrac{a_n x^n + \ldots + a_0}{b_m x^m + \ldots + b_0}$.

  2. Mostre que $\displaystyle \lim_{x \to \infty} f(x) = \displaystyle \lim_{x \to -\infty} -f(x)$.

  3. Mostre que $\displaystyle \lim_{x \to 0^-} \dfrac{1}{f(x)} = \displaystyle \lim_{x \to -\infty} f(x)$.

36   

Calcule os seguintes limites:

  1. $\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{3}+2}\right)$

  2. $\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x^{2}+2}\right)$

  3. $\lim\limits_{x\rightarrow \infty }\left( x-\sqrt{x+2}\right)$

  1.   $-\infty$
  2. $0$
  3. $\infty$

41   

Calcule os seguintes limites:

  1. $\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{x}\right)  ^{x+2}$

  2. $\lim\limits_{x\rightarrow \infty }\left( 1+\dfrac{1}{2x}\right) ^{x}  $

  3. $\lim\limits_{x\rightarrow \infty }\left( \dfrac{x+2}{x+1}\right)  ^{x}$

56   

Verifique se os seguintes limites existem. Explique.

  1. $\lim\limits_{x\rightarrow\infty}2^{1/x}$.

  2. $\lim\limits_{t\rightarrow\infty}\sin x$.

  3. $\lim\limits_{x\rightarrow 2^-}\tan^{-1}\left(\frac{1}{2x-4}\right)$.

50   

Avalie os seguintes limites de acordo com o gráfico da função:

  $f(x) = x^2\sin (\pi x)$

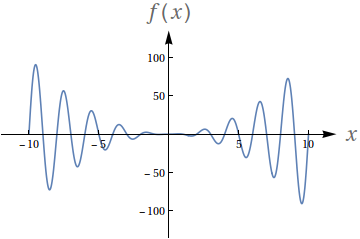
fig_assintotas_horizontais_22.png

  1. $\lim\limits_{x\to -\infty} f(x)$

  2. $\lim\limits_{x\to \infty} f(x)$

723   

Calcule o limite:

$\lim\limits_{x\rightarrow +\infty }\left( x-\sqrt{x^{2}+4x}\right)$.

$-2$.