Limites fundamentais
Um limite especial
Considere a função $f(x)=\left(1+\dfrac{1}{x}\right)^x$.
O que acontece quando $x$ tende ao infinito?
O expoente aumentará infinitamente mas a base $\left(1+\dfrac{1}{x}\right)$ vai se aproximar do valor $1$.
O que você acha que acontecerá? O tamanho do expoente crescerá rápido o suficiente para fazer o limite "explodir" OU o valor da base decrescerá rápido o suficiente, de modo que o limite tenderá a um valor finito?
Interaja com o aplicativo por alguns minutos.
Deslize o botão Graph Function! para observar o gráfico de $f(x)$ ser traçado. Depois, arraste os botões roxo e vermelho para observar os valores de (x, f(x)).
Então responda as questões a seguir:
- Depois de arrastar os botões deslizantes completamente para a direita, arraste o botão roxo o mais para a esquerda possível. Se preciso, varie o zoom da tela. Há um valor do qual a função parece se aproximar conforme $x$ assume valores cada vez menores? Qual?
- Depois de arrastar os botões deslizantes completamente para a direita, arraste o botão vermelho o mais para a direita possível. Se preciso, varie o zoom da tela. Há um valor do qual a função parece se aproximar conforme $x$ assume valores cada vez maiores? Qual?
- Se você responde "Sim" para as duas questões anteriores, como você relaciona o valor que responde ao item 1. com o valor que responde ao item 2?
Limite fundamental trigonométrico - $\lim_\limits{x\to 0}\dfrac{\sin(x)}{x}$
O segmento CD mede o sendo do ângulo CÂD.
Você se lembra da fórmula do comprimento do arco de circunferência cujo raio é $r$ e o ângulo é $x$?
Tendo a fórmula em mente, podemos afirmar que, como a circunferência tem raio 1, o comprimento do arco BC coincidirá com a medida do ângulo CÂD.
Ao mover o ponto C, compare o valor do segmento CD com o valor do ângulo CÂD. O valor de L é a razão entre CD e o ângulo CÂD. Qual é a tendência de L quando C tende para B?
Essa simulação contribui no estudo do limite fundamental $\lim_\limits{x\to 0}\dfrac{\sin(x)}{x}$? Reflita!
Limite fundamental da função - $f(x)=\dfrac{\sin(x)}{x}$
Observe o gráfico de $f(x)$, sabemos que esta função não está definida em $x=0$.
Siga as instruções do aplicativo.
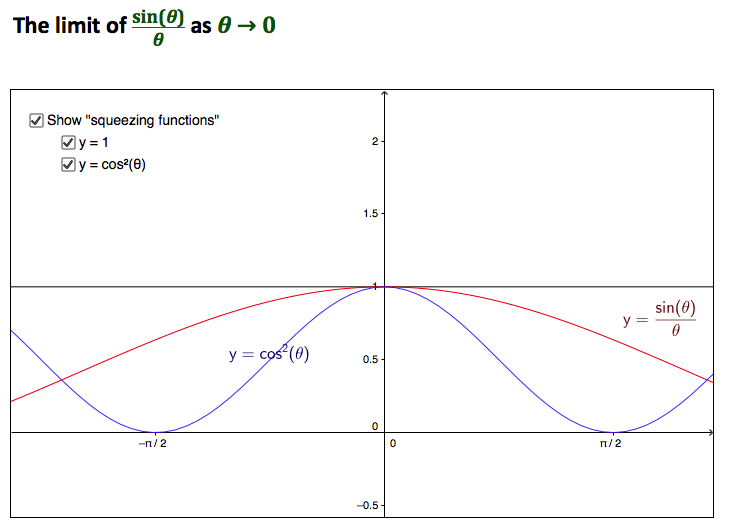
Limite de $\sin(x)/x$ com $x\rightarrow 0$
Observe o gráfico de $f(x)$ e a comparação com as funções $g(x)=1$ e $h(x)=\cos^2(x)$. Siga as instruções para visualizar um dos limite fundamentais.
Applet em inglês
Outros applets disponíveis na página do Prof. Marc Renault.

