Definição de função contínua
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Mostre que a função $f\left( x\right) =\sqrt[n]{x}$ é contínua em seu domínio.
Dê um exemplo de uma função definida em $\mathbb{R}$ que não seja contínua em $2$ mas que $\lim\limits_{x\rightarrow 2^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 2^{-}}f\left( x\right) .$
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
\frac{x^2+5x+4}{x^2+3x+2}, & & \text{se } x\neq -1\\
3, & &\text{se } x=-1
\end{array}\right.$
- $x=-1$
- $x=10$
- Sim.
- Sim.
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
\frac{x^2-64}{x^2-11 x+24}, & & \text{se } x\neq 8\\
5, & & \text{se } x=8
\end{array}\right.$
- $x=0$
- $x=8$
- Sim.
- Não. $\lim_{x\to 8} f(x) = 16/5 \neq f(8) = 5$.
Dê um exemplo de uma função definida em $\mathbb{R}$ que não seja contínua em $0$ mas que $\lim\limits_{x\rightarrow0^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 0^{-}}f\left( x\right) .$
- Se $f$ é contínua em $c$, então $\lim_{x\to c^+}f(x) = f(c)$.
- Se $f$ é contínua em $c$, então $\lim_{x\to c}f(x)$ existe.
- Se $f$ é definida em um intervalo aberto contendo $c$, e $ \lim_{x\to c}f(x)$ existe, então $f$ é contínua em $c$.
- Verdadeiro
- Verdadeiro
- Falso
Determine os valores para os quais a função \begin{align*} f(x) =\left\{ \begin{array} [c]{c} x^{2}+1,\text{ se }x\leq0 \\ \cos x, \text{ se } 0<x<1 \\ x^{2}+1, \text{ se }1 \leq x \end{array} \right.\end{align*} é contínua. Justifique sua resposta.
Dê um exemplo de uma função que seja contínua em todos os pontos da reta, exceto nos pontos da forma $k \pi$, $k \in \mathbb{Z}$.
$f(x)=1$, se $x=k \pi$, $k \in \mathbb{Z}$; $f(x)=0$, caso contrário.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ h(k) = \sqrt{1-k}+\sqrt{k+1}$.
$[-1,1]$
Mostre que a função \begin{align*} f\left( x\right) =\left\{ \begin{array}{cc} \dfrac{x^{3}-4x}{x^{2}-4}, & \text{se } x\neq \pm 2 \\ 2, & \text{se } x=2 \\ -3, & \text{se } x=-2 \end{array} \right. \end{align*} é contínua em todos os pontos, com exceção do ponto $x=-2$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(s) = \ln s$.
$(0,\infty)$
$f(x)=1, x \neq 0$; $f(0)=2$.
Mostre que a função $f\left( x\right) =\dfrac{1}{x}$ é contínua em seu domínio.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(x) = e^x$.
$(-\infty,\infty)$
A afirmação: $`` \lim\limits_{x\rightarrow p^+} f(x) = \lim\limits_{x\rightarrow p^-} f(x)\Rightarrow f \mbox{ contínua em } p. "$ é verdadeira ou falsa? Justifique.
É falsa. Só seria verdadeira se o valor dos limites laterais fosse igual a $f(p)$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$f(x) = x^2-3x+9$.
$(-\infty,\infty)$
Seja $f$ uma função contínua e decrescente em $\left[a,b\right]$. Mostre que $f$ tem uma inversa decrescente em $\left[f(b),f(a)\right]$.
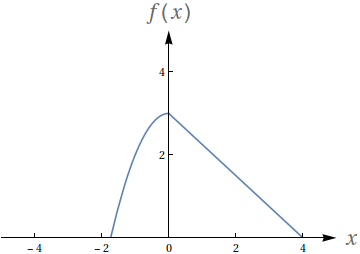
$f$ é contínua em $x=0$.
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc} 1, & & \text{se } x=0\\ \frac{\sin x}{x}, & &\text{se } x>0 \end{array}\right.$
- $x=0$
- $x=\pi$
- Sim.
- Sim.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ h(t) = \cos t$.
$(-\infty,\infty)$
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(x) = \frac{1}{1+x^2}$.
$(-\infty,\infty)$
Mostre, usando a definição, que a função $f\left( x\right) =ax+b$ é contínua em seu domínio.
Para a função a seguir, responda se a mesma é contínua nos pontos abaixo (e, caso não o seja, justifique)
$ f(x) = \left\{\begin{array}{ccc}
x^3-x, & & \text{se } x<1\\
x-2, & & \text{se } x\geq 1
\end{array}\right.$
- $x=0$.
- $x=1$.
- Sim.
- Não: Os limites pela direita e pela esquerda não são iguais em $x=1$.
Mostre que a função $f\left( x\right) =x^{n}$ é contínua em seu domínio.
O domínio da função é $\mathbb{R}$. Logo, para $x \in \mathbb{R}$, temos:
$\lim_\limits{x \to a} x^n = a^n$
e
$f(a) = a^n$.
Isto é, $\lim_\limits{x \to a} f(x) = f(a)$, e portanto a função é contínua.
- Se $f$ é contínua em $[0,1)$ e $[1,2)$, então $f$ é contínua em $[0,2)$.
- A soma de funções contínuas também é contínua
- Se $f$ é contínua em $[a,b]$, então $\lim_{x\to a^-}f(x) = f(a)$.
- Falso
- Verdadeiro
- Falso
Se você investir $1000$ reais em uma aplicação que paga $7$% de juros compostos em $n$ vezes por ano, então em $10$ anos sua aplicação terá no total $1000(1+0,07/n)^{10n}$ reais.
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta trimestralmente ($n=4$)?
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta mensalmente ($n=12$)?
Quanto dinheiro você terá em $10$ anos se a taxa de juros é composta mensalmente ($n=365$)?
Pesquise a taxa de juros paga pela poupança, e o período em que ela é composta. Calcule a quantidade de dinheiro que você terá se investir uma certa quantia de dinheiro (pense no dinheiro você tem disponível para investir) em $1$, $2$, $5$ e $10$ anos com essa taxa e período de composição. Interprete os resultados pensando em seu futuro!
Quanto dinheiro você terá em $10$ anos se os juros forem compostos continuamente, isto é, se $n\to\infty$?
Mostre, usando a definição, que a função dada por $f(x) = 3x$ é contínua para todo $x$ real.
É possível que uma função $f:{\mathbb{R} \to \mathbb{R}}$
seja tal que $\lim\limits_{x\rightarrow 2^{+}}f\left( x\right) =\lim\limits_{x\rightarrow 2^{-}}f\left(x\right)$ e ao mesmo tempo não seja contínua em $2$? Justifique e/ou dê um exemplo.
Responda os itens:
- Dada $f:{\mathbb{R} \to \mathbb{R}}$, defina (em termos de $\varepsilon $ e $\delta $) $\lim\limits_{x\rightarrow p}f\left( x\right) =L.$ Ilustre elaborando um gráfico para uma função genérica.
- Qual é a condição sobre esse limite para que a função seja contínua?
Mostre que função $f\left( x\right) =\dfrac{1}{x^2}$ é contínua em seu domínio.
Seja $f:\mathbb{R\rightarrow R}$ a função
definida por
\begin{equation*}
f\left( x\right) =\left\{
\begin{array}{cc}
x^{2} & \text{se }x\leq 1 \\
2x-1 & \text{se }x>1
\end{array}
\right. ,
\end{equation*}
e defina $g\left( x\right) =\lim\limits_{x\rightarrow h}\dfrac{f\left(
x+h\right) -f\left( x\right) }{h}$. Mostre que $g\left( x\right) $ é contínua.
Seja $f:\mathbb{R\rightarrow R}$ a função
definida por
\begin{equation*}
f\left( x\right) =\left\{
\begin{array}{cc}
x^{2}, & \text{se }x\leq 1 \\
2x-1, & \text{se }x>1
\end{array}
\right. ,
\end{equation*}
e defina $g\left( x\right) =\lim\limits_{x \rightarrow h}\dfrac{f \left(x+h \right) -f \left( x\right) }{h}$.
Mostre que $g\left( x\right) $ é contínua.
\begin{eqnarray*} g\left( x\right) &=&\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left( x+h\right) ^{2}-x^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{x^{2}+2hx+h^{2}-x^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2hx+h^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0}\left( 2x+h\right) =2x. \end{eqnarray*}
Já para $x>1$ temos que
\begin{eqnarray*} g\left( x\right) &=&\lim\limits_{h\rightarrow 0}\dfrac{f\left( x+h\right) -f\left( x\right) }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ 2\left( x+h\right) -1\right] - \left[ 2x-1\right] }{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2h}{h}=2. \end{eqnarray*}
Para $x=1$ temos que
\begin{eqnarray*} \lim\limits_{h\rightarrow 0^{+}}\dfrac{f\left( 1+h\right) -f\left( 1\right) }{h} &=&\lim\limits_{h\rightarrow 0}\dfrac{\left[ 2\left( 1+h\right) -1 \right] -1}{h} \\ &=&\lim\limits_{h\rightarrow 0}\dfrac{2h}{h}=2 \\ \lim\limits_{h\rightarrow 0^{-}}\dfrac{f\left( 1+h\right) -f\left( 1\right) }{h} &=&\lim\limits_{h\rightarrow 0^{-}}\dfrac{\left( 1+h\right) ^{2}-1}{h} \\ &=&\lim\limits_{h\rightarrow 0^{-}}\dfrac{2h+h^{2}}{h} \\ &=&\lim\limits_{h\rightarrow 0^{-}}\left( 2+h\right) =2. \end{eqnarray*}
Temos então que $g$ é bem definida também no ponto $x=1$ e, de modo geral, $g$ pode ser expressa por \begin{equation*} g\left( x\right) =\left\{ \begin{array}{cc} 2x & \text{se }x\leq 1 \\ 2 & \text{se }x>1 \end{array} \right. \text{.} \end{equation*}
Como as funções $h\left( x\right) =2x$ e $p\left( x\right) \equiv 2$ são contínuas, temos que $g\left( x\right) $ é contínua para todo $x\neq 1$.
Além disto, como $\lim\limits_{x\rightarrow 1^{-}}g\left( x\right) =\lim\limits_{x\rightarrow 1}2x=2=\lim\limits_{x\rightarrow 1^{+}}2=\lim\limits_{x\rightarrow 1^{+}}g\left( x\right) $, segue que $\lim\limits_{x\rightarrow 1}g\left(x\right) =2$. Mas como $g\left( 1\right) =2$, segue que a função $ g\left( x\right) $ também é contínua no ponto $x=1$.
Dê exemplo de uma função $f$ que seja descontínua, mas tal que $|f|$ seja contínua.
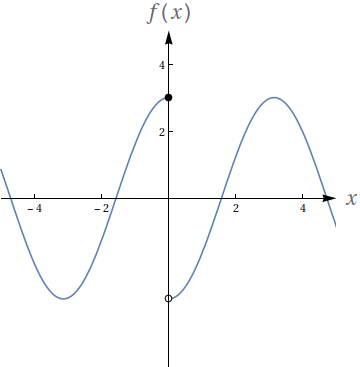
$f$ não é contínua em $x=0$.
Considere uma função contínua $\phi:\mathbb{R} \to \mathbb{R}$ tal que
\[ \forall \quad {x \in \mathbb{R}},\quad \phi(x)\geq x^2.\]
Mostre que existe $a\geq 0$ tal que $\left[a,+\infty\right[$ é o contradomínio de $\phi$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(x) = \sin(e^x+x^2)$.
$(-\infty,\infty)$
Justifique sua resposta.
$c=-1$ ou $c=2$.
Dada uma função $f:{\mathbb{R} \to \mathbb{R}}$, defina sua continuidade no ponto $p\in \mathbb{R}.$
É verdade que, ao se esticar um elástico puxando-o por suas extremidades em direções opostas, algum ponto do elástico permanecerá em sua posição inicial? Justifique sua resposta.
Prove que se $f$ e $g$ são ambas funções contínuas, então $f+g$ é contínua.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(t) = \frac{1}{\sqrt{1-t^2}}$.
$(-1,1)$
Calcule:
- $ \lim\limits_{x\to 5^-} f(x)$
- $ \lim\limits_{x\to 5^+} f(x)$
- $ \lim\limits_{x\to 5} f(x)$
- $f(5)$
- $f$ é contínua em $x=5$?
1. $20$.
2. $25$.
3. Não existe.
4. $25$
5. Não.
Dê um exemplo de uma função tal que $\lim\limits_{x\rightarrow p}\left| f\left( x\right) \right| $ exista mas $\lim\limits_{x\rightarrow p}f\left( x\right) $ não exista.
Uma das propriedades da potenciação é que $a^0=1$, $\forall a \neq 0$. Além disso, também sabe-se que $0^n=0,\quad \forall n>0$. A extensão destas regras para incluir, respectivamente, $a=0$ e $n=0$ levam a resultados conflitantes quanto ao valor de $0^0$(O que não implica em contradição, dado que as propriedades não foram estabelecidas para $a=0$ e $n=0$).
Sendo assim, avalie $x^x$ para $x=0,1;0,01;0,001;\ldots$. Qual o padrão observado? Com o auxílio de recursos computacionais, observe o gráfico de $y=x^x$ para valores positivos de $x$, se aproximando da origem. Para qual valor a função parece convergir para $x=0$?
Sugestão: Procure, no site, o exercício 1528. Compare os resultados obtidos.
Mostre que a função $f\left( x\right) =\left\{ \begin{array}{cc} \dfrac{x^{3}-8}{x-2}, & \text{se }x\neq 2 \\ 12, & \text{se }x=2 \end{array}\right. $ é contínua em seu domínio.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(t) = \sqrt{5t^2-30}$.
$(-\infty,-\sqrt{6}]\cup [\sqrt{6},\infty)$
A função pode tender a valores diferentes pela esquerda e pela direita, a função pode crescer de maneira ilimitada, ou a função pode oscilar em torno de um valor.
Suponha que $\left| f\left( x\right) -f\left( 1\right) \right| \leq \left( x-1\right) ^{2}$. Demonstre que $f\left( x\right) $ é contínua em $1$.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ f(k) = \sqrt{1-e^k}$.
$(-\infty,0]$
Considere a função \begin{align*} f\left( x\right) =\left\{ \begin{array}{cc} a-x, & \text{se } x<-1 \\ x, & \text{se } -1\leq x<1 \\ \dfrac{2}{x}+b, & \text{se } 1\leq x \end{array} \right. . \end{align*}
- Encontre os limites laterais a direita e a esquerda de $f$ nos pontos $1$ e $-1.$
- Determine os valores de $a$ e $b$ que tornam $f$ contínua em toda a reta.
- Calcule $\lim\limits_{x\rightarrow \infty }f\left(x\right) $ e $\lim\limits_{x\rightarrow -\;\infty }f\left( x\right) $.
Calcule $\displaystyle\lim_{x\rightarrow 0}\frac{\frac{2}{x} - 5\cos(\frac{1}{x^2+2x})}{-\frac{5}{x} + 2\cos(\frac{1}{x^2+2x})}$.
Existe algum número real $a$ tal que a função $f(x) = \left\{\begin{array}{ccl}\displaystyle\frac{\frac{2}{x} - 5\cos(\frac{1}{x^2+2x})}{-\frac{5}{x} + 2\cos(\frac{1}{x^2+2x})},& \mbox{se} & x\neq 0\\ a, & \mbox{se} & x=0 \end{array} \right.$ seja contínua?
f(x)=\frac{\sqrt{1-x^2}}{1-tg x} \end{align*}
- Determine o domínio de $f$.
- Estude $f$ quanto a continuidade.
Para a função a seguir, dê os intervalos nos quais ela é contínua:
$ g(x) = \sqrt{x^2-4}$.
$(-\infty,-2]\cup [2,\infty)$
Dê um exemplo para mostrar que o produto de uma função contínua por uma função descontínua, pode ser uma função contínua.
Conforme $x$ aumenta, tanto $1/x$ quanto $1/(ln\ x)$ tendem a zero. Dada a função: $f(x)=\left(\frac{1}{x}\right)^{1/(ln\ x)}$ avalie $f(x)$ para valores cada vez maiores de $x$. Qual o padrão observado? Com o auxílio de recursos computacionais, observe o gráfico de $f(x)$ para valores grandes de $x$.
Sugestão: Procure, no site, o exercício 1527. Compare os resultados obtidos.

