Áreas e Distâncias
Selecione os exercícios por
Dificuldade
Categoria
Outros
Os botões acima permitem selecionar que tipos de exercício você deseja ver na lista.
Para retirar alguma categoria da lista, clique sobre o botão para toná-lo inativo. Para adicioná-la, clique novamente no botão.
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x^3$ no intervalo $[0,b]$ é $b^4/4$.
Mostre o mesmo resultado utilizando somas inferiores.
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x$ no intervalo $[0,b]$ é $b^2/2$.
Mostre o mesmo resultado utilizando somas inferiores.
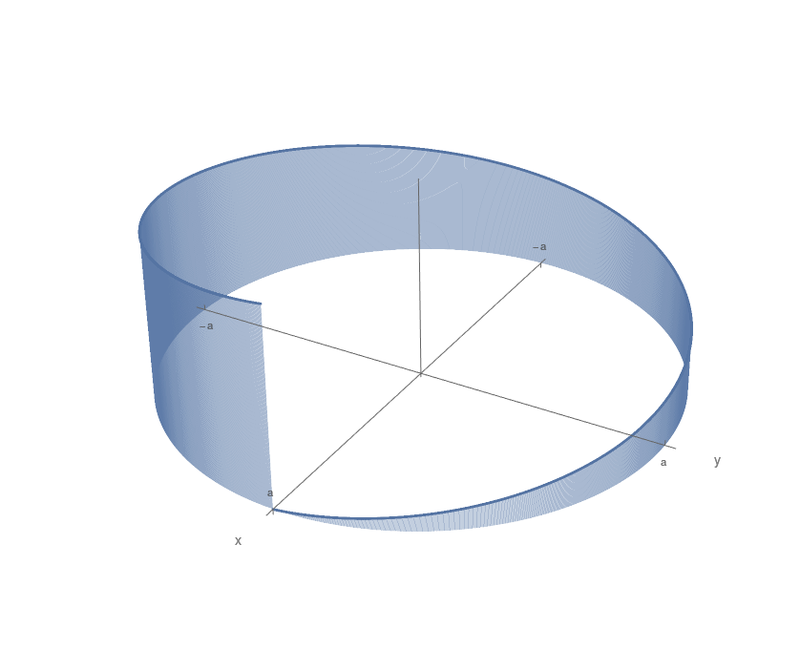
Uma superfície é criada a partir de segmentos de reta perpendiculares traçados sobre um círculo de raio $a$, perpendiculares ao plano do círculo. O comprimento de um segmento correspondente a um ponto $p$ sobre o círculo é $ks$, sendo $k$ uma constante positiva e $s$ o comprimento de arco do círculo no sentido anti-horário de $(a,0)$ até o ponto $p$.
Determine a área desta superfície, conforme a figura a seguir, em função de $k$.
Mostre que a área $A$ de um círculo de raio $r$ é $A=\pi r^{2}$.
Determine um número $0\leq b\leq 2$ tal que a reta $x=b$ divide a região delimitada por $y=\sqrt{4-x^{2}}$ e $y=0$ e $x=0$ em duas regiões de mesma área.
Utilizando somas superiores, mostre que a área sob o gráfico de $y=x^2$ no intervalo $[0,b]$ é $b^3/3$.
Mostre o mesmo resultado utilizando somas inferiores.
Um objeto é atirado do nível do mar para cima com uma velocidade inicial de $100m/s$.
Supondo que a gravidade seja a única força que atua sobre este objeto superestime sua veocidade depois de $5$ segundos. Use $g=10m/s^2$.
Calcule uma estimativa inferior para a altura atingida depois de $5s$.
Considere a área entre a curva $y=x^{4}$ e o eixo $x$, primeiro no intervalo $\left[ -1,1\right] $ e depois no intervalo $\left[1,a\right] $. Determinar $a\geq 1$ tal que estas áreas sejam iguais.
Mostre que, para toda parábola dada por $y=ax^2$, com $a>0$, temos: $$\displaystyle \int_0^b a x^2 \, dx = a \dfrac{b^3}{3}.$$
Use este fato para provar que a área do setor parabólico delimitado por $y=ax^2$ e a reta $y=ab^2$ é igual a quatro terços da área do triângulo com vértices $(0,0)$, $(b,ab^2)$ e $(-b,ab^2)$. Este resultado é um caso particular do Teorema de Arquimedes sobre a área de um setor parabólico.
Um objeto é solto de um helicóptero. O objeto cai cada vez mais rápido, mas sua aceleração diminui com o passar do tempo devido à resistência do ar. A aceleração foi medida nos primeiros cinco segundos, quando ele atingiu o chão, e o resultado está na tabela a seguir:
$
\begin{array}{ccccccc} \hline
t & 0 & 1 & 2 & 3 & 4 & 5 \\\hline
a & 9,81 & 5,95 & 3,61 & 2,19 & 1,33 & 0,81 \\\hline
\end{array}
$
Faça uma estimativa superior para o módulo da velocidade quando $t=5$.
Faça uma estimativa superior para o módulo da posição quando $t=5$.
Faça uma estimativa superior para a altura da queda.

